Vertical Electronic Excitations in Solution with the EOM-CCSD Method Combined with a Polarizable Explicit/Implicit Solvent Model

Abstract

The accurate calculation of electronic transition energies and properties of isolated chromophores is not sufficient to provide a realistic simulation of their excited states in solution. In fact, the solvent influences the solute geometry, electronic structure, and response to external fields. Therefore, a proper description of the solvent effect is fundamental. This can be achieved by combining polarizable explicit and implicit representations of the solvent. The former provides a realistic description of solvent molecules around the solute, while the latter introduces the electrostatic effect of the bulk solution and reduces the need of too large a number of explicit solvent molecules. This strategy is particularly appealing when an accurate method such as equation of motion coupled cluster singles and doubles (EOM-CCSD) is employed for the treatment of the chromophore. In this contribution, we present the coupling of EOM-CCSD with a fluctuating charges (FQ) model and polarizable continuum model (PCM) of solvation for vertical excitations in a state-specific framework. The theory, implementation, and prototypical applications of the method are presented. Numerical tests on small solute-water clusters show very good agreement between full EOM-CCSD and EOM-CCSD-FQ calculations, with and without PCM, with differences ≤ 0.1 eV. Additionally, approximated schemes that further reduce the computational cost of the method are introduced and showed to perform well compared to the full method (errors ≤ 0.1 eV).

1 Introduction

The accurate simulation of photochemical processes has become increasingly important in the past decade as an invaluable tool to assist and often guide experiments. The study of electronic excited states is at the frontier of modern science and goes beyond traditional chemistry to include multidisciplinary research fields, as in energy and material science. This kind of applications, however, requires a realistic description of the complex environment around the chromophore because of the important effects on its electronic structure. The computational resources required for treating large systems are still much larger than what is achievable with standard quantum mechanical (QM) tools especially when accurate methods are employed as, for instance, the series of methods provided by coupled cluster theory (CC)^1,2. A reasonable compromise between accuracy and computational effort can be achieved by resorting to multiscale or “focused” models, where the system is separated in multiple layers and the target structure is treated with a higher level of theory while the rest is described with less accurate but computationally less demanding approaches.

The prototypical “environment” surrounding a chromophore is a solvent. Much effort has been devoted to reliable and yet affordable modeling of the large number of molecules required to properly describe solution phase. In general, solvation models can be separated in two large categories: explicit and implicit models. The former maintain an atomistic representation of the solvent, thus are able to describe specific solute-solvent interactions (e.g., hydrogen bonds) and provide a more realistic picture. The drawback is that explicit models require a large number of solvent molecules to properly describe bulk effects and, consequently, require the consideration of a large number of configurations in order to achieve a statistical average of a given property. Implicit models, on the other hand, replace the atomistic representations of the solvent with a continuum, polarizable medium. The advantage here is a lower computational cost since long-range bulk effects and statistical averaging are naturally accounted for. The drawback is that specific solute-solvent interactions cannot be properly described. A large number of models have been developed in both families and a comprehensive account of all of them is beyond the scope of this work^3–50.

The best of the two worlds can be obtained by a judicious combination of the two approaches, which would limit the number of explicit solvent molecules to the first few solvation shells (to account for specific solute-solvent interactions) while including long-range effects through a continuum model. In this way, the number of explicit solvent configurations (and corresponding QM calculations) necessary for statistical averaging can be greatly reduced. This strategy assumes critical importance when a member of the CC family of methods is used, such as the equation of motion singles and doubles (EOM-CCSD)^1,2,51–54. In recent publications, Lipparini et al.^19–21 reported the combination of a fluctuating charge (FQ)^16–18 model and the polarizable continuum model (PCM)^22–25,27 for ground and excited states while Caricato^49,50 reported the combination of EOM-CCSD with PCM. In this contribution, we present the combination of these approaches in the EOM-CCSD-FQ and EOM-CCSD-FQ-PCM methods, and their implementation. The formulation of FQ and FQ-PCM in Ref. 19^,20, whose equations are formally very similar to those for PCM, allows for a relatively direct extension of the EOM-CCSD-PCM method to this explicit/implicit approach, including approximate schemes that can be used to further reduce computational cost^49,50.

The test systems presented in this work are small solute-water clusters (including up to six explicit water molecules). These are certainly not enough to provide a realistic representation of a solvation shell but can be treated entirely at EOM-CCSD level, thus providing a direct comparison between full QM and hybrid calculations. Larger, more realistic solvation shells will be the subject of future investigation. The results in this paper show the efficacy of this focused model for the reliable computation of solvatochromic shifts compared to full QM calculations and open new avenues for the application of accurate QM methods to simulation of real-life systems.

This paper is organized as follows. The theory and implementation of the FQ-PCM models and their coupling with EOM-CCSD is presented in 2. Numerical tests are reported in 3, and a discussion of the results and concluding remarks are presented in 4.

2 Theory

In this section, we review the theory for the FQ model combined with PCM and their coupling with the potent EOM-CCSD method for electronic excited states. Thanks to the formulation of the FQ and FQ-PCM models in Ref. 19^,20, the coupling with EOM-CCSD straightforwardly follows that with PCM^49,50, as discussed in 2.2. Therefore, here we only report the main expressions and refer the reader to Refs. 19^,20,49,50 for details on their derivation and implementation.

2.1 FQ-PCM

In the FQ model, the polarizability of the force field is introduced by endowing each atom with a point charge, whose value depends on the environment¹⁶ according to the electronegativity equalization principle (EEP).^55,56 The EEP can be recast in a variational formulation, which is a convenient way to define FQs as the ones minimizing the following functional:

$$\begin{array}{cc}\hfill F(\mathbf{Q},\lambda )& =\sum _{\alpha ,i}{Q}_{\alpha i}{\chi }_{\alpha i}+\frac{1}{2}\sum _{\alpha ,i}\sum _{\beta ,j}{Q}_{\alpha i}{J}_{\alpha i,\beta j}{Q}_{\beta j}+\sum _{\alpha }{\lambda }_{\alpha }(\sum _i{Q}_{\alpha i}-Q_{\alpha }^{\mathit{tot}})\hfill \\ \hfill & =\mathbf{Q}\cdot \chi +\frac{1}{2}\mathbf{Q}\cdot \mathbf{JQ}+\lambda \cdot \mathbf{Q}\hfill \end{array}$$ (1)

where the Greek indexes α and β run on molecules and the Latin ones on the atoms of each molecule. In 1, the χ vector contains the electronegativities of the atoms, the matrix J represents the (screened) electrostatic interaction between the fluctuating charges Q, and a set of Lagrangian multipliers λ_α is used to impose charge conservation constraints. By introducing a compact notation (see Ref. 19 for a detailed derivation and description of the various parameters that define the model), the stationarity conditions read

$${\mathbf{DQ}}_{\lambda }=-{\mathbf{C}}_Q$$ (2)

where C_Q is a vector containing atomic electronegativities and total charge constraints, D is the matrix composed by J and the Lagrange multipliers related blocks, whereas Q_λ is a vector containing charges and Lagrange multipliers.

Consistently with the semi-classical nature of a QM/MM approach, we introduce the coupling with a QM (SCF) description by treating the interaction between the two densities of charge (i.e., the one represented by the FQs and the QM one) classically, i.e., through a simple Coulomb interaction:

$$E_{\mathit{QM}∕\mathit{MM}}=\sum _{i=1}^{N_q}\Phi \left[{\rho }_{\mathit{QM}}\right]\left({\mathbf{r}}_i\right){\overline{Q}}_i$$ (3)

where the sum runs over the N_q FQs and Φ[ρ_QM](r_i) is the electrostatic potential due to the QM density of charge at the i-th FQ placed at r_i:

$$\Phi \left[{\rho }_{\mathit{QM}}\right]\left({\mathbf{r}}_i\right)\stackrel{\mathit{def}}{=}{\overline{V}}_i\left(\mathbf{P}\right)={\overline{V}}_i^N\left(\mathbf{P}\right)+{\overline{V}}_i^e\left(\mathbf{P}\right)=\sum _{\zeta =1}^{N_n}\frac{Z_{\zeta }}{\mid {\mathbf{r}}_i-{\mathbf{R}}_{\zeta }\mid }-{\int }_{{\mathbb{R}}^3}d\mathbf{r}\frac{{\rho }^{\mathit{el}}\left(\mathbf{r}\right)}{\mid {\mathbf{r}}_i-\mathbf{r}\mid }$$

Here, the ζ-labeled sum runs over the N_n QM nuclei, whose position we call R_ζ (see Ref. 20^,21 for a detailed discussion of the coupling). For later convenience, we have introduced a slightly modified notation, indicating with and overbar the expectation values of the electrostatic potential and of the charges to distinguish them by the associated operators. This distinction can be made clearer for the second term of the potential by expanding the electronic density ρ^el(r) in terms of an atomic basis set:

$${\overline{V}}_i^e\left(\mathbf{P}\right)=-\sum _{\mu \nu }{P}_{\mu \nu }{\int }_{{\mathbb{R}}^3}d\mathbf{r}\frac{{\chi }_{\mu }\left(\mathbf{r}\right){\chi }_{\nu }\left(\mathbf{r}\right)}{\mid {\mathbf{r}}_i-\mathbf{r}\mid }=\sum _{\mu \nu }{P}_{\mu \nu }{V}_{\mu \nu ,i}$$ (4)

where the “uncontracted” potential V_μν, which is the representation of the potential operator in the atomic orbitals (AO) basis set, is introduced and the double sum runs on the AO: the expectation value is obtained by contracting the operator with the density matrix.

The definition of the interaction adopted yields a QM/MM energy functional that is variational with respect to both densities of charge, once the suitable constraints have been taken into account, in a similar fashion to what has been proposed by some of the present authors for PCM^35,57. Therefore:

$$\mathcal{E}[\mathbf{P},\overline{\mathbf{Q}},\lambda ]=\text{tr}\mathbf{hP}+\frac{1}{2}\text{tr}\mathbf{PG}\left(\mathbf{P}\right)+\overline{\mathbf{Q}}\cdot \chi +\frac{1}{2}\overline{\mathbf{Q}}\cdot \mathbf{J}\overline{\mathbf{Q}}+\lambda \cdot \overline{\mathbf{Q}}+\overline{\mathbf{Q}}\cdot \overline{\mathbf{V}}\left(\mathbf{P}\right)$$ (5)

where h and G are the usual one- and two-electron matrices. It is possible to introduce the coupled Fock/FQ equations by introducing an extended Fock operator, which can be computed as the gradient of the energy functional 5 with respect to the density matrix:

$$\tilde{F}=\frac{\partial \mathcal{E}}{\partial \mathbf{P}}=\mathbf{h}+\mathbf{G}\left(\mathbf{P}\right)+\overline{\mathbf{Q}}\cdot \mathbf{V}$$ (6)

The FQs are obtained by imposing the stationarity of the global functional with respect to the charges and the Lagrangian multipliers; with respect to 2, a new source term appears:

$$\mathbf{D}\overline{\mathbf{Q}}=-\mathbf{C}-\overline{\mathbf{V}}\left(\mathbf{P}\right)$$ (7)

Such term represents the coupling between the QM and MM portions of the system. The inclusion of a further layer treated by means of the PCM approach (in particular, we choose to the conductor-like PCM^58–61) is easily obtained by redefining the charges and the D matrix so as to also include PCM contributions:

$$\left(\begin{array}{cc}\hfill \mathbf{D}\hfill & \hfill {\Omega }^{†}\hfill \\ \hfill \Omega \hfill & \hfill \mathbf{S}∕f\left(\epsilon \right)\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\overline{\mathbf{Q}}}^{\mathit{FQ}}\hfill \\ \hfill {\overline{\mathbf{Q}}}^{\mathit{PCM}}\hfill \end{array}\right)=-\left(\begin{array}{c}\hfill \mathbf{C}\hfill \\ \hfill 0\hfill \end{array}\right)-\left(\begin{array}{c}\hfill {\overline{\mathbf{V}}}^{\mathit{FQ}}\left(\mathbf{P}\right)\hfill \\ \hfill {\overline{\mathbf{V}}}^{\mathit{PCM}}\left(\mathbf{P}\right)\hfill \end{array}\right).$$ (8)

where S and Ω represent the Coulomb interaction of the PCM charges with themselves and with the FQs, respectively, and we have introduced the superscripts FQ and PCM to distinguish the two sets of charges. In addition, a PCM contribution ${\overline{\mathbf{Q}}}^{\mathit{PCM}}\cdot \mathbf{V}$ is to be added to ${\overline{\mathbf{Q}}}^{\mathit{FQ}}\cdot \mathbf{V}$ in 6. Further details on the coupling of the PCM with the FQ model can be found elsewhere.^19,20

2.2 EOM-CCSD-FQ-PCM

The coupling of CCSD for ground and excited states with the FQ model directly follows its coupling with PCM^44–50. The complete scheme is called PTED (perturbation theory energy and density) for historical reasons^62,63, and the solvent reaction field depends on the correlation density (thus the D in the acronym). For the ground state, a CC free energy functional can be written as:

$$G_0^{\mathit{PTED}}=G_{\mathit{ref}}^{\xi }+\langle {\Phi }_0\mid (1+\Lambda )e^{-T}{H}_N^{\xi }{e}^T\mid {\Phi }_0\rangle +\frac{1}{2}{\overline{\mathbf{V}}}_N\cdot {\overline{\mathbf{Q}}}_N^{\xi }$$ (9)

where Φ₀ is the reference wave function (HF in most cases), G_ref is the associate reference solvation free energy, T and Λ are the CC excitation and de-excitation operators. The subscript N indicates the normal-product form of an operator (X_N = X − ⟨Φ₀ |X| Φ₀⟩), and the Hamiltonian $H_N^{\xi }$ includes the reference charges:

$$H_N^{\xi }=H_N+{\mathbf{V}}_N\cdot {\overline{\mathbf{Q}}}_0^{\xi }.$$ (10)

The superscript ξ refers to the solvation model in use: FQ or FQ-PCM. For FQ-only, the reference charges ${\overline{\mathbf{Q}}}_0^{\mathit{FQ}}$, which depend on the nuclei and SCF electronic charge density, are computed by solving 7. The charges ${\overline{\mathbf{Q}}}_N^{\mathit{FQ}}$, on the other hand, depend on the correlation density:

$${\gamma }_{\mathit{pq}}=\langle {\Phi }_0\mid (1+\Lambda )e^{-T}\left\{p^{†}q\right\}{e}^T\mid {\Phi }_0\rangle .$$ (11)

where p, q are two generic molecular orbitals (MOs). The charges ${\overline{\mathbf{Q}}}_N^{\mathit{FQ}}$ are then obtained by solving:

$$\mathbf{D}{\overline{\mathbf{Q}}}_N^{\mathit{FQ}}=-{\overline{\mathbf{V}}}_N\left(\gamma \right).$$ (12)

For the combined FQ-PCM approach, the reference charges are computed by solving 8 while the correlation charges by solving:

$$\left(\begin{array}{cc}\hfill \mathbf{D}\hfill & \hfill {\Omega }^{†}\hfill \\ \hfill \Omega \hfill & \hfill \mathbf{S}∕f\left(\epsilon \right)\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\overline{\mathbf{Q}}}_N^{\mathit{FQ}}\hfill \\ \hfill {\overline{\mathbf{Q}}}_N^{\mathit{PCM}}\hfill \end{array}\right)=-\left(\begin{array}{c}\hfill {\overline{\mathbf{V}}}_N^{\mathit{FQ}}\left(\gamma \right)\hfill \\ \hfill {\overline{\mathbf{V}}}_N^{\mathit{PCM}}\left(\gamma \right)\hfill \end{array}\right).$$ (13)

In this case, the dimension of the charges vector in 9 is the sum of the number of FQ and PCM charges. From the point of view of the CC equations (and associated computer code), however, the choice of solvation model is transparent and the same machinery introduced for CC-PCM can be employed^44,46,47. In this work, we have developed the interface of the code that computes the FQ and FQ-PCM charges in 12-13 with the code that produces the corresponding operators that enter the CC equations for the evaluation of 9. It is important to note that the computational cost for the evaluation of the charges in 7, 8, 12, and 13 is negligible compared to the solution of the CC equations.

$G_0^{\mathit{PTED}}$ is computed by minimizing the expression in 9 with respect to the T and Λ amplitudes. The computational demand is thus at least twice as large as that for the corresponding gas phase calculation. Similar to PCM, approximations can be introduced to avoid the need of solving for the Λ amplitudes. These approximate schemes, called PTE, PTE(S), and PTES do not require the calculation of the entire correlation density but only the CC amplitudes. In PTE, the explicit solvation term in the correlation part (last term in 9) is completely neglected, and the solvent effect is only introduced in the reference wave function through an explicit energy term and implicit orbital polarization. In PTE(S) and PTES, an explicit solvation term is introduced in the correlation equations but is computed by approximating the correlation density with the only term that does not depend on the Λ amplitudes, i.e., the T singles amplitudes (thus the “S” in the name). In PTE(S), such term is only a correction to the PTE free energy while in PTES there is an explicit operator in the T equations. Details for these schemes can be found in Refs. 46^,47,49,50.

Similarly to ground state, the K-th excited state free energy functional takes the form:

$$\begin{array}{cc}\hfill G_K^{\mathit{PTED}}=& G_{\mathit{ref}}^{\xi }+\langle {\Phi }_0\mid L_K\left[e^{-T_K}{H}_N^{\xi }{e}^{T_K},R_K\right]\mid {\Phi }_0\rangle \hfill \\ & +\langle {\Phi }_0\mid (1+{\Lambda }_K)e^{-T_K}{H}_N^{\xi }{e}^{T_K}\mid {\Phi }_0\rangle \hfill \\ & +{\omega }_K(1-\langle {\Phi }_0\mid L_K{R}_K\mid {\Phi }_0\rangle )+\frac{1}{2}{\overline{\mathbf{V}}}_N^K\cdot {\overline{\mathbf{Q}}}_N^{K,\xi }\hfill \end{array}$$ (14)

where ω_K, L_K, and R_K are the EOM-CC similarity tranformed Hamiltonian K-th eigenvalue, left, and right eigenvectors, respectively. The charges ${\overline{\mathbf{Q}}}_N^{K,\xi }$ are computed by solving 12 or 13 for FQ or FQ-PCM approaches, respectively, with the K-th state density:

$$\begin{array}{cc}\hfill {\gamma }_{\mathit{pq}}^K=& \langle {\Phi }_0\mid L_K\left[e^{-T}\right\{p^{†}q\}{e}^T,R_K]\mid {\Phi }_0\rangle \hfill \\ & +\langle {\Phi }_0\mid (1+{\Lambda }_K)e^{-T}\left\{p^{†}q\right\}{e}^T\mid {\Phi }_0\rangle .\hfill \end{array}$$ (15)

$G_K^{\mathit{PTED}}$ is obtained after minimization of the functional in 14 with respect to the T_K, Λ_K, L_K, and R_K amplitudes. Since this is a state-specific approach, this set of amplitudes is different for each excited state. In order to avoid the computation of the Λ_K amplitudes and decouple the ground state from the excited state part of the calculation, the PTE, PTE(S), and PTES approximate schemes can be introduced also for EOM-CC. For excited states, the PTE scheme includes state-specific solvent terms in the EOM equations. Therefore, the scheme where no explicit term appears in the CC equation is called FRF, for frozen-reaction-field (FRF and PTE are the same for the ground state). More details can be found in Ref. 49^,50.

When vertical transition calculations are performed with a continuum solvation model, the different response-time of the electrons and nuclei of the solvent molecules must be taken into account. This is achieved in PCM by introducing a nonequilibrium solvation regime^25,64,65, which represents the situation where only the solvent electron response is allowed to equilibrate with the new solute electronic density while the solvent nuclei response is kept frozen in the initial state. This approach is not necessary for the FQ method alone since a nonequilibrium response is automatically implied as the solvent molecules are not allowed to move. An explicit nonequilibrium calculation is, on the other hand, necessary for the FQ-PCM approach. The solvent electrons response is obtained by replacing the equilibrium dielectric constant ε in 13 with the optical dielectric constant ε_∞. The nonequilibrium EOM-CCSD-FQ-PCM expressions for the PTED, PTES, PTE(S), and PTE schemes are identical to those for EOM-CCSD-PCM as reported in Ref. 50, provided that the charges ${\overline{\mathbf{Q}}}_N^{K,\mathit{FQ}-\mathit{PCM}}$ in 13 are computed using ε_∞.

3 Results

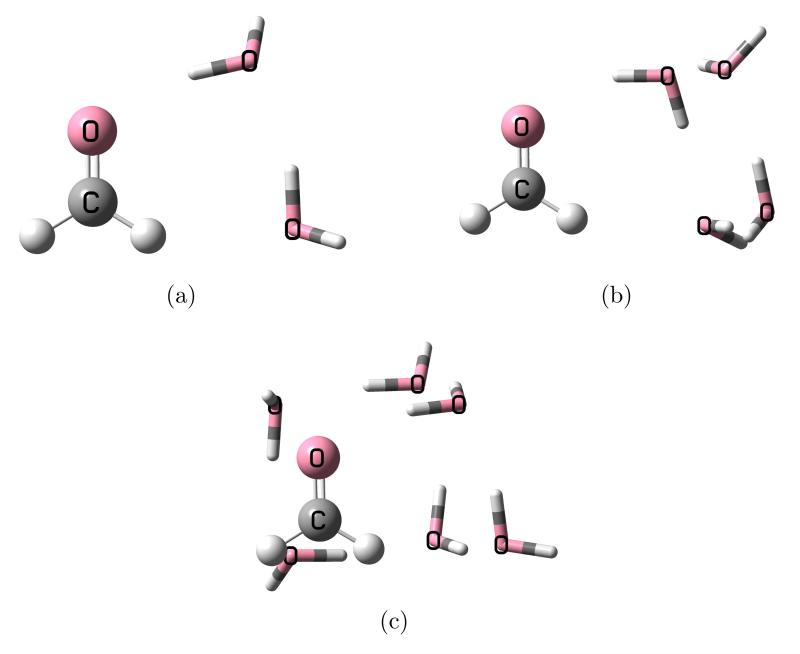
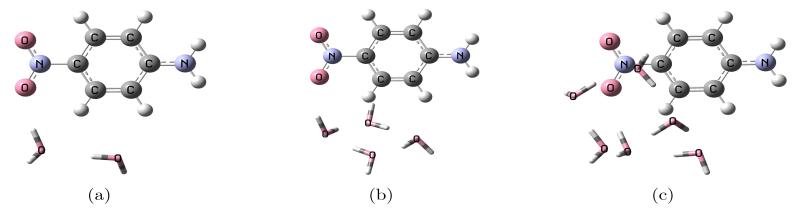
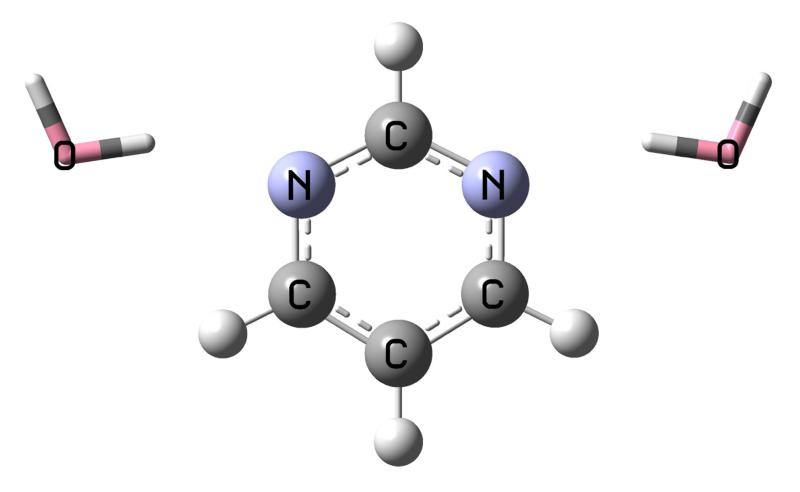
The methods described in the previous section, for the complete and approximate schemes, are tested here on three molecules with small water clusters: formaldehyde, p-nitroaniline (PNA), and pyrimidine. The first two molecules are considered with two, four and six water molecules, and are shown in figure 1, 2 where the “solute” molecules are depicted as balls and sticks while the water molecules as tubes. The geometries are taken from Ref. 12 where EOM-CCSD was combined with the effective fragment potential (EFP)^8,9 method. This allows for a direct comparison of the two approaches, FQ and EFP. Although, it is important to mention some differences between them: FQ is an electrostatic-only model but includes mutual solute-solvent polarization effects in the CC equations due to the iterative solution of 9 and 14; EFP in Ref. 12, on the other hand, includes other effects at the SCF level (i.e., dispersion, exchange-repulsion, and polarization) but only a polarization correction to the excitation energy after conversion of the EOM equations. We also consider the effect of a continuum solvation model around the entire cluster. The latter molecule, pyrimidine, is considered with two water molecule around it in such a way that the cluster structure maintains C_2v symmetry, shown in 3. The geometry of this cluster is taken from Ref. 20. In general, the comparison will be made between the full EOM-CCSD calculation for the solute-water clusters and that with the EOM-CCSD-FQ approach, both with and without PCM.

Figure 1.

Structure of the formaldehyde-water clusters.

Figure 2.

Structure of the PNA-water clusters.

The 6-31+G(d) basis set is used for the calculations on formaldehyde and PNA, as in Ref. 12. For formaldehyde, also aug-cc-pVDZ⁶⁶ is used to assess some basis set effects. For pyrimidine, the aug-N07 basis set⁶⁷ is used as in Ref. 20. The core orbitals are kept frozen in the CC part of the calculation except for formaldehyde with the 6-31+G(d) basis set. The PCM cavity is built with a series of interlocking spheres centered on the nuclei and employing solvation model D (SMD) radii⁶⁸. The CPCM^58–61 flavor of PCM is used for all calculations. The FQ parameters for water are η_O = 367.0 kcal/mol², η_H = 392.2 kcal/mol², and χ_OH = 73.33 kcal/mol. These parameters are taken directly from Ref. 16, and no optimization was attempted. All calculations are performed with a development version of the GAUSSIAN suite of programs⁶⁹.

3.1 Formaldehyde

The n → π* transition energy for the isolated formaldehyde is 4.137 eV with the 6-31+G(d) basis set. The excitation energies for the formaldehyde-water clusters in gas phase computed with the same basis set are shown in 1. The “Full” results refer to the calculations computed entirely at EOM-CCSD level, while the following rows report the results obtained by considering the water molecules as classical, polarizable charges according to the various schemes described in 2.2. Finally, the last row reports the results using the EFP method from Ref. 12. The agreement between the EOM-CCSD-FQ method and the full EOM-CCSD calculations is very good: 0.02 eV, 0.01 eV, and 0.10 eV for the 2-, 4-, and 6-water clusters, respectively, with the complete PTED scheme. The performance of FQ and EFP is similar, with the former method being closer to the reference data for the two smaller clusters, and the latter being better for the larger cluster. A comparison between the various approximate schemes for the EOM-CCSD-FQ approach indicates differences not larger than 0.02 eV. This is important from a computational point of view since the complete PTED scheme requires two separate calculations, for the ground and excited states, thus it is roughly twice as expensive as the approximate schemes. Even the FRF scheme (where the FQ charges are frozen at their SCF values) performs well, although, as we shall see when the PCM contribution is added, this approximation is in general too drastic. Among the approximate schemes, PTE is the closest to PTED, consistently with Ref. 49^,50.

Introducing bulk solvation effects through PCM shifts the excitation energies of the clusters considerably. The data is reported in 2. “Full-PCM” refers to the full QM calculations while “FQ-PCM” indicates the QM-classical approach. Since various schemes can be also defined for the full EOM-CCSD-PCM calculations, the comparison between the Full-PCM and FQ-PCM results can be directly carried out for all schemes. First, however, notice that the PCM effect on the full PTED calculation shifts the transition energy by 0.09 eV, 0.11 eV, and 0.04 eV for the 2-, 4-, and 6-water clusters, respectively. This is a indication that these small clusters cannot be considered a realistic representation of a solvated system. However, since our goal is to compare with full-EOM calculations, we are limited in the system size we can treat. The agreement between the Full-PCM and FQ-PCM is very good: of the order of 0.02 eV in most cases; the largest difference is found for the 6-water cluster with the PTED scheme, 0.08 eV, which is smaller than the same results in gas phase (0.10 eV, see 1). The difference between the approximate schemes and PTED is small 0.02-0.04 eV, except for the FRF scheme where the difference can be > 0.1 eV. The best agreement with PTED is achieved with the PTE scheme.

Changing basis set, from 6-31+G(d) to aug-cc-pVDZ, does not significantly change the transition energy. The data with the latter basis is reported in 3 for the gas phase clusters. The transition energy for the isolated molecule becomes 4.125 eV, thus a little more than 0.01 eV lower than with the Pople basis set. Similar changes are obtained for the full QM cluster calculations. The FQ calculations also follow similar trends, so the results are consistent with those discussed above for the 6-31+G(d) basis. The effect of PCM, shown in 4, is to reduce even further the difference between basis sets. Overall, the best agreement with PTED is again obtained by employing the PTE approximate scheme.

3.2 PNA

The π → π* transition energy for the PNA-water clusters in gas phase is reported in 5. The difference between the FQ results with the PTED scheme and the full EOM calculations is 0.11 eV, 0.07 eV, and 0.11 eV for the 2-, 4-, and 6-water cluster, respectively, which is slightly worse than the EFP results but still much smaller than the shift compared to isolated PNA (0.28 eV, 0.19, and 0.26 eV, respectively). All the approximate schemes perform very well, with differences below 0.01 eV from PTED.

The introduction of bulk solvation effects shifts the excitation energy to much lower values as shown in 6 when the effect of PCM is considered. This red-shift of about 0.9 eV (for all clusters) indicates a strong stabilization of the excited state energy compared to the ground state. This is due to a charge separation in the excited state that is stabilized by the presence of a polar solvent like water. The difference between the energy of various clusters is now within 0.01 eV for all Full-PCM calculations with the PTED scheme, contrary to differences of more 0.1 eV for the corresponding results in gas phase (c.f. 5). The difference between the various schemes for the Full-PCM calculations is slightly larger than compared to gas phase. The PTES results are less than 0.1 eV from the complete PTED scheme, while the FRF scheme provides the worst performance with difference above 0.15 eV. More importantly, the comparison between the Full-PCM and FQ-PCM results shows very good agreement, with differences below 0.04 eV.

3.3 Pyrimidine

The summary of the results for the pyrimidine-water cluster is reported in 7. The transition considered is the lowest n → π* (B₁ symmetry). The transition energy for the isolated molecule and the cluster in gas phase for the full QM calculation is 4.581 eV and 4.899 eV, respectively. Therefore, the two water molecules produce a shift of 0.32 eV. This can be compared with the shift obtained with PCM on pyrimidine alone (see the “P/PCM” column in 7), which is 0.19 eV. Note that the approximate schemes in this case are within 0.04 eV from PTED. The comparison between the full EOM calculation for the water cluster in gas phase and that with the FQ schemes indicates a very good performance of the FQ approach (see the “P+2W/FQ” column in 7): the difference of the PTED scheme from the full EOM result is below 0.03 eV, while the difference between the approximate schemes and PTED is below 0.01 eV (except for FRF). The addition of PCM on top of the pyrimidine-water cluster blue shifts the transition energy of about 0.1 eV (see the “P+2W/FQ-PCM” column in 7). The comparison between the full EOM-PCM and the EOM-FQ-PCM calculation is very positive, with differences below 0.01 eV. For this system, PTE is the closest approximate scheme to PTED.

4 Discussion and Conclusions

This work reports the coupling of the highly accurate EOM-CCSD method for excited states with a combination of explicit/implicit polarizable solvent models: FQ and PCM. This approach aims at introducing the essential solvent effect on excitation energies when these are computed with computationally demanding methods such as those offered by CC theory while maintaining a reasonable balance between accuracy and computational cost. In this direction, the combination of the FQ and PCM approaches is a decisive step towards a reliable description of direct solute-solvent interaction and bulk solvent effects. Indeed, the use of a continuum model like PCM has the potential advantage of reducing the number of explicit solvent molecules necessary to obtain convergence on long-range interactions, which otherwise can only be reproduced by considering a large number of solvent configurations (provided, for instance, by a molecular dynamics simulation). Reducing the number of configurations is extremely important when the solute is treated at CC level because it reduces the number of EOM-CC calculations.

Although our goal is to use the EOM-CCSD-FQ-PCM method for realistic modeling of solvated systems, which still implies a relatively large number of explicit solvent molecules, the examples reported in this paper focus on small solute-water clusters, with and without PCM. In this way, the entire cluster can be treated at EOM-CCSD level thus allowing for a direct comparison with the full QM calculation. The first two systems, formaldehyde and PNA (see 3.1 and 3.2), were used to test the popular EFP approach¹² and thus offer an opportunity for a comparison with a different solvation model. Note, however, that our approach includes mutual-polarization between solute and solvent, which are reported only as an a posteriori correction in Ref. 12. Although such effects are small for transition energies, they can be significant for excited state properties⁴⁹. The performance of FQ for the gas phase clusters is rather good, with differences ≤ 0.1 eV from the full QM calculations and comparable to EFP. Further improvements in our method may be obtained by including other effects, like dispersion and exchange-repulsion, already present in EFP. Also, a better parameterization of the model for post-SCF methods would be beneficial.

Since Lipparini et al.^19–21 casted the FQ expressions in a way formally similar to those of PCM, the coupling of the two models is straightforward, as summarized in 2.1. This has also the advantage that the (EOM-)CCSD-PCM series of methods^44–50 can be seamlessly extended to the coupling with FQ and FQ-PCM. When the EOM-CCSD-FQ-PCM results are compared with those from full EOM-CCSD-PCM calculations, the agreement is even better than in gas phase, see 2, 4, and 6. The results reported in 3.3 for the last test system, a cluster of pyrimidine and two water molecule in C_2v configuration, show an even better performance of both the FQ and FQ-PCM approaches compared to the full QM calculations, with differences below 0.04 eV and 0.01 eV, respectively.

The approximate schemes perform all quite well. The FRF scheme, which does not include mutual-polarization effects, provides errors larger than 0.1 eV (and larger than 0.15 eV for PNA, see 6) and is, as expected, the least reliable. The appeal of the approximate schemes is that the transition energy can be computed in one step, while PTED requires two separate calculations for the ground and the excited states.

In summary, the results presented in this work hold the promise of reliable and yet computationally feasible calculations of excited states of chromophores in solution by judiciously coupling a highly accurate method for the solute (EOM-CCSD) and an approximate polarizable explicit/implicit model (FQ-PCM) for the solvent. Simulations of realistic solvated systems are currently in progress in our laboratories.

Figure 3.

Structure of the pyrimidine-water cluster.

Table 1.

Formaldehyde excitation energy (eV) for the n → π* transition with the 6-31+G(d) basis set with two, four, and six water molecules. “Full” refers to the calculation done on the entire system with the EOM-CCSD method. The EFP results are from Ref. 12. The excitation energy for the isolated molecule is 4.137 eV.

	2	4	6
Full	4.283	4.240	4.421
FRF	4.278	4.246	4.337
PTE	4.257	4.231	4.313
PTE(S)	4.255	4.228	4.310
PTES	4.255	4.229	4.311
PTED	4.261	4.234	4.318
EFP	4.334	4.286	4.430

Table 2.

Formaldehyde excitation energy (eV) for the n → π* transition with the 6-31+G(d) basis set with two, four, and six water molecules and PCM. “Full-PCM” refers to the calculation done on the entire system with the EOM-CCSD-PCM schemes.

	2		4		6
	Full-PCM	FQ-PCM	Full-PCM	FQ-PCM	Full-PCM	FQ-PCM
FRF	4.436	4.472	4.410	4.451	4.510	4.479
PTE	4.351	4.362	4.325	4.344	4.431	4.373
PTE(S)	4.319	4.327	4.292	4.310	4.402	4.340
PTES	4.330	4.339	4.303	4.322	4.413	4.352
PTED	4.374	4.360	4.349	4.342	4.457	4.373

Table 3.

Formaldehyde excitation energy (eV) for the n → π* transition with the aug-cc-pVDZ basis set with two, four, and six water molecules. “Full” refers to the calculation done on the entire system with the EOM-CCSD method. The excitation energy for the isolated molecule is 4.125 eV.

	2	4	6
Full	4.276	4.227	4.410
FRF	4.273	4.239	4.334
PTE	4.251	4.222	4.309
PTE(S)	4.248	4.219	4.306
PTES	4.248	4.220	4.307
PTED	4.254	4.225	4.314

Table 4.

Formaldehyde excitation energy (eV) for the n → π* transition with the aug-cc-pVDZ basis set with two, four, and six water molecules and PCM. “Full-PCM” refers to the calculation done on the entire system with the EOM-CCSD-PCM schemes.

	2		4		6
	Full-PCM	FQ-PCM	Full-PCM	FQ-PCM	Full-PCM	FQ-PCM
FRF	4.436	4.472	4.408	4.451	4.503	4.479
PTE	4.348	4.358	4.319	4.341	4.422	4.369
PTE(S)	4.317	4.323	4.287	4.306	4.395	4.335
PTES	4.328	4.335	4.298	4.318	4.405	4.347
PTED	4.374	4.356	4.347	4.338	4.451	4.368

Table 5.

PNA excitation energy (eV) for the π → π* transition with the 6-31+G(d) basis set with two, four, and six water molecules. “Full” refers to the calculation done on the entire system with the EOM-CCSD method. The EFP results are from Ref. 12. The excitation energy for the isolated molecule is 4.654 eV.

	2	4	6
Full	4.375	4.461	4.391
FRF	4.490	4.536	4.511
PTE	4.479	4.525	4.490
PTE(S)	4.480	4.527	4.492
PTES	4.480	4.527	4.492
PTED	4.482	4.529	4.497
EFP	4.384	4.459	4.415

Table 6.

PNA excitation energy (eV) for the π → π* transition with the 6-31+G(d) basis set with two, four, and six water molecules and PCM. “Full-PCM” refers to the calculation done on the entire system with the EOM-CCSD-PCM schemes.

	2		4		6
	Full-PCM	FQ-PCM	Full-PCM	FQ-PCM	Full-PCM	FQ-PCM
FRF	3.902	3.908	3.916	3.915	3.929	3.922
PTE	3.612	3.598	3.625	3.605	3.645	3.607
PTE(S)	3.650	3.639	3.664	3.646	3.684	3.648
PTES	3.650	3.639	3.664	3.646	3.684	3.648
PTED	3.743	3.779	3.757	3.786	3.775	3.789

Table 7.

Pyridine excitation energy (eV) for the n → π* (B₁) transition with the aug-N07 basis set. “P” refers to pyrimidine alone while “P+2W” indicate the cluster with two water molecules. The transition energy computed with full EOM-CCSD on the isolate molecule and the water cluster without PCM are 4.581 eV and 4.899 eV, respectively.

	P/PCM	P+2W/FQ	P+2W/PCM	P+2W/FQ-PCM
FRF	4.814	4.908	5.015	5.068
PTE	4.741	4.864	4.952	4.962
PTE(S)	4.735	4.862	4.949	4.956
PTES	4.737	4.862	4.950	4.957
PTED	4.771	4.870	4.982	4.990