Abstract
A mechanism-based model was developed to characterize the crosstalk between proinflammatory cytokines, bone remodeling biomarkers, and bone mineral density (BMD) in collagen-induced arthritic (CIA) rats. Male Lewis rats were divided into five groups: healthy control, CIA control, CIA receiving single 0.225 mg kg−1 subcutaneous (SC) dexamethasone (DEX), CIA receiving single 2.25 mg kg−1 SC DEX, and CIA receiving chronic 0.225 mg kg−1 SC DEX. The CIA rats underwent collagen induction at day 0 and DEX was injected at day 21 post-induction. Disease activity was monitored throughout the study and rats were sacrificed at different time points for blood and paw collection. Protein concentrations of interleukin (IL)-1β, IL-6, receptor activator of nuclear factor kappa-B ligand (RANKL), osteoprotegerin (OPG), and tartrate-resistant acid phosphatase 5b (TRACP-5b) in paws were measured by enzyme-linked immunosorbent assays (ELISA). Disease progression and DEX pharmacodynamic profiles of IL-1β, IL-6, RANKL, and OPG were fitted simultaneously and parameters were sequentially applied to fit the TRACP-5b and BMD data. The model was built according to the mechanisms reported in the literature and modeling was performed using ADAPT 5 software with naïve pooling. Time profiles of IL-1β and IL-6 protein concentrations correlated with their mRNAs. The RANKL and OPG profiles matched previous findings in CIA rats. DEX inhibited the expressions of IL-1β, IL-6, and RANKL, but did not alter OPG. TRACP-5b was also inhibited by DEX. Model predictions suggested that anti-IL-1β therapy and anti-RANKL therapy would result in similar efficacy for prevention of bone loss among the cytokine antagonists.
Keywords: Biomarkers, bone modeling, dexamethasone, pharmacodynamics, systems model
Introduction
Bone remodeling is a tightly controlled dynamic process that is regulated by many different factors. Two major cell types that are responsible for bone homeostasis are osteoblasts and osteoclasts. Osteoblasts are bone-forming cells that synthesize the bone matrix and mineralization. Osteoclasts are responsible for bone resorption (Tanaka et al. 2005). When the activity of osteoblasts exceeds that of osteoclasts, bone formation dominates as is the case during the growth period in childhood. In bone-related disease conditions such as osteoporosis and rheumatoid arthritis (RA), the activity of osteoclasts becomes dominant; active bone resorption occurs and leads to bone destruction. To understand the pathogenesis of bone loss in RA, it is important to study the mediators and pathways controlling the activities of osteoblasts and osteoclasts.
One of the major mechanisms governing the balance between osteoblasts and osteoclasts is the RANK/RANKL/OPG system. RANK (∼67 kDa) is expressed on osteoclast precursors, and its activation is required for maturation of osteoclast precursors to active osteoclasts. This activation is mediated by the binding between RANK and RANKL (∼35 kDa), which is a member of the tumor necrosis factor (TNF)-family of cytokines and is produced by osteoblasts. Upon maturation of osteoclasts, they can elicit their bone-resorbing activity and initiate the bone breakdown process. This process is counter-regulated by the action of OPG (∼120 kDa as a homodimer), which is a natural decoy receptor for RANKL synthesized primarily by osteoblasts (Nelson et al. 2012). In healthy conditions, this system is at steady-state and is responsible for maintaining normal bone metabolism. However, in bone-related diseases, especially in immune diseases such as RA, the components in this system are under the influence of other immune stimulants, resulting in the disruption of the osteoblast/osteoclast balance.
Rheumatoid arthritis is characterized as a chronic inflammatory condition that is mediated mainly by immune cells such as macrophages and fibroblasts, as well as proinflammatory cytokines TNF-α, IL-1β, and IL-6 (Choy and Panayi 2001). The immune cascade caused by cytokines results in two parallel processes: joint inflammation and joint destruction. Joint inflammation is primarily driven by the cytokines and leads to pain and swelling. Joint destruction is partly driven by the inflammation process and has a more complicated pathology. It involves the effects of cytokines, the RANK/RANKL/OPG system, together with other factors such as metalloproteinases (MMPs) (Klareskog et al. 2009). Our laboratory previously published a mechanism-based model that described the dynamics and the interplay between DEX, endogenous corticosterone (CST), glucocorticoid receptor (GR), proinflammatory cytokines (TNF-α, IL-1β, and IL-6), and their regulation of disease endpoints (paw swelling and bone mineral density) in rats with collagen-induced arthritis, which is a common animal model of RA (Earp et al. 2008a,b). The current study aimed to further expand this model with added information regarding the temporal changes of the components in the RANK/RANKL/OPG pathway and osteoclast activity, and thus provide better insights into bone destruction in RA.
Many mathematical models were published exploring the dynamics of bone remodeling with the incorporation of the RANK/RANKL/OPG signaling pathway (Pivonka et al. 2008, 2010; Peterson and Riggs 2010, 2012; Schmidt et al. 2011; Post et al. 2013). Most were built according to literature findings and focused on the effects of calcium and hormones such as parathyroid hormone (PTH) and transforming growth factor (TGF)-β on bone remodeling. They adequately predict BMD progression under different situations such as aging, osteoporosis, and sustained glucocorticoid therapy, and are also useful in making recommendations for therapeutic interventions that may lead to desirable clinical outcomes. However, to our knowledge, no such model has been developed for RA. Our current study develops a similar mechanism-based model for RA and includes experimental data regarding RANKL and OPG disease progression. The model presented in this study is a combination of our Earp et al. model developed for CIA disease progression and the bone remodeling model developed by Lemaire et al. (2004). The model as a whole characterizes the crosstalk between the immune cascade, the RANK/RANKL/OPG pathway, as well as BMD during RA disease progression.
Materials and Methods
Animals
Male Lewis rats (6–9 weeks old) were purchased from Harlan (Indianapolis, IN) with weights of 150–175 g. The rats were housed individually in the University Laboratory Animal Facility and acclimatized for 1 week under constant temperature (22°C), humidity (72%), and 12-h light/12-h dark cycle. Rats had free access to rat chow and water. All protocols followed the Principles of Laboratory Animal Care (Institute of Laboratory Animal Resources, 1996) and were approved by the University at Buffalo Institutional Animal Care and Use Committee.
Induction of collagen-induced arthritis in Lewis rats
The induction of collagen-induced arthritis (CIA) in Lewis rats followed protocols and reagents supplied by Chondrex, Inc. (Redmond, WA). The day of first collagen induction was regarded as day 0 in the study. Detailed procedures of the collagen induction were described previously (Earp et al. 2008b; Lon et al. 2011).
Experimental design
A number of rats were assigned as healthy controls and did not undergo collagen induction. One or two healthy control rats were sacrificed on days 9, 15, 19, 21, 23, 30, and 34 for baseline assessment. For CIA rats, paw edema and body weights were monitored throughout the entire study starting from day 0. Paw sizes were determined using digital calipers with details described previously (Earp et al. 2008a,b, 2009; Liu et al. 2011; Lon et al. 2011). Edema was indicated by the sum of the paw and ankle area measurements for each hind foot. On day 20 post-induction, rats with paw volume increases of at least 50% in one or two paws were selected and randomly assigned to four groups: vehicle control group, SC low-dose group which received 0.225 mg kg−1 subcutaneous (SC) DEX on day 21, SC high-dose group which received 2.25 mg kg−1 SC DEX on day 21, and SC multiple-dose group which received once a day doses of 0.225 mg kg−1 SC DEX on days 21–27. For the CIA control group, one to four rats were sacrificed on days 9, 15, 19, 21, 23, 30, 34, and 40. For the DEX groups, three or four rats were sacrificed at each time point. For rats in the SC low-dose and high-dose groups, these times points were at 1, 2, 4, 6, 8, 12, 24, 36, 48, 96, 216, and 336 h after dosing, while for SC multiple-dose rats, time points were at 36, 84, 132, 180, 264, and 336 h after the first dose.
All rats were sacrificed by aortal exsanguinations and blood was collected in syringes containing EDTA as anticoagulant. Blood samples were centrifuged at 2000g for 10 min at 4°C. Plasma was then collected and aliquots were transferred into microfuge tubes. Paw tissues (above ankle excluding skin and toenails) were also collected during the sacrifice and were flash-frozen in liquid nitrogen. After collection, all blood and paw samples were immediately stored at −80°C before further analysis.
Protein extraction from the rat paws
Frozen paw tissue was pulverized with a mortar and pestle under liquid nitrogen. For CIA rats, only swollen paws (indicated by paw edema measurements) were processed and included in our analysis. The protein extraction buffer was composed of 50 mmol L−1 Tris buffer at pH 7.4, 0.1 mol L−1 NaCl, and 0.1% Triton X-100 with the addition of protease inhibitor cocktail from Roche (cOmplete, Mini; one tablet per 10 mL buffer, Indianapolis, IN). The composition of the buffer was reported previously for protein extraction (Stolina et al. 2008, 2009). Pulverized paw tissue was weighed in a polypropylene tube and mixed with the protein extraction buffer. The mixture was then homogenized using a Kinematica Polytron homogenizer (model PT10-35; Kinematica Inc., Newark, NJ) on speed setting at five in an ice-bath for three 10-sec durations, with a 30-sec interval for cooling. The homogenization probe was rinsed three times with double distilled water, chilled with ice, and completely dried between samples. The homogenate was transferred to a centrifuge tube and centrifuged at 10,000 rpm for 10 min. The supernatant was collected and aliquots were stored at −80°C. Total protein concentrations in the homogenate samples were determined using the microplate procedure with a BCA assay kit (Pierce Biotechnology, Rochford, IL).
Measurements of protein concentration by ELISA methodology
Concentrations of IL-1β, IL-6, RANKL, OPG, and TRACP-5b in paw homogenates were determined by ELISA. For IL-1β, IL-6, and RANKL, undiluted homogenates were added during the ELISA procedure. For TRACP-5b, homogenates were diluted two- to four-fold with homogenization buffer before analysis. The assay results were normalized with the total protein concentrations obtained by the BCA assay. For OPG, protein concentrations of the homogenate samples were adjusted to 1 mg mL−1 before the procedure to minimize the matrix effects observed in a preliminary test.
Quantikine Rat Immunoassay kits from R&D Systems, Inc. (Minneapolis, MN) were used for measuring concentrations of IL-1β and IL-6. Quantikine Mouse RANKL Immunoassay kit from the same company was used for rat RANKL protein determination. This use is based on the high (96%) similarity between the mouse and rat RANKL amino acid sequence (Xu et al. 2000) and its successful application reported previously (Stolina et al. 2005). Osteoprotegerin ELISA kit (for mouse/rat OPG) from Alpco Diagnostics (Salem, NH) was used for measuring OPG. RatTRAP assay kit from Immunodiagnostic Systems Ltd (IDS Ltd, Fountain Hills, AZ) was used for TRACP-5b. The assay procedures followed the manufacturers’ instructions. All samples were run in duplicate and quality control (QC) samples were prepared for each plate for between-assay variability assessment. Calibration curves for IL-1β, IL-6, and RANKL were constructed by plotting the absorbance of each standard versus its concentration on a log/log graph with the best-fitted line determined by regression analysis. Calibration curves for OPG and TRACP-5b were built by fitting the standards and the absorbance readings into a 4-parameter logistic model. The lower limits of quantification for IL-1β, IL-6, RANKL, OPG, and TRACP-5b were 31.2, 62.5, 31.2, 62.5 pg mL−1, and 0.52 U L−1. The between-assay coefficients of variability were 7.86%, 9.09%, 3.35%, 8.49%, and 2.01%.
Mechanism-based disease progression model
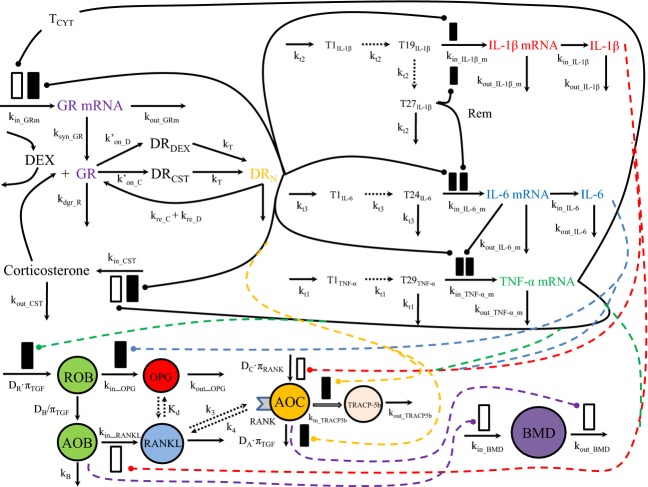
Figure 1 displays a schematic of the mechanistic model. The components describing the dynamics of corticosterone (CST), glucocorticoid receptor (GR) mRNA, and the three proinflammatory cytokines (TNF-α, IL-1β, and IL-6) mRNAs utilized our previous model (Earp et al. 2008a, b). Intramuscular (IM) DEX PK characteristics in both healthy and CIA rats have been investigated (Earp et al. 2008c), and preliminary study has shown the similarity between IM and SC PK profiles. Thus, the IM PK model was used for SC DEX. All parameters regarding these components were fixed in the analysis, except for α2 (0.0002894 nmol GR nmol IL-1β−1) and β2 (0.00001159 ng CST mL−1 GR nmol IL-1β−1), which describe the intrinsic activity of IL-1β on GR mRNA and CST as described in the Earp et al. article. These two values are close to zero and simulations indicated that their removal did not alter the model fittings; thus these two parameters were fixed to 0 for simplicity. The time profiles of IL-1β, IL-6, RANKL, and OPG protein concentrations were fitted simultaneously, and the resulting parameters were fixed and applied to fit the TRACP-5b and BMD data.
Figure 1.
Schematic of the mechanistic model of disease progression of glucocorticoid receptor (GR), proinflammatory cytokines (TNF-α, IL-1β, and IL-6), RANK/RANKL/OPG system, and bone mineral density (BMD) in collagen-induced arthritic (CIA) rat model. The bone homeostasis-related components of the model are displayed in colored circles. Black solid lines indicate the interactions described by the previous Earp model. Dashed lines specify the action of IL-1β (red), IL-6 (blue), and TNF-α (green) on different components of the bone remodeling system. Yellow-dashed lines indicate the action of DRN on active osteoclasts (AOC) and its activity, and purple dashed lines show the action of active osteoblasts (AOB) and AOC on BMD. CIA, collagen-induced arthritic; RANKL, receptor activator of nuclear factor kappa-B ligand.
Dynamics of IL-1β and IL-6 proteins
In the Earp model, mRNA concentration-time profiles of cytokines IL-1β and IL-6 after arthritis induction were well described by a series of transduction compartments with incorporation of the effects of bound CST-GR complex in the nucleus (DRN) and the remission compartment (Rem) (Earp et al. 2008a,b). The protein concentrations of IL-1β and IL-6 are modeled here as catenary compartments following the IL-1β and IL-6 mRNA transduction process. The equations for fitting IL-1β and IL-6 protein concentration-time profiles in both CIA and DEX-treated CIA rats are as follows:
| 1 |
| 2 |
where kin2P and kin3P represent the synthesis rates of IL-1β and IL-6 proteins (shown as kin_IL-1β and kin_IL-6 in Fig.1), S2 and S3 are the proportionality constants between the disease-stimulated IL-1β and IL-6 mRNAs and their protein concentrations, IL-1βM0 and IL-6M0 are the baseline mRNA concentrations, and IL-1βP0 and IL-6P0 are the baseline protein concentrations (determined by the average values in healthy rats). The elimination rates of IL-1β and IL-6 proteins (shown as kout_IL-1β and kout_IL-6 in Fig.1), are represented by  and
and 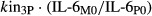 .
.
Dynamics of the bone remodeling system in healthy rats
The RANKL and OPG concentration-time profiles were fitted in a model expanded from a bone turnover model proposed by Lemaire et al. to describe the interactions between osteoblasts and osteoclasts during bone remodeling (Lemaire et al. 2004). This model was developed based on the effects of PTH and TGF-β, which are two important mediators regulating calcium homeostasis and bone remodeling, and it incorporates the regulation of the RANK/RANKL/OPG pathway in osteoblast/osteoclast activities. The original model, when unaltered, can describe the steady state and relationships of all the components, including, responding osteoblasts (ROB, referred as “R” in the Lemaire model), active osteoblasts (AOB, referred as “B” in the Lemaire model), active osteoclasts (AOC, referred as “C” in the Lemaire model), RANKL, and OPG.
In our model, most parameters remain the same as in the Lemaire model, while some are modified to fit the experimental data. Under healthy conditions, the dynamics of ROB, AOB, AOC, RANKL, and OPG are described by
| 3 |
| 4 |
| 5 |
where DR and DC are the differentiation rate constants of osteoblast progenitors and osteoclast precursors, and kB and DA are elimination rate constants of active osteoblasts and osteoclasts. DB is the product of a fixed proportion (f0) and the differentiation rate constant of responding osteoblasts (dB). The πTGF and πRANK are receptor occupancies of TGF-β and RANK as given by
| 6 |
| 7 |
where AOCS is half the concentration of active osteoclasts yielding maximum TGF-β receptor occupancy, KL is the concentration of RANK-RANKL complex, K is the concentration of RANK, and k3 and k4 are the binding and dissociation rate constants of the RANK-RANKL complex. The equation for the pseudo steady-state concentrations of RANKL (L) and OPG (O) are as follows:
| 8 |
| 9 |
where kinL (shown as kin_RANKL in Fig.1) is the production rate constant of RANKL, Kd is the equilibrium dissociation constant of the OPG-RANKL complex, and kinO and kO are the production and loss rate constants of OPG (shown as kin_OPG and kout_OPG in Fig.1). In the Lemaire model, productions of RANKL and OPG are subject to PTH binding and are governed by PTH receptor occupancy (πP). Since experimental data for both RANKL and OPG were obtained in our study, we estimated their production rate constants. The use of one parameter (kinL or kinO) is for simplicity and to minimize overparameterization. The Kd for the OPG-RANKL complex is used instead of separate binding and dissociation rate constants (k2/k1) for the same purpose. Details of the derivations of equations 7-9 can be found in supporting information Data S1.
Dynamics of the bone remodeling system in CIA rats
Under arthritic conditions, proinflammatory cytokines are stimulated and they can affect the bone turnover process via multiple pathways. The ultimate result of these effects is bone loss, with is a significant risk in RA. There are numerous reports in the literature studying the mechanisms by which TNF-α, IL-1β, and IL-6 disrupt the osteoblast/osteoclast balance in RA. We aimed to include those mechanisms that are most commonly recognized and test their suitability in explaining our experimental data. The relationships between the inflammatory cytokines and the important components in bone remodeling and the model that can best describe our data are delineated below.
TNF-α is often regarded as one of the dominant mediators in RA and is also a potent inducer for other cytokines (Karmakar et al. 2010). In bone remodeling, TNF-α has been shown to inhibit the differentiation and maturation of osteoblasts (Gilbert et al. 2000; Nanes 2003), and stimulate the formation and activity of osteoclasts through both RANKL-dependent and –independent pathways (Goldring 2002; Walsh et al. 2005). TNF-α can directly increase the numbers of osteoclast precursors through up-regulation of c-Fms expression (Yao et al. 2006), and promote osteoclast differentiation with IL-1α (Kobayashi et al. 2000). It can induce the expression of RANKL in bone marrow cells (Wei et al. 2005) and activate RANKL signaling pathway (Lam et al. 2000).
IL-1β also stimulates the production of RANKL in bone. Some studies suggested that the regulation of IL-1β on RANKL expression may be downstream of the TNF-α-mediated bone destructive cascade (Wei et al. 2005; Zwerina et al. 2007), but there are also other studies that suggested this mechanism is TNF-α-independent (Ma et al. 2004; Wei et al. 2005). In vitro evidence from Wei et al. indicated that expressions of IL-1 receptor 1 (IL-1R1) were up-regulated in osteoclast precursor cells after addition of TNF-α, and, in turn, IL-1 augmented the osteoclast differentiation via the RANKL pathway. On the other hand, in IL-1R1 deficient mice, administration of TNF-α resulted in around 50% reduction in osteoclastogenesis, suggesting TNF-α can mediate this process without IL-1β (Wei et al. 2005). IL-1β has also been shown to have a direct stimulatory effect on osteoclasts (Goldring 2002; Walsh et al. 2005; Lorenzo et al. 2008). In the absence of osteoblasts, IL-1 can induce the maturation and bone-resorbing activity of osteoclasts (Jimi et al. 1999).
IL-6 has been shown to regulate bone resorption via the differentiation and maturation of osteoclasts (Goldring 2002; Lorenzo et al. 2008), and this may be mediated in a RANKL-independent manner (Kudo et al. 2003). Its effect on the RANKL-mediated pathway is controversial. Some studies suggested that it directly or indirectly induces RANKL expression (Palmqvist et al. 2002; Hashizume et al. 2008), but there are also studies that had contradictory results (Braun and Zwerina 2011; Suzuki et al. 2011). Liu et al. investigated the crosstalk between IL-6 and prostaglandin E2 (PGE2) signaling pathways and how they govern osteoclastogenesis (Liu et al. 2005), and found that IL-6 participated in cyclooxygenase (COX)-2 mediated PGE2 synthesis, which can promote osteoclast production though inhibition of OPG and stimulation of RANKL. There is also a positive feedback mechanism between PGE2 and IL-6 in bone, by which one can augment the secretion of the other. The results of the Liu study also suggested that IL-6/PGE2-mediated osteoclastogenesis is mainly via the blockade of OPG production, whereas the increase in RANKL expression is minimal.
Since DEX is a potent immunosuppressant and is effective in eliciting a broad array of immune responses, it is difficult to differentiate its specific effects on bone remodeling apart from the suppression it causes in cytokines. It is well known that prolonged use of DEX and other glucocorticoids cause bone loss and fractures (Cooper et al. 1995), but its exact mechanism is not clear. Studies have suggested that DEX may directly or indirectly stimulate the production of osteoclasts via the RANKL pathway (Auphan et al. 1995), and prevent apoptosis of osteoclasts (Weinstein et al. 2002; Kim et al. 2006). Although the lifespan and number of osteoclasts may be increased by DEX, it suppresses the bone-resorbing activity of osteoclasts (Kim et al. 2006). The reduction in bone-resorbing activity is likely due to the disruption of the osteoclast cytoskeleton mediated by a macrophage colony-stimulating factor (M-CSF)-dependent pathway (Kim et al. 2006). The final effect of DEX on BMD in CIA rats is essentially the result of these complicated interactions.
Taking all of these findings into consideration, the selected model was constructed with the change in each cytokine or DRN from its baseline affecting the components in the Lemaire model. It should be noted in the model, TNF-α (TNF-αM) represents mRNA concentrations as described in the Earp et al. article, whereas IL-1β (IL-1βP) and IL-6 (IL-6P) represent protein concentrations as described in equations 1 and 2. The equations are as follows:
 |
10 |
| 11 |
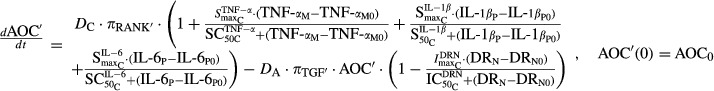 |
12 |
where ROB′, AOB′, and AOC′ are the concentrations of responding osteoblasts, active osteoblasts, and active osteoclasts after CIA induction, 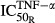 is the sensitivity constant of the inhibition by TNF-α on osteoblast production,
is the sensitivity constant of the inhibition by TNF-α on osteoblast production, 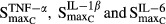 reflect stimulation of production of osteoclasts by cytokines TNF-α, IL-1β, and IL-6, while
reflect stimulation of production of osteoclasts by cytokines TNF-α, IL-1β, and IL-6, while 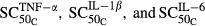 are the respective sensitivity constants, and
are the respective sensitivity constants, and 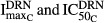 are the parameters regarding the effect of DRN on osteoclast apoptosis.
are the parameters regarding the effect of DRN on osteoclast apoptosis.
Receptor occupancies (πTGF′ and πRANK′), RANKL (L′), and OPG (O′) in CIA rats were modeled as follows:
| 13 |
| 14 |
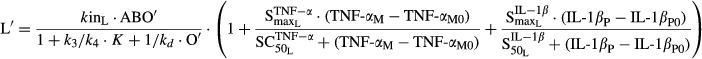 |
15 |
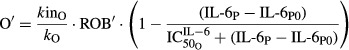 |
16 |
where 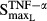 and
and 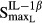 reflect the stimulation of RANKL production by TNF-α and IL-1β,
reflect the stimulation of RANKL production by TNF-α and IL-1β, 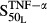 and
and 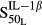 are sensitivity constants, and
are sensitivity constants, and 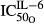 is the sensitivity constant for inhibition of OPG production by IL-6.
is the sensitivity constant for inhibition of OPG production by IL-6.
Dynamics of TRACP-5b
TRACP-5b is derived from osteoclasts and is a marker for bone resorption (Halleen et al. 2000). In our model, TRACP-5b concentrations are linked to active osteoclasts (AOC), by which the ratio change controls the progression of TRACP-5b. The equation for TRACP-5b in CIA rats and its temporal changes after DEX is as follows:
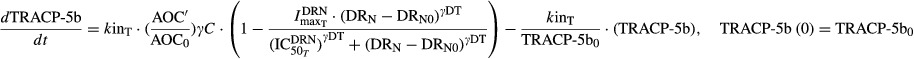 |
17 |
where kinT is the production rate constant of TRACP-5b (shown as kin_TRACP5b in Fig.1), γC is the amplification factor 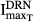 , and
, and 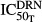 are the capacity and sensitivity constants for inhibition of TRACP-5b by DRN, and γDT is the Hill function for the inhibition. The elimination process (koutT, shown as kout_TRACP5b in Fig.1) is given by (kinT)/(TRACP-5b0). TRACP-5b0 is the baseline concentration and is the average value in healthy rats.
are the capacity and sensitivity constants for inhibition of TRACP-5b by DRN, and γDT is the Hill function for the inhibition. The elimination process (koutT, shown as kout_TRACP5b in Fig.1) is given by (kinT)/(TRACP-5b0). TRACP-5b0 is the baseline concentration and is the average value in healthy rats.
Dynamics of bone mineral density
Bone mineral density (BMD) data were obtained previously (Earp et al. 2008a,b). BMD is determined by the balance between osteoblasts and osteoclasts. In our model, the production of bone turnover is linked to the ratio change in active osteoblasts (AOB), and the bone breakdown process is connected to the ratio change in active osteoclasts (AOC). Since the model was built to describe the whole bone system at the steady state, the profiles of AOB and AOC in healthy rats are flat and the ratio changes remain 1. Thus, in healthy animals the effect of AOB or AOC on BMD is not turned on and the equations are as follows:
| 18 |
| 19 |
| 20 |
| 21 |
| 22 |
A logistic function was used in each bone region to describe the natural growth (with rate constant kgrow) of the bone. Parameters kinLR, kinTF, kinDF, kinMF, and kinEF are the production rate constants of lumbar vertebrate regions 1–4 (LR), total femur (TF), diaphyseal femur (DF), metaphyseal femur (MF), and epiphyseal femur (EF). The BMDLR0, BMDTF0, BMDDF0, BMDMF0, and BMDEF0 are the baseline values of BMD in the respective regions, and BMDLRSS, BMDTFSS, BMDDFSS, BMDMFSS, and BMDEFSS are the steady-state BMD values at the end of the experiment.
For CIA rats, the ratio changes of AOB and AOC during natural disease progression and after DEX are incorporated in the equations as follows:
| 23 |
| 24 |
| 25 |
| 26 |
| 27 |
where γBLR, γBTF, γBDF, γBMF, and γBEF are the amplification factors of the effects of AOB on the production of BMD in the five bone regions, and γCLR, γCTF, γCDF, γCMF, and γCEF are the amplification factors of the effects of AOC on the loss of BMD in the respective bone regions. This portion of the model resembles the equation used previously to model the progression of lumbar spine BMD in humans after treatment with denosumab (Peterson and Riggs 2012).
Model fitting and data analysis
The area under the effect curves (AUEC) of concentration-time profiles of the IL-1β, IL-6, RANKL, OPG, and TRACP-5b in healthy, CIA, and DEX-dosed CIA rats were statistically compared by the two-sided Bailer-Satterthwaite method (Bailer 1988; Nedelman et al. 1995), and the t-statistic was calculated as follows:
| 28 |
where AUECC and AUECA are the AUEC of the control rats and CIA rats, and s2 (AUEC) is the variance of the AUEC. The profiles were considered statistically different if tobs ≥ 2.58, which is the Bonferroni-corrected critical value (zcrit) in this analysis.
Model fittings were performed by nonlinear regression analysis using the maximum likelihood algorithm in the ADAPT 5 program (D'Argenio et al. 2009). Profiles of natural disease progression and all DEX dosing groups were fitted simultaneously and data from all the animals were naïve-pooled. The IL-1β, IL-6, RANKL, and OPG protein concentration-time profiles were fitted first, and the resulting parameters were fixed and applied to fit the TRACP-5b and BMD data. The variance model used is as follows:
| 29 |
where Vi represents the variance of the ith data point, σ1 and σ2 are variance model parameters, and Yi is the ith model prediction. A separate variance model was applied for each biomarker or disease endpoint. The final model was selected based on the success of minimization, modeling fittings, and reasonability and precision of parameter estimation.
Results
Measurements of protein concentrations in paw extracts
Our initial interest was to measure the protein concentrations of the three cytokines assessed in the Earp model (TNF-α, IL-1β, and IL-6) and incorporate them into the current model. We successfully measured and implemented the profiles of IL-1β and IL-6 protein concentrations in rat paws. However, preliminary experiments showed that the TNF-α protein concentration was not detectable, and hence it was not included in our model development. Instead, mRNA concentrations of TNF-α was included in the modeling analysis of this study.
Dynamics of IL-1β and IL-6 proteins
Comparison of IL-1β and IL-6 mRNA and protein disease progression profiles is shown in Figure2. The cytokine mRNA profiles were adopted from our previous study (Earp et al. 2008b). It appeared that the mRNA and protein concentration profiles for both IL-1β and IL-6 correlated well, and the disease-state stimulation of mRNA was much higher than for the protein products. The disease onset times for mRNA and protein were similar, and the protein profiles of both cytokines generally followed the tendencies of their mRNA expressions (Earp et al. 2008b), where the concentration reached a steady state for IL-1β, and rose and fell off for IL-6 after disease onset.
Figure 2.
Disease progression of IL-1β and IL-6 mRNA and protein concentrations in CIA rats. Mean mRNA and protein concentrations at each time points were normalized with their respective baseline concentrations obtained on the first sacrifice time (day 9, 216 h post-induction). Solid and open circles depict normalized mRNA and protein profiles, and accompanying lines are normalized model predictions.
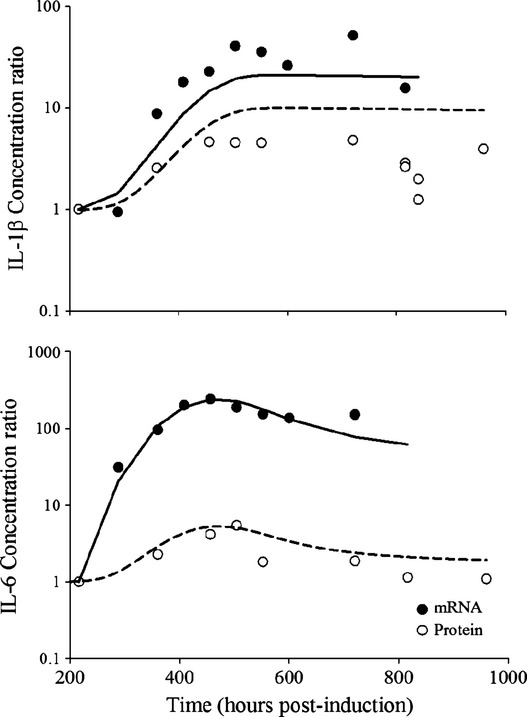
Figure3 depicts the profiles of IL-1β and IL-6 proteins in rat paws during CIA natural disease progression and DEX dosing. DEX caused a rapid drop in the protein concentrations of both cytokines in a manner similar to its effects to mRNA (Earp et al. 2008a). Chronic DEX effectively suppressed both cytokines to their baseline concentrations during the dosing period and the profiles returned to predose state after dosing is terminated.
Figure 3.
Disease progression and PD of DEX for IL-1β and IL-6 protein concentrations in CIA rats. The gray areas indicate the range of baseline concentrations (mean ± SD) in healthy animals. Symbols and lines depict data from CIA control (∆, long dashed line), CIA receiving single 0.225 mg kg−1 dose (□, short dashed line), CIA receiving single 2.25 mg kg−1 dose (◊, dotted line), and CIA receiving chronic doses of 0.225 mg kg−1 groups (○, long dashed-dotted line). Model predictions for the respective groups are depicted by accompanying lines. CIA, collagen-induced arthritic; DEX, dexamethasone; PD, pharmacodynamic.
Comparisons of AUEC revealed that CIA rats had significantly higher expressions of IL-1β (7.47 pmol mg_protein−1 h) and IL-6 (2.11 pmol mg_protein−1 h) than in healthy rats (1.06 and 1.17 pmol mg_protein−1 h). After dosing, the AUEC of IL-1β in CIA rats receiving single 0.225 mg kg−1, single 2.25 mg kg−1, and chronic 0.225 mg kg−1 SC DEX are 3.41, 2.57, and 1.52 pmol mg_protein−1 h and were statistically lower than in CIA control rats and were significantly different from each other. For IL-6, the AUECs after dosing were 1.56, 1.09, and 0.704 pmol mg_protein−1 h, respectively. The chronic dosing group exhibited significantly lower IL-6 than the CIA control and single-dose groups. No difference was found between the CIA control and CIA single-dose rats for IL-6.
The proposed model provided reasonable fittings of the profiles of both cytokines in CIA natural disease progression and under DEX dosing (Figs.2, 3). There was a slight underestimation of protein concentrations of IL-1β during the rising phase in the CIA rats, (Fig.3), which corresponds to the overestimation at the plateau phase in the normalized profiles in Figure2. However, it was acceptable, given that there are considerable variabilities among the CIA animals and the plateau phase was adequately captured. The parameter estimates for IL-1β and IL-6 proteins are listed in Table1. The synthesis rate constants for IL-1β and IL-6 were 3.94 × 10−5 and 1.63 × 10−4 pmol mg_protein−1 h−1 nmol_mRNA−1, reflecting the slow translation process from mRNA to protein. The proportionality constants (S2 and S3) between mRNA and protein concentrations for IL-1β and IL-6 were 0.454 and 0.00332.
Table 1.
Model parameter estimates for the dynamics of IL-1β and IL-6 proteins
| Parameter (Units) | Definition | Estimate | CV % |
|---|---|---|---|
| kin2P (pmol h−1 nmol_mRNA−1) | Synthesis rate constant for IL-1β protein | 3.94 × 10−5 | 7.45 |
| S2 | Proportionality constant of disease-stimulated IL-1β mRNA and protein | 0.454 | 0.674 |
| IL-1βP0 (pmol mg_protein−1) | IL-1β protein baseline | 0.00129 | FIXED |
| kin3P (pmol h−1 nmol_mRNA−1) | Synthesis rate constant for IL-6 protein | 1.63 × 10−4 | 38.2 |
| S3 | Proportionality constant of disease-stimulated IL-6 mRNA and protein | 0.00332 | 5.33 |
| IL-6P0 (pmol mg_protein−1) | IL-6 protein baseline | 0.00116 | FIXED |
CV %, coefficient of variation.
Dynamics of the bone remodeling system
The predicted profiles of ROB, AOB, and AOC under healthy and CIA conditions are presented in Figure4. In healthy animals, ROB, AOB, and AOC are at homeostasis and the model predictions showed that the profiles of the three components remained flat throughout the study period. Under the arthritic conditions, the simulations indicated that both ROB and AOB gradually declined and reached new steady states, whereas AOC demonstrated a rise and fall profile similar to IL-6.
Figure 4.
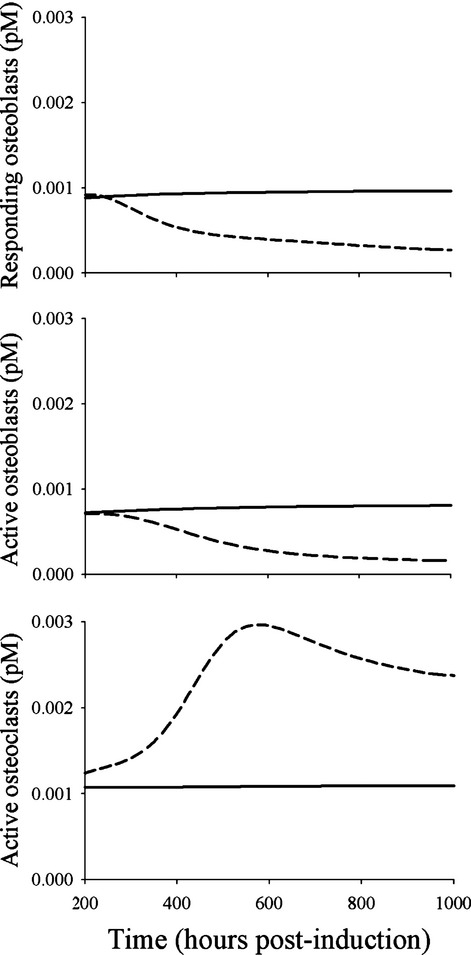
Model predicted concentration-time profiles of responding osteoblasts, active osteoblasts, and active osteoclasts under healthy (solid lines) and CIA disease (long dashed lines) conditions. CIA, collagen-induced arthritic.
Figure5 shows the disease progression and PD of DEX for RANKL and OPG proteins. The profile of RANKL disease progression in CIA rats exhibited a similar pattern to IL-6, where it rose around day 14 (336 h) post-induction, peaked at around day 21 (504 h), and then gradually declined. Analysis of AUEC showed that RANKL was significantly higher in CIA rats (4.10 pmol mg_protein−1 h) than in healthy rats (1.25 pmol mg_protein−1 h). DEX rapidly decreased RANKL expression after administration, and there was a small rebound of RANKL concentration after dosing ceased. Chronic DEX caused a sustained suppression of RANKL during the dosing period, and the reduction caused RANKL to drop below the baseline concentration (as shown in Fig.5). Postdose AUECs of RANKL were 1.86, 1.63, and 1.19 pmol mg−1 protein−1 h after single 0.225 mg kg−1, single 2.25 mg kg−1, and chronic 0.225 mg kg−1 DEX, and statistical analyses showed that these are all significantly lower than CIA control rats. The AUEC values also differed among all the treatment groups.
Figure 5.
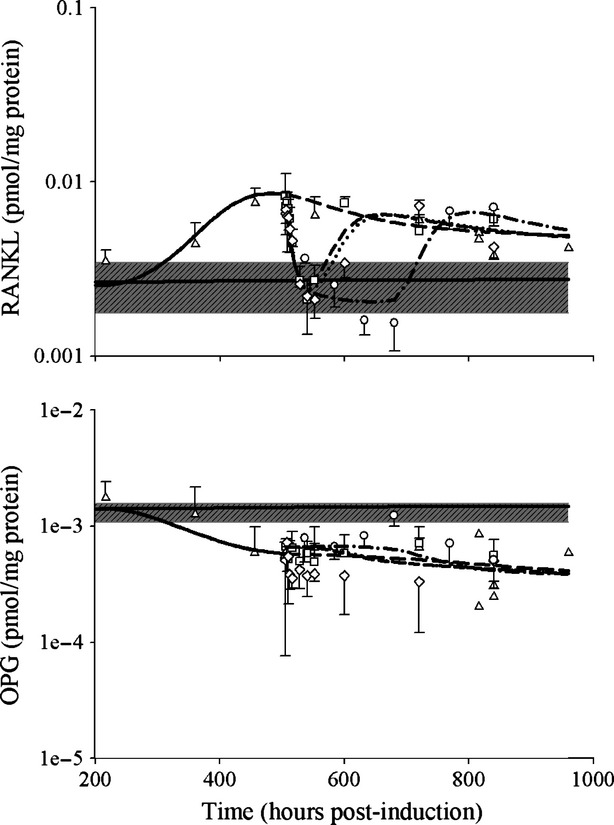
Disease progression and PD of DEX for RANKL and OPG protein concentrations in CIA rats. The gray areas indicate the range of baseline concentrations (mean ± SD) in healthy animals. Symbols and lines depict data from CIA control (∆, long dashed line), CIA receiving single 0.225 mg kg−1 dose (□, short dashed line), CIA receiving single 2.25 mg kg−1 dose (◊, dotted line), and CIA receiving chronic doses of 0.225 mg kg−1 groups (○, long dashed-dotted line). CIA, collagen-induced arthritic; DEX, dexamethasone; PD, pharmacodynamic; OPG, osteoprotegerin.
OPG, as a decoy receptor of RANKL, showed an opposite profile compared to RANKL after CIA induction. At around the time (day 14 post-induction) that concentrations of cytokines and RANKL began to rise, OPG started to drop and then reached a new steady state around day 21 (504 h). This decrease is statistically significant with AUECs of 0.833 and 0.552 pmol mg_protein−1 h for healthy and CIA rats. The effects of DEX on OPG disease progression appeared to be modest and no significant difference was revealed when comparing the AUEC of the CIA control rats with any of the dosing groups. However, there seemed to be a slightly increasing trend observed in the chronic dosing group (Fig.5).
The parameter estimates of the system are listed in Table2. All fixed parameters were adapted from the Lemaire model. The two parameters reflecting the activity of osteoblasts and osteoclasts that were estimated are Kd (dissociation rate constant of the RANKL-OPG complex) as 1.21 × 10−4 pmol mg_protein−1 and DC (differentiation rate of osteoclast precursors) as 0.0757 pmol L−1 h−1. The estimate for the production rate constant of RANKL (kinR) was 46.5 pmol mg_protein−1 h−1 pmol L−1 and was 0.0224 pmol mg_protein−1 h−1 pmol L−1 for OPG (kinO). Estimates of Smax revealed that IL-1β (4.57) had a stronger effect on the production of RANKL than TNF-α (0.00554). The effect of IL-6 (0.0599) on the stimulation of osteoclasts was higher than both TNF-α (0.0231) and IL-1β (0.0198). Estimates of IC50 and SC50 suggested that all three cytokines had sensitive effects on osteoclasts. The SC50 of TNF-α on osteoclasts was 0.00425 pmol mg_RNA−1, which is lower than its effect on osteoblasts (IC50 = 0.0138 pmol mg_RNA−1) and on RANKL (SC50 = 0.0659 pmol mg_RNA−1). The stimulation of IL-1β on osteoclasts (SC50 = 7.20 × 10−4 pmol mg_protein−1) was more sensitive than its effect on RANKL (SC50 = 0.0137 pmol mg_protein−1). The sensitivity of IL-6 on osteoclasts was 7.02 × 10−4 pmol mg_protein−1, which is also much lower than its sensitivity on OPG inhibition (IC50 = 0.0294 pmol mg_protein−1).
Table 2.
Model parameter estimates for the bone remodeling system
| Parameter (Units) | Definition | Estimate | CV % |
|---|---|---|---|
| DR (pmol L−1h−1) | Differentiation rate of osteoblast progenitors | 2.92 × 10−5 | FIXED |
| f0 | Fixed proportion | 0.05 | FIXED |
| AOCs (pmol L−1) | Value of C to get half differentiation flux | 5 × 10−3 | FIXED |
| dB (h−1) | Differentiation rate of responding osteoblasts | 0.0292 | FIXED |
| kB (h−1) | Elimination rate of active osteoblasts | 7.88 × 10−3 | FIXED |
| k3 (pmol L−1 h−1) | Rate of RANK-RANKL binding | 2.42 × 10−5 | FIXED |
| k4 (h−1) | Rate of RANK-RANKL dissociation | 7.08 × 10−4 | FIXED |
| kO (h−1) | Elimination rate of OPG | 0.0146 | FIXED |
| DA (h−1) | Osteoclast apoptosis rate due to TGF-β | 0.0292 | FIXED |
| K (pmol L−1) | Concentration of RANK | 10 | FIXED |
| ROB0 (pmol L−1) | Responding osteoblast baseline | 7.73 × 10−4 | FIXED |
| AOB0 (pmol L−1) | Active osteoblast baseline | 7.28 × 10−4 | FIXED |
| AOC0 (pmol L−1) | Active osteoclast baseline | 9.13 × 10−4 | FIXED |
| kinL (pmol mg_protein−1 h−1 pmol L−1) | Production rate constant of RANKL | 46.5 | 73.8 |
| Kd (pmol mg_protein−1) | Dissociation rate constant of RANKL-OPG | 1.21 × 10−4 | 76.4 |
| kinO (pmol mg_protein−1 h−1 pmol L−1) | Production rate constant of OPG | 0.0224 | 29.0 |
| DC (pmol L−1 h−1) | Differentiation rate of osteoclast precursors | 0.0757 | 41.7 |
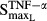 |
Stimulation of RANKL via TNF | 0.0554 | 130 |
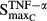 |
Stimulation of osteoclasts via TNF | 0.0231 | 327 |
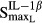 |
Stimulation of RANKL via IL-1β | 4.57 | 28.9 |
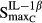 |
Stimulation of osteoclasts via IL-1β | 0.0198 | 122 |
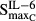 |
Stimulation of osteoclasts via IL-6 | 0.0599 | 252 |
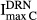 |
Inhibition of osteoclasts by DRN | 0.423 | 46.0 |
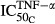 (pmol mg_RNA−1) (pmol mg_RNA−1) |
Sensitivity of TNF inhibition on osteoblasts | 0.0138 | 45.7 |
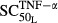 (pmol mg_RNA−1) (pmol mg_RNA−1) |
Sensitivity of TNF stimulation on RANKL | 0.0659 | 234 |
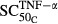 (pmol mg_RNA-1) (pmol mg_RNA-1) |
Sensitivity of TNF stimulation on osteoclasts | 0.00425 | 485 |
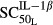 (pmol mg_protein−1) (pmol mg_protein−1) |
Sensitivity of IL-1β stimulation on RANKL | 0.0137 | 49.6 |
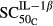 (pmol mg_protein−1) (pmol mg_protein−1) |
Sensitivity of IL-1β stimulation on osteoclasts | 7.20 × 10−4 | 280 |
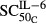 (pmol mg_protein−1) (pmol mg_protein−1) |
Sensitivity of IL-6 stimulation on osteoclasts | 7.02 × 10−4 | 77.8 |
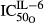 (pmol mg_protein−1) (pmol mg_protein−1) |
Sensitivity of IL-6 inhibition on OPG | 0.0294 | 82.5 |
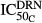 (nmol L−1) (nmol L−1) |
Sensitivity of DRN inhibition on osteoclasts | 5.49 × 10−7 | 310 |
CV %, coefficient of variation; RANKL, receptor activator of nuclear factor kappa-B ligand; OPG, osteoprotegerin.
Dynamics of TRACP-5b
Concentration-time profiles, the TRACP-5b, and predicted profiles of active osteoclasts (AOC) after DEX dosing are shown in Figure6. Disease progression of TRACP-5b after CIA induction exhibited a profile similar to that of RANKL or IL-6 and had the typical pattern of delay, rise to peak, and then fall off (Fig.6). Statistical analysis indicated that the AUEC of TRACP-5b expression in CIA rats (1444 U g_protein−1·h) was significantly higher than in healthy rats (356 U g_protein−1·h). DEX dosing effectively decreased TRACP-5b concentrations, and all DEX dosing groups had a significantly lower AUEC (608, 433, and 527 U g_protein−1·h after single 0.225 mg kg−1, single 2.25 mg kg−1, and chronic 0.225 mg kg−1 doses) than the CIA control rats after drug administration at day 21. No differences were revealed among the DEX dosing groups.
Figure 6.
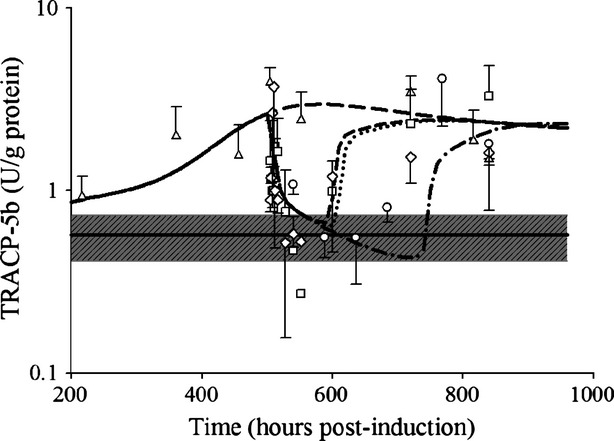
Disease progression and PD of DEX for TRACP-5b in CIA rats. The closed circles (●) depict healthy animals. The gray area indicates the range of baseline concentrations (mean ± SD) in healthy animals. Symbols and lines depict data from CIA control (∆, long dashed line), CIA receiving single 0.225 mg kg−1 dose (□, short dashed line), CIA receiving single 2.25 mg kg−1 dose (◊, dotted line), and CIA receiving chronic doses of 0.225 mg kg−1 groups (○, long dashed-dotted line). CIA, collagen-induced arthritic; DEX, dexamethasone; PD, pharmacodynamic; TRACP-5b, tartrate-resistant acid phosphatase 5b.
Since TRACP-5b is a marker of bone resorption, it was of interest to compare its progression with that of the bone-resorbing osteoclasts. The proposed model assumed that DEX not only affected the apoptosis of osteoclasts (i.e. 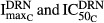 ), but also inhibited their activity(i.e.
), but also inhibited their activity(i.e. 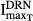 and
and 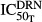 ) and hence decreased the production of TRACP-5b. Model fittings (Fig.6) indicated that the model well captured the rapid drop of TRACP-5b concentrations after DEX, reflecting the suitability of this model to explain the PD of DEX on TRACP-5b disease progression. The parameter estimates are listed in Table3. All parameters were estimated with good precision (low CV %). The maximum inhibition on TRACP-5b production by DEX (
) and hence decreased the production of TRACP-5b. Model fittings (Fig.6) indicated that the model well captured the rapid drop of TRACP-5b concentrations after DEX, reflecting the suitability of this model to explain the PD of DEX on TRACP-5b disease progression. The parameter estimates are listed in Table3. All parameters were estimated with good precision (low CV %). The maximum inhibition on TRACP-5b production by DEX (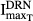 ) was estimated to be 67.8%, with
) was estimated to be 67.8%, with 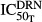 of 31.1 nmol L−1.
of 31.1 nmol L−1.
Table 3.
Model parameter estimates for the dynamics of TRACP-5b
| Parameter (Units) | Definition | Estimate | CV % |
|---|---|---|---|
| kinT (U L−1 h−1) | Synthesis rate constant for TRACP-5b | 0.0918 | 34.6 |
| TRACP-5β0 (U L−1) | TRACP-5b baseline | 0.570 | FIXED |
| γc | Amplification factor of osteoclasts on TRACP-5b | 1.38 | 4.31 |
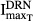 |
Inhibition of TRACP-5b by DRN | 0.678 | 22.0 |
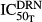 (nmol L−1) (nmol L−1) |
Sensitivity constant of DRN inhibition on TRACP-5b | 31.1 | 8.29 |
| γDT | Hill function of the DRN inhibition on TRACP-5b | 10 | FIXED |
CV %, coefficient of variation; TRACP-5b, tartrate-resistant acid phosphatase 5b.
Dynamics of bone mineral density
The profiles of BMD in the five bone areas (lumbar vertebrate 1–4, total femur, diaphyseal femur, metaphyseal femur, and epiphyseal femur) are shown in Figure7. In healthy rats, there were gradual increases in BMD of all five bone regions during the experiment period, and the logistic model well captured these behaviors. In CIA rats, bone loss began at around 420 h after disease induction, and BMD stayed low throughout the rest of experiment. DEX chronic dosing at 0.225 mg kg−1 did not seem to have strong protective effects against bone loss, and in most cases the profiles after DEX largely overlap with the natural disease progression profiles. By linking the bone formation process with the osteoblasts and the bone breakdown process with the osteoclasts, our proposed model could reasonably describe the BMD during disease progression and DEX effects in all five bone regions. Parameter estimates (in Table4) showed that kin values for all bone regions have small values (about 1 × 10−4 g cm−2 h−1), reflecting the slow bone turnover process. The AOB and AOC appeared to have various degrees of contribution toward the five bone regions, which are reasonable considering the differences in their bone compositions. It is also interesting that the estimates of the amplification factors (γBLR = 0.170 and γCLR = 0.0542) for lumbar vertebrate 1-4 (LR) are surprisingly close to the values reported by Peterson and Riggs for lumbar spine (γOB = 0.0739 and γOC = 0.0679) (Peterson and Riggs 2012).
Figure 7.
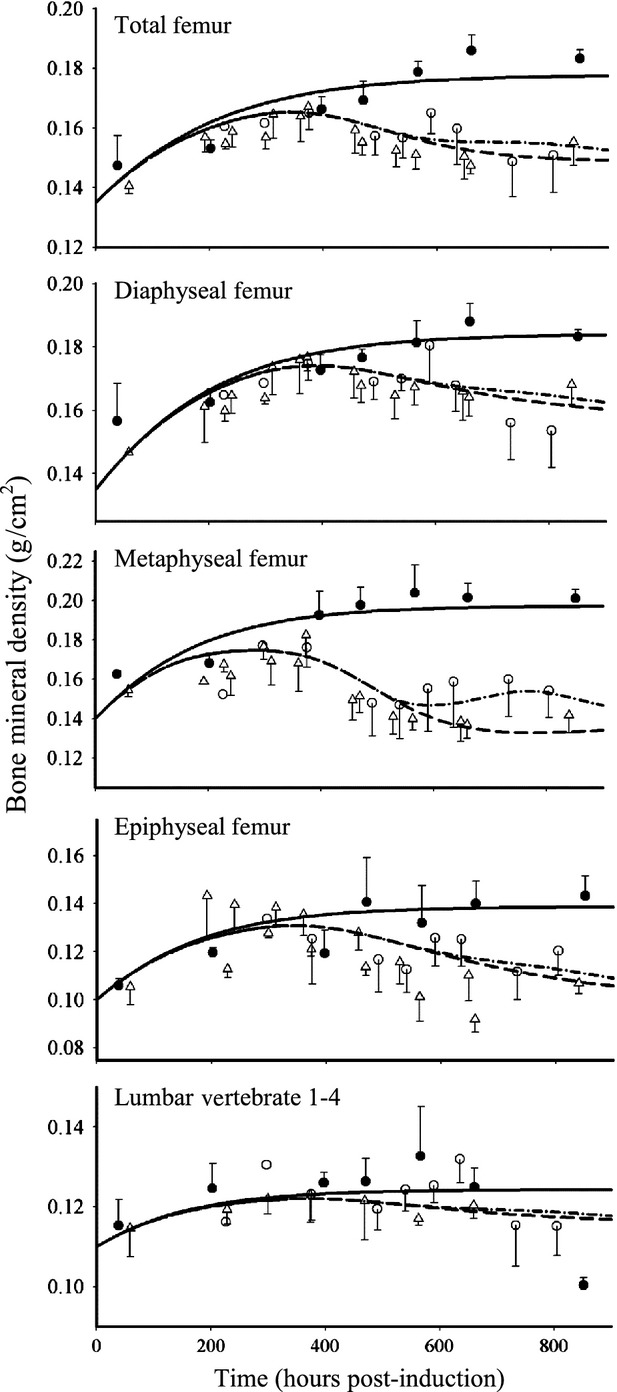
Profiles of BMD in different bone regions in healthy (●) and CIA rats. Symbols depict data from CIA control (∆) and CIA rats receiving chronic doses of 0.225 mg kg−1 DEX (○). Lines depict model predictions in corresponding groups. BMD, bone mineral density; CIA, collagen-induced arthritic; DEX, dexamethasone; RANKL, receptor activator of nuclear factor kappa-B ligand.
Table 4.
Model parameter estimates for bone mineral density
| Parameter (Units) | Definition | Estimate | CV % |
|---|---|---|---|
| kgrow (g cm−2 h−1) | Natural growth rate of BMD | 5.43 × 10−3 | 15.8 |
| L0 (g cm−2) | Lumbar vertebrate 1–4 initial BMD | 0.110 | FIXED |
| TF0 (g cm−2) | Total femur initial BMD | 0.135 | FIXED |
| DF0 (g cm−2) | Diaphyseal femur initial BMD | 0.135 | FIXED |
| MF0 (g cm−2) | Metaphyseal femur initial BMD | 0.140 | FIXED |
| EF0 (g cm−2) | Epiphyseal femur initial BMD | 0.100 | FIXED |
| LRss (g cm−2) | Lumbar vertebrate 1–4 steady-state BMD | 0.129 | 12.4 |
| TFss (g cm−2) | Total femur steady-state BMD | 0.183 | 2.82 |
| DFss (g cm−2) | Diaphyseal femur steady-state BMD | 0.195 | 7.13 |
| MFss (g cm−2) | Metaphyseal femur steady-state BMD | 0.233 | 13.9 |
| EFss (g cm−2) | Epiphyseal femur steady-state BMD | 0.162 | 20.9 |
| kinLR (g cm−2 h−1) | Production rate constant of lumbar vertebrate 1–4 BMD | 1.98 × 10−4 | 360 |
| kinTF (g cm−2 h−1) | Production rate constant of total femur BMD | 8.24 × 10−5 | 80.1 |
| kinDF (g cm−2 h−1) | Production rate constant of diaphyseal femur BMD | 1.54 × 10−4 | 124 |
| kinMF (g cm−2 h−1) | Production rate constant of metaphyseal femur BMD | 4.05 × 10−4 | 68.4 |
| kinEF (g cm−2 h−1) | Production rate constant of epiphyseal femur BMD | 2.83 × 10−4 | 126 |
| γBLR | Amplification factor of osteoblast on lumbar vertebrate | 0.170 | 437 |
| γBTF | Amplification factor of osteoblast on total femur | 3.19 | 151 |
| γBDF | Amplification factor of osteoblast on diaphyseal femur | 1.02 | 293 |
| γBMF | Amplification factor of osteoblast on metaphyseal femur | 0.00643 | 37.3 |
| γBEF | Amplification factor of osteoblast on epiphyseal femur | 0.746 | 232 |
| γCLR | Amplification factor of osteoclast on lumbar vertebrate | 0.0542 | 480 |
| γCTF | Amplification factor of osteoclast on total femur | 0.528 | 136 |
| γCDF | Amplification factor of osteoclast on diaphyseal femur | 0.119 | 259 |
| γCMF | Amplification factor of osteoclast on metaphyseal femur | 0.588 | 46.0 |
| γCEF | Amplification factor of osteoclast on epiphyseal femur | 0.0827 | 225 |
CV %, coefficient of variation.
Discussion
In this study, we aimed to incorporate as many biomarkers as possible in order to construct a more comprehensive model for RA. We also attempted to measure TNF-α protein, but it could not be detected in the paws of either healthy or CIA rats. This is consistent with findings in a previous study (Stolina et al. 2008). The joint damage caused by TNF-α may be further mediated by IL-1 (Zwerina et al. 2007), where IL-1 augments the TNF-α-activated RANKL up-regulation (Walsh et al. 2005; Karmakar et al. 2010). Our model seemed to support these findings. The estimated sensitivity constants for RANKL induction were 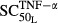 = 0.0659 pmol mg_RNA−1 (4.40-fold from the baseline value 0.0150 pmol mg_RNA−1) for TNF-α, and
= 0.0659 pmol mg_RNA−1 (4.40-fold from the baseline value 0.0150 pmol mg_RNA−1) for TNF-α, and 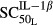 = 0.0137 pmol mg_protein−1 (10.6-fold from the baseline value 0.00129 pmol mg_protein−1) for IL-1β. This indicated that TNF-α responded to RANKL activation faster than IL-1β. Our results also showed that the maximum effects on RANKL induction by TNF-α (
= 0.0137 pmol mg_protein−1 (10.6-fold from the baseline value 0.00129 pmol mg_protein−1) for IL-1β. This indicated that TNF-α responded to RANKL activation faster than IL-1β. Our results also showed that the maximum effects on RANKL induction by TNF-α (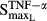 ) and IL-1β (
) and IL-1β (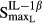 ) were 0.0554 and 4.57, which is consistent with the findings that IL-1β was the main mediator for RANKL induction.
) were 0.0554 and 4.57, which is consistent with the findings that IL-1β was the main mediator for RANKL induction.
TNF-α appeared to be the most sensitive in its stimulation of osteoclast production (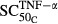 = 0.00425 pmol mg_RNA−1) compared with its effects on osteoblasts (
= 0.00425 pmol mg_RNA−1) compared with its effects on osteoblasts (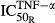 = 0.0138 pmol mg_RNA−1) and RANKL (
= 0.0138 pmol mg_RNA−1) and RANKL (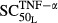 = 0.0659 pmol mg_RNA−1), and this is true for both IL-1β and IL-6 as well. These results suggest that the immune cascade in RA primarily affects osteoclasts in the regulation of bone loss and emphasizes the importance of osteoclasts. Other studies also found that osteoclasts are the primary driver for bone loss in RA, whereas osteoblasts indirectly modulate the process (Walsh et al. 2005; Karmakar et al. 2010).
= 0.0659 pmol mg_RNA−1), and this is true for both IL-1β and IL-6 as well. These results suggest that the immune cascade in RA primarily affects osteoclasts in the regulation of bone loss and emphasizes the importance of osteoclasts. Other studies also found that osteoclasts are the primary driver for bone loss in RA, whereas osteoblasts indirectly modulate the process (Walsh et al. 2005; Karmakar et al. 2010).
The disease progression of IL-1β and IL-6 proteins appeared consistent with previous studies (Stolina et al. 2008). It also appeared that their protein concentrations corresponded well with the mRNA profiles, which is consistent with the findings in a CIA mouse model (Rioja et al. 2004). The PD effects of DEX on IL-1β and IL-6 proteins resembled observations of their mRNA profiles, and such relationships allowed the use of a simple proportionality constant to link the mRNA and protein profiles. These suggested that IL-1β and IL-6 mRNAs are good surrogates for assessing the dynamics of their protein concentrations in CIA rats, and the assumptions which the Earp model applied were valid.
The disease progression profiles of RANKL and OPG in CIA rat paws agreed with previous findings, where the two progressed in the opposite direction and then reached the steady state as time proceeded (Stolina et al. 2008). In our study, RANKL:OPG ratios in CIA rats increased over time and remained elevated at the end of the study, which suggested the presence of active bone resorption. Our model assumptions about the cytokine regulation of RANKL, OPG, osteoblasts, and osteoclasts were all obtained from the literature, and the modeling results revealed that connecting these mechanisms together can adequately explain the progression of RANKL and OPG in RA and, surprisingly, also capture the PD effects of DEX dosing.
Our results regarding the disease progression profile of TRACP-5b confirmed the previous findings that TRACP-5b is significantly raised after disease onset slightly later than RANKL (Stolina et al. 2005). It was suggested that secreted TRACP-5b represents the number of osteoclasts (Alatalo et al. 2004; Rissanen et al. 2008). Thus, in our model, we first attempted to link the ratio changes of the AOC compartment directly to TRACP-5b, and it functioned well in describing its disease progression. However, DEX caused a much faster drop in TRACP-5b concentrations than in the simulated AOC compartment, which suggested there may be undescribed inhibitory pathways. The inhibition described by Kim et al. regarding the DEX effect on osteoclast function was then applied to fit the data (Kim et al. 2006), and it appeared to capture the profiles of TRACP-5b well.
By incorporating the ratio changes of AOB and AOC into the formation and elimination processes of bone turnover, our modeling well captured CIA disease progression and DEX PD profiles of the BMD in all five bone regions. Although DEX could effectively suppress cytokine expressions, it appeared that it only had modest effects on BMD. This is likely because DEX can simultaneously modulate the activity of osteoblasts and osteoclasts, and it can shift the balance in both directions. This bidirectional nature is the reason why dosages and dosing regimens are critical for DEX monotherapy, and dose optimization is important for DEX therapy to attain therapeutic benefits and prevent bone loss.
We performed simulations to predict scenarios where individual mediators (IL-1β, IL-6, or RANKL) are completely inhibited (Fig.8). The effect of inhibition of IL-1β or RANKL seems to be similar, resulting in comparable degree of improvement in the BMD profiles and RANKL:OPG ratios. On the contrary, inhibition of IL-6 appears to be the least effective in obviating bone loss. It was shown that tocilizumab (anti-IL-6 antibody) may induce OPG expression but not RANKL (Kanbe et al. 2012). Although this matches our model predictions, it is important to consider that the efficacy of anti-IL-6 therapy against bone loss may be related to the Wnt signaling pathway (Corrado et al. 2013), which was not included in our model. The efficacy of tocilizumab toward bone loss is likely to be resulted from both mechanisms.
Figure 8.
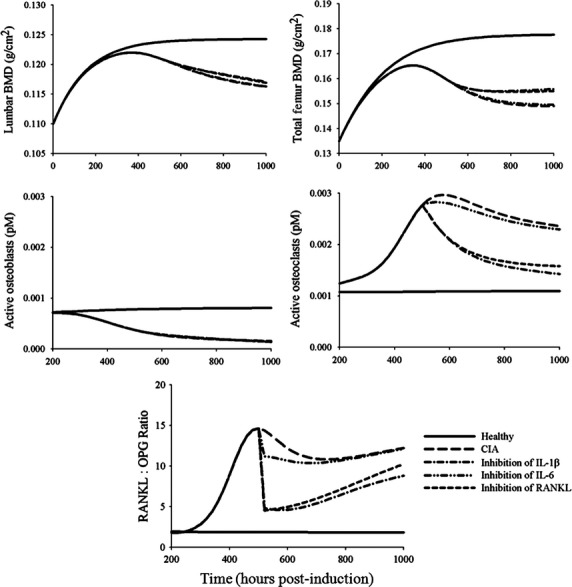
Model predictions of time profiles of lumbar BMD, total femur BMD, active osteoblasts, active osteoclasts, and the RANKL:OPG ratios under different potential therapeutic approaches. Therapeutic interventions were assumed to start at 504 h (21 days) post-induction and continue to 1000 h. Solid and long-dashed lines depict the profiles in healthy and CIA rats. Lines show profiles under complete inhibition of indicated agents. BMD, bone mineral density; CIA, collagen-induced arthritic; RANKL, receptor activator of nuclear factor kappa-B ligand; OPG, osteoprotegerin.
It should be noted that there are limitations in our model. One caveat is that some assumptions may be oversimplified. An example is that simple additive relationships were assumed for processes where several mediators simultaneously come into effect. This might not be true considering the tight regulations among the cytokines. For instance, TNF-α and IL-1 may be synergistic for their induction of RANKL (Wei et al. 2005). Another point to keep in mind is the exclusion of other RA pathological pathways or signals in our model. We assumed that effects of hormones PTH and TGF-β on bone were minimal compared with cytokines in RA, and this is because most reports emphasize the roles of cytokines and there have been controversies regarding the roles of PTH (Af Ekenstam et al. 1990; Rossini et al. 2011) and TGF-β (Lorenzo et al. 2008; Rico et al. 2010) in RA. There is also evidence that others pathways, such as the Wnt signaling pathway and the IL-17 cytokine family, are critical in RA but were not described in our model. Owing to the model complexity, making such assumptions is essential to describe our experimental data together.
To fully appreciate the interplay between these cytokines, biomarkers, and the bone turnover process, disease progression and dynamic profiles of all involved mediators under the condition where only one single component is in effect or inhibited (for example, by the use of specific inhibitors such as TNF-α, IL-1, IL-6, or RANKL antagonists) would be necessary. This type of information is essential for better assessment of the interactions between different mediators, in the same manner that PK/PD information for the individual drugs is required in drug–drug interaction studies. Incorporation of other signaling pathways is critical for better understanding of the entire mechanisms governing RA and bone destruction. Subsequent studies may be designed and help in resolving these relationships.
Conclusions
A mechanism-based systems model is developed to describe the immune pathways involved in bone destruction during disease progression in CIA rats. The interplay between GR, proinflammatory cytokines (TNF-α, IL-1β, IL-6), RANK/RANKL/OPG system, and BMD is characterized. The disease progressions of RANKL, OPG, TRACP-5b, and BMD are shown to be controlled by the disease progressions of cytokines and endogenous CST. DEX suppresses the expressions of cytokines and RANKL after dosing and subsequently modulates the activities of bone-forming osteoblasts and bone-resorbing osteoclasts. Although the model only describes a simple version of probable bone remodeling processes and there are probably other crucial pathways that may require consideration, it allows the characterization of all measured biomarkers under CIA disease progression and the intervention of DEX. Future experiments may be conducted to study the crosstalk between the cytokines, the RANK/RANKL/OPG system, and other mediators such as the Wnt signaling family, PTH, and calcium and investigate how they function on the bone remodeling process in RA.
Acknowledgments
This work was supported by funding from NIH Grant GM 24211 and a fellowship for Lon from Amgen, Inc. We thank Marina Stolina from Amgen, Inc. for sharing the protocol for paw homogenate preparation, and Yanlin Wang for her technical support in the animal experiments.
Glossary
- (IL)-1β
interleukin-one-beta
- AOB
active osteoblasts
- AOC
active osteoclasts
- AUEC
area under the effect curves
- BCA
bicinchoninic acid
- BMD
bone mineral density
- CIA
collagen-induced arthritic
- COX
cyclooxygenase
- CST
corticosterone
- DEX
dexamethasone
- DF
diaphyseal femur
- EDTA
ethylenediaminetetraacetic acid
- EF
epiphyseal femur
- ELISA
enzyme-linked immunosorbent assays
- GR
glucocorticoid receptor
- IL-6
interleukin-six
- LR
lumbar vertebrae
- M-CSF
macrophage-colony-stimulating factor
- MF
metaphyseal femur
- MMPs
metalloproteinases
- mRNA
messenger ribonucleic acid
- OPG
osteoprotegerin
- PD
pharmacodynamic
- PGE2
prostaglandin E2
- PK
pharmacokinetic
- PTH
parathyroid hormone
- QC
quality control
- RANKL
receptor activator of nuclear factor kappa-B ligand
- RANK
receptor activator of nuclear factor kappa-B
- RA
rheumatoid arthritis
- ROB
responding osteoblasts
- SC
subcutaneous
- TGF-β
transforming growth factor-β
- TF
total femur
- TNF-α
tumor necrosis factor-alpha
- TRACP-5b
tartrate-resistant acid phosphatase 5b
Author Contributions
Participated in research design: Lon, DuBois, Earp, Almon, Jusko. Conducted experiments: Lon, DuBois, Earp. Performed data analysis: Lon, Earp. Wrote or contributed to the writing of the manuscript: Lon, DuBois, Earp, Almon, Jusko.
Disclosure
None declared.
Supporting Information
Additional Supporting Information may be found in the online version of this article:
Data S1. Derivations of equations 7-9.
References
- Af Ekenstam E, Benson L, Hallgren R, Wide L, Ljunghall S. Impaired secretion of parathyroid hormone in patients with rheumatoid arthritis: relationship to inflammatory activity. Clin Endocrinol. 1990;32:323–328. doi: 10.1111/j.1365-2265.1990.tb00873.x. [DOI] [PubMed] [Google Scholar]
- Alatalo SL, Ivaska KK, Waguespack SG, Econs MJ, Vaananen HK, Halleen JM. Osteoclast-derived serum tartrate-resistant acid phosphatase 5b in Albers-Schonberg disease (type II autosomal dominant osteopetrosis) Clin Chem. 2004;50:883–890. doi: 10.1373/clinchem.2003.029355. [DOI] [PubMed] [Google Scholar]
- Auphan N, DiDonato JA, Rosette C, Helmberg A, Karin M. Immunosuppression by glucocorticoids: inhibition of NF-kappa B activity through induction of I kappa B synthesis. Science. 1995;270:286–290. doi: 10.1126/science.270.5234.286. [DOI] [PubMed] [Google Scholar]
- Bailer AJ. Testing for the equality of area under the curves when using destructive measurement techniques. J Pharmacokinet Biopharm. 1988;16:303–309. doi: 10.1007/BF01062139. [DOI] [PubMed] [Google Scholar]
- Braun T, Zwerina J. Positive regulators of osteoclastogenesis and bone resorption in rheumatoid arthritis. Arthritis Res Ther. 2011;13:235. doi: 10.1186/ar3380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choy EH, Panayi GS. Cytokine pathways and joint inflammation in rheumatoid arthritis. N Engl J Med. 2001;344:907–916. doi: 10.1056/NEJM200103223441207. [DOI] [PubMed] [Google Scholar]
- Cooper C, Coupland C, Mitchell M. Rheumatoid arthritis, corticosteroid therapy and hip fracture. Ann Rheum Dis. 1995;54:49–52. doi: 10.1136/ard.54.1.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corrado A, Neve A, Maruotti N, Cantatore FP. Bone effects of biologic drugs in rheumatoid arthritis. Clin Dev Immunol. 2013;2013:945945. doi: 10.1155/2013/945945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D'Argenio DZ, Schumitzky A, Wang X. ADAPT 5 user's guide: pharmacokinetic/pharmacodynamic systems analysis software. Los Angeles: Biomedical Simulations Resource; 2009. [Google Scholar]
- Earp JC, Dubois DC, Molano DS, Pyszczynski NA, Almon RR, Jusko WJ. Modeling corticosteroid effects in a rat model of rheumatoid arthritis II: Mechanistic pharmacodynamic model for dexamethasone effects in Lewis rats with collagen-induced arthritis. J Pharmacol Exp Ther. 2008a;326:546–554. doi: 10.1124/jpet.108.137414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Earp JC, Dubois DC, Molano DS, Pyszczynski NA, Keller CE, Almon RR. Modeling corticosteroid effects in a rat model of rheumatoid arthritis I: mechanistic disease progression model for the time course of collagen-induced arthritis in Lewis rats. J Pharmacol Exp Ther. 2008b;326:532–545. doi: 10.1124/jpet.108.137372. , et al. ( [DOI] [PMC free article] [PubMed] [Google Scholar]
- Earp JC, Pyszczynski NA, Molano DS, Jusko WJ. Pharmacokinetics of dexamethasone in a rat model of rheumatoid arthritis. Biopharm Drug Dispos. 2008c;29:366–372. doi: 10.1002/bdd.626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Earp JC, Dubois DC, Almon RR, Jusko WJ. Quantitative dynamic models of arthritis progression in the rat. Pharm Res. 2009;26:196–203. doi: 10.1007/s11095-008-9711-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert L, He X, Farmer P, Boden S, Kozlowski M, Rubin J. Inhibition of osteoblast differentiation by tumor necrosis factor-alpha. Endocrinology. 2000;141:3956–3964. doi: 10.1210/endo.141.11.7739. , et al. ( [DOI] [PubMed] [Google Scholar]
- Goldring SR. Bone and joint destruction in rheumatoid arthritis: what is really happening? J Rheumatol Suppl. 2002;65:44–48. [PubMed] [Google Scholar]
- Halleen JM, Alatalo SL, Suominen H, Cheng S, Janckila AJ, Vaananen HK. Tartrate-resistant acid phosphatase 5b: a novel serum marker of bone resorption. J Bone Miner Res. 2000;15:1337–1345. doi: 10.1359/jbmr.2000.15.7.1337. [DOI] [PubMed] [Google Scholar]
- Hashizume M, Hayakawa N, Mihara M. IL-6 trans-signalling directly induces RANKL on fibroblast-like synovial cells and is involved in RANKL induction by TNF-alpha and IL-17. Rheumatology (Oxford) 2008;47:1635–1640. doi: 10.1093/rheumatology/ken363. [DOI] [PubMed] [Google Scholar]
- Institute of Laboratory Animal Resources. Guide for the Care and Use of Laboratory Animals. 7th ed. Commission on Life Sciences, National Research Council, Washington DC: Institute of Laboratory Animal Resources; 1996. [Google Scholar]
- Jimi E, Nakamura I, Duong LT, Ikebe T, Takahashi N, Rodan GA. Interleukin 1 induces multinucleation and bone-resorbing activity of osteoclasts in the absence of osteoblasts/stromal cells. Exp Cell Res. 1999;247:84–93. doi: 10.1006/excr.1998.4320. , et al. ( [DOI] [PubMed] [Google Scholar]
- Kanbe K, Nakamura A, Inoue Y, Hobo K. Osteoprotegerin expression in bone marrow by treatment with tocilizumab in rheumatoid arthritis. Rheumatol Int. 2012;32:2669–2674. doi: 10.1007/s00296-011-2021-9. [DOI] [PubMed] [Google Scholar]
- Karmakar S, Kay J, Gravallese EM. Bone damage in rheumatoid arthritis: mechanistic insights and approaches to prevention. Rheum Dis Clin North Am. 2010;36:385–404. doi: 10.1016/j.rdc.2010.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim HJ, Zhao H, Kitaura H, Bhattacharyya S, Brewer JA, Muglia LJ. Glucocorticoids suppress bone formation via the osteoclast. J Clin Invest. 2006;116:2152–2160. doi: 10.1172/JCI28084. , et al. ( [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klareskog L, Catrina AI, Paget S. Rheumatoid arthritis. Lancet. 2009;373:659–672. doi: 10.1016/S0140-6736(09)60008-8. [DOI] [PubMed] [Google Scholar]
- Kobayashi K, Takahashi N, Jimi E, Udagawa N, Takami M, Kotake S. Tumor necrosis factor alpha stimulates osteoclast differentiation by a mechanism independent of the ODF/RANKL-RANK interaction. J Exp Med. 2000;191:275–286. doi: 10.1084/jem.191.2.275. , et al. ( [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kudo O, Sabokbar A, Pocock A, Itonaga I, Fujikawa Y, Athanasou NA. Interleukin-6 and interleukin-11 support human osteoclast formation by a RANKL-independent mechanism. Bone. 2003;32:1–7. doi: 10.1016/s8756-3282(02)00915-8. [DOI] [PubMed] [Google Scholar]
- Lam J, Takeshita S, Barker JE, Kanagawa O, Ross FP, Teitelbaum SL. TNF-alpha induces osteoclastogenesis by direct stimulation of macrophages exposed to permissive levels of RANK ligand. J Clin Invest. 2000;106:1481–1488. doi: 10.1172/JCI11176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemaire V, Tobin FL, Greller LD, Cho CR, Suva LJ. Modeling the interactions between osteoblast and osteoclast activities in bone remodeling. J Theor Biol. 2004;229:293–309. doi: 10.1016/j.jtbi.2004.03.023. [DOI] [PubMed] [Google Scholar]
- Liu XH, Kirschenbaum A, Yao S, Levine AC. Cross-talk between the interleukin-6 and prostaglandin E(2) signaling systems results in enhancement of osteoclastogenesis through effects on the osteoprotegerin/receptor activator of nuclear factor-{kappa}B (RANK) ligand/RANK system. Endocrinology. 2005;146:1991–1998. doi: 10.1210/en.2004-1167. [DOI] [PubMed] [Google Scholar]
- Liu D, Lon HK, Dubois DC, Almon RR, Jusko WJ. Population pharmacokinetic-pharmacodynamic-disease progression model for effects of anakinra in Lewis rats with collagen-induced arthritis. J Pharmacokinet Pharmacodyn. 2011;38:769–786. doi: 10.1007/s10928-011-9219-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lon HK, Liu D, Zhang Q, DuBois DC, Almon RR, Jusko WJ. Pharmacokinetic-pharmacodynamic disease progression model for effect of etanercept in Lewis rats with collagen-induced arthritis. Pharm Res. 2011;28:1622–1630. doi: 10.1007/s11095-011-0396-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenzo J, Horowitz M, Choi Y. Osteoimmunology: interactions of the bone and immune system. Endocr Rev. 2008;29:403–440. doi: 10.1210/er.2007-0038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma T, Miyanishi K, Suen A, Epstein NJ, Tomita T, Smith RL. Human interleukin-1-induced murine osteoclastogenesis is dependent on RANKL, but independent of TNF-alpha. Cytokine. 2004;26:138–144. doi: 10.1016/j.cyto.2004.02.001. , et al. ( [DOI] [PubMed] [Google Scholar]
- Nanes MS. Tumor necrosis factor-alpha: molecular and cellular mechanisms in skeletal pathology. Gene. 2003;321:1–15. doi: 10.1016/s0378-1119(03)00841-2. [DOI] [PubMed] [Google Scholar]
- Nedelman JR, Gibiansky E, Lau DT. Applying Bailer's method for AUC confidence intervals to sparse sampling. Pharm Res. 1995;12:124–128. doi: 10.1023/a:1016255124336. [DOI] [PubMed] [Google Scholar]
- Nelson CA, Warren JT, Wang MW, Teitelbaum SL, Fremont DH. RANKL employs distinct binding modes to engage RANK and the osteoprotegerin decoy receptor. Structure. 2012;20:1971–1982. doi: 10.1016/j.str.2012.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmqvist P, Persson E, Conaway HH, Lerner UH. IL-6, leukemia inhibitory factor, and oncostatin M stimulate bone resorption and regulate the expression of receptor activator of NF-kappa B ligand, osteoprotegerin, and receptor activator of NF-kappa B in mouse calvariae. J Immunol. 2002;169:3353–3362. doi: 10.4049/jimmunol.169.6.3353. [DOI] [PubMed] [Google Scholar]
- Peterson MC, Riggs MM. A physiologically based mathematical model of integrated calcium homeostasis and bone remodeling. Bone. 2010;46:49–63. doi: 10.1016/j.bone.2009.08.053. [DOI] [PubMed] [Google Scholar]
- Peterson MC, Riggs MM. Predicting nonlinear changes in bone mineral density over time using a multiscale systems pharmacology model. CPT Pharmacometrics Syst Pharmacol. 2012;1:e14. doi: 10.1038/psp.2012.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pivonka P, Zimak J, Smith DW, Gardiner BS, Dunstan CR, Sims NA. Model structure and control of bone remodeling: a theoretical study. Bone. 2008;43:249–263. doi: 10.1016/j.bone.2008.03.025. , et al. ( [DOI] [PubMed] [Google Scholar]
- Pivonka P, Zimak J, Smith DW, Gardiner BS, Dunstan CR, Sims NA. Theoretical investigation of the role of the RANK-RANKL-OPG system in bone remodeling. J Theor Biol. 2010;262:306–316. doi: 10.1016/j.jtbi.2009.09.021. , et al. ( [DOI] [PubMed] [Google Scholar]
- Post TM, Schmidt S, Peletier LA, de Greef R, Kerbusch T, Danhof M. Application of a mechanism-based disease systems model for osteoporosis to clinical data. J Pharmacokinet Pharmacodyn. 2013;40:143–156. doi: 10.1007/s10928-012-9294-9. [DOI] [PubMed] [Google Scholar]
- Rico MC, Rough JJ, Del Carpio-Cano FE, Kunapuli SP, DeLa Cadena RA. The axis of thrombospondin-1, transforming growth factor beta and connective tissue growth factor: an emerging therapeutic target in rheumatoid arthritis. Curr Vasc Pharmacol. 2010;8:338–343. doi: 10.2174/157016110791112296. [DOI] [PubMed] [Google Scholar]
- Rioja I, Bush KA, Buckton JB, Dickson MC, Life PF. Joint cytokine quantification in two rodent arthritis models: kinetics of expression, correlation of mRNA and protein levels and response to prednisolone treatment. Clin Exp Immunol. 2004;137:65–73. doi: 10.1111/j.1365-2249.2004.02499.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rissanen JP, Suominen MI, Peng Z, Halleen JM. Secreted tartrate-resistant acid phosphatase 5b is a Marker of osteoclast number in human osteoclast cultures and the rat ovariectomy model. Calcif Tissue Int. 2008;82:108–115. doi: 10.1007/s00223-007-9091-4. [DOI] [PubMed] [Google Scholar]
- Rossini M, Bagnato G, Frediani B, Iagnocco A, La Montagna G, Minisola G. Relationship of focal erosions, bone mineral density, and parathyroid hormone in rheumatoid arthritis. J Rheumatol. 2011;38:997–1002. doi: 10.3899/jrheum.100829. , et al. ( [DOI] [PubMed] [Google Scholar]
- Schmidt S, Post TM, Peletier LA, Boroujerdi MA, Danhof M. Coping with time scales in disease systems analysis: application to bone remodeling. J Pharmacokinet Pharmacodyn. 2011;38:873–900. doi: 10.1007/s10928-011-9224-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stolina M, Adamu S, Ominsky M, Dwyer D, Asuncion F, Geng Z. RANKL is a marker and mediator of local and systemic bone loss in two rat models of inflammatory arthritis. J Bone Miner Res. 2005;20:1756–1765. doi: 10.1359/JBMR.050601. , et al. ( [DOI] [PubMed] [Google Scholar]
- Stolina M, Bolon B, Dwyer D, Middleton S, Duryea D, Kostenuik PJ. The evolving systemic and local biomarker milieu at different stages of disease progression in rat collagen-induced arthritis. Biomarkers. 2008;13:692–712. doi: 10.1080/13547500802651911. , et al. ( [DOI] [PubMed] [Google Scholar]
- Stolina M, Bolon B, Middleton S, Dwyer D, Brown H, Duryea D. The evolving systemic and local biomarker milieu at different stages of disease progression in rat adjuvant-induced arthritis. J Clin Immunol. 2009;29:158–174. doi: 10.1007/s10875-008-9238-8. , et al. ( [DOI] [PubMed] [Google Scholar]
- Suzuki M, Hashizume M, Yoshida H, Shiina M, Mihara M. Intercellular adhesion molecule-1 on synovial cells attenuated interleukin-6-induced inhibition of osteoclastogenesis induced by receptor activator for nuclear factor kappaB ligand. Clin Exp Immunol. 2011;163:88–95. doi: 10.1111/j.1365-2249.2010.04276.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka Y, Nakayamada S, Okada Y. Osteoblasts and osteoclasts in bone remodeling and inflammation. Curr Drug Targets Inflamm Allergy. 2005;4:325–328. doi: 10.2174/1568010054022015. [DOI] [PubMed] [Google Scholar]
- Walsh NC, Crotti TN, Goldring SR, Gravallese EM. Rheumatic diseases: the effects of inflammation on bone. Immunol Rev. 2005;208:228–251. doi: 10.1111/j.0105-2896.2005.00338.x. [DOI] [PubMed] [Google Scholar]
- Wei S, Kitaura H, Zhou P, Ross FP, Teitelbaum SL. IL-1 mediates TNF-induced osteoclastogenesis. J Clin Invest. 2005;115:282–290. doi: 10.1172/JCI23394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinstein RS, Chen JR, Powers CC, Stewart SA, Landes RD, Bellido T. Promotion of osteoclast survival and antagonism of bisphosphonate-induced osteoclast apoptosis by glucocorticoids. J Clin Invest. 2002;109:1041–1048. doi: 10.1172/JCI14538. , et al. ( [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Tan JW, Huang L, Gao XH, Laird R, Liu D. Cloning, sequencing, and functional characterization of the rat homologue of receptor activator of NF-kappaB ligand. J Bone Miner Res. 2000;15:2178–2186. doi: 10.1359/jbmr.2000.15.11.2178. , et al. ( [DOI] [PubMed] [Google Scholar]
- Yao Z, Li P, Zhang Q, Schwarz EM, Keng P, Arbini A. Tumor necrosis factor-alpha increases circulating osteoclast precursor numbers by promoting their proliferation and differentiation in the bone marrow through up-regulation of c-Fms expression. J Biol Chem. 2006;281:11846–11855. doi: 10.1074/jbc.M512624200. , et al. ( [DOI] [PubMed] [Google Scholar]
- Zwerina J, Redlich K, Polzer K, Joosten L, Kronke G, Distler J. TNF-induced structural joint damage is mediated by IL-1. Proc Natl Acad Sci USA. 2007;104:11742–11747. doi: 10.1073/pnas.0610812104. , et al. ( [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1. Derivations of equations 7-9.