Detecting Compartmental non-Gaussian Diffusion with Symmetrized Double-PFG MRI

Abstract

Diffusion in tissue and porous media is known to be non-Gaussian and has been used for clinical indications of stroke and other tissue pathologies. However, when conventional NMR techniques are applied to biological tissues and other heterogeneous materials, the presence of multiple compartments (pores) with different Gaussian diffusivities will also contribute to the measurement of non-Gaussian behavior. Here we present Symmetrized Double PFG (sd-PFG), which can separate these two contributions to non-Gaussian signal decay as having distinct angular modulation frequencies. In contrast to prior angular d-PFG methods, sd-PFG can unambiguously extract kurtosis as an oscillation from samples with isotropic or uniformly oriented anisotropic pores, and can generally extract a combination of compartmental anisotropy and kurtosis. The method further fixes its sensitivity with respect to the time-dependence of the apparent diffusion coefficient. We experimentally demonstrate the measurement of the fourth moment (kurtosis) of diffusion and find it consistent with theoretical predictions. By enabling the unambiguous identification of contributions of compartmental kurtosis to the signal, sd-PFG has the potential to help identify the underlying micro-structural changes corresponding to current kurtosis based diagnostics and act as a novel source of contrast to better resolve tissue micro-structure.

1 Introduction

Nuclear Magnetic Resonance (NMR) has long been used as a non-invasive probe of material micro structure [1] with applications in medical MRI and oil well logging [2, 3, 4, 5, 6] through the relationship between the apparent diffusion coefficient and pore structure [2, 7]. In bulk fluid, the molecular diffusion displacement R is distributed in a Gaussian fashion log[P(R)] ∝ R², and thus the presence of higher order terms (e.g. 4th order term, kurtosis) is a reflection of restricted diffusion. In medical MRI, the experimental detection of the fourth moment has been used for clinical indications in diffusion kurtosis imaging (DKI) and has been linked to stroke [8] and other tissue pathologies [9, 10], and its direct measurement is desirable as a clinical diagnostic tool.

A complication arises in that sample heterogeneity can also contribute to deviations from a Gaussian signal decay, even in complete absence of non-Gaussian diffusion. For example, while diffusion in bulk fluids is Gaussian, a diffusion measurement of a water and an oil vial next to each other (without imaging) would still yield non-Gaussian behavior. This is simply due to their differing diffusion coefficients and the superposition of their signals.

In the case of imaging tissue, a single voxel can contain variety of distinct microscopic environments of differing size and anisotropy. As with the vial of water and oil, these different environments can represent independent components. Thus, while ‘free water’ in tissue is well-characterized by Gaussian diffusion [11], variations in the tissue can lead to a distribution of observed diffusivities that would still register as a fourth order decay in DKI. If these contributions could instead be separated from the contributions to kurtosis from restricted water, these different environments could be unambiguously identified.

Isolation of hidden ‘local’ features of restricted diffusion is still possible. For example, oscillating the gradients such that the effective encoding (‘q-vector’) is spun at the magic angle will average out the influence of anisotropy, both macroscopic and compartmental [12]. Alternatively, correlating the direction of diffusion over successive displacements with double pulsed field gradient techniques (d-PFG) has been shown to be effective to extract ‘local’ features of diffusion [13, 14, 15]. For instance, the signal difference between parallel (0°) and anti-parallel (180°) gradients have been used to unambiguously identify restricted diffusion [13]. However, the multiple diffusive displacements measured in these angular techniques are interdependent, complicating their interpretation and design.

This work identifies mirror symmetries of diffusional motion when measured over multiple displacements, and formulates two corresponding independent measures (or modes) of stationary stochastic processes [16]. These modes lack the intrinsic interdependence found between measurements of 2-point displacements, greatly simplifying the design of d-PFG measurements. Thus, their utilization enables a new class of techniques where these independent modes are experimentally controlled to engineer sequences that isolate features of diffusion.

We introduce one particular implementation for MRI, the symmetrized double pulsed-field-gradient (sd-PFG) experiment. By fixing the encoding strength for both diffusion modes while varying their physical orientations, the technique can separate Gaussian and non-Gaussian diffusion processes as modulations of the NMR signal at different “angular frequencies” in isotropic and uniformly oriented anisotropic pores. Any Gaussian moment can only contribute to zero or 2-cycle modulations, whereas kurtosis will also produce a distinct 4-cycle modulation. Generally, this procedure will identify a combination of CSA and compartmental kurtosis. We will describe the theory and experimental verification of the method in a well-characterized restricted diffusion phantom and a plant specimen. We also include additional detailed proofs and simulations as a part of the supplementary information (SI).

2 Theory

The conventional PFG experiment uses a pair of field gradient pulses of equal duration (δ) and strength (but effectively in opposite directions, +g and −g) separated by a time Δ. A spin with a displacement of R will acquire a phase ψ = q · R in the limit of short pulse widths δ where q ≡ γδg (γ is the gyromagnetic ratio)[17]. The d-PFG experiment [18, 13, 14] adds a second and independently varied PFG pair, q₂, some time τ_m after the first PFG pair, q₁. The phase encoded by the d-PFG experiment is then¹ ψ = q₁ · R₁ + q₂ · R₂, where R₁ and R₂ are the net displacements occurring during q₁ and q₂, respectively. The NMR signal without relaxation is then

$$E({\mathbf{q}}_{\mathbf{1}},{\mathbf{q}}_{\mathbf{2}})=\langle e^{-i{\mathbf{q}}_{\mathbf{1}}\cdot {\mathbf{R}}_{\mathbf{1}}-i{\mathbf{q}}_{\mathbf{2}}\cdot {\mathbf{R}}_{\mathbf{2}}}\rangle ,$$ (1)

where 〈〉 denotes the ensemble average. In this work, we only consider τ_m = 0 and use identical diffusion times Δ during q₁ and q₂ (Fig. 1).

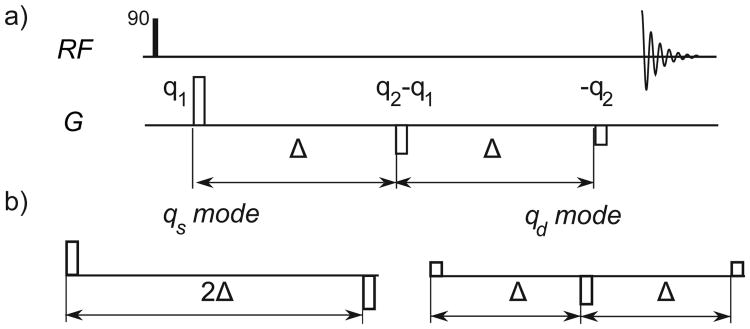
Figure 1.

(a) The basic d-PFG pulse sequence with zero mixing time. An initial 90° RF pulse excites the spins, then three gradient pulses acting as 2 PFG encoding pairs imprint and refocus the spatial modulation of the spin magnetization across the sample, after which the signal is acquired. (b) The alternate encoding axes q_s and q_d are linear combinations of q₁ and q₂ that divide the total encoding period into segments of 2Δ and Δ respectively and are the principal signal axes.

In absence of flow, the second order cumulant expansion of E(q₁, q₂) depends only on the mean square of the phase, $\frac{1}{2}\langle {\psi }^2\rangle$ [20]. This is a function of the mean square net displacements 〈R₁R₁^T〉 = 〈R₂R₂^T〉 and their correlations 〈R₁R₂^T〉 = 〈R₂R₁^T〉, where the equalities follow from diffusion being a stationary process and the use of the identical encoding times Δ [21]. The mean square displacement defines the diffusion tensor as a function of the diffusion time, D̄_Δ = 〈RR^T〉 /2Δ. The correlation tensor 〈R₁R₂^T〉 is also a function of the diffusion tensor, but for two different diffusion times, 2Δ [D̄_2Δ – D̄_Δ], as shown in [19] for τ_m = 0. With these relations, the second order moment approximation of the d-PFG signal is then

$$ln[E({\mathbf{q}}_{\mathbf{1}},{\mathbf{q}}_{\mathbf{2}})]\approx -\mathrm{\Delta }[{{\mathbf{q}}_{\mathbf{1}}}^T{\overline{\mathbf{D}}}_{\mathrm{\Delta }}{\mathbf{q}}_{\mathbf{1}}+{{\mathbf{q}}_{\mathbf{2}}}^T{\overline{\mathbf{D}}}_{\mathrm{\Delta }}{\mathbf{q}}_{\mathbf{2}}+2{{\mathbf{q}}_{\mathbf{1}}}^T({\overline{\mathbf{D}}}_{2\mathrm{\Delta }}-{\overline{\mathbf{D}}}_{\mathrm{\Delta }}){\mathbf{q}}_{\mathbf{2}}]$$ (2)

Using the basis with symmetric and anti-symmetric gradient waveforms as shown in (Fig. 1b), q_s ≡ (q₁ + q₂), and q_d ≡ (q₂ − q₁), Eq. 2 yields

$$ln[E({\mathbf{q}}_{\mathbf{s}},{\mathbf{q}}_{\mathbf{d}})]\approx -\frac{\mathrm{\Delta }}{2}[{{\mathbf{q}}_{\mathbf{s}}}^T{\overline{\mathbf{D}}}_{2\mathrm{\Delta }}{\mathbf{q}}_{\mathbf{s}}+{{\mathbf{q}}_{\mathbf{d}}}^T(2{\overline{\mathbf{D}}}_{\mathrm{\Delta }}-{\overline{\mathbf{D}}}_{2\mathrm{\Delta }}){\mathbf{q}}_{\mathbf{d}}].$$ (3)

Thus, q_d and q_s independently encode for the apparent diffusion coefficient for two different diffusion times (D̄_2Δ and 2D̄_Δ – D̄_2Δ) and are the principal signal axes of the d-PFG experiment when Δ₁ = Δ₂ [16]. These independent encoding modes reflect a more general symmetry than what eq. 3 would imply. The q_s, q_d decomposition also holds for all mixing times τ_m [16] and represent the axes of mirror symmetry of the d-PFG signal as proved and simulated in the supplementary information (see SI).

By decomposing the signal equation according to these independent encoding modes, the task of designing a d-PFG experiment that isolates or intentionally correlates different terms is greatly simplified. For example, correlating the values of the apparent diffusion coefficient at different diffusion times is a matter of systematically varying the relative strengths of q_s and q_d [16].

Alternatively, the technique this paper introduces utilizes the q_s, q_d formulation to develop a sequence that removes terms in order to highlight higher-order effects. Specifically, by performing the experiment holding |q_s| = |q_d| = q constant, it symmetrically and consistently weights the underlying encoding modes. We further focus on one specific implementation,

$${\mathbf{q}}_{\mathbf{1}}(\varphi )=qcos(\varphi )\widehat{\mathbf{x}},{\mathbf{q}}_{\mathbf{2}}(\varphi )=qsin(\varphi )\widehat{\mathbf{y}}.$$ (4)

where the angle ϕ acts as a modulation phase between the magnitude of q₁ and q₂. (fig. 2 left) Note that the orientations of the PFG pulses do not vary. However, ϕ, does represent the physical orientation of the principal encoding modes relative to ±x̂

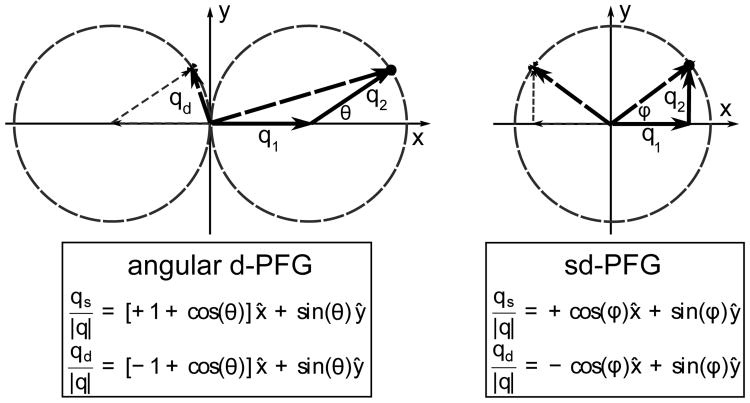
Figure 2.

Gradient trajectories for angular d-PFG (left) and sd-PFG (right) in q_s, q_d and q₁, q₂ coordinates, this varies the relative magnitudes of q_s and q_d and so modulates the measurement's sensitivity to D̄_Δ and D̄_2Δ. sd-PFG modulates the relative amplitudes of q₁ and q₂, but never orientation, in a manner so to fix the corresponding magnitudes of q_s and q_d for a constant relative sensitivity to D̄_Δ and D̄_2Δ

$${\mathbf{q}}_{\mathbf{s}}(\varphi )=qcos(\varphi )\widehat{\mathbf{x}}+qsin(\varphi )\widehat{\mathbf{y}},{\mathbf{q}}_{\mathbf{d}}(\varphi )=-qcos(\varphi )\widehat{\mathbf{x}}+qsin(\varphi )\widehat{\mathbf{y}}.$$ (5)

We title this specific sequence symmetrized double PFG (sd-PFG) because it symmetrically weights both the underlying encoding modes, and uniformly samples all orientations within the x/y plane for both encoding modes. As a consequence, sd-PFG modulations due to the variation in D_Δ with Δ for isotropic diffusion are eliminated, where Eq. 3 evaluates to

$$ln[E(q,\varphi )]\approx -\mathrm{\Delta }{q}^2{D}_{\mathrm{\Delta }},$$ (6)

and for anisotropic samples, sd-PFG is equally sensitive to diffusion along both directions in the encoding plane where

$$ln[E(q,\varphi )]\approx -\frac{\mathrm{\Delta }}{2}{\mathrm{q}}^2\{(D_{\mathrm{\Delta },xx}+D_{\mathrm{\Delta },yy})+cos(2\varphi )(D_{\mathrm{\Delta },xx}-D_{\mathrm{\Delta },yy})+2sin(2\varphi )(D_{2\mathrm{\Delta },xx}-D_{\mathrm{\Delta },yy})\},$$ (7)

In contrast, traditional angular d-PFG based techniques [13] lack these symmetries (fig. 2 left). In these experiments, the direction of motion between successive diffusion periods (instead of independent modes) is measured by fixing the magnitudes of the q₁ and q₂ encoding strengths and varying their relative orientation θ.

$${\mathbf{q}}_{\mathbf{1}}(\theta )=q\widehat{\mathbf{x}},{\mathbf{q}}_{\mathbf{2}}(\theta )=q(cos(\theta )\widehat{\mathbf{x}}+sin(\theta )\widehat{\mathbf{y}}).$$ (8)

$${\mathbf{q}}_{\mathbf{s}}=q((1+cos(\theta ))\widehat{\mathbf{x}}+sin(\theta )\widehat{\mathbf{y}}),{\mathbf{q}}_{\mathbf{d}}=q((-1+cos(\theta ))\widehat{\mathbf{x}}+sin(\theta )\widehat{\mathbf{y}}).$$ (9)

As a result, time dependent diffusion will generally cause a cos θ modulation for isotropic diffusion [13, 21],

$$ln[E(q,\varphi )]\approx -2{\mathrm{\Delta }}_{q^2}\{D_{\mathrm{\Delta }}+cos(\theta )(D_{2\mathrm{\Delta }}-D_{\mathrm{\Delta }})\}$$ (10)

and will produce a stronger encoding along the direction of the first gradient pulse.

$$ln[E(q,\varphi )]\approx -\frac{1}{2}{\mathrm{\Delta }}_{q^2}\{3D_{\mathrm{\Delta },xx}+D_{\mathrm{\Delta },yy}+4cos(\theta )(D_{2\mathrm{\Delta },xx}-D_{\mathrm{\Delta },xx})+4sin(\theta )(D_{2\mathrm{\Delta },xy}-D_{\mathrm{\Delta },xy})+cos(2\theta )(D_{\mathrm{\Delta },xx}-D_{\mathrm{\Delta },yy})+2sin(2\theta )D_{\mathrm{\Delta },xy}\}$$ (11)

sd-PFG also removes the angular d-PFG modulation present when non-negligible pulse widths are employed and the q₁ and q₂ gradient pulses overlap (see SI). Then, the angular d-PFG signal oscillates even for isotropic time independent diffusion due to the encoding strength (b-value) varying [22],

$$ln[E(g,\theta )]\approx -\frac{1}{3}{g}^2{\delta }^2(6\mathrm{\Delta }-2\delta -\delta cos(\theta ))D.$$ (12)

whereas the sd-PFG signal remains constant (see SI)

$$ln[E(g,\varphi )]\approx -\frac{1}{3}{g}^2{\delta }^2(3\mathrm{\Delta }-\delta )D.$$ (13)

High-order cumulants will cause interference like effects, leading to additional modulations with ϕ in the sd-PFG signal. The fourth moment, kurtosis, is the next higher moment in the cumulant expansion of the signal and will contribute to a 4-cycle modulation in the sd-PFG signal as the terms sin(4ϕ) and cos(4ϕ). Using the tensor notation in Ref. [21] and assuming the narrow gradient pulse limit, the sd-PFG signal to the fourth moment is

$$ln[E(q,\varphi )]\approx -\frac{\mathrm{\Delta }{q}^2}{2}((D_{\mathrm{\Delta },xx}+D_{\mathrm{\Delta },yy})+cos(2\varphi )(D_{\mathrm{\Delta },xx}-D_{\mathrm{\Delta },yy})+2sin(2\varphi )(D_{2\mathrm{\Delta },xy}-D_{\mathrm{\Delta },xy}))-\frac{q^4}{4!}\{\frac{3+cos(4\varphi )}{8}(K_{xxxx}+K_{yyyy})+\frac{cos(2\varphi )}{2}(K_{xxxx}-K_{yyyy})+\frac{3}{4}(1-cos(4\varphi ))Z_{xxyy}+(sin(2\varphi )-\frac{1}{2}sin(4\varphi ))(S_{xxxy}-S_{yyyx})\}$$ (14)

where K̄ reflects the mean of the fourth power of net displacement over Δ, and the other tensors correlate R₁, R₂ between the times defined by q₁ and q₂. As defined in [21], these are

$$K_{ijkl}=\langle R_{1i}{R}_{1j}{R}_{1k}{R}_{1l}\rangle -\langle R_{1i}{R}_{1j}\rangle \langle R_{1k}{R}_{1l}\rangle -\langle R_{1i}{R}_{1k}\rangle \langle R_{1j}{R}_{1l}\rangle -\langle R_{1i}{R}_{1l}\rangle \langle R_{1j}{R}_{1k}\rangle$$

$$Z_{ijkl}=\langle R_{1i}{R}_{1j}{R}_{2k}{R}_{2l}\rangle -\langle R_{1i}{R}_{1j}\rangle \langle R_{2k}{R}_{2l}\rangle -\langle R_{1i}{R}_{2k}\rangle \langle R_{1j}{R}_{2l}\rangle -\langle R_{1i}{R}_{2l}\rangle \langle R_{1j}{R}_{2k}\rangle$$

$$S_{ijkl}=\langle R_{1i}{R}_{1j}{R}_{1k}{R}_{2l}\rangle -\langle R_{1i}{R}_{1j}\rangle \langle R_{1k}{R}_{2l}\rangle -\langle R_{1i}{R}_{1k}\rangle \langle R_{1j}{R}_{2l}\rangle -\langle R_{1i}{R}_{2l}\rangle \langle R_{1j}{R}_{1k}\rangle .$$

Because kurtosis will typically induce a 4-cycle modulation in the signal with respect to ϕ and Gaussian terms can only cause 0 and 2 cycle modulations, sd-PFG can unambiguously identify a combination of kurtosis and higher-order moments of the signal decay via a Fourier decomposition of ln[E(q, ϕ)] with respect to ϕ. These oscillations are a consequence of the signal equation for a tensor term of order 2n involving a product of 2n terms of sin(ϕ) and cos(ϕ) with sd-PFG sampling, yielding oscillations at up to 2n-cycles.

In comparison, correlating the direction of motion between subsequent times with angular d-PFG [13] exhibits a very different signal structure. Despite the angular d-PFG terms also consisting of trigonometric polynomials of order 2n, due to the symmetry of the tensors and the |q₁| = |q₂| sampling, no such 4-cycle oscillations are produced for kurtosis with isotropic diffusion [15, 21]. Thus, sd-PFG has both the advantages of removing the additional modulation due to time-dependence of the diffusion coefficient and the ability to identify kurtosis by this Fourier analysis including the common case of isotropic diffusion which angular d-PFG techniques cannot. This analysis also indicates that traditional angular d-PFG indicators of CSA can be contaminated by kurtosis. Kurtosis in angular d-PFG will still produce 2-cycle modulations for isotropic pores [21], but for anisotropic pores will also produce 2 and 4-cycle modulations that can be mistaken for CSA.

Typically, natural samples contain a distribution of restriction shapes and sizes, whereas the analysis so far has assumed a homogeneous sample with a single pore type. Given isotropic pores, the Fourier identification of local kurtosis is robust. In this case, the sd-PFG signal arising directly from the Gaussian moments of a heterogeneous distribution of pore sizes is simply

$$E(q,\varphi )=\int d{D}_{\mathrm{\Delta }}f(D_{\mathrm{\Delta }})e^{-\mathrm{\Delta }{q}^2{D}_{\mathrm{\Delta }}}$$ (15)

where f(D_Δ) is the corresponding distribution of isotropic diffusion coefficients. A distribution f(D_Δ), will cause a non-Gaussian decay of E(q, ϕ) as a function of q, but will maintain invariance with respect to ϕ. Thus, given isotropic pores, the observation of a 4–cycle modulation with sd-PFG can distinguish compartmental kurtosis (CK) from the presence of a distribution of apparent diffusion coefficients. In contrast, s-PFG measurements and current d-PFG analyses cannot make this distinction. Furthermore, these oscillating components of the sd-PFG signal can be isolated by Fourier analysis robustly and could unambiguously identify far weaker non-Gaussian components than the traditional means of extracting kurtosis, such as fitting the second and fourth order terms from the signal q-decay.

There is an additional source to the 4ϕ modulation in the case of compartment shape anisotropy (CSA), where the individual pores are anisotropic but together have no net preferential orientation (see SI). Then, the 2-cycle modulations in the sd-PFG signal due to local Gaussian anisotropy can combine to form a 4-cycle modulation as a 4^th order decay of the observed signal. A ‘frequency doubling’ of the oscillating terms cos(2ϕ) and sin(2ϕ) occurs because the observed signal is the sum of the exponent, a non-linear operation, of these terms for multiple orientations. Thus, in general the observation of a 4-cycle sd-PFG modulation in a heterogeneous sample reflects the presence of a combination of CSA and kurtosis as a 4^th order decay.

3 Methods

We acquired sd-PFG data for a glass capillary array and a plant sample on separate instruments. To minimize artifacts, the sd-PFG sequence in figure 1a-b must be modified to include refocusing pulses, and could further utilize bi-polar gradient pulses [23]. For both sets of measurements, we incorporate a double spin echo, during sd-PFG encoding and use an appropriate acquisition scheme.

For the glass capillary array phantom (GCA) (Photonis, Sturbridge, MA), MR acquisition was carried out on a 7-Tesla Bruker ADVANCE III spectrometer with microimaging gradients (Bruker BioSpin, Germany) using a double-PFG filtered imaging sequence [24]. The nominal pore diameter was 10 μm with a maximum variation of 5% between capillaries. The sample temperature was set to 19°C. The sd-PFG parameters were: δ=3.15 ms, Δ=25 ms, and q/2π= 41.9 and 83.9 mm⁻¹, respectively. The sample was placed parallel to the main magnetic field, which defines the z-axis. The first and second gradients were fixed along the x- and y-axes, respectively. For each of the q-values, a set of 37 measurements were performed with ϕ values increased in increments of 10°. The imaging parameters were: TE=12ms, TR=7s, slice thickness=0.5 mm, field of view=16×16 mm², matrix size=128×128, resolution=0.125×0.125 mm², bandwidth=50 kHz and number of averages=2. The signal was averaged over a large region of interest of the sd-PFG images to improve the signal-to-noise ratio. To fit the observed sd-PFG signal to simulation as in [24], a bi-compartmental model was assumed and a Levenberg-Marquardt numerical fitting procedure was employed to estimate the unknown parameters: S₀ (signal with no diffusion-weighting), f_cyl (fraction of the restricted compartment), and the inner diameter (ID). To obtain the sd-PFG signal model, we employed (SI) a general theory of NMR signal for restricted diffusion [25], which involves the generalization of the multiple correlation function method originally developed by Robertson [26] and extended by others [27, 28].

For the asparagus sample, the center was cored with a 3mm NMR tube and kept at room temperature ≈28±1°C. Data was collected on an Oxford 1 T horizontal bore magnet with a Bruker ADVANCE II spectrometer and a custom double-PFG filtered CPMG sequence. The encoding parameters were: δ=4.0ms, Δ=120 ms, and q/2π spanned 0 to 38.2 mm⁻¹ and ϕ spanned 180° in 11.25° increments omitting the angles where either q₁ or q₂ is exactly zero and fail to also act as a crusher pulse. A 16×14 array of q-values and ϕ were acquired with a CPMG acquisition employing TE=0.5ms, TR=6s and 8 averages. The q-values were incremented as an inner loop and the signal is normalized to most recent q = 0 acquisition to minimize the effects of temperature and other instrumental drifts.

4 Results and Discussion

4.1 Glass Capillary Array

The distinct features of sd-PFG are the absence of modulations due to time dependence in the apparent diffusion coefficient and a 4-cycle modulation corresponding that remains even for isotropic diffusion. In contrast, when correlating the direction of motion between diffusion periods, these conditions will yield a cosine modulation due to time dependent diffusion and no modulation for isotropic kurtosis.

The GCA phantom consists of aligned cylindrical pores using capillaries (10 μm ID) filled with water. For purely Gaussian diffusion, sd-PFG should give a constant signal as a function of ϕ. However, the signal will also produce an oscillation at 4 cycles (4ϕ) in the presence of compartmental kurtosis. This oscillation cannot arise from CSA because the cylindrical pores are isotropic within the x, y-plane. These modulations are clearly observed at high q (Fig. 3) and still observable even at lower q. This oscillation is notably absent in previous GCA measurements with angular d-PFG [24], in agreement with Jespersen's prior predictions [21], and confirms that angular d-PFG cannot isolate CK as an oscillation for this simple pore geometry. The 1-cycle oscillation characteristic of restricted diffusion in angular d-PFG (cos(θ)) is notably absent from this data in agreement with our strategy of symmetrization of the sd-PFG sampling and our q_s, q_d decomposition.

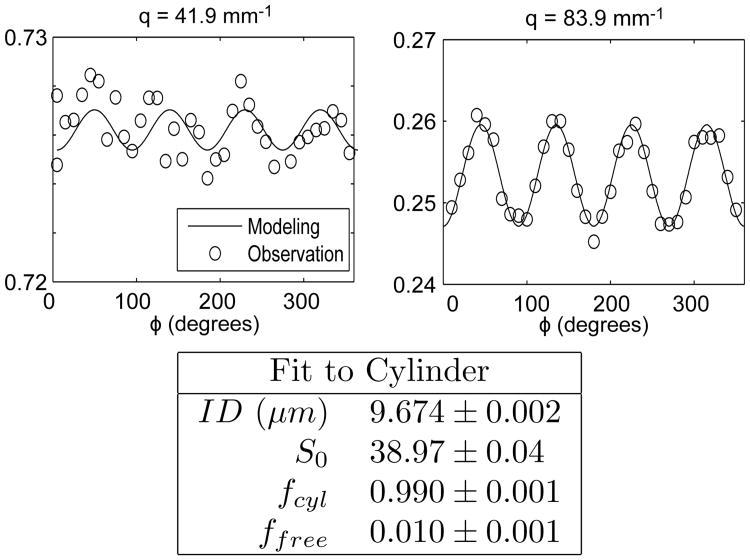
Figure 3.

The sd-PFG signal of a glass capillary array (GCA) consisting of 10μm ID cylinders oriented perpendicular to the gradient axes (g_x, g_y) for low (41.9 mm⁻¹) and higher (83.9 mm⁻¹) q. The 4-cycle angular oscillation unambiguously indicates the presence of non-Gaussian diffusion. The d-PFG signal modeling is confirmed by its fit to the observed signal where the deviations are dominated by variations in q due to gradient resolution limitations. The fitting results, assuming a cylindrical geometry and a free fluid component, yield a cylinder diameter very close to the nominal 10μm ID of the sample's fibers.

The observed sd-PFG signal quantitatively fits the full numerical simulation of the cylinder model. Assuming a cylindrical geometry and a variable fraction of free fluid, the fit to the data yields a diameter of 9.67 μm for the 10 μm cylinders. Deviations from the fit are dominated by the inability to maintain constant q as a function of ϕ due to the limited digital resolution of the gradient electronics. The experimental gradient amplitude exhibits a noticeable variation (q/2π = 41.930 ± 0.124 mm⁻¹ and 83.943 ± 0.066 mm⁻¹).

4.2 Compartmental kurtosis in a plant sample

The utility of sd-PFG is not when there is a homogeneous system and the observation of the bulk properties matches ‘local’ diffusive behavior, but when there is a mixture of different environments obscuring local structure such as for restricted diffusion in samples of interest for biological and material applications. A visual analysis of the sd-PFG data, as used for the GCA, is not generally practical because any anisotropic regions, can contribute to large 0- and 2-cycle modulations and visually obscure any small 4-cycle signals. In this case, a harmonic decomposition by a Fourier transform of ln [E(q, ϕ)] with respect to ϕ will be effective to separate Gaussian and non-Gaussian behaviors. Then the signals corresponding to the 0- and 2ϕ modulation should largely reflect the Gaussian moments, while the signal at the 4ϕ modulation can contain contributions from only higher order moments (kurtosis and CSA). We denote these components as E_0̃ for zero angular signal modulation, E_2̃ for the 2ϕ modulation, E_4̃ for the 4ϕ modulation etc, and focus on only the components corresponding to the cosine transform,

$$ln[E(q,\varphi )]=E_{\stackrel{\sim }{0}}(q)+E_{\stackrel{\sim }{2}}(q)cos(2\varphi )+E_{\stackrel{\sim }{4}}(q)cos(4\varphi )+\dots$$ (16)

More generally, the oscillations of the sd-PFG signal can have non-trivial sin components (Eqs. 7,14). Their contributions are not shown for clarity, as their amplitudes are comparatively negligible for the sample. Only E_2̃(q) has a significant sin component corresponding to time dependence in the cross term of the apparent diffusion coefficient. (see SI)

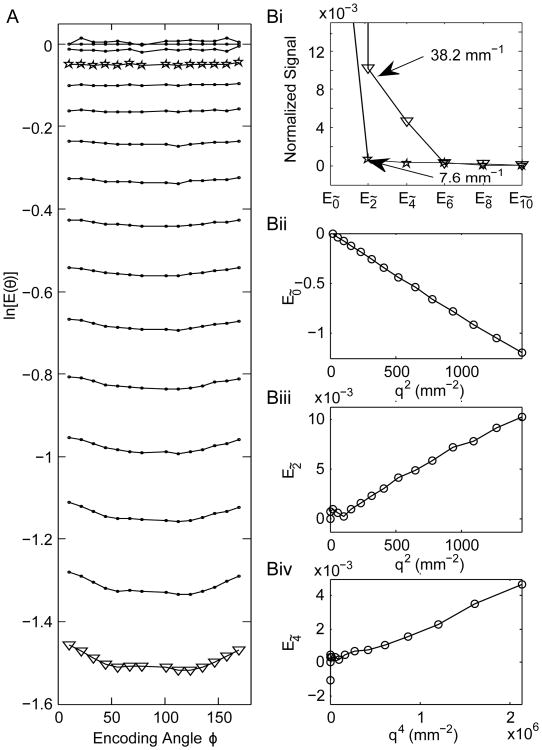
For the asparagus sample (Fig. 4), the constant and 2ϕ contributions dominate the signal, especially at small q (Left panel), and the 4ϕ modulation is not immediately identifiable from the raw E(q, ϕ) signal. However, in the frequency decomposition this 4ϕ modulation is clearly observable. As components with a nϕ modulation largely correspond to a nth or first non-zero higher moment, E_4̃ corresponds to kurtosis and its plot forms a linear curve with respect to q⁴. Similarly, E_0̃ and E_2̃ correspond to Gaussian decays and form straight lines when plotted against q². The positive slopes of E_2̃(q) and E_4̃(q) do not contradict having a signal decay, and instead reflect the phase of the oscillation resulting from the structure of the corresponding diffusion tensors. For example, the positive slope of E_2̃(q) simply implies that D_Δ,xx < D_Δ,yy.

Figure 4.

sd-PFG signal of asparagus and the Fourier analysis. A. The raw signal as a function of ϕ for different gradient pulse strengths uniformly spanning q = 0 to 38.2 mm⁻¹. B. The angular frequency decomposition of the signal. (i) The signal modulation as a function of angular frequency for two q values (stars and triangles correspond to the same values of q in A). Components corresponding to a nϕ oscillation in ln [E(q, ϕ)] largely correspond to a nth moment decay (or to the first non-zero higher order moment) and so (ii) E_0̃ and (iii) E_2̃, the 0 and 2ϕ oscillations, correspond to the Gaussian decay and form a linear curve with q². (iv) The plot for 4ϕ (E_4̃) of ln [E(q, ϕ)] corresponds to kurtosis and forms a linear curve as a function of |q|⁴.

In a strict sense, the moments 2n and higher will all contribute to a coefficient E_2ñ according to the moment analysis of the sd-PFG (eqs. 7,14). Thus, E_0̃ and E_2̃ will also have contributions from kurtosis and higher order moments, but these moments are typically much smaller and dominated by the lowest order term. What this relation ensures is the ability to isolate the signal from typically much larger lower order moments, and so E_4̃ isolates the far smaller component due to kurtosis from the Gaussian contributions. This still holds true for the case of CSA, where the superposition of signal from anisotropic Gaussian diffusion can lead to a 4ϕ modulation, as this nonetheless only occurs for the 4th moment of the total signal (see SI). The structure of this sample allows us to rule out CSA as a contributing factor. In general, other techniques would have to be employed to differentiate CK and CSA, such as Eriksson et. al's magic-angle spinning q-vector technique [12]. Traditional angular d-PFG CSA indicators cannot be used to make this distinction, since these would also be affected by kurtosis.

4.3 Generalization: Correlation of Independent Diffusion Modes

The use of principal diffusion encoding modes, as demonstrated in the design of sd-PFG with q_s and q_d, enables the systematic analysis and construction of the correlations between different measures of diffusion. In contrast to Mitra's initial work [13], where the relative direction of motion is compared between adjacent times (q₁ and q₂), the influence of basic features such as time dependent diffusion are immediately apparent and easily controlled in our framework. This greatly simplifies the design of d-PFG experiments to isolate terms as shown here or to directly correlate them as done previously [16].

The use of these modes can enable the generation of a new class of diffusion techniques. In particular, sd-PFG is but one modulation technique possible when fixing the encoding strength for the separate diffusion modes. Instead, alternative modulation schemes could sample all the distinct angles between q_s, q_d in the plane, or use different fixed strengths for the two different modes. For example, in a manner analogous to Jespersen's recent approach to angular d-PFG measurements [29], the sd-PFG experiment could be repeated varying the orientation of the encoding x/y-plane between measurements to obtain rotationally invariant measures of the signal. Finally, the distinct diffusion encoding modes q_s, q_d are unlikely to be the only unique pair and there are possibly many more independent modes. For example, a whole range of gradient sequences that are independent to the second moment have been incidentally identified to eliminate background gradient cross-terms [17]. Whether signal from these other sequences exhibit the same mirror symmetry in the signal as q_s, q_d is the focus of current work.

5 Conclusions

This paper describes a novel d-PFG design (sd-PFG) to directly measure compartmental non-Gaussian diffusion (e.g. kurtosis) through a unique 4-cycle modulation. The presence of a diffusion distribution and bulk anisotropy in natural materials do not affect this measurement as they appear as zero or 2-cycle modulations, easily distinguishable from the 4-cycle modulation through Fourier analysis. The pulse sequence described here can be readily implemented in conventional NMR systems and on clinical MRI scanners, and the sequence parameters such as gradient strength q (up to 40 mm⁻¹) and encoding times Δ (10-100 ms) are well within the range of the capability of these systems. Thus, we expect this technique to find applications in medical research and clinical diagnostics to examine tissue pathology resulting from changes in tissue microstructure. More broadly, this work identifies basic symmetries underlying multiple point diffusion measurements, and sd-PFG represents one of a new class of multi-dimensional NMR techniques based on correlating the distinct modes of diffusive motion.

Abbreviations

ADC

apparent diffusion coefficient

PFG

Pulsed-Field-Gradient Experiment

d-PFG

Double Pulsed-Field-Gradient Experiment

sd-PFG

Symmetrized Double Pulsed-Field-Gradient Experiment

CK

Compartmental Kurtosis