Incorporation of Non-zero Echo Times in the SPGR and bSSFP Signal Models used in mcDESPOT

Abstract

Purpose

To analyze the effect of neglecting non-zero echo times (TEs) in the conventional model of multicomponent driven equilibrium single pulse observation of T₁ and T₂ (mcDESPOT).

Theory and Methods

Formulations of the two-component spoiled gradient recalled echo (SPGR) and balanced steady state free precession (bSSFP) models that incorporate non-zero TE effects are presented in the context of mcDESPOT and compared to the conventionally-used SPGR and bSSFP models which ignore non-zero TEs. Relative errors in derived parameter estimates from conventional mcDESPOT, omitting TE effects, are assessed using simulations over a wide range of experimental and sample parameters.

Results

The neglect of non-zero TE leads to an overestimate of the SPGR signal and an underestimate of the bSSFP signal. These effects can introduce large errors in parameter estimates derived from conventional mcDESPOT under realistic imaging conditions.

Conclusion

SPGR and bSSFP signal models accounting for non-zero TE effects should be incorporated into quantitative mcDESPOT analyses.

INTRODUCTION

Combining spoiled gradient recalled echo (SPGR) and balanced steady state free precession (bSSFP) imaging sequences, as in multicomponent driven equilibrium single pulse observation of T₁ and T₂ (mcDESPOT) (1–2), results in relatively high signal-to-noise ratio (SNR) and rapid image acquisitions in studies of multicomponent systems. This facilitates, in principle, bicomponent, high-resolution, maps of component fractions and corresponding relaxation times across the entire human brain or knee (3–6), overcoming the main limitations of conventional multi-spin-echo pulse sequences (7–9).

Although it is often restricted to a two-pool model (1–2, 9), mcDESPOT has been extended to include a third pool to account for either partial volume effects (10) or magnetization transfer (11). However, in all variants of mcDESPOT, the magnetization relaxation that occurs between the pulse preceding signal acquisition and the acquisition itself is neglected; that is, non-zero TE effects are neglected in analysis of both the SPGR and bSSFP signals. In a recent study (12), it was shown that the neglect of non-zero TE in the two-component SPGR signal model introduces considerable errors into derived parameter estimates from mcDESPOT. However, neglect of nonzero TE effects in the bSSFP model, and the resulting errors in mcDESPOT parameter estimates, were not investigated.

mcDESPOT is a multicomponent extension of the well established DESPOT₁ and DESPOT₂ methods used for accurate and rapid whole-brain T₁ and T₂ mapping (13–15). It is clear that, given the long mean relaxation times in brain or other soft tissues, the neglect of non-zero TE effects in DESPOT₁ and DESPOT₂ signal models will have negligible impact on the derived parameter estimates. However, it remains unclear if this assumption still holds for multicomponent studies, since underlying signal components will exhibit differential amplitude weighting during relaxation.

Here, we evaluate formulations of the SPGR and bSSFP signal models that account for nonzero TE in the context of mcDESPOT analysis. Next, numerical simulations are presented to determine the impact of neglecting non-zero TEs on derived parameter estimates from conventional two-pool mcDESPOT (1–2, 5–6, 9, 12). Since our focus is on the effect of underlying signal models, we restricted our analyses to the case of infinite SNR.

THEORY

Under conditions of chemical equilibrium and in the presence of two-pool exchange between a slowly relaxing species S and a fast-relaxing species F, the steady-state (SS) bSSFP magnetization, M^SS, immediately preceding each radio-frequency (RF) pulse is given by (1–2, 10, 16)

$${\mathbf{M}}^{SS}={\left(\mathbf{I}-e^{\mathbf{A}·{TR}_{\mathit{bSSFP}}}\mathbf{R}(\alpha )\right)}^{-1}(e^{\mathbf{A}·{TR}_{\mathit{bSSFP}}}-\mathbf{I}){\mathbf{A}}^{-1}\mathbf{C}$$ [1]

where $\mathbf{M}=[M_{x,S}^{SS}{M}_{x,F}^{SS}{M}_{y,S}^{SS}{M}_{y,F}^{SS}{M}_{z,S}^{SS}{M}_{z,F}^{SS}]$, C = M₀[0 0 0 0 f_S/T_1,S f_F/T_1,F]^T,

$$\mathbf{A}=\left[\begin{array}{cccccc}-\frac{1}{T_{2,S}}-k_{SF}& k_{FS}& \frac{{\theta }_{RF}}{{TR}_{\mathit{bSSFP}}}+\mathrm{\Delta }\omega & 0& 0& 0\\ k_{SF}& -\frac{1}{T_{2,F}}-k_{FS}& 0& \frac{{\theta }_{RF}}{{TR}_{\mathit{bSSFP}}}+\mathrm{\Delta }\omega & 0& 0\\ -\frac{{\theta }_{RF}}{{TR}_{\mathit{bSSFP}}}-\mathrm{\Delta }\omega & 0& -\frac{1}{T_{2,S}}-k_{SF}& k_{FS}& 0& 0\\ 0& -\frac{{\theta }_{RF}}{{TR}_{\mathit{bSSFP}}}-\mathrm{\Delta }\omega & k_{SF}& -\frac{1}{T_{2,F}}-k_{FS}& 0& 0\\ 0& 0& 0& 0& -\frac{1}{T_{1,S}}-k_{SF}& k_{FS}\\ 0& 0& 0& 0& k_{SF}& -\frac{1}{T_{1,F}}-k_{FS}\end{array}\right],$$

and

$$\mathbf{R}(\alpha )=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& cos\alpha & 0& sin\alpha & 0\\ 0& 0& 0& cos\alpha & 0& sin\alpha \\ 0& 0& -sin\alpha & 0& cos\alpha & 0\\ 0& 0& 0& -sin\alpha & 0& cos\alpha \end{array}\right],$$

where M₀ represents the signal amplitude at TE = 0 ms and incorporates proton density and various machine factors, I is the 6 × 6 identity matrix, TR_bSSFP is the repetition time that corresponds to the time between two successive RF pulses, θ_RF is the phase increment of the RF excitation pulse, f_F and f_S are the fractions of the fast and slow T₂ components, respectively, with f_F = 1 − f_S, T₂ and T₁ are the transverse and longitudinal relaxation times, respectively, k_FS is the exchange rate from F to S, k_SF is the exchange rate from S to F, Δω is the off-resonance frequency, with the assumption that both components exhibit the same chemical shift, and α represents flip angle (FA) with pulse phase taken arbitrarily as x.

In the conventional implementation of mcDESPOT (1–2, 10), the theoretical two-component bSSFP signal is taken as

$$S^{SS}=\mid (M_{x,S}^{SS}+M_{x,F}^{SS})+i(M_{y,S}^{SS}+M_{y,F}^{SS})\mid$$ [2]

or, in the absence of chemical exchange, by the following summation (17)

$$S_{no-\mathit{exchange}}^{SS}=\left|M_0\left(f_s(M_{a,S}^{SS}+i{M}_{b,S}^{SS})+(1-f_s)(M_{a,F}^{SS}+i{M}_{b,F}^{SS})\right)\right|$$ [3]

where

$$M_{a,j}^{SS}=\frac{E_{2,j}(1-E_{1,j})sin{\theta }_{n}sin{\phi }_j}{(1-E_{1,j}cos{\theta }_n)(1-E_{2,j}cos{\phi }_j)-E_{2,j}(E_{1,j}-cos{\theta }_n)(E_{2,j}-cos{\phi }_j)}$$

and

$$M_{b,j}^{SS}=\frac{E_{2,j}(1-E_{1,j})(cos{\phi }_j-E_{2,j})sin{\theta }_n}{(1-E_{1,j}cos{\theta }_n)(1-E_{2,j}cos{\phi }_j)-E_{2,j}(E_{1,j}-cos{\theta }_n)(E_{2,j}-cos{\phi }_j)}$$

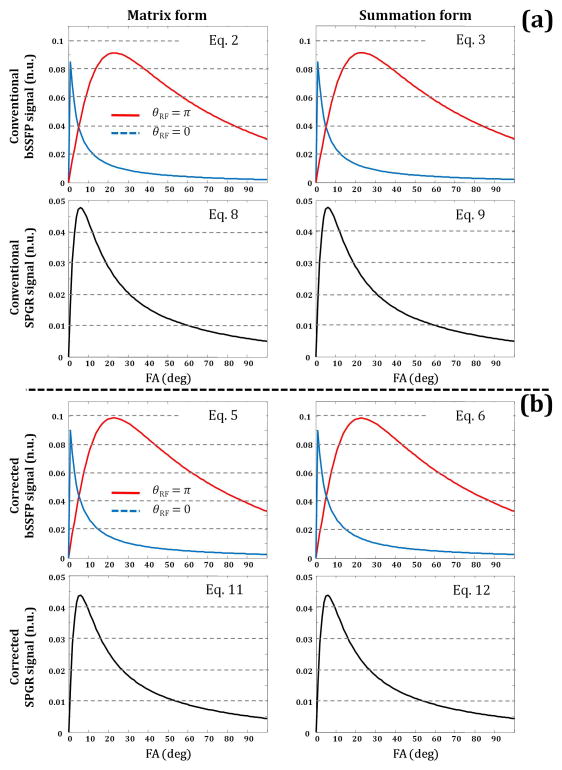
where φ_j = θ_RF + TRΔω_j, E_2,j = exp(−TR_bSSFP/T₂,j) and E_1,j = exp(−TR_bSSFP/T₁,j), and j stands for the j^th component (i.e. S or F). The equivalence of Eqs. 2 and 3 is shown in Fig. 1a, upper row. However, Eqs. 1–3 do not account for the relaxation occurring between a bSSFP excitation pulse and the subsequent acquisition that occurs at TE_bSSFP = TR_bSSFP/2 (18–19). The corrected bSSFP magnetization, ${\mathbf{M}}_{\mathit{Corr}}^{\mathit{bSSFP}}$, is described by application of Eq. 1 to the magnetization M^SS prior to the pulse that precedes echo acquisition

Fig. 1.

Comparison of the matrix (left column) and summation (right column) forms of the two-component bSSFP and SPGR signals in the absence of chemical exchange as a function of flip angle (FA) when non-zero TE effects were (a) omitted or (b) incorporated in the signal models. The modeled equations are indicated in the figure panels. Signals were generated using the following underlying input and experimental parameters: f_F = 0.2, T_2,F = 10 ms, T_2,S = 90 ms, T_1,F = 450 ms, T_1,S = 2000, k_FS = k_SF = 0 ms⁻¹, Δω = 0 Hz, TE_SPGR = 2.5 ms, and TR_bSSFP = TR_SPGR = 7 ms. Note the increase in the corrected bSSFP and the decrease in the corrected SPGR signal when these non-zero TE effects were incorporated as compared to the conventional bSSFP and SPGR signal forms used in mcDESPOT that neglect TEs.

$${\mathbf{M}}_{\mathit{Corr}}^{\mathit{bSSFP}}=e^{{\mathbf{A}}^{\ast }·\frac{{TR}_{\mathit{bSSFP}}}{2}}\mathbf{R}(\alpha ){\mathbf{M}}^{SS}+\left(e^{{\mathbf{A}}^{\ast }·\frac{{TR}_{\mathit{bSSFP}}}{2}}-\mathbf{I}\right){\mathbf{A}}^{\ast -1}\mathbf{C}$$ [4]

where the matrix A* is identical to the matrix A as defined above, but with TR_bSSFP replaced by TE_bSSFP throughout. Then the corrected theoretical two-component bSSFP signal is given by

$$S_{\mathit{Corr}}^{\mathit{bSSFP}}=\mid (M_{\mathit{Corr},x,S}^{\mathit{bSSFP}}+M_{\mathit{Corr},x,F}^{\mathit{bSSFP}})+i(M_{\mathit{Corr},y,S}^{\mathit{bSSFP}}+M_{\mathit{Corr},y,F}^{\mathit{bSSFP}})\mid$$ [5]

where the x- and y-components of the transverse magnetization are indicated by subscripts, or, in the absence of chemical exchange, by the following summation

$$S_{\mathit{Corr},no-\mathit{exchange}}^{\mathit{bSSFP}}=\left|M_0\left(f_s(M_{\mathit{Corr},a,S}^{\mathit{bSSFP}}+i{M}_{\mathit{Corr},b,S}^{\mathit{bSSFP}})+(1-f_s)(M_{\mathit{Corr},a,F}^{\mathit{bSSFP}}+i{M}_{\mathit{Corr},b,F}^{\mathit{bSSFP}})\right)\right|$$ [6]

where

$$M_{\mathit{Corr},a,j}^{\mathit{bSSFP}}=\frac{\sqrt{E_{2,j}}(1-E_{1,j})sin{\theta }_{n}sin{\phi }_j}{(1-E_{1,j}\text{cos}{\theta }_n)(1-E_{2,j}\text{cos}{\phi }_j)-E_{2,j}(E_{1,j}-cos{\theta }_n)(E_{2,j}-cos{\phi }_j)}$$

and

$$M_{\mathit{Corr},b,j}^{\mathit{bSSFP}}=\frac{\sqrt{E_{2,j}}(1-E_{1,j})(cos{\phi }_j-E_{2,j})sin{\theta }_n}{(1-E_{1,j}\text{cos}{\theta }_n)(1-E_{2,j}\text{cos}{\phi }_j)-E_{2,j}(E_{1,j}-cos{\theta }_n)(E_{2,j}-cos{\phi }_j)}$$

This form of the numerator, in which $\sqrt{E_{2,j}}$ appears instead of E_2,j, reflects the fact that relaxation prior to echo formation occurs over a time period TE_bSSFP = TR_bSSFP/2 (18–19), rather than over the time period TR_bSSFP. The equivalence of Eqs. 5 and 6 is shown in Fig. 1b, upper row.

Similarly, for spoiled steady state (SSS) transverse magnetization prior to each RF pulse as in the case of SPGR, the magnetization M^SSS immediately following each RF pulse is given by (1–2, 16)

$${\mathbf{M}}^{\mathit{SSS}}={(\mathbf{I}-e^{\mathbf{B}·{TR}_{\mathit{SPGR}}}\text{cos}\alpha )}^{-1}(\mathbf{I}-e^{\mathbf{B}·{TR}_{\mathit{SPGR}}})\mathbf{D}\text{sin}\alpha$$ [7]

where I is the 2 × 2 identity matrix, D = M₀[f_S f_F]^T and

$$\mathbf{B}=\left[\begin{array}{cc}-\frac{1}{T_{1,S}}-k_{SF}& k_{FS}\\ k_{SF}& -\frac{1}{T_{1,F}}-k_{FS}\end{array}\right].$$

In the conventional implementation of mcDESPOT (1–2, 10), the theoretical two-component SPGR signal is taken as

$$S^{\mathit{SSS}}=|M_{z,S}^{\mathit{SSS}}+M_{z,F}^{\mathit{SSS}}|$$ [8]

which, in the absence of chemical exchange, reduces to the following summation (Fig. 1a, second row) (20)

$$S_{no-\mathit{exchange}}^{\mathit{SSS}}=M_0\text{sin}\alpha \left(f_S\frac{1-E_{1,S}}{1-E_{1,S}\text{cos}\alpha }+(1-f_S)\frac{1-E_{1,F}}{1-E_{1,F}\text{cos}\alpha }\right)$$ [9]

Eqs. 7–9 do not account for the relaxation occurring between an excitation pulse and the subsequent acquisition (12). The corrected two-component SPGR magnetization, ${\mathbf{M}}_{\mathit{Corr}}^{\mathit{SPGR}}$, is described by (21)

$${\mathbf{M}}_{\mathit{Corr}}^{\mathit{SPGR}}=e^{{\mathbf{A}}_{\mathit{SPGR}}·T{E}_{\mathit{SPGR}}}\mathbf{R}(\alpha )\mathbf{S}{\mathbf{M}}_{\mathit{Corr}}^{\mathit{SSS}}+\mathbf{S}(e^{{\mathbf{A}}_{\mathit{SPGR}}·T{E}_{\mathit{SPGR}}}-\mathbf{I}){{\mathbf{A}}_{\mathit{SPGR}}}^{-1}\mathbf{C}$$ [10]

where the matrix A_SPGR is given by

$${\mathbf{A}}_{\mathit{SPGR}}=\left[\begin{array}{cccccc}-\frac{1}{T_{2,S}}-k_{SF}& k_{FS}& 0& 0& 0& 0\\ k_{SF}& -\frac{1}{T_{2,F}}-k_{FS}& 0& 0& 0& 0\\ 0& 0& -\frac{1}{T_{2,S}}-k_{SF}& k_{FS}& 0& 0\\ 0& 0& k_{SF}& -\frac{1}{T_{2,F}}-k_{FS}& 0& 0\\ 0& 0& 0& 0& -\frac{1}{T_{1,S}}-k_{SF}& k_{FS}\\ 0& 0& 0& 0& k_{SF}& -\frac{1}{T_{1,F}}-k_{FS}\end{array}\right],$$

and ${\mathbf{M}}_{\mathit{Corr}}^{\mathit{SSS}}={(\mathbf{I}-\mathbf{R}(\alpha )e^{{\mathbf{A}}_{\mathit{SPGR}}·{TR}_{\mathit{SPGR}}}\mathbf{S})}^{-1}\mathbf{S}\left((e^{{\mathbf{A}}_{\mathit{SPGR}}·{TR}_{\mathit{SPGR}}}-\mathbf{I}){{\mathbf{A}}_{\mathit{SPGR}}}^{-1}\mathbf{C}\right)$, I is the 6 × 6 identity matrix, and S is the spoiler matrix given by

$$\mathbf{S}=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right],$$

from which the corrected theoretical two-component SPGR signal is given by

$$S_{\mathit{Corr}}^{\mathit{SPGR}}=\mid (M_{\mathit{Corr},x,S}^{\mathit{SPGR}}+M_{\mathit{Corr},x,F}^{\mathit{SPGR}})+i(M_{\mathit{Corr},y,S}^{\mathit{SPGR}}+M_{\mathit{Corr},y,F}^{\mathit{SPGR}})\mid$$ [11]

or, in the absence of chemical exchange, by the following simple summation (Fig. 1b, second row)

$$S_{\mathit{Corr},no-\mathit{exchange}}^{\mathit{SPGR}}=S_0\text{sin}\alpha \left(f_S\frac{E_{2,S}^{†}(1-E_{1,S})}{1-E_{1,S}\text{cos}\alpha }+(1-f_s)\frac{E_{2,F}^{†}(1-E_{1,F})}{1-E_{1,F}\text{cos}\alpha }\right)$$ [12]

where $S_0=M_0\mathit{exp}(-T{E}_{\mathit{SPGR}}/T_2^{\prime })$ and $E_{2,j}^{†}=\mathit{exp}(-T{E}_{\mathit{SPGR}}/T_{2,j})$, and where $T_2^{\prime }$ describes mesoscopic or macroscopic field inhomogeneities common to both relaxation components (12).

METHODS

Effect of non-zero TE_SPGR on SPGR and non-zero TE_bSSFP on bSSFP signals

Corrected SPGR and bSSFP signals generated using Eq. 11 and Eq.5, respectively, explicitly accounting for transverse relaxation during non-zero TE_SPGR and TE_bSSFP were compared to conventional SPGR and bSSFP signals generated using Eq. 8 and Eq. 2, respectively, which neglect non-zero TE_SPGR and TE_bSSFP effects. Signal differences were calculated as 100 * (S_Conv − S_Corr)/S_Corr, where S_Conv and S_Corr are conventional and corrected signals, respectively, as a function of FA. Analyses were performed for corrected SPGR signals generated with TR_SPGR = 7 ms, and over a range of TE_SPGR from 0.5 to 6 ms in 0.25 ms increments and for FAs ranging from 1° to 100° in increments of 1°. The signal difference between conventional and corrected bSSFP signals was likewise calculated for values of TE_bSSFP (= TR_bSSFP/2) ranging from 0.5 to 6 ms in 0.25 ms increments for FAs ranging from 1° to 100° in increments of 1°. To correspond to actual practice (2–6, 9–12), two corrected bSSFP signals were generated with θ_RF of 0 or π(bSSFP₀ or bSSFP_π), respectively. All simulations used input parameters f_F = 0.2, T_2,F = 10 ms, T_2,S = 90 ms, T_1,F = 450 ms, T_1,S = 2000, k_FS = k_SF = 0 ms⁻¹ and Δω = 0 Hz; these are based on reported values from human brain imaging (1–4, 8–10).

Effects of non-modeled non-zero TE_SPGR and TE_bSSFP on mcDESPOT-derived parameter estimates

Effects of non-zero TE_SPGR

Corrected SPGR signals were simulated using Eq. 11 for values of TE_SPGR ranging from 0.5 to 6 ms in 0.25 ms increments and corrected bSSFP signals were generated using Eq. 5 with fixed TE_bSSFP value of 3.5 ms and for θ_RF of 0 or π. Corrected SPGR and bSSFP were generated for values of f_F ranging from 0.025 to 0.5 in increments of 0.025. For each TE_SPGR and f_F combination, corrected SPGR and bSSFP signals were then fitted simultaneously to Eqs. 11 and 5, explicitly accounting for non-zero TE_SPGR and TE_bSSFP (TE-Corrected mcDESPOT; TEC-mcDESPOT), or to Eqs. 8 and 2, neglecting non-zero TE_SPGR and TE_bSSFP (Conventional mcDESPOT). Using typical values of experimental parameters (1–6, 9–12, 22–28), SPGR signals were generated for α^o = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, while, bSSFP signals were generated for α^o = {2, 6, 14, 22, 30, 38, 46, 54, 62, 70}. The other experimental and input parameters were identical to those noted above. Relative parameter errors were calculated according to 100 * |P̂ − P|/P, where P̂ and P are the estimated and true parameter values, respectively.

Parameter estimates were derived using the stochastic region contraction (SRC) algorithm (1–2, 9, 12, 29). For each iteration of the SRC algorithm, 20000 random samples were generated within specified parameter bounds. The 50 solutions with the smallest least squares residual were used to construct bounds for the next iteration. Iterations were terminated after convergence was achieved, defined as a difference between the minimum and maximum values for all parameters of less than 1%, or after 30 iterations. The initial parameter bounds were: 0 ≤ f_F ≤ 0.8, 1 ms ≤ T_2,F ≤ 40 ms, 40 ms ≤ T_2,S ≤ 200 ms, 100 ms ≤ T_1,F ≤ 700 ms and 700 ms ≤ T_1,S ≤ 3000 ms. To avoid the need to explicitly fit for M₀, each dataset was normalized with respect to its mean value over the full range of FA (1–2, 9, 12).

Effects of non-zero TE_bSSFP

Corrected SPGR signals were simulated using Eq. 11 with a fixed TE_SPGR value of 2 ms. Corrected bSSFP signals were generated using Eq. 5 for values of TE_bSSFP (= TR_bSSFP/2) ranging from 1.5 to 6 ms in 0.25 ms increments and for θ_RF of 0 or π. Corrected SPGR and bSSFP were generated for values of f_F ranging from 0.025 to 0.5 in increments of 0.025. For each TE_bSSFP and f_F combination, corrected SPGR and bSSFP signals were then fitted simultaneously to Eqs. 11 and 5, explicitly accounting for non-zero TE_SPGR and TE_bSSFP (TEC-mcDESPOT), or to Eqs. 8 and 2, neglecting non-zero TE_SPGR and TE_bSSFP (Conventional mcDESPOT). The other experimental and underlying input parameters were identical to those used in the previous analyses. Parameter estimates were derived using the SRC algorithm with relative parameter errors calculated as described above.

RESULTS

Figure 2 shows the relative differences between conventional (Eqs. 8 and 2) and corrected (Eqs. 11 and 5) two-component SPGR and bSSFP signals for different values of TE_SPGR and TE_bSSFP as a function of FA. As seen, conventional SPGR signals are overestimated to an extent that increases with increasing TE_SPGR or FA. In contrast, conventional bSSFP₀ and bSSFP_π are underestimated to an extent increasing with increasing TE_bSSFP and with increasing FAs for bSSFP₀, and decreasing with respect to increasing FA for bSSFP_π.

Fig. 2.

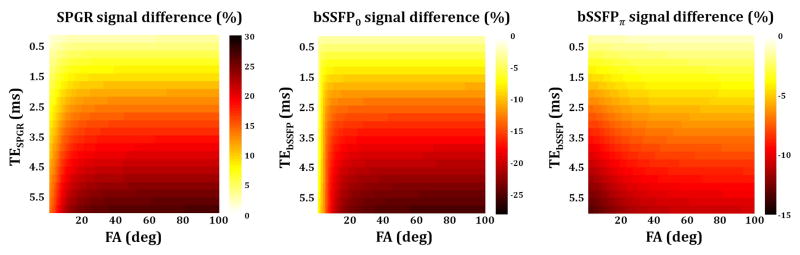
Relative difference between corrected and conventional SPGR and bSSFP signals. The corrected signals incorporate non-zero TE_SPGR and TE_bSSFP as discussed in the text, while the conventional signals omit these. Results are shown for different values of TE and as a function of flip angle (FA). Signals were generated using the following underlying input and experimental parameters: f_F = 0.2, T_2,F = 10 ms, T_2,S = 90 ms, T_1,F = 450 ms, T_1,S = 2000, k_FS = k_SF = 0 ms⁻¹, Δω = 0 Hz, and TR_bSSFP = TR_SPGR = 7 ms. As shown, for all TEs and FA combinations, the conventional SPGR signal was overestimated while the conventional bSSFP signal was underestimated.

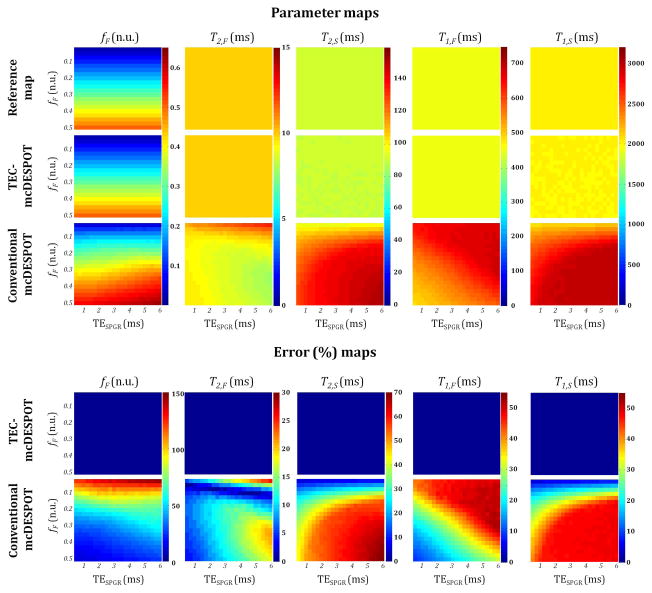
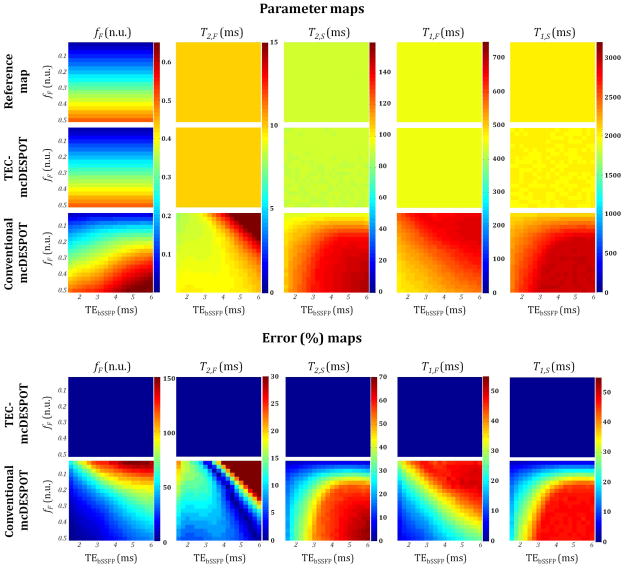
Parameter estimate errors resulting from conventional mcDESPOT are shown in Figs. 3 and 4. When data were simulated with non-zero TEs (i.e. TE_SPGR or TE_bSSFP) using Eqs. 11 and 5 and fit with the correct models (TEC-mcDESPOT), Eqs. 11 and 5, true input values were obtained for all parameters, shown as zero errors in derived parameter estimates. This indicates the ability of the SRC fitting procedure to determine the correct least-squares minima for these multiparametric signal models at infinite SNR. Figures 3 and 4 also show parameter estimates and the corresponding relative error maps for conventional mcDESPOT-derived parameter estimates obtained by fitting data generated from Eqs. 11 and 5, correctly incorporating non-zero TE effects, with Eqs. 8 and 2, which do not include appropriate correction for TEs. Results are shown for different combinations of f_F and TEs. For all TEs and f_F combinations, estimated parameter values of f_F, T_2,S, T_1,F and T_1,S were clearly overestimated, while estimated parameter values of T_2,F showed more complex patterns. In all cases, conventional mcDESPOT led to substantial errors in derived parameter estimates over the entire ranges of TEs and f_F. Relative error was seen to increase with increasing TE_SPGR or TE_bSSFP for all parameters, while error increased for T_2,S and T_1,S and decreased for f_F and T_1,F as a function of f_F. However, the relative error in the estimated values of T_2,F showed more complex patterns as a function of TEs and f_F.

Fig. 3.

Parameter value and relative error maps obtained from fitting simulated data with TEC-mcDESPOT (Eqs. 5 and 11) or conventional mcDESPOT (Eqs. 2 and 8) signal models for different combinations of TE_SPGR and f_F. Analyses were performed at infinite SNR with, in all cases, corrected bSSFP signals generated using Eq. 5 for a fixed TE_bSSFP value of 3.5 ms. Note that the color bars were set to correspond to the dynamic range of each parameter, and therefore differ between parameters.

Fig. 4.

Parameter and relative error maps obtained from fitting simulated data with TEC-mcDESPOT (Eqs. 5 and 11) or conventional mcDESPOT (Eqs. 2 and 8) signal models for different combinations of TE_bSSFP and f_F. Analyses were performed at infinite SNR with, in all cases, corrected SPGR signals were generated using Eq. 11 for a fixed TE_SPGR value of 2 ms. Note that the color bars were set to correspond to the dynamic range of each parameter, and therefore differ between parameters.

DISCUSSION

The introduction of mcDESPOT in 2008 (1) permitted for the first time high-resolution whole-brain analysis of myelin water fraction in human brain (1–4, 10, 22–28), and proteoglycan associated water fraction in human knee cartilage (5–6, 11). In light of the importance of this method, we have re-examined the signal models used in mcDESPOT and noted that the approximations used in single-component analyses, that is in DESPOT₁ and DESPOT₂, may not hold for the multicomponent mcDESPOT analysis. For DESPOT₁ and DESPOT₂, non-zero TE effects may be neglected due to the long mean relaxation times in brain and other soft tissues. However, while the resulting errors in signal amplitudes may appear to be negligible for mcDESPOT as well (Figs. 1–2), our detailed analysis has indicated that in fact these small deviations may result in large errors in parameter estimates under realistic imaging conditions (Figs. 3–4). This is likely due to the inherent and unavoidable sloppiness of this high dimensional signal model (12, 30–31), and to the fact that differential relaxation between the two components can introduce substantial errors.

Our simulation analyses showed that, as expected, neglect of non-zero TE_SPGR in the SPGR model leads to overestimates of signal values (Figs. 1–2), due to the omission of the signal decay between the RF pulse and the read-out gradient (12, 21, 32). In contrast, neglect of non-zero TE in the bSSFP model leads to signal underestimates (Figs. 1–2) since, in effect, this neglect incorporates transverse relaxation over a period of TR_bSSFP rather than TR_bSSFP/2 prior to echo acquisition (18–19, 33). That is, the incorrect signal model evaluates the signal after an echo time of TR, rather than after the shorter echo time of TR/2. Thus, in this case, incorrect modeling of transverse relaxation results in an underestimate of signal intensity. More importantly, neglect of non-zero TEs in mcDESPOT leads to significant errors in derived parameter estimates (Figs. 3–4).

The impact of noise on the accuracy and precision of derived parameter estimates has been the subject of extensive previous investigations. It was demonstrated that high quality parameter estimates may be obtainable from mcDESPOT with SNR that is clinically achievable (12, 34). However, the errors in parameter estimation described herein and due to the neglect of TE effects were considerably larger than those introduced due to noise (12, 34). In fact, the relative error calculated over 1000 noise realizations in the estimation of f_F was ~10% with the above underlying and experimental parameters and SNR = M₀/σ = 1000; achievable in clinical setting (12, 34), where σ represents the standard deviation of zero-mean Gaussian noise. The error due to neglect of TEs under comparable circumstances with TE_SPGR = 2 ms and TE_bSSFP = 3.5 ms was however ~60% (Figs. 3–4). Since our focus is on the effect of underlying signal models, we restricted our analyses to the case of infinite SNR and evaluated simulation results to explicitly determine the magnitude of the effects, without the manifold additional complications inherent in analysis of experimental data.

We assumed no exchange in the mcDESPOT signal model for several reasons. First, a recent study suggests that the incorporation of two-site exchange has a minimal effect on the estimated values of the rapidly-relaxing fraction of a two-component model (9), which is the main parameter of interest for characterization of cartilage and brain (3–11). In addition, we have found (data not shown) that the inclusion of exchange as an additional unknown parameter requires further constraints on the initial parameter bounds of the SRC algorithm for reliable parameter estimates, even at infinite SNR. This is likely due to the increased complexity of the local minima structure or the further flatness of the parameter energy surfaces as compared to the five unknown parameters model adopted in our analysis and analyzed elsewhere (12). In addition, we neglected finite RF pulse length effects in the current study in order to correspond to the conventional analysis of mcDESPOT. However, it has been shown that the neglect of relaxation during RF pulses can lead to further deviations of the measured signals from the theoretical SPGR and bSSFP models (21, 35–38). Moreover, again as with the conventional mcDESPOT approach, we assumed perfect spoiling of transverse magnetization prior to each RF pulse in the SPGR sequence. However, it has been shown that there may be a degree of preservation of transverse coherence in fast RF spoiled sequences with concomitant deviation of the signal behavior from the idealized model (32, 39). In the experimental setting, all of these additional effects would presumably be additive to those discussed here, which are based on considerations of the underlying signal models used in mcDESPOT analysis. Finally, we note that our results are equally applicable to other steady-state approaches such as mcRISE (11).

CONCLUSIONS

Neglect of non-zero TE_SPGR and TE_bSSFP leads to signal models that overestimate SPGR signal intensity and underestimate bSSFP signal intensity. We have shown that this can result in substantial errors in mcDESPOT-derived parameter estimates and propose the use of the SPGR and bSSFP signal models described herein for quantitative analyses using mcDESPOT.