Connectivity‐based whole brain dual parcellation by group ICA reveals tract structures and decreased connectivity in schizophrenia

Abstract

Mapping brain connectivity based on neuroimaging data is a promising new tool for understanding brain structure and function. In this methods paper, we demonstrate that group independent component analysis (GICA) can be used to perform a dual parcellation of the brain based on its connectivity matrix (cmICA). This dual parcellation consists of a set of spatially independent source maps, and a corresponding set of paired dual maps that define the connectivity of each source map to the brain. These dual maps are called the connectivity profiles of the source maps. Traditional analysis of connectivity matrices has been used previously for brain parcellation, but the present method provides additional information on the connectivity of these segmented regions. In this paper, the whole brain structural connectivity matrices were calculated on a 5 mm³ voxel scale from diffusion imaging data based on the probabilistic tractography method. The effect of the choice of the number of components (30 and 100) and their stability were examined. This method generated a set of spatially independent components that are consistent with the canonical brain tracts provided by previous anatomic descriptions, with the high order model yielding finer segmentations. The corpus‐callosum example shows how this method leads to a robust parcellation of a brain structure based on its connectivity properties. We applied cmICA to study structural connectivity differences between a group of schizophrenia subjects and healthy controls. The connectivity profiles at both model orders showed similar regions with reduced connectivity in schizophrenia patients. These regions included forceps major, right inferior fronto‐occipital fasciculus, uncinate fasciculus, thalamic radiation, and corticospinal tract. This paper provides a novel unsupervised data‐driven framework that summarizes the information in a large global connectivity matrix and tests for brain connectivity differences. It has the potential for capturing important brain changes related to disease in connectivity‐based disorders. Hum Brain Mapp 36:4681–4701, 2015. © 2015 Wiley Periodicals, Inc.

Abbreviations

DTI

diffusion tensor imaging

GFA

generalized fractional anisotropy

GICA

group independent analysis

HARDI

high angular resolution diffusion imaging

ICA

independent component analysis

IFG

inferior frontal gyrus

TBSS

tract based spatial statistics

INTRODUCTION

Connectivity diagram plays a key role in brain function and behavior. Many neuropsychiatric disorders, e.g. schizophrenia, have been suggested caused by abnormal communication between disparate brain networks. However, compared with the conventional region‐of‐interest or volume based morphometric analysis, connectivity analysis is not that straightforward, as it represents the interregional or intervoxel relationships. This makes it difficult to interpret, track, and visualize neurophysiological biomarkers. The aim of this study is to demonstrate that group independent analysis (GICA) [Calhoun and Adali, 2012; Calhoun et al., 2001] is capable of accomplishing such tasks.

Brain connectivity can de described in terms of a connectivity matrix $C$, whose element $C(i,j)$ describes the strength of the morphometric link between nodes $i$ and $j$ (structural connectivity) or describes a statistical link, such as the correlation between the BOLD (or EEG, MEG) activation at the two nodes (functional connectivity). In this paper, we show that group ICA of the connectivity matrix (cmICA) can be used for dual parcellation of the brain connectivity. The dual parcellation consists of a set of spatially independent maps { $s_k$} and a corresponding dual set of spatial maps { $r_k$}, such that $r_k$ defines the brain regions connected to $s_k$. $r_k$ is called the connectivity profile of $s_k$. We focus on such a dual parcellation based on structural connectivity matrices calculated from diffusion imaging data by probabilistic tractography.

This is a new method for understanding brain connectivity based on diffusion fiber tractography. Fiber tractography using diffusion imaging is an important noninvasive technique to quantitatively evaluate anatomical or structural connectivity between different brain regions. A major application of these connectivity maps is regional (cortical or subcortical) segmentation/parcellation of the brain. These studies include segmentation of the thalamus [Behrens et al., 2003a], medial frontal cortex [Johansen‐Berg et al., 2004], inferior frontal cortex [Anwander et al., 2007], and cingulate cortex [Beckmann et al., 2009, Cloutman and Ralph, 2012] for a recent review). So far the same topic has not yet been systematically studied for the whole brain, mainly because of the computational demands. A connectivity matrix computed from diffusion tractography does not directly give tract parcellations, but only gives a distribution of fiber counts between different brain regions. Further processing is required to interpret the connectivity matrix. In this study, we propose cmICA, a group independent component analysis (ICA) for decomposing connectivity matrices. We apply it to a large whole brain voxel‐to‐voxel tractographic connectivity matrix and examined its capability of blind neuronal tract separation in an unsupervised learning of connectivity properties, rather than predefining a region of interests (ROI) and/or segmenting specific brain regions as in some of the previous studies. We further evaluate cmICA's ability to distinguish groups of subjects with possible differences in brain structural connectivity by applying it to data from schizophrenia patients and healthy controls.

The data‐driven group ICA approach [Calhoun and Adali, 2012; Calhoun et al., 2001] has been used previously to extract functional network sources during a task or at rest based on fMRI data [Beckmann et al., 2005; Calhoun and Adali, 2012; Calhoun et al., 2008; Calhoun et al., 2002]. This work applies the same technology to connectivity matrices. In fMRI the data is space‐by‐time, while in the present application the data is space‐by‐space. Although seems like a trivial difference, it does make it harder to interpret the results. One of our goals is to give a clear interpretation of the results for the GICA analysis of connectivity matrices. Spatial GICA decomposes fMRI data into linked statistically independent spatial maps and the corresponding representative time series. Here also the connectivity matrix is decomposed in two linked spatial maps. We obtain spatially independent maps and their corresponding pairs describing their connectivity profile.

This is also a new framework to look for differences between connectivity matrices of two groups of subjects. Functional connectivity matrix differences have previously been studied by looking at difference of each element $C(i,j)$ across the groups and checking for significant differences after correcting for multiple comparisons [Allen et al., 2014; Smith, 2012; Van Essen et al., 2013]. Typically, in these studies $C(i,j)$ represented macroscopic brain areas (ROIs) defined on apriori knowledge, while we define $C(i,j)$ at a voxel level. Then in an unsupervised manner, cmICA reduces the connectivity matrix into fewer components, which capture the essential connectivity properties and differences are sought among them.

We calculate the structural connectivity from diffusion tensor imaging data and use probabilistic tractography to calculate the connectivity matrix elements. $C(i,j)$ is calculated as the percentage of fiber tracts that start from the i ^th node and reach the j ^th node. There are different methods for calculating the connectivity matrix, among them one is the streamline tracking [Mori et al., 1999]. This method is not well suited for modeling crossing/kissing fibers and more susceptible to noises because of its deterministic properties; where probabilistic tracking [Behrens et al., 2003b] minimizes these problems by taking into account the uncertainty of the local fiber orientation. Also, compared with supervised ROI‐based methods for calculating connectivity matrices, cmICA provides a data‐driven view of the connectivity in a comprehensive and relatively unbiased manner, which may increase sensitivity to subtle changes between subjects [Allen et al., 2011; Koch et al., 2010]. Moreover, cmICA can be extended to analyze a subset of the structural connectivity matrix focusing on specific interregional connections, such as thalamocortical pathways [Behrens et al., 2003a; O'Muircheartaigh et al., 2011], functional connectivity matrices obtained from fMRI [Van Essen et al., 2013], other neuronal imaging approaches [Oh et al., 2014], or any mathematical adjacent matrices representing a graph. While our cmICA technique does not depend on the choice of the method for calculating a connectivity matrix, the interpretation of the final results will depend on how the connectivity matrix was calculated. In this paper, we only focus on cmICA application to structural connectivity.

Just as in the GICA application to fMRI data, the maps $r_k$ and $s_k$ are calculated for each subject, and can be used to look for connectivity differences between groups of subjects. We apply the method to look for connectivity differences between a group of schizophrenia patients and healthy controls. One theory proposed to understand schizophrenia has been the functional disconnection hypothesis [Friston, 1998]. It is based on a dysfunctional connection of the brain leading to cognitive impairment. This raises the possibility of functional disconnection being accompanied by damage or disorganization of white matter tracts that connect the respective functional gray matter regions. More recent genetic and histopathological studies provide further indirect evidence that patients with schizophrenia may be more susceptible to oligodendrocyte dysfunction and impaired myelination, leading to white matter abnormalities [Aston et al., 2004; Davis and Haroutunian, 2003; Hakak et al., 2001; Sugai et al., 2004].

Previous diffusion based analysis to study schizophrenia has mostly focused on scalar parameters, such as fractional anisotropy (FA) to look for white matter integrity differences between healthy controls and schizophrenia patients. The group differences were tested based either on a voxel based analysis or a tract based spatial statistics (TBSS) [Smith et al., 2006] method. The finding of reduced FA in patients is interpreted as an indicator of ‘altered’ connectivity [Camchong et al., 2011; Caprihan et al., 2011; Clark et al., 2011; Fitzsimmons et al., 2013; Lee et al., 2013]. However, a drawback of these methods is that FA is a local measure, and although a reduction in FA can lead to reduced connectivity between regions connected by the fiber tracts passing through that region of reduced FA, the FA analysis does not directly identify the compromised network. FA is a ‘proxy’ marker for anatomical integrity, and thus limited in capturing the global connection information [Kim et al., 2008].

A more direct analysis of structural connectivity between different regions has been used previously in schizophrenia studies to look at connectivity differences between inferior frontal gyrus (IFG) and superior temporal gyrus (STG) in patients [Kubicki et al., 2011]. It was also used in Kubota's study [Kubota et al., 2013] to calculate connectivity within the thalamocortical pathways. Nonetheless, these studies sought connectivity differences in a limited number of anatomically predefined ROIs' between schizophrenia and controls. In this paper, we present an alternative method of analyzing diffusion imaging based structural connectivity matrices, which capture the networks effected by white matter pathologies [Behrens et al., 2003b; Mori et al., 1999; Skudlarski et al., 2008]. Although our focus is on a general method of connectivity matrix analysis, simultaneous analysis of structural and functional activity in schizophrenia patients can give a more comprehensive picture of connectivity changes [Skudlarski et al., 2010].

In addition, we look at the effect of the number of ICA components on the maps generated by cmICA and also study their stability with respect to the choice of the initialization parameters in the GICA algorithm. In summary, the cmICA algorithm segments the brain into tracts and generates their dual connectivity profiles based on the connectivity matrix. These dual maps are useful to study connectivity differences caused by white matter injury.

METHOD

Theory

The connectivity matrix C is a $N_b\times N_a$ matrix, representing the connectivity strength between all node pairs across two brain regions Region A ( $N_a$ nodes) and Region B ( $N_b$ nodes). After reformatting a connectivity matrix, the proposed cmICA can be easily related to previous ICA applications in fMRI, as such a connectivity matrix is similar to the spatial‐temporal data generated in fMRI experiment expressed as a $N_b\times N_a$ dimension matrix, with the 3D brain voxels as rows, and the corresponding time courses as columns. Each column is a fMRI time‐course of one voxel, which is very similar to the connectivity profile of the voxel in our example. In fMRI we have Time by Space as input for further analysis; in our case both dimensions of the connectivity matrix are different regions of space, so Region B by Region A connectivity is the input for further analysis. This analogy opens up the possibility of using tools developed for fMRI analysis for analyzing structural connectivity data.

The cmICA approximates the connectivity matrix $C$ by a matrix $\widehat{C}$ such that it has been factorized into

$$\widehat{C}=RS$$ (1)

where $R$ is a $N_b\times N_c$ matrix and $S$ is a matrix. If our notation is to represent all vectors as column vectors, then with $S={(s_1,s_2,\mathrm{...},s_{N_c})}^T$ and $R=(r_1,r_2,\mathrm{...},r_{N_c})$, we can write

$$\widehat{C}={\displaystyle \sum _{k=1}^{N_c}{r}_k{s}_k^T}$$ (2)

Following the analogy of GICA analysis to fMRI data, each ‘spatial map’ $s_k$ represents an independent source over Region A, and each ‘loading coefficient’ $r_k$ represents a brain map over Region B that indicates the common connectivity pattern shared by the region $s_k$. Figure 1 illustrates the cmICA factorization in brain. In the Region A to Region B case (Fig. 1A), cmICA decomposes an asymmetrical connectivity matrix (Fig. 1A Left) that is derived from the structural connectivity (Fig. 1A Middle, see Supporting Information A for the details of constructing connectivity matrix from diffusion imaging) into independent spatial maps $s_k$ in Region A (Fig. 1A Right, marked in purple, green and brown areas), with all the nodes within each spatial map $s_k$ share the similar connectivity profile $r_k$ in Region B (Fig. 1A Right, marked in lighter purple, green and brown areas) and $r_k$ conveys two types of information – (1) the regions which are connected to $s_k$ (the nodes' location in Region B) and (2) the strength of the connectivity (the nodes' intensity projected from the connectivity lines into Region B). In the case of whole brain connectivity (Fig. 1B), cmICA is performed on a symmetric connectivity matrix (Fig. 1B Left); therefore $s_k$ can be highly correlated with $r_k$, resulting in independent connectivity parcels (Fig. 1B Right, marked in dark blue, red, yellow, blue, and dark green areas), simply because $s_k$ and $r_k$ are defined over the same spatial region and the connectivity profile is shared by the intraparcel nodes. The interpretation of the relationship between $S$ and $R$ has special significance when the connectivity matrix is symmetric. The question of similarity between S and R only arises when the regions A and B are identical, a point which we discuss in more detail later. We believe that if the tract map S and its connectivity profile map R have highly similar spatial patterns, then this shows that the connectivity structure of tract S is from itself, suggesting a ‘tightly’ connected parcel; if not then it indicates a ‘loose’ parcel. In addition, the segmentations derived from cmICA can overlap (the purple, orange, and green dots in Fig. 1B Right), e.g. representing the crossing fibers in different tracts. This is different from most hard segmentation methods commonly used in connectivity matrix parcellation [Anwander et al., 2007; Johansen‐Berg et al., 2004].

Figure 1.

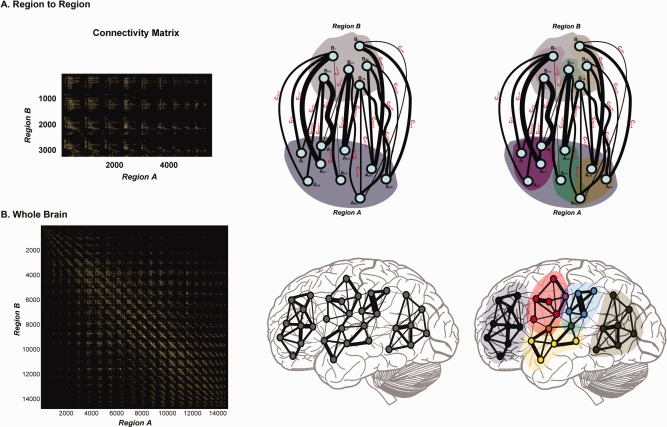
cmICA factorizes the connecitivity as follows. In the Region to Region case (A), cmICA decomposes an asymmetrical connectivity matrix into independent spatial maps $s_k$ in Region A (purple, green and brown areas), with all the nodes within each spatial map $s_k$ share the similar connectivity profile $r_k$ in Region B (lighter purple, green and brown areas). The $r_k$ represents the location and strength of how $s_k$ connects to Region B. In the whole brain connectivity case (B), cmICA decomposes a symmetric connectivity matrix into independent connectivity parcels (B Right, dark blue, red, yellow, blue and dark green areas). In this case $s_k$ can be highly correlated with $r_k$. Each intracomponent connectivity network can be computed by $r_k{s}_k^T$, and the cmICA segments can overlap (purple, orange and green dots in Figure 1B Right), representing the crossing regions in different connectivity networks. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

A number of options are available for implementing GICA and the subsequent back‐reconstruction [Erhardt et al., 2011]. We describe the method below in four steps‐1. PCA data reduction of connectivity matrix $C_k$ for a single subject; 2. Group concatenation of reduced data $C^{*}$ and second level PCA reduction; 3. ICA on group data into maps S; 4. Back‐reconstruction of group S and R into subject level $S_k$ and $R_k$.

Notations

• S: ICA independent spatial components, parcels, or tracts (for diffusion tractographic data).

• R: ICA connectivity profile, paired with S and representing its connection strength across brain.

• Connectivity matrix: a $N_b\times N_a$ matrix, representing the connectivity strength between all node pairs across two brain regions Region A (size $N_a$) and Region B (size $N_b$); S separate Region A, and R separate Region B.

• Nodes: Single elements in Region A or Region B.

• Connection: Single elements in connectivity matrix.

Subjects

Subjects were recruited via the Center for Biomedical Research Excellence (COBRE, http://cobre.mrn.org) program at the Mind Research Network. We used diffusion tensor imaging data from a large data set of schizophrenia subjects (n = 64, age = 38.8 $\pm$13.3 years) and healthy control subjects (n = 64, age = 35.3 $\pm$ 11.0 years). COBRE data are also shared via the COINS data exchange (http://coins.mrn.org/dx) [Scott et al., 2011; Wood et al., in press]. Each subject provided written informed consent according to guidelines at the University of New Mexico and was compensated for their participation. Prior to inclusion in the study, all healthy subjects were screened to ensure they were free from neurological or psychiatric diseases (DSM‐IV Axis I or Axis II). Structural clinical interviews for DSM‐IV (SCID) and case file reviews confirmed diagnosis of schizophrenia for the patients. The specific clinical screening protocol can be referred to our recent work [Cetin et al., 2014], including retrospective and prospective clinical stability, medical history, etc. Patients and control were matched with age, gender, race, parental socioeconomic status (education and occupation levels), a less biased premorbid intelligence estimate [Saykin et al., 1991; Yeo et al., 2014]. Table 1 provides demographic and clinical information in details. The data was all collected on a 3T Siemens Trio scanner with identical imaging parameters.

Table 1.

Demographic and clinical information

	Schizophrenia patients (n = 64)	Healthy controls (n = 64)	P‐value
Age (Years)	38.8 ± 13.3	35.3 ± 11.0	0.11
Gender (Male:female)	50:14	45:19	0.32
Racea	2:2:4:1:55	2:0:5:0:57	0.63
Marital statusb	7:8:47:2	17:9:38:0	8.9e‐3
Socioeconomic status
Highest level of educationc	3.8 ± 1.4	4.6 ± 1.3	1.6e‐3
Parental education levelc(primary/secondary caretaker)	4.2 ± 2.0/4.5 ± 2.2	4.7 ± 1.9/4.9 ± 2.3	0.25/0.39
Highest level of occupationd	5.1 ± 1.5	3.8 ± 1.3	1.4e‐6
Parental occupation leveld(primary/secondary caretaker)	4.3 ± 1.7/4.3 ± 1.7	3.6 ± 1.5/3.9 ± 1.8	0.03/0.25
Family psychosis historye	16 (25%)	1 (1.6%)	6.6e‐5
Psychiatric onset agef	22.0 ± 8.4
WTAR IQg	99.4 ± 16.4	109.8 ± 12.8	2.0e‐4
WASI Sum IQh	98.0 ± 17.4	111.2 ± 11.8	5.8e‐6
MATRICS composite scorei	30.9 ± 13.6	50.4 ± 8.3	1.9e‐14
PANSSj
Positive	15.0 ± 4.6
Negative	14.6 ± 4.6
General	29.7 ± 8.3

^aRace: American Indian (or Alaska native): Asian: black (or African American): native Hawaiian (or other pacific islander): white.

^bMarital status: married: divorced: single: separated.

^cHighest level of education/parental education level ‐ ‘1’ grade 6 or less, ‘2’ grade 7 ‐ 12 (without graduating high school), ‘3’ graduated high school or high school equivalent, ‘4’ part college, ‘5’ graduated 2 yr college, ‘6’ graduated 4 yr college, ‘7’ part graduate/professional school, ‘8’ completed graduate/professional.

^dHighest level of occupation/parental occupation level ‐ ‘1’ higher executives, proprietors of large concerns, and major professionals, ‘2’ business managers, proprietors of medium‐sized business, and lesser professionals, ‘3’ administrative personnel, small independent businesses, and minor professionals, ‘4’ clerical and sales workers, technicians, owners of small businesses and minor professionals, ‘5’ skilled manual employees, ‘6’ machine operators and semi‐skilled employees, ‘7’ unskilled employees.

^eFamily psychosis history: having first degree relative with psychosis.

^fPsychiatric onset age: age at first diagnoses of schizophrenia or schizoaffective disorder.

^gWTAR: Wechsler test of adult reading.

^hWASI: Wechsler abbreviated scale of intelligence.

ⁱMATRICS: ‘Measurement and treatment research to improve cognition in schizophrenia’ consensus cognitive battery.

^jPANSS: Positive and negative syndrome scale.

Data Acquisition

Diffusion data were acquired via a single‐shot spin‐echo echo planar imaging (EPI) with a twice‐refocused balanced echo sequence to reduce eddy current distortions. The DTI sequence had 30 directions, b = 800 s/mm² and five measurements of b = 0, for 6 minutes of acquisition time. The b = 0 measurements were interleaved after every six non‐zero b‐value measurements. DTI was obtained in the axial direction along the AC‐PC line. The FOV was 256 × 256 mm with a 2 mm slice thickness, 72 slices, 128 × 128 matrix size, voxel size = 2 mm × 2 mm × 2 mm, TE = 84 ms, TR = 9,000 ms, NEX=1, partial Fourier encoding of 3/4, and with a GRAPPA acceleration factor of 2.

Diffusion Analysis

Quality control of diffusion images were based on an automatic algorithm based on several criteria. The signal drop‐outs caused by large or abrupt motion were identified and removed by a custom in‐house program written in IDL (http://www.exelisvis.com). These typically appear as zipper like artifacts in the sagital view. The smaller and the gradual motion through the scan, and the eddy current induced distortions were corrected by registering images to the first b = 0 image by flirt/FSL (http://fsl.fmrib.ox.ac.uk) with an affine transform and mutual information cost index. A gradient direction requiring more 3 mm of displacement on 100 cm radius sphere was not included. The back ground noise level threshold was automatically calculated from regions outside the image (mean + two times the standard deviation). The mean image signal for a given gradient direction had to be greater than this threshold, otherwise the gradient direction was dropped. Subjects with greater than 10% of the gradient directions removed were not included because of the possible bias in their calculated diffusion parameters. The effect of removing gradient directions on FA calculation has been previously studied by our group [Ling et al., 2012]. We have not studied the effect of removing gradient directions on connectivity calculations. Gradient directions were adjusted for any image rotation required during the motion correction step. This was followed by calculating the orientation distribution function (ODF) by bedpostx/FSL and probabilistic tractography by probtrackx/FSL.

During tractography, we performed bedpostx on native space and then warped onto the standard MNI FA maps. Also in this application, we used the entire brain's voxels as the seed region as well as the target region, without predefining any ROI masks to ensure pure data driven blind source separation. To balance the computation demands and performance, a 5 mm spatial resolution and 250 streamlines from each seed voxel were used. Down‐sampling at this stage reduced the number of voxels and the connectivity matrix to a large, yet manageable size. The spatial resolution of 5 mm was the smallest voxel size we could handle based on our memory limits, with ∼200 Gb RAM cost for 128 subjects. On three subjects we did single subject cmICA with 250, 500, and 1000 streamlines, and the tract patterns were essentially similar to those obtained by using 250 streamlines. We then proceeded to do further analysis with 250 streamlines for reasons of computational speed.

Connectivity Analysis

After probabilistic tractography, whole brain voxel‐paired connectivity were converted with a two‐dimensional connectivity matrix for further analysis, as illustrated in Supporting Information A. The connectivity matrices from the two groups of subjects were then subjected to a multi‐subject cmICA and followed by back‐reconstruction for each subject [Calhoun et al., 2001]. The whole analysis pipeline is shown in Figure 2, with steps of data acquisition, diffusion analysis, connectivity matrix construction described in Methods 2‐4 and the final cmICA. The group‐level cmICA implemented here is equivalent to the temporal‐concatenated group ICA algorithm applied previously in fMRI [Calhoun and Adali, 2006; Wu et al., 2010]. Similar to the fMRI in group‐level analysis, we concatenate the input Region B by Region A data of individuals along Region B. The cmICA calculates maximally spatial independent maps S for Region A that are representative across all subjects in the group. These maps were back‐reconstructed into subject‐specific spatial maps S_k and their shared connectivity profile maps R_k, where k is the subject index. And the group‐level connectivity profile maps R are calculated as the aggregation of R_k. (Note that the aggregation of S_k is mathematically close to S). The cmICA produces spatially independent maps S over Region A and their connectivity profile maps R over Region B across all subjects.

Figure 2.

The cmICA connectivity analysis pipeline includes the initial DTI preprocessing, FA map calculation, bedpostx/probtrackx to retrieve connectivity information, connectivity matrix construction, and the final ICA parcellation. ICA can be employed for a single subject analysis (left) or for group level analysis (right). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

We examined the similarity between S and R based on our data and further discuss this point later. In addition a mathematical condition is derived when there will be perfect correlation between $s_k$ and $r_k$ (Supporting Information B). All components were thresholded to display the strongest tract regions based on the distribution of voxelwise t‐statistics [Allen et al., 2011]. ICASSO with multiple re‐runs and random initial conditions was used to arrive at a robust decomposition [Himberg et al., 2004].

Since this is the first attempt to apply ICA to whole‐brain tractography at the group level, we chose both low order (30) and high order (100) to understand the effect of model order selection. These model orders were chosen based upon our previous extensive experience in ICA in fMRI and EEG [Calhoun and Adali, 2012; Calhoun et al., 2010; Wu et al., 2010]. The choice of low and high model orders lets us study the fine‐grained regional separation obtained by higher order models for our diffusion based data. In contrast to fMRI applications [Allen et al., 2014; Kiviniemi et al., 2009; Wu et al., 2010], as well as to maintain more variance of information (>80%), we also evaluated ICASSO results across several high model orders from 50 to 150, and empirically determined that 100 was the best choice in terms of covering all the expected tracts and providing the most stability within our dataset. We also ran cmICA on three individual subjects separately as well as on group analysis at both model orders to look at reproducibility and stability of the model.

Group Difference Analysis

After cmICA back‐reconstructions, each subject has its own independent tract maps S_k and their shared connectivity profile R_k corresponding to each ICA components. We ran two‐sample t‐tests separately for both S_k and R_k for all the subjects to look for connectivity based group differences. Previous schizophrenia studies have demonstrated that brain structural connectivity is highly associated with age or illness duration [Jones et al., 2006; Kyriakopoulos et al., 2009; Voineskos et al., 2010]. In this study, we first used a multivariate model selection procedure to check the impact of different factors by performing a multivariate analysis of covariance (MANCOVA) on effects of age, gender, race and group label as well as their dependences to see which one(s) predictor in the design matrix showed variabilities in the multivariate response. And we found that for these 128 subjects only the age predicted a significant variability whereas the age × group or any other factors in the design matrix didn't indicate a significant variability. We then only removed age‐related effects and their likely influence on cross‐group comparison by matching ages across groups and testing the statistical differences with age as a covariate. Lastly, the significant regions were adjusted for multiple comparisons using the false discovery rate (FDR) corrected P < 0.05 and cluster size > 5 voxels.

RESULTS

Low Model Order Tract Clusters S

We broadly classified 30 cmICA spatial maps into three major functional categories, seen in Figure 3, consisting of commissural (right‐left hemispheric cortex), association (same hemispheric cortex‐cortex) and projection (cortex‐spinal, cortex‐thalamic) fibers [Mori et al., 2005; Wakana et al., 2004], with detailed names in each category aided by the 20 region ‘JHU white‐matter tractography atlas’ [FSL‐Atlases; Hua et al., 2008; Wakana et al., 2007]. The cmICA spatial maps were converted to ROIs for visualization purposes by a suitable threshold. The ROI was generated by t‐statistics and thresholded at $t>\mu +4\sigma$, with $\mu$ being the mean and $\sigma$ the standard deviation of spatial component (as discussed by [Allen et al., 2011] in Appendix B). Note that we do not use these ROIs for looking at group differences.

Figure 3.

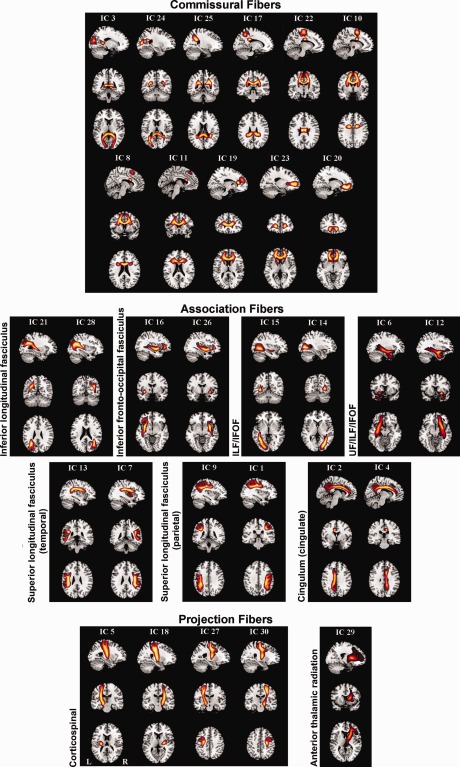
cmICA connectivity maps are shown for the low (30) model order. All S components are categorized into three groups consisting of commissural, association, and projection tracts. The detailed subcategories (following JHU atlas) are shown as well. All atlas labels were found, except the hippocampal part of cingulum and the left anterior thalamic radiation.

The commissural fibers define the fibers that go across the corpus callosum connecting both hemispheres of the brain. We found that eleven out of the thirty ICA components belonged to this category. The association fibers connect different parts of the brain within the same cerebral hemisphere. Fourteen of the thirty ICA components belonged to this category. These include the inferior longitudinal fasciculus (ILF), inferior frontal‐occipital fasciculus (IFOF), superior longitudinal fasciculus (SLF, temporal and parietal), uncinate fasciculus (UF) and cingulum (superior cingulate part, supracallosal). The projection fibers connect the cortex to the lower parts of the brain and spinal cord, and include the corticospinal tracts and anterior thalamic radiation (ATR). Five ICA components from our data were classified as the projection fibers.cmICA segmented the corpus callosum into eleven segments based on the connectivity of these regions (Fig. 4). The JHU atlas does not provide the segments of the corpus callosum (CC), other than forceps major and forceps minor. We did not find any of atlases, JHU or others, that parcellate commissural tracts across other CC locations, probably because it is more difficult to track consistent commissural tracts in varying orientations across different subjects. This is similar to Hofer's tractography based findings [Hofer and Frahm, 2006] but with a finer corpus callosum segmentation.

Figure 4.

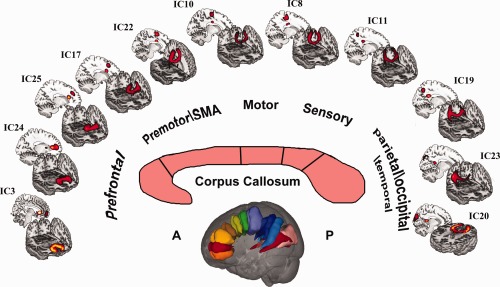
This is an example of connectivity based segmentation of corpus callosum. These eleven components belong to commissural fiber tracts, and connect both hemispheres through the corpus callosum. These tract components spread along different orientations, connecting different parts of cortical area to the corpus callosum. These areas include prefrontal, premotor, motor, sensory and parietal/occipital/temporal brain regions. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

cmICA Maps Correspondence to JHU Tractography Atlas

All the spatial tract components were numerically compared to the JHU 20 region white matter tract atlas, based on the overlap of the ICA components to the JHU atlas regions. Table 2 shows the percentage overlap of ICA maps converted to an ROI to the JHU atlas (JHU‐ICBM‐tracts‐maxprob‐thr0‐1mm from the FSL atlas library) [Hua et al., 2008; Mori et al., 2005; Wakana et al., 2007; Wakana et al., 2004]. The ICA maps are rank ordered to indicate the maximum two overlap regions of the JHU atlas. For example, 68.8% of IC 18 overlaps with the left corticospinal tract and 16.3% with left superior longitudinal fasciculus. Figure 5 shows the 10 different ICA maps that had the maximum overlap with the JHU atlas. These maps are marked with asterisks on IC index in the first column of Table 2. Two other maps (IC26 and IC11) are also shown in Figure 5 to make the left/right pairs complete. The major part of IC11 is a commissural fiber segmenting the corpus callosum.

Table 2.

Thirty‐component cmICA maps correspondence to JHU tractography atlas

IC index	Fiber type	JHU atlas region	%	JHU atlas region	%
IC 7a	Association	Superior longitudinal fasciculus L	90.4	Anterior thalamic radiation L	0.8
IC 9a	Association	Superior longitudinal fasciculus R	84.2	Inferior longitudinal fasciculus R	2.1
IC 1	Association	Superior longitudinal fasciculus L	82.6	Corticospinal tract L	1.8
IC 13	Association	Superior longitudinal fasciculus R	82.6	Superior longitudinal fasciculus (temporal) R	7.4
IC 4a	Association	Cingulum (cingulate gyrus) L	76.3	Forceps minor	2.4
IC 3a	Commissural	Forceps major	75.4	Inferior fronto‐occipital fasciculus R	3.4
IC 5a	Projection	Corticospinal tract R	71.5	Superior longitudinal fasciculus R	17.3
IC 23a	Commissural	Forceps minor	69.4	Anterior thalamic radiation R	13.2
IC 18a	Projection	Corticospinal tract L	68.8	Superior longitudinal fasciculus L	16.3
IC 16a	Association	Inferior fronto‐occipital fasciculus R	67.8	Anterior thalamic radiation R	10.9
IC 2a	Association	Cingulum (cingulate gyrus) R	64.5	Forceps minor	9.1
IC 29a	Projection	Anterior thalamic radiation L	63.2	Inferior fronto‐occipital fasciculus L	22.3
IC 19	Commissural	Forceps minor	62	Anterior thalamic radiation L	12.7
IC 20	Commissural	Forceps minor	59.8	Uncinate fasciculus R	7.6
IC 26a	Association	Inferior fronto‐occipital fasciculus L	48	Inferior longitudinal fasciculus L	11.6
IC 15	Association	Inferior longitudinal fasciculus R	45.5	Inferior fronto‐occipital fasciculus R	33.4
IC 14	Association	Inferior longitudinal fasciculus L	44.1	Inferior fronto‐occipital fasciculus L	25.6
IC 24	Commissural	Forceps major	43.6	Inferior fronto‐occipital fasciculus R	21.2
IC 28	Association	Inferior longitudinal fasciculus L	37.6	Superior longitudinal fasciculus L	27.9
IC 21	Association	Inferior fronto‐occipital fasciculus R	35.4	Inferior longitudinal fasciculus R	17.1
IC 27	Projection	Corticospinal tract R	33.6	Superior longitudinal fasciculus R	31.9
IC 30	Projection	Superior longitudinal fasciculus L	30.1	Corticospinal tract L	24.2
IC 12b	Association	Inferior fronto‐occipital fasciculus L	27.2	Inferior longitudinal fasciculus L	22.2
IC 6b	Association	Inferior fronto‐occipital fasciculus R	21	Anterior thalamic radiation R	15.1
IC 22c	Commissural	Corticospinal tract R	17.8	Corticospinal tract L	17.5
IC 11 a,c	Commissural	Anterior thalamic radiation R	14.4	Forceps minor	12.1
IC 17c	Commissural	Cingulum (cingulate gyrus) L	13	Corticospinal tract L	11.7
IC 25c	Commissural	Anterior thalamic radiation L	11.6	Superior longitudinal fasciculus L	11.1
IC 10c	Commissural	Anterior thalamic radiation R	6.7	Anterior thalamic radiation L	6.1
IC 8c	Commissural	Anterior thalamic radiation L	5.4	Anterior thalamic radiation R	4.9

^aMarks the components plotted in Figure 6.

^bIC12 and IC6 have overlaps with uncinate fasciculus 17.4% and 14.1%.

^cMarks the tracts not covered by JHU atlas (<20% overlap), which visually identified as commissural fibers across corpus callosum. ‘Fiber type’ is labeled based on the actual tract trajectory.

Figure 5.

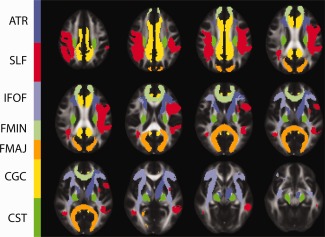
Ten cmICA tract maps are shown with maximum spatial overlaps with the JHU atlas' JHU‐ICBM‐tracts‐maxprob‐thr0‐1mm in FSL's atlas library. These maps included forcep major (FMAJ), forcep minor (FMIN), right inferior‐fronto‐occipital fasciculus (IFOF), left anterior thalamic radiation, and left and right hemisphere superior longitudinal facsciculus (SLF), cortico‐spinal tract (CST), cingulated gyrus (CGC). We have also included left inferior‐fronto‐occipital fasciculus (IFOF, IC 26) and right anterior thalamic radiation (ATR IC 11) for completing the left/right pairs. Table II computes all thirty cmICA components' overlapping percentage with JHU atlas regions. Six out of eleven commissural components that were not covered by the JHU atlas, excluding FMAJ and FMIN, were labeled according to the atlas region with which they had maximum correspondence. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

High Model Order Tract Clusters S

As expected, at the higher order model of 100, seen in Figure 6, the cmICA component split into finer regions. However, the majority of these components could still be associated with the broad atlas definitions, but with smaller coverage. Figure 6B shows that the numbers of association components, especially covering ILF and IFOF, as well as thalamic radiations were significantly increased. Some of the tracts that were not detected in lower order model, such as infracallosal cingulum in the hippocampus (Fig. 6B, component 18 and 27), were recovered at the higher order. Thalamic radiations (Fig. 6C) of different orientations (anterior, superior, posterior) were also identified instead of anterior regions only in the case of lower model and in JHU atlas.

Figure 6.

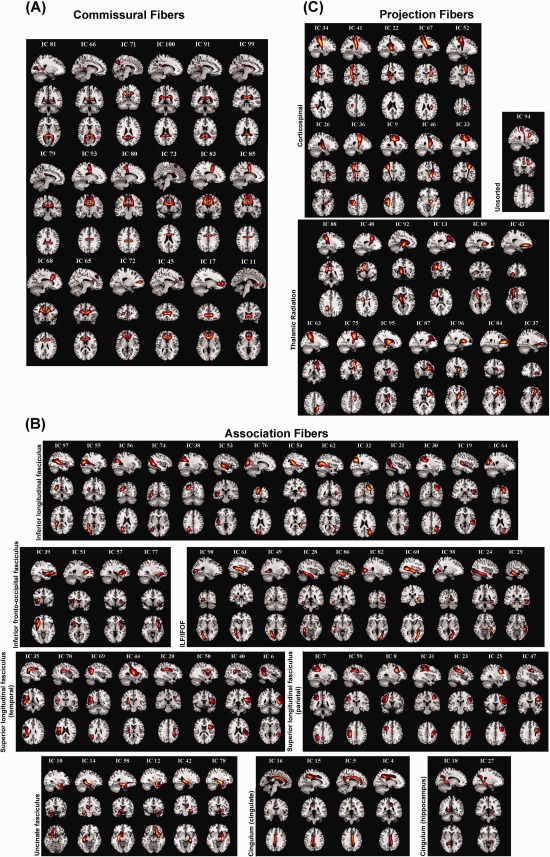
cmICA connectivity maps are shown for the high (100) model order. Ninety seven S components at model order of one hundred are plotted in a format similar to that of Figure 4, with commissural fibers shown in (A), association fibers in (B) and projection fibers in (C). The tracts split into finer regions, but overall follow the atlas definitions. One component (IC94) covered two disjoint atlas tracts. There were no missing JHU atlas defined tracts in the ICA maps. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 7 demonstrates a case of component splitting related to UF because of the higher order choice. The leftmost and rightmost plots are component 6 and 12 from model order 30, which cover tracts of the UF and partial IFOF. The two plots in the middle are from model order 100, corresponding to the low order model precisely. Besides increased splitting of the components, some of the cluster definitions are refined in higher model order. For example, components 10 and 12 in the model order 100 case show fine‐grained tracts with more precise segmentation and better alignment to the UF (hook‐shape only).

Figure 7.

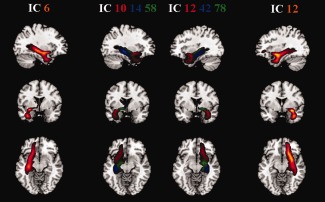
This is an example of how a high model order analysis can split components obtained from a low model order analysis and improve the definition of the connected region. The component IC6 (right hemisphere, and leftmost plot) and IC12 (left hemisphere, and rightmost plot) are from low order analysis. They cover uncinate fasciculus and parts of the inferior fronto‐occipital fasciculus. The corresponding high order analysis components (shown in the middle) are IC10, IC14, IC58 (right hemisphere) and IC12, IC42, IC78 (left hemisphere). They clearly demonstrate the splitting of the low model order component, and the better definition of the hook‐shape of uncinate fasciculus as captured by the high order components IC10 and IC12. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Each cmICA analysis gives components in an arbitrary order. Hence, in order to compare the low order and the high order cmICA analysis, the components have to be sorted to match. Sorting of the components here was based on three criteria: (1) high spatial correlation to the lower model component above 0.5, (2) atlas regions overlapping above 50% and (3) manual verifications. Out of one hundred components, three were categorized as artifacts because the mask was slightly larger and included parts of the cerebellum and the spatial pattern is different compared to the useful components (Supporting Information C). After artifact removal, component IC94 (Fig. 6C Unsorted) was the only one that covered two disjoint (projection) tract structures (corticospinal and thalamic radiation, both on the left).

To ensure the validity of model order selections on our dataset, we tested the convergence during ICA training and the stability via ICASSO on both low and high model orders (Supporting Information D). The results showed that both model orders are fairly reliable.

S and R Comparisons

The group‐specific components of S and R can both be seen as the aggregated subject‐specific tract maps S_k and conjugate tract maps R_k. S defines the group independent spatial components (parcels) of the predominant fiber bundles from the entire brain, and R defines the common connectivity profile or which (fiber) region of the brain that S is most connected to. In Figure 8, we examine the correlation between $s_k$, the row of S, and $r_k$, the column of R. Each pair $(s_k,r_k)$ defines two different spatial maps, and they contribute to the connectivity matrix through the outer product $r_k{s}_k^T$ (Eq. [2]). High correlation between $s_k$ and $r_k$, means that $s_k$ is highly connected to itself, within its own spatial map. An example of perfect correlation between $s_k$ and $r_k$ makes it clearer. In this case $r_k{s}_k^T$ would be a symmetric connectivity matrix which can be reordered to give a tight connected cluster. A low correlation between $s_k$ and $r_k$ means, that although $s_k$ defines a region which has high structural connectivity, this region is also connected to other regions not part of $s_k$.

Figure 8.

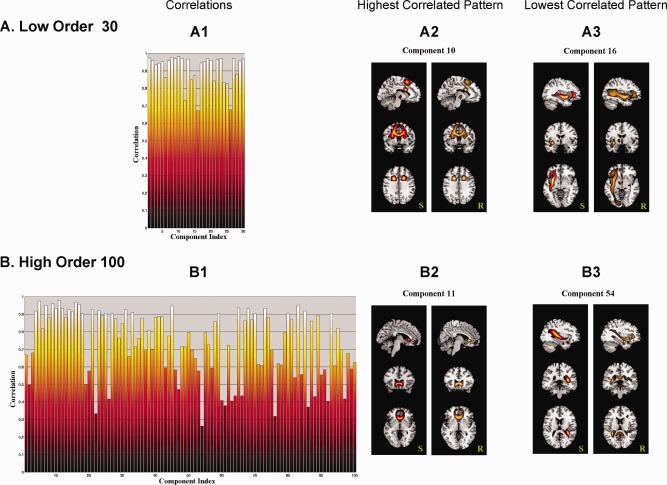
The spatial correlation between rows of S and the corresponding columns of R for the low model order analysis (A) are compared to those of the high model order analysis (B). A1 and B1 are the correlations between all S and R pairs for the two model orders, A2 and B2 are the tract patterns of the pairs with the highest correlation, and A3 and B3 are the tract patterns of the pairs with the lowest correlation between S and R pairs. The S part of component 16 (A3) is connected to a broader region in R, lowering the correlation; whereas the S part of component 54 (B3) is connected to regions in the opposite hemisphere, lowering the correlation. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

At low order model of 30, the majority of the S and R pairs are highly correlated to each other (Fig. 8 A1), with the highest correlation of 0.982 for component 10 (Fig. 8 A2) and the lowest correlation of 0.671 for component 16 (Fig. 8 A3). At high order model of 100, correlations decreased for many components because of more detailed region definitions (Fig. 8 B1). The highest correlation was 0.979 for component 11 (Fig. 8 B2) and the lowest correlation was 0.262 for component 54 (Fig. 8 B3). However, we found that the patterns of components in the high order case are similar to those of the matching components of the lower model order case. For example, component 10 in low order and component 11 in high order were either in or close to the corpus callosum ‐ forcep major tracts. This was also true for component 16 in low order and component 54 in high order for the IFOF/ILF tract. Finally, we found that the low correlations between S and R was due to R extending more broadly to neighboring regions, meaning S was highly connected to itself as well as neighbor fibers (e.g., low model order, component 16 in Fig. 8 A3); alternately, the low S and R correlation can be seem when R reaches to the same tract region of S, but in the opposite hemisphere (e.g., high model order, component 54 in Fig. 8 B3).

Group Difference Between Schizophrenia Patients and Healthy Controls

One of the benefits of using cmICA is that it not only detects similar patterns across the group, but at the same time captures intersubject variability. Figure 9 illustrates group differences between patients diagnosed with schizophrenia and healthy controls as captured by low and high order cmICA for components divided into three main categories of commissural, association, and projection fiber bundles. Each category includes significant results from all the components belonging to that category. After the removal of age effects, FDR correction, and removal of clusters smaller than 5 voxels, we found that: (1) the connectivity strength was significantly reduced in schizophrenia across large regions of the brain. (2) The blank pictures for S are there to indicate no significant regions. The group differences in tract maps S are smaller (volume‐size) than in conjugate maps R. This is partially due to the group ICA concatenation orientation, and in general R was more sensitive than S, see discussion for details. (3) The group differences for the high order model were across more components, but the overall regions (e.g., coverage and intensity) are similar to those in the low order model. (4) Most of the group differences were found in the right hemisphere. The effect of interhemispheric coordination or lateralization cannot be fully determined at this point. However, it has been reported that one of the important trait markers in schizophrenia is reduced laterality [Hoptman et al., 2012; Oertel et al., 2010]. The significant components are presented in detail in Table 3, including the identified cluster sizes and the peak voxel coordinates and t values.

Figure 9.

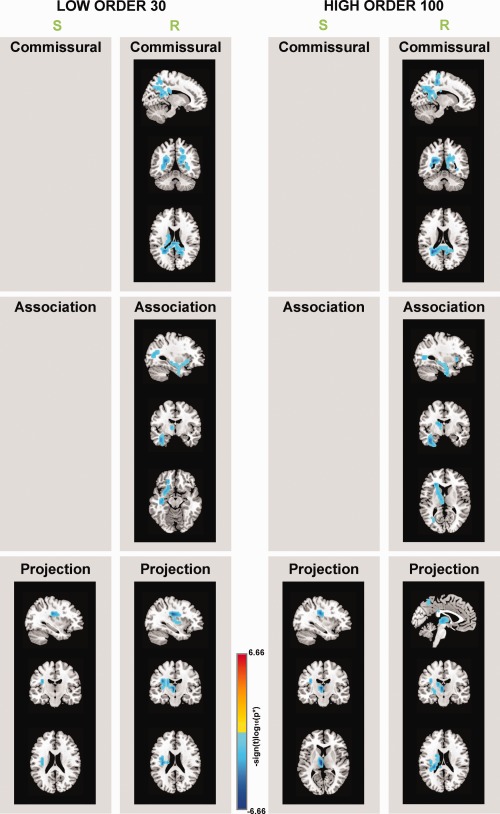
The regions with significant group differences (P < 0.05*) between patients with schizophrenia and healthy controls are separately illustrated for the low and the high order models, and for S and R. The effect of age was removed, the significance was after FDR correction and significant clusters larger than five voxels are shown. The blank areas mean that there were no significant differences found in these categories. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 3.

MNI table of group difference components

S	Sizea	Peak	R	Sizea	Peak
Low order 30
Commissural
			R 3	6	(−15,51,18), −6.074
			R 17	46	(20,31,28), −5.937
			R 25	60	(−15,61,48), −4.694
Association
			R 6	18	(40,6, −27), −4.780
			R 16	38	(25,61,28), −4.946
Projection
S 5	7	(35,21,28), −5.354	R 5	61	(5,31,73), −5.776
			R 29	9	(5,21,‐1), −5.889
High Order 100
Commissural
			R 71	112	(25,51,23), −5.679
			R 80	21	(−15,31,48), −6.178
			R 91	7	(−35,31, −7), −3.895
Association
			R 14	32	(40,6, −32), −4.760
			R 39	6	(25,76,3), −4.315
			R 51	8	(35, −19,3), −4.592
			R 58	41	(10,16,3), −5.395
Projection
S 34	7	(35,21,28), −5.531	R 22	9	(15,16,13), −3.791
S 92	16	(5,16,8), −6.656	R 34	6	(35,21,23), −4.949
			R 63	18	(25,36,33), −4.070
			R 88	32	(25,36,33), −4.743
			R 89	15	(5,21, −2), −6.017

^a‘Size’ is calculated in units of voxels, 1 voxel = 5 × 5 × 5 mm³.

DISCUSSION

Structural Connectivity in Schizophrenia

There has been a growing interest in brain connectivity studies [Allen et al., 2014; Cloutman and Ralph, 2012; Deco et al., 2011; Honey et al., 2009] describing communication across different brain regions, in contrast to traditional analysis regarding properties of single brain regions (ROIs), such as volumes, magnitudes, or diffusivities. Previous studies [Deco et al., 2011; Honey et al., 2009] suggest a clear consensus that structural connectivity is highly associated with functional connectivity, whereas functional connectivity directly impacts normal cognition, cognitive abnormality, and cognitive status. Our approach presents a promising method to study how brain disease (e.g. schizophrenia) is related to changes in brain structural connectivity. Although a full discussion of various findings and models of schizophrenia is beyond the scope of this paper, it has been shown [Ashtari et al., 2007; Camchong et al., 2006] that schizophrenia is associated with reduced brain structural connectivity, as indicated by reduced FA, a marker for fiber tract integrity. Diffusion tensor model based calculations and FA brain maps are believed to reflect the diffusion direction, myelin structure, and fiber density. In addition FA is relatively easy and fast to compute. However, we recognize that FA and connectivity as measured here are sensitive to different tract properties. Although, both FA and connectivity matrix are calculated from diffusion data, FA is a measure of a local tract property while connectivity is a larger scale interregional tract property. The two quantities are related, because local white matter damage, as indicated by a FA decrease, can change a global connectivity measure. But this need not be so, because brain can develop alternate pathways connecting the two regions. The connectivity matrix measures how well any two regions are connected regardless of the exact local pathways. FA being a local property can be more sensitive to detect changes in small regional areas. These differences imply that FA and connectivity provide different measures of white matter integrity. Other anisotropy measures such as generalized fractional anisotropy (GFA) [Tuch, 2004] have been defined with high angular resolution diffusion imaging (HARDI), but these measures are also local tissue properties (e.g. GFA is simply an extension of local FA with a generalization to more than three eigenvalues [Cohen‐Adad et al., 2011; Tuch, 2004]), and are again ‘proxy’ markers for anatomical connectivity.

We observed significant decrease in white matter connectivity in patients diagnosed with schizophrenia (compared with healthy controls) in the corticospinal tract, thalamic radiation, uncinate fasciculus, forcep major and inferior fronto‐occipital fasciculus. The affected tracts are consistent with previous analysis based only on FA [Camchong et al., 2011; Caprihan et al., 2011; White et al., 2011] but the significant differences seen here in connectivity are for broader spatial regions. An ICA based method has been used previously to decompose FA maps into spatially independent brain structures [Caprihan et al., 2011; Li et al., 2012]. The group differences were seen in terms of the loading coefficients, which was one number per map per subject. In our present analysis, the loading coefficient is itself a spatial map, and gives better localization of the spatial region where there are connectivity differences. We directly probe for connectivity differences.

The present tractography‐based connectivity technique is better in terms of identifying (major) axonal bundles. The ICA components in our data‐driven study matched well with an established white matter tract atlas [Hua et al., 2008; Mori et al., 2005; Wakana et al., 2007]; whereas ICA components from FA based maps [Caprihan et al., 2011] have only partial coverage of the brain, being restricted to the white matter regions. Schizophrenia is believed to be an information processing incapability or a brain connectivity abnormality [Fitzsimmons et al., 2013]. Tractography should increase the sensitivity of capturing the difference between patients diagnosed with schizophrenia and healthy controls, because it provides information regarding ‘connectivity’ within white matter tracts. To fully understand the relative advantages of fractional Anisotropy versus connectivity based analysis, it is still required to compare on a common data set.

This study focused on probabilistic tractography and cmICA to implement connectivity‐based parcellations. Probabilistic tractography has been used to segment thalamus, cortical regions or subcortical regions [Behrens et al., 2003a; Jbabdi et al., 2009; Johansen‐Berg et al., 2004; O'Muircheartaigh et al., 2011]. Considering the plethora of methods related to our work, we discuss some brief comparisons with two popular methods commonly used in connectivity‐based tractography studies, namely streamline tractography and spectral clustering [Cloutman and Ralph, 2012]. Streamline tractography, which relies on a deterministic model, does not perform well in regions where we expect crossing fibers, and is not a good approach for cortical parcellation due to the subthreshold FA in gray matter. Spectral clustering, a graph‐based segmentation method, focuses on ‘all‐or‐nothing’ hard clusters, which may cause false parcellations in regions exhibiting crossing fibers. Comparing clustering with cmICA and clustering with spectral clustering we note that the cuts in spectral clustering depend heavily on the similarity matrix measures and global normalization. This can be especially inconsistent and inefficient when the model order is high and the cut number increases. These observations are consistent with many previous studies [Behrens et al., 2007; Behrens et al., 2003b; Nadler and Galun, 2006; Von Luxburg, 2007].

ICA in Connectivity

ICA has achieved great success in neuroimaging applications, particular in fMRI [Beckmann et al., 2005; Calhoun and Adali, 2006; Greicius et al., 2004; Kiviniemi et al., 2003; McKeown et al., 2003]. The goal of ICA for fMRI analysis is to study the spatio‐temporal structure of the signal. One can choose to work with either spatially or temporally independent components, but most applications use the former and recover maximally spatially independent and temporally coherent sources. In this study, ICA was applied to structural connectivity. In this case, we sought components that were maximally spatially independent in tract regions (Region A) but exhibited shared connectivity profile (Region B). This approach opens avenues to explore structural connectivity maps in a data‐driven way, which we believe is useful and straightforward, compared to other parcellation methods requiring details in clustering priors and/or projections [O'Muircheartaigh et al., 2011].

Standard single‐subject ICA does not draw group inferences from multiple subject analysis naturally [Calhoun et al., 2001]. Different individuals may have very different mixing ‘loadings’ (time courses in fMRI, connectivity profile in connectivity) and matching components among subjects is imperfect. Our implementation follows the temporal concatenation approach in the GIFT toolbox, which has been extensively studied and discussed in previous papers [Allen et al., 2014; Calhoun and Adali, 2012; Calhoun et al., 2001; Erhardt et al., 2011]. The cmICA performs ICA on connectivity matrices from the entire group, capturing the common group components, then later back‐reconstructing into subject‐specific components, making subject variability and group difference comparisons relatively straightforward. In our case, cmICA assumes a common model for the spatial tract maps to avoid the single‐subject ICA problem. The GIFT software has been optimized to work with very large numbers of subjects and is not limited by the RAM of the computer used [Rachakonda and Calhoun, 2013]. To improve the execution of cmICA in large‐scale structure connectivity, we also chose ARPACK, a fast SVD method on large sparse matrices, to support PCA, and used the infomax algorithm to perform the ICA.

Compared to our strategy, another approach for performing group inference with ICA is called tensorial ICA, which was used in O'Muircheartaigh's connectivity parcellation for a similar goal [O'Muircheartaigh et al., 2011]. In tensorial ICA it is assumed that each subject's mixing matrix is a common matrix scaled by the subject's loading coefficients. In fMRI this assumption is approximately valid for a stimulus driven fMRI experiment with identical timing among subjects but not for resting‐state fMRI. A similar limitation of tensorial ICA applies here, because we are interested in regional differences of connectivity profile, which are not captured in the tensorial ICA approach beyond a simple amplitude parameter for the entire component [Beckmann et al., 2005; Calhoun et al., 2009; Guo and Pagnoni, 2008].

The ICA method has been applied previously to FA maps [Caprihan et al., 2011] and on the maps generated by TBSS analysis [Li et al., 2012]. The input data in our method is a connectivity matrix, which is also based on diffusion imaging, but the nature of the input data is different from the previous two applications. The connectivity matrix for each subject is two dimensional, and its ICA decomposition segmented the brain and gave the connectivity profile for each segment, which itself was an image. In the previous applications of ICA to diffusion imaging data the input was essentially one‐dimensional and ICA segmented the brain but only gave a scalar loading coefficient for each segment.

This is a general method to understand group differences in connectivity matrices. Connectivity matrices obtained from resting‐state fMRI data by an ICA or a seed based analysis can be further analyzed by cmICA proposed here for teasing out significant brain structures that show group differences. Another important thing to note is that once a whole brain connectivity matrix is calculated, we can extract an asymmetric submatrix between two regions and perform cmICA. This would place greater weight on the connections between the two specific regions considered, and the conclusions will have greater sensitivity to the connectivity between these two regions. In our analysis we have noted that the connectivity matrix had stronger values within white matter and consequently tracts were obtained in these regions. If connectivity between two regions within gray matter, or from white‐to gray matter needs to be emphasized then a connectivity matrix can be obtained specifically for these regions.

Relationship Between S and R

From the results of Figure 9, it is apparent that the connectivity profile maps R capture more differences than the spatial tract maps S. The fundamental reason for this result lies in the assumptions of group ICA in our model. In a manner similar to the temporal concatenation approach of fMRI data, ICA mathematical model assumes spatial stationarity across subjects, i.e. assuming common group spatial maps [Calhoun et al., 2001], while allowing for unique time courses for each subject. Subject specific spatial maps are calculated by some back‐reconstruction method. Although individual spatial maps can show differences across subjects, the differences will be small because of ICA's stationarity assumption on S [Allen et al., 2014] . A greater proportion of the difference is captured by R. This is consistent with our observation that the R maps are more sensitive than S maps in terms of inter‐subject variability, and therefore the former captures more group difference than the latter.

The connectivity matrix properties that influence the correlation between S and R to be lower or higher requires further study. Regarding the decrease of correlations between group‐specific S and R maps in the higher order model, we provide several possible explanations. First, a high order model results in more S spatial map splitting, consistent with fMRI studies [Abou‐Elseoud et al., 2010; Kiviniemi et al., 2009]. However, the corresponding R is not necessarily following the same splitting pattern. Instead, the subcomponents of R in the high order model may share similar maps as in the original R in the low order model. This has been observed in fMRI as well. For example, in the high dimensional model, the default mode network spatial component S may split into multiple non‐overlapping spatial sub‐components, although they still share high correlations on time course components R [Allen et al., 2014] as well as with the R of the original DMN component in the low order model. In this sense, the high order model will decrease the original large spatial correlation of S and R from the low order model. Secondly, we noticed that with the higher order model, S can define a region in one hemisphere but its connectivity profile R can capture connections to the opposite hemispheres, see Figure 8, B3 component 54. We believe that these tract components with low spatial correlations are still physiologically significant. And finally, the high order model captured more subtle ‘loose’ tract parcels S (e.g., thalamic radiations in different orientations beyond the anterior), with lower connectivity strength which may not be recovered in lower dimensional PCA. It is possible that these tracts S were connected with more extensive regions R than those ‘tight’ tract bundles (e.g., commissural fiber tract bundles across corpus callosum) with high connectivity strength that shares the common S and R.

The above discussion refers to the case when Region A and Region B are identical in the original connectivity matrix. When these regions are not identical, such as in the case of most commonly explored thalamo‐cortical connectivity matrix, cmICA will yield S and R in different spaces as well. Theoretically, we can apply ICA in either direction of the connectivity matrix, e.g. searching independent maps S on thalamus (thalamic parcealltion) and connected cortical areas R, or S on cortical regions (cortical parcellation) and finding connected thalamic subset R.

Limitations and Future Work

One limitation of this study is that the diffusion sequence used in our data collection, such as low b‐values of 800 s/mm² and low gradient directions of 30. This study was based on a previously collected data set fora large schizophrenia study (http://cobre.mrn.org/). However our approach is generally applicable to other data sets and the purpose of the paper is to introduce the cmICA method. The low number of gradient directions limits the number of multiple fiber orientations and the angular resolution that can be resolved in a voxel, and reduces the accuracy of the calculated connectivity matrix. The bedpost algorithm used automatic relevance determination (ARD) to limit the number of multiple fiber orientation in the model to that supported by the data [Behrens et al., 2007]. The cost of low b‐value is to reduce the sensitivity of diffusion coefficient estimation and the capability of detecting intravoxel heterogeneity, therefore resulting in reduced connectivity matrix accuracy. With these drawbacks in mind, we would like to improve our sequence quality in future. The present analysis also has a limitation of 5mm spatial resolution used for the whole brain connectivity calculation. We were interested in whole brain analysis because we wanted to develop a ‘blind’ source separation method that could look for connectivity difference not only between the white matter but also between the white and the gray matter. The primary limitation of 5 mm spatial resolution was the memory to calculate SVD of the connectivity matrix. The connectivity matrices are sparse (Supporting Information A) and it may be possible to use clever computational techniques for SVD calculation which take advantage of this sparsity. We are working on this and plan to relax this constraint in future work [Rachakonda and Calhoun, 2013]. The proposed approach is general and will work better as data quality and resolution is improved.

Although we tested our algorithm for both low model order 30 and the high model order 100 in numerous ways (see Methods), it is still hard to know the ideal number of ICA components without the ground truth and further simulation studies. It is difficult to compare our work with previous approaches because they are sufficiently different. Our review of previous work revealed that existing work typically requires a seed ROI or terminal ROI or use only a pre‐defined subset of the brain region, and hence are not purely data‐driven [Anwander et al., 2007; Catani and Thiebaut de Schotten, 2008; Cloutman and Ralph, 2012; Jin et al., 2014; Johansen‐Berg et al., 2004; Lawes et al., 2008; O'Muircheartaigh et al., 2011; Oishi et al., 2009]. We did find one similar work that utilized ICA into connectivity‐based parcellation from O'Muircheartaigh [O'Muircheartaigh et al., 2011], which was applied to thalamus‐cortical connectivity. In this paper, the authors separated left‐right hemispheres and ran ICA of model order 30 (out of 1770 thalamic volumes) on each side without further validation on model selection, and found that ICA generated similar thalamus parcellations as Behrens' hard segmentation method [Behrens et al., 2003a] in the same datasets but with increased sensitivity. Using a similar approach, we ran ICA in our subset of thalamus‐cortical connectivity matrix, and found similar parcellation results. However, we can also compare the thalamocortical regional connectivity differences in our ICA model which O'Muircheartaigh's tensorial ICA doesn't allow. These results can be replicated and validated with multiple b‐value and higher number of gradient direction data sets, as they become available.

In this study, we did not study the effect of distance on connectivity. Long range connections will be weaker. Although, the algorithm probtrackx/FSL gives on option for calculating connectivity with a distance correction, we have not studied it. This correction may alter the connectivity group differences found in this study.

The patients and the control group of subjects were matched based on age, gender, and race. They were also matched on the basis of their parental socio‐economic status (SES), which has been indicated as a more unbiased potential confounder associated with premorbid intelligence in previous works [Calvin et al., 2011; Saykin et al., 1991; Yeo et al., 2014]. However, both the WTAR and WASI IQ scores of patients were significantly lower than those of controls. Thus it is possible that connectivity differences we see are because of cognitive differences and not because of schizophrenia. All the patients are on some form of medication and its effect on connectivity is another confounding factor in this study.

CONCLUSION

This methods paper presents a general framework (cmICA) to look for differences between connectivity matrices of two groups of subjects. The connectivity matrix can be functional or structural. Our focus was on connectivity matrices derived from diffusion tractography. The method to analyze the connectivity matrix is different from other previous methods in that it gives a dual segmentation of the brain (S and R). The previous connectivity matrix analysis methods have been used to segment the brain but they do not give the connectivity profiles of these segments. A whole brain connectivity matrix based on diffusion data has not been studied before. The whole brain connectivity matrix was symmetric but as we discuss before this method can be used to study connectivity between any two different regions. The field of diffusion imaging based connectivity studies has been advanced by this method to look directly at connectivity rather than a local property such as fractional anisotropy. Finally, we applied cmICA to probe for connectivity differences between brains of patients diagnosed with schizophrenia and healthy subjects and the differences were in the connectivity profiles of tracts which included forceps major, right inferior fronto‐occipital fasciculus, uncinate fasciculus, thalamic radiation, and corticospinal tract.

Supporting information

Supporting Information Figure 1.

Supporting Information Figure 2.

Supporting Information Figure 3.

Supporting Information Figure 4.

Supporting Information Figure 5.

Supporting Information Figure 6.

Supporting Information Figure 7.

Supporting Information Figure 8.

Supporting Information Figure 9.

Supporting Information Figure 10.