Resting state functional MRI reveals abnormal network connectivity in neurofibromatosis 1

Abstract

Neurofibromatosis type I (NF1) is a genetic disorder caused by mutations in the neurofibromin 1 gene at locus 17q11.2. Individuals with NF1 have an increased incidence of learning disabilities, attention deficits, and autism spectrum disorders. As a single‐gene disorder, NF1 represents a valuable model for understanding gene–brain–behavior relationships. While mouse models have elucidated molecular and cellular mechanisms underlying learning deficits associated with this mutation, little is known about functional brain architecture in human subjects with NF1. To address this question, we used resting state functional connectivity magnetic resonance imaging (rs‐fcMRI) to elucidate the intrinsic network structure of 30 NF1 participants compared with 30 healthy demographically matched controls during an eyes‐open rs‐fcMRI scan. Novel statistical methods were employed to quantify differences in local connectivity (edge strength) and modularity structure, in combination with traditional global graph theory applications. Our findings suggest that individuals with NF1 have reduced anterior–posterior connectivity, weaker bilateral edges, and altered modularity clustering relative to healthy controls. Further, edge strength and modular clustering indices were correlated with IQ and internalizing symptoms. These findings suggest that Ras signaling disruption may lead to abnormal functional brain connectivity; further investigation into the functional consequences of these alterations in both humans and in animal models is warranted. Hum Brain Mapp 36:4566–4581, 2015. © 2015 Wiley Periodicals, Inc.

INTRODUCTION

Neurofibromatosis type I (NF1) is a genetic disorder caused by heterozygous mutations in the neurofibromin 1 gene at locus 17q11.2 [Barker et al., 1987; Cawthon et al., 1990; Viskochil et al., 1990; Wallace et al., 1990]. The intact neurofibromin 1 protein is expressed during early embryonic neural development and plays a critical role in central nervous system (CNS) neural differentiation by regulating the p21Ras GTP‐ase signaling pathway [North, 2000; Trovó‐Marqui and Tajara, 2006]. Over 1000 mutations in the NF1 gene have been documented, although a clear genotype–phenotype correlation has yet to be established [Friedman, 1999; van Minkelen et al., 2014]. NF1 is one of the most common human genetic disorders (prevalence 1:3,500) that affects neurological, cognitive, social, and physical development [Hyman et al., 2006; Kayl and Moore, 2000; Pride et al., 2013]. Individuals with NF1 experience highly variable phenotypic expression of physical symptoms, including neurofibromas (benign tumors), skeletal malformations, and Lisch nodules [Kayl and Moore, 2000]. Despite typically having intelligence quotients (IQ) in the average to low‐average range, children with NF1 have high rates of specific learning disabilities [Hyman et al., 2006], autism spectrum disorders [Garg et al., 2013], and attention deficits [Hyman et al., 2005].

As a single‐gene disorder, NF1 represents a valuable model for understanding gene–brain–behavior relations. Mouse models have provided insight into the molecular and cellular mechanisms underlying cognitive deficits in NF1. In a seminal paper, Costa et al. showed that the spatial learning deficits seen in mice with NF1 mutations are caused by an increase in the p‐21 Ras signaling pathway. By pharmacologically decreasing Ras levels, the learning deficits were rescued [Costa et al., 2002]. Later studies showed that the increased Ras levels led to increases in MAPK activity, enhanced GABA release, and deficits in long‐term potentiation that likely contribute to the learning deficits in mice [Cui et al., 2008]. Furthermore, recent studies have substantiated the finding that hyperactive Ras/mitogen‐activated protein kinase (MAPK) cascade is critically involved in many pathogenic features of NF1 [Sharma et al., 2013]. More work is needed to elucidate the mechanisms by which these signaling alterations impact neural connectivity in individuals with NF1.

In a parallel line of investigation, neuroimaging studies have recently begun to examine structural and functional properties of the NF1 brain to understand the neural consequences of NF1 mutations in humans. Enlarged brain volume is one of the most consistent neuroanatomic findings in individuals with NF1, with about 50% of individuals meeting criteria for macrocephaly [Greenwood et al., 2005; Moore et al., 2000; Payne et al., 2010]. This is likely attributable to disrupted cell proliferation and differentiation due to mutation of the neurofibromin protein [Lee et al., 2010]. This finding is notable given that early brain overgrowth is one of the earliest signs of autism [Courchesne et al., 2003], which is present at elevated rates in individuals with NF1 and other disorders involving mutations in the Ras/MAPK signaling pathway [“Ras‐opathies”; Adviento et al., 2014]. Some studies have attributed this enlargement in NF1 individuals to globally increased white matter volume [Dubovsky et al., 2001; Margariti et al., 2007]. A recent diffusion tensor imaging (DTI) investigation revealed disproportionate disruption of white matter tracts connecting frontal regions in young adults with NF1, as well as an overall increase in diffusivity [Karlsgodt et al., 2012]. Together, these studies suggest that thicker, less organized white matter pathways may contribute to the increased brain size in individuals with NF1 [Alkan et al., 2005; Eastwood et al., 2001; Tognini et al., 2005].

Much less is known about the functional consequences of these structural abnormalities. Limited task‐based functional magnetic resonance imaging (fMRI) studies suggest that individuals with NF1 recruit vastly different brain regions than controls to process the same stimuli. Violante et al. (2012) found that NF1 individuals showed deficient activation in visual cortex during a low‐level visual processing paradigm, while other studies have observed reduced activation in frontal regions in NF1 subjects during reading, visuo‐spatial [Billingsley et al., 2003, 2004], and spatial working memory tasks [Shilyansky et al., 2010]. Although task studies provide insight into particular behavioral deficits, the more fundamental question remains: how does the resting NF1 brain compare to that of healthy controls? This can be addressed via resting state functional connectivity (rs‐fcMRI), a method for evaluating intrinsic network activity in the brain while a subject is alert but not performing an explicit task [Biswal et al., 1995; Dijk et al., 2010]. Only one previous study has examined neural activity in individuals with NF1 during “pseudo‐resting‐state” activity (i.e., subjects are presented with a task, but task‐related activation is removed). Findings suggested that use of the drug Lovastatin increased previously deficient long‐range connectivity in seven NF1 subjects [Chabernaud et al., 2012]. However, lack of demographically matched controls limited interpretability of these intriguing findings. Without a demographically well‐matched control group, it is impossible to quantify the extent and magnitude of functional connectivity alterations in NF1 patients. To our knowledge, the only existing study of resting functional connectivity in NF1 [Chabernaud et al., 2012] did not include a control group, and thus could only qualitatively compare their findings to those of prior studies to infer “abnormal” baseline connectivity in the patient group.

One of the primary goals of rs‐fcMRI is to quantify the functional relationship between multiple brain regions (nodes) by constructing a network of significant relationships between regions (edges). Once the subject‐ and group‐level network variance is accounted for [Narayan and Allen, 2013], a network graph is estimated and local properties such as edge strength can be compared between groups [Tomson et al., 2013]. Further application of graph theoretical techniques are applied to the network to characterize the global organization and structure of the resulting network [Bullmore and Sporns, 2009, 2012; Rubinov and Sporns, 2010; van den Heuvel and Sporns, 2011]. Graph theory has been recently applied to many studies in healthy individuals and in various clinical populations [Buckner et al., 2009; Delmonte et al., 2013; Lynall et al., 2010] to quantify the location of hubs, characterize the makeup of modules (neighborhoods), and network flexibility during learning [Bassett et al., 2011]. This technique provides a unique window into how brain regions communicate and how such communication may break down in the context of a disease that may disrupt neural connectivity like NF1 [Buckner et al., 2009; Lynall et al., 2010].

This study represents, to our knowledge, the first rs‐fcMRI investigation to study the functional architecture of the resting brain in subjects with NF1 relative to demographically matched healthy controls. Here we sought to elucidate how the intrinsic network structure of the NF1 brain differs from typically developing controls by inferring network structure, comparing the strength of individual edges, and calculating graph theoretical metrics from true resting state data. In addition to furthering our understanding of NF1, our analysis also applies novel methods for estimating network structure and evaluating differences in edge strength between groups. We demonstrate that these methods improve upon existing statistical frameworks and are robust to the uncertainty inherent in rs‐fcMRI data.

METHODS

Subjects

Thirty participants diagnosed with NF1 (mean age 27 ± 12; 12 males) and 30 healthy controls (mean age 29 ± 11; 16 males) were recruited for this study (Table 1). All individuals provided written consent for participation, as approved by the Institutional Review Board of the University of California, Los Angeles (UCLA), after study procedures were fully explained. NF1 participants were diagnosed with NF1 by a physician familiar with the disorder and recruited via IRB‐approved advertisements at UCLA. All NF1 participants fulfilled the diagnostic criteria specified by the National Institutes of Health Consensus Development Conference (1987), as confirmed by clinical interview and physical examination. Healthy controls were recruited through advertisements at UCLA for ongoing research studies. Controls did not have any Axis‐I psychiatric disorders or medical conditions that might affect cognitive function, as assessed by the Structured Clinical Interview for DSM‐IV [First et al., 1997]. All participants were screened for significant substance use in the last 6 months, history of head injury, mental retardation (IQ < 70), and/or insufficient fluency in the English language. All participants received a brief cognitive assessment on the day of the MRI scan, the Wechsler Abbreviated Scale of Intelligence [WASI, 1999]. NF1 participants younger than 18 completed the standard psychological assessment tool, the Child Behavioral Checklist [CBCL; Achenbach, 1992]. NF1 participants over 18 completed the Youth Adult Self Report [YASR; Achenbach, 1997], derived directly from the CBCL and adapted for participants older than 18.

Table 1.

Demographic information for NF1 and control participants

	NF1 participants (n = 30)	Control participants (n=30)	p‐value
Age (years, ±SD) [range]	27.1 (12.1) [10‐46]	25.5 (11.1) [10‐45]	0.596
Gender (N, % female)	18 (60%)	14 (47%)	0.309
Full Scale IQ (mean, ±SD)	97 (12.6)	113 (19.1)	<0.001
Years education (±SD)	14 (2.6)	12 (4.1)	0.062
Motion (mm, ±SD)	0.160 (.31)	0.269 (.21)	0.187
Scanner Location 1 (N)	19	5
Scanner Location 2 (N)	11	25

Magnetic Resonance Imaging Acquisition

All subjects were scanned at either the Ahmanson–Lovelace Brain Mapping Center (BMC) or the Staglin Center for Cognitive Neuroscience (CCN) in Los Angeles, CA, USA. Both sites had identical three Tesla Siemens Trio systems, utilizing a 12‐channel head coil. A T2 matched‐bandwidth structural image was acquired for the purposes of registration to the functional data (voxel size 1.5 × 1.5 × 4.0 mm, TR = 5,000 ms, TE = 34 ms, echo spacing = 0.89 ms, 34 axial slices, slice thickness 4.0 mm, flip angle 90°, FOV = 192, matrix size = 128 × 128). Functional T2 scans were collected while participants were instructed to fixate on a crosshair for 5 minutes. 152 volumes were collected (voxel size 3.0 × 3.0 × 4.0 mm, TR = 2,000 ms, TE = 30 ms, echo spacing = 0.79 ms, 34 axial slices, slice thickness 4.0 mm, flip angle 90°, FOV = 192, matrix size = 64 × 64).

MRI Pre‐Processing

All functional data underwent basic preprocessing using the FMRIB Software Library (http://fsl.fmrib.ox.ac.uk/fsl). Preprocessing steps included brain extraction, motion correction, spatial smoothing with a 5‐mm Gaussian kernel, band‐pass temporal filtering (0.01 Hz < f < 0.1 Hz), registration to matched bandwidth structural scan, and final registration to MNI standard space. No subject exceeded 2 mm translational mean framewise displacement prior to motion correction [Power et al., 2012], and after motion correction, no subject exceeded 1 mm FD. Global signal, 24 motion parameters, and motion confound files were regressed from the resting time‐series data [Power et al., 2014] in lieu of “scrubbing” [Carp, 2013]. There were no significant differences in motion between groups, before or after motion correction (Table 1). Additionally, there were no significant differences in global signal between groups (p = 0.82). All volumes were subsequently parcellated into 113 regions using the Harvard–Oxford atlas [Desikan et al., 2006]. All voxel time‐series within a brain region were averaged together to yield a single time‐series for each brain region. Each subject's individual data consisted of 113 time‐series with 152 timepoints.

Constructing Networks

We inferred one network for each subject to represent the pairwise relationship between all brain regions under consideration. Partial correlation coefficients were used to estimate the relationship between BOLD activity traces in each of the 113 Harvard–Oxford brain regions [Smith et al., 2011]. We whiten the time‐series assuming an AR(1) model and used the QuIC implementation [Hsieh et al., 2011] of Graphical Lasso [Friedman et al., 2008] to produce Markov networks that quantify the relationship between each pair of regions [Smith et al., 2011] for each subject. Stability selection [Liu et al., 2010; Meinshausen and Bühlmann, 2010] was used to determine the optimal network sparsity or number of edges in the network. The primary benefit of stability selection is that it retains only the most stable edges in the network, therefore eliminating the need for “hard” thresholding of the network (i.e., all values less than 0.3 would be arbitrarily discarded). This approach results in a sparse network whose remaining edges represent direct connections between nodes [Narayan and Allen, 2013; Ryali et al., 2012; Tomson et al., 2013]. To estimate a network for each group, all NF1 time‐series were whitened and then concatenated into a single time‐series. The single NF1 concatenated time‐series was subjected to the same procedures described above for single subject network estimation. The same procedure was performed for controls.

Testing for Group Differences in Edges

Once individual subject networks were constructed and sparsified, we tested whether individual edges were stronger in one group than the other. A strong edge (i.e., with a high partial correlation coefficient) will be sufficiently robust to remain in the network after sparsification, and thus will be present in the final sparsified network. A weak edge (i.e., with a low partial correlation coefficient) will not survive sparsification, and will be removed from the network. In this way, we can test each edge individually for its presence or absence in the network and compare whether an edge exists more often in one group's network than the other. This is challenging using standard methods [Narayan and Allen, 2013; Narayan et al., 2015], which often miss true edge differences and find false positives, as seen in the motivating example in Figure 1. Existing methods first estimate the connectivity network for each subject, use a two‐sample binomial Wald test for each edge, and then correct for multiple testing [Palaniyappan et al., 2013; Tao et al., 2013; Zalesky et al., 2010]. To improve the accuracy of edge testing, we developed a novel procedure called the R3 approach that obtains both a better estimate of edge presence and also accounts for inter‐ and intra‐subject variability in multi‐subject networks (described below).

Figure 1.

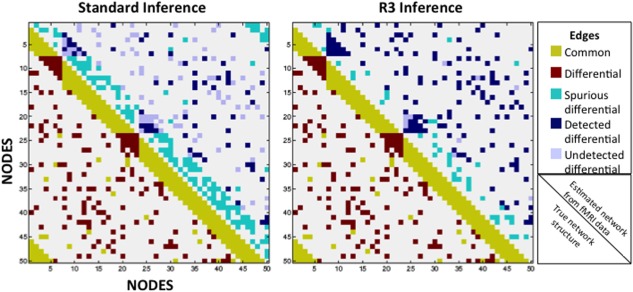
The R3 approach detects fewer spurious differences and more true edge differences, while also controlling the false discovery rate more effectively than standard inference tests (two‐sample Wald tests with FDR adjustments for multiple testing). Two artificial networks of 50 nodes and 510 edges were constructed, with 360 edges common to both graphs, and only 150 edges existing exclusively in one graph. Using standard inference tests and the novel R3 approach, we compared each technique's ability to uncover the latent graph structure beneath simulated functional MRI data from two groups of 20 subjects. Upper halves represent inference results, detailing common edges that were incorrectly identified as differential between groups (turquoise; false positives), differential edges that were correctly identified as differential (navy; true positives), and differential edges that went undetected (lilac; false negatives). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

R3 Edge Testing

The R3 method utilizes three primary procedures: resampling, random penalization, and random effects. The motivation for resampling arises from the fact that networks are estimated from noisy fMRI measurements. Thus, estimated edges in the network possess some variance. By determining whether an edge remains in a network after small perturbations to the time‐series, we are able to quantify uncertainty in estimated edges. We use subsampling to perturb the data and provide us with pseudo‐replicates of fMRI measurements. For every perturbation of the data, we estimate a corresponding network. Stable edges are present across a majority of these perturbations, and are less likely to occur by chance.

To determine whether individual edges exist exclusively in one group, we resample the 152 fMRI observations (timepoints) with replacement 100 times for every subject (bootstrapping), estimate the Markov network for each resample with random penalties [Meinshausen and Bühlmann, 2010; Narayan and Allen, 2013; Narayan et al., 2015], and then compute how often an edge is present or absent in each network estimate. This resampling procedure does not address temporal change throughout the time‐series. Because the preliminary whitening step removes correlation between all timepoints, we can randomly select a subset of the total time‐points 100 times with replacement. These 100 resampled networks allow us to calculate a variance on any network metric in which we are interested (in this case, the existence of a single edge in a single subject). Since the presence or absence of an edge is binary, we aggregate these estimates per subject to obtain an edge proportion, where proportions can vary between 0 and 1. This procedure allows us make the following exemplar statement: “Subject 1 has an edge connecting regions 4 and 5 in 81 of the 100 total resamplings (i.e., 81% of the time).” As the number of subjects is relatively small (<100), we model the probability of observing an edge using a beta‐binomial distribution and construct a corresponding two‐sample random effects test statistic [Crowder, 1978; Liang and Hanfelt, 1994; Narayan et al., 2015]. These test statistics do not follow known distributions, so we perform a basic permutation test, permuting subject labels to determine whether any significant difference is due to chance or actual group assignment [Good, 2005; Tomson et al., 2013]. We also test whether the total number of edges (after R3 sparsification) differed between groups. Finally, we use Storey's direct false discovery rate (FDR) procedure [Storey, 2002] to control for FDR at the 10% level.

As an illustration of the efficacy of our approach, we provide a simulated example for two groups of 20 subjects each with 50 nodes, 400 time‐points, and 150 truly differential edges. In comparison to standard techniques, the R3 approach finds over twice as many true edges, with substantially fewer false‐positive differences (Fig. 1).

Modularity

Modularity is a traditional graph theory metric that describes how nodes in a network organize into neighborhoods, or modules. A module consists of a group of nodes that have more edges connecting one another than connecting the group to the rest of the network. However, current clustering algorithms assign nodes to modules based on a single snapshot of the network, providing no information about how consistently a node falls into a particular module. For this reason, we improve on the existing graph theoretical metric by using a modularity stability measurement [Dudoit and Fridlyand, 2002] to score the strength of the module allegiance of each node. In other words, rather than assuming that each node belonged to only one module based on a single estimate, we perturbed the data by resampling it, then re‐estimating and reclustering the networks, finally arriving at a co‐occurrence frequency that determines how consistently two nodes belonged to the same module [Tomson et al., 2013]. Thus, in each resample, we obtain a binary statistic for every pair of nodes, indicating a co‐occurrence. We aggregated these co‐occurrences across all resamples to obtain a co‐occurrence frequency. Just as in edge‐testing, as described above, we used a two‐sample beta binomial test statistic to compare the co‐occurrence frequencies of all pairs of nodes between two groups. To determine how nodes cluster into modules, we applied Newman's modularity algorithm [Newman, 2006] to each group‐level graph. Prior to testing for statistical significance, we screened out node‐pairs that consistently had low co‐occurrences (below 40%) across all subjects in all groups. We use the terminology “clustering” to describe nodes that fall into modules with a significantly greater co‐occurrence frequency between groups. To determine whether clustering patterns differed between groups, we used permutation tests [Good, 2011] to obtain p‐values for group differences, and controlled for FDR at 10% [Storey, 2002].

Graph Theory

After testing networks for edge strength differences and modularity clustering, we also studied the networks for differences in traditional graph theory metrics [Buckner et al., 2009; Fornito et al., 2013; Telesford et al., 2010; van den Heuvel and Hulshoff Pol, 2010], including the number of edges belonging to each node (degree), the average shortest path length between nodes (global efficiency), the overall number of modules (modularity coefficient; Q), and the index of balance between connections that are made within and between modules (participation coefficient). Graph metrics of degree and participation coefficient, which are computed separately for each individual node, were then compared at both the node level (i.e., Is the degree of node X higher in controls?) and at the average network level (i.e., Is the average degree of all nodes greater in controls than in Nf1 participants?). Rather than using a standard t‐test to find differences in these metrics between groups, we computed the relevant graph metric for each resampled network in each subject and used a linear mixed effects two‐sample test statistic to determine whether the group networks differed significantly. We subsequently used permutation tests [Good, 2011] to obtain p‐values. We corrected for multiplicity for all node level tests, using Storey's method [Storey, 2002] to estimate the false discovery rate (FDR) at 10% [Benjamini and Hochberg, 1995].

Nuisance Variables

Estimating Markov networks for large networks in fMRI is statistically challenging, and we lack adequate statistical power and error control to adjust for a large number of covariates at the edge level [Narayan et al., 2015]. Thus, we chose to account for nuisance covariates at the region of interest (ROI) level. Since the ROI time‐series comprise the input to the network analyses, we employed an ANOVA to model the whitened time‐series using group, scanner location and group × scanner location interaction as fixed effects and a subject‐level random effect. We found no significant relationship with scanner, group, nor a group by scanner interaction effect for any of the 113 ROIs after correcting for multiple comparisons at 10% FDR using the Benjamini–Yekutieli procedure (all p > 0.05). We also tested for scanner effects on the global sparsity (total number of edges) of each network using another linear mixed effects model and found no significant relationship between network sparsity and scanner location (p = 0.54), nor a patient by group interaction (p = 0.41). These results indicate no evidence of a main effect of scanner on the ROI time‐series, the fundamental unit upon which edge structure, graph theory, and modularity calculations were made.

Relationships to Clinical Measures

We examined three clinical measures as they related to our network findings: IQ as estimated by the WASI (for all subjects), Total Internalizing Score (only NF1 subjects), and Total Problem Score (only NF1 subjects). Internalizing and Problem scores were acquired using the widely used standardized measure in child psychology, the Childhood Behavioral Checklist (CBCL) [Achenbach, 1992]. NF1 participants older than 18 were given the Youth Adult Self Report (YASR), which was derived from the CBCL [Achenbach, 1997].

To test the hypothesis that graph metric measurements could predict clinical measures, we fit a separate mixed effects model between each clinical variable, and each graph metric. We used standard linear mixed effects models for the continuous responses: sparsity, global efficiency, anterior–posterior sparsity, and bilateral sparsity. In the case of edges and co‐modularity, which produce discrete proportions, we used nonlinear beta‐binomial models. We focused these tests on the 10 most significant differential edges and the 10 most significant differential modular pairs.

RESULTS

Demographics

As shown in Table 1, control and NF1 participants were matched for age and gender. NF1 participants did not differ significantly from controls in years of education, but had significantly lower Full Scale IQ, as measured by the WASI. Although IQ scores for NF1 participants are in the average range, this downward shift in IQ is consistent with previous findings [Kayl and Moore, 2000; Hyman et al., 2005].

R3 Edge Testing

The goal of R3 edge testing is to find edges that are significantly stronger in one group than the same edge in another group. Therefore, we report only differential edges. We first tested whether the total number of edges remaining in the sparsified networks was significantly different between groups, and found no difference in overall sparsity. Differential edge testing revealed 26 edges that were significantly stronger in controls than in NF1 participants (Fig. 2 and Table 2). These 26 edges connect nodes across hemispheres and across the anterior–posterior plane. Ten unique edges were significantly stronger in NF1 participants than controls. By comparison, these edges were short‐range, unilateral, and demonstrated less anterior–posterior connectivity relative to the edges that were significantly stronger in the control network.

Figure 2.

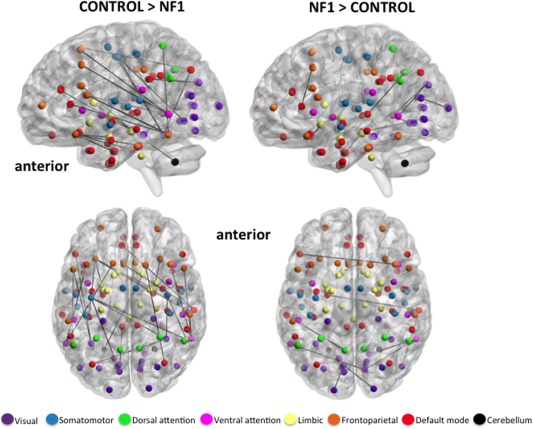
Axial and medial view (left hemisphere) of significantly stronger edges in healthy controls (left) and participants with NF1 (right), indicating relatively greater anterior–posterior connectivity in controls vs NF1 participants. Spheres represent the center coordinate of brain regions from the Harvard–Oxford atlas, and black lines represent exclusive maps of edges that exist in each cohort. Spheres are colored to demonstrate membership to one of seven functional networks derived from resting state studies of 1000 subjects [Yeo et al., 2011]. All edges are significant at FDR 10% corrected for multiple comparisons. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 2.

Differential edge testing on whole‐brain networks

		“The edge connecting nodes 1 and 2 is stronger in group X than in group Y…”
	P	Node 1	Node 2
Controls	1e−6	Right precentral gyrus	Right inferior temporal gyrus
	0.00003	Right inferior frontal gyrus, pars opercularis	Right middle temporal gyrus
	0.00009	Right inferior frontal gyrus, pars opercularis	Left middle temporal gyrus
	0.00014	Right middle temporal gyrus, posterior division	Left paracingulate gyrus
	0.00015	Right middle temporal gyrus, posterior division	Left cingulate gyrus, anterior division
	0.00031	Right middle frontal gyrus	Left temporal occipital fusiform cortex
	0.00047	Right amygdala	Left frontal orbital cortex
	0.00059	Right middle frontal gyrus	Right middle temporal gyrus
	0.00059	Left frontal orbital cortex	Left temporal fusiform cortex, posterior division
	0.00105	Left cingulate gyrus, posterior division	Left cuneal cortex
	0.00108	Right superior frontal gyrus	Right lateral occipital cortex, superior division
	0.00118	Left frontal orbital cortex	Right parahippocampal gyrus, anterior division
	0.00119	Right frontal orbital cortex	Right parahippocampal gyrus, anterior division
	0.00122	Left precentral gyrus	Right temporal occipital fusiform cortex
	0.00123	Left inferior frontal gyrus, pars opercularis	Left inferior temporal gyrus
	0.00172	Right middle temporal gyrus	Right supramarginal gyrus, anterior division
	0.00193	Left lateral occipital cortex, superior division	Right temporal occipital fusiform cortex
	0.00227	Right precentral gyrus	Right temporal occipital fusiform cortex
	0.00227	Right caudate	Left cerebellum
	0.00227	Left amygdala	Left frontal orbital cortex
	0.00227	Left precentral gyrus	Left lingual gyrus
	0.00230	Left superior frontal gyrus	Left middle temporal gyrus
	0.00236	Left superior parietal lobule	Left temporal occipital fusiform cortex
	0.00241	Left inferior frontal gyrus, pars opercularis	Left temporal occipital fusiform cortex
	0.00245	Right inferior temporal gyrus, posterior division	Left frontal orbital cortex
	0.00253	Left precentral gyrus	Right inferior temporal gyrus
NF1	0.00001	Right middle temporal gyrus, posterior division	Right lateral occipital cortex, inferior division
	0.00022	Right middle temporal gyrus, posterior division	Left parahippocampal gyrus, anterior division
	0.00072	Left supracalcarine cortex	Right occipital pole
	0.00152	Left supracalcarine cortex	Left occipital pole
	0.00162	Left accumbens	Right subcallosal cortex
	0.00162	Left middle temporal gyrus	Right cuneal cortex
	0.00162	Left superior temporal gyrus, posterior division	Left precuneous cortex
	0.00163	Right middle temporal gyrus	Right lingual gyrus
	0.00164	Right middle frontal gyrus	Left inferior frontal gyrus, pars triangularis
	0.00287	Right middle temporal gyrus	Right cuneal cortex

Results indicate that 26 edges are stronger in controls than NF1 participants, and 10 edges are stronger in NF1 participants than controls. Only significant results are shown (corrected for multiple comparisons with false discovery rate at 10% using Benjamini–Hochberg). Bold text indicates one edge, significantly stronger in controls than NF1, that correlates positively with IQ in both groups.

Modularity

The modularity analysis is also differential: we only test/report which nodes cluster more often in one group than another. Results from the differential modularity analysis revealed 19 node pairs (16 unique nodes; Table 3) clustering more often in controls than in NF1 participants (Fig. 3 and Table 3). We plotted the node locations on a map of seven functional networks defined by a previous study of resting state data obtained from 1000 subjects (Fig. 3; Yeo et al., 2011), and found that the vast majority (13) of these nodes observed in controls belonged to either the visual or the default mode network, with many bilateral pairs clustering together. NF1 participants, by contrast, clustered 6 node pairs (9 unique nodes) significantly more often than controls. The 9 unique nodes were distributed throughout five of the seven functional networks shown (Fig. 3) and were not preferentially aligned to any particular network. The clustering pattern of NF1 nodes reveals a right‐lateralized pattern and no bilateral pairs, when compared with control clustering patterns.

Table 3.

Differential Modularity Clustering Results Reveal That Healthy Controls Cluster Visual and Default Mode Networks More Often Than NF1 Participants

		“Nodes 1 and 2 cluster into the same functional module more often in group X than in group Y”
	P	Node 1	Network	Node 2	Network
Control	1.24E‐05	Left lateral occipital cortex, inferior division	Visual	Left intracalcarine cortex	Visual
	3.15E‐05	Left lateral occipital cortex, inferior division	Visual	Right intracalcarine cortex	Visual
	3.47E‐05	Left lateral occipital cortex, inferior division	Visual	Left supracalcarine cortex	Visual
	3.99E‐05	Left intracalcarine cortex	Visual	Left occipital pole	Visual
	4.19E‐05	Left temporal pole	Default	Right middle temporal gyrus, posterior division	Default
	4.79E‐05	Left intracalcarine cortex	Visual	Left occipital fusiform cortex	Visual
	6.88E‐05	Right intracalcarine cortex	Visual	Left occipital fusiform cortex	Visual
	7.43E‐05	Left lateral occipital cortex, inferior division	Visual	Right cuneal cortex	Visual
	7.48E‐05	Left lateral occipital cortex, inferior division	Visual	Right supracalcarine cortex	Visual
	8.13E‐05	Left supracalcarine cortex	Visual	Left occipital pole	Visual
	8.14E‐05	Brainstem	Limbic	Right amygdala	Limbic
	8.41E‐05	Left lateral occipital cortex, inferior division	Visual	Left cuneal cortex	Visual
	0.00011	Brainstem	Limbic	Left amygdala	Limbic
	0.00011	Right intracalcarine cortex	Visual	Left occipital pole	Visual
	0.00016	Left occipital fusiform cortex	Visual	Left supracalcarine cortex	Visual
	0.00018	Right temporal pole	Default	Right superior temporal gyrus, anterior division	Default
	0.00019	Right supracalcarine cortex	Visual	Left occipital pole	Visual
	0.00021	Right cuneal cortex	Visual	Left occipital pole	Visual
	0.00024	Left cuneal cortex	Visual	Left occipital pole	Visual
NF1	0.00011	Right frontal orbital cortex	Frontoparietal	Right parahippocampal gyrus, anterior division	Default
	0.00037	Right amygdala	Limbic	Right frontal orbital cortex	Frontoparietal
	0.00077	Left intracalcarine cortex	Visual	Right cingulate gyrus, posterior division	Default
	0.00084	Right lateral occipital cortex, superior division	Default	Right supplementary motor cortex	Somatomotor
	0.00090	Right cingulate gyrus, posterior division	Default	Left supracalcarine cortex	Visual
	0.00095	Right hippocampus	Limbic	Right frontal orbital cortex	Frontoparietal

By contrast, NF1 participants show more sporadic clustering of nodes from diverse networks and a bias toward clusters in the right hemisphere. Only significant results are shown (adjusted for false discovery rate at 10% using Benjamini–Hochberg procedure). Bold text indicates modular clustering that varies inversely with Total Internalizing Symptoms in NF1 participants; i.e., as internalizing symptoms become more severe, these nodes cluster less often.

Figure 3.

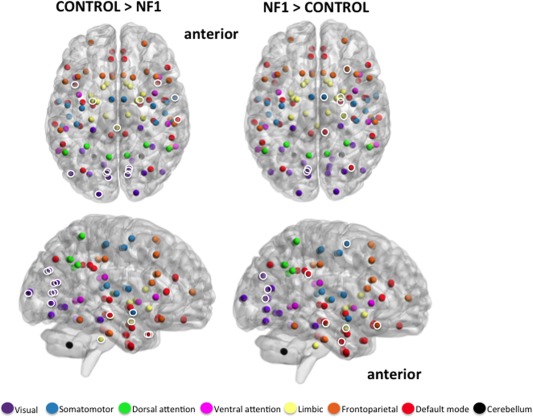
Axial and medial view (right hemisphere) of significantly greater modular clustering in controls (left; 15 unique nodes) and NF1 participants (right; 9 unique nodes). Brain networks consist of several modules, or smaller “neighborhoods” of brain regions more connected to one another than to the rest of the network. “Modular clustering” evaluates the frequency with which any two nodes are members of the same module, and identifies nodes that are functionally related to one another. Highlighted nodes (white circles) are brain regions that consistently fall in the same module together, and do so significantly more often than identical nodes in the opposing group. Uncircled nodes have modular clustering patterns, but the pattern is not significantly different between groups. Results suggest that the largest difference between groups is in the clustering patterns of the visual (purple) and default mode (red) networks. Controls demonstrate a tightly clustered visual network and bilateral clustering of visual, default‐mode, and limbic nodes. NF1 participants show broader and more diffuse clustering patterns, combining nodes from visual, default mode, limbic, frontoparietal, and somatomotor networks. NF1 clustering is primarily in the right hemisphere. Anatomical locations of all 113 nodes are represented by spheres. Sphere colors match those specified in Figure 2. Module clusters shown at FDR 10%. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Graph Theory

We found no significant differences between the controls and NF1 participants for any traditional graph theory metric (degree, global efficiency, modularity coefficient, or participation coefficient) at the average group level. At the node level, we tested whether any individual nodes had higher degree or participation coefficient in either group, finding no significant differences for either metric.

Relationships to Clinical Measures

Modular clustering tests revealed a significant correlation with internalizing symptoms in patients with NF1 in five node‐pairs, each of which contains the inferior left lateral occipital cortex. The five significant node pairs (corrected at FDR 10%) are inferior left lateral occipital cortex paired with (1) left intracalcarine cortex (P = 0.01), (2) right intracalcarine cortex (P = 0.009), (3) left supracalcarine cortex (P = 0.007), (4) right cuneal cortex (P = 0.003), and (5) right supracalcarine cortex (P = 0.004). Edge testing also revealed a significant relationship between the most significantly differential edge (connecting right precentral gyrus with the right inferior temporal gyrus) and IQ (P = 0.01, FDR 10%). However, we found no significant relationships between clinical metrics (IQ, TIS, or TPS) and graph‐based measures of overall sparsity, global efficiency, anterior–posterior sparsity, or bilateral sparsity.

DISCUSSION

We present this study elucidating resting state functional network architecture in individuals with the monogenic disorder NF1. Novel analysis techniques introduced here allowed us to evaluate all network edges for greater strength (i.e., increased connectivity) in each group. As such, one of the primary findings of this study is reduced anterior–posterior connectivity in NF1 participants compared with healthy controls. After stringent corrections for multiple comparisons, 26 edges were found to be significantly stronger in controls than NF1 participants, while 10 edges were stronger in NF1 participants than those same edges in controls. Importantly, the pattern of differential edge distribution provides insight into the nature of connectivity deficits in NF1. In Figure 2, we show exclusive maps of all edges that were significantly stronger in one group than another. If an edge appears in the control network, for example, it is significantly stronger than the identical edge in NF1 subjects, hence there is no edge overlap shown. Comparing the NF1 and control networks in Figure 2, the edge distribution suggests a pattern of long‐range anterior–posterior connectivity in controls that is noticeably absent from the NF1 cohort. In other words, although anterior–posterior edges are present in both groups, our results suggest that these types of edges are significantly weaker in NF1 subjects.

These findings are in accord with previous suggestions of connectivity impairments in NF1 assessed using different methodologies, including task‐based fMRI studies of visual, spatial, and working memory, in which NF1 patients generally show a pattern of increased short‐range and diminished long‐range connectivity [Billingsley et al., 2004; Chabernaud et al., 2012; Shilyansky et al., 2010; Violante et al., 2012]. Using a seed‐based approach, Chabernaud et al. (2012) found that, prior to treatment with the Ras‐inhibiting drug lovastatin, patients with NF1 showed an absence of typical long‐range resting state functional connectivity between the posterior cingulate and medial prefrontal cortex, two hubs within the default mode network of the brain. Although the absence of a healthy control group limits the extent to which these findings deviate from typical resting state connectivity patterns, our findings of reduced anterior–posterior connectivity relative to control subjects appear to align well with this report. Notably, many studies have observed diminished long‐range connectivity in adolescents and adults with idiopathic autism spectrum disorders [Dichter, 2012; Müller et al., 2011; Verly et al., 2013; von dem Hagen et al., 2013], as well as local over‐connectivity in posterior brain regions [Maximo et al., 2013]. Given that our findings are derived from resting state data, we speculate that these connectivity differences represent an intrinsic difference between control and NF1 network structures, which might predispose NF1 participants to further difficulties when task requirements are involved. Additionally, this convergence of findings between our study and those observed in idiopathic ASD is important and suggests specific points of convergence in patterns of resting state alterations, e.g., altered anterior–posterior connectivity, which may be informative regarding shared downstream circuit malformations (albeit possibly caused by distinct molecular mechanisms). Translational studies in mouse models of NF1 will be critical to elucidate the underlying molecular basis of the observed functional connectivity disturbances.

Another novel finding is altered modularity clustering patterns in NF1 participants. In large brain networks, it is valuable to understand how brain regions organize into neighborhoods or modules. Although existing modularity algorithms accurately assign nodes into neighborhoods (modules; Newman 2006), these algorithms are not equipped to quantify the allegiance of a node to a module (i.e., Does node 5 fall into module 1 90% of the time, or just 5% of the time?). For this reason, we discarded the notion of absolute module allegiance in favor of a metric that examines how often each pair of nodes falls into the same module together. We call this metric “clustering”. For example, if we resample the modularity calculation and find that nodes 5 and 6 consistently fall into module 1 together, we conclude that the nodes have similar behavior and are functionally connected. This modularity clustering test estimates how well any two nodes share modularity affiliation, and can be thought of as a metric of functional connectivity. When we compare two groups, we ask which nodal pairs cluster together more frequently in one group than another. For example, if nodes 5 and 6 cluster into module 1 90% of the time for group A, but only 10% of the time for group B, we can conclude that nodes 5 and 6 cluster together more often (and are thus more functionally related) in group A than group B. Overall, the edge and modularity clustering metrics describe two very different properties of the network. All edge strength differences in these data represent direct edges, while modularity clustering can be affected by direct or indirect relationships between shared neighbors.

Our modularity results reveal differential clustering patterns in 16 unique nodes (19 total pairs) in controls (Fig. 3). These 16 nodes belong primarily to the visual and default mode networks, with only three nodes (brainstem and bilateral amygdala) belonging to the limbic network. Notably, every node pair belongs to the same network affiliation, labels which were imposed from a separate dataset after modularity results were calculated [Yeo et al., 2011]. This pattern suggests that the visual and default mode networks are more tightly clustered in controls than in individuals with NF1. It is important also to consider that of the 16 unique nodes that differentially cluster in controls relative to NF1 participants, the two most frequently appearing are the inferior division of the left lateral occipital cortex and the left occipital pole. Each node shows up six times in clustered pairs, and both nodes are within the visual network. We cannot speculate about the relationship between these two visual nodes and perceptual experience, but it does raise an important question for future studies about why we see such a compelling difference in the visual network between groups.

By contrast, NF1 participants cluster six node pairs more frequently than controls and have nine unique nodes (compared to 16 unique nodes in controls). The important distinction between groups is that the nine unique NF1 cluster nodes span five of the seven functional networks (visual, default mode, limbic, fronto‐parietal, and somatomotor). This contrasts with controls, whose 16 unique nodes were found largely within two primary networks (visual and default mode). In further contrast to controls, for which each node pair belongs to the same module, no node pair in NF1 participants belongs to the same assigned module. The observed intra‐module clustering pattern suggests that NF1 networks have stronger between‐module connectivity and weaker within‐module connectivity than controls. These findings are in line with the two prior resting state functional MRI studies of NF1, in which (using seed‐based approaches) the investigators find altered short‐range connectivity patterns in NF1 participants compared to controls [Chabernaud et al., 2012; Loitfelder et al., 2015]. Together, these data indicate less tightly organized clustering of visual and default mode networks and potentially impaired intra‐modular affiliation.

In addition to evaluating individual edge strength and modularity clustering abnormalities in NF1 participants, we characterized the networks using graph theory metrics including degree, global efficiency, modularity coefficient, and participation coefficient. These metrics have become popular in network analyses as descriptors of network structure [Buckner et al., 2009; Fornito et al., 2013; Telesford et al., 2010; van den Heuvel and Hulshoff Pol, 2010]. After accounting for inter‐subject variance and performing permutation testing, we saw no significant group differences in degree (average number of edges connected to each node), global efficiency (average number of edges required to connect all node pairs), modularity coefficient (number of neighborhoods that divide the network), or participation coefficient (average number of edges connecting a node to modules outside its affiliation). Given the tremendous dependence of graph theory metrics on network sparsity and variability, we were not surprised to find an insignificant difference between groups when sparsity and variability were accounted for in the model. A lack of group differences in these graph theory metrics suggest that NF1 participants overall have similar global network properties, but differ from controls in more localized structure, such as edge strength and module composition. For example, although NF1 functional networks have the same raw number of modules as controls, the clustering pattern of nodes within those modules is not identical. Thus, while traditional graph properties appear to be indistinct in individuals with NF1, local differences in edge strength and modular affiliation may be relevant to characteristic behavioral findings in the disorder.

To further investigate the influence of edge strength and modularity on clinical measures, we evaluated three behavioral metrics: IQ (all subjects), Total Internalizing Score (NF1 participants only), and Total Problem Score (NF1 participants only), from the Childhood Behavioral Checklist (CBCL; for participants under 18) and the Youth Adult Self Report (YASR; for participants over 18). We found a significant negative relationship between internalizing symptoms from the Problem Score and clustering patterns in NF1 subjects. Specifically, five clustered pairs varied inversely with internalizing symptoms (blue highlight, Fig. 3). Notably, each of the five significant pairs contained one node in common, the left inferior lateral occipital cortex (LOC). The LOC is the same node that showed up in six of the 19 node pairs that clustered less often in NF1 participants than controls, indicating that the left LOC in patients becomes more disconnected to the remaining 5 nodes as internalizing symptoms increase. In other words, a higher internalizing score in NF1 patients (which is associated with anxiety and mood symptoms) is correlated with a weaker affiliation between these six nodes. Additionally, we found one edge (connecting right precentral and right temporal gyri) that correlated significantly with IQ in both groups (Table 2, bold highlight). Regardless of group identity, this finding suggests that the relationship between the right precentral and right temporal gyri is weaker in individuals with low IQ. Larger, external datasets are necessary to validate this finding, and further explore the relationship between functional connectivity of these regions. Finally, we investigated the relationship between clinical metrics and graph metrics such as global sparsity and global efficiency; no significant relationship was observed. Additionally, the total number of anterior–posterior and total bilateral connections was not associated with these clinical variables. Nonetheless, the observed edge‐IQ and modularity‐internalizing relationships are promising and warrant further exploration in independent datasets.

Although direct relationships between structural and functional connectivity in typically developing populations have yet to be fully elucidated [Grayson et al., 2014; Lohse et al., 2014], it is notable that abnormal white matter structure has been reported in several studies of both children and adults with NF1, particularly in the context of hyperintensities on T2‐weighted images in the brain, or unidentified bright objects (UBOs) [Moore et al., 2000; Pride et al., 2010]. While the exact nature of the UBOs is not known, histological analysis has revealed that they are often transient and can be caused by intramyelinic edema [DiPaolo et al., 1995]. A few studies to date have explored structural connectivity in NF1 applying a region of interest (ROI)‐based approach to diffusion tensor imaging (DTI) data; these studies have generally shown decreases in fractional anisotropy (FA), an indicator of water's directional coherence in white matter, as well as increases in overall diffusivity [Zamboni et al., 2007; van Engelen et al., 2008; Wignall et al., 2010]. To our knowledge, ours is the only previous DTI study to take a whole‐brain approach. In an independent sample of young adult NF1 patients [Karlsgodt et al., 2012], we found that, relative to healthy controls, NF1 patients showed widespread reductions in white matter integrity across the entire brain, as reflected by decreased FA and significantly increased absolute diffusion (ADC). We additionally found pronounced differences in radial diffusion in NF1 patients, indicative of either decreased myelination or increased space between axons. FA and radial diffusion effects were of greatest magnitude in the frontal lobe [Karlsgodt et al., 2012].

Notably, NF1 mutations are known to impact myelin, as the gene encoding the oligodendrocyte‐myelin glycoprotein (OMgp) is embedded within an intron of the NF1 gene [Viskochil et al., 1991]. This protein has been the focus of much interest as a potential mechanism underlying overproliferation of oligodendrocytes, which may explain structural neuroanatomic findings of enlarged white matter. Increased corpus callosum area and/or callosal thickening has been frequently reported in studies of patients with NF1[Cutting et al., 2002; Duarte et al., 2014; Dubovsky et al., 2001; Kayl and Moore, 2000; Pride et al., 2010; Violante et al., 2013]. Additionally, two cross‐sectional studies have found increased corpus callosum size to be associated with lower IQ and poorer performance on measures of academic achievement, abstract concept formation, verbal memory, and visual‐spatial and motor skills in children with NF1, indicating that greater callosal size is associated with impaired functional computations the brain in patients with NF1 [Moore et al., 2000; Pride et al., 2010]. Additionally, prior work in a mouse model of NF1 found that developmental Nf1 loss throughout the brain resulted in corpus callosum enlargement that could be reduced in size by treatment with a MEK/ERK inhibitor during neonatal stages [Wang et al., 2012]. Mapping the network topology of structural alterations in white matter fiber tracts in NF1 patients using similar methods—in order to determine whether core topological properties characterize both structural and functional connectivity alterations—is an important next step. This will be critical for elucidating the relationships between structural and functional brain alterations in NF1.

A limitation of the present study is a lack of a priori knowledge of the functional architecture of the resting brain in NF1. In order to explore a wide range of possible findings, we included all nodes, all edges, and many graph theory metrics in our analyses. Consequently, our penalties for multiple comparisons were perhaps overly stringent. In addition, our sample included a wide age range. Although groups were age‐matched, the broad range provides a substantial challenge when considering the pace of network reorganization during development [Supekar et al., 2009; Zielinski et al., 2010]. A larger sample size would have allowed us to either narrow the age range or bin the subject pool to examine network changes in NF1 during development. It should also be noted that we employed global signal regression as a preprocessing step [Power et al., 2014]. Global signal regression helps remove influences that affect signal all over the brain, thereby highlighting the relationship between smaller, individual regions. There is some debate about the effect that this procedure has on the resulting time‐series [Power et al., 2014; Schwarz and McGonigle, 2011; Weissenbacher et al., 2009], but in our dataset, we found that global signal regression produced a more Gaussian distribution of correlation coefficients than if we eliminated this step. Another methodological consideration is our use of an anatomical atlas to define regions of interest. The benefit of this method is that the identity of each brain region is accepted by the field. A limitation is that different brain regions are often markedly different in size, which means that the number of voxels averaged together to create a single regional time‐series varies as well. The alternative, using functionally derived regions, has its own set of distinct limitations, however, and we chose anatomical labeling to avoid problems of region identification.

Although the underlying biological basis for these altered connectivity findings is not yet known, a recent magnetic resonance spectroscopy study [Violante et al., 2012] found reduced gamma‐aminobutyric acid (GABA; an inhibitory neurotransmitter) levels in visual cortex in participants with NF1, whereas no alterations were observed in glutamine levels, indicating an imbalance in the excitatory/inhibitory push–pull mechanism in NF1 participants. This study also found that GABA/total creatine levels were inversely correlated with neural activity (peak BOLD amplitude) during a low‐level visual processing task in both NF1 participants and controls, suggesting that BOLD response is sensitive to excitatory‐inhibitory balance and, in turn, to GABA concentrations [Chen et al., 2005]. Previous studies in NF1 rodent models have shown evidence of increased inhibitory postsynaptic potentials, which was attributable to higher levels of GABA release [Cui et al., 2008]. The NF1 protein is highly expressed in rodent and human oligodendrocytes [Daston et al., 1992]. A recent study in an NF1 loss of function mouse model examined the role of H‐Ras activation in oligodendrocytes [Mayes et al., 2013], finding gross enlargement of optic nerves, consistent with findings of white matter enlargement in human patients with Nf1; further, Ras pathway activation in oligodendrocytes upregulated nitric oxide synthases (NOS) in white matter and elevated oligodendrocyte reactive oxygen species, including NO, which contributed to behavioral abnormalities in the mouse. These findings suggest a potential cellular and molecular mechanism of Nf1‐associated brain abnormalities.

In summary, here we applied novel network analysis methods to study the functional architecture of the resting brain in individuals with NF1 mutations. Our data suggest that NF1 is indeed characterized by diminished anterior‐posterior connectivity and disorganized, unilateral modular clustering compared with controls. Investigation of the global features of NF1 and control networks indicates that both groups have similar hubs, are equally efficient, and divide into the same number of modules. However, local network differences in edge strength and modular clustering may contribute to the cognitive deficits experienced by individuals with NF1. Future, larger‐scale studies are warranted in order to evaluate how these local features are relevant to learning and memory deficits common to the NF1 population.