Abstract
The selection of a primary model to describe microbial growth in predictive food microbiology often appears to be subjective. The objective of this research was to check the performance of different mathematical models in predicting growth parameters, both by absorbance and plate count methods. For this purpose, growth curves of three different microorganisms (Bacillus cereus, Listeria monocytogenes, and Escherichia coli) grown under the same conditions, but with different initial concentrations each, were analysed. When measuring the microbial growth of each microorganism by optical density, almost all models provided quite high goodness of fit (r 2 > 0.93) for all growth curves. The growth rate remained approximately constant for all growth curves of each microorganism, when considering one growth model, but differences were found among models. Three-phase linear model provided the lowest variation for growth rate values for all three microorganisms. Baranyi model gave a variation marginally higher, despite a much better overall fitting. When measuring the microbial growth by plate count, similar results were obtained. These results provide insight into predictive microbiology and will help food microbiologists and researchers to choose the proper primary growth predictive model.
1. Introduction
Predictive microbiology enables, through the use of mathematical models, estimating the behaviour of microorganisms under certain circumstances [1], based upon the premise that the responses of microorganisms to environmental factors are reproducible. The ability to predict both the growth of microorganisms, as affected by different environmental factors, and the survival of microorganisms as a result of preservative treatments is an important tool for evaluating the safety and shelf life of food products.
Before predictive microbiology can be applied to the food industry, mathematical models that adequately describe microbial behaviour are needed. There are a number of sigmoid equations and several models that have been used as growth functions. They all differ in “ease of use” and number of parameters in the equation. Some authors have compared the behaviour of different growth models, from different viewpoints, including mathematical measures of goodness of fit [2] and/or other statistical criteria [3–5]. The usual measures of goodness of fit for model comparison in previous studies were done by calculating the bias (B f) and accuracy (A f) indices as provided by Ross [6], the coefficient of determination (r 2), the residual mean square error (RMSE), or the F-test. Other authors [7, 8] have focussed on direct comparisons of particular growth parameters as predicted by various models.
These studies have reached different conclusions. Hence, there is significant disagreement in literature on which is the best-fitting model for predictive microbiology. The selection of a model in predictive food microbiology often appears to be subjective. Based on reports in the literature, Gompertz, Baranyi, Richards, logistic, and three-phase linear models are the most widely used [5, 9–11].
The growth curve has been mostly expressed in terms of microbial numbers (concentration of colony forming units), but also in terms of optical density as an indirect measurement. The measurement of absorbance is a rapid, nondestructive, inexpensive, and relatively easy-to-automate method to monitor bacterial growth, as compared to many other techniques and particularly when compared to classical viable count methods. When modelling optical density growth curves, the fitted parameters are different from the population growth parameters derived from viable counts. The rate of increase of the optical density does not express the maximum specific growth rate and the detection time is not equivalent to the lag time, unless the initial inoculum is greater than the detection limit. In spite of the limitations related to detection thresholds, correlation with the parameters derived from viable count growth curves, and inability to model growth in turbid liquid foods and in solid food matrixes, numerous techniques and mathematical growth models have been used in recent years for estimation of growth rates and lag times from absorbance data [5, 7, 8, 12–14]. In the opinion of Dalgaard and Koutsoumanis [7], absorbance techniques should be limited to conditions where high cell densities are reached, such as those resembling the growth of spoilage bacteria in foods. Even assuming the limitations of absorbance to build growth curves, it may be useful, if not to obtain very precise growth kinetic parameters, at least to compare the growth of different cultures or of the same cultures but in different conditions.
Work modelling the behaviour of bacteria in foods has shown that the lag phase is more difficult to predict than is the specific growth rate [15], mainly because of the influence in lag time of the physiological state of individual bacterial cells and, to a minor extent, of the inoculum size. The physiological state of the cells is affected by their previous growth environment and by exposure to stress conditions, which can extend the lag time considerably and also increase individual cell lag time variability [16–18]. However, microorganisms with a similar precultural history exposed to the same favourable growth conditions should be in a similar optimum physiological state and, thus, its effect on lag time variability is negligible [19]. Regarding the inoculum size, Baranyi and Pin [20] showed that as the cell number in the inoculum decreases, the population lag increases by an amount that depends on the distribution of individual lag times and the maximum specific growth rate. Augustin et al. [21] showed that the inoculum level effect can be explained by an increasing variability in individual cell lag time when stress factors become more stringent, and Baranyi and Pin [20] found that, under optimum growth conditions, this effect would only be expected at inoculum levels below about 102-103 cells, because the impact of variability among a small population of cells can become more important on lag time [2, 22].
Hence, a sufficiently large population of microorganisms exposed to exactly the same favourable growth conditions and with a similar precultural history behave in a similar way; that is, they should show the same growth parameters, growth rate, and lag phase duration.
The objective of this research was to check the performance of different mathematical models in predicting growth parameters, by both absorbance and plate count methods. For this purpose, growth curves of three different microorganisms (Bacillus cereus, Listeria monocytogenes, and Escherichia coli) grown, each species, under the same conditions, but with different initial concentrations, were analysed.
2. Materials and Methods
2.1. Microorganisms
Bacillus cereus, Listeria monocytogenes, and Escherichia coli were chosen as representative microorganisms for spore-forming, Gram-positive, and Gram-negative bacteria, respectively.
B. cereus INRA-AVTZ415 was kindly provided by the Institut National de la Recherche Agronomique (INRA, Avignon, France). L. monocytogenes and E. coli type strains (CECT 4031 and CECT 515, resp.) were provided by the Spanish Type Culture Collection (CECT).
To inoculate the growth media, B. cereus vegetative cells were grown at 30°C in brain heart infusion broth (BHI; Scharlau Chemie S.A., Barcelona, Spain), until the stationary phase of growth was reached. L. monocytogenes vegetative cells were grown at 37°C in tryptic soy broth (TSB; Scharlau Chemie) supplemented (w/v) with 0.6% yeast extract (YE; Scharlau Chemie), until the stationary phase of growth was reached. E. coli vegetative cells were grown at 37°C in TSB+YE acidified to pH 5 with ClH (Panreac Química, Barcelona, Spain) until the stationary phase of growth was reached. These growth conditions were chosen as favorable for these microorganisms.
2.2. Optical Density Growth Curves
100-well microtitre plates were filled with 400 μL of the growth media (BHI for B. cereus, TSB+YE for L. monocytogenes, and pH 5 TSB+YE for E. coli) and were inoculated with the microorganisms and incubated in a Bioscreen C analyzer (Oy Growth Curves Ab Ltd., Helsinki, Finland). Initial concentrations in the growth media were 101, 102, 103, 104, 105, and 106 CFU mL−1 for B. cereus, 102, 103, 104, 105, 106, and 107 CFU mL−1 for L. monocytogenes, and 102, 104, and 106 CFU mL−1 for E. coli. In order to avoid variability derived from differences in the physiological state of different cultures, all the growth curves from each bacterium were obtained from a single bacterial culture. Growth media were incubated at 30°C for B. cereus and at 37°C for L. monocytogenes and E. coli. At 20 min intervals, the optical density (OD) of the samples using a wideband filter (420–580 nm) was measured.
For each combination of microorganism and initial concentration, 25–30 repetitions were performed, except for B. cereus 101 and 102 CFU mL−1 initial concentrations, where 13 and 21 repetitions were performed, and for L. monocytogenes 103, 105, and 107 CFU mL−1 initial concentrations, where 5 repetitions each were performed. Growth curves were obtained by plotting the OD against the exposure time. A total of 345 individual growth curves were generated by absorbance measurements.
2.3. Plate Count Growth Curves
50 mL flasks of the growth media were inoculated with the microorganisms and incubated with agitation at 500 rpm. Growth media and incubation temperatures were the same as those used for optical density growth curves. Initial concentrations in the growth media were 101, 103, and 105 CFU mL−1 for B. cereus and 102, 104, and 106 CFU mL−1 for L. monocytogenes and E. coli. At preset time intervals, samples were taken, properly diluted in buffered peptone water (BPW, Scharlau Chemie), and incubated in BHI agar (BHIA, Scharlau Chemie) for 24 h at 30°C for B. cereus and in tryptic soy agar (TSA, Scharlau Chemie) + YE for 24 h at 37°C for L. monocytogenes and E. coli. Growth curves were performed in duplicate.
Growth curves were obtained by plotting log CFU mL−1 against the exposure time.
2.4. Mathematical Models
Analyses of the growth curves were performed using five primary growth models. These growth models were based on either linear (derived from the Monod model) or nonlinear (Gompertz, Logistic, Richards, and Baranyi) equations (Table 1) and reparameterized to reflect microbial growth parameters as derived by Zwietering et al. [3].
Table 1.
Primary growth models.
| Model | Equationa |
|---|---|
| Three-phase linear | y = y 0 t ≤ λ |
| y = y 0 + μ(t − λ) λ < t < t s | |
| y = y max t ≥ t s | |
|
| |
| Gompertz | y = y 0 + C(e (−e(μe(λ−t)/C+1))) |
|
| |
| Logistic | |
|
| |
| Richards | |
|
| |
| Baranyi |
|
a y: log count or absorbance at time t; y 0: initial log count or absorbance; μ: maximum growth rate; λ: lag time; t s: time to reach stationary growth phase; y max: final log count or absorbance; C: increase in log count or absorbance from y 0 to y max; β: model coefficient.
Curve fitting of three-phase linear, Gompertz, logistic, and Richards models was done using the curve-fitting tool of Matlab 7.0 (Math Works, Natick, USA) with which 95% confidence limits (CL) for growth parameters and r 2, RMSE, and sum of square error (SSE) of fit were calculated.
The curve fitting of Baranyi's equation was done using DMFit 2.0 program and the model of Baranyi and Roberts [23] as kindly provided by Dr. József Baranyi. This program provided standard error for each growth parameter and r 2 and standard error of fit. With these values, 95% CL of growth parameters and RMSE of fit were calculated.
Analysis of variance, medians, and quartiles for box and whisker plots were calculated using StatGraphics (StatPoint Technologies, Warrenton, USA). p values were always lower than 0.05.
3. Results and Discussion
3.1. Optical Density Growth Curves
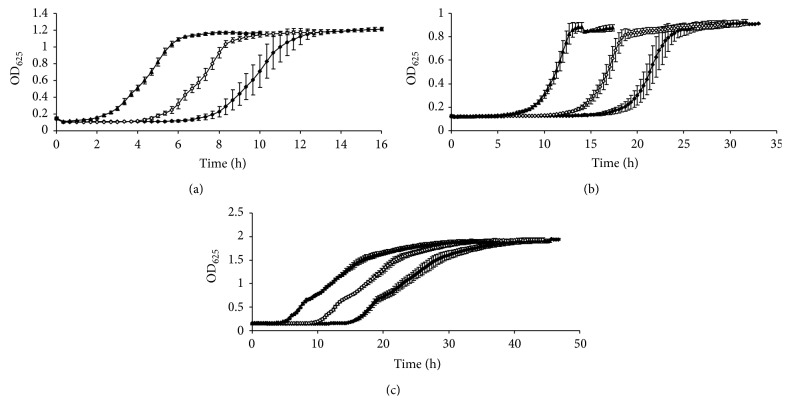
Figure 1 shows the optical density growth curves plotted with the average OD values at each sampling time of B. cereus INRA-AVTZ 415 at 30°C in BHI (a), L. monocytogenes CECT 4031 at 37°C in TSB+YE (b), and E. coli CECT 515 at 37°C in pH 5 TSB+YE (c) starting at 102, 104, and 106 CFU mL−1. These average growth curves correspond to 25–30 individual growth curves each. The slopes of all the growth curves corresponding to a microorganism were parallel in the exponential growth phase; that is, the growth rates were similar, as they should correspond to different cultures of the same microorganism growing exactly in the same conditions. However, a progressive decrease of lag phase duration was observed as the initial concentration increased. This decrease in lag time can be easily explained because the culture spends less time in reaching a concentration where the absorbance increases. Actually, several authors have recently used simple equations to derive real lag time and provided the initial concentration of microorganisms and the observed lag time from OD measurements [24–26]. The relatively low standard deviation values obtained, especially for growth curves starting at 104 and 106, are indicative of the repetitivity of the growth curves. It can be noticed that error bars are bigger as the initial concentration decreases, as a consequence of the increased variability among a small population of cells [2].
Figure 1.
Optical density growth curves plotted with the average OD values (±standard deviation) at each sampling time of Bacillus cereus INRA-AVTZ 415 at 30°C in BHI (a), Listeria monocytogenes CECT 4031 at 37°C in TSB+YE (b), and Escherichia coli CECT 515 at 37°C in pH 5 TSB+YE (c). Initial number of microorganisms: (⧫) 102 CFU mL−1; (◊) 104 CFU mL−1; (▲) 106 CFU mL−1.
Table 2 shows the growth parameters given by three-phase linear, Gompertz, logistic, Richards, and Baranyi models for the growth curves of B. cereus plotted with the average OD values shown in Figure 1(a). All the models tested provided the values that could be expected for growth parameters of the three growth curves selected of this microorganism. Figure 1(a) shows that all three average growth curves of B. cereus were approximately parallel in their exponential growth phases. Although the curve starting at 102 CFU mL−1 had a slightly lower slope, only logistic and Richards models showed significant differences between this and the other two curves of B. cereus starting at higher initial concentrations (Table 2). When comparing the growth rate values given by the different models, three-phase linear model gave the lowest values (0.27–0.30 OD units h−1), followed by Baranyi model (0.28–0.31 OD units h−1), logistic and Gompertz (0.31–0.35 OD units h−1), and Richards model (0.30–0.42 OD units h−1). Also, all models provided shorter lag phases at higher initial concentrations, as shown in Figure 1(a). Initial absorbance (y 0) had values between 0.071 and 0.180 for all growth curves and models. The increase in absorbance from initial to final optical density (C) had values between 0.975 and 1.107 for all growth curves and models. Hence all models seemed to perform adequately, providing expected growth parameter values for these growth curves. r 2 values were higher than 0.995 for all growth curves and all models, except for three-phase linear model, which gave values as low as 0.989, hence being the model which provided worst fit to the data, as also it could be expected from a model consisting of three straight lines. All models gave RMSE values lower than 0.035.
Table 2.
Growth parameters and their 95% confidence limits and coefficients of determination (r 2), SSE, and RMSE of fit obtained with different growth models for the average OD growth curves of Bacillus cereus INRA-AVTZ 415 at 30°C in BHI inoculating 102, 104, and 106 CFU mL−1 shown in Figure 1(a).
| Growth model | Initial concentration (CFU mL−1) | Lag time (h) | Growth rate (OD units h−1) |
y
0
(OD units) |
C
(OD units) |
β | r 2 | SSE | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| Three-phase linear | 102 | 7.81 (7.68–7.94) |
0.269 (0.253–0.285) |
0.130 (0.042–0.217) |
1.056 | 0.994 | 0.0034 | 0.0207 | |
| 104 | 5.47 (5.29–5.66) |
0.304 (0.274–0.334) |
0.140 (0.019–0.261) |
0.999 | 0.989 | 0.0042 | 0.0268 | ||
| 106 | 2.82 (2.68–2.95) |
0.293 (0.273–0.312) |
0.180 (0.027–0.332) |
0.975 | 0.994 | 0.0032 | 0.0215 | ||
|
| |||||||||
| Gompertz | 102 | 7.95 (7.87–8.03) |
0.312 (0.301–0.329) |
0.117 (0.109–0.124) |
1.107 (1.095–1.120) |
0.999 | 0.0166 | 0.0179 | |
| 104 | 5.50 (5.35–5.64) |
0.342 (0.314–0.370) |
0.118 (0.103–0.133) |
1.078 (1.050–1.106) |
0.996 | 0.0281 | 0.0283 | ||
| 106 | 2.87 (2.69–3.04) |
0.349 (0.315–0.382) |
0.142 (0.119–0.166) |
1.057 (1.019–1.095) |
0.995 | 0.0252 | 0.0311 | ||
|
| |||||||||
| Logistic | 102 | 8.01 (7.97–8.06) |
0.313 (0.307–0.319) |
0.105 (0.102–0.109) |
1.104 (1.099–1.110) |
0.999 | 0.0031 | 0.0077 | |
| 104 | 5.56 (5.47–5.65) |
0.345 (0.329–0.360) |
0.105 (0.096–0.150) |
1.070 (1.056–1.085) |
0.999 | 0.0081 | 0.0152 | ||
| 106 | 2.87 (2.75–2.99) |
0.347 (0.329–0.365) |
0.114 (0.098–0.110) |
1.066 (1.045–1.088) |
0.999 | 0.0070 | 0.0164 | ||
|
| |||||||||
| Richards | 102 | 8.00 (7.96–8.05) |
0.303 (0.285–0.321) |
0.106 (0.103–0.110) |
1.104 (1.099–1.110) |
0.911 (0.769–1.054) |
0.999 | 0.0030 | 0.0076 |
| 104 | 5.63 (5.54–5.72) |
0.401 (0.373–0.429) |
0.096 (0.086–0.100) |
1.071 (1.058–1.084) |
1.693 (1.257–2.130) |
0.999 | 0.0060 | 0.0132 | |
| 106 | 2.85 (2.75–2.95) |
0.420 (0.400–0.439) |
0.071 (0.048–0.090) |
1.099 (1.076–1.122) |
2.490 (1.823–3.158) |
0.999 | 0.0029 | 0.0108 | |
|
| |||||||||
| Baranyi | 102 | 7.80 (7.70–7.90) |
0.275 (0.264–0.286) |
0.155 | 1.047 (1.040–1.054) |
0.999 | 0.0155 | ||
| 104 | 5.40 (5.29–5.51) |
0.307 (0.291–0.323) |
0.141 | 1.020 (1.010–1.030) |
0.999 | 0.0178 | |||
| 106 | 2.76 (2.66–2.87) |
0.312 (0.298–0.326) |
0.152 | 1.015 (1.006–1.023) |
0.999 | 0.0148 | |||
Table 3 shows the growth parameters given by the five models for the growth curves of L. monocytogenes shown in Figure 1(b). Similar results were obtained, although in this case the only model which did not provide significant differences for the three growth rate values for the three initial concentrations tested was the three-phase linear. Again, the same order was obtained, three-phase linear model giving the lowest values (0.15–0.17 OD units h−1), followed by Baranyi model (0.15–0.20 OD units h−1), logistic and Gompertz (0.17–0.22 OD units h−1), and Richards model giving the highest values (0.18–0.32 OD units h−1). Also, all models provided shorter lag phases at higher initial concentrations. y 0 values were between 0.119 and 0.149 and C values between 0.712 and 0.784. Again, r 2 values were higher than 0.990 for all growth curves and all models, except for three-phase linear model, which gave values as low as 0.930. Three-phase linear model also gave RMSE values as high as 0.061.
Table 3.
Growth parameters and their 95% confidence limits and coefficients of determination (r 2), SSE, and RMSE of fit obtained with different growth models for the average OD growth curves of Listeria monocytogenes CECT 4031 at 37°C in TSB+YE inoculating 102, 104, and 106 CFU mL−1 shown in Figure 1(b).
| Growth model | Initial concentration (CFU mL−1) | Lag time (h) | Growth rate (OD units h−1) |
y
0
(OD units) |
C
(OD units) |
β | r 2 | SSE | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| Three-phase linear | 102 | 19.11 (18.96–19.27) |
0.163 (0.154–0.173) |
0.142 (0.069–0.214) |
0.742 | 0.994 | 0.0013 | 0.0127 | |
| 104 | 14.61 (14.42–14.81) |
0.173 (0.159–0.187) |
0.143 (0.065–0.222) |
0.724 | 0.989 | 0.0026 | 0.0181 | ||
| 106 | 8.79 (8.23–9.35) |
0.150 (0.126–0.174) |
0.149 (0.072–0.227) |
0.712 | 0.930 | 0.0490 | 0.0614 | ||
|
| |||||||||
| Gompertz | 102 | 18.99 (18.87–19.10) |
0.169 (0.161–0.177) |
0.132 (0.128–0.136) |
0.784 (0.776–0.792) |
0.998 | 0.0221 | 0.0153 | |
| 104 | 14.46 (14.31–14.62) |
0.179 (0.167–0.191) |
0.133 (0.127–0.139) |
0.757 (0.746–0.768) |
0.997 | 0.0353 | 0.0204 | ||
| 106 | 9.33 (9.09–9.56) |
0.218 (0.190–0.245) |
0.141 (0.129–0.154) |
0.755 (0.726–0.783) |
0.990 | 0.0491 | 0.0320 | ||
|
| |||||||||
| Logistic | 102 | 19.06 (18.99–19.12) |
0.168 (0.163–0.171) |
0.128 (0.126–0.130) |
0.779 (0.775–0.783) |
0.999 | 0.0052 | 0.0074 | |
| 104 | 14.55 (14.43–14.67) |
0.178 (0.170–0.186) |
0.128 (0.123–0.132) |
0.755 (0.748–0.762) |
0.999 | 0.0160 | 0.0137 | ||
| 106 | 9.40 (9.22–9.58) |
0.217 (0.199–0.235) |
0.135 (0.126–0.144) |
0.747 (0.730–0.765) |
0.996 | 0.0227 | 0.0218 | ||
|
| |||||||||
| Richards | 102 | 19.12 (19.05–19.19) |
0.183 (0.175–0.191) |
0.126 (0.124–0.128) |
0.778 (0.774–0.781) |
1.333 (1.152–1.514) |
0.999 | 0.0045 | 0.0069 |
| 104 | 14.74 (14.61–14.87) |
0.219 (0.205–0.233) |
0.123 (0.119–0.128) |
0.754 (0.748–0.760) |
2.040 (1.565–2.515) |
0.999 | 0.0123 | 0.0121 | |
| 106 | 9.93 (9.81–10.06) |
0.318 (0.303–0.333) |
0.119 (0.115–0.123) |
0.748 (0.742–0.754) |
6.730 (4.925–8.536) |
0.999 | 0.0028 | 0.0078 | |
|
| |||||||||
| Baranyi | 102 | 18.79 (18.65–18.93) |
0.148 (0.142–0.155) |
0.120 | 0.781 (0.776–0.786) |
0.998 | 0.0138 | ||
| 104 | 14.04 (13.87–14.21) |
0.163 (0.153–0.173) |
0.130 | 0.745 (0.739–0.752) |
0.997 | 0.0178 | |||
| 106 | 8.95 (8.75–9.15) |
0.201 (0.183–0.218) |
0.139 | 0.731 (0.718–0.743) |
0.995 | 0.0219 | |||
Table 4 shows the growth parameters given by the five models under study for the growth curves of E. coli shown in Figure 1(c). In this case, some unexpected results were obtained. Three-phase linear, Gompertz, logistic, and Baranyi models behaved as previously described for B. cereus and L. monocytogenes. Each model provided very similar values for the growth rates of the three growth curves, with only slight differences among them. However, only logistic and Baranyi models did not provide significant differences. For this microorganism, again, the three-phase linear model gave the lowest value for the growth rate (0.10–0.11 OD units h−1), but in this case together with Baranyi model, and again logistic and Gompertz models gave higher values (0.12–0.13 OD units h−1). However, Richards model gave unexpectedly low values for growth rates (<0.001 OD units h−1). All models provided shorter lag phases at higher initial concentrations. y 0 values were between 0.060 and 0.176 for all growth curves and models, except for the logistic model, which gave an exceptional low y 0 value of 0.000 (fixed at bound) for growth curve starting at 106 CFU mL−1. Logistic model gave values of SSE higher than 0.1 for all three growth curves of E. coli, which were almost twice the values obtained for any other growth curve shown in Table 2, 3, or 4. In this case all r 2 values were higher than 0.99 for all growth curves and all models, including the three-phase linear model.
Table 4.
Growth parameters obtained and their 95% confidence limits and coefficients of determination (r 2), SSE, and RMSE of fit with different growth models for the average OD growth curves of Escherichia coli CECT 515 at 37°C in pH 5 TSB+YE inoculating 102, 104, and 106 CFU mL−1 shown in Figure 1(c).
| Growth model | Initial concentration (CFU mL−1) | Lag time (h) | Growth rate (OD units h−1) |
y
0
(OD units) |
C
(OD units) |
β | r 2 | SSE | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| Three-phase linear | 102 | 14.80 (14.60–15.00) |
0.103 (0.100–0.105) |
0.161 (0.115–0.207) |
1.622 | 0.995 | 0.0200 | 0.0250 | |
| 104 | 9.70 (9.53–9.86) |
0.110 (0.107–0.112) |
0.167 (0.111–0.223) |
1.656 | 0.996 | 0.0150 | 0.0220 | ||
| 106 | 4.44 (4.27–4.61) |
0.111 (0.108–0.113) |
0.176 (0.113–0.239) |
1.600 | 0.996 | 0.0150 | 0.0224 | ||
|
| |||||||||
| Gompertz | 102 | 15.46 (15.29–15.62) |
0.117 (0.115–0.119) |
0.144 (0.137–0.152) |
1.794 (1.780–1.807) |
0.999 | 0.0700 | 0.0227 | |
| 104 | 10.29 (10.13–10.46) |
0.125 (0.123–0.128) |
0.146 (0.137–0.155) |
1.799 (1.785–1.812) |
0.999 | 0.0663 | 0.0227 | ||
| 106 | 4.65 (4.42–4.89) |
0.125 (0.122–0.127) |
0.123 (0.106–0.140) |
1.783 (1.761–1.805) |
0.999 | 0.0597 | 0.0237 | ||
|
| |||||||||
| Logistic | 102 | 15.51 (15.12–15.90) |
0.117 (0.113–0.121) |
0.105 (0.088–0.121) |
1.784 (1.758–1.810) |
0.997 | 0.2544 | 0.0433 | |
| 104 | 9.95 (9.56–10.33) |
0.123 (0.119–0.126) |
0.078 (0.057–0.094) |
1.834 (1.808–1.860) |
0.997 | 0.1825 | 0.0376 | ||
| 106 | 3.67 (3.46–3.89) |
0.120 (0.117–0.123) |
0.000a | 1.875 (1.864–1.887) |
0.997 | 0.1232 | 0.0339 | ||
|
| |||||||||
| Richards | 102 | 15.46 (15.18–15.73) |
0.00008 (−0.016–0.016) |
0.144 (0.137–0.152) |
1.794 (1.772–1.816) |
0.00024 (−0.049–0.049) |
0.999 | 0.0670 | 0.0228 |
| 104 | 10.29 (9.98–10.61) |
0.0001 (−0.063–0.063) |
0.146 (0.135–0.156) |
1.799 (1.778–1.819) |
0.00041 (−0.185–0.186) |
0.999 | 0.0663 | 0.0228 | |
| 106 | 4.65 (4.41–4.90) |
0.0002 (−0.107–0.107) |
0.123 (0.086–0.159) |
1.783 (1.743–1.824) |
0.00062 (−0.316–0.317) |
0.999 | 0.0598 | 0.0239 | |
|
| |||||||||
| Baranyi | 102 | 14.31 (13.87–14.75) |
0.101 (0.097–0.105) |
0.126 | 1.742 (1.727–1.756) |
0.996 | 0.0445 | ||
| 104 | 8.96 (8.50–9.41) |
0.107 (0.103–0.111) |
0.115 | 1.777 (1.763–1.789) |
0.996 | 0.0445 | |||
| 106 | 2.72 (2.07–3.38) |
0.104 (0.099–0.109) |
0.060 | 1.791 (1.776–1.806) |
0.994 | 0.0483 | |||
aValue fixed at bound.
After the results shown in Figure 1 and Tables 2, 3, and 4, the growth models selected for the rest of the investigation were three-phase linear, Gompertz, and Baranyi. The three selected models provided expected values for the growth parameters and fitted data properly, as shown by the statistics analysed, even in the case of the three-phase linear model, which was the one to provide worse goodness of fit, that is, lowest r 2 and highest RMSE values. Richards and logistic models were disregarded because they were not able to fit properly all these typical growth curves; that is, they gave abnormal values for growth parameters in some occasions.
Each model had a trend in providing higher or lower values, three-phase linear model giving consistently the lowest values, followed by Baranyi and Gompertz models, in this order, for both the growth rate and the lag phase. In a previous comparison of these three models, Buchanan et al. [2] already noticed and explained this effect on the basis of the nature of each model. These authors also highlighted the correlation existing between lag phase duration and specific growth rate values. This gives an explanation for the differences found in the values provided for growth rate and lag phase among these predictive models.
Hence, it seems that, depending on the predictive model chosen, values for growth rates and lag times will be consistently higher or lower. Then the question is which growth model can be considered the best for describing the true population growth and why. This can be answered with a deep analysis of the analytical aspects of the models, mechanistic elements, number of parameters, fitting properties, and so forth. However, such analyses have already been performed in the past [3], but researchers continue to use and compare different growth models [5, 12], probably because concluding results have not been reached yet.
In this context, our viewpoint is that the best performing model is the one which, for the growth parameters of different cultures of one microbial strain growing under exactly the same conditions and with the same precultural history, gives closer values.
With this purpose, an extensive analysis of growth curves was performed with the three selected growth models. Only growth rate was considered at this stage, since this parameter should be similar for all growth curves of the same microbial strain, even when starting from different initial inocula levels. A total of 345 individual growth curves were analysed, including those individual growth curves used to build the average OD growth curves shown in Figure 1.
Table 5 shows, as an example, growth rate values obtained for all E. coli individual growth curves with three-phase linear, Gompertz, and Baranyi growth models. With these data and those for the individual growth curves of B. cereus and L. monocytogenes, extensive statistical analyses were performed, including analyses of variance, medians, and quartiles. Analyses of variance showed that initial concentration did not influence growth rate and that significant differences were found among growth rate values given by the different models, as already pointed out. The statistical analyses also showed that, within models, growth rate data were not normally distributed, and significant differences were also found among median growth rate values.
Table 5.
Growth rate values and their 95% confidence limits and coefficients of determination (r 2) and RMSE of fit obtained with three-phase linear, Gompertz, and Baranyi growth models for the growth curves of Escherichia coli CECT 515 at 37°C in pH 5 TSB+YE inoculating 102, 104, and 106 CFU mL−1.
| Initial concentration (CFU mL−1) | Three-phase linear model | Gompertz model | Baranyi model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Growth rate | r 2 | RMSE | Growth rate | r 2 | RMSE | Growth rate | r 2 | RMSE | |
| (OD units h−1) | (OD units h−1) | (OD units h−1) | |||||||
| 102 | 0.076 (0.073–0.078) | 0.988 | 0.0425 | 0.094 (0.092–0.097) | 0.997 | 0.0346 | 0.091 | 0.993 | 0.0516 |
| 0.086 (0.084–0.088) | 0.994 | 0.0295 | 0.100 (0.097–0.102) | 0.998 | 0.0296 | 0.112 | 0.995 | 0.0469 | |
| 0.091 (0.089–0.093) | 0.995 | 0.0284 | 0.106 (0.103–0.108) | 0.998 | 0.0283 | 0.112 | 0.995 | 0.0478 | |
| 0.100 (0.096–0.105) | 0.982 | 0.0516 | 0.118 (0.115–0.121) | 0.998 | 0.0317 | 0.112 | 0.995 | 0.0456 | |
| 0.082 (0.078–0.085) | 0.990 | 0.0414 | 0.100 (0.097–0.102) | 0.998 | 0.0319 | 0.116 | 0.996 | 0.0412 | |
| 0.091 (0.088–0.094) | 0.988 | 0.0478 | 0.114 (0.112–0.116) | 0.999 | 0.0203 | 0.115 | 0.995 | 0.0453 | |
| 0.095 (0.093–0.097) | 0.994 | 0.0348 | 0.113 (0.112–0.115) | 0.999 | 0.0179 | 0.113 | 0.995 | 0.0482 | |
| 0.097 (0.095–0.099) | 0.996 | 0.0230 | 0.111 (0.109–0.113) | 0.999 | 0.0239 | 0.113 | 0.995 | 0.0465 | |
| 0.102 (0.100–0.104) | 0.998 | 0.0173 | 0.116 (0.114–0.118) | 0.999 | 0.0204 | 0.111 | 0.995 | 0.0489 | |
| 0.087 (0.085–0.089) | 0.994 | 0.0300 | 0.100 (0.098–0.103) | 0.998 | 0.0297 | 0.114 | 0.995 | 0.0475 | |
| 0.109 (0.107–0.111) | 0.997 | 0.0215 | 0.125 (0.122–0.127) | 0.999 | 0.0217 | 0.109 | 0.995 | 0.0458 | |
| 0.111 (0.108–0.114) | 0.995 | 0.0285 | 0.126 (0.124–0.129) | 0.999 | 0.0234 | 0.111 | 0.995 | 0.0444 | |
| 0.114 (0.111–0.117) | 0.994 | 0.0319 | 0.132 (0.129–0.136) | 0.999 | 0.0269 | 0.113 | 0.994 | 0.0499 | |
| 0.110 (0.106–0.114) | 0.986 | 0.0516 | 0.132 (0.129–0.136) | 0.999 | 0.0286 | 0.109 | 0.993 | 0.0543 | |
| 0.116 (0.113–0.119) | 0.994 | 0.0330 | 0.136 (0.133–0.139) | 0.999 | 0.0224 | 0.104 | 0.994 | 0.0516 | |
| 0.104 (0.101–0.106) | 0.995 | 0.0318 | 0.120 (0.117–0.123) | 0.998 | 0.0292 | 0.003 | 0.156 | 0.9944 | |
| 0.107 (0.105–0.109) | 0.997 | 0.0223 | 0.122 (0.120–0.124) | 0.999 | 0.0215 | 0.110 | 0.995 | 0.0465 | |
| 0.106 (0.104–0.109) | 0.994 | 0.0332 | 0.122 (0.120–0.125) | 0.999 | 0.0297 | 0.115 | 0.996 | 0.0443 | |
| 0.106 (0.103–0.108) | 0.993 | 0.0378 | 0.123 (0.120–0.126) | 0.999 | 0.0264 | 0.109 | 0.995 | 0.0456 | |
| 0.112 (0.106–0.118) | 0.977 | 0.0629 | 0.136 (0.132–0.139) | 0.999 | 0.0282 | 0.091 | 0.993 | 0.0501 | |
| 0.085 (0.083–0.087) | 0.990 | 0.0415 | 0.106 (0.104–0.108) | 0.999 | 0.0240 | 0.083 | 0.991 | 0.0576 | |
| 0.108 (0.106–0.110) | 0.997 | 0.0223 | 0.121 (0.119–0.123) | 0.999 | 0.0217 | 0.103 | 0.994 | 0.0499 | |
| 0.084 (0.081–0.088) | 0.984 | 0.0507 | 0.098 (0.095–0.102) | 0.996 | 0.0440 | 0.098 | 0.994 | 0.0500 | |
| 0.108 (0.106–0.110) | 0.996 | 0.0260 | 0.125 (0.122–0.128) | 0.999 | 0.0261 | 0.109 | 0.995 | 0.0458 | |
| 0.108 (0.106–0.111) | 0.996 | 0.0277 | 0.125 (0.123–0.128) | 0.999 | 0.0262 | 0.098 | 0.993 | 0.0525 | |
| 0.110 (0.106–0.114) | 0.988 | 0.0484 | 0.132 (0.129–0.135) | 0.999 | 0.0257 | 0.101 | 0.994 | 0.0498 | |
| 0.109 (0.106–0.111) | 0.994 | 0.0338 | 0.128 (0.125–0.131) | 0.999 | 0.0259 | 0.102 | 0.993 | 0.0517 | |
| 0.102 (0.100–0.104) | 0.995 | 0.0264 | 0.116 (0.114–0.119) | 0.999 | 0.0252 | 0.102 | 0.993 | 0.0536 | |
| 0.104 (0.101–0.108) | 0.991 | 0.0394 | 0.121 (0.118–0.124) | 0.998 | 0.0329 | 0.104 | 0.994 | 0.0499 | |
| 0.118 (0.115–0.121) | 0.996 | 0.0275 | 0.137 (0.135–0.140) | 0.999 | 0.0216 | 0.095 | 0.993 | 0.0510 | |
|
| |||||||||
| 104 | 0.090 (0.088–0.093) | 0.993 | 0.0331 | 0.105 (0.102–0.107) | 0.998 | 0.0319 | 0.090 | 0.996 | 0.0432 |
| 0.099 (0.096–0.102) | 0.991 | 0.0429 | 0.120 (0.117–0.1229) | 0.998 | 0.0292 | 0.106 | 0.996 | 0.0437 | |
| 0.102 (0.099–0.104) | 0.995 | 0.0283 | 0.117 (0.115–0.119) | 0.999 | 0.0283 | 0.101 | 0.996 | 0.0477 | |
| 0.101 (0.099–0.103) | 0.995 | 0.0304 | 0.117 (0.115–0.120) | 0.998 | 0.0290 | 0.104 | 0.996 | 0.0418 | |
| 0.101 (0.099–0.104) | 0.995 | 0.0283 | 0.115 (0.112–0.118) | 0.998 | 0.0304 | 0.102 | 0.996 | 0.0452 | |
| 0.102 (0.100–0.104) | 0.996 | 0.0295 | 0.118 (0.115–0.121) | 0.998 | 0.0302 | 0.105 | 0.996 | 0.0433 | |
| 0.095 (0.093–0.098) | 0.989 | 0.0464 | 0.116 (0.113–0.119) | 0.998 | 0.0308 | 0.101 | 0.996 | 0.0476 | |
| 0.101 (0.098–0.103) | 0.995 | 0.0279 | 0.115 (0.112–0.117) | 0.998 | 0.0283 | 0.100 | 0.996 | 0.0450 | |
| 0.102 (0.100–0.104) | 0.996 | 0.0257 | 0.116 (0.114–0.118) | 0.999 | 0.0216 | 0.100 | 0.995 | 0.0477 | |
| 0.074 (0.070–0.079) | 0.950 | 0.1039 | 0.116 (0.113–0.118) | 0.999 | 0.0249 | 0.100 | 0.995 | 0.0479 | |
| 0.094 (0.091–0.096) | 0.993 | 0.0315 | 0.110 (0.108–0.113) | 0.998 | 0.0264 | 0.096 | 0.995 | 0.0465 | |
| 0.098 (0.095–0.100) | 0.992 | 0.0431 | 0.118 (0.115–0.120) | 0.999 | 0.0258 | 0.103 | 0.996 | 0.0431 | |
| 0.113 (0.111–0.116) | 0.996 | 0.0264 | 0.131 (0.128–0.134) | 0.999 | 0.0267 | 0.116 | 0.997 | 0.0427 | |
| 0.111 (0.109–0.114) | 0.995 | 0.0278 | 0.126 (0.123–0.130) | 0.998 | 0.0286 | 0.111 | 0.996 | 0.0453 | |
| 0.108 (0.106–0.110) | 0.997 | 0.0231 | 0.123 (0.121–0.126) | 0.999 | 0.0244 | 0.108 | 0.996 | 0.0444 | |
| 0.112 (0.109–0.115) | 0.992 | 0.0362 | 0.128 (0.124–0.131) | 0.998 | 0.0338 | 0.113 | 0.996 | 0.0452 | |
| 0.110 (0.107–0.112) | 0.996 | 0.0256 | 0.125 (0.122–0.128) | 0.999 | 0.0280 | 0.111 | 0.996 | 0.0429 | |
| 0.105 (0.102–0.107) | 0.995 | 0.0302 | 0.123 (0.121–0.126) | 0.999 | 0.0239 | 0.107 | 0.996 | 0.0460 | |
| 0.111 (0.107–0.116) | 0.982 | 0.0638 | 0.140 (0.137–0.143) | 0.999 | 0.0275 | 0.124 | 0.996 | 0.0443 | |
| 0.119 (0.117–0.121) | 0.997 | 0.0225 | 0.137 (0.134–0.140) | 0.999 | 0.0265 | 0.122 | 0.997 | 0.0400 | |
| 0.117 (0.113–0.120) | 0.992 | 0.0399 | 0.140 (0.137–0.143) | 0.999 | 0.0236 | 0.123 | 0.996 | 0.0454 | |
| 0.120 (0.118–0.122) | 0.998 | 0.0218 | 0.138 (0.135–0.142) | 0.999 | 0.0260 | 0.123 | 0.997 | 0.0401 | |
| 0.120 (0.117–0.122) | 0.996 | 0.0274 | 0.137 (0.134–0.140) | 0.999 | 0.0271 | 0.120 | 0.996 | 0.0471 | |
| 0.116 (0.113–0.119) | 0.995 | 0.0304 | 0.132 (0.129–0.135) | 0.999 | 0.0249 | 0.117 | 0.997 | 0.0397 | |
| 0.120 (0.117–0.123) | 0.994 | 0.0329 | 0.137 (0.133–0.141) | 0.998 | 0.0326 | 0.123 | 0.997 | 0.0424 | |
| 0.117 (0.114–0.119) | 0.997 | 0.0247 | 0.135 (0.132–0.138) | 0.999 | 0.0239 | 0.121 | 0.997 | 0.0374 | |
| 0.105 (0.101–0.109) | 0.980 | 0.0715 | 0.137 (0.133–0.141) | 0.998 | 0.0292 | 0.123 | 0.997 | 0.0371 | |
| 0.112 (0.110–0.114) | 0.997 | 0.0216 | 0.128 (0.125–0.130) | 0.999 | 0.0218 | 0.112 | 0.996 | 0.0458 | |
| 0.120 (0.117–0.122) | 0.996 | 0.0278 | 0.137 (0.134–0.140) | 0.999 | 0.0249 | 0.120 | 0.996 | 0.0449 | |
| 0.109 (0.106–0.112) | 0.993 | 0.0318 | 0.124 (0.121–0.126) | 0.999 | 0.0246 | 0.105 | 0.994 | 0.0531 | |
|
| |||||||||
| 106 | 0.092 (0.089–0.096) | 0.989 | 0.0400 | 0.112 (0.109–0.114) | 0.998 | 0.0269 | 0.091 | 0.993 | 0.0516 |
| 0.114 (0.111–0.117) | 0.994 | 0.0302 | 0.130 (0.126–0.134) | 0.998 | 0.0325 | 0.112 | 0.995 | 0.0469 | |
| 0.101 (0.096–0.105) | 0.979 | 0.0667 | 0.130 (0.127–0.134) | 0.998 | 0.0278 | 0.112 | 0.995 | 0.0478 | |
| 0.115 (0.112–0.117) | 0.996 | 0.0248 | 0.129 (0.126–0.132) | 0.998 | 0.0267 | 0.112 | 0.995 | 0.0456 | |
| 0.112 (0.109–0.115) | 0.995 | 0.0310 | 0.131 (0.128–0.135) | 0.998 | 0.0303 | 0.116 | 0.996 | 0.0412 | |
| 0.115 (0.113–0.117) | 0.996 | 0.0245 | 0.132 (0.129–0.135) | 0.999 | 0.0259 | 0.115 | 0.995 | 0.0453 | |
| 0.117 (0.114–0.119) | 0.997 | 0.0243 | 0.131 (0.128–0.135) | 0.998 | 0.0280 | 0.113 | 0.995 | 0.0482 | |
| 0.113 (0.110–0.115) | 0.995 | 0.0319 | 0.130 (0.126–0.134) | 0.998 | 0.0321 | 0.113 | 0.995 | 0.0465 | |
| 0.114 (0.112–0.117) | 0.995 | 0.0294 | 0.130 (0.126–0.133) | 0.998 | 0.0298 | 0.111 | 0.995 | 0.0489 | |
| 0.114 (0.111–0.117) | 0.995 | 0.0282 | 0.132 (0.129–0.134) | 0.998 | 0.0284 | 0.114 | 0.995 | 0.0475 | |
| 0.111 (0.108–0.113) | 0.997 | 0.0223 | 0.127 (0.124–0.130) | 0.998 | 0.0269 | 0.109 | 0.995 | 0.0458 | |
| 0.112 (0.109–0.115) | 0.995 | 0.0292 | 0.128 (0.125–0.132) | 0.998 | 0.0309 | 0.111 | 0.995 | 0.0444 | |
| 0.116 (0.114–0.118) | 0.997 | 0.0227 | 0.131 (0.128–0.135) | 0.998 | 0.0261 | 0.113 | 0.994 | 0.0499 | |
| 0.069 (0.063–0.074) | 0.903 | 0.1575 | 0.129 (0.127–0.132) | 0.999 | 0.0248 | 0.109 | 0.993 | 0.0543 | |
| 0.108 (0.106–0.111) | 0.996 | 0.0250 | 0.123 (0.120–0.126) | 0.999 | 0.0243 | 0.104 | 0.994 | 0.0516 | |
| 0.120 (0.117–0.122) | 0.995 | 0.0289 | 0.137 (0.133–0.140) | 0.998 | 0.0291 | 0.003 | 0.156 | 0.9944 | |
| 0.112 (0.110–0.115) | 0.996 | 0.0250 | 0.127 (0.124–0.131) | 0.998 | 0.0289 | 0.110 | 0.995 | 0.0465 | |
| 0.113 (0.111–0.116) | 0.996 | 0.0279 | 0.132 (0.129–0.136) | 0.998 | 0.0284 | 0.115 | 0.996 | 0.0443 | |
| 0.102 (0.098–0.106) | 0.987 | 0.0494 | 0.126 (0.123–0.129) | 0.998 | 0.0261 | 0.109 | 0.995 | 0.0456 | |
| 0.086 (0.082–0.089) | 0.982 | 0.0543 | 0.109 (0.106–0.112) | 0.998 | 0.0278 | 0.091 | 0.993 | 0.0501 | |
| 0.079 (0.076–0.083) | 0.975 | 0.0603 | 0.101 (0.098–0.105) | 0.997 | 0.0353 | 0.083 | 0.991 | 0.0576 | |
| 0.106 (0.104–0.109) | 0.995 | 0.0286 | 0.122 (0.119–0.125) | 0.998 | 0.0281 | 0.103 | 0.994 | 0.0499 | |
| 0.102 (0.099–0.105) | 0.993 | 0.0306 | 0.117 (0.114–0.119) | 0.998 | 0.0261 | 0.098 | 0.994 | 0.0500 | |
| 0.111 (0.108–0.113) | 0.996 | 0.0234 | 0.127 (0.124–0.130) | 0.999 | 0.0251 | 0.109 | 0.995 | 0.0458 | |
| 0.102 (0.099–0.105) | 0.992 | 0.0345 | 0.119 (0.116–0.121) | 0.999 | 0.0240 | 0.098 | 0.993 | 0.0525 | |
| 0.104 (0.101–0.107) | 0.993 | 0.0293 | 0.119 (0.116–0.122) | 0.998 | 0.0258 | 0.101 | 0.994 | 0.0498 | |
| 0.071 (0.066–0.076) | 0.931 | 0.1209 | 0.121 (0.118–0.124) | 0.998 | 0.0250 | 0.102 | 0.993 | 0.0517 | |
| 0.105 (0.102–0.108) | 0.994 | 0.0312 | 0.122 (0.119–0.125) | 0.998 | 0.0266 | 0.102 | 0.993 | 0.0536 | |
| 0.106 (0.103–0.109) | 0.993 | 0.0341 | 0.123 (0.120–0.126) | 0.998 | 0.0270 | 0.104 | 0.994 | 0.0499 | |
| 0.094 (0.091–0.098) | 0.989 | 0.0399 | 0.114 (0.111–0.117) | 0.998 | 0.0292 | 0.095 | 0.993 | 0.0510 | |
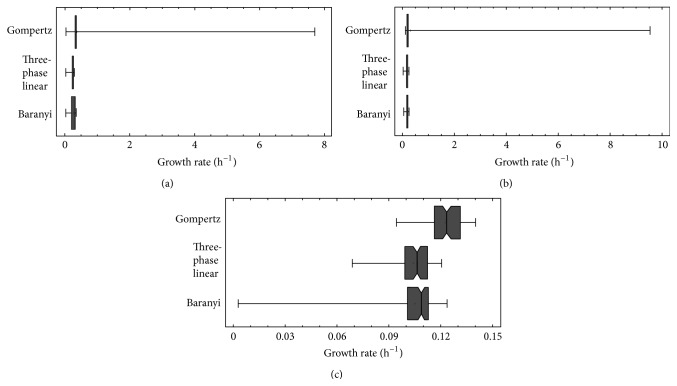
The last step of this research was to analyse variation of growth rate values. Table 6 shows average and standard deviation for growth rate of all three microorganisms as obtained by three-phase linear, Gompertz, and Baranyi models, and Figure 2 shows box and whiskers plots for the growth rate of the three microorganisms. These plots are based on the median and withstand perturbations caused by outliers better than plots based on the average. Since growth rate data were not normally distributed, box and whiskers plots are more appropriate than average and standard deviation shown in Table 6.
Table 6.
Average ± standard deviation of growth rate values (OD units h−1) obtained with three-phase linear, Gompertz, and Baranyi growth models for all the growth curves of Bacillus cereus INRA-AVTZ 415 at 30°C in BHI, Listeria monocytogenes CECT 4031 at 37°C in TSB+YE, and Escherichia coli CECT 515 at 37°C in pH 5 TSB+YE.
| Growth model | B. cereus | L. monocytogenes | E. coli |
|---|---|---|---|
| Three-phase linear | 0.226 ± 0.062 | 0.170 ± 0.022 | 0.104 ± 0.011 |
| Gompertz | 0.364 ± 0.627 | 0.296 ± 0.941 | 0.123 ± 0.011 |
| Baranyi | 0.261 ± 0.085 | 0.164 ± 0.042 | 0.105 ± 0.018 |
Figure 2.
Box and whiskers plots for growth rate values of Bacillus cereus INRA-AVTZ 415 at 30°C in BHI (a), Listeria monocytogenes CECT 4031 at 37°C in TSB+YE (b), and Escherichia coli CECT 515 at 37°C in pH 5 TSB+YE (c).
The results shown in Figure 2 clearly show that Gompertz model has a higher degree of variation in the growth rate values than the three-phase linear and Baranyi models. Gompertz model also generated some outlier growth rate values which extended the “whiskers” several units in the case of B. cereus and L. monocytogenes. It is certainly possible to obtain correct values for these outliers by changing the initial values when performing the nonlinear regression, but the purpose of this research was not to optimize the models, but to test them in order to choose the model that performs best. Hence initial values were not changed. Three-phase linear model provided slightly less variation than Baranyi, although the goodness of fit of this model is considerably worse than that of Baranyi model.
3.2. Plate Count Growth Curves
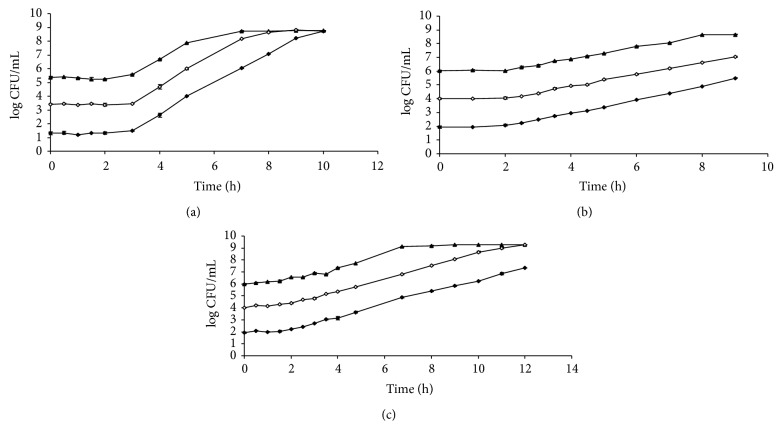
In order to double check the results obtained, several plate count growth curves of these same microorganisms were modelled with the five growth models. Figure 3 shows the growth curves plotted with the average log CFU mL−1 at each sampling time of B. cereus INRA-AVTZ 415 at 30°C in BHI (a), L. monocytogenes CECT 4031 at 37°C in TSB+YE (b), and E. coli CECT 515 at 37°C in pH 5 TSB+YE (c) starting at different initial concentration of microorganisms. As usual for plate count growth curves, these curves included less data per curve and did not show data points in all growth phases. In this way, models were forced into the common situation of scarce data points. Tables 7, 8, and 9 show the growth parameters given by three-phase linear, Gompertz, logistic, Richards, and Baranyi models for the growth curves of B. cereus, L. monocytogenes, and E. coli shown in Figures 3(a), 3(b), and 3(c), respectively.
Figure 3.
Plate count growth curves plotted with the average plate count values (±standard deviation) at each sampling time of Bacillus cereus INRA-AVTZ 415 at 30°C in BHI (a), Listeria monocytogenes CECT 4031 at 37°C in TSB+YE (b), and Escherichia coli CECT 515 at 37°C in pH 5 TSB+YE (c). Initial number of microorganisms: (⧫) 102 CFU mL−1; (◊) 104 CFU mL−1; (▲) 106 CFU mL−1.
Table 7.
Growth parameters and their 95% confidence limits and coefficients of determination (r 2), SSE, and RMSE of fit obtained with different growth models for average plate count growth curves of Bacillus cereus INRA-AVTZ 415 at 30°C in BHI inoculating 10, 103, and 105 CFU mL−1 shown in Figure 3(a).
| Growth model | Initial concentration (CFU mL−1) | Lag time (h) | Growth rate (log cycles h−1) |
y
0
(log CFU mL−1) |
C
(log cycles) |
β | r 2 | SSE | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| Three-phase linear | 10 | 2.75 (2.59–2.91) |
1.112 (1.073–1.115) |
1.343 (1.202–1.484) |
7.701 | 0.993 | 0.2880 | 0.2400 | |
| 103 | 2.92 (2.79–3.05) |
1.182 (1.121–1.138) |
3.414 (3.338–3.490) |
5.337 | 0.927 | 0.7295 | 0.4931 | ||
| 105 | 2.77 (2.64–2.91) |
1.143 (1.049–1.232) |
5.367 (5.289–5.444) |
3.372 | 0.920 | 0.8099 | 0.4025 | ||
|
| |||||||||
| Gompertz | 10 | 3.06 (2.59–3.52) |
1.276 (1.112–1.440) |
1.211 (0.983–1.440) |
9.049 (7.519–10.580) |
0.996 | 0.2846 | 0.1886 | |
| 103 | 3.30 (3.08–3.53) |
1.598 (1.380–1.816) |
3.403 (3.302–3.504) |
5.521 (5.284–5.757) |
0.998 | 0.0811 | 0.1007 | ||
| 105 | 3.00 (2.82–3.17) |
1.386 (1.206–1.565) |
5.319 (5.257–5.382) |
3.469 (3.363–3.574) |
0.999 | 0.0301 | 0.0613 | ||
|
| |||||||||
| Logistic | 10 | 3.04 (2.12–3.96) |
1.318 (1.081–1.556) |
0.914 (0.408–1.421) |
8.529 (6.904–10.150) |
0.992 | 0.5385 | 0.2595 | |
| 103 | 3.39 (3.00–3.79) |
1.651 (1.296–2.006) |
3.330 (3.154–3.507) |
5.433 (5.112–5.754) |
0.996 | 0.1747 | 0.1478 | ||
| 105 | 3.10 (2.84–3.36) |
1.451 (1.193–1.709) |
5.288 (5.194–5.381) |
3.461 (3.320–3.603) |
0.997 | 0.0551 | 0.0830 | ||
|
| |||||||||
| Richards | 10 | 3.06 (1.92–4.19) |
0.0006 (−4.543–4.544) |
1.211 (0.779–1.643) |
9.049 (5.176–12.920) |
0.00017 (−1.310–1.311) |
0.995 | 0.2846 | 0.2016 |
| 103 | 3.30 (3.05–3.55) |
0.004 (−2.950–2.958) |
3.403 (3.288–3.519) |
5.520 (5.229–5.812) |
0.0009 (−0.681–0.683) |
0.998 | 0.0811 | 0.1070 | |
| 105 | 3.02 (2.82–3.21) |
0.536 (−1.052–2.125) |
5.316 (5.247–5.385) |
3.460 (3.350–3.571) |
0.181 (−0.508–0.871) |
0.998 | 0.0275 | 0.0627 | |
|
| |||||||||
| Baranyi | 10 | 2.88 (2.39–3.37) |
1.187 (1.054–1.324) |
1.172 | 7.869 | 0.996 | 0.1792 | ||
| 103 | 3.09 (2.77–3.41) |
1.313 (1.137–1.324) |
3.360 | 5.387 | 0.997 | 0.1248 | |||
| 105 | 2.95 (2.75–3.15) |
1.275 (1.121–1.429) |
5.309 | 3.436 | 0.999 | 0.0604 | |||
Table 8.
Growth parameters and their 95% confidence limits and coefficients of determination (r 2), SSE, and RMSE of fit obtained with different growth models for average plate count growth curves of Listeria monocytogenes CECT 4031 at 37°C in TSB+YE inoculating 102, 104, and 106 CFU mL−1 shown in Figure 3(b).
| Growth model | Initial concentration (CFU mL−1) | Lag time (h) | Growth rate (log cycles h−1) |
y
0
(log CFU mL−1) |
C
(log cycles) |
β | r 2 | SSE | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| Three-phase linear | 102 | 2.00 (1.85–2.14) |
0.487 (0.467–0.506) |
1.988 (1.820–2.150) |
— | 0.997 | 0.0346 | 0.0620 | |
| 104 | 1.95 (1.75–2.06) |
0.432 (0.424–0.441) |
4.006 (3.970–4.040) |
— | 0.986 | 0.1525 | 0.1235 | ||
| 106 | 2.00 (1.78–2.24) |
0.423 (0.402–0.441) |
6.113 (5.870–6.360) |
2.554 | 0.985 | 0.0916 | 0.1070 | ||
|
| |||||||||
| Gompertz | 102 | 2.13 (1.63–2.63) |
0.542 (0.510–0.574) |
1.803 (1.599–2.007) |
6.071 (4.105–8.038) |
0.997 | 0.0406 | 0.0672 | |
| 104 | 2.22 (1.63–2.81) |
0.503 (0.443–0.564) |
3.932 (3.755–4.109) |
3.917 (2.982–4.852) |
0.993 | 0.0691 | 0.0870 | ||
| 106 | 2.27 (1.70–2.83) |
0.485 (0.417–0.554) |
6.009 (5.856–6.163) |
3.227 (2.604–3.85) |
0.992 | 0.0655 | 0.0853 | ||
|
| |||||||||
| Logistic | 102 | 1.73 (0.75–2.71) |
0.559 (0.511–0.606) |
1.501 (1.086–1.917) |
5.297 (3.521–7.073) |
0.995 | 0.0614 | 0.0826 | |
| 104 | 1.91 (0.72–3.10) |
0.513 (0.428–0.597) |
3.715 (3.340–4.091) |
3.739 (2.689–4.79) |
0.989 | 0.1087 | 0.1099 | ||
| 106 | 2.12 (1.18–3.06) |
0.501 (0.415–0.587) |
5.863 (5.599–6.127) |
3.073 (2.465–3.681) |
0.990 | 0.0841 | 0.0967 | ||
|
| |||||||||
| Richards | 102 | 2.13 (1.41–2.85) |
0.003 (−2.733–2.738) |
1.803 (1.282–2.323) |
6.068 (0.701–11.440) |
0.002 (−1.865–1.868) |
0.996 | 0.0407 | 0.0713 |
| 104 | 2.22 (1.57–2.86) |
0.0008 (−2.303–2.304) |
3.932 (3.614–4.250) |
3.917 (2.384–5.450) |
0.0006 (−1.686–1.687) |
0.992 | 0.0691 | 0.0929 | |
| 106 | 2.27 (1.70–2.84) |
0.013 (0.011–0.015) |
6.008 (5.854–6.163) |
3.222 (2.601–3.843) |
0.01a | 0.992 | 0.0657 | 0.0854 | |
|
| |||||||||
| Baranyi | 102 | 2.07 (1.84–2.31) |
0.514 (0.494–0.534) |
1.891 | — | 0.999 | 0.0453 | ||
| 104 | 1.86 (1.34–2.37) |
0.447 (0.410–0.483) |
3.896 | — | 0.993 | 0.0875 | |||
| 106 | 2.14 (1.64–2.64) |
0.460 (0.402–0.517) |
5.996 | 2.774 | 0.993 | 0.0774 | |||
aValue fixed at bound.
Table 9.
Growth parameters and their 95% confidence limits and coefficients of determination (r 2), SSE, and RMSE of fit obtained with different growth models for average plate count growth curves of Escherichia coli CECT 4031 at 37°C in pH 5 TSB+YE inoculating 102, 104, and 106 CFU mL−1 shown in Figure 3(c).
| Growth model | Initial concentration (CFU mL−1) | Lag time (h) | Growth rate (log cycles h−1) |
y
0
(log CFU mL−1) |
C
(log cycles) |
β | r 2 | SSE | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| Three-phase linear | 102 | 1.61 (1.41–1.81) |
0.518 (0.507–0.526) |
2.011 (1.800–2.220) |
— | 0.992 | 0.3897 | 0.1731 | |
| 104 | 1.63 (1.39–1.89) |
0.521 (0.508–0.544) |
4.108 (3.790–4.430) |
5.175 | 0.991 | 0.4079 | 0.1771 | ||
| 106 | 1.74 (1.45–2.02) |
0.574 (0.523–0.627) |
6.052 (5.920–6.180) |
3.229 | 0.948 | 0.9450 | 0.2931 | ||
|
| |||||||||
| Gompertz | 102 | 1.49 (0.57–2.42) |
0.576 (0.531–0.620) |
1.687 (1.330–2.043) |
7.489 (5.845–9.132) |
0.997 | 0.1518 | 0.1125 | |
| 104 | 1.55 (0.97–2.13) |
0.580 (0.549–0.611) |
3.862 (3.641–4.083) |
7.252 (6.270–8.234) |
0.999 | 0.0669 | 0.0747 | ||
| 106 | 2.25 (1.63–2.88) |
0.692 (0.515–0.869) |
6.180 (5.988–6.372) |
3.233 (2.898–3.568) |
0.985 | 0.3275 | 0.1652 | ||
|
| |||||||||
| Logistic | 102 | 0.41 (−1.52–2.34) |
0.578 (0.520–0.635) |
1.011 (0.223–1.799) |
7.501 (5.528–9.474) |
0.995 | 0.2043 | 0.1305 | |
| 104 | 0.85 (−0.11–1.81) |
0.593 (0.557–0.630) |
3.344 (2.965–3.722) |
6.952 (6.051–7.852) |
0.998 | 0.0727 | 0.0778 | ||
| 106 | 2.28 (1.64–2.93) |
0.728 (0.576–0.880) |
6.065 (5.866–6.265) |
3.264 (2.987–3.541) |
0.992 | 0.1763 | 0.1212 | ||
|
| |||||||||
| Richards | 102 | 1.49 (−0.21–3.19) |
0.002 (−3.220–3.224) |
1.686 (0.453–2.919) |
7.488 (4.798–10.180) |
0.001 (−2.065–2.067) |
0.996 | 0.1519 | 0.1175 |
| 104 | 1.53 (0.45–2.60) |
0.061 (−1.745–1.867) |
3.839 (3.100–4.578) |
7.214 (5.605–8.822) |
0.041 (−1.248–1.330) |
0.998 | 0.0671 | 0.0781 | |
| 106 | 2.11 (1.08–3.14) |
0.953 (0.749–1.157) |
5.573 (4.954–6.192) |
3.691 (3.069–4.312) |
7.363 (−3.876–18.600) |
0.996 | 0.0874 | 0.0891 | |
|
| |||||||||
| Baranyi | 102 | 1.32 (0.71–1.92) |
0.523 (0.489–0.556) |
1.807 | — | 0.996 | 0.1176 | ||
| 104 | 1.79 (1.45–1.92) |
0.568 (0.539–0.598) |
4.040 | 5.512 | 0.999 | 0.0624 | |||
| 106 | 2.35 (1.76–2.93) |
0.687 (0.528–0.849) |
6.181 | 3.093 | 0.991 | 0.1288 | |||
Similar results to those obtained with absorbance data were obtained when modelling the data from plate count growth curves. Three-phase linear model gave the lowest values for growth rates and lag times, followed by Baranyi, Gompertz, and logistic, in that order, for all three microorganisms. For these plate count growth curves, Richards model was not able to provide satisfactory values for growth rate for any of the curves. It is worth noting that some of the growth curves did not reach the stationary growth phase, and both three-phase linear and Baranyi models did not provide values for maximum population levels in these cases, while all other models provided uncertain estimations for this parameter. Again, three-phase linear was the model which had the worst goodness of fit, with r 2 values as low as 0.92 and RMSE values as high as 0.49.
Table 10 shows average and standard deviation for growth rate of all three microorganisms as obtained by three-phase linear, Gompertz, logistic, and Baranyi models with plate count growth curves. Again, when comparing the similarities in the growth rate values (Table 10), three-phase linear was the model to give less variation (lower standard deviation) for the different growth curves.
Table 10.
Average ± standard deviation of growth rate values (log cycles h−1) obtained with three-phase linear, Gompertz, and Baranyi growth models for all the growth curves of Bacillus cereus INRA-AVTZ 415 at 30°C in BHI, Listeria monocytogenes CECT 4031 at 37°C in TSB+YE, and Escherichia coli CECT 515 at 37°C in pH 5 TSB+YE.
| Growth model | B. cereus | L. monocytogenes | E. coli |
|---|---|---|---|
| Three-phase linear | 1.146 ± 0.035 | 0.447 ± 0.035 | 0.538 ± 0.032 |
| Gompertz | 1.420 ± 0.164 | 0.510 ± 0.029 | 0.616 ± 0.066 |
| Logistic | 1.473 ± 0.168 | 0.524 ± 0.031 | 0.633 ± 0.083 |
| Baranyi | 1.258 ± 0.065 | 0.474 ± 0.036 | 0.593 ± 0.085 |
Comparisons of the behaviour of different growth models reported in literature have reached different conclusions. Zwietering et al. [3] studied the growth of Lactobacillus plantarum in MRS medium at different temperatures and concluded that the Gompertz model was the best-fitting model. When these authors [3] extended the study to several microorganisms they reached similar conclusions. Buchanan et al. [2] reported that the three-phase linear model was more robust than the Gompertz and Baranyi models in terms of successfully fitting growth curve data. In their research [2] they fitted experimental data for E. coli O157:H7. Schepers et al. [27] found that the Richards model was the best growth model for Lactobacillus helveticus grown at different pH values, and Dalgaard and Koutsoumanis [7] also agreed that Richards model gave the best estimates for absorbance growth curves obtained with mixtures of different microbial strains isolated from spoiled seafood and incubated in different conditions to obtain a wide range of growth yields. López et al. [5] concluded, after a detailed statistical evaluation, that the Baranyi model showed the best behaviour for the growth curves studied. Baranyi and three-phase linear models showed the best fit for plate count data of Yersinia enterocolitica grown under different conditions of pH, temperature, and CO2. Richards model was the best-fitting optical density data of different bacterial and fungal species grown under different conditions. However, Mytilinaios et al. [12] found more recently that Baranyi was the most capable model to fit optical density data obtained for L. monocytogenes at different temperatures and pH values. The Weibull model also adequately described microbial growth [5]. Baty and Delignette-Muller [4] found that Baranyi was the best curve-fitting model for most curves, although they noted that the intermodel variability was frequently minor comparing to the imprecision of the parameter estimates, due to the low quantity and quality of the data used to build the growth curves. Actually, the low quality data used by these authors correspond to the datasets tabulated in the work by Buchanan et al. [2]. Pal et al. [28] also showed that Baranyi model provided the best fit for a majority of growth curves obtained for L. monocytogenes at low temperatures in liquid cultures, although there was no significant difference among all the primary growth models analysed. Maybe the use of so many microorganisms growing under such different growth conditions could explain, at least in part, the differences in the conclusions reached by authors regarding the best-fitting model.
4. Conclusions
Our results show that both Baranyi and three-phase linear models provide low variability for growth rate values when analysing similar growth curves, hence being the models of choice. Three-phase linear model gives the lowest variation for growth rates, while Baranyi gives a variation marginally higher, despite much better overall fitting.
These results provide insight into predictive microbiology and will help food microbiologists and researchers to choose the proper primary growth predictive model.
Acknowledgments
This research was financially supported by the Ministerio de Economía y Competitividad of the Spanish Government and Fondo Europeo de Desarrollo Regional (FEDER) through Projects AGL2010-19775 and AGL2013-48993-C2-1-R.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
References
- 1.McMeekin T. A., Olley J., Ross T., Ratkowsky D. A. Predictive Microbiology: Theory and Application. New York, NY, USA: John Wiley and Sons; 1993. [Google Scholar]
- 2.Buchanan R. L., Whiting R. C., Damert W. C. When is simple good enough: a comparison of the Gompertz, Baranyi, and three-phase linear models for fitting bacterial growth curves. Food Microbiology. 1997;14(4):313–326. doi: 10.1006/fmic.1997.0125. [DOI] [Google Scholar]
- 3.Zwietering M. H., Jongenburger I., Rombouts F. M., van't Riet K. Modeling of the bacterial growth curve. Applied and Environmental Microbiology. 1990;56(6):1875–1881. doi: 10.1128/aem.56.6.1875-1881.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Baty F., Delignette-Muller M.-L. Estimating the bacterial lag time: which model, which precision? International Journal of Food Microbiology. 2004;91(3):261–277. doi: 10.1016/j.ijfoodmicro.2003.07.002. [DOI] [PubMed] [Google Scholar]
- 5.López S., Prieto M., Dijkstra J., Dhanoa M. S., France J. Statistical evaluation of mathematical models for microbial growth. International Journal of Food Microbiology. 2004;96(3):289–300. doi: 10.1016/j.ijfoodmicro.2004.03.026. [DOI] [PubMed] [Google Scholar]
- 6.Ross T. Indices for performance evaluation of predictive models in food microbiology. Journal of Applied Bacteriology. 1996;81(5):501–508. doi: 10.1111/j.1365-2672.1996.tb03539.x. [DOI] [PubMed] [Google Scholar]
- 7.Dalgaard P., Koutsoumanis K. Comparison of maximum specific growth rates and lag times estimated from absorbance and viable count data by different mathematical models. Journal of Microbiological Methods. 2001;43(3):183–196. doi: 10.1016/s0167-7012(00)00219-0. [DOI] [PubMed] [Google Scholar]
- 8.Perni S., Andrew P. W., Shama G. Estimating the maximum growth rate from microbial growth curves: definition is everything. Food Microbiology. 2005;22(6):491–495. doi: 10.1016/j.fm.2004.11.014. [DOI] [Google Scholar]
- 9.Huang L. Optimization of a new mathematical model for bacterial growth. Food Control. 2013;32(1):283–288. doi: 10.1016/j.foodcont.2012.11.019. [DOI] [Google Scholar]
- 10.Jewell K. Comparison of 1-step and 2-step methods of fitting microbiological models. International Journal of Food Microbiology. 2012;160(2):145–161. doi: 10.1016/j.ijfoodmicro.2012.09.017. [DOI] [PubMed] [Google Scholar]
- 11.Coroller L., Kan-King-Yu D., Leguerinel I., Mafart P., Membré J.-M. Modelling of growth, growth/no-growth interface and nonthermal inactivation areas of Listeria in foods. International Journal of Food Microbiology. 2012;152(3):139–152. doi: 10.1016/j.ijfoodmicro.2011.09.023. [DOI] [PubMed] [Google Scholar]
- 12.Mytilinaios I., Salih M., Schofield H. K., Lambert R. J. W. Growth curve prediction from optical density data. International Journal of Food Microbiology. 2012;154(3):169–176. doi: 10.1016/j.ijfoodmicro.2011.12.035. [DOI] [PubMed] [Google Scholar]
- 13.Augustin J.-C., Rosso L., Carlier V. Estimation of temperature dependent growth rate and lag time of Listeria monocytogenes by optical density measurements. Journal of Microbiological Methods. 1999;38(1-2):137–146. doi: 10.1016/s0167-7012(99)00089-5. [DOI] [PubMed] [Google Scholar]
- 14.Periago P. M., Conesa R., Delgado B., Fernández P. S., Palop A. Bacillus megaterium spore germination and growth inhibition by a treatment combining heat with natural antimicrobials. Food Technology and Biotechnology. 2006;44(1):17–23. [Google Scholar]
- 15.Baty F., Flandrois J. P., Delignette-Muller M. L. Modeling the lag time of Listeria monocytogenes from viable count enumeration and optical density data. Applied and Environmental Microbiology. 2002;68(12):5816–5825. doi: 10.1128/aem.68.12.5816-5825.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pascual C., Robinson T. P., Ocio M. J., Aboaba O. O., Mackey B. M. The effect of inoculum size and sublethal injury on the ability of Listeria monocytogenes to initiate growth under suboptimal conditions. Letters in Applied Microbiology. 2001;33(5):357–361. doi: 10.1046/j.1472-765x.2001.01012.x. [DOI] [PubMed] [Google Scholar]
- 17.Mackey B. M., Derrick C. M. The effect of sublethal injury by heating, freezing, drying and gamma-radiation on the duration of the lag phase of Salmonella typhimurium . Journal of Applied Bacteriology. 1982;53(2):243–251. doi: 10.1111/j.1365-2672.1982.tb04683.x. [DOI] [PubMed] [Google Scholar]
- 18.Swinnen I. A. M., Bernaerts K., Dens E. J. J., Geeraerd A. H., van Impe J. F. Predictive modelling of the microbial lag phase: a review. International Journal of Food Microbiology. 2004;94(2):137–159. doi: 10.1016/j.ijfoodmicro.2004.01.006. [DOI] [PubMed] [Google Scholar]
- 19.Baranyi J., Pin C. Modelling the history effect on microbial growth parameters and survival. In: McKellar R. C., Lu X., editors. Modelling Microbial Responses in Food. Boca Raton, Fla, USA: CRC Press; 2003. pp. 285–302. [Google Scholar]
- 20.Baranyi J., Pin C. Estimating bacterial growth parameters by means of detection times. Applied and Environmental Microbiology. 1999;65(2):732–736. doi: 10.1128/aem.65.2.732-736.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Augustin J.-C., Brouillaud-Delattre A., Rosso L., Carlier V. Significance of inoculum size in the lag time of Listeria monocytogenes . Applied and Environmental Microbiology. 2000;66(4):1706–1710. doi: 10.1128/aem.66.4.1706-1710.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Whiting R. C., Bagi L. K. Modeling the lag phase of Listeria monocytogenes . International Journal of Food Microbiology. 2002;73(2-3):291–295. doi: 10.1016/s0168-1605(01)00662-6. [DOI] [PubMed] [Google Scholar]
- 23.Baranyi J., Roberts T. A., McClure P. J. A non-autonomous differential equation to model bacterial growth. Food Microbiology. 1993;10(1):43–59. doi: 10.1006/fmic.1993.1005. [DOI] [Google Scholar]
- 24.Smelt J. P. P. M., Otten G. D., Bos A. P. Modelling the effect of sublethal injury on the distribution of the lag times of individual cells of Lactobacillus plantarum . International Journal of Food Microbiology. 2002;73(2-3):207–212. doi: 10.1016/s0168-1605(01)00651-1. [DOI] [PubMed] [Google Scholar]
- 25.Métris A., George S. M., Baranyi J. Use of optical density detection times to assess the effect of acetic acid on single-cell kinetics. Applied and Environmental Microbiology. 2006;72(10):6674–6679. doi: 10.1128/aem.00914-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Valero A., Pérez-Rodríguez F., Carrasco E., García-Gimeno R. M., Zurera G. Modeling the growth rate of Listeria monocytogenes using absorbance measurements and calibration curves. Journal of Food Science. 2006;71(7):257–264. doi: 10.1111/j.1750-3841.2006.00139.x. [DOI] [Google Scholar]
- 27.Schepers A. W., Thibault J., Lacroix C. Comparison of simple neural networks and nonlinear regression models for descriptive modeling of Lactobacillus helveticus growth in pH-controlled batch cultures. Enzyme and Microbial Technology. 2000;26(5-6):431–445. doi: 10.1016/s0141-0229(99)00183-0. [DOI] [PubMed] [Google Scholar]
- 28.Pal A., Labuza T. P., Diez-Gonzalez F. Comparison of primary predictive models to study the growth of Listeria monocytogenes at low temperatures in liquid cultures and selection of fastest growing ribotypes in meat and turkey product slurries. Food Microbiology. 2008;25(3):460–470. doi: 10.1016/j.fm.2008.01.009. [DOI] [PubMed] [Google Scholar]