Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Oct 25.
Published in final edited form as: Rep U S. 2011 Sep;2011:2564–2569. doi: 10.1109/IROS.2011.6094945

Feasibility Study of an Optically Actuated MR-compatible Active Needle

Seok Chang Ryu 1, Pierre Renaud 2, Richard J Black 3, Bruce L Daniel 4, Mark R Cutkosky 5
PMCID: PMC4620048  NIHMSID: NIHMS724971  PMID: 26509100

Abstract

An active needle is proposed for the development of MRI guided percutaneous procedures. The needle uses internal laser heating, conducted via optical fibers, of a shape memory alloy (SMA) actuator to produce bending in the distal section of the needle. Active bending of the needle as it is inserted allows it to reach small targets while overcoming the effects of interactions with surrounding tissue, which can otherwise deflect the needle away from its ideal path. The active section is designed to bend preferentially in one direction under actuation, and is also made from SMA for its combination of MR and bio-compatibility and its superelastic bending properties. A prototype, with a size equivalent to standard 16G biopsy needle, exhibits significant bending with a tip rotation of more than 10°. A numerical analysis and experiments provide information concerning the required amount of heating and guidance for design of efficient optical heating systems.

I. Introduction

In the field of interventional radiology, procedures such as biopsies or punctures are performed using an imaging device for guidance. MR scanners are very interesting devices in this context: the radiologist and the patient are not exposed to any ionizing radiation, and the images provided by MR scanners have a high level of contrast and sufficient resolution to identify small structures such as early stage tumors.

One of the factors limiting today the accuracy of such gestures is the needle deflection during the insertion [1]. The control of the needle path, previously achieved with a rigid body assumption [2], thus evolved towards needle steering [3] by including needle-tissue interaction models, to predict the behavior of the needle from its geometry and tissue modeling. A simple insertion strategy was introduced in [4], the needle is simply rotated by 180° when the estimated deflection reaches a given threshold. More complex control strategies have subsequently been developed to compensate for needle deflections and even to avoid anatomical obstacles. In [5], [6], the authors propose to manipulate the needle from its base, outside the patient body, using a robotic system to create forces and moments on the needle in a similar way to the approach used by clinicians. The stiffness of the tissues at the entry point may limit such a steering strategy and the robotic system must be designed to provide mobilities in addition to those required for needle insertion and rotation about the long axis.

In [7], [8], [9] relative displacements between concentric needles, or a prebent needle integrated into a straight cannula, are used to generate a needle trajectory. From a design point of view, an even simpler approach to steer a needle is to use the asymmetry of the needle to create forces on the needle during its insertion. The only degrees of freedom to control are then the insertion and the axial rotation of the needle. Needles with asymmetric bevels are submitted to an unbalanced field of forces during the insertion [10], [11]. This phenomenon can be used [12] to steer thin needles. Various complex curves are obtained by combining the needle insertion and self-rotation movements [13], [14], [15].

In this paper, we propose an extension of needle steering using interactions between the needle and the tissues. The design consists of a needle capable of active bending that, in combination with the normal insertion forces and the ability to rotate the needle about its long axis, allow it to be steered to reach small tumors or other sites. The actuation system is entirely compatible with MR imaging and the diameter, at 1.65 mm, is compatible with standard prostate biopsy needles. In section II, the main design features are introduced. An experimental study of the device characteristics and assessment of the optical heating requirements are then provided in section III before concluding on the next steps in the development of the active needle.

II. Active needle design

A. Related work

The design of an active needle was considered of interest in [16], but no entirely MR-compatible active biopsy needle has been presented in the literature. Tang et al. developed a needle with a magnetized compliant section near the tip that is controlled by an external magnetic force [17], which is obviously not MR-compatible. The thin tip also makes the needle susceptible to buckling. Yan et al. proposed a smart needle concept, with a piezoelectric material deposited on the needle to create a continuous bending effect along the needle [18]. However, this design is not optimized for steering the needle tip during insertion.

The principle of an active needle can also be related to active catheters [19] e.g., for navigation in blood vessels. Several such systems have been developed [20], [21], [22], however their design cannot be directly exploited for an active needle because of the very different mechanical interactions that exist between a needle and tissues, as compared to the interaction of a catheter with blood flow.

MR-compatible actuation technologies have also been developed for robotic devices. Pneumatic [23] or hydraulic [24], [25] systems are of interest, the latter presenting an impressive power/volume ratio. However, integrating such technologies in a 1–2 mm diameter needle remains a formidable challenge. Among the actuation technologies that present a high power/volume ratio and MR-compatibility, Shape Memory Alloys (SMA) are of particular interest. By activating thermally a phase transition in the SMA microstructure, this material can be used as an actuator.

Joule heating with an electric current is usually adopted to obtain SMA contraction. An MR-compatible device can be designed using such an approach [26], however artifacts will be created if actuation and MR imaging are performed concurrently. Optical heating has been proposed to actuate an SMA forceps for minimally invasive surgery in [27] and for contraction of an embedded SMA in a smart composite [28]. Both studies demonstrate the feasibility of optical SMA actuation, and therefore MR-compatibility can be obtained by considering the use of optical fibers to direct laser light to an SMA wire actuator.

B. Main design features

1) Principle of an active biopsy needle

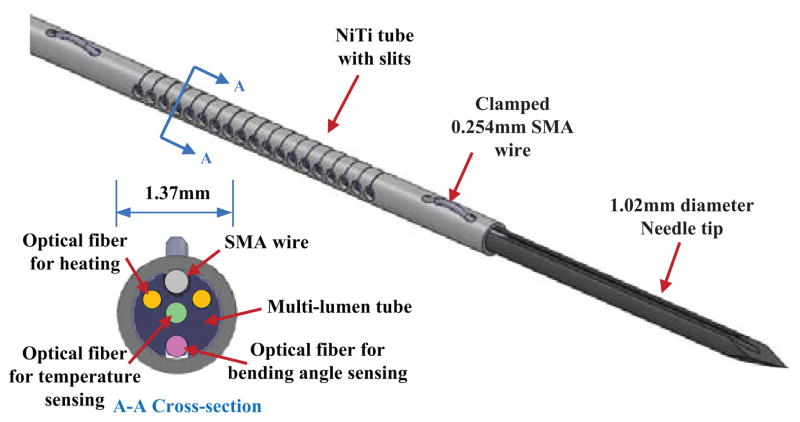
A biopsy needle is considered for the design of the active needle. It is composed of two main parts: an inner stylet and an outer cannula. During a biopsy, the two elements are inserted together to reach the biopsy site. Then, the inner stylet is removed and a biopsy probe is inserted to perform the biopsy. For the proposed device, the active element is the inner stylet initially inserted with the cannula (Fig. 2).

Fig. 2.

Fig. 2

Open in a new tab

The inner stylet of an active needle design

The active element introduces one degree of freedom in the needle body. Combinging active bending with needle insertion and axial rotation movements, it becomes possible to control the needle trajectory, following a similar approach as used previously for needle steering with beveled needles.

The inner stylet has a maximum diameter of 1.35 mm, at the location of the active element, corresponding to a 18G needle. With the external cannula, the overall diameter is equal to 1.65mm, which is equivalent to 16G devices, used for instance for prostate biopsies.

2) SMA for actuation with TFBG for optical activation

To promote compactness and effective heat transfer, the optical fibers should run parallel to the needle axis and transmit heat over a finite length of the SMA wire. The core diameter of the optical fiber is approximately 100 μm and the exiting laser illumination can produce excessive local heating if it is not distributed. One solution to this problem is to use tilted fiber bragg gratings (TFBG) to heat the SMA wire from the side of an optical fiber.

A TFBG is written on the core of the optical fiber. It acts as a wavelength-specific reflector [29], characterized by the grating period d and its tilt angle θ. The tilt angle can be on the order of 45°, and the grating length is usually about 5 mm. The reflected wavelength is defined by λ = 2dneff with neff the effective refractive index in the fiber core. By removing the fiber cladding, the power emission out of the fiber is maximized, and can reach 55% of the laser power emitted through the fiber [30]. In this manner, homogeneous heating can be obtained over lengths up to 50mm [31].

3) SMA for MR compatible superelastic structure

The phase transition of SMA is used for actuation, but also to provide the flexibility needed to deflect the needle. SMA exhibits a so-called superelastic domain: if the temperature is high enough, the material is in its austenite phase. A stress increase can then induce a phase transition towards the martensite phase. This stress-induced phase transition is characterized by a large plateau in the stress-strain domain. We propose here, in a similar way to the needle design introduced in [32], to use this large elasticity domain for the body of the active device. This approach allows the needle to achieve high deflections, due to device actuation or to interaction with tissues, without the occurrence of any plastic deformation.

C. Design implementation

1) Integration

The actuation mechanism is based on a machined SMA tube and SMA wire. The flexible part of the SMA tube is 25 mm long, with a series of slits with rounded ends (to reduce stress concentrations) on one side (Fig. 2). The number of slits and the distance of 30 μm between two consecutive slits are chosen so that the slits close fully under maximum actuation. In this way, the device is always in a configuration for which the wire can generate a tension during its contraction, independent of the external interaction forces. Once the slits have closed, the needle becomes considerably stiffer with respect to additional bending loads.

In addition to the SMA wire, the SMA tube contains optical fibers for heating and sensing. These elements, presented in the following section, are inserted in a flexible multi-lumen PTFE tube to obtain and maintain their alignments. High density PTFE material is relatively transparent to mid-infrared light, thereby allowing most of the emitted power from the fibers to reach the SMA wire.

2) Actuation

The SMA wire has a diameter of 0.25 mm. In the current design, a Flexinol wire is chosen (Dynalloy Inc, Tustin, CA). It can generate, according to the manufacturer’s specifications, up to 4% of strain when heated to 90°C. This temperature is high compared to safe temperatures for human tissues, which are on the order of 45°C. However, SMA alloys can receive heat treatments to lower their phase transition temperature to 55°C [33]. The outer cannula, made of PTFE, introduces an additional thermal insulation with respect to tissue. Moreover, the bending actuation will be applied only for short periods of time, to alter the path taken by the needle as it is inserted. Under these conditions, surrounding tissues should be able to sustain the resulting temperature increases.

Two fibers are embedded in the device to heat the SMA wire. Each of them integrates a TFBG so that four heating areas, including the fiber tips, are positioned along the 18 mm of SMA wire.

3) Sensing

Optical sensing techniques are preferred for an MR-compatible device. In addition to the fibers with TFBGs, the design includes one optical fiber with a standard FBG and one optical fiber for estimating temperature and curvature, respectively. The estimated curvature information can be converted into mechanical strain along the temperature sensing fiber and the SMA wire. The strain-compensated temperature and the strain on the SMA wire enable closed loop control of bending angle.

D. Behavior evaluation using numerical simulation

Steering performance is intrinsically linked to the steering control strategy and the mechanical properties of the tissues in interaction with the needle. In this paper, we focus on two intrinsic properties of the device. The first is the maximum deflection of the needle when no force is applied on the needle tip is determined. This deflection describes the achievable trajectory correction when using a simple retract-then-insert strategy, where the needle is almost completely retracted, deflected, and inserted again. Second, the needle stiffness is evaluated to estimate, with a very simple interaction model, the potential behavior of the device in tissue.

Finite Element Analysis (FEA) is performed using An-sys software. Superelastic behavior of the SMA can be simulated, in isothermal conditions. As a consequence, we do not perform a thermo-mechanical simulation but only a mechanical simulation, using the SMA wire specifications provided by the manufacturer and an experimentally identified Young’s modulus for the tube under the conditions of interest.

1) Needle deflection

The SMA wire can be described [34], [35] as a spring for which displacement depends on the force generated by the phase transition in the material and the stiffness of the surrounding elements connected to the wire. The deflection is therefore evaluated in 3 steps. First, the stiffness describing the action of the flexible tube on the wire is evaluated. Next, the wire behavior during contraction is determined. Then, the needle deflection is found by simulating the bending of the SMA tube with the determined loading conditions.

The axial wire stiffness is 29 N/mm, and the stiffness of the tube is estimated using FEA equal to 43 N/mm. Using the wire description introduced in [34] and the manufacturer’s specifications, the action of the wire on the SMA tube can thus be modeled as a 10 N force. The simulated needle deflection is represented in Fig. 4(a). The maximum deflection is 2.23 mm, which represents a bending angle of 4.6°, considering from the FEA results that the rotation begins at the first slit on the SMA tube. The Von Mises stress reaches 233 MPa in the tube (Fig. 4(b)). The superelastic plateau is defined for the material by a stress of 520 MPa. The superelastic effect is therefore not required during contraction of the wire but may be used to remain in an elastic domain when external loads are applied.

Fig. 4.

Fig. 4

Open in a new tab

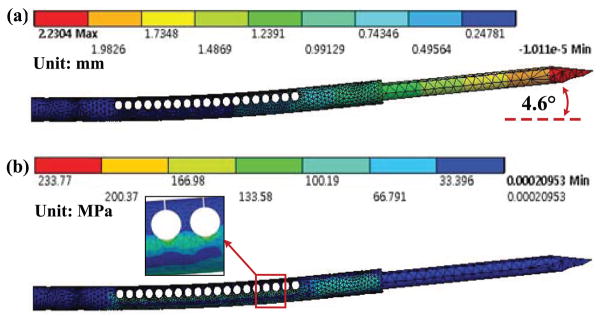
FEA: (a)Tip deflection(scale 1), (b)von-Mises stress in the tube

If a simple retract-then-insert needle insertion strategy is used, the deflection angle results in a trajectory deviation of 4.8 mm when the needle is inserted by 60 mm, an average length to reach the prostate during a biopsy [36]. The device performance seems therefore relevant for the application. As outlined earlier, its performance in terms of needle steering depends on the control strategy that will be implemented. A more detailed analysis will be achieved in a future work.

2) Needle stiffness

The SMA tube is not symmetric with respect to the needle axis. As a consequence, axial forces exerted by tissues at the tip will induce bending, similarly to a needle with an asymmetric bevel. Compensating for this phenomenon is straightforward, and involves rotating the needle about its long axis. We wish, however, to estimate the magnitude of force that will cause the slits to close up, i.e. beyond which active steering is no longer possible until the needle is rotated.

The bending stiffness, defined as the ratio between the moment applied on the active part of the needle and its curvature, is estimated using FEA at 1493 Nmm2. Let us consider a very simple model of interaction with the tissue, with a purely axial force exerted on the needle tip. This force must then be equal to 12.6 N to reach the maximum deflection estimated previously. This value seems satisfactory, as the axial force only reaches for instance 10 N when puncturing a prostate capsule [37], and is significantly lower after this puncture.

III. Prototype and Experimentation

A. Prototype

For this preliminary study, only the SMA tube and wire are assembled (Fig. 1). The tube slits are laser machined (Lumenous Inc, Sunnyvale, CA) on a NiTI tube (Johnson Matthey Medical Inc, West Chester, PA). In this version of the device, the SMA wire is pressed on the SMA tube using a grooved needle, manufactured using electro-discharge machining.

Fig. 1.

Fig. 1

Open in a new tab

Inner stylet of the proposed active biopsy needle

B. Evaluation of the prototype

1) Active needle deflection

In this experiment, the active needle prototype is activated using conventional Joule heating (Fig. 5). The vertical deflection is evaluated using a vision-based measurement of the 15 mm long needle tip. The measurement accuracy of the tip displacement is approximately 0.17 mm, so that the angle is evaluated with an accuracy of 0.25°.

Fig. 5.

Fig. 5

Open in a new tab

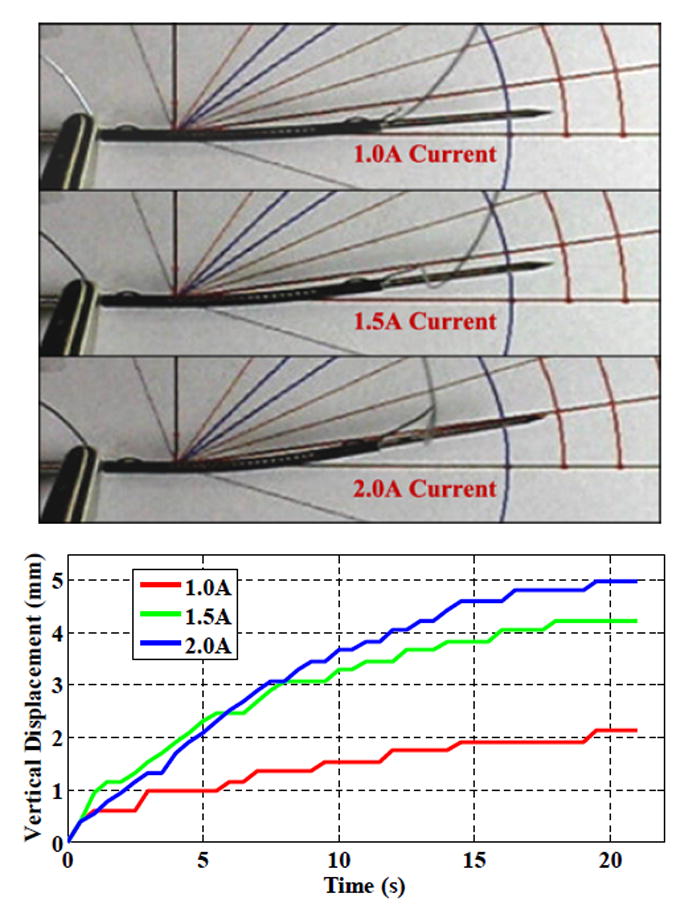
Vertical deflection of the active needle tip with Joule heating

First, the heating is performed with a current of 1A, the current suggested by the manufacturer. The power emitted by Joule heating is then equal to 0.36 W. The tip reaches a maximum deflection of 2.12 mm, within 5% of the value predicted with FEA.

The current in the wire can be increased without wire breakage. Higher deflection is then observed: 4.21 mm (8.8°) and 4.98 mm (10.4°) for currents of 1.5 A and 2.0 A, respectively.

2) Device stiffness

Stiffness evaluation is achieved by clamping the one end of the active part on a metallic breadboard to minimize the presence of any additional flexibility. Different masses are attached to a fixed point on the part to create a force perpendicular to the needle axis, and the vertical tip deflections are measured.

The relationship between the displacement of the needle tip and the applied force is represented in Fig. 6. The behavior predicted using FEA is superimposed. Assuming simple beam bending, the bending stiffness of the device corresponds to 1451 Nmm2, which is consistent with the expected bending stiffness. However, the prototype has a 5% lower stiffness than the value assessed numerically. The main potential source of discrepancy is the SMA behavior; the Young’s modulus may be lower than expected. In particular, the laser cutting of the slits may have affected the structure with the presence of martensite, the most flexible material phase, at room temperature. Further investigation with material testing is needed.

Fig. 6.

Fig. 6

Open in a new tab

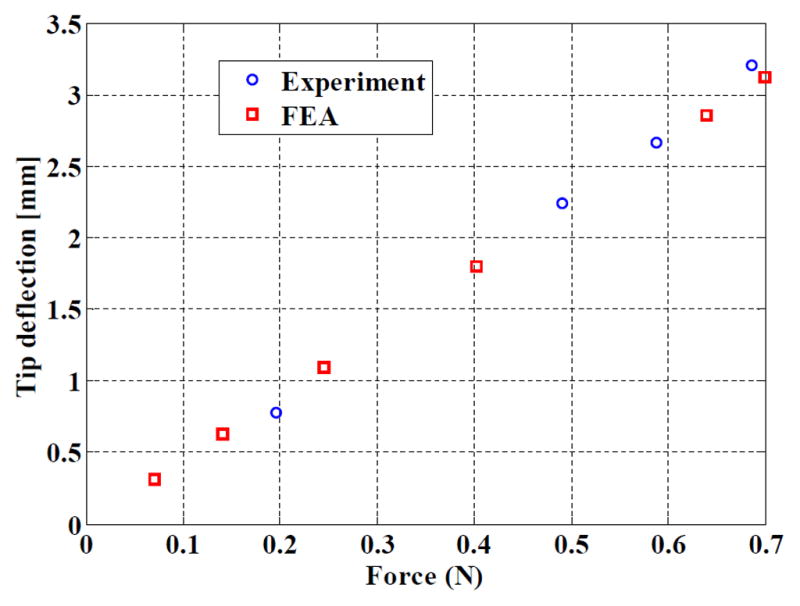
Comparison of experimental and simulated stiffnesses

C. Optical heating

An experimental study was performed to help in the design of the optical heating system, and evaluate the efficiency of the optical heating that may be expected.

1) The experimental set-up

An apparatus was constructed to assess the heating performance using optical fibers of a single SMA wire. The apparatus (Fig. 7) is a lever mechanism, actuated by the SMA wire, whose displacement is measured using a spring-loaded dial gauge. The dial gauge applies a resisting force of approximately 1 N to the lever tip. A 0.25 mm diameter, 40 mm long, Dynalloy wire is used. Measurement resolution is 0.025 mm at the tip of the lever, which makes it possible determine the wire contraction using a kinematic model with a resolution of 2 μm. To perform the heating, two multimode fibers (105μm core diameter) are connected to 976nm lasers (Alfalight Inc, Madison, WI). The use of two fibers allows a simulation of multi-point heating, albeit less evenly distributed than with TFBGs. The optical fibers and the SMA wire are positioned in the same plane. The fibers are spaced 15 mm apart and oriented perpendicular to the wire, almost in contact with it.

Fig. 7.

Fig. 7

Open in a new tab

Experimental set-up for the evaluation of the optical heating

2) Results

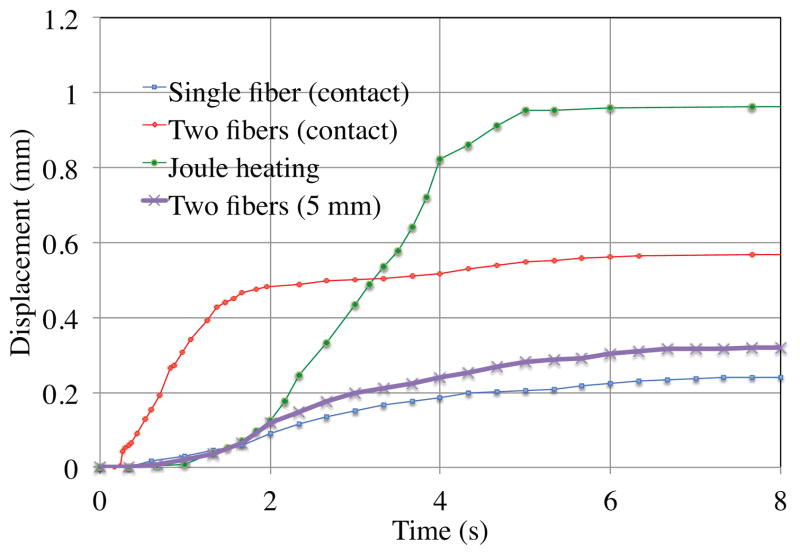
The wire contraction is represented in Fig. 8. The displacements observed when using only one fiber, with two fibers, and after displacing the two fibers 5 mm distant from the wire. The results are compared to the results obtained when the wire is heated uniformly by Joule heating using a constant current of 1.4 A, producing 2 W for the 40 mm of wire. The dynamics and the amplitude of the contraction in this case provide a reference for the optical heating results.

Fig. 8.

Fig. 8

Open in a new tab

Comparison of wire displacement during optical and Joule heating

First, the maximum power from the optical fiber tip is evaluated. Above 0.38 W, heating with the fiber tip nearly in contact with the wire leads to the wire breakage due to the small spot size.

Using one fiber to perform the heating, the wire contraction is equal to 25% of the displacement obtained with Joule heating, with a comparable initial contraction rate. This tends to show that about 10 mm of wire has contracted during the 8 seconds of heating.

With two fibers, the total power emitted is 0.76 W. The wire displacement reaches 58% of the 40 mm wire contraction obtained by Joule heating. In other words, about 23 mm of wire is contracted with the optical heating in about 8 seconds. The initial contraction is faster than with the Joule heating. Since the heating is more localized, the wire is submitted to strong thermal gradients, and the maximum temperatures exceed those from Joule heating.

When increasing the distance between the fibers and the SMA wire, the wire no longer receives most of the power emitted by the fiber tips. Measurement with a power meter shows that each fiber sends 0.16 W to approximately 5 mm of wire. The heating effect is still significant: the wire displacement is slightly greater than obtained with a single fiber in contact, with comparable dynamics. This configuration, similar to the effect that can be obtained with the use of TFBGs, appears promising: the power for optical heating remains limited, with 0.32 W to obtain a contraction of more than 10 mm of wire, and heating along the length of the wire, instead of spot heating, limits overheating that can lead to breakage. With refinement of the optical heating system and of the transfer of power into the wire, the bending requirements can be satisfied.

IV. Conclusion

In this paper, a new design for an MR-compatible active needle is proposed. Combining SMA, for its shape memory and superelastic effects, and optical heating using TFBGs allows us to propose a device matching the size of a standard biopsy needle with significant active deflection capabilities. A first prototype is presented, with an evaluation of its performances. The potential of optical heating is then experimentally evaluated. Information about the required power for the SMA wire heating has been determined, and the effect of uniformity of heating are evaluated. Further work will focus on the integration of TFBGs to actuate the needle with SMA wires, presenting a lower contraction temperature, and on the development of closed-loop bending and temperature control strategies adapted to the steering capabilities of the device.

Fig. 3.

Fig. 3

Open in a new tab

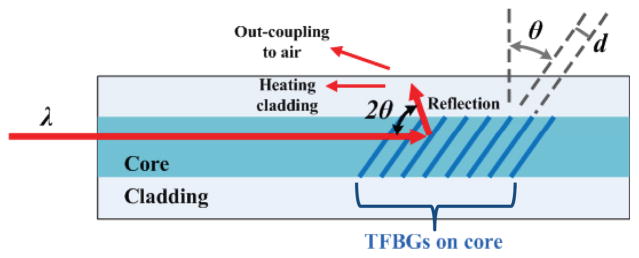
Principle of a Tilted Fiber Bragg Grating

Acknowledgments

S. C. Ryu was supported by a seed grant program of Center for Biomedical Imaging at Stanford and P. Renaud by a Fulbright fellowship at Stanford University.

Contributor Information

Seok Chang Ryu, Email: scryu@stanford.edu, Center for Design Research, Stanford University, Stanford, CA, USA.

Pierre Renaud, Email: pierre.renaud@insa-strasbourg.fr, LSIIT, Strasbourg University - CNRS - INSA, Strasbourg, France.

Richard J. Black, Email: rjb@ifos.com, Intelligent Fiber Optic Systems Corporation (www.ifos.com), Santa Clara, CA, USA

Bruce L. Daniel, Email: bdaniel@stanford.edu, Department of radiology, Stanford University, Stanford, CA, USA

Mark R. Cutkosky, Email: cutkosky@stanford.edu, Center for Design Research, Stanford University, Stanford, CA, USA

References

  • 1.Blumenfeld P, Hata N, DiMaio S, Zou K, Haker S, Fichtinger G, Tempany C. Transperinal prostate biopsy under magnetic resonance image guidance: A needle placement accuracy study. Journal of Magnetic Resonance Imaging. 2007;26:688–694. doi: 10.1002/jmri.21067. [DOI] [PubMed] [Google Scholar]
  • 2.Buonocore E, Skipper G. Steerable real-time sonographically guided needle biopsy. Am J Roentgenol. 1981;136(2):387–392. doi: 10.2214/ajr.136.2.387. [DOI] [PubMed] [Google Scholar]
  • 3.DiMaio S, Salcudean S. Needle steering and model-based trajectory planning. Medical Image Computing and Computer-Assisted Intervention. 2003 [Google Scholar]
  • 4.Abolhassani N, Patel R, Ayazi F. Effects of different insertion methods on reducing needle deflection. Proc. 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society EMBS; 2007; 2007. pp. 491–494. [DOI] [PubMed] [Google Scholar]
  • 5.DiMaio SP, Salcudean SE. Needle steering and motion planning in soft tissues. IEEE Transactions on Biomedical Engineering. 2005 Jun;52(6):965–974. doi: 10.1109/TBME.2005.846734. [DOI] [PubMed] [Google Scholar]
  • 6.Glozman D, Shoham M. Image-guided robotic flexible needle steering. IEEE Transactions on Robotics. 2007;23(3):459–467. [Google Scholar]
  • 7.Sears P, Dupont P. A steerable needle technology using curved concentric tubes. Proc. IEEE/RSJ International Conference on Intelligent Robots and Systems; 2006. pp. 2850–2856. [Google Scholar]
  • 8.Okazawa S, Ebrahimi R, Chuang J, Salcudean SE, Rohling R. Hand-held steerable needle device. IEEE/ASME Transactions on Mechatronics. 2005;10(3):285–296. [Google Scholar]
  • 9.Webster I, Okamura RJAM, Cowan N. Toward active cannulas: Miniature snake-like surgical robots. Proc. IEEE International Conference on Int. Robots and Systems; 2006. pp. 2857–2863. [Google Scholar]
  • 10.Kataoka H, Washio T, Audette M, Mizuhara K. A model for relations between needle deflection, force, and thickness on needle penetration. Medical Image Computing and Computer-Assisted Intervention. 2001:966–974. [Google Scholar]
  • 11.Okamura AM, Simone C, O’Leary MD. Force modeling for needle insertion into soft tissue. IEEE Transactions on Biomedical Engineering. 2004 Oct;51(10):1707–1716. doi: 10.1109/TBME.2004.831542. [DOI] [PubMed] [Google Scholar]
  • 12.Alterovitz R, Goldberg K, Okamura A. Planning for steerable bevel-tip needle insertion through 2d soft tissue with obstacles. Proc. IEEE International Conference on Robotics and Automation ICRA; 2005; 2005. pp. 1640–1645. [Google Scholar]
  • 13.Engh JA, Podnar G, Khoo SY, Riviere CN. Flexible needle steering system for percutaneous access to deep zones of the brain. Proc. IEEE 32nd Annual Northeast Bioengineering Conference; 2006. pp. 103–104. [Google Scholar]
  • 14.Ding J, Stoianovici D, Petrisor D, Mozer P, Avila R, Ibanez L, Turner W, Yankelvitz D, Wilson E, Banovac F, Cleary K. Medical needle steering for lung biopsy: Experimental results in tissue phantoms using a robotic needle driver. Proc. 8th IEEE International Conference on BioInformatics and Bio Engineering BIBE; 2008; 2008. pp. 1–5. [Google Scholar]
  • 15.Misra S, Reed KB, Benjamin WS, Ramesh KT, Okamura AM. Observations and models for needle-tissue interactions. Proc. IEEE Int. Conf. on Robotics and Automation; 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Li BN, Nguyen PB, Ong SH, Qin J, Yang LJ, Chui CK. Image processing and modeling for active needle steering in liver surgery. Proc. Int. Asia Conf. Informatics in Control, Automation and Robotics CAR ’09; 2009. pp. 306–310. [Google Scholar]
  • 17.Tang L, Chen Y, He X. Magnetic force aided compliant needle navigation and needle performance analysis. Proc. IEEE International Conference on Robotics and Biomimetics ROBIO 2007; 15–18 Dec. 2007; pp. 612–616. [Google Scholar]
  • 18.Yan K, Podder T, Ng WS, Yu Y. Smart needle for percutaneous surgery: Influential factor investigation. Proc. 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society EMBS; 2007; 2007. pp. 461–464. [DOI] [PubMed] [Google Scholar]
  • 19.Lim G, Park K, Sugihara M, Minami K, Esashi M. Future of active catheters. Sensors and Actuators A: Physical. 1996;56(1–2):113–121. [Google Scholar]
  • 20.Haga Y, Tanahashi Y, Esashi M. Small diameter active catheter using shape memory alloy. Proc. Workshop The Eleventh Annual Int Micro Electro Mechanical Systems MEMS 98; 1998. pp. 419–424. [Google Scholar]
  • 21.Ikuta K, Ichikawa H, Suzuki K, Yajima D. Multi-degree of freedom hydraulic pressure driven safety active catheter. Proc. IEEE Int. Conf. Robotics and Automation ICRA; 2006; 2006. pp. 4161–4166. [Google Scholar]
  • 22.Tung AT, Park BH, Niemeyer G, Liang DH. Laser-machined shape memory alloy actuators for active catheters. IEEE/ASME Transactions on Mechatronics. 2007;12(4):439–446. [Google Scholar]
  • 23.Fischer G, Iordachita I, Csoma C, Tokuda J, DiMaio S, Tempany C, Hata N, Fichtinger G. MRI-compatible pneumatic robot for transperineal prostate needle placement. IEEE/ASME Transactions on Mechatronics. 2008;13(3):295–305. doi: 10.1109/TMECH.2008.924044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Ganesh G, Gassert R, Burdet E, Bleuler H. Dynamics and control of an MRI compatible master-slave system with hydrostatic transmission. IEEE Conf on Robotics and Automation. 2004:1288–1294. [Google Scholar]
  • 25.Okayasu H, Okamoto J, Fujie M, Umezu M, Iseki H. Development of a hydraulic-driven flexible manipulator for neurosurgery. International Congress Series. 2003;1256:607–612. [Google Scholar]
  • 26.Pappafotis W, ad Bejgerowki N, Gullapalli R, Simard J, Gupta S, Desai J. Towards design and fabrication of a miniature MRI-compatible robot for applications in neurosurgery. ASME Mechanisms and Robotics Conference; 2008. [Google Scholar]
  • 27.Nakamura Y, Shimizu K. Optical drive of sma active forceps for minimally invasive surgery. Journal of the Robotics Society of Japan. 1999;17(3):439–448. [Google Scholar]
  • 28.Zhao Z-m, Chen Y-m, Yu X-l. The parameters selection of sma optically activated and its application. Journal of Wuhan University of Technology-Materials Science Edition. 2002;17 [Google Scholar]
  • 29.Nemova G, Chauve J, Kashyap R. Design of sidetap fiber bragg grating filters. Optics Communications. 2006;259(2):649–654. [Google Scholar]
  • 30.Seihyoung L, Shinyoung Y, Jong JL, Chong HY, Hyun SK. Optical signal is coupled out using fiber grating. SPIE. 2007 [Google Scholar]
  • 31.Westbrook P, Feder KS, CGE Fiber-grating distributed lighting for sensing applications. SPIE. 2008 [Google Scholar]
  • 32.Webster I, Memisevic RJJ, Okamura AM. Design considerations for robotic needle steering. Proc. IEEE International Conference on Robotics and Automation ICRA; 2005; 2005. pp. 3588–3594. [Google Scholar]
  • 33.Luo Y, Takagi T, Matsuzawa K. Thermal responses of shape memory alloy artificial anal sphincters. Smart Materials and Structures. 2003;12(4):533. [Online]. Available: http://stacks.iop.org/0964-1726/12/i=4/a=304. [Google Scholar]
  • 34.Kode V, Cavusoglu MC, Azar MT. Design and characterization of a novel hybrid actuator using shape memory alloy and D.C. motor for minimally invasive surgery applications. IEEE Int Conf on Mechatronics and Automation. 2005 [Google Scholar]
  • 35.Kim S, Hawkes E, Cho K, Joda M, Foley J, Wood R. Micro artificial muscle fiber using NiTi spring for soft robotics. IEEE Conf on Int Robots and Systems. 2009:2228–2234. [Google Scholar]
  • 36.Plante J-S, Devita L, Tadakuma K, Dubowsky S. MRI Compatible Device for Robotic Assisted Interventions to Prostate Cancer. John Wiley & Sons, Ltd; 2009. pp. 411–425. [Google Scholar]
  • 37.Yan K, Li L, Joseph J, Rubens D, Messing E, Liao L, Yu L. A real-time prostate cancer detection technique using needle insertion force and patient-specific criteria during percutaneous intervention. Med Phys. 2009;36(7) doi: 10.1118/1.3148834. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES