Multivariate analysis of the volumetric capnograph for PaCO₂ estimation

Abstract

Purpose: End-tidal CO₂ (eTCO₂) can be used to estimate the arterial CO₂ (PaCO₂) under steady-state conditions, but that relationship deteriorates during hemodynamic or respiratory instability. We developed a multivariate method to improve our ability to estimate the PaCO₂, by using additional information contained in the volumetric capnograph (Vcap) waveform. We tested this approach using data from a porcine model of chest trauma/hemorrhage. Methods: This experiment consisted of 3 stages: pre-injury, injury/resuscitation, and post-injury. In stage I, anesthetized pigs (n=26) underwent ventilator maneuvers (tidal volume and respiratory rate) to induce hypo-or hyper-ventilation. In stage II, pigs underwent either (A) unilateral pulmonary contusion, hemorrhage, and resuscitation (n=13); or (B) bilateral pulmonary contusion (n=13) followed by 30 min of monitoring. In stage III, the ventilator maneuvers were repeated. The following Vcap features were measured: eTCO₂, phase 2 slope (p2m), phase 3 slope (p3m), and inter-breath interval. The data were fit to 2 models: (1) multivariate linear regression and (2) a machine-learning model (M5P). Results: 1750 10-breath sets were analyzed. Univariate models employing eTCO₂ alone were adequate during stages I and III. During stage II, mean error for the linear model was -8.44 mmHg (R²=0.14, P<0.001) and for M5P it was -5.98 mmHg (R²=0.13, P<0.01). By adding Vcap features, all models exhibited improvement. In stage II, the mean error of the linear model improved to -4.64 mmHg (R²=0.11, P<0.01), and that of the M5P model improved to -1.62 mmHg (R²=0.25, P<0.01). Conclusions: By incorporating Vcap waveform features, multivariate methods modestly improved PaCO₂ estimation, especially during periods of hemodynamic and respiratory instability. Further work would be needed to produce a clinically useful CO₂ monitoring system under these challenging conditions.

Introduction

Capnography is the measurement and display of the partial pressure of carbon dioxide in the exhaled breath. Capnographic monitoring is increasingly recognized as an important tool in critical care and emergency medicine, because it helps achieve the 4 immediate priorities of resuscitation: airway, breathing, circulation, and disability [1]. For airway management, it confirms endotracheal tube placement and alerts the provider if the tube becomes dislodged. For breathing management, end-tidal carbon dioxide (eTCO₂), under hemodynamically stable conditions, correlates with arterial carbon dioxide (PaCO₂) and provides a non-invasive estimate of ventilation adequacy. For circulation management, onset of cardiac arrest and hemorrhagic shock are quickly reflected in decreases in eTCO₂ [2]. Conversely, eTCO₂ rises during adequate chest compressions [3]. For disability management, capnography is indicated for the treatment of intubated patients with head injury, since cerebral blood flow is adversely affected by hypocapnia [4]. Because of these and similar considerations, capnography is recommended by the American Society of Anesthesiologists [5], the Advanced Trauma Life Support course [6] the Advanced Cardiovascular Life Support course [3], and the Brain Trauma Foundation’s prehospital guidelines [7].

In several of the above applications, a close relationship between the eTCO₂ and PaCO₂ is assumed. However, rapidly changing hemodynamic or respiratory conditions alter the relationship between eTCO₂ and PaCO₂. For example, an increase in alveolar dead space due to deterioration of pulmonary function increases the divergence between eTCO₂ and PaCO₂. In patients with healthy lungs, this divergence is small, justifying the use of eTCO₂ as a surrogate for PaCO₂. In patients with diseased lungs, the baseline eTCO₂-to-PaCO₂ difference must be measured, allowing subsequent estimates of the PaCO₂ to be more accurately estimated [8]. But if the dead space changes with worsening (or improving) disease, then eTCO₂ becomes less reliable as a PaCO₂ surrogate.Decreased perfusion of the lung, e.g. in cardiogenic shock or hemorrhagic shock, also increases the eTCO₂-to-PaCO₂ difference and interferes with the utility of the eTCO₂ as a surrogate for PaCO₂ [9].

In a porcine model of chest trauma and hemorrhage, we recently confirmed the close correlation between eTCO₂ and PaCO₂ across a wide range of minute-ventilation levels, both before injury and after resuscitation. However, the eTCO₂-to-PaCO₂ relationship deteriorated significantly immediately after injury and during hemorrhagic shock [10].

Because of these limitations and in order to improve our ability to predict PaCO₂ in unstable patients, we reexamined the information content of the exhaled CO₂ waveform. We employed the volumetric capnograph (Vcap), which is the result of plotting the exhaled CO₂ against the exhaled breath volume on a breath-by-breath basis. This differs from the usual capnograph, in which exhaled CO₂ is displayed as a function of time. Certain features of the Vcap waveform correlate with ventilation-perfusion (V/Q) dispersion, a global index of V/Q mismatch [11]. Previously, a multivariate approach was applied to data obtained from Vcap waveform features, to predict the presence of pulmonary embolism [12]. The purpose of the current study was to develop and evaluate an improved algorithm for estimating PaCO₂ using readily available features of the volumetric capnograph. We hypothesized that multivariate assessment of these features could improve our ability to estimate PaCO₂ noninvasively, despite rapidly changing pulmonary and hemodynamic conditions.

Materials and methods

This study was approved by the U.S. Army Institute of Surgical Research, Institutional Animal Care and Use Committee. It was conducted in compliance with the Animal Welfare Act and the implementing Animal Welfare Regulations and in accordance with the principles of the Guide for the Care and Use of Laboratory Animals.

Animal preparation

This study consisted of analysis of data from previously reported animal experiments [10]. Briefly, 26 female Yorkshire pigs (Midwest Research Swine, Gibbon, MN) weighing 30 to 45 kg were fasted overnight and premedicated with glycopyrolate. Inhaled isoflurane (0.5-3.0 vol%) was used to induce anesthesia. Animals were intubated, and midazolam (25 mg/h), ketamine (250 μg/kg/min), and propofol (150 μg/kg/min) were administered for total intravenous anesthesia (TIVA). A tracheostomy was performed. The femoral arteries, femoral veins, and right external jugular vein were catheterized. The animals were then placed in the sternal recumbent position. They were mechanically ventilated using a Dräger EVITA XL ventilator (Dräger Medical, Telford, Pa), initially with a tidal volume (TV) of 10 mL/kg and a respiratory rate (RR) of 12 breaths/min. The fraction of inspired oxygen (FiO₂) and the positive end-expiratory pressure were set to 21% and 5 mmHg, respectively. A mainstream Vcap monitor (CO₂SMO; Philips Respironics, Amsterdam, Netherlands) was connected to the endotracheal tube. A pulse oximeter (Oxisensor II 1-20: Covidien; Nellcor, Mansfield, Mass) was placed on the tail to measure peripheral saturation of oxygen (SpO₂). Blood gases were measured using a point-of-care device (iSTAT, Abbott Laboratories, Abbott Park, IL). The FiO₂ of the ventilator was adjusted to maintain a minimum SpO₂ of 90%.

Experimental protocol

Both experiments consisted of 3 stages. On day 1, the animals were surgically prepared as described above, and underwent a sequence of respiratory maneuvers (stage I; see below). The animals were then rested overnight in the animal ICU. The next day, they were placed in the dorsal recumbent position and underwent stage II. This consisted of either unilateral (right-sided) (Group A, n=13) or bilateral pulmonary contusions (Group B, n=13) [13]. Those animals in Group A then underwent hemorrhage (12 mL/kg over 10 min), a shock period of 30 min, and rapid resuscitation with lactated Ringer’s (3 times the shed volume) and shed blood. No respiratory maneuvers were performed during stage II. After resuscitation, the animals were returned to the sternal recumbent position and the same respiratory maneuvers as in stage I were performed again (stage III). Upon completion of stage III, the animals were euthanized with high-dose sodium pentobarbital solution (Fatal-Plus, Dearborn, MI).

For the respiratory maneuvers in stages I and III, a sequence of ventilator changes were performed by varying the RR or TV to induce hypoventilation or hyperventilation. After baseline measurements, each animal was randomized into 1 of 4 groups to determine the sequence by which the respiratory maneuvers would be done. Before respiratory maneuvers and after ensuring adequate analgesia, animals were administered a vecuronium bolus (1 mg/kg) to ensure the absence of spontaneous respiration. Blood gas analysis was performed at 5 and 7 min after each respiratory maneuver; PaCO₂ values were recorded and the results were averaged.

Capnographic analysis

Ventilator settings and continuous capnography waveforms were recorded from the CO₂SMO device to a computer by custom-built software, the Integrated Data Exchange and Archival (IDEA) system.

A Java-based computer program was written to analyze the ventilator waveforms and to segment each breath. The Vcap curves were obtained by plotting the partial pressure of CO₂ as a function of the volume of exhaled breath. The curves were then parameterized as described previously by Fletcher [14,15]. The Vcap curve is characterized by three phases (Figure 1). Phase 1 is an initial flat phase, low in CO₂, which corresponds to exhalation of air from the anatomical dead space that has not undergone gas exchange at the alveoli. Phase 2 is characterized by a rapid rise in CO₂ due to mixing of air from the dead space and the alveoli. Phase 3 is consists of alveolar gas and is characterized by a plateau, with a slight incline, that terminates in the CO₂ partial pressure recognized as eTCO₂.

Figure 1.

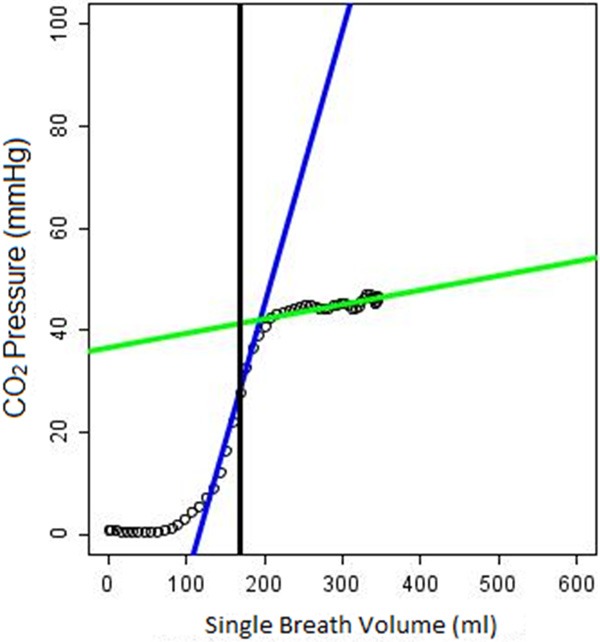
Example of Vcap waveform. Blue line: phase 2 slope (p2m), phase 2 intercept (p2i), Green line: phase 3 slope (p3m), phase 3 intercept (p3i), Black line: Airway Dead Space (in mL).

Slopes and intercepts for each phase were determined and named as follows: phase 2 slope (p2m), phase 2 intercept (p2i), phase 3 slope (p3m), phase 3 intercept (p3i). In addition, standard ventilator settings were recorded including respiratory rate, tidal volume, minute volume, FiO₂, and I:E ratio. The inter-breath interval, IBI, was defined as the time between the start of consecutive breaths measured in seconds. Breath-by-breath Vcap and flow curves were generated by the software and exported as JPEG files for manual review, i.e. to identify artifacts and to assess segmentation quality. For each time point, the last 10 consecutive artifact-free breaths for each ventilator setting were identified and the Vcap parameters calculated and averaged. A composite capnograph overlay image was created to display these last 10 breaths superimposed on each other (Figure 2). The IBIs of the 10 breaths at each of the ventilator settings were manually reviewed for each time point and for each animal. Any breaths deviating from the respiratory rate set by the ventilator by > ± 0.02 seconds were automatically excluded. If marked variability was present for at least 4 of the 10 breaths, the time point was discarded.

Figure 2.

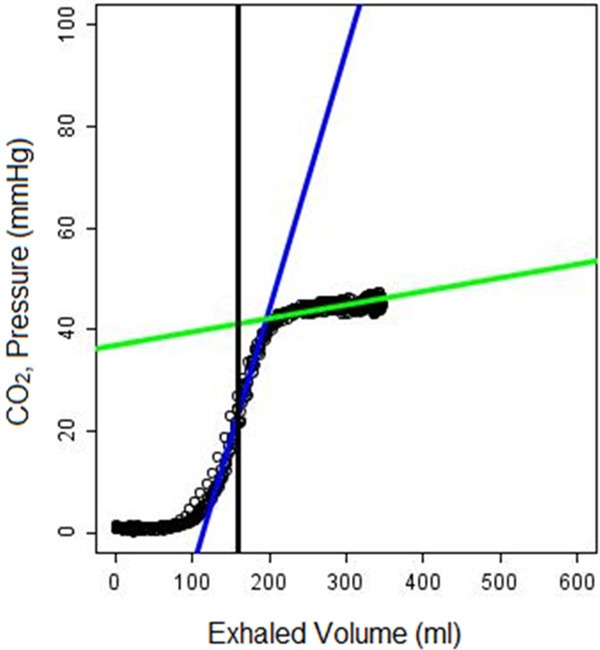
Composite Vcap curve consisting of ten overlaid breaths.

The following software-derived Vcap variables were used in multivariate analysis to derive estimates of PaCO₂: eTCO₂, IBI, p2m, p2i, p3m, p3i, and anatomical dead space. It was determined through model testing that p2i, p3i, and anatomical dead space did not contribute significantly, and these were subsequently dropped from the models. We evaluated 2 models: a standard multivariate linear model and M5P, a well-known machine-learning model. Each of these 2 models encompassed all 3 stages of the experiment; that is, the 2 models were developed using data from all 3 stages, and then were applied to the individual stages.

The M5P model is a regression-tree model [16-18] and is implemented as a part of Weka [19]. It combines an automated classifier which creates clusters of similar data elements together with an independent least-squares fit for each set of values in the cluster. In our case, the leaves of this tree represent a linear regression of closely related clusters of PaCO₂ test results. The segmentation of clusters was determined automatically by the data heuristics using the M5P algorithm. The resulting model had the advantage of being both transparent to the observer as well as providing an efficient and classical mechanism for prediction through the linear regression component. The resulting model is piecewise linear.

Statistical analysis

Analysis was performed using R Version 3.02 and the RWeka package [20,21]. All results are expressed as correlations or means ± SD.

Results

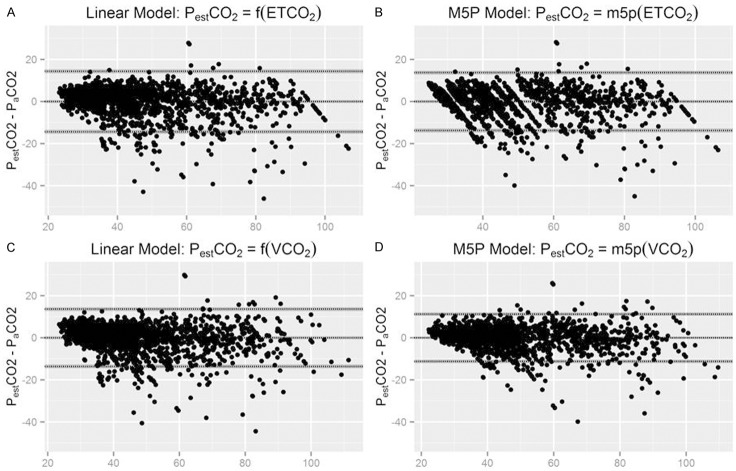
We analyzed a total of 1750 10-breath sets. Results of fitting the data to the 2 models are shown in Table 1. Bland-Altman analysis of the overall data is shown in Figure 3A-D. The following equations describe the results of linear regression:

Table 1.

Summary of the results

Features	Model	Stage I		Stage II		Stage III		Overall
		N=867		N=75		N=808		N=1750
		R2	Bias (Mean ± SD)	R2	Bias (Mean ± SD)	R2	Bias (Mean ± SD)	R2	Bias (Mean ± SD)
eTCO2	Linear	0.96#	2.91±3.87	0.14#	-8.44±6.45	0.81#	-5.47±7.97	0.83#	-1.45±7.59
eTCO2	M5P	0.95#	3.65±4.10	0.13*	-5.98±6.17	0.83#	-3.43±7.46	0.84#	-0.03±7.01
eTCO2, IBI, p2m, p3m	Linear	0.96#	-3.97±3.92	0.11*	-4.64±5.83	0.80#	-2.82±7.93	0.85#	0.00±6.94
eTCO2, IBI, p2m, p3m	M5P	0.96#	1.89±3.84	0.25#	-1.62±5.06	0.86#	-1.92±6.71	0.90#	-0.01±5.73

^# P<0.001;

^* P<0.01.

Figure 3.

Bland-Altman analysis. A: eTCO₂-based linear regression model; B: eTCO₂-based M5P model; C: Vcap-based linear regression model; D: Vcap-based M5P model. X axes represent the average of PaCO₂ and P_ESTCO₂.

Linear Regression: PaCO₂=0.8933 * eTCO₂+6.2825;

Multiple Linear Regression: PaCO₂=0.6307 * eTCO₂+9.7282 * p2m+3.0249 * p3m+1.4702 * IBI+6.6849.

M5P models for single and multiple variables are provided in the supplemental digital content. Using eTCO₂ alone, PaCO₂ could be accurately estimated in uninjured animals (stage I) with a mean error of 2.91 mmHg (R²=0.96, P<0.001) in the linear model, or of 3.65 mmHg (R²=0.95, P<0.001) in the M5P model. After resuscitation (stage III), the mean error for the linear model was -5.47 mmHg (R²=0.81, P<0.001) and for the M5P model -3.43 mmHg (R²=0.83). As expected, the relationship deteriorated considerably during the injury/resuscitation stage (stage II), with the mean error for the linear model of -8.44 mmHg (R²=0.14, P<0.001) and for M5P of -5.98 mmHg (R²=0.13, P<0.01).

By using the additional features of the Vcap curve, all models exhibited improvement in estimation with decreases in the mean error and increases in correlation. Most notable was the improvement in stage II, in which the mean error of the linear model improved to -4.64 mm Hg (R²=0.11, P<0.01), and that of the M5P model improved to -1.62 mm Hg (R²=0.25, P<0.01). For stages I and III, slight improvements in the average error and correlation were also noted (Table 1).

Discussion

The principal finding of this study is that multivariate analysis of the Vcap waveform improved our ability to estimate PaCO₂ during unstable conditions in a porcine model of chest trauma and resuscitation, compared with the eTCO₂ alone. Having an accurate assessment of PaCO₂ is important in clinical practice, as it could reduce the need for invasive blood gas sampling to verify adequacy of ventilation. This capability is needed for any intubated patient, but is especially important for maintaining normoventilation in patients with traumatic brain injury [4,22].

Previously, we showed that end-tidal capnography provides an accurate estimate of PaCO₂ under stable hemodynamic and respiratory conditions, but fails during unstable conditions [10,23]. Several techniques have been described in an effort to improve the non-invasive PaCO₂ estimate. One of them, described by Fletcher [24], involves halving the ventilator respiratory rate and doubling the tidal volume while keeping the inspiratory time constant. The change in eTCO₂ is expected to be proportional to the original PaCO₂-eTCO₂ difference. However, the actual results were mixed and the maneuver had a variable effect on eTCO₂, depending on lung function. Another technique for estimation of PaCO₂ from eTCO₂ was described by Tavernier et al. [25]. It involves prolonged expiration maneuvers. This technique is based on the assumption that a prolonged or forced expiration for 5-15 seconds may provide a better correlation with PaCO₂. However, end-expiration PCO₂ correlated poorly with PaCO₂. A recent work by Khemani et al. [26] described application of a multivariate Gaussian process model, which incorporated ventilator-derived data with non-invasive variables such as the eTCO₂ and pulse oximetry to improve estimation of the PaCO₂. The authors reported that this model predicted PaCO₂ within ± 6 mmHg of the observed values, 80% of the time.

In the present study, we retrospectively applied multivariate modeling techniques to a set of capnographic waveform data. Morphology of the recorded waveforms was parameterized using a custom-designed Java-based program. The slopes of phases 2 and 3 were retained in this model. These variables provide important information on ventilation-perfusion relationships in the lungs [15,27,28]. Fowler (29) proposed that a sloping phase 3 reflected non-uniformity of ventilation. He attributed this in turn to 2 factors. First (the regional theory), there is regional non-uniformity of ventilation; inspired gas is distributed unevenly to different zones in the lung. Second (the sequential theory), there is temporal non-uniformity of alveolar expansion, such that some areas fill before and empty after other areas. This causes dead space gas to be distributed preferentially to the latter regions [30].

Clinically, Tusman [27] showed that both slope II and slope III were proportional to pulmonary blood flow in patients coming off of cardiopulmonary bypass. Relatedly, slope III is abnormal in patients with pulmonary embolus [31]. Several studies have demonstrated that patients with chronic obstructive lung disease have abnormal Vcap data, which deteriorate with advanced disease [32]. Mechanically ventilated patients with ARDS differ from normal patients on multiple Vcap variables [33].

In the present study, we used a well-characterized model of unilateral pulmonary contusion followed by hemorrhage and aggressive resuscitation, as well as a new model of bilateral pulmonary contusion without additional hemorrhage. We previously used the multiple inert gas elimination technique (MIGET) to establish that a large increase in true shunt (from 4 to 33%) occurs in the unilateral contusion model. Initially, blood flow increased to low and very low V/Q compartments as well [34]. Thus, our data are consistent with the concept that V/Q mismatch influences the Vcap waveform, and specifically the phase 3 slope, in ARDS [35].

We analyzed our data using multivariate linear regression or a tree-based machine-learning model, which permitted us to calculate P_ESTCO₂ values solely based on non-invasive capnographic parameters. Unlike the method described by Fletcher, our process did not require any alterations to ventilator parameters, e.g. respiratory rates or tidal volumes [24]. Our approach would be useful for critically ill patients, in whom such changes may be detrimental.

Our study had the following limitations. This analysis was carried out retrospectively using stringent selection criteria for breath quality, as well as manual review of the waveforms. The utility of such method when applied prospectively without human oversight is yet to be proven. In order to improve the quality of data, we completed manual review of the 10-breath datasets for noise and spurious detection prior commencing the final analysis. This resulted in the inclusion of only 75 10-breath sets from stage II (injury/resuscitation). Due to the relatively small size of the set, especially during the acute injury state, we used the entire data set for developing the models and did not use a separate data set for testing [36]. Such approach may have resulted in higher accuracy of P_ESTCO₂ than would have been achieved otherwise. Finally, the clinical utility of this approach has yet to be proven.

Conclusions

Porcine models of chest trauma and hemorrhage were used to develop models for predicting PaCO₂ from the exhaled PCO₂. Multiple features of the Vcap curve, including eTCO₂, the inter-breath interval, and the slopes of phases 2 and 3 of the curve, were incorporated into a model that improves PaCO₂ estimation over that obtained from the eTCO₂ alone. This model functioned well for subsets of the data from before injury, during injury/resuscitation, and after recovery. This approach merits prospective validation in other models of disease and injury.

Disclosure of conflict of interest

None.