Abstract
This article highlights the role of a positive feedback gating mechanism at the cellular level in the robustness and modulation properties of rhythmic activities at the circuit level. The results are presented in the context of half-center oscillators, which are simple rhythmic circuits composed of two reciprocally connected inhibitory neuronal populations. Specifically, we focus on rhythms that rely on a particular excitability property, the postinhibitory rebound, an intrinsic cellular property that elicits transient membrane depolarization when released from hyperpolarization. Two distinct ionic currents can evoke this transient depolarization: a hyperpolarization-activated cation current and a low-threshold T-type calcium current. The presence of a slow activation is specific to the T-type calcium current and provides a slow positive feedback at the cellular level that is absent in the cation current. We show that this slow positive feedback is required to endow the network rhythm with physiological modulation and robustness properties. This study thereby identifies an essential cellular property to be retained at the network level in modeling network robustness and modulation.
Keywords: modulation, robustness, networks, central pattern generators, postinhibitory rebound
biological rhythms play a major role in the functioning of the brain, but much remains to be understood regarding their control, regulation, and function. Many advances in this important question have come from experimental and computational studies of central pattern generators (CPGs), which endogenously produce precise rhythmic outputs directly related to motor functions (Getting 1989; Grillner and Wallén 1985; Harris-Warrick 2011; Marder and Bucher 2001; Marder and Calabrese 1996). In this effort, experimental work benefits from computational models, but models at the circuit level usually rely on mathematical simplifications at the component level. The question of which cellular details must be retained at the network level is largely open (Marder and Goaillard 2006).
Motivated by this general question, we highlight a simple feedback mechanism at the cellular level that has a key influence on circuit robustness and modulation. We illustrate this property via the computational study of an archetype model of CPG circuits, the half-center oscillator (HCO): two neurons, or neuronal populations, that do not oscillate in isolation but oscillate in an anti-phase rhythm when reciprocally connected (Brown 1911; Perkel and Mulloney 1974; Satterlie 1985). Because of the widespread occurrence of this circuit motif, the mechanisms have been extensively studied, both computationally and experimentally (Calabrese and De Schutter 1992; Daun et al. 2009; Harris-Warrick 2011; Marder and Calabrese 1996; Skinner et al. 1993, 1994; Wang and Rinzel 1992). A specific cellular excitability property, the postinhibitory rebound (PIR) (Perkel and Mulloney 1974), and its two specific ionic currents, hyperpolarization-activated cation current, IH, and a low-threshold T-type calcium current, ICa,T (Angstadt et al. 2005), are well-known key players in circuit oscillations.
Previous studies have focused on distinguishing those two currents from their contribution to the escape or release mechanism (Daun et al. 2009; Skinner et al. 1994; Wang and Rinzel 1992) and their modulation of rhythmic activity (Cymbalyuk et al. 2002; Doloc-Mihu and Calabrese 2011; Olypher et al. 2006; Sorensen et al. 2004). This article highlights that those two currents differ in another simple yet fundamental aspect: both generate a PIR, but only one of them acts as a source of positive feedback through its slow activation (in a timescale critical for the rhythm generation). The present work demonstrates through a computational study that this particular feedback is fundamental for the robustness and modulation properties of the circuit rhythm and that its absence is detrimental to both robustness and modulation at the circuit level.
Our results predict that PIR per se is not a sufficient cellular excitability property to be retained at the network level. In addition, the slow regenerative nature of the current dynamics must be retained as an important parameter. We emphasized in previous work the importance of this positive feedback at the cellular level in defining bursting excitability (Franci et al. 2014) and its widespread regulation in different neuron types (Franci et al. 2013). The present study suggests the important role of regenerativity at the cellular level for robustness and modulation at the circuit level.
MATERIALS AND METHODS
All the numerical simulations and analyses were performed with MATLAB (The MathWorks). The models were implemented in a MATLAB code and simulated using a forward Euler method with a time step of 0.005 ms.
Cellular model.
The cellular model is inspired from the crab stomatogastric ganglion (STG) conductance-based neuron model (Liu et al. 1998; Turrigiano et al. 1995). The model contains Hodgkin-Huxley (HH)-type currents (Hodgkin and Huxley 1952): the transient sodium current, INa, a fast depolarizing current, and the delayed-rectifier potassium current, IK,DR, a slower hyperpolarizing current, plus a leak current, Ileak. The two currents responsible for PIR are ICa,T and IH, defined above. The membrane potential dynamics writes as follows:
where C = 1 μF/cm2 is the membrane capacitance and Iapp is the applied current.
Each ionic current i takes the standard HH form:
where ḡi is the maximal conductance for current i, pi and qi are integers, and Ei is the reversal potential of the ion i. Table 1 lists the values of ḡi, pi, qi, and Ei for the different currents.
Table 1.
Parameters for membrane currents of the cellular model
| Ii | ḡi | pi | qi | Ei |
|---|---|---|---|---|
| INa | 60 | 3 | 1 | 50 |
| IK,DR | 40 | 4 | 0 | −80 |
| Ileak | 0.035 | 0 | 0 | −49 |
| ICa,T | 0.3 | 3 | 1 | 120 |
| IH | 0.12 | 1 | 0 | −20 |
Notation is explained in the text. All conductance values are given in mS/cm2 and membrane potentials in mV.
Activation and inactivation variable dynamics follow the classical formalism:
where the functions for τm,i, m∞,i, τh,i, and h∞,i are given in Table 2. Note that if pi = 0 and/or qi = 0, then and τm,i and m∞,i and/or τh,i, and h∞,i are not listed, respectively.
Table 2.
Functions for membrane currents of the cellular model
| m∞,i(Vm) | h∞,i(Vm) | τm,i(Vm) | τh,i(Vm) | |||||
|---|---|---|---|---|---|---|---|---|
| INa | ||||||||
| IK,DR | ||||||||
| ICa,T | ||||||||
| IH |
Notation is explained in the text. All time constants are given in ms.
Reduced model.
To capture the cellular dynamics at the network level (see Figs. 3–7), we use a reduced cellular model with three ionic currents: the two HH currents responsible for action potentials, INa and IK,DR, and a single “PIR current,” IPIR, responsible for the PIR. On the basis of the observation (Fig. 2) that the excitability properties of a restorative model are similar with an instantaneously activated T-type calcium current and with an IH current, we model the IPIR current with the T-type calcium channel parameters and functions of Tables 1 and 2, but with an instantaneous activation when considering a restorative current and with a slow activation when considering a regenerative current. In this way, the two PIR currents only differ in the nature of their slow feedback, but they possess identical current-voltage curves. Our reduced model does not capture the physiological sag brought by an IH current, but the present results do not depend on that cellular property. We insist that the variation of the activation time constant in our reduced model is not physiological but only meant to capture the restorative or regenerative nature of the PIR in an otherwise identical reduced model. Our PIR current can be thought of as the aggregated current resulting from all physiological currents contributing to the PIR.
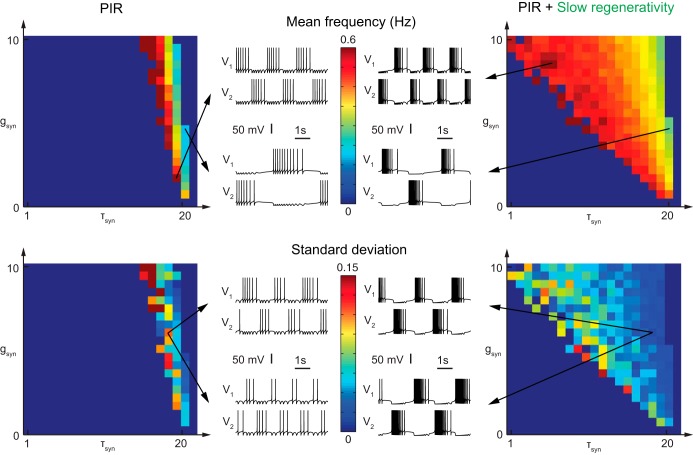
Fig. 3.
Frequency modulation with extrinsic parameters is fragile without slow regenerativity. Modulation of the network frequency by varying synaptic parameters, ḡsyn (in mS/cm2) and τsyn (in ms), is robust with slow regenerativity but fragile without. Left: PIR only. Right: PIR + slow regenerativity. Mean frequency (top) and standard deviation (bottom) are shown for 10 simulations with 40% variability in ḡsyn and 20% variability in τsyn (see materials and methods for a description of mean frequency and standard deviation). Membrane potentials V1 and V2 at top represent maximal and minimal oscillation frequency, respectively, with parameters as indicated by the arrows. Membrane potentials at bottom represent 2 different simulations with the same ḡsyn and τsyn parameters. ḡsyn and τsyn are affected by parameter variability.
Fig. 7.
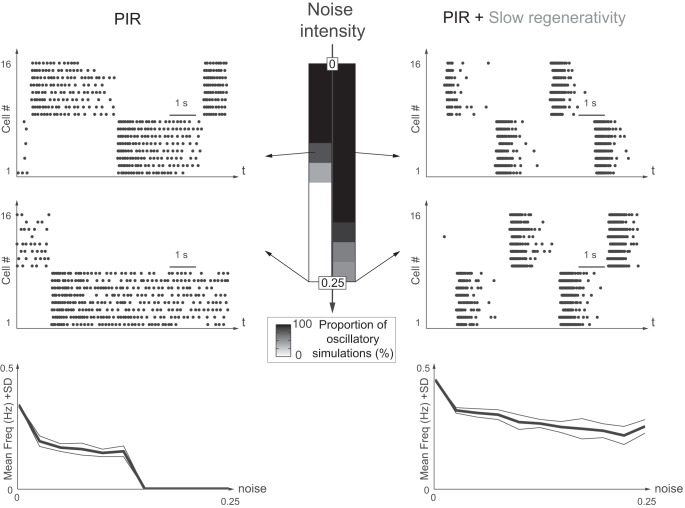
Slow regenerativity makes network oscillations robust against exogenous noise. Network oscillations are robust toward exogenous noise only with slow regenerativity. Left: PIR only. Right: PIR + slow regenerativity. Gaussian white noise (noise intensity, D, ranges from 0 to 0.25 mV2) is added to the neurons (see materials and methods for a description of noise). The grayscale code indicates the proportion of simulations with stable rhythmic activity out of 10 simulations. Upper and lower raster plots indicate noise intensity D of 0.10 and 0.25 mV2, respectively. Bottom: plots of the mean frequency (bold line) and 1 SD variation (thin lines) for each noise level for the 10 simulations with oscillations.
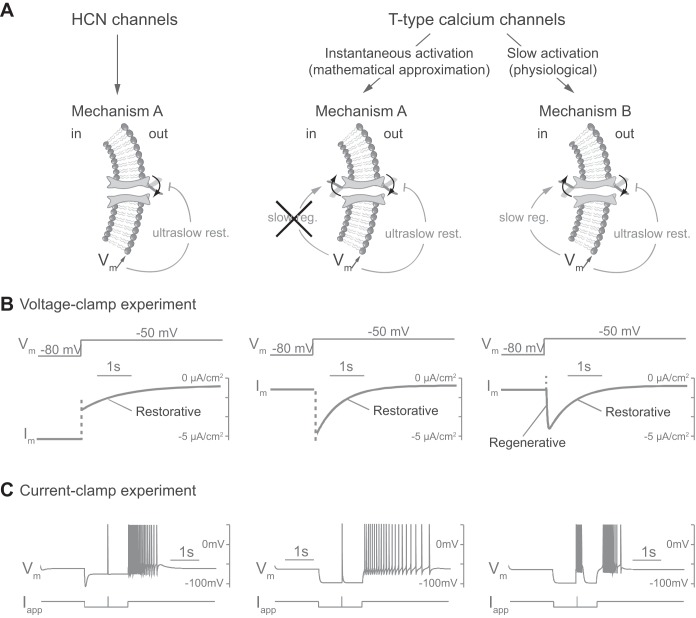
Fig. 2.
Slow activation of T-type calcium channels is the distinctive difference between the PIR mechanisms A and B. A: schemes representing ion channel gating in different cases. HCN, hyperpolarization-activated cyclic nucleotide-gated channels. B: voltage-clamp experiment in silico. Responses of transmembrane current (Im) to a varying externally applied potential (Vm, varies from −80 to −50 mV) for each case. C: current-clamp experiment in silico. Responses of membrane potential (Vm) to a varying external applied current (Iapp) for each case. The applied current is identical to that in Fig. 1 but takes a value of 10 μA/cm2 for 10 ms for the fast depolarizing input. Both mechanisms trigger a PIR via an ultraslow inward current in response to hyperpolarization, which brings ultraslow restorativity (ultraslow rest.) to the neuron (see materials and methods for a description of cellular models and applied currents). In addition, T-type calcium channels in mechanism B, because of their slow activation, are a source of slow regenerativity (slow reg.). An instantaneous activation of the T-type calcium channels, i.e., steady-state approximation of their activation, suppresses this slow regenerativity and produces a mechanism A PIR. The mechanism B PIR is endogenous, as revealed by the specific signature during hyperpolarization.
Network model.
There are two types of network studied: a 2-neuron network and a 16-neuron network, with two populations of eight neurons. The 16-neuron network is used in Figs. 5–7 to study the impact of variability in the parameters and the effect of different noise sources. For each network, the two neuronal populations (either 1 neuron or 8 neurons) are reciprocally connected all-to-all with γ-aminobutyric acid (GABA) synapses between populations; there is no intrapopulation connection. The synaptic currents are graded synaptic currents, which are responsible for the inhibition of the opposite cell and the removal of inactivation from IPIR (Nadim et al. 1995). Graded synapses are commonly found in central pattern generators. The GABA synapses follow first-order kinetics for simplicity, and the synaptic current between two populations takes the form (Golomb et al. 1994)
where Vj is the presynaptic membrane potential and N is the number of presynaptic neurons (1 or 8). If not stated otherwise, ḡsyn = 4 mS/cm2, Esyn = −80 mV, kfA = 2 ms−1, krA = 0.1 ms−1, θs = −45 mV, and σs = 2 mV.
Fig. 5.
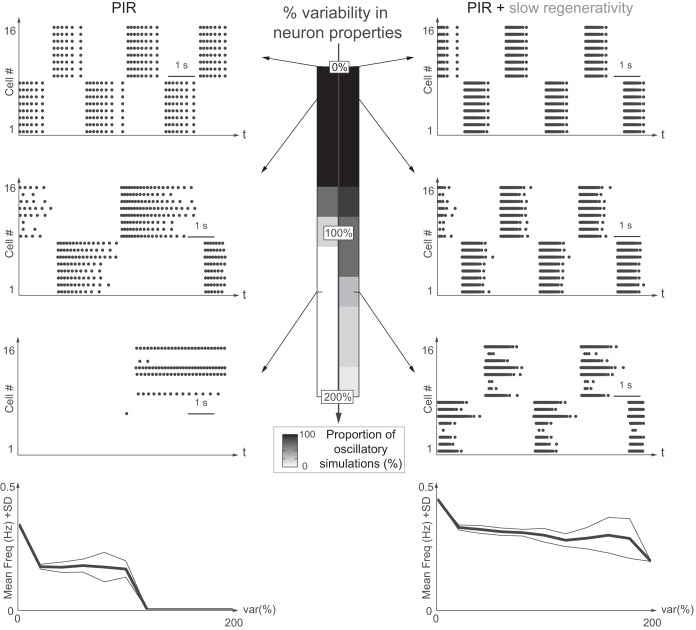
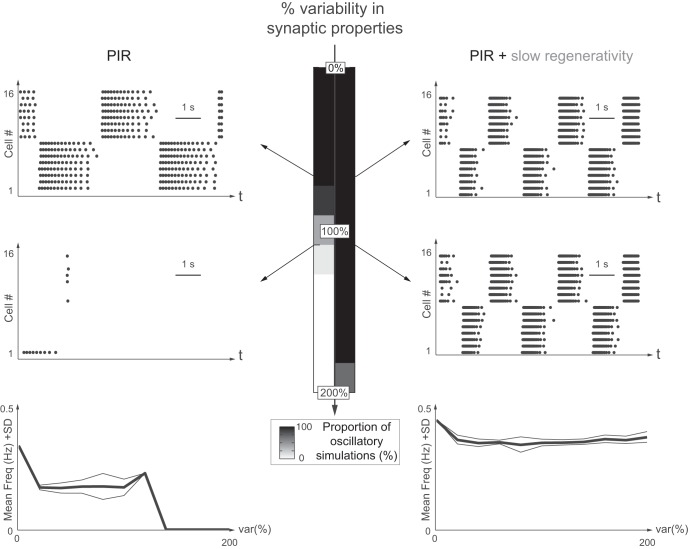
Slow regenerativity makes network oscillations insensitive to intrinsic variability. Network oscillations are robust toward intrinsic variability only with slow regenerativity. Left: PIR only. Right: PIR + slow regenerativity. Variability (level: 0 to 200%) is indicated in the maximal conductance of the PIR current, ḡPIR. The grayscale code indicates the proportion of simulations with stable rhythmic activity out of 10 simulations. From upper to lower, raster plots show 0, 20, and 140% variability, respectively. Bottom: plots of the mean frequency (mean freq.; bold line) and 1 standard deviation (SD) variation (thin lines) for each variability level (var%) for the 10 simulations with oscillations.
Variability.
Physiological variability is modeled by randomly selecting (by generation of uniformly distributed pseudorandom numbers with the MATLAB function “rand”) the values for the parameter subjected to variability in an interval, called variation range, centered on a given parameter value. The variability level quantifies the width of this interval, as a percentage of the given value. For instance, a 200% variability in ḡPIR means that for a given parameter value of 0.3 mS/cm2, the variation range has a width of 200% × 0.3 = 0.6 and is centered on 0.3. The parameters are therefore randomly selected out of the interval [0 mS/cm2, 0.6 mS/cm2].
Analyses.
A network is categorized as having a stable rhythmic activity if all the neurons in the network are still bursting in the stationary state (after the transient initiation phase). Because of the specific network structure (connection all-to-all from one population to the other, and vice versa), all the neurons in one population receive the same input (coming from all the neurons in the other population). Therefore, if all the neurons are bursting, the bursts have been elicited by the same transient hyperpolarizing input (bursting cannot happen without this hyperpolarization) and the bursts are synchronous; i.e., all the bursts overlap, but not necessarily the spikes. This provokes HCO anti-phase oscillations. Bursting in neurons is detected by having two consecutive spikes less than 100 ms apart.
The frequency is the inverse of the time duration between the beginning of two bursts, or period, averaged over the two neurons of the two-neuron network. The duty cycle is the ratio between the burst duration and the period, averaged over the two neurons. The duty cycle ratio is the ratio between the duty cycle in neuron 1 (the neuron upon which acts the external hyperpolarization) and in neuron 2 (the other neuron). Each value for the mean frequency, mean duty cycle, and mean duty cycle ratio was computed from 10 simulations with the same set of parameters but with 40% variability in ḡsyn and 20% variability in ḡPIR. Only simulations endowed with rhythmic activity in the sense defined previously were considered to compute the means and standard deviations. If no rhythmic activity was detected, the computed means and standard deviations were set to 0. The proportion of oscillatory simulations quantifies the percentage of simulations that showed rhythmic activity out of the 10 simulations with the same set of parameters. The oscillations are called stable if this percentage is above 50%.
Simulation details.
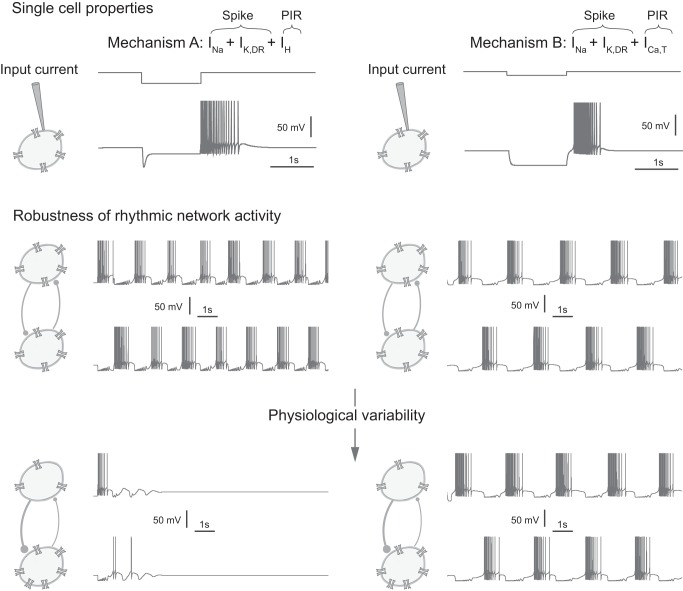
The simulations shown in Fig. 1 are performed using the cellular model described above, with ḡCa,T = 0 mS/cm2 and ḡH = 0.12 mS/cm2 for mechanism A and ḡH = 0 mS/cm2 and ḡCa,T = 0.14 mS/cm2 for mechanism B. The applied current, Iapp, takes values of −0.8 and −3.8 μA/cm2 for mechanism A and values of −0.65 and −1.85 μA/cm2 for mechanism B. Simulations in Fig. 1, middle, do not present any parameter variability; the two neurons and synaptic connections are identical. Physiological variability is simulated in Fig. 1, bottom, with 40% variability in ḡsyn and 20% variability in ḡH and ḡCa,T.
Fig. 1.
Network rhythmic activities generated by distinct postinhibitory rebound (PIR) mechanisms strongly differ in their robustness properties. Top: mechanism A (left) generates a PIR with a hyperpolarization-activated cation (IH)-type current, and mechanism B (right) generates a PIR with a slowly activating T-type calcium (ICa,T)-type current (see materials and methods for a description of cellular models). The IH and ICa,T ion channel traces are shown, and the input current is applied externally as indicated by the cartoon. The input currents are different, to trigger PIRs of similar time duration from different mechanisms (see materials and methods for precise values). Middle: in a half-center 2-neuron network configuration, both mechanisms generate anti-phase oscillations. The density of ion channels in both neurons is identical, representing homogeneous cellular properties. Similarly, the synaptic connections are identical, representing homogeneous synaptic properties without variability. Bottom: physiological variability (see materials and methods for a description of variability) in both the synaptic (40% variability in ḡsyn) and cellular properties (left, 20% variability in ḡH; right, 20% variability in ḡCa,T) makes the oscillations unstable with mechanism A but not with mechanism B. The density of ion channels differs between the 2 neurons, and the synaptic connections are different, representing physiological variability in the cellular and synaptic properties, respectively.
The cell models in Fig. 2 were performed using the cellular model described above, with ḡCa,T = 0 ms/cm2 and ḡH = 0.12 mS/cm2 (left), ḡH = 0 mS/cm2, ḡCa,T = 0.14 mS/cm2, and instantaneous activation (center), and ḡH = 0 mS/cm2, ḡCa,T = 0.14 mS/cm2, and slow activation (right). The applied current is identical to that in Fig. 1 but takes a value of 10 μA/cm2 for 10 ms for the fast depolarizing input.
In Fig. 3, the maximal synaptic conductance, ḡsyn (from 0 to 10 mS/cm2), and the synaptic time constant to 1/krA (τsyn; krA varies from 0 to 1 ms−1), vary simultaneously for the two neurons. The variability level is 40% for ḡsyn and 20% for ḡPIR. Membrane potential plots (ḡsyn [mS/cm2], krA [ms−1]) [top left, (1.5, 0.1) and (4.5, 0.05); top right, (8.5, 0.75) and (4.5, 0.05); bottom, (6, 0.15)] with variability. In Fig. 4, the maximal PIR conductances, ḡPIR,1 for neuron 1 and ḡPIR,2 for neuron 2 (from 0.25 to 0.75 mS/cm2), vary independently for the two neurons. The variability level is 40% for ḡsyn and 20% for ḡPIR. The zoom for the duty cycle and duty cycle ratio covers a range from 0.25 to 0.50 mS/cm2.
Fig. 4.
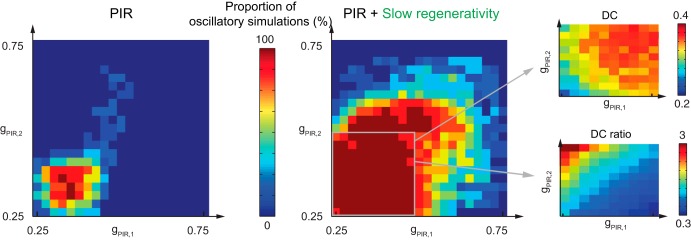
Duty cycle modulation with intrinsic parameters is fragile without slow regenerativity. Modulation of the duty cycle and duty cycle ratio by varying intrinsic parameters of neuron 1 (ḡPIR,1; in mS/cm2) and neuron 2 (ḡPIR,2; in mS/cm2) is robust with slow regenerativity but fragile without. Left: PIR only. Right: PIR + slow regenerativity. The proportion of simulations with stable rhythmic activity is shown for 10 simulations with 40% variability in ḡsyn and 20% variability in ḡPIR (see materials and methods for a description of detection of rhythm and proportion of half-center oscillations). For the case with slow regenerativity, enlarged views of the stable region for mean duty cycle (DC; top far right) and mean duty cycle ratio (DC ratio; bottom far right) from the 10 simulations are shown (see materials and methods for a description of duty cycle and duty cycle ratio). The arrows indicate the direction of DC and DC ratio modulation.
For Fig. 5, the intrinsic neuron parameter is ḡPIR = 0.3 mS/cm2 with a variability level from 0 to 200%. For Fig. 6, the extrinsic neuron parameter is ḡsyn = 2 mS/cm2 with a variability level from 0 to 200%. In Fig. 7, a Gaussian white noise is added in the voltage equation to model the typical spike train input received from the many other unmodeled neurons (Lindner et al. 2003). The noise is 2Dξ(t), where D is the noise intensity and varies from 0 to 0.25, and ξ(t) is drawn from a normal distribution with zero mean and unitary standard deviation and is different for each neuron.
Fig. 6.
Slow regenerativity makes network oscillations insensitive to extrinsic variability. Network oscillations are robust toward synaptic variability only with slow regenerativity. Left: PIR only. Right: PIR + slow regenerativity. Variability (level: 0 to 200%) in the maximal conductance of the synaptic connection, ḡsyn. The grayscale code indicates the proportion of simulations with stable rhythmic activity out of 10 simulations. Upper and lower raster plots show membrane potentials with 80 and 110% variability, respectively. Bottom: plots of the mean frequency (bold line) and 1 SD variation (thin lines) for each variability level for the 10 simulations with oscillations.
RESULTS
Slow activation of T-type calcium channels is critical to robustness of network rhythmic activity.
To assess the role of cellular properties in network rhythms, we consider one of the simplest and most studied networks: the half-center oscillator, HCO. The network rhythm results from the mutual inhibition of two neurons that do not oscillate endogenously in isolation (Brown 1911; Perkel and Mulloney 1974; Satterlie 1985). HCOs have been identified at the core of most endogenous rhythmic circuits, such as CPGs governing locomotion (Brown 1911; Calabrese and De Schutter 1992; Daun et al. 2009; Grillner and Wallén 1985; Perkel and Mulloney 1974; Satterlie 1985) or respiration (Butera et al. 1999; Daun et al. 2009). Oscillations in HCOs can be triggered by hyperpolarizing pulses. When released from hyperpolarization, the cell generates a burstlike transient depolarization with one or more spikes. This activity hyperpolarizes the other cell via the inhibitory synaptic connection, which in turn triggers a transient burst. The cycle repeats leading to an anti-phase rhythm between the two neurons.
The transient depolarization following the termination of a hyperpolarizing input is an essential cellular property for the network rhythm, best known in the literature as postinhibitory rebound (PIR; Perkel and Mulloney 1974). Two major ionic currents have been shown to underlie the PIR (Fig. 1, top): 1) IH, a hyperpolarization-activated inward current that contributes to rebound responses in a diverse array of neurons in invertebrates and vertebrates (Angstadt et al. 2005); and 2) the low-threshold T-type calcium current ICa,T, which is deinactivated by hyperpolarization and then activates on release from inhibition (Steriade et al. 1990). Many studies have highlighted the distinction between these two currents in HCOs from an “escape or release” mechanism perspective, with T-type calcium currents inducing the release mechanism and IH-like currents promoting the escape mechanism (Daun et al. 2009; Skinner et al. 1994; Wang and Rinzel 1992): either the active cell “releases” its inhibitory effect on the silent cell (release mechanism), or the silent cell “escapes” from inhibition via the activation of an IH-like current (escape mechanism).
Separately, the two types of current generate similar PIR traces in single cells (Fig. 1, top; see materials and methods for a description of cellular models and model difference between mechanisms A and B). Although both mechanisms are redundant for the generation of oscillations in a two-neuron network with reciprocal inhibition (Fig. 1, middle), we emphasize a fundamental difference between the two: in the presence of physiological variability, i.e., variability in the intrinsic cellular properties and synaptic connections (see materials and methods for a description of variability), the rhythm generated by mechanism A is fragile (Fig. 1, bottom). This fragility toward heterogeneity and noise (see following sections) highlights a fundamental difference between the two mechanisms.
This difference lies in the specific gating properties of the two currents generating the PIR. IH is an inward, depolarizing current that activates ultraslowly (τm,h around 600 ms at threshold potential) during membrane potential hyperpolarization. This current thus counteracts the hyperpolarization that causes its activation, acting as a source of negative feedback on membrane potential variations in an ultraslow timescale (i.e., over the course of several action potentials). This property is termed (ultraslow) restorativity (Fig. 2A, left) (Drion et al. 2015; Franci et al. 2013). Likewise, ICa,T is an inward, depolarizing current that inactivates ultraslowly (τh,CaT around 600 ms at threshold potential) and therefore shares the ultraslow restorativity property of IH (Fig. 2A, center and right). This ultraslow restorativity is the foundation of the PIR.
On the other hand, in contrast to IH that is present during the whole hyperpolarization, ICa,T also needs to be activated by membrane potential depolarization. This activation, which is typically faster than the inactivation (τm,CaT around 20 ms at threshold potential), tends to amplify membrane depolarization, acting as a source of positive feedback on membrane potential variations in a slow timescale (over the course of a single action potential). This property is termed (slow) regenerativity (Fig. 2A, right). The absence or presence of this slow regenerativity is the sole difference between mechanism A and mechanism B, respectively.
These dynamical properties can be directly measured in a voltage-clamp experiment (Drion et al. 2015). Figure 2B shows a simulated voltage-clamp experiment in the model with IH (left) or ICa,T (center and right; Vm varies from −80 to −50 mV). The dashed lines correspond to instantaneous changes in transmembrane current that do not play any dynamical role (changes in driving forces and/or instantaneous activation of ICa,T). In the presence of IH, a subthreshold depolarizing step induces an ultraslow monotonic decrease of the inward transmembrane current (Fig. 2B, left). This ultraslow restorative event is carried by the deactivation of IH. In the presence of ICa,T, a subthreshold depolarizing step induces a biphasic change in the transmembrane current: the inward current first increases due to the activation of ICa,T (slow regenerative event), peaks at around 60 ms, and then decreases ultraslowly due to the inactivation of ICa,T (ultraslow restorative event; Fig. 2B, right). It is important to note that the steady-state value of the transmembrane current is very similar in both cases. This subtle difference in transmembrane current dynamics has a large impact on neuron excitability properties (Drion et al. 2012, 2015; Franci et al. 2013), as illustrated in Fig. 2C: a transient excitatory pulse that triggers a single spike in mechanism A (IH; left) triggers a burst in mechanism B (ICa,T; right). This signature reveals that bursts, or plateau properties, are solely endogenously generated with a PIR with slow regenerativity (mechanism B).
A frequent modeling simplification is to neglect the slow activation kinetics of T-type calcium channels and to consider the activation at steady state (i.e., instantaneous). It should be noted that the slow regenerativity is lost in this approximation, which eliminates the bursting signature observed in mechanism B, as illustrated in Fig. 2, center.
In the rest of this article, we investigate the impact of the difference between mechanisms A and B at the network level. More specifically, we look at a few simple quantities that characterize the network rhythm in a two-neuron network: the network or interburst frequency, i.e., the inverse of the time duration between two burst onsets; the duty cycle, which is the ratio between the burst duration and the period, averaged over the two neurons; and the ratio between the duty cycle in neuron 1 (the neuron upon which acts the external hyperpolarization) and in neuron 2 (the other neuron). In the next section we investigate to what extent the two mechanisms withstand robust oscillations in a network with neuronal populations.
Robust modulation of network properties requires slow regenerativity.
Experimentally, the network properties of CPGs, i.e., network frequency and duty cycle (or phase relation) can be modulated via both intrinsic neuron parameters (such as ionic conductances across neurons) and synaptic parameters (such as synaptic conductances) on multiple timescales (Dayan 2012; Dickinson 2006; El Manira and Wallén 2000; Fellous and Linster 1998; Harris-Warrick 2011; Harris-Warrick and Marder 1991; Marder 2012; Marder and Thirumalai 2002; Nadim and Bucher 2014). In this section, we investigate how the rhythmic activity of a two-neuron network responds to these modulations, both with PIR without slow regenerativity and with PIR with slow regenerativity, and in presence of parameter variability (see materials and methods for network description and details of the simulations).
Extrinsic parameters, i.e., the synaptic parameters ḡsyn and τsyn, given intrinsic (cellular) characteristics, modulate the network frequency. Synaptic coupling is very plastic (Dayan and Abbott 2005; Gerstner and Kistler 2002), and synapses are a primary target of modulators (Nadim and Bucher 2014). Synaptic currents can be generated by the cooperation of several ion channel subtypes, which have slightly different kinetics. Variation of the synaptic parameters results from a variation of the contribution of all the subtypes. Absolute variation of the different ion channels influences the maximal conductance, whereas their relative variation can modulate the time constant of the synaptic current that aggregates all the different subtypes in a model (for instance, combination of GABAA and GABAB synapses). Therefore, both the synaptic magnitude, ḡsyn (reflecting a variation in the absolute magnitude), and the synaptic kinetics, τsyn (reflecting a variation in the relative magnitude), can be sources of modulation.
Oscillations with cellular slow regenerativity can be modulated over a large range by extrinsic parameters (Fig. 3, right). Variation of the ḡsyn and τsyn parameters generates a 150% increase in network frequency (see materials and methods for a description of mean frequency). Such a span of modulation is observed in physiological rhythms: for instance, there is a 150% increase in frequency from slow-wave sleep (∼4 Hz) to sleep spindles (∼10 Hz) and a 250% increase from beta-band oscillations (∼20 Hz) to gamma-band oscillations (∼70 Hz). In addition, with slow regenerativity, the network frequency is only weakly sensitive to the variability in parameters as shown by the standard deviation plot and the highly similar network frequencies in the membrane voltage traces (see materials and methods for a description of standard deviation). In contrast, variations of ḡsyn without slow regenerativity allow for network frequency modulation for a much smaller parameter range (Fig. 3, left). Moreover, this modulation is very fragile and very sensitive to variability: the standard deviation reaches higher values than with slow regenerativity, and membrane potential traces are different for a same set of parameters but different simulations (Fig. 3, bottom left). Variation of τsyn is almost impossible: τsyn must lie in a very specific timescale for the oscillations to develop in the network. In the absence of positive feedback at the cellular level, the modulation requires a tight coupling between intrinsic and extrinsic parameters: the network oscillations are a direct image of the unicellular activity. The synaptic dynamics must be close to the neuron intrinsic dynamics and cannot deviate from a tiny range of parameters.
Intrinsic parameters, i.e., the cellular parameter ḡPIR for each neuron (ḡPIR,1 for neuron 1 and ḡPIR,2 for neuron 2), given extrinsic (synaptic) characteristics, modulate the duty cycle and duty cycle ratio (see materials and methods for a description of duty cycle and duty cycle ratio). Many neuromodulators act on the neuron intrinsic properties by altering the balance of conductances, modifying their excitability properties (Marder and Thirumalai 2002). The maximal conductance of the PIR current is a natural candidate for modulation by intrinsic parameters.
The high robustness brought by cellular slow regenerativity allows also for the modulation by intrinsic parameters even in presence of variability in the network (Fig. 4). Covariation of the maximal PIR conductances ḡPIR,1 and ḡPIR,2 leads to an increase in duty cycle of 100% (Fig. 4, top right). Independent variation of the same parameters, i.e., varying ḡPIR,1 and ḡPIR,2 independently, modulates the duty cycle ratio up to a factor of 3 (Fig. 4, bottom right). Variations in phase relation have been observed, for instance, in cats during normal locomotion, where the shortening, by a factor of 2 or 3, of one of the phases (the extensor phase) leads to faster walking (Halbertsma 1983). In contrast, our computational model suggests that modulation with PIR without slow regenerativity is so fragile that it is physiologically unrealistic. Stable oscillations with variation of intrinsic parameters do not cover a large parameter range (Fig. 4, left).
To summarize, the high robustness brought by cellular slow regenerativity allows for the modulation by both extrinsic and intrinsic parameters. In addition, the network frequency and duty cycle can be modulated independently and in the presence of physiological variability in the network.
Robustness of network oscillations requires PIR with slow regenerativity.
There exists extensive experimental evidence that the rhythmic activity of neuronal circuits is robust against variability in intrinsic parameters, extrinsic parameters, and exogenous noise (such as synaptic currents external to the circuit) (Destexhe and Rudolph-Lilith 2012; Goldman et al. 2001; Golowasch et al. 1999a, 1999b; Liu et al. 1998). We tested the robustness of HCOs in a 16-neuron network with PIR without slow regenerativity against a network with PIR with slow regenerativity. The results show the drastic influence of cellular slow regenerativity in the robustness of the network.
Intrinsic variability of the network was studied by introducing variability in the maximal conductance of the PIR current, ḡPIR. Variability in the cellular properties dramatically impacts the rhythmic activity of the network without slow regenerativity (Fig. 5, left). The network rhythm becomes unstable beyond 80% of variability and is significantly perturbed for smaller values. In sharp contrast, the network oscillations with slow regenerativity are robust against intrinsic variability up to 120% (Fig. 5, right). Remarkably, the network frequency is almost unaffected by the intrinsic variability, a consequence of the positive feedback brought by slow regenerative currents.
The robustness of the network oscillations against variability in extrinsic parameters was studied by introducing variability in the maximal synaptic conductance parameters, ḡsyn. Without slow regenerativity, a small variability in the synaptic conductances dramatically affects the network activity (Fig. 6, left; compare with Fig. 5, left, for the case without variability): identical maximal synaptic conductances generate oscillations, but oscillations become unstable when the maximal synaptic conductances differ between the two populations. Oscillations with a PIR without slow regenerativity are fragile with network variability. In sharp contrast, variability in the synaptic conductances is possible for a much larger range with slow regenerativity, and the network frequency is also almost independent of the synaptic variability. Oscillations persist up to a variability of 200%. A source of slow positive feedback in the PIR mechanism is therefore essential to robustness of network oscillations against network variability.
The robustness of the network oscillations against exogenous disturbances was investigated by adding a Gaussian white noise in the equation that models membrane potential variations (see materials and methods for a description of noise). This emulates the external perturbations (spike train inputs from surrounding neurons) received by a network when studied in a noisy environment rather than in isolation (Lindner et al. 2003). We simulated a 16-neuron network with 2 populations, with a different noise source for each neuron (Fig. 7).
The results are consistent with the robustness against parameter variability. Without slow regenerativity, oscillations are sensitive to noise and completely disappear with a noise level >0.125 mV2. With slow regenerativity, oscillations are robust to noise up to a level of 0.25 mV2. Similarly to the introduction of variability in intrinsic and extrinsic parameters, the network frequency is also less affected in the presence of slow regenerativity.
DISCUSSION
Slow regenerativity is essential to robustness and modulation of network rhythmic activity.
The main message of this article is to highlight the role of slow regenerativity, a cellular excitability property, in endowing network oscillations with modulation and robustness properties that seem ubiquitous in physiological neuronal networks. An ionic current is slowly regenerative if it provides a source of positive feedback around resting potential in the slow timescale of repolarization (Franci et al. 2013). The importance of this cellular property was assessed in one of the simplest and best understood network oscillation mechanisms, the anti-phase rhythm observed between two populations of neurons reciprocally connected by inhibitory synaptic connections. Many earlier studies have emphasized the role of PIR at the cellular level as a core mechanism for the network oscillation and have identified IH and ICa,T as two distinct ionic currents that can participate in the PIR. Our novel contribution is to observe that the cellular PIR will enable a robust network oscillation that is subject to modulation only in the presence of a slow regenerative ionic current. Because both IH and ICa,T are sources of PIR currents but only ICa,T is slow regenerative, i.e., ICa,T provides a slow positive feedback via its slow activation variable that is absent in the cation current, our work suggests a novel and somewhat fundamental complementarity between T-type calcium and IH channels in PIR mechanisms.
As a source of positive feedback, regenerative currents make the PIR endogenous, that is, robust in the presence of intrinsic and extrinsic sources of variability. As a consequence, a PIR with slow regenerative currents allows for robust network oscillations and enables robust modulation. The network oscillation is robust because it can sustain large variability across the neuronal population in both intrinsic (cellular) and extrinsic (synaptic) parameters. It is also subject to modulation because the frequency and phase properties of the oscillation can be controlled over a broad range by a relative modulation of extrinsic or intrinsic conductances. Our computational investigation illustrated that these robustness and modulation properties are lost when the PIR is purely ultraslow restorative.
Our results also predict that PIR per se is not a sufficient cellular excitability property to ensure modulation and robustness of HCO oscillations. Determining the dynamics of the PIR current is also primordial. At the cellular level, this suggests an experimental essay to detect the presence or absence of a slow positive feedback source. Slow regenerativity can be detected by the neuron-specific response, single spike or burst, to a transient excitatory pulse, when the neuron is under the influence of a hyperpolarization current. The triggering of a burst indicates the existence of a slow regenerative source and predicts modulation and robustness properties at the network level.
Future work could target the differentiation of the two types of PIR for HCOs in regard to their response to inputs. A tool largely used to quantify how oscillators response to inputs in biology, and more specifically in neuroscience, is the phase-response curve (PRC). PRCs express a perturbation of the state of the oscillators as a perturbation of the phase. In other words, PRCs describe the dependence of the phase shift on the phase at the perturbation time (see Smeal et al. 2010 for a review). A recent work in this direction can be found in the study by Zhang and Lewis (2013), for instance. Current work by the authors focuses on relaxing the weakly coupled condition for PRCs of HCOs (Smeal et al. 2010). In addition, investigating the impact of a different mode of synaptic transmission (e.g., spike-mediated transmission) could reveal further insights (Nadim et al. 1995).
Complementarity between the two types of PIR currents.
In the context of HCOs, many neurons possess both IH and ICa,T, the two main currents that contribute to PIR (Calabrese and De Schutter 1992; Cymbalyuk et al. 2002; De Schutter et al. 1993; Doloc-Mihu and Calabrese 2011; Nadim et al. 1995; Olypher et al. 2006; Sorensen et al. 2004). When those two currents are present, both IH and ICa,T can be a source of modulation. In this case, the presence of T-type calcium currents as a source of slow regenerativity is sufficient to guarantee network oscillation robustness. On the other hand, the hyperpolarization-activated cation current can modulate drastically the network frequency and duty cycle (Cymbalyuk et al. 2002; Sorensen et al. 2004). However, our computational model suggests that this is only the case if a slow regenerative current is supplied by another mechanism. It is noteworthy that slow restorativity can be provided by other means, such as the presence of high-threshold calcium channels. For instance, recent experiments have highlighted the involvement of a slowly activating, low-threshold inward current, i.e., slow regenerative current, in the generation of rhythmic oscillations in a crab CPG (Rodriguez et al. 2013). This requirement for slow regenerativity reveals a somewhat fundamental complementarity, distinct from the release or escape view, between the two channels: ICa,T allows for stable rhythmic oscillations to emerge, and IH enlarges the modulation possibilities.
Positive feedback as a source of endogenous activity.
Slow regenerativity is nothing but a source of positive feedback in the slow timescale of repolarization. It is a slow analog of the positive feedback brought by sodium activation in the fast timescale of spike upstroke. In previous work (Franci et al. 2013), we showed that this positive feedback is essential for bistability, i.e., the robust coexistence of hyperpolarized and spiking states at the cellular level. We subsequently showed (Franci et al. 2014) that this positive feedback is essential for modulation and robustness of bursting activities. In the present work we show that the same positive feedback at the cellular level is also essential for robustness and modulation at the network level. The common feature of the positive feedback in those three phenomena is that it makes the neuronal excitability in the slow timescale an endogenous property, robust in the presence of intrinsic and extrinsic variability. Making an activity endogenous is the very nature of positive feedback and has been emphasized in a number of contexts. The results presented in this article are in line with the discussion of the role of positive feedback in other biological models such as, for instance, the biochemical mechanisms underlying the mitotic oscillator (Novak and Tyson 1993; Pomerening et al. 2003; Tyson and Novak 2008): the oscillator is endogenous and robust in the presence of positive feedback, whereas it becomes exogenous and entrainable when the source of positive feedback disappears. Therefore, the importance at the network level of positive feedback at the cellular level is thought to be general, and its role in other neuronal networks should be investigated.
Slow regenerativity in half-center oscillator models.
There is a rich literature on computational models of oscillations generated by reciprocal inhibition. HCOs have been used to model rhythmic motor outputs in many invertebrates and vertebrates (Brown 1911; Calabrese and De Schutter 1992; Harris-Warrick 2011; Marder and Calabrese 1996; Perkel and Mulloney 1974; Satterlie 1985). In a different context, models of thalamocortical spindle oscillations suggest that the rhythm originates from the thalamic reticular nucleus, which consists in interacting inhibitory nonoscillatory neurons (Destexhe et al. 1994; Golomb et al. 1994; Wang and Rinzel 1992, 1993).
It is of interest to observe the varying degree of cellular regenerativity in published models of HCOs. Early models are conductance based and usually include at the cellular level both IH and ICa,T, the two main physiological currents eliciting the PIR (Calabrese and De Schutter 1992; De Schutter et al. 1993; Destexhe et al. 1994; Huguenard and Prince 1992; Nadim et al. 1995). However, network computational studies often lead to subsequent mathematical simplifications of the cellular details, and the cellular slow positive feedback is often lost in this reduction process. A frequent simplification in the literature (see e.g., Daun et al. 2009; Golomb and Rinzel 1993; Rinzel et al. 1998; Wang and Rinzel 1992, 1993) is to resort to a steady-state approximation of the calcium activation in the same way as it is normally done for sodium activation, but this approximation rests on neglecting fast dynamics, which amounts to considering calcium channels as a source of fast rather than slow positive feedback. The resulting reduced models have therefore lost their source of slow regenerativity, which makes them unsuitable for robustness and modulation studies at the network level.
The alternative model reduction consists of modeling the cellular level as Morris-Lecar-type neurons, retaining the slow calcium currents but neglecting the fast sodium currents (Skinner et al. 1993, 1994). Those models do retain the slow positive feedback source necessary for robustness, but they lose the spike interpretability since the model describes the envelope of the bursting and nonbursting dynamics. This prevents exogenous modulation of the rhythm. In addition, if sodium spikes were added to a Morris-Lecar neuron with the addition of the spike currents (as suggested by Kopell and Ermentrout 2002) while the calcium activation was kept at steady state, the slow regenerativity would be destroyed.
It should be highlighted that it is possible to derive reduced neuronal models that do retain the balance of slow positive and negative feedbacks as an explicit parameter (see, e.g., the recent models in Drion et al. 2012; Franci et al. 2014). The results of the present study suggest that it is an important feature to retain in a simplified model aimed at network computational studies. The reduced model has the physiological interpretation of a reduced conductance-based model and provides a route to bursting (Franci et al. 2014). By comparison, most reduced models in the literature do not allow study of modulation and robustness because their parameters do not have physiological correlates.
GRANTS
This work was supported by Belgian Science Policy Grant IAPVII/19. J. Dethier is supported by the Fonds de la Recherche Scientifique-FNRS (Belgian Fund for Scientific Research). G. Drion is a Marie-Curie COFUND postdoctoral fellow at the University of Liege, co-funded by the European Union.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
J.D., G.D., and R.S. conception and design of research; J.D. and G.D. performed experiments; J.D. analyzed data; J.D., G.D., A.F., and R.S. interpreted results of experiments; J.D. and G.D. prepared figures; J.D. drafted manuscript; J.D., G.D., A.F., and R.S. edited and revised manuscript; J.D., G.D., A.F., and R.S. approved final version of manuscript.
ACKNOWLEDGMENTS
We acknowledge constructive discussions with Dr. Timothy O'Leary (Brandeis University) and Prof. Eve Marder (Brandeis University).
REFERENCES
- Angstadt JD, Grassmann JL, Theriault KM, Levasseur SM. Mechanisms of postinhibitory rebound and its modulation by serotonin in excitatory swim motor neurons of the medicinal leech. J Comp Physiol A Neuroethol Sens Neural Behav Physiol 191: 715–732, 2005. [DOI] [PubMed] [Google Scholar]
- Brown TG. The intrinsic factors in the act of progression in the mammal. Proc R Soc Lond B 84: 308–319, 1911. [Google Scholar]
- Butera RJ Jr, Rinzel J, Smith JC. Models of respiratory rhythm generation in the prebötzinger complex. II. Populations of coupled pacemaker neurons. J Neurophysiol 82: 398–415, 1999. [DOI] [PubMed] [Google Scholar]
- Calabrese RL, De Schutter E. Motor-pattern-generating networks in invertebrates: modeling our way toward understanding. Trends Neurosci 15: 439–445, 1992. [DOI] [PubMed] [Google Scholar]
- Cymbalyuk GS, Gaudry Q, Masino MA, Calabrese RL. Bursting in leech heart interneurons: cell-autonomous and network-based mechanisms. J Neurosci 22: 10580–10592, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daun S, Rubin JE, Rybak IA. Control of oscillation periods and phase durations in half-center central pattern generators: a comparative mechanistic analysis. J Comput Neurosci 27: 3–36, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P. Twenty-five lessons from computational neuromodulation. Neuron 76: 240–256, 2012. [DOI] [PubMed] [Google Scholar]
- Dayan P, Abbott LF. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge, MA: The MIT Press, 2005. [Google Scholar]
- De Schutter E, Angstadt JD, Calabrese RL. A model of graded synaptic transmission for use in dynamic network simulations. J Neurophysiol 69: 1225–1235, 1993. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Contreras D, Sejnowski TJ, Steriade M. A model of spindle rhythmicity in the isolated thalamic reticular nucleus. J Neurophysiol 72: 803–818, 1994. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Rudolph-Lilith M. Neuronal noise. In: Springer Series in Computational Neuroscience, edited by Destexhe A, Brette R. New York: Springer, volume 8, 2012. [Google Scholar]
- Dickinson PS. Neuromodulation of central pattern generators in invertebrates and vertebrates. Curr Opin Neurobiol 16: 604–614, 2006. [DOI] [PubMed] [Google Scholar]
- Doloc-Mihu A, Calabrese RL. A database of computational models of a half-center oscillator for analyzing how neuronal parameters influence network activity. J Biol Phys 37: 263–283, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drion G, Franci A, Dethier J, Sepulchre R. Dynamic input conductances shape neuronal spiking. eNeuro 2: 0031–14, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drion G, Franci A, Seutin V, Sepulchre R. A novel phase portrait for neuronal excitability. PLoS One 7: e41806, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Manira A, Wallén P. Mechanisms of modulation of a neural network. News Physiol Sci 15: 186–191, 2000. [DOI] [PubMed] [Google Scholar]
- Fellous JM, Linster C. Computational models of neuromodulation. Neural Comput 10: 771–805, 1998. [DOI] [PubMed] [Google Scholar]
- Franci A, Drion G, Sepulchre R. Modeling the modulation of neuronal bursting: a singularity theory approach. SIAM J Appl Dyn Syst 13: 798–829, 2014. [Google Scholar]
- Franci A, Drion G, Seutin V, Sepulchre R. A balance equation determines a switch in neuronal excitability. PLoS Comput Biol 9: e1003040, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W, Kistler W. Spiking Neuron Models: Single Neurons, Populations, Plasticity. Cambridge, UK: Cambridge University Press, 2002. [Google Scholar]
- Getting PA. Emerging principles governing the operation of neural networks. Annu Rev Neurosci 12: 185–204, 1989. [DOI] [PubMed] [Google Scholar]
- Goldman MS, Golowasch J, Marder E, Abbott LF. Global structure, robustness, and modulation of neuronal models. J Neurosci 21: 5229–5238, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golomb D, Rinzel J. Dynamics of globally coupled inhibitory neurons with heterogeneity. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics 48: 4810–4814, 1993. [DOI] [PubMed] [Google Scholar]
- Golomb D, Wang XJ, Rinzel J. Synchronization properties of spindle oscillations in a thalamic reticular nucleus model. J Neurophysiol 72: 1109–1126, 1994. [DOI] [PubMed] [Google Scholar]
- Golowasch J, Abbott LF, Marder E. Activity-dependent regulation of potassium currents in an identified neuron of the stomatogastric ganglion of the crab Cancer borealis. J Neurosci 19: RC33, 1999a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Casey M, Abbott LF, Marder E. Network stability from activity-dependent regulation of neuronal conductances. Neural Comput 11: 1079–1096, 1999b. [DOI] [PubMed] [Google Scholar]
- Grillner S, Wallén P. Central pattern generators for locomotion, with special reference to vertebrates. Annu Rev Neurosci 8: 233–261, 1985. [DOI] [PubMed] [Google Scholar]
- Halbertsma JM. The stride cycle of the cat: the modelling of locomotion by computerized analysis of automatic recordings. Acta Physiol Scand Suppl 521: 1–75, 1983. [PubMed] [Google Scholar]
- Harris-Warrick RM. Neuromodulation and flexibility in central pattern generator networks. Curr Opin Neurobiol 21: 685–692, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris-Warrick RM, Marder E. Modulation of neural networks for behavior. Annu Rev Neurosci 14: 39–57, 1991. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117: 500–544, 1952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huguenard JR, Prince DA. A novel T-type current underlies prolonged Ca2+-dependent burst firing in gabaergic neurons of rat thalamic reticular nucleus. J Neurosci 12: 3804–3817, 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopell N, Ermentrout G. Mechanisms of phase-locking and frequency control in pairs of coupled neural oscillators. In: Handbook of Dynamical Systems II: Towards Applications, edited by Fielder B, Iooss G, Kopell N. Amsterdam: Elsevier, vol. 2, chapt. 1, 2002, p. 3–54. [Google Scholar]
- Lindner B, Longtin A, Bulsara AR. Analytic expressions for rate and CV of a type I neuron driven by white Gaussian noise. Neural Comput 15: 1761–8178, 2003. [DOI] [PubMed] [Google Scholar]
- Liu Z, Golowasch J, Marder E, Abbott LF. A model neuron with activity-dependent conductances regulated by multiple calcium sensors. J Neurosci 18: 2309–2320, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E. Neuromodulation of neuronal circuits: back to the future. Neuron 76: 1–11, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Bucher D. Central pattern generators and the control of rhythmic movements. Curr Biol 11: R986–R996, 2001. [DOI] [PubMed] [Google Scholar]
- Marder E, Calabrese RL. Principles of rhythmic motor pattern generation. Physiol Rev 76: 687–717, 1996. [DOI] [PubMed] [Google Scholar]
- Marder E, Goaillard JM. Variability, compensation and homeostasis in neuron and network function. Nat Rev Neurosci 7: 563–574, 2006. [DOI] [PubMed] [Google Scholar]
- Marder E, Thirumalai V. Cellular, synaptic and network effects of neuromodulation. Neural Netw 15: 479–493, 2002. [DOI] [PubMed] [Google Scholar]
- Nadim F, Bucher D. Neuromodulation of neurons and synapses. Curr Opin Neurobiol 29C: 48–56, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadim F, Olsen OH, De Schutter E, Calabrese RL. Modeling the leech heartbeat elemental oscillator. I. Interactions of intrinsic and synaptic currents. J Comput Neurosci 2: 215–235, 1995. [DOI] [PubMed] [Google Scholar]
- Novak B, Tyson JJ. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos. J Cell Sci 106: 1153–1168, 1993. [DOI] [PubMed] [Google Scholar]
- Olypher A, Cymbalyuk G, Calabrese RL. Hybrid systems analysis of the control of burst duration by low-voltage-activated calcium current in leech heart interneurons. J Neurophysiol 96: 2857–2867, 2006. [DOI] [PubMed] [Google Scholar]
- Perkel DH, Mulloney B. Motor pattern production in reciprocally inhibitory neurons exhibiting postinhibitory rebound. Science 185: 181–183, 1974. [DOI] [PubMed] [Google Scholar]
- Pomerening JR, Sontag ED, Ferrell JE Jr. Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat Cell Biol 5: 346–351, 2003. [DOI] [PubMed] [Google Scholar]
- Rinzel J, Terman D, Wang X, Ermentrout B. Propagating activity patterns in large-scale inhibitory neuronal networks. Science 279: 1351–1355, 1998. [DOI] [PubMed] [Google Scholar]
- Rodriguez JC, Blitz DM, Nusbaum MP. Convergent rhythm generation from divergent cellular mechanisms. J Neurosci 33: 18047–18064, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterlie RA. Reciprocal inhibition and postinhibitory rebound produce reverberation in a locomotor pattern generator. Science 229: 402–404, 1985. [DOI] [PubMed] [Google Scholar]
- Skinner FK, Kopell N, Marder E. Mechanisms for oscillation and frequency control in reciprocally inhibitory model neural networks. J Comput Neurosci 1: 69–87, 1994. [DOI] [PubMed] [Google Scholar]
- Skinner FK, Turrigiano GG, Marder E. Frequency and burst duration in oscillating neurons and two-cell networks. Biol Cybern 69: 375–383, 1993. [PubMed] [Google Scholar]
- Smeal RM, Ermentrout GB, White JA. Phase-response curves and synchronized neural networks. Philos Trans R Soc Lond B Biol Sci 365: 2407–2422, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorensen M, DeWeerth S, Cymbalyuk G, Calabrese RL. Using a hybrid neural system to reveal regulation of neuronal network activity by an intrinsic current. J Neurosci 24: 5427–5438, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Gloor P, Llinas RR, Lopes da Silva FH, Mesulam MM. Basic mechanisms of cerebral rhythmic activities. Electroencephalogr Clin Neurophysiol 76: 481–508, 1990. [DOI] [PubMed] [Google Scholar]
- Turrigiano G, LeMasson G, Marder E. Selective regulation of current densities underlies spontaneous changes in the activity of cultured neurons. J Neurosci 15: 3640–3652, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyson JJ, Novak B. Temporal organization of the cell cycle. Curr Biol 18: R759–R768, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Rinzel J. Alternating and synchronous rhythms in reciprocally inhibitory model neurons. Neural Comput 4: 84–97, 1992. [Google Scholar]
- Wang XJ, Rinzel J. Spindle rhythmicity in the reticularis thalami nucleus: synchronization among mutually inhibitory neurons. Neuroscience 53: 899–904, 1993. [DOI] [PubMed] [Google Scholar]
- Zhang C, Lewis TJ. Phase response properties of half-center oscillators. J Comput Neurosci 35: 55–74, 2013. [DOI] [PubMed] [Google Scholar]