Modeling and simulating the neuromuscular mechanisms regulating ankle and knee joint stiffness during human locomotion

Abstract

This work presents an electrophysiologically and dynamically consistent musculoskeletal model to predict stiffness in the human ankle and knee joints as derived from the joints constituent biological tissues (i.e., the spanning musculotendon units). The modeling method we propose uses electromyography (EMG) recordings from 13 muscle groups to drive forward dynamic simulations of the human leg in five healthy subjects during overground walking and running. The EMG-driven musculoskeletal model estimates musculotendon and resulting joint stiffness that is consistent with experimental EMG data as well as with the experimental joint moments. This provides a framework that allows for the first time observing 1) the elastic interplay between the knee and ankle joints, 2) the individual muscle contribution to joint stiffness, and 3) the underlying co-contraction strategies. It provides a theoretical description of how stiffness modulates as a function of muscle activation, fiber contraction, and interacting tendon dynamics. Furthermore, it describes how this differs from currently available stiffness definitions, including quasi-stiffness and short-range stiffness. This work offers a theoretical and computational basis for describing and investigating the neuromuscular mechanisms underlying human locomotion.

human locomotion results from afferent and efferent neural activity being translated into mechanical output by muscles acting on skeletal joints and in the subsequent exchange of interaction forces with the external environment (Zajac et al., 2002; Enoka, 2008; Winter, 2009). Humans are remarkably capable of physically interacting across large varieties of terrains and naturally adjusting to their demand. This efficient adaptation process occurs subconsciously, and normally involves little or no mental effort (Morton and Fuller, 1952). It is largely managed at the neuromuscular level by continuous modulation of viscoelastic characteristics in multiple musculotendon units (MTUs) simultaneously (Latash and Zatsiorsky, 1993; Todorov, 2000; Enoka, 2008; Wakeling et al., 2012). The viscoelasticity of individual MTUs spanning multiple skeletal joint degrees of freedom (DOFs) determines the resulting viscoelasticity (i.e., impedance) at the joint level (Latash and Zatsiorsky, 1993; McIntyre et al., 1996; Hu et al., 2011; Pfeifer et al., 2012). It is worth stressing that in physics, the term “viscoelasticity” traditionally refers to the property of materials to mechanically respond to deformations by exhibiting both elastic and viscous characteristics (Stachurski, 2009). Although the classical definition of viscoelasticity is naturally applicable to biological MTUs, it does not directly apply to a skeletal joint, which cannot be considered to be a “body” that responds to deformations with viscoelastic material properties. In this context, we will refer to “joint viscoelasticity” as the combined viscoelastic response of the joint constituent biological tissues, the spanning MTUs, to joint kinematics variations as previously proposed (Latash and Zatsiorsky, 1993).

Accessing MTU and joint viscoelasticity estimates at any particular instant in time is crucial for explaining the neurophysiology, biomechanics, and energetics of natural movement with direct implications in the development of neurorehabilitation and augmentation technologies (Farris and Sawicki, 2012; Farris et al., 2014; Collins et al., 2015). The MTU viscoelasticity can be expressed at the level of stiffness (i.e., resistive force due to MTU elastic characteristics) and damping (i.e., resistive force due to MTU viscous characteristics) (Winter, 2009). This study focuses on the stiffness level.

During locomotion, joint elastic properties have been investigated by means of the quasi-stiffness (QS) estimates (Stefanyshyn and Nigg, 1998; Kuitunen et al., 2002; Charalambous et al., 2012; Shamaei et al., 2013a,b,c). This represents the slope of the best linear fit on the joint moment-angle characteristics throughout a specific phase of the gait cycle. Therefore, QS provides only a representative stiffness estimate within a specific gait phase. System identification methods in conjunction with joint perturbation techniques have also been used to infer joint stiffness by determining the dynamic relationship between experimental recordings of joint angles and moments both in isometric and dynamic conditions (Weiss et al., 1986a,b; Bennett et al., 1992; Ludvig and Perreault, 2012; Plocharski and Plocharski, 2013; Lee and Hogan, 2015; Rouse et al., 2014). Several theoretical and empirical planar spring-mass models have been used to describe the equivalent linear spring stiffness coefficient of the whole lower extremity needed to describe walking and running under different conditions including speed, stride length, stride frequency, and duty factor (Alexander, 1992; Farley and González, 1996; Morin et al., 2005; Geyer et al., 2006; Blum et al., 2009; Dean and Kuo, 2009). Theoretical planar spring-mass models have also been used to investigate QS at the joint level (Günther and Blickhan, 2002).

Recently, musculoskeletal modeling methods have been applied to estimate “endpoint stiffness” in the human arm (Hu et al., 2011) and joint stiffness in the human knee (Pfeifer et al., 2012) in isometric conditions. In this, the term endpoint stiffness refers to the spring-like behavior that the human arm endpoint displays when the arm is constrained to operate in the horizontal plane (McIntyre et al., 1996). These studies (Hu et al., 2011; Pfeifer et al., 2012) showed that net isometric stiffness could be well reconstructed from the muscle fiber short-range stiffness (SRS) and the series elastic tendon stiffness. However, whereas SRS is an appropriate model for characterizing muscle stiffness during isometric conditions, it could not be applied to characterize muscle stiffness during dynamic movement.

Muscle SRS describes the initial steep rise in force when contractile muscle fibers are stretched within a 3% of their length (Walmsley and Proske, 1981). This represents the intrinsic stiffness of the fibers' myofilaments, resulting from the deformation of existing cross-bridges without significant breakdown or reformation (i.e., no change in fiber length) (Walmsley and Proske, 1981). From a modeling point of view, SRS is viably computed as the scaled ratio between muscle force and optimal fiber length (see materials and methods) (Cui et al., 2007, 2008; Hu et al., 2011). This substantially relaxes the modeling requirements because it provides a formulation that is invariant to changes in fiber contraction length and velocity, which do not need to be modeled and estimated. However, during dynamic movement, muscle fibers are stretched beyond the limits of SRS. This results in fiber stiffness being dominated by changes in fiber length, contraction velocity, and activation, with a substantial drop in the fiber resistive force with respect to what is observed within the SRS range (Walmsley and Proske, 1981; Campbell and Moss, 2000). This is referred to as the thixotropic behavior of skeletal muscles (Campbell and Moss, 2000). Therefore, during dynamic movement, SRS is not descriptive of the elastic characteristics of muscle fibers because it would overestimate the underlying stiffness, as previously discussed (Walmsley and Proske, 1981; Campbell and Moss, 2000; Cui et al., 2007, 2008; de Vlugt et al., 2011; Hu et al., 2011). The joint stiffness decrease in transitioning from an isometric pose to dynamic movement was also recently observed experimentally in humans (van Eesbeek et al., 2010; de Vlugt et al., 2011; Ludvig et al., 2012). In this context, it was also shown that SRS is a temporal-dependent feature of muscle contraction lasting ∼30 ms from the joint movement initiation (de Vlugt et al., 2011), thus not persisting during regime locomotion.

Furthermore, the previous modeling studies could not account for physiological co-contraction ratios between agonist and antagonist muscles. Dynamic locomotion is strongly characterized by variable co-contraction ratios between agonist and antagonist muscles (Collins, 1995; Lloyd and Buchanan, 2001; Besier et al., 2003a, 2009). Physiological co-contraction plays a major role in determining the net stiffness of a joint (Hirokawa et al., 1991; Nielsen and Kagamihara, 1993; Todorov, 2000, 2004). Therefore, it needs to be properly accounted for in musculoskeletal modeling methods that aim to characterize muscle and joint stiffness during natural movement. Previous studies used static optimization methods (e.g., Crowninshield and Brand, 1981; Anderson and Pandy, 2001) to solve for muscle force patterns that track experimental net joint moments (Hu et al., 2011) or flexion/extension moments linearly derived from the average flexors'/extensors' electromyography (EMG) readings (Pfeifer et al., 2012) during isometric tasks. This results in force patterns that satisfy constraints imposed by an objective function (i.e., minimal sum of squared forces). In this, the a priori chosen optimization criterion characterizes muscle function only within a specific regime (Todorov, 2004). However, it is known that the same joint angle and moment can underlie substantially different patterns of muscle excitation and co-contraction. These vary with the control task and demand of the external environment (Tax et al., 1990) and can include reflex-based excitation components (Sinkjær et al., 1988; Perreault et al., 2000; Geyer and Herr, 2010). This all cannot be accounted for by a single optimization criterion (Todorov, 2004).

None of the studies examined thus far have provided a modeling framework for estimating instantaneous modulations of muscle and joint stiffness during natural locomotion. This requires a musculoskeletal modeling method that accounts for physiological muscle recruitment strategies and contraction dynamics. In this study we address this challenge by using an EMG-driven musculoskeletal model of the human leg (Lloyd and Besier, 2003; Buchanan et al., 2004; Krishnaswamy et al., 2011; Sartori et al., 2012b; Farris et al., 2014). The term “leg” is used throughout this manuscript according to its anatomical definition. In this, experimental EMG signals are used to directly drive the individual MTUs spanning the knee and ankle joints. The underlying musculoskeletal model is scaled and calibrated to match an individual's anthropometry and EMG-to-force generating properties. The major benefit is the possibility of determining the subject-specific relationships between patterns of MTU excitation and the resulting MTU force without making any a priori assumption on how MTUs are recruited and excited (Sartori et al., 2014).

This enabled the use of EMG-driven modeling for predicting a number of internal musculoskeletal variables that directly emerge from physiological muscle co-contraction strategies during locomotion. They included joint moments (Lloyd and Besier, 2003; Buchanan et al., 2004; Sartori et al., 2012b, 2013, 2014), in vivo knee joint contact forces (Winby et al., 2009; Gardinier et al., 2013; Gerus et al., 2013), and hip joint compressive forces (Fernandez et al., 2014). Furthermore, it enabled studying individuals with neuromuscular or orthopedic impairments that underlay abnormal neuromuscular control strategies. Patients included those with anterior cruciate ligament rupture (Shao et al., 2011), patellofemoral pain (Besier et al., 2009), osteoarthritis (Fregly, 2009; Kumar et al., 2012), stroke (Fregly, 2009; Shao et al., 2009), and upper extremity neuromuscular injuries (Manal and Buchanan, 2005).

In this study we show, for the first time, the use of EMG-driven musculoskeletal modeling for deriving instantaneous estimates of joint stiffness from the stiffness of constituent MTUs during locomotion. We illustrate how this approach fundamentally differs from alternative stiffness estimates, including the SRS and the QS. In five healthy subjects we validate our method's ability of generating simulations of ground-level walking and running that are both electrophysiologically consistent (i.e., driven by experimental EMG data) and dynamically consistent (i.e., the simulated moments match experimental joint moments). We investigate the resulting joint stiffness profiles emerging from these subjects during the performed motor tasks. We assess the major muscles contributing to the estimated joint stiffness and how muscle co-contraction contributes to its modulation. Finally, we compare and further validate our results with findings available in the literature.

MATERIALS AND METHODS

Data collection.

The Human Research Ethics Committee at the University of Western Australia approved all procedures, and participants provided their informed, written consent. Motion-capture data were recorded from five healthy men (age 26.6 ± 1.3 yr, weight 73.9 ± 11.8 kg, height 1.77 ± 0.1 m) who performed one static anatomical pose, and repeated trials of ground-level fast walking (7.8 ± 0.8 trials, 1.9 ± 0.25 m/s) and fast running (8.6 ± 1.9 trials, 4.6 ± 0.38 m/s). The locomotion speed was not controlled across trials and subjects, hence the substantial speed variability observed over the entire dataset.

Recordings of dynamic trials included the full gait stance phase of the subjects' right leg. Each subject had 27 retro-reflective markers placed on their lower extremities, pelvis, and trunk (Dempsey et al., 2009; Sartori et al., 2012b). Three-dimensional (3-D) marker locations were recorded at 250 Hz using a 12-camera Vicon MX Motion Analysis System (Oxford Metrics, Oxford, UK). The ground reaction forces (GRFs) and EMG data were recorded at 2,000 Hz using an in-ground force plate (AMTI, Watertown, MA) and a 16-channel acquisition system (Noraxon, Scottsdale, AZ), respectively. GRFs and marker trajectories were both low-pass filtered with the same zero-phase second-order Butterworth filter. Cut-off frequencies (between 8 and 14 Hz) were determined by a trial-specific residual analysis (Winter, 2009). The EMG data were collected from 13 leg muscles: tensor fascia latae, gracilis, lateral and medial hamstrings, rectus femoris, sartorius, vastus lateralis and medialis, gastrocnemius lateralis and medialis, soleus, peroneus group, and tibialis anterior. Raw EMG recordings were band-pass filtered (30–450 Hz), full-wave rectified, and low-pass filtered (6 Hz) using a zero-phase second-order Butterworth filter (Lloyd and Besier, 2003). For each subject and muscle, the resulting EMG linear envelopes were normalized with respect to the peak-processed values obtained from the entire set of recorded trials. We will refer to processed and normalized EMG signals as “excitations.” From the dynamic trials two distinct data sets were created. One was for the EMG-driven model calibration, which consisted of two walking and two running trials per subject. The second set was for the EMG-driven model test, which consisted of 5.8 ± 0.8 trials of walking and 6.6 ± 1.9 trials of running per subject.

Movement analysis.

Using the open-source software OpenSim (Delp et al., 2007), a 12-segment, 19 DOF, generic rigid-body model of the human skeletal geometry was scaled to match each individual subject's anthropometry (Sartori et al., 2012b). The scaling process used experimentally measured marker positions recorded from the static standing poses, and from the estimated location of the hip, knee, and ankle joint centers using functional trials (Besier et al., 2003b). In this procedure, virtual markers were created and placed on the generic rigid-body model on the basis of the position of the experimental markers. The rigid-body model anthropometric properties were linearly scaled on the basis of the relative distances between experimental and corresponding virtual markers (Delp et al., 2007). This adjusted anatomical segment length, width, depth, center of mass location, and mass moment of inertia. The OpenSim inverse kinematics (IK) algorithm solved for joint angles that minimized the least-squared error between experimental and virtual marker locations from the scaled rigid-body model (Lu and O'Connor, 1999). The IK-generated joint angles and the experimental GRFs were used to obtain joint moments via inverse dynamics (ID) and residual reduction analysis (RRA) using the scaled rigid-body model (Thelen and Anderson, 2006). This ensured the resulting joint moments and joint angles were dynamically consistent (Thelen and Anderson, 2006; Delp et al., 2007), thus addressing inverse dynamics uncertainties (Piovesan et al., 2011). The joint moments produced by this pathway were referred to as the experimental joint moments. The alternative pathway to estimate joint moments was by the use of calibrated, subject-specific, EMG-driven musculoskeletal model.

EMG-driven model-based estimation of MTU forces and joint moments.

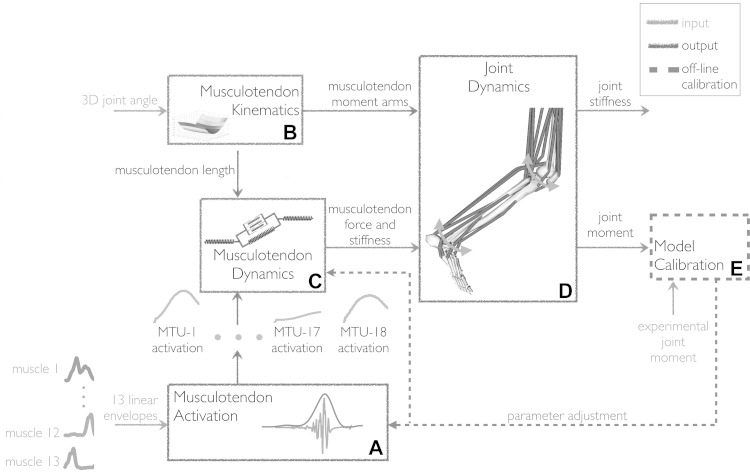
The EMG-driven model employed in this study was previously presented in details (Lloyd and Besier, 2003; Buchanan et al., 2004; Sartori et al., 2012b). The model structure (Fig. 1) is outlined below. It is composed of four main blocks, all of which are internally consistent (Lloyd and Besier, 2003; Sartori et al., 2014).

Fig. 1.

The schematic structure of the electromyography (EMG)-driven musculoskeletal model. It comprises five components: musculotendon activation, A; musculotendon kinematics B; musculotendon dynamics, C; joint dynamics, D; and model calibration, E. The EMG-driven model is initially calibrated (E) using experimental EMG-excitations, experimental three-dimensional (3-D) joint angles, and matching experimental joint moments from a set of calibration trials. After calibration, the model is operated in open-loop (i.e., it does not require experimental joint moments to track). The calibrated model is validated on its ability to blindly match experimental joint moments from a set of novel trials that were not used for calibration. The musculotendon activation component (A) maps initial EMG-excitations recorded from 13 muscle groups to activations for 18 musculotendon units (MTUs, Table 1). Subsequently, MTU force and stiffness are determined (C) as a function of muscle activation (A) and experimental 3-D musculotendon kinematics derived from experimental 3-D joint kinematics (B). The resulting MTU forces and stiffness are simultaneously projected (D) on two degrees of freedom including the knee flexion-extension and the ankle plantar-dorsi flexion.

The MTU activation block (Fig. 1A) receives excitations recorded from 13 muscle groups (see Data collection) and uses them to drive 18 MTUs (Table 1) (Sartori et al., 2012b). Experimental excitations are processed using an infinite impulsive response filter to model the twitch response of the muscle fibers to the excitation onset (Lloyd and Besier, 2003). These are further processed by a nonlinear transfer function to account for the nonlinearity in the excitation-to-force relationship and to determine the resulting muscle activation (Lloyd and Besier, 2003; Buchanan et al., 2004).

Table 1.

Electromyograms, musculotendon units, and moment arm sign

Experimental Muscle EMG	Musculotendon Unit*	Knee Flexion-Extension Moment Arm		Ankle Plantar-Dorsi-Flexion Moment Arm
		Positive	Negative	Positive	Negative
Tensor fasciae latae	Tfl	Knee extensor
Gracilis	Gra		Knee flexor
Lateral hamstring	Bicfemlh		Knee flexor
	Bicfemsh		Knee flexor
Medial hamstring	Semimem		Knee flexor
	Semiten		Knee flexor
Rectus femoris	Recfem	Knee extensor
Sartorius	Sar		Knee flexor
Vastus lateralis	Vaslat	Knee extensor
Vastus medialis	Vasmed	Knee extensor
(Vastus lateralis + vastus medialis)/2	Vasint	Knee extensor
Gastrocnemius lateralis	Gaslat		Knee flexor		Plantar flexor
Gastrocnemius medialis	Gasmed		Knee flexor		Plantar flexor
Soleus	Sol				Plantar flexor
Peroneus group	Perlong				Plantar flexor
	Perbrev				Plantar flexor
	Pertert			Dorsi flexor
Tibialis anterior	Tibant			Dorsi flexor

Muscle groups from which experimental electromyograms (EMG) were recorded and the associated musculotendon units (MTUs) that were driven by these EMGs. In this, the vastus intermedius EMG activity was derived as the mean between the vastus lateralis and vastus medialis EMGs (Lloyd and Besier, 2003). The biceps femoris long head and short head were driven by the same EMG signal. The same applied to the semimembranosus and semitendinosus as well as to the peroneus longus, brevis and tertius (Sartori et al., 2012b). The MTUs spanning a specific joint DOF were gathered into agonist and antagonist groups based on the moment arm sign observed during walking and running and using the moment arm sign convention from (Sartori et al., 2012).

^*Tfl, tensor fasciae latae; Gra, gracilis; Bicfemlh, biceps femoris long head; Bicfemsh, biceps femoris short head; Semimem, Semimembranosus; Semiten, semitendinosus, Recfem, rectus femoris; Sar, sartorius; Vaslat, vastus lateralis; Vasmed, vastus medialis; Vasint, vastus intermedius; Gaslat, gastrocnemius lateralis; Gasmed, gastrocnemius medialis; Sol, soleus; Perlong, peroneus longus; Perbrev, peroneus brevis; Pertert, peroneus tertius; Tibant, tibialis anterior.

The MTU kinematics block (Fig. 1B) employs a five-DOF, 18-MTU, generic model of the human muscle geometry (Sartori et al., 2012a). This is adjusted to match the dimensions of the scaled OpenSim rigid-body model used for the IK, ID, and RRA calculations (see Movement analysis). In this, each MTU's insertion, origin, and MTU-to-bone wrapping point is linearly scaled to remain in the same relative position with respect to the segment dimensions of the scaled rigid-body model. The MTUs in the muscle geometry model span five kinematic DOFs including hip adduction-abduction, hip internal-external rotation, hip flexion-extension, knee flexion-extension, and ankle plantar-dorsi flexion. The IK-generated angles about these five DOFs directly inform the MTU kinematics block, which computes instantaneous MTU length, ℓ^mt; velocity, v^mt; and moment arms, r (Sartori et al., 2012a). In this, a multidimensional cubic B-spline function is created for each MTU and is used to represent how MTU length, velocity, and moment arms change vs. IK-generated joint angles as discussed in our previous work (Sartori et al., 2012a).

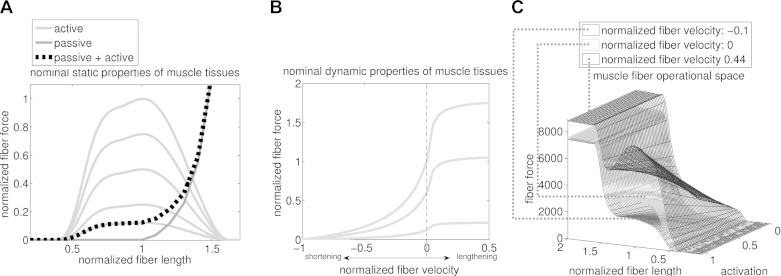
The MTU dynamics block (Fig. 1C) takes as its input MTU activation, a(t); and ℓ^mt and v^mt from the previous blocks. It uses a Hill-type muscle model to estimate instantaneous length, contraction velocity, and force in the muscle fibers, and strain and force in the series-elastic tendon within each MTU (Lloyd and Besier, 2003; Buchanan et al., 2004; Winby et al., 2009; Sartori et al., 2012b). The static properties of fibers are modeled using parallel force-length passive f_p(l̃^m) and activation-dependent f_A(l̃^m) curves (Fig. 2A) (Lloyd and Besier, 2003). The dynamic properties of fibers are modeled using an activation-dependent force-velocity f(ṽ^m) curve (Fig. 2B), which includes a passive parallel damping element to prevent any singularities of the mass-less model when activation or isometric force are zero (Schutte et al., 1993; Lloyd and Besier, 2003). These curves are normalized to maximum isometric muscle force (F^max), whereas l̃^m and ṽ^m represent fiber length and velocity normalized to optimal fiber length, l_o^m, and maximum muscle contraction velocity, respectively (Zajac, 1989). The coupling between l_o^m and a(t) is incorporated as described by Lloyd and Besier (2003). The tendon properties are modeled using a force-strain function, f(ε), with nonlinear toe region normalized to F^max (Zajac, 1989). The total MTU force, F^MTU, is calculated as a function of a(t) normalized fiber length, l^m, and contraction velocity, ṽ^m:

$$F^{MTU}=F^t=F^m\cos (\varphi (l^m))=\lfloor a(t)f({\tilde{l}}^m)f({\tilde{v}}^m)+f_P({\tilde{l}}^m)\rfloor F^{\max }\cos (\varphi (l^m))$$ (1)

where F^t and F^m are the tendon and fiber force, respectively. The ϕ(l^m) term represents the pennation angle, which changes with instantaneous fiber length assuming the muscle belly had a constant thickness and volume (Scott and Winter, 1991). At each time frame, fiber length, l̃^m; velocity, ṽ^m; and tendon strain, ε; are determined so to guarantee the equilibrium between F^m and F^t in Equation 1. This occurs using a Wijngaarden-Dekker-Brent optimization routine (Brent, 1973), which finds the root of the equilibrium between the muscle fibers and the tendon forces.

Fig. 2.

A: nominal static properties of muscle tissues. These are determined by the active and passive isometric force-length curves. Fiber force and length values are normalized by the maximal isometric force, F^max, and optimal fiber length, l_o^m, respectively. B: nominal dynamic properties of muscle tissues. These are determined by the active force-velocity curve. Fiber force and contraction velocity values are normalized by the F^max and maximal contraction velocity, v^max, respectively. Both active force-length and force-velocity curves are depicted for different levels of muscle activation. C: solution space of the fiber force. This results from combining passive and active force-length and force-velocity curves. Note how muscle force is modulated simultaneously by activation, fiber length, and contraction velocity.

The joint dynamics block (Fig. 1D) computes joint moments about the knee flexion-extension and ankle plantar-dorsi flexion DOFs as the product of each MTU force (Equation 1) and their associated moment arms from the MTU kinematics block (Lloyd and Besier, 2003; Sartori et al., 2012b, 2013).

The model calibration block (Fig. 1E) determines subject-specific parameters for the EMG-driven model as described extensively previously (Sartori et al., 2012b, 2013). Very briefly, calibrated parameters in the MTU activation block (Fig. 1A) include two MTU-specific excitation-to-activation filtering coefficients, which are varied between ±1 to realize a stable positive solution and a critically damped impulsive response for the EMG-excitation recursive filter (Lloyd and Besier, 2003), and one MTU-specific shape factor parameter that is altered between −3 and 0 to account for the nonlinear EMG-to-force relationship (Lloyd and Besier, 2003; Buchanan et al., 2004). In the MTU dynamics block (Fig. 1C), MTU strength coefficients, γ, adjust MTU-specific nominal F^max to match the person's strength (i.e., F^max = γ·nomial F^max). Strength coefficients are varied between 0.5 ≤ γ ≤ 1.5 and gather MTUs in seven groups according to their functional action, including uniarticular knee flexors, uniarticular knee extensors, uniarticular ankle plantar flexors, uniarticular ankle dorsi flexors, biarticular knee extensors, biarticular knee flexors, and biarticular calf muscles. The nominal F^max for MTUs within the same group are scaled by the same γ coefficient. The nominal F^max values are taken from Yamaguchi et al. (1990). Muscle tendon slack length, l_s^t, and optimal fiber length, l_o^m, are adjusted so that l_s^t = initial value ±5% and l_o^m = initial value ±2.5% with initial values obtained using the methodology presented in Winby et al. (2008) that accounts for how l_s^t and l_o^m vary nonlinearly with an individual's anthropometry. A simulated annealing algorithm (Goffe et al., 1994) varies the parameters within the predefined boundaries to minimize the sum of the mean square differences between the predicted and experimental joint moments calculated over the two DOFs and the four calibration trials (see Data collection) recorded for a specific subject (Sartori et al., 2012b, 2013, 2014). In this, the mean square differences relative to one specific joint DOF are normalized by the reference DOF-moments variance (Lloyd et al., 2008; Winby et al., 2009). We do this to prevent inadvertently assigning greater emphasis to longer trials with higher joint moment values and assure that error terms across all DOFs are equally minimized. Moreover, the objective function also includes a penalty factor that penalizes instances of normalized fiber length being less than 0.5 or greater than 1.5, thus operating outside physiological ranges (Lloyd and Besier, 2003). After calibration, the model is validated on its ability to blindly match experimental ankle and knee joint moments during novel validation trials that are not used for calibration (see Data collection). During the validation step, optimization is no longer used, with joint moments and stiffness being blindly predicted as a function of EMG signals and joint angles. Therefore, the calibrated model operates according to an open-loop paradigm.

EMG-driven model-based estimation of MTU and joint stiffness.

The calibrated, subject-specific EMG-driven model (Fig. 1) is used to estimate instantaneous stiffness in 18 leg MTUs (Table 1). The MTU-specific stiffness is then projected to the joint level to derive the resulting stiffness about two DOFs (i.e., knee flexion-extension and ankle plantar-dorsi flexion). The net stiffness about a joint DOF, K^DOF, is determined as:

$$K^{DOF}={\displaystyle \sum }_{i=1}^{\#MTU}{K}_i^{MTU}\cdot r_i^2+\frac{\partial r_i}{\partial {\theta }^{DOF}}\cdot F_i^{MTU}$$ (2)

where K_i^MTU and r_i, respectively, represent the stiffness and moment arm of the i^th MTU spanning the specific DOF, whereas θ^DOF is the joint angle about the specific DOF, as previously described (McIntyre et al., 1996; Hu et al., 2011; Pfeifer et al., 2012). The moment arm partial derivative $\frac{{\partial r}_i}{{\partial \theta }^{DOF}}$ in Equation 2 is calculated by creating a cubic B-spline function per MTU (Sartori et al., 2012a). The MTU-specific spline represents how r changes with respect to θ^DOF (i.e,. $\forall$ DOFs∈ MTU). The nominal data (i.e., θ^DOF and r, $\forall$ DOFs∈ MTU) needed to compute the spline coefficients are created using the MTU kinematics block (Fig. 1B) and by sampling each DOF range of motion in 100 equidistant values. The K^DOF term represents the instantaneous torque response about a joint-DOF, for every degree of perturbation, from its current angular position, θ^DOF.

The total stiffness K_i^MTU in each MTU is modeled as muscle fiber stiffness K^m in series with tendon stiffness K^t (Latash and Zatsiorsky, 1993; Cui et al., 2008; Pfeifer et al., 2012):

$$K^{MTU}={\left(\frac{1}{K^m}+\frac{1}{K^t}\right)}^{-1}$$ (3)

Tendon stiffness, K^t, is estimated from the slope of the nonlinear force-strain relationship, f(ε), in the correspondence of the instantaneous tendon strain value, ε. Muscle fiber stiffness, K^m, is calculated as the partial derivative of fiber force, F^m (Equation 1), with respect to the normalized fiber length, l̃^m:

$$K^m=\frac{\partial F^m(a,{\tilde{l}}^m,{\tilde{v}}^m)}{\partial {\tilde{l}}^m}$$ (4)

The partial derivative in Equation 4 is calculated by creating a multidimensional cubic spline function per muscle (Sartori et al., 2012a). The muscle-specific spline describes how F^m changes simultaneously with respect to its states, which include activation, a; normalized fiber length, l̃^m; and normalized fiber velocity, ṽ^m (Fig. 2C). The nominal data (i.e., a, l̃^m, ṽ^m, and F^m) needed to compute the spline coefficients are generated using the subject-specific EMG-driven model (Sartori et al., 2012a,b). Nominal data are chosen so that they sample the entire F^m solution space (i.e., 0 < a < 1, 0 < l̃^m < 2, and −1 < ṽ^m < 1, with the same sample step = 0.05 for all three variables). In this context, K^m (i.e., Equation 4) is the directional derivative computed from the force-length-velocity-activation surface (Fig. 2C) along the normalized fiber length directional axis, for given instantaneous states (a, l̃^m, ṽ^m) and corresponding force level, F^m.

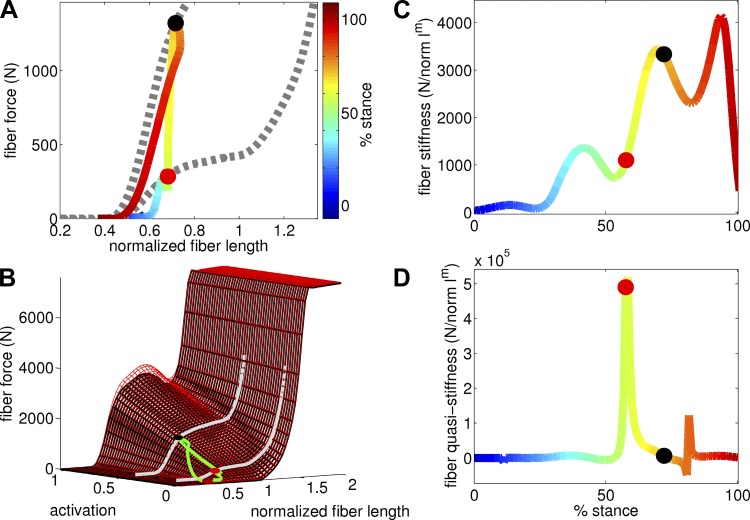
This is further exemplified in Fig. 3, A and B. These depict the soleus fiber force-length profile throughout the stance phase of walking for one subject. Figure 3B also shows the force-length profile projected on the force-length-velocity-activation surface (Equations 1–4). As the stance phase progresses, the triplet (a, l̃^m, ṽ^m) is modulated dynamically and contributes to define instantaneous F^m points that lay both on the force-length profile and on the force-length-velocity-activation surface. [See the two points at 57.6% and 72% stance (the red dot and black dot, respectively), in Fig. 3, A and B.] Note how these two points lay on the same force-length profile (Fig. 3A) but on two different surfaces (Fig. 3B), each of which is relative to a different instantaneous ṽ^m value. The instantaneous stiffness in a point of the gait cycle is calculated from the slope of the surface cross-section along the l̃^m-axis (see dotted lines in Fig. 3A). The surface cross section is modulated as a function of a and ṽ^m, and the force slope (i.e., stiffness) is computed in the correspondence of the current l̃^m value (Fig. 3, A and B).

Fig. 3.

A: Profile of the fiber force-length of the soleus muscle over the stance phase of walking (i.e., see continuous colored workloop) with 0% being heel-strike and 100% toe-off events. Two cross-sections of the force-length-velocity-activation solution space along the fiber length axis are depicted in the correspondence of 57.6% stance (red dot) and 72% (black dot) respectively (i.e., see dotted lines). In these two stance points, the respective cross-sections differ with that of each other because they underlie different muscle activations, fiber lengths, and contraction velocities. Furthermore, note how in a specific stance point, the slope derived from the fiber force-length profile differs substantially from that derived from the force-length-velocity-activation cross section. B: force solution surfaces of the soleus muscles in the correspondence of 57.6% stance (red 3-D surface and red dot) and 72% (black 3-D surface and black dot). The fiber force-length profile of soleus muscles (i.e., green work loop) throughout the stance phase of walking (as in A) is also projected on the muscle force solution spaces. C: instantaneous stiffness of soleus (K^m, Equation 4) throughout the stance phase of walking. This is predicted from the slope of the fiber force-length-velocity-activation surface in B as the slope along the normalized fiber length directional axis in the correspondence of the instant normalized fiber length predicted by our EMG-driven method (also see materials and methods). D: instantaneous quasi-stiffness (QS, Equation 6) of soleus throughout the stance phase of walking. This is predicted from the tangent of the fiber force-length profile in A. Note how stiffness and QS can predict substantially different slopes in the correspondence of the same stance point. QS relates changes in fiber force with changes in fiber length without accounting for the fact that force may be instead varying because of the activation or contraction velocity components, hence the peaks in (B) relative to the steep tangents in (A). The reported data are relative to subject 1 and are calculated as a function of normalized fiber length and contraction velocity values. Also see Supplemental Video S1.

This formulation properly accounts for changes in fiber force, F^m, that occur due to rapid, dynamic changes in fiber length for given instantaneous values of contraction velocity and activation (Figs. 2 and 3). Note that this is different than simply estimating the slope on the isometric force-length relationship f_A(l̃^m) + f_P(l̃^m) in Fig. 2A. This would describe only the “static state” of muscle fibers, as previously discussed (Hu et al., 2011) (i.e., the isometric force that muscle fibers can generate at a specific length and activation). Our proposed modeling methodology also accounts for the “dynamic state” of the muscle fibers, which also depends on the contraction velocity of the fibers, ṽ^m, and activation, as shown in Equations 1–4 and Fig. 2, B and C. Furthermore, it accounts for how fibers interact with the series-elastic tendon. In this scenario, the ability to drive each individual MTU as a function of experimental EMG-excitations is crucial to properly account for physiological co-contraction strategies in agonist and antagonist MTUs during dynamic motor tasks.

Relation to QS and SRS.

QS is used to estimate joint stiffness properties throughout entire gait phases during dynamic locomotion (Stefanyshyn and Nigg, 1998; Coyles et al., 2011; Charalambous et al., 2012; Shamaei et al., 2013a,b,c). It reflects a fundamentally different physical variable with respect to the instantaneous stiffness discussed in the present study (i.e., Equations 2–4) (Latash and Zatsiorsky, 1993; Rouse et al., 2013). At the muscle fiber level, QS can be derived from the slope of the force-length curve over time (Fig. 3A). Mathematically, this represents the ratio between the total differential of the fiber force function [i.e., dF^m(a,l̃^m, ṽ^m)] and the differential of fiber length (dl̃^m) over time. The total differential of fiber force is reported below:

$$d{F}^m(a,{\tilde{l}}^m,{\tilde{v}}^m)=\frac{\partial F(a,{\tilde{l}}^m,{\tilde{v}}^m)}{\partial a}da+\frac{\partial F(a,{\tilde{l}}^m,{\tilde{v}}^m)}{\partial {\tilde{l}}^m}d{\tilde{l}}^m+\frac{\partial F(a,{\tilde{l}}^m,{\tilde{v}}^m)}{\partial {\tilde{v}}^m}d{\tilde{v}}^m$$ (5)

By dividing Equation 5 with respect to dl̃^m and by substituting Equation 4 (i.e., K^m) into it, we derive a compact mathematical formalization of QS:

$$QS(t,dt)=\frac{\partial F(a,{\tilde{l}}^m,{\tilde{v}}^m)}{\partial a}\frac{da}{d{\tilde{l}}^m}+K^m+\frac{\partial F(a,{\tilde{l}}^m,{\tilde{v}}^m)}{\partial {\tilde{v}}^m}\frac{d{\tilde{v}}^m}{d{\tilde{l}}^m}=A(t,dt)+K^m(t)+V(t,dt)$$ (6)

showing that muscle fiber QS does not solely represent changes in muscle force due to changes in fiber length [i.e., the muscle fiber stiffness term K^m(t) in Equation 4] but also incorporates terms that vary with the activation [i.e., A(t, dt)] and contraction velocity [i.e., V(t, dt)] differentials as well as with the time interval, dt, used to compute the slope on the force-length curve. At the joint level, QS is biased by all these terms for all MTUs spanning that joint.

SRS reflects the intrinsic stiffness of the myofilaments of the fibers when contractile fibers are stretched within a 3% of their length (Walmsley and Proske, 1981). This can be estimated using the model developed by Cui et al. (2008) for muscles in the cat hindlimb:

$$SRS=\gamma \frac{F^m}{l_O^m}$$ (7)

where γ = 23.4 is a dimensionless scaling constant (Cui et al., 2008), whereas l_o^m is the optimal fiber length. This formulation was subsequently used in conjunction with human musculoskeletal models to study isometric joint stiffness in the arm and knee joint (Hu et al., 2011; Pfeifer et al., 2012). In Equation 7, SRS is proportional to muscle fiber force and is invariant to changes in fiber length and contraction velocity. SRS well describes the isometric characteristics of muscle stiffness but would overestimate them in dynamic conditions, as previously discussed (Walmsley and Proske, 1981; Campbell and Moss, 2000; Cui et al., 2007, 2008; de Vlugt et al., 2011; Hu et al., 2011).

Validation procedures and analyses.

After scaling and calibrating the EMG-driven model to each individual subject, it was examined in a series of validation tests. The first test assessed the subject-specific EMG-driven model's ability to blindly predict dynamically consistent joint moments, from experimental excitations, about the knee flexion-extension and ankle plantar-dorsi flexion DOFs and across the 12.4 ± 2.6 validation trials performed by each of the five subjects (i.e., 62 validation trials across all subjects). Therefore, across all validation trials the model was validated on 124 estimations (i.e., 62 trials and two degrees of freedom).

The second test analyzed the muscle and joint stiffness underlying the dynamically consistent EMG-driven simulations of walking and running for all subjects. The contribution of each MTU to the net stiffness about a specific joint DOF was determined by means of the variability accounted for (VAF) index (d'Avella et al., 2003; Ivanenko et al., 2006; Sartori et al., 2013):

$$VA{F}_{DOF}^{MTU}=1-\frac{{\displaystyle \sum }_{s=0\%}^{100\%}{(K{(s)}^{DOF}-K{(s)}_{MTU}^{DOF})}^2}{{\displaystyle \sum }_{s=0\%}^{100\%}{(K{(s)}^{DOF})}^2}$$ (8)

where K_MTU^DOF is the single MTU stiffness projected on the specific DOF using Equation 2, whereas s represents a stance phase point.

The third test assessed the co-contraction ratio (CCR) between agonist and antagonist muscles spanning a joint DOF (Lloyd and Buchanan, 2001):

$$\{\begin{array}{lll}CCR(t)\hspace{0.17em}=\hfill & \frac{EMG{(t)}_{antagonist}}{EMG{(t)}_{agonist}}-1,\hfill & if\hspace{0.17em}EMG{(t)}_{antagonist}<EMG{(t)}_{agonist}\hfill \\ CCR(t)\hspace{0.17em}=\hfill & 1-\frac{EMG{(t)}_{agonist}}{EMG{(t)}_{antagonist}},\hfill & \hspace{0.17em}otherwise\hfill \end{array}$$ (9)

where EMG(t)_agonist and EMG(t)_antagonist, respectively, represent the average across all agonist and antagonist muscle excitations at time instant, t. The CCR index varies between −1 (i.e., reflecting solely agonist excitation) and 1 (i.e., reflecting solely antagonist excitation), with 0 reflecting a balanced contribution between agonist and antagonist muscle excitation. The MTUs spanning a specific joint DOF were gathered between agonist and antagonist groups on the basis of the moment arm sign throughout specific joint DOF range of motion observed during walking and running (Table 1).

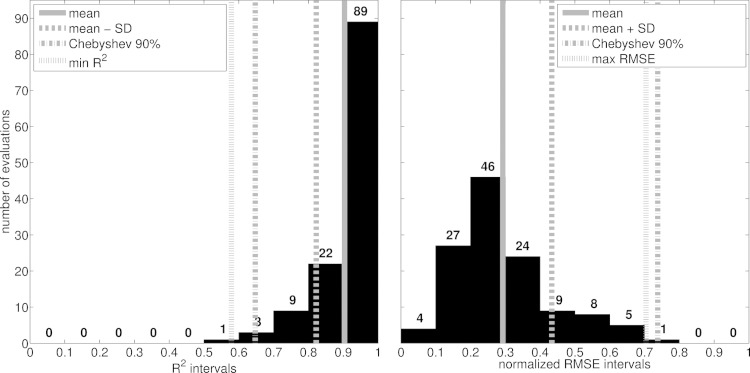
Across the validation tests and analyses, all EMG-driven model estimates were time-normalized to 100 samples using cubic splines. Experimental and predicted joint moments were further normalized to a subject's body mass. Similarity between predicted and experimental quantities (i.e., joint moments and stiffness) was calculated using the coefficient of determination (R², square of the Pearson product moment correlation coefficient) and the root mean squared error normalized with respect to the root mean squared sum of the corresponding experimental quantity (NRMSE). The 90% confidence interval was estimated for R² and NRMSE using the Chebyshev's theorem (i.e., expected interval = mean ± 3.16·std). This could be applied with no assumption on the normality of R² and NRMSE distributions (Fig. 6).

Fig. 6.

Distribution of the similarity indexes computed between experimental and predicted joint moments from all validation trials and subjects. Similarity indexes include the coefficient of determination (R²) and the root mean square error normalized to the root mean square sum of the experimental joint moments (RMSE). Histograms gather the R² and RMSE values in intervals with a 0.1-fixed-width in the (zero-to-1) range. In this range, vertical lines highlight a number of variables including the average indexes (i.e., mean) and those within one standard deviation (i.e., SD), the maximum expected RMSE and the minimum expected R² calculated using the Chebyshev's theorem assuming a 90% confidence interval (i.e., Chebyshev 90%), as well as the most unfavorable index values including R² = 0.58 (i.e., min R²) and RMSE = 0.704 (i.e., max RMSE).

RESULTS

We first provide representative comparisons between our proposed instantaneous stiffness estimates (Equations 2–4) and those derived from QS (Equations 5–6) and SRS (Equation 7), respectively. These representative comparisons are used to further illustrate the conceptual differences between stiffness estimation methods. We then report quantitative results across the tests in Validation procedures and analyses. Finally, we compare our results with those available from the literature.

Figure 3A shows how the soleus force slope (i.e., stiffness) in the correspondence of a specific stance point of walking (i.e., 57.6% and 72% stances, respectively) can substantially differ when estimated directly from the force-length profile (i.e., see the continuous workloop profile, QS) or from the force-length-velocity-activation surface cross section (i.e., see the dotted gray line, K^m). Instantaneous stiffness throughout the stance phase is reported in Fig. 3C (i.e., K^m) and 3D (i.e., QS). This further illustrates how differences between instantaneous estimates of K^m and QS can be of several orders of magnitude even at the single muscle level (also see Supplemental Video S1, available in the data supplement online at the Journal of Neurophysiology Web site). The force-length profile (Fig. 3A) from which QS is derived, directly relates changes in F^m with changes in l̃^m without accounting for the fact that F^m may be instead varying because of a and ṽ^m. In this, the chosen time interval, dt, from which we compute QS, impacts the final stiffness estimate (Equation 6). Short intervals are most affected by the instantaneous peaks depicted in Fig. 3D. These peaks directly relate to the activation and contraction velocity differentials (Equation 6), which make fiber force vary with no underlying changes in fiber length, hence the vertical tangent on the force-length profile as depicted in Fig. 3, A and B in the correspondence of the point at 57.6% stance. In these conditions, QS estimates do not reflect changes in muscle force due to changes in fiber length, thus biasing the final stiffness result.

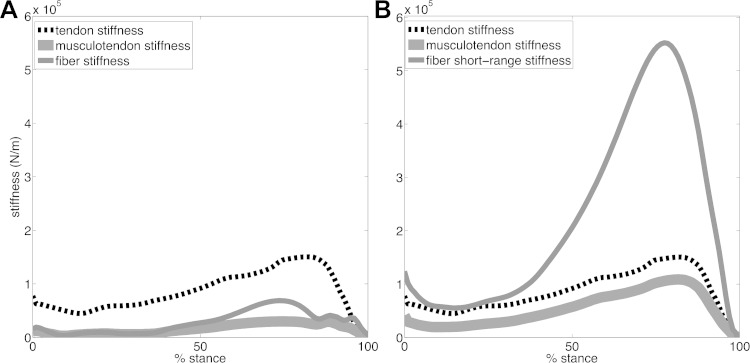
Figure 4 shows the gastrocnemius medialis MTU stiffness and how this delineates into individual tendon and fibers stiffness (i.e., using our proposed K^m and SRS, respectively). Reported stiffness curves are averaged across all walking trials performed by all subjects. Figure 4A shows that our proposed method (K^m, Equation 4) results in fibers that are more compliant than the series elastic tendon, thus dominating the resulting MTU stiffness as previously reported in experimental and theoretical studies (Walmsley and Proske, 1981; Zajac, 1989; Latash and Zatsiorsky, 1993; Cook and McDonagh, 1996; Endo and Herr, 2014). Notably, the peaks in the tendon stiffness of the gastrocnemius medialis predicted by our proposed method (i.e., 160 ± 69 N/mm, Fig. 4A) are within literature values available for this muscle (Lichtwark and Wilson, 2005, 2008; Krishnaswamy et al., 2011). In this context, the tendon stiffness in the linear region of the force-strain relationship was investigated for the gastrocnemius medialis in relation to MTU efficiency during the stance phase of walking. Optimal tendon stiffness for the gastrocnemius medialis was found to be 144 N/mm as reported by Lichtwark and Wilson (2008), and ranged between 103 N/mm and 150 N/mm as reported by Krishnaswamy et al. (2011). Experimental studies found in vivo gastrocnemius tendon stiffness in the range of 174 ± 38 N/mm (Maganaris and Paul, 2002; Lichtwark and Wilson, 2005). Conversely, SRS (Equation 7) resulted in gastrocnemius medialis fibers being substantially stiffer than the series elastic tendon (Fig. 4B), which does not represent physiological MTU behavior (Walmsley and Proske, 1981; Latash and Zatsiorsky, 1993; Lichtwark and Wilson, 2008; Endo and Herr, 2014).

Fig. 4.

A: stiffness predicted by our proposed method (Equation 4) for fibers of the gastrocnemius medialis, tendon, and musculotendon unit. B: short-range stiffness (Equation 7) predicted for fibers of the gastrocnemius medialis, as well as tendon stiffness and resulting musculotendon unit stiffness. Values are averaged across all walking trials performed by all subjects and are reported throughout the stance phase of walking with 0% being heel-strike and 100% being toe-off events.

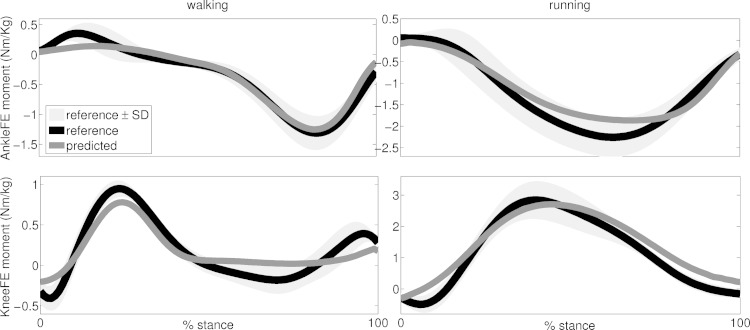
In the first test described in the Validation procedures and analyses section, the subject-specific EMG-driven model predicted joint moments that matched the experimental moments across all 124 performed estimations (i.e., 62 validation trials of walking and running from all 5 subjects) from which joint moments were estimated about two DOFs: the knee flexion extension and the ankle plantar-dorsi flexion (Fig. 5). The similarity indexes ranged between 0.1 ≤ NRMSE ≤ 0.7 and 0.57 ≤ R² ≤ 0.99 (Fig. 6). Of all 124 performed estimations, 77% had R² >0.9 and NRMSEs <0.3, across all tasks, subjects, and DOFs (Fig. 6). The average values were distributed toward low NRMSEs (i.e., 0.29 ± 0.14) and high R² (i.e., 0.9 ± 0.08) values (Fig. 6).

Fig. 5.

Predicted and experimental joint moments from all validation trials and subjects. The ensemble average (continuous lines) curves are depicted for experimental and predicted joint moments. The standard deviations (shaded area) are also depicted for the experimental joint moments. Experimental and predicted joint moments are reported about two degrees of freedom including knee flexion-extension (KneeFE) and ankle plantar-dorsi flexion (AnkleFE). The reported data are from the stance phase with 0% being heel-strike and 100% being toe-off events.

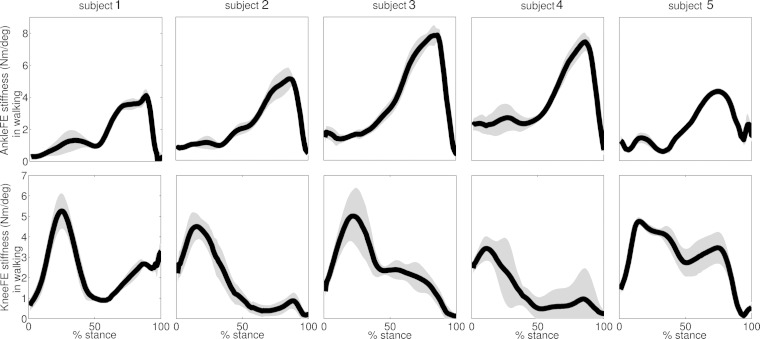
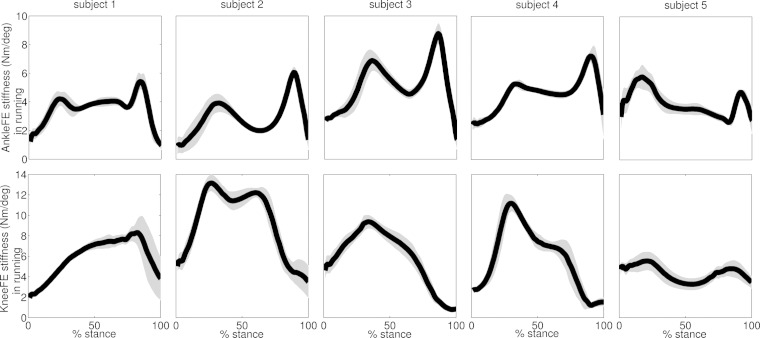
The second test revealed distinct stiffness mechanisms across joints and motor tasks, which were consistent across subjects (Figs. 7–9). Across all performed trials and subjects, walking was characterized by a knee stiffness peak (i.e., 4.8 ± 1.1 Nm/deg) occurring at 19.3 ± 6.5% stance, followed by a higher and minimally overlapped ankle stiffness peak (i.e., 5.9 ± 1.8 Nm/deg) at 83.9 ± 5.4% stance (Fig. 7). Running displayed different stiffness mechanisms with respect to walking (Fig. 8). It was characterized by double-peak stiffness curves both at the ankle and knee, with levels of synchronization across joints. The ankle stiffness first peak (i.e., 5.5 ± 1.3 Nm/deg) occurred at 27.8 ± 10.7% stance, whereas the second peak (i.e., 6.5 ± 1.6 Nm/deg) occurred at 89.4 ± 3.1% stance. Knee stiffness had two pronounced peaks in subjects 2 and 5. The first peak (8.7 ± 3.8 Nm/deg) occurred at 20.3 ± 8.1% stance and a second peak (i.e., 7.9 ± 3.9 Nm/deg) at 74.1 ± 11.7% stance. Subjects 1, 3, and 4 generated knee stiffness with a single pronounced peak. Subject 1 had a peak of 8.9 ± 1.3 Nm/deg occurring at 84.7 ± 5.1%. Subjects 3 and 4 had peaks of 10.2 ± 1.3 Nm/deg occurring at 32 ± 7.4% stance.

Fig. 7.

The ensemble average curves (continuous line) and standard deviation (shaded area) for the stiffness predicted about two degrees of freedom including ankle plantar-dorsi flexion (AnkleFE) and knee flexion-extension (KneeFE) during walking across all validation trials and subjects. Data are reported for the stance phase of walking with 0% being heel-strike and 100% being toe-off events.

Fig. 9.

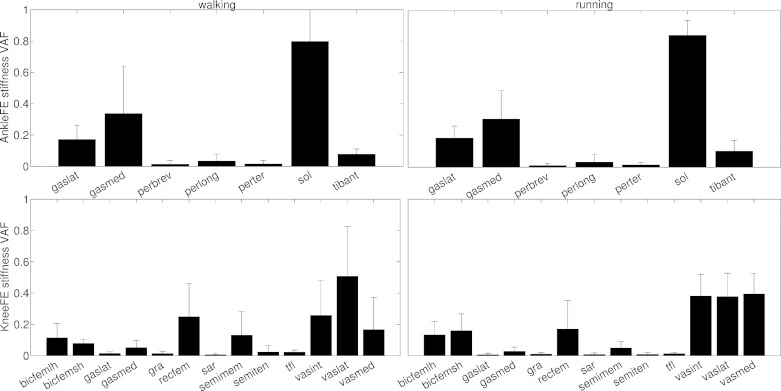
Variability accounted for (VAF) by all 18 musculotendon units in the model in the net joint stiffness about two degrees of freedom including ankle plantar-dorsi flexion (AnkleFE) and knee flexion-extension (KneeFE). VAF values are averaged from all performed trials and subjects (black bar) and are reported together with the standard deviation (vertical line).

Fig. 8.

The ensemble average curves (continuous line) and standard deviation (shaded area) for the stiffness predicted about two degrees of freedom including ankle plantar-dorsi flexion (AnkleFE) and knee flexion-extension (KneeFE) during running across all validation trials and subjects. Data are reported for the stance phase of running with 0% being heel-strike and 100% being toe-off events.

The joint moment and stiffness predicted by our proposed method resulted from muscles operating on the ascending portion of the force-length-velocity-activation surface (Table 2, Fig. 3, and Supplemental Video S1) across all trials and subjects. The muscles that accounted for most of the ankle stiffness variability (i.e., VAF index in Equation 8, Fig. 9) were the plantar flexors including the soleus (VAF_walking = 0.79 ± 0.2 and VAF_running = 0.84 ± 0.1), the gastrocnemius medialis (VAF_walking = 0.34 ± 0.3 and VAF_running = 0.31 ± 0.2) and the gastrocnemius lateralis (VAF_walking = 0.17 ± 0.1 and VAF_running = 0.19 ± 0.1) with peroneus brevis and longus displaying negligible values (i.e., VAF_{walking/running} ≤0.05). Small VAFs were observed in the dorsi flexors including tibialis anterior (i.e., VAF_{walking/running} = 0.09 ± 0.05) and peroneus tertius (i.e., VAF_{walking/running} ≤0.03). Unlike for the ankle, the muscles that accounted for most of the knee stiffness variability were apportioned between the extensors and the antagonist flexors groups (Fig. 9). Extensor muscles included the vastus medialis (i.e., VAF_walking = 0.19 ± 0.2 and VAF_running = 0.36 ± 0.1), intermedius (i.e., VAF_walking = 0.28 ± 0.2 and VAF_running = 0.35 ± 0.1), lateralis (i.e., VAF_walking = 0.47 ± 0.3 and VAF_running = 0.4 ± 0.2), and the rectus femoris (i.e., VAF_walking = 0.26 ± 0.2 and VAF_running = 0.2 ± 0.2) with negligible contribution coming from the tensor fasciae latae (i.e., VAF_{walking/running} = 0.01 ± 0.01). Flexor muscles included the medial hamstrings (i.e., cumulative VAF_walking = 0.14 ± 0.2 and VAF_running = 0.04 ± 0.04) and lateral hamstrings (i.e., cumulative VAF_walking = 0.19 ± 0.1 and VAF_running = 0.3 ± 0.1) with negligible contributions from the gastrocnemii (i.e., cumulative VAF_{walking/running} = 0.05 ± 0.04), sartorius (i.e., VAF_{walking/running} = 0.01 ± 0.01) and gracilis (i.e., VAF_{walking/running} = 0.01 ± 0.01).

Table 2.

Normalized muscle fiber lengths

	Bicfemlh	Bicfemsh	Gaslat	Gasmed	Gra	Perbrev	Perlong	Pertert	Recfem	Sar	Semimem	Semiten	Sol	Tfl	Tibant	Vasint	Vaslat
WK	0.5 (0.1)	0.72 (0.1)	0.9 (0.1)	0.89 (0.2)	0.61 (0.1)	0.66 (0.1)	0.61 (0.1)	1.12 (0.1)	0.69 (0.1)	0.85 (0.1)	0.38 (0.1)	0.57 (0.1)	0.62 (0.1)	1.23 (0.1)	0.9 (0.1)	0.43 (0.1)	0.51 (0.1)
RN	0.55 (0.1)	0.71 (0.1)	0.88 (0.1)	0.79 (0.2)	0.59 (0.1)	0.7 (0.1)	0.65 (0.1)	1.1 (0.1)	0.76 (0.1)	0.84 (0.1)	0.39 (0.1)	0.58 (0.1)	0.7 (0.1)	1.22 (0.1)	0.84 (0.1)	0.63 (0.1)	0.72 (0.1)

Normalized fiber length for all 18 musculotendon units in the model.

Data reported in this table are mean (SD) values averaged across all trials and subjects within each motor task, which included walking (WK) and running (RN). Musculotendon unit names are defined in Table 1.

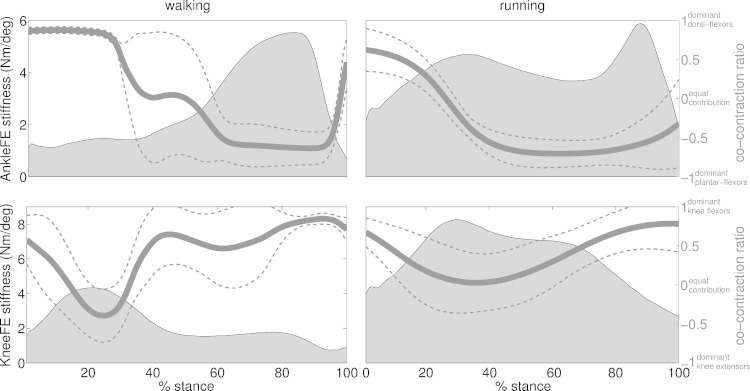
The third test revealed that joint stiffness emerged from substantial modulation of the underlying co-contraction ratios (CCRs, Equation 9) of the muscles across all performed trials and subjects (Fig. 10). In the early stance of walking (i.e., 0% ≤ stance ≤ 25%), the knee stiffness peak underlay muscle activity that shifted from dominant knee flexors (i.e., CCR = 0.62 ± 0.2 at 0% stance) to lesser dominant knee extensors (i.e., CCR = −0.4 ± 0.3 at 25% stance). This enabled shock absorption and weight acceptance functions predominantly at the knee joint with low ankle joint stiffness corresponding to dominant dorsi flexors activity (i.e., CCR = 0.86 ± 0.01 between 0% ≤ stance ≤ 25%). Throughout the midstance (i.e., 25% ≤ stance ≤ 85%), ankle stiffness increased as a function of dominant plantar flexors activity (i.e., CCR = −0.63 ± 0.2 at 85% stance), whereas knee stiffness decreased as a function of dominant knee flexors activity (i.e., CCR = 0.6 ± 0.1 between 45% ≤ stance ≤ 85%). This corresponded to foot push-off and body propulsion with production of joint moment (Fig. 5) and stiffness (Fig. 10) mainly at the ankle joint. In the terminal stance (i.e., stance ≥85%), both ankle and knee stiffness reached their lowest values in the correspondence of dominant dorsi flexors (CCR = 0.6 ± 0.2 at 100% stance) and knee flexors activity (CCR = 0.65 ± 0.2 at 100% stance), in preparation for the swing phase.

Fig. 10.

Ensemble average joint stiffness (shaded area) and co-contraction ratio (solid line). Data are averaged across all trials performed by all subjects across walking and running trials, respectively. Standard deviation curves are also reported relative to the co-contraction ratio (dotted lines). Data are reported about the ankle plantar-dorsi flexion (AnkleFE) and knee flexion-extension (KneeFE) degrees of freedom and throughout the stance phase with 0% being heel-strike and 100% being toe-off events.

In the early stance of running (i.e., 0% ≤ stance ≤ 30%) the synchronized stiffness peaks in the ankle and knee joints, indicated highly balanced (i.e., CCR ≈0) CCRs between agonist and antagonist muscles [i.e., CCR_knee = 0.02 ± 0.2 and CCR_ankle = −0.15 ± 0.1 at 30% stance (Fig. 10)]. This enabled shock absorption and weight acceptance functions both at the knee and ankle joints. Throughout the midstance (30% ≤ stance ≤ 65%), muscle activity transitioned toward dominant ankle plantar flexors (CCR = −0.6 ± 0.1), with a resulting sharp drop in ankle stiffness, whereas co-contraction remained balanced at the knee joint (CCR = 0.14 ± 0.1) with no substantial drop in joint stiffness. In the terminal stance (i.e., stance ≥65%), the second ankle stiffness peak corresponded to dominant plantar-flexor activity transitioning toward ankle dorsi flexors in the terminal stance (CCR = −0.18 ± 0.5 at 100% stance). In this phase, knee joint stiffness dropped substantially as a result of dominant knee flexors activity (CCR = 0.66 ± 0.1) in preparation for the swing phase.

DISCUSSION

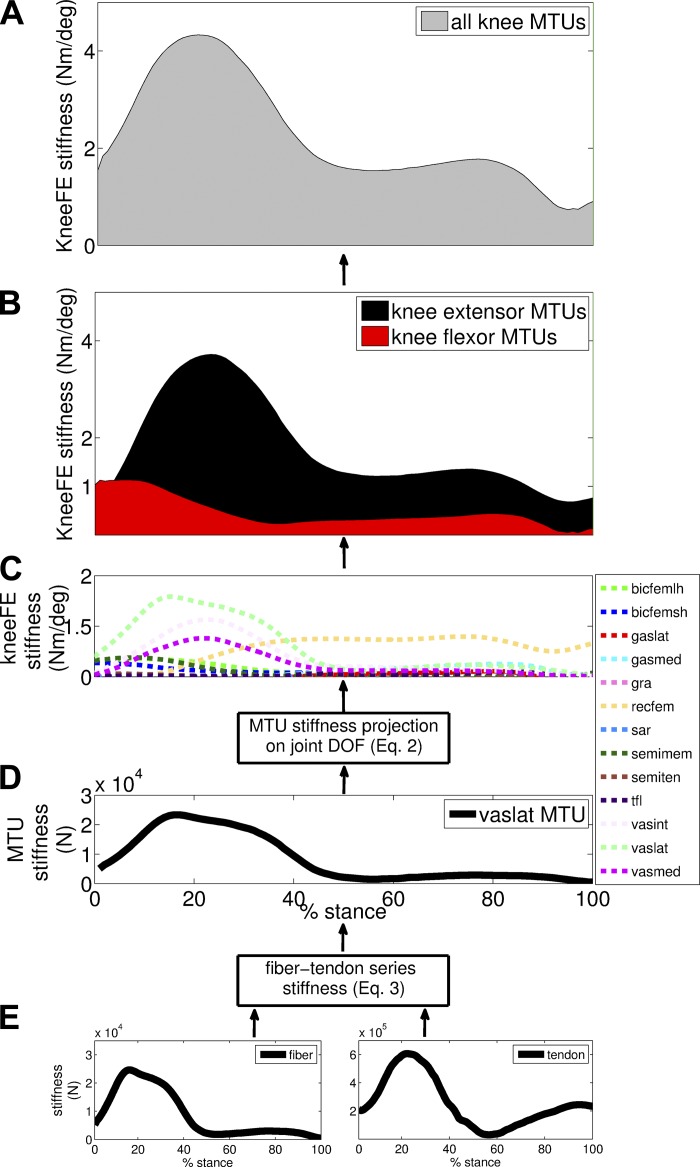
This study explored the theoretical and experimental aspects of a subject-specific EMG-driven model of the human leg to predict electrophysiologically and dynamically consistent estimates of ankle and knee joint stiffness directly from the joint constituent MTUs during dynamic locomotion. In this scenario, we aimed to highlight the hierarchical nature of how stiffness emerges at the joint. That is, how net joint stiffness (Figs. 7, 8, and 10) emerges from the contribution of individual MTUs (Figs. 9), and how individual MTU stiffness emerges from the contribution of muscle fibers in series with elastic tendons (Figs. 2–4). This is further highlighted in Fig. 11. This study also highlighted how our proposed stiffness estimates fundamentally differ with respect to SRS and QS estimates.

Fig. 11.

Hierarchical structure of how net joint stiffness (A) emerges, in our framework, from the stiffness contribution of the joint constituent muscle-tendon units (MTUs) (B and C) as well as how MTU stiffness (D) results from the stiffness of constituent fibers in series with tendon stiffness (E). Data are averaged across all trials performed by all subjects across walking trials. Data are reported about the knee flexion-extension (KneeFE) degrees of freedom, for the associated MTUs with names as defined in Table 1, and throughout the stance phase with 0% being heel-strike and 100% being toe-off events. Results show that the early stance of walking (i.e., 0% ≤ stance ≤ 25%) underlies a progressive decrease in joint stiffness of knee flexors (B) and a simultaneous increase in net joint stiffness (A) mainly contributed by knee extensors (B). Throughout the midstance (i.e., 25% ≤ stance ≤ 85%), net knee stiffness (A) decreased due to a gradual decrease in joint stiffness of knee extensors (B). In the terminal stance (i.e., stance ≥85%), net knee stiffness (A) reached its lowest value in the correspondence of activity of knee flexors in preparation for the swing phase.

Previous work based on musculoskeletal modeling focused on isometric tasks only and did not use experimental EMG-excitations to calibrate and drive forward dynamic subject-specific musculoskeletal models (Hu et al., 2011; Pfeifer et al., 2012). Furthermore, previous work was based on the SRS component of muscle fibers. The SRS mathematical formulation (Cui et al., 2008) provides estimates that are directly proportional to muscle isometric force and invariant to changes in fiber contraction length and velocity. Therefore, MTU forces could be determined, in these studies, directly from external isometric joint moments with no need for explicitly solving for the underlying fiber contraction and tendon dynamics (Hu et al., 2011; Pfeifer et al., 2012). That is, by balancing external (i.e., measured) and internal (i.e., unknown MTU force by the known moment arms) moments while solving for the MTU force distribution problem by imposing a static optimization criterion chosen a priori (Crowninshield and Brand, 1981; Anderson and Pandy, 2001). This predicts muscle forces and SRS that directly reflect isometric joint moments but do not account for force/stiffness modulations due to changes in the neural drive to muscles and in the underlying muscle fiber compliance, which are dominant factors in dynamic motor tasks. In this context, it is known that SRS would overestimate muscle stiffness (and therefore joint stiffness) during dynamic locomotion (Walmsley and Proske, 1981; Hu et al., 2011; Pfeifer et al., 2012). This was illustrated in our representative comparisons (Fig. 4). Moreover, the a priori chosen static optimization criterion used in these previous works (Hu et al., 2011; Pfeifer et al., 2012) could not explain large repertoires of muscle co-contraction typically observed across dynamically different motor tasks such as walking and running (Tax et al., 1990; Besier et al., 2003a; Heintz and Gutierrez-Farewik, 2007; Vigouroux et al., 2007; Sartori et al., 2012b, 2013). Nevertheless, SRS is an important mechanism for inclusion in current modeling methods to characterize the stiffness mechanisms underlying isometric muscle function, as well as postural tasks and gait initiation (Hu et al., 2011; Pfeifer et al., 2012).

Our proposed method addressed some of the above-described limitations. It provided a framework that for the first time enabled the investigation of MTU and joint stiffness estimates during dynamic locomotion tasks. This could be performed by 1) ensuring physiological CCRs in the simulated muscles via experimental EMG-excitations used as a direct input drive (Fig. 10), 2) modeling the nonlinear transfer function between EMG-excitation and MTU force, and 3) modeling the dynamic contraction of muscle fibers (due to activation, contraction length, and velocity) and their interaction with the series elastic tendon (Figs. 2–4) (Lloyd and Besier, 2003; Sartori et al., 2012b, 2013, 2014). The resulting joint stiffness estimates were directly produced by experimental excitations and physiological muscle operations that matched experimental joint moments about multiple DOFs, subjects, and across different motor tasks (Figs. 2–6).

This work revealed for the first time the elastic interplay between the knee and ankle joints. Results showed regularities in the production of muscle and joint stiffness with distinctive strategies for walking (Fig. 7) and running (Fig. 8). Observed regularities included stiffness peak timings (see results and Figs. 7, 8, and 10), muscle fibers consistently operating on the ascending portion of the force-length-velocity-activation surface (Table 2, Fig. 3, and Supplemental Video S1), and consistent CCR modulations (see results and Fig. 10). Specifically, results indicated that locomotion is characterized by joint stiffness strategies of impulsive nature (i.e., having burst-like transients) (Figs. 7, 8, and 10). During walking, the knee and ankle joints displayed minimally overlapped burst-like transients, thus reflecting interjoint, low elastic coupling. This was characterized by an initial stiffness burst in the knee joint in the early stance followed by a minimally overlapped stiffness burst in the ankle joint during the terminal stance (Figs. 7 and 10). Running displayed higher elastic coupling between the two joints (Figs. 8 and 10). This was characterized by double-burst stiffness curves both at the ankle and knee joints, which emerged in the early (i.e., weight-acceptance phase) and terminal (i.e., push-off phase) stance phases (Latash, 2010). Stiffness peaks underlay co-contraction ratios that were always more balanced (i.e., CCR closer to zero) in the knee joint than in the ankle joint (Fig. 10). This was also reflected by the fact that net knee joint stiffness was contributed both by knee extensors and flexors (Fig. 9), whereas ankle stiffness was predominantly contributed by plantar-flexors (Fig. 9) as previous related work (Farris and Sawicki, 2012) confirmed. This suggested that the ankle joint modulates stiffness for propelling the body while knee joint stiffness appeared to be modulated for body weight acceptance and joint stability functions.

There are limitations to this study. This work was based on five subjects. Therefore, it may not be possible to completely generalize the results. However, this study aimed at developing the theoretical and computational modeling framework for investigating the neuro-musculo-skeletal mechanisms that regulate dynamic stiffness on a subject-specific basis. This step needs to be necessarily taken before a framework can be systematically applied to a large population of subjects. In this context, the proposed EMG-driven musculoskeletal model was first scaled and then calibrated to each subject to account for subject-specific anthropometry, EMG-to-activation mapping, and MTU force-generating properties. This enabled our methods to be specifically applied across individuals, while accounting for the subject's actual muscle activation patterns. This represents an improvement in current state-of-the-art modeling methodologies in which the recruited subjects are chosen to have a similar build as that of the anatomical model (Lloyd and Besier, 2003; Martelli et al., 2011, 2015) or the model anthropometric properties are scaled with no identification of subject-specific EMG-to-force parameters (Hamner and Delp, 2013; Hicks et al., 2015). Future studies will couple our proposed modeling methods with dimensionality reduction techniques (Lee and Seung, 1999; Sartori et al., 2013), thus enabling the characterization of robust regularities in the neuromuscular control of joint stiffness across a large population of subjects, something this study could address only partially due to the small subject population size.

Results were generated during the walking and running stance phases only. We did this because the model calibration included running trials for which the swing phase occurred either partially or entirely out of the motion-capture volume. Therefore, incomplete swing-phase data were available for calibration and validation across trials. However, contrary to the stance phase, the human leg during swing undergoes a ballistic movement largely supported by the hip with no considerable muscular effort in knee and ankle joints (Collins et al., 2005; Hamner et al., 2010; Hamner and Delp, 2013; Shamaei et al., 2013a,c). Therefore, our proposed analysis allowed an observation of the major phases underlying stiffness modulation at the knee and ankle. Future work will, however, include an analysis of the swing phase and stiffness estimation from the hip joint.

Our methods employed Hill-type muscle models that did not characterize a number of important muscle-tendon force-generating mechanisms. Future work will address this limitation by 1) including more detailed models of the triceps surae mechanical contribution to the Achilles tendon strain and stiffness (Gerus et al., 2012; Shim et al., 2014), 2) modeling history-dependent muscle force-generating mechanisms that include stretch-induced force enhancement and shortening-induced force depression (McGowan et al., 2012), 3) incorporating more realistic damping and force-velocity characteristics (Haeufle et al., 2014), and 4) incorporating muscle energetics characteristics resulting from MTU stiffness modulation (Umberger and Rubenson, 2011; Endo and Herr, 2014).

Surface EMG provides only a surrogate measurement of the neural drive received by muscles, from which it is currently not possible to discern the underlying afferent and efferent components or their contribution to muscle and skeletal joint stiffness regulation (Farina and Negro, 2012). Future work will employ high-density EMG in conjunction with decomposition techniques to experimentally decode single-motor-unit action potential and spiking events (Farina et al., 2014b). In combination with our proposed musculoskeletal modeling framework, this will enable the identification of different neural components in the drive to muscles (Farina et al., 2014a). This will open new avenues for investigating the roles of central and peripheral circuitries in the modulation of stiffness (Piovesan et al., 2013). Furthermore, it will enable an estimation of the effective muscle excitation level as a direct function of motor unit spikes. This will address limitations in current EMG amplitude estimation methods, which rely heavily on EMG linear envelope maxima and filtering parameters identification (Sartori et al., 2014).

The joint stiffness predicted during walking and running could not be directly validated with experimental stiffness recordings. Although joint stiffness can be viably recorded in isometric or postural tasks (Perreault et al., 2001, 2004; Pfeifer et al., 2012), the reliable measurement of stiffness during natural locomotion still remains an open challenge and currently relies on noncommercial instrumentation and nonstandard identification procedures. However, in this current study, we compared our results directly with experimental stiffness recordings available from the literature (Plocharski and Plocharski, 2013; Lee and Hogan, 2015; Rouse et al., 2014). See Comparison with experimental stiffness estimates from the literature. It is worth stressing that comparing results with perturbation-based studies in the literature needs to occur with caution due to inherent differences including subject population size and type, locomotion speed, system identification method, and perturbation properties. These factors introduce variability across perturbation-based studies and with respect to the results derived from our study, which involved different locomotion speeds and unperturbed locomotion conditions. In this context, it was previously shown that experimentally recorded joint stiffness varies with the perturbation amplitude and speed, and as a function of muscle stretch reflexes elicited by the perturbation system (Bennett, 1994; Loram and Lakie, 2002; Vlutters et al., 2015). Finally, our results reflect only joint stiffness contributed from muscles for which surface EMG data are available (Table 1). This may further contribute to the differences observed in experimental studies in which the experimentally measured stiffness encompasses all muscles spanning the joint (Plocharski and Plocharski, 2013; Lee and Hogan, 2015; Rouse et al., 2014). Future studies will seek to employ wearable joint perturbation systems (Andersen and Sinkjaer, 1995; Plocharski and Plocharski, 2013) in combination with system identification methodologies (Ludvig and Perreault, 2012) for a more direct validation of the modeling methods presented in our study.

It is worth stressing that the aim of our proposed work was not that of addressing, in a single study, all limitations existing in the fields of model-based estimation and system identification of musculoskeletal stiffness. Our aim was to provide a theoretical and computational framework for calculating joint stiffness that explained both measured electrophysiological and mechanical data. Furthermore, our aim was to investigate how the predicted stiffness modulates during locomotion and to indicate how this differs from current stiffness estimates, including QS and SRS. Notably, our results demonstrated that our proposed method could use EMG signals recorded from 13 muscles to blindly predict dynamically consistent estimates of ankle plantar-dorsi flexion and knee flexion-extension moments, and resulting stiffness during walking and running and across five subjects by means of 124 evaluations (i.e., see Validation procedures and analyses). In this, validation was performed according to an open-loop paradigm in which joint moments were predicted with no knowledge of the corresponding experimental values (Sartori et al., 2012b). Although this does not directly validate the stiffness estimates, it does prove that the predicted joint stiffness is consistent with the subjects' actual electrophysiological activity and resulting multijoint moments.

Future studies will employ our recently proposed closed-loop EMG-informed modeling paradigm (Sartori et al., 2014). This will ensure precise and consistent tracking of reference joint moments by minimally adjusting the input experimental EMGs and by synthesizing excitations for muscles with no experimental EMG data available (Sartori et al., 2014). This will open several possibilities, including 1) estimating stiffness at the hip joint, for which the major flexor muscles (i.e., iliacus and psoas) are deeply located; 2) computing the stiffness contribution of intrinsic ankle muscles for which surface EMG is not accessible, including tibialis posterior, flexor digitorum/hallucis muscles, and extensor digitorum/hallucis muscles; 3) assessing differences in joint stiffness estimation with respect to the fully predictive open-loop paradigm of this study, which may not preserve prediction accuracy across validation trials (Fig. 6); and 4) coupling our modeling methods with numerical forward integrators and postural controllers (Leroux et al., 2002; Latash, 2010; Wang et al., 2012) for computing segmental/articular kinematics emerging from the predicted joint moments and stiffness.

Remarkably, our validation results also showed that our methodology estimated gastrocnemius tendon stiffness that was in line with literature values available for this muscle [i.e., see results (Maganaris and Paul, 2002; Lichtwark and Wilson, 2005, 2008; Krishnaswamy et al., 2011)]. Moreover, our simulations resulted from muscle fibers predominantly operating on the ascending portion of the force-length-velocity-activation surface (Table 2, Fig. 3, and Supplemental Video S1). This may underlie a metabolic advantage because on the ascending portion, muscle activation, length, and contraction velocity have the most influence on the mechanical force output. This enables muscle force production with minimally required activation and contraction modulations, thus saving the metabolic cost necessary to actively recruit muscle fibers (Collins et al., 2015). This is also in agreement with experimental findings that reported normal muscle fiber operation in the ascending portion of the force-length relationship (Maganaris, 2001; Rubenson et al., 2012) with contractions within confined ranges of the sarcomere length (Burkholder and Lieber, 2001). Future studies will also employ ultrasound imaging and in vivo measurements to further validate our methods at the MTU level (Farris et al., 2014).

These observations provide some confidence that the physiological aspects of our proposed EMG-driven simulations are valid. Furthermore, they place further emphasis on the importance of using experimental EMG data for driving the underlying musculoskeletal model. Because normalized fiber length varies around rather confined ranges (Table 2) as opposed to EMG-derived muscle activation that largely varies between 0 and 1 (Fig. 3), abnormal muscle activation patterns (i.e., from static optimization-based methods) would have the most impact on the predicted muscle and joint stiffness and would adversely bias their final estimations (Burkholder and Lieber, 2001).

Comparison with QS estimates from the literature.

The estimates of joint QS available in the literature were always greater than the instantaneous stiffness estimates computed by our method (Figs. 7–10) when averaged across the respective gait phases (Stefanyshyn and Nigg, 1998; Günther and Blickhan, 2002; Coyles et al., 2011; Charalambous et al., 2012; Plocharski and Plocharski, 2013; Shamaei et al., 2013a,c). This may be a direct consequence of the time interval, dt, needed to compute QS (Equation 6). As previously discussed (i.e., see Relation to QS and SRS), a small dt would make QS more sensitive to vertical tangents on the torque-angle relationship similarly to what is shown in our results at the muscle level (i.e., see Fig. 3D and results). However, QS estimates were generally in agreement with instantaneous stiffness peaks predicted by our method at specific points within the same gait phases.

A modeling study that used a 2-D spring-mass model reported QS estimates at the ankle and knee over the stance phase of running (i.e., 4.8 ± 0.5 m/s) in the order of 7.1 ± 1.9 Nm/deg and 10.8 ± 3.0 Nm/deg, respectively (Günther and Blickhan, 2002). These were 1–3 Nm/deg higher than the stiffness peaks predicted by our method at the ankle (i.e., 5.9 ± 1.8 Nm/deg, at 88.9 ± 3.2% stance) and knee (8.2 ± 3.3 Nm/deg, at 29.8 ± 8.0% stance) joints (Fig. 10).

Experimental studies reported knee QS, throughout the weight-acceptance phase of walking, in the order of 4.9 ± 1.3 Nm/deg (Shamaei et al., 2013c). This reflected the knee stiffness early peak (i.e., 4.3 ± 1.1 Nm/deg, at 20.7 ± 6.5% stance) predicted using our EMG-driven modeling method (see second test and Figs. 7 and 10). Throughout the push-off phase of walking, the ankle QS was reported to be in the order of 17 Nm/deg (Shamaei et al., 2013a). This was substantially higher than the highest ankle stiffness values (i.e., 7.8 ± 0.5 Nm/deg, at 85.3 ± 7.2% stance) predicted using our EMG-driven modeling methods (see second test and Figs. 7, subject 3). Throughout the push-off phase of sprint running, the ankle QS was reported to be in the order of 5.93 ± 0.75 Nm/deg (Stefanyshyn and Nigg, 1998; Coyles et al., 2011; Charalambous et al., 2012). This reflected ankle stiffness peak values (i.e., 5.8 ± 1.8 Nm/deg, at 88.9 ± 3.2% stance) predicted using our EMG-driven modeling method (see second test and Figs. 7 and 10). Throughout the first 100 ms of the stance phase of running (4.5 ± 0.2 m/s), the knee QS was reported to be in the order of 8.74 ± 2.73 Nm/deg (Coyles et al., 2011), which was in agreement with knee stiffness peaks (8.2 ± 3.3 Nm/deg, at 29.8 ± 8.0% stance) predicted using our EMG-driven modeling method.

Comparison with experimental stiffness estimates from the literature.

Experimental recordings of ankle stiffness were reported (Plocharski and Plocharski, 2013) from 11 subjects walking on a treadmill (1.1 ± 0.04 m/s) and wearing an ankle joint perturbation system (Andersen and Sinkjaer, 1995). Ankle joint stiffness was derived from the data that recorded the perturbation system (i.e., joint angle and moment), which were post-processed using a multisegment system identification algorithm (Ludvig and Perreault, 2012). This provided quasi-instantaneous recordings of ankle joint stiffness at 20%, 50%, and 90% gait cycle, resulting from fast perturbations (i.e., the perturbation window, 100 ms; angular velocity, 300 deg/s; amplitude, 8 deg; and hold-window, 200 ms). At 20% gait cycle (i.e., ≈33% stance), the experimentally measured ankle stiffness was in the order of 4.7 ± 1.9 Nm/deg over the 100-ms-perturbation window and was 2.0 ± 1.8 Nm/deg over the 200-ms-hold phase (Plocharski and Plocharski, 2013). At the same stance point, our EMG-driven modeling method predicted instantaneous peaks of ankle stiffness (i.e., 1.4 ± 0.8 Nm/deg) that were in line with values extracted from the 100-ms-perturbation window. At 50% gait cycle (i.e., ≈ 83% stance), the experimentally measured ankle stiffness was in the order of 5.3 ± 2.6 Nm/deg over the 100-ms-perturbation window and 2.9 ± 3.0 Nm/deg over the 200-ms-hold phase (Plocharski and Plocharski, 2013). At the same gait cycle point, our EMG-driven modeling method predicted instantaneous peaks of ankle stiffness (i.e., 5.3 ± 1.7 Nm/deg) that are in line with values extracted from the 100-ms-perturbation window. The 90% gait cycle corresponded to the swing phase of walking, which was not recorded in our proposed study.

Rouse and colleagues (2014) reported experimental ankle stiffness estimates during the locomotion stance phase from 10 subjects walking overground (85–90 steps/min) on a perturbation platform. A second-order parametric model was established on the basis of recorded ankle torque and kinematics to characterize ankle impedance during perturbation (Rouse et al., 2012). This provided recordings of ankle joint stiffness at about 20%, 35%, 55%, and 70% stance, resulting from mild perturbations (i.e., perturbation window, 75 ms; angular velocity, 45 deg/s; amplitude, 2 deg). Stiffness increased by a factor of four from 20% to 70% of stance phase, starting at ∼1.5 Nm·rad⁻¹·kg⁻¹ (i.e., ≈ 20% stance phase) and increasing to 6.5 Nm·rad·⁻¹·kg⁻¹ (i.e., ≈ 70% stance phase). Results reported by Rouse et al. (2012, 2014) are within one to two standard deviations from our reported values (i.e., ankle stiffness increasing throughout the stance phase starting at 1.01 ± 0.6 Nm·rad⁻¹·kg⁻¹; that is, ≈ 20% stance phase) and increasing to 3.8 ± 2.6 Nm·rad⁻¹·kg⁻¹ (i.e., ≈ 80% stance phase).

Lee and Hogan reported experimental ankle stiffness estimates during the locomotion initial stance phase from 13 subjects walking on a treadmill (0.7 ± 0.1 m/s) and wearing a perturbation robot (Khanna et al., 2010; Lee and Hogan, 2015). A time-varying ensemble-based system identification method was used to extract ankle stiffness during perturbation (MacNeil et al., 1992). This provided recordings of ankle joint stiffness in the order of 1.1 ± 0.1 Nm/deg at about 5% stance, resulting from random torque perturbations (i.e., peak-to-peak perturbation torque amplitude, ±7.7 Nm/rad; stop frequency, 100 Hz) (Lee and Hogan, 2015). Results are in line with our reported values (i.e., 1.2 ± 1.5 Nm/deg at 5% stance).

Conclusions

The proposed method is an internally consistent, subject-specific musculoskeletal model for estimating MTU and joint stiffness that results from experimental EMG-excitations and that underlie MTU forces that match experimental joint moments measured from dynamic locomotion. This differs fundamentally from current stiffness estimates, including QS and SRS. In this context, our methods and results show the following points.

Quasi-stiffness (QS, Equation 6) and stiffness (K^m, Equations 3–4) are two distinct concepts and are equivalent only in a passive system (Rouse et al., 2013). This is mathematically formulated in Equation 6, which relates QS to K^m in the context of an active muscle. In this, QS = K^m only if the muscle activation and contraction velocity components [i.e., A(dt,t) and V(dt,t) respectively] were disregarded. Our results showed that in the context of a muscle (i.e., active system), QS would directly relate changes in muscle force to changes in muscle fiber length without accounting for the fact that muscle force may be instead varying because of other factors such as muscle activation or contraction velocity (Equation 6 and Fig. 3). Therefore, QS provides biased estimates of the mechanical stiffness of an active system, such as a muscle or a human joint [i.e., estimates that do not strictly describe resistive force responses due to MTU or joint elastic characteristics (Rouse et al., 2013)].

Although SRS is an important model for describing isometric muscle stiffness, it would predict nonphysiological MTU stiffness when applied to dynamic locomotion (Equation 7 and Fig. 4).

In contrast, this study proposed a modeling formulation of how muscle and joint stiffness modulate as a function of muscle activation, fiber contraction, and interacting tendon dynamics. As a result, this formulation can be applied to dynamic locomotion (i.e., unlike SRS) and can generalize across passive and active systems (i.e., unlike QS).

This methodology could be used in the future in conjunction with predictive models of muscle recruitment and modularity (Sartori et al., 2013) for synthesizing the neuromuscular mechanisms that underlie human-like locomotion (Wang et al., 2007; Song and Geyer, 2015) in artificial systems such as bipedal robots or prosthetic limbs (Farahat and Herr, 2010; Beyl et al., 2011; Markowitz et al., 2011; Karavas et al., 2013).

The ability of our proposed methodology to characterize subject-specific and motor task-specific MTU and joint stiffness is critical for creating wearable robots with actuator power and spring stiffness that are attuned to an individual users' joint properties and external mechanical demands (Shamaei et al., 2013a).

The ability to estimate net joint stiffness in real-time from EMG signals could be used in scenarios involving patients with unilateral impairments (Pfeifer et al., 2012, 2015). In this context, stiffness could be estimated from healthy-side joints and used for controlling variable-stiffness prostheses and orthoses that would act on the contralateral affected leg and restore healthy-leg behavior across different locomotion tasks and terrains.

The ability to estimate the stiffness of individual muscle fibers and tendons in real-time could be used to modulate the metabolic cost of locomotion in individuals who wear orthoses. In this context, the orthosis could be controlled so that the user's muscle fibers always operate on the most favorable portion of the force-length-velocity-activation surface (Farris and Sawicki, 2012; Collins et al., 2015).

Finally, the ability to translate an individual's EMG activity into muscle and joint stiffness estimates could enable developing strategies to address abnormal stiffness in patients with neurological and orthopedic conditions and to deliver personalized rehabilitation treatments that restore physiological properties (Wolbrecht et al., 2008; Ogawa et al., 2014).

In conclusion, the proposed method is a theoretical and computational framework for investigating the neuromuscular basis of locomotion and motor control. This may open up new avenues for examining human neuromuscular control and musculoskeletal mechanics, with implications for the development of neurorehabilitation technologies.

GRANTS

Support for this work was provided by the European Research Council (ERC) via the ERC Advanced Grant DEMOVE (267888) and by the European Seventh Framework Programmes FP7-ICT-2011-9 and FP7-ICT-2013-10 via the H2R (60069) and BIOMOT (611695) Projects.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.S. conception and design of research; M.S. performed experiments; M.S. and M.M. analyzed data; M.S. and M.M. interpreted results of experiments; M.S. and M.M. prepared figures; M.S. and D.F. drafted manuscript; M.S., M.M., C.P., M.R., and D.F. edited and revised manuscript; M.S. and D.F. approved final version of manuscript.