Modeling Dynamic Fluctuations in Type 1 Diabetes Progression: Quantifying β-cell variation after the appearance of islet-specific autoimmune responses

Abstract

Type 1 diabetes (T1DM) is a chronic autoimmune disease with a long prodrome, which is characterized by dysfunction and ultimately destruction of pancreatic β-cells. Because of the limited access to pancreatic tissue and pancreatic lymph nodes during the normoglycemic phase of the disease, little is known about the dynamics involved in the chain of events leading to the clinical onset of the disease in humans. In particular, during T1DM progression there is limited information about temporal fluctuations of immunologic abnormalities and their effect on pancreatic β-cell function and mass. Therefore, our understanding of the pathoetiology of T1DM relies almost entirely on studies in animal models of this disease. In an effort to elucidate important mechanisms that may play a critical role in the progression to overt disease, we propose a mathematical model that takes into account the dynamics of functional and dysfunctional β-cells, regulatory T cells, and pathogenic T cells. The model assumes that all individuals carrying susceptible HLA haplotypes will develop variable degrees of T1DM-related immunologic abnormalities. The results provide information about the concentrations and ratios of pathogenic T cells and regulatory T cells, the timing in which β-cells become dysfunctional, and how certain kinetic parameters affect the progression to T1DM. Our model is able to describe changes in the ratio of pathogenic T cells and regulatory T cells after the appearance islet antibodies in the pancreas. Finally, we discuss the robustness of the model and its ability to assist experimentalists in designing studies to test complicated theories about the disease.

1 Introduction

Mathematical modeling has played a critical role in our understanding of various pathogenic aspects of human diseases, such as infectious diseases (1; 2; 3; 4), cancer (5; 6), cardiac arrhythmias (7), and diabetes (8; 9). Thus far, modeling in diabetes research has mainly focused on the kinetics of glucose-induced insulin secretion and sensitivity (10; 11; 12), bursting properties of pancreatic β-cells (13; 14), and glucose-calcium oscillations in β-cells (15). Only recently has mechanistic modeling begun to explore specific pathways associated with the effects of T cells in the chain of events causing β-cell destruction that leads to T1DM (16). Work by Wang et al. studied the heterogeneity between young- and adult-onset type 1 diabetes (17), and Entelos developed a large scale model of a virtual NOD mouse (18) are some examples.

T1DM is a chronic autoimmune disease in which β-cells are gradually destroyed by pathogenic (autoreactive) T cells. This process is the end result of complex interactions among genetic, immunologic, and environmental factors (19). There is compelling evidence in (20) suggesting that T1DM results from an altered balance between pathogenic T cells mediating disease and regulatory T cells (Tregs) controlling auto-immunity (21). Type 1 diabetes is a polygenic disease for which there are a small number of genes with large effects (i.e., HLA) and a large number of genes with small effects (22; 23). Risk of T1DM progression is mainly conferred by specific HLA DR/DQ alleles [e.g., DRB1*03-DQB1*0201 (DR3) or DRB1*04-DQB1*0302 (DR4)] (24; 25; 26). Conversely, the DQB1*0602 allele is associated with dominant (80%–95%)protection from T1DM (26).

Although autoreactive CD4⁺ and CD8⁺ T cells are required for the initiation and progression of the disease (27; 28), the cellular dynamics leading to disease progression are not well understood. It has been postulated that in T1DM there is an imbalance of pathogenic (effector) T cells and regulatory T cells (Tregs) (21). Regulatory T cells (formerly suppressor T cells) are a specialized sub-population of T cells that suppress activation of the immune system thereby maintaining the homeostasis and tolerance to self molecules. Tregs represent less than 2% of the T cells in the peripheral blood. Using a number of experimental protocols, Treg cells can be expanded in vitro and in vivo and eventually could be harnessed therapeutically to treat T1DM or facilitate tolerance of transplanted pancreatic islets (29).

The fundamental pathophysiology shared by all patients with T1DM is the progressive loss in the ability of pancreatic β-cells to secrete insulin in response to glucose (30). This progressive decline in β-cell function may be secondary to a defect of regulatory T cells. A number of studies have demonstrated that any approach aiming to achieve immune hypo-responsiveness or tolerance in established T1DM will have to address the β-cell mass and function remaining at the time of clinical diagnosis of T1DM to permit a recovery of a metabolically-functional mass over the long-term (31; 32).

Convincing findings from prospective studies in first degree relatives of T1DM probands have shown a long latent period between the first appearance of circulating autoantibodies directed against islet autoantigens and clinical onset (33; 34). In T1DM a long prodrome offers a wide window of opportunities for identifying individuals at risk and conducting intervention to delay or even prevent the clinical onset of the disease. Algorithms based on immunologic and metabolic measurements have been developed in an effort to improve prediction of type 1 diabetes. However, during the natural history of the disease the mechanisms determining the imbalance between pathogenic T cells and regulatory T cells and are far from been resolved. Thus, in the following sections, we model their fluctuations occurring during the progression to disease onset. We pose questions about dynamic changes in the number and function of pathogenic (effector) and regulatory T cells in relation to pancreatic β-cell mass and function. These conjectures will lay the groundwork to identify gaps in the current knowledge of the pathoetiology of T1DM. Once these knowledge gaps during disease progression are identified, their dynamics can be further explored by formulating and evaluating hypotheses which may lead to the design of new experimental approaches with the potential to dramatically enhance our understanding of the disease process and interventions that prevent progression of T1DM.

2 Model development

Our intention is to study the relationship between immune cells and regulatory T cells by specifically looking at the ratio of pathogenic T cells and regulatory T cells, to determine the level of β-cell decrease after the appearance of islet antibodies in the pancreas, and to make prediction as to the key parameters that are controlling this behavior prior to the clinical onset of T1DM. We do so by developing a model that accounts for glucose, insulin, functioning β-cells, dysfunctional β-cells, normal regulatory T cells, defective regulatory T cells, IL-2, and pathogenic T cells. The key components of this model are its ability to track the concentration and functionality of both the β-cells and the regulatory T cells.

2.1 Glucose and Insulin

Insulin and glucagon are hormones that control the glycemic levels and are secreted in the pancreas by functioning β-cells and α-cells, respectively. Hence, it is important to track insulin (I) and glucose (G) in the model due to the direct correlation between their measured concentrations in the plasma and the assumed concentration of functioning β-cells in the pancreas.

Previous models have successfully shown a sigmoidal relationship for glucose concentration and activity in the pancreas (35). Topp et al. (8) modeled insulin production as a function of β-cells and glucose but only considered one type of β-cell. We modify their model by considering the existence of two types of β-cells: a functioning class (β_f ) that produces insulin at normal levels and a dysfunctional class (β_nf ) that produces no insulin. We also allow for small numbers of dysfunctional β-cells to regain some level of functionality and therefor return to the insulin producing class. Hence, in our model, the insulin secretion rate will depend on glucose concentration and only the functioning β-cells,

$$\frac{dG}{dt}=R_0-G(E{g}_0+S_{i}I),$$ (1)

$$\frac{dI}{dt}=\frac{\sigma B_f{G}^2}{\alpha +G^2}-{\delta }_{I}I.$$ (2)

In (1), R₀ is the net rate of production at zero glucose, Eg₀ is the total glucose effectiveness at zero insulin, and S_i is the insulin sensitivity. Glucose effectiveness is defined as the ability of glucose to stimulate its own uptake and inhibit its own production; insulin’s effect on glucose uptake and production is defined as Insulin sensitivity (36). Bergman et al. (37) provided experimental evidence for this relationship using the glucose clamp technique. The parameter σ represents the rate of insulin secretion due to β_f cells, α represents glucose concentration where the levels reach half saturation, and δ_I is the rate of removal of insulin.

2.2 β-cells

We consider two compartments for β-cells. For the functioning β-cells we use the same source term given in (8). Topp et al. assume that new β-cells can be formed by the replication of pre-existing β-cells or by neogenesis, the differentiation of new β-cells from a precursor or progenitor cell (38). Presently, it is very difficult to quantify rates of neogenesis or of trans-differentiation, the switch from pancreatic ductal cells to β-cells. However, there is a body of research that suggests, albeit indirectly, that these mechanisms make negligible contributions to β-cell mass dynamics except during development and in response to extreme physiological or chemically induced trauma (39; 40; 41; 42). For these reasons, neogenesis and trans-differentiation are not incorporated into the present model.

The first term in (3) describes the replication, r₁, and apoptotic death, d₀, rates of existing β-cells. In vitro studies show that the percentage of β-cells undergoing replication varies as a nonlinear function of glucose level in the medium (8; 43). Replication rates for β-cells increase with increasing glucose levels; however, at extreme hyperglycemia (> 400mg/ml), β-cell replication may be reduced at a constant rate, r₂ (39). Apoptotic death has been shown to vary nonlinearly with glucose (44; 45). Specifically, increasing the glucose level from very low levels to approximately 110 mg/ml in the medium surrounding cultured β-cells reduced their death rate; however, above 110 mg/ml glucose, the rate of β-cell death either remained low or increased.

In addition to death by apoptosis, cells can be lost from the functioning β-cell pool by losing the ability to produce insulin (46). This feature was not considered in (8) but is a key feature of our model. Functioning β-cells may lose the ability to produce insulin as a result of CD4⁺ T cell infiltration and their subsequent production of harmful cytokines and cytotoxins, such as IL-1 and TNF-α leading to iNOS (47). This process is accounted for in the second term in (3) by assuming pathogenic T cells T_b are directly affecting the β-cells and causing a switch from functional to non-functional. The maximal rate at which this happens is α₁ and k₁ represents the half-saturation constant. With this we have,

$$\frac{d{B}_f}{dt}=(r_{1}G-d_0-r_2{G}^2)B_f-\frac{a_1{T}_b{B}_f}{k_1+T_b}+\epsilon B_{nf}.$$ (3)

An important feature of (3) is the loss of functioning β-cells does not occur at a constant rate; instead, their loss of function and death rate will depend on the presence of pathogenic T cells. The observation that actual death/loss of β-cells may occur in phases is considered through the saturation term in (3) which transitions functioning β-cells to the dysfunctional β-cell class as seen in (4). Once β-cells are no longer capable of producing insulin, they either undergo apoptosis or necrosis at an elevated, but glucose independent rate, d₁, or are directly destroyed by cytotoxic T-cells which we account for by the scaling term, γ_T. This term simply increases the rate of removal of cells from this class. In the results that follow, we will show the model’s ability to provide clues to the significance of this result. For instance, we will consider the possibility that the β-cells that become dysfunctional may actually, at some future time, be able to reverse this effect and hence begin to produce some levels of insulin. We incorporate this result with a simple linear term εB_nf;

$$\frac{d{B}_{nf}}{dt}=\frac{a_1{T}_b{B}_f}{k_1+T_b}-{\gamma }_T{d}_1{B}_{nf}-\epsilon B_{nf}.$$ (4)

Together, (3) and (4) model the rate of change in the total β-cell mass. In this way, the fraction of functioning β-cells is not constant, rather it is dynamically varying.

2.3 Immune Cells

T cells possess the ability to directly destroy β-cells in a cytotoxic manner and by directly influencing β-cell destruction through the release of cytotoxic molecules such as cytokines and perforin. In type 1 diabetes, there is evidence that when the immune system is unbalanced, favoring islet inflammation and pathogenicity, the system is prone to islet autoimmunity development. This situation can also occur if there is a defect in regulation.

We can test this hypothesis by allowing our model to account for two classes of regulatory T cells: normal regulatory T cells, R, and a second class that represents regulatory T cells that have lost some form of functionality, R_b. This defect leads to an “unregulated” immune response, due to a class of pathogenic T cells, that affects the characteristics of insulin-producing β-cells by reducing their numbers or changing their functionality. Hence, we consider two main components of the immune response: regulatory T cells and the cells which are being regulated. The regulated cells are considered to be pathogenic T cells, T_b, which have migrated to the pancreas from the thymus and are unresponsive to the regulatory T cells (see Fig. 1).

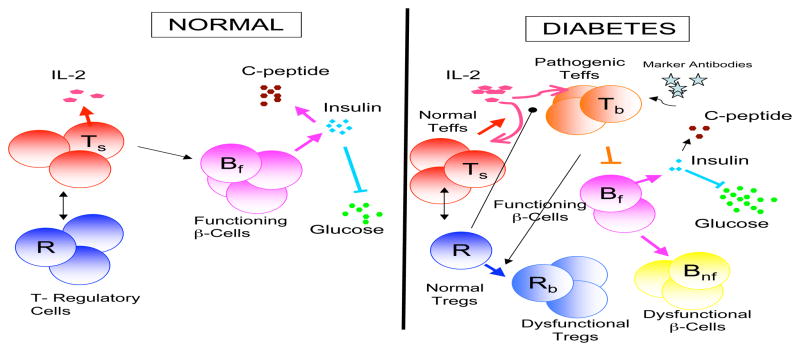
Fig. 1.

Diagram presenting the basic features of our model. The left side shows a normal individual and the right side shows a T1DM patient. For a normal individual there exists a healthy balance between the regulatory T cells, immune cells and functioning β-cells. The functioning β-cells produce insulin which then controls the levels of glucose. IL-2 is produced by the immune cells. The path to T1DM is shown on the right were we introduce two compartments, R_b and T_b, that show the model’s ability to track the changes in functionality and concentration of functioning β-cells, B_f, and regulatory T cells, R. We also show the islet autoantibodies which we hypothesis correlates in time with an increase in pathogenic T cells, T_b, that are attacking the functioning β-cells. Notice the resulting changes in the level of glucose and insulin.

Taking the information above, we are able to generate the next set of equations used to describe the immune response that play a key role in the progression to T1DM. We recognize regulatory T cells (R) and a compartment of pathogenic T cells (T_b) which are considered to be dangerous effector T-cells and become increasingly resistant to control from regulatory T cells. Evidence shows that infiltration of these dangerous pathogenic T cells is gradual initially and directly relates to the two-phase loss of β-cell mass (48);

$$\frac{d{T}_b}{dt}=S(t)+\frac{a_3{T}_b}{k_4+T_b}(1-\frac{T_b+R+R_b+B_f+B_{nf}}{K_p})-d_3{T}_r-\delta T_{b}R,$$ (5)

$$\frac{dR}{dt}=\frac{a_{4}R{I}_2}{k_2+I_2}(1-\frac{T_b+R+R_b+B_f+B_{nf}}{K_p})-d_{2}R-\alpha R.$$ (6)

Of note that in (6) the proliferation rate of regulatory T cells depends on the amount of I₂ available in the pancreas, which is assumed to vary according to $\frac{d{I}_2}{dt}=\frac{{\rho }_1{I}_{2}R}{k_4+R}-\mu I_2$. The rate of production of the pathogenic T cells, however, correlates with the presence of certain types of islet autoantibodies, S(t), that are produced by B cells. K_p represents the carrying capacity in the pancreas of both immune cells and β-cells, d_i is the death rate of immune cells, δ is the rate at which regulatory T cells can kill pathogenic T cells, and the k_i’s are the half-saturation constants that control the rate of increase of cells in the pancreas.

A unique aspect of our model is the function S(t) which will allow for the inclusion of the autoantibodies ICA, GAD65, IAA and IA2, which are well known to appear many years before the clinical onset of T1DM (49). The immune cells produce these autoantibodies against self-antigens in response to the damage of the β-cells. We assume that due to some unknown event, the pathogenic T cells begin to attack the β-cells, which leads to the release of islet autoantibodies and an increased level of proliferation of pathogenic T cells. We will consider this function to be time-dependent in accordance with a function that allows us to introduce them in the system at specific times over the course of a patient developing T1DM. Hence we consider

$$S(t)=({\alpha }_{1}H(t-{\tau }_1)+{\alpha }_{2}H(t-{\tau }_2)+{\alpha }_{3}H(t-{\tau }_3)+{\alpha }_{4}H(t-{\tau }_4))\frac{t^3}{K+t^3}.$$ (7)

We can also use a hyperbolic tangent function which allows for a more continuous dynamic but both functions show similar results.

Finally, we consider the inclusion of a class of non-functioning regulatory T cells (R_nf ). Evidence suggests that there is a gradual switch between functioning and non-functioning regulatory T cells (50). By modeling this class of regulatory T cells we are able to suggest possible pathways for disease progression that have yet to be considered. The rate of transition from functioning to non-functional regulatory T cells is given by F₁(R, R_b, T_b) = αR,

$$\frac{d{R}_b}{dt}=\alpha R-{\delta }_R{R}_b.$$ (8)

3 Results

The results presented here provide evidence of the model’s ability to study the dynamics of T1DM. For each figure, we assume specific values for the disease parameters and the results are based on these assumptions. In all cases, we can find and will show variations in these results by simply changing one or two of the key parameters.

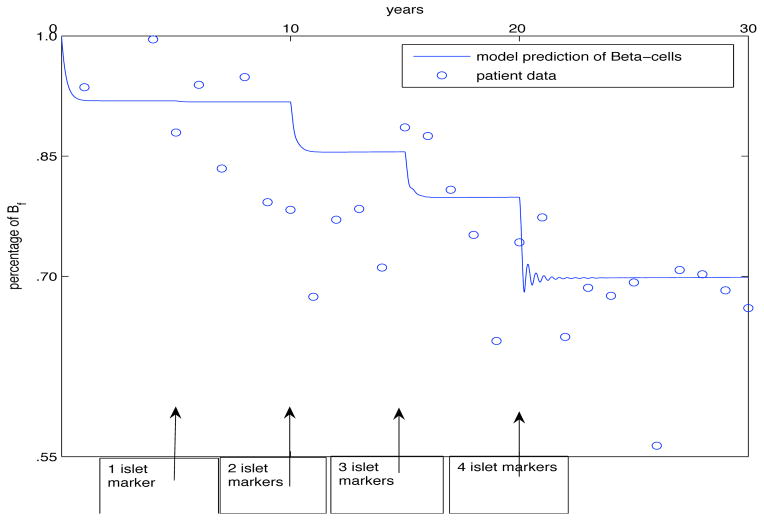
We first model immunologic fluctuations which may occur during the progression to clinical T1DM. These assumptions may explain the stepwise decline in β-cell mass and function that occurs after the appearance of multiple autoantibodies which are strong predictors of disease development (see Fig. 2). The model assumes all individuals carrying a disease-prone HLA genotype (i.e. DRB1*03-DQB1*0201 (DR3) or DRB1*04-DQB1*0302 (DR4)] will develop a degree of islet autoimmunity. The pathogenic phenotype can be viewed as a spectrum with destructive autoimmunity, loss of β-cell mass, multiple autoantibodies and clinical disease observed at one end, and non-destructive autoimmunity, preservation of β-cell mass, and generally absence of islet autoantibodies, at the opposite end of the spectrum. In the initial phase of the disease, the number of pathogenic T cells is controlled by an increase in number of functional regulatory T cells. As the disease process becomes more prominent, autoreactive effector (pathogenic) T cells that mediate disease exceed the number of regulatory T cells, which no longer suppress pathogenic autoimmune responses and in turn lose their ability to actively control unwanted immunity even after the onset of pathological manifestations.

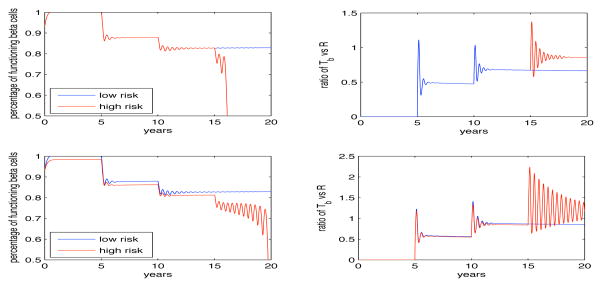
Fig. 2.

During T1DM progression there is an imbalance between the degree of epitope spreading, the cytotoxic potential of autoreactive T cells, the efficiency of regulatory responses and, possibly, the rate of regeneration of β-cells in response to immune-mediated β-cell destruction. These immunologic responses are cyclic and if autoreactive T cells (Teffs) exceed in number and/or function Tregs or there are functional defects in Tregs (top panel), which would no longer counteract the cytotoxic potential of Teffs, this leads to β-cell dysfunction and ultimately destruction. This destructive process may take years, as for childhood type 1 diabetes or decades (middle panel), or for instance in Latent Autoimmune Diabetes of the Adulthood (LADA). Islet autoantibodies manufactured by the immune system are directed against one of more of hosts self-proteins and they serve as reliable surrogate predictive markers of disease. The bottom panel shows cyclic variations of Teffs and Tregs in individuals with low risk or no risk of T1DM progression, such as those with single islet autoantibody responses. In this case there is a compensatory regulatory response counteracting effectively the cytotoxic potential of autoreactive T cell responses.

3.1 Relationship between islet autoantibodies, ratio of pathogenic T cells to regulatory T cells, and β-cell mass

The discovery of islet cell antibodies (ICA) was the prelude to the understanding that type 1 diabetes mellitus (T1DM) is a chronic autoimmune disease (51). We previously (49) summarized the current evidence for multiple islet autoantibodies as predictive markers for T1DM progression. We incorporated these islet autoantibodies into our model for T1DM to study the dynamics and progression of the disease for individuals considered to be low risk, i.e., present less than three islet autoantibodies, or high risk, i.e., greater than two islet autoantibody markers.

Our results (see Fig. 3 through Fig. 5) show the model’s prediction, over a 30 year period of time, for the concentration of functioning β-cells and for the ratio of pathogenic T cells to regulatory T cells. In each simulation we allow for the appearance of one islet antibody every five years from the start of our simulation, i.e., in (7) τ₁ = 5 years, τ₂ = 10 years, and τ₃ = 15 years. It must be emphasized that this is just one test case and that we can consider an infinite number of others. For instance, the appearance of certain islet antibodies can occur in as early as 5 months in young kids or over 20 years in the elderly. Each of these scenarios can be tested with our model, by varying τ_i in (7), but we only present the case here where they occur every 5 years. Our initial results, which we vary α_i and K in (7), suggest that the β-cells receive most of their damage during the first attack by the pathogenic T cells, i.e., which coincides with the appearance of the first islet autoantibody. We found roughly a 12% (see Fig. 3) to 28% (see Fig. 5) decrease in the level of functioning β-cells. However, after the appearance of the second antibody we find a smaller reduction in the β-cells. This result is contrary to some current beliefs and by varying the parameter values, we can describe events where the β-cell decrease is more gradual over time, instead of a more rapid reduction, proving the robustness of our model (see Fig. 8.)

Fig. 3.

Important figure showing the model’s capabilities of simulating T1DM results. The mathematical model presented in this paper accounts for the functionality and concentration of regulatory T cells. The top two panels show the decline of functioning β-cells (left) and the ratio of pathogenic T cells to regulatory T cells (right) when we allow for the dysfunctional β-cells to regain some of their functionality (ε > 0). What we find is for low risk individuals (≤ 2 islet autoantibodies) that the β-cells decline between 10 – 15% over a 20 year period and the person remains in a pre-diabetic state. However if the person moves to high risk, i.e., > 2 islet autoantibodies, the β-cells begin to significantly decline and with-in three years drop to zero. The right panel shows the ratio of T_b vs R and how the regulatory T cells are trying to control the pathogenic T cells (through the quickly damped oscillations) but become too stressed after the third antibody appears (as seen by the sustained oscillations). The bottom set of panels show the same dynamics but when we do not allow for the return of dysfunctional β-cells (ε = 0). The significant difference we find is that after the appearance of the third antibody the β-cells decline with-in one year instead of three years but they do so while the regulatory T cells seem to be still controlling the pathogenic T cells (as seen by the ratio of T_b to R being less then one and hence the concentration of R is greater than T_b).

Fig. 5.

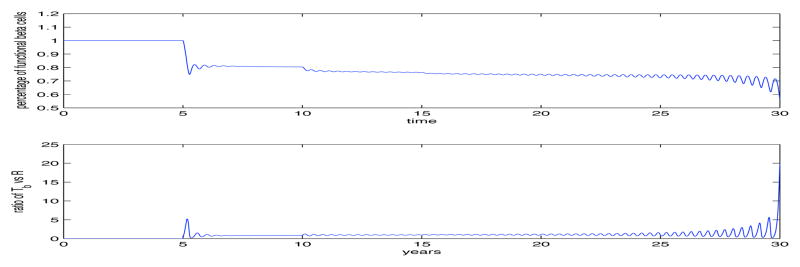
Figure similar to Fig. 4, except we change the values of α_i and K by 20%, showing that the functioning β-cells can be predicted by the model to maintain a reduced level for over 20 years after we see the third islet autoantibody. Again, showing the model’s robustness to describe a wide variety of dynamics.

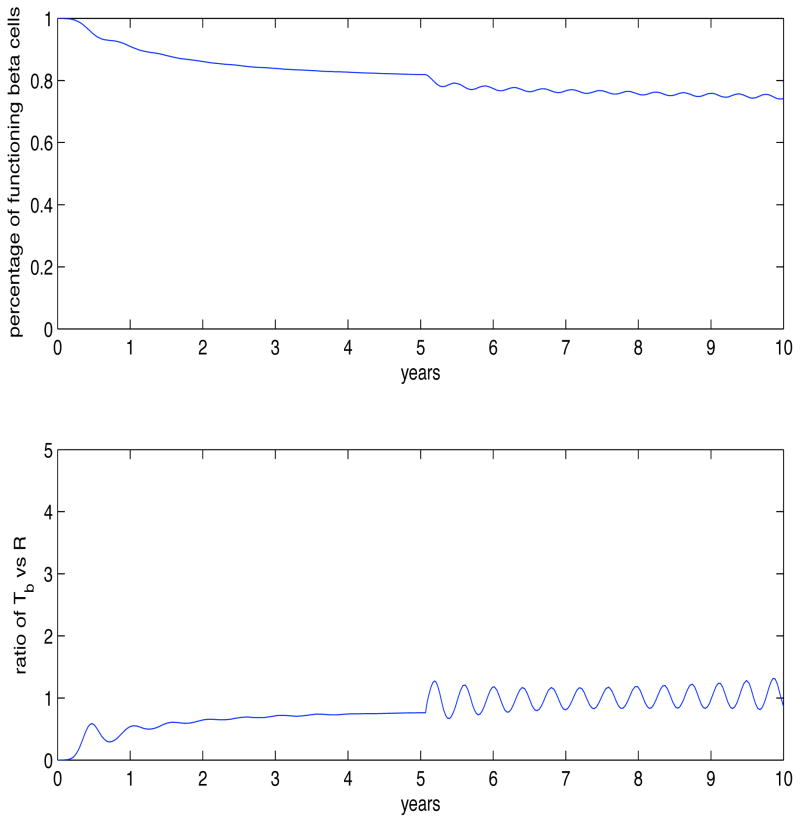
Fig. 8.

With modifications in our function, S(t), we can describe early events in the onset of T1DM in young adults. Top figure shows the gradual decline in functioning β-cells. The initial decline could be due to the subjects genetic disposition to the disease. Once T cell and autoantibody responses occur, we continue to see a decline in the number of functioning β-cells. In conjunction with this, we see the ratio of pathogenic to regulatory T cells (bottom figure) starting to oscillate about 1. With the proper adaption to experimental data, our model can help understand the complex dynamics associated with this disease.

What happens next depends on the assumption that either a third islet autoantibody will appear or not. If we assume no more islet autoantibodies appear then the individual is predicted to stay in a pre-diabetic state, i.e., the level of functioning β-cells is decreased but settles to level that is lower then what is seen in a normal individual (Fig. 3 panel A blue line). These results can be dramatically different if we change the values of α_i in (7) and in fact, we can show the biggest decrease in functioning β-cells can occur after the appearance of the second islet autoantibody and not the first (results not shown). When we compared these results with the ratio of pathogenic T cells to regulatory T cells (Fig. 3 panel B blue line) we find damped oscillations that occur for a few months after initiation of the pathogenic T cells attack of the β-cells. This leads us to believe that the pathogenic T cells are trying to overtake the system but the regulatory T cells are able to maintain control. Another theory is that an environmental factor, such as a virus, can trigger pathogenic T cells, which can destroy insulin secreting cells. We discuss this more in the future work section.

If we allow for a third attack by pathogenic T cells (shown by the appearance of a third islet autoantibody at 15 years), we find this control is only temporarily as seen in Fig. 3 (panel B red line) when after a third marker becomes present (high risk) the oscillations become larger and in fact for the first time, the ratio T_b/R becomes greater than one. This result shows comparable dynamics with the experimental evidence presented in Fig. 2 (panel C).

We ran a second test that studies the impact of assuming that the pathway for dysfunctional β-cells to return to a functioning state no longer exists, i.e., ε = 0 in (3) and (4). Hence we assume that once a β-cell becomes dysfunctional that they remain dysfunctional. When we run these simulations we find similar results to the above case when we consider a low risk individual (less then 3 islet autoantibodies) Fig. 3 (panel C and D, blue lines). However when we consider a high risk individual we find an interesting result: the time it takes for the β-cells to rapidly decline to zero is only one year instead of three years, however, the pathogenic T cells do not fluctuate as much as the case when ε > 0 (see Fig. 3 panel C and D red lines) and in fact show that the disease appears to be more severe but while we would expect the ratio of T_b/R to be greater than in the previous example, we find a non-intuitive result that shows the ratio to be 32% less then the previous case.

As mentioned above, by varying the rates α_i, τ_i, and K we can see quite different dynamics. For instance, in Fig. 3 we found that after the appearance of the third islet autoantibody, the individual will experience a significant reduction of functioning β-cells within a few years. However, this may not be the case in all individuals and if we allow for slight changes in α_i and K we find that the individual can actually maintain some level of functioning β-cells for between 12 years (Fig. 4) to 30 years (Fig. 5) after the third autoantibody is present. During this time, the ratio of pathogenic T cells to regulatory T cells shows some rapid, large amplitude oscillations, with pathogenic T cells exceeding regulatory T cells in number, showing a highly dynamic process between these two immune cells. In fact, we find that even though the β-cells maintain some level of function, the ratio of $\frac{T_b}{R}$ is much larger then the case when the patient experiences a nearly complete annihilation of functioning β-cells.

Fig. 4.

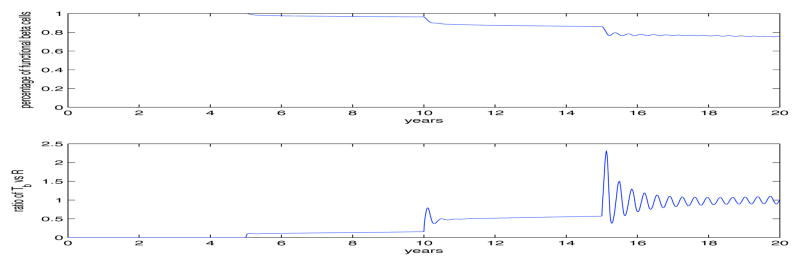
In this figure we provide an example that allows for the appearance of three islet autoantibodies but different from Fig. 3 we see that the patient responded with only a 10% decrease in functioning β-cells after the first islet autoantibody appeared, however, after the third autoantibody, the level of functioning β-cells maintains a level that is only reduced by 20% and maintains this level for over 12 years. This dynamic is very different then the one presented in the previous figure. All the model parameters were kept the same except for the ones that control the S(t). In fact, the change in dynamics seen in this figure are due to a doubling of α_i and a two order of magnitude change in K, showing the robustness of our model and the critical need for data to validate our results.

4 Describing the number and function of regulatory T cells and β-cells

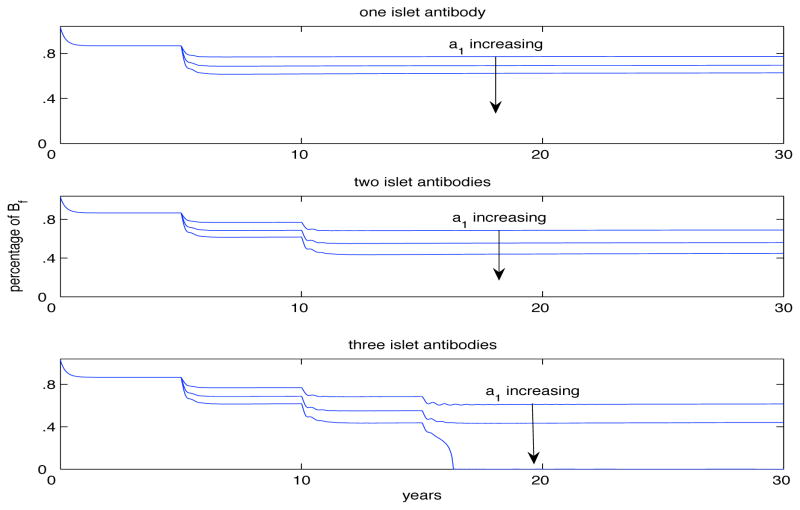
Our model allows for the transition of β-cells from functioning to dysfunctional as seen in (3) with the saturation term $\frac{a_1{T}_b{B}_f}{k_1+T_b}$. In the previous results we allowed for a₁ = 8 per day. This term is the source of the dysfunctional β-cells as seen in (4) and can change the model’s description. As seen in Fig. 6 our model can account for various declines in functioning β-cells by varying the rate at which they switch over, a₁. In the following graph we provide three simulations that allow for one (Fig. 6 top panel), two (Fig. 6 middle panel) or three islet antibodies (Fig. 6 bottom panel). In each figure we start a₁ = 8 per day and then double it and then triple it. As the value for a₁ increases, the level of β-cells begins to decrease and we found that when there are three islet antibodies that if a₁ > 18 per day then the level of functioning β-cells drops to zero. Comparing Fig. 3 and Fig. 6 we found similar results showing the decline of β-cells occurs either through an increase of the rate of switch from functioning to dysfunctional or if we keep this rate fixed, through a change in the level of dysfunctional β-cells returning to the functional class. This provides direct evidence for the importance of the rate at which this occurs.

Fig. 6.

Model describing β-cell resilience where the functional form for their transformation to dysfunctional β-cells is given by $\frac{a_1{T}_b{B}_f}{k_1+T_b}$ and hence is considered to be dependent solely on the T cells that have become resistant to regulator T cell responses. The panels allow for one (top) islet autoantibody, two (middle), and three (bottom). In each case we set a₁ = 8 per day and then double it and then triple its value. In all cases, the level of functioning β-cells decreases as a₁ increases and in fact, there exists a dramatic drop when we allow for three islet autoantibodies and let a₁ > 18 as seen in the bottom panel.

5 Islet antibodies and describing onset of T1DM

Finally, we consider applying the model to a generated random set of data points showing the gradual decline of functional β-cells over a 30 year period of time. We were able to keep the model parameters fixed from before and focus on the timing in which the islet antibodies appear in the pancreas. They appear at 5, 10, 15 and 20 years post start of the simulation, and we are able to describe, using a Monte Carlo algorithm, the level of response needed by the pathogenic T cells in order to fit the data. For this simulation we set $S(t)=({\alpha }_{1}H(t-1825)+{\alpha }_{2}H(t-3650)+{\alpha }_{3}H(t-5475)+{\alpha }_{4}H(t-7300))\frac{t^3}{K+t^3}$, where the H represents the heaviside (step) function and time is in days. From our data set we were able to show an increase in the response of pathogenic T cells after each islet antibody entered. As seen in Fig. 7 we used α₁ = 10, α₂ = 50, α₃ = 100, and α₄ = 150. With the application of real data, we feel we can make significant contributions to the understanding of T1DM.

Fig. 7.

Now we consider the predictive ability of the model and show how it can be of use for understanding T1DM. The previous figures have focused on the model’s description of changes in β-cell numbers over time. In this figure, we generated a random set of data points that simulates the gradual decline of functional β-cells over a 30 year period of time. Keeping the model parameters fixed from before, we focused on the timing of the appearance of the islet autoantibodies in the pancreas. We assumed they appeared at 5, 10, 15 and 20 years, post start of the simulation, and then described the level of response the pathogenic T cells needed to fit the data. The equation we used was $S(t)=({\alpha }_{1}H(t-1825)+{\alpha }_{2}H(t-3650)+{\alpha }_{3}H(t-5475)+{\alpha }_{4}H(t-7300))\frac{t^3}{K+t^3}$, where the H represents the heaviside (step) function. From our data set we were able to show an increase in the response of pathogenic T cells after the number of islet autoantibodies increase. As seen in Fig. 7 we used α₁ = 10, α₂ = 50, α₃ = 100, and α₄ = 150.

6 Discussion

One of the common characteristics of chronic autoimmune disorders, such as lupus, rheumatoid arthritis and T1DM, is their relapsing-remitting nature, which implies a cyclic process of their autoimmune responses. The intensity and duration of cyclic variations of pathogenic immune responses and pro-inflammatory cytokines can cause flare ups of rheumatoid arthritis or T1DM. The fundamental pathophysiology shared by all patients with type 1 diabetes is the progressive loss in the ability of the β-cells in the pancreas to secrete insulin in response to glucose and the progressive decline in β-cell mass. As autoimmunity in type 1 diabetes progresses from initial activation to a chronic state, there is an increase in number of islet autoantigens targeted by T cells and autoantibodies which precede the onset of clinical disease. Multiple antibodies reacting with these autoantigens (i.e., insulin, glutamic acid decarboxylase (GAD65) and the islet antigen IA-2), are detected in the majority of newly diagnosed T1DM patients and their presence is highly predictive of disease progression in otherwise healthy first-degree relatives of T1DM probands. Islet autoantibodies serve as surrogate markers for specific autoimmune responses targeting pancreatic β-cells (33; 34; 49). Although in our armamentarium we have reliable autoantibody markers predicting with accuracy T1DM progression (33; 34), the negative results from the Diabetes Prevention Trial-Type 1 Diabetes Study Group (52) and the European Nicotinamide Diabetes Intervention Trial (ENDIT) Group (53) have for now clouded our vision that effective prevention is around the corner. One reason that could explain these negative results is that the mechanisms of the disease process prior to diabetes onset are largely unknown.

In the past two decades tremendous progress has been made in the understanding of the genetics, pathophysiology and prediction of the disease. However, there are critical gaps that have yet to be filled. Prompted by an interest in trying to fill some of these gaps, we modeled a few crucial aspects of the disease process. The model that we present is an attempt to address complicated questions about the decline of functioning β-cells, about the ratio of pathogenic T cells to regulatory T cells, and describe the onset of the disease. As seen in Fig. 3 we found in low risk individuals (less then three islet autoantibodies) that the person can have a 10 – 20% decline in the number of functioning β-cells but still stay in a pre-diabetic state. In fact, we can find declines up to 25% in these pre-diabetic individuals (results not shown). During the pre-diabetic state we also can predict the ratio of pathogenic T cells to regulatory T cells. We found a significant result when allowing dysfunctional β-cells to return to the functioning class. When we assumed ε > 0 in (3) we found $\frac{T_b}{R}>1$ and when the third islet autoantibody appears that the person will have a catastrophic decrease within 3 years of functioning β-cells without intervention. If we do not allow for the return to the functioning class (seen in (3) with ε = 0) we see the catastrophic decrease within one year, however, $\frac{T_b}{R}<1$, which implies the regulatory T cells still out number the pathogenic T cells. A result that is somewhat non-intuitive when compared with Fig. 2 and shows the model’s ability to describe dynamics that are not mainstream and may lead to important conjectures that must be tested experimentally.

Another unique feature of our model is the term $\frac{a_1{T}_b{B}_f}{k_1+T_b}$ which allows for a dynamic change in functionality of β-cells over time and hence does not assume the change to be constant. We tested the model’s ability to fit a generated random set of data points showing the gradual decline of functional β-cells over a 30 year period of time. The model allows us to focus on certain kinetics associated with the disease and in Fig. 7 we showed how we can use this model to simulate the decay of β-cells in relation to the islet autoantibodies in the pancreas. These results show the potential of our model to make significant contributions to the understanding of T1DM when applied to real clinical data sets.

Albeit evidence indicates that T1DM is the end result of an altered balance between pathogenic T cells and regulatory Tregs, the mechanisms determining this imbalance have not yet been determined. One hypothesis is that the rate of T1DM progression depends on the degree of epitope spreading, the efficiency of regulatory responses and, possibly, the rate of regeneration of β-cells in response to immune-mediated beta cell injury (54). Treg cells prevent activation of autoreactive T cells in the lymph nodes by limiting their access to dendritic cells and thus their expansion and achievement of effector functions. These activities are largely mediated by thymus-derived natural Tregs. When immune homeostasis is perturbed and inflammation erupts in the tissues, both natural Tregs and cytokine-induced adaptive Tregs traffic to the site of inflammation and inhibit the functions of fully differentiated pathogenic effector T cells in the target tissue. If regulatory responses are defective, as postulated in our model, we can find effector T cell responses that outnumber regulatory responses leading to impairment, destruction of β-cell mass and disease onset. However, we can also find disease onset in patients whose regulatory T cells still outnumber the pathogenic T cells, suggesting a more complex implicit dynamic.

Despite significant advances, a simple, scalable, non-toxic, and highly-effective therapeutic strategy that can indefinitely lead to a recovery of β-cell function or mass remains elusive. At least in theory β-cell mass and function could be rescued by blocking the ability to generate pathogenic T cell responses to islet auto antigen(s) thought to signal the beginning stages of the disease, and by either developing Treg-based cellular therapeutics or delete pathogenic T cells in an attempt to suppress autoimmune responses. In vivo potential mechanisms of action with the ultimate goal of safety and efficacy trials in pre-clinical and new-onset Type 1 diabetic patients may be valuable to help design future prevention trials for Type 1 diabetes. T1DM is a chronic autoimmune disease characterized by dysfunction and ultimately destruction of β-cells in the islets of Langerhans. T1DM presents a complex interaction between genetic, immunological, and environmental factors, most of which have yet to be identified. Hence, we proposed in this paper the first model of its kind to study this complex interaction. For instance, while it is known that when the level of β-cell function is no longer sufficient to maintain metabolic homeostasis, the individual is then dependent on endogenous insulin to sustain life, it is not known why or how these β-cells lose function. Also, the fundamental pathophysiology shared by all patients with T1DM is the progressive loss in the ability of the β-cells of the pancreas to secrete insulin in response to glucose. This progressive decline in beta cell function may be secondary to a defect of regulatory T cells.

With this information at hand we have provided the groundwork for the next stage of models to study T1DM. With real connections between experiment and theory, we expect significant advances in our understanding of this disease.

7 Future Studies

We have developed a dynamical systems model that describes β-cells, immune cells, cytokines, glucose and insulin. Our current work describes the relationship between functional β-cells and islet autoantibodies. Our results suggest that the timing in which the β-cells switch over from functional to dysfunctional plays a critical role in the model’s predictive ability. As seen in (3) we assume the switch is modeled by $\frac{a_1{T}_b{B}_f}{k_1+T_b}+\epsilon B_{nf}$. While we allow for a dynamic change seen in the levels of T_b and B_f, however, it is assumed to occur at a constant rate a₁. We plan to study a switch that is time dependent such that a₁ = a(t).

A second area of interest is focusing more on the regulatory T cells. We assumed that regulatory T cells can switch over to a dysfunctional class and that these cells become unable to control the pathogenic T cells. However, what causes this switch is unknown. We want to expand the model to test specific hypotheses about the causes for the change in regulatory T cells: Is it an imbalance in the regulatory T cells? Is it caused by the migration of pathogenic T cells in the pancreas? or is it a combination of both?

Third, we plan to begin a mathematical study to evaluate the association between infectious diseases and T1DM (55). Evidence suggests that the recent increase in the incidence of T1DM that cannot be explained by hereditary events leads one to look for environmental causes, such as childhood infectious diseases (56). Our mathematical model will allow us to study this in detail.

Finally, Pietropaolo’s group has recently found that an antibody response against an epitope localized within the extracellular domain of the neuroendocrine autoantigen IA-2 can predict a rapid progression of T1DM in adolescents as well as young adults (unpublished results). We are working to apply our model to study the pathogenesis of T1DM in young adults. Our model can describe this early and rapid progression as seen in Fig. 8 and with proper connections to experimental data should be able to help in the understanding of this dynamic.