Longitudinal spread of mechanical excitation through tectorial membrane traveling waves

Significance

The sharp frequency selectivity of auditory neurons, which is a hallmark of mammalian hearing, originates mechanically in the cochlea. Local resonance of the tectorial membrane (TM) is thought to play a key role. However, the presence of TM traveling waves suggests an entirely different mechanism. In this paper, we present experiments to measure longitudinal spread of mechanical excitation via TM traveling waves and discuss implications for the resulting tuning. We show that increasing viscosity or decreasing stiffness of the TM reduces the longitudinal spread of mechanical excitation, which would sharpen frequency selectivity. These trends are opposite those trends for a resonant TM, where increasing viscous loss or decreasing stiffness would broaden tuning.

Abstract

The mammalian inner ear separates sounds by their frequency content, and this separation underlies important properties of human hearing, including our ability to understand speech in noisy environments. Studies of genetic disorders of hearing have demonstrated a link between frequency selectivity and wave properties of the tectorial membrane (TM). To understand these wave properties better, we developed chemical manipulations that systematically and reversibly alter TM stiffness and viscosity. Using microfabricated shear probes, we show that (i) reducing pH reduces TM stiffness with little change in TM viscosity and (ii) adding PEG increases TM viscosity with little change in TM stiffness. By applying these manipulations in measurements of TM waves, we show that TM wave speed is determined primarily by stiffness at low frequencies and by viscosity at high frequencies. Both TM viscosity and stiffness affect the longitudinal spread of mechanical excitation through the TM over a broad range of frequencies. Increasing TM viscosity or decreasing stiffness reduces longitudinal spread of mechanical excitation, thereby coupling a smaller range of best frequencies and sharpening tuning. In contrast, increasing viscous loss or decreasing stiffness would tend to broaden tuning in resonance-based TM models. Thus, TM wave and resonance mechanisms are fundamentally different in the way they control frequency selectivity.

The sharp frequency selectivity of auditory nerve fiber responses to sound is a hallmark of mammalian cochlear function. This remarkable signal processing originates in the mechanical stage of the cochlear signal processing chain (1–7), as evidenced by measured motions and mechanical properties of the basilar membrane (BM) (2–9) and tectorial membrane (TM) (10–24). Although the hydromechanical mechanisms underlying BM motions have been characterized based on experimental and theoretical studies, the mechanisms underlying TM motions remain unclear.

The TM is an acellular matrix that overlies the hair bundles of sensory receptor cells. Based on its strategic position above the organ of Corti, conventional cochlear models (25–29) have implicated local mechanical properties (i.e., mass, stiffness) of the TM in stimulating the sensory hair bundles of hair cells and in cochlear tuning. Recent dynamic measurements of the TM, in vitro (17, 30–33) and in vivo (34), suggest that the TM supports longitudinal coupling, with large spatial extents across a broad range of frequencies. This longitudinal coupling manifests in the form of propagating traveling waves that are thought to contribute to hearing mechanisms (17, 21, 30, 35–40). Genetic modification studies provide further support that the spatial extent of TM waves may play a significant role in cochlear tuning (30, 32). Although these measurements, models, and genetic modification studies have confirmed the importance of TM mechanical properties in hearing, they have not isolated the distinct roles of TM stiffness and viscosity in generating longitudinally propagating traveling waves of the TM.

To understand the contributions of TM material properties on traveling waves better, we developed chemical manipulations to alter the stiffness and viscosity of the TM selectively and reversibly. Because the TM is poroelastic (32, 41), we expect that changes in bath composition can have a direct effect on the mechanical properties of the TM mechanical matrix and its interstitial fluid, which makes up 97$\text{\%}$ of TM wet weight (42). The addition of PEG has previously been shown to generate an osmotic response that could be accounted for by the permeability of these molecules through the matrix rather than by direct changes to the matrix itself (41). In contrast, changing bath pH has little effect on the osmotic pressure or viscosity of the bath but has been shown to have a direct effect on the macromolecular matrix (43). In this paper, we apply these physicochemical manipulations to alter TM material properties reversibly, and thereby probe their role in controlling longitudinal spread of excitation through the TM.

Results

Chemically Altering TM Stiffness and Viscosity.

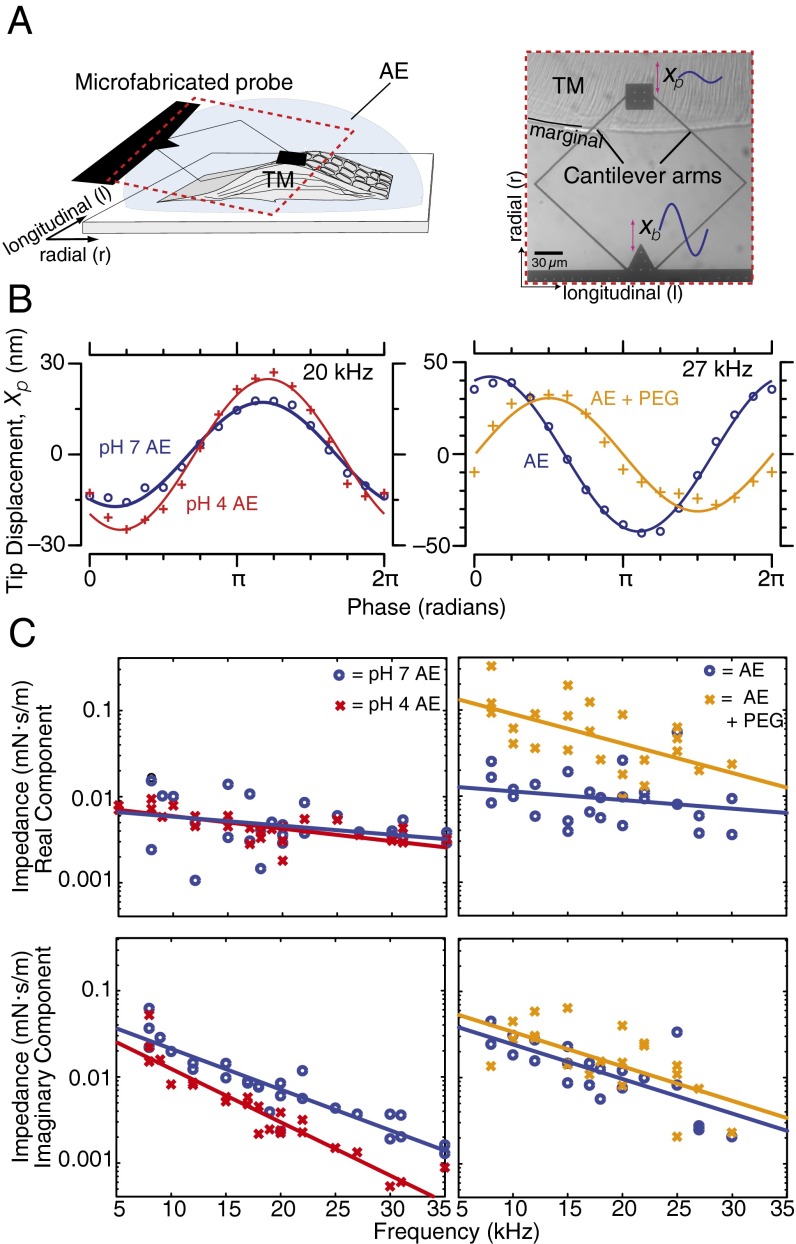
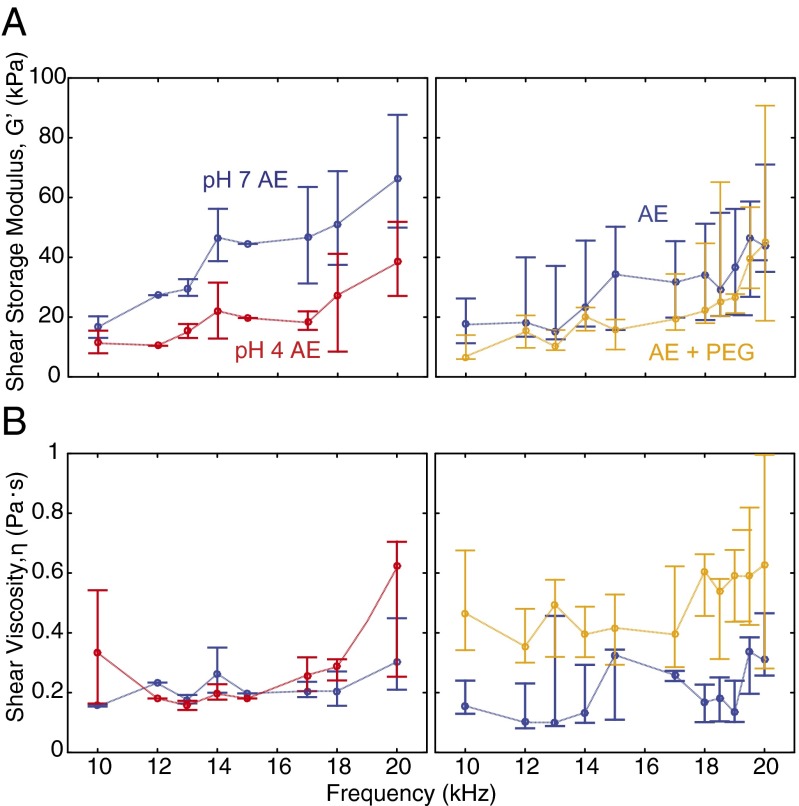
The sensory receptor cells in the inner ear are mechanically stimulated by shear motions of the overlying TM. To understand the relative contributions of TM shear stiffness and viscosity in determining motion of the TM, we developed chemical manipulations to alter these material properties selectively. Using microfabricated shearing probes, we measured TM shear impedance in three different solutions of artificial endolymph (AE) (Fig. 1A, Materials and Methods, and SI Materials and Methods). Fig. 1B (Left) shows results when the TM is bathed in AE at physiological and reduced pH. Fig. 1B (Right) shows results when the TM is bathed in AE with and without the addition of PEG. The frequency dependence of TM impedance in AE with reduced pH (Fig. 1C, Left; n = 4 preparations) and with added PEG (Fig. 1C, Right; n = 4 preparations) provides insight into the changes in mechanical properties induced by chemical manipulations. Decreasing bath pH had little effect on the real (lossy) component of shear impedance but significantly reduced the imaginary (stiffness) component (by $\sim$2.2-fold) of shear impedance across frequencies. In contrast to pH, adding PEG significantly increased the real component of TM shear impedance by $\sim$4.4-fold and had little effect on the imaginary component of TM shear impedance. The effects of reducing pH and adding PEG to the bath surrounding the TM were largely reversed upon reequilibration to physiological AE (Fig. S1). These results show that effects of pH and PEG on TM viscoelastic properties are complementary, and provide useful tools for probing TM wave properties.

Fig. 1.

Dynamic shear impedance of the TM in response to chemical manipulations. (A, Left) Microfabricated shear probe, consisting of a base and a shear plate connected by flexible arms, is used to apply shear forces to TM segments immersed in an AE bath. (A, Right) Optical image (40× magnification) of a basal TM segment attached to a glass slide with the shear probe engaged on the TM’s top surface. X_b, displacement of the probe base; X_p, displacement of the probe tip. (B) Representative motions of the TM in response to shear forces. (C) Real (Top) and imaginary (Bottom) components of TM shear impedance vs. frequency in normal AE and in response to reduced bath pH (Left) and elevated viscosity (Right). The line represents linear regression through data.

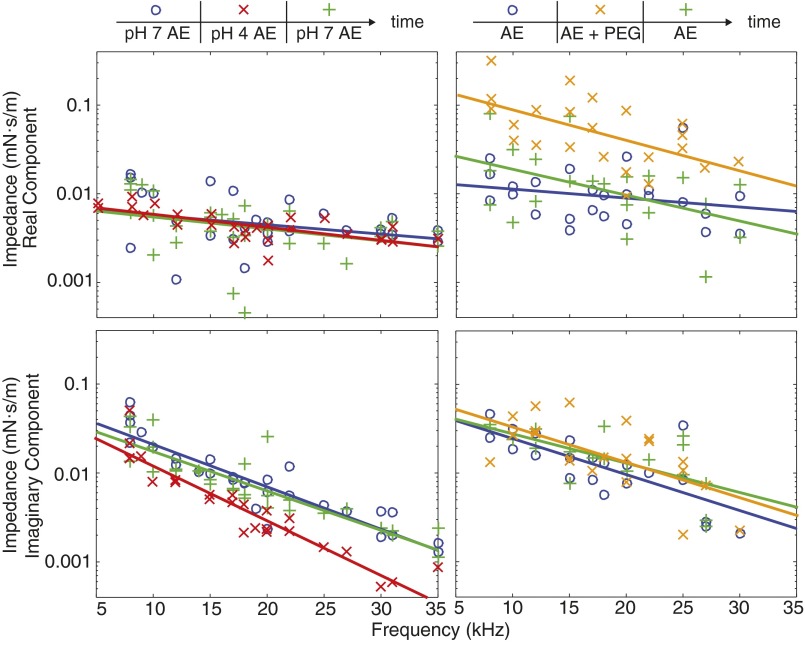
Fig. S1.

Dynamic shear impedance of the TM measured under physiological conditions (pH 7.3 AE, blue circles), in response to chemical manipulations (reduced pH, red crosses; elevated viscosity, orange crosses), and after returning the bath to physiological conditions (green plusses). (Upper Left) Reducing bath pH from 7.3 to 4 had little effect on the real component of impedance. (Lower Left) However, reducing bath pH decreases the imaginary component of impedance by a factor of $\sim$2.2-fold (averaged across all measured frequencies), and then returning the bath to pH 7.3 increases the imaginary component of impedance by a factor of $\sim$2.1-fold. (Upper Right) Increasing bath viscosity increases the real component of impedance by a factor of $\sim$4.4-fold (averaged across all measured frequencies), and returning the bath to physiological viscosity reversed the change in the real component (by a factor of $\sim$3.9-fold). (Lower Right) Both increasing bath viscosity and returning the bath to physiological viscosity had little effect on the imaginary component of impedance.

Effects of Chemical Manipulations on TM Waves.

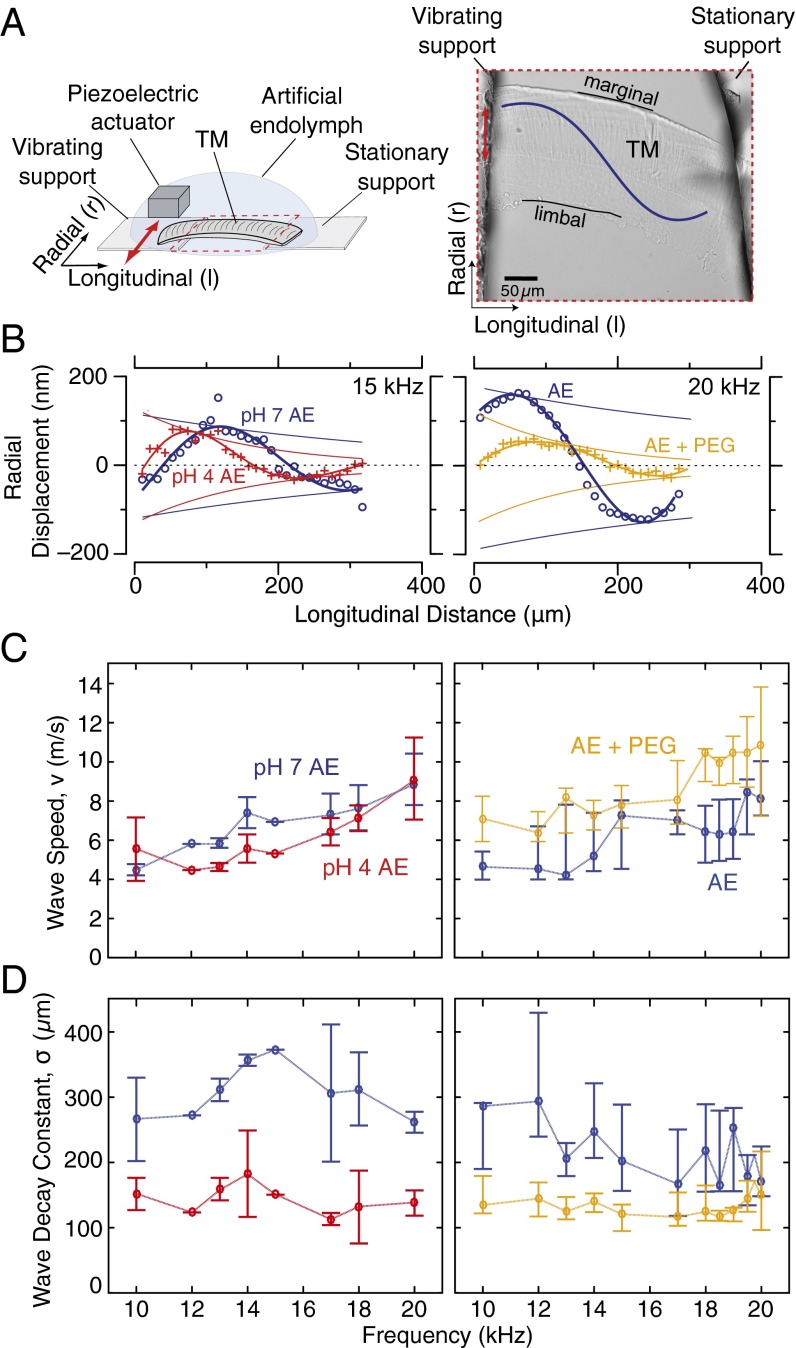
Point impedance measurements (e.g., Fig. 1) characterize local relations between force and displacement. However, motions of adjacent parts of the TM are also coupled, so that motions at one point can generate motions and forces at other points. To characterize the roles of stiffness and viscosity on coupling, we measured wave properties of isolated TMs in AE with reduced pH and added PEG (Materials and Methods). TM segments were excised from the basal turn, suspended between two supports, and immersed in a physiological AE bath (Fig. 2A). Audio frequency vibrations of a piezoelectric crystal attached to one of the supports generated radial vibrations of the TM that propagated longitudinally as traveling waves (e.g., Movie S1). Traveling waves were visualized using motion magnification algorithms (44) and quantified using a previously published computer microvision technique (45) (Materials and Methods and SI Materials and Methods). The magnitude and phase of displacement at each longitudinal position were determined from stroboscopic images at eight phases of the sinusoidal stimulus (Fig. S2). Results across longitudinal distance z (Fig. 2B) were fit to complex exponentials of the form $A{e}^{-z/\sigma }{e}^{-j2\pi z/\lambda }$ to determine wavelength λ, wave speed $V=f\lambda$ (Fig. 2C), and wave decay constant σ (Fig. 2D), where f represents frequency. Fig. 2B shows snapshots of representative TM waves under physiological conditions, in a bath with reduced pH, and in AE with PEG [15 mM and 8 kDa, which increases bath viscosity by 8.9-fold (46)].

Fig. 2.

TM wave measurements in response to chemical manipulations. (A, Left) Schematic drawing of TM wave chamber showing the position of the TM relative to the piezoelectric actuator, optics, and support structures. (A, Right) Optical image (20× magnification) of a basal TM segment attached between two supports. (B, Left) TM wave snapshot in AE at pH 7.3 (blue) and following equilibration in an AE bath at pH 4 (red). (B, Right) TM wave snapshot in AE (blue) and after increasing bath viscosity with addition of 15 mM 8-kDa PEG (orange). (C, Left) TM wave speed (median and interquartile range) in AE at physiological pH and following reduction to pH 4 (n = 4 preparations). (C, Right) TM wave speed in AE and in a high-viscosity bath equilibrated with PEG (n = 7 preparations). Wave speeds dropped slightly at most measured frequencies in response to low pH, whereas high viscosity caused an increase in wave speed across all frequencies. (D) TM wave decay constants (median and interquartile range) in AE at physiological pH and following reduction to pH 4. TM wave decay constants in AE and in a high-viscosity bath equilibrated with PEG. In AE with physiological viscosity, TM wave decay constants ranged from 160 to 450 μm at 10–20 kHz, whereas increasing bath viscosity caused a decrease in the wave decay constant (medians below 150 μm) at every measured frequency.

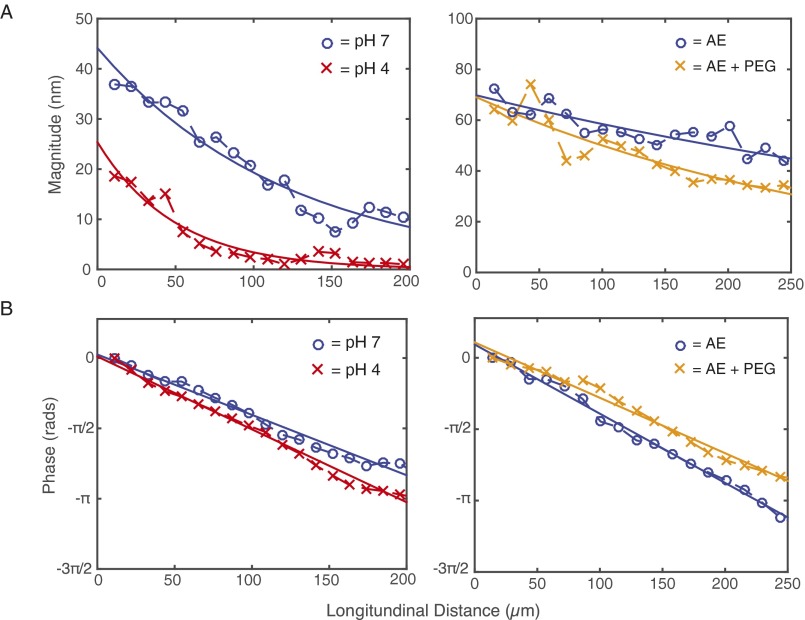
Fig. S2.

TM displacements vs. longitudinal distance at a stimulus frequency of 18 kHz for TM segments from Fig. 2. Magnitude (A) and phase (B) of displacement at pH 7 (blue circles) and pH 4 (red crosses) (Left) and in physiological AE (blue circles) and increased bath viscosity (orange crosses) (Right).

Pooled results for frequencies from 10 to 20 kHz were compared for TMs bathed in normal AE (n = 13 preparations), reduced pH (n = 4 preparations), and increased viscosity (n = 7 preparations). Reducing bath pH from 7.3 to 4 caused only a slight decrease in wavelengths and speeds of TM waves at most measured frequencies (Fig. 2C, Left). In contrast, increasing bath viscosity to 8.9-fold the viscosity of water caused large ($\sim$49$\text{\%}$) increases in wavelengths and speeds (Fig. 2C, Right) across all frequencies.

Although reducing bath pH caused little effect on TM wave speed, it did have a significant effect on decay constants. Reducing bath pH from pH 7.3 to pH 4 caused the spatial extent of TM waves to drop by $\sim$42$\text{\%}$ (Fig. 2D, Left). Similar to the changes in wave properties caused by reducing pH, increasing bath viscosity caused a reduction in the spatial extent of TM waves by $\sim$58$\text{\%}$ across all frequencies (Fig. 2D, Right).

Viscoelastic Model of Traveling Waves and Material Properties of the TM.

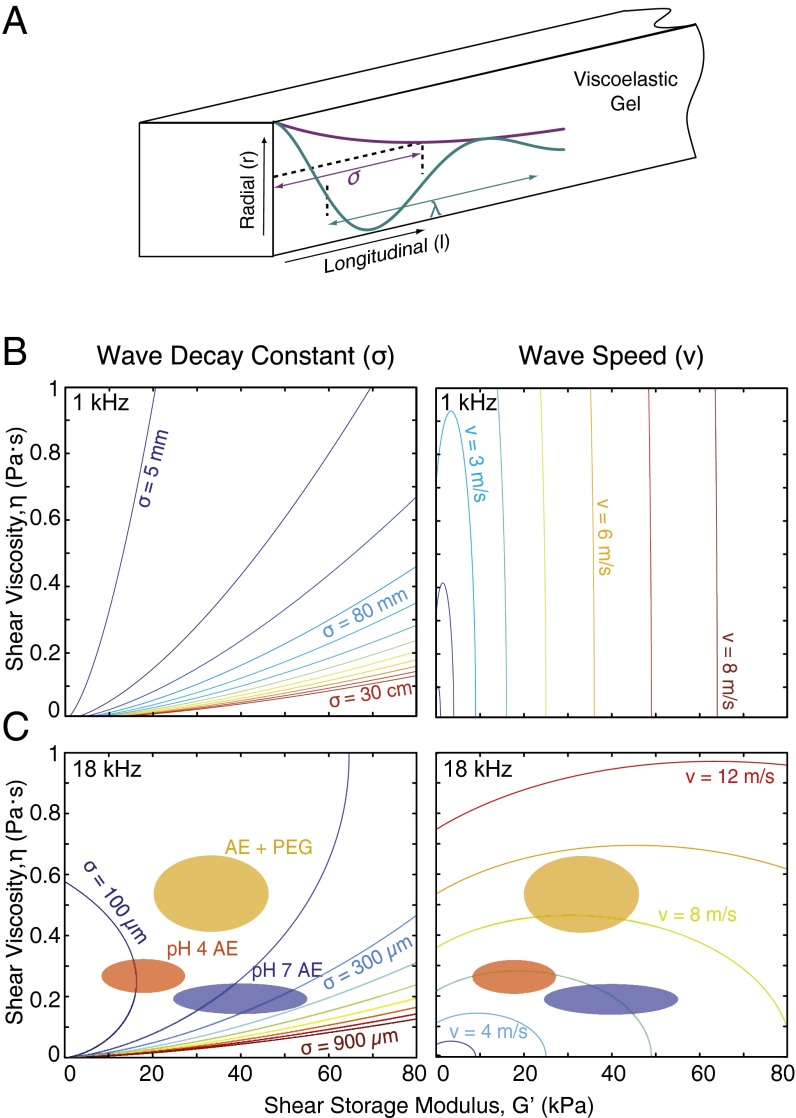
We observed a simple relationship between the chemical manipulations applied to the TM and impedance measurements: (i) Adding PEG to the bath increased the real part of the point impedance with little change in the imaginary part, suggesting that the effect was predominantly viscous, and (ii) lowering bath pH decreased the imaginary part with little change in the real part, suggesting that the effect was predominantly stiffness. However, both chemical manipulations altered both the speed and decay of TM waves. To understand the relation between these results, we analyzed an analytical model of viscoelastic gels. In this model, TM waves are represented by shearing motions of a semiinfinite viscoelastic gel. This analytical model has the advantage that wave motions can be described by two simple equations (47):

$$\mathit{\sigma }=\sqrt{\frac{2\left({G\prime }^2+{\omega }^2{\eta }^2\right)}{\rho {\omega }^2\left(\sqrt{{G\prime }^2+{\omega }^2{\eta }^2}-G\prime \right)}},$$ [1]

$$v=\sqrt{\frac{2\left({G\prime }^2+{\omega }^2{\eta }^2\right)}{\rho \left(\sqrt{{G\prime }^2+{\omega }^2{\eta }^2}+G\prime \right)}},$$ [2]

where ρ is the density of water, $G\prime$ is the shear storage modulus of the TM, η is the shear viscosity of the TM, and ω is the angular frequency.

We used this model to compute TM material properties from TM wave measurements (Fig. 3). Results were similar to results for the shearing probe (Fig. 1): Reducing bath pH tends to reduce shear storage modulus (with little change in shear viscosity), and adding PEG to the bath tends to increase shear viscosity of the TM (with little change in storage modulus). Although these results show that TM wave properties can be understood by thinking about the TM as a viscoelastic solid, they give little insight into the relatively complex dependence of TM wave properties on TM material properties. To understand this dependence better, we computed contour plots to relate wave and material properties at low (1 kHz) and high (18 kHz) frequencies (Fig. 4).

Fig. 3.

TM dynamic material properties under normal conditions, in low pH, and with high viscosity as a function of frequency (median and interquartile range). TM shear storage modulus (A) and shear viscosity (B) under physiological conditions (blue), in reduced pH (red), and with increased viscosity (orange) are shown. Reducing bath pH reduces the TM shear storage modulus, with little change in shear viscosity. Conversely, increasing bath viscosity with PEG primarily increases TM shear viscosity, with little change in the shear storage modulus.

Fig. 4.

Viscoelastic gel model predictions of TM material properties and wave properties. (A) Schematic drawing of wave propagation through a viscoelastic gel. Contours denote the range of values for wave decay constants and wave speeds at 1 kHz (B) and 18 kHz (C). Colored ellipses pasted on the decay constant and speed contours indicate mean and SD of $G\prime$ and η calculated from 17- to 19-kHz wave properties at (i) physiological bath pH and viscosity (blue), (ii) decreased bath pH (red), and (iii) increased bath viscosity with 15 mM 8-kDa PEG (orange).

At low frequencies, wave speed depends almost entirely on shear storage modulus $G\prime$ and very little on shear viscosity η (Fig. 4B). At high frequencies, the reverse is true: wave speed is affected very little by $G\prime$ and significantly by η (Fig. 4C). In both low- and high-frequency cases, the wave decay constant depends on both $G\prime$ and η. To illustrate the use of these contour plots to understand our measurements, we have plotted the mean and SDs of the wave and material properties as ellipses (Fig. 4C). Reducing pH decreases shear storage modulus with little change to shear viscosity, which reduces the wave decay constant but has little effect on wave speed. By contrast, adding PEG increases shear viscosity with little change to shear storage modulus, which decreases wave decay constant and increases wave speed. These results highlight the complex dependence of TM wave parameters on TM material properties.

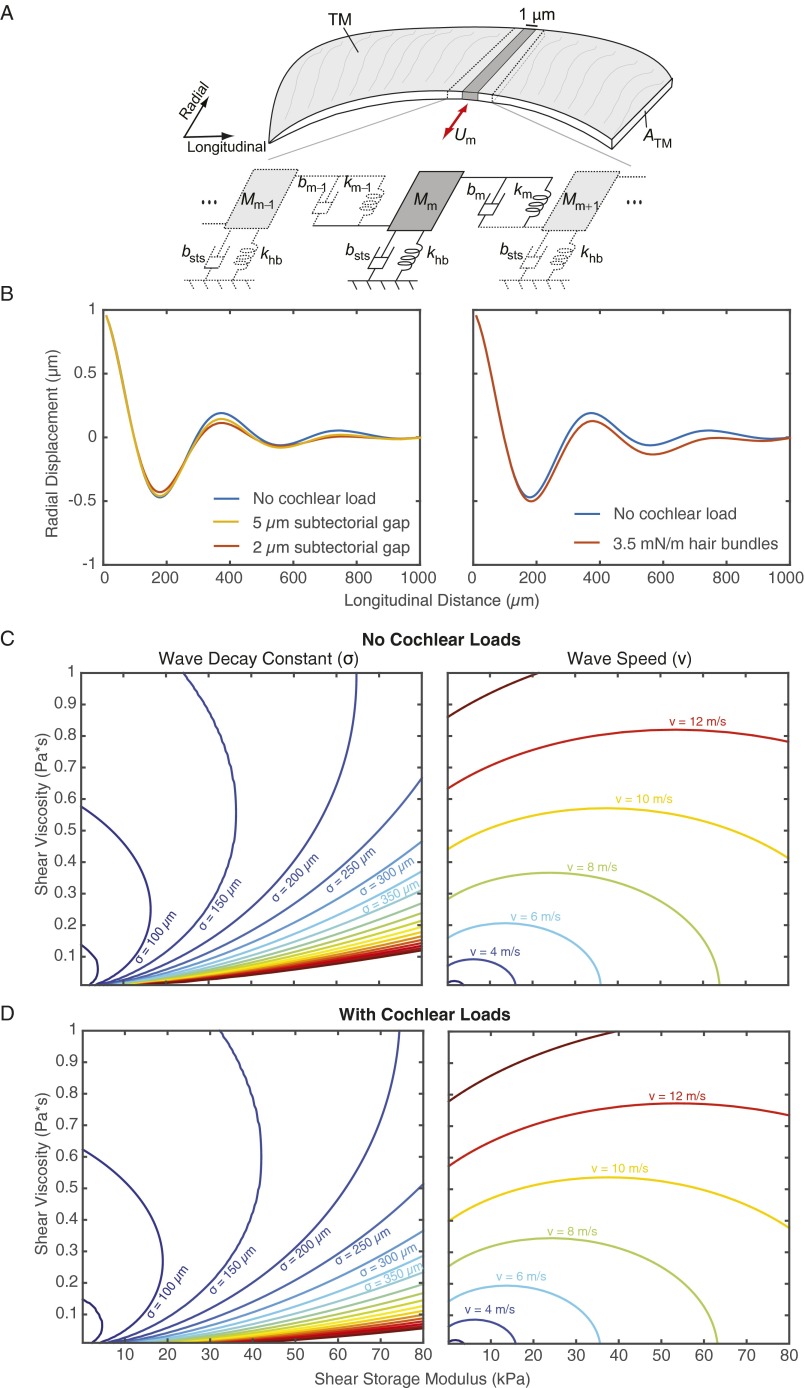
To investigate effects of cochlear loads on TM waves, we calculated the relation between wave parameters and TM material properties before and after the addition of springs to represent the mechanical loading of hair cells and dashpots to represent fluid loading in the subtectorial space (Fig. S3). Adding stiffnesses on the order of the measured stiffness of hair bundles (48) and adding damping that would result from a 2-μm subtectorial gap change wave speed and decay constants by less than $\sim$10%.

Fig. S3.

Effect of cochlear loads on a lumped parameter model of TM traveling waves. (A) TM is represented by a sequence of 1-μm longitudinal sections. Each section is represented by its mass ($M_m$), which moves with radial velocity ($U_m$), and is coupled to adjacent masses by springs ($k_m$) and dashpots ($b_m$) that represent the elastic and viscous material properties of the TM, respectively. Each mass is also loaded by a dashpot ($b_{sts}$) that represents the subtectorial fluid and by springs ($k_{hb}$) that represent the stiffnesses of underlying hair bundles. (B, Left) Loading by subtectorial fluid decreases the amplitude of the wave by less than $\sim$3% when the gap is 5 μm (yellow line) and by less than $\sim$10% when the gap is 2 μm (red line). (B, Right) Loading by hair bundles [0.0035 N/m (48)] increased the wave decay constant by ∼1% (red line). (C and D) Effect of cochlear loads on the relation between TM wave parameters and TM material properties. (C) Contours indicate wave decay constants and wave speeds at 18 kHz. (D) Adding cochlear loads due to hair bundles and fluid loss in a 2-μm subtectorial gap shifts the contours less than $\sim$10$\text{\%}$.

SI Materials and Methods

Calculating TM Impedance.

The impedance of the TM was determined by analyzing the relative motions of the TM and probe based on the following equation:

$$Z_{TM}\left(\omega \right)=k_{mp}\frac{X_b\left(\omega \right)-X_p\left(\omega \right)}{j\omega X_p\left(\omega \right)},$$ [S1]

where $X_b$ is the displacement of the probe base, $X_p$ is the displacement of the probe tip, and $k_{mp}$ is the stiffness of the probe in the radial direction (57 mN/m).

Optical Imaging System.

The computer vision system consisted of an optical light microscope with magnifications of 20× (wave measurements) and 40× (point impedance measurements), water immersion objectives (0.5 N.A. and 0.75 N.A, respectively; Zeiss Axioplan; Carl Zeiss), and a transmitted-light condenser (0.8 N.A.). Images were captured with a 5-megapixel CCD camera (Stingray; Allied Vision Technologies). A stroboscopically pulsed light-emitting diode was synchronized with the piezoelectric actuator used in both shear impedance and wave measurements. The TM was illuminated, and images were captured at eight evenly spaced phases over several cycles. The collected images were then analyzed with motion-tracking algorithms (45) to determine the magnitude and phase of TM displacement at multiple regions of interest along the surface of the TM in both the point impedance and wave measurements.

Discussion

Chemical Manipulations to Test the Role of Stiffness and Viscosity on TM Dynamics.

Although it is widely accepted that the TM is a viscoelastic structure (13, 16, 32, 49), the relative contributions of viscosity and stiffness to TM dynamics have not previously been examined systematically. In this study, we have developed a method to modulate TM dynamic properties by altering the pH and viscosity of the bath surrounding the TM. Results (Fig. 4) show that decreasing pH caused the shear storage modulus of the TM to decrease by nearly a factor of 2 (from 49.8 $\pm$ 14.5 to 22.1 $\pm$ 11.2 kPa, mean $\pm$ SD; range: 17–19 kHz) with little change in shear viscosity (from 0.21 $\pm$ 0.040 to 0.27 $\pm$ 0.044 Pa⋅s). In contrast, increasing bath viscosity increased the loss modulus of the TM by nearly a factor of 3 (from 0.19 $\pm$ 0.07 to 0.51 $\pm$ 0.13 Pa⋅s) with little change in shear storage modulus (from 34.9 $\pm$ 14.0 to 28.4 $\pm$ 14.0 kPa). Furthermore, both of these manipulations are almost completely reversible (Fig. S1). Thus, we can alter the chemical composition of the bath to alter TM dynamic material properties selectively and reversibly.

Frequency-Dependent Effects of Stiffness and Viscosity on TM Waves.

By chemically modulating TM material properties, we demonstrated that changes in material properties have a profound effect on wave speeds and decay constants. In particular, we showed that at high frequencies, reducing TM stiffness primarily results in a decrease in TM wave decay constant, whereas increasing TM viscosity results in an increase in TM wave speed and a decrease in TM wave decay constant (Fig. 2). These measurements fit our model predictions of shear viscosity and shear storage modulus on wave behavior (Fig. 4). The viscoelastic contour plots at low frequencies (Fig. 4B) reveal that wave speed is controlled almost exclusively by shear storage modulus at physiological conditions. In contrast, at high frequencies, speed is primarily determined by shear viscosity (Fig. 4C). This result is counterintuitive. Typically, the storage element in a transmission line controls the speed; here, we see that the loss element plays a more important role in determining wave speed at high frequencies. Thus, at high frequencies, viscous coupling of the TM must be precisely maintained to allow the TM wave speeds to match the wave speeds of the BM wave for effective cochlear amplification (50, 51).

TM Stiffness and Viscosity Are Both Essential for Maintaining Longitudinal Spread of Mechanical Excitation.

The viscoelastic contour plots (Fig. 4 B and C) reveal that both TM shear viscosity and shear storage modulus play significant roles in controlling TM wave decay constants at all frequencies. Small changes from the physiological values of either $G\prime$ or η cause nearly proportional changes in wave decay constants. Changes to both TM shear storage modulus and shear viscosity alter longitudinal coupling at all frequencies, and thereby change longitudinal spread of mechanical excitation through TM waves. These wave decay constant contour plots thus provide a basis for evaluating alterations to TM dynamics, and their effects on spread of mechanical excitation in the cochlea.

Effects of Cochlear Attachments.

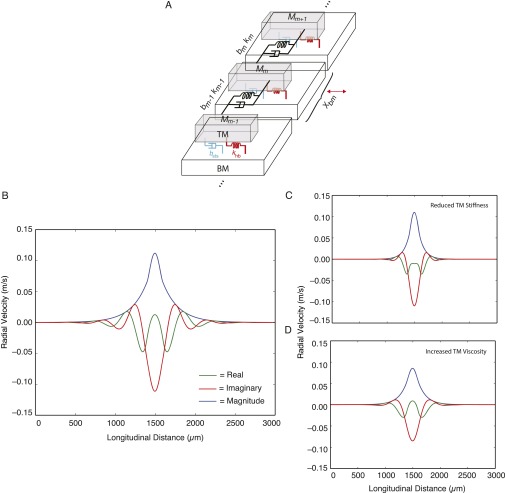
In this study, we investigated response properties of TMs that were isolated from their normal cochlear attachments. In vivo, we expect cochlear attachments to stimulate motions of the TM and present loads that could alter wave propagation. We investigated these possibilities with a model in which the TM was represented as a distributed series of masses coupled by viscous and elastic elements, the BM was represented by an underlying parallel plate, hair bundles were represented as discrete springs, and subtectorial fluid was represented as Couette flow (Fig. S4A). In the absence of BM motion, the hair bundles and subtectorial fluid had little effect on properties of TM waves (Fig. S3 B–D).

Fig. S4.

TM wave propagation in the presence of surrounding cochlear structures. (A) Distributed impedance model of the TM, where hair bundles and the subtectorial space act both as a load on the TM and as force generators by which the BM can excite forces on the TM. (B) Real (green) and imaginary (red) components and magnitude (blue) of TM velocity in response to stimulating a 200-μm region of the BM ($X_{bm}$) at 20 kHz with a constant velocity of 1 m/s. Parameters are as follows: TM width of 30 μm (marginal edge to start of limbal attachment), TM height of 50 μm, TM segment length of 1,000 μm, subtectorial gap size of 2 μm, hair bundle stiffness of 0.0035 N/m, TM shear storage modulus of 47 kPa, and TM shear viscosity of 0.22 Pa⋅s. (C) TM velocity at reduced shear storage modulus (23 kPa). (D) TM velocity at increased shear viscosity (0.60 Pa⋅s).

In addition to generating loads, the subtectorial fluid and hair bundles couple the BM and TM, thereby providing a means by which the BM can launch TM waves. Oscillating a portion of the BM with constant radial velocity launched waves on the TM (Fig. S4) with similar decay constants to those decay constants observed in Fig. 2 for the isolated preparation at physiological conditions (Fig. S4B), reduced stiffness (Fig. S4C), and increased viscosity (Fig. S4D). These results show that the impedance of a portion of the TM is comparable to impedance of the hair bundles and subtectorial space in that portion. In a sense, the impedance of the TM is “matched” to the impedance of the structures that couple the TM to the organ of Corti (i.e., the impedance of the TM is small enough to be stimulated by subjacent structures but large enough to resist the decay of traveling waves).

Implications for Cochlear Tuning Mechanisms.

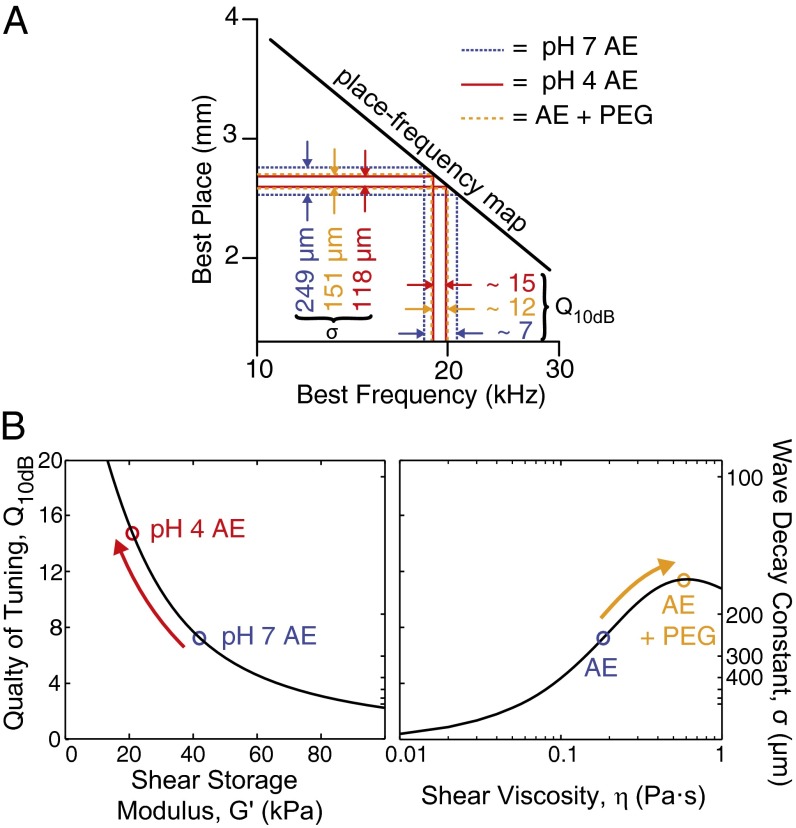
Previous cochlear models have represented the TM as a resonant structure that plays an important role in cochlear tuning (25–29). However, the presence of TM waves demonstrates substantial longitudinal coupling, which has an impact on response properties at each longitudinal location. Consider a simple model of the cochlea that consists of a bank of resonators tuned for higher frequencies at the base and progressively lower frequencies near the apex. In such a model, longitudinal coupling would tend to increase the sensitivity of each resonator to neighboring best frequencies, and thereby broaden the apparent tuning of each resonator. The TM wave decay constant provides a measure of the distance over which TM coupling is significant. This distance spans some range of best frequencies as given by the cochlear map, and this range of best frequencies determines an effective quality of tuning Q (Fig. 5A). For physiological bath conditions, the $Q_{10dB}$ predicted from TM wave decay constants closely matches measurements from neural recordings (52).

Fig. 5.

Relationship between TM material properties and tuning. (A) TM wave decay constants, in conjunction with the slope of a place-frequency map, are used to calculate quality of tuning. The solid black line represents the relation between best place and best frequency (54). Horizontal lines and single-sided arrows denote the spatial extent of TM waves (i.e., wave decay constants) for TMs at physiological conditions (mean of 17–19 kHz, blue, 249 μm), with increased viscosity (orange, 146 μm), and reduced pH (red, 118 μm). Vertical dashed lines and single-sided arrows denote the frequency bandwidth around the best frequency. The ratio of frequency bandwidth and best frequency yields ${\text{Q}}_{10dB}$ in physiological conditions ($\sim$7), with increased bath viscosity ($\sim$12), and with reduced bath pH ($\sim$15). (B) Tuning quality factor (${\text{Q}}_{10dB}$) estimates determined from the viscoelastic model as a function of shear storage modulus and shear viscosity at 18 kHz. Open circles indicate ${\text{Q}}_{10dB}$ predicted from experimental conditions (mean of 17–19 kHz). (Right) ${\text{Q}}_{10dB}$ estimates increase with increasing shear viscosity, η, when the shear storage modulus is fixed (40 kPa). (Left) In contrast, ${\text{Q}}_{10dB}$ estimates decrease with increasing shear storage modulus, $G\prime$, when shear viscosity is fixed (0.20 Pa⋅s).

Because wave decay constants depend on stiffness (Fig. 4) and the $Q_{10dB}$ depends on wave decay constants (Fig. 5A), it follows that $Q_{10dB}$ will depend on stiffness as well. Estimates of $Q_{10dB}$ as a function of shear storage modulus show that increasing TM stiffness broadens cochlear tuning (Fig. 5B, Left). Strikingly, the opposite trend is predicted in resonant models of the TM, where increasing TM stiffness would give rise to sharper cochlear tuning.

TM wave decay constants also depend on shear viscosity, which suggests that in addition to stiffness, $Q_{10dB}$ would depend on TM shear viscosity. Estimates of $Q_{10dB}$ as a function of TM shear viscosity show that increasing shear viscosity sharpens cochlear tuning (Fig. 5B, Right). This finding further contradicts resonant models, in which increasing viscous damping would tend to broaden cochlear tuning. Thus, the effects of stiffness and viscosity in controlling tuning via TM waves are opposite in direction and fundamentally different from resonant models of the TM.

Materials and Methods

Isolated TM Preparations.

The cochleae of adult mice (strains 129SvEv/C57BL6J, B6129F1, and CD-1; 4–8 wk old) were excised using a previously published surgical technique (53). No strain-dependent differences were found. The organ of Corti and TM were exposed by chipping away the bony enclosure of the cochlea. We used transmitted light illumination to visualize the TM spiraling around the cochlear turns. Using a sterilized eyelash, segments of the TM were teased apart from the basal turn of the cochlea. These TM segments were kept in an AE solution containing 174 mM KCl, 5 mM Hepes, 3 mM dextrose, 2 mM NaCl, and 0.02 mM CaCl₂ (equilibrated at pH 7.3 at room temperature). The care and use of animals in this study were approved by the Massachusetts Institute of Technology Committee on Animal Care.

Measuring TM Point Impedance.

Radial TM shear impedance was measured using microfabricated probes (18). The probe design consisted of a base structure that was driven by a piezoactuator, a 30 × 30-μm shearing plate, and flexible arms that connected the base structure to the plate. To measure TM point impedances, basal TM samples were first immersed in AE and adhered to a glass slide using commercially available bioadhesive (Cell-Tak; Collaborative Research). The microfabricated shear probe’s shearing plate was then engaged on the surface of the TM using a micromanipulator (Rucker and Kolls). The relative motion of the shearing plate and the base depends on the relative impedance of the TM and the cantilever arms. The shearing plate was designed to approximate the shear forces exerted by a cluster of hair bundles. To reduce variability caused by radial gradients in stiffness, the shearing plate was centered on Hensen’s stripe. The base of the probe was stimulated in the radial direction using the piezoelectric actuator across a broad range of frequencies (5–35 kHz) with displacements of $\sim$0.5–1 μm. The impedance of the TM was determined by analyzing the relative motions of the TM and probe (SI Materials and Methods, Calculating TM Impedance).

Measuring TM Wave Properties.

Isolated TM segments were suspended between vibrating and stationary supports in a wave chamber (17, 30). The vibrating support consisted of a piezoelectric actuator (Thorlabs) that delivered oscillatory motions at audio frequencies (10–20 kHz). The stationary support was firmly attached to the underlying glass slide. Both supports were coated with 2 μL of tissue adhesive (Cell-Tak) and perfused with AE. The TM was then injected into the AE bath and carefully attached to the surfaces of the supports in the regions coated with Cell-Tak. TM wave motions were generated by stimulating the piezoelectric actuator coupled to the vibrating support. These motions launched longitudinally propagating waves in the radial direction. TM motions were then fit with a decaying sinusoid to extract wave motion parameters. These fits had two free parameters: wavelength (λ, distance the wave travels while going through a full cycle of motion) and wave decay constant (σ; distance the wave travels before dissipating by a factor of e in amplitude).

TM Point Impedance and Wave Properties in PEG-Buffered AE.

We added PEG (15 mM of 8-kDa PEG; Sigma–Aldrich) to the AE bath surrounding the TM to alter the shear viscosity of the TM. To ensure equilibration of PEG, the bath (5 mL) was exchanged four times over the course of ∼5 min. The final solution was equilibrated for 5 min before TM shear impedance and wave measurements. Once measurements were completed, the bath was reequilibrated to normal AE and wave measurements were repeated.

TM Point Impedance and Wave Properties in pH 4-Buffered AE.

In a separate set of experiments, we altered the pH of the bath surrounding the TM by exchanging AE equilibrated at pH 7.3 with AE at pH 4. To ensure equilibration, the bath surrounding the TM was perfused continuously for 5 min and monitored for changes in pH levels. TM shear impedance and wave measurements were completed under physiological conditions (pH 7.3) and at pH 4. Each test bath was perfused twice to test for repeatability.