Coexistence of both gyroid chiralities in individual butterfly wing scales of Callophrys rubi

Significance

Arthropod biophotonic nanostructures provide a plethora of complex geometries. Although the variety of geometric forms observed reflects those found in amphiphilic self-assembly, the biological formation principles are more complex. This paper addresses the chiral single gyroid in the Green Hairstreak butterfly Callophrys rubi, robustly showing that the formation process produces both the left- and right-handed enantiomers but with distinctly different likelihood. An interpretation excludes the molecular chirality of chitin as the determining feature of the enantiomeric type, emphasizing the need to identify other chirality-specific factors within the membrane-based biological formation model. These findings contribute to an understanding of nature’s ability to control secondary features of the structure formation, such as enantiomeric type and crystallographic texture, informing bioinspired self-assembly strategies.

Abstract

The wing scales of the Green Hairstreak butterfly Callophrys rubi consist of crystalline domains with sizes of a few micrometers, which exhibit a congenitally handed porous chitin microstructure identified as the chiral triply periodic single-gyroid structure. Here, the chirality and crystallographic texture of these domains are investigated by means of electron tomography. The tomograms unambiguously reveal the coexistence of the two enantiomeric forms of opposite handedness: the left- and right-handed gyroids. These two enantiomers appear with nonequal probabilities, implying that molecularly chiral constituents of the biological formation process presumably invoke a chiral symmetry break, resulting in a preferred enantiomeric form of the gyroid structure. Assuming validity of the formation model proposed by Ghiradella H (1989) J Morphol 202(1):69–88 and Saranathan V, et al. (2010) Proc Natl Acad Sci USA 107(26):11676–11681, where the two enantiomeric labyrinthine domains of the gyroid are connected to the extracellular and intra-SER spaces, our findings imply that the structural chirality of the single gyroid is, however, not caused by the molecular chirality of chitin. Furthermore, the wing scales are found to be highly textured, with a substantial fraction of domains exhibiting the <001> directions of the gyroid crystal aligned parallel to the scale surface normal. Both findings are needed to completely understand the photonic purpose of the single gyroid in gyroid-forming butterflies. More importantly, they show the level of control that morphogenesis exerts over secondary features of biological nanostructures, such as chirality or crystallographic texture, providing inspiration for biomimetic replication strategies for synthetic self-assembly mechanisms.

Although the formation of chiral structures is fascinating, their occurrence can often be rationalized by simple energy or free energy considerations without a need to resort to their possible biological origin. For example, handed structures are observed in the simplest models of phyllotaxis (1) and self-assembly of biological fibers (2). In such models, there is no energetic distinction between and hence, a balance of the two enantiomers [that is, the right-handed (RH) and left-handed (LH) versions of the chiral structure]. Chiral symmetry breaking, the process by which one enantiomer occurs exclusively or with prevalence, is commonly observed in biological materials on a range of scales from molecular dimensions and the structure of DNA to the macroscopic size of snails (3). The dominance of one enantiomer is driven by the presence of a force or molecular building block that favors one enantiomer over the other; constituent chiral molecules (4), genetically controlled molecular pathways (3), and biological generation of torque (5) are possible causes.

Here, we investigate the chiral symmetry breaking of the single-gyroid structure, a complex network-like ordered nanostructure observed in the wing scales of various butterfly species, including Callophrys rubi (6–9), and other arthropod species (10). The gyroid geometry, which serves as biophotonic crystals, has cubic symmetry (I4₁32) and is characterized by the topologically particularly simple srs-net (the label for the chiral degree-three network modeled on SrSi2) (11). As a chiral structure, it can be realized as one of two enantiomers (related by mirror symmetry) that are here called RH and LH. [By convention, we refer to the enantiomer of the single gyroid as LH, which has a screw axis along the <111> direction centered within the void domain that is an LH helix (compare with Fig. 3A, row 4). An RH helix is defined by (x, y, z)(t) = (cos t, sin t, t) for t = [0,4π] in a conventional RH coordinate system. For the so-defined LH single-gyroid enantiomer, this convention implies that the parallel screw axis along the same direction but centered within the solid domain is RH, that the 4₁ screw axis along the <100> direction centered within the void domain is RH (compare with Fig. 3A, row 3), and that the screw axis along the <100> direction centered within the solid domain is LH. The enantiomer displayed in figure 2 in ref. 12 is LH.] The chirality of the single gyroid is complicated by the presence of the distinct screw axis of opposite handedness (12). Our results provide a clear indication that nature’s morphogenesis of this complex nanostructure exerts control over secondary features of the formed complex nanostructure, leading to specific enantiomeric form and specific crystallographic texture (meaning the occurrence of preferential crystal orientation of the micrometer-sized gyroid domains with regard to the wing scale surface). Within the wing scales, the single gyroid is realized at a large length scale (lattice parameters around 300 nm), well beyond the size of the constituent molecular components. This length scale leads to structural coloration effects caused by photonic crystal properties of the gyroid in the visible or near-UV spectrum. The chiral geometry suggests possible circular polarization effects (13), which have been observed in nanofabricated replica and used for proposed biomimetic nanoengineered devices (14). Given the biological precedence of circular polarization-sensitive vision [mantis shrimp (15)] and the range of strongly circularly polarizing biological materials (16–19) (based on Bouligand structures reminiscent of cholesteric liquid crystal phases), circular polarization effects in the butterfly wing scales would seem to be a possibility, but direct measurements of macroscopic reflections fail to detect a circular polarization signal (12, 20).

Fig. 3.

Exemplary ET datasets of two crystallites with opposite chirality. (A) LH srs-net and (B) RH srs-net. In row 1, STEM images from the respective tilt series (horizontal tilt axis) of the investigated crystallites are shown with direct view along the fourfold [001] zone axes. Row 2 shows representations of the tomograms (volume rendering; parallel view and visualization adapted to match the respective STEM projections in row 1) of the respective crystals; Insets show surface renderings of smaller parts of the crystallites. In rows 3 and 4, perspective views along the pore channels of the tomograms and the respective views in the theoretical gyroid structure are shown (compare with Fig. 1D). The directions of the channels within the respective crystallites are indicated by circles ([001]) and arrows ([111]). Fig. S2 shows the respective views in the tomograms along the [111] zone axes. Movies S1 and S2 show animations of the tomograms from A and B.

In light of their role for circular polarization effects, it has been questioned by Saranathan et al. (6), Mille et al. (21), and Saba et al. (12) whether both single-gyroid enantiomers occur within the wing scales of C. rubi (racemic mixtures with equal proportions of RH and LH enantiomers would clearly annihilate any circular polarization signal). Saranathan et al. (6) proposed the existence of both chiralities from SEM images of the scale surface. Mille et al. (21) reported that the RH and LH gyroid networks occur with a ratio of 1:7, which was as well derived from SEM images. Because reliable chirality information is hard to obtain only from single projections or surface topography images, single-image transmission electron microscopy (TEM) or SEM techniques make it difficult to identify the enantiomeric type of a given single-gyroid structure (22). Small-angle X-ray scattering, which has been successfully used to identify the geometric forms observed across a large sweep of arthropod species, cannot be used to identify the enantiomeric type.

A second important aspect is the relative orientation of the nanostructured crystallites (that is, the degree of crystallographic texture). It is an essential determinant of color uniformity, because the photonic properties of the single gyroid strongly depend on the crystal orientation (12, 23). Yoshioka et al. (9) observed a highly textured crystal orientation within scales of the butterfly Parides sesostris. Although the scales of P. sesostris exhibit a multicrystalline structure on the micrometer scale, they appear to be rather uniform in color, which is linked to the preferential orientation of the nonchiral <110> direction of the individual crystallites parallel to the surface normal of the scales. This kind of crystallographic texture is not expected for C. rubi, because the crystallites differ in color and light intensity, which is clearly visible in the light microscopy images (Figs. 1 A and B and 2A).

Fig. 1.

Butterfly C. rubi and its wing scales microstructure. (A) Photo of the ventral side of C. rubi. (B) Light microscopic image (reflection mode) of its hindwing ventral surface showing hundreds of scales attached to the wing—the shimmering, mostly green scales contain the gyroid structure (imaged region marked by the black rectangle in A). (C) SEM image (top view) of the ventral scale surface indicating the periodic gyroid structure. (D) Model of the expected gyroid structure (2 × 2 × 2 unit cells), with a chitin volume fraction of 0.3 along (Left) the oppositely handed fourfold screw axis <001> and (Right) the threefold screw axis <111> (a formal description of the gyroid is in SI Text).

Fig. 2.

Microscopic analysis of microstructure and sample preparation for ET. (A) Light microscopic image (reflection mode) of a single scale comprising differently oriented interconnected nanostructured crystallites, which reflect the incoming light in a varying spectral range and intensity. (B) STEM image of a single scale with several adjacent crystal domains. (C) Light microscopic image of several butterfly wing scales glued onto a Cu grid with rectangular holes. (D) Low-magnification STEM image of a scale after machining a defined bar with several adjacent crystallites by FIB milling. The original scale outline is indicated by the dotted line, whereas the removed regions are dashed in magenta. (E) STEM image of such a typical bar. The distinct contrast in the STEM images is interpreted in local projected mass density, because the solid material consists of amorphous chitin (bright), whereas the pores are unfilled (dark).

The level of structural detail described by our study is only accessible because of advances in 3D imaging technology for biological tissue and materials. Systematic application of scanning TEM (STEM) electron tomography (ET) here enables us to obtain sufficiently detailed and reliable real-space spatial data to assert firmly the chirality of the crystallites and the orientation relation of crystallites within single butterfly wing scales of C. rubi. Although individual tomograms have been analyzed for specific biological tissue [including bluebird feathers (24), the butterfly Teinopalpus imperialis (25), and also, C. rubi (8)], our study clearly shows the potential that systematic application of ET holds for understanding the finer but important secondary characteristics, such as chirality or crystallographic texture, for biological matter.

Results

A photograph of a butterfly of the investigated species C. rubi is shown in Fig. 1A. The ventral side of its wings is covered by approximately rectangular scales (compare Fig. 1B with Fig. 2A), which are composed of a self-supporting chitin structure with a thickness of a few micrometers containing differently oriented interconnected nanostructured crystallites with a diameter of up to 10 µm (Figs. 1C and 2 A and B). Fig. 2A shows a light microscopic image with these nanostructured crystal domains being distinguishable by reflecting light (in a spectral range from yellow to blue with varying intensities). The clear correlation between those separated regions (Fig. 2A) and the highly crystalline domains in SEM (Fig. 1C) and especially, STEM imaging (Fig. 2B) can be drawn. Single scales glued onto a TEM grid before focused ion beam (FIB) preparation are depicted in Fig. 2C. The STEM image in Fig. 2B clearly shows the highly periodic structure of several crystallites, which cover the whole scales and are connected to parallel arranged ribs (bright horizontal line contrast) and cross-ribs (compare with Fig. 1C). Those ribs are supposed to provide mechanical stability of the scales and furthermore, serve as additional interference reflectors (26). To optimize the sample geometry for ET, we used a dual-beam FIB instrument to produce a bar geometry by systematically removing material from the scales as shown in Fig. 2D (details in Methods). The bars with a width of around 2 µm typically comprise a few interconnected crystallites (Fig. 2E), which are accessible for tilt-series acquisition (Fig. S1 shows a scheme of ET). The bar geometry assures minimal projected sample thickness at high tilt angles, which drastically enhances the quality of the 3D reconstructions, enabling reliable evaluation of the chiral gyroid morphology. Like the single STEM images in Figs. 2B, 3, and 4, the resulting 3D reconstructions exhibit chitin-filled space that can be clearly distinguished from the unfilled pore channels (Fig. 3). Here, the gyroid surface divides space into one subvolume filled with chitin and the empty pore system (Figs. 1–3). The pore channels of this gyroid structure exhibit a threefold symmetry with a certain handedness along the <111> axis and a fourfold symmetry with opposite handedness along the <001> axis (compare with Fig. 1D). The network exhibiting an LH screw along <111> is defined as LH srs-network, and the one with an RH screw along <111> is named RH srs-net (13, 22). All reconstructed crystallites contain several unit cells of the expected cubic gyroid structure, from which the chirality of each crystallite is determined.

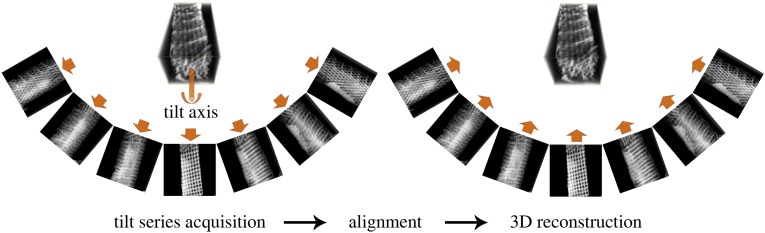
Fig. S1.

Scheme of ET. A tilt series of projections (same for both bright-field TEM and STEM tomography) from different viewing angles of an object (here, butterfly wing scale crystallites) is acquired and aligned to a common tilt axis. The aligned tilt series is then used to reconstruct the 3D structure of the butterfly wing scales.

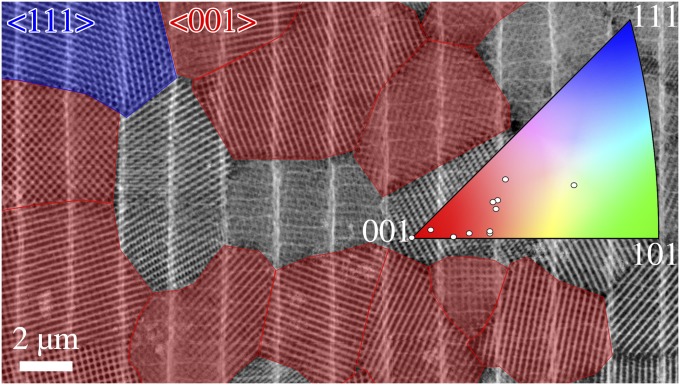
Fig. 4.

Crystallographic texture analysis of butterfly wing scales. STEM overview image with viewing direction perpendicular to the scale surface (larger overviews are in Figs. S3 and S4)—crystallites exhibiting a fourfold symmetry (<001> axes oriented very close or parallel to the scale surface normal) are highlighted in red, and those with a threefold symmetry (<111> axes oriented parallel to the scale surface normal) are highlighted in blue (<101> zone axes are not considered, because they are very hard to identify from projections only). Inset shows the partial inverse pole figure displaying the orientation of the scale surface normal w.r.t. the 12 reconstructed crystallites.

Fig. S2.

ET datasets of two crystallites (different scales) with opposite chirality. (A) The crystal domain in Fig. 3A oriented nearly along its threefold symmetry axis [111]: (Upper Left) STEM image from the respective tilt series (tilt angle of +60°), (Lower Left) representation of the tomographic reconstruction (volume rendering; parallel view and visualization adapted to match the respective STEM projection), (Lower Right) surface rendering (parallel view; viewing direction indicated with an arrow in Fig. 3A) of a smaller part of the crystallite, and (Upper Right) magnified perspective view of the surface rendering. (B) The crystal domain in Fig. 3B oriented along its threefold symmetry axis [111]: (Lower) surface rendering (parallel view; viewing direction indicated with an arrow in Fig. 3B) of a smaller part of the crystallite and (Upper) magnified perspective view of the surface rendering.

The tomographic reconstructions of two exemplary gyroid crystals from different scales of the same butterfly (Fig. 3) unambiguously reveal that both possible mirror symmetric chiralities are found. Rows 3 and 4 in Fig. 3 show magnified perspective views along the respective zone axes ([001] and [111]) into the reconstructed tomograms and the theoretically expected gyroid surfaces (volume fraction of 0.3). In total, 12 crystallites from four different wing scales of one butterfly were characterized. Ten of them exhibit LH srs-nets, whereas only two are RH crystals (Table S1). From a statistical point of view, this strongly indicates (with a significance level <5%) that both chiral networks appear but with unequal probabilities (a significance test is in SI Text). Both RH crystallites were directly situated adjacent to crystals with opposite chirality (LH srs-net). In one measurement, we were even able to reconstruct three neighboring crystallites, where two LH ones directly bordered one RH crystal. However, another longer bar contained only five LH crystals in a row.

Table S1.

Characteristics of reconstructed photonic crystal domains

Crystallite	Chitin fraction	Chirality	a1/nm [100]	a2/nm [010]	a3/nm [001]
1	0.34 ± 0.08	LH srs	332	292	261
2	0.31 ± 0.05	LH srs	349	289	226
3	0.32 ± 0.06	LH srs	379	247	242
4	0.35 ± 0.05	RH srs	340	285	233
5	0.28 ± 0.03	LH srs	377	248	239
6	0.29 ± 0.03	RH srs	332	266	245
7	0.30 ± 0.03	LH srs	320	296	234
8	0.29 ± 0.03	LH srs	352	255	292
9	0.29 ± 0.03	LH srs	387	271	231
10	0.30 ± 0.05	LH srs	340	330	260
11	0.36 ± 0.05	LH srs	320	282	250
12	0.30 ± 0.05	LH srs	365	230	247

Chitin volume fraction, chirality information, and edge lengths of the average unit cell of each respective reconstructed photonic crystal domain.

The chitin filling fraction is directly determined from the reconstructed volumes. So far, the volume fraction had been determined indirectly by comparing simulations with experimental SEM or TEM images (7, 21). For two exemplary crystallites with opposite chirality, Fig. 3 shows a comparison of STEM images from the respective tilt series (compare with Fig. 3, row 1) and semitransparent volume renderings in parallel view (compare with Fig. 3, row 2) of the reconstructions, which are used to adjust the optimum segmentation threshold. These two crystallites exhibit chitin filling fractions of 0.31 ± 0.05 (Fig. 3A) and 0.29 ± 0.03 (Fig. 3B), respectively. For all investigated crystallites, the chitin volume fraction ranges from 0.28 to 0.36. This is in the range of the values reported in the literature, with a spread of the volume fraction of smaller [0.15–0.70 (8) and 0.17 (7)] or comparable size [0.25–0.35 (21)]. The periodicity of the gyroid microstructure of the reconstructed crystallites is 230–390 nm (SI Text has an explanation of this quite broad range and compare with Table S1), which is agreement with values mentioned in the literature (8, 21).

Already from single STEM images of scales (Figs. 2B and 4), there is a clear indication for a preferred orientation of the <001> axes of the gyroid crystallites perpendicular to the scale surface. This pronounced <001> crystallographic texture is confirmed by a systematic analysis of a large number of crystallites from STEM overview images (Fig. 4 and Figs. S3 and S4). In total, using this technique, 248 of 763 analyzed crystals could be clearly identified to have the <001> axis exactly or closely aligned with respect to (w.r.t.) the scale surface normal (a detailed description is in SI Text). This corresponds to 32.5%, which indicates a crystallographic texture with a significantly higher probability than the value of 1.14% expected for a random isotropic orientation (calculation is in SI Text). The result is further supported by the orientation of 12 crystallites studied by ET. The partial inverse pole figure in Fig. 4, Inset shows the relative orientation of each scale surface normal w.r.t. the nearest highly symmetric axes of the reconstructed crystallites (more details are in SI Text). As expected from the STEM images, most of the crystals show their <001> axis being closely aligned with the scale surface normal. The above-mentioned STEM analysis furthermore showed that the <111> axis also is more frequently aligned along (or close to) the scale surface normal (12.5%) than expected for random isotropic distribution (1.52%) (SI Text). There is no indication of a preferred in-plane (azimuthal) crystal orientation, which was shown by an analysis using the above-mentioned STEM images of crystals having the <001> axis parallel aligned w.r.t. the scale surface normal (compare with Fig. S5).

Fig. S3.

Crystallographic texture analysis using STEM images. Stitched STEM overview images of various interconnected crystallites with a view perpendicular to the wing scale; the field of view is bordered on the left and the right by glue. Crystallites exhibiting a fourfold symmetry (<001> zone axis oriented very close or parallel to the scale surface normal) are highlighted in red, and those crystallites with a threefold symmetry (<111> zone axis oriented parallel to the scale surface normal) are highlighted in blue. The area shown in Fig. 4 is cropped from this figure.

Fig. S4.

Additional crystallographic texture analysis using STEM images. Additional stitched STEM overview images of various interconnected crystallites with a view perpendicular to the wing scale; the field of view is bordered on the left and the right by glue. Crystallites exhibiting a fourfold symmetry (<001> zone axis oriented very close or parallel to the scale surface normal) are highlighted in red, and those crystallites with a threefold symmetry (<111> zone axis oriented parallel to the scale surface normal) are highlighted in blue.

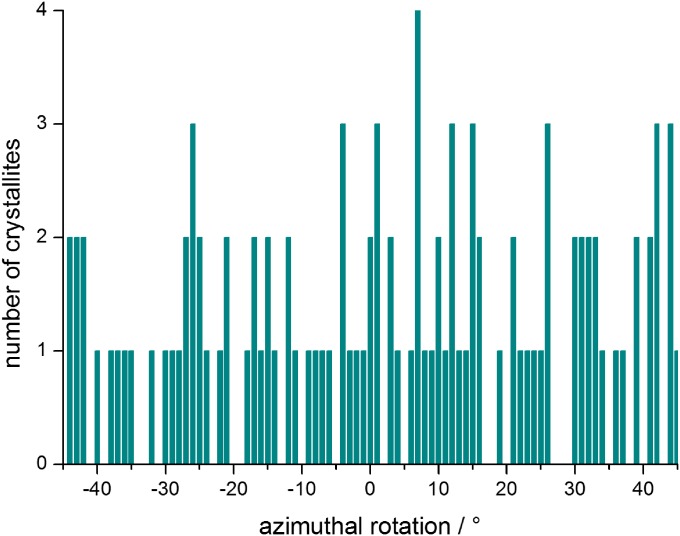
Fig. S5.

Azimuthal orientation relationship. Analysis of 107 crystallites oriented with the [001] axis parallel aligned with the scale surface normal (derived from STEM images) (compare with Figs. S3 and S4); at 0° azimuthal rotation, the [010] crystallite axes (or equal) are parallel to the main supporting ridges (the long axis of the butterfly wing scales).

SI Text

Gyroid Description.

The triply periodic gyroid surface (55), which was introduced by Alan Schoen (28), can be mathematically described by

$$\sin x\hspace{0.17em}\cos y+\sin y\cos z+\sin z\cos x=t\text{.}$$ [S1]

This surface divides two subvolumes, and t defines the respective volume fraction. For t = 0, the surface is minimal, and the volume fraction is 0.5; for t = +0.61 (RH srs-net) and t = −0.61 (LH srs-net), the volume fraction is 0.3 (55). For 0 < |t| < 1.413, the resulting gyroid surface is completely connected (55). The chiral gyroid structure is based on the srs-network with the cubic symmetry group I4₁32 (13).

Bright-Field TEM Tomography.

To test the impact of different imaging modes, one tilt series was acquired in bright-field TEM imaging mode. However, because of the well-interpretable mass–thickness contrast and the high depth of field, STEM tomography was favored over bright-field TEM tomography. However, the reconstructed crystallite was used for additional analysis.

STEM Tomography.

The reduced semiconvergence angle of the electron beam causes a reduced lateral resolution because of the Abbe diffraction limit but is negligible at the applied magnifications. STEM imaging mainly exhibits a well-interpretable mass–thickness contrast between the amorphous chitin structure and the empty pores. It was performed at an intermediate camera length (115 mm) to realize a short exposure time per projection (sufficient signal-to-noise ratio) and thus, prevent morphological changes of the chitin structure during tilt-series acquisition.

The final voxel edge lengths in the tomograms were 2.61 and 3.69 nm (depending on the magnification used for image acquisition), and the minimum reconstructed domain size was 2,560 × 652 × 1,129 nm³.

Tomogram Analysis.

The tomograms (16-bit grayscale) were binarized without additional postprocessing to separate the pore space from the chitin phase. The best-suited threshold was determined using the method by Otsu (56). Furthermore, we adjusted the threshold [using VSG Amira ResolveRT and ImageJ (54)], so that the surfaces of the chitin (projection through the reconstructed volumes and semitransparent volume rendering in parallel view) match the measured intensity distributions in the experimental STEM images (projected information through the whole crystallite).

Because of reconstruction artifacts resulting from the missing tilt-angle range (missing wedge artifacts) (57) and therefore, blurring of image details, like the edges from chitin to vacuum, the threshold value and thus, the volume fraction can only be determined with certain accuracy. Depending on the orientation of the respective nanostructured crystal (e.g., tilt-axis orientation along or perpendicular to certain lattice planes of the nanostructured crystal) and therefore, the resulting contrast in STEM imaging, some volumes could be segmented more accurately, which results in a lower error of the volume fraction.

We determined the edge lengths of the average unit cell of each nanostructured crystal by measuring the distances of the main maximum to the first side maxima of the respective 3D autocorrelation functions [calculated with ImageJ (54)] viewed along the respective gyroid zone axes.

The orientation of the reconstructed crystallites with respect to the scale surface normal was analyzed using the tilt-series projections, the reconstructed volumes, and their 3D autocorrelation functions.

Because of the high degree of symmetry of the cubic gyroid crystal along its zone axes (crystal orientation with high symmetry) in each of these different representations, the main zone axes <001> (fourfold rotational symmetry) and <111> (threefold rotational symmetry) are clearly identifiable.

We determined the chiral information of each reconstructed crystallite by tilting the tomogram (visualized as surface and volume rendering in the VSG Amira ResolveRT software) into the respective zone axes of the gyroid crystal and directly observing the handedness of the chitin structure by following the screw axis along the pore channels (see Movies S1 and S2).

Inverse Pole Figure.

The inverse pole figure was drawn using stereographic projection of the respective penetration points of the scale surface normal and the unit spheres of the reconstructed nanostructured crystal domains (points of intersection of the equatorial plane and the connection line between the penetration point and the “south pole” of the unit spheres, respectively). The cubic unit cells of the reconstructed crystals were, thereby, considered to be undistorted.

Deformation of Microstructure Caused by Preparation.

The preparation of samples suitable for ET investigation using FIB milling (compare with Fig. 2 D and E) introduces distortion to the chitin structure because of the release of inner stresses (drying of glue) parallel to the long axis of the thin bar. The lattice parameters are, therefore, affected, and the periodicity of the gyroid microstructure of the reconstructed crystallites ranges from 230 to 390 nm (compare with Table S1). However, the chirality of the crystallites is unaffected by this distortion.

The chirality of each crystallite was unambiguously identified by orientating the reconstructed volumes (3D visualization) with viewing direction along the most obvious periodically ordered and handed chitin channels: either the <001> or <111> directions of the cubic gyroid crystal. In most cases, the distinct zone axes could already be identified from the periodic pattern of the channels exhibiting either three- or fourfold rotational symmetry. In case of ambiguous symmetry caused by distortion, tilting the 3D reconstructions from one zone axis to the other by checking the chirality of the respective void domain, the sequence of LH and RH helices in the void domains of the channels finally enabled the unambiguous assignment of the <001> or <111> zone axes to the reconstructed crystals.

Significance Test of Equal Probability of both Chiralities.

A hypothesis testing is performed with the null hypothesis H₀:

$$H_{\text{0}}:\hspace{0.17em}\mathrm{both}\hspace{0.17em}\mathrm{chiralities}\hspace{0.17em}\mathrm{exist}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\mathrm{equal}\hspace{0.17em}\mathrm{probability},\hspace{0.17em}\text{and}{H}_{\text{0}}\text{:\hspace{0.17em}}p=\mathrm{0.5.}$$

The level of significance of the binomial test is set to 5%. For the probability of wrong decision and therefore, the error of the first kind, it follows that

$$P(\text{reject}\hspace{0.17em}{H}_0|H_0\hspace{0.17em}\text{is correct})\hspace{0.17em}\text{and that}$$

$$P(X\ge c|p=0.5)={\displaystyle \sum }_{i=c}^{12}B\left(i\right|0.5,12)\le 0.05,$$

with binomial distribution B, critical value c, number of trials n = 12, and success probability of each trial p = 0.5. For c = 10, the probability of wrong decision is

$$P(X\ge 10|p=0.5)={\displaystyle \sum }_{i=\mathrm{10}}^{12}B\left(i\right|0.5,12)\approx 0.0193\approx 2\%.$$

In our case, 10 of 12 crystallites show the same chirality. With a probability of wrong decision (error of the first kind) of about 2% (c = 10), we refuse the hypothesis that both chiralities appear with equal probability. Therefore, our experiment is situated within a level of significance of 5% of the binomial test.

Identification of Crystal Orientation in STEM Images.

STEM images (e.g., Fig. 4 and Figs. S3 and S4) with viewing direction perpendicular to the scale surface were used to identify crystallites having the <001> and <111> axes exactly or almost parallel, respectively, aligned with respect to the scale surface normal. Of a total number of 763 crystals, 248 were aligned along <001> (32.5%), and 95 were aligned along <111> (12.5%). The majority of these crystallites shows a very unique fourfold rotational symmetry (for <111>: threefold rotational symmetry) pattern with similar periodicity that is easy to identify. Some regions of the wing scales seem to be covered by (or filled with) some layers of chitin, which complicate or even impede the clear identification of the crystallite orientation. These regions were not considered for the orientation analysis. Therefore, some of the crystallites exhibiting a rather gray and uniform contrast could still be crystallites oriented with <001> (or <111>) along the surface normal.

Estimation of Orientation Probability.

To determine the angular range, which allows the identification of whether a crystallite is oriented along <001> (<111>) from projections (STEM images), the sample was tilted to have the viewing (electron beam) direction parallel to the respective <001> (<111>) axes of the crystallite. By carefully tilting several crystallites away from these zone axes, an angular range of ±5° was determined, within which it is still possible to identify whether the viewing direction is closely aligned to the <001> (<111>) axis of the crystallite. This information was used to estimate the expected orientation probability of observing crystallites oriented with the <001> (<111>) axis parallel to the scale surface normal in STEM images, assuming that the crystal orientation is random.

Therefore, the surface area of the spherical cap with an aperture of $2\theta =10°$,

$$A_{cap}=2\pi rh,$$

is calculated with sphere radius r and height $h=r(1-\text{cos}\theta )$. The area fraction of six equal spherical caps around six <001> axes (eight for <111>) of a cubic crystal and the complete sphere is

$$\frac{6\mathrm{\cdot }{A}_{cap}}{A_{sphere}}=\hspace{0.17em}\frac{12\pi r^2\left(1-\text{cos}5°\right)}{4\pi r^2}=3\left(1-\text{cos}5°\right)\approx 0.0114=1.14\%$$

and equals the probability to observe crystallites oriented with the <001> axis parallel to the scale surface normal. The probability to observe crystallites oriented with the <111> axis parallel to the scale surface normal is $8\mathrm{\cdot }{A}_{cap}/A_{sphere}\approx 1.52\text{\%}$.

Discussion

This study represents the first investigation, to our knowledge, by ET of the enantiopurity of the 3D chitin single-gyroid structure within butterfly wing scales. ET reconstructions of the real-space chitin distribution provide clear and direct evidence that both enantiomers (that is, the two possible mirror-symmetric realizations) of the single gyroids exist within butterfly scales, with a strong indication that the LH srs-net occurs with a significantly higher probability (10 of 12). This finding is important for a better understanding of the morphogenesis of the single-gyroid structure within the wing scales of C. rubi. In all likelihood, the formation of the chitin single-gyroid structure proceeds by a two-stage process involving the formation of convoluted inner-cellular membranes with cubic symmetry that act as precursor structures in which the chitin polymerization takes place or where extracellularly synthesized chitin biopolymers are deposited (6, 10). Such cubic membranes, which are fluid membranes draped onto negatively curved bicontinuous surface geometries with cubic symmetry, are commonly found within cell organelles, such as the mitochondrion, the endoplasmic reticulum, or plant cell chloroplast (27). Although also based on the gyroid geometry (28), the topology of these fluid membranes is different from the chitin single-gyroid structure. The latter is composed of a single connected solid network-like subspace, with a complement that is a single connected hollow network-like pore space [a network solid (29)]. The former, the cubic fluid membranes, are represented by a single lipid membrane draped onto a periodic saddle surface that represents the interface between two distinct nonconnected aqueous domains. These cubic membranes are reminiscent of self-assembled water–lipid cubic phases but with important differences (30), including of importance in this context, an imbalance or asymmetry of the two aqueous domains. In synthetic lipid–water systems that form the Q₂₃₀ (inverted or type II) gyroid phase (31, 32), the two aqueous domains are symmetry-related [that is, in particular, they hold the same water content, and the membrane midplane traces the location of a symmetric saddle surface (mathematically speaking, a minimal surface)]. For the Q₂₃₀ phase based on the gyroid, the two channels are mirror images of each other (one RH and one LH) related by inversion symmetry operations in the space group Ia3d, which are absent from the symmetry group I4₁32 of the single gyroid. In biological cubic membranes, the two aqueous domains are not necessarily of equal water content, in which case the symmetry group is that of the oriented (single) structures, which exclude operations that interchange the two aqueous domains; this behavior is particularly well-verified for the thylakoid membrane in plant prolamellar bodies, where X-ray scattering experiments clearly give the space groups of the nonoriented (single) version of the bicontinuous diamond membrane (33). The possible asymmetry between the two domains in biological cubic membranes can be rationalized by the possibility that they are connected to different cellular spaces, such as the extracellular, intracellular, or the intrasmooth endoplasmic reticulum (intra-SER) space (10); the asymmetry is also evident in the proposed flow-growth process for the formation of cubic bicontinuous structures by complicated folds of the plasma membrane. For membranes based on the gyroid geometry, the two aqueous domains can differ in two regards. First, geometrically, one domain is RH (the choice of which of the two is called RH is purely convention), and one is LH. Second, in terms of their function or formation, the channels can differ (e.g., being connected to the inner-cellular, extracellular, or intra-SER space). Whether and if so, how these two properties correlate are key points in understanding the formation of the single-gyroid chitin structure.

Saranathan et al. (6) have proposed a specific model that strongly relies on an asymmetric channel arrangement, where one network domain represents the extracellular space and the other one is the intra-SER space [in addition, Saranathan et al. (6) suggest the presence of another aqueous compartment, the intracellular space, such that the arrangement resembles the single-gyroid phase in linear ABC-type triblock copolymers (34)]. By virtue of the proposed difference between the two channels (connected to the extracellular and intra-SER spaces, respectively), this membrane geometry is (functionally) a single-gyroid structure. The formation of the single-gyroid chitin structure is then proposed as a second stage consisting in a chitin deposition and polymerization process extruded from the extracellular space. In this two-stage model, whether the RH channel represents the extracellular space and the LH channel represents the intra-SER space or vice versa is determined in the first stage, when chitin is assumed not to be present; hence, the molecular chirality of chitin has no influence on whether the LH or the RH network represents the extracellular space and hence, eventually, the solid chitin domain. Saranathan et al. (6) have argued that the “initiation of gyroid chirality during development is random” and have cautiously claimed that a balanced occurrence of both enantiomers is commensurate with their analysis of SEM images. Our study conclusively shows that this is incorrect, with a preference for LH chitin gyroid structures in C. rubi. For the model by Saranathan et al. (6) to be correct given the shown enantiomer imbalance, an alternative mechanism for enantiomer preference in the formation of the cubic membrane needs to be identified. Note that this, in particular, implies that the membrane formation process and the chitin deposition process are noninteracting; if, indeed, the two processes occurred simultaneously, the membrane folding process could be influenced by the presence of chitin. Available SEM data of biological cubic membranes in the literature cannot conclusively rule out alternatives to the model by Saranathan et al. (6), considering, in particular, that bicontinuous cubic arrangements where the membrane consists of multiple parallel bilayers are common (27, 35, 36). If the chitin deposition, indeed, occurred within a cubic membrane arrangement where both network-like channels were connected to the extracellular space, then the preferential occurrence of one enantiomer would be the result of the deposition or self-assembly of chiral molecular entities (chitin) within chiral domains (either the RH or LH domain). In that case, the prevalence of one enantiomer would seem to be a natural consequence.

Our findings show that the morphogenesis of the single gyroid is a complex process, with control over the chiral symmetry. Beyond the relevance for this biological structure formation problem, this formation process may give inspiration for chirality control in synthetic self-assembly strategies for single-gyroid structures. This includes both the formation process of single-gyroid mesoporous silicates, where the formation of single gyroids has been shown presumably with a racemic (balanced) mix of enantiomers (37), and platinum and gold replicas from copolymeric templates (38, 39). Considering the recent interest in gyroid-like structures for photonic and plasmonic applications (reviewed in ref. 40) as well as their potential for chiral sieves, gaining control over the chirality is an important goal. The outcome of our study emphasizes the need for substantially more comprehensive investigations of cubic bicontinous inner-cellular membranes—a proposition with a scope that is significantly broader than the enigma of the formation of the butterfly single gyroid. Despite their ubiquity in biological tissue in essential functional units—including the mitochondrion as the cell’s power house and the thylakoid membrane involved in photosynthesis—our understanding of their formation is limited to an incomplete analogy to synthetic cubic phases and an appreciation of their likely biological role largely absent from mainstream cell biology.

Our identification of a preferred enantiomer within the wing scales of C. rubi renews the question of the purpose, if any, of a well-defined chirality in this system. The single-gyroid material (of a given fixed handedness) has been clearly shown to discriminate between LH and RH circular polarized light (13, 14, 38, 41, 42). Given the prevalence of the LH enantiomer of the single gyroid and the frequent occurrence of the <001> inclination [being the sole direction with strong circular dichroism (12, 23)], the wing scales of C. rubi fulfill the prerequisites for the existence of an optical circular polarization signal. However, spectral measurements on the wings of C. rubi (and T. imperialis, another gyroid-forming butterfly species) have failed to record any discrimination between left and right circularly polarized light (12, 20). Given these observations and given the lack of physiological evidence of circular polarization sensitivity in insects, it seems that the structural chirality does not relate to biologically relevant circular polarization. The possibility of other functional purposes of the chiral structure cannot be eliminated, although the structure size is almost certainly too large for it to act as a chirality-selective molecular sieve [noting that, e.g., many pheromones are chiral molecules (43)]. Evidently, it is possible that the chirality of the single gyroid and the prevalence of one enantiomer within the butterfly system are solely a byproduct of the evolutionary optimization w.r.t. nonpolarized optical properties (44, 45). In this context, the intimate relationship of the gyroid to the closely related single-diamond structure is noteworthy; this latter achiral structure, which has been observed and related to optical function in weevils (10, 45–47), is likely to emerge by a similar process to the single gyroid [indeed, Saranathan et al. (10) report the coexistence of a single gyroid and a single-diamond structure within Lamprocyphus weevil]. Considering, in particular, the similar properties w.r.t. nonpolarized light (e.g., figure 5 in ref. 45), photonic properties do not provide the need for differentiation between these two bicontinuous forms. In the context of the enantiomeric composition and the question if the molecular chirality of chitin contributes to the selection of the enantiomeric type, it is useful to consider a structurally unrelated chiral manifestation of chitin: the Bouligand structure observed in a variety of beetles (17, 19, 48); in these beetles, which are strongly circularly polarizing (19, 49, 50) and where the chirality is widely believed to result from a process analogous to a cholesteric phase formation, only the LH enantiomer is observed. Interestingly, in the analogous phase found in the cellulose structure of a particular plant, Pollia condensata, both enantiomers are observed (18).

In addition to the question of enantiomeric type, our analysis emphasizes another aspect of nature’s ability to control secondary features of morphogenesis, which is manifest in the crystallographic texture of the polycrystalline arrangement. The polycrystalline arrangement of the single-gyroid chitin structure shows a preferred alignment of certain crystallographic directions w.r.t the scale’s outer surface normal, named crystallographic texture. Our findings of 12.5% and 32.5% of crystallites oriented along the <111> and <100> crystallographic directions, respectively, are in stark contrast to the observation in another gyroid-forming butterfly, P. sesostris, where a strong prevalence of the <110> direction is observed (9). This difference in the degree of crystallographic texture between these two species is in accordance with the optical appearance of the wing scales, which show a rather uniform color in the case of P. sesostris and spatial variations of reflectivity for C. rubi. We can hypothesize that these differences are related to the biological function of the coloration, which for C. rubi, is almost certainly camouflage and for P. sesostris, is more likely aposematism (10, 51). It is also interesting to note that the scales of P. sesostris are covered with a highly efficient UV filter on their top surface (51); any reflections from crystallites with <100> or <111> direction [which reflect predominantly in the near-UV (12, 23)] would be strongly dampened by this filter, and it seems logical that these inclinations do not occur in P. sesostris. By contrast, C. rubi (44, 51) does not exhibit a frontally covering absorbing filter covering the photonic structures [note the existence of colocalized pigment within the gyroidal structure in C. rubi (12)]; it is conceivable that the occurrence of UV-reflecting inclinations contributes to the camouflage effect. The presence of different preferred inclinations in P. sesostris and C. rubi hints at evolutionary control over this secondary feature of the spatial structure (44). Like for the enantiomer specificity, a deeper understanding of how the butterfly structure formation controls the crystallographic texture could lead to useful strategies to gain control over crystallographic texture in synthetic self-assembly processes of cubic bicontinuous phases.

In conclusion, ET has been used here to show the high level of control that morphogenetic processes in butterfly wing scales exert over secondary features of the nanostructure. In particular, a preferred enantiomeric form (chirality) has been identified along with a crystallographic texture that deviates from that of the same nanostructural forms in other butterfly species. More investigation of the precursor inner-cellular cubic membranes is needed to fully resolve the formation process of this intriguing chiral structure, with a view to replication in chirality-specific synthetic self-assembly strategies as well.

Methods

Site-Specific FIB Preparation.

Individual scales were carefully detached from the butterfly wings (C. rubi specimens were obtained from The Insect Company; www.insectcompany.com) and glued onto copper TEM grids (400 × 100 mesh; glue M-Bond 610) with the long side of the scales being perpendicularly aligned w.r.t. with the bars of the grid (Fig. 2C). To minimize reconstruction artifacts in ET caused by a drastic increase of projected mass thickness at high tilt angles, we fabricated narrow bars (around 2 μm wide and 10 to 15 μm long) by removing material from both sides using an FIB instrument (30 kV, 30 pA; FEI Strata 235) as indicated in Fig. 2D. The bars were chosen to be parallel to the long axis of the scales and therefore, also parallel to the supporting ridges of the scale (bright horizontal lines in Fig. 2B). To avoid any damage of the sensitive chitin structure, we conducted FIB milling without imaging or irradiating the regions of interest directly with the Ga-ion beam. The locations of the bars were randomly selected. Each bar contained several directly neighboring crystallites. No further thinning of the scales was applied, because their thickness is usually lower than 2 µm, providing sufficient electron transparency. In total, we analyzed 12 crystallites chosen from four different scales of one butterfly. Sample precharacterization was performed using a Zeiss Merlin Scanning Electron Microscope (Carl Zeiss AG).

Electron Tomography.

Electron tomography (ET) was performed using an FEI Titan³ 80–300 Transmission Electron Microscope operated at an acceleration voltage of 300 kV. We used annular dark-field STEM imaging because of the advantages of high depth of field and mass–thickness contrast (Rutherford scattering). To image the quite thick chitin specimens (1–2 µm) with a sufficient depth of field, we reduced the semiconvergence angle α of the electron probe to α = 1.2 mrad (µProbe STEM imaging mode) (additional details are in SI Text) (52). Tilt series covering a large tilt-angle range of ±75° with tilt increments of 1°–2° were obtained with an ultrathin single-tilt tomography holder (model 2020; Fischione). The 3D reconstructions were computed using the FEI Inspect 3D software and applying the simultaneous iterative reconstruction technique algorithm (53) with 50 iterations. We performed the 3D analysis and visualization of the datasets using VSG Amira ResolveRT software and ImageJ (54). A detailed description of the tomogram analysis can be found in SI Text.