Microtubules self-repair in response to mechanical stress

Abstract

Microtubules - which define the shape of axons, cilia and flagella, and provide tracks for intracellular transport - can be highly bent by intracellular forces, and microtubule structure and stiffness are thought to be affected by physical constraints. Yet how microtubules tolerate the vast forces exerted on them remains unknown. Here, by using a microfluidic device, we show that microtubule stiffness decreases incrementally with each cycle of bending and release. Similar to other cases of material fatigue, the concentration of mechanical stresses on pre-existing defects in the microtubule lattice is responsible for the generation of larger damages, which further decrease microtubule stiffness. Strikingly, damaged microtubules were able to incorporate new tubulin dimers into their lattice and recover their initial stiffness. Our findings demonstrate that microtubules are ductile materials with self-healing properties, that their dynamics does not exclusively occur at their ends, and that their lattice plasticity enables the microtubules' adaptation to mechanical stresses.

Microtubules are dynamic polymers that span the intracellular space. The self-organization of microtubule arrays defines the shape of axons, cilia, flagella, centrioles as well as the structure of mitotic spindles and of intracellular transport networks ¹. Therefore the growth dynamics and mechanical properties of microtubules, which determine network architecture, are central to cell physiology. The dynamics of microtubule growth has been exhaustively investigated and is now fairly well described ^2,3 compared to microtubules mechanical properties, which are poorly understood despite their critical role in the regulation of microtubule network geometry ^4–7.

The large and hollow cross-section of a microtubule’s tubular shape confers it a high bending stiffness ⁸. Microtubule persistence length - of a few millimeters - surpasses by several orders of magnitude the stiffness of other cytoskeleton polymers ^7,9. The regular lattice of adjacent protofilaments has been an inspiring structure and the subject of various physical models of microtubule mechanics. Cracks, defects and holes in the lattice, as well as breathing or sliding of adjacent protofilaments have all been proposed to modulate microtubule mechanical properties ^8,10–17. In vivo, microtubules are submitted to various types of external forces; produced by fluid flow in the case of cilia and flagella, or by molecular motors and deformation of other cytoskeleton networks in the cytoplasm ^18–24. Microtubules can move, bend or break in response to those constraints ^25,26. Yet, it is currently not known how microtubules respond to the vast forces exerted on them and if cracks and defects actually modulate this response.

Optical tweezers and fluid flow have been used to bend microtubules and estimate microtubule stiffness ^7,27. They revealed key microtubule features such as stiffness length dependency and the softening effect of microtubule stabilizing drugs ^28,29. However, investigations into the mechanical properties of dynamic microtubules in response to external forces critically need a new method that does not sacrifice throughput for accuracy and is compatible with high quality imaging. Here we developed a device that can be used to apply controlled hydrodynamic constraints on arrays of dynamic microtubules and monitor their deformation.

Microtubules soften under mechanical stress

To study the effect of mechanical stress on microtubules, we attached microtubule seeds onto micropatterns³⁰, grew dynamic microtubules and applied a calibrated (and locally quantifiable) flow orthogonal to the microtubule axis using microfluidics (Fig. 1A). When subjected to a transient hydrodynamic flow, microtubules bent and recovered their original straight shape with no apparent hysteresis (i.e. microtubules demonstrated elastic deformation, Supplementary video S1 and Fig. 1B). Surprisingly, repeated bending cycles using identical flow revealed that microtubules bent further with each cycle. The maximal deflection increased incrementally with each mechanical cycle (Supplementary video S2, Fig. 2A and 2B) suggesting that microtubules became softer –i.e. exhibited material fatigue– under repeated mechanical stress. Microtubule persistence length, a direct correlate of microtubule stiffness, can be inferred from the microtubule shape and the velocity of the fluid exerting the hydrodynamic force on the microtubule ²⁹ (see Methods). While the initial persistence length varied from 2 to 4 mm, the majority of microtubules (60%, n=15), which were assembled in the presence of 20 μM of tubulin, displayed a progressive reduction of stiffness cycle after cycle (Fig. 2C). On average, those microtubules became twice as soft as their initial state after 6 bending cycles.

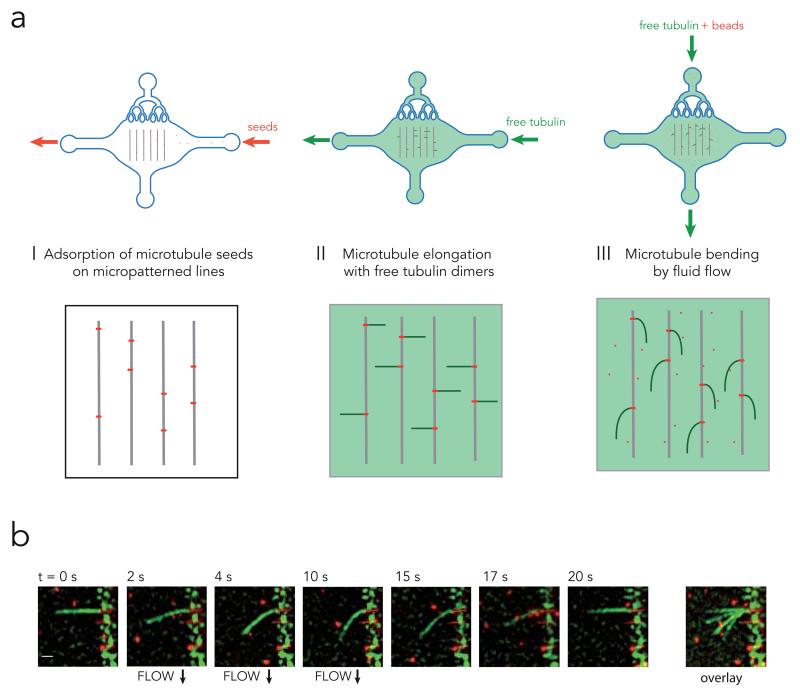
Figure 1. Microtubule bending device.

a, Illustration of the work flow. Red fluorescent microtubule seeds (short red lines), were flowed into the microfluidic device and grafted on micropatterned lines (grey lines) (step I). Free green fluorescent tubulin dimers were then added onto the seeds to grow microtubules (green lines) (step II). The same mix was then flowed normal to the microtubules and used as a hydrodynamic constraint to bend microtubules (step III). Red fluorescent beads were added to the mix to measure fluid flow next to microtubules.

b, Time lapse sequence of microtubule (green) bending in response to fluid flow. Scale bar is 3 μm. Overlay of images during the bending steps conveniently shows the magnitude of microtubule deformation (right image).

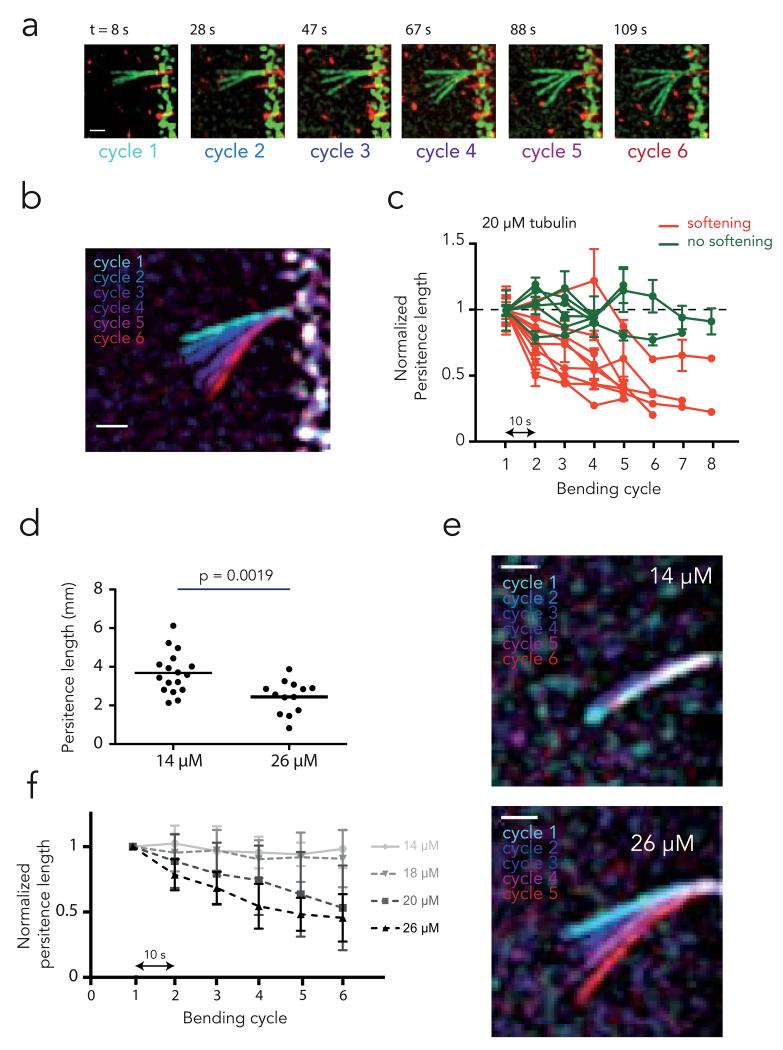
Figure 2. Microtubule softening upon external constraint.

a, Sequence of bending cycles. Images show the overlay of microtubule deformations during each successive bending cycle. Bending flows were applied during 10 seconds. A pause of 10 second was respected between bending steps. Deformations appeared larger cycle after cycle. Scale bar is 3 μm.

b, Overlay of microtubule maximal deformation during each bending cycle. Distinct colors have been attributed to each bending cycle. Scale bar is 3 μm.

c, Measurements of microtubule persistent length evolution over the successive bending cycles. Delay between bending cycles was 10 s. Microtubule persistent lengths were normalized to their initial value. Error bars correspond to the standard deviation calculated from 5 consecutive frames for each bending cycle. As a test of tendency, Spearman correlation tests for persistent length values over the successive cycles were performed. Green curves show microtubules for which the persistent length was not significantly affected over the bending cycles, whereas red curves show those that have been soften during the cyclic stress.

d, Comparison of initial microtubule persistent length for microtubules assembled in the presence of 14 μM or 26 μM of free tubulin dimers. Values were compared with an unpaired t test (two-tailed).

e, Overlay of microtubule maximal deformation during bending cycles for microtubules assembled in the presence of 14 μM or 26 μM of free tubulin dimers.

f, Measurements of microtubule persistent length evolution over the successive bending cycles for microtubules assembled in the presence of various concentration of free tubulin dimers (26 μM: n=9; 20 μM: n=15, 18 μM: n=15; 14 μM: n=13). Microtubule persistent lengths were normalized to their initial values. Values correspond to average persistent length of individual measurements shown in Supplementary Figure 1. Error bars show standard deviation between distinct microtubule bending experiments. All curves were considered significantly different using a two-way ANOVA test, except 14 and 18 μM. A T test on the average persistent length showed all these differences became significant at the fourth bending cycle.

Lattice defects promote microtubule softening

Material fatigue of highly ordered polymers and crystal-like structures is known to stem from pre-existing structural defects that concentrate stresses and spread into larger damages³¹. Pre-existing structural defects in the microtubules lattice, such as lack of dimers, abrupt variations of protofilament number, or of helix start number have been reported^32,33. By altering the regularity of the lattice, defects introduce areas of weakness that concentrate stresses and undergo local protofilament disorganization and partial lattice disassembly. We use the term “defect” to refer to initial lattice imperfections and the term “damage” to refer to the lattice disorganization and destruction that results from stress accumulation on defects. Defects in the microtubule lattice have already been proposed to alter mechanical properties but this hypothesis remains untested ^8,11,13,14. Consistently, rapidly polymerized microtubules harbour a greater frequency of defects and tend to display lower stiffness^32,34. We confirmed that rapidly assembled microtubules are softer than slowly assembled microtubules (Fig. 2D). To test whether the amount of pre-existing defects is responsible for microtubule softening through the generation of larger damages, we subjected microtubules assembled at various speeds to repeated bending cycles. It appeared that the magnitude of microtubule fatigue in response to cyclic stress was indeed larger in rapidly assembled microtubules (Fig. 2E). All microtubules assembled at the highest tested concentration of free tubulin (26 μM) displayed material fatigue whereas softening was undetectable for microtubules assembled at the lowest concentration (14 μM) (Fig. 2F, Supplementary Fig. S1). These results demonstrate that the stress alone is not sufficient to fatigue microtubules and they suggest that pre-existing lattice defects may be responsible for this mechanical property. Of note, highly curved microtubules in cells have long puzzled investigators considering the intrinsic stiffness of pure microtubules. While microtubule curvature in cells may result from the large forces exerted by actin network contraction³⁵, the microtubule fatigue we describe here suggests that repeated mechanical constraints may soften microtubules in cells.

Softened microtubules can self-repair

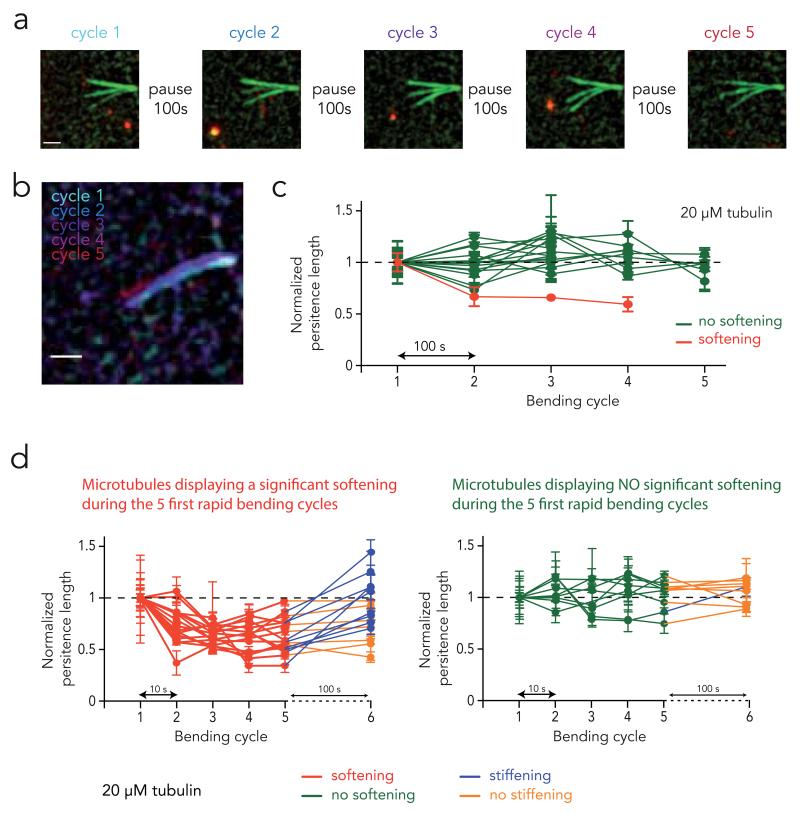
Some structures made of long-lived microtubules in sensory organelles, such as sensory cilia or axons, maintain their mechanical properties despite being continuously subjected to external constraints^24,36. This raises the possibility that mechanisms may protect long-lived microtubules from material fatigue or allow them to recover from the effect of injurious bending. We tested this hypothesis by letting microtubules recover for long periods of time between the bending cycles (Fig. 3A). Microtubules were assembled at 20 μM of free tubulin. As the duration of the rest period increased from 10 to 100 s, the proportion of microtubules affected by fatigue was progressively reduced (Supplementary Fig. S2). Remarkably, when microtubules remained at rest for 100 s between the bending cycles, microtubule stiffness was unchanged from one cycle to another (Fig. 3B-C). Since microtubules were subjected to the same bending forces in all recovery experiments, the absence of softening when resting time is increased to 100 s suggests that microtubules underwent repair in between the bending cycles. To further test whether microtubules recover their mechanical properties after being damaged, we induce softening with five rapid bending cycles and followed by a 100 s rest (Figure 3d). The majority of microtubules that had softened during the five bending cycles displayed a significant stiffness increase during the rest period. Meanwhile, for most of the microtubules that did not soften, stiffness did not increase during the rest period. These findings demonstrate that damaged microtubules have the ability to recover their stiffness through self-repair.

Figure 3. Microtubule mechanical recovery.

a, Sequence of bending cycles. Images show the overlay of microtubule deformations during each successive bending cycle. Bending flows were applied during 10 seconds. A pause of 100 second was respected between bending steps. Deformations appeared similar for all cycles. Scale bar is 3 μm.

b, Overlay of microtubule maximal deformation during each bending cycle. Distinct colors have been attributed to each bending cycle. Scale bar is 3 μm.

c, Measurements of microtubule persistent length evolution over the successive bending cycles. Delay between bending cycles was 100 s. Error bars correspond to the standard deviation calculated from 5 consecutive frames for each bending cycle. As a test of tendency, Spearman correlation tests for persistent length values over the successive cycles were performed. Green curves show microtubules for which the final persistent length was not significantly different from their initial one, whereas red curves show those that have been soften during the cyclic stress.

d, Evolution of microtubule persistent length following five rapid bending cycles. Delay between the five first bending cycles was 10 s. To distinguish softening from non-softening microtubules, we used the distance between the minimum normalized Lp and the Lp during the first cycle (=1) as a parameter for a k-means clustering. The clustering algorithm found one group with a low distance, which corresponds to non-softening microtubules (shown on the left graph), and another group with a high distance, corresponding to softening microtubules (shown on the right graph). The recovery after a 100 s pause time was assessed by comparing Lp before and after the pause with a Wilcoxon matched-pairs test. Microtubules displaying significant recovery are shown in blue, the other in orange.

Microtubules have self-healing properties

We propose two hypotheses for the recovery of mechanical properties during the pauses: 1- incorporation of new tubulin to patch damages in the lattice and 2- lateral realignment of protofilaments that underwent sliding or separation. In the former hypothesis, stiffness recovery should involve the incorporation of new dimers in the lattice. To test the possibility that tubulin incorporation can actually heal microtubules, we generated large, but locally and temporally controlled, structural damages to microtubules with laser pulses (Supplementary video S3 and Supplementary Fig. S4). To visualize possible tubulin incorporation into the microtubule lattice, red microtubules were bathed in a solution of green tubulin and damaged by laser pulses. Upon switching the solution back to red tubulin, it was apparent that the green tubulin had become incorporated not only at the end but also at the impact site on the red microtubule (Supplementary video S4 and Fig. 4A). This suggests that microtubule lattice repair can take place and be directly visualized in the case of large damages.

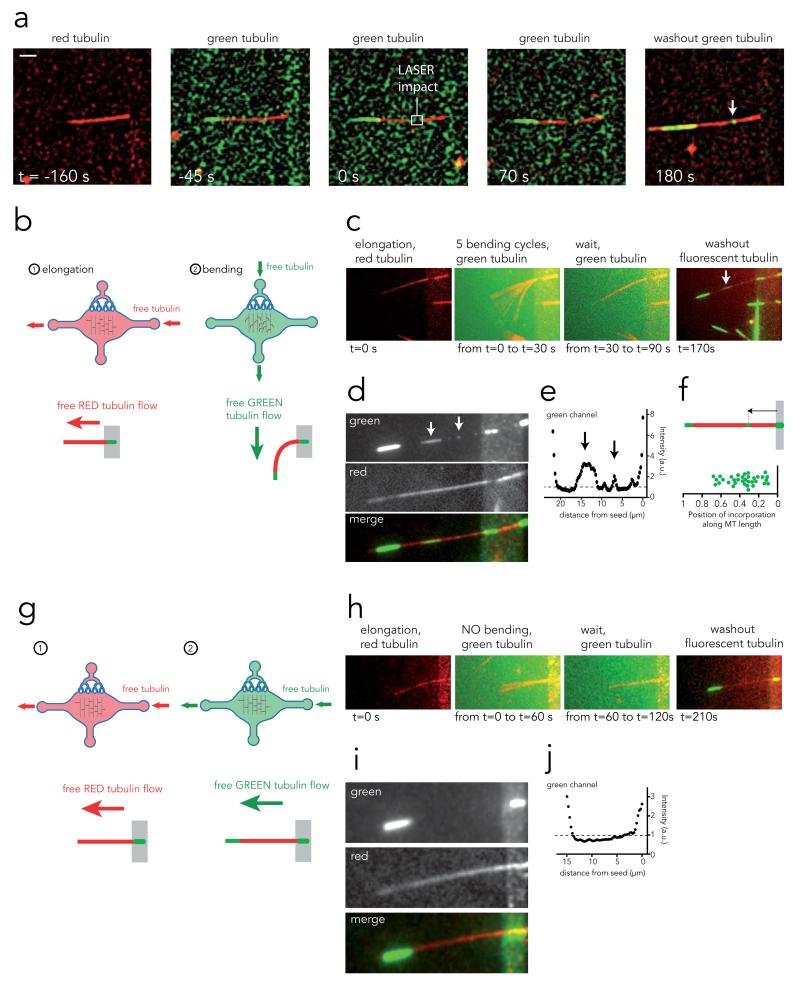
Figure 4. Microtubule self-healing.

a, Image sequence showing a microtubule assembled with red tubulin (t=−160s), bathed in a solution of green tubulin (t=−45s), damaged (but not cut) with laser pulses (t=0) and let in the presence of green tubulin for 70s. Green tubulin was washed away and replaced by red tubulin. Removal of the green fluorescent background revealed incorporation of tubulin dimers at the damaged site (arrow). Scale bar is 5 μm.

b, Experimental procedure to grow microtubules with red tubulin and bend them in the presence of green tubulin.

c, Image sequence showing from left to right: a red microtubule, the overlay of 5 bending cycles in the presence of green tubulin, the 1-minute-long pause, followed by the green tubulin washout revealing incorporation of tubulin dimers along the microtubule length (arrow).

d, Averages of 30 images taken successively in the red and green channels at the end of the image sequence shown in c in order to improve signal to noise ratio. Stretches of green tubulin along the red lattice become more visible (arrows).

e, Green fluorescence intensity linescan along the microtubule length on the image shown in d. Arrows correspond to incorporation sites between the microtubule seed (right peak) and the growing end (left peak).

f, Measurement of external tubulin incorporation site positions along microtubule length. Distances were normalized with respect to microtubule length.

g, Experimental procedure to grow microtubules with red tubulin and flow green tubulin along their length without bending them.

h, Image sequence showing from left to right: a red microtubule, the overlay of pictures taken during green tubulin flow along microtubule length, the 1-minute-long pause, followed by the green tubulin washout revealing the absence of incorporation of tubulin dimers along the microtubule length.

i, Averages of 30 images taken successively in the red and green channels at the end of the image sequence shown in h in order to improve signal to noise ratio. No stretch of green tubulin could be detected along the red lattice.

j, Green fluorescence intensity linescan along the microtubule length on the image shown in i. Fluorescence linescans showed no fluorescence peak between the microtubule seed (right peak) and the growing end (left peak).

Incorporation of tubulin along the microtubule length has previously been hypothesized³⁷. Stabilized, end-to-end annealed axonemes were shown to adopt curved shapes upon removal of free tubulin dimers in solution and to resume their original straight shapes upon dimer addition. This suggested that microtubule shape recovery depended on intra-lattice dimer incorporation³⁷. To test whether bent microtubules heal by local incorporation of tubulin at areas of high stress, we subjected red-labelled microtubules to five bending cycles with prolonged recovery periods in the presence of green-labelled tubulin (Fig. 4B). Concentrates of green fluorescence were found along the red microtubules (Supplementary video S5 and Fig. 4C and D) in more than 80% (n=24) of microtubules that had been repeatedly bent. Green fluorescence peaks 1.5 to 4 times higher than the adjacent background were found in line scans (Fig. 4E and Supplementary Fig. S5). The appearance of new tubulin along the microtubule length takes place preferentially in the proximal and most curved half of the microtubule (Fig. 4F), thus suggesting that the areas subjected to the greatest local stress underwent damages that were repaired by local tubulin incorporation. Meanwhile, we did not detect any incorporation of green-labelled tubulin into red-labelled microtubules subjected to a longitudinal –rather than orthogonal– flow (Fig. 4G-J, Supplementary video S6, and Supplementary Fig. S6). In addition, slowly assembled microtubules (with 14 μM tubulin) that did not display material fatigue (Fig. 2E) also failed to incorporate new tubulin into their lattice under repeated cycles of bending (Supplementary Fig. S7). Thus free tubulin dimers incorporate systematically along the sidewall of microtubules recovering their stiffness after having been damaged by external forces but they do not incorporate in microtubules in which stiffness is not changing (whether they had been bent or not). Therefore tubulin dimer incorporation along the lattice appears to be a key correlate of microtubule stiffness recovery.

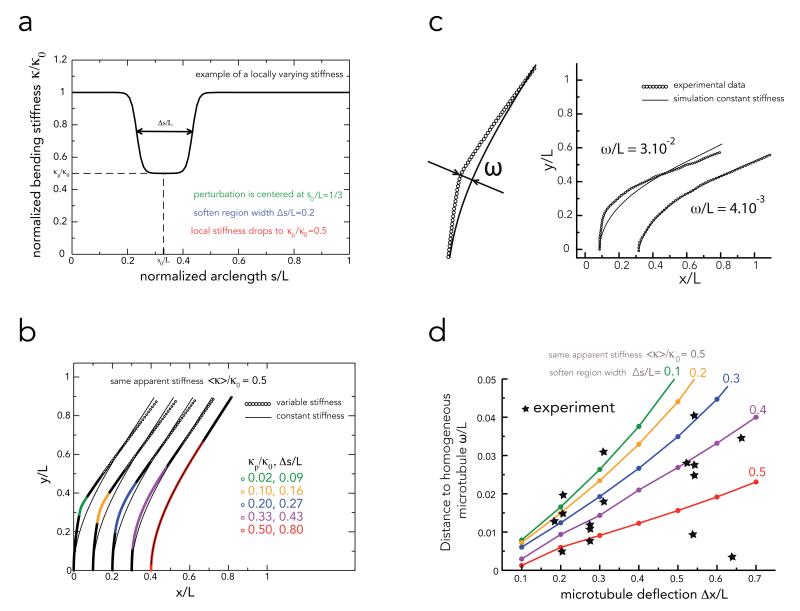
Intriguingly, curvature seems to vary smoothly along the length of the bent microtubule even though the size of the tubulin incorporation area –i.e. the repaired area– is rather limited (green fluorescent sites were 1.2 μm +/− 1 μm long (n=26)). Local damage should intuitively lead to localized kinks rather than homogeneous global deformations. Since we could not measure experimentally the size of the softened regions, which seems to differ from the size of the repair region, we developed a method to estimate it by comparing the experimental deformations we measured to those of numerical microtubules of known stiffness profile. We performed numerical simulations in which softening was limited to defined length segments (Figure 5a and Methods). In our simulations, both the width and the degree of local softening contributed to the deformation and the apparent average stiffness of the entire microtubule (Figure 5b and Supplementary Fig. S8). Then, in order to characterize microtubule deviation from homogeneous deformation, we measured the distance ω between experimentally bent microtubules and numerical microtubules of constant stiffness showing similar deformations (Figure 5c). Large distances corresponded to microtubules showing local kinks whereas low distances corresponded to more homogeneous deformation. We compared experimental values to those of numerically simulated microtubules with various rigidity profiles but similar apparent stiffness (see Methods and Figure 5d). Some experimental data points were close to numerical simulations of microtubule with small soften region (Δs/L = 0.1) but others were closer to simulation of microtubules with long soften region (Δs/L = 0.5). This showed that, in our experiments, the bending induced damages were not always highly localized but often extended over a large portion of the microtubule. Thus, the two working hypotheses we formulated for microtubule repair, ie local structure healing by incorporation of free dimers and lattice rearrangement over long distances, are both compatible with our experimental observations.

Figure 5. Numerical simulations of microtubule deformations in response to local or global stiffness reduction.

a, This graph represents the parameters used for the simulation. Microtubules had a length L, and a bending stiffness κ₀. Their stiffness was locally reduced to κ_p/κ₀ over a normalized length Δs/L positioned at the arc length s₀₀/L. In this example as well as in all simulations s₀/L = 0.33.

b, Examples of microtubule equilibrium shapes in response to distinct combinations local softenings parameters (κ_p/κ₀ and Δs/L) leading to the same apparent bending stiffness (<κ>/κ₀=0.5). Shown are also the fits against a model with the constant stiffness 0.5 (full lines).

c, Measurement of the distance ω/L between the shapes of experimental microtubules to shapes of microtubules with a constant rigidity as explained in Methods section. Two examples illustrate a high and low distance suggestive of local and global softening process respectively.

d, Comparison of distances to homogeneous microtubules between experimental observations and simulated microtubules. Colored lines show the theoretical dependence of the distance ω/L on the microtubule deflection Δx/L for different extent of the softened region Δs/L (different colors) and the same given apparent stiffness ⟨κ⟩/κ₀ = 0.5. Stars correspond to experimental measurements of the distance ω/L and the deflection Δx/L for different deflection for different microtubules. Shown are only values obtained from microtubules with an apparent stiffness comprised between 0.4 and 0.6 after five bending cycles.

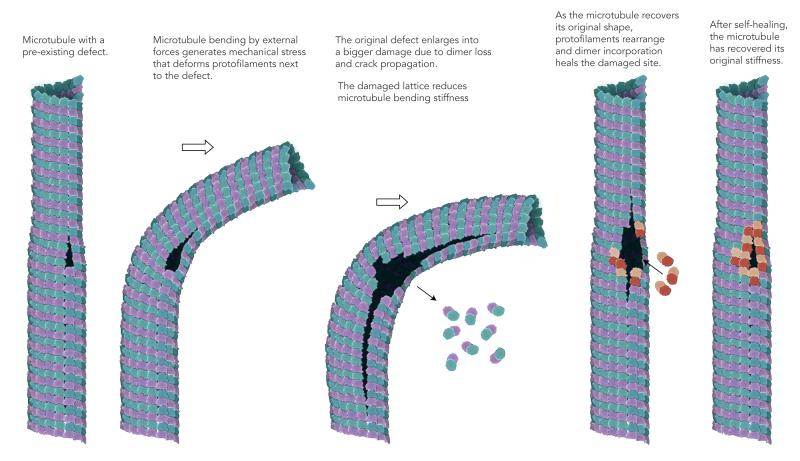
Here we report the softening and self-healing of microtubules in response to mechanical constraints. While softening upon repetitive constraints, or fatigue, is common to all materials, self-healing is much less frequent^38,39 and appears here as the remarkable natural feature of a biological polymer. Defects in microtubule lattice, such as variations of protofilaments number^32,33, are likely to play a central role in microtubule fatigue and self-healing since in the absence of defects microtubules deformed elastically with no fatigue and no repair (Figure 2F and supplementary Figure S7). Exactly how the accumulation of stress at lattice defects alters microtubule architecture and bending stiffness remains a key question. Our data suggest that two processes may operate: 1- a local disassembly spreading from the pre-existing defect (Figure 4) and 2- a long-range disorganization of microtubule lattice (Figure 5). We speculate that structural defects may initiate lattice disorganization by allowing a higher degree of freedom to adjacent protofilaments (Figure 6). Protofilaments adjacent to the defect have fewer lateral interactions and are thus easier to separate making their deformation less constrained (Figure 6ii). This favours the propagation of cracks in the lattice as well as protofilament rupture and disassembly (Figure 6iii). These effects contribute to global and local microtubule softening. They can be further amplified in repeated bending sequences generating microtubule fatigue (Figure 6iii). As the microtubule recover its original straight shape, due to the remaining stiffness of the intact protofilaments, separated protofilaments spontaneously realign and progressively re-establish lateral interactions (Figure 6iv). Meanwhile, free tubulin in the medium binds to the newly generated protofilament ends and completes the healing of the structure (Figure 6iv). Thereby, the microtubule recovers its original stiffness (Figure 6v).

FIGURE 6. Model of microtubule softening and self-repairing under mechanical stress.

Speculative interpretation of microtubule lattice defect contribution to microtubule deformation, softening and self-healing under mechanical stress. Illustration by Dr. Agnieszka Kawska at IlluScientia.com.

These new properties of microtubule softening and self-repairing and the plasticity of microtubule lattice profoundly change our appreciation of microtubule mechanics and dynamics. It should prompt us to revise our understanding of the regulation of microtubule network architectures.

Methods

Tubulin purification and labeling

Tubulin was purified from fresh bovine brain by three cycles of temperature-dependent assembly and disassembly in Brinkley Buffer 80 (BRB80 buffer; BRB buffer: 80 mM PIPES, pH 6.8, 1 mM EGTA, and 1 mM MgCl₂ plus 1 mM GTP) ⁴⁰. MAP-free neurotubulin was purified by cation-exchange chromatography (EMD SO, 650 M, Merck) in 50 mM PIPES, pH 6.8, supplemented with 1 mM MgCl₂, and 1 mM EGTA ⁴¹. Purified tubulin was obtained after a cycle of polymerization and depolymerization. Fluorescent tubulin (ATTO-488 and ATTO-565-labeled tubulin) and biotinylated tubulin were prepared as previously described ⁴². Microtubules from neurotubulin were polymerized at 37°C for 30 min and layered onto cushions of 0.1 M NaHEPES, pH 8.6, 1 mM MgCl₂, 1 mM EGTA, 60% v/v glycerol, and sedimented by high centrifugation at 30°C. Then Microtubules were resuspended in 0.1 M NaHEPES, pH 8.6, 1 mM MgCl₂, 1 mM EGTA, 40% v/v glycerol and labeled by adding 1/10 volume 100 mM NHS-ATTO (ATTO Tec), or NHS-Biotin (Pierce) for 10 min at 37°C. The labeling reaction was stopped using 2 volumes of 2X BRB80, containing 100 mM potassium glutamate and 40% v/v glycerol, and then Microtubules were sedimented onto cushions of BRB80 supplemented with 60% glycerol. Microtubules were resuspended in BRB80, and a second cycle of polymerization and depolymerization was performed before use.

Cover glass micropatterning

The micropatterning technique was adapted from Portran et al.³⁰. Cover glasses were cleaned by successive chemical treatments: 30 min in acetone, 15 min in ethanol (96 %), rinsing in ultrapure water, 2 h in Hellmanex III (2 % in water, Hellmanex), and rinsing in ultrapure water. Cover glasses were dried using nitrogen gas flow and incubated for three days in a solution of tri-ethoxy-silane-PEG (30 kDa, PSB-2014, creative PEG works) 1 mg/ml in ethanol 96% and 0.02% of HCl, with gentle agitation at room temperature. Cover glasses were then successively washed in ethanol and ultrapure water, dried with nitrogen gas, and stored at 4°C. Passivated cover glasses were placed into contact with a photomask (Toppan) with a custom-made vacuum-compatible holder and exposed to deep UV (7 mW/cm² at 184 nm, Jelight) for 2 min 30 s. Deep UV exposure through the transparent micropatterns on the photomask created oxidized micropatterned regions on the PEG coated cover glasses.

Microfluidic circuit fabrication and flow control

The microfluidic device was fabricated in PDMS (Sylgard 184, Dow Corning) using standard photolithography and soft lithography ⁴³. The master mold was fabricated by patterning 50 μm thick negative photoresist (SU8 2100, Microchem, MA) by photolitography. A positive replica was fabricated by replica molding PDMS against the master. Prior to molding, the master mold was silanized (trichloro(1H,1H,2H,2H-perfluorooctyl)silane, Sigma) for easier lift-off. Four in-and outlet ports were made in the PDMS device using 0.5 mm soft substrate punches (UniCore 0.5, Ted Pella, Redding, CA). Connectors to support the tubing were made out of PDMS cubes (0.5 cm side length) with a 1.2 mm diameter through hole. The connectors were bonded to the chip ports using still liquid PDMS as glue, which was used to coat the interface between the chip and the connectors, and was then rapidly cured on a hotplate at 120°C. Teflon tubing (Tefzel, inner diameter: 0.03", outer diameter: 1/16", Upchurch Scientific) was inserted into the two ports serving as outlets. Tubing with 0.01" inner and 1/16" outer diameter was used to connect the inlets via two three-way valves (Omnifit labware, Cambridge, UK) that could be opened and closed by hand to a computer-controlled microfluidic pump (MFCS-4C, Fluigent, Villejuif, France). Flow inside the chip was controlled using the MFCS-Flex control software (Fluigent). For repeated bending experiments, a script was used that automatically set the flow to a defined value for 10 s, then turning off the flow for 10 s or 100 s, and then repeating this cycle up to ten times. Custom rubber pieces that fit onto the tubing were used to close the open ends of the outlet tubing when needed.

Microtubule growth on micropatterns

Microtubule seeds were prepared at 10 μM tubulin concentration (30% ATTO-488-labeled or ATTO-565-labeled tubulin and 70 % biotinylated tubulin) in BRB80 supplemented with 0.5 mM GMP-CPP at 37°C for 1 h. The seeds were incubated with 1 μM Taxotere (Sigma) at room temperature for 30 min and were then sedimented by high centrifugation at 30°C and resuspended in BRB80 supplemented with 0.5 mM GMP-CPP and 1 μM Taxotere. Seeds were stored in liquid nitrogen and quickly warmed to 37°C before use.

The PDMS chip was placed on a micropatterned cover glass and fixed on the microscope stage. The chip was perfused with neutravidin (25 μg/ml in BRB80; Pierce), then washed with BRB80, passivated for 20 s with PLL-g-PEG (Pll 20K-G35-PEG2K, Jenkam Technology) at 0.1 mg/ml in 10 mM Hepes (pH = 7.4), and washed again with BRB80. Microtubule seeds were flowed into the chamber at high flow rates perpendicularly to the micropatterned lines to ensure proper orientation of the seeds. Non-attached seeds were washed out immediately using BRB80 supplemented with 1% BSA. Seeds were elongated with a mix containing 14, 18, 20 or 26 μM of tubulin (30% labeled) in BRB80 supplemented with 50 mM NaCl, 50 25 mM NaPi, 1 mM GTP, an oxygen scavenger cocktail (20 mM DTT, 2 mg/ml glucose, 80 μg/ml catalase and 0.67 mg/ml glucose oxidase), 1% BSA, 0.025% methyl cellulose (1500 cp, Sigma) and 0.02% red fluorescent beads (Fluoro-Max polymer spheres, 0.52 μm diameter, Thermo Scientific). The same mix was used to subject microtubules to flow. For the experiments showing tubulin incorporation after bending, a mix was prepared with 100% labeled tubulin for bending the microtubules.

Imaging

Microtubules were visualized using an objective-based azimuthal ilas2 TIRF microscope (Nikon Eclipse Ti, modified by Roper Scientific) and an Evolve 512 camera (Photometrics). The microscope stage was kept at 37°C using a warm stage controller (LINKAM MC60). Excitation was achieved using 491 and 561 nm lasers (Optical Insights). Time-lapse recording was performed using Metamorph software (version 7.7.5, Universal Imaging). Movies were processed to improve the signal/noise ratio (smooth and subtract background functions of ImageJ, version 1.47n5). Images were typically taken every 150 ms.

Laser-induced microtubule damages

Laser induced microtubule damage was performed using a Laser illuminator iLas2 (Roper Scientific) set up on an inverted microscope (Ti-E, Nikon) with a 60x Nikon APO TIRF Oil objective. iLas2 is a dual axis galvanometer based optical scanner that focuses the Laser beam on the sample (diffraction limited spot size) on the whole field of view of the camera. Laser displacement, exposure time and repetition rate were controlled using Metamorph software (version 7.7.9.0, Universal Imaging). To damage Alexa-561 labeled microtubules, a 50 mW / 561 nm laser was used at 90% power performing 30 repetitions within a field of approx. 4 μm × 4 μm size. To merely photobleach microtubules, 20 repetitions were carried out at 80% laser power. In order to break microtubules, 50 repetitions at 100% laser power were used.

Measurement of microtubule persistence length

The microtubule is described as an inextensible slender filament with length L and bending rigidity κ, which is bent in two dimensions by the fluid flow. Its elastic energy E is given by

$$\mathrm{E}\left[\mathbf{r}\right]={\int }_0^{\mathrm{L}}\left\{\frac{\mathrm{\kappa }}{2}{\left(\frac{{\mathrm{d}}^2\mathbf{r}}{{\mathrm{ds}}^2}\right)}^2+\frac{\lambda }{2}\left[{\left(\frac{\mathrm{d}\mathbf{r}}{\mathrm{ds}}\right)}^2-1\right]\right\}\mathrm{ds}.$$ (1)

The vector r(s) denotes the position of the filament parameterized by the arc length s and λ denotes a Lagrange multiplier associated with the inextensibility condition ∣dr/ds∣=1. The force exerted on the filament is given by the functional variation of the potential E with respect to the filament position vector r

$${\mathbf{F}}_{\mathrm{B}}=-\frac{\mathrm{\delta }\mathrm{E}}{\mathrm{\delta }\mathbf{r}}.$$ (2)

The filament orientation is fixed by the seed orientation at s=0, whereas the other end of the filament at s=L is force-free. The hydrodynamic drag exerted by the fluid flow on a slender filament is given by

$${\mathbf{F}}_{\mathrm{H}}=\mathrm{g}\mathrm{\mu }\left(\mathrm{I}-\frac{1}{2}\frac{\mathrm{d}\mathbf{r}}{\mathrm{ds}}\otimes \frac{\mathrm{d}\mathbf{r}}{\mathrm{ds}}\right){\mathbf{v}}_{\mathrm{b}},$$ (3)

where v_b denotes the velocity field measured by the bead displacements, μ denotes the viscosity of the fluid and g denotes a geometrical factor of order 1, which depends on the distance of the filament from the surface, the radius of the filament and the distance of the beads from the surface. ⨂ denotes the outer product and I is the identity tensor. In mechanical equilibrium

$${\mathbf{F}}_{\mathrm{B}}+{\mathbf{F}}_{\mathrm{H}}=0,$$ (4)

which determines the equilibrium shape of the filament subject to the appropriate boundary conditions. The filament rigidity was determined by solving Eqs. (1-4) using the AUTO-07p softwage package ⁴⁴ and by minimizing the function

$${\mathrm{\omega }}^2\left(\mathrm{\kappa }\right)=\frac{1}{\mathrm{L}}{\int }_0^{\mathrm{L}}{\left[{\mathbf{r}}_{\mathrm{R}}\right(\mathrm{S})-\mathbf{r}(\mathrm{S}\left)\right]}^2\mathrm{ds}$$ (5)

where r_R(s) denotes the measured position of the filament. The persistence length is then given by L_p=κ/(K_BT). ω is a measure for the distance between the shapes of two microtubules. In the fitting routine for the experimentally measured microtubule shapes, ω denotes the distance between the shape of the experimental snake and an inextensible flexible filament subjected to the same flow as the experimental snake.

We assumed that the origin of the microtubule was clamped in the direction of the seed. To correct for a measurement error of the microtubule origin, we optimized Eq. 5 also for the position of the microtubule origin.

The analytic determination of the geometrical factor g is difficult, since (i) the distance of the filament from the surface is not known but is <100 nm (the depth of the evanescent wave field), (ii) the fluid velocity is determined by imaging of beads with a radius of 250 nm, which are visible with TIRF and (iii) the velocity field close to the surface is distorted by the PEG brush. We assume that g is approximately constant for all experiments. From an independent measurement of microtubule persistence length based on thermal fluctuations ⁹ we have calculated g = 0.27 ± 0.11.

Modelling of microtubule softening

Using numerical simulations we tested whether the observed bending-induced softening of microtubules was localized or rather extended over a larger portion of the microtubule. To that end we calculated theoretically the shapes of microtubules with a spatially dependent rigidity of the form

$$\mathrm{\kappa }={\mathrm{\kappa }}_{\mathrm{p}}+\frac{{\mathrm{\kappa }}_0-{\mathrm{\kappa }}_{\mathrm{p}}}{2}\left\{2+\text{tanh}\left[\frac{2(\mathrm{s}-{\mathrm{s}}_0)-\Delta \mathrm{s}}{\mathrm{\epsilon }}\right]-\text{tanh}\left[\frac{2(\mathrm{s}-{\mathrm{s}}_0)+\Delta \mathrm{s}}{\mathrm{\epsilon }}\right]\right\}.$$ (6)

where κ₀ (κ_p) denotes the microtubule rigidity in the unsoftened (softened) region, s₀ and Δs denote the center position and the width of the softened region and ε denotes the width of the transition region between the softened and unsoftened part of the microtubule. The shapes of microtubules with an inhomogeneous rigidity [Eq. (6)] were fitted to the shapes of microtubules with a homogeneous rigidity to obtain an apparent average stiffness ⟨κ⟩, as we did for experimentally obtained microtubules shapes using Eq. (5). For the calculations all lengths were scaled by the length L of the microtubule and the forces were scaled by the hydrodynamic drag force per cross-section gηv. The shape of a microtubule with homogenous stiffness then depends on a single dimensionless parameter $\langle \tilde{\kappa }\rangle =\langle \kappa \rangle ∕\left(\mathrm{L}^3\mathrm{g}\mathrm{\eta }\mathrm{v}\right)$.

Apparent stiffness (<κ>/κ₀) is the stiffness of an homogeneous microtubule whose shape best fits the observed (or simulated) deformation. It is higher than the stiffness of the soft part except when this part gets long enough and the two values match.

In figure 5d, we worked with numerical microtubules with an apparent stiffness of ⟨κ⟩/κ₀ = 0.5. We calculated the scaled fit parameter ω/L for microtubule with varying parameters of the perturbation Δs/L and κ_p/κ₀ and different ratios κ₀/L³gηv, corresponding to different deflections of the unsoftened microtubule. All other parameters were kept constant, i.e. s₀/L = 0.33 and ε/L=0.02.

To match experimentally obtained scaled fit parameters ω/L to theoretical ones, we picked bending cycles were microtubules showed a scaled effective rigidity ratio $\langle {\tilde{\kappa }}_{\mathrm{n}}\rangle ∕\langle {\tilde{\kappa }}_1\rangle \approx 0.4...0.6$ (The subscript denotes the number of the bending cycle.). We then matched the deflection of the first bending cycle x/L and the experimental fit quality parameter ω_n/L_n to the theoretical curves to obtain an estimation of the width of the softened region (see Fig. 5d). Experimental points were spread between Δs/L =0 and 0.6, which supports the hypothesis that the bending induced damages were not always highly localized but often extended over a larger portion of the microtubule.