Polarizable Molecular Dynamics in a Polarizable Continuum Solvent

Abstract

We present for the first time scalable polarizable molecular dynamics (MD) simulations within a polarizable continuum solvent with molecular shape cavities and exact solution of the mutual polarization. The key ingredients are a very efficient algorithm for solving the equations associated with the polarizable continuum, in particular, the domain decomposition Conductor-like Screening Model (ddCOSMO), a rigorous coupling of the continuum with the polarizable force field achieved through a robust variational formulation and an effective strategy to solve the coupled equations. The coupling of ddCOSMO with non variational force fields, including AMOEBA, is also addressed. The MD simulations are feasible, for real life systems, on standard cluster nodes; a scalable parallel implementation allows for further speed up in the context of a newly developed module in Tinker, named Tinker-HP. NVE simulations are stable and long term energy conservation can be achieved. This paper is focused on the methodological developments, on the analysis of the algorithm and on the stability of the simulations; a proof-of-concept application is also presented to attest the possibilities of this newly developed technique.

1 Introduction

In the last few years polarizable molecular mechanics (MM) has been an intense field of development.^1–8 In particular, polarizable molecular dynamics (MD) simulations open new routes to study difficult systems ranging from metalloproteins and heavy metal complexes to polar and ionic liquids that require more sophisticated potentials. Moreover, an increasing number of studies show that the lack of polarization can be a serious limitation for ionic systems but also for a correct estimation of weak interaction, with direct implications in protein folding and protein-ligand binding.^8–12

The potential increase of accuracy which can be reached by introducing a polarizable force field (PFF) faces however the disadvantage of a more costly simulation;¹³ this is particularly true when a large set of solvent molecules have to be included in the system to account for bulk solvation effects. To overcome this problem, continuum solvation models^14–17 (CSM) can be effectively used and in fact different combinations of standard nonpolarizable FF and CSMs are available in various MD softwares. The mixed strategy is advantageous with respect to a fully atomistic one as the continuum easily takes into account the long-range interactions that would require a huge number of solvent molecules, increasing significantly the computational cost of the simulation, and implicitly includes the statistical average of their configurations. However, until now the coupling between polarizable force fields and polarizable continuum models has been mostly used to obtain an alternative approach to the Periodic Boundary Conditions and a simplified spherical model has been used to represent the boundary between the atomistic and the continuum model. A notable example is the Generalized Solvent Boundary Potential (GSBP) approach developed by Roux and coworkers¹⁸ but also approaches based on apparent surface charge (ASC) methods have been presented.^19–23 Alternatively, the coupling between PFFs and continuum models have been proposed for simplified versions of CSMs in which the atomistic part of the system can be polarized by the continuum part but not vice versa;²⁴ the Generalized Born Model²⁵ (GBM) is the typical continuum approach used even if more recently a Generalized Kirkwood model²⁶ and a linearized Poisson-Boltzmann model²⁷ have been presented in combination with the AMOEBA polarizable force field.^28,29

To get a more realistic description of the environment effects, it would be important to have a fully polarizable scheme in which the two subsystems mutually polarize in a self consistent way. This characteristic is one of the main reasons of the success of CSMs when coupled to quantum-mechanical descriptions.^14,30 In fact, the QM electronic density is self-consistently adapted to the solvent polarization in QM/CSM formulations and this allows to account for the important effects that the solvent can have on molecular properties and processes of solvated systems. We can therefore expect that the same important effects can be seen in the classical simulation of processes when a polarizable description is used for the atomistic part of the system. Unfortunately, it is not straightforward to extend the CSMs which have been optimized for the coupling with a QM description, to classical and polarizable descriptions. In the QM cases, in fact, the cost of the overall calculation is largely dominated by the QM step and therefore the computational effectiveness of the polarizable CSMs is not a real issue. When the polarizable CSM has to be coupled to classical descriptions, instead, the picture can be completely reverted and the resolution of the self-consistent scheme which determines the response of the CSM to the atomistic but classical subsystem can become so severe a bottleneck to make the whole approach practically useless when applied to MD simulations.^31,32 To have a really usable fully polarizable MM/CSM approach, the continuum approach has thus to be reformulated in a very efficient way.

In this paper, we present the first scalable formulation of a fully polarizable MM/CSM that can be used in MD simulations of systems of real (bio)chemical interest. This formulation is achieved by coupling PFFs with the continuum model we have recently proposed, the domain decomposition Conductor-like Screening Model^33–36 (ddCOSMO). The latter is a continuum model which represents the polarization of the solvent in terms of a response limited to the surface of the molecular cavity embedding the atomistic subsystem (which can be either treated classically or quantum-mechanically). The ddCOSMO is characterized by linear scaling properties with respect to the size of the system and is well suited for parallel implementations. Its capabilities were recently demonstrated for QM methods enabling the optimization of large molecules in solvent with gain of up to 3 orders of magnitude in time with respect to other CSMs.³⁵ We propose here a totally new implementation of the method in combination with different PFFs based on induce dipoles, including variational and non variational PFFs.

The paper is organized as follows. In section 2, theory and algorithms are presented with a special focus on the coupling issue in the framework of both variational and non-variational PFFs. In section 3, the numerical stability of the simulations is demonstrated and an application to the simulation of solvent effects on the IR spectrum of a small polypeptide system is reported. Some conclusions and perspectives end the paper in section 4.

2 Theory

In this section, we briefly recap the polarization equations for both point-dipole based^37,38 PFFs and the COSMO solvation model,³⁹ accordingly to the ddCOSMO discretization; we focus on the coupling of such models and discuss the special case of non-variational force fields.²⁸ The algorithm implemented to solve the final, coupled equations is also briefly presented.

In a dipole-based polarizable force field, the electrostatics of each atom i is described through a set of static multipoles and a polarizability α_i, a 3-dimensional rank 2 symmetric tensor which describes the linear response of such an atom to a polarizing electric field E⃗_i. The static multipoles are usually point charges, but more advanced force fields can include higher order multipoles, such as dipoles and quadrupoles; nevertheless, the field created by the multipolar distribution induces, at each polarizable site i, a point dipole μ⃗_i such that the interaction between the inducing field E⃗_i and the induced dipoles is maximized, while the work to induce the dipoles and the interaction between the induced dipoles are minimized. In a recent paper,¹³ we have thoroughly analyzed the properties of the polarization equations and we have introduced a Jacobi-DIIS scheme that has been shown to be robust, enjoy fast convergence properties and be suitable for parallel implementations due to low communications between processes. All the details of the derivation can be found in reference 13. Here, it is sufficient to say that the induced dipoles are the minimizers of the following energy functional

$$ℰ=-\sum _{i=1}^N{E}_i^{\alpha }{\mu }_i^{\alpha }+\frac{1}{2}\sum _{i=1}^M{[{\alpha }_i^{-1}]}^{\alpha \beta }{\mu }_i^{\alpha }{\mu }_i^{\beta }+\frac{1}{2}\sum _{i=1}^M\sum _{j\ne i}{𝒯}_{ij}^{\alpha \beta }{\mu }_i^{\alpha }{\mu }_j^{\beta },$$ (1)

where $E_i^{\alpha }$ is the α-th component of the inducing field E⃗_i and ${\mu }_i^{\alpha }$ the α-th component of the induced dipole μ⃗_i, both at the polarization site i; the Latin indexes run over the M polarization sites and the Greek ones over the Cartesian coordinates of the various quantities, for the latter indexes, Einstein summation is used.

$${𝒯}_{ij}^{\alpha \beta }=-\frac{{\delta }_{\alpha \beta }}{r_{ij}^3}{\lambda }_3(u_{ij})+3\frac{r_{ij}^{\alpha }{r}_{ij}^{\beta }}{r_{ij}^5}{\lambda }_5(u_{ij})$$ (2)

is the dipole-dipole interaction matrix, δ_αβ is the Kronecker symbol, r_ij = |r_j − r_i| is the distance between site i and site j and u_ij = r_ij/(〈α_i〉〈α_j〉)^1/6 is the effective distance as a function of the averaged polarizabilities of sites i and j, 〈α_i〉 = 1/3 tr α_i. Such a matrix includes Thole’s damping through the functions

$${\lambda }_3(u)=1-e^{-a{u}^3},$$ (3)

$${\lambda }_5(u)=1-(1+a{u}^3)e^{-a{u}^3}.$$ (4)

Other functional forms are used in the literature for the damping functions; a detailed analysis can be found in references 40, 41. It is possible to introduce a more compact notation by introducing a 3M-dimensional symmetric matrix T, which we will refer to as the polarization matrix, and the 3M-dimensional fields and dipoles vectors according to

$$\mathbf{T}=\left(\begin{array}{ccccc}\hfill {\alpha }_1^{-1}\hfill & \hfill {𝒯}_{12}\hfill & \hfill {𝒯}_{13}\hfill & \hfill \cdots \hfill & \hfill {𝒯}_{1M}\hfill \\ \hfill {𝒯}_{21}\hfill & \hfill {\alpha }_2^{-1}\hfill & \hfill {𝒯}_{23}\hfill & \hfill \cdots \hfill & \hfill {𝒯}_{2M}\hfill \\ \hfill {𝒯}_{31}\hfill & \hfill {𝒯}_{32}\hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill {𝒯}_{M1}\hfill & \hfill {𝒯}_{M2}\hfill & \hfill \hfill & \hfill \cdots \hfill & \hfill {\alpha }_M^{-1}\hfill \end{array}\right),\mathbf{E}=\left(\begin{array}{c}\hfill {\overrightarrow{E}}_1\hfill \\ \hfill {\overrightarrow{E}}_2\hfill \\ \hfill ⋮\hfill \\ \hfill {\overrightarrow{E}}_M\hfill \end{array}\right),\mathit{\mu }=\left(\begin{array}{c}\hfill {\overrightarrow{\mu }}_1\hfill \\ \hfill {\overrightarrow{\mu }}_2\hfill \\ \hfill ⋮\hfill \\ \hfill {\overrightarrow{\mu }}_M\hfill \end{array}\right).$$ (5)

where the 𝒯_ij ∈ ℝ^3×3 blocks are the ones defined in Eq. (2). The energy functional defined in eq. 1 becomes

$$ℰ=\frac{1}{2}{\mathit{\mu }}^{†}\mathbf{T}\mathit{\mu }-{\mathbf{E}}^{†}\mathit{\mu };$$ (6)

finally, the minimum condition leads to the following linear system:

$$\mathbf{T}\mathit{\mu }=\mathbf{E}.$$ (7)

Continuum solvation models require to solve or to approximate a partial differential equation which, for polarizable models, is either the Poisson equation or the Poisson-Boltzmann equation. In particular, in the COSMO model the solvent is represented as an infinite, uniform conductor that occupies the whole space but a cavity that accommodates the solute. There are several definitions for such a cavity,¹⁴ the most common being the Van der Waals cavity, the solvent accessible surface (SAS) and solvent excluded surface (SES): in the present work, we use a scaled Van der Waals cavity, which we obtain as the union of interlocking spheres, one per atom, the radii of which are the Van der Waals radii of the atoms scaled with a constant factor of 1.1. In the ddCOSMO framework, an iterative procedure based on Schwarz’s domain decomposition method is used together with a discretization scheme based on spherical harmonics, which corresponds to solving a non-symmetric linear system³³

$$LX=g_0,$$ (8)

where L is the ddCOSMO matrix, X is the unknown used to represent the solvent polarization and g₀ is the solute’s potential weighted with suitable switching factors. More details can be found in references 33, 34 and in appendix A. The ddCOSMO matrix is formed by M² blocks, each block corresponding to a sphere (and hence to an atom) and being sized (N +1)², where N is the maximum angular momentum used for the spherical harmonics expansion of the solution. Such a matrix is sparse, as only intersecting spheres are interacting, with any off-diagonal block corresponding to two spheres that do not intersect being zero. The ddCOSMO reaction energy, i.e., the electrostatic contribution to the solvation energy, is computed as

$$E_s=\frac{1}{2}f(ℰ)\langle {\mathrm{\Psi }}_0,X\rangle ,$$ (9)

where f(ε) is an empirical scaling introduced to account for the dielectric nature of the solvent³⁹ (typically, $f(\epsilon )=\frac{\epsilon -1}{\epsilon }$ where ε is the macroscopic dielectric constant of the solvent), Ψ is a vector containing the solute’s (static) multipolar distribution scaled with suitable factors and we denote

$$\langle a,b\rangle =\sum _{j=1}^M\sum _{l=0}^N\sum _{m=-l}^l{[a_j]}_l^m{[b_j]}_l^m.$$ (10)

The coupling of a dipole-based polarizable force field and ddCOSMO can be obtained through a variational formulation.^13,20,31 Given the ddCOSMO equations, it is in fact possible to write an energy functional which is variational with respect to the dipoles and includes mutual polarization between the dipoles and the continuum. Such a functional is the sum of the dipoles functional, as in eq. 6, and the ddCOSMO energy:

$$𝒢(\mathit{\mu })=\frac{1}{2}{\mathit{\mu }}^{†}\mathbf{T}\mathit{\mu }-{\mathit{\mu }}^{†}{\mathbf{E}}_0+\frac{1}{2}f(ℰ)\langle \mathrm{\Psi },X\rangle ,$$ (11)

where

$$X=L^{-1}g$$ (12)

according to the ddCOSMO equation. Notice that we have introduced, for ddCOSMO, the quantities

$$g=g(\mu )=g_0+g_{\mu },\hspace{1em}\mathrm{\Psi }=\mathrm{\Psi }(\mu )={\mathrm{\Psi }}_0+{\mathrm{\Psi }}_{\mu }.$$ (13)

Such quantities are affine functions of μ and correspond to the potential generated by the solute, including the induced dipoles, and to the scaled multipoles and induced dipoles (see eq. 48 in Appendix A), respectively, and account for the interaction between the solute and the solvent. Notice that, as g_μ and Ψ_μ are linear in μ, we can write:

$$g_{\mu }=B^{*}\mu ,\hspace{1em}{\mathrm{\Psi }}_{\mu }=A^{*}\mu .$$ (14)

The ddCOSMO term in eq. 11 introduces a combination of constant, linear and quadratic terms with respect to the induced dipoles, correctly implying the mutual polarization of the dipoles with the continuum, as the dipoles and ddCOSMO equations will be coupled. The coupled equations can be derived by imposing the stationarity of the new energy functional with respect to the induced dipoles:

$$\frac{\partial 𝒢}{\partial \mathit{\mu }}=\mathbf{T}\mathit{\mu }-{\mathbf{E}}_0+{\mathbf{E}}_c=0,$$ (15)

where we have introduced the COSMO field E_c, which is obtained by differentiating the COSMO energy with respect to the induced dipoles:

$${\mathbf{E}}_c=\frac{1}{2}f(ℰ)\frac{\partial }{\partial \mathit{\mu }}\langle \mathrm{\Psi },X\rangle =\frac{1}{2}f(ℰ)[\langle \frac{\partial \mathrm{\Psi }}{\partial \mathit{\mu }},X\rangle +\langle \mathrm{\Psi },\frac{\partial X}{\partial \mathit{\mu }}\rangle ].$$ (16)

Both terms of eq. 16 are obtained with a linear transformation of either the ddCOSMO solution X or the solution to the ddCOSMO adjoint equations L*S = Ψ; in particular:

$${\mathbf{E}}_c=\frac{1}{2}f(ℰ)[AX+BS].$$ (17)

The expressions of the A and B matrices, together with the derivation of equations 17 and 14 can be found in appendix B. We are now ready to write the coupled equations for the dipoles and the continuum. By putting everything together, eq. 15 becomes

$$\mathbf{T}\mu +\frac{1}{2}f(ℰ)AX+\frac{1}{2}f(ℰ)BS={\mathbf{E}}_0,$$ (18)

where the direct and adjoint ddCOSMO equations, which we need to compute X and s, are

$$LX=g=g_0+B^{*}\mathit{\mu }$$ (19)

and

$$L^{*}S=\mathrm{\Psi }={\mathrm{\Psi }}_0+A^{*}\mathit{\mu }.$$ (20)

We can put everything together into a global linear system:

$$\left(\begin{array}{ccc}\hfill \mathbf{T}\hfill & \hfill \frac{1}{2}f(ℰ)A\hfill & \hfill \frac{1}{2}f(ℰ)B\hfill \\ \hfill -B^{*}\hfill & \hfill L\hfill & \hfill 0\hfill \\ \hfill -A^{*}\hfill & \hfill 0\hfill & \hfill L^{*}\hfill \end{array}\right)\left(\begin{array}{c}\hfill \mathit{\mu }\hfill \\ \hfill X\hfill \\ \hfill S\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\mathbf{E}}_0\hfill \\ \hfill g_0\hfill \\ \hfill {\mathrm{\Psi }}_0\hfill \end{array}\right).$$ (21)

Once the linear system in eq. 21 has been solved, the total polarization energy, i.e., including both the dipoles polarization and the continuum polarization, is computed according to eq. 11.

2.1 A special case: non variational force fields

In the previous derivation, we have assumed that the polarization energy is a variational functional of the induced dipoles. This assumption is not respected in the AMOEBA force field,^28,29 where the polarization energy is computed as the electrostatic interaction between the induced dipoles, computed according to eq. 7 (and therefore as the solution to a variational problem), and an electric field which is different from the inducing one. The two fields differ for the local interaction scaling: while the inducing field (usually called “direct field”, E_d) at polarization site i is the field produced by all the multipoles on all the other sites, the contributions to the interacting field (usually called “polarization field”, E_p) from the closest neighbors (i.e., 1–2, 1–3 and 1–4) are scaled in order to take into account that the interaction energy between such atoms is usually accounted for by the bonding terms. To summarize, the AMOEBA polarization energy is defined as follows:

$$E_A=-\frac{1}{2}{({\mathit{\mu }}_d)}^{†}{\mathbf{E}}_p,$$ (22)

where the “direct” dipoles are solution to the polarization equations as in eq. 7:

$$\mathbf{T}{\mathit{\mu }}_d={\mathbf{E}}_d.$$

In order to couple the AMOEBA force field with ddCOSMO, it is possible to manipulate the AMOEBA polarization energy in order to write it as a combination of variational terms. Let μ_p be the solution to

$$\mathbf{T}{\mathit{\mu }}_p={\mathbf{E}}_p.$$

According to our derivation, the “p” dipoles will be the minimizers of

$$ℰ({\mathit{\mu }}_p)=\frac{1}{2}{({\mathit{\mu }}_p)}^{†}\mathbf{T}{\mathit{\mu }}_p-{({\mathit{\mu }}_p)}^{†}{\mathbf{E}}_p.$$

It is easily shown that

$$E_A=\frac{1}{2}{({\mathit{\mu }}_d)}^{†}{\mathbf{E}}_p=ℰ({\mathit{\mu }}_d+{\mathit{\mu }}_p)-ℰ({\mathit{\mu }}_d)-ℰ({\mathit{\mu }}_p),$$ (23)

where the two sets of dipoles are the variational minimizers of the associated energy functional: the AMOEBA polarization energy can therefore be expressed as the combination of three variational expressions. We proceed to couple ddCOSMO to the AMOEBA force field by replacing each term in eq. 23 with the corresponding “solvated” energy functional, eq. 11:

$$G_A≔𝒢({\mathit{\mu }}_d+{\mathit{\mu }}_p)-𝒢({\mathit{\mu }}_d)-𝒢({\mathit{\mu }}_p).$$ (24)

Here, both sets of dipoles are determined by minimizing the associated 𝒢 functional, i.e., by solving the coupled linear system in eq. 21 for two different right-hand sides:

$$\left(\begin{array}{ccc}\hfill \mathbf{T}\hfill & \hfill \frac{1}{2}f(ℰ)A\hfill & \hfill \frac{1}{2}f(ℰ)B\hfill \\ \hfill -B^{*}\hfill & \hfill L\hfill & \hfill 0\hfill \\ \hfill -A^{*}\hfill & \hfill 0\hfill & \hfill L^{*}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathit{\mu }}_d\hfill \\ \hfill X_d\hfill \\ \hfill S_d\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\mathbf{E}}_d\hfill \\ \hfill g_0\hfill \\ \hfill {\mathrm{\Psi }}_0\hfill \end{array}\right)$$ (25)

and

$$\left(\begin{array}{ccc}\hfill \mathbf{T}\hfill & \hfill \frac{1}{2}f(ℰ)A\hfill & \hfill \frac{1}{2}f(ℰ)B\hfill \\ \hfill -B^{*}\hfill & \hfill L\hfill & \hfill 0\hfill \\ \hfill -A^{*}\hfill & \hfill 0\hfill & \hfill L^{*}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathit{\mu }}_p\hfill \\ \hfill X_p\hfill \\ \hfill S_p\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\mathbf{E}}_p\hfill \\ \hfill g_0\hfill \\ \hfill {\mathrm{\Psi }}_0\hfill \end{array}\right).$$ (26)

The AMOEBA/ddCOSMO energy expression can be simplified by substituting the explicit expression of the various functionals: through some trivial, but cumbersome algebra we get:

$$G_A=\frac{1}{2}{({\mathit{\mu }}_d)}^{†}\mathbf{T}{\mathit{\mu }}_p-\frac{1}{2}{\mathit{\mu }}_d^{†}{\mathbf{E}}_p-\frac{1}{2}{\mathit{\mu }}_p^{†}{\mathbf{E}}_d+\frac{1}{4}f(ℰ)[\langle {\mathrm{\Psi }}_p,X_d\rangle +\langle {\mathrm{\Psi }}_d,X_p\rangle ],$$ (27)

where we have introduced the short notations Ψ_d = Ψ₀ + Ψ_μd and Ψ_p = Ψ₀ + Ψ_μp.

2.2 Analytical derivatives of the polarization energy

Analytical derivatives can be easily assembled by differentiating eq. 11, remembering that, having solved the coupled polarization equations, such a functional is stationary with respect to the dipoles:¹³

$${𝒢}^x=\frac{\partial 𝒢}{\partial x}+\frac{\partial 𝒢}{\partial \mathit{\mu }}\frac{\partial \mathit{\mu }}{\partial x},$$ (28)

where x denotes a generic coordinate of an atom.

In the variational case, the last term in eq. 28 vanishes and the derivatives of the dipoles do not need to be assembled. By expanding eq. 28, we get:

$${𝒢}^x=\frac{1}{2}{\mathit{\mu }}^{†}{\mathbf{T}}^x\mathit{\mu }-{\mathit{\mu }}^{†}{\mathbf{E}}_0^x+\frac{1}{2}f(ℰ)(\langle {\mathrm{\Psi }}^x,X\rangle +\langle \mathrm{\Psi },X^x\rangle ).$$ (29)

The derivatives of the T matrix and of the electric field have been discussed extensively in ref. 13. The derivatives of the Ψ vector are nonzero only if the solute’s multipolar distribution contains static multipoles of angular momentum greater than zero, i.e., dipoles, quadrupoles and higher order terms: such multipoles are in fact vector or tensor quantities which need to be defined in a local frame and rotated in the lab frame: such a transformation depends on the position of the atoms and contributes to the total derivatives. This contributions have also been extensively discussed in ref. 13. The derivatives of the X expansion coefficients can be computed by differentiating the ddCOSMO equations:

$$L^{x}X+L{X}^x=g^x\Rightarrow X^x=L^{-1}(g^x-L^{x}X).$$ (30)

By substituting into the last term of eq. 29:

$$\langle \mathrm{\Psi },X^x\rangle =\langle \mathrm{\Psi },L^{-1}(g^x-L^{x}X)\rangle =\langle S,g^x-L^{x}X\rangle .$$ (31)

Notice that the solution to the adjoint system is already available, as it is necessary to compute it in order to solve the coupled linear system. A complete derivation of the ddCOSMO analytical derivatives, including the expressions of g^x and L^x can be found in ref. 34.

Analytical derivatives for the non-variational case can be formulated using the same procedure elucidated in the previous section, i.e., by writing the energy as a combination of variational contributions, differentiating each variational contribution and putting everything together. Through some algebra, we get

$$G_A^x=\frac{1}{2}{\mathit{\mu }}_p^{†}{\mathbf{T}}^x{\mathit{\mu }}_d-\frac{1}{2}{\mathit{\mu }}_p^{†}{\mathbf{E}}_d^x-\frac{1}{2}{\mathit{\mu }}_d^{†}{\mathbf{E}}_p^x+\frac{1}{4}f(\epsilon )[\langle {\mathrm{\Psi }}_d^x,X_p\rangle +\langle {\mathrm{\Psi }}_d,X_p^x\rangle +\langle {\mathrm{\Psi }}_p^x,X_f\rangle +\langle {\mathrm{\Psi }}_p,X_d^x\rangle ].$$ (32)

2.3 Implementation details

The solution to the coupled polarization equations is a computationally demanding task, as the size of the linear system can easily become very large. Direct techniques, such as LU decomposition, can not be employed, as even for medium-sized systems the matrix in eq. 21 can be too large to be stored in memory. Fortunately, the sparsity of the ddCOSMO matrix allows for a very efficient, linear-scaling iterative procedure to solve the direct and adjoint ddCOSMO equations: such an iterative procedure can be coupled with an iterative solver for the dipoles linear system. In particular, we use Jacobi Iterations (JI) coupled with the Direct Inversion in the Iterative Subspace (DIIS) extrapolation both for ddCOSMO³⁴ and for the dipoles.¹³ The details of the implementation and a thorough analysis of the various possible algorithm to treat the polarization equations can be found elsewhere^13,42 Three families of iterative strategies are possible, in principle, to solve the coupled equations. The first is the so-called monolithic approach, i.e., to deal with the full linear system at once through an iterative procedure; the second is to iterate on the dipoles (macroiterations) and, at each macroiteration, fully solve the COSMO direct and adjoint equations (microiterations); the third is to iterate on the COSMO direct and adjoint equations (macroiterations) fully solving, at each macroiteration, the dipoles system (microiterations). Various refinements, such as doing an adaptive number of macroiteration depending on the convergence, or using a varying threshold for the microiteration depending on the convergence of the macroiterations, can be adopted to speedup the process. The three strategies have been implemented and explored: the second and third ones resulted to be the most competitive. Nevertheless, in the perspective of performing MD simulations, the ability of providing a very good guess for the dipoles led us to adopt the second strategy, which we will now detail.

Initial computation and guess

The first step of the computation is to assemble the right-hand side of eq. 21, that is, the electric field of the solute at the polarizable sites, its potential at the cavity and the Ψ₀ vector, which is formed by scaling the solute multipolar distribution according to eq. 48. A guess is also formed for the dipoles: in a previous paper¹³ we analyzed various possibilities and we found that using the predictor step of Kolafa’s integrator⁴³ as a guess provided a very effective form of convergence acceleration. Kolafa’s guess requires one to know the solution at the six previous point: for the first six steps in a MD simulation, we use what we called in the previous paper the direct field guess, i.e., we initialize the dipoles to

$${\overrightarrow{\mu }}_i={\alpha }_i{\overrightarrow{E}}_i^0.$$

Both the ddCOSMO X and S coefficients are initialized to zero. Given the guessed dipoles, the total potential Φ and the total Ψ vector are assembled.

Main loop

The main iteration loop starts with two calls to the ddCOSMO iterative solver - for the direct and adjoint systems, respectively. Such calls are completely independent and can be run in parallel. The ddCOSMO linear systems are solved iteratively by Jacobi/DIIS using a variable convergence threshold; in particular, we start with a threshold of 10⁻³ and, along the macroiterations, we set it to one tenth of the root-mean-square (RMS) increment on the dipoles. Also, at macroiteration i, we use X[ⁱ⁻¹] and S^[i−1] as guesses. Once the two ddCOSMO linear systems have been solved, the COSMO electric field is computed according to equation 17 and added to the E₀ field. A Jacobi step is then performed on the dipoles and the RMS of the increment and its maximum are computed. Convergence is achieved when the RMS is smaller than a threshold provided by the user and the maximum smaller than ten times such a threshold. If convergence has not been reached, the DIIS extrapolation is carried out on the dipoles. Finally, the total potential and Ψ vector are updated for the following iteration. Notice that for the non-variational case, two sets of dipoles (and hence of ddCOSMO coefficients) are dealt with; nevertheless, the matrix is formed on the fly and multiplied with both sets of dipoles, with limited - but not negligible - computational overhead. This step is the most time-consuming, as several matrix-vector products are to be evaluated.

Energy and Forces

Once the coupled equations have been solved, we proceed to compute the solvation and polarization energy according to equation 11 or 27 in the non-variational case. The forces are then computed according to equation 28, or 32, in order to be used for the integration of the equations of motion in the MD simulation.

This strategy has been implemented in the Tinker Package and parallelized according to either the OpenMP or the MPI paradigms. The implementation of the ddCOSMO field has been checked by comparing the computed field with the one obtained by numerically differentiating the energy with respect to the dipoles; the same validation has been carried out with the forces, which have been compared with numerical derivatives of the energy with respect to the positions of the nuclei. In both cases, an agreement up to numerical precision was observed; also, the forces rigorously sum to zero independent of the discretization and of the convergence threshold used.

3 Results

3.1 Numerical tests

In this section, we will analyze the behavior of a MD simulation performed with a PFF coupled to ddCOSMO with respect to the convergence used for the linear equations and to the time step used in the MD. We will also comment on the timings and on the performances of our code on parallel architectures.

Computational details

All the computation have been performed with a locally modified module of the TINKER⁴⁴ package, named Tinker-HP, dedicated to parallel implementations. The iterative solver used for the polarization equations and the ddCOSMO algorithm were implemented in such a module and parallelized according to either the OpenMP or the MPI paradigms. As a test case, we performed a 100ps NVE MD simulation on a small protein (PDB reference: 1FSV) using increasing convergence thresholds and timesteps. The PDB structure was minimized with analytical gradients and a 20ps NVT equilibration was run with the Berendsen Thermostat⁴⁵ in order to provide a starting point for the NVE simulations. Both a variational force field, namely the AMBER ff99 force field with the parametrization of Wang et al.^40,46 for the polarizable electrostatics, and a non variational one, namely the AMOEBA99bio²⁸ force field, were employed. All the computations were performed on a dual Xeon E5-2650 cluster node (16 cores, 2GHz) equipped with 64GB of DDR3 memory.

For each simulation, we report: (i) the short time average fluctuation, which we compute as the average of the RMS, 100 steps fluctuation of the total energy; (ii) the long range energy drift, which we compute by fitting the total energy as a function of time with a linear function

$$E(t)=at+b$$

and by computing the value of such a function at 100ps; (iii) the average computational time per time step, which we compute as the total computational time over the number of time steps. The results are summarized in Table 1 for the AMBER/Wang variational force field and in table 2 for the AMOEBA force field. From the results reported in Tables 1 and 2 we can infer the good stability of the polarizable dynamics. Short time fluctuations are always smaller than 1 kcal/mol, even using the sleaziest convergence threshold and the longer time step, for both the variational and the non variational force field. This proves the good quality of the computed forces, which not only sum rigorously to zero (i.e., the total momentum is conserved), but are also little sensitive to the small error on the dipoles and ddCOSMO equations solution due to a non fully-converged iterative procedure. Furthermore, such a drift shows little or no dependence on the threshold and a test performed with very tight convergence does not show further improvements: the short term fluctuations are therefore mainly a consequence of the Velocity Verlet integrator. Notice how the STF illustrates that such an integration scheme is second order in the time step. Long term stability is more subtle to analyze, as it is the result of several interacting causes. The Velocity Verlet is a second-order simplectic integrator and its time reversibility grants, in exact precision, the long term stability of the simulation; however, round-off errors and a non-perfect convergence of the polarization degrees of freedom can spoil energy conservation producing a drift. Furthermore, the guess for the iterative solution can break the overall time-reversibility of the simulation, either being itself non time-reversible (for instance, using the solution at the previous step produces a non-symmetric expression with respect to time inversion) or being time-reversible only for fully converged solutions and infinite precision. The latter is the case for our choice of a guess: as mentioned in section 2.3, we use the prediction step of Kolafa’s predictor-corrector, the reversibility of which, when used as a guess, is spoiled by convergence and round-off errors. Such effect is more marked for longer time steps and sleazier convergence thresholds, producing a drift which can be as large as 20 kcal/mol per 100ps. This analysis is further complicated by the interaction of the various sources of long time effects, which can produce error cancellation: this explains, for instance, the non systematic behavior we observed, for instance, for the AMOEBA simulation, where, for a convergence threshold fixed to 10⁻⁴, the 1fs time-step simulation is more stable than the 0.5fs one.

Table 1.

Stability of NVE simulations as a function of the convergence threshold for the coupled polarization equations and of the time step (AMBER/Wang variational force field). For each combination, the short time average fluctuation (STF), the long time drift (LTD) and the average computational time per time step (ACT) are reported. All the energies are in kcal/mol, all timings in seconds.

	Convergence 10−4			Convergence 10−5			Convergence 10−6
Time step	STF	LTD	ACT	STF	LTD	ACT	STF	LTD	ACT
1.00fs	0.42	20.7	0.35	0.46	18.5	0.46	0.43	20.7	0.75
0.50fs	0.11	8.7	0.35	0.10	2.1	0.46	0.10	4.4	0.75
0.25fs	0.03	3.6	0.35	0.02	0.0	0.46	0.02	0.5	0.75

Table 2.

Stability of NVE simulations as a function of the convergence threshold for the coupled polarization equations and of the time step (AMOEBA force field). For each combination, the short time average fluctuation (STF), the long time drift (LTD) and the average computational time per time step (ACT) are reported. All the energies are in kcal/mol, all timings in seconds.

	Convergence 10−4			Convergence 10−5			Convergence 10−6
Time step	STF	LTD	ACT	STF	LTD	ACT	STF	LTD	ACT
1.00fs	0.46	−1.6	1.18	0.46	3.1	1.34	0.45	9.0	1.72
0.50fs	0.11	10.4	1.18	0.11	1.5	1.34	0.11	1.2	1.72
0.25fs	0.03	2.1	1.18	0.03	0.2	1.34	0.03	−0.1	1.72

Nevertheless, our results show that it is indeed possible to perform a stable MD simulation with a polarizable force field coupled to a polarizable continuum by choosing an appropriate combination of time step and convergence thresholds. We also remark that, thanks to the excellent short-time behavior, it is possible to correct the long time behavior by using a thermostat: even the 1fs step - 10⁻⁴ threshold can be used with a noticeable saving in computational time. We stress that Kolafa’s predictor as a guess, as shown in a recent publication,¹³ is a very effective guess, which greatly reduces the number of iterations needed to converge the polarization equations: the small instabilities introduced are a price worth to be paid for the computational saving produced.

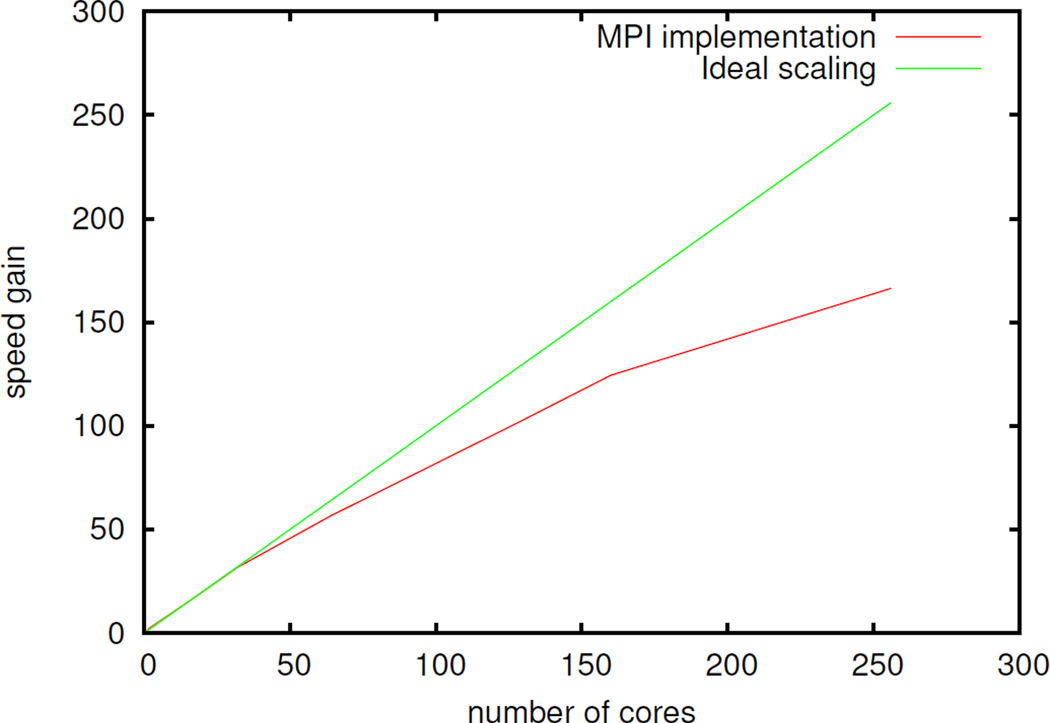
We conclude this section by discussing briefly the MPI parallel implementation of our procedure. For the ddCOSMO solver, which needs to be called twice per iteration, a spacial decomposition load balancing strategy is used to ensure that each process is given a similar workload; moreover, non-blocking communication is used to mask the communication overhead. Once the two ddCOSMO linear system have been solved, the solutions are broadcasted to all the processes in order to compute the COSMO field and the next iteration dipoles are computed. This are in turn broadcasted in order to compute the potential and Ψ vector for the next ddCOSMO computation. The overall scaling properties of the algorithm for a system composed by roughly 10000 atoms are reported in figure 1. While the scaling deviates from the ideal one, the overall performances of the code are quite good and allow one to use our implementation on parallel computers. It appears that the ddCOSMO solver is the limiting part in terms of parallel scaling; furthermore, while a hybrid OpenMP/MPI implementation showed very promising results for the direct-space solution of the polarization equations, this was not the case for the ddCOSMO equations and, therefore, for the coupled PFF/ddCOSMO ones. A more efficient parallel implementation is under active investigation.

Figure 1.

Scaling of the MPI code for the coupled induced dipoles/ddCOSMO problem, with respect to a single node (16 cores) computation.

3.2 Solvatochromism of a α-helical polypeptide

In order to test the ability of ddCOSMO to introduce solvation effects in a MD simulation, we have studied the solvatochromism of a model peptide in its alpha-helix secondary structure. MD simulations have been performed by using a development version of Tinker program⁴⁴ and the AMOEBA99bio force field.²⁸ The system consists of a single α-helical polypeptide composed by twenty amino-acids. To consider the solvatochromism, two sets of 5 trajectories have been considered both in vacuo and in water by means of the ddCCOSMO implicit scheme described in this paper. For both sets of trajectories, a first set of simulations of 20ps were performed in the canonical (NVT) ensemble at room temperature to ensure the thermalization step, using Berendsen thermostat;⁴⁵ subsequent trajectories of 20ps in the microcanonical ensemble (NVE) for production have been computed. Equations of motion have been integrated with the velocity-Verlet scheme⁴⁷ and a timestep of 0.1 fs. IR spectra are obtained from the Fourier transform of the dipole autocorrelation function:⁴⁸

$$I(\omega )\propto {\int }_0^T\langle \mu (0)\mu (t)\rangle e^{-i\omega t}dt,$$ (33)

where μ is the molecular dipole and T is the simulation time. The assignment of vibrational bands in terms of atomic displacements can be achieved through vibrational density of states, calculated as the Fourier transform of the velocity correlation function:

$$P(\omega )=\sum _{j=1}^M{\int }_0^T\langle {\upsilon }_j(0)·{\upsilon }_j(t)\rangle e^{-i\omega t}dt,$$ (34)

where υ_j is the velocity of the j-th atom. We then projected the velocity autocorrelation function on internal coordinates or selected atoms (C and O atoms of amide in our cases) for a more comprehensive assignment of the peaks.⁴⁸

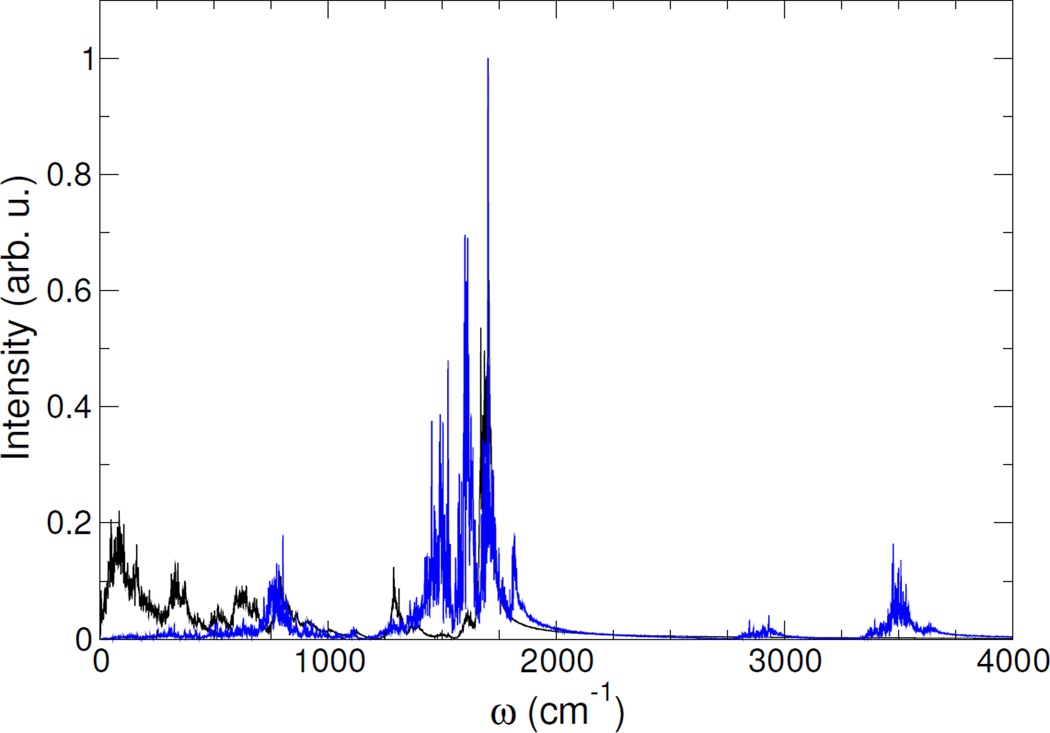
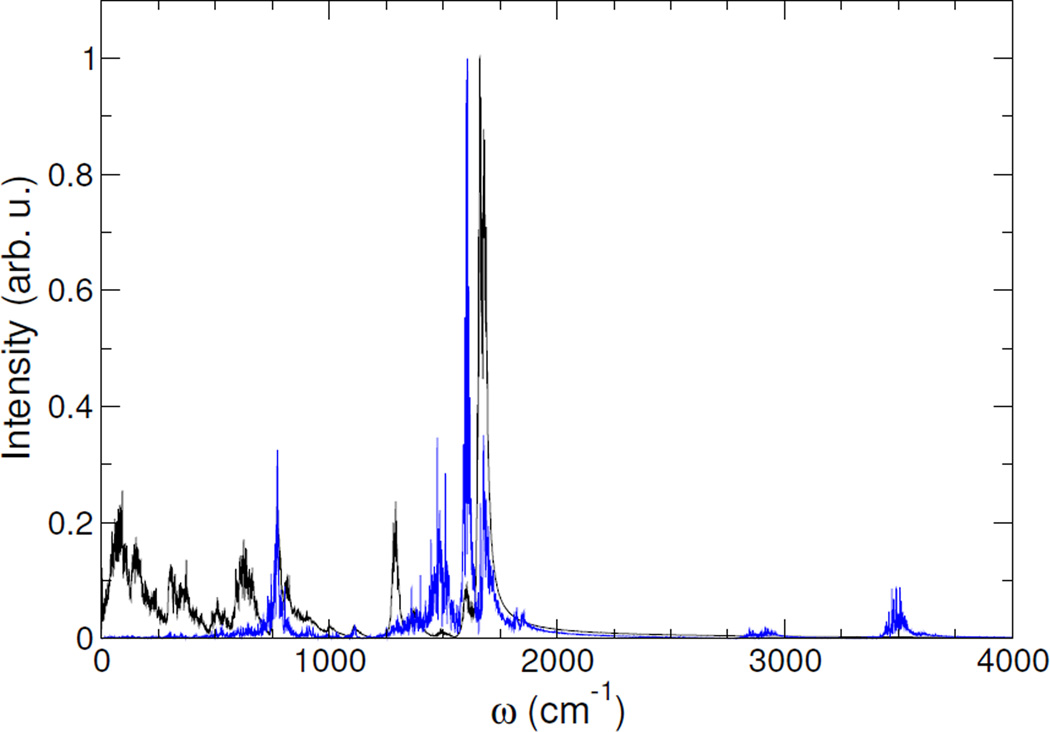
Computed IR spectra (black lines) and vibrational densities of states projected on the C and O atoms of all amide groups (blue lines) for the α-helix model are shown on fig. 2 and 3 for the in vacuo and in water computations, respectively. Assignments of the active IR bands corresponding of the amide I region can be easily achieved through the vibrational density of states projected on C and O atoms of all amide groups (blue lines): the bands of the IR spectrum with maximal overlap with the main bands of the power spectrum are assigned to the motion of the C and O atoms of the amide groups.

Figure 2.

Computed IR spectra (black) and projected vibrational density of states (blue) on C and O atoms of all amide groups for a α-helix polypeptide model in vacuo

Figure 3.

Computed IR spectra (black) and projected vibrational density of states (blue) on C and O atoms of all amide groups for a α-helix polypeptide model in water

Indeed, the amide I mode frequency is found to be 1700 cm⁻¹ in vacuo and between 1665–1680 cm⁻¹ in water, which is in fair agreement with the expected range of frequencies of α-helix (1654 cm⁻¹). Moreover, the solvation-induced amide I mode frequency shift was found to be in between −20 cm⁻¹ and −35 cm⁻¹, which is in excellent agreement with previous classical MD simulations using an explicit treatment of the solvation of a α-helix model.⁴⁹ This result demonstrates the ability of the ddCOSMO scheme to correctly reproduce the solvatochromism of the amide I region for a α-helix model without the explicit treatment of solvent molecules.

4 Conclusions and Perspectives

We have presented for the first time a formulation and implementation of polarizable MD in a polarizable continuum solvent without restrictions on the cavity shape and without approximations on the coupling between the polarization degrees of freedom. A solid variational formulation has been proposed to introduce the coupling and derive the equations; a generalization to non-variational polarizable force fields has then been achieved by writing the non-variational energy as a linear combination of variational functionals. Thanks to a new formulation for the continuum, ddCOSMO, it is indeed possible to solve the mutual polarization equations for both the continuum and the dipoles very efficiently; furthermore, the algorithm is highly suited for parallelization and a scalable implementation is already available. The combination of algorithmics, code optimization and parallelization makes the method fully operational and not just a proof of concept: while being more expensive than standard ones, polarizable MD simulations in a polarizable continuum can be performed for medium-large systems even on a single computer node in reasonable times, i.e., roughly one second per time-step. Nevertheless, in order to apply this methodology to larger systems, the use of the MPI code on large computers becomes mandatory. Furthermore, the use of linear scaling techniques, such as the Fast Multipole Method, to overcome the quadratic bottlenecks connected to the evaluation of the MM/Continuum couplings and of the induced dipoles iterations, will also make possible computations on larger systems.

Momentum and energy conservation have been rigorously assessed. The analytical forces always sum to zero, implying the momentum conservation and a very good behavior of NVE simulations with respect to short-time fluctuations; long-time energy conservation can be obtained by combining the use of a tight convergence threshold for the polarization equations, an adequate time-step and a non-biased guess for the dipoles. Nevertheless, the long term stability remains acceptable even for sleazy converge thresholds, long time steps and a non fully time-reversible guess for the dipoles: the small and slow long-term drift can be easily controlled by a weakly coupled thermostat. The capabilities of this new methodology have been sketched with a test-case application, where we succeeded in reproducing the solvatochromic shift of the amide I mode of an α-helix oligopeptide. We would like to point out that we have obtained such a result without any re-parametrization of either the force field (and in particular, the electrostatic and van der Waals terms) or the continuum (in particular, the atomic radii used to define the cavity): more accurate results can be easily obtained by a better tailoring of the method.

The ddCOSMO algorithm has been implemented for both standard and polarizable force fields in a new Tinker module implemented in our groups and devoted to massively parallel implementation; it will coexist with a parallel implementation of both the electrostatic and polarization energies and forces in the context of periodic boundary conditions simulations with the Particle Mest Ewald approach^50,51

While this article already proposes a fully operational strategy, many developments can be considered. From a methodological point of view, further investigations on the molecular cavity are needed, as the Van der Waals cavity can be not completely satisfactory: artificial holes in the cavity, which expose the solute to the solvent in non-physical regions, could be avoided by using a more advanced definition of the cavity itself, such as the so-called solvent excluded surface. Also, non-equilibrium effects, due to retardation effects in the solvent response, are currently neglected: while the role of the continuum is here mainly to provide a suitable boundary for the simulation, such effects can be important and need to be included in a complete model. From a computational point of view, several developments are possible. Due to the characteristics of the algorithm, a GPU implementation is particularly interesting and should produce noticeable performance gains. A possibility worthy of investigation would be to propagate the induced dipoles in a Car-Parrinello fashion; however, this would require a careful choice of the fictitious mass of the dipoles and could produce numerical instabilities or artifacts. Some coarse-graining of the cavity, for instance, by not endowing the hydrogen atoms with their own sphere, but by including them in the sphere of the heavy atom they are attached to, could also produce large performance gains without compromising the accuracy if the motion of an hydrogen atom is not the aim of the study. Further code optimization and parametrization, with particular focus on the non-electrostatic terms for solvation, could then open the way to free energy computations, with interesting applications in the field of biochemistry and pharmacology.

A The ddCOSMO discretization of the COSMO model

The Conductor-like Screening Model (COSMO) is a polarizable continuum solvation model which models the solvent as a structureless, uniform continuum conductor. The solute is accommodated into a molecule-shaped cavity Ω and the interaction with the environment is described as the electrostatic interaction of the density of charge of the solute with the polarization field created by the conductor. Throughout this paper, we will assume that the molecular cavity is a scaled Van der Waals cavity, built as the union of spheres centered at the atoms, with radius the Van der Waals radius of the atom scaled by a factor 1.1. This interaction energy is then scaled with an empirical factor f(ε) in order to account for the dielectric nature of the solvent. The polarization of the conductor is computed by numerically solving Poisson’s equation, usually recast as an integral equation on the cavity boundary Γ = ∂Ω. As a conductor has a constant, zero potential, the potential produced by the solute in vacuo Φ plus the potential due to the polarization W of the metal (the so-called reaction potential) must add up to zero at the boundary:

$$\forall \mathbf{s}\in \mathrm{\Gamma }\hspace{1em}W(\mathbf{s})+\mathrm{\Phi }(\mathbf{s})=0$$

The reaction potential can be represented in terms of an apparent surface charge (ASC) σ induced at the boundary:

$$\forall \mathbf{r}\in \mathrm{\Omega }\cup \mathrm{\Gamma },\hspace{1em}W(\mathbf{r})={\int }_{\mathrm{\Gamma }}\frac{\sigma (\mathbf{s})}{|\mathbf{r}-\mathbf{s}|}d\mathbf{s}$$ (35)

By putting together the two relations, one obtains the COSMO Integral equation:

$${\int }_{\mathrm{\Gamma }}\frac{\sigma (\mathbf{s}\prime )}{|\mathbf{s}-\mathbf{s}\prime |}d\mathbf{s}\prime ≔({𝒮}_{\mathrm{\Gamma }}\sigma )(\mathbf{s})=-\mathrm{\Phi }(\mathbf{s})$$ (36)

The solvation energy is then computed as

$$E_s=\frac{1}{2}f(\epsilon ){\int }_{\mathrm{\Omega }}\rho (\mathbf{r})W(\mathbf{r})=\frac{1}{2}f(\epsilon ){\int }_{\mathrm{\Gamma }}\mathrm{\Phi }(\mathbf{s})\sigma (\mathbf{s})$$ (37)

where ρ is the solute’s density of charge, $f(\epsilon )=\frac{\epsilon -1}{\epsilon }$ is the scaling factor, ε is the solvent dielectric constant and the 1/2 factor takes into account the work needed to polarize the conductor. The COSMO equation is usually discretized using the Boundary Element Method (BEM), which transforms the integral equation into a dense linear system which can be solved iteratively; as the matrix-vector products implied in the iterative solution correspond to computing the potential produced by a given set of charges, the Fast Multipole Method (FMM) can be used to achieve linear scaling in computational cost; nevertheless, to solve the COSMO equation remains a demanding task in terms of computational resources.

Recently, we have presented a new discretization for COSMO based on Schwarz’s Domain Decomposition method: we will refer to the new discretization as ddCOSMO. The ddCOSMO algorithm is an iterative procedure that decomposes the COSMO problem in the molecular cavity Ω into a collection of coupled problems in each of the spheres Ω_j that compose the cavity. At iteration it, for each sphere Ω_j, a COSMO-like integral equation is solved on its boundary Γ_j = ∂Ω_j:

$$\forall \mathbf{s}\in {\mathrm{\Gamma }}_j\hspace{1em}({𝒮}_j{\sigma }_j^{(it)})(\mathbf{s})=g(\mathbf{s})$$ (38)

The expression of the right-hand side g depends on whether the point s belongs to the global cavity’s boundary (i.e., it is exposed to the solvent) or it is inside one or more other spheres (i.e., it is buried inside the cavity). If the point is exposed, the right-hand side is equal to minus the solute’s electrostatic potential Φ(s); if the point is buried, i.e., if the point s is inside some other sphere Ω_k, the right-hand side g is computed from the reaction potential inside Ω_k at the previous iteration, which is in turn computed from ${\sigma }_k^{(it-1)}$ according to eq.35, where ${\sigma }_k^{(it-1)}$ is the solution to the integral equation on sphere k at iteration it − 1. If the point s belongs to more than one sphere, g is computed as the average of the reaction potentials in each sphere s belongs to. Let 𝒩_j(s) be the list of spheres that intersect Ω_j at s and let |𝒩_j(s)| be the number of such spheres. Let also χ_k be the characteristic function of Ω_k, i.e., χ_k(r) = 1 if r ∈ Ω_k and χ_k(r) = 0 otherwise. A point s ∈ Γ_j is external if and only if the characteristic functions of all the spheres Ω_k, k ≠ j, are zero, i.e., if

$$\sum _{k\in {𝒩}_j(\mathbf{s})}\frac{{𝒳}_k(\mathbf{s})}{|{𝒩}_j(\mathbf{s})|}=\sum _{k\in {𝒩}_j(\mathbf{s})}{\omega }_{jk}(\mathbf{s})=0$$ (39)

where, for later convenience, we have introduced the normalized weights ${\omega }_{jk}(\mathbf{s})=\frac{{\chi }_k(\mathbf{s})}{|{𝒩}_j(\mathbf{s})|}$ and we adopt the convention 0/0 = 0. Note that, in practice, the functions χ_k have to be smoothed out to obtain regular potential energy surfaces. This technical point is detailed in Ref. 34. We can now express the right-hand side of eq. 38 as

$$\forall \mathbf{s}\in {\mathrm{\Gamma }}_j\hspace{1em}g(\mathbf{s})=-(1-\sum _{k\in {𝒩}_j(\mathbf{s})}{\omega }_{jk}(\mathbf{s}))\mathrm{\Phi }(\mathbf{s})+\sum _{k\in {𝒩}_j(\mathbf{s})}{\omega }_{jk}(\mathbf{s})({𝒮}_k{\sigma }_k^{(it-1)}(\mathbf{s})$$ (40)

This leads, for each sphere j, to the following equation:

$$\forall \mathbf{s}\in {\mathrm{\Gamma }}_j(𝒮{\sigma }_j^{(it)})(\mathbf{s})=-(1-\sum _{k\in {𝒩}_j(\mathbf{s})}{\omega }_{jk}(\mathbf{s}))\mathrm{\Phi }(\mathbf{s})+\sum _{k\in {𝒩}_j(\mathbf{s})}{\omega }_{jk}(\mathbf{s})({𝒮}_k{\sigma }_k^{(it-1)})(\mathbf{s})$$ (41)

Notice how eq. 41 represents a Jacobi iteration for a linear system of integral equations, which defines the COSMO model:

$$\forall \mathbf{s}\in {\mathrm{\Gamma }}_j\hspace{1em}(𝒮{\sigma }_j)(\mathbf{s})-\sum _{k\in {𝒩}_j(\mathbf{s})}{\omega }_{jk}(\mathbf{s})({𝒮}_k{\sigma }_k)(\mathbf{s})=-(1-\sum _{k\in {𝒩}_j(\mathbf{s})}{\omega }_{jk}(\mathbf{s}))\mathrm{\Phi }(\mathbf{s})$$ (42)

The ddCOSMO system of integral equations is easily discretized in a real spherical harmonics basis through the following Ansatz:

$${\sigma }_j(\mathbf{s})=\sum _{lm}{[X_j]}_l^m{Y}_l^m\left(\frac{\mathbf{s}-{\mathbf{r}}_j}{|\mathbf{s}-{\mathbf{r}}_j|}\right)$$

For each sphere, each operator in eq. 42 (i.e., either the “diagonal” 𝒮_j or the “off-diagonal” 𝒮_jk) is represented through a matrix L_jj (or L_jk) whose size is given by the number of spherical harmonics used for the discretization. The ddCOSMO global matrix L will hence be made of M × M blocks of size N_b × N_b, where N_b = (L_max + 1)² and L_max is the maximum angular momentum in the spherical harmonics basis.

The choice of real spherical harmonics is particularly advantageous, as the 𝒮 operator is diagonal in such a basis:

$${[L_{jj}]}_{ll\prime }^{mm\prime }=\langle l,m|𝒮|l\prime ,m\prime \rangle =\frac{4\pi }{2l+1}{\delta }_{ll\prime }\delta mm\prime$$ (43)

where we have used Dirac’s notation and |l, m〉 represents the spherical harmonic of quantum numbers l, m. The discretization of the 𝒮_jk operators is less straightforward, as it is not possible to compute the integrals analytically. However, an efficient numerical quadrature exists for the unit sphere: the numerical integration can therefore be easily computed through the Lebedev rule. Let ${\{{\mathbf{y}}_n,w_n\}}_{n=1}^{N_g}$ be a set of Lebedev points and weights: the final expression for the off-diagonal blocks of the ddCOSMO matrix is

$${[L_{jk}]}_{ll\prime }^{mm\prime }=-\langle l,m|{\omega }_{jk}{𝒮}_k|l\prime ,m\prime \rangle =-\sum _{n=1}^{N_g}{w}_n{Y}_l^m({\mathbf{y}}_n)W_n^{jk}\frac{4\pi }{2l\prime +1}{(t_n^{jk})}^{l\prime }{Y}_{l\prime }^{m\prime }({\mathbf{s}}_n^{jk})$$ (44)

A complete derivation of eq. 44 and all the details of the ddCOSMO method can be found in ref. 33 and 34; here it is sufficient to notice that the quantities $t_n^{jk},{\mathbf{s}}_n^{jk}$ and $W_n^{jk}$ depend only on the Lebedev grid and on the geometry of the system. Moreover, the $W_n^{jk}$ coefficient - which correspond to ω_jk(y_n), defined in eq. 39 - vanishes if the spheres j and k do not intersect: as a consequence, all the blocks of the ddCOSMO matrix concerning non-intersecting spheres are zero, and the matrix is block-sparse. The right-hand side of the ddCOSMO linear system is assembled from the molecular potential, the $W_n^{jk}$ coefficients and the spherical harmonics:

$${[g_j]}_l^m=-\sum _{n=1}^{N_g}{w}_n{Y}_l^m({\mathbf{y}}_n)U_n^j{\mathrm{\Phi }}_n^j$$ (45)

where $U_n^j=1-{\sum }_{k\in {𝒩}_j}{W}_n^{jk}$ 𝒩_j is the list of spheres that intersect Ω_j and ${\mathrm{\Phi }}_n^j$ is the solute’s potential at y_n on sphere Ω_j. It is now possible to write the discretized ddCOSMO linear system. Let ${[X_j]}_l^m$ be the l − m expansion coefficient of σ_j in the spherical harmonics basis (i.e., the unknown of the ddCOSMO linear system): the ddCOSMO equation reads:

$$\left(\begin{array}{ccc}\hfill L_{11}\hfill & \hfill \dots \hfill & \hfill L_{1M}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill L_{M1}\hfill & \hfill \dots \hfill & \hfill L_{MM}\hfill \end{array}\right)\left(\begin{array}{c}\hfill X_1\hfill \\ \hfill ⋮\hfill \\ \hfill X_M\hfill \end{array}\right)=\left(\begin{array}{c}\hfill g_1\hfill \\ \hfill ⋮\hfill \\ \hfill g_M\hfill \end{array}\right)$$ (46)

For the sake of brevity, and for convenience in the following manipulations, we introduce, for the ddCOSMO equation, the notation

$$LX=g$$

The solvation energy can now be computed as in eq. 37, where, if the solute’s density is a collection of point multipoles, the integral can be easily computed. Let L_s be the maximum angular momentum of the solute’s multipolar distribution (i.e., 0 for point charges only, 2 for distributions up to the quadrupole) and let ${[Q_j]}_l^m$ be the l − m (real, spherical) multipole on the j-th atom of the solute. The polarization energy will be:

$$E_s=\frac{1}{2}f(\epsilon )\sum _{j=1}^M\sum _{l=0}^{L_s}\sum _{m=-l}^l\frac{4\pi }{2l+1}{[Q_j]}_l^m{[X_j]}_l^m=\frac{1}{2}f(\epsilon )\langle \mathrm{\Psi },X\rangle$$ (47)

where, for each 0 ≤ l ≤ N, −l ≤ m ≤ l we have introduced the vector Ψ such that

$${[{\mathrm{\Psi }}_j]}_l^m=\frac{4\pi }{2l+1}{[Q_j]}_l^m{\delta }_{l\le L_s}$$ (48)

δ_l≤Ls is one if l ≤ L_s and zero otherwise and we use the notation

$$\langle a,b\rangle =\sum _{j=1}^M\sum _{l=0}^N\sum _{m=-l}^l{[a_j]}_l^m{[b_j]}_l^m$$

B Derivation of the coupled equations

In this appendix, we will derive the coupled polarization equations for a variational force field. We recall that the COSMO field E_c is obtained by differentiating the COSMO energy with respect to the induced dipoles:

$${\mathbf{E}}_c=\frac{1}{2}f(\epsilon )\frac{\partial }{\partial \mathit{\mu }}\langle \mathrm{\Psi },X\rangle =\frac{1}{2}f(\epsilon )[\langle \frac{\partial \mathrm{\Psi }}{\partial \mathit{\mu }},X\rangle +\langle \mathrm{\Psi },\frac{\partial X}{\partial \mathit{\mu }}\rangle ].$$ (49)

The first term of eq. 49 is easily assembled:

$${[E_{c,j}^1]}_1^m=\frac{1}{2}f(\epsilon )\frac{4\pi }{3}{[X_j]}_1^m$$ (50)

Equation 50 introduces a linear transformation of the ddCOSMO X coefficients, which we denote with the matrix A. Notice that we assume that the dipoles are in their spherical representation; in the actual implementation, the dipoles are treated as Cartesian multipoles and the spherical-to-cartesian conversion is folded inside the matrix, so that we can write

$${\mathbf{E}}_c^1=\frac{1}{2}f(\epsilon )AX.$$

We notice from eq. 48 that such a transformation is the adjoint of the transformation that, given the (cartesian) induced dipoles, produces the Ψ_μ vector:

$${\mathrm{\Psi }}_{\mu }=A^{*}\mathit{\mu }$$

The second contribution to the COSMO field involves the derivatives of the X coefficients with respect to the induced dipoles:

$$\langle \mathrm{\Psi },\frac{\partial X}{\partial \mathit{\mu }}\rangle =\langle \mathrm{\Psi },L^{-1}\frac{\partial g}{\partial \mathit{\mu }}\rangle =\langle S,\frac{\partial g}{\partial \mathit{\mu }}\rangle$$

where we have introduced the solution the the adjoint ddCOSMO linear system

$$L^{*}S=\mathrm{\Psi }$$ (51)

The derivatives of g_μ are obtained by differentiating the solute’s potential with respect to the dipoles and then assembling with the potential derivative a term such as the one in eq. 45. In particular, let ${\overrightarrow{\upsilon }}_n^{jk}$ be the vector pointing from the position of the k-th atom to the gridpoint y_n on the j-th sphere. The potential produced by the induced dipoles at the latter point is

$${[{\mathrm{\Phi }}_{\mu }]}_n^j=-\sum _{k=1}^M\frac{{\overrightarrow{\upsilon }}_n^{jk}·{\overrightarrow{\mu }}_k}{{|{\overrightarrow{\upsilon }}_n^{jk}|}^3}$$

where for convenience we are using the cartesian representation of the dipoles, which allows us to compute the second contribution to the ddCOSMO field as

$${\overrightarrow{E}}_{c,j}^2=-\frac{1}{2}f(\epsilon )\sum _{k=1}^M\sum _{lm}\sum _{n=1}^{N_g}{w}_n{Y}_l^m({\mathbf{y}}_n)U_n^k{[S_k]}_l^m\frac{{\overrightarrow{\upsilon }}_n^{jk}}{{|{\overrightarrow{\upsilon }}_n^{jk}|}^3}$$ (52)

As before, eq. 52 introduces a linear transformation which converts the solution to the ddCOSMO adjoint system into the second component of the COSMO field:

$${\mathbf{E}}_c^2=\frac{1}{2}f(\epsilon )BS$$

Again, the adjoint of B is the linear transformation that, given the (cartesian) induced dipoles, produces the g_μ vector:

$$g_{\mu }=B^{*}\mathit{\mu }.$$