Helicase Processivity and Not the Unwinding Velocity Exhibits Universal Increase with Force

Abstract

Helicases, involved in a number of cellular functions, are motors that translocate along single-stranded nucleic acid and couple the motion to unwinding double-strands of a duplex nucleic acid. The junction between double- and single-strands creates a barrier to the movement of the helicase, which can be manipulated in vitro by applying mechanical forces directly on the nucleic acid strands. Single-molecule experiments have demonstrated that the unwinding velocities of some helicases increase dramatically with increase in the external force, while others show little response. In contrast, the unwinding processivity always increases when the force increases. The differing responses of the unwinding velocity and processivity to force have lacked explanation. By generalizing a previous model of processive unwinding by helicases, we provide a unified framework for understanding the dependence of velocity and processivity on force and the nucleic acid sequence. We predict that the sensitivity of unwinding processivity to external force is a universal feature that should be observed in all helicases. Our prediction is illustrated using T7 and NS3 helicases as case studies. Interestingly, the increase in unwinding processivity with force depends on whether the helicase forces basepair opening by direct interaction or if such a disruption occurs spontaneously due to thermal fluctuations. Based on the theoretical results, we propose that proteins like single-strand binding proteins associated with helicases in the replisome may have coevolved with helicases to increase the unwinding processivity even if the velocity remains unaffected.

Introduction

Helicases are molecular motors that can translocate along single-stranded (ss) nucleic acids (NAs) and can unwind double-stranded (ds) NAs when confronted by a ss-ds junction (1–4). These remarkable motors, found in all organisms, are involved in a variety of cellular functions ranging from DNA and RNA replication, remodeling of chromatin, translation, and other aspects of nucleic acid metabolism (5–14), and are classified into six families based on their sequence (15,16). Various ensemble assays have been developed (17–21) to decipher how they step on single strands of nucleic acids, how they interact with ss-ds junctions, and how often they dissociate from their track. Single-molecule manipulation techniques, such as laser optical tweezers and magnetic tweezers, have also been used to probe the kinetics of stepping and nucleic acid unwinding at the level of individual helicase molecules (22–25). These experiments are particularly suited to obtain quantitative measurements of helicase processivity and unwinding velocity under force. From such measurements, one can obtain insights into the mechanisms of helicase function and how various helicases differ from each other.

In a number of single molecule experiments, a variety of interesting observations have been made on the response of helicase velocity and processivity to force. Processivity is a measure of the average number of basepairs unwound by the helicase in a single binding event (see below for a more detailed discussion of various other definitions). Dessinges et al. (24), who used magnetic tweezers to follow the unwinding of dsDNA by the UvrD helicase, showed that the unwinding velocity depends only weakly over a broad range (3–35 pN) of applied forces on the ds termini of the DNA. However, the unwinding processivity was much larger (265 bp) in their experiment compared to previous results (45 bp) from zero-force ensemble assays (18), suggesting that force possibly plays a part in enhancing the processivity of UvrD. It should be kept in mind that the stoichiometry of helicase attachment to DNA was not explicitly determined in Dessinges et al. (24). This is particularly relevant because enhanced processivity is achieved by UvrD dimers (26,27). In sharp contrast, Johnson et al. (28) discovered, using laser optical tweezer experiments, that both the unwinding velocity and processivity of T7 helicase are highly tension-dependent. Indeed, the unwinding rate increased by an order of magnitude when the tensile force applied to destabilize the ss-dsDNA junction was increased from 5 to 11 pN. Finally, Lionnet et al. (29) examined the unwinding kinetics of the gp41 helicase. Like the T7 helicase, the unwinding velocity depends strongly on the value of the tension destabilizing the ss-dsDNA junction. From these experiments, we surmise that while different helicases exhibit very different unwinding velocity responses to force, the processivity always increases appreciably with force. Here, we provide a theory that explains the differing dependencies of unwinding velocity and processivity on force.

Some aspects of the varied responses in helicase velocities have been qualitatively justified in a previous work (30), based upon an insightful theoretical model of helicases originally proposed by Betterton and Jülicher (31–33). The model quantifies the crucial ideas of active and passive unwinding by a helicase—a classification that has been the basis for understanding helicase mechanisms for a number of years (1,2,21,28,29,34–38). A passive helicase utilizes the thermal breathing of the ss-ds junction of a nucleic acid, to opportunistically step in front. Because the double-strand closes on itself on average, the helicase frequently faces a barrier and hence moves ahead relatively slowly (as compared to its unimpeded single-strand velocity). An active helicase, on the other hand, promotes dsDNA melting by lowering the stability of basepairs at the junction, either by utilizing free energy from ATP hydrolysis or the binding free energy of the protein at the junction. The resulting increase in unwinding velocity of an active helicase depends on the extent of the destabilization of the ds junction due to interaction with the helicase. This suggests that the helicase can be active to various degrees.

An optimally active helicase would unwind at a maximum velocity that is close to or equals the single-strand velocity, V_SS (32). For helicases with negligible back-stepping rates, it was argued in Manosas et al. (30) that when a helicase is passive, an external force can assist in the opening of the double-strand junction, thus increasing the velocity of the helicase. On the other hand, because the unwinding velocity of an optimally active helicase is ∼V_SS, an external force should not increase the unwinding velocity significantly. These physically motivated arguments suggest that the velocity of a passive helicase should increase appreciably with force while the velocity of an optimally active helicase will be similar to V_SS. Manosas et al. (30) did not investigate the processivities of helicases, and hence their work provided only an incomplete understanding of the nature of helicase motion. By generalizing the model of Betterton and Jülicher (31–33) to include force dependence for both velocities and processivities, we show that even though the velocity can vary with external force in a helicase-dependent manner, the unwinding processivity always increases significantly with force. This is a remarkable result, as it predicts a universal behavior—unlike the velocity, the processivity will increase rapidly with external force for all helicases regardless of their architecture. In addition, our work highlights another surprising finding—the more active a helicase is (the stronger its interaction with the ss-ds junction), the less processive is its motion. The effect of increasing the external force at a given interaction strength is therefore opposite to the effect of increasing the interaction strength at a given external force. Finally, the sequence-dependent behavior of the unwinding velocity and processivity show complex behavior depending on the percentage of GC content. We predict that details of the energy landscape of basepair opening, GC content, and the extent to which the helicase is active, determine the unwinding velocity and processivity.

Materials and Methods

As illustrated schematically in Fig. 1, in the model of Betterton and Jülicher (31–33) the nucleic acid (NA) is represented by a one-dimensional lattice with n denoting the lattice position of the helicase, while m specifies the position of the ss-ds junction. Models similar in spirit, but differing significantly in formulation and application, have also been used to analyze motility of kinesin (39). We extended the model of Betterton and Jülicher (31–33) to include a constant external force or tension (F), which is applied to the complementary termini of the NA, in order to investigate the dependence of velocity and processivity on load. In accord with the single-molecule optical tweezers experiments (28,40), tension is applied in a manner that increases the opening rate of the junction and decreases the closing rate while maintaining detailed balance.

Figure 1.

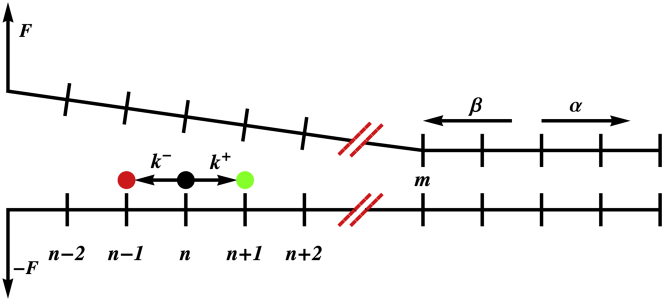
A schematic illustration of the extension of the Betterton and Jülicher model for helicases. The position of the helicase (black circle) on an underlying one-dimensional lattice representing the nucleic acid substrate is denoted by the variable n, while the variable m refers to the location of the ss-dsNA junction. At infinite separation between the helicase and ss-ds NA junction, n → n + 1 transitions occur at rate k⁺, while n → n − 1 transitions occur at rate k⁻. Similarly, m → m + 1 transitions occur at rate α, and m → m − 1 transitions occur at rate β. The tension F is applied to the ends of the nucleic acid. To see this figure in color, go online.

If the helicase and ss-ds junction are in proximity, there is an effective interaction. The passive unwinding mechanism is realized by a hard-wall coupling potential,

$$U\left(j\right)=\{\begin{array}{cc}\infty & \left(j\le 0\right)\\ 0& \left(j>0\right),\end{array}$$ (1)

where j ≡ m – n (Fig. 1). Similarly, we represent an active unwinding mechanism by a coupling potential consisting of both a step-function and a hard-wall,

$$U\left(j\right)=\{\begin{array}{cc}\infty & \left(j\le -1\right),\\ U_0& \left(j=0\right),\\ 0& \left(j>0\right),\end{array}$$ (2)

where the energy U₀ is in units of k_BT.

Unwinding velocity of a helicase

The mean velocity (V) of the helicase/junction complex is proportional to a sum over all j of a product of the probability of being at separation j and the net rate at which the centroid coordinate (l = m + n, Fig. 1) increases:

$$V=\frac{1}{2}\sum _j\left(k_j^{+}+{\alpha }_j-k_j^{-}-{\beta }_j\right)P_j,$$ (3)

where α_j is the rate constant associated with junction opening when the helicase and junction are at separation j. Similarly, β_j, k⁺_j, and k⁻_j are the j-dependent rate constants associated with junction-closing, helicase forward-stepping, and helicase backward-stepping, respectively.

Because experiments are performed at a constant temperature and F, opening and closing of the ss-ds junction can only be attributed to thermal fluctuations or the applied tension. Thus, the ratio of the rate at which the junction opens (α_j−1) to that at which it closes (β_j) satisfies

$$\begin{array}{l}\begin{array}{c}\frac{{\alpha }_{j-1}}{{\beta }_j}=\frac{\alpha }{\beta }{e}^{\left[U\left(j-1\right)-U\left(j\right)\right]}{e}^{\Delta G_F},\\ \frac{\alpha }{\beta }=e^{-\Delta G},\end{array}\\ \end{array}$$ (4)

where α (β) is the j → ∞ junction opening (closing) rate; ΔG is the stability of the junction basepair in the absence of either force or helicase; U(j) is the value of the coupling potential when the helicase and junction are at separation j; and ΔG_F is the destabilization in the free energy of the basepair at the junction, caused by the applied force F. For simplicity, we choose ΔG_F = FΔx (for further details, see the Discussion), where Δx is roughly twice the length of ssDNA separating two bases. When ATP hydrolysis is tightly coupled to helicase transitions, the hopping rates approximately satisfy a relation akin to detailed balance (31), as

$$\frac{k_j^{+}}{k_{j-1}^{-}}\approx \frac{k^{+}}{k^{-}}{e}^{-\left[U\left(j-1\right)-U\left(j\right)\right]},$$ (5)

where $k^{+}={\text{lim}}_{j\to \infty }{k}_j^{+}$ and $k^{-}={\text{lim}}_{j\to \infty }{k}_{j-1}^{-}$. Note that when the helicase traverses on a single-strand, there is no ss-ds junction confronting the helicase, and hence the hopping rates that describe its motion are k⁺ and k⁻. Thus, the single-strand velocity is V_SS = k⁺ − k⁻. For a number of helicases like T7, T4, NS3, and UvrD that translocate directionally on ss nucleic acids, the forward rate k⁺ can be assumed to be much larger than k⁻, near the physiological ATP concentrations (∼1 mM, close to saturating conditions for most helicases) that are usually used in experiments (21,28–30,36). We therefore work under this approximation throughout this article. However, while unwinding the double-strand, the forward rate decreases and the backward rate increases (as evident from Eq. 5 and the equations for the individual rates below), making back-stepping much more likely. A high probability of back-stepping was indeed observed in a recent experiment on the XPD helicase (37). Finally, individual rates are affected by the coupling potential and the applied tension as follows: $k_j^{+}=k^{+}{e}^{-f\left[U\left(j-1\right)-U\left(j\right)\right]}$, $k_{j-1}^{-}=k^{-}{e}^{-\left(f-1\right)\left[U\left(j-1\right)-U\left(j\right)\right]}$, ${\beta }_j=\beta e^{-f\left[U\left(j-1\right)-U\left(j\right)+F\Delta x\right]}$, and ${\alpha }_{j-1}=\alpha e^{-\left(f-1\right)\left[U\left(j-1\right)-U\left(j\right)+F\Delta x\right]}$, where f (0 < f < 1) is the location (in units of lattice spacing) of the transition state separating the closed and open states. Note that the applied tension, F, affects only the nucleic acid breathing rates (α_j−1 and β_j), not the hopping rates.

The rates of a passive helicase are independent of j for j > 1, and at j = 1 we have k⁺₁ = β₁ = 0. The force-velocity relation for a hard-wall (passive) helicase, calculated using Eq. 3, is

$$V_{\text{HW}}=\frac{{\alpha }^{\prime }{k}^{+}-{\beta }^{\prime }{k}^{-}}{{\beta }^{\prime }+k^{+}},$$ (6)

where V_HW ≡ V_HW (F, f), α′ ≡ αe^{–(f−1)FΔx}, and β′ ≡ βe^−fFΔx. For convenience, while referring to V_HW in the rest of the text, we explicitly show the functional dependence of only the parameter pertinent to the particular discussion. Note that for F = 0, Eq. 6 coincides with Eq. 22 in Betterton and Jülicher (32). By making the approximation k⁻ ≈ 0, we obtain $V_{\text{HW}}\approx \left({\alpha }^{\prime }/{\beta }^{\prime }\right)\left(k^{+}/\left(1+k^{+}/{\beta }^{\prime }\right)\right)$ and $\left(V_{\text{HW}}\left(F\right)\right)/\left(V_{\text{HW}}\left(F=0\right)\right)\approx \left({\alpha }^{\prime }/\alpha \right)/\left({\beta }^{\prime }/\beta \right)\left(\left(1+k^{+}/\beta \right)/\left(1+k^{+}/{\beta }^{\prime }\right)\right)$. Finally, making the approximation β′ >> k⁺, we conclude that

$$\frac{V_{\text{HW}}\left(F\right)}{V_{\text{HW}}\left(F=0\right)}\approx e^{F\Delta x}.$$ (7)

(The approximation β >> k⁺ is typically valid because β ≃ 10⁵–10⁸ s⁻¹, while k⁺ ≃ 1–10³ s⁻¹.) A passive helicase must wait for the junction to open to step forward and prevent the newly separated basepair from reannealing. From Eq. 7 it follows that the application of force exponentially increases the probability that the junction is open relative to the probability that it is closed, resulting in an exponential increase in the unwinding velocity relative to the F = 0 value.

For a single-step active helicase (modeled with Eq. 2), the rates are independent of j for all j > 1. A straightforward calculation of Eq. 3 leads to

$$\frac{V_1}{V_{\text{HW}}}=\frac{c^{\prime }+\left(1-c^{\prime }\right)e^{-f{U}_0}}{c^{\prime }+\left(1-c^{\prime }\right)e^{-U_0}},$$ (8)

where V₁ ≡ V₁(F, f, U₀), c′ = (αe^{−(f−1)FΔx} + k⁻)/k⁺ + βe^−fFΔx), and the subscripts 1 and HW denote the step (active) and hard-wall (passive) coupling potentials, respectively. When the step potential goes to zero (U₀ = 0), the unwinding velocity is just equal to the hard-wall (passive) helicase velocity as can be seen from Eq. 8. As with V_HW, while referring to V₁ in the rest of the text, we show only the functional dependence of the parameters pertinent to the particular discussion. Finally, using the results of Eqs. 7 and 8, we find $\left(V_1\left(F\right)\right)/\left(V_1\left(F=0\right)\right)=\left(\left(c^{\prime }+\left(1-c^{\prime }\right)e^{-f{U}_0}\right)/\left(c^{\prime }+\left(1-c^{\prime }\right)e^{-U_0}\right)\right)e^{F\Delta x}\left(\left(c+\left(1-c\right)e^{-U_0}\right)/\left(\left(c+\left(1-c\right)e^{-f{U}_0}\right)\right)\right)$, where c = c′(F = 0) = (α + k⁻)/(k⁺ + β).

Helicase processivity

The processivity of a helicase has been defined in various ways (33): 1) the mean attachment time of the helicase 〈τ〉; 2) the average number of basepairs unwound in a single binding event 〈δm〉 (in other words, the average number of basepairs by which the junction moves ahead before the helicase detaches); and 3) the average number of basepairs translocated before the helicase detaches 〈δn〉; 〈δm〉 and 〈δn〉 (termed “unwinding” and “translocation” processivities, respectively) in principle could be very different. For instance, if the helicase binds very far from the junction (j₀ >> 1), the double-strand will close rapidly before the helicase can translocate by a significant amount, thus making the unwinding processivity (〈δm〉) negative. However, if the helicase binds very close to the junction (j₀ ∼ 1), 〈δm〉 and 〈δn〉 are almost identical (33). The double-strand would always have a larger closing rate as compared to the opening rate, thus making the strands close on average. This would hold even in the presence of external forces, as long as they are less than the force needed to unzip the double-strand. In such physically relevant situations, after a very brief transition period the helicase is likely to be very close to the junction, and hence the relevant initial condition can always be taken as j₀ = 1.

In the single molecule experiments measuring unwinding velocity and processivity, typically a DNA hairpin serves as a model double-strand. The upstream single-strand overhangs allow the helicase to load (29,30,36,40). At forces less than the critical force required to unzip the hairpin in the absence of a helicase, the arrival of a helicase at the junction and subsequent unwinding causes the end-to-end distance to increase. As a result, the presence of the helicase on the hairpin can only be discerned by observing the sudden change in the end-to-end distance, which happens when j₀ ∼ 1. In this work, therefore, we work with the initial condition j₀ = 1, and hence the unwinding processivity 〈δm〉 and translocation processivity 〈δn〉 are almost identical.

To model a helicase with finite processivity, we incorporate an unbinding rate γ_j, which depends implicitly on the separation j through the relation γ_j = γe^U(j) (33). We assume that U(j) → 0 as j → ∞. It is physically reasonable that the unbinding rate should increase as U(j) increases, because the repulsion between the helicase and the nucleic acid would cause the former to dissociate. This has indeed been observed in experiments—the dissociation rate of T7 from dsDNA is roughly 100 times larger (21) than that from ssDNA (41), at the same dTTP concentration of 2 mM. The exponential dependence of γ_j on U(j) is further justified by noting that it is built on the celebrated Bell model, which has been used successfully to describe unbinding of cell-adhesion molecules and other complexes. Because the velocity of unwinding is unaffected by introduction of the unbinding rate γ_j, the analytical results derived above for the unwinding velocity hold good even for finitely processive helicases. For the physically relevant initial condition j₀ ∼ 1 (explained above), the velocity of active unwinding is given by

$$V_1\approx \langle \delta m\rangle /\langle \tau \rangle \approx \langle \delta n\rangle /\langle \tau \rangle .$$ (9)

For the initial condition j₀ ∼ 1, the two expressions for unwinding velocity given by Eqs. 8 and 9 are equivalent. Betterton and Jülicher (33) derived the following expressions for the three measures of processivity:

$$\begin{array}{l}\langle \tau \rangle =\sum _j{R}_j,\\ \langle \delta m\rangle =\frac{\langle \delta l\rangle +\langle \delta j\rangle }{2},\\ \langle \delta n\rangle =\frac{\langle \delta l\rangle -\langle \delta j\rangle }{2}.\end{array}$$ (10)

Here, the parameters {R_j} are obtained by solving the infinite set of second-order recurrence relations

$$-{\delta }_{j{j}_0}=-\left(k_j^{+}+k_j^{-}+{\alpha }_j+{\beta }_j+{\gamma }_j\right)R_j+\left({\alpha }_{j-1}+k_{j-1}^{-}\right)R_{j-1}+\left({\beta }_{j+1}+k_{j+1}^{+}\right)R_{j+1},$$ (11)

where j₀ is the value of j at time t = 0; δ_jj0 is the Kronecker delta; $\langle \delta j\rangle ={\sum }_j\left(j-j_0\right){\gamma }_j{R}_j$, where 〈δl〉 is given by the expression $\langle \delta l\rangle =b{\left(1+a-y_{-}-\left(a-b\right)/y_{+}\right)}^{-1}\left[\left(y_{-}/{\left(1-y_{-}\right)}^2\right)-\left(y_{+}/{\left(1-y_{+}\right)}^2\right)\right]$, and the y_± values are the roots of the equation y² − (1 + a) y + (a – b) = 0; a = (1 + p)/q; b = 1/q; $p={\sum }_j\left({\alpha }_j+k_j^{+}\right)R_j$; and $q={\sum }_j\left({\beta }_j+k_j^{-}\right)R_j$. The model of Betterton and Jülicher (31–33) derived Eq. 11 by taking the Laplace transform of the time evolution equation of P(j,l,t), the joint probability density of finding the helicase-junction system in state (j,l) at time t. The equation P(j,l,t) obeys a Master equation accounting for the movement of the helicase in the forward and backward directions as well as detachment from the NA.

When the helicase is passive, U(j) = 0 for j > 0 (Eq. 1) and hence the dissociation rate γ_j = γ for all j. As a result, the mean attachment time for a passive helicase 〈τ〉_HW is given by

$${\langle \tau \rangle }_{\text{HW}}=\frac{1}{\gamma },$$ (12)

for all values of the external force F.

Results

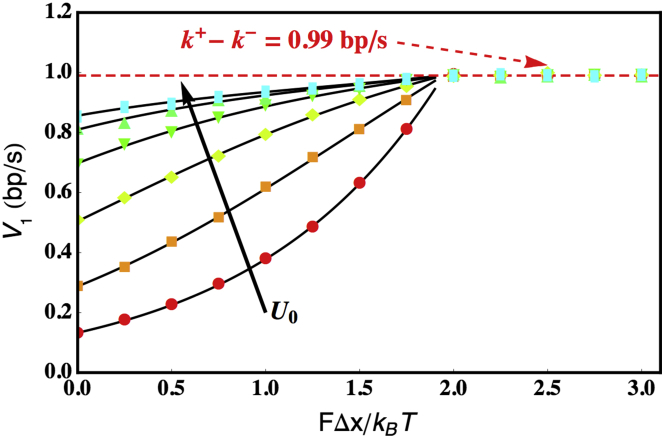
In order to determine the velocity and processivity, we solve the sparse linear system given by Eq. 11 for {R_j}. All our results have been numerically obtained for the case where the back-stepping rate of the helicase in the absence of dsDNA (k⁻) is small compared to the forward rate in the absence of dsDNA (k⁺). We use a grid of size M = 10,000 in j to solve Eq. 11. A larger grid size than that used by the Betterton and Jülicher model (M = 100 was used in Betterton and Jülicher (33)) is necessitated by the external tension applied to the NA substrate. From a numerical standpoint, as FΔx/k_BT increases, {R_j} converges to zero increasingly slowly, thus requiring more and more terms to guarantee the convergence of the sums used to calculate 〈τ〉, 〈δj〉, and 〈δl〉. For FΔx/k_BT > 1.95, a grid of size M = 10⁶ in j proves to be insufficient to solve Eq. 11. It is not possible to explore forces >1.95 k_BT/Δx because such large forces result in the melting of the duplex. This is because our choice of α = 10⁵ s⁻¹ and β = 7 × 10⁵ s⁻¹ correspond to ΔG = 1.95 k_BT. At these forces, 〈δm〉 is very large and 〈δm〉 ≈ 〈τ〉(k⁺ = k⁻). These results are confirmed in Fig. 2, which shows (in addition to the numerical results) simulation results at these larger forces (see below for additional information).

Figure 2.

Unwinding velocity V₁(F,U₀) as a function of the tension (FΔx/k_BT), for various coupling potentials U₀/k_BT = 0 (red circles), 1 (orange squares), 2 (yellow diamonds), 3 (green down-triangles), 4 (green up-triangles), and 5 (cyan rectangles). (Solid black lines) Numerical results obtained using Eqs. 9 and 11. Each symbol represents an average of 1000 independent KMC simulations. For forces exceeding FΔx/k_BT = 1.9, the duplex melts and it is no longer possible to numerically solve the system given by Eq. 11, but the robustness of our simulation algorithm allows us to explore this regime confirming that the duplex has melted. The parameters used were f = 0.01, α = 10⁵ s⁻¹, β = 7 × 10⁵ s⁻¹, k⁺ = 1 bp/s, k⁻ = 0.01 bp/s, γ = 0.01 s⁻¹, and j₀ = 1. To see this figure in color, go online.

Unwinding velocity

To understand how the unwinding velocity depends on the model parameters, we plot the F-dependent unwinding velocity V₁(F,U₀) for several values of U₀ (Fig. 2). This figure reveals several interesting features: 1) Fig. 2 shows that for a small value of f = 0.01 << 1 (f is the transition state location along the reaction coordinate separating the closed and open states of a basepair), if the helicase is passive U₀ = 0 or weakly active (U₀ < ΔG), the unwinding velocity is highly sensitive to the external force. As U₀ increases, making the helicase increasingly more active, the unwinding velocity is less sensitive to increase in force. In the parameter range f << 1 and U₀/K_BT >> 1, the helicase is optimally active. 2) The parameters used in Fig. 2 correspond to a single-strand translocation velocity V_SS = 0.99 bp/s. In the optimally active regime, the unwinding velocity is close to V_SS for a large range of forces. This observation, along with the first point, qualitatively describes the velocity behavior of a number of helicases (30). For example, UvrD is optimally active while T7 is passive or at best, only weakly active. 3) When U₀ = 0, the results revert to those expected for a hard-wall coupling potential. Thus, as illustrated in Fig. 2, the effect of tensile force at U₀ = 0 is simply to increase the mean velocity exponentially relative to the zero force value (Eq. 7).

Processivity and lifetimes

For finitely processive helicases, the primary results of numerically solving Eq. 11 are plotted in Figs. 3, 4, 5, and 6, illustrating several points worthy of note:

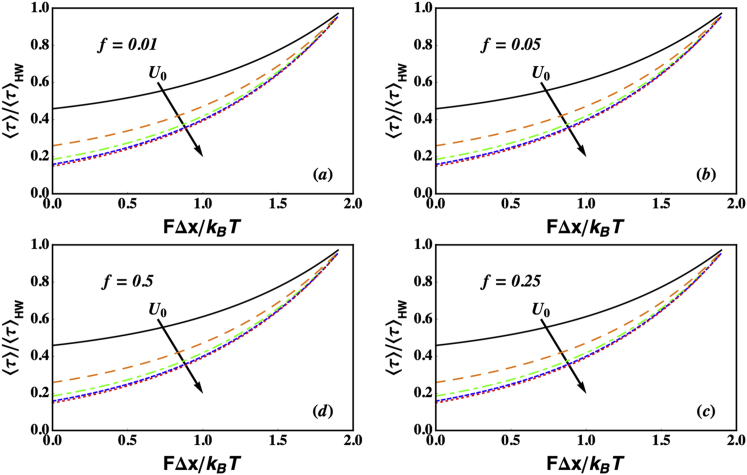
• 1)The variations in the average lifetime of the helicase 〈τ〉 (normalized by the lifetime of the passive helicase) with F, f, and U₀ (Eq. 10) are displayed in Fig. 3. Evidently, a passive helicase (U₀ = 0) has the largest lifetime. As U₀ increases, lifetimes monotonically decrease at any given force value. This is not surprising because the lifetime is controlled by the detachment rate γ_j, which increases exponentially with increase in U₀. As F increases, the opening rate of the double-strand becomes larger, thus increasing the probability of the helicase to find an open adjacent base whenever it steps ahead. This results in fewer occasions where the helicase has to pay the extra U₀ energy to plow ahead, resulting in larger lifetimes. At forces close to the double-strand rupture force, the helicase always finds a clear path ahead and hence rarely interacts with the junction, making the lifetime increasingly approach the passive helicase lifetime. Finally, Fig. 3 also demonstrates that the mean attachment time of the helicase relative to that of a passive helicase depends on both U₀ and F, but is insensitive to the parameter f.
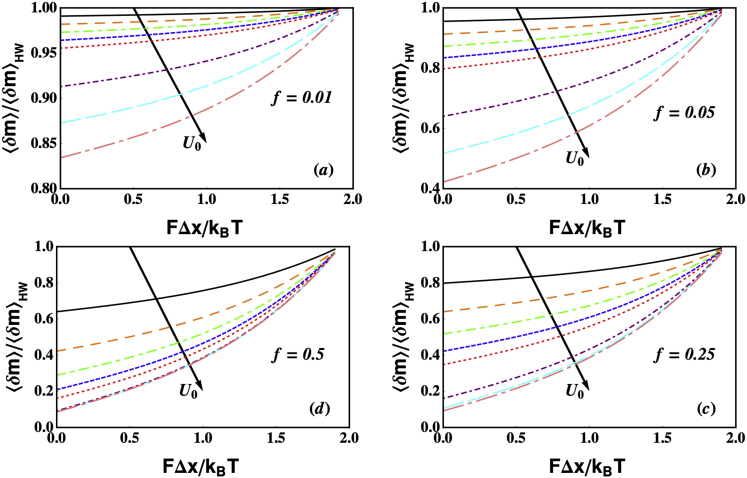
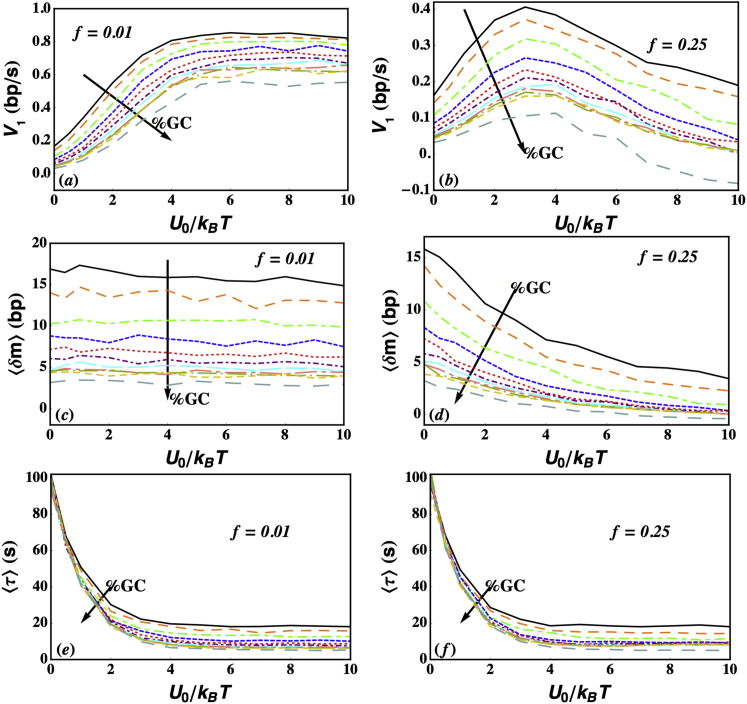
• 2)Fig. 4 shows the mean unwinding processivity of an active helicase relative to a passive helicase. Because the translocation processivity is very similar, we do not show a separate figure and all results discussed for 〈δm〉, also hold good for 〈δn〉. It is evident from the figure that similar to the lifetime (Fig. 3), the unwinding processivity is also maximum for a passive helicase, and monotonically decreases as the helicase becomes more active. This interesting result can be physically understood as follows: 〈δm〉 depends on the unwinding velocity and mean lifetime as 〈δm〉 = V₁(F,U₀)〈τ〉. At a given force, as U₀ increases, V₁(F,U₀) initially increases (see Fig. 6, a and b) but 〈τ〉 decreases (see Figs. 3 and Fig. 6, e and f). The rate at which these two quantities increase/decrease determines the trend for 〈δm〉. Our results show that the rate of decrease of 〈τ〉 is faster than the rate at which V₁(F,U₀) increases. This can be most clearly seen in Fig. 6, b and f, where the velocity and mean processivities have been plotted as functions of U₀, respectively, for f = 0.25. The value 〈τ〉 decreases faster than V₁(F,U₀) increases, and hence the overall result is that 〈δm〉 decreases as a function of U₀ regardless of the GC content (Fig. 6 d).
• 3)The unwinding processivity depends strongly on the parameter f. For f = 0.01 and F = 0, 〈δm〉/〈δm〉_HW > 0.8 even when the coupling potential U₀ = 20 k_BT (pink dot-dashed line in Fig. 4). For f = 0.05 and F = 0, the coupling potential U₀ must exceed 5 k_BT for 〈δm〉/〈δm〉_HW to decrease to <0.8 (red dotted curve in Fig. 4). Thus, the effects of the barriers to translocation and NA breathing on 〈δm〉 are the principal determinants of the velocity of a processive helicase (see also Sequence Effects below).
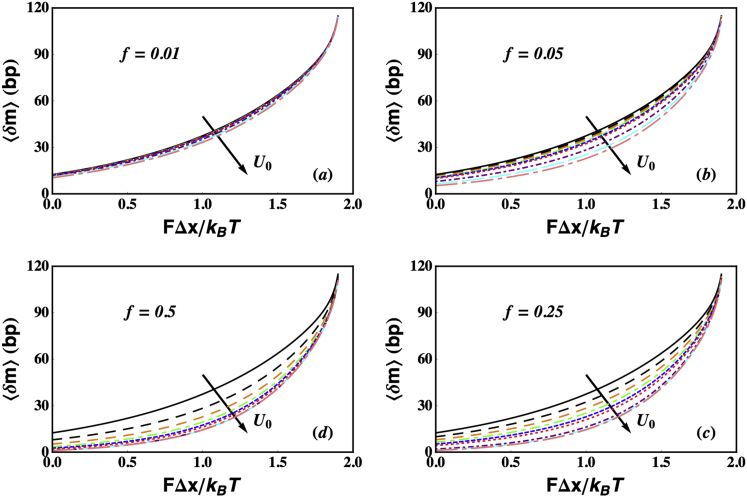
• 4)The equation 〈δm〉 = V₁(F,U₀)〈τ〉 gives key insights into the force dependence of processivity. As was discussed above, for a passive helicase with U₀ = 0, the velocity V_HW increases rapidly as the force increases (Fig. 2). However, the lifetime of a passive helicase 〈τ〉_HW does not change and is constant at 〈τ〉_HW = 1/γ (Eq. 12). This immediately means that 〈δm〉 will increase rapidly with increase in force (solid black lines in Fig. 5). In the other extreme limit of an optimally active helicase (U₀/K_BT >> 1 and f << 1), our discussions above show that V₁ will not significantly change with force (Fig. 2). However, unlike the passive situation, 〈τ〉 increases rapidly with force (Fig. 3). This result follows again from the discussion in the previous points—as a helicase becomes more active, the increased interaction with the junction reduces its lifetime. An external force reduces the probability of this interaction, which in turn results in an increase in 〈τ〉, the lifetime of the helicase. As a result, 〈δm〉 will increase rapidly as the external force increases (Fig. 5 a). For intermediate values of U₀ and higher values of f, the increase in 〈δm〉 with force is a result of contributions from both the velocity as well as the lifetime. Thus, the phenomenon of rapid increase in unwinding processivity as F increases, arises due to very different reasons, depending on how active the helicase is. These arguments lead to the surprising prediction that no matter how active (or passive) the helicase is, the processivity is sensitive to external force. Our prediction, which we believe is universal for unwinding helicases, is borne out in the few experiments that have analyzed the variation of unwinding processivity over a range of forces (28,40). This behavior is to be contrasted with the dependence of unwinding velocity on F, which varies significantly when the helicase is passive, but less so for active helicases.

Figure 3.

Ratio of the mean attachment time of an active to a passive helicase 〈τ〉/〈τ〉_HW as a function of FΔx/k_BT, for U₀/k_BT = 1 (black solid line), 2 (orange dashed line), 3 (green short and long dashed line), 4 (blue short dashed line), and 5 (red dotted line). The value 〈τ〉/〈τ〉_HW increases with FΔx/k_BT and decreases with increasing U₀/k_BT. Interestingly, the mean attachment time is unaffected by f (all curves with the same value of U₀/k_BT can be superimposed). Parameters used to solve Eq. 11 were α = 10⁵ s⁻¹, β = 7 × 10⁵ s⁻¹, k⁺ = 1 bp/s, k⁻ = 0.01 bp/s, γ = 0.01 s⁻¹, j₀ = 1, and M = 10⁴. (a)–(d) correspond to f = 0.01, 0.05, 0.25, and 0.5, respectively. To see this figure in color, go online.

Figure 4.

Mean unwinding processivity of an active helicase (relative to that of a passive helicase) as a function of FΔx/k_BT, for U₀/k_BT = 1, 2, 3, 4, 5, 10, 15, and 20. For all values of U₀, the processivity always increases with increasing tension destabilizing the ss-dsNA junction and decreases with increasing step height. Unlike the mean attachment time (Fig. 3), the unwinding processivity is highly sensitive to the kinetic parameter f, further confirming that the processivity is likely to exert a strong influence over the kinetics of unwinding. Parameters used to solve Eq. 11 were α = 10⁵ s⁻¹, β = 7 × 10⁵ s⁻¹, k⁺ = 1 bp/s, k⁻ = 0.01 bp/s, γ = 0.01 s⁻¹, j₀ = 1, and M = 10⁴. (a)–(d) correspond to f = 0.01, 0.05, 0.25, and 0.5, respectively. To see this figure in color, go online.

Figure 5.

Plots of the mean unwinding processivity of a helicase as a function of the applied tension, for U₀/K_BT = 0 (passive), 1, 2, 3, 4, 5, 10, 15, and 20. The processivity always increases with increasing tension destabilizing the ss-dsNA junction and decreases with increasing step height. We used the same parameters as in Fig. 4. (a)–(d) correspond to f = 0.01, 0.05, 0.25, and 0.5, respectively. To see this figure in color, go online.

Figure 6.

The dependence of 〈τ〉, 〈δm〉, and 〈δm〉/〈τ〉 on the step-height (U₀/K_BT) for varying amounts of GC content for the sequence given in the text. Simulations were performed at U₀/k_BT = 0, 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Each data point corresponds to an average over 1000 independent KMC simulations. All quantities decrease with increasing %GC. Interestingly, the mean attachment time 〈τ〉 is again very insensitive to f. The value 〈δm〉 is, however, sensitive to f, leading to disparate behaviors for 〈δm〉/〈τ〉. When f = 0.25, 〈δm〉/〈τ〉 shows a very distinct maximum when %GC = 0.0 but a very weak maximum when %GC = 1.0. When f = 0.01, 〈δm〉/〈τ〉 shows saturating behavior with increasing U₀. Thus, sequence plays a crucial role in determining the kinetics of unwinding. Parameters used in the simulations were α = 10⁵ s⁻¹, β = 7 × 10⁵ s⁻¹, k⁺ = 1 bp/s, k⁻ = 0.01 bp/s, γ = 0.01 s⁻¹, and j₀ = 1. (a), (c), and (e) correspond to f = 0.01, while (b), (d), and (f) correspond to f = 0.25. To see this figure in color, go online.

Sequence effects

The quantitative insights obtained for helicase velocity (Fig. 2) and processivity (Fig. 5) as a function of force prompted us to use a similar model to explore the effects of NA sequence. Helicase unwinding and translocation can be modeled as a discrete-state continuous-time stochastic process (42). Instead of adopting Eq. 11 to include sequence effects, we used the kinetic Monte Carlo (KMC) method (43) to simulate the model. We chose KMC in this case because grid sizes larger than M = 10⁴ would be needed to solve Eq. 11, which contributes to numerical stability problems. The transitions in the KMC are stochastically implemented, and a given trajectory is generated until the helicase disassociates.

From detailed balance, it follows that $\alpha /\beta =e^{-\Delta G}$, where ΔG ≈ 2 is the sequence-averaged free energy per basepair in the absence of the helicase. To incorporate sequence effects, we let ΔG = g(δm), where δm ≡ m – m₀ with m₀ being the initial position of the ss-dsNA junction on the lattice, and the sequence-dependent function g is constructed from the nearest-neighbor parameters provided in Table 3 of SantaLucia et al. (44). For example, if the junction is a GC basepair and the downstream pair is AT, we assign ΔG(δm) = 1.46 kcal/mol ≈ 2.43 k_BT. Following Betterton and Jülicher (33), we assume β to be constant and then assign α = βe^−ΔG. As the sequence composition is varied, the average free energy per basepair ranges from $\overline{\Delta G}=1.7$ when the GC content is 0% to $\overline{\Delta G}=2.95$ if the GC content is 100%. We investigated the NA sequences organized in a block copolymer fashion. For example, the infinitely repeating unit of the sequence used to investigate 40% GC content was

$$\begin{array}{cccccccccccc}{5}^{\prime }& G& G& G& G& A& A& A& A& A& A& 3^{\prime }\\ 3^{\prime }& C& C& C& C& T& T& T& T& T& T& 5^{\prime }\end{array}.$$

We investigated sequences with fractional GC content varying from 0 to 1 in increments of 0.1. All simulations were performed with initial separation j₀ = 1 and with the junction located at the first GC pair of the repeating unit of the sequence.

The mean attachment time is calculated as $\langle \tau \rangle \equiv 1/N{\sum }_{i=1}^N{\tau }_i$, where N is the number of simulations (N = 1000 for every data point we collected), and τ_i is the attachment time in simulation i. The mean translocation processivity is calculated using $\langle \delta n\rangle \equiv 1/N{\sum }_{i=1}^N\left(n_i^f-n_i^0\right)$, where n_i⁰ is the initial position of the helicase is simulation i and n_i^f is its final position. Finally, the mean unwinding processivity is calculated as $\langle \delta m\rangle \equiv 1/N{\sum }_{i=1}^N\left(m_i^f-m_i^0\right)$, where m_i⁰ is the initial position of the ss-dsNA junction and m_i^f is its final position.

The results of our simulations investigating sequence dependence are provided in Fig. 6, and we note the following points of interest: 1) Not surprisingly, processivity (both 〈δm〉 and 〈τ〉) and V₁ = 〈δm〉/〈τ〉 decrease as the fraction of GC content is increased. 2) The decrease in attachment time with increasing U₀ is similar at both f = 0.01 and f = 0.25. The behavior of 〈δm〉 with increasing U₀ at f = 0.25, however, differs substantially from its behavior at f = 0.01. At f = 0.01, 〈δm〉 is essentially constant with respect to U₀. This leads to an eventual saturation of 〈δm〉/〈τ〉 at large U₀. At f = 0.25, on the other hand, sequence effects are more pronounced. For example, 〈δm〉 decreases substantially with U₀ when %GC = 0 (Fig. 6, black solid line), but negligibly when %GC = 1 (Fig. 6, gray dashed line). This behavior leads to a pronounced peak in V₁ when %GC = 0, but a very small peak when the fractional GC content is 1. Indeed, at %GC = 100, we see that 〈δm〉 can actually become negative leading to a negative V₁ for helicases with too strong a coupling. The surprising finding that velocity and processivity can be negative can be explained as follows: If the base ahead of the helicase is very stable, with a large ΔG, and if the helicase back-stepping rate (during unwinding) is comparable in magnitude to the forward stepping rate, it is possible that on average the helicase steps backward before the base in front opens from a thermal fluctuations. In such a situation, the velocity and processivity would be negative. It remains to be ascertained whether this is realized in practice.

Discussion

Effect of ssDNA elasticity

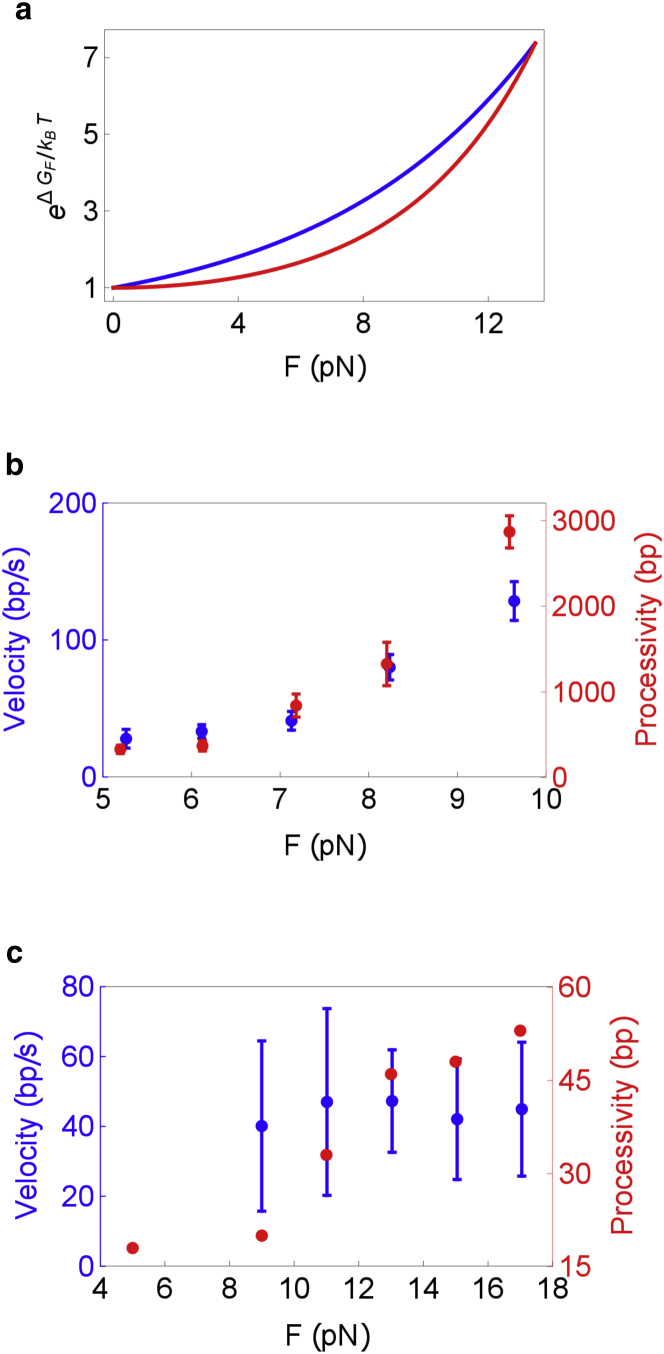
To simplify our analysis, we used the Bell model ΔG_F = FΔx, for the effect of force on the destabilization of the junction basepair. It might be more accurate to use $\Delta G_F=2L/l\text{log}\left(1/\left(Fl\right)\text{sinh}\left(Fl\right)\right)$ (29,45), because a freely-jointed-chain model has been shown to be appropriate to describe single-strand DNA elasticity (46). As shown in Fig. 7 a, $e^{\Delta G_F}$ values for both the models are similar, and hence using the simpler Bell model does not make any qualitative difference in our results.

Figure 7.

(a) Dependence of $e^{\Delta G_F}$ on F for two models: ΔG_F = FΔx (blue curve), and $\Delta G_F=2L/l\text{log}\left(1/\left(Fl\right)\text{sinh}\left(Fl\right)\right)$ (red curve). The parameters Δx = 0.594 nm, L = 0.6 nm/nucleotide, and l = 1.3 nm were chosen such that for both models, the critical force (force at which ΔG = ΔG_F) is 13.5 pN, a typical value for DNA hairpins. To be consistent with the rest of our analysis, ΔG was chosen to be 1.95 k_BT. (b and c) Experimental data suggesting a universal behavior of the unwinding processivity as a function of force. Velocity (blue) and processivity (red) data on (b) the T7 helicase (28) and (c) the NS3 helicase (40). The data shows that the unwinding velocity of the two helicases can be strongly or weakly dependent on external force. The processivity clearly increases as F increases, for both the helicases. To see this figure in color, go online.

Effect of back-stepping rate

We analyzed the model for the case where the back-stepping rate of the helicase k⁻ is much smaller than the forward stepping rate k⁺, in the absence of the double-strand junction. Most molecular motors fall in this regime, where k⁺ >> k⁻. For example, the ratio k⁺/k⁻ was measured to be ∼221 in Kinesin (47) and is expected to be large for helicases as well (30). As long as this holds good, which has experimental support, all the results obtained in this work will remain valid.

Mechanism for increase in processivity with force is different for passive and active helicases

From the recent single molecule experiments on three helicases (24,28,40), we have surmised that the dependence of unwinding processivity on F may be universal (Fig. 7, b and c). Irrespective of whether the unwinding velocity increases rapidly with force, the processivity seems to increase with the external force. In this work, we have provided a theoretical explanation of this behavior. Based on the theory, we predict that the sensitivity of processivity to force should indeed be a universal feature of all helicases, whether they are active or passive. Our argument hinges on the observation that the processivity of a helicase is very well approximated by the product of two quantities, the unwinding velocity and the attachment time of the helicase: 〈δm〉 ≈ V₁〈τ〉. The origin of the universal increase of 〈δm〉 with F is dramatically different for passive and active helicases. We have shown that when the helicase is passive, V₁(= V_HW) increases rapidly with force while 〈τ〉_HW stays constant, independent of the force. In contrast, when the helicase is optimally active, V₁ hardly changes as a function of force, while 〈τ〉 increases rapidly as the force is ramped up. Thus, in both these extreme situations of helicase activity, the processivity 〈δm〉 shows significant variation as a function of force. This leads to the prediction that irrespective of the nature of interaction of the helicase with the double-strand junction, the processivity should always increase as the force is increased.

We note in passing that the relationship, 〈δm〉 ≈ V₁〈τ〉, can be used to anticipate the effect of ATP concentration on 〈δm〉. If for a particular helicase 〈τ〉 is independent of ATP concentration, it follows that processivity is determined by V₁. So we expect that decreasing ATP concentration should decrease V₁, and hence 〈δm〉. Interestingly, this was observed in an experiment on RecBCD some time ago (48).

Is there a general role for partner proteins in the replisome?

Our demonstration that helicase processivity always increases with F regardless of the underlying architecture of the enzyme, is likely to be relevant in vivo as well. It is becoming increasingly evident that helicases function most efficiently only in the presence of the macromolecular machinery with which it interacts in the cellular milieu (6,35). Significant increase in the unwinding velocity and processivity of a number of helicases has been reported in Stano et al. (49), Rajagopal and Patel (50), and Manosas et al. (51), when coupled to partner proteins like the polymerase or single-stranded binding proteins (SSB). This naturally suggests a possibility that by partially destabilizing the ss-dsDNA junction, the partner proteins could be mimicking external forces that are applied in single molecule experiments.

A number of explanations have been proposed in the literature, to account for the effect of partner proteins on helicases (35). For example, dsDNA destabilization, prevention of back-slippage of the helicase, specific interactions with the helicase leading to longer helicase lifetimes on the nucleic acid track, are some of the commonly invoked methods by which partner proteins are conjectured to increase the efficiency of helicases. Although it is likely that some or all of these mechanisms together contribute in increasing a helicase’s speed and processivity, there is evidence to suggest that partial destabilization of the ss-dsDNA junction may be essential. It has been known for a long time that by binding tightly to ssDNA, SSB can destabilize the bases of dsDNA (52,53), at least the first few bases near the ss-ds junction (54). A similar double-strand destabilization effect caused by the polymerase was shown to be critical in explaining single molecule data on the T4 helicase (51). To explain the sometimes order-of-magnitude increase in velocity/processivity of helicases, it therefore seems likely that an essential requirement is at least partial destabilization of a few basepairs at the ss-dsDNA junction, by partner proteins.

If partner proteins indeed mimic external forces resulting in destabilization of the ss-dsDNA junction, we would predict that they would have distinctly different effects on T7 (weakly active) and NS3 (active) helicases. The effects should be similar to the force response (Fig. 7, b and c)—both the velocity and processivity of T7 helicase should be increased by partner proteins, while only the processivity should be enhanced of the NS3 helicase. Remarkably, this has indeed been observed in experiments. Rajagopal and Patel (50) showed that SSB increase only the processivity of NS3 while Stano et al. (49) and previous works (55) showed that both velocity and processivity of T7 helicase increases due to the presence of a polymerase.

It is worth reemphasizing that we are drawing a parallel between the effect of partner proteins on the ss-dsDNA junction and the basepair destabilization effect (reduction in ΔG) due to external mechanical forces. We are not predicting the effect of partner proteins on the individual rates whose ratio determines ΔG (see Eq. 4). Therefore, destabilization of the junction by partner proteins could happen either by increasing the dsDNA opening rate α or by decreasing the dsDNA closing rate β. The latter mechanism was shown to hold in a particular study of the effect of single-strand binding proteins on dsDNA (56), and hence is another example supporting our claim.

Our work therefore suggests a very general role for the partner proteins associated with helicases in the replisome. Even though these associated proteins may or may not increase the unwinding velocity of a helicase depending on the specifics of the helicase’s interaction with the dsDNA, they should universally increase the processivity of the helicase. This seems to be borne out in experiments, and the generality of our statement can be tested in future experiments. In a related context, it was shown earlier that the interactions between separate domains of the same helicase could potentially lead to a higher velocity than either individual domain (57). This mechanism could also play a role in understanding the reason for increase in velocity of different oligomeric states of helicases or helicases interacting with partner proteins.

Conclusions

There has been no unified explanation for the recent experimental observations that the unwinding processivity of helicases is always enhanced by force while the velocity shows a multitude of helicase-dependent responses. By extending the theory of Betterton and Jülicher to include force effects, we have provided an understanding of these varied observations. The velocity of unwinding depends crucially on the extent to which a helicase is active. Optimally active helicases show little or no change in velocity while the velocity of passive helicases is highly sensitive to external forces that destabilize the double-strand. In stark contrast, we predict that the unwinding processivity of a helicase should always increase with force, irrespective of how active or passive it is. The reason for this universal behavior of the processivity, however, depends on the nature of the helicase. Our prediction is general, and seems to be borne out in structurally diverse helicases like T7, UvrD, and NS3. Future experimental measurements of load-dependent processivity can test our assertion that associated partner proteins may have coevolved with helicases to increase the processivity, not the velocity of unwinding nucleic acids. Finally, our sequence-dependent simulations show that the velocity can display nonmonotonic behavior that is strongly dependent on GC content as well as saturating behavior at very small f. Many of our predictions await future experiments.

Author Contributions

D.L.P., S.C., and D.T. designed and performed research and wrote the article.

Editor: Timothy Lohman.