Structural Origins of Misfolding Propensity in the Platelet Adhesive Von Willebrand Factor A1 Domain

Abstract

The von Willebrand factor (VWF) A1 and A3 domains are structurally isomorphic yet exhibit distinct mechanisms of unfolding. The A1 domain, responsible for platelet adhesion to VWF in hemostasis, unfolds through a molten globule intermediate in an apparent three-state mechanism, while A3 unfolds by a classical two-state mechanism. Inspection of the sequences or structures alone does not elucidate the source of this thermodynamic conundrum; however, the three-state character of the A1 domain suggests that it has more than one cooperative substructure yielding two separate unfolding transitions not present in A3. We investigate the extent to which structural elements contributing to intermediate conformations can be identified using a residue-specific implementation of the structure-energy-equivalence-of-domains algorithm (SEED), which parses proteins of known structure into their constituent thermodynamically cooperative components using protein-group-specific, transfer free energies. The structural elements computed to contribute to the non-two-state character coincide with regions where Von Willebrand disease mutations induce misfolded molten globule conformations of the A1 domain. This suggests a mechanism for the regulation of rheological platelet adhesion to A1 based on cooperative flexibility of the α2 and α3 helices flanking the platelet GPIbα receptor binding interface.

Introduction

The von Willebrand factor (VWF) A1 and A3 domains function in hemostasis to capture platelets from rheological blood flow and deposit them onto collagen and other exposed subendothelial matrix proteins at sites of vascular injury to form a platelet plug and arrest bleeding. The platelet GPIbα binding A1 domain facilitates the capture of platelets via rheological regulation of its conformation under shear stress, resulting in a balanced feat of catch-and-release while A3 anchors VWF to collagen in the vascular wall (1,2). A myriad of human mutations causing both loss and gain of platelet adhesive function occurring in the A1 domain contribute to a dynamic range of bleeding severity and thrombocytopenia in the most common inherited bleeding disorder, von Willebrand disease (VWD) (3,4).

The energetic differences between A1 and A3 domain structures are intimately linked to VWF function. In the disease state, the platelet-binding function of the A1 domain is significantly affected by its propensity to populate intermediate molten globule states with misfolding occurring in two-thirds of the most common biophysically and thermodynamically characterized VWD A1 domain variants (4–7). Population of these intermediate states causes distinctive three-state chemical and thermal denaturation profiles for A1 (7,8). In contrast, the chemical and thermal unfolding of the collagen-binding A3 domain exhibits classical two-state character but with the added complication of denatured state expansion (9). A3 also imparts stability to the association of domains in an A1A2A3 tridomain fragment of VWF, providing an additional regulatory role for the conformational activation of VWF under shear stress (10). Despite their functionally and thermodynamically distinct properties, the structures of these domains are isomorphic (11). These observations present a genuine challenge to decipher the thermodynamics of these domains from their chemical structures.

To investigate the origins of the observed differences in the unfolding thermodynamics of the A1 and A3 domains, we have employed the structure-energy-equivalence-of-domains (SEED) algorithm (12), which uses residue-specific water → 1M urea-group transfer free energies (13) to define thermodynamic subdomains of protein structures consistent with experimentally determined equilibrium folding intermediates. In initiating the studies to be described, our goal was to resolve regions of the A1 domain structure that contribute to its propensity to unfold to intermediate conformations by using the A3 domain structure as an experimentally verified two-state reference. Transfer free energies have been used to successfully predict the global thermodynamic cooperativity of urea-induced unfolding and osmolyte-induced folding of a comprehensive collection of proteins and osmolytes (14). Here, we analyze A1 and A3 using a modified implementation of SEED to parse these structures into their constituent thermodynamically cooperative components with residue specificity and provide experimental data that support the conclusions derived from SEED.

The SEED analysis revealed clear differences in regional folding cooperativity between the two domains. In particular, the second and third α-helical elements identified with low structural cooperativity indicate a thermodynamic potential for local unfolding. These two helical structures span 50 residues that flank both sides of the GPIbα binding interface and coincide with residue positions where point mutations induce the pathological molten globule conformations that cause VWD (4). Mutations in the α2 helix concomitantly reduce the helical content and enhance the adhesion pause times of platelets translocating on the A1 domain corresponding to an increased bond strength and a diminished dissociation rate of the A1-GPIbα complex. Mutations in the α3 helix result in a greater loss of secondary structure content with complete loss of platelet adhesion. The results suggest a potential dynamic regulatory competition between the folding propensities of these helical elements as a mechanism for the catch-and-release of platelets under rheological shear flow.

Materials and Methods

Structure and sequence similarity

Structural alignment of the crystallographic structures of A1 (1AUQ, residues 509–698) and A3 (1AO3, residues 1–187) was performed using the CE algorithm (15) with manual inspection of the residue equivalences (see Fig. S1 in the Supporting Material). In this sequence alignment implicated from structure matching, a pair of residues, aligned in space, is considered aligned in sequence; and a residue without a close spatial match in the structure alignment is aligned to a gap in the sequence alignment. The fraction of identical and similar residues from this structure-based alignment is in agreement with a purely sequence-based approach using the software ALIGN (16), but implies a different set of equivalent residues. The significant structural similarity is further confirmed by evaluating the optimal residue equivalence using root-mean-square distance difference (RMSDD) (17), an alignment-invariant metric based on the pairwise internal distances within each structure. To emphasize the importance of using the correct residue equivalence, arbitrarily removing three C-terminal residues from A1 (which has 190 residues) and comparing to A3 (187 residues) yields an RMSDD of 3.4 Å. The lowest RMSDD achievable from removing any three residues from A1 is 2.3 Å. After 100,000 iterations of randomly removing nine residues from A1 and six from A3 and computing the RMSDD of the resulting 181 equivalent residues, the minimum structural equivalence observed was 2.4 Å.

SEED calculations

SEED is used to parse domain structures both linearly through sequence (sequential parsing) and nonsequentially through nearest neighbors in space (spatial parsing) to assess sequential context independently from spatial relationships between elements of structure. This parsing implementation of SEED uses a ratiometric approach of comparing m values calculated for structural fragments to define an empirical representation of fold cooperativity with residue resolution. The m values of both excised and in situ fragments generated by sequential or spatial parsing of the structurally aligned A1 and A3 domain coordinates were calculated using the methods previously described for whole proteins (13,14). The m values for each fragment were normalized by the number of amino acids contained (F) and plotted as a distribution for all fragments in which amino acid i (AA_i) was the central residue of sequential parsing or the root residue for spatial parsing. The median m/F was taken as AA_i’s residue-specific contribution. AA_i specific cooperativity ratios were calculated from the ratio of m values of excised, relative to in situ, fragments, CR = (m/F)_excised/(m/F)_{in situ}.

As an example of sequential parsing, if (17,7) designates a fragment beginning at residue 17 and extending to residue 23 (of length 7 with residue 20 in the center), the contribution of residue 20 would be the median value from the set of fragments {(17,7), (16,9), (15,11),…}. The termini are allowed to wrap together in this procedure. For the A3 domain (which has 187 residues), one example of wrapping would be the fragment (180,15). This fragment is assigned a center of 187 and is comprised of the eight most C-terminal residues and seven most N-terminal residues. In the spatial parsing, AA_i acts as the root; i.e., the first residue in a growing fragment. Nearest-neighbor amino acids are added to the growing fragment by ranking through space proximities between α-carbons of all residues relative to AA_i, the closest being added first, until the entire structure has been recapitulated. As each residue is added, m values of the fragments are calculated as above and the median across all fragments for which AA_i was the root, determines AA_i’s thermodynamic contribution.

The SEED algorithm, as implemented in this article, is available upon request.

The m value calculations

The m values of all fragments parsed from the structures were calculated using the transfer model and Eqs. 1–3 as described by the literature (13,14,18):

$$\begin{array}{c}{m}_{\text{calc}}=\Delta G_{tr,D}^{1M}-\Delta G_{tr,N}^{1M}\\ =\sum _{i=AA\text{type}}{n}_i\Delta {\alpha }_i^{sc}\Delta g_{tr,i}^{sc}\\ +\sum _{i=AA\text{type}}{n}_i\Delta {\alpha }_i^{bb}\Delta g_{tr,i}^{bb}.\end{array}$$ (1)

$$\Delta {\alpha }_i^{sc}=\underset{j}{\sum ^{n_i}}\frac{1}{n_i}\cdot \frac{AS{A}_{i,j,D}^{sc}-AS{A}_{i,j,N}^{sc}}{AS{A}_{\text{gly}-A{A}_i-\text{gly}}^{sc}},$$ (2)

$$\Delta {\alpha }_i^{bb}=\underset{j}{\sum ^{n_i}}\frac{1}{n_i}\cdot \frac{AS{A}_{i,j,D}^{bb}-AS{A}_{i,j,N}^{bb}}{AS{A}_{\text{gly}-A{A}_i-\text{gly}}^{bb}}.$$ (3)

The n_i value is the number of groups i in the protein, and Δα_i is the average fractional number of backbone (bb) or side-chain (sc) groups of type i that are newly exposed upon transfer to a one molar urea solution (13). The value Δg_tr,i is the corresponding transfer free energy of backbone or side-chain groups i from buffer to the one molar urea solution. ASA_i,j for the N and D states is determined using the algorithms described in Auton and Bolen (18), Lesser and Rose (19), and Creamer et al. (20).

To convert the ASA_i,j values to numbers of backbone or side-chain equivalents, we divide by a representative backbone (bb) or side-chain (sc) area of amino acid i. The model we chose is the backbone and side-chain areas of the central species of the gly-AA_i-gly tripeptide because it gives the maximal solvent exposure for these groups. Division of backbone or side-chain area differences, (ASA_i,j,D - ASA_i,j,N), by their corresponding group areas in gly-AA_i-gly gives an equivalent number of protein backbone or side-chain group units (n_i,U - n_i,N) that are newly exposed upon denaturation, as specified by the transfer model.

Results

Thermodynamic dissimilarity of structurally isomorphic domains

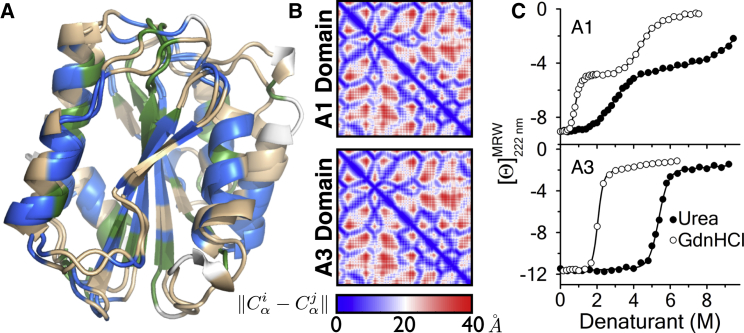
The structural alignment of the A1 and A3 domains in Fig. 1 A was performed using the CE algorithm (15). Residues are 23% identical, and an additional 40% of the residues are composed of physicochemically similar amino acids. The fraction of identical and similar residues is in agreement with a purely sequence-based approach using the software ALIGN (16), but implies a different set of equivalent residues. Despite the low sequence identity, the two domains are nearly identical in structure. After an optimal alignment and manual curation of the implicated residue equivalence, 40% of aligned residues are within 1 Å and 73% within 2 Å. The spatial fit of the 181 equivalent residues (those not aligned to a gap) was evaluated with the alignment-free RMSDD (17) to compare the differences of internal α-carbon distances (Fig. 1 B). This metric gives an excellent fit of 1.48 Å. The structures of A1 and A3 are highly similar, and the superpositioning is optimally aligned.

Figure 1.

(A) Structural alignment of A1 and A3 domains colored by sequence similarity (green, identical; blue, similar; tan, dissimilar; and white, aligned to gap). (B) Distance-difference matrix of all aligned backbone atoms. (C) Urea and guanidine hydrochloride denaturation at 25°C monitored by circular dichroism at λ = 222 nm. To see this figure in color, go online.

Although these domains are structurally isomorphic, the denaturant-induced unfolding of the A1 and A3 domains (Fig. 1 C) demonstrates a classical two-state unfolding of A3 with a single cooperative transition and a three-state unfolding of A1 through an intermediate state with two cooperative transitions. Urea denaturation cooperatively unfolds A1 in the first transition, but unlike GndHCl, urea is unable to completely denature the A1 domain in the second transition due to its solubility limit. GndHCl denaturation is used only to fully illustrate the three-state character of the A1 domain. The urea m values for A3, m = −2.3 ± 0.1 kcal/mol/M, and the sum of m values for each transition of A1, m_total = (−1.12 ± 0.04) + (−0.8 ± 0.15) = −1.92 ± 0.16 kcal/mol/M, give the overall global unfolding cooperativities for complete denaturation of these domains. Using the transfer model, the urea m-values of the entire A3 and A1 domain structures are calculated to be −2.4 and −2.6 kcal/mol/M, respectively. These values are in reasonable agreement with the experimental m values and are within the 95% confidence interval (±0.68 kcal/mol/M) for whole protein m-value predictions (14), although the experimental sum of m values for A1 is significantly less than calculated due to the non-two-state character.

SEED analysis of structural cooperativity

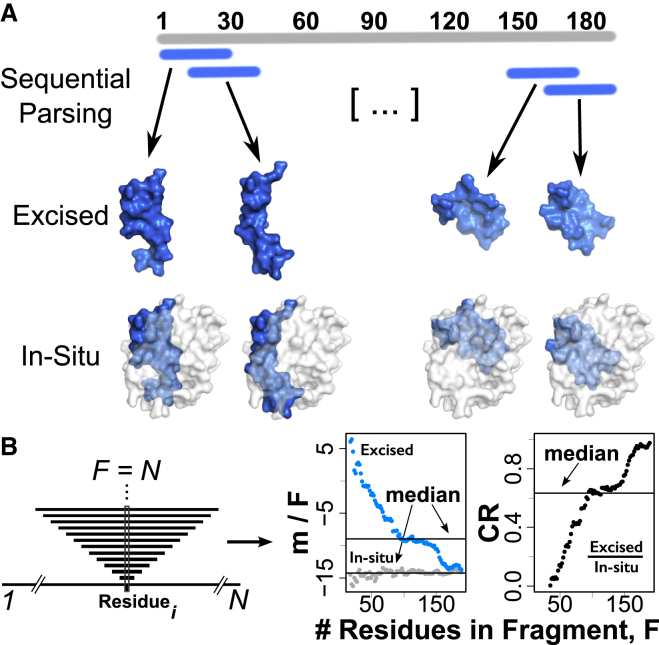
While denaturation experiments provide m-value measurements of entire proteins, computational approaches allow the calculation and assignment of per-residue contributions from experimentally determined group transfer free energies. Fig. 2 A illustrates how group transfer free energies are parsed over sequential substructures using SEED to assess the residue contributions to the unfolding cooperativity of the entire protein. A structural fragment of the domain is defined by each pair (R, W) of starting residue (R∈[1…N]) and an odd-number window size (W∈[1…N]), where N is the greatest odd number of residues in the structure. This enumeration produces N²/2 unique fragments of the domain structures: 18,050 for A1 and 17,485 for A3. Urea m-values are computed for each fragment within the context of the whole structure (m_{in situ}) and as isolated fragments without any contribution from the rest of the structure (m_excised) and normalized to the fragment length, F (Fig. 2 B). Because m values are scaled by solvent accessibility, the difference between the in situ and excised contexts is the per-residue burial of the fragment by the remainder of the structure. The cooperativity ratio (CR = m_excised/m_{in situ}) evaluates the extent to which a fragment acts as an independent folding unit (Fig. 2 B) (12). In essence, when native tertiary structure contacts are disrupted, a low CR corresponds to a predisposition to unfold, whereas a high CR indicates a propensity to remain folded. In this procedure, the termini are allowed to wrap together to account for the possibility of N- and C-terminal residues to exist within the same folding unit. This procedure is particularly appropriate for A1 and A3 because both domains contain a single disulfide bridge linking the N- and C-termini. Under nonreducing conditions, both molecules are folded cyclical peptides, making the wrapping behavior of our algorithm reflective of their native covalent topology.

Figure 2.

Sequential parsing by SEED. (A) Examples of excised and in situ fragments derived from sequentially contiguous regions of structure. (B) Fragments are centered on each residue i and extended to increasing lengths up to the full length of the protein. The sequence is circularized to account for fragments containing both N- and C-terminal residues. The m values are calculated for both excised and in situ fragments, normalized to the number of residues in the fragments (m/F), and the median (horizontal lines) is calculated with respect to all fragment lengths with a common central residue, i. The median cooperativity ratio is CR = (m_excised/F)/(m_in situ/F). To see this figure in color, go online.

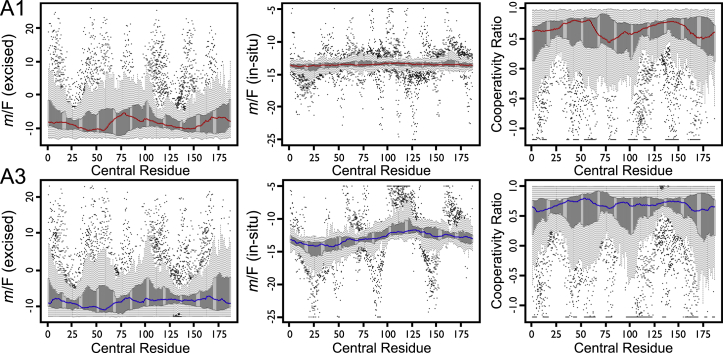
Each residue i is assigned the median m/F value across all contiguous sequential fragments for which residue i is the center of the fragment (Fig. 2 B) because it best represents the central distribution tendency of the series. The median was chosen because the distribution of m/F as a function of the number of residues per fragment is skewed, and because medians eliminate contributions of short fragment outliers (<20 residues) that significantly affect the average. These skewed distributions of m/F values across the residue sequence illustrate the heterogeneity of the residue-specific contributions to the m value (Fig. 3). The median is appropriate considering that a minimum of 30 residues was needed to identify a domain in the original SEED algorithm as implemented by Porter and Rose (12). The per-residue median values provide an empirical thermodynamic profile for comparing protein structures. The distribution of m/F values in Fig. 3 associated with each residue across all sequential fragments reveals significant differences between these domains. As fragments approach the length of the whole protein, excised and in situ m values both limit to the value computed for the whole protein, and CR limits to unity, but the path is not strictly monotonic (Fig. 2 B).

Figure 3.

Sequential parsing of the m value by SEED. A box plot of the distribution of m/F values across all fragments of the A1 domain (top) and the A3 domain (bottom) for excised (left) and in situ (middle) fragments, and the cooperativity ratio (right). (The thick bar covers half the fragments, the dotted line extends up to 1.5× that range, and the dots represent short fragment outliers.) The median values are highlighted for each residue (red, A1 or blue, A3). Note the large difference in scale and overall variance between the excised and in situ contexts. For plotting purposes, values of m/F, excised, are truncated at 22; values of m/F, in situ, are truncated between −5 and −25; and cooperativity ratio (CR) values are truncated at −1.2. While fragments of all sizes are computed, only those of at least seven residues, shown as very short fragments, have an expected high variability. To see this figure in color, go online.

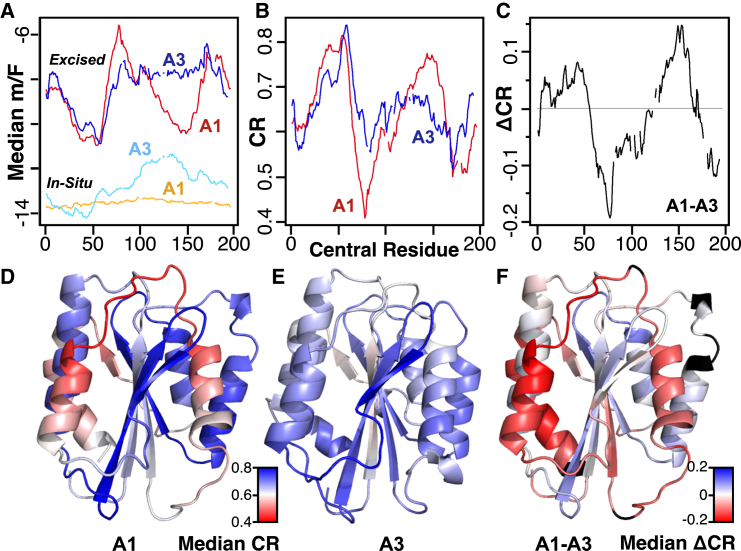
The median m/F values for each domain’s excised and in situ fragments, the CR, and the CR difference between domains, ΔCR, are plotted in Fig. 4, A–C. These data identify the region between residues 60 and 110 as significantly less cooperative in A1 relative to their cooperativity in A3. The unfolding cooperativity of the A1 C-terminus is also reduced. Some intervening residues between these regions are more cooperative. As the range of CR values for A3 is less than for A1, the domain differences highlighted using ΔCR values largely follow variations in structural cooperativity within A1. The per-residue CR values are projected onto each structure, emphasizing the structural relationship between differentiating regions (Fig. 4, D–F). The least cooperative helix-loop-helix structural element surrounding the leading strand of the central β-sheet is an important binding interface between A1 and platelet receptor GPIbα (4). The C-terminus on the opposite face of the A1 domain structure also has a low computed cooperativity.

Figure 4.

Median per residue contribution to cooperative unfolding by sequential parsing using SEED. (A) Median per-residue m/F values for excised and in situ fragments. (B) Median cooperativity ratio, CR. (C) Cooperativity ratio difference, ΔCR. (D and E) Median CR of A1 and A3 mapped to structure. (F) Difference, ΔCR mapped to the A1 structure. (Black) Residues that do not structurally align. (A–C) Line breaks correspond to residues aligned to a gap (no structurally equivalent residue). To see this figure in color, go online.

Three computational controls were performed to assess the robustness of the SEED results as described in the Materials and Methods and the Supporting Material. 1) Spatial parsing of the m value was performed to assess whether the thermodynamic differences between the domain structures could be deciphered in the context of sequentially discontiguous fragments by parsing next-nearest neighbors from a residue-distance difference matrix. 2) Sequential parsing of the m value was performed while omitting residue-specific transfer free energies to assess surface area contributions alone. 3) Transfer free energies of two denaturants and five osmolytes were used in the sequential parsing to assess whether the observed computations are independent of the type of cosolute used to probe the structural thermodynamic differences. These computational controls (illustrated in Figs. S2–S4) demonstrate: spatial parsing does not reveal thermodynamic differences between these domains; sequential parsing of the surface area alone is not distinguishing; and cooperativity ratios are qualitatively similar when using different osmolyte dependent transfer free energy data sets. The results reveal that group transfer free energies within sequential context specifically recognize thermodynamic properties of the A1 domain structure that are discernibly different from that of the A3 domain structure.

Correlation to mutation effects on cooperativity

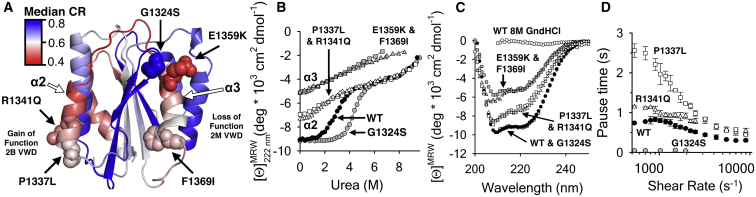
Mutation-induced loss of A1 domain helical secondary structure is a defining characteristic of the von Willebrand disease state. Of the 18 biophysically characterized A1 domain variants, 12 have a nonnative molten globule structure that results in a reduced or absent cooperative transition from the native to intermediate state (4). Fig. 5 A illustrates the structural locale of two gain-of-function Type-2B VWD mutations (R1341Q and P1337L) and three loss-of-function Type-2 M VWD mutations (G1324S, E1359K, and F1369I). Fig. 5 A shows that the four mutations that induce misfolding occur in the α2-helix-loop-α3-helix secondary structure elements that are calculated by SEED to have low cooperativity ratios. The effects of these mutations also show a concomitant loss of secondary structure and a loss of a urea-induced unfolding transition (Fig. 5 B). The loss of helical structure caused by the type-2M mutations in α3 is greater than that for the type-2B mutations in α2, but both mutations in α2 and in α3 remain partially unfolded in the absence of urea and retain significant helical content relative to the completely denatured state in 8-M GndHCl as demonstrated by the far-ultraviolet circular dichroism spectra in Fig. 5 C. Consequently, this greater loss of secondary structure caused by the type-2M mutations inactivates the platelet adhesive function of the A1 domain. The type-2B mutations in α2 retain much of the intermediate state character of the wild-type (WT) A1 domain and enhance the platelet adhesion pause times, resulting in a gain-of-function phenotype consistent with the disease classification. Increased pause times correspond to greater bond strengths and decreased dissociation rates under shear flow (Fig. 5 D). In contrast, the type-2M G1324S mutation, located in the β-hairpin loop region of high cooperativity, stabilizes the A1 domain (Fig. 5 B), resulting in greatly diminished platelet adhesion pause times due to reduced flexibility imposed by the serine side chain. The biophysical characterization of these pathological mutations, in combination with the SEED calculations, suggest that cooperativity and stability issues in the 2-helix-loop-3-helix region of A1 have key regulatory roles in platelet adhesion, which are discussed below.

Figure 5.

(A) Head-on view of the GPIbα binding interface of the A1 domain illustrating the location of type-2B VWD mutations (R1341Q and P1337L) in α2 and type-2M mutations in the β-hairpin (G1324S) and α3 (E1359K and F1369I). (B) Urea unfolding of WT (solid circles), G1324S (shaded circles), R1341Q and P1337L (open triangles and squares), and E1359K and F1369I (shaded triangles and squares). (C) Far-UV CD spectra of the protein variants (indictaed in B) in the absence of urea. WT A1 in 8M GndHCl is included as a completely unfolded reference. (D) Shear-dependent platelet pause times on WT (solid circles), R1341Q (triangles), P1337L (squares), and G1324S (shaded circles). The type-2M loss-of-function variants (F1369I and E1359K), did not adhere platelets. Data in (B)–(D) are published in Tischer et al. (4). To see this figure in color, go online.

Discussion

The translation of structure to energetics and thermodynamic parameters has been a long-sought-after goal in the discipline of protein folding. Divergent protein sequences that fold to isomorphic structures demonstrate compelling cases that challenge the development of accurate and predictive thermodynamic models. In our implementation of SEED, we perform transfer free energy calculations on substructures, fragments of the native structure, that are defined by either sequential or spatial parsing so that cooperativity can be assessed through sequence context independently from spatial context. Both parsing methods assume that all regions of structure are intrinsically two-state. Partial structure is defined only by how the structures are parsed; therefore, non-two-state character should be implicitly revealed if the residue-specific thermodynamics are correct. Fragment m values are calculated independently and within the context of the entire domain, and ratiometrically compared to empirically compute the relative propensity of each fragment to unfold with or without contributions from the remaining structure. The cooperativity ratio was previously used by Porter and Rose (12) as a metric to qualify the partitioning of protein structures into discrete thermodynamic domains using a coarse-grained 30-residue window size and a simple scoring function. Residue-level specificity is attained empirically by calculating the median of cooperativity ratios of all fragments with common central residues that increases the detail with which protein fold cooperativity can be queried within domains.

The magnitude of the cooperativity ratio has physical contributions from solvent-accessible surface area as well as thermodynamic contributions from group transfer free energies. Within the context of this ratiometric computation, the ΔASA contributions of these A domains are highly similar because of the structural isomorphism (Fig. S2); thus, the cooperativity ratio can be interpreted primarily as a thermodynamic potential for cooperative folding. When native tertiary contacts are disrupted, low cooperativity regions could easily unfold while the rest of the protein structure remains folded. In contrast, high cooperativity regions would have a propensity to stay folded when local unfolding events disrupt native contacts. Such cooperativity issues are characteristic of the A1 domain, which has fundamentally different thermodynamic properties persisting over a range of denaturation conditions and mutational effects that define the presence of intermediates in A1’s three-state character as opposed to the two-state character of the A3 domain (4–10,21).

The experimentally distinct thermodynamics between A1 and A3 are contrasted by nearly identical tertiary structures. Using the A3 domain as a reference two-state unfolder, the sequential parsing by SEED identifies structural regions of differential thermodynamic character that could contribute to partially structured intermediates in the A1 domain. Specifically, the computed low cooperativity ratio of the α2-loop-α3 secondary structure elements indicates a potential for local unfolding independent from the remainder of the protein. These helices each flank the GPIbα binding interface, and mutations in and around these structural regions are known to induce pathological molten globule conformations of the A1 domain leading to VWD (4). Interestingly, mutations occurring in this structural region cause misfolding to molten globule states with opposite phenotypes. Misfolding in α3 causes loss of function, whereas misfolding in α2 strengthens the interaction of A1 with platelet GPIbα. This opposition implicates a requirement that α3 remain structured for binding to occur and a regulatory role for local unfolding of α2 that modulates the strength of platelet adhesion (Fig. 5).

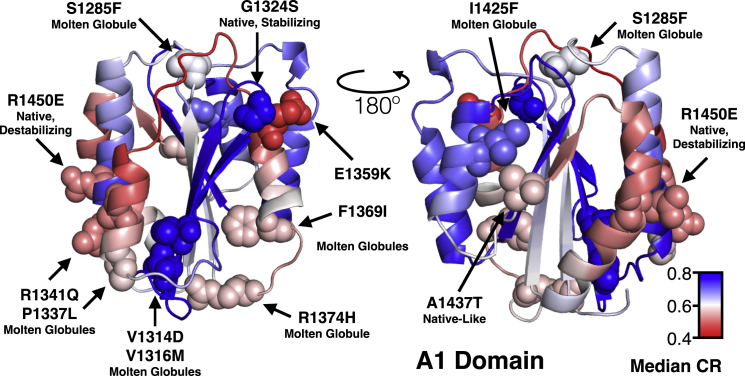
Fig. 6 illustrates a qualitative relationship between the structural locations of a more comprehensive list of disease mutations in the A1 domain and the local sequential folding cooperativity calculated by SEED. We have previously discussed the possible structural defects (hydrophobic packing, cavity formation, steric and charge effects) that contribute to these mutations’ destabilizing and molten-globule propensities in the A1 domain (4). These mutations were classified according to secondary structure content and the presence of a native to intermediate unfolding transition as being native, or nativelike with reduced secondary structure, or molten globule, having no cooperative native to intermediate unfolding transition. Most destabilizing and molten-globule variants occur from mutations that are within peripheral solvent-exposed helical structures computed to have low folding cooperativity by SEED. Exceptions are V1314D and V1316M, which introduce a negative charge and steric hindrances in the hydrophobic core causing substantial destabilizing effects on neighboring secondary structure elements such as the α2 helix. I1425F and S1285F also introduce local hydrophobic packing issues affecting local secondary structures. In the native class, a charge reversal mutation, R1450E, in the α6 helix thermodynamically destabilizes the A1 domain, leading to an allosteric activation of platelet adhesive function at lower rheological shear rates (10,22). In contrast, G1324S, located in a high cooperativity region, stabilizes the native-to-intermediate unfolding transition due to a reduction in conformational degrees of freedom provoked by the serine side chain (Fig. 5) (5). The structural correlations between cooperativity ratios and known mutations are not perfect, but, given only WT structures and residue-specific group transfer free energies, the sequential parsing results do highlight the structural regions known to be important in VWD pathology.

Figure 6.

Correlation of SEED sequential parsing median CR with locations of known clinical amino-acid substitutions that cause von Willebrand disease (4). Gain-of-function (type-2B VWD) clinical mutations are R1341Q, P1337L, V1324D, and V1316M. Loss-of-function (type-2M VWD) clinical mutations are E1359K, F1369I, I1425F, A1437T, and R1374H. Allosteric gain-of-function R1450E in α6 helix. To see this figure in color, go online.

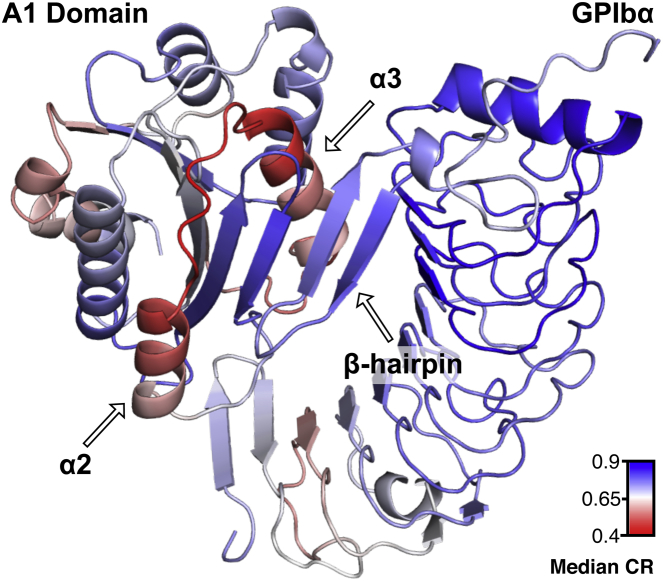
Fig. 7 illustrates the sequential cooperativity ratio with respect to the A1-GPIbα complex. Cooperativity ratios were calculated for both the A1 domain and GPIbα chains separately and combined for illustration. This perspective particularly emphasizes the relationship between the low cooperativity α2-loop-α3 structures of the A1 domain and the GPIbα β-hairpin that extends the A1 domains central β-sheet. The calculated residue-specific cooperativities suggest that the α2 and α3 helices of A1 could provide flexibility to the binding interface, via local unfolding reactions, to mediate the mechanical properties of adhesion under rheological flow. The validity of this idea, to our knowledge, has not yet been completely tested, but other computational methods have also implicated a localized dynamic role of the α2 helix (23). Taking into account the fact that GPIbα has been cocrystallized with a helical peptide (OS1) that inhibits platelet interactions with VWF, it is possible that the α2-loop-α3 helices could play a direct role in the binding under shear stress (24). The OS1 peptide also sterically overlaps with the A1 domain α3 helix when the GPIbα-OS1 structure is superimposed on the GPIbα-VWF-A1 complex (24). Additional evidence in support of a direct interaction between A1 domain helices and GPIbα is the observed on-pathway structural interactions between GPIbα leucine-rich-repeat residues and K1371 at the C-terminus of the α3 helix in a directed-evolution disulfide-bond variant of the A1 domain (25). Given that clinical disease mutations in α3 cause loss of function and those in and around α2 cause gain of function (Fig. 5), this dynamic and competitive interplay between the folding propensities of the α2 and α3 helices not only determines a predisposition for disease but also regulates the strength of platelet adhesion under rheological shear stress (4). Viewed from the perspective of cooperativity ratios, Fig. 7 implies that the mechanics of catch-and-release driven by local unfolding of the A1 domain α2-loop-α3 helices could simply be due to entanglement with the GPIbα β-hairpin under shear flow.

Figure 7.

The A1-GPIbα complex (1SQ0) as observed by SEED using the median sequential parsing cooperativity ratio. To see this figure in color, go online.

The computational comparisons of these VWF domains establish the feasibility of deciphering thermodynamic properties of isomorphic proteins using a representative structure. The observed thermodynamic conundrum given here is not unique to the A1 and A3 domains of VWF. Homologous mesophilic and thermophilic proteins are also known to be structurally indistinguishable but thermodynamically distinct (26,27). The utility of SEED is clear, but not without its limitations. It cannot distinguish the local stability (ΔG) of substructures because it is based on the m value, the derivative of stability with respect to urea concentration (∂ΔG/∂c_urea). It is also limited in its ability to distinguish isomorphic structures with highly identical sequences, such as structures with point mutations, unless the mutation causes a significant change in the experimentally determined structure. Despite these limitations, SEED can decipher isomorphic structures that are divergent in sequence, and it has potential for proteins with high sequence identity but different folds (28).

In conclusion, through comparison of two thermodynamically distinct isomorphic domains, the structural components of proteins that give rise to folding cooperativity can be assessed using a thermodynamic scale based on residue-specific group contributions. SEED identifies contiguous regions of A1 domain structure with significantly lower cooperative folding propensities than A3. The correlation of these regions with the locale of known clinical mutations that induce misfolding of the A1 domain provides evidence that they could contribute to the population of intermediate conformations both under equilibrium and in the presence of rheological shear.

Author Contributions

M.T.Z. and A.T. performed research and analyzed data; M.A., M.T.Z., and S.T.W. designed research and coded the software; and M.A., M.T.Z., and S.T.W. wrote the article.

Editor: Dr. H. Jane Dyson.