Indirect estimation of a discrete-state discrete-time model using secondary data analysis of regression data

SUMMARY

Multi-state models of chronic disease are becoming increasingly important in medical research to describe the progression of complicated diseases. However, studies seldom observe health outcomes over long time periods. Therefore, current clinical research focuses on the secondary data analysis of the published literature to estimate a single transition probability within the entire model. Unfortunately, there are many difficulties when using secondary data, especially since the states and transitions of published studies may not be consistent with the proposed multi-state model. Early approaches to reconciling published studies with the theoretical framework of a multi-state model have been limited to data available as cumulative counts of progression. This paper presents an approach that allows the use of published regression data in a multi-state model when the published study may have ignored intermediary states in the multi-state model. Colloquially, we call this approach the Lemonade Method since when study data give you lemons, make lemonade. The approach uses maximum likelihood estimation. An example is provided for the progression of heart disease in people with diabetes.

1. INTRODUCTION

This research was motivated by a model of diabetes progression through various states (or stages). Researchers are beginning to use computer models and simulations to provide a composite view of the natural history of diseases, such as cancer [1, 2], diabetes [3–6], and infectious diseases [7]. A discussion on disease models can be found in [8]. Using diabetes as an example, a large number of groups of researchers are developing diabetes model independently. A partial list of diabetes models includes the Michigan Model 2005 [3], the U.K. Prospective Diabetes Study (UKPDS) Outcomes Model 2004 (UKPDS 68) [4], and the CDC/RTI model [5]. Many others were reported in the Mount Hood Conference [9]. In fact, the American Diabetes Association consensus panel has published a set of guidelines for modeling of Diabetes [6]. Using these computer models, researchers can investigate long-term benefits of early intervention such as reduced prevalence, morbidity, mortality, and costs. Currently, however, parameter uncertainty remains one of the major limitations for such models.

Because most clinical studies do not collect enough data to model every state of interest, modelers have to find a single ‘best’ estimate for each transition in the model from the medical literature and plug that single estimate into a multi-state model of progression, thereby constructing one disease model from many clinical studies. For example, to model the cardiovascular disease (CVD) sub-processes in a diabetes patient, one could use a model as illustrated in Figure 1, which includes five states and eight transition probabilities. Unfortunately, many well-designed studies cannot be used in disease models because the study design is based on a different theoretical model and state-definition than the proposed disease model. For example, the well-known UKPDS group [4, 10, 11] has developed the UKPDS Risk Engine Model for coronary heart disease and published their risk equation [11]. This model has the strength of being based on a single, prospective, longitudinal cohort. However, the UKPDS did not study the risk of progression from no CVD to angina, angina to myocardial infarction (MI), and some other transitions in the above model. Instead it estimated the risk of progression from no CVD to MI. As such, their single estimate is a function of four transition probabilities of interest in our theoretical model: p₀₁, p₀₂, p₁₂, p₁₄. Proper use of the UKPDS data in our theoretical model requires integration between the estimates provided by secondary data analysis and the parameters defining our theoretical model.

Figure 1.

A model of the CVD process within diabetes.

To our knowledge, no previous work has attempted to integrate information from such studies into parameters in the disease models. Using the traditional techniques, modelers cannot use the UKPDS data to model progression of a finer detailed model. Traditional statistical approaches like compartmental analysis, longitudinal models, Markov models, and survival models are limited to use with a single study and, thus, have the limitations discussed above related to the UKPDS study (That is, most clinical studies do not collect enough data to model every state of interest.). Moreover, most traditional statistical approaches do not accommodate grouped states and other consequences of secondary data analysis. Isaman et al. [12] present an approach to multi-state models for discrete-time chronic disease models. Their approach uses supplementary data (such as those that either group states or omits intermediate states) in the likelihood for parameter estimation. Their method differentiates between direct data, which denote the data used to estimate a single transition parameter in a multi-state model of disease progression, and complementary (augmentary) data, which denote the data that arise from a process that is a function of more than one model parameter (i.e. not direct). For example, the UKPDS data described above would be denoted as the complementary data. Isaman et al. [12] uses a likelihood method to produce indirect estimates using complementary data. Using this approach, the data are summary statistics provided by a study, not the raw data collected by a study.

In [12], the authors implicitly assume that the transition probabilities between disease stages are the same for all the subjects. However, study populations of interest are often collections of individuals with varying characteristics, which are potential risk factors for disease progression. For example, the Ovarian Cancer Screening Simulation program [1] is a comprehensive representation of ovarian cancer biology, detection, screening behavior, interventions, and costs in a simulation of a defined population of women. The likelihood of an ovarian tumor occurring and its detection through screening vary, depending on the characteristics of the individual and the intervention that is being considered.

Therefore, it is important to model transition probabilities as a function of characteristics of the individual. One approach is to partition the baseline population into groups of unique individuals and estimate transition probabilities for each partition. If a study provides cumulative counts on different partition, then the partitions can be viewed as independent studies on the restricted population and the methods developed in [12] can be extended to use this information for estimating transition probabilities for each partition.

In addition to the above type of studies, more information may be available in studies like UKPDS, which provides a risk equation. Isaman et al.’s work [12] has been limited to data provided in the medical literature as cumulative counts and is not amenable to utilize information in regression parameters of a risk equation. In particular, the UKPDS CVD model described above provides a risk equation based on not only categorical covariates such as gender, but also continuous covariates such as age and blood pressure. To use this study requires both the ability to adjust for skipped states and the ability to incorporate regression parameters into the estimation procedure. Incorporating regression parameters into the likelihood is complicated due to the fact that the studies being used may not have been designed to estimate the theoretical model of interest. As such, there may be nuisance parameters estimated by the study that are of no interest in the theoretical model being developed. One statistical approach to issues of insufficient data in disease models has been presented by Manton et al. [13, 14]. Manton et al. considered the situation where information regarding covariates was unknown or only known in aggregate. Using conditioning and smoothing, he proposed a method for incorporating this augmentary data. Another approach is to assume a known form for transitions to unknown intermediary states, and use the EM algorithm [15]. However, we have much secondary data available and it should be possible to use these valuable data to evaluate the likelihood and estimate the parameters of interest despite their imperfect study designs.

This paper builds upon Isaman et al.’s results [12] and provides a method for incorporating regression parameters into the estimation of transition parameters for discrete-state discrete-time models of chronic disease. We call this approach the Lemonade Method in the spirit of when study data give you lemons, make lemonade. Examples to investigate the behavior of the Lemonade Method are provided, and we apply the results to a model of diabetic CVD.

2. THE MODEL

Following the approach of [12], we assume that

• (1) the disease process operates as a discrete-time, Markov process,

• (2) the data are independent realizations generated from either the theoretical model, a sub-process, or a grouped process of the theoretical model,

• (3) the data are informative, i.e. there is large enough number of events of interest during the study period to provide informative data, and

• (4) the data are consistent estimates of the parameters they measure.

Note that our data are the summary statistics provided by a study, not the raw data collected by a study. When using complementary data (e.g. grouped nodes or nuisance parameters) in estimation, the distinction between the theoretical model and the study data is critical. We first introduce notation for the theoretical model. Note that the Examples section follows this notation and provides further explanation with details and calculation. Let

(i, j ) denote the path from state i to state j

N denote the number of states in the theoretical model,

P be the N x N transition matrix of the theoretical model.

In [12], the authors implicitly assume that P is the same for all subjects. However, in reality the rate of disease progression is often associated with the demographic covariates such as gender, race, BMI, etc. In this paper, we extend the approach in [12] by modeling transition probabilities as a conditional expectation expressed as a function of covariates in the theoretical model. In this paper the function notation is restricted to multivariate step function representation using categorical covariates (e.g. gender, race, age category). Let

α denote a vector of unknown model parameters to be estimated. Note that each transition in the model may depend upon one or more of the members of this vector,

Z denote the 1xR vector of covariates in the theoretical model, indexed by r; again, note that we use vector form to simplify notation later on. In practice each transition may depend on different covariates,

π_ij(α, Z) denote the unknown transition probability between two states i and j under the theoretical model, with possible dependence on model covariates, i.e. {P}_ij = π_ij(α, Z). Note that this function defines which members of α and Z participate in defining each transition.

While making a distinction between the theoretical model and the study we define the following notation, which depends on the study (indexed by k). Note that for simplicity, in this paper, we assume that a single study provides information on a single transition and therefore its index k will from hereon imply related start and end states. With this in mind, let

T_(k) denote the length of the study period,

Π_(k)ij(α, Z, t) denote the cumulative probability of transition from model state i to model state j by time t restricted by the design of study k. This matrix depends on both the structure of P and the design of the clinical study. To derive it one can rewrite P with appropriate absorbing states to represent the counting process of the clinical study. For details, please see [12, 16].

In addition to accommodating covariates in the theoretical model, we must accommodate two types of studies. The first type provides cumulative counts. Note that if the baseline population is partitioned into groups of unique individuals and estimates are made separately for each partition (by the study), then the partitions can be viewed as independent studies on a restricted population. The method for using information provided by this type of study was developed by Isaman et al. [12] and further extended in [16].

The second type of study provides a risk equation depending on a set of covariates for the transition probability between two states i and j. For example, in the UKPDS study, the risk equation depends on age, gender, race, and blood pressure for the transition probability between no CVD and MI. The focus of this paper is to extend the approach in [12] to integrate information from the second type of study. Let

Y_(k) denote the vector of length S_(k) of covariates measured in study k. Note that Y_(k) and Z do not necessarily overlap. In addition note that the study index _(k) does not denote members of this vector, rather this distinguishes this vector from covariate vectors in other studies,

{Y_(k)m} denote a population data set with M_(k) individuals associated with study k describing the distribution of covariates in the population. Each member of this set Y_(k)m is a vector on its own that is suitable for substituting all the covariates in Y_(k) ∪Z,

λ_(k), ${\widehat{\lambda }}_{\left(k\right)}$ denote the vector of length Q_(k) of unknown parameters associated with Y_(k) and their observed estimates, respectively. For example, the model of the UKPDS study we used in Section 4 is approximately a proportional hazard model; λ_(k) is then approximately the relative risk associated with the risk factors [11],

Σ_(k) denote the estimated variance–covariance matrix of ${\widehat{\lambda }}_{\left(k\right)}$,

F_(k)(Y_(k), λ_(k), t) denote the expected value of cumulative probability of transition from state i to state j as provided by the risk function in study k by time t. Note that the set of covariates used in a particular study Y_(k) do not necessarily overlap with those involved in Π_(k)ij(α, Z, t). In addition note that the indices i and j do not explicitly appear in the notation since study k implicitly indicates this transition.

2.1. Likelihood function and parameter estimation

To integrate information from the second type of study, which provides a risk equation for the transition probability based on covariates, is not as straight forward as for the first type of study (See [12, 16] for details). We describe our strategy as follows.

When the sufficient statistics provided by a study are estimates of regression coefficients and their standard errors, the approximate joint distribution of the observed regression coefficients ${\widehat{\lambda }}_{\left(k\right)}$ is multivariate Normal (λ_(k), Σ_(k)). The standard approach for direct data assumes that the approximate likelihood function of unknown parameters λ_(k) is Normal (${\widehat{\lambda }}_{\left(k\right)}$, Σ_(k)) [17, 18]. Specifically, in our situation, to accommodate complementary data in the form of regression coefficients, the partial likelihood associated with the kth study,

$$L_{\left(k\right)ij}\propto {\left(2\pi \right)}^{-Q_{\left(k\right)}∕2}\mid {\Sigma }_{\left(k\right)}{\mid }^{-1∕2}\text{exp}(-\frac{1}{2}{({\lambda }_{\left(k\right)}-{\widehat{\lambda }}_{\left(k\right)})}^{\mathrm{T}}{\Sigma }_{\left(k\right)}^{-1}({\lambda }_{\left(k\right)}-{\widehat{\lambda }}_{\left(k\right)}))\text{is}\text{a}\text{function}\text{of}{\lambda }_{\left(k\right)}$$

Note that Π_(k)ij (α, Z, t) and F_(k)(Y_(k), λ_(k), t) are the two functions that both model the expected transition probability for a subject with the given characteristics, but conditional on potentially two different sets of covariates. To simplify notations we will refer to Π_(k)ij(α, Z, t) and F_(k)(Y_(k), λ_(k), t) as Π_(k)ij and F_(k) from here on. If λ_(k) can be explicitly written as a function of α, i.e. λ_(k)(α), the above partial likelihood function can be directly integrated into the full likelihood function. For example, assume in a theoretical model, the transition probability from no CVD to angina in 1 year is allowed to differ between gender and subjects younger or older than 65 years of age. Imagine a study that provides a estimated risk equation for the same transition in 1 year, and F_(k) = λ_(k)0+λ_(k)1Gender+λ_(k)2Age, where Age is a continuous variable and Gender is a dichotomous variable. One can easily calculate the transition probability for the four unique populations based on the age and gender distribution in this study. It is not hard to see that in this case λ_(k) can be written as an explicit function of the parameters in this study.

However, in many cases, covariates in Y_(k) are not necessarily of interest in the theoretical model. For example, in the CVD model in Figure 1, the transition probability from no CVD to MI in the theoretical model does not condition on any covariate. But some studies (e.g. UKPDS) might provide a risk equation of covariates such as age and blood pressure for this transition probability. In addition, some of the covariates in the theoretical model might not be considered in these studies.

Because of these discrepancies between F_(k) and Π_(k)ij, in order to use information provided by such risk equations to estimate α in the theoretical model, we first create a mapping from λ_(k) to α. Note that Π_(k)ij(α, Z, t) and F_(k)(Y_(k), λ_(k), t) are two functions that both model the expected transition probability for a subject with given characteristics. Therefore, a good estimator of α should minimize the difference between F_(k)and Π_(k)ij at subject level. Following this logic, we create a mapping from λ_(k) to α through minimizing the sum of squared difference between F_(k) and Π_(k)ij over the study’s population, i.e. we minimize $\Omega ={\sum }_{m=1}^{M_{\left(k\right)}}{(F_{\left(k\right)}({\mathbf{Y}}_{\left(k\right)m},{\lambda }_{\left(k\right)},T_{\left(k\right)})-{\Pi }_{\left(k\right)ij}(\alpha ,{\mathbf{Z}}_m,T_{\left(k\right)}))}^2$, where M_(k) is the total number of subjects in study k.

Because the theoretical model is based on parameters that define unique population categories according to covariates Z, the cumulative transition probability Π_(k)ij is the same within each population category ν = 1,…, V. When model parameters that are involved in Π_(k)ij for each of these population categories are independent, minimizing Ω is equivalent to minimizing ${\Omega }_{\nu }={\sum }_{m_{\nu }=1}^{M_{\left(k\right)\nu }}{(F_{\left(k\right)}({\mathbf{Y}}_{\left(k\right)m_{\nu }},{\lambda }_{\left(k\right)},T_{\left(k\right)})-{\Pi }_{\left(k\right)ij}(\alpha ,{\mathbf{Z}}_{\nu },T_{\left(k\right)}))}^2$ simultaneously, where M_(k)ν is the total number of subjects in the νth population category according to the theoretical model in study k and Y_(k)mν and Z_v are the study and model covariates associated with the m_ν individual in this category.

By differentiating each Ω with respect to α, the α’s that minimize Ω_ν satisfy ${\sum }_{m_{\nu }=1}^{M_{\left(k\right)\nu }}{F}_{\left(k\right)}({\mathbf{Y}}_{\left(k\right)m_{\nu }},{\lambda }_{\left(k\right)},T_{\left(k\right)})∕M_{\left(k\right)\nu }={\Pi }_{\left(k\right)ij}(\alpha ,{\mathbf{Z}}_{\nu },T_{\left(k\right)})$. Let $G_{\nu }\left({\lambda }_{\left(k\right)}\right)={\sum }_{m_{\nu }=1}^{M_{\left(k\right)\nu }}{F}_{\left(k\right)}({\mathbf{Y}}_{\left(k\right)m_{\nu }},{\lambda }_{\left(k\right)},T_{\left(k\right)})∕M_{\left(k\right)\nu }$ and let H_(k)ν(α) = Π_(k)ij(α, Z_ν, T_(k)). These notations create two vectors G(λ_(k)) and H_(k)(α) that simplify the notation of the previous equation set to G_ν(λ_(k)) = H_(k)ν(α) for all ν = 1,…, V or even simpler G(λ_(k)) = H_(k)(α). We now use G in the Delta method to perform a change of variable under the usual regularity conditions. For J, the Jacobian of the transformation of size Q_(k)xR (which depends implicitly on study k), the contribution to the likelihood for the kth study for the transition between state i and state j is

$$L_{\left(k\right)ij}\propto {\left(2\pi \right)}^{-Q∕2}\mid \mathbf{J}{\Sigma }_{\left(k\right)}{\mathbf{J}}^{\mathrm{T}}{\mid }^{-1∕2}\text{exp}(-\frac{1}{2}{(\mathbf{G}\left({\lambda }_{\left(k\right)}\right)-\mathbf{G}\left({\widehat{\lambda }}_{\left(k\right)}\right))}^{\mathrm{T}}{\left(\mathbf{J}{\Sigma }_{\left(k\right)}{\mathbf{J}}^{\mathrm{T}}\right)}^{-1}(\mathbf{G}\left({\lambda }_{\left(k\right)}\right)-\mathbf{G}\left({\widehat{\lambda }}_{\left(k\right)}\right)))$$

Substituting G(λ_(k)) for H_(k)(α) we get the likelihood as a function of α. i.e.

$$L_{\left(k\right)ij}(\alpha )\propto {\left(2\pi \right)}^{-Q∕2}\mid \mathbf{J}{\Sigma }_{\left(k\right)}{\mathbf{J}}^{\mathrm{T}}{\mid }^{-1∕2}\text{exp}(-\frac{1}{2}{({\mathbf{H}}_{\left(k\right)}(\alpha )-\mathbf{G}\left({\widehat{\lambda }}_{\left(k\right)}\right))}^{\mathrm{T}}{\left(\mathbf{J}{\Sigma }_{\left(k\right)}{\mathbf{J}}^{\mathrm{T}}\right)}^{-1}({\mathbf{H}}_{\left(k\right)}(\alpha )-\mathbf{G}\left({\widehat{\lambda }}_{\left(k\right)}\right)))$$

Often, Π_(k)ij and H_(k)(α) will be a function of several parameters α, which will be estimable only in combination with data from other studies in the full likelihood. This method can be further extended to cover more complicated situations. We will discuss this extensions and limitations in the discussion section.

For studies not involving regression parameters, L_(k)ij is defined as in [12]. Briefly, Isaman constructs a study-specific K matrix that transforms the transition matrix of the theoretical model, P, into a transition matrix that is correct for the design of the kth study. This transformation involves a method called designed absorption, and involves pooling transitions from grouped states to define L_(k)ij. In this fashion, the full likelihood for all studies providing information about the model can be calculated as L = Π_k Π_i Π_i L_(k)ij. Using likelihood estimation, our estimates will have the usual properties of MLE’s.

Note that for simplicity and for the sake of focusing on the main topic of this paper, Isaman et al.’s notation [12] has been simplified and adapted specifically to deal with the issue addressed in the paper. Other aspects related to this technique as described in [12, 16] use a slightly different notation.

2.2. Practical considerations

There are several practical considerations when applying this technique. First, the least-squares technique used to associate the study parameters with the model parameters assumes the availability of the population on which the study’s model was developed. These raw data are rarely available; otherwise, we would use the raw data rather than the regression parameters. However, published studies virtually always are published with a table of demographic characteristics of the population. This table should include descriptors for all important covariates in the study’s model. From this table of demographics, we can construct the marginal distribution of the population and use these simulated marginal data in the least-squares expression. Assuming that the study’s model fits the data, the regression parameters are sufficient statistics for the outcome being measured. Interaction effects are captured by the study’s model. Note that the population {Y_(k)m} requires information about not only the study covariates, Y_(k), in the regression equation but also the covariates, Z, in the theoretical model. If Z is a subset of Y_(k), this is automatic. When the population descriptors are not available such as in the reports of the U.S. Renal System [19], the population descriptors may be garnered from national statistics or from populations such as National Health and Nutrition Examination Survey (NHANES).

A second practical consideration is the availability of the covariance matrix of the study’s regression parameters. Usually, regression parameters are published with standard errors or confidence intervals, from which the variances of the estimates can be derived. However, the covariance between regression parameters are often unpublished. In the simulations below, we explore the influence of the covariances in the estimation using the Lemonade Method.

2.3. Computational considerations

Our proposed method quickly becomes computationally intensive. Specific examples and their solutions will be presented below via the examples. Briefly, our computational approach involves the use of symbolic math and numerical analysis techniques. Symbolic math is used to construct the likelihood expression and to calculate the function derivatives as preparation to numerical solution. The use of symbolic math allows accurate depiction of the expression calculated and is generally not limited to the machine precision. However, symbolic techniques may fail when the expression size is large. Moreover, since the expressions generated by the system are general, an analytic solution is not always possible. Thus, numerical techniques are essential.

We used standard numerical analysis techniques such as finite differences to compute the Jacobian and constrained optimization to maximize the likelihood. However, numerical techniques also have limitations: they are limited by floating point number representation defined by the machine precision, and by the solver technique and its parameters and tolerances. When large expressions are generated as in the case of many parameters or studies, then precision issues may be encountered. We addressed issues with precision in a variety of standard and custom methods. Standard approaches included using multiple initial points for each solution and using the log-likelihood rather than the likelihood. We also supplied the numerical solver with symbolic differentiation to improve the accuracy, and solver parameters were manually optimized to find tolerances that enabled convergence. Custom methods included placing safeguards that make sure that symbolic and numeric calculations agree to a tolerance before and after the optimization. With these techniques and safeguards in place, it was possible to derive the results demonstrated below.

To test the computational stability of our approach, we compared our results (using the above numerical techniques) to examples where the exact solution was known in order to estimate the magnitude of the imprecision. For the examples to be presented in section 3, our results using the Lemonade Method agreed with the theoretical values of the probabilities (computed using symbolic math) within the tolerance better than 3e–9. In addition, our technique was compared with an additional set of mockup examples built to test the system. These mockup examples are published with the software prototype online at [20]. In this set of examples there were 38 mockup examples with known answers that generated 122 probabilities as answers. With the above techniques and safeguards in place, our results using the Lemonade Method agreed with the theoretical values within a tolerance smaller than 4e–5. Figure 2 describes the distribution of these errors on a logarithmic scale to demonstrate the rarity of extreme error values. We expect these numerical issues to decrease as computing technology and theory improve.

Figure 2.

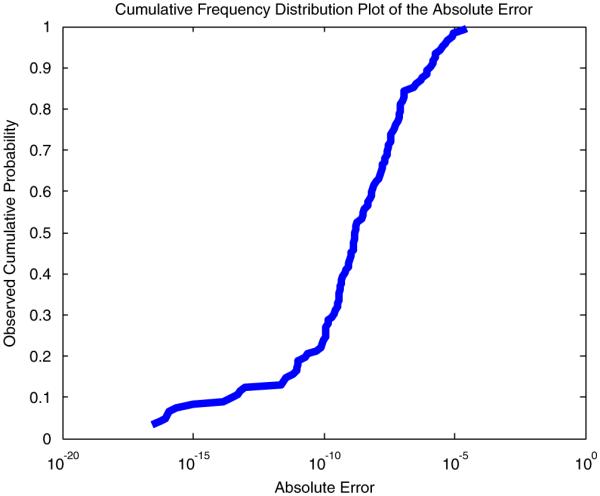
Cumulative frequency distribution plot of computational errors. This graph shows the computational sensitivity of the method considering for 38 mockup examples that generated 122 probabilities as results.

3. EXAMPLES

The properties of our estimates and intuition regarding use of this method will be investigated using a series of simple examples. The first set of examples investigates the bias and efficiency of the Lemonade Method in a simple setting where exact solutions are known. The second set of simulations will investigate the sensitivity of estimates to variance–covariance changes. Finally, we will discuss limitations of the Lemonade Method as illustrated by the simulated examples.

3.1. Base example

For all of the examples, we will work from a ‘base’ model and study as defined below. Our theoretical model has only two states and the parameters of interest are the transition probability between the two states for men and women, respectively. The model is illustrated below in Figure 3. We assume that state 1 is an absorbing state such that p₁₁ = 1 and p₁₀ = 0. In formal terms, the model can be expressed as follows:

Figure 3.

A simple model containing two states and one transition.

N = 2, indicating, two states as can be seen in Figure 3.

α =[p_01f p_01m ], indicating the two unknown coefficients to be estimated

Z = [Gender] and R = 1, indicate a single covariate associated with the model

$${\pi }_{01}(\alpha ,\mathbf{Z})=\{\begin{array}{cc}\hfill & p_{01f}\mid \text{Gender}=0\hfill \\ \hfill & p_{01m}\mid \text{Gender}=1\hfill \end{array}\phantom{\}}$$

indicates the probability to transit from state 0 to state 1, other probabilities are either 0 or 1. The Probability matrix is therefore

$$\mathbf{P}=\left[\begin{array}{cc}\hfill 1-{\pi }_{01}(\alpha ,\mathbf{Z})\hfill & \hfill {\pi }_{01}(\alpha ,\mathbf{Z})\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]=\{\begin{array}{cc}\hfill & \left[\begin{array}{cc}\hfill 1-p_{01f}\hfill & \hfill p_{01f}\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\mid \text{Gender}=0\hfill \\ \hfill & \left[\begin{array}{cc}\hfill 1-p_{01m}\hfill & \hfill p_{01m}\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\mid \text{Gender}=1\hfill \end{array}\phantom{\}}$$

Note that the P matrix is different for male and female.

We will index the study with k = 0 and formally define the study using the following notations:

i = 0 and j = 1 define the start state and end state of the study using model terminology. Π_(0)ij(α, Z, t) will be the model matrix restricted by the study design. In this case, it does not change when the study design is applied on the model since the study end state is the terminal state of the model. To clarify this example, the transition probabilty from state 0 to state 1 after 2 years is extracted from the first row and second column of the matrix P*P and formalized as

$${\Pi }_{\left(0\right)01}(\alpha ,\mathbf{Z},t=2)=\{\begin{array}{cc}\hfill & (1-p_{01f})p_{01f}\mid \text{Gender}=0\hfill \\ \hfill & (1-p_{01m})p_{01m}\mid \text{Gender}=1\hfill \end{array}\phantom{\}}$$

This result is provided here to remind the reader that the model describes the transition probability as a polynomial generated by a Markov Model. For this base example, however, this 2 years result will not be used as the study associated is only 1 year long, i.e. the transition probability to be used is

$${\Pi }_{\left(0\right)01}(\alpha ,\mathbf{Z},t=1)=\{\begin{array}{cc}\hfill & p_{01f}\mid \text{Gender}=0\hfill \\ \hfill & p_{01m}\mid \text{Gender}=1\hfill \end{array}\phantom{\}}$$

T₍₀₎ = 1 i.e. Consider the simple case where the study period is 1 year.

Y₍₀₎ = (Gender, HDL), this means that the study data depend on S₍₀₎ = 2 covariates: Gender and HDL cholesterol.

{Y_(0)m}={(Gender, HDL)}={(0, 1.25) (0, 1.15) (1, 1.25) (1, 1.15)} is the population of M₍₀₎ = 4 individuals associated with the study and represents the distribution on covariate values in it.

λ₍₀₎ = (λ₍₀₎₀, λ₍₀₎₁, λ₍₀₎₂), ${\widehat{\lambda }}_{\left(0\right)}$ = (0.1, 0.2, 0.5) denote the vector of length Q₍₀₎ = 3 associated with the intercept, gender, and HDL, respectively.

Σ₍₀₎ = diag(0.1, 0.1, 0.1) is the reported variance–covariance matrix from study 0. Note that in this simple example the covariance values are set to 0.

F(Y₍₀₎, λ₍₀₎, t) = 1−exp(−(λ₍₀₎₀+λ₍₀₎₁Male+λ₍₀₎₂HDL)t) denote the expected value of the probability provided by the study to move from state 0 to state 1 in time t.

To solve the example above, there is a need to bridge the different formulation between the study and the theoretical model. This is performed by writing the following least-squares equation:

$$\begin{array}{cc}\hfill \Omega =& \sum _{m=1}^{M_{\left(0\right)}}{(F_{\left(0\right)}({\mathbf{Y}}_{\left(0\right)m},{\lambda }_{\left(0\right)},T_{\left(0\right)})-{\Pi }_{\left(0\right)ij}(\alpha ,{\mathbf{Z}}_m,T_{\left(0\right)}))}^2={(1-\text{exp}(-({\lambda }_{\left(0\right)0}+{\lambda }_{\left(0\right)2}\ast 1.25)\ast 1)-p_{01f})}^2\hfill \\ \hfill & +{(1-\text{exp}(-({\lambda }_{\left(0\right)0}+{\lambda }_{\left(0\right)2}\ast 1.15)\ast 1)-p_{01f})}^2+(1-\text{exp}(-({\lambda }_{\left(0\right)0}+{\lambda }_{\left(0\right)1}+{\lambda }_{\left(0\right)2}\ast 1.25)\ast 1)\hfill \\ \hfill & {-p_{01m})}^2+{(1-\text{exp}(-({\lambda }_{\left(0\right)0}+{\lambda }_{\left(0\right)1}+{\lambda }_{\left(0\right)2}\ast 1.15)\ast 1)-p_{01m})}^2\hfill \end{array}$$

Before proceeding, let us examine the equation above. There are two unique population categories in this model, male and female, i.e. V = 2. Accordingly Ω can now be separated into two parts: ν = 1 corresponding to the first two components depending on p_{01 f} and ν = 2 corresponding to the last two components depending on p_01m, each having a quadratic form. Setting each quadratic to zero and solving these equations provide an estimate for female and male, respectively.

This allows finding estimates for the model transition probabilities and therefore bridging between the study and model terminology. This link can be defined in a vector of functions representing male and female transition probabilities:

$$\begin{array}{cc}\hfill \mathbf{G}\left({\lambda }_{\left(0\right)}\right)& \hfill \\ \hfill & =\left[\begin{array}{c}\hfill (1-\text{exp}(-({\lambda }_{\left(0\right)0}+{\lambda }_{\left(0\right)2}\ast 1.25)\ast 1)+1-\text{exp}(-({\lambda }_{\left(0\right)0}+{\lambda }_{\left(0\right)2}\ast 1.15)\ast 1))∕2\hfill \\ \hfill (1-\text{exp}(-({\lambda }_{\left(0\right)0}+{\lambda }_{\left(0\right)1}+{\lambda }_{\left(0\right)2}\ast 1.25)\ast 1)+1-\text{exp}(-({\lambda }_{\left(0\right)0}+{\lambda }_{\left(0\right)1}+{\lambda }_{\left(0\right)2}\ast 1.15)\ast 1))∕2\hfill \end{array}\right]\hfill \\ \hfill & \leftrightarrow \left[\begin{array}{c}\hfill p_{01f}\hfill \\ \hfill p_{01m}\hfill \end{array}\right]={\mathbf{H}}_{\left(0\right)}(\alpha )\hfill \end{array}$$

This vector still depends on vector of unknowns λ₍₀₎ and we can use it to explore the relation between the study and model parameters. We can calculate the estimated values for the model transition probabilities by substituting the study-reported values for the unknowns in this function vector:

$$\begin{array}{cc}\hfill {\mathbf{H}}_{\left(0\right)}\left(\widehat{\alpha }\right)=& \left[\begin{array}{c}\hfill {\widehat{p}}_{01f}\hfill \\ \hfill {\widehat{p}}_{01m}\hfill \end{array}\right]\leftarrow \mathbf{G}\left({\widehat{\lambda }}_{\left(0\right)}\right)\hfill \\ \hfill =& \left[\begin{array}{c}\hfill (1-\text{exp}(-(0.1+0.5\ast 1.25)\ast 1)+1-\text{exp}(-(0.1+0.5\ast 1.15)\ast 1))∕2\hfill \\ \hfill (1-\text{exp}(-(0.1+0.2+0.5\ast 1.25)\ast 1)+1-\text{exp}(-(0.1+0.2+0.5\ast 1.15)\ast 1))∕2\hfill \end{array}\right]\hfill \\ \hfill =& \left[\begin{array}{c}\hfill 0.5033\hfill \\ \hfill 0.5933\hfill \end{array}\right]\hfill \end{array}$$

We can also derive additional information regarding the behavior of this expression around the expected values in the form of the Jacobian:

$$\mathbf{J}\left({\lambda }_{\left(0\right)}\right)=\frac{\partial \mathbf{G}\left({\lambda }_{\left(0\right)}\right)}{\partial {\lambda }_{\left(0\right)}}$$

Although this can be expressed analytically, it is numerically derived around the expected value using finite differences. This results in the following value:

$$\mathbf{J}=\mathbf{J}\left({\widehat{\lambda }}_{\left(0\right)}\right)=\left[\begin{array}{ccc}\hfill 0.4967\hfill & \hfill 0\hfill & \hfill 0.5955\hfill \\ \hfill 0.4067\hfill & \hfill 0.4067\hfill & \hfill 0.4875\hfill \end{array}\right]$$

This allows constructing the Likelihood function for this study:

$$L_{\left(0\right)01}(\alpha )\propto {\left(2\pi \right)}^{-Q_{\left(0\right)}∕2}\mid \mathbf{J}{\Sigma }_{\left(0\right)}{\mathbf{J}}^{\mathrm{T}}{\mid }^{-1∕2}\text{exp}(-\frac{1}{2}{({\mathbf{H}}_{\left(0\right)}(\alpha )-\mathbf{G}\left({\widehat{\lambda }}_{\left(0\right)}\right))}^{\mathrm{T}}{\left(\mathbf{J}{\Sigma }_{\left(0\right)}{\mathbf{J}}^{\mathrm{T}}\right)}^{-1}({\mathbf{H}}_{\left(0\right)}(\alpha )-\mathbf{G}\left({\widehat{\lambda }}_{\left(0\right)}\right)))$$

In logarithmic form this can be written as

$$\begin{array}{cc}\hfill \text{log}\left(L_{\left(0\right)01}(\alpha )\right)=& (28.58\ast p_{01f}+0.3018-24.75\ast p_{01m})\ast (p_{01f}-0.50933)\hfill \\ \hfill & -(-24.75\ast p_{01f}-5.480+30.23\ast p_{01m})\ast (p_{01m}-0.5933)\hfill \end{array}$$

Numerically optimizing the above likelihood expression results in the expected values,

$$\widehat{\alpha }=\left[\begin{array}{c}\hfill p_{01f}\hfill \\ \hfill p_{01m}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 0.5033\hfill \\ \hfill 0.5933\hfill \end{array}\right]$$

and the covariance matrix for $\widehat{\alpha }$ resulting from this optimization is

$$\left[\begin{array}{cc}\hfill 0.0601\hfill & \hfill 0.0492\hfill \\ \hfill 0.0492\hfill & \hfill 0.0568\hfill \end{array}\right]$$

Note that in the absence of other studies, the covariance matrix is equivalent to JΣ₍₀₎J^T.

In this simple case, the above result can be obtained without the likelihood optimization. However, when several studies with varying lengths are involved, this may not be as trivial and the likelihood optimization step is essential to merge information from different studies together.

3.2. Variations on the base example

Based on this example, we considered variations from the base case that vary the number of years, T₍₀₎, followed by the study, and we also considered a larger population (M₍₀₎ = 150), which is comprised of random draws from a Bernoulli(0.5) distribution for Gender and a Normal(1.2,0.1) for HDL. These are presented in Table I.

Table I.

Results for simple examples varying population size and length of study.

Population	Years	$\widehat{p}$01 f	$\widehat{p}$01m	V($\widehat{p}$01 f ) variance	V($\widehat{p}$01m) variance	V($\widehat{p}$01m, $\widehat{p}$01 f ) covariance
N =4	1	0.5033	0.5933	0.0601	0.0568	0.0492
	2	0.5031	0.5932	0.0601	0.0568	0.0492
	3	0.5029	0.5930	0.0601	0.0568	0.0492
N =150	1	0.5023	0.5879	0.0600	0.0573	0.0492
	2	0.5018	0.5875	0.0599	0.0572	0.0491
	3	0.5012	0.5870	0.0598	0.0572	0.0490

The slight difference between estimates for the population of size 4 and the population of size 150 can be explained by the natural variation caused by the sampling error when constructing the marginal distribution of HDL from the Normal distribution. The variance terms are also close to the expected for T₍₀₎ = 1, and do not vary substantially as the sample size increases. This is expected since the influence of the sample size is incorporated into the covariance matrix for the study’s estimates, which we have held constant in these examples.

In the case of our base example for 1 year and a population M₍₀₎ = 4, the expected incidence (variance) is 0.5933 (0.1206) for men and 0.5033 (0.125) for women using Isaman’s method [12]. Isaman’s method, in contrast to the method presented in this paper, requires the user to summarize the study data as the expected cumulative count. As a matter of fact, this method does not incorporate the uncertainty of the regression coefficient in the study into the model parameters. Since it uses the expected cumulative count as if it is the observed count, the estimated variance of the estimated model parameters is directly related to the number of subjects, instead of the covariance matrix of the regression coefficient in the study. Using our transformation approach, we are not only able to obtain a better estimation of the variances by correctly incorporating the uncertainty in the regression coefficient estimates, more importantly, we can also account for the covariance between published estimates if these covariance terms are provided.

Table II and Figure 4 present results obtained from variations on the base example where the variance–covariance matrix Σ₍₀₎ is modified. The example in the first row of Table II annotated ‘Scaling Variance’ demonstrates the influence of the covariance matrix on model results. When using the identity matrix for variance–covariance, the likelihood function was changed (as illustrated in the contour plots of Figure 4(1)) and the variance of estimates increased by a factor of 10, as would be expected.

Table II.

Variations on the base example, varying scale parameters, and covariance.

Test #	Test name	$\widehat{p}$01 f	$\widehat{p}$01m	V($\widehat{p}$01 f ) variance	V($\widehat{p}$01m) variance	V($\widehat{p}$01m,$\widehat{p}$01 f ) covariance
1	Scaling variance	0.5033	0.5933	0.6013	0.5685	0.4923
2	Covariance, c=0.05	0.5033	0.5933	0.0601	0.0734	0.0593
3	Covariance, c=0.07	0.5033	0.5933	0.0601	0.0800	0.0634
4	Covariance, c=0.1	0.5033	0.5933	0.0601	0.0899	0.0694
5	Covariance, c=−0.05	0.5033	0.5933	0.0601	0.0403	0.0391

Figure 4.

Log likelihood plots corresponding to Table II results. The iso-curves at the bottom of each graph are helpful to understand the shape of the log-likelihood function. Note the different scales on the vertical axis and the cross section projections to recognize differences between plots: (0) reference; (1) scaling variance; (2) covariance, c = 0.05; (3) covariance, c = 0.07; (4) covariance, c = 0.1; and (5) covariance, c = −0.05.

The last four examples in Table II and in Figure 4 illustrate the influence of varying the correlation between parameters. Rather than assuming that the regression estimates provided by the study are independent, we used a covariance matrix of the form

$${\Sigma }_{\left(0\right)}=\left(\begin{array}{ccc}\hfill 0.1\hfill & \hfill c\hfill & \hfill 0\hfill \\ \hfill c\hfill & \hfill 0.1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0.1\hfill \end{array}\right)\text{where}c\in \{0.05,0.07,0.1,-0.05\}$$

The correlation between λ₍₀₎₁ and λ₍₀₎₂, c, varied from c = −0.05 to c = 0.1. Because of the parameterization used, the correlation does not change the variance of ${\widehat{p}}_{01f}$ since λ₍₀₎₁ is the indicator for male gender. However, the variance for ${\widehat{p}}_{01m}$ increases with c as well as the covariance between ${\widehat{p}}_{01f}$ and ${\widehat{p}}_{01m}$. The influence on the likelihood function can be seen in Figures 4(2)–(5). It can be seen that the estimated probability does not change, yet the likelihood function changes its shape as the variance dictated by (JΣ₍₀₎J^T) changes.

Note that in all the examples presented in Table II, the final estimated probabilities are similar since the peak of the likelihood function does not change. However, when this datum is combined with the data arriving from another study, the changes in the variances may lead to different results. The difference will arise from the different shape of the likelihood function that in combination with another likelihood function generated for another study may create a different peak and hence a difference in estimates.

Understanding the influence of correlation on the variances of estimates is important because often when data are available only as regression coefficients, the full covariance matrix Σ₍₀₎ is unavailable. Covariance terms may not be reported in the literature. In this case, the Lemonade Method produces liberal confidence intervals. Further work is needed to minimize the influence of this missing information on covariances. In addition, we encourage the clinical researchers to publish the correlation between their estimates, perhaps in an appendix.

4. APPLICATION

In this section we present a model of progression of CVD in people with type 2 diabetes. The CVD model is a part of a larger model of diabetes progression published previously [3]. The theoretical model, describing the disease progression, was chosen in collaboration with the clinical investigators, and the data were extracted from the medical literature after an extensive literature review. This review provided us with the best available literature providing primary and augmentary estimates for the model. We desired to use the method in [12] to combine these data into a single model of diabetes progression; however, one important study, the UKPDS [11], provided a risk equation rather than the cumulative counts. In this section, we use the UKPDS risk equation in combination with the cumulative counts from other studies to compute estimates of CVD progression. We then compare those results with the results generated by summarizing the UKPDS risk engine as cumulative counts using Isaman et al.’s method.

The theoretical model for CVD has five states, ordered 0 to 4 respectively for No CVD, Angina, MI, History of MI, and Death from CVD. Figure 1 depicts the model as boxes and the model transitions using dark thick arrows. An MI is depicted as a rhombus and is defined as an event such that patients pass through MI and either die or enter a state called ‘history of MI’. The parameters of interest, π_ij(α, Z), are denoted by the initial and terminal states of transfer, i.e. α =[p₀₁, p₀₂, p₁₂, p₁₄, p₂₃, p₃₂, p₃₄], Z = ϕ. For example p₀₁ denotes the probability of progression from state 0 to state 1. Note that the model supports MI recurrence in individuals with History of MI ( p₃₂) and note that p₂₄ = 1− p₂₃.

Figure 5 extends Figure 1 and contains information about the existing studies in the literature. Study paths are presented as dotted pale arrows. The study paths are interpreted to connect the proper states using the model terminology. The study paths are depicted by Letters A–G. Each such transition may represent one or more studies. Detailed information about the studies and the form of the data provided is presented in Table III. The path letters on the first column in the table correspond to the transitions in the figure.

Figure 5.

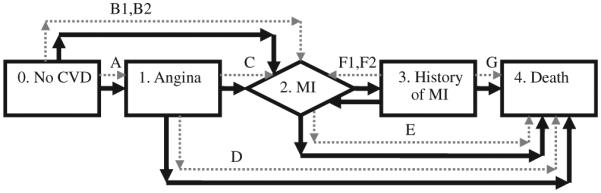
The CVD model in dark thick lines and associated studies in dotted pale arrows.

Table III.

Clinical studies used to estimate parameters of the CVD model.

Study index k	Transition	Population count M(k)	Incident count	Years	Annualized	Reference
1	A: 0 to 1	1138	72	10	0.0065	UKPDS 33, 1998 [21]
2	B1: 0 to 2	890	180	7	0.0318	Haffner, 1998 [22]
3	B2: 0 to 2	4540	See UKPDS risk equation	10		Stevens, 2001 (UKPDS 56) [11]
4	C: 1 to 2	569	61	2	0.0551	Malmberg, 2000 [23]
5	D: 1 to 4	569	53	2	0.0477	Malmberg, 2000 [23]
6	E: 2 to 4	437 (male) 183 (female)	197 71	1	0.4508 0.3880	Miettinen, 1998 [24]
7	F1: 3 to 2	73 (male)	13	1	0.1781	Ulvenstam, 1985 [25]
			20	2	0.1479
			34	5	0.1178
8	F2: 3 to 2	169	76	7	0.0818	Haffner, 1998 [22]
9	G: 3 to 4	256 (male) 147 (female)	79 58	5	0.0711 0.0955	Lowel, 2000 [26]

Each study provides the following information: (1) the study index, (2) the transition reported by the study presented using the model terminology, (3) initial population count, (4) the cumulative incident count reaching the end state at the end of the study, (5) the study length in years for which incident counts were reported, (6) the annualized rates that were calculated from this information for comparison with model results, and (7) the reference from where the data were extracted.

The data extracted from the medical literature are presented in Table III. Note that several of the studies provide gender-specific data that do not appear in the model.

Incorporating the UKPDS risk engine into the estimation procedure requires additional information. The UKPDS provides us with a risk equation that has the form

$$\begin{array}{cc}\hfill F_{\left(3\right)}=& 1-\text{exp}(-{\lambda }_{\left(3\right)1}{{\lambda }_{\left(3\right)2}}^{(\text{AGE}-55)}{{\lambda }_{\left(3\right)3}}^{(1-\text{Male})}{{\lambda }_{\left(3\right)4}}^{(1-\text{WHITE})}{{\lambda }_{\left(3\right)5}}^{\left(\text{SMOKE}\right)}\phantom{)}\hfill \\ \hfill & \phantom{(}\times {{\lambda }_{\left(3\right)6}}^{(\text{BP}-135.7)∕10}\left(\frac{1-{{\lambda }_{\left(3\right)7}}^{\mathrm{T}\left(3\right)}}{1-{\lambda }_{\left(3\right)7}}\right))\hfill \end{array}$$

Although we cannot modify the form of the equation provided by the UKPDS, we have simplified the equation for our example, assuming that the population has Hemoglobin A1C and Lipid ratios at the population average modeled by the UKPDS. The parameter coefficients, published by the UKPDS, are

$$\begin{array}{cc}\hfill {\widehat{\lambda }}_{\left(3\right)}=& \left[0.01121.05900.52500.39001.35001.08801.078\right]\hfill \\ \hfill {\Sigma }_{\left(3\right)}=& \text{diag}(2.0408\ast {10}^{-6},3.1497\ast {10}^{-5},0.0028699,0.010412,\hfill \\ \hfill & 0.014994,0.00070387,0.00026656)\hfill \end{array}$$

For this example, we assume that the covariance between estimators is 0.

Thus, the partial likelihood contributed by the UKPDS is

$$L_{\left(3\right)02}\propto {\left(2\pi \right)}^{-7∕2}\mid {\Sigma }_{\left(3\right)}{\mid }^{-1∕2}\text{exp}(-\frac{1}{2}{({\lambda }_{\left(3\right)}-{\widehat{\lambda }}_{\left(3\right)})}^{\mathrm{T}}\Sigma {\left(3\right)}^{-1}(\lambda \left(3\right)-\widehat{\lambda }\left(3\right)))$$

prior to application of our transformation of variable. The cumulative function under our theoretical model (illustrated in Figure 5) is a function of several unknown parameters p₀₁, p₀₂, p₁₂, p₁₄ ∈ α, and has no overlap with covariates Y₍₃₎ of the UKPDS. Using Isaman’s method of designed absorption, the terminal state of the UKPDS (MI) is treated as a sink and matrix multiplication of a study-specific transition matrix maps π₀₂ to the transition probabilities.

The model probability matrix specific to this study is therefore

$${\Pi }_{\left(3\right)}(\alpha ,\mathbf{Z},t)={\left[\begin{array}{ccccc}\hfill 1-p_{01}-p_{02}\hfill & \hfill p_{01}\hfill & \hfill p_{02}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1-p_{12}-p_{14}\hfill & \hfill p_{12}\hfill & \hfill 0\hfill & \hfill p_{14}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill p_{32}\hfill & \hfill 1-p_{32}-p_{34}\hfill & \hfill p_{34}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]}^t$$

Least squares was used to map between Π₍₃₎₀₂ and F₍₃₎₀₂. To conduct this least-squares fit, we used the marginal distributions for covariates as published in Table 1 of [11] to generate a random population of 4540 people representing the UKPDS sample. Using these data, we calculated estimates for the CVD model using the Lemonade Method. The results are displayed in Table IV.

Table IV.

Estimation results for the CVD model.

	Using incident counts for the UKPDS		Using the UKPDS risk equation
	Point estimate	Standard Error	Point estimate	Standard Error	Difference of model estimates
$\widehat{p}$ 01	0.0070	0.0008	0.0071	0.0008	1.60E–04
$\widehat{p}$ 02	0.0119	0.0006	0.0218	0.0014	9.93E–03
$\widehat{p}$ 12	0.0569	0.0069	0.0549	0.0068	−2.00E–03
$\widehat{p}$ 14	0.0225	0.0072	0.0237	0.0072	1.21E–03
$\widehat{p}$ 23	0.5686	0.0199	0.5688	0.0199	1.61E–04
$\widehat{p}$ 32	0.1032	0.0088	0.1032	0.0088	3.81E–06
$\widehat{p}$ 34	0.0362	0.0070	0.0362	0.0070	9.39E–06
−Log (L)	4277.75		1993.67

For comparison, the first column presents point estimates for the transition probability obtained for the model when UKPDS outcomes in study B2 were represented as a table of incident counts. The incident counts were estimated by using the expected value of the UKPDS risk engine formula for men and for women separately by using the mean substitution of averages defined in Table 1 in [11] and rounding the obtained number. The expected incident counts for 2643 men and 1897 women respectively are 49, 105, 169, 241, 322 and 21, 45, 73, 104, 140 for 2, 4, 6, 8, and 10 years. This approach using incident counts is used for reference, to demonstrate the existing approach. The second column contains results obtained by using the method described in this paper using the UKPDS risk function.

Comparing results with and without the UKPDS risk function shows changes between estimates that are related to Π₍₃₎₀₂; $\widehat{p}$₀₁, $\widehat{p}$₀₂, $\widehat{p}$₁₂, $\widehat{p}$₁₄ ∈ $\widehat{\alpha }$. The parameter most influenced by the change was $\widehat{p}$₀₂. This is not surprising as this is the parameter most clearly related to the UKPDS (which estimates progression from state 0 to state 2).

Note that some ambiguity may be created when using study information with our model. For example, in the UKPDS risk engine study sudden death cases were counted as CHD events. Sudden death cases are defined by as death cases with the unknown reasons (ICD9 code 798.9) and are therefore difficult to match with our theoretical model. For example in our model, a transition is possible from angina directly to death. For simplicity, we assume that these kinds of deaths are excluded from the UKPDS risk engine outcome and that the incident counts are associated with state 2 (MI). Another assumption we make is that the number of sudden deaths is small and therefore does not create a significant bias.

The computational errors for the above application example were estimated using a mockup example we created that simulates the problem under known and ideal conditions. The mockups were created by employing the following steps:

1. Assigning known transition probability values to all unknown probabilities and therefore effectively creating the transition probability matrix.

2. For each study,

   1. 2.1. The transition probability matrix was modified to reflect proper absorption states.

   2. 2.2. The probability matrix was used to calculate what portion of the population reaches the end state at the end of the study.

   3. 2.3. Special treatment was created for regression studies, where study parameters were solved symbolically using a known predefined population to calculate the values that will produce a certain known transition probability associated with the study. For example for the UKPDS regression study, we adjust the intercept so that the marginal transition probability for the known simplified population matched the assigned mock up value.

3. The above calculated values were used as input data to estimate model parameters.

4. The estimation results were analyzed and compared with the assigned probabilities generated at the beginning of the mockup to deduce estimability and accuracy of our calculations for this model.

Table V shows the results of using a mockup model. The mockups used the exact same model with a simplified small population set. The results of the estimation engine were compared with the exact results expected for these mockups. For these two mockup models, the errors in the probability numbers were smaller than 7e–8 in all cases. Although this number may be different for the real-non-mockup examples, it provides some estimate of the accuracy of the calculations in ideal simplified conditions similar to the actual models.

Table V.

Mockup accuracy for the CVD model.

		Using incident counts for the UKPDS		Using the UKPDS risk equation
	Mockup probability values	Absolute Error	Relative Error	Absolute Error	Relative Error
$\widehat{p}$ 01	0.005	−8.8E–12	−1.8E–09	−1.2E–11	−2.5E–09
$\widehat{p}$ 02	0.03	1.85E–11	6.16E–10	−3.8E–11	−1.3E–09
$\widehat{p}$ 12	0.05	4.29E–10	8.58E–09	2.3E–10	4.6E–09
$\widehat{p}$ 14	0.05	3.48E–09	6.96E–08	1.08E–09	2.16E–08
$\widehat{p}$ 23	0.8	8.32E–09	1.04E–08	−3.3E–09	−4.2E–09
$\widehat{p}$ 32	0.1	−3.1E–10	−3.1E–09	−2.2E–09	−2.2E–08
$\widehat{p}$ 34	0.08	2.3E–09	2.88E–08	−1.1E–10	−1.4E–09

The first two columns represent the model input probabilities which are also the expected estimation results. The following columns show the accuracy of the estimation engine from these expected results for both models.

5. DISCUSSION

As disease models become increasingly important in health care and clinical decision making, statisticians need to be involved in the methods used for estimation. Currently, there are very few statistical methods available for researchers developing multi-state models from a variety of clinical studies. The Lemonade Method provides a step toward the statistical integration of available data into a multi-state or multi-process model.

Our use of the delta method for parameter estimation is novel because in most statistical applications, the data collected are designed to measure the parameters of interest. The complication that arises in the secondary data analysis is that the data rarely measure exactly the parameters of interest. If the data do directly measure the parameters of interest, our technique is not necessary and an ordinary meta-analysis can be conducted. However, in our application, the data are not direct estimates. Thus, a change of variable allows us to estimate the parameters of interest.

The use of regression parameters in the estimation procedure has several benefits. First, it uses the best results available to researchers in the form presented. More importantly, the use of regression parameters allows us to use the covariates measured in a study and summarized in a risk function. As such, we can use the data as they are presented in the literature. We also have the potential to use the covariance matrices of published regression coefficients to provide a more appropriate variance estimate of our parameter estimates.

When using the secondary data analysis, publication bias is a common concern. However, models of disease progression and complication are generally less prone to publication bias than many other techniques using meta-analysis because the data are drawn from population-based studies (such as the UKPDS or Framingham), national registries (such as SEER or USRDS), or from the control arm of clinical studies (such that publication bias would imply conservatively low estimates). In addition, a risk equation or a model is not in the form of a single number (usually a relative risk) whose magnitude might directly influence publication decisions. Although, when it comes to covariates, spurious covariate effects will be published often due to random chance as a part of a larger model. When a number of studies that provide risk equations are used, such spurious effect would be expected to be insignificant in the final model. Thus, models of disease progression are an application where using the published data could be advantageous.

The Lemonade Method has potential for generalization. For example, although we limited ourselves to examples with binary covariates, our approach generalizes to accommodate any categorical covariates. In addition, our current implementation is limited in the sense that it requires the unknown cumulative transition probabilities to be independent for each population category. This independence can be satisfied by the user who creates the model. Relaxing this limitation is a future research direction. Moreover, this technique can be generalized for transition probabilities as a function of both categorical and continuous covariates. This generalization will allow disease models to use functions in the multi-state models as Manton and Stallard suggested in [27]. This approach can also be generalized in the future to accommodate more sophisticated models such as random effects.

An important limitation of this technique is computational feasibility. Several techniques to improve the computational burden of this method have been mentioned previously. It is important to note that numerical difficulties were observed and resolved during this research. As the number of parameters being estimated increases and as the number of studies grows, the computational burden will grow. However, as technology improves and more research is invested in these problems, the difficulties should lessen. The migration of the program to an environment with increased accuracy such as an environment using quad precision [28] or variable precision arithmetic [29] may decrease the numerical difficulties. In addition, the improvement of the symbolic math techniques may improve the accuracy, and the numerical methods such as Gaussian quadrature may improve the computational efficiency. Despite the computational difficulties encountered, we were able to cope with these issues. Computation time was negligible compared with the data collection time and even data entry to the system. Computations were completed in minutes at worst and in seconds for the simpler examples. Examples similar to those provided in the paper are available online for reference [20].

Note that our method reduces to a simple form of conventional meta-analysis when (1) there is only one transition of interest, (2) there are several studies that all provide incidence rate or transition probability for this transition, and (3) all studies measure exactly the states of interest the trivial case where the theoretical model is identical to the published models). In the future we hope to accommodate random effects in our approach as a less naive approach to meta-analysis, but this would require far greater amounts of available data estimating each transition. Moreover, we expect that estimability under a random effects model would require numerous studies using the exact same state definitions. Currently we have neither the technology nor the data to correctly model random effects of our parameter estimates.

In summary, we have presented a new approach for incorporating secondary data into the disease models where a longitudinal study is not feasible. We have demonstrated that the approach is unbiased and efficient, as expected for a likelihood technique. We presented a clinical example where the approach was useful and provided better information than the previous approaches allow. Thus, The Lemonade Method has been shown to be flexible and well behaved, providing a new technique for modelers of chronic diseases.

The Software Prototype implementing the approach in this paper has been released under the GPL license and can be downloaded from the project web site at [20].