Abstract
The heat-shock response is a key factor in diverse stress scenarios, ranging from hyperthermia to protein folding diseases. However, the complex dynamics of this physiological response have eluded mathematical modeling efforts. Although several computational models have attempted to characterize the heat-shock response, they were unable to model its dynamics across diverse experimental datasets. To address this limitation, we mined the literature to obtain a compendium of in vitro hyperthermia experiments investigating the heat-shock response in HeLa cells. We identified mechanisms previously discussed in the experimental literature, such as temperature-dependent transcription, translation, and heat-shock factor (HSF) oligomerization, as well as the role of heat-shock protein mRNA, and constructed an expanded mathematical model to explain the temperature-varying DNA-binding dynamics, the presence of free HSF during homeostasis and the initial phase of the heat-shock response, and heat-shock protein dynamics in the long-term heat-shock response. In addition, our model was able to consistently predict the extent of damage produced by different combinations of exposure temperatures and durations, which were validated against known cellular-response patterns. Our model was also in agreement with experiments showing that the number of HSF molecules in a HeLa cell is roughly 100 times greater than the number of stress-activated heat-shock element sites, further confirming the model’s ability to reproduce experimental results not used in model calibration. Finally, a sensitivity analysis revealed that altering the homeostatic concentration of HSF can lead to large changes in the stress response without significantly impacting the homeostatic levels of other model components, making it an attractive target for intervention. Overall, this model represents a step forward in the quantitative understanding of the dynamics of the heat-shock response.
Introduction
The heat-shock response is a cellular-level regulatory mechanism to mitigate the cytotoxic effects of damaged or misfolded proteins. In addition to heat stress, a variety of other physiological stressors can lead to the accumulation of misfolded proteins in the cell. Therefore, despite its name, the heat-shock response is important not just in hyperthermia but also in many other scenarios, such as toxic chemical exposure (1), aging (2), cancer (1,3), protein folding diseases (4), and gene therapy (5). By improving our knowledge and understanding of the heat-shock response, progress may be made in all of these areas (6).
Dating back to the discovery of the heat-shock response in the 1960s (7), there has been much interest in unraveling its molecular mechanisms. It is now known that the core of the heat-shock response is the activation of the transcription factor for heat shock, known as the heat-shock factor (HSF), leading to the production of heat-shock proteins (HSPs), which serve to ameliorate the effects of accumulated misfolded proteins (MFPs) (2,8,9). However, experiments have also found a great deal of complexity in the regulation of the heat-shock response. The amount of HSF activated in response to hyperthermia is extremely sensitive to small changes in temperature (10), and the relationships between temperature, exposure duration, and damage, are nonlinear (11). Furthermore, there are many molecular pathways that regulate the extent of the response (2,12) in a tissue-specific manner (12,13).
The importance of understanding the heat-shock response and the complexities involved in doing so have motivated the development of mathematical models. For example, we believe that Peper et al. (14) constructed the first model of the heat-shock response and used it to investigate mechanisms of thermotolerance without including a detailed description of transcriptional regulation. In contrast, Rieger et al. (15) studied the dynamics of HSP expression and HSF regulation in more detail to identify the critical steps in the regulatory control. This work was recently extended in the models of Petre et al. (16) and Szymańska and Zylicz (17) to further investigate the dynamics of the response, sensitivities of parameters, and interrelations between molecular species. A major drawback of these prior models is the limited number of comparisons with experimental data, both in terms of parameter identification and model validation. Without rigorous comparisons between models and data, such works serve as useful tools to conceptualize the dynamics of the heat-shock response, but are limited in their quantitative and predictive capabilities.
In the literature, copious data exist on the heat-shock response for a variety of experimental conditions. We leveraged these data to develop a mathematical model of the heat-shock response starting from the model of Petre et al. (16). By restricting our analysis to experiments studying hyperthermia in HeLa cells in vitro, we obtained a collection of relatively consistent data suitable for the development of a coarse biochemical model. Constructing a model that would be consistent with these data required the incorporation of several molecular mechanisms, such as temperature-dependent transcription, translation, and HSF oligomerization, as well as the representation of HSP mRNA, that were not included in prior models of the heat-shock response. However, their inclusion is justified by the literature to describe specific responses, such as temperature-varying DNA binding dynamics, the presence of free HSF during homeostasis and the initial phase of the heat-shock response, and HSP dynamics in the long-term heat-shock response. By successfully calibrating our model with a wide range of experimental data from several different research groups, we semiquantitatively demonstrated its ability to capture these relevant molecular mechanisms. We performed model validation by comparing the predictions of our model with a previously derived relationship between time and temperature of exposure obtained from a wide variety of experimental models (11). Finally, a sensitivity analysis revealed potential targets to modulate the stress-induced levels of key components of the heat-shock response while maintaining normal homeostatic function. This model represents a step forward in the quantitative understanding of the dynamics of the heat-shock response, and lays a foundation for future work investigating further regulatory intricacies.
Materials and Methods
Model structure
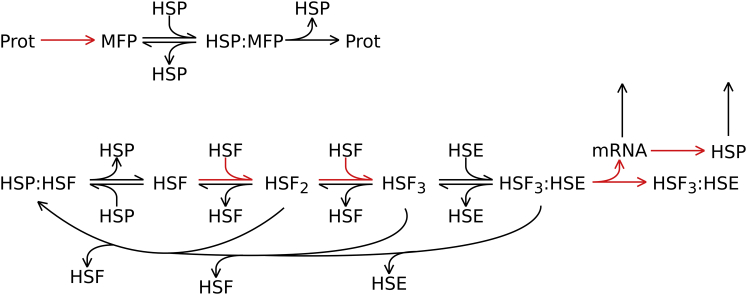
The core of the heat-shock response is the stress-induced activation of the heat-shock transcription factor (HSF), leading to the production of HSPs, which have dual roles of limiting damage caused by a stressor and acting as a negative feedback regulator of HSF. Fig. 1 shows the network diagram of our model, which comprised 11 molecular species (Table 1), 14 reactions (Eqs. 1–14), and 25 parameters (Table 2). We based our model heavily on the previously published model of Petre et al. (16), but with some critical changes, which are detailed below.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
Figure 1.
Network diagram of the heat-shock response model. Highlighted reactions (red or gray) are those that have explicit temperature dependences, as described by Eqs. 15, 19, and 20. (HSE, heat-shock element; HSF, heat-shock factor; HSP, heat-shock protein; MFP, misfolded protein; mRNA, heat-shock protein messenger RNA; and Prot, healthy protein.) To see this figure in color, go online.
Table 1.
Species in the heat-shock response model
| Species | Description |
|---|---|
| HSF | heat shock factor |
| HSF2 | HSF dimer |
| HSF3 | HSF trimer |
| HSE | free heat-shock element (HSE) site on DNA |
| HSF3:HSE | HSF3 bound to HSE |
| mRNA | mRNA of heat-shock protein |
| HSP | free heat-shock protein |
| HSP:HSF | HSP bound to HSF |
| Prot | healthy protein |
| MFP | free misfolded protein |
| HSP:MFP | HSP bound to misfolded protein |
Table 2.
Model parameters and total amounts of conserved species
| Parametera | Value | Units |
|---|---|---|
| k1f | 5.13 × 10−3 | mL/n/s |
| k1r | 8.58 × 10−2 | 1/s |
| k2f | 7.97 × 10−5 | mL/n/s |
| k2r | 6.42 × 10−3 | 1/s |
| k3f | 2.21 × 10−1 | mL/n/s |
| k3r | 1.49 × 103 | 1/s |
| k4 | 1.85 | 1/s |
| k5 | 1.26 × 10−5 | 1/s |
| k6 | 1.70 × 10−4 | 1/s |
| k7f | 6.38 × 101 | mL/n/s |
| k7r | 3.42 × 103 | 1/s |
| k8 | 2.47 × 101 | mL/n/s |
| k9 | 1.53 × 10−2 | mL/n/s |
| k10 | 4.73 × 10−1 | mL/n/s |
| k11 | 3.22 × 10−4 | 1/s |
| k13f | 2.19 × 10−2 | mL/n/s |
| k13r | 6.49 × 102 | 1/s |
| k14 | 4.04 × 101 | 1/s |
| kS1 | 1.65 | none |
| kS2 | 4.11 × 101 | °C |
| kS3 | 7.97 × 10−1 | none |
| kS4 | 4.08 × 101 | °C |
| Total HSF (HSF0) | 5.19 × 103 | n |
| Total HSE (HSE0) | 7.34 × 101 | n |
| Total Prot (Prot0) | 9.88 × 108 | n |
Here, n, number; HSF, heat-shock factor; HSE, heat-shock element; Prot, healthy protein.
kif and kir denote forward and reverse reaction rates, respectively, for the ith equation number (i = 1,2,…14 for Eqs. 1–14, respectively) if the reaction is reversible. Otherwise, the reaction rate for the ith equation number is given by ki. See Eqs. 19 and 20 for the terms ks1–ks4.
The heat-shock response is initiated by a stressor, hyperthermia in this case, leading to the conversion of healthy proteins (Prots) into misfolded proteins (MFPs) via Eq. 12. In this model, no distinction was made between different types of healthy and misfolded protein, so Prot and MFP represent lumped variables across all of the proteins in a cell. We used Eq. 15, which was obtained from calorimetry data in Lepock et al. (18) and gives the specific dependence of protein misfolding on temperature, to specify the temperature-dependent reaction rate (φT) for Eq. 12. This is consistent with prior models of the heat-shock response (14,16). In Eq. 15, T represents the temperature (in °C), with a default homeostatic value of 37°C:
| (15) |
Free MFPs form HSP:MFP complexes with free HSP (see Eq. 13), which may facilitate the refolding of MFP back to Prot (see Eq. 14). However, in homeostasis, much of the cell’s HSPs are in the inactive form as HSP:HSF complexes. As MFPs are produced in response to elevated temperatures, HSP:HSF complexes break down (see Eq. 7) as MFP competes with HSF for HSP binding. This frees HSF to form activated trimers that can bind to heat-shock elements (HSE) on the DNA (HSF3:HSE) (see Eqs. 1–3). Binding of the activated transcription factor to DNA leads to the production of HSP and, consequently, there is an increased concentration of free HSP available to bind to both MFP and HSF. Eventually, when sufficient amounts of HSP are produced relative to its substrates, it will again sequester HSF in inactive HSP:HSF complexes. In this manner, the magnitude of the stress response is tuned based on the amount of misfolded proteins, and the response self-regulates when sufficient amount of HSP has been produced.
Based on the reactions shown in Eqs. 1–14, we specified conservation relationships in our model for three species (total HSF, total protein, and total HSE sites in Eqs. 16–18, respectively), thereby defining a unique homeostatic steady state at T = 37°C:
| (16) |
| (17) |
| (18) |
The above description of our model is consistent with the model of Petre et al. (16), which is the basis of our work. In addition, we made several data-driven modifications to the model:
-
1)
We added an mRNA variable to represent the mRNA of HSP (Eqs. 4–6) rather than assuming that activation of the transcription factor directly leads to HSP production. This is important because HSP mRNA can persist for several hours after transcription ends, accounting for patterns of HSP production that cannot otherwise be reconciled with HSF activation data.
-
2)
We used the sigmoidal term (S1) shown in Eq. 19 to scale the rates of transcription and translation in Eqs. 4 and 6, based on experimental evidence that both transcription and translation rates diminish when cells are exposed to very high temperatures (19,20):
| (19) |
A similar sigmoidal relationship between temperature and translation in the heat-shock response was previously explored in the model of Rieger et al. (15).
-
3)
We used the sigmoidal term (S2) shown in Eq. 20 to scale the rates of the HSF oligomerization reactions in Eqs. 1 and 2, based on the known temperature dependence of HSF oligomerization potentially caused by multiple molecular mechanisms (2):
| (20) |
The need for these modifications to the model is detailed in the Results, where model simulations are compared against a variety of experimental data from prior studies. The formulas for S1 and S2 do not have mechanistic origins. They are phenomenologically derived sigmoid functions designed to mimic observed experimental results of molecular species in the model. S1 is meant to account for the fact that both transcription and translation rates diminish when cells are exposed to very high temperatures (19,20). S2 represents the effect of temperature on HSF oligomerization, which could plausibly be caused by several mechanisms (2). A larger model would be required to potentially derive more-mechanistic representations of these effects. The parameters in the equations for S1 and S2 were fit along with the reaction rate parameters as described in the Parameter Estimation, below. This was ultimately done because, as discussed above, S1 and S2 do not have precise biological meaning and direct experimental data were not available. Hence, their fit to the available experimental data is only meaningful in that their presence allows the entire model to fit all of the experimental data shown in Results.
In total, the 11 differential equations used to simulate the 11 species in our mass action kinetics model are given below:
Comparisons with experimental data
We obtained the experimental data for the model, shown and described in detail in Results, for a variety of heat-stress conditions from Abravaya et al. (10), Theodorakis and Morimoto (19), Andrews et al. (21), Baler et al. (22), Kline and Morimoto (23), Mosser et al. (24), Shi et al. (25), and Stege et al. (26). All data in these studies were from experiments involving HeLa cells exposed to hyperthermia.
In our model, we included only one HSP variable to represent all HSPs. In reality, there are multiple HSPs, typically grouped by their molecular masses. The HSP model variable was intended to represent the collective action of all HSPs. However, separate measurements for all of the different HSPs are generally not available. Therefore, data for 70-kDa HSP (Hsp70) were used to calibrate the HSP variable in our model because Hsp70 data were the most abundant and well characterized. The HSF variable in our model represented the HSF1 transcription factor. Although there are several other isoforms of HSF, HSF1 is the primary regulator of the response to stressors such as elevated temperature.
All of the published experimental data used here was qualitative, which complicated the comparison of model output to data. For most of the data, all that could be done was to run the model for the same temperature stimulus as in the experiment and then scale both the experimental data and model output so that they had the same peak value. However, in some cases, it was possible to derive additional information from the experimental datasets. When multiple experiments in the same article were reported on the same scale (10,25), data and model output were normalized together for all of those experiments/simulations by scaling them relative to the overall maximum peak values. Additionally, due to the fact that HSF1 levels remain constant during heat stress, studies measuring HSF in its different complexes (free, trimerized, and bound to HSP) (22) were collectively scaled with a denominator equal to the total amount of HSF in the experimental data or the model simulation. A complete implementation of the data normalization process can be found in Model S1 in the Supporting Material.
Parameter estimation
We estimated the model parameters based on the data and normalization described above. The parameters in the model include reaction rates corresponding to the reactions in Eqs. 1–14 (kif for forward rate and kir for the reverse rate if the reaction is reversible and ki otherwise, where i is the reaction number), temperature constants that define the sigmoidal functions in Eqs. 19 and 20, and the initial concentrations of the conserved species in Eqs. 16–18. To start, we fixed the model parameters and performed simulations for each experimental study. Next, we computed the objective function as the sum of the squared errors between the model outputs and the experimental data from all studies. Finally, we minimized this objective function using a pattern-search algorithm available in the software MATLAB (The MathWorks, Natick, MA: via the PATTERNSEARCH function). This algorithm was observed to produce a lower value of the objective function than the other global optimization algorithms available in MATLAB. Briefly, the PATTERNSEARCH algorithm works by iteratively searching within a mesh surrounding an established local optimal point in the parameter space to identify the next local optimal point. By repeating this procedure, the pattern-search algorithm identifies a path toward the optimal solution in the parameter space. In the optimization process, all of the parameters shown in Table 2 were allowed to vary. For each set of parameters generated during the optimization, the model was allowed to reach steady state before hyperthermia was applied, thus ensuring that all simulations were done for heat-shock response models at homeostatic 37°C steady states before heating.
Sensitivity analysis
We performed a local one-at-a-time sensitivity analysis to identify parameters and initial conditions that most influence model outputs, using the same procedure as prior models of the heat-shock response (15,16). We computed the sensitivity coefficients (si,j) for each combination of output metrics [fi(x,T)] and parameters (pj) in Eq. 21,
| (21) |
where p represents the vector of parameters and initial conditions shown in Table 1, x denotes the time course output of the model, and T represents the temperature profile. We used three output metrics: steady-state levels of the HSP and MFP variables, respectively, at 37°C; and the AUC of MFP in response to a 1 h 43°C heat shock.
Code availability
The MATLAB software code for this study is available in Model S1 in the Supporting Material. This includes the model described in the text, data normalization, parameter estimation, cumulative equivalent minutes at 43°C (CEM43) analysis, sensitivity analysis, and generation of all figures.
Results
Comparisons to experimental data
Prior modeling studies have focused largely on qualitative comparisons between model simulations and limited experimental datasets. Given the large amount of published experimental data on the heat-shock response, we sought to perform a comprehensive comparison of our model against the data. A major challenge in this regard was the heterogeneity in the experimental data. For this reason, we focused exclusively on in vitro studies of HeLa cells where the only applied stressor was hyperthermia. Literature search using these constraints produced a largely consistent set of data made up of 17 time-series measurements of six model components from eight publications (10,19,21–26). We used these data to calibrate the model (Figs. 2, 3, and 4).
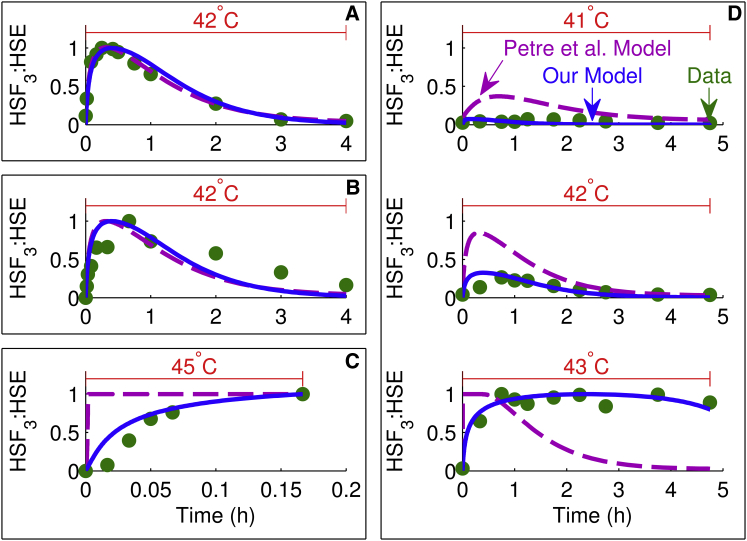
Figure 2.
Comparison of model simulations with HSF DNA-binding data. Each plot shows the heat-stress temperature at the top, experimental data (circles), our model simulation (solid line), and model simulation of Petre et al. (16) (dashed line). Each box enclosing one or more plots is denoted by a letter and represents either one experiment or experiments from the same study plotted on the same scale: (A) (23), (B) (10), (C) (22), and (D) (10). To see this figure in color, go online.
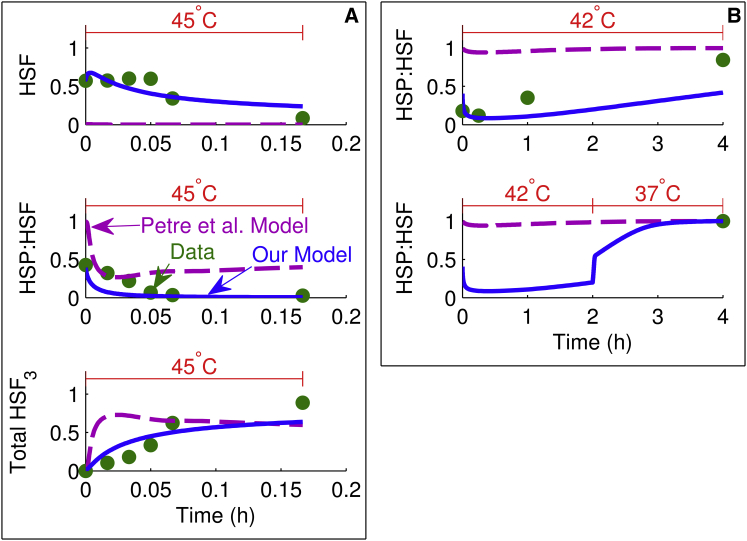
Figure 3.
Comparison of model simulations with HSP/HSF dynamics data. Each plot shows the heat-stress temperature at the top, experimental data (circles), our model simulation (solid line), and the model simulation of Petre et al. (16) (dashed line). Each box enclosing multiple plots is denoted by a letter and represents experiments from the same study plotted on the same scale: (A) (22) and (B) (25). To see this figure in color, go online.
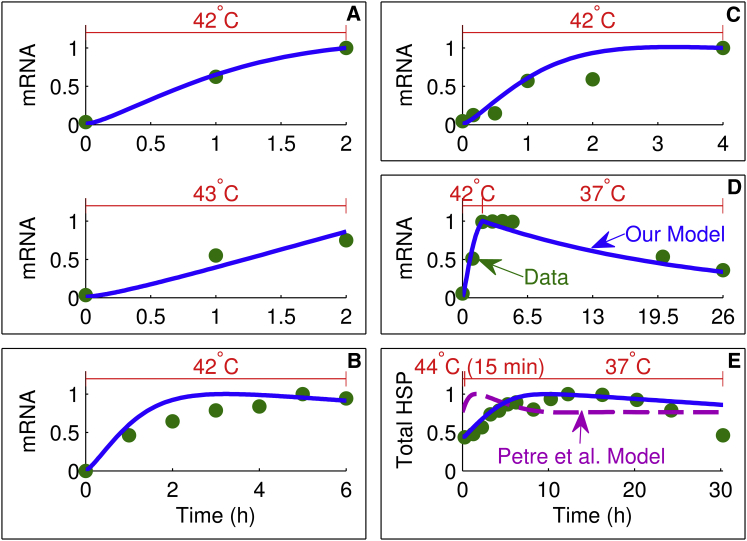
Figure 4.
Comparison of model simulations with HSP transcription and translation data. Each heat-stress temperature at the top, experimental data (circles), our model simulation (solid line), and the model simulation of Petre et al. (16) (dashed line). Results from the model of Petre et al. (16) are only shown in (E) because (A)–(D) correspond to the mRNA variable, which was not included in their model. Each box enclosing one or more plots is denoted by a letter and represents either one experiment or experiments from the same study plotted on the same scale: A (19), B (21), C (24), D (21), and E (26). To see this figure in color, go online.
HSF DNA binding
A critical step in the activation of the heat-shock response is the binding of activated HSF trimers to DNA, allowing for the transcriptional regulation of HSP (Eqs. 3 and 4). Fig. 2 shows four experimental datasets from three HSF DNA-binding studies (two different datasets were from the same study) (10,22,23) compared against the HSF3:HSE variable from both Petre et al. (16) and our model. The model of Petre et al. (16) fit well to the data for heat shock at 42°C in Fig. 2 A, which was used in their model calibration, and to the similar data in Fig. 2 B. However, it poorly fit the data for heat shock at other temperatures (Fig. 2, C and D). Fig. 2 D (10) shows an important feature of HSF DNA binding observed from the experimental data: namely, that there was a huge difference in the binding dynamics as the heat-shock temperature is increased from 42 to 43°C, which was not captured by the model of Petre et al. (16). In contrast, our model was successful in capturing the dynamics for heat shock across a range of temperatures from 41 to 45°C by accounting for the diminished transcriptional and translational efficiency at higher temperatures (Eq. 19). In response to low temperatures, the heat-shock response is acute and self-limiting due to the negative feedback loop between HSF and HSP. However, at high temperatures, diminished transcriptional and translational efficiency inhibit the function of the negative feedback loop, leading to much more persistent activation of the transcription factor. Without accounting for this mechanism that allows for long-term DNA binding, it would not be possible to model the data shown in Fig. 2 D.
Although the simulations shown in Fig. 2, A and B, are identical to the 42°C simulations in Fig. 2 D (middle plot), the scaling of the output is different because the simulations in Fig. 2 D were plotted on a scale relative to the highest of the three temperatures. In Fig. 2, A and B, only one temperature was available from the experimental data, allowing only relative comparisons at that one temperature.
HSP:HSF dynamics
We obtained the data on binding between HSF and HSP from two studies (22,25). Fig. 3 A shows the data from the protocol proposed by Baler et al. (22), in which the concentration of HSF was measured in three different forms: monomeric; bound to HSP; and trimeric. Prior computational models (15,16), including the model of Petre et al. (16), have qualitatively captured the well-known heat-stress responses of HSP:HSF complex dissociation and HSF trimerization (Fig. 3 A, middle and bottom, respectively). However, the experimental data (Fig. 3 A, top) also showed a substantial amount of free HSF in homeostasis and early in the heat-stress response, which is consistent with other studies (22,27,28) but could not be explained by previously published computational models (15,16). In contrast, using a temperature-dependent term in Eq. 20 to represent the increased propensity for HSF oligomerization with temperature increase, we were not only able to describe HSP:HSF complex dissociation and HSF trimerization but also the presence of free HSF during homeostasis and the initial phase of the heat-stress response. The behavior of the prior models showing no free homeostatic HSF, and thereby contradicting the experimental data (Fig. 3 A), can be explained based on a common misconception that HSF is inactivated solely by binding to HSP and thus free HSF always rapidly oligomerizes. However, Anckar and Sistonen (2) showed that although HSP-mediated sequestration of HSF is a popular model for the regulation of HSF oligomerization, there are several alternative mechanisms supported by experimental evidence, including regulation by heat-sensitive noncoding RNA, HSF conformational changes, and neuronal control. Because the specific molecular pathways and relative contributions of the aforementioned regulatory mechanisms are not known as of this writing, using the generic temperature-dependent term in Eq. 20 to account for the total contributions from these mechanisms allowed us to consistently reproduce the experimental data shown in Fig. 3 A.
Fig. 3 B shows the data from the protocol investigated by Shi et al. (25), in which cells were exposed to two different heating regimes: 42°C for 4 h and 42°C for 2 h followed by 2 h of recovery at 37°C. An interesting characteristic of the response was the increased concentration of HSP:HSF in the latter case when heating was stopped due to a combined effect of reduced MFP production and increased efficiency of HSP transcription and translation at a lower temperature (37°C), leading to greater availability of free HSP to bind to HSF. We included both of these mechanisms in our model (Eqs. 15 and 19), thereby allowing us to capture the dynamics (Fig. 3 B), as opposed to the model of Petre et al. (16), and other prior models.
Transcription and translation of HSP
The production of HSP is the main mechanism by which the heat-shock response exerts its protective effect as a result of stress. Activation of the heat-shock transcription factor (HSF) leads to transcription of HSP mRNA and ultimately the translation of new HSP proteins. Transcription is relatively rapid in response to hyperthermia, with mRNA reaching maximal levels within hours of the initiation of stress, as shown in Fig. 4, A–D (19,21,24). Even in response to heat stress being discontinued after a relatively short 2 h period (Fig. 4 D), mRNA levels persisted for several hours (21). The experimental data shown in Fig. 4 A are also interesting because, being from the same study, this information provides a semiquantitative comparison on the relative levels of transcription in response to 42 and 43°C heating (19), clearly illustrating that the higher temperature leads to diminished transcription. By incorporating temperature-dependent transcription and translation rates in the model (Eq. 19), we were successfully able to capture the temporal mRNA dynamics for these different heat-stress conditions. None of these transcriptional data can be compared with the model of Petre et al. (16), which does not explicitly include mRNA; instead, in their model, HSP is produced directly from HSF:HSE. More importantly, it is not possible to model the long-term heat-shock response, as shown in Fig. 4 E (26), using their formulation. Fig. 4 E shows the change in total HSP as a result of heat stress at 44°C for 15 min followed by recovery at 37°C. Although hyperthermia was only applied for 15 min, HSP mRNA persisted in the system after transcription ended (similar to Fig. 4 D), leading to a HSP profile that peaked ∼10 h after the heat stress ended. Therefore, by incorporating an mRNA variable into our model, we were successfully able to account for the experimental mRNA and protein dynamics shown in Fig. 4.
Cumulative equivalent minutes at 43°C
There has long been interest in comparing the effects of thermal doses of different temperatures and durations. For instance, is it worse to be exposed to 43°C for 15 min or 44°C for 10 min? Experimental work in a variety of different cell lines and tissues has resulted in an empirical formula to facilitate these comparisons through a metric called “cumulative equivalent minutes at 43°C” (CEM43) (11,29,30), as given by Eq. 22,
| (22) |
where Δt is the duration of the exposure, R is the gas constant, and T is the temperature of the exposure.
CEM43 was designed to reflect the equivalent damage, such as the fraction of cells killed (or tissue necrosis fraction), for different time-temperature combinations. For example, using Eq. 22 for CEM43, damage at 44°C for 10 min is equivalent to that at 43°C for 20 min. In the absence of a direct variable in our model that maps to damage, we used free MFP concentration as a representative of damage because free misfolded proteins are known to play a critical cytotoxic role in the response to hyperthermia (31). Therefore, we used the area under the curve (AUC) of the MFP variable as a damage metric to evaluate whether our model predictions were consistent with the temperature-time equivalence given by the CEM43 relationship (Eq. 22). Fig. 5 A shows the MFP concentration as a function of time for various heat-stress temperatures, and, as expected, MFP increased for higher exposure temperatures. Fig. 5 B shows the changes in MFP AUC (relative to MFP AUC at 43°C) with temperature when the heating duration was either kept constant (blue line) or set in a temperature-dependent manner (red line) using the CEM43 formula (Eq. 22). To obtain the blue line in Fig. 5 B, we selected 20 different temperatures at equal intervals between 42 and 45°C. For each temperature, we performed model simulations to calculate the MFP AUC for 20 different heating durations equally spaced from 10 to 120 min, performing 400 simulations in total. Next, we calculated the ratio of MFP AUC at a particular temperature to that at 43°C for the same duration. Finally, we calculated the average (blue line) and standard deviation (shaded blue region) of MFP AUC ratio for each temperature to obtain the results shown in Fig. 5 B. As expected, and consistent with Fig. 5 A, the MFP AUC ratio, which gives the relative damage at a specific temperature with respect to damage at 43°C, increased significantly as the temperature increased beyond 43°C.
Figure 5.
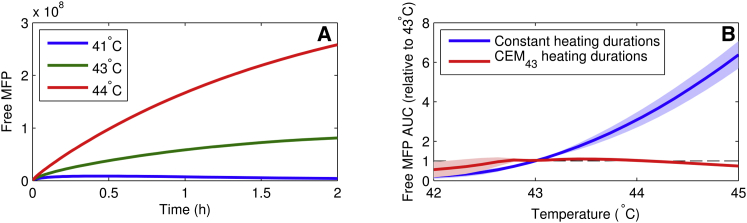
Analysis of protein misfolding as a function of temperature and duration of exposure. (A) MFP versus time for three different temperatures. (B) AUC for 800 simulations similar to those in (A) for a variety of heating duration and temperature combinations. (Blue curve) Ratio of MFP AUC at a particular temperature to that at 43°C for the same duration. (Red curve) Ratio of MFP AUC at a particular temperature and duration to that at 43°C for the corresponding cumulative equivalent minutes at 43°C (CEM43) duration. (Shaded regions) Standard deviation over multiple different heating durations.
Similarly, to obtain the red line in Fig. 5 B, we first determined Δt from the CEM43 relationship (Eq. 22) corresponding to the 20 different CEM43 durations from 10 to 120 min for the 20 different temperature used above. For example, for heating at 42°C, the CEM43 time of 10 min corresponded to Δt of 40 min (using Eq. 22). Next, we performed model simulations for these calculated durations for each temperature, again resulting in a total of 400 simulations. Subsequently, we calculated the ratio of MFP AUC at a particular temperature and duration to that at 43°C for the corresponding CEM43 duration. Finally, we calculated the average (red line) and standard deviation (shaded red region) of the MFP AUC ratio for each temperature to obtain the results shown in Fig. 5 B. Based on the definition of CEM43, these ratios should be 1 (dashed line in Fig. 5 B) for each case if our model predictions were to be consistent with the CEM43 formulation. We indeed found that the MFP AUC ratio (red line) was roughly constant across the temperature range and close to 1, indicating that the model corresponded well with prior studies on heat-induced damage and CEM43 time-temperature equivalence. The only exception was observed at low temperatures, where longer temperature exposures produced lower levels of MFP AUC because the model predicted that the heat-shock response was sufficient to keep MFP at very low levels after an initial acute response. These results served as model validation because MFP AUCs and CEM43 values were not computed until after model calibration was completed. Furthermore, as evidenced by Fig. S1 (in the Supporting Material) showing the equivalent of Fig. 5 for the model of Petre et al. (16) (which does not produce an isoeffect for temperatures and durations set by the CEM43 formula), it is not true that all models of the heat-shock response capture the effect of the CEM43 relationship.
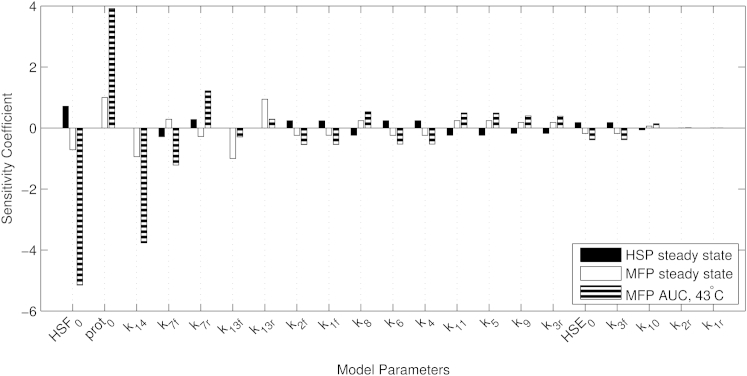
Sensitivity analysis
We performed sensitivity analysis to investigate the relationship between model output and parameter values. We used three different output metrics to calculate sensitivities: 1) steady-state value of HSP at 37°C, 2) steady-state value of MFP at 37°C, and 3) MFP AUC in response to heat stress. Using the HSP and MFP variable for sensitivity analysis allowed for comparison with the results of Petre et al. (16), and the MFP AUC variable served as a reasonable metric of damage, as described above. Fig. 6 shows the sensitivities of these three output metrics relative to each of the parameters shown in Table 2. Several parameters had very low sensitivities, indicating that their specific values did not substantially impact the model output. These include the rates governing HSF deoligomerization (k1r and k2r), which Petre et al. (16) also identified as among the most insensitive parameters in their model. In general, steady-state sensitivity coefficients from our model corresponded well with those of Petre et al. (16), as is shown in Fig. S2. The MFP AUC sensitivities revealed a subset of parameters that had differential sensitivities in stress and in homeostasis, such as HSF0 (the total amount of HSF), k14 (rate of MFP refolding by HSP), and k7f and k7r (forward and reverse rates for the binding of HSP and HSF, respectively).
Figure 6.
Sensitivities of steady-state values and stress responsiveness of the heat-shock response relative to all parameters.
Discussion
Building on an existing model and experimental data, we developed a more detailed model of the heat-shock response. The model presented here is not the first heat-shock response model (14–17), but it differs from previous works in its use of a wide range of published experimental studies for both calibration and validation. Although prior models did well to qualitatively investigate the core mechanisms of the heat-shock response, a more quantitative approach is necessary to ensure that a model can be reliably applied as a component within a larger system, such as during heat-stress progression (32), which is a major potential application of this type of work. Simple models of the heat-shock response have already been used as components of larger mathematical models for predicting inflammation in heat stroke (33) and optimizing cancer therapy (3,34). A more-complete and realistic model could aid in further applications where understanding the extent of the heat-shock response is important.
Our model builds on the work of Petre et al. (16), which itself was more comprehensively calibrated and validated than any of the other previous models of the heat-shock response. Petre et al. (16) calibrated their model with data on HSF DNA binding, which was used here in Fig. 2 A. Subsequently, they validated their model based on novel data of cells transfected to express yellow fluorescent protein in response to HSF activation. However, calibration using a single time series is not sufficient to identify parameter sets that produce reasonable results for variables not involved directly in the calibration process. We observed this throughout the model development process, where it was not uncommon for an incomplete version of our model to be consistent with some but not all of the experimental data. It was only in the context of the complete set of experimental data that all the limitations of prior models became apparent, thus motivating our structural modifications to model components responsible for HSF oligomerization, transcription, and translation.
In general, it is possible to fit any model to any data if enough free parameters are added to the model. Therefore, it is important to stress the point that the modifications we made to the model of Petre et al. (16) were not just arbitrary free parameters; instead, they were all based on mechanisms described in the literature. For instance, transcriptional data clearly shows that although HSP mRNA is produced in response to heat stress, there is a point around, roughly, 43°C where further increases in temperature lead to less transcription (19). It is similarly well established that HSF can in fact exist as a free monomer without immediately oligomerizing, due to HSF-inactivating factors besides the HSF-HSP negative feedback loop (2). Making relatively simple modifications to the model of Petre et al. (16) to incorporate these mechanisms resulted in a model that was consistent with the experimental data shown in Figs. 2, 3, and 4. Furthermore, these changes appeared to be necessary to explain the data, as we were not successful in attempts to simply recalibrate the model of Petre et al. (16) to all of the data in the same manner as the calibration procedure described here.
In addition to calibrating our model with data, we sought to validate it by testing its performance relative to data not used in calibration. Ideally, this would have been done by simply reserving some experimental data as validation data, but this was not feasible due to the complexity of the model relative to the limited amount of available data. Instead, the analysis of time-temperature equivalence in our model, shown in Fig. 5, serves as an important validation of model behavior. The ability of our model to reproduce the breakpoint at 43°C in the CEM43 equation (Eq. 22) is facilitated by the same mechanisms that were added to the model to explain the HSF DNA-binding data shown in Fig. 2 and the mRNA data shown in Fig. 4. As temperature increases beyond a certain threshold near 43°C, transcriptional and translational efficiency diminish, resulting in a weakened heat-shock response even in the presence of a more severe heat stress. The amount of weakening required to describe the molecular-level data turned out to also be the amount of weakening required to accurately capture the higher-level characteristics of the CEM43 breakpoint, which serves as validation of our model.
Another source of validation comes from comparing the total concentrations of conserved species with known values from the literature. Two of the three conserved species in our model are HSF, the transcription factor; and HSE, its DNA-binding site. As shown in Table 2, our model calibration procedure resulted in an HSF concentration that is roughly 100 times higher than that of HSE, which naively seems like an unrealistically large disparity. However, it is in line with experimental data showing that the number of molecules of HSF in a HeLa cell is roughly 100 times larger than the number of stress-activated HSE sites (35,36). This again confirms the ability of our model to reproduce experimental results that were not used in calibration.
The steady-state sensitivity analysis results for our model were largely in agreement with those of Petre et al. (16), as shown in Fig. S2. This is surprising given the additional mechanisms in our model and the large differences in the time-course simulation results of Figs. 2, 3, and 4. The stress-responsive sensitivity analysis results were most interesting because they revealed certain parameters of the model that can lead to large changes in stress responsiveness without substantially altering homeostasis. This is important because HSPs are molecular chaperones involved in numerous cellular signaling pathways, so it may be desirable to modulate the heat-shock response without altering homeostatic levels of its components.
We found that the parameter with both the largest overall sensitivity in the stress response and the largest ratio of stress-responsive and homeostatic sensitivities was the total amount of HSF in the cell (HSF0), making it an attractive target for intervention (Fig. 6). HSF0 was a conserved quantity in our model based on experimental evidence that HSF levels remain roughly constant during heat stress (35). Our model, based on HeLa cells, predicted that overexpression of HSF leads to diminished free MFP accumulation (and therefore decreased cytotoxicity) through the increased production of HSP (Fig. S3). The effects of HSF overexpression have been previously studied in a murine fibroblast cell line (37). They found that cells that overexpressed HSF were more resistant to the cytotoxic effects of heat stress, but this effect did not appear to be directly caused by the production of more HSP. However, a more recent study of HSF overexpression in human colon carcinoma cells did observe that overexpression of HSF led to increased HSP levels in response to a chemical stimulus (38), in agreement with our model. Because it is known that the heat-shock response varies by cell type (39), sensitivities relative to perturbations, such as HSF overexpression, could be heterogeneous in different cell types. Given sufficient training data for different types of cells, mathematical models could be used to predict these kinds of potentially important cell-type-specific effects of modulating the expression and action of components of the heat-shock response.
When modeling chemical reactions occurring at different temperatures, it is important to consider the inherent effect that temperature has on reaction rates, which has not been done previously, to our knowledge, in models of the heat-shock response. In our model, certain reactions known to be highly sensitive to temperature based on specific biological mechanisms have explicit temperature dependences in their reaction rates, which is highlighted in Fig. 1. More generally, each reaction rate should have some dependence on temperature, which can be approximated through a relatively simple exponential model based on the concept of temperature coefficients (40). However, because incorporating this type of global temperature dependence did not substantially alter our ability to explain the data, we chose to pursue the simpler formulation of the model without these temperature coefficient terms.
Even with the larger amount of data we used for our model development relative to prior models, data availability was still a significant challenge. The scope of our model and analysis was purposely limited to make it feasible to identify parameter values based on the available data. The lack of consistent, quantitative data complicated the calibration process, and improvements in this regard could result in a better parameterized model. Additionally, several components in our model could be expanded to become more realistic if adequate data were available. The regulation of HSF activation is a complex process involving multiple different pathways (2), which we combined in Eq. 20, representing our uncertainty of the relative contributions of different mechanisms. The HSP variable of our model was meant to collectively represent the action of the many classes of HSPs, and more comprehensive and consistent time-course data would be valuable in modeling the heterogeneous behaviors of different HSPs. Furthermore, a significant challenge in all hyperthermia research is the high variability observed in responses to subtly different heating methods (41). For these reasons, the parameter set shown in Table 2 is likely not the only parameterization that allows our model to fit the data reasonably well. However, the fact that this model, unlike prior models, is able to explain experimental data through a set of well-established reactions implies that it can serve as a basis for further exploration into the intricacies of the heat-shock response.
In addition to the limitations described above, the main challenge in terms of data availability is the paucity of information about the dynamics of protein misfolding. The only published data came from the calorimetry studies of Lepock et al. (18), which we used in Eq. 15 to set the rate of protein misfolding similar to prior models (14,16). However, these data are problematic for two reasons: 1) they are unable to distinguish between protein misfolding and other thermodynamic processes; and 2) measurements were taken as temperature was increased 1°C/min, which may not be valid for longer-term heating. Although it is plausible that protein misfolding could be the dominant component measured in those calorimetry experiments and Lepock et al. (42) claimed that longer exposures do not drastically change the total amount of misfolding, more data on protein misfolding would be desirable, including data on the association of misfolded proteins with HSPs and the formation of aggregates of misfolded proteins. Despite these significant limitations in terms of data availability, this work still represents a step forward in that it does encompass multiple data sets from multiple different experiments on most of the components in the model. From a mathematical perspective, the problem of limited data could be somewhat assuaged by nondimensionalization, which could reduce the number of parameters in the model and facilitate the analysis of the different timescales inherent in the chemical reactions (15,43).
Because cells respond differently to different types of heat-shock-response-inducing stimuli and different cell types have heterogeneous responses to heat stress (39), we considered data only from hyperthermia experiments in HeLa cells. Prior models have, to some extent, investigated cell-type differences in the heat-shock response. Rieger et al. (15) qualitatively set some reaction rates in their model to compare differences in HSF activation mechanisms between human and yeast cells. Yet, even within different types of human cells, there can be important differences in the heat-shock response. An in vivo study (13) has shown significant variability between responses in different tissues exposed to very similar heating profiles. By focusing on HeLa cells (the cell line with the most available data), our work represents a foundation for future models aimed at exploring cell-type heterogeneity in more detail. However, this will require novel experimental data in which multiple cell types are probed in consistent conditions. In 2013, there has been progress on understanding tissue-specific differences in the regulation of the heat-shock response (12), but much work remains to gather the knowledge required to build dynamical molecular-level models that capture this heterogeneity.
We chose not to explore the problem of consecutive heat shocks or thermotolerance in this article. Although this problem has been explored by prior models of the heat-shock response, including the model of Petre et al. (16), given the challenges discussed here in accurately modeling a single heat shock, it is unlikely that existing models (including ours) would provide reasonable agreement with experimental data and provide novel insights about consecutive heat shocks. Moreover, experimental studies exploring dual-hit heat shocks (26,39,44) contain additional degrees of freedom in the experimental design (length of each pulse; gap between pulses; temperatures before, during, and after each pulse), which further exacerbate the modeling challenges discussed here and would require novel experimental data to be fully described in a mathematical framework.
Modeling the heat-shock response is a critical task in understanding the overall response to heat stress, which in addition to the heat-shock response also includes several other physiological responses, such as altered blood-flow patterns and inflammation (45). If cell-type-specific models of the heat-shock response can be developed and validated in vitro similar to our approach here for HeLa cells, that would facilitate linking the cellular heat-shock response with models of interlinked processes, such as inflammation (33) and heat transfer (46), culminating in a multiscale model of in vivo heat stress. The work presented here is a step toward that ultimate goal.
Author Contributions
J. D. Scheff, J. D. Stallings, J. Reifman, and V. Rakesh designed research. J. D. Scheff performed research. J. D. Scheff, J. D. Stallings, J. Reifman, and V. Rakesh analyzed data. J. D. Scheff, J. D. Stallings, J. Reifman, and V. Rakesh wrote the article.
Acknowledgments
The research was supported by the U.S. Army Network Science Initiative and the Military Operational Medicine Research Program, U.S. Army Medical Research and Materiel Command, Fort Detrick, MD.
The opinions and assertions contained herein are the private views of the authors and are not to be construed as official or as reflecting the views of the U.S. Army or of the U.S. Department of Defense. This article has been approved for public release with unlimited distribution.
Editor: Ruth Baker.
Footnotes
This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Three figures and one model zip file are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00610-4.
Supporting Material
References
- 1.Jolly C., Morimoto R.I. Role of the heat shock response and molecular chaperones in oncogenesis and cell death. J. Natl. Cancer Inst. 2000;92:1564–1572. doi: 10.1093/jnci/92.19.1564. [DOI] [PubMed] [Google Scholar]
- 2.Anckar J., Sistonen L. Regulation of HSF1 function in the heat stress response: implications in aging and disease. Annu. Rev. Biochem. 2011;80:1089–1115. doi: 10.1146/annurev-biochem-060809-095203. [DOI] [PubMed] [Google Scholar]
- 3.Rylander M.N., Feng Y., Diller K.R. Optimizing heat shock protein expression induced by prostate cancer laser therapy through predictive computational models. J. Biomed. Opt. 2006;11:041113. doi: 10.1117/1.2241310. [DOI] [PubMed] [Google Scholar]
- 4.Valastyan J.S., Lindquist S. Mechanisms of protein-folding diseases at a glance. Dis. Model. Mech. 2014;7:9–14. doi: 10.1242/dmm.013474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rome C., Couillaud F., Moonen C.T. Spatial and temporal control of expression of therapeutic genes using heat shock protein promoters. Methods. 2005;35:188–198. doi: 10.1016/j.ymeth.2004.08.011. [DOI] [PubMed] [Google Scholar]
- 6.Balch W.E., Morimoto R.I., Kelly J.W. Adapting proteostasis for disease intervention. Science. 2008;319:916–919. doi: 10.1126/science.1141448. [DOI] [PubMed] [Google Scholar]
- 7.Ritossa F. Discovery of the heat shock response. Cell Stress Chaperones. 1996;1:97–98. doi: 10.1379/1466-1268(1996)001<0097:dothsr>2.3.co;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Riezman H. Why do cells require heat shock proteins to survive heat stress? Cell Cycle. 2004;3:61–63. [PubMed] [Google Scholar]
- 9.Morimoto R.I. Cells in stress: transcriptional activation of heat shock genes. Science. 1993;259:1409–1410. doi: 10.1126/science.8451637. [DOI] [PubMed] [Google Scholar]
- 10.Abravaya K., Phillips B., Morimoto R.I. Attenuation of the heat shock response in HeLa cells is mediated by the release of bound heat shock transcription factor and is modulated by changes in growth and in heat shock temperatures. Genes Dev. 1991;5:2117–2127. doi: 10.1101/gad.5.11.2117. [DOI] [PubMed] [Google Scholar]
- 11.Yarmolenko P.S., Moon E.J., Dewhirst M.W. Thresholds for thermal damage to normal tissues: an update. Int. J. Hyperthermia. 2011;27:320–343. doi: 10.3109/02656736.2010.534527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guisbert E., Czyz D.M., Morimoto R.I. Identification of a tissue-selective heat shock response regulatory network. PLoS Genet. 2013;9:e1003466. doi: 10.1371/journal.pgen.1003466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Beck S.C., Paidas C.N., De Maio A. Depressed expression of the inducible form of HSP 70 (HSP 72) in brain and heart after in vivo heat shock. Am. J. Physiol. 1995;269:R608–R613. doi: 10.1152/ajpregu.1995.269.3.R608. [DOI] [PubMed] [Google Scholar]
- 14.Peper A., Grimbergen C.A., van Wijk R. A mathematical model of the hsp70 regulation in the cell. Int. J. Hyperthermia. 1998;14:97–124. doi: 10.3109/02656739809018218. [DOI] [PubMed] [Google Scholar]
- 15.Rieger T.R., Morimoto R.I., Hatzimanikatis V. Mathematical modeling of the eukaryotic heat-shock response: dynamics of the hsp70 promoter. Biophys. J. 2005;88:1646–1658. doi: 10.1529/biophysj.104.055301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Petre I., Mizera A., Back R.J. A simple mass-action model for the eukaryotic heat shock response and its mathematical validation. Nat. Comput. 2011;10:595–612. [Google Scholar]
- 17.Szymańska Z., Zylicz M. Mathematical modeling of heat shock protein synthesis in response to temperature change. J. Theor. Biol. 2009;259:562–569. doi: 10.1016/j.jtbi.2009.03.021. [DOI] [PubMed] [Google Scholar]
- 18.Lepock J.R., Frey H.E., Ritchie K.P. Protein denaturation in intact hepatocytes and isolated cellular organelles during heat shock. J. Cell Biol. 1993;122:1267–1276. doi: 10.1083/jcb.122.6.1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Theodorakis N.G., Morimoto R.I. Posttranscriptional regulation of hsp70 expression in human cells: effects of heat shock, inhibition of protein synthesis, and adenovirus infection on translation and mRNA stability. Mol. Cell. Biol. 1987;7:4357–4368. doi: 10.1128/mcb.7.12.4357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lipan O., Navenot J.M., Peiper S.C. Heat shock response in CHO mammalian cells is controlled by a nonlinear stochastic process. PLOS Comput. Biol. 2007;3:1859–1870. doi: 10.1371/journal.pcbi.0030187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Andrews G.K., Harding M.A., Adamson E.D. The heat shock response in HeLa cells is accompanied by elevated expression of the c-fos proto-oncogene. Mol. Cell. Biol. 1987;7:3452–3458. doi: 10.1128/mcb.7.10.3452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Baler R., Zou J., Voellmy R. Evidence for a role of Hsp70 in the regulation of the heat shock response in mammalian cells. Cell Stress Chaperones. 1996;1:33–39. doi: 10.1379/1466-1268(1996)001<0033:efaroh>2.3.co;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kline M.P., Morimoto R.I. Repression of the heat shock factor 1 transcriptional activation domain is modulated by constitutive phosphorylation. Mol. Cell. Biol. 1997;17:2107–2115. doi: 10.1128/mcb.17.4.2107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mosser D.D., Theodorakis N.G., Morimoto R.I. Coordinate changes in heat shock element-binding activity and HSP70 gene transcription rates in human cells. Mol. Cell. Biol. 1988;8:4736–4744. doi: 10.1128/mcb.8.11.4736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shi Y., Mosser D.D., Morimoto R.I. Molecular chaperones as HSF1-specific transcriptional repressors. Genes Dev. 1998;12:654–666. doi: 10.1101/gad.12.5.654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stege G.J., Brunsting J.F., Konings A.W. Thermotolerance and nuclear protein aggregation: protection against initial damage or better recovery? J. Cell. Physiol. 1995;164:579–586. doi: 10.1002/jcp.1041640316. [DOI] [PubMed] [Google Scholar]
- 27.Guo Y., Guettouche T., Voellmy R. Evidence for a mechanism of repression of heat shock factor 1 transcriptional activity by a multichaperone complex. J. Biol. Chem. 2001;276:45791–45799. doi: 10.1074/jbc.M105931200. [DOI] [PubMed] [Google Scholar]
- 28.Xia W., Voellmy R. Hyperphosphorylation of heat shock transcription factor 1 is correlated with transcriptional competence and slow dissociation of active factor trimers. J. Biol. Chem. 1997;272:4094–4102. doi: 10.1074/jbc.272.7.4094. [DOI] [PubMed] [Google Scholar]
- 29.Dewhirst M.W., Viglianti B.L., Hoopes P.J. Basic principles of thermal dosimetry and thermal thresholds for tissue damage from hyperthermia. Int. J. Hyperthermia. 2003;19:267–294. doi: 10.1080/0265673031000119006. [DOI] [PubMed] [Google Scholar]
- 30.Sapareto S.A., Dewey W.C. Thermal dose determination in cancer therapy. Int. J. Radiat. Oncol. Biol. Phys. 1984;10:787–800. doi: 10.1016/0360-3016(84)90379-1. [DOI] [PubMed] [Google Scholar]
- 31.Friant S., Meier K.D., Riezman H. Increased ubiquitin-dependent degradation can replace the essential requirement for heat shock protein induction. EMBO J. 2003;22:3783–3791. doi: 10.1093/emboj/cdg375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bouchama A., Knochel J.P. Heat stroke. N. Engl. J. Med. 2002;346:1978–1988. doi: 10.1056/NEJMra011089. [DOI] [PubMed] [Google Scholar]
- 33.Rodriguez-Fernandez M., Grosman B., Doyle F.J., 3rd Modeling the intra- and extracellular cytokine signaling pathway under heat stroke in the liver. PLoS One. 2013;8:e73393. doi: 10.1371/journal.pone.0073393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rylander M.N., Feng Y., Diller K.R. Measurement and mathematical modeling of thermally induced injury and heat shock protein expression kinetics in normal and cancerous prostate cells. Int. J. Hyperthermia. 2010;26:748–764. doi: 10.3109/02656736.2010.486778. [DOI] [PubMed] [Google Scholar]
- 35.Sarge K.D., Murphy S.P., Morimoto R.I. Activation of heat shock gene transcription by heat shock factor 1 involves oligomerization, acquisition of DNA-binding activity, and nuclear localization and can occur in the absence of stress. Mol. Cell. Biol. 1993;13:1392–1407. doi: 10.1128/mcb.13.3.1392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gonsalves S.E., Moses A.M., Westwood J.T. Whole-genome analysis reveals that active heat shock factor binding sites are mostly associated with non-heat shock genes in Drosophila melanogaster. PLoS One. 2011;6:e15934. doi: 10.1371/journal.pone.0015934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mivechi N.F., Shi X.Y., Hahn G.M. Stable overexpression of human HSF-1 in murine cells suggests activation rather than expression of HSF-1 to be the key regulatory step in the heat shock gene expression. J. Cell. Biochem. 1995;59:266–280. doi: 10.1002/jcb.240590215. [DOI] [PubMed] [Google Scholar]
- 38.Cai J., Kirlin W.G., Sartorelli A.C. Overexpression of heat shock factor 1 inhibits butyrate-induced differentiation in colon cancer cells. Cell Stress Chaperones. 2006;11:199–207. doi: 10.1379/CSC-180R.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mizzen L.A., Welch W.J. Characterization of the thermotolerant cell. I. Effects on protein synthesis activity and the regulation of heat-shock protein 70 expression. J. Cell Biol. 1988;106:1105–1116. doi: 10.1083/jcb.106.4.1105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mitrophanov A.Y., Rosendaal F.R., Reifman J. Computational analysis of the effects of reduced temperature on thrombin generation: the contributions of hypothermia to coagulopathy. Anesth. Analg. 2013;117:565–574. doi: 10.1213/ANE.0b013e31829c3b22. [DOI] [PubMed] [Google Scholar]
- 41.Wu W., Zhang C., Yang J. Differences in heating methods may account for variation in reported effects on γH2AX focus formation. Mutat. Res. 2009;676:48–53. doi: 10.1016/j.mrgentox.2009.03.003. [DOI] [PubMed] [Google Scholar]
- 42.Lepock J.R., Frey H.E., Kruuv J. Thermal analysis of CHL V79 cells using differential scanning calorimetry: implications for hyperthermic cell killing and the heat shock response. J. Cell. Physiol. 1988;137:14–24. doi: 10.1002/jcp.1041370103. [DOI] [PubMed] [Google Scholar]
- 43.Mirams G.R., Byrne H.M., King J.R. A multiple timescale analysis of a mathematical model of the Wnt/β-catenin signalling pathway. J. Math. Biol. 2010;60:131–160. doi: 10.1007/s00285-009-0262-y. [DOI] [PubMed] [Google Scholar]
- 44.Theodorakis N.G., Drujan D., De Maio A. Thermotolerant cells show an attenuated expression of Hsp70 after heat shock. J. Biol. Chem. 1999;274:12081–12086. doi: 10.1074/jbc.274.17.12081. [DOI] [PubMed] [Google Scholar]
- 45.Epstein Y., Roberts W.O. The pathophysiology of heat stroke: an integrative view of the final common pathway. Scand. J. Med. Sci. Sports. 2011;21:742–748. doi: 10.1111/j.1600-0838.2011.01333.x. [DOI] [PubMed] [Google Scholar]
- 46.Rakesh V., Stallings J.D., Reifman J. A 3-D mathematical model to identify organ-specific risks in rats during thermal stress. J. Appl. Physiol. 2013;115:1822–1837. doi: 10.1152/japplphysiol.00589.2013. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.