Abstract
We have developed a technique to directly quantify cell-substrate adhesion force using micropipette aspiration. The micropipette is positioned perpendicular to the surface of an adherent cell and a constant-rate aspiration pressure is applied. Since the micropipette diameter and the aspiration pressure are our control parameters, we have direct knowledge of the aspiration force, whereas the cell behavior is monitored either in brightfield or interference reflection microscopy. This setup thus allows us to explore a range of geometric parameters, such as projected cell area, adhesion area, or pipette size, as well as dynamical parameters such as the loading rate. We find that cell detachment is a well-defined event occurring at a critical aspiration pressure, and that the detachment force scales with the cell adhesion area (for a given micropipette diameter and loading rate), which defines a critical stress. Taking into account the cell adhesion area, intrinsic parameters of the adhesion bonds, and the loading rate, a minimal model provides an expression for the critical stress that helps rationalize our experimental results.
Introduction
Cell adhesion is involved in a plethora of physiological and pathological cellular processes, and cell-substrate adhesion affects several cellular functions, such as migration, proliferation, and differentiation. Molecules involved in cell-substrate adhesion have been thoroughly studied (1), yet quantitative experimental techniques are still needed to provide a better understanding of the mechanics of cell adhesion. In the context of atherosclerosis, the early stage of the disease involves the transmigration of monocytes in abnormally high numbers, which then accumulate in arterial walls and participate in the formation of atherosclerotic plaques (2). Measuring changes in the adhesion of endothelial cells should help shed light on this process, as mechanical changes in endothelial cells after monocyte adhesion might play a crucial role in pathologically elevated transmigration rates. Indeed, results of a study by Kataoka et al. suggest that in vitro, the contact between white blood cells and endothelial cells modifies the strength of endothelial cell adhesion to their substrate (3). The authors found indirect evidence of a reduced adhesion in the presence of white blood cells by measuring a change in the electrical resistance of a population of endothelial cells. They interpreted the observed decrease of electrical resistance in the presence of white blood cells as evidence of a nanometer-scale increase in the distance between the ventral cell surface and the substrate. However, a more direct characterization of the mechanical properties of endothelial cells is still needed to better understand their response to leukocyte adhesion.
Although the behavior of red blood cells detaching from a surface has been experimentally and numerically investigated while monitoring the applied force (4,5), and though several techniques exist to measure the adhesion of cells adhering weakly to a substrate or to another cell, data are scarce on strongly adherent cells such as endothelial cells. Previous techniques at the single-cell level relied on pulling a micro- or nanoneedle inserted into the cell body (6–8), pulling (9,10) or scraping (11,12) the cell of interest with a bending cantilever, and aspirating the cell with a micropipette (13–16). Experiments were also carried out on cell populations in which cell detachment was induced by centrifugation or hydrodynamic stress (17,18), yielding ensemble-averaged values for the quantities of interest. However, some of these studies involve technical difficulties, such as the need for protein scaffolding of the cells to avoid membrane rupture when they are pulled by a nanoneedle (8). Moreover, knowing the detachment force is not always straightforward. For instance, in the case of aspirating micropipettes used as cantilevers (9,10), the detachment force measured from the cantilever deflection may not be independent of the aspiration pressure used to hold the cell and micropipette in contact, as other experiments with static micropipettes indicate that a high aspiration pressure is enough to detach a cell without having to bend the micropipette (13). In turn, in the latter work, the micropipette was not held in direct contact with the cells, so that the flow of medium into the pipette is expected to have contributed to the detachment force; indeed, in a related study, this was taken into account using fluid-flow simulations (16).
This work presents, to our knowledge, a new technique designed to investigate the detachment of endothelial cells adhering to a substrate. This method allows for direct measurement of the detachment force by placing an aspirating micropipette in contact with the surface of an endothelial cell so that a seal is formed and fluid flow into the micropipette can be neglected. We can perform detachment assays on a number of individual cells in a single experimental run, thus exploring a range of cell sizes, while imposing the micropipette diameter and the aspirating pressure rate (or loading rate). Finally, interference reflection microscopy (IRM) is used to monitor the adhesion areas, as was previously done in the case of adhering blood cells (9) and tumor cells (18). In a nutshell, this technique enables us to fully probe the influence of geometric parameters, such as cell surface, adhesion areas, and micropipette size, as well as dynamical parameters such as the loading rate. We present a minimal model that captures the features of the mechanical behavior observed in our experiments.
Materials and Methods
Endothelial cells
Primary bovine aortic endothelial cells were kindly provided by A.-C. Vion and C. Boulanger and used between passages 4 and 11. They were cultured in Dulbecco’s modified Eagle’s medium (Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum (Invitrogen) and 1% penicillin/streptomycin (Invitrogen) at 37°C with 5% CO2. The cells were passaged three times a week and resuspended in fresh culture medium. One to two days before each experiment, the cells were trypsinated with trypLE (Invitrogen) and plated at a subconfluent density onto thin-bottom dishes (standard-bottom low-walled 35-mm μ-Dish, IBIDI, Martinsried, Germany). In another set of experiments, the cells were grown on glass microbeads instead of a petri dish. Typically, 50 dextran Cytodex-3 microcarrier beads (Sigma-Aldrich, Taufkirchen, Germany) were first deposited at the bottom of a μ-Dish in phosphate-buffered saline (PBS; Invitrogen). The PBS was then removed and ∼10,000 trypsinated bovine aortic endothelial cells were introduced into the μ-Dish.
Before any experiment, a μ-Dish was brought onto the stage of the microscope, where experiments were performed, at room temperature in cultured medium with 20 mM HEPES (Invitrogen) added, on cells that had been plated onto the petri dish a few hours to a few days earlier. Dependence of the detachment force on the length of time after plating was not examined in this study. For experiments in which the cells were exposed to cytochalasin D, the cells were incubated for 30 min in a solution containing 1 μg/mL cytochalasin D from Zygosporium masonii (Sigma-Aldrich). The solution containing the cytochalasin D was then aspirated, and fresh medium was introduced. When treated with nocodazole, cells were incubated for 1 h in culture medium containing 10 μg/mL of nocodazole (Sigma-Aldrich).We verified using live-cell microtubule staining (tubulin tracker green, Life Technologies, Saint Aubin, France) that in these conditions, microtubules were properly destabilized.
Micropatterns
Micropatterned coverslips were prepared as described by Azioune et al. (19). The coverslips were first sonicated in ethanol and plasma-treated. They were then incubated in 10 mM HEPES buffer in the presence of 0.1 mg/mL of polylysine-grafted polyethyleneglycol (PLL-g-PEG; Surface Solutions, Dübendorf, Switzerland). After washing with PBS and water, the coverslips were illuminated with deep ultraviolet (UV) light (UVO Cleaner, 342 Series, Jelight, CA) through a photomask and then incubated for 1 h in 100 mM NaHCO3 in the presence of 50 μg/mL fibronectin. The cells were then plated onto the coverslips, which were mounted on magnetic chambers (Chamlide, Live Cell Instrument, Seoul, South Korea) before each experiment.
Micropipette fabrication
Borosilicate glass capillaries (1 mm outside diameter, 0.78 mm inside diameter, Harvard Apparatus, Holliston, MA) were pulled on a P-97 micropipette puller (Sutter Instruments, Novato, CA). To fabricate the micropipettes used in cell aspiration, a MF-900 microforge (Narishige, Tokyo, Japan) was used to cut the extremity of pulled capillaries to the desired diameter, ranging from 4.6 to 30 μm. The body of the micropipettes was then bent at a 45° angle so that their extremity could be held perpendicular to the plane of cell adherence. The micropipettes used to hold the Cytodex-3 beads were fabricated in the same fashion but with a 50-μm diameter at the tip.
Microscope setup
The setup was mounted on a TE300 inverted microscope (Nikon, Tokyo, Japan) located on an air suspension table (CVI Melles Griot, Didam, Netherlands). It was equipped with a 100× oil immersion, 1.3 NA objective for experiment monitoring (Nikon), and lower magnification objectives (40×, 20×, 10×, 4×, and 2×, Nikon Instruments) for micropipette positioning. Images were acquired with a Flash4.0 CMOS camera (Hamamatsu Photonics, Hamamatsu City, Japan) controlled using the software Micromanager (20). The experiments were performed using either brightfield microscopy or IRM. Timelapse movies were acquired at a rate of 1 frame/s under a 100 ms exposure time for IRM.
Interference reflection microscopy
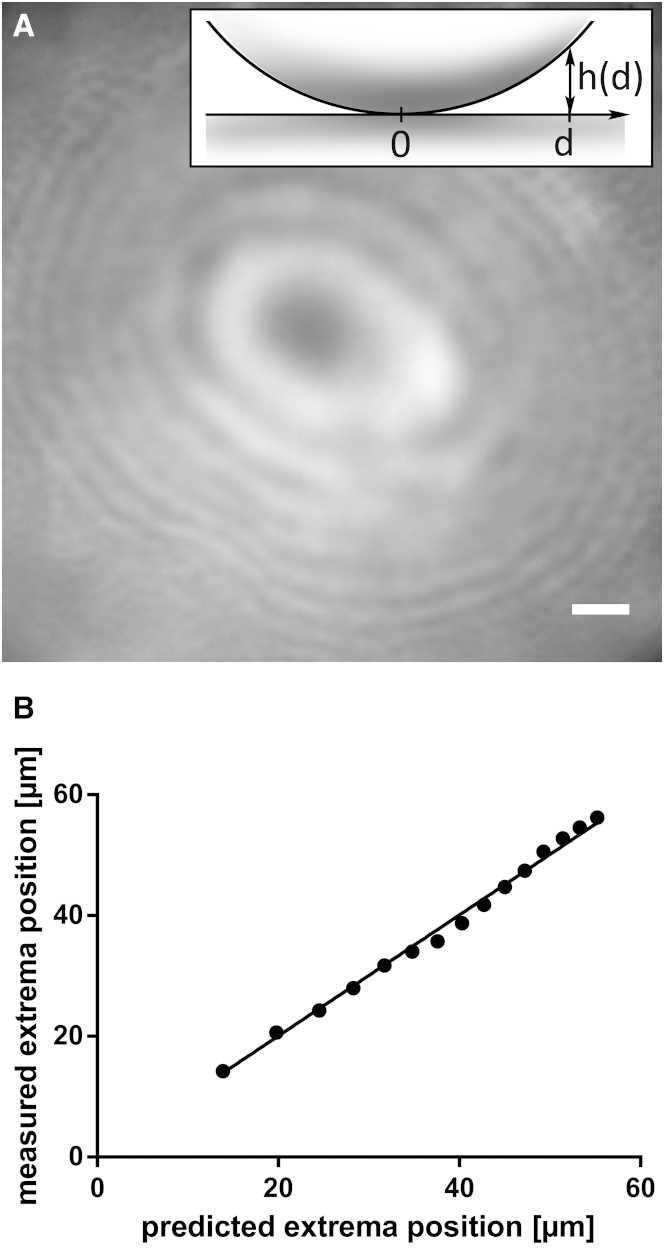
In performing IRM, we used a filter cube equipped with a dual-edge dichroic mirror and a dual-band bandpass emission filter (505/606-nm BrightLine and 524/628-nm BrightLine, respectively, Semrock, Rochester, NY). As an illumination source, we used an Intensilight (Nikon) with an ND8 neutral density filter, and no excitation filter. The polarization of the incoming light was assured by the dichroic mirror, but our illumination was not strictly monochromatic due to the dual-band emission filter. Raw images were processed to remove their background using the software ImageJ (21). See the Supporting Material for details on image processing. To validate this configuration, we tested the setup using 2.2-mm glass beads (Dominique Dutscher, Brumath, France) placed at the bottom of a petri dish in the presence of cell culture medium (see the raw picture obtained in Fig. 1 A). The distance between the surface of the glass bead and the surface of the petri dish is given by , where R = 1.1 mm is the radius of the bead and d is the distance from the bead center projected on the dish plane, (Fig. 1 A, inset). We measured the positions of the local intensity extrema as a function of h and verified that they follow the established equation (18,22)
| (1) |
where and are the maximum and minimum intensity levels, respectively, and (Fig. 1 B). The best fit was obtained for a characteristic wavelength of nm.
Figure 1.
Determination of the IRM wavelength. (A) IRM image showing the intensity minima and maxima (from destructive and constructive interference, respectively) of the light refracted from a 2.2-mm glass bead. Scale bar, 10 μm. (Inset) For each point on the bead surface, the distance to the petri dish is , where R = 1.1 mm is the bead radius and d is the projected distance from the center of the bead. (B) Plot of the experimental intensity extrema positions versus the predictions from Eq. 1 (18,22), for nm. The good fit for this value of λ is evidenced by the slope of the linear regression: 1.003 ± 0.007.
When performing experiments with continuous IRM imaging, we qualitatively observed that the illumination seemed to affect the cell mechanics. Indeed, a primary detachment event occurred during which a significant part of the cell detached, but the pipette tip then had to be slightly translated in the xy plane to detach the remaining part of the cell (Movie S2). During our experiments under brightfield illumination, we also observed cell detachment, but no additional micropipette motion was necessary to fully detach the cells. We hypothesize that this change in cell mechanics is due to the UV light used in our IRM setup. Under continuous illumination, the cells are exposed to a very large amount of UV light, which likely causes phototoxic damage. In most experiments, however, we only used IRM to take a snapshot of the adhesive areas in the initial state and thus expect cell damage to be minimal.
Micromanipulators
The microscope was equipped with a motorized micromanipulator carrying a first micropipette holder at a 45° angle, and a manual three-axis stage linked to a UT-2 joint to orient a second micropipette holder (MP285 micromanipulator, Sutter Instruments, Novato, CA; IM-H1 micropipette holders and UT-2 joint, Narishige, Tokyo, Japan; three-axis stage, Thorlabs, Newton, NJ). The first micropipette was used to aspirate adherent endothelial cells, whereas the other was used to hold Cytodex-3 beads.
Results and Discussion
A constant-rate aspiration technique for cell-detachment assays
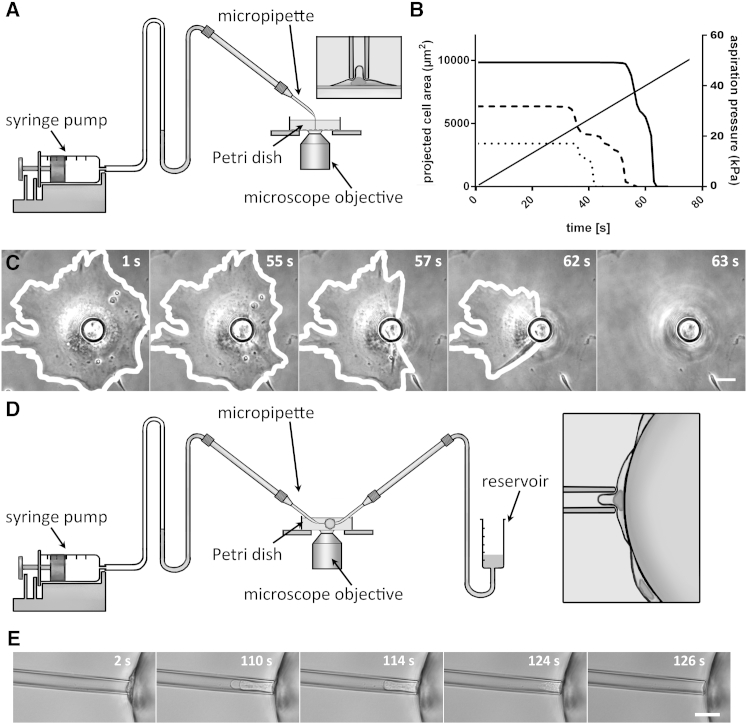
We have developed, to our knowledge, a new technique to apply a well-controlled aspiration force to a single endothelial cell adhering to a substrate while quantitatively monitoring the detachment mechanics. We impose an aspiration pressure, , at a constant rate, , via a micropipette held in contact with the cell body, its tip perpendicular to the substrate (Fig. 2). The aspiration force applied to the cell, , is readily known, since we control both the aspiration pressure, , and the pipette section, . Two different setup configurations allow us to visualize and follow the detachment mechanics either in bottom or side view, which we refer to as in-plane and profile modes, respectively.
Figure 2.
Setup: in-plane (A–C) and profile modes (D and E). (A) Experimental setup for in-plane aspiration experiments. In this case, the micropipette is positioned perpendicular to the surface of adherent endothelial cells cultured on the bottom of a petri dish. The syringe pump on the left creates a constant-rate aspiration pressure increase. (B) Plot of the projected cell area versus time for three different cells. The projected cell area is measured from pictures taken throughout the detachment. (C) Time-lapse of a cell throughout a detachment assay (corresponding to the solid line in B, and to the cell on the right in Movie S1). Scale bar, 10 μm. (D) Experimental setup for profile aspiration experiments. In this case, the aspiration micropipette is still positioned perpendicular to the surface of the endothelial cells, but they adhere to a Cytodex-3 bead, held in position by a second, larger micropipette (on the right). (E) Time lapse of the detachment assay of an endothelial cell adhering to a Cytodex-3 bead. Scale bar, 10 μm.
In the first configuration, or in-plane mode, we designed our setup to be able to work directly with cells cultured on the bottom of a thin-bottom petri dish: this allows us to test a significant number of cells in a single run of experiments (up to 100/day). The petri dish is placed above the microscope objective, parallel to the observation plane. An aspiration micropipette fabricated as described above is micromanipulated so that its tip is brought into contact perpendicular to the luminal surface of the adherent endothelial cells (see Fig. 2 A and Movie S1). Monitoring the detachment in the substrate plane allows us to measure the projected cell area over time (see Fig. 2 B). Using IRM also gives access to evolution of adhesion areas (see Fig. 4 A).
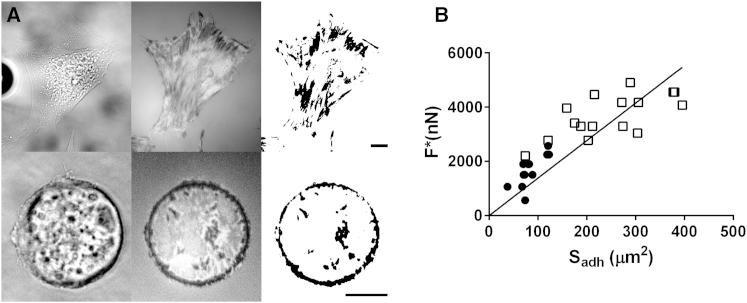
Figure 4.
Detachment force scales with the adhesion area obtained from IRM images. (A) Each row shows, from left to right, the brightfield picture, the IRM picture, and the binary picture, with the adhesion patches shown in black. (Upper) Cell adhering to an unpatterned petri dish. (Lower) Cell constrained on a circular micropattern. Scale bars, 10 μm. (B) Detachment force versus adhesion area. The detachment forces obtained with (●) and without (□) micropatterns scale with the adhesion area (the solid line shows the linear fit of both data sets).
To better understand the detachment process, we performed complementary experiments in a second configuration, the profile mode. In this case, endothelial cells adhering to a microsphere held by a second micropipette are aspirated in a direction parallel to the observation plane, enabling us to observe the detachment from the side (see Fig. 2 D). More precisely, the cells were grown on 200-μm dextran Cytodex-3 microspheres initially designed to culture adherent cells in agitation. We used a 50-μm-diameter micropipette to firmly hold a Cytodex-3 bead. We positioned the bead to place endothelial cells perpendicular to the equatorial plane of the microsphere (Fig. 2 D, inset), which allowed us to visualize a single endothelial cell in profile. We then brought the aspiration micropipette into contact with the endothelial cell, perpendicular to its surface (Fig. 2, D and E). This visualization method does not give access to the projected cell area, but it provides additional insight into the cell-detachment dynamics.
Detachment force and geometric parameters
The time evolution of the projected cell area is shown in Fig. 2 B for three different cells. Although the initial area covered by the cells varies, each case follows a qualitatively similar scenario: the projected area is constant over time until a breaking point when the projected area rapidly collapses until the cell is fully detached, at a critical aspiration pressure, . This indicates that the detachment of cells from their substrate is a well-defined event in our assay. Moreover, for a constant micropipette diameter, we find that larger cells require a higher aspiration pressure, i.e., a higher aspiration force, , to detach from the substrate.
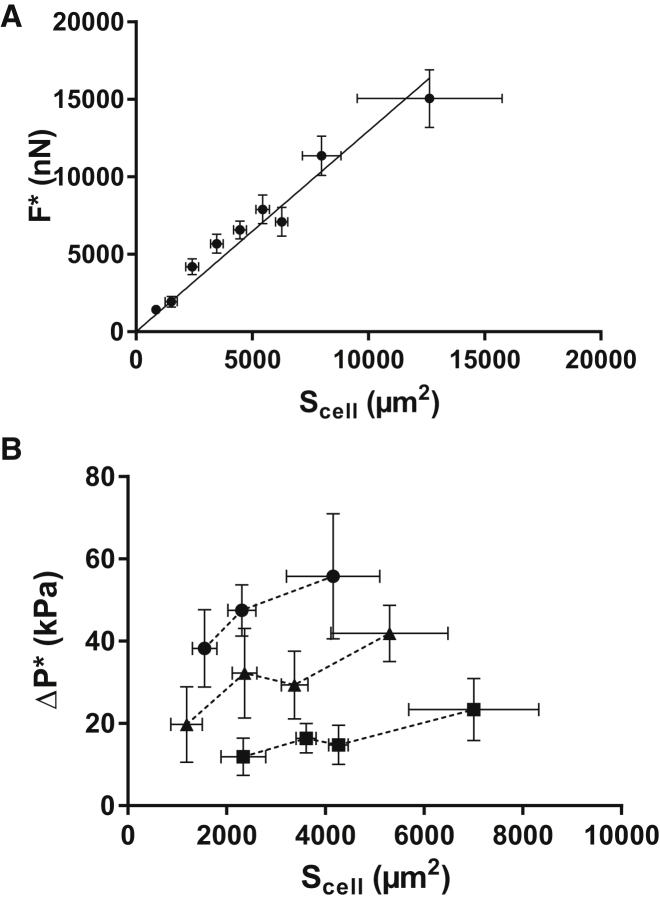
To further quantify the relation between projected area and detachment force, we performed in-plane detachment experiments on 325 cells (over several dishes and days). We found the detachment force, , to be, at a first approximation, proportional to the initial projected cell area, (Fig. 3 A). We can then write
| (2) |
A linear fit of the experimental data yields a critical stress of 1300 ± 50 Pa. All points in this data set collapse on the master curve from Eq. 2, regardless of cell size or pipette diameter. Indeed, both and vary widely here: ranges from to and from to (which corresponds to pipette radii of 2.3–15 ). Conversely, we found to depend on , as shown in Fig. 3 B. We thus conclude that , not , is the relevant observable quantity that characterizes cell detachment.
Figure 3.
Critical stress. (A) Plot of binned experimental data showing that the detachment force scales linearly with the initial projected cell area, , implying that a critical stress, 1300 Pa ± 50 Pa, induces cell detachment. Error bars show the standard deviation. N = 335 experimental data points. (B) Critical aspiration pressure, , versus projected cell area for different micropipette diameters. depends on the micropipette section, , used in the experiments (●: , ▲: , ▪: ). Error bars show the standard deviation.
Since cells resist an aspiration force via cell-substrate adhesions, we used IRM to investigate the relationship between detachment force and adhesive areas at the cell-substrate interface. Indeed, these adhesive areas appear as dark patches in IRM images taken in the in-plane mode (18,22,23). By monitoring the evolution of these adhesive areas over the duration of a complete detachment event, we found that the detachment does not occur by peeling from the periphery but rather appears to be initiated in the region directly under the micropipette, see Movie S2 and Fig. 4 A. These experiments lead us to assume that the adhesive areas share the pulling force throughout the aspiration assay and remain stable until rupture. However, a quantification of these experiments during the detachment process is difficult, as the cell membrane areas that are pulled further than half a wavelength (i.e., 170 nm) away from the substrate become as dark as the adhering areas. In what follows, we consider the initial adhesive area, .
We relate the rupture force, , to the initial adhesive area, , instead of the initial projected cell area, , by expressing as
| (3) |
which defines a second critical stress, 16700 ± 5600 Pa (N = 16) (see Fig. 4 B). The rupture force, , scales with both and , and consistently, and are correlated (Spearman’s correlation r = 0.54, N = 16 cells), with = 0.09 ± 0.04 (N = 16 cells, mean ± SD).
The scaling of with is easier to interpret, since the resistance to the aspiration force comes from these adhesion areas. However, the correlation between and does not allow us to conclude whether is truly a more relevant parameter than . To constrain , we cultured cells on circular micropatterns of different sizes, so that was imposed by the disk shape ( = 520 ± 30 μm2 on 25-μm patterns, N = 12; = 760 ± 210 μm2 on 30-μm patterns, N = 10). We took advantage of the fact that still varied, = 0.16 ± 0.05 (mean ± SD), to study how the detachment force, , relates to . Interestingly, when detaching cells from the micropatterns, still scaled linearly with as in Eq. 3, and the values obtained for the critical stress, , were comparable to those obtained without micropatterns: 16,700 ± 5600 Pa without a micropattern (N = 16) versus 20,300 ± 5500 Pa on micropatterns (N = 12). Note that to account for the fibronectin thickness of the micropatterns, we considered a 60 nm threshold to define the adhesion areas on the IRM pictures—instead of 50 nm on petri dishes. Consequently, a single IRM picture of the cell-substrate interface should be sufficient to compute the aspiration force necessary to detach the cell at a given loading rate.
Membrane rupture does not entail cell detachment
The complete detachment process was also monitored in profile mode, in which the aspirated endothelial cell was visualized from the side under brightfield illumination (Fig. 2, D and E). We found that the cell membrane appeared to break systematically before detachment (Movie S3). To assess whether the membrane rupture was a triggering event for cell detachment, we performed in-plane experiments in the presence of propidium iodide in the surrounding medium. Propidium iodide is an intercalating agent that becomes fluorescent when it gains access to intracellular nucleic acids: membrane rupture is thus indicated by a sharp increase in fluorescence (see Movie S4). We measured the force at which the membrane broke for several pipette radii and compared it to the detachment force predicted by Eq. 2 (with = 1300 Pa). This computed detachment force was systematically higher than the force at which the membrane was observed to break, i.e., membrane rupture always occurred before cell detachment within this range of pipette radii (Fig. 5). In profile mode, we ran a second series of experiments in which we stopped aspirating and waited for 2 min immediately after membrane rupture. None of the 10 cells we tested detached during that period of time. At the end of this waiting period, we aspirated these cells again and verified that they could still resist a significant amount of aspiration before detaching. We ran a set of complementary experiments in in-plane mode. We applied an aspiration pressure of 5.5 kPa on cells in the presence of propidium iodide, until the rapid increase in fluorescence showed that the membrane was ruptured. As soon as rupture was detected, we set the aspiration pressure back to zero while leaving the micropipette in place, and we waited for up to 300 s. During the whole process, we imaged the cell-substrate interface with IRM at a rate of one image every 4 s. The quantification of these experiments showed that stayed relatively constant even in the presence of a broken membrane (see the Supporting Material, Fig. S3, and Movie S5).
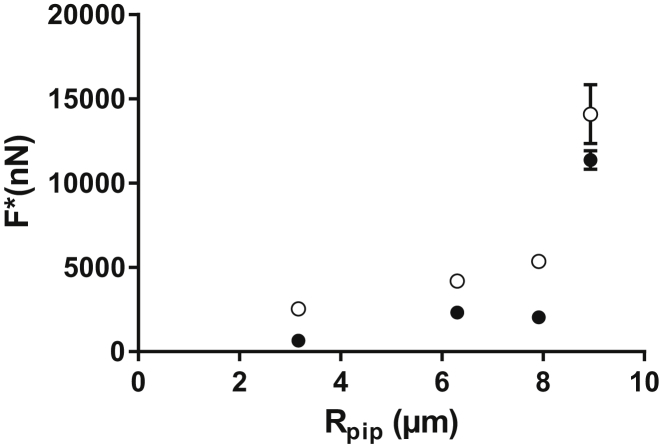
Figure 5.
Aspiration force at membrane rupture and detachment force. The force at rupture (●), based on experimental data, and the detachment force (○) are predicted using Eq. 2. The membrane systematically breaks before the cell detaches from the substrate. Error bars represent the standard error.
To test whether detachment force would still scale with in the absence of membrane rupture, we grew endothelial cells on a low-adhesion surface consisting of a glass coated with a low concentration of PLL-g-PEG molecules (see the Supporting Material). When left for 2 h to adhere, cells developed a limited . Detachment force in these conditions still scaled with both and (Fig. S4). The critical stress, = 1500 ± 500 (N = 9 cells), was very consistent with the one obtained on glass substrates, although = 4300 ± 2300 Pa was significantly lower (see the Supporting Material for further discussion).We ran another set of detachment experiments on cells grown on PLL-g-PEG in the presence of propidium iodide, and they showed that for the majority of cells (17 of 20 cells tested), the cell membrane did not break before detachment. These sets of experiments strongly suggest that membrane rupture does not necessarily lead to cell detachment, and that it has no influence on the scaling of detachment force with cell projected area. This suggests that membrane integrity is not essential for transmitting forces to the cell-substrate interface. The consideration that membrane rupture does not seem to influence the rupture force, together with our IRM observation of cells detaching first in the region directly beneath the micropipette instead of peeling from the outer rim toward the center, led us to conclude that the aspiration force is not transmitted to the substrate through membrane tension but rather through the whole cell body. In what follows, we then make the simplifying assumption that the adhesive bonds share the aspiration force in parallel.
Existence of intact adhesion area after cell detachment
As can be observed in Movie S2, some traces that appear dark in the IRM images can be seen after cell detachment. We examined whether the presence of what we will henceforth call dark traces was systematic. Indeed, after the detachment of each of nine cells, although these traces were hard to observe in brightfield illumination, they were systematically present in IRM (see Fig. S7). To investigate the nature of the dark traces, we performed immunostaining of the substrate after cells were detached and found that the dark traces were rich in vinculin (see the Supporting Material and Fig. S8). We quantified the area, , of these dark traces relative to measured before detachment. By using the same thresholding procedure of IRM images (see the Supporting Material) before and after detachment on N = 13 cells, we obtained = 0.06 ± 0.07. Thus, on average, 94% of all adhesive areas detach during cell detachment, so we made the simplifying assumption that we could neglect the potential contribution of the undetached adhesion area. However, this raised an interesting question about the process occurring locally to these remaining adhesion areas during cell detachment. One possible scenario is that at these locations, the membrane broke instead of adhesive bonds. We tried to test this hypothesis by running detachment experiments in the presence of propidium iodide while acquiring time lapses. We could not detect such local membrane rupture, and we only observed a major rupture close to the micropipette tip (as shown in Movies S2 and S5). These nanoscale membrane ruptures could still exist, but get repaired too quickly (24), thus avoiding diffusion of propidium inside the cell.
Dynamic force spectroscopy of cell adhesion: cell detachment force depends on the loading rate
Since the seminal work of Evans et al. and further developments by other groups in the field of dynamic force spectroscopy, it has been established that when submitted to a pulling force, f, increasing linearly in time, a single adhesive bond breaks at a force level that is stochastic due to thermal fluctuations and that the most probable value of this rupture force, , depends on the loading rate, i.e., the rate of force increase, (25–29). All of the aspiration experiments described above were performed with an aspirating pressure that increased linearly with time, so that the aspirating force applied to the cell at any time is given by
| (4) |
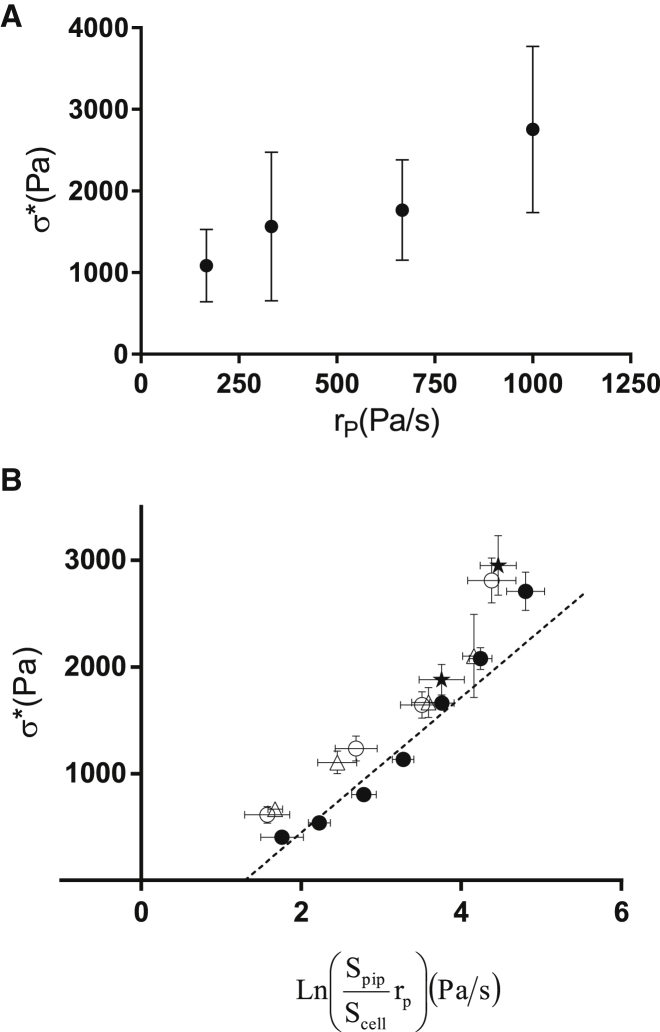
where is the applied aspiration pressure at time t, and the aspiration rate, , is the constant rate at which the aspiration pressure increases. As shown in Fig. 6 A, we find that the critical stress, , increases with the aspiration rate, .
Figure 6.
Critical stress as a function of the aspiration rate and master equation. (A) Critical stress versus aspiration rate, from experimental data. Error bars represent the standard deviation. (B) Critical stress versus for the conditions where varies while is constant (data points shown in A) (○), varies while is constant (●), cells are exposed to cytochalasin D (Δ), and cells are treated with nocodazole (★). All data collapse along the master curve, in good agreement with the prediction from Eq. 8. Error bars represent the standard error.
Making a number of simplifying assumptions, we can write a minimal model to rationalize our experimental results for the detachment dynamics, notably the relationship between detachment force, aspiration rate, and adhesive areas. As mentioned above, we first assume that the adhesive bonds share the aspiration force in parallel. Taking a mean-field approach, we assume that each adhesive bond breaks at the same rupture force, , and approximate the number of bonds, N, as , where is the average area occupied by a single biological adhesive bond. Assuming a negligible transmission of the aspiration force through the membrane, a quasistatic equilibrium between the aspiration force, , and the force shared by the N bonds adhering to the substrate is expressed as . Note that most experiments were conducted under brightfield illumination so that we measured instead of , but as the ratio is well-defined, we can write
| (5) |
which relates cell-scale stresses to molecular-scale forces. We further assume that for a single adhesive bond, the rupture force, , follows a slip-bond behavior with a single energy barrier dominating its dynamics (28,30,31),
| (6) |
where is the Boltzmann constant, the microscopic distance characteristic of the bond, and an off-rate (equivalently the inverse of a lifetime) under no applied force.
The loading rate of the bond is then
and hence,
| (7) |
Combining Eqs. 5–7, we obtain the master equation,
| (8) |
which predicts the dependence of on , , , , and the microscopic parameters , , and . This new expression for now captures the dependence on both the geometric parameters and .
Since and the pipette radius were our control parameters, we readily tested the dependency of on and independently. We maintained = 667 Pa/s constant while varying the pipette surface area from to (over N = 335 cells), or kept Spipette = constant while varying over four different trials, 167 Pa/s, 333 Pa/s, 667 Pa/s, and 1000 Pa/s (N = 55 cells). Based on data from the literature (32,33), we took for the average surface area per adhesive bond, and verified that the data satisfactorily collapsed on the master curve given by Eq. 8 (Fig. 6). A linear fit of the data in Fig. 6 B yields a slope of 634 Pa and an intercept with the y axis, at , of −821 Pa. Taking the average value = 0.09 and at room temperature, we obtain a characteristic lengthscale of = 0.11 nm and an off rate of 0.006 .
This off rate is consistent with values obtained in single-molecule force spectroscopy; for instance, Evans et al. measured zero-force off rates ranging from to s−1. However, although a microscopic distance, , of only 0.1 nm is not unrealistic compared to distances measured in other bonds (34), larger microscopic distances ranging from 0.4 to 0.6 nm were measured for ICAM1- integrin bonds (35,36).
Note that to keep our model simple, we neglected the stochastic nature of the bond rupture by assuming that all bonds would all break at the most probable rupture force, , and implicitly considered that once broken, adhesive bonds could not reform. However, we are applying very weak loading rates on each bond ( pN/s), and rebinding might play a role. Litvinov et al. (32) found much larger off rates for fibrinogen-integrin interactions than we did in this study, on the order of . This large discrepancy with our value for could be a signature of the rebinding that we neglected in our model. Another major assumption we made was to consider slip bonds, although evidence of both slip and catch bonds was reported for integrins (see Zhang et al. (37,38), Li et al. (39), and Jiang et al. (40) for slip bonds and a more recent work by Jiang et al. (41) for catch bonds). One technical advantage of considering slip bonds is that the relationship between the rupture force, , of a single slip bond submitted to a loading rate is simple and involves only two microscopic parameters. On the other hand, there are multiple catch-bond models, and they involve more parameters (30,42).
The master equation (Eq. 8) underestimates the detachment stress, , at large values of , i.e., at large loading rates, according to Eq. 7: this might be due to our model for the dynamics of adhesive bonds, as it has been shown that the dynamics of some adhesive bonds are dictated by more than one major energy barrier (26,28). To take this into account, Eq. 6 could be refined to include multiple linear terms in the relationship between and , with coefficients depending on the energy barrier governing the dissociation dynamics (26,28,29,43). Nevertheless, our simple model captures well the dependence on geometric parameters (, , ), on intrinsic characteristics of adhesive bonds ( and ), and notably on the rate at which the aspiration pressure is applied. This validates our global picture of detachment dynamics relying on adhesive areas sharing the aspiration stress in parallel.
Effect of cytoskeletal inhibitors
To assess the role of the cytoskeleton, we also investigated the effect of actin depolymerization. To do so, we incubated cells for 30 min with a high concentration of cytochalasin D (). The cells affected by the drug displayed a starlike form instead of the convex polygonal shapes of untreated cells (see Fig. S9), but showed only a slight decrease in their ratio in the remaining cell area ( = 0.07 ± 0.02, N = 30, in the presence of cytochalasin D, versus 0.09 ± 0.04, N = 16, without cytochalasin D). We could roughly estimate before treatment by measuring the surface of the convex polygon in which the cell surface is inscribed. Such a rough estimate made on five cells led us to assume that was reduced by a factor of 0.7 ± 0.1 by cytochalasin D. The fact that is comparable to untreated cells means that both and were affected by cytochalasin D. Interestingly, even though we again varied the aspiration rate, the measured collapsed on the same master curve defined by Eq. 8 (see Fig. S10). We further investigated the potential role of cytoskeleton by destabilizing the microtubule network with nocodazole. We obtained an adhesion area, , that was larger relative to than in the control case without nocodazole ( = 0.17 ± 0.09%, N = 15), consistent with the slightly higher values for than would have been predicted by the master curve for a comparable aspiration rate and pipette diameter (Fig. 6 B). These experiments with cytoskeletal inhibitors show that to be transmitted to the substrate, the aspiration force does not require an intact actin or microtubule cytoskeleton. Although this might be surprising, it is worth noting that force (stress) can be transmitted through a pure liquid, in the same way that aspiration force (pressure) is transmitted through the water inside the body of the micropipette. Hence, one can envision that a solid-like cytoskeletal meshwork is not necessarily required to transmit the forces that detach the cell.
Comparison with other studies
Although direct comparison is not straightforward, we can place our results in the context of the literature on cell detachment. Experiments on biotinylated red blood cells adhering to streptavidin-coated surfaces (4) also led to a detachment process in two phases. During the first phase, the contact radius slowly decreased, and then the adhesive contact underwent a “catastrophe-like” diminution until separation (4). We do not see a slow reduction of adhesion area in our experiments, but the catastrophic diminution of adhesive area found in that study quite matches what we observe. Those authors also introduced a critical force, , over which the adhesive contact cannot withstand a force in static conditions, where W is the adhesion energy per unit area and the contact radius. From their critical force, we can estimate a critical stress, , as 100 Pa. Shortly before the Pierrat et al. study, Prechtel et al. (44) ran similar experiments but with vesicles decorated with lipopeptides and adhering to endothelial cells via integrins. Those authors also observed very rapid detachment of the vesicle (within ∼40 ms). They performed experiments at larger loading rates than ours, but extrapolating their rupture force versus loading-rate relationship leads to detachment forces as low as 100 pN for adhesive patches of typical radius 1 , hence a critical stress of only tens of pascals. Francis et al. (9) used flexible aspirating micropipettes as cantilevers to detach red blood cells and Dictyostelium discoideum amoeba from hydrophobic or hydrophilic substrates while monitoring the adhesion areas with IRM. For red blood cells, they obtained detachment forces of ∼1 nN for an adhesion area of ∼ 0.3 , based on which we can estimate a critical stress of ∼ 3000 Pa. For the detachment of Dictyostelium discoideum, the authors found a detachment force of ∼10 nN for an adhesion area of ∼2 , leading to a critical-stress value of ∼ 5000 Pa, close to the one they obtained with red blood cells. We have information neither on the loading rate used nor on the ratio in that case, but based on the figures by Francis et al. (9), we can roughly estimate that ∼ 0.3, so that 1000 Pa. These values are larger than the one estimated above based on studies by Pierrat et al. and Prechtel et al., but one major reason might be that the latter groups used specific bonds, whereas Francis et al. used a hydrophilic or hydrophobic glass substrate with no serum in the medium (hence no extracellular matrix molecules). We stress that a difference in the red blood cell detachment in the above-mentioned studies is that the force was expected by the authors to act only at the perimeter of the adhesion zone, in a ring of finite width (44), as opposed to our case, where force is shared by adhesive bonds in parallel. Coman used microneedles to pull on cell-cell adhesions (6,7) and obtained typical rupture forces of nN (1 mg) for nontumoral cells, but without including information about the cell-cell adhesion area. By (roughly) estimating lateral contact between the epithelial cells used by Coman as ∼100 , we obtain a critical-stress estimate of Pa, much larger than our measurements, although with no information about the applied loading rate and allowing for the fact that we may be overestimating the area and cell-cell contacts. Ryu et al. (8) pulled with a nanoneedle on cells covered with a proteic scaffold and obtained detachment forces of ∼500 nN. By estimating the area of the cell-substrate interface as ∼100 , we can estimate a critical stress of ∼5 kPa. The authors used nanoneedles of spring constant ∼1 N/m and a retraction velocity of 5 μm/s, leading to a force increasing at a rate of 5000 nN/s, which, because it is larger than the maximal loading rate (on the whole cell) of ∼ 700 nN/s used in this study, makes their larger critical-stress value consistent with our measurements. In a different experimental configuration, Salánki et al. performed detachment assays using an aspirating micropipette held near (but not in contact with) an adhering cell, with a stepwise increment in aspiration pressure (16). The detachment force was not measured but rather was computed using fluid-flow simulations, and they obtained typical values of 2000 nN. Their cells had a projected area of 500–700 , yielding a typical stress of 3000–4000 Pa that might be consistent with our measured critical stress . However, Salánki et al. did not correlate the detachment force with the cell projected area for a given cell type, so it is difficult to speculate whether their data regarding applied loading rate are directly comparable to ours.
Regarding techniques that employ cell detachment by shear, a study using a cantilever of known stiffness to measure the force necessary to scrape cells from their substrate found a constant critical shear stress of 530–750 Pa (11,12). Since their cantilever stiffness was 3.12 and its approach velocity 20 , the loading rate applied to the cell was . At our highest aspiration rate, , and our largest , we impose a loading rate on the whole cell of ∼ 700 , which corresponds to a critical stress of ∼ 3000 Pa (Fig. 6 B), which is larger compared to their critical shear stress (11,12) and would be even larger if we were to interpolate to a higher loading rate. Studies performed in microfluidic channels apply a fluid shear stress to a cell population. Klein et al. (18) increased the shear stress in a stepwise manner and measured a critical fluid shear stress of 3–4 Pa over which 50% of adhered cells would detach. Assuming that this value is representative of a critical stress obtained by shearing cells, this is very small compared to all of the previously mentioned studies, including ours. However, the authors used a model to deduce adhesion forces of ∼200 nN and ∼300 nN per cell for two different cell types. By dividing by the measured projected cell areas of ∼300 and ∼80 , respectively, we can estimate critical stress values of 700 and 400 Pa, respectively, for the two cell types used in that study. It is not clear whether this critical stress is not strongly model-dependent, or whether it can be considered as a critical stress that would be obtained by pulling cells, whereas the critical fluid shear stress of only a few pascals is representative of the critical stress obtained by a dezipping of adhesion molecules. Finally, Christ et al. (17) measured a critical fluid shear stress of 50–100 Pa.
Overall, our measurements are in better agreement with pulling techniques (6–9) than with shearing techniques (11,12,17,18). Scrapping might be more similar to an unzipping of the adhesion molecules on a frontline, as opposed to our situation, where adhesive bonds seem to withstand the pulling force in parallel.
Conclusions
We have developed, to our knowledge, a new micropipette-based technique to quantify adhesion force at the single-cell level. This technique enables us to fully probe the influence of geometric parameters such as projected cell area, adhesion areas, and micropipette size, as well as dynamical parameters such as the loading rate. We found cell detachment to be a well-defined event and established a clear correlation between the detachment force and the cell adhesion area. Furthermore, we demonstrated that the detachment force is not a constant but depends on how the force is applied to the cell. Finally, a minimalist model helped us rationalize how the critical stress characterizing cell detachment depends on the cell adhesive area, intrinsic parameters of the adhesive bonds, and the rate at which the force is applied to the cell. We showed that we can predict the force necessary to detach a cell from a substrate by acquiring a single IRM picture of that cell and measuring the area covered by the adhesive bonds. In the context of leukocyte-endothelium interactions, it is therefore reasonable to postulate that the formation of microgaps after monocyte adhesion, described by Kataoka et al. (3), should be detectable directly through IRM. We believe this technique should prove useful for studying in detail the changes at the single-endothelial-cell level induced by monocyte adhesion. It would also be interesting to test how the adhesion of other leukocytes affects the mechanical properties of endothelial cells. Kang et al. (45) have shown that neutrophil adhesion induces a local decrease in endothelial stiffness at the adhesion point that lasts <1 min, but also a stiffness increase in adjacent endothelial cells. Forthcoming results on monocyte and lymphocyte adhesion should help elucidate whether those changes are a universal mechanical response of endothelial cells to the adhesion of leukocytes, or whether these cells can adapt their response to the type of leukocyte adhering to them.
Author Contributions
J.H. designed the research; B.H., A.B., and Y.H. performed the research; B.H. and J.H. analyzed the data; and B.H., A.I.B., and J.H. wrote the article.
Acknowledgments
The authors acknowledge Julie Lafaurie-Janvore for introducing them to the micropatterning technique. J.H. acknowledges Caroline Foubert, Caroline Frot, Daniel Guy, Antoine Garcia, Delphine L’Huillier, and Do Chi Toai Vu for technical support and David Gonzalez-Rodriguez and Maria-Elisabetta Serrentino for fruitful discussions.
This work was supported by a permanent endowment in cardiovascular cellular engineering from the AXA Research Fund.
Editor: Cecile Sykes.
Footnotes
Supporting Results and Discussion, ten figures, and five movies and are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00597-4.
Supporting Material
The projected area of the three cells is shown in Fig. 2 B. The cell on the right corresponds to Fig. 2 C. The acquisition was performed at one frame per second, and the movie plays at 20 frames per second (i.e., time accelerated 20 times).
The arrows indicate dark areas that correspond to adhesive areas of the cell to its substate. The acquisition was performed at one frame per second, and the movie plays at 20 frames per second (i.e., time accelerated 20 times).
The movie corresponds to Fig. 2 E. The acquisition was performed at one frame per second, and the movie plays at 10 frames per second (i.e., time accelerated 10 times). The arrow indicates membrane rupture.
When the cell membrane breaks, propidium iodide gains access to intracellular nucleic acids and becomes fluorescent. The scale bar is 10 μm. The acquisition was performed at one frame per second, and the movie plays at 5 frames per second (i.e., time accelerated 5 times).
A 5.5 kPa-aspiration pressure is applied to a cell imaged with IRM (left). The contour of the adhesion areas have been superimposed in white. When the cell membrane breaks, propidium iodide gains access to intracellular nucleic acids and becomes fluorescent (right). The scale bars are 10 μm. The acquisition was performed at one frame every 4 seconds, and the movie plays at 20 frames per second (i.e., time accelerated 80 times).
References
- 1.Zaidel-Bar R., Geiger B. The switchable integrin adhesome. J. Cell Sci. 2010;123:1385–1388. doi: 10.1242/jcs.066183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ross R. Atherosclerosis—an inflammatory disease. N. Engl. J. Med. 1999;340:115–126. doi: 10.1056/NEJM199901143400207. [DOI] [PubMed] [Google Scholar]
- 3.Kataoka N., Iwaki K., Kajiya F. Measurements of endothelial cell-to-cell and cell-to-substrate gaps and micromechanical properties of endothelial cells during monocyte adhesion. Proc. Natl. Acad. Sci. USA. 2002;99:15638–15643. doi: 10.1073/pnas.242590799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pierrat S., Brochard-Wyart F., Nassoy P. Enforced detachment of red blood cells adhering to surfaces: statics and dynamics. Biophys. J. 2004;87:2855–2869. doi: 10.1529/biophysj.104.043695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Erdmann T., Schwarz U.S. Adhesion clusters under shared linear loading: a stochastic analysis. Europhys. Lett. 2004;66:603–609. [Google Scholar]
- 6.Coman D.R. Decreased mutual adhesiveness, a property of cells from squamous cell carcinomas. Cancer Res. 1944;4:625–629. [Google Scholar]
- 7.Coman D.R. Adhesiveness and stickiness: two independent properties of the cell surface. Cancer Res. 1961;21:1436–1438. [PubMed] [Google Scholar]
- 8.Ryu S., Hashizume Y., Nakamura C. Measurement of cell adhesion force by vertical forcible detachment using an arrowhead nanoneedle and atomic force microscopy. Biochem. Biophys. Res. Commun. 2014;451:107–111. doi: 10.1016/j.bbrc.2014.07.078. [DOI] [PubMed] [Google Scholar]
- 9.Francis G.W., Fisher L.R., Gingell D. Direct measurement of cell detachment force on single cells using a new electromechanical method. J. Cell Sci. 1987;87:519–523. doi: 10.1242/jcs.87.4.519. [DOI] [PubMed] [Google Scholar]
- 10.Colbert M.J., Raegen A.N., Dalnoki-Veress K. Adhesion and membrane tension of single vesicles and living cells using a micropipette-based technique. Eur. Phys. J. E Soft Matter. 2009;30:117–121. doi: 10.1140/epje/i2009-10514-7. [DOI] [PubMed] [Google Scholar]
- 11.Yamamoto A., Mishima S., Sumita M. A new technique for direct measurement of the shear force necessary to detach a cell from a material. Biomaterials. 1998;19:871–879. doi: 10.1016/s0142-9612(97)00248-2. [DOI] [PubMed] [Google Scholar]
- 12.Sagvolden G., Giaever I., Feder J. Cell adhesion force microscopy. Proc. Natl. Acad. Sci. USA. 1999;96:471–476. doi: 10.1073/pnas.96.2.471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Athanassiou G., Deligianni D. Adhesion strength of individual human bone marrow cells to fibronectin. Integrin β1-mediated adhesion. J. Mater. Sci. Mater. Med. 2001;12:965–970. doi: 10.1023/a:1012809115479. [DOI] [PubMed] [Google Scholar]
- 14.Sung K.L., Sung L.A., Chien S. Determination of junction avidity of cytolytic T cell and target cell. Science. 1986;234:1405–1408. doi: 10.1126/science.3491426. [DOI] [PubMed] [Google Scholar]
- 15.Martinez-Rico C., Pincet F., Dufour S. Integrins stimulate E-cadherin-mediated intercellular adhesion by regulating Src-kinase activation and actomyosin contractility. J. Cell Sci. 2010;123:712–722. doi: 10.1242/jcs.047878. [DOI] [PubMed] [Google Scholar]
- 16.Salánki R., Hős C., Szabó B. Single cell adhesion assay using computer controlled micropipette. PLoS ONE. 2014;9:e111450. doi: 10.1371/journal.pone.0111450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Christ K.V., Turner K.T. Methods to measure strength of cell adhesion to substrates. J. Adhes. Sci. Technol. 2010;24:2027–2058. [Google Scholar]
- 18.Klein K., Rommel C.E., Spatz J.P. Cell membrane topology analysis by RICM enables marker-free adhesion strength quantification. Biointerphases. 2013;8:28. doi: 10.1186/1559-4106-8-28. [DOI] [PubMed] [Google Scholar]
- 19.Azioune A., Storch M., Piel M. Simple and rapid process for single cell micro-patterning. Lab Chip. 2009;9:1640–1642. doi: 10.1039/b821581m. [DOI] [PubMed] [Google Scholar]
- 20.Edelstein A., Amodaj N., Stuurman N. Computer control of microscopes using μManager. Curr. Protoc. Mol. Biol. 2010;Chapter 14:20. doi: 10.1002/0471142727.mb1420s92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schneider C.A., Rasband W.S., Eliceiri K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods. 2012;9:671–675. doi: 10.1038/nmeth.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pierres A., Benoliel A.M., Bongrand P. Cell fitting to adhesive surfaces: a prerequisite to firm attachment and subsequent events. Eur. Cell. Mater. 2002;3:31–45. doi: 10.22203/ecm.v003a04. [DOI] [PubMed] [Google Scholar]
- 23.Curtis A.S.G. The mechanism of adhesion of cells to glass. A study by interference reflection microscopy. J. Cell Biol. 1964;20:199–215. doi: 10.1083/jcb.20.2.199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Andrews N.W., Almeida P.E., Corrotte M. Damage control: cellular mechanisms of plasma membrane repair. Trends Cell Biol. 2014;24:734–742. doi: 10.1016/j.tcb.2014.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Evans E., Ritchie K., Merkel R. Sensitive force technique to probe molecular adhesion and structural linkages at biological interfaces. Biophys. J. 1995;68:2580–2587. doi: 10.1016/S0006-3495(95)80441-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Merkel R., Nassoy P., Evans E. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 1999;397:50–53. doi: 10.1038/16219. [DOI] [PubMed] [Google Scholar]
- 27.Dudko O.K., Filippov A.E., Urbakh M. Beyond the conventional description of dynamic force spectroscopy of adhesion bonds. Proc. Natl. Acad. Sci. USA. 2003;100:11378–11381. doi: 10.1073/pnas.1534554100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pincet F., Husson J. The solution to the streptavidin-biotin paradox: the influence of history on the strength of single molecular bonds. Biophys. J. 2005;89:4374–4381. doi: 10.1529/biophysj.105.067769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Husson J., Pincet F. Analyzing single-bond experiments: influence of the shape of the energy landscape and universal law between the width, depth, and force spectrum of the bond. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;77:026108. doi: 10.1103/PhysRevE.77.026108. [DOI] [PubMed] [Google Scholar]
- 30.Evans E., Leung A., Zhu C. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA. 2004;101:11281–11286. doi: 10.1073/pnas.0401870101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dembo M., Torney D.C., Hammer D. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. B Biol. Sci. 1988;234:55–83. doi: 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
- 32.Litvinov R.I., Mekler A., Weisel J.W. Resolving two-dimensional kinetics of the integrin αIIbβ3-fibrinogen interactions using binding-unbinding correlation spectroscopy. J. Biol. Chem. 2012;287:35275–35285. doi: 10.1074/jbc.M112.404848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Selhuber-Unkel C., López-García M., Spatz J.P. Cooperativity in adhesion cluster formation during initial cell adhesion. Biophys. J. 2008;95:5424–5431. doi: 10.1529/biophysj.108.139584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Merkel R. Force spectroscopy on single passive biomolecules and single biomolecular bonds. Phys. Rep. 2001;346:343–385. [Google Scholar]
- 35.Evans E., Kinoshita K., Leung A. Long-lived, high-strength states of ICAM-1 bonds to β2 integrin, I: lifetimes of bonds to recombinant αLβ2 under force. Biophys. J. 2010;98:1458–1466. doi: 10.1016/j.bpj.2009.09.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kinoshita K., Leung A., Evans E. Long-lived, high-strength states of ICAM-1 bonds to β2 integrin, II: lifetimes of LFA-1 bonds under force in leukocyte signaling. Biophys. J. 2010;98:1467–1475. doi: 10.1016/j.bpj.2009.12.4316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhang X., Wojcikiewicz E., Moy V.T. Force spectroscopy of the leukocyte function-associated antigen-1/intercellular adhesion molecule-1 interaction. Biophys. J. 2002;83:2270–2279. doi: 10.1016/S0006-3495(02)73987-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhang X., Chen A., Goligorsky M.S. Atomic force microscopy measurement of leukocyte-endothelial interaction. Am. J. Physiol. Heart Circ. Physiol. 2004;286:H359–H367. doi: 10.1152/ajpheart.00491.2003. [DOI] [PubMed] [Google Scholar]
- 39.Li F., Redick S.D., Moy V.T. Force measurements of the α5β1 integrin-fibronectin interaction. Biophys. J. 2003;84:1252–1262. doi: 10.1016/S0006-3495(03)74940-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Jiang G., Giannone G., Sheetz M.P. Two-piconewton slip bond between fibronectin and the cytoskeleton depends on talin. Nature. 2003;424:334–337. doi: 10.1038/nature01805. [DOI] [PubMed] [Google Scholar]
- 41.Kong F., García A.J., Zhu C. Demonstration of catch bonds between an integrin and its ligand. J. Cell Biol. 2009;185:1275–1284. doi: 10.1083/jcb.200810002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pereverzev Y.V., Prezhdo O.V., Thomas W.E. The two-pathway model for the catch-slip transition in biological adhesion. Biophys. J. 2005;89:1446–1454. doi: 10.1529/biophysj.105.062158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bartolo D., Derényi I., Ajdari A. Dynamic response of adhesion complexes: beyond the single-path picture. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:051910. doi: 10.1103/PhysRevE.65.051910. [DOI] [PubMed] [Google Scholar]
- 44.Prechtel K., Bausch A.R., Merkel R. Dynamic force spectroscopy to probe adhesion strength of living cells. Phys. Rev. Lett. 2002;89:028101. doi: 10.1103/PhysRevLett.89.028101. [DOI] [PubMed] [Google Scholar]
- 45.Kang I., Wang Q., Doerschuk C.M. Effect of neutrophil adhesion on the mechanical properties of lung microvascular endothelial cells. Am. J. Respir. Cell Mol. Biol. 2010;43:591–598. doi: 10.1165/rcmb.2006-0381OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The projected area of the three cells is shown in Fig. 2 B. The cell on the right corresponds to Fig. 2 C. The acquisition was performed at one frame per second, and the movie plays at 20 frames per second (i.e., time accelerated 20 times).
The arrows indicate dark areas that correspond to adhesive areas of the cell to its substate. The acquisition was performed at one frame per second, and the movie plays at 20 frames per second (i.e., time accelerated 20 times).
The movie corresponds to Fig. 2 E. The acquisition was performed at one frame per second, and the movie plays at 10 frames per second (i.e., time accelerated 10 times). The arrow indicates membrane rupture.
When the cell membrane breaks, propidium iodide gains access to intracellular nucleic acids and becomes fluorescent. The scale bar is 10 μm. The acquisition was performed at one frame per second, and the movie plays at 5 frames per second (i.e., time accelerated 5 times).
A 5.5 kPa-aspiration pressure is applied to a cell imaged with IRM (left). The contour of the adhesion areas have been superimposed in white. When the cell membrane breaks, propidium iodide gains access to intracellular nucleic acids and becomes fluorescent (right). The scale bars are 10 μm. The acquisition was performed at one frame every 4 seconds, and the movie plays at 20 frames per second (i.e., time accelerated 80 times).