Summary
The hippocampus is essential for spatiotemporal cognition. Sequences of neuronal activation provide a substrate for this fundamental function. At the behavioral timescale, these sequences have been shown to occur either in the presence of successive external landmarks or through internal mechanisms within an episodic memory task. In both cases, activity is externally constrained by the organization of the task and by the size of the environment explored. Therefore, it remains unknown whether hippocampal activity can self-organize into a default mode in the absence of any external memory demand or spatiotemporal boundary. Here we show that, in the presence of self-motion cues, a population code integrating distance naturally emerges in the hippocampus in the form of recurring sequences. These internal dynamics clamp spontaneous travel since run distance distributes into integer multiples of the span of these sequences. These sequences may thus guide navigation when external landmarks are reduced.
Highlights
-
•
Without external cues, hippocampal dynamics spontaneously display recurring sequences
-
•
Recurring sequences span across a fixed traveled distance
-
•
Sequences are an internal cognitive template that shapes mouse behavior
-
•
Sequences display an internally hardwired functional structure
The hippocampus supports spatiotemporal cognition. Using calcium imaging in the hippocampus of awake mice, Villette and Malvache et al. show that stereotyped sequences of neuronal activation, integrating spatiotemporal components of behavior, spontaneously recur, without any external drive, under the influence of self-motion.
Introduction
Hippocampal networks can display sequences of neuronal activation at the temporal resolution of behavior, or compressed within the period of network oscillations (Buzsáki, 2010). The occurrence and organization of these sequences are thought to underlie numerous fundamental operations of the hippocampus, from the sensing of sensory cues and building a cognitive map of the environment, to mnemonic and planning functions (Dragoi and Tonegawa, 2011; Skaggs and McNaughton, 1996; Wilson and McNaughton, 1994). At the behavioral timescale, these sequences were first shown to occur in the presence of external landmarks that provide successive cues organizing neuronal activity through exteroception. For example, hippocampal place cells are sequentially activated at consecutive positions in space when a rodent explores an environment naturally delivering serially ordered external landmarks (Dragoi and Buzsáki, 2006), even when only tactile and visual cues are provided (Royer et al., 2012). However, the sequential activation of hippocampal neurons at the behavioral timescale can also be disengaged from external landmarks and instead occur in the absence of changing sensory or feedback cues. This involves self-organized internal mechanisms but happens within a behaviorally relevant context—for example, during the delay period of a memory task (Itskov et al., 2011; Kraus et al., 2013; Pastalkova et al., 2008; Wang et al., 2014).
To some extent, the reward that guides an animal’s behavior within a defined task also provides an external drive on hippocampal dynamics. Hence, so far it remains unknown whether hippocampal activity can also be organized at population level in the absence of any driving external goal. It is also unknown whether the span of hippocampal sequences is intrinsically predetermined in time or space in the absence of any temporal and spatial boundary. Indeed, both externally and internally triggered sequences observed until now at the timescale of behavior always cover a finite spatial and temporal extent that is constrained by external factors such as the temporal organization of the task (Pastalkova et al., 2008) or the size of the environment explored in space (Ravassard et al., 2013). This is an important issue, since it defines the intrinsic determinants and behavioral reach of hippocampal population coding.
Here, large-scale two-photon calcium imaging was used to capture population dynamics while resolving single-cell behavior in the CA1 region of awake mice. A simple experimental paradigm was implemented to record spontaneous dynamics while minimizing the influence of external spatiotemporal landmarks or limits, which allows separating the contributions of time, distance, and external motivation to neuronal firing. In these conditions, we show that hippocampal dynamics self-organize into sequences of neuronal activation recurring one after another within discrete run epochs and each spanning accross a fixed traveled distance. These recurring sequences translate into a behavioral correlate, since spontaneous run epochs display some stereotypy: they distribute as multiple integers of the distance unit represented in the sequences. We propose that such sequences could be a default internal dynamic template for spatiotemporal processing in the hippocampus.
Results
Recurring Sequences of Neuronal Activation in CA1 under the Presence of Self-Motion Cues
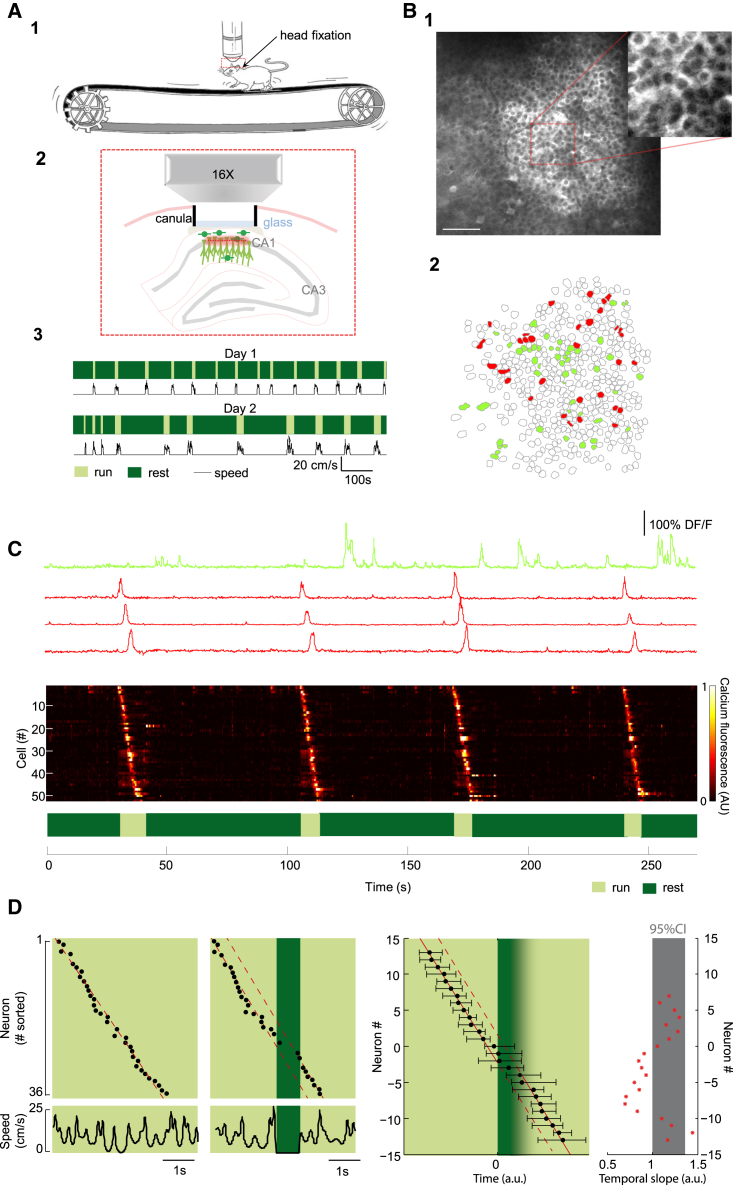
To observe hippocampal dynamics, we examined the spatiotemporal distribution of neuronal activity in the CA1 pyramidal layer using two-photon calcium imaging of awake head-restrained mice allowed to self-regulate their motion in the dark on a nonmotorized treadmill (Royer et al., 2012) (Figure 1A). In contrast to previous studies, we chose not to deprive mice of water or food so that their behavior was not guided toward receiving any reward. In this way, during each daily imaging session, mice spontaneously traveled on the track through the alternation of run epochs (interquartile range 4–10 s; see Figure S1 available online) and rest epochs (from 10 to 74 s; Figure 1A). Within run epochs, mice moved at various speeds (average 10.4 cm/s, range: 5–20 cm/s) and displayed short periods of immobility (< 2 s; Figures 1D and S1; see Experimental Procedures). To map neuronal activity across consecutive days, we used a viral vector (AAV2/1.syn-GCaMP5G) that makes GABAergic and glutamatergic CA1 neurons express the calcium indicator GCaMP5 (Akerboom et al., 2012). In order to image from a large population of neurons (∼1,000 cells, Figure 1), we used a low-magnification objective that allows for imaging a 400 × 400 μm2 field of view centered on the stratum pyramidale (Figure 1B) after surgical implantation of a chronic glass window on the hippocampus (Dombeck et al., 2010). This surgical procedure was previously shown to allow for the reliable recording of place cell activity (Dombeck et al., 2010), and we show it has no impact on exploratory activity (Figure S2).
Figure 1.
CA1 Dynamics Display Recurring Sequences of Neuronal Activation during Run Epochs
(A) (A1) Cartoon of the experimental setup with the mouse head-fixed below the objective (allowing for two-photon imaging, red box, A2) but free to run on a non-motorized treadmill. (A2) Schematic of the imaging conditions. (A3) Representative behavior on two imaging sessions shows alternation between run (light) and rest (dark) periods. Corresponding speed as a function of time is displayed below (black).
(B) (B1) Two-photon in vivo GCAMP5 fluorescence image of the CA1 pyramidal layer; scale bar, 100 μm. (B2) Contour map of imaged cells with neurons recruited in a sequence (red), and other active neurons (green).
(C) Individual calcium fluorescence signals as a function of time (top) of one representative cell displaying sustained firing (green) and three cells (red) recruited in four consecutive sequences visible on the rasterplot (middle) displaying a heatmap of the signal of all the neurons involved. Corresponding mouse behavior is indicated on the box below.
(D) (Left) Rasterplots of neuronal activation as a function of time for two sequences occurring either during continuous run or including a short immobility period (dark green) and slope fit (red line); bottom plots indicate mouse speed as a function of time. Right rasterplot represents the pooled distribution of neuronal activation onsets (median and interquartile range) for all the sequences including a short immobility period, taking the start of the pause as a time reference (time 0, neuron #0, n = 91 pauses, 5 sessions, 3 mice). Temporal slopes before and after the pauses are indicated (red lines). Right plot shows the evolution of the normalized temporal slope (red); 95% confidence interval is indicated (CI, gray area, see Experimental Procedures).
After three to five habituation sessions, mice running on an empty self-paced treadmill in the dark were imaged (Figure 1A), an experimental configuration that allows studying CA1 dynamics under the sole influence of self-motion cues. Spontaneous behavior remained highly variable and did not display any significant repetition pattern from one day to the next (Figures S1C–S1F). This lack of behavioral stereotypy enabled disentangling the relative contributions of time and distance to the firing of neurons. Most of the activity was observed during run epochs (Figure 1C). Unexpectedly (Kentros et al., 2004; Pastalkova et al., 2008), out of 65 imaging sessions (Figure S1G), we found that CA1 dynamics displayed recurring sequences of neuronal firing exclusively during run epochs in 28 imaging sessions (five mice; Figure 1C; Movie S1). Statistical analysis using data reshuffling established that sequences were not occurring by chance (p < 0.001, see Experimental Procedures). These sequences repeatedly engaged a sparse and scattered neuronal population that represented about 5% of all imaged neurons and 36% of the total fraction of active cells during run (Figure 1B). Cells engaged in these sequences were spatially intermingled with other run active cells that displayed variable activity patterns (Figures 1B and 1C), including sustained firing (25% of active cells, Figure 1C), or uncorrelated and sparse activation onsets (39% of active cells, Figure S3). Recent studies have addressed the relative influence of external sensory cues or behavioral context on the patterning of hippocampal dynamics, and it is now well established that, at the single-cell level, these can be controlled by absolute or relative location and time depending on the available and relevant stimulus for the task at hand (Aghajan et al., 2014; Chen et al., 2013; Itskov et al., 2011; Kraus et al., 2013; Ravassard et al., 2013). We thus asked whether the sequences of neuronal activation observed here were driven by absolute location or time. We can exclude a modulation of neuronal firing by the absolute position on the treadmill (as could occur if an undetected cue was left on the track) since (1) sequence recurrence never matched the length of the treadmill (180 cm, Figure 2D) and (2) as expected from a 0.05 statistical cutoff, less than 5% of the cells recruited in sequences displayed significantly location-modulated activation (1,048 cells out of 28 sessions, p < 0.05, Kolmogorov-Smirnoff uniformity test on firing onset distribution along the treadmill, Figure 2E). Similarly, sequences could not be integrating absolute elapsed time because (1) sequences could repeat one after another either within the same run epoch (defined as periods where speed exceeds 2 cm/s, Figure 3A) or separated by rest periods of variable duration (Figures 1A and S1); and (2) sequences could be transiently perturbed during short immobility gaps (Figure S1) and then resumed when running restarted, since the slope during the pause was significantly different from that before and after it (Figure 1D). Thus the sequences observed are independent from absolute time or location. Analysis was therefore next restricted only to run epochs in order to determine whether neuronal sequences were constrained by the integration of time or distance during mouse travel.
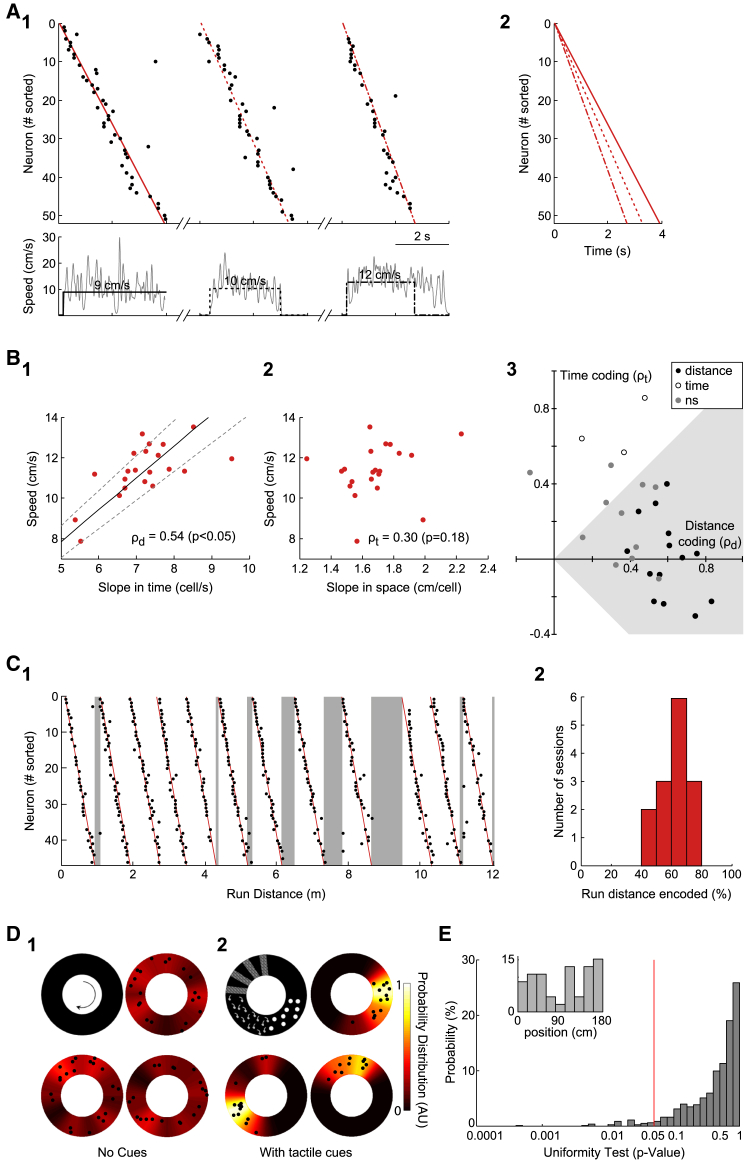
Figure 2.
Distance-Modulated Sequences
(A) (A1) Rasterplots of neuronal activation as a function of run time (black) and robust fits (red) of three sequences occurring at different running speeds (bottom, raw data gray, median speed black). (A2) Superimposed fits for the three examples in (A1).
(B) (B1) Graph of speed versus temporal slope for each sequence (dots) recorded in this representative imaging session; solid line indicates fit through origin while dashed line indicates ±10% interval (slope, 0.64 cell/cm). (B2) Graph plotting speed versus spatial slope for the same set of sequences (dots). Spearman correlation coefficient and corresponding p value are indicated. (B3) Graph plotting, for each imaging session (n = 28 sessions, 5 mice), the Spearman correlation coefficients for the spatial (ρt) and the temporal slope (ρd). Many sessions fell in the area where more information is carried by run distance (gray). Significant sessions for distance, time or nonsignificant representations are indicated by black, open or gray dots, respectively.
(C) (C1) Representative rasterplot of neuronal activation as a function of run distance displaying successive sequences within an imaging session. Sequences were recurring but separated by gaps of non-encoded run distance (gray areas). (C2) Histogram plotting the distribution of 14 imaging sessions as a function of the fraction of the total run distance encoded within a distance sequence.
(D) Polar representation of the firing field of representative neurons with 360° corresponding to one lap as schematized on the top left; firing probability is represented by the heatmap while black dots indicate activation onsets; three cells from an experiment on an empty treadmill (D1), three with tactile cues (D2). Heatmap represents the probability distribution of activation onsets.
(E) p values obtained from the uniformity test (Kolmogorov-Smirnoff) applied to the distribution of firing onsets of individual cells along the track (1,048 cells, pooled data over all sessions displaying sequences); red line indicates the statistical threshold (0.05). (Inset) Representative distribution of the onsets of one cell displaying a uniform distribution (p = 0.43).
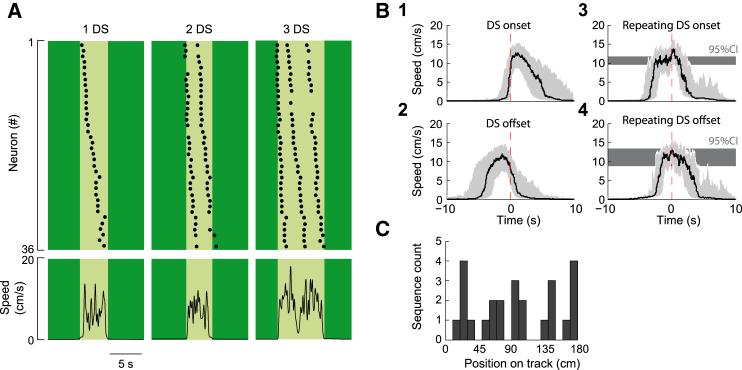
Figure 3.
Distance-Modulated Sequences Can Repeat One after the Other within a Continuous Run
(A) Representative rasterplots of neuronal activation as a function of time for three run epochs (light green) displaying an integer number of sequences during the same imaging session. Bottom graphs indicate corresponding speed as a function of time.
(B) (B1 and B2) Perievent triggered distribution of the mouse speed (median: black line, inter-quartile range: gray area) aligned to the onset (B1) or to the offset (B2) of all first DS detected in each run epoch (n = 325 DS). (B3 and B4) Same as (B1) and (B2), but speed distribution now uses the onsets (B3) or the offsets (B4) of the DS that repeated after another in the middle of a run epoch (n = 64 DS). Gray area indicates the 95% confidence interval (CI).
(C) Representative plot showing the uniform distribution on the absolute track position of repeating DS onsets for one imaging session (n = 25 DS, Kolmogorov-Smirnoff test, p > 0.1).
Distance Sequences: Sequential Neuronal Activation Integrating Traveled Distance
To test whether sequences integrated travel duration or distance, we analyzed, for each imaging session, the correlation between the slopes of the sequences (in the temporal or spatial domain) and the median mouse speed of the corresponding run epochs. If the progress of neuronal activation was set by the run distance, then the temporal slope of the sequences (expressed as cell/s) should correlate with speed while the spatial slope (in cm/cell) should be constant and thus independent from speed (Figures 2A and 2B). For each imaging session, we calculated the Spearman correlation coefficient between the temporal or spatial slope and the speed (Figure 2B); this analysis is a robust way to assess distance or time representation in noisy data (see data simulation in Figures S3B–S3D). Across sessions, sequences could be modulated by time and distance (28 imaging sessions, n = 5 mice, Figures 2B and S1). However, in many cases they were principally modulated by distance alone (14 out of 28 sessions, Spearman p < 0.05; Table S1). In the intermediate cases, both time and distance representations seemed to intermingle (11 out of 28), whereas time alone was organizing neuronal activation in a minority of the sessions (3 out of 28). This demonstrates that, as previously described at single-cell level, hippocampal dynamics capture both spatial and temporal information at the population level (Kraus et al., 2013). However, when integrating information at the population level over each imaging session, we observe that on average distance is more likely to be represented in our experimental conditions (Figures 2B and S1).
As distance-modulated sequences were frequent, analysis was next restricted to the imaging sessions in which these were observed (n = 14 sessions, 5 mice, 493 sequences, Experimental Procedures, and Figure S1G). Such distance-modulated sequences (DS) repetitively engaged the same neurons within an imaging session (Figures 1C and 2C, on average 70%). They spanned most but not all the distance traveled within a run epoch. A period of travel could therefore sometimes not be represented within neuronal dynamics (a “nonencoded travel distance,” Figure 2C). This indicated that DSs do not provide a metric integrating the total distance covered by the mouse but instead display a finite size that is intrinsically set. This “nonencoded travel distance” did not involve the coordinated firing of another group of cells, as only one recurring pattern of neuronal activation was detected per session. Also, as expected, the onsets of the calcium transients of the neurons engaged in the DS (DS neurons) were not locked to the treadmill lap in contrast to those of the neurons displaying location-dependent firing after a few days of spontaneous run in the presence of serial tactile cues (i.e., place cells, n = 3 mice, Figure 2D). Neither were these onsets periodic, given the occurrence of “nonencoded traveled distances” between sequences. Nor were the DSs triggered by a undetectable cue on the track (Figure 2E). Therefore, in conditions dominated by idiothetic cues, some fixed distance metric can be represented in the hippocampus in the form of recurring sequences of neuronal activation.
We next asked whether the finite size of the DS was due to experimental limitations, or instead could represent an intrinsic metric for distance. To this aim, we first analyzed the topographical arrangement of DS neurons. The spatial distribution of DS neurons within the pyramidal layer did not display any remarkable pattern since these were not more clustered than expected by chance, even when taking into account their time of recruitment within the sequence (Figure S4). This indicates that our imaging field of view sampled from a random representative subset of DS neurons and that the distance span covered by each sequence was unlikely to be truncated.
The “Distance Unit”: An Internal Cognitive Template that Varies on a Daily Basis and Shapes Mouse Behavior
Mouse behavior may control or be controlled by the firing of hippocampal neurons. Thus, the distance encoded at population level in the DS could be set by the mouse behavior or conversely, spontaneous runs could be internally predetermined by the spatial extent of the DS. In order to address the former hypothesis, we have plotted the distribution of the mouse speed centered on the time of DS start or stop. We first used the first DS of each run epoch as a reference (Figure 3B). In this case, DS onsets were time-locked to the start of the run (Figure 3B1) whereas DS offsets occurred before its end (Figure 3B2). DS could also repeat in the middle of a run epoch one after another (Figure 3A), and this repetition is expected to be triggered by an external drive, such as a short pause in mouse run or a cue on the track. To test the first possibility, the onsets and offsets of these DS were specifically used as a reference for the mouse speed distribution plots (Figures 3B3 and 3B4). Surprisingly, no significant pause or deceleration were observed. However, speed significantly increased by about 20% (Figure 3B3). This is a potentially interesting finding that may relate to the mechanisms of sequence initiation given that the firing frequency of CA1 pyramidal neurons increases with speed (Hirase et al., 1999; Geisler et al., 2007; Fuhrmann et al., 2015). In addition, DS repetition was not linked to a cue on the track (uniformity Kolmogorov-Smirnov test Figure 3C, p > 0.1). Hence, both the onset and offset of a DS could be uncorrelated to the start and end of the run, in contrast to previous reports where the span of neuronal activation sequences was constrained by the underlying task (Kraus et al., 2013; Pastalkova et al., 2008; Ravassard et al., 2013; Royer et al., 2012). This shows the intrinsic finite extent of sequences of neural activation in CA1 that encode traveled distance without being locked to behavior. We thus refer to such discrete span of the DS as the “distance unit” (DU) encoded at population level within the imaging session.
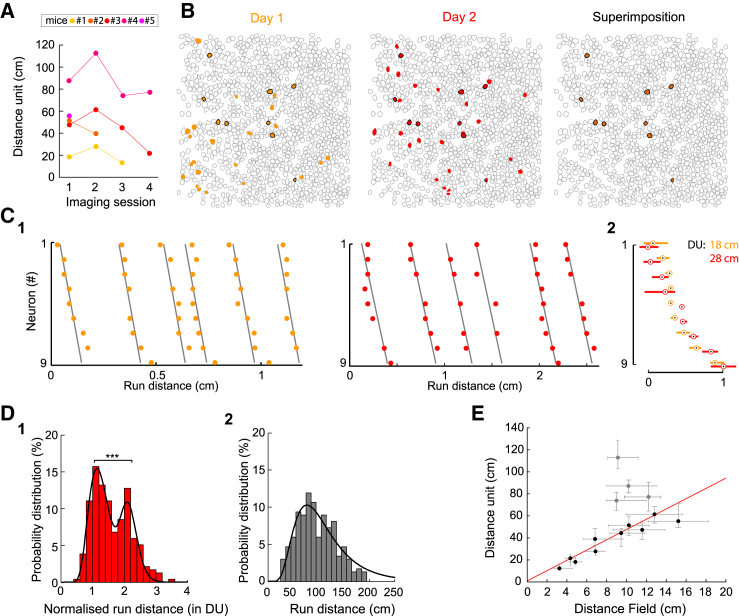
Quantification of the DU for each imaging session revealed that these spanned across a wide range (12–112 cm, Figure 4A), even for the same mouse across imaging days, indicating that this value is not preset. We took advantage of this variability to test if, as for place cells where the size of place fields scales with that of the explored environment (Diba and Buzsáki, 2008; Muller and Kubie, 1987; O’Keefe and Burgess, 1996), the “average distance field width” (Experimental Procedures) linearly scaled with the DU. Such a relationship could be observed (Figure 4E, Pearson, R = 0,94, p < 0.001), indicating a shared property between distance and place fields.
Figure 4.
The Distance Unit Provides an Internal Template that Varies on a Daily Basis
(A) Evolution of the “distance unit” over four daily imaging sessions for five mice (colored lines).
(B) Representative example of the contour maps of imaged cells indicating neurons involved in distance sequences on the first day where sequences could be imaged (yellow, left) and the next (middle, red) or both (orange, right and black contours on all three maps).
(C) (C1) Rasterplots showing the activation, as a function of distance, of the nine cells involved in distance sequences on both days. Neurons are ordered based on their average activation delay on the first day; day 1 (left), day 2 (right). (C2) Superimposed average rasterplot of the sequences on both days (day 1, orange; day 2, red); the median delay of onset (dot) and the corresponding interquartile range (rectangle) are indicated for each cell and calculated taking cell #5 as reference. Note that the “distance unit” (DU) calculated for each day (same color code) varied significantly.
(D) Probability distribution histograms of the normalized (1) and absolute (2) run distance (n = 235 run epochs, 10 sessions with a median run distance smaller than 2 DU). The normalized run distance displays a bimodal distribution (r2 = 0.98) with a first peak at 1.1. DU and a significant second one at 2.1 DU (Figures S4D–S4H, ∗∗∗p < 0.001). The absolute distance histogram distribution is log-normal (r2 = 0.91) with a peak at 77 cm.
(E) Graph indicating the correlation between the average size of single-cell distance fields (median values and interquartile ranges, see Experimental Procedures) and the “distance unit”; the fit (red, Pearson, R = 0,94, p < 0.001) indicates that the average distance field represents one-fifth of the distance unit.
Since the DU could considerably vary across days, we compared the set of neurons involved within the DS from one imaging session to the next. Almost one-third of the cells involved within a DS one day were still recruited the next (28% ± 8%, three sessions paired, two mice, Figures 4B and 4C). In addition, although no serial external cues were provided to support and recall the sequence organization, the relative order of the neurons within the sequences was also maintained (Figures 4C and S4B). This indicates that DS rely on intrinsically prewired functional links between neurons. DS thus provide an internal template for the integration of incoming sensory signals.
Last, we asked whether the template metric provided by the DU shaped spontaneous mouse runs. To this aim, analysis was focused on the distribution of the distance traveled within single run epochs (that comprised a detected DS), expressed in DU (rather than cm). The median value of this normalized distance, calculated per imaging session, segregated into two groups (group 1, 1–2 DU, 235 run epochs, 10 sessions; group 2, 2.5–3.2 DU, 90 run epochs, 4 sessions; Figure S4C; Table S1). When pooling together group 1, we noticed that the distribution was significantly bimodal with peaks at 1.1 and 2.1 DU (Figures 4D and S4; p < 0.001, see Experimental Procedures), whereas it was log-normal without normalization. Regarding group 2 distribution bimodality, the occurrence of imaging sessions displaying a majority of run epochs with more than 2DS was too infrequent to draw any significant conclusion. Thus, spontaneous run epochs tended to distribute as integer multiples of the distance intrinsically integrated in the respective DS. This further supports the idea that DSs are a representation of distance encoded in the hippocampal network.
Discussion
This study shows that sparse and stereotyped chains of neuronal activation, integrating spatiotemporal components of behavior, spontaneously recur one after another, without any external drive, in the hippocampus under the influence of self-motion. We show that the “distance unit” associated to these intrinsically finite sequences provides a population metric for distance encoded in CA1 dynamics. This DU is not entirely engraved, as it could vary on a daily basis. However, the partial replay of sequences from one day to the next strongly suggests the existence of internally prewired networks (Dragoi and Tonegawa, 2014). Animals were more likely to travel spontaneously once or twice the “distance unit,” suggesting that linear path integration may use dead reckoning cycles and that this internal representation is limited. In natural environments, this function is complemented by landmark recognition (McNaughton et al., 1991). In contrast, in the absence of external cues, integer multiples of the DU operate as attractor states for spontaneous behavior. This finding was made possible by a combination of factors that were not gathered before (Chen et al., 2013; Kraus et al., 2013; Pastalkova et al., 2008; Poucet et al., 2014; Ravassard et al., 2013) and that include (1) the absence of sensory or cognitive external drive, (2) the absence of reward, (3) the absence of temporal or spatial borders (Solstad et al., 2008), (4) the sampling of activity from a large number of neurons, (5) a large range of running speeds to allow disentangling elapsed time from distance even for short travels, and (6) the use of a one dimensional environment. Last, we cannot exclude that keeping head direction signals constant also contributed in revealing such stereotyped dynamics (Cowen and Nitz, 2014; Sargolini et al., 2006). It is also possible that the filtering of neuronal spiking, an experimental limitation of the use of calcium indicators, is here providing a first integration step of hippocampal dynamics.
Besides spatial cognition and memory, sequences of neuronal activation have been previously reported in different brain regions and species where they have been associated with a variety of brain computations, including song generation (Long et al., 2010), odor encoding (Wehr and Laurent, 1996), choice decision (Harvey et al., 2012; Pastalkova et al., 2008), associative learning (Modi et al., 2014), or brain-state transitions (Luczak et al., 2007). Here we show that sequences can display an intrinsic finite spatiotemporal extent. They can repeat one after another within a continuous behavioral episode, sometimes following a spatiotemporal gap lacking any significant neuronal activity pattern. Interestingly, spontaneous repetition of neuronal activation has been reported at the single-cell level for example for cells displaying multiple place fields when large environments are explored (Rich et al., 2014), and at the population level when identical repeating environments are successively explored (Mizuseki et al., 2012). The same way that cells with multiple place fields somehow provide a natural segmentation of large environments, it is possible that the repetition of finite sequences reflects a similar phenomenon where an infinite environment is divided into discrete cognitive chunks (Gupta et al., 2012). This activity repetition may reflect a self-generated behavioral strategy (Cabral et al., 2014) or the limit of the internal representation of the world, the latter being more likely for we show that behavior tends to follow hippocampal dynamics and not the opposite. Hence, for a given imaging session, we observed that mice could run once or twice the DU, with no strategical preference for either one of these options. Therefore, DS may represent the full capacity of the available working memory for a given experience. When animals are trained for a particular task, sequential neuronal activation covers the entire length of the task at hand (in time or space) (Dragoi and Buzsáki, 2006; Itskov et al., 2011; Kraus et al., 2013; Pastalkova et al., 2008; Royer et al., 2012; Wang et al., 2014). As a consequence of the intrinsic finite size, sequences scale to match the experienced episode, which implies that the coding resolution is inversely proportional to the size of the task. Hence, we observed that “average distance field width” linearly scaled with the DU.
Absolute distance from a fixed starting point has recently been reported to be represented in hippocampal firing at single-cell level (Kraus et al., 2013) and to contribute to place coding in the absence of visual cues (Chen et al., 2013) or in virtual environments (Ravassard et al., 2013). The critical implication of self-body cues in the distance representation within place fields has recently been demonstrated in virtual environments (Chen et al., 2013). From that, it was thus expected, in our particular conditions where self-motion cues are prominent, that sequential neuronal firing integrates traveled distance. However, the single-cell activity recorded here cannot provide a measure of run distance since run epochs comprise periods of non-encoded distance. In addition, in the case of the DS described here, as reported before for single-cell hippocampal activity (Kraus et al., 2013), it is very likely that time is also contributing to single-cell firing. Probably best supporting that point is the fact that the organization of sequences was not affected by short rest periods, indicating that some cells are bridging the temporal gap between two diconstinuous runs within a single sequence. Alternatively, information may be transiently stored and hidden for example in the decaying synaptic weights over time accross short temporal gaps (less than one second long) (Buonomano and Maass, 2009).
Distance was known to be represented within hippocampal dynamics at a shorter timescale, in the form of the sequential firing of place cells sharing overlapping place fields within a theta cycle (Dragoi and Buzsáki, 2006). Interestingly, theta phase precession is preserved after stimulation-induced perturbation of hippocampal activity (Zugaro et al., 2005), the same way sequences described here resumed after a short immobility period. In addition, theta sequences were recently shown to be critically related to internally generated hippocampal sequences formed during an episodic memory task (Wang et al., 2014). It will thus be important to examine the link between these two temporal scales of distance representation, which may ultimately require determining the translation of distance sequences in a two-dimensional environment. Sequences were also shown to occur at an even more compressed timescale, during sharp wave activity and quiet wakefulness. These sequences reflect previous sensory experience (Buzsáki et al., 1992; Karlsson and Frank, 2009). In the same way, distance sequences may recapitulate a recent experience thus supporting the view of the hippocampus as a “relational processing system” (Eichenbaum and Cohen, 2014), linking sequential body movements to an existing distance template supported by internally preconfigured networks. In this way, these may contribute to the generation of place fields in the absence of proximal sensory cues as likely occurs in the dark (Poucet et al., 2014), or when large environments are explored (Wang et al., 2014). These may also contribute to temporal integration when time becomes a more prominent component (MacDonald et al., 2013).
Future studies are needed to address the cellular mechanisms of sequence generation, in particular their link to entorhinal inputs from grid cells, the standard metric for space in the brain (Moser and Moser, 2008), or to medial septum inputs that pace the internal hippocampal clock at theta frequency. The preconfigured character of hippocampal dynamics, dominated by a small minority of active cells in many states and contexts (Mizuseki and Buzsáki, 2013), may provide a cellular substrate by which hippocampal dynamics spontaneously collapse into these default sequences, based on the preferential activation of a highly excitable subset of neurons triggering a chain of pre-existing functional links. Interestingly, sequences of neuronal activation lacking spatial specificity (Cheng and Ji, 2013) have been recently observed in an Alzheimer disease model, suggesting that these may represent the minimum default operational mode of the hippocampus when sensory perception is reduced.
Experimental Procedures
Mice
All protocols were performed under the guidelines of the French National Ethic Committee for Sciences and Health report on “Ethical Principles for Animal Experimentation” in agreement with the European Community Directive 86/609/EEC under agreement #01413. Male adult wild type Swiss mice (n = 8, 25–40 g body weight) were used for experiments. All mice were housed in standard conditions (12 hr light/dark cycles light off at 7:30 a.m., housed one per cage, water and food ad libitum). Mice were handled before recording sessions to limit head restraint associated stress and experiments were performed during the dark cycle.
Virus Infection
In order to perform large-scale calcium imaging, mice were injected with a viral solution (titer, ∼1012 genomes copy/ml; Penn Vector Core) of AAV2/1.Syn.GCaMP5G.WPRE.SV40. Mice were first anesthetized (100 mg/kg ketamine, 10 mg/kg xylazine), and 500 nl of viral solution was injected at a rate of 100 nL/min into the left dorsal hippocampus at following coordinates: AP, 2 and 2.5; ML, 1.6 and 2.1 relative to bregma; DV, 1.3 relative to brain surface. The constrained tissue was allowed to recover for 1 min prior and 3 min after injections to prevent injection backwash. Craniotomy was then protected with skin stapled. Mice were allowed to recover for a minimum of 7 days.
Implantation of Chronic Hippocampal Window
This procedure was inspired from Dombeck et al. (2010) and adapted for large-scale imaging. After 4 days of water deprivation to transiently modify hemodynamics to help for the surgery (1.5 ml/24 hr; <20% loss of initial body weight), mice were anesthetized with ketamine (100 mg/kg) and xylazine (10 mg/kg), and a 3 mm diameter craniotomy centered over virus injection sites was performed. The dura was gently cut and a portion of the overlying cortex was aspirated to allow optical access to the hippocampus. The cortex was continuously irrigated to limit bleeding during cortex withdrawal. Similarly to the original method, the external capsule was exposed and allowed to dry until tacky, upon which a stainless steel canula (Microgroup) attached to a glass coverslip was placed in the hole, sealed with uncured kwik sil (WPI), and fixed to the skull using Super-bond (DSM Dentaire). A custom-made bar was fixed at the back of the head. Mice were allowed to recover for 4–6 days and then handled for 2 days in order to limit head restraint-associated stress.
Imaging Procedure and Treadmill Setup
Mice were head-fixed on a nonmotorized treadmill (adapted from Royer et al., 2012) allowing them self-paced locomotion, and all experiments were performed in the dark. No reward was given. After three to five habituation sessions, mice were watchful but calm and alternated between periods of moving and resting activity during recordings. The treadmill was made from a 180 cm black velvet seamless belt for the experiments done in the absence of external cue (n = 5 mice). In the experiments aiming at imaging place cell firing (n = 3 mice), the belt was enriched in tactile cues as follows: we delineated four zones of 45 cm displaying the following items: (1) 2 cm wide disks of white Velcro; (2) small white pressure buttons; (3) gray diamond shaped textured plastic fabric; (4) no cue. For all experiments, extra sound, odor, touch, and light were minimized during the imaging session (in preliminary experiments where the seam was too prominent we observed cue-related firing; data not shown). The mouse speed and instantaneous position were tracked using a graded wheel, as previously described (Royer et al., 2012) (1 cm position resolution). Imaging was performed with a single beam multiphoton pulsed laser scanning system coupled to a microscope (TriM Scope II, LaVision Biotech). The Ti:sapphire excitation laser (Chameleon Ultra II, Coherent) was operated at 920 nm. GCaMP fluorescence was isolated using a bandpass filter (510/25). Images were acquired through a GaSP PMT (H7422-40, Hamamatsu) using a 16 immersion objective (NIKON, NA 0.8). Using Imspector software (LaVision Biotech), the fluorescence activity from a 400 μm2 field of view was acquired at 9.62 Hz with a 1.85 μs dwell time per pixel (2 μm/pixel). Imaging fields were selected to sample the dorsal CA1 area and maximize the number of imaged neurons in the stratum pyramidale. Speed, position, and image triggers were synchronously acquired and digitized using a 1440A Digidata (Axon instrument, 2 kHz sampling) and the Axoscope 10 software (Axon instrument). A typical imaging session occurred as follows: (1) the mouse was handled then fixed on the treadmill; (2) five consecutive 3,000 frames movies were acquired; (3) the mouse returned to its homecage. The next imaging session occurred 24 hr after. Mice were imaged once a day for up to 4 weeks.
Data Analysis
Active Cell Detection during Run Epochs
Run epochs were defined as continuous periods of time during which the average mouse speed exceeded 2 cm/s. A custom-made algorithm based on PCA/ICA was used and combined to morphological identification. Movement correction was first performed for each frame using the cross-correlation with a reference image. Only frames corresponding to mouse run were used for cell detection. The offset PCA method was next applied (Kaifosh et al., 2013). Principal components displaying a variance greater than noise were fed to an iterative ICA algorithm (Mukamel et al., 2009). Cells were identified in the output of the ICA using 2D-spatial wavelet filtering matching the expected cell size (7–15 μm diameter). Cell contours were next extracted. The obtained ROI were finally smoothed using a closing algorithm thus defining the active cell population. The fluorescence trace of each cell was calculated by averaging over the ROI.
Detection of Recurring Activity Patterns
Principal component analysis was performed on the fluorescence traces of active cells. GCaMP fluorescence traces were smoothed in time (Gaussian filtering, s=5s) before fed to the offset PCA algorithm (Kaifosh et al., 2013). The smoothing adds correlation between neighbouring time points in order to gather the activity of cells that fire successively. The principal component which displayed recurring fluorescence patterns during each run epoch (among the five with the highest variance) was manually selected. The reason for manual selection was (1) the need to select a principal component that contained information about population activity during run epochs (i.e., displaying transients at each run); and (2) among the five extracted principal components, it also often happened that traces reflecting for example high activity of a single neuron outside from run epochs or movement artifacts, were considered as holding the most information by the PCA. The derivative of that principal component (Figure S3, green) was then cross-correlated with the activity of each individual cell. The use of the derivative preferentially select cells with short calcium transient and thus remove cells that fire during the entire run epoch which are not part of a sequence. The correlation coefficients thus obtained were used as a metric to determine the participation of each cell to recurring activity: a threshold was calculated applying Otsu's method (Otsu, 1979) to the distribution of this metric in the cell population (Figure S3). Cells whose correlation was higher than the threshold were considered as involved in such recurring activity. Note that in several instances (37 out of 65 imaging sessions from five mice, see Figure S1G), no recurring pattern was detected. To identify another group of cells that would display another recurring pattern, we reiterate this procedure with the previously identified cells removed. After reshuffling between active cells independently in each run epoch, i.e., the fluorescence trace is divided in different time interval inside which cells activity is permuted (e.g., cell 1 gets the activity of cell 5 during the first run epoch and of cell 3 during the second one, etc.), no recurring activity (at least two sequences of five cells) was detected which validated our detection method (0 occurrence out of 1,000 reshufflings).
Sequence Slope Analysis
For each recurring activity pattern, cell activation onset was defined by the maximum of the first derivative of the smoothed trace (Gaussian filtering, s = 2s). Onsets displaying a maximal derivative smaller than 5% DF/F.s1 were discarded. Cells were then ordered in a sequence according to their median onset delay in each run epoch. The sequences that involved at least half of the cells were linearly fitted using a regression algorithm that ignores outliers (Matlab function robustfit). The fits displaying a robust root mean square error exceeding 20% of the duration of the sequence were discarded. The remaining sequences were used for all quantitative analysis (n = 389 fitted sequences, 79% of all sequences). This linear fit provided the slope (in cell/s) of each sequence. To assess whether the dynamics of these sequences depended on run distance, we analyzed the correlation between the slope and the corresponding median speed. In the case of a statistically significant correlation (p < 0.05, Spearman, n = 14 out of 28 sessions), a distance unit DU that links the speed v, the slope S, and the number of cells N could be defined as follows: DU is the spatial extent of the run distance from the first to the last cell of the sequence. Such recurring sequences were classified as distance sequences (DS).
The same analysis was performed in the spatial domain by converting activation onsets in time to onsets in space using the measured mouse position. A few sessions (3 out of 28) displayed a significant correlation, which indicated that run time could also modulate sequence dynamics.
Statistics on Short Pauses within Run Epochs
Short pauses were defined as the periods when the speed was lower than 2 cm/s for more than 500 ms and less than 2 s. To analyze whether the occurrence of short pauses affected the dynamics of DS, the distribution of neuronal activation onsets centered on each pause start was computed. The five sessions that displayed more than ten pauses (n = 3 mice) were kept for further analysis. In addition, only pauses which roughly occurred in the middle of a sequence (20%–80% of sequence completion, n = 91 pauses) could be analyzed, since information was needed about cell activation before and after the pause. We next used the onset of the last cell before the pause as a reference to center all sequences on the pause. The temporal slope of the sequences was normalized to the average. In that way, the arrangement of the sequences around the pauses could be pooled across sessions. The evolution of the normalized temporal slope was measured using a linear fit over a sliding window of six cells; the 95% confidence interval was calculated using the distribution of these slopes before the pause (n = 8 slope values, Gaussian approximation).
Distribution of Speed around DS
In order to reveal a potential link between the animal's speed and the dynamics of the DS, speed was normalized across sessions and pooled using a 20 s time window centered either on the onsets or the offsets of DS. These were calculated using the median activation onsets of the first or last five cells in the sequence, respectively. The 95% confidence interval was calculated using the speed distribution before the pause (from the time when speed plateaus to pause onset, Gaussian approximation).
Statistical Analysis of Distribution Peaks
In order to assess whether a second peak in an apparently uniform distribution was significant, tests were performed as follows. First, the distribution histogram was fitted using an ad hoc uniform function (log-normal in our case) and a least-squares fit algorithm (lsqcurvefit function in matlab). Second, the probability distribution for the value of each bin was calculated by computing random samples (n = 105 samples) using the fitted distribution. Third, a significance curve was defined by applying the same percentile to all bins (equiprobability). The value of the percentile was chosen so that the probability of having at least one peak bigger than the significance curve was 5% (see Figure S4). This statistical test was robust against binning phase and size as long as the peak was not split between two bins (see Figures S4F–S4H).
Distance Field Calculation
For each cell involved in a “distance sequence,” we detected the onset and offset of its mean fluorescence transient over all sequences; the onset being the time when the fluorescence transient reached 10% of its maximum value and the offset the time when the trace derivative reached its minimum value. This gave an estimate of the firing duration for each cell; the distance field was defined as the product of the median speed and the firing duration thus calculated.
Author Contributions
V.V., A.M., and R.C. designed the research. V.V., A.M., and T.T. designed the experimental setup. V.V. collected the data. A.M. and N.D. designed the analysis. A.M. analyzed the data. V.V., A.M., and R.C. wrote the paper.
Acknowledgments
Work was supported by the INSERM, CNRS (R.C.), FP7-ERC “GABA Networks” grant (#242842), France Life Imaging, and the Fondation pour la Recherche Médicale. We gratefully acknowledge the GENIE Program and the Janelia Farm Research Campus specifically for GCAMP5Gs: L.L. Looger, PhD; J. Akerboom, PhD, and D.S. Kim, PhD. We also thank Professor D. Dombeck, Professor S. Royer, R. Martinez, and Dr. M. Ros for their help in setting up the experiments; we are grateful to S. Heuet for the treadmill cartoon. We are indebted to Drs. Y. Ben-Ari, C. Boccara, J. Epsztein, R. Khazipov, P.P. Lenck-Santini, B. Poucet, D. Robbe, and the team members for helpful comments on the manuscript.
Published: October 21, 2015
Footnotes
This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Supplemental Information includes four figures, one table, and one movie and can be found with this article at http://dx.doi.org/10.1016/j.neuron.2015.09.052.
Contributor Information
Arnaud Malvache, Email: arnaud.malvache@inserm.fr.
Rosa Cossart, Email: rosa.cossart@inserm.fr.
Supplemental Information
(Left panel) Movie of the GCaMP5G fluorescence signal imaged in the CA1 stratum pyramidale of a mouse running in the dark on a treadmill without cues. (Right panel) Fluorescence traces from three neurons in the movie involved in recurrent sequences of neuronal firing as the mouse spontaneously travels on the treadmill. Bottom graph indicates mouse speed.
References
- Aghajan Z.M., Acharya L., Moore J.J., Cushman J.D., Vuong C., Mehta M.R. Impaired spatial selectivity and intact phase precession in two-dimensional virtual reality. Nat. Neurosci. 2014;18:121–128. doi: 10.1038/nn.3884. [DOI] [PubMed] [Google Scholar]
- Akerboom J., Chen T.W., Wardill T.J., Tian L., Marvin J.S., Mutlu S., Calderón N.C., Esposti F., Borghuis B.G., Sun X.R. Optimization of a GCaMP calcium indicator for neural activity imaging. J. Neurosci. 2012;32:13819–13840. doi: 10.1523/JNEUROSCI.2601-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buonomano D.V., Maass W. State-dependent computations: spatiotemporal processing in cortical networks. Nat. Rev. Neurosci. 2009;10:113–125. doi: 10.1038/nrn2558. [DOI] [PubMed] [Google Scholar]
- Buzsáki G. Neural syntax: cell assemblies, synapsembles, and readers. Neuron. 2010;68:362–385. doi: 10.1016/j.neuron.2010.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G., Horváth Z., Urioste R., Hetke J., Wise K. High-frequency network oscillation in the hippocampus. Science. 1992;256:1025–1027. doi: 10.1126/science.1589772. [DOI] [PubMed] [Google Scholar]
- Cabral H.O., Vinck M., Fouquet C., Pennartz C.M., Rondi-Reig L., Battaglia F.P. Oscillatory dynamics and place field maps reflect hippocampal ensemble processing of sequence and place memory under NMDA receptor control. Neuron. 2014;81:402–415. doi: 10.1016/j.neuron.2013.11.010. [DOI] [PubMed] [Google Scholar]
- Chen G., King J.A., Burgess N., O’Keefe J. How vision and movement combine in the hippocampal place code. Proc. Natl. Acad. Sci. USA. 2013;110:378–383. doi: 10.1073/pnas.1215834110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng J., Ji D. Rigid firing sequences undermine spatial memory codes in a neurodegenerative mouse model. eLife. 2013;2:e00647. doi: 10.7554/eLife.00647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowen S.L., Nitz D.A. Repeating firing fields of CA1 neurons shift forward in response to increasing angular velocity. J. Neurosci. 2014;34:232–241. doi: 10.1523/JNEUROSCI.1199-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diba K., Buzsáki G. Hippocampal network dynamics constrain the time lag between pyramidal cells across modified environments. J. Neurosci. 2008;28:13448–13456. doi: 10.1523/JNEUROSCI.3824-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dombeck D.A., Harvey C.D., Tian L., Looger L.L., Tank D.W. Functional imaging of hippocampal place cells at cellular resolution during virtual navigation. Nat. Neurosci. 2010;13:1433–1440. doi: 10.1038/nn.2648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dragoi G., Buzsáki G. Temporal encoding of place sequences by hippocampal cell assemblies. Neuron. 2006;50:145–157. doi: 10.1016/j.neuron.2006.02.023. [DOI] [PubMed] [Google Scholar]
- Dragoi G., Tonegawa S. Preplay of future place cell sequences by hippocampal cellular assemblies. Nature. 2011;469:397–401. doi: 10.1038/nature09633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dragoi G., Tonegawa S. Selection of preconfigured cell assemblies for representation of novel spatial experiences. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014;369:20120522. doi: 10.1098/rstb.2012.0522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichenbaum H., Cohen N.J. Can we reconcile the declarative memory and spatial navigation views on hippocampal function? Neuron. 2014;83:764–770. doi: 10.1016/j.neuron.2014.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuhrmann F., Justus D., Sosulina L., Kaneko H., Beutel T., Friedrichs D., Schoch S., Schwarz M.K., Fuhrmann M., Remy S. Locomotion, theta oscillations, and the speed-correlated firing of hippocampal neurons are controlled by a medial septal glutamatergic circuit. Neuron. 2015;86:1253–1264. doi: 10.1016/j.neuron.2015.05.001. [DOI] [PubMed] [Google Scholar]
- Geisler C., Robbe D., Zugaro M., Sirota A., Buzsaki G. Hippocampal place cell assemblies are speed-controlled oscillators. Proc. Natl. Acad. Sci. USA. 2007;104:8149–8154. doi: 10.1073/pnas.0610121104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta A.S., van der Meer M.A., Touretzky D.S., Redish A.D. Segmentation of spatial experience by hippocampal θ sequences. Nat. Neurosci. 2012;15:1032–1039. doi: 10.1038/nn.3138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey C.D., Coen P., Tank D.W. Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature. 2012;484:62–68. doi: 10.1038/nature10918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirase H., Czurko A., Csicsvari J., Buzsaki G. Firing rate and theta-phase coding by hippocampal pyramidal neurons during “space clamping.”. Eur. J. Neurosci. 1999;11:4373–4380. doi: 10.1046/j.1460-9568.1999.00853.x. [DOI] [PubMed] [Google Scholar]
- Itskov V., Curto C., Pastalkova E., Buzsáki G. Cell assembly sequences arising from spike threshold adaptation keep track of time in the hippocampus. J. Neurosci. 2011;31:2828–2834. doi: 10.1523/JNEUROSCI.3773-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaifosh P., Lovett-Barron M., Turi G.F., Reardon T.R., Losonczy A. Septo-hippocampal GABAergic signaling across multiple modalities in awake mice. Nat. Neurosci. 2013;16:1182–1184. doi: 10.1038/nn.3482. [DOI] [PubMed] [Google Scholar]
- Karlsson M.P., Frank L.M. Awake replay of remote experiences in the hippocampus. Nat. Neurosci. 2009;12:913–918. doi: 10.1038/nn.2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kentros C.G., Agnihotri N.T., Streater S., Hawkins R.D., Kandel E.R. Increased attention to spatial context increases both place field stability and spatial memory. Neuron. 2004;42:283–295. doi: 10.1016/s0896-6273(04)00192-8. [DOI] [PubMed] [Google Scholar]
- Kraus B.J., Robinson R.J., 2nd, White J.A., Eichenbaum H., Hasselmo M.E. Hippocampal “time cells”: time versus path integration. Neuron. 2013;78:1090–1101. doi: 10.1016/j.neuron.2013.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long M.A., Jin D.Z., Fee M.S. Support for a synaptic chain model of neuronal sequence generation. Nature. 2010;468:394–399. doi: 10.1038/nature09514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luczak A., Barthó P., Marguet S.L., Buzsáki G., Harris K.D. Sequential structure of neocortical spontaneous activity in vivo. Proc. Natl. Acad. Sci. USA. 2007;104:347–352. doi: 10.1073/pnas.0605643104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacDonald C.J., Carrow S., Place R., Eichenbaum H. Distinct hippocampal time cell sequences represent odor memories in immobilized rats. J. Neurosci. 2013;33:14607–14616. doi: 10.1523/JNEUROSCI.1537-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNaughton B.L., Chen L.L., Markus E.J. “Dead reckoning,” landmark learning, and the sense of direction: a neurophysiological and computational hypothesis. J. Cogn. Neurosci. 1991;3:190–202. doi: 10.1162/jocn.1991.3.2.190. [DOI] [PubMed] [Google Scholar]
- Mizuseki K., Buzsáki G. Preconfigured, skewed distribution of firing rates in the hippocampus and entorhinal cortex. Cell Rep. 2013;4:1010–1021. doi: 10.1016/j.celrep.2013.07.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizuseki K., Royer S., Diba K., Buzsáki G. Activity dynamics and behavioral correlates of CA3 and CA1 hippocampal pyramidal neurons. Hippocampus. 2012;22:1659–1680. doi: 10.1002/hipo.22002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Modi M.N., Dhawale A.K., Bhalla U.S. CA1 cell activity sequences emerge after reorganization of network correlation structure during associative learning. eLife. 2014;3:e01982. doi: 10.7554/eLife.01982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moser E.I., Moser M.B. A metric for space. Hippocampus. 2008;18:1142–1156. doi: 10.1002/hipo.20483. [DOI] [PubMed] [Google Scholar]
- Mukamel E.A., Nimmerjahn A., Schnitzer M.J. Automated analysis of cellular signals from large-scale calcium imaging data. Neuron. 2009;63:747–760. doi: 10.1016/j.neuron.2009.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller R.U., Kubie J.L. The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. J. Neurosci. 1987;7:1951–1968. doi: 10.1523/JNEUROSCI.07-07-01951.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Keefe J., Burgess N. Geometric determinants of the place fields of hippocampal neurons. Nature. 1996;381:425–428. doi: 10.1038/381425a0. [DOI] [PubMed] [Google Scholar]
- Otsu N. Threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybernet. 1979;9:62–66. [Google Scholar]
- Pastalkova E., Itskov V., Amarasingham A., Buzsáki G. Internally generated cell assembly sequences in the rat hippocampus. Science. 2008;321:1322–1327. doi: 10.1126/science.1159775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poucet B., Sargolini F., Song E.Y., Hangya B., Fox S., Muller R.U. Independence of landmark and self-motion-guided navigation: a different role for grid cells. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014;369:20130370. doi: 10.1098/rstb.2013.0370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravassard P., Kees A., Willers B., Ho D., Aharoni D., Cushman J., Aghajan Z.M., Mehta M.R. Multisensory control of hippocampal spatiotemporal selectivity. Science. 2013;340:1342–1346. doi: 10.1126/science.1232655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich P.D., Liaw H.P., Lee A.K. Place cells. Large environments reveal the statistical structure governing hippocampal representations. Science. 2014;345:814–817. doi: 10.1126/science.1255635. [DOI] [PubMed] [Google Scholar]
- Royer S., Zemelman B.V., Losonczy A., Kim J., Chance F., Magee J.C., Buzsáki G. Control of timing, rate and bursts of hippocampal place cells by dendritic and somatic inhibition. Nat. Neurosci. 2012;15:769–775. doi: 10.1038/nn.3077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargolini F., Fyhn M., Hafting T., McNaughton B.L., Witter M.P., Moser M.B., Moser E.I. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- Skaggs W.E., McNaughton B.L. Replay of neuronal firing sequences in rat hippocampus during sleep following spatial experience. Science. 1996;271:1870–1873. doi: 10.1126/science.271.5257.1870. [DOI] [PubMed] [Google Scholar]
- Solstad T., Boccara C.N., Kropff E., Moser M.B., Moser E.I. Representation of geometric borders in the entorhinal cortex. Science. 2008;322:1865–1868. doi: 10.1126/science.1166466. [DOI] [PubMed] [Google Scholar]
- Wang Y., Romani S., Lustig B., Leonardo A., Pastalkova E. Theta sequences are essential for internally generated hippocampal firing fields. Nat. Neurosci. 2014;18:282–288. doi: 10.1038/nn.3904. [DOI] [PubMed] [Google Scholar]
- Wehr M., Laurent G. Odour encoding by temporal sequences of firing in oscillating neural assemblies. Nature. 1996;384:162–166. doi: 10.1038/384162a0. [DOI] [PubMed] [Google Scholar]
- Wilson M.A., McNaughton B.L. Reactivation of hippocampal ensemble memories during sleep. Science. 1994;265:676–679. doi: 10.1126/science.8036517. [DOI] [PubMed] [Google Scholar]
- Zugaro M.B., Monconduit L., Buzsáki G. Spike phase precession persists after transient intrahippocampal perturbation. Nat. Neurosci. 2005;8:67–71. doi: 10.1038/nn1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(Left panel) Movie of the GCaMP5G fluorescence signal imaged in the CA1 stratum pyramidale of a mouse running in the dark on a treadmill without cues. (Right panel) Fluorescence traces from three neurons in the movie involved in recurrent sequences of neuronal firing as the mouse spontaneously travels on the treadmill. Bottom graph indicates mouse speed.