Abstract
Atomically detailed simulations of HIV RT are performed to investigate the contributions of the conformational transition to the overall rate and specificity of enzyme catalysis. A number of different scenarios are considered within Milestoning theory to provide a more complete picture of the process of opening and closing the enzyme. We consider the open to closed transition in the absence of and with the correct and incorrect substrates. We also consider the free energy profile and the kinetics of the conformational change after the chemistry step in which a new base was added to the DNA, but the DNA was not yet displaced. We partition the free energy along the reaction coordinate and analyze the importance of different protein domains. Strikingly, significant influence on the free energy profile is detected for amino acids far from the active site. The overall long-range impact is about fifty percent of the total. We also illustrate that the overall rate is not necessarily determined by the highest free energy barrier along the reaction path (with respect to the free enzyme and substrate) and that the specificity is not necessarily determined by the same reaction step that determines the rate.
Keywords: DNA polymerase, potential of mean force, Milestoning, reaction coordinate, specificity
I. Introduction
In our previous work we showed that a substrate-induced change in enzyme structure from an open to a closed state can be the major determinant of enzyme specificity even if the conformational change is not rate determining, and we examined the kinetics of this structural transition by computer simulations at atomic resolution1. Here we extend these studies to explore the conformational change in the absence of substrate and after the chemical reaction in order to provide a more complete description of the role of conformational dynamics in a complete enzyme cycle.
Because the relevance of the conformational change to enzyme specificity has been controversial, it is necessary for us to first address recent criticisms. If the conformational change step is rate-determining, it will be the major determinant of enzyme specificity2, and there seems to be no dispute of that conclusion. However, the disagreement arises when the conformational change is not rate-determining. In particular, Warshel3 has made two claims that we disagree with: (i) “the highest activation barrier (relative to the unbound state) absolutely determines the overall rate”, (see legend to figure 1 of reference 3), and (ii) “as long as the free energy barriers associated with any of the prechemistry steps are not rate limiting, they could not contribute to the catalysis and then to the fidelity” (see abstract of reference 3).
The error in these statements stems from equating overall rate of catalysis to specificity. Stated in terms familiar to enzymologists, enzyme specificity is a function of the apparent second order rate constant for substrate binding (and subsequent product formation) and is defined by kcat/Km, the so-called specificity constant. In contrast, the net rate is defined by kcat, the maximum rate of turnover at saturating substrate concentration. While enzyme specificity is determined by the highest activation barrier relative to the unbound state, the overall rate (or net rate) is a function of the highest absolute barrier relative to their local minima. Although in some cases these two aspects of enzyme catalysis (specificity and net rate) can be attributed to a single step in the reaction sequence, the specificity-determining step can differ from the rate-determining step when the specificity-determining step is largely irreversible and precedes the rate-determining step.
To illustrate this point, we provide counter examples to the above claims using two simple kinetic schemes below that serve as pedagogical examples. We first consider the elementary Michaelis-Menten model for enzyme kinetics for a single substrate and then consider competing reactions with two similar substrates.
We derive the results in considerable detail to remove any suspicion that our argument is merely verbal and to show that our conclusions are based on simple mathematical analysis of a minimal model widely used in biochemistry. This analysis can easily be extended to a more complex kinetic scheme that includes an explicit step for the conformational transition preceding chemistry.
We first illustrate that the rate determining step can be a step in which the barrier height is not the highest relative to the separated enzyme and substrate. Consider a simple scheme of a reaction of an enzyme E with substrate A.
| (1) |
We use the steady state approximation on the intermediate EA to write
| (2) |
and obtain
| (3) |
An explicit expression for the amount of the free enzyme [E] is derived using the total concentration (or the number of enzyme molecules) [E0], to give [E] = [E0] − [EA] and therefore
| (4) |
Finally, the expression for the rate is
| (5) |
This is the Michaelis-Menten equation as derived by Briggs and Haldane4 and written with explicit rate constants rather than being reduced to kcat and Km parameters.
In order to demonstrate our argument, we consider the limit where k−1 ≡ k2
| (6) |
Physically this limit means that the backward reaction after complex formation is unlikely and the process becomes essentially irreversible kinetically. This is an important limit found in the action of a number of enzymes and we have illustrated such a process, computationally and experimentally in1.
We consider next two other limits which are a function of substrate concentration (i) k2 >> k1 [A] and (ii) k2 << k1 [A]. Note that k1 [A] is a pseudo first order rate coefficient for a fixed concentration of substrate. We have for the two cases (i) rate ≅ k1 [E0][A] and (ii) rate ≅ k2 [E0]. It should be clear at this point that the term “overall rate” is useful only with reference to a state defined by the substrate concentration. Generally the terms, “net rate” or “overall rate” refer to the maximum rate achieved at high substrate concentration. Thus, the only reasonable interpretation of the term “overall rate” is to mean the maximum rate, which in this model is defined by rate ≅ k2 [E0] when k2 << k1[A]. This corresponds to the definition of kcat = k2 for this simple model.
To make the connection to free energy we write the rate coefficients using Arrhenius expressions kx = ω exp(−βΔFx) where for simplicity we use the same pre-exponential factor for all rate coefficients. Consider the free energy diagram in Figure 1.
Figure 1.
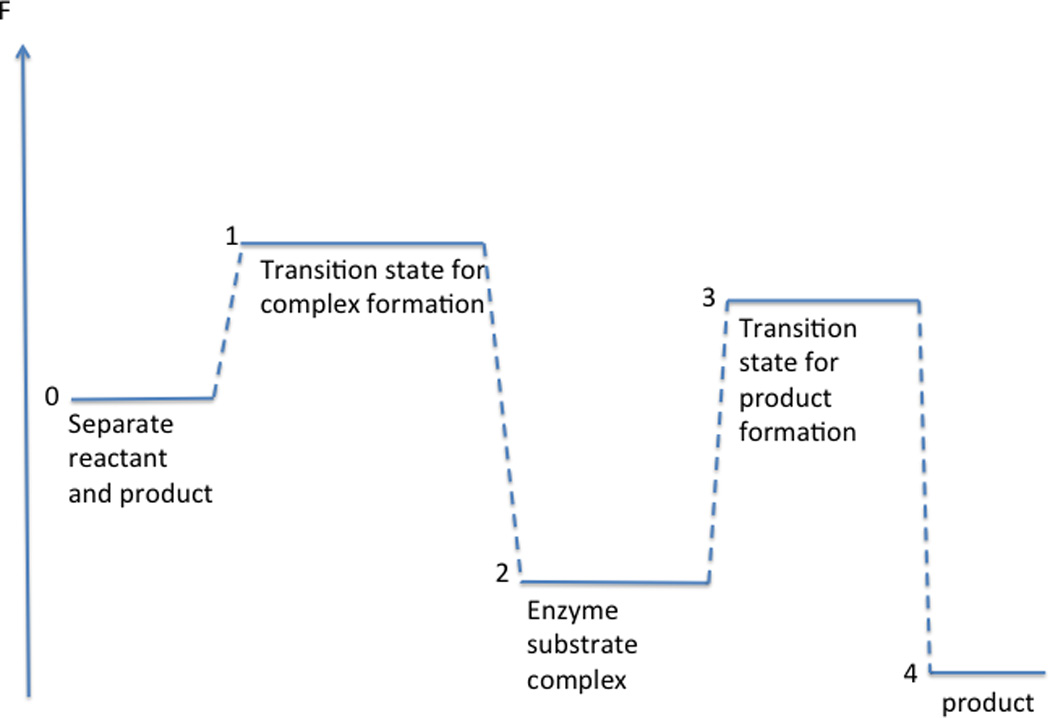
A schematic free energy diagram illustrating a case in which the rate determining state is not with the highest free energy barrier with respect to separate reactants and products. The dashed line is to guide the eye. See text for more details.
According to the free energy diagram we have k1 = ω exp(−β(F1 − F0)), k−1 = ω exp(−β(F2 − F1)), and k2 = ω exp(−β(F3 − F2)). From the diagram it is obvious that we have k−1 << k2 and k2 << k1[A] which illustrates the subtitle of I.1. The important conclusion from this analysis is that even though substrate binding (barrier 1) is faster than chemistry (barrier 3), the barrier to release the substrate (reverse reaction) is sufficiently high (barrier 2) such that the barrier for catalysis relative to free enzyme and substrate becomes lower than that for the binding step.
We consider next the fidelity of the enzyme. We show that under the same circumstances the selectivity is controlled by a step that is not rate-determining; namely, step 1.
Consider two substrates A and B that compete for the same enzyme E to produce [PA] and [PB] respectively. The reaction schemes are
| (7) |
We define the specificity as the ratio of the two rates
| (8) |
Assuming steady states for the two intermediates [EA] and [EB] we have
| (9) |
As before assume that k−1 << k2
| (10) |
From this analysis we demonstrate that the specificity depends on the rate coefficients of step 1, which is not rate determining! Stated in terms that are commonly used in enzymology, the net rate is determined by kcat = k2, while specificity is determined by kcat/Km = k1 (for this simple model). Our simple analysis here shows that when a binding step is largely irreversible, specificity and net rate are a function of different steps in the pathway. Moreover, this analysis provides clear exceptions to Warshel’s general assertions. Specifically, we demonstrate that: (i) the highest activation barrier (relative to the unbound state) does not necessarily determine the overall rate, (ii) even when the free energy barrier associated with a pre-chemistry step is not rate limiting, it can contribute to fidelity.
We have extended our analysis to a real-life example based upon our data defining the kinetics of DNA polymerization. DNA polymerases represent an ideal model for understanding enzyme specificity because their alternative substrates are well known in the form of noncognate base pairs, and enzyme fidelity is biologically important so specificity in discriminating against similar substrates is quite high. In order to better understand the molecular details underlying enzyme conformational dynamics in governing specificity we previously examined the kinetics of closing of the structure of the HIV reverse transcriptase (HIV-RT) with a nucleotide substrate bound1, 5 using atomically detailed simulations and the Milestoning theory6, 7. We showed that while a correct substrate induces a fast conformational change to bind the substrate tightly and facilitates fast catalysis, an incorrect substrate fails to stabilize the closed state or organize the active site residues for catalysis. Thus, the conformational change is a major determinant of enzyme specificity. In this report, we extend these studies to examine the conformational dynamics in the absence of nucleotide and following nucleotide incorporation and pyrophosphate release.
We also consider the individual contributions of amino acids to the free energy change along the transition pathways. Such partitions can be a useful tool to identify the critical residues that can be targets of site directed mutagenesis experiments. We note however, that partition of the free energy to individual components has long been a controversial issue computationally. In general the partition depends on the path between two end states. The dependence of free energy partition on the path makes this type of analysis ill defined8. However, in the present case we have fixed the path. It is the minimum free energy coordinate for the conformational transition under considerations9 that was determined using the String method10. The assumption that we made in the additional analysis discussed in this paper, is of a small perturbation, such that the reaction coordinate does not change significantly from the initial guess in response to substrate and protein variations. Hence the analysis we present here is well defined formally. It provides unambiguous information about the participation of different protein parts in the reaction once a reaction coordinate is available.
This manuscript is organized as follows. In Method we discuss the theory of minimum free energy calculation and Milestoning, the setup of the calculations and the novel analysis of free energy partition. In Results we outline the kinetics and thermodynamics of enzyme conformational transition in different substrate conditions and we discuss the potential impact of our free energy partition calculations for future experiments. Conclusions are in the last section.
II. Methods
II.1 Theory
In this section we briefly review the computational methods used in this manuscript. We describe the Locally Updated Planes (LUP)11 and the finite temperature String method12 as implemented in our molecular dynamics code MOIL13, to compute minimum free energy pathways. We also outline the computational aspects of the Milestoning method14–16. Finally, we consider the exact partition of the free energy along the reaction pathway.
II.1.1 The Locally Updated Planes and string methods
The string method is an iterative algorithm to refine a whole curve to determine a minimum free energy coordinate (MFEP). Consider a one-dimensional curvilinear coordinate and hypersurfaces perpendicular to it (Figure 2) that defines a reaction coordinate. A frequent approximation to the hypersurfaces is hyperplanes that are orthogonal to the curvilinear path. In the present study we use hyperplanes similarly to previous investigations17, 18,19. In our code, the String method is a direct extension of the Locally Updated Planes method (LUP11) that was published in 1990 to compute minimum energy pathways (MEPs). In LUP a discrete representation of the reaction coordinate is quenched, keeping the end points of the first and last structures (reactant and product) fixed. Let x ∈ R3N be the coordinate vector of the whole system, N is the number of atoms, and let xR and xP be the coordinate vectors of the reactant and product respectively. Let x(l, τ) be a curve connecting the reactant and product and parameterized by l such that x(l = 0, τ) is the reactant and x(l = L, τ) is the product. Hence the two end points are fixed and are independent of the value of τ. The variable τ is a fictitious time that is used to monitor the path quenching process. The path is approaching the correct solution (the Steepest Descent Path - SDP) monotonically as τ increases. We define the path slope, which is a unit vector along the direction of the path at l
| (11) |
Figure 2.
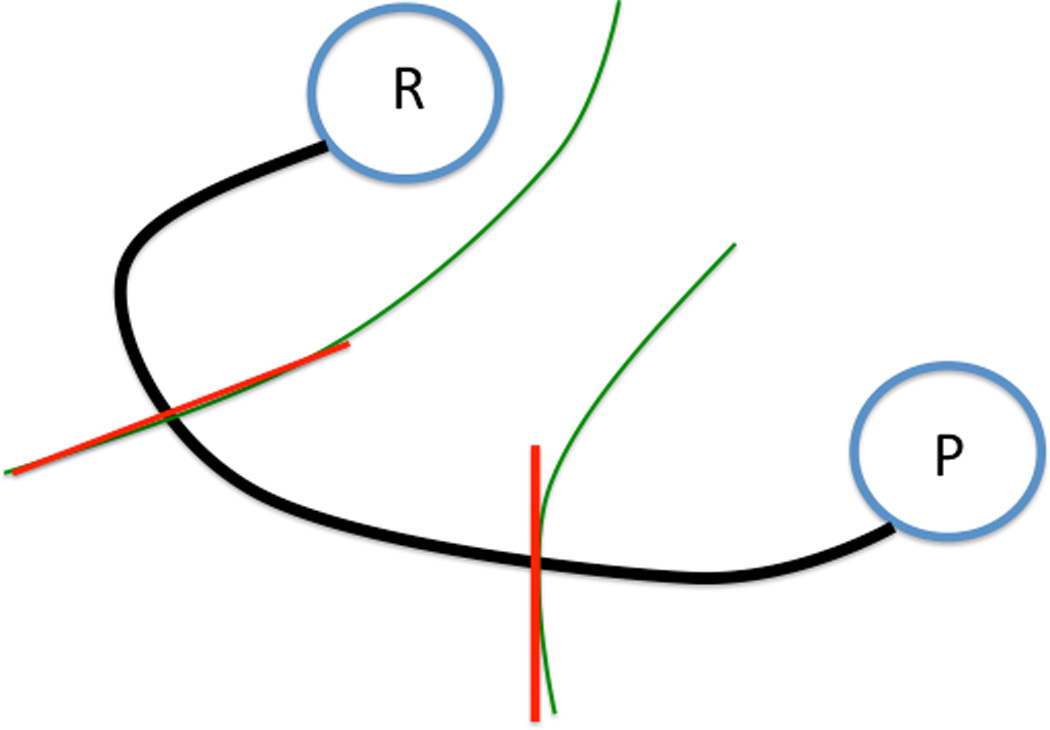
The schematic representation of the path connecting reactant (R) and product (P). Milestones (green curves) are hypersurfaces that are normal to the curvilinear reaction coordinate. In the practical application of the string method the hypersurfaces are replaced by hyperplanes (red straight lines) locally orthogonal to the line connecting the reactants and products.
The calculation of the minimum energy path is the minimization of the energy of each of the points along the curve, x(l, τ). The potential energy is U(x) and the minimization is subject to the constraint that the point remains on the curve.
| (12) |
The projection operator in Eq. (12), , forces the displacement, dx, to remain in the hyperplane orthogonal to the current direction of the curvilinear coordinate. At the limit of τ → ∞, provided that the potential is bound from below, the curve is reaching a stationary solution in which the right hand side is zero for all points along the path. The asymptotic path is one possible realization of the steepest descent path, also called the minimum energy path or the intrinsic reaction coordinate.
Let a discrete set of coordinates x(l, = i, τ) i = 0, …, L approximates the continuous curve. In the discrete representation x(0, τ) is the vector coordinate of the reactants, x(L, τ) is the coordinate vector of the products, and both of them are fixed. There are L − 1 intervals interpolating between the end states. We assume that the lengths of the intervals are sufficiently small to provide adequate representation of the continuous curve. This assumption can be enforced by additional constraints, which are either penalty functions20, or holonomic constraints9 to keep the distance between sequential points along the path the same21, for example
| (13) |
To find the minimum energy path we solve the quenched equation at the limit τ → ∞ for the discrete positions along the path
| (14) |
We estimate the path slope using a finite difference between positions along the reaction coordinate as shown in the second line. Note that the path slope is changing dynamically as the individual discrete points along the path are modified and couple the coordinate vectors along the path.
To compute the minimum free energy path in the space of coarse variables we consider the potential of mean force instead of the potential, and optimize the curve in a subspace of coarse variables. In general the coarse variables can be curvilinear coordinates, which complicates the analysis. We restrict our implementation in MOIL13 to a subset of coarse variables, which are Cartesian coordinates. For example we considered all the Cartesian coordinates of the Cα atoms of the amino acids in a protein. Let y ∈ Rn be the vector of the coarse variables in n dimensions and let z be the vector of the coordinates that supplements y to obtain x. Let sl be the path slope in the space of coarse variables (similarly to el in full space). To obtain the minimum free energy path in the space of coarse variables the String extension of LUP12 uses the potential of mean force (PMF) instead of the full potential in Eq. (12). We have
| (15) |
where the average in the lower equation is conducted on the subspace, Z. The joined Cartesian spaces Z and Y make the complete space X. We were able to write the average without a Jacobian factor for transformation between coordinate sets (X→Y, Z) since we restrict the representation of the coarse variables to Cartesian only. In practice, we use constant temperature Molecular Dynamics simulations to perform the spatial average in Eq. (15). Hence, we replace the spatial average by a temporal average in accord with the ergodic hypothesis. The values of the coarse variables are kept fixed during the averaging process and are modified only when propagating the curve according to the top formula of Eq. (15) for one fictitious time step. Hence, the curve quenching is conducted only in the coarse space.
In summary Eq. (15) is the String formula that is implemented in MOIL13 and is a direct extension of the LUP algorithm. The result of these calculations is a sequential set of points in coarse space - yi=1,…,L. This set is a discrete approximation to the curve that defines the reaction coordinate.
The reaction coordinate is the set of hypersurfaces orthogonal to the curve computed earlier. In II.1.1 we generated a sequence of points in coarse space that are parameterized by a single scalar variable l. The reaction coordinate is characterized by the values of the coarse variables at points, y(l), and by the slope of the path, ql. The change in the free energy along the path is given by
| (16) |
The sum over j is over the coarse variables. Since we have chosen the coarse variables to be Cartesian, the individual contributions in the above sum can be separated and grouped to different subsets (e.g. atoms that belong to a particular amino acid or to a particular secondary structure element). The final expression shows that the free energy differences can be written as contributions from displacements along different coarse variables. Of course, this exact partition is conditioned on the availability of a reaction coordinate.
Milestoning is a theory and an algorithm that was introduced to compute thermodynamics and long time kinetics along reaction coordinates. While Milestoning at present is a general and rigorous theory7 which is exact and is not limited to one reaction coordinate, here we exploit the simpler, approximate, and less expensive to compute versions of the algorithm6, 14, 22. Since Milestoning was discussed extensively elsewhere we only define below the important variables and introduce the final formulas.
Definitions in the context of the Milestoning theory:
Milestones: Milestones are orthogonal hypersurfaces normal to the curve of the reaction coordinate (Figure 2). A trajectory is in state α if the last milestone that it crossed is α.
Probability: The probability, pα (xα, t), is the probability that at time t the last milestone crossed by a trajectory at position xα, is α. The stationary probability is defined as the limit
Free energy: the free energy of state α is defined as Fα (xα) = −kT log (pα, stat (xα)) where k is the Boltzmann constant and T is the temperature.
Flux: The flux, qα (xα, t) is the number of trajectories that pass through a milestone α at phase space point xα in unit time. By construction it is always positive.
Mean First Passage Time (MFPT): The MFPT, 〈τ〉, is the time that it takes a trajectory, on the average, to start at the reactant and ends the product state for the first time. In systems that follow exponential kinetics, it is the inverse of the rate coefficient.
Conditional or transition probability (kernel): The kernel Kβα (xβ, xα, t) is the probability that a trajectory will cross milestone α at point xα and at time t given that it passes milestone β at point xβ at time 0. The kernel in current Milestoning implementation depends only on the time differences between crossing events.
The starting equation in Milestoning is the equation that accounts for conservation of the flux.
| (17) |
The summation over β is over other milestones that can access directly milestone α (without crossing other milestones in between). The integration in the expression on the right is over the phase space of the milestone Γβ, and of the time of entry to the other milestones, in an earlier time t'.
Consider a stationary version of Eq. (17), which we provide without proof. A complete discussion can be found elsewhere14, 16. A stationary flux is obtained at sufficiently long times in which the system is approaching a steady state. The result of a long time analysis of Eq. (17) is a linear, integral, and exact equation for the stationary flux
| (18) |
If the system is close to equilibrium in the NVT ensemble7 one may assume that the initial flux at milestone qβ(x) is distributed according to the canonical weight
| (19) |
where wβ is a weight to be determined. If the initial conditions for the trajectories are already sampled from the canonical ensemble conditioned to be at milestone β, the flux is
| (20) |
where i is the running index of the sampled trajectories and L is their total number.
Plugging Eq. (19) into Eq. (18) and integrating over xα we have
| (21) |
The first line of Eq. (21) is a linear matrix equation for the coefficients, wα. The matrix element Kβα is estimated from short trajectories between the milestones. For convenience we also denote the full matrix with bold face, K, of dimension M × M where M is the number of milestones. The physical interpretation of Kβα is the probability that a thermal trajectory initiated in milestone β will hit milestone α before any other milestone.
For computational purposes we define two types of transition kernels. The first, KC, is set with cyclic boundary condition. Trajectories that enter the product state are immediately returned to the reactant. This kernel conserves probability and is appropriate to study stationary flux. The second kernel, KA, is absorbing or terminating; every trajectory that enters the final state disappears. The absorbing kernel does not conserve probability and is appropriate for the study of the mean first passage time as we outline below.
We also define the life-time of the milestone, tβ as follows: Given that a trajectory started from a point xβ in Milestone β, we ask what is the average time for this trajectory to hit for the first time a milestone different from β.
We note that the kernel with periodic boundary conditions is a probability function and is normalized as
| (22) |
The life-time is therefore (written for a point in a milestone and for an average over a milestone)
| (23) |
Given the stationary flux and the milestone lifetime we have shown7 that the stationary probability that the last milestone that was crossed and the free energy of α are
| (24) |
The final formula for this section is for the overall mean first passage time, (definition 5) which is derived under similar assumptions as for Eq. (19)
| (25) |
Note the use of an absorbing kernel in the derivation of the MFPT.
Eq. (24) and (25) are the central expressions of this section.
The models of the open and closed forms of the enzyme were based on the structures 1RTD23, 24 and 1J5O24 respectively from the Protein Data Bank25. The molecular model of the enzyme-DNA complex with incoming nucleotide is shown in Figure 3. The molecular modeling of the enzyme and DNA complex with an incoming nucleotide was discussed in detail in Reference 1. This section discusses the modeling of the two other molecular systems: enzyme-DNA complex with no nucleotide bound (NN) and the complex after correct nucleotide undergoes chemical reaction denoted as After Chemistry (AC).
Figure 3.
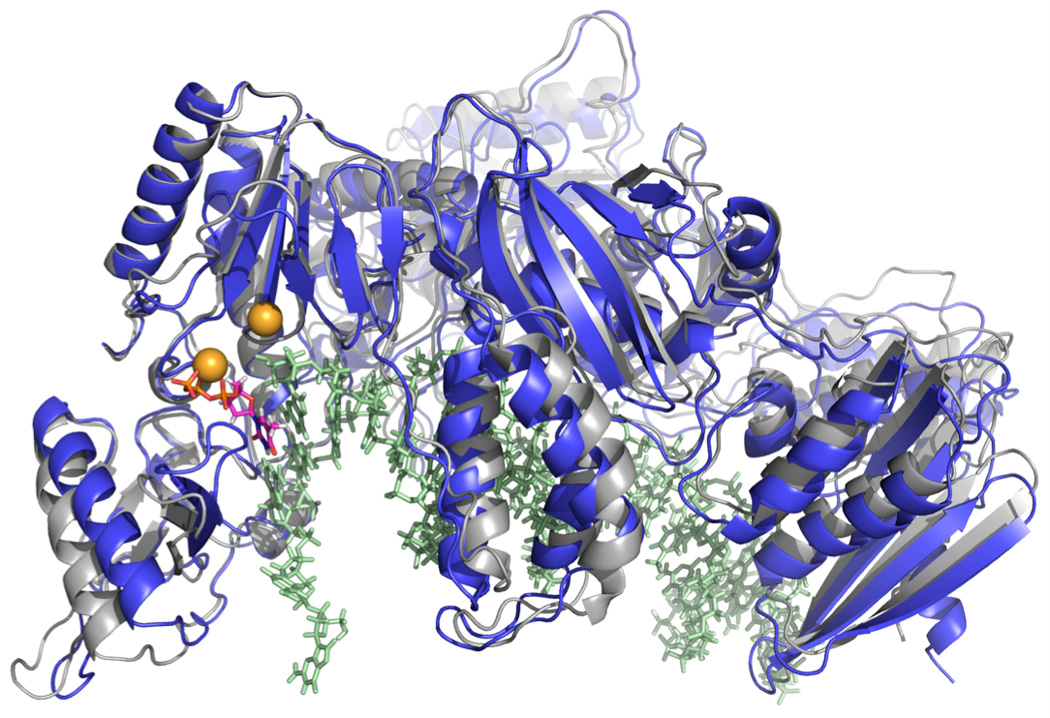
Molecular structure of the HIV Reverse Transcriptase that is used in molecular dynamic simulations. The protein-DNA complex is shown in open (grey) and closed (blue) forms. Shown in colored spheres are Magnesium ions. The incoming nucleotide bound to the active site is shown with purple-orange sticks.
To model NN we use the existing crystal structures in the two end points mentioned above. We remove the matching nucleotide (here, TTP) from the crystal structure of the closed complex and perform a short minimization to relax the structure to a local energy minimum. The open state 1J5D does not have an incoming nucleotide bound so we used it as is. To model the AC structure we added the matching nucleotide (Thymine in our case) to the growing strand and removed pyrophosphate group and the two catalytic magnesium ions at the active site. These models were used to compute the minimum free energy paths for open to closed transition of HIVRT. The paths were then used to compute the thermodynamics and kinetics of the conformational transitions in different substrate conditions.
All calculations were performed with the MOIL suit of programs13. The OPLSAAL all atom force field was used to model the protein and the nucleic interactions26, 27. As detailed in Reference 28 bonding terms of the nucleic acids were adopted from AMBER f9929. The simulated system consists of the enzyme (984 residue) in complex with 25bp DNA duplex with a sequence of 5′ -GCCTCGCAGCCGTCCAACCAACTCA-3′ base pair with 3′CGGAGCGTCGGCAGGTTGGTTGAGTAGCAGCTAGGTTACGGCAGG-5′. The entire complex is embedded in 40,300 TIP3P water molecules. A periodic rectangular box of 108.5×108.5×118.5A3 was used. Magnesium and chloride ions were added to ensure neutrality and to mimic experimental conditions of concentration of 50mM. The geometry of individual water molecules was fixed with matrix SHAKE30. Particle Mesh Ewald Summation31 was used for long-range summation of electrostatics with a grid size of 64 angstrom in each direction. Velocity scaling was applied to keep the temperature constant at 311K and configurations perpendicular to the reaction coordinate were sampled using Lagrangian constraints as implemented in Reference 32. Initial phase space points were sampled at constant temperature, i.e. from the NVT ensemble. Short trajectories initiated from the sample points to estimate the transition kernel matrix followed the Newton’s equations of motion.
We constructed the transition path that minimizes the free energy barrier using the string method. As an initial guess for NN and AC paths we used our path for the correct match computed in Reference 1. Each configuration of the enzyme along the discrete representation of the path in coarse space is modified to NN or AC condition and then solvated with water and ions. Solvated configurations were further equilibrated for about 200ps by freezing the enzyme-DNA complex but allowing the solution atoms to move. We used the Cartesian coordinates of the α-carbons of the enzyme and all heavy atoms of the fingers domain (1–85, 115–150) as our coarse variable set. We evolved the configurations at constant temperature in the hyperplane orthogonal to the path32 sampling conformations from canonical ensemble. We computed the average force perpendicular to the path in 5ps time intervals. The average force was used to quench the path and adjust the distances between the points (Eq. (14)). The path is updated for about ~250 times to achieve a converged path.
The calculations of the optimal curve (Eq. (15)) are meaningful if the distances separating sequential points along the path are small such that the variations in the sequential forces are small as well. That is, the finite difference approximation of the curve is accurate. One way of avoiding a particularly large distance is to spread the points uniformly along the curve, which minimizes the worst distance. Uniform density of points along the path was proposed and enforced in the past by the addition of equi-distance restraints21, Lagrange multipliers9, or path re-parameterization33. We combined the use of restraints, which are more stable numerically, with a refinement step of the re-parameterization.
To ensure the convergence of the path we computed the RMSD (Root Mean Square Deviation) of the path after each update. We stopped adjusting the path when the change in RMSD (Root Mean Square Difference) between two paths in a sequence was smaller than 0.001 angstrom.
Three-nanosecond simulations at the hyperplane normal to the reaction coordinate (the milestone) were used to sample configurations. Snapshots were saved every 0.5ps and were examined to check if they are sampled from First Hitting Point Distribution (FHPD). The FHPD points are identified by integration backward in time and verifying that the first milestone that is crossed during the backward integration is different from the originating milestone. If the trajectory first hits the initiating milestone, it is not sampled from FHPD and is removed from the statistics. The acceptance ratio varied from a milestone to a milestone and was between 0.1–0.9. Verified FHPD points were then integrated forward in time until they hit for the first time another milestone16. In the forward integration we allow for re-crossing of the originating milestone. The typical time for the termination is about 10–30ps. The identity of the initiating and terminating milestones were recorded as well as the lifetime of the trajectories. At each milestone a minimum of 200 trajectories are used to estimate the matrix element of the transition kernel.
We estimate the free energy change along the reaction coordinate by Milestoning and by integration of the mean force (Eqs. (16) and (24)). These two calculations are possible in a single Milestoning calculation since the sampling at the milestone for initial conditions for trajectories can be used to estimate the average force in the hypersurface orthogonal to the reaction coordinate. Estimating the free energy profile by two different approaches enhances the confidence in the conclusions of the computations.
III. Results
In Figure 4 we summarize the main result of this article on the overall free energy landscapes of different binding modes of the ligand. The free energy profiles presented are computed using integration of the PMF. All the curves are matched at the left with the state of physical binding of the nucleotide to the open state. While differences in physical binding can be significant and will be addressed in future work, we focus in the present study on the conformational transition step. Interestingly, the right side of the free energy profile of binding a mismatch nucleotide (dATP, blue curve) is the highest of the curves. This makes the closed state of a bound mismatch unlikely, even with respect to the enzyme with no nucleotide bound. A conformational transition from an open to closed state without the presence of a ligand (red curve) is almost free-energy neutral. There is no strong preference of the enzyme for the open or closed states in the absence of ligand according to our findings. Correct ligand binding makes a significant change in free energy landscape shifting the equilibrium to the closed state (black curve).
Figure 4.
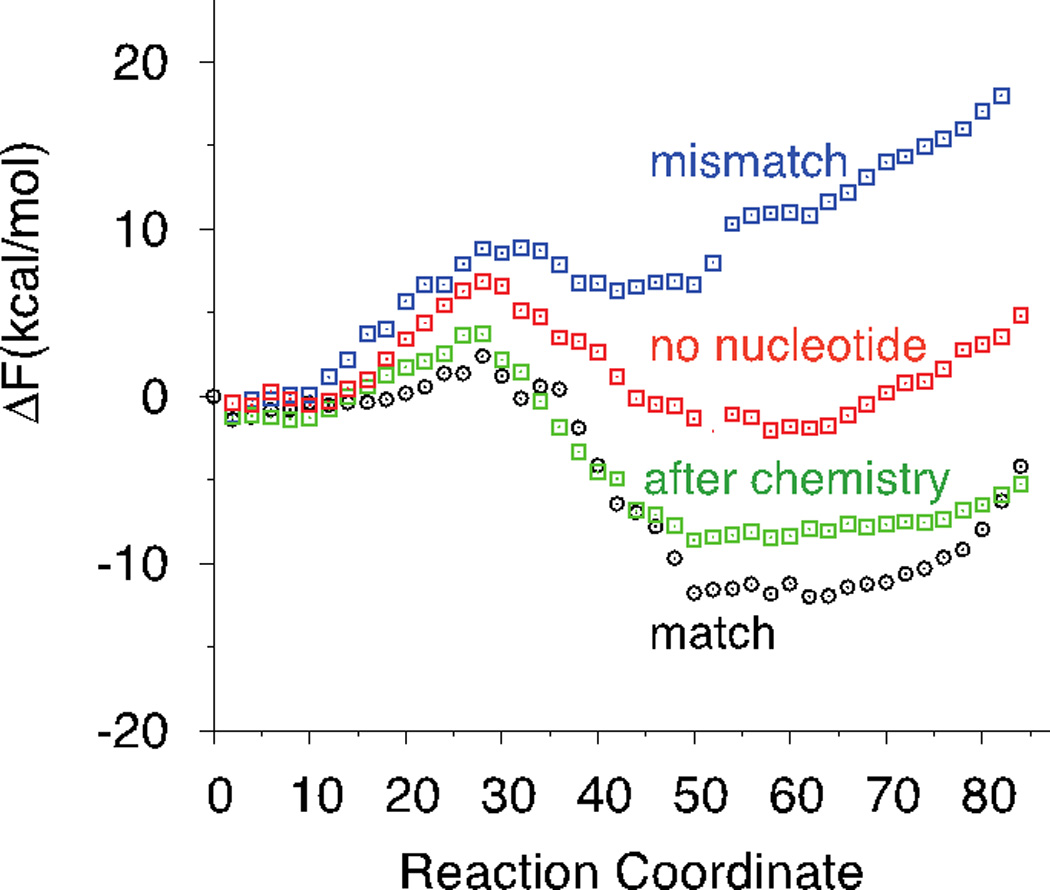
Potential of Mean Force along the open to closed transition of the HIV RT. Each color represents the PMF with a different substrate bound Correct Nucleotide TTP (Black), Mismatch dATP (Blue), Correct Nucleotide after addition to the growing strand and release of pyrophosphate group (Green), and No nucleotide (Red).
Addition of the nucleotide to the growing strand results in a moderate change of the free energy profile at the closed state (green curve). Releasing of the pyrophosphate group together with two magnesium ions at the conserved ion binding pockets reduces also the free energy barrier going from open to closed, causing a rapid collapse to the closed state when the enzyme is open and at the same time the absence of magnesium ions at the active site reduces the stability of the closed state relative to the enzyme with the correct nucleotide bound. However, the changes are still not enough to shift the equilibrium towards the opening after chemistry. Hence the translocation of the DNA after the chemical reaction may be necessary to destabilize the closed state.
In Figure 5 we compare the free energy profiles that are obtained by the two different computational approaches described in Methods section. The widely used protocol is the integration of PMF along a reaction coordinate, (Eq. (16)) which we showed already in Figure 4. The second approach is based on the stationary flux in Milestoning formulation (Eq. (24)). The two entities are not exactly the same since in Milestoning the probability is defined by the last milestone that was passed by a trajectory (and not an average over an interval). However, for sufficiently small displacements between the milestones which is about 0.05 angstrom in our case we expect them to be similar, as we illustrate for a dipeptide in Reference 14. Of course the displacement should not be too small to violate the de-correlation assumption of the current Milestoning algorithm.
Figure 5.
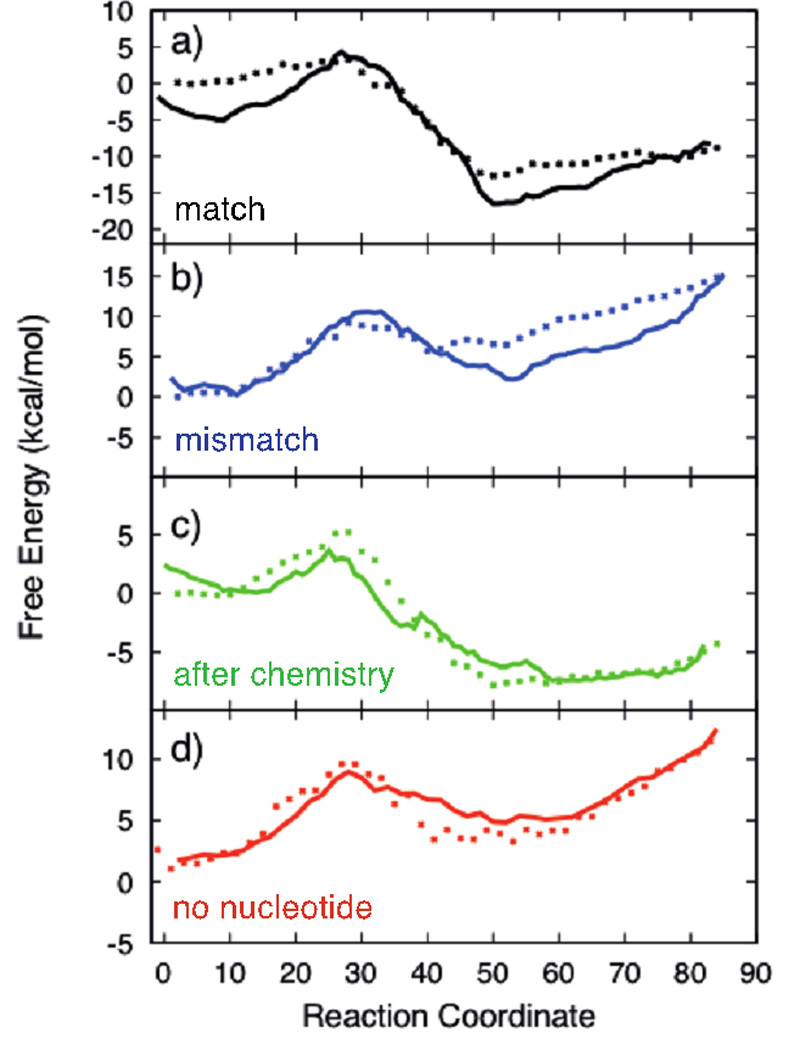
Comparison of the free energy calculations along the enzyme conformational transition pathway with different binding modes of incoming substrate using the two different methods: Points are computed from the average of the projection of force along the path (PMF), Solid lines are the free energy estimates from the stationary probability of milestones computed from unconstrained molecular dynamic simulations. The plots correspond to different substrates: a-Correct nucleotide bound, b-Mismatch bound, c-Correct Nucleotide after pyrophosphate release, d-No Incoming nucleotide bound.
Besides the definition of free energy the theories behind the calculations are markedly different. The PMF is based on equilibrium sampling of configurations, while Milestoning is based on kinetic analysis of trajectory fragments. The observation that the long time behavior of the kinetic matrix agrees with straightforward equilibrium calculations is a useful testimony for the convergence of the calculations.
In Table 1 we provide the rate constants for the conformational transitions computed by Milestoning theory. In parenthesis we give the experimental rate coefficients, when available. Figure 6 shows the mean first passage time, computed with Milestoning, starting from the reactant and terminating at a specific position along the reaction coordinate.
Table 1.
The rate coefficients for the transition between open to closed states (k2 and k−2) computed by Milestoning. The experimental results are provided in parentheses when available.
| Substrate | k2(s−1) | k−2(s−1) |
|---|---|---|
| Correct | 2500–20000 (2000) | 40 (3) |
| Mismatch | 200–400 (>500) | 4000 (>1200) |
| No-Nucleotide | 100–2000 | 40000 |
| After Chemistry | 8×10^6 | 4400 |
Figure 6.
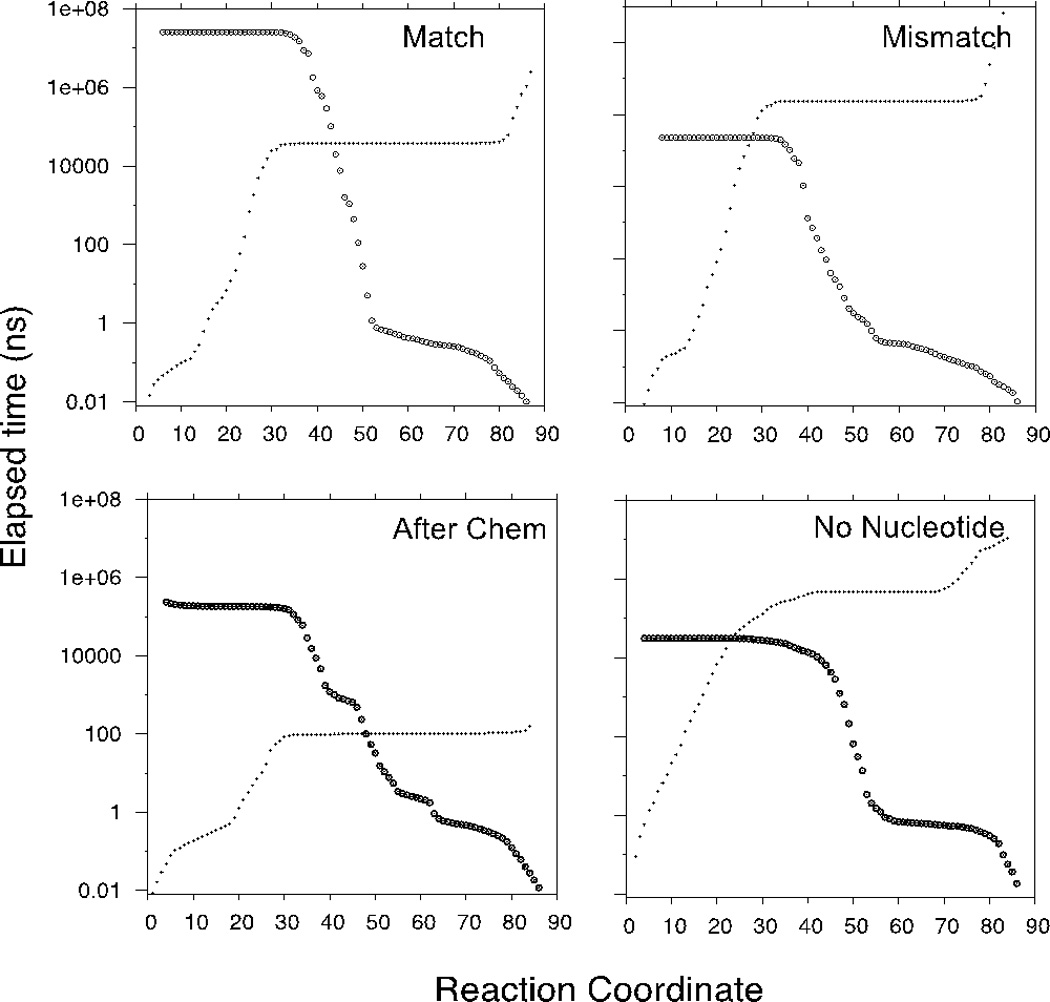
Mean First passage time for the conformational transition of HIV RT between two functional states with different substrate binding states. Open state is represented with 1 in the Reaction Coordinate while the closed structure is 85. Small dots show the elapsed time from open to closed while circles are the time for the reverse transition.
We simulated the opening of the complex, after the chemical step is completed, by adjusting the structures of the path we defined previously1. We started from the closed state structure with a bound nucleotide and completed the bond between the 3’OH end of the primer strand and incoming nucleotide. We then removed the pyrophosphate and two metal ions, and used the string method to refine the path starting from the previously computed reaction coordinate for the correct nucleotide computed previously. With the reaction coordinate at hand we used Milestoning to compute kinetics and thermodynamics of the process going from an open to a closed state with the elongated DNA occupying the nucleotide binding site. The order of events in the pathway involving release of the bound metal ions and the pyrophosphate and the opening of the enzyme is not known. For this analysis we modeled the reaction as sequential with release of pyrophosphate preceding opening. First, the small molecules leave with no significant change in the protein structure, and second the conformational transition takes place without the presence of the ion or the leaving group. Our MD simulations suggest that opening is fast (4400 s−1) relative to the rate of opening before chemistry (40 s−1). In future work, we will consider the alternative reaction sequence with opening preceding pyrophosphate release.
To get further insight to the free energy profiles and to the molecular factors that determine the dramatic changes in the rate and equilibrium binding of nucleotide to the HIV RT we exploit the exact partitioning of the mean force potential that was discussed earlier: If the molecular force is written as a sum, then the mean force potential along the reaction coordinate can also be written as a sum of the same type of terms (Eq. (16)).
Figure 7 shows the results of the subdivision of the protein into individual domains thought to make important contributions to the free energy of the open to closed transition. In particular, for each condition we compare the contributions of the fingers domain (Residues 1–88, 121–146) to the results obtained for the whole protein and the whole protein minus the fingers domain. In addition, we also consider the contribution of a small subset of key amino acids in the two loops of the fingers domain; the loops connecting β3–β4 and β7–β8 (residues 65–74 and 137–144). Figure 7a shows the partition of free energy change from open to the closed with correct nucleotide bound. Interestingly, the results indicate that the fingers domain contributes about half of the net free energy difference between open and closed states, while changes in structure in the remainder of the protein contribute the rest. It is obvious that the nearest residues to the active site (finger domain) will have a significant contribution to the free energy profile. However, the significant contribution of the rest of the protein is surprising.
Figure 7.
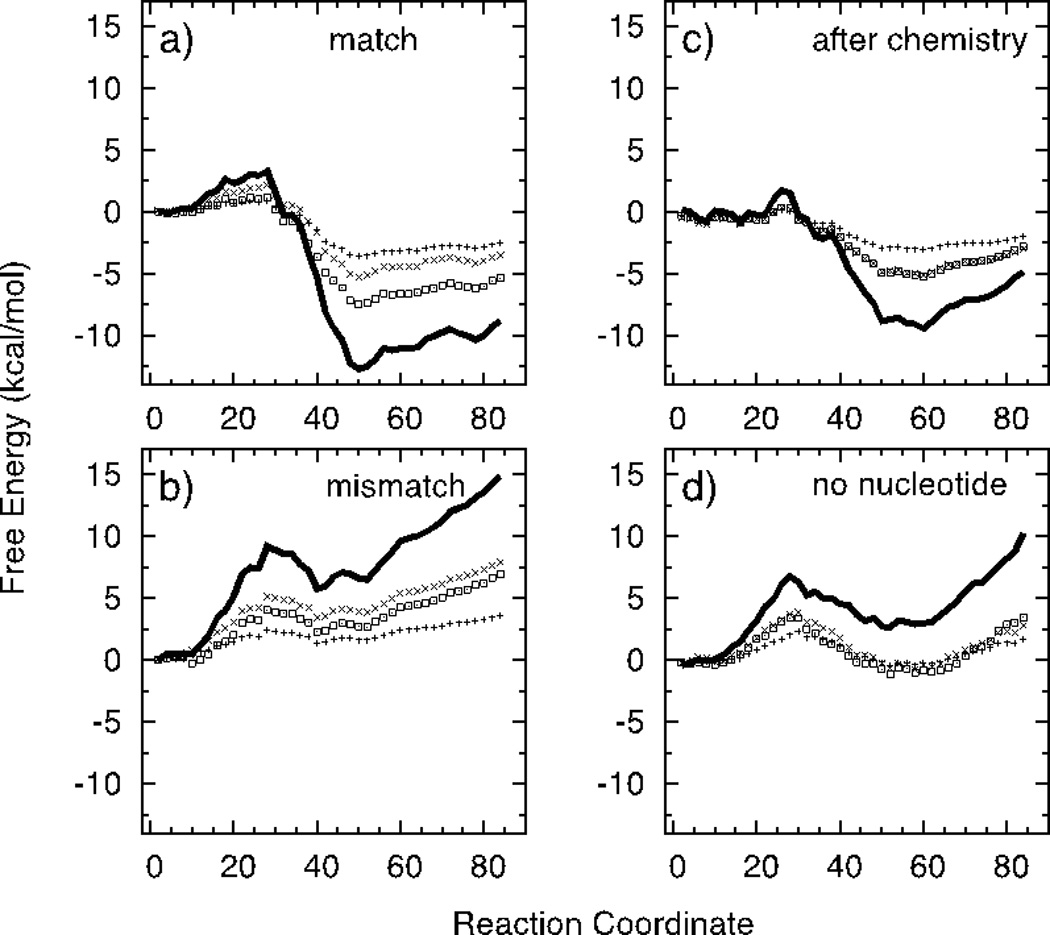
PMF for the systems studied (with the same order as in Figure 5). Solid lines are the PMF for the whole enzyme (Residue 1–984). Points are the contributions from a subset of particles from the enzyme; (x) represents the contribution from fingers domain (Residues 1–88, 121–146), (□) is the whole enzyme other than fingers domain, and (+) is the contribution from a subset of fingers domain (65–74, 137–144).
Figure 7b shows the results obtained with a mismatched nucleotide bound. Here, contributions of the fingers domain and the remainder of the protein to the unfavorable free energy difference between the open and closed states are approximately equal. In addition, the fingers domain and the remainder of the protein contribute comparable amounts to the free energy barrier at the transition state. The important conclusion of these studies is that the fingers domain and the remainder of the protein each contribute to the mismatch recognition, and this implies that a mismatched nucleotide-template interaction causes changes in protein structure both at the local level due to changes in the fingers domain interaction energies, but also causes global changes in protein structure. These changes were already reported in our earlier work1. Figure 7c shows the results obtained for the open to closed transition after chemistry, that is, with the DNA primer terminus occupying the nucleotide-binding site. Again the contributions of the fingers domain and the remainder of the protein are approximately equal for both the net free energy difference and the activation barrier. Thus both local and global protein and DNA structure elements tend to stabilize the closed state. Finally, in Figure 7d, we consider the change from the open to closed state in the absence of added nucleotide, and again, the changes in free energy contributed by the fingers domain are approximately equal to the contributions of the remainder of the protein.
Clearly these results indicate that motions throughout the protein are coupled to the reorganization of the residues in the immediate vicinity of the active site. Long distance interactions may act to gate the transition from the open to the closed state and could reflect the interaction of the DNA primer/template with the protein. For example, it is known that mismatches in the primer/template slow the rate of incorporation of a correct base pair34–37. This could be accomplished through these long-range interactions, or could be a result of misalignment of active site residues caused by the altered structure of the mismatched base pair in the DNA. Further experimental and computational analysis will be required to address the effect of mismatches in the DNA on nucleotide-induced conformational changes and incorporation. Our analysis provides novel predictions that will need to be tested experimentally in future work.
Partitioning of the PMF calculations provide an estimate of the contributions of individual amino acids to conformational change in enzyme structure. In Table 2, we list the free energy contributions of the most important amino acids, both at the transition state (TS) and to the net free energy difference between open and closed states. In this list, some of the amino acids are in line with expectations regarding the importance of charged residues at the active site such as R72, K65 and K66. Other predictions are unexpected, but could be rationalized post hoc, and will require further experimental tests. In particular during the open to closed transition, W71 slides along a hydrophobic face of the αA-helix. This motion was un-noticed from examination of static structures, but is quite evident in a movie generated by the minimum free energy pathway. Charged residues N137 and E138 interact with the charged groups of αA-helix and come in close contact while enzyme closes. Figure 8 shows the location and contribution of each of these residues to the overall free energy change as a heat map. One striking result is that the side chains far from the active site play a significant role in nucleotide recognition and stabilization of the incoming cognate nucleotide, while the same residues destabilize non-cognate one leading to the opening of the complex.
Table 2.
Residues that contribute most to the PMF. We report the change in the free energy from open to transition state (TS) and from open to closed state. The locations of these residues are depicted in Figure 6. All values are in kcal/mole.
| Correct | Mismatch | No-Nucleotide | After-Chem | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Res ID |
TS | Closed | Res ID |
TS | Closed | Res ID |
TS | Closed | Res ID |
TS | Closed |
| N137 | 0.2 | −1.1 | K66 | 0.5 | 0.45 | K67 | 0.75 | 0.4 | N137 | 0 | −0.7 |
| K66 | 0.15 | −0.5 | W71 | 0.4 | 0.45 | N137 | 0.4 | −0.3 | K66 | 0 | −0.5 |
| E138 | 0.05 | −0.3 | N137 | 0.25 | 0.4 | E138 | 0.2 | 0.35 | S68 | 0 | −0.4 |
| K32 | 0.15 | −0.15 | R72 | 0.2 | 0.4 | C38 | 0.05 | −0.25 | K65 | 0 | −0.3 |
| K65 | 0.05 | −0.25 | E138 | 0.2 | 0.3 | K65 | 0.35 | 0.2 | T139 | 0 | 0.2 |
Figure 8.
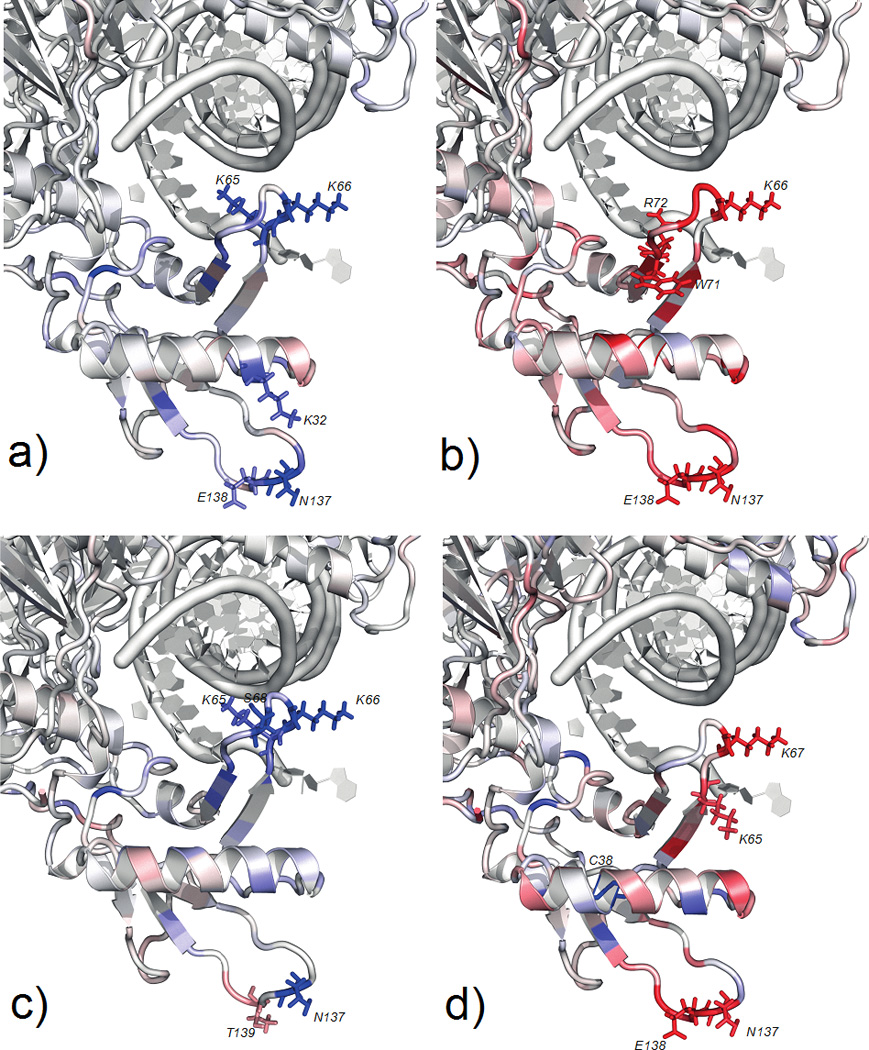
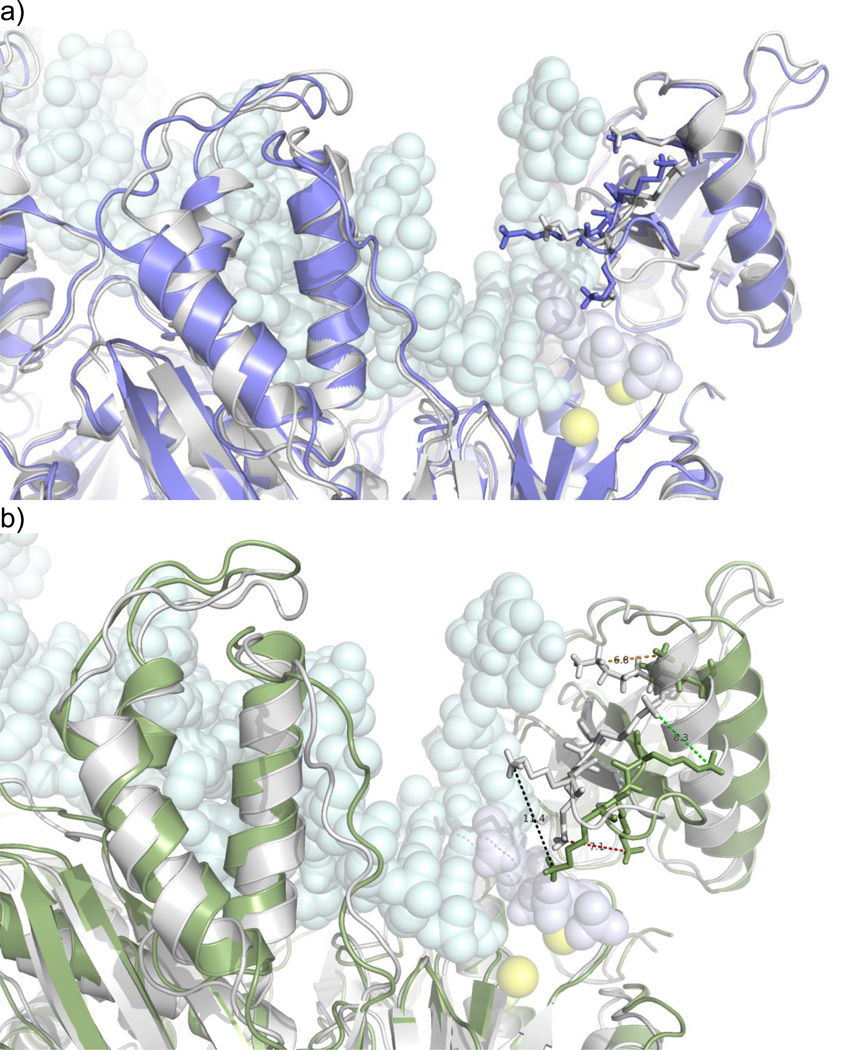
Contribution of each residue to the free energy difference going from open to closed states of the enzyme. Color changes in red–white-blue with Red being free energy contribution of ≥+0.5 kcal/mole to the closing conformational change, white being 0.0 kcal/mole and blue is ≤−0.5 kcal/mole. Contributions of individual residues to the overall free energy changes with substrate states studied. The contributions are depicted on the open state structure of the enzyme for comparison. a) Shows the free energy difference when a correct match is bound, b) for mismatch, c) after the chemical reaction of the correct substrate and d) in the absence of incoming nucleotide. Residues that contribute the most to the free energy change summarized in Table 2 and their side chains are drawn here explicitly in sticks representation.
In addition to the free energy contributions we show snapshot of structures sampled from the transition state ensembles for the two different modes of binding considered (see Figure 9). Transition State (TS) structures are compared with the case when correct nucleotide is bound, which was described in detail in our earlier work1. TS structure of correct substrate is similar even after the chemical reaction (Figure 9a). In the TS ensemble, positively charged groups bring together the finger domain in close contact to the DNA and terminal nucleotide. Interestingly a significant difference is observed in the TS structures of the transition in no nucleotide bound transition when compared with the correct substrate bound (see Figure 9b). The most significant difference is the displacement of the observed lysine side chains. Lysine chains did not align towards the DNA nor come close enough, an observation reported earlier for the mismatch1. Perhaps not surprisingly this gives the dramatic change in the local charge distribution around the active site and caused the slow rate of closing reported here. Also αA-helix that is sandwiched by the two loops connecting β3–β4 and β7–β8 stayed further from the active site relative to the correct nucleotide
Figure 9.
Structures selected from the Transition State (TS) shown in Figure 5 for different substrate binding states. Gray is the structure of protein when the ligand is correct in comparison when the enzyme a) after chemical reaction and b) without a nucleotide bound. Lysine side chains in the fingers domain show the most variation and they are shown with sticks for comparison.
IV. Discussions and Conclusions
In summary our investigation of the conformational transition (step 2) includes now the following scenarios
| (26) |
where EDn represents a complex of enzyme with DNA containing n nucleotides, E’ represents the closed enzyme state, D’ represents DNA where the primer terminus occupies the nucleotide binding site (the pre-translocation state), NC represents a correct nucleotide and NI represents an incorrect nucleotide.
In scenario (a) we considered the conformational transition with a correct ligand bound to the protein, in (b) with an incorrect ligand bound, in (c) with no ligand bound, and in (d) after the chemical step, but without the displacement of the DNA to free space to a new substrate. Step (c) is of particular interest from the perspective of mechanisms. Calculation (c) helps differentiate between a sequential binding mechanism and a mechanism of a conformational selection in which the conformational change precedes substrate binding. The conformational selection picture assumes a rapid equilibrium between the different states of the proteins (open or close), which are accomplished without the presence of the substrate. If step (c) is indeed much faster than steps (a) or (b), then conformational selection is a possible mechanism, but one key determinant is the rate of nucleotide binding to the open state, which we have not yet addressed. However, we have measured the maximum rate of the observed conformational change with different ligands yielding different rates38, 39, which argues against the conformational selection mechanism which predicts that the maximum rate of the observed conformational change will be independent of the ligand.
Step (d) is concerned with the completion of a cycle of the molecular machine. For the enzyme to be ready to accept another incoming nucleotide after the chemical step, the complex must transition to the beginning of the cycle. This transition includes two steps: The DNA must translocate further from the finger domain to free up the nucleotide binding site for the incoming nucleotide and a second step involves the opening of the finger domain of the protein so that a new ligand can bind. But what is the order of events? Does the DNA slide while the protein is still in the closed form, or does it slide after the protein changes its conformation to the open state? Scenario (d) prepares the ground for a fuller investigation of this question. Here we consider the feasibility of sliding after the closed to open transition. The reverse of the scheme in (c) is indeed similar to the second scenario: there the transition is after the DNA is translocated and ready for the incoming nucleotide binding and suggests that translocation should proceed chemistry to de-stabilize the closed state and afford rapid opening of the enzyme for a new nucleotides.
Our analysis provides a novel insight into the molecular details underlying substrate recognition by HIV reverse transcriptase. By comparing the molecular trajectories of the open to closed transitions in the presence and absence of nucleotide, with a mismatched nucleotide and the process after the chemical reaction, we have revealed new features of the complex reactions’ energy landscape. First, it is clear that the binding of a correct nucleotide precedes the open to closed transition in keeping with an induced-fit model. A view of the induced fit model according to the present calculations is a shift or tilting of the free energy landscape of the protein that follows the binding of the substrate. The tilting pushes the protein to a new alternative structural state, more stable from free energy perspective than the stable state of the unbound form, and hence it induces the conformational transition. Without the presence of the ligand, weakly attached to the surface of the protein, the energy landscape would have been less likely to motivate the conformational transition. Of course, for the case of enzymatic reaction, the open state of the unbound form must be present with high probability. If it is not open the ligand may not be able to enter the active site and bind. Indeed Figure 4 indicates that the transition is more likely to occur after the substrate binds physically at the surface of HIV-RT. The closed form is about 0.5–1 kcal/mol higher in free energy than the open form in the absence of a substrate. The same form is more stable (lower in free energy) by about 10 kcal/mol once the ligand is bound.
Our study also provides a method to estimate the free energy contribution of each individual amino acid to the observed free energy profile. The assumption is that the reaction coordinate following point mutations of the HIV RT protein is stable and the changes can be thought of as perturbations. Hence the mechanism of the conformational transition is not changing significantly. This analysis makes predictions that can be approached by site directed mutagenesis, but experimental data must also be interpreted with caution. Conservative mutations to disrupt hydrogen bonds, ionic interactions or hydrophobic interactions generally lead to changes in apparent free energy (as a ΔΔG based upon changes in rate or equilibrium constants) in the range of 1–3 kcal/mole, and these results overestimate the net contribution of an individual interaction due to secondary effects of the amino acid substitution. For example, the sum of the effects of mutations of all residues surrounding the active site a tyrosyl tRNA synthetase leads to a net change in free energy, which is twice that measured directly40. In our analysis, each amino acid is predicted to contribute less than 1 kcal/mol of interaction energy so that the sum of all interactions is consistent with the net free energy difference. Further experimental and computational approaches are required to resolve the contributions of individual amino acids, and the current results present a novel approach that has the potential to provide new insights into protein structure/function relationships. For example, in some cases single or multiple amino acid substitutions in HIV reverse transcriptase lead to resistance to nucleoside analogs used to treat HIV infections. The computational methods hold the potential to provide new theories to understand the changes in protein structure leading to resistance based upon computation of the free energy profile comparing the native nucleotides with the nucleotide analogs for wild-type and mutant forms of the enzyme. This extensive computational effort will be facilitated by PMF methods.
Supplementary Material
Acknowledgements
This research was supported by grants from the NIH GM59796 and Welch Foundation F-1783 to RE, and by grants from the NIH GM084741 and Welch Foundation F-1604 to KAJ and AD181 faculty research grant to SK.
Footnotes
Open to Closed transition of HIV Reverse transcriptase along the minimum free energy path is shown with a supplementary movie. Residues represented in stick are key residues in the motion for the correct incoming nucleotide (see main text for more detail). This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Kirmizialtin S, Nguyen V, Johnson KA, Elber R. How Conformational Dynamics of DNA Polymerase Select Correct Substrates: Experiments and Simulations. Structure. 2012;20:618–627. doi: 10.1016/j.str.2012.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Johnson KA. Conformational Coupling in DNA polymerase fidelity. Annu. Rev. Biochem. 1993;62:685–713. doi: 10.1146/annurev.bi.62.070193.003345. [DOI] [PubMed] [Google Scholar]
- 3.Prasad BR, Kamerlin SCL, Florian J, Warshel A. Prechemistry Barriers and Checkpoints do not Contribute to Fidelity and Catalysis as Long as They are not Rate Limiting. Theor. Chem. Acc. 2012;131:1288. [Google Scholar]
- 4.Briggs G, Haldane JBS. A Note on The Kinetics of Enzyme Action. Biochem. J. 1925;19:338–339. doi: 10.1042/bj0190338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Elber R, Kirmizialtin S. Molecular Machines. Curr. Opin. Struct. Biol. 2013;23:206–211. doi: 10.1016/j.sbi.2012.12.002. [DOI] [PubMed] [Google Scholar]
- 6.Kirmizialtin S, Elber R. Revisiting and Computing Reaction Coordinates with Directional Milestoning. J. Phys. Chem. A. 2011;115:6137–6148. doi: 10.1021/jp111093c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bello-Rivas JM, Elber R. Exact Milestoning. J. Chem. Phys. 2015;142:094102. doi: 10.1063/1.4913399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boresch S, Archontis G, Karplus M. Free-Energy Simulations - the Meaning of the Individual Contributions from a Component Analysis. Prot.-Stru. Func. and Gen. 1994;20:25–33. doi: 10.1002/prot.340200105. [DOI] [PubMed] [Google Scholar]
- 9.E WN, Ren WQ, Vanden-Eijnden E. String Method for the Study of Rare Events. Phys. Rev. B. 2002;66:052301. doi: 10.1021/jp0455430. [DOI] [PubMed] [Google Scholar]
- 10.Maragliano L, Fischer A, Vanden-Eijnden E, Ciccotti G. String Method in Collective Variables: Minimum Free Energy Paths and Isocommittor Surfaces. J. Chem. Phys. 2006;125:024106. doi: 10.1063/1.2212942. [DOI] [PubMed] [Google Scholar]
- 11.Ulitsky A, Elber R. A New Technique to Calculate Steepest Descent Paths in Flexible Polyatomic Systems. J. Chem. Phys. 1990;92:1510–1511. [Google Scholar]
- 12.E W, Ren WQ, Vanden-Eijnden E. Finite Temperature String Method for the Study of Rare Events. J. Phys. Chem. B. 2005;109:6688–6693. doi: 10.1021/jp0455430. [DOI] [PubMed] [Google Scholar]
- 13.Elber R, Roitberg A, Simmerling C, Goldstein R, Li HY, Verkhivker G, Keasar C, Zhang J, Ulitsky A. MOIL: a Program for Simulations of Macrmolecules. Comp. Phys. Comm. 1995;91:159–189. [Google Scholar]
- 14.West AMA, Elber R, Shalloway D. Extending Molecular Dynamics Time Scales with Milestoning: Example of Complex Kinetics in a Solvated Peptide. J. Chem. Phys. 2007;126:145104. doi: 10.1063/1.2716389. [DOI] [PubMed] [Google Scholar]
- 15.Majek P, Elber R. Milestoning Without a Reaction Coordinate. J. Chem. Theo. Comp. 2010;6:1805–1817. doi: 10.1021/ct100114j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kirmizialtin S, Elber R. Revisiting and Computing Reaction Coordinate with Directional Milestoning. J. Phys. Chem. A. 2011;115:6137–6148. doi: 10.1021/jp111093c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Elber R, West A. Atomically Detailed Simulation of the Recovery Stroke in Myosin by Milestoning. Proc. Natl. Acad. Sci. U.S.A. 2010;107:5001–5005. doi: 10.1073/pnas.0909636107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Elber R. A Milestoning Study of the Kinetics of an Allosteric Transition: Atomically Detailed Simulations of Deoxy Scapharca Hemoglobin. Biophys. J. 2007;92:L85–L87. doi: 10.1529/biophysj.106.101899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vanden-Eijnden E, Venturoli M. Revisiting the Finite Temperature String Method for the Calculation of Reaction Tubes and Free Energies. J. Chem. Phys. 2009;130:194103. doi: 10.1063/1.3130083. [DOI] [PubMed] [Google Scholar]
- 20.Czerminski R, Elber R. Self Avoiding Walk Between 2 Fixed End Points as a Tool to Calculate Reaction Paths in Large Molecular Systems. Int. J. Quant. Chem. 1990:167–186. [Google Scholar]
- 21.Elber R, Karplus M. A Method for Determining Reaction Paths in Large Molecules - Application to Myoglobin. Chem. Phys. Lett. 1987;139:375–380. [Google Scholar]
- 22.Shalloway D, Faradjian AK. Efficient Computation of the First Passage Time Distribution of the Generalized Master Equation by Steady-State Relaxation. J. Chem. Phys. 2006;124:054112. doi: 10.1063/1.2161211. [DOI] [PubMed] [Google Scholar]
- 23.Huang HF, Chopra R, Verdine GL, Harrison SC. Structure of a Covalently Trapped Catalytic Complex of HIV-I Reverse Transcriptase: Implications for Drug Resistance. Science. 1998;282:1669–1675. doi: 10.1126/science.282.5394.1669. [DOI] [PubMed] [Google Scholar]
- 24.Sarafianos SG, Das K, Clark AD, Ding JP, Boyer PL, Hughes SH, Arnold E. Lamivudine (3TC) Resistance in HIV-1 Reverse Transcriptase Involves Steric Hindrance with Beta-Branched Amino Acids. Proc. Natl. Acad. Sci. U. S. A. 1999;96:10027–10032. doi: 10.1073/pnas.96.18.10027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nuc. Acid Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kaminski G, Friesner R, Tirado-Rives J, Jorgensen WL. Evaluation and Reparameterization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B. 2001;105:6474–6487. [Google Scholar]
- 27.Pranata J, Wierschke SG, Jorgensen WL. OPLS Potential Functions for Nucleotide Bases- Relative Association Constants of Hydrogen-Bonded Base Pairs in Chloroform. J. Am. Chem. Soc. 1991;113:2810–2819. [Google Scholar]
- 28.Kirmizialtin S, Elber R. Computational Exploration of Mobile Ion Distributions Around RNA Duplex. J. Phys. Chem. B. 2010;114:8207–8220. doi: 10.1021/jp911992t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang JM, Cieplak P, Kollman PA. How Well Does a Restrained Electrostatic Potential (RESP) Model Perform in Calculating Conformational Energies of Organic and Biological Molecules? J. Comp. Chem. 2000;21:1049–1074. [Google Scholar]
- 30.Weinbach Y, Elber R. Revisiting and Parallelizing SHAKE. J. Comp. Phys. 2005;209:193–206. [Google Scholar]
- 31.Darden T, York D, Pedersen L. Particel Mesh Ewald an N. Log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 32.Elber R. Calculation of the Potential of Mean Force Using Molecular Dynamics with Linear Constraints -An Application to a Conformational Transition in a Solvated Dipeptide. J. Chem. Phys. 1990;93:4312–4321. [Google Scholar]
- 33.E WN, Vanden-Eijnden E. Transition-Path Theory and Path-Finding Algorithms for the Study of Rare Events. Annu. Rev. Phys. Chem. 2010;61:391–420. doi: 10.1146/annurev.physchem.040808.090412. [DOI] [PubMed] [Google Scholar]
- 34.Donlin MJ, Patel SS, Johnson KA. Kinetic Partitioning Between the Exonuclease and Polymerase Sites in DNA Error Correction. Biochemistry. 1991;30:538–546. doi: 10.1021/bi00216a031. [DOI] [PubMed] [Google Scholar]
- 35.Wong I, Patel SS, Johnson KA. An Induced-Fit Kinetic Mechanism for DNA Replication Fidelity: Direct Measurement by Single-Turnover Kinetics. Biochemistry. 1991;30:526–537. doi: 10.1021/bi00216a030. [DOI] [PubMed] [Google Scholar]
- 36.Patel SS, Wong I, Johnson KA. Pre-Steady-State Kinetic-Analysis of Processive Dna-Replication Including Complete Characterization of An Exonuclease-Deficient Mutant. Biochemistry. 1991;30:511–525. doi: 10.1021/bi00216a029. [DOI] [PubMed] [Google Scholar]
- 37.Kati WM, Johnson KA, Jerva LF, Anderson KS. Mechanism and Fidelity of HIV Reverse Transcriptase. J. Biol. Chem. 1992;267:25988–25997. [PubMed] [Google Scholar]
- 38.Kellinger MW, Johnson KA. Nucleotide-Dependent Conformational Change Governs Specificity and Analog Discrimination by HIV Reverse Transcriptase. Proc. Natl. Acad. Sci. U.S.A. 2010;107:7734–7739. doi: 10.1073/pnas.0913946107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kellinger MW, Johnson KA. Role of Induced Fit in Limiting Discrimination Against AZT by HIV Reverse Transcriptase. Biochemistry. 2011;50:5008–5015. doi: 10.1021/bi200204m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Johnson KA, Benkovic SJ. Analysis of Protein Function by Mutagenesis. The Enzymes. 1990;XIX:159–211. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.