Dipole-Potential-Mediated Effects on Ion Pump Kinetics

Abstract

The kinetics of conformational changes of P-type ATPases necessary for the occlusion or deocclusion of transported ions are known to be sensitive to the composition of the surrounding membrane, e.g., phospholipid content, mole percentage of cholesterol, and the presence of lipid-bound anions. Research has shown that many membrane components modify the dipole potential of the lipid head-group region. Based on the observation that occlusion/deocclusion reactions of ion pumps perturb the membrane surrounding the protein, a mechanism is suggested whereby dipole potential modifiers induce preferential stabilization or destabilization of occluded or nonoccluded states of the protein, leading to changes in the forward and backward rate constants for the transition. The mechanism relies on the assumption that conformational changes of the protein are associated with changes in its hydrophobic thickness that requires a change in local lipid packing density to allow hydrophobic matching with the membrane. The changes in lipid packing density cause changes in local lipid dipole potential that are responsible for the dependence of conformational kinetics on dipole potential modifiers. The proposed mechanism has the potential to explain effects of lipid composition on the kinetics of any membrane protein undergoing significant changes in its membrane cross-sectional area during its activity.

Main Text

Ion pumps, such as the Na⁺,K⁺-ATPase (present in the plasma membrane of all animals), the sarcoplasmic reticulum Ca²⁺-ATPase, and the H⁺,K⁺-ATPase of the stomach utilize the energy derived from ATP hydrolysis to transport ions against an electrochemical potential gradient across the membranes in which the pumps are embedded. In the case of the Na⁺,K⁺-ATPase, the pumping of Na⁺ and K⁺ ions is essential for the maintenance of cell volume as well as playing a crucial part in allowing the excitability of nerve and muscle cells and in the reabsorption of nutrients in the kidney. The sarcoplasmic reticulum Ca²⁺-ATPase is essential for muscle relaxation, and the H⁺,K⁺-ATPase maintains the acidic environment of the stomach necessary for digestion. These three examples of ion pumps belong to the P-type ATPase family, so-called because they all form phosphorylated intermediates. Many other ion pumps exist, and not all derive their energy from ATP. Other sources of energy include light and the energy released from redox or other chemical reactions.

Common to all ion pumps belonging to the P-type ATPase class is the existence of occluded states, i.e., states in which the transported ions are entrapped within the protein matrix so that access to the solution on either side of the membrane is limited. Experimental evidence for an occluded K⁺ state as an important intermediate in the Na⁺,K⁺-ATPase ion translocation mechanism was first reported in 1972 by Post et al. (1). Occlusion enhances the effectiveness of ion pumping, because simultaneous access of the ions to the solution on both sides of the membrane would allow the ions to flow down their electrochemical potential gradients rather than being pumped against them. The enzymatic cycles of these ion pumps, therefore, must undergo a series of conformational changes between occluded and nonoccluded states. The enzymatic mechanism of P-type ATPases can be summarized schematically by the Albers-Post or E1-E2 cycle (see Fig. 1). States in which ions are occluded are signified by brackets around the ions. The scheme shown in Fig. 1 is actually drawn for the Na⁺,K⁺-ATPase, but the corresponding scheme for any other P-type ATPase can be obtained by exchanging for the relevant ions. For example, in the case of the sarcoplasmic reticulum Ca²⁺-ATPase, the 3 Na⁺ should be replaced by 2 Ca²⁺ ions and the 2 K⁺ ions should be replaced by 2 or 3 H⁺ ions (2, 3).

Figure 1.

Albers-Post or E1-E2 reaction cycle, describing the sequence of partial reactions that P-type ATPases undergo. The scheme shown is for the Na⁺,K⁺-ATPase, but analogous schemes for other P-type ATPases can be drawn by substituting the Na⁺ (green) and K⁺ ions (orange) with the relevant ions. The dotted box highlights the reaction on which this article concentrates, the E1P(Na⁺)₃ → E2PNa⁺₃ reaction, which involves a conformational change deoccluding the ions from within the protein matrix. Modified from Gadsby et al. (16) with permission. To see this figure in color, go online.

Recent crystallographic data obtained on several P-type ATPases has shown that the conformational changes the enzymes undergo during their pumping cycles are significant, extending throughout the molecules (4, 5, 6, 7, 8). In the course of this Perspective article I argue that these large conformational changes are at least in part responsible for the well-established high sensitivity of the activity of P-type ATPases to the composition of their surrounding membrane (5, 9, 10). Of course, some effects of lipid composition may simply be because of an electrostatic interaction with the transported ions. For example, lipids with negative charges would be expected to produce a negative surface potential, attracting cations to the membrane surface and hence influencing the occupation of ion binding sites (9). Ion binding and release equilibria have also been found to be sensitive to the transmembrane electrical potential (11, 12, 13, 14, 15, 16), particularly on the extracellular side of the protein. These steps, involving charge transport, are termed electrogenic. However, the kinetics of nonelectrogenic conformational transitions between occluded and nonoccluded states in which there is no significant movement of charge across the membrane have also been found to be sensitive to the lipid surroundings or additives to them (15, 17, 18, 19, 20, 21, 22). These effects cannot be explained by a simple electrostatic attraction or repulsion of the transported ions. Because the mechanism by which nonelectrogenic steps are modified by their membrane surroundings is still unclear, it is on these steps that I wish to concentrate.

Two particularly interesting and relevant case studies are the kinetic changes of ion pumps caused by the membrane binding of lyotropic anions of the Hofmeister series (e.g., ClO₄⁻, SCN⁻, I⁻, Br⁻, and NO₃⁻) and by the membrane enrichment or removal of cholesterol. Lyotropic ions have been found to slow down the E1P → E2P transition, both for the Na⁺,K⁺-ATPase (20) and the sarcoplasmic reticulum Ca²⁺-ATPase (22). Based initially on experiments by Post and Suzuki (17), subsequently supported by many other studies (15, 18, 19), lyotropic anions stabilize the occluded E1P state. In contrast, cholesterol has been found to stabilize the nonoccluded E2P state, as well as to accelerate deocclusion of K⁺ on the cytoplasmic face of the Na⁺,K⁺-ATPase (21). Thus, lyotropic anions and cholesterol have opposite effects on the E1P-E2P distribution. Interestingly, lyotropic anions and cholesterol have also been found to have an opposite effect on the membrane dipole potential. (For those readers unfamiliar with the concept of the dipole potential, a brief overview is given later.) Experimentally it has been found that lyotropic anions decrease the dipole potential (23, 24), whereas cholesterol, up to the physiological level of 30 to 50 mol % in the membrane, increases the dipole potential (25, 26, 27, 28, 29, 30, 31, 32). A reasonable hypothesis would, therefore, be that the effect of these membrane components or additives on the kinetics of the E1P → E2P transition are linked to their effect on the dipole potential. The ultimate aim of this study is to provide a structural mechanism explaining how such a link might come about.

Membrane cross-sectional area

X-ray crystallographic data obtained on P-type ATPases has shown that the conformational changes these ion pumps undergo as part of their reaction cycle are so large that the cross-sectional area they occupy within the membrane is significantly different in different conformational states (5, 10). If one just considers cross-sectional area changes at the membrane/aqueous solution interface, then the free energy change associated with a change in cross-sectional area depends on the surface tension, γ, of the membrane. For a conformational transition between two states with different cross-sectional areas in the membrane, the dependence of the equilibrium constant, K, between the two states is related to γ by the following:

$${\left(\frac{d\ln K}{d\gamma }\right)}_T=-\frac{\Delta A}{RT},$$ (1)

where ΔA is the change in cross-sectional area in the membrane that the protein occupies on undergoing the transition per mole of protein, R is the ideal gas constant, and T is the absolute temperature. This equation is simply the surface pressure version of the well-known van’t Hoff equation for the dependence of an equilibrium constant on temperature. What the equation shows is that any membrane additive or component that either increases or decreases the surface tension would be expected to shift the equilibrium between the two conformational states. Thus, the state that occupies a larger membrane cross-sectional area would be favored in a membrane with a low surface tension, whereas the state occupying a smaller cross-sectional area would be favored in a membrane with a higher surface tension.

The rationale just presented for explaining shifts in membrane protein conformational equilibria based on the effect of surface pressure or surface tension is in accordance with a theory described previously by Cantor (33) and it has been taken up by others as an explanation for membrane-mediated effects on ion pump kinetics (10, 34). Although such an approach is perfectly valid, surface tension or surface pressure are macroscopic quantities. Their origins lie in the intermolecular forces involved. For example, the high surface tension of water is because of the strong hydrogen bonding between water molecules. Thus, a deeper understanding at the molecular level of the basis of membrane composition on membrane protein conformational changes can only be achieved if one considers the intermolecular forces involved. However, before discussing the forces present within a lipid membrane, first we must consider in more detail the perturbation that a protein conformational change causes on its surrounding membrane, in particular on the membrane thickness.

Hydrophobic thickness

Assuming that the external three-dimensional pressure is constant (normally atmospheric pressure), then the total membrane-embedded volume occupied by a membrane protein when it undergoes a conformational transition (equivalent to a chemical isomerization) should be constant. This means that if a conformational transition involves an increase in the area that the protein occupies within the membrane, this must be compensated for by a decrease in its transmembrane width. If the width of the protein decreases, the thickness of the surrounding lipid membrane must also decrease to prevent water from contacting hydrophobic regions of the protein, which would be energetically prohibitive. Thus, there must be hydrophobic matching between the protein and its membrane (35, 36, 37).

For a phospholipid bilayer, the only way the membrane can become thicker is if the hydrocarbon chains become more extended and ordered. Greater extension of the chains means that the lipid molecules come closer together and the area occupied per lipid head-group in the membrane must decrease. Conversely, if a membrane gets thinner, the lipid chains must become more disordered and the area per lipid molecule in the membrane surface increases. Most importantly for the argument here, when the packing density of lipids in the membrane changes this changes the electrical dipole potential within the glycerol backbone region of the membrane (38, 39, 40). Therefore, I will now briefly review the concept of the dipole potential.

Membrane dipole potential

The membrane dipole potential, ψ_d, is an electrical potential difference located within lipid membranes in the narrow region between the glycerol backbone of the phospholipids and the interface with the neighboring aqueous solution (41, 42, 43, 44). Depending on the lipid composition, its value is normally in the range of 100 to 500 mV. Because it drops over a small distance, it produces very large field strengths of 10⁸ to 10⁹ V m⁻¹. This is far in excess of the field strengths typically produced by the transmembrane electrical potential, which results in field strengths of ∼10⁷ V m⁻¹. In spite of the large field strength the dipole potential produces, it seems to have little effect on the binding or conduction of transported ions through membrane proteins. The reason for this is that, except for the case of small pore-forming peptides such as gramicidin (45) or syringomycin E (46), the ions are largely shielded from the high electric field by the intervening protein mass (47, 48). However, if a transmembrane protein undergoes a conformational transition that deforms the surrounding membrane, then the dipole potential is likely to play a crucial role because in this case the lipids have to move simultaneously with the protein. This could be the case for ion occlusion or deocclusion reactions of ion pumps and secondary transporters or for conformational transitions responsible for gating in the case of ion channels.

At this stage the molecular origin of the dipole potential is not entirely clear, but the general consensus is that a major contribution is oriented water dipoles associated with the carbonyl groups in the ester linkage between the lipid head-group and the hydrocarbon chains (39, 49, 50, 51). It is certainly not simply because of charges on the lipid head-groups themselves.

Dipole-dipole interactions

Because the dipoles that produce the dipole potential are located more or less parallel to one another in the membrane, their interaction is repulsive. The energy, E, of interaction of two parallel dipoles in isolation is given by the following:

$$E=\frac{1}{4\pi {\epsilon }_0\epsilon }\frac{{\mu }^2}{r^3},$$ (2)

where μ is the dipole moment, r is the distance between the two dipoles, ε₀ is the permittivity of free space, and ε is the dielectric constant of the medium (52). In a two-dimensional array of dipoles as present in a membrane surface, the magnitude of the repulsive energy would be increased by a factor M because of interactions with all of the neighboring dipoles, where M is a Madelung constant determined by the geometric packing of the dipoles. For example, if one assumes a hexagonally close-packed array of dipoles, the value of M can be estimated by extrapolation to an infinite distance from a central lipid molecule to be ∼10.2. For such a lattice, r is related to the cross-sectional area, A, occupied by a lipid in the membrane by the following:

$$r=\sqrt{A/\text{cos}30}.$$ (3)

Substituting for r in Eq. 2 and incorporating the Madelung constant and Avogadro’s constant, N_A, then gives the following for the repulsive energy per mole of lipid:

$$E=\frac{N_A}{4\pi {\epsilon }_0\epsilon }\frac{{\mu }^2{\left(\text{cos}30\right)}^{3/2}}{A^{3/2}}M.$$ (4)

From this equation one can see that an increase in packing density of dipoles, i.e., dipole moment per unit area, and, thus, an increase in ψ_d would be expected to result in a destabilization or an increase in energy.

The exact relationship between the dipole packing density, μ/A, and ψ_d is given by the following Helmholtz equation:

$${\psi }_d=\frac{\mu }{A{\epsilon }_0\epsilon }.$$ (5)

From this equation an effective dipole moment per lipid molecule perpendicular to the surface of the membrane can be estimated. If one assumes typical values for ψ_d and A of ∼300 mV and 0.65 nm² (38), respectively, and a dielectric constant in the lipid head-group region where the dipole potential drops of 75 (48), one obtains a value for μ of 1.3 × 10⁻²⁸ Cm or 39 D. Now, utilizing this value in Eq. 4, the repulsive energy of interaction per mole of lipid can be estimated to be 19 kJ mol⁻¹.

Now, we turn our attention to the effect that the dipole packing density or the dipole potential will have on the conformational equilibrium of an ion pump.

Conformational equilibrium

Let us consider a particular conformational equilibrium, the interconversion of the occluded state E1P(M⁺) and the nonoccluded E2PM⁺ state of a P-type ATPase. M⁺ represents here any ion that is transported by a P-type ATPase. The precise ion stoichiometry is irrelevant for the present argument. It is only important that the ions are occluded in the E1P state and unoccluded in the E2P state. In the case of the Na⁺,K⁺-ATPase, E1P(M⁺) would correspond to E1P(Na⁺₃) and E2PM⁺ would correspond to E2PNa⁺₃. In the case of the sarcoplasmic reticulum Ca²⁺-ATPase, E1P(M⁺) would be E1P(Ca²⁺₂) and E2PM⁺ would be E2PCa²⁺₂.

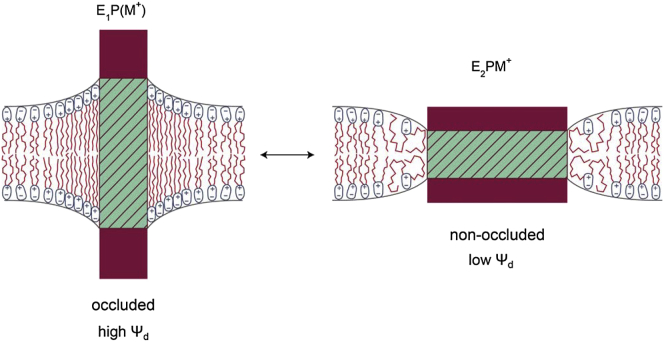
When the ions are released, i.e., to the extracellular medium in the case of the Na⁺,K⁺-ATPase or to the lumen of the sarcoplasmic reticulum in the case of the Ca²⁺-ATPase, they are thought to pass along a relatively deep access channel (12, 14, 53). In the occluded E1P state this channel must be closed, whereas in the nonoccluded E2P state the channel must be open. In the E1P closed state at least part of the protein must, therefore, be more compact. For the purposes of the clarity of the argument, this is shown in an exaggerated fashion in Fig. 2. Here, because we are primarily concerned with the effect of the protein conformational change on the lipid surroundings, for simplicity we also ignore the fact that the protein is not symmetrical and treat it merely as a deformable box in the membrane.

Figure 2.

Conformational transition between an ion-occluded E1P(M⁺) state and a nonoccluded E2PM⁺ state. The E1P(M⁺) state is assumed to have a wider hydrophobic thickness (shaded portion of the protein) and a smaller cross-sectional area in the membrane, whereas the E2PM⁺ state has a narrower hydrophobic thickness and a larger membrane cross-sectional area. To allow for hydrophobic matching between the protein and membrane in each state, the membrane must locally increase its thickness around the E1P(M⁺) state and decrease its thickness around the E2PM⁺ state. The increase in membrane thickness around the E1P(M⁺) state requires an extension of the lipid hydrocarbon chains and an increase in local lipid packing density, producing a high local dipole potential. The decrease in membrane thickness around the E2PM⁺ state requires a spreading or disordering of the lipid hydrocarbon chains and a decrease in local lipid packing density, producing a low local dipole potential. To see this figure in color, go online.

In the more compact occluded E1P state, one can see on the left of Fig. 2 that the smaller membrane cross-sectional area of the protein increases its hydrophobic thickness. To match this, the chains of the lipids surrounding the protein must extend and the lipid packing density must increase. This results in a high local dipole potential around the protein. Conversely, in the case of the nonoccluded E2P state, on the right of Fig. 2, the larger membrane cross-sectional area of the protein decreases its hydrophobic thickness. In this case the lipid chains must spread out and become more disordered to decrease the hydrophobic thickness of the surrounding membrane. The lipid molecules, thus, become less tightly packed, resulting in a low local dipole potential around the protein.

Now let us consider the effect of membrane composition or membrane additives on this conformational equilibrium. Le Châtelier’s principle states that any equilibrium will shift to decrease the magnitude of a perturbation. Applying this to the problem at hand, if a substance is included in the membrane that increases the dipole potential, then the equilibrium must shift to the side with a lower dipole potential, i.e., toward E2P. If a substance is added to the membrane that decreases the dipole potential, the equilibrium must shift to the side with a higher dipole potential, i.e., toward E1P.

The expected shifts based on Le Châtelier’s qualitative principle can also be understood in terms of the intermolecular forces involved. In the E1P state there is a high local dipole potential around the protein and hence a much larger degree of electrostatic repulsion between the tightly packed dipoles. If a substance were added that decreases the dipole potential, this would energetically stabilize this state relative to E2P and shift the equilibrium toward E1P. This corresponds to the effects that have been observed with lyotropic anions (15, 17, 18, 19, 20, 22), which are known to decrease the dipole potential (23, 24).

In the E2P state, on the other hand, there is a low local dipole potential around the protein and a low packing density of the lipid molecules. The low packing density weakens the favorable van der Waals attractions between the lipid chains. If a substance were added that increases the lipid packing density and increases the dipole potential, this would energetically stabilize this state relative to E1P and shift the equilibrium toward E2P. This corresponds to the effect that has been observed with cholesterol (21), a molecule known to enhance the dipole potential (25, 26, 27, 28, 29, 30, 31, 32).

The effects of substances that either increase or decrease the dipole potential on the energetics of the E1P-E2P equilibrium are shown in Fig. 3. Substances that lower the dipole potential increase the activation energy for the reaction E1P → E2P and this reaction hence becomes slower. This also coincides precisely with what has been observed experimentally after addition of lyotropic anions such as perchlorate or nitrate, which decrease the dipole potential, to membrane fragments containing the Na⁺,K⁺-ATPase (20) or the sarcoplasmic reticulum Ca²⁺-ATPase (22). On the other hand, substances that increase the dipole potential increase the activation energy for the backward reaction E2P → E1P, hence effectively inhibiting the reverse reaction and promoting the conversion to E2P.

Figure 3.

Effects of substances that modify the dipole potential on the activation energy of the E1P(M⁺) ↔ E2PM⁺ transition. In a native reference state (solid gray line reaction profile), the activation energy of the forward E1P(M⁺) → E2PM⁺ reaction is given by ΔG^‡_f and that of the backward E2PM⁺ → E1P(M⁺) transition is given by ΔG^‡_r. Substances that lower ψ_d (dashed line reaction profile) stabilize the E1P(M⁺) state and increase the activation energy of the forward reaction to ΔG^‡_f^’, thus slowing the forward reaction. Substances that increase ψ_d (dotted line reaction profile) stabilize the E2PM⁺ state and increase the activation energy of the backward reaction to ΔG^‡_r^”, thus slowing the backward reaction.

Although I have been describing the energetics of a single ion pump reaction, it is important to realize that ion pumps are not in equilibrium. Ions are continually moving across membranes along their electrochemical potential gradients in the opposite direction to which they are being pumped. Ion pumps must always be provided with energy (e.g., in the form of ATP) to continue to pump in the forward direction of their catalytic cycle. Depending on the forward and backward rate constants of deocclusion or occlusion reactions, these reactions may or may not be in equilibrium on the timescale of the overall turnover of the enzyme and the contribution of occlusion and deocclusion reactions to rate determination of the enzyme’s steady-state activity will depend on the values of the rate constants of all of the partial reactions of the reaction cycle. Nevertheless, any membrane component that via its effect on the dipole potential enhances the forward rate of a necessary deocclusion or occlusion must, to a greater or lesser extent, enhance the overall turnover.

Finally, I consider quantitatively whether modifications in the dipole potential could be expected to significantly change the relative energies of occluded and nonoccluded enzyme states. Earlier it was shown that the repulsive energy of interaction between dipoles in the membrane interface in an unperturbed lipid bilayer is ∼19 kJ mol⁻¹. This is of a similar magnitude as the attractive energy on formation of a hydrogen bond, i.e., not a particularly strong interaction in comparison with covalent bond formation. However, it is important to bear in mind that the conformational change of a single ion pump molecule is likely to perturb the packing of many lipid molecules. For the Na⁺,K⁺-ATPase there are 35 and for the sarcoplasmic reticulum Ca²⁺-ATPase there are ∼20 annular lipid molecules in direct contact with the protein (10). However, it is likely that any membrane perturbation involved with a conformational change of the protein would extend further out from the protein past the annular lipids (although not into the bulk lipid phase), so that many more lipid molecules than this would be involved. Nevertheless, the repulsive energy because of the interactions of the dipoles associated solely with the 35 annular lipids around the Na⁺,K⁺-ATPase, calculated simply by multiplying the interaction energy by the number of lipid molecules, would be 665 kJ mol⁻¹ of protein. For comparison, the free energy of ATP hydrolysis, which provides the driving force for P-type ATPases, is expected to be ∼−60 kJ mol⁻¹ for animal cells (53). Thus, a change in the energy of dipole interactions of only 10% would be expected to provide free energy changes equivalent to the entire driving force of the enzyme. Even minor changes in the dipole potential are likely to produce significant modifications in the relative energies of the E1P and E2P conformational states.

Conclusions

The modification of the kinetics of conformational transitions between membrane protein states of differing hydrophobic thicknesses by the effects of membrane components on the dipole potential, as shown schematically in Figs. 2 and 3, provides a framework for understanding how membrane composition influences not just the kinetics of ion pumps, but any membrane protein that undergoes a conformational change large enough to perturb the surrounding membrane. Hence, the theoretical framework and structural mechanism presented in this article could potentially also be applied to secondary transporters, ion channels, and membrane receptors.

As described in this article, the effects of dipole potential on an ion pump or any other ion-transporting membrane protein are expected to be local, because the perturbation of the membrane that the protein produces is local. The dipole potential in the bulk lipid far from the protein is expected to have no direct protein effect. The bulk dipole potential does, however, significantly affect the passive membrane permeability, particularly toward cations (25).

Every individual ion pump or membrane protein will have its own mechanism and its own variations in hydrophobic thickness as part of its mechanism. On this basis one would expect significant variation in the magnitude of the dipole potential across the surface of a cell. In fact this has already been experimentally observed. Using fluorescence microscopy together with a voltage-sensitive fluorescent dye sensitive to the dipole potential, Bedlack et al. (54) found that the magnitude of the dipole potential varies considerably laterally across the surface of a differentiating neuroblastoma cell. They suggested that the variations in dipole potential they observed could originate in variations in the local concentration of cholesterol in the membrane. In subsequent experiments, the same group (55) showed, furthermore, via cell-attached patch-clamp measurements, that the kinetics of activation, i.e., gating, of Na⁺ channels varied across the surface of the cell and that the variations in gating kinetics spatially coincided with those of the dipole potential. Thus, they concluded that Na⁺ channel gating kinetics is dependent on the local dipole potential. However, as one would expect from the size of the channel and screening of the Na⁺ ions from the dipole potential by the intervening protein (47), they observed no spatial variation in single-channel conductance. If the gating of these channels involves significant changes in protein hydrophobic thickness, these observations could be explained by the mechanism presented in Fig. 2. However, as pointed out by Zhang et al. (55), because the Na⁺ channels they were investigating were voltage-gated, a direct interaction between the gating charges on the protein and the dipole potential is in this case also a definite possibility.

Returning to ion pumps, the activity of some pumps could possibly be optimized by a high local dipole potential, others by a lower local dipole potential. In the case of the Na⁺,K⁺-ATPase, cholesterol significantly enhances its activity (10, 56, 57). Although the role of specific cholesterol-protein interactions cannot be excluded, particularly because cholesterol has been found to co-crystallize with the protein (8, 58), an important contribution to the pump activity increase caused by cholesterol could lie in its dipole-potential-induced stabilization of the E2P state. Regarding the effects of lyotropic anions, the possibility that these could affect the relative stabilities of occluded and nonoccluded ion pump conformational states via direct interaction with the protein as well as through the membrane deserves attention, particularly because it is known that the stability of water-soluble proteins is affected by the addition of anions belonging to the Hofmeister series (59).

As just explained, the importance of dipole potential in modifying the kinetics of occlusion and deocclusion reactions of ion pumps via the structural mechanism shown in Fig. 2 still requires further testing. Fortunately experimental methods are available for quantifying the dipole potential (42, 44), among others via the use of voltage-sensitive fluorescent dyes. An interesting new technique for more precise quantification of the local electric field within membranes is the use of the vibrational Stark effect on the absorption frequency of the nitrile group linked to transmembrane peptides via an unnatural amino acid (60). Many methods for resolving the kinetics of partial reactions of ion pumps are also available, e.g., stopped-flow, quenched-flow, voltage-jump, and flash photolysis (53, 61). Thus, the testing of the validity of the hypotheses presented in this article does not rely solely on theoretical methods, such as molecular dynamics simulations, although these will certainly provide valuable new insights. For example, combining molecular dynamics simulations with low-resolution x-ray crystallography, Sonntag et al. (62) already found evidence that conformational changes between occluded and nonoccluded states of the sarcoplasmic reticulum Ca²⁺-ATPase are accompanied by local deformation of the surrounding membrane, consistent with the structural hypothesis shown in Fig. 2. Another fortunate circumstance is that more and more crystal structures of ion pumps in different conformational states are being published. Analysis of these structures will allow changes in membrane cross-sectional area that the proteins occupy as well as changes in their hydrophobic thickness to be quantified, so that the degrees of membrane perturbation they cause can be more accurately assessed.

In the past, research in the area of ion-transporting membrane proteins has naturally tended to concentrate on the effect of the transmembrane electrical potential, because this can be precisely controlled by electrophysiological techniques. Probably because it is more difficult to control and measure, the role of the dipole potential has tended in comparison to be somewhat neglected. Now that the structures of these proteins and their interaction with the surrounding membrane are becoming better understood, hopefully this situation will change. The reason for the vast variety of lipids in biological membranes has always been a puzzle. The dipole potential could be a key piece in solving the puzzle.

Editor: Brian Salzberg