Computation of pH-Dependent Binding Free Energies

Abstract

Protein-ligand binding accompanies changes in the surrounding electrostatic environments of the two binding partners and may lead to changes in protonation upon binding. In cases where the complex formation results in a net transfer of protons, the binding process is pH-dependent. However, conventional free energy computations or molecular docking protocols typically employ fixed protonation states for the titratable groups in both binding partners set a priori, which are identical for the free and bound states. In this review, we draw attention to these important yet largely ignored binding-induced protonation changes in protein-ligand association by outlining physical origins and prevalence of the protonation changes upon binding. Following a summary of various theoretical methods for pK_a prediction, we discuss the theoretical framework to examine the pH dependence of protein-ligand binding processes.

Introduction

Complex formation between a protein and small molecules comprises one of the most fundamental reactions in biology. The association may not only result in conformational rearrangements, but also may induce changes in the pK_a values of titratable groups on either binding partner due to the altered electrostatic environment upon binding.¹ While the binding-induced structural changes have been explored extensively,² however, the shifts in the pK_a, or protonation state, of the titratable groups that accompany the binding have been less well explored. In addition, the changes in protonation accompanying protein-small molecule binding^1,3 have been relatively rarely analyzed compared to the analogous changes in protein-protein complex formation.^4-8 However, as an estimated 60-80% of orally administered drugs are weak acids or bases, the protonation states of bound ligands can also be tuned by cellular pH and electrostatic environment of their protein binding partners.^9,10 In cases where protein-ligand binding accompanies a net transfer of protons to either binding partner, the binding process is pH-dependent, i.e., the observed binding free energy is a function of pH.

However, conventional biomolecular modeling or free energy computations involving the complex formation typically employ fixed protonation states for the titratable groups in both binding partners set a priori, which are identical for the free and bound states. Clearly, in cases where ligand binding accompanies a net proton transfer to the system, this assumption ignores the possibility of protonation states changing while the chemical environments change upon binding. Consequently, when the true ensemble of conformations consists of various electrostatic environments, the use of a single, fixed protonation state may hinder the accurate description of the ensemble and can lead to significant errors.¹

In this review, we outline the physical origins and prevalence of changes in protonation that accompanies the protein-small molecule complex formation; a recent review by Onufriev and Alexov very thoroughly analyzed the binding-induced pK_a shifts for protein-protein, protein-small molecule, and protein-nucleic acid binding.¹ We further review the theoretical methods for predicting the pK_a values of titratable groups in protein-ligand binding. Finally, we address the computational protocol for obtaining pH-dependent binding free energies for the associations accompanying a net proton transfer and provide a brief outlook on the field.

Physical Origins and Prevalence of Binding-induced Protonation Changes

The observed pK_a value of a titratable residue is generally obtained as a sum of the residue's intrinsic pK_a in solution, pK_a^int, and the shift in pK_a arising from the surrounding environment, ΔpK_a:^11,12

$${\mathrm{pK}}_{\mathrm{a}}^{\mathrm{obs}}={\mathrm{pK}}_{\mathrm{a}}^{\mathrm{int}}+\Delta {\mathrm{pK}}_{\mathrm{a}}.$$ (1)

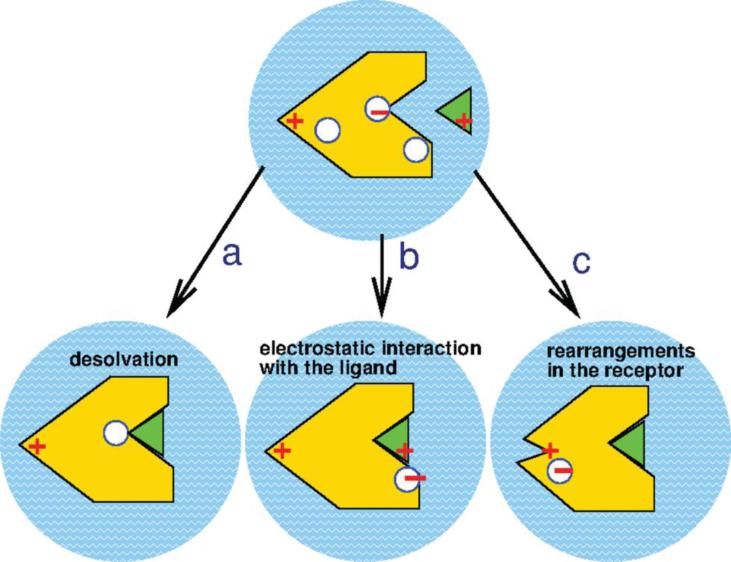
The shift in pK_a of titratable residues from its pK_a^int is typically due to the (a) desolvation penalty; (b) direct electrostatic interaction between the protein and bound ligand; and (c) charge rearrangement following the structural change upon binding (Figure 1). The desolvation, also referred to as the Born contribution, typically favors uncharged residue because the solvent-protein interaction at the binding site is replaced by the bound ligand. The last two causes of ΔpK_a together comprise the “background” contribution to the ΔpK_a and include changes in hydrogen bonding pattern and interactions involving other polar or charged groups. These background effects may propagate to the titratable groups distant from the immediate binding interface due to the structural and electrostatic rearrangement, resulting in the so-called allosteric effect on the pK_a shift.

Figure 1.

Three major mechanisms behind the shift in pK_a. (a) Desolvation. (b) Direct protein-ligand electrostatic interaction. (c) Charge rearrangement upon structural change. The figure is adopted from Onufriev and Alexov (2013).¹

A recent computational survey by Aguilar et al. showed the prevalence of binding-induced protonation changes for protein-small molecule complexes as well as protein-protein and protein-nucleic acid complexes by performing continuum electrostatic calculations on both free and bound forms of either binding partner.¹³ In 60% of protein-small molecule complexes considered, it was shown that at least one titratable residue completely changed its protonation state at neutral pH upon binding. It was found that all three of the above-mentioned causes of ΔpK_a play roles in the changes in protonation, where the direct electrostatic effects, i.e., (a) and (b), are short-ranged and the strongest, while the charge rearrangement upon structural reorganization, i.e. (c) affects more distant residues, propagating as far as 24 Å from the binding interface.¹³

While the work by Aguilar et al. comprises the largest scale survey for protein-small molecule complexes to date, individual instances of binding-induced shifts in pK_a were reported as well both experimentally^14-23 and computationally.^3,24-28 From Table 1, it is apparent that the pK_a shifts of varying magnitudes are observed for the titratable residues in protein upon binding of inhibitor. In addition, several works noted the changes in pK_a of titratable groups in the bound ligand upon binding to receptor, highlighting that the binding-induced changes in pK_a are not limited to the protein partner.^29-31

Table 1.

Experimentally observed shifts in pK_a (ΔpK_a) in protein-small molecule binding.

Protein	Ligand	Titratable group	ΔpKa	PDB ID of free protein	PDB ID of complex
HIV-1 protease	Pepstatin	Asp25	>+2.214	3HVP	1HPX
		Asp25’	<−1.514	3HVP	1HPX
HIV-1 protease	DMP-32	Asp25/Asp25’	+2.1915	1HHP	1QBS
Plasmepsin II	Pepstatin	Asp34/Asp214	+0.116	1PFZ	1SME
		His164	+1.516	1PFZ	1SME
Chymotrypsin	N-Acetyl-L-Pbhe-CF3	His57	+3.317	6GCH	6GCH
Xylanase	2FXb	Glu172	−2.518	1BVV	1BVV
Hydroxynitrile lyase	Thiocyanate	His235	+5.519	2YAS	2YAS
TSG-6	Hyaluronan	His4	+0.520	1O7B	1O7C
Galectin-1	β-Galactoside	His44/His52	+0.321	1W6N	2ZKN

Theoretical Methods for pK_a Prediction

The majority of computational pK_a prediction algorithms employ continuum electrostatics models for their simplicity and speed. In the continuum electrostatics, the bulk aqueous environment is represented as an infinite, high-dielectric continuum and the protein is modeled as a low-dielectric, polarizable cavity with fixed point charges.^11,32,33 The continuum approach includes Poisson-Boltzmann method^34,35 and more simplified generalized Born (GB) approximation,^36,37 whose underlying theories are well described in the references provided. The continuum approaches allow enhanced conformational sampling through an instantaneous dielectric response of the solute partial charges to the change in solvent dielectric and shows reliable results in computational pK_a prediction.^{11,12,25,38-42}

Structural flexibility of protein^4,36,43-46 and dielectric heterogeneity^47,48 have been further taken into account for more realistic description of protein conformational variability in pK_a computation. The protein-dipole Langevin dipole (PDLD) model of Warshel and coworkers represents protein as polarizable dipole while the nearby solvent is described as Langevin dipoles.⁴⁹ Also, quantum mechanics/molecular mechanics (QM/MM) method has been coupled with free energy computations for more rigorous pK_a computations.^50,51

More recent advances in the computational pK_a prediction protocols couple conformational and protonation sampling by applying molecular dynamics (MD) technique that employs pH as an external thermodynamic variable. In these constant pH MD (CpHMD) methods, conformations of the system are sampled with MD and the electrostatics are periodically analyzed using various methods including continuum electrostatics, MD, or Monte Carlo (MC). Various flavors of the CpHMD techniques have been developed, which are often classified as either continuous or discrete models depending on the treatment of titratable protons in the simulation. The former considers protonation state as a continuous titration parameter that propagates with the atomic coordinates of the system.^52-54 The use of mean-field approximation in the earlier implementation of the continuous CpHMD methods, however, allowed the unphysical fractional protonation states. Therefore, Lee et al. developed a novel continuous titration approach to avoid fractional protonation states by coupling λ-dynamics and applying an artificial titration barrier.⁵⁵

On the other hand, in the discrete protonation state model, the titratable site is considered either protonated or deprotonated, avoiding the intermediate charge state.^56-58 The stochastic titration model of Baptista et al. comprises of short segments of MD simulations periodically interrupted by MC for electrostatic energy evaluation using PB.⁵⁶ Mongan et al. further applied the GB implicit solvent in the MC sampling scheme to the stochastic method of Baptista et al. for enhanced computational and sampling efficiency.⁵⁹ On the other hand, Bürgi et al. avoided the continuum approach by computing electrostatic free energy by more rigorous yet expensive thermodynamic integration.⁶⁰ Recent improvements on both continuous and discrete protonation models of the CpHMD methods include the application of enhanced sampling techniques such as replica exchange^61-64 or accelerated MD⁶⁵ in order to increase the convergence. To date, CpHMD methods have been successfully applied to predict pK_a values of titratable groups in proteins^{28,53-56,59-65} and nucleic acids,^66-68 as well as to explain the acid-base catalysis by RNase A⁶⁹ and to understand the mechanisms behind the pH-dependent conformational changes critical to the function of proteins such as nitrophorin,⁷⁰ rhodopsin,⁷¹ and BACE-1.²⁸

Computation of pH-dependent binding free energies for protein-ligand complex

As stated above, simulations of protein-ligand systems are typically preceded by the assignment of fixed protonation states to titratable groups on the two binding partners. Further, docking studies often employ empirical prediction algorithms to assign fixed protonation states to the free ligands being docked. These approaches, however, fail to account for changes in protonation that may follow from the altered electrostatic environment surrounding the two binding partners upon complex formation. For instance, the pK_a values of the titratable groups reported in Table 1 fall into the physiological pH range between 4 and 8, indicating that the changes in protonation upon binding can occur in biologically relevant conditions. Clearly, in cases where ligand binding is linked to the (un)binding of protons, the error in assigning incorrect protonation states in free energy computations without correcting for the pH dependence of the binding free energy can give errors greater in magnitude than the errors from typical free energy computations.⁷²

Recently, groups of Jensen and Alexov examined the pH dependence of protein-protein binding^6,8 through an application of the binding polynomial formalism devised by Wyman⁷³ and used by Tanford to describe protein folding/unfolding.⁷⁴ Based on the binding polynomial, the pH dependence of the binding free energy can be expressed as:

$$\Delta {\mathrm{G}}^{°}\left(\mathrm{pH}\right)=\Delta {\mathrm{G}}_{\mathrm{ref}}^{°}-{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\ln \left(\sum _{\mathrm{i}=\mathrm{Asp},\mathrm{Glu},\mathrm{His},\mathrm{C}-\mathrm{term}}\frac{1+{10}^{{\mathrm{pK}}_{\mathrm{a}}^{\mathrm{C}}-\mathrm{pH}}}{1+{10}^{{\mathrm{pK}}_{\mathrm{a}}^{\mathrm{F}}-\mathrm{pH}}}\right)-{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\ln \left(\sum _{\mathrm{i}=\mathrm{Arg},\mathrm{Lys},\mathrm{Cys},\mathrm{Tyr},\mathrm{N}-\mathrm{term}}\frac{1+{10}^{\mathrm{pH}-{\mathrm{pK}}_{\mathrm{a}}^{\mathrm{C}}}}{1+{10}^{\mathrm{pH}-{\mathrm{pK}}_{\mathrm{a}}^{\mathrm{F}}}}\right)$$ (2)

where the last two terms are corrections to the reference binding affinity, ΔG°_ref, in which the binding-induced protonation change is ignored. The pK_a^C and pK_a^F are the pK_a value of the complexed and free states of the receptor, respectively. This formalism for obtaining ΔG as a function of pH can further be applied to cases where multiple ligand and receptor groups titrate in the pH range considered, assuming that proton binding occurs independently. In other words, Eq. 2 can only be applied when all titratable groups are uncoupled from each other.

As protein active sites often contain multiple titratable groups whose protonation states are coupled to perform a given function, it will sometimes be wrong to assume that all titratable groups remain uncoupled upon ligand binding. In such cases, the use of a relation devised by Wyman⁷⁵ provides a thermodynamic relation for proton-linked ligand binding where titratable sites may interact:

$$\Delta {\mathrm{G}}^{°}\left(\mathrm{pH}\right)=\Delta {\mathrm{G}}_{\mathrm{ref},\mathrm{pH}}^{°}-{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\ln \left(10\right){\int }_{{\mathrm{pH}}_{\mathrm{ref}}}^{\mathrm{pH}}\left\{{\mathrm{Z}}_{\mathrm{PL}}\left(\mathrm{pH}\right)-{\mathrm{Z}}_{\mathrm{P}}\left(\mathrm{pH}\right)-{\mathrm{Z}}_{\mathrm{L}}\left(\mathrm{pH}\right)\right\}\mathrm{dpH},$$ (3)

where Z_PL, Z_P, and Z_L are the total charges for protein-ligand complex, protein, and ligand, respectively. This approach has been used to account for the pH dependence of protein-protein^6,8 and protein-ligand binding,^3,28 as well as protein stability.^74,76

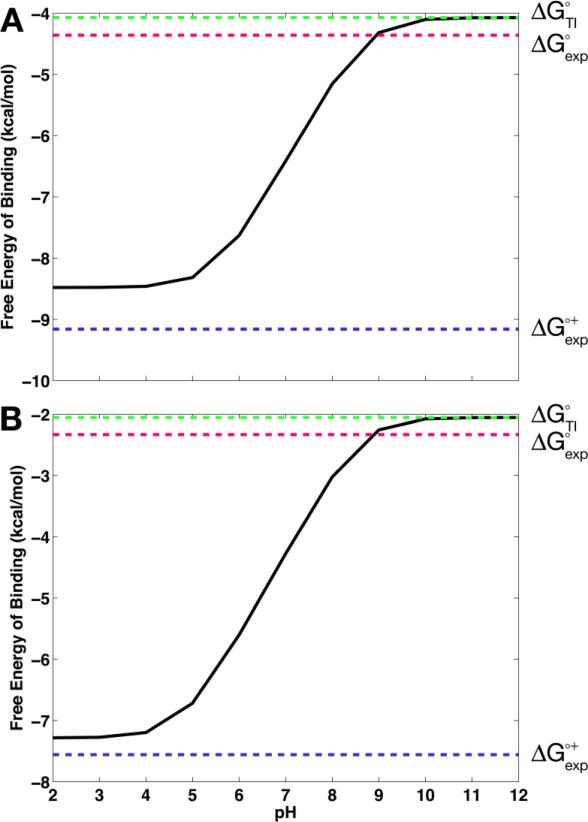
Within the binding framework, these expressions have often been used in conjunction with computational pK_a predictions such as PROPKA⁷⁷ or MCCE,⁴⁶ as in Mason and Jensen⁶ and Mitra et al.⁸ However, due to the limited conformational sampling in such pK_a computation algorithms, the coupling of conformational and protonation equilibria has not been fully accounted for. In addition, while the binding polynomial-based method has been applied to protein-protein^6,8 and protein-nucleic acid binding, there had been no standard protocol to rigorously account for proton-linked ligand binding.^67,78,79 Therefore, following the theoretical foundations of these studies, we recently applied the binding polynomial formalism with the CpHMD framework to compute the pH-dependent binding free energies.⁸⁰ In this computational protocol, the correction terms in Eqs. 2 and 3 are obtained from the CpHMD simulations while ΔG°_ref can be taken either from experiment or from thermodynamic integration (TI) computations, where the latter provides a full computational prediction of the pH dependence of binding processes. When applied to binding of small molecules to the cucurbit[7]uril (CB[7]) host, this CpHMD-based free energy method accurately obtained the pH-dependent binding free energy profiles (Figure 2).⁸⁰ For instance, in Figure 2, the binding free energy profiles of CB[7] binding to benzimidazole and fuberidazole are shown, computed with the ΔG°_ref obtained from the TI computation, i.e., ΔG°_TI. While the CpHMD/TI computation of pH-dependent binding free energies is prone to greater error than the use of ΔG°_ref from experiment (ΔG°_exp), the authors found that the errors in assigning incorrect protonation states in free energy computations without correcting for the pH dependence of the binding free energy can give errors in excess of the errors from the typical free energy computations.⁸⁰ The method has been further applied to several inhibitor-bound structures of BACE-1 in order to capture the pH dependence of protein-ligand systems and highlighted the significance of correctly accounting for the binding-induced protonation changes in free energy computations.²⁸

Figure 2.

Binding free energies of cucurbit[7]uril host to the guests, (A) benzimidazole and (B) fuberidazole. ΔG°_TI is the absolute reference binding free energy obtained from thermodynamic integration computations for the reference deprotonated state of the guest; ΔG°_exp is the experimental binding free energy for the reference deprotonated guest; and ΔG°⁺_exp is the binding free energy for the protonated guest derived from ΔG°_exp. The figure is adopted from Kim et al. (2015).⁸⁰

Outlook

We have presented a brief review of pH dependence of protein-ligand complex formation. While the prevalence of binding-induced changes in pK_a or protonation state has been well appreciated especially due to the recent progress in this field, it is true that these phenomena are not always accounted for in the majority of free energy computations or computational drug discovery. The use of the expressions applying the binding polynomial formalism to address the pH dependence of binding free energies is promising in these fields, and the application of the CpHMD technique particularly enables the coupling of conformational and protonation equilibria. Though not specifically addressed, similar philosophies may also be applicable to the scoring functions in docking protocols.

Several challenges, however, still remain. The lack of binding free energies experimentally measured at various pH levels, preferably for large protein-ligand datasets, imposes a challenge to incorporating the pH-dependent effects into computational studies; availability of the experimental reference binding free energies will be of great importance to pushing the free energy computation field forward. Also, the accuracy of current pK_a prediction algorithms strongly affects the quality the studies on the pH dependence. The pK_a cooperative, a collaborative effort to advance structure-based calculation of pK_a and electrostatics, noted that significant progress is still needed to improve the results from the current computational pK_a predictions.⁸¹ Besides the performance of the pK_a computation algorithms, the pK_a values obtained from such computations are known to be sensitive to the details of the input structure.⁸² While the advances in X-ray and NMR techniques for protein structural determination are clearly encouraging, the lack of availability of high-resolution structures of both protein monomer and protein-ligand complex in many cases still hinders the progress in the study of binding-induced protonation changes. Despite these challenges, however, we strongly believe that the growing attention to this field of study is promising.