Patient-specific dose calculations for pediatric CT of the chest, abdomen and pelvis

Abstract

Background

Organ dose is essential for accurate estimates of patient dose from CT.

Objective

To determine organ doses from a broad range of pediatric patients undergoing diagnostic chest–abdomen–pelvis CT and investigate how these relate to patient size.

Materials and methods

We used a previously validated Monte Carlo simulation model of a Philips Brilliance 64 multi-detector CT scanner (Philips Healthcare, Best, The Netherlands) to calculate organ doses for 40 pediatric patients (M:F=21:19; range 0.6–17 years). Organ volumes and positions were determined from the images using standard segmentation techniques. Non-linear regression was performed to determine the relationship between volume CT dose index (CTDI_vol)-normalized organ doses and abdominopelvic diameter. We then compared results with values obtained from independent studies.

Results

We found that CTDI_vol-normalized organ dose correlated strongly with exponentially decreasing abdominopelvic diameter (R²>0.8 for most organs). A similar relationship was determined for effective dose when normalized by dose-length product (R²=0.95). Our results agreed with previous studies within 12% using similar scan parameters (i.e. bowtie filter size, beam collimation); however results varied up to 25% when compared to studies using different bowtie filters.

Conclusion

Our study determined that organ doses can be estimated from measurements of patient size, namely body diameter, and CTDI_vol prior to CT examination. This information provides an improved method for patient dose estimation.

Introduction

The high image contrast and good spatial resolution of CT make it an essential diagnostic tool in medicine. However, concerns about radiation exposure from CT examinations have been amplified in recent years. There has been a dramatic increase in the contribution of medical sources to the overall annual radiation exposure to humans [1]. Furthermore, the workload percentage of CT in diagnostic radiology rose 13% between 1989 and 2007, with CT examinations contributing as much as 75% of the collective dose from medical radiation [2]. Concerns of increased risk from radiation exposure are heightened in children because of their greater radiosensitivity [3] and extended lifespan in which long-term radiation effects may develop [4, 5]. Efforts such as the Image Gently campaign [6, 7] have raised awareness of radiation protection for children receiving CT examinations with the goal of minimizing dose while maintaining imaging quality.

Accurate dose calculations are essential to understand the risk–benefit relationship of any medical procedure requiring ionizing radiation. The most commonly used method for assessing CT dose is based on the vendor-supplied volume CT dose index (CTDI_vol) and dose-length product (DLP) [8]. The CTDI_vol estimates the average dose within a scan volume from dose measurements in a standard 16-cm- or 32-cm-diameter acrylic cylindrical phantom and is assigned equally to all patients [9]. DLP accounts for the total dose delivered to the irradiated region of the body, defined as the product of CTDI_vol and the specific scan length [10]. However, because patients vary in size and shape, single metrics such as these are insufficient to accurately estimate actual patient dose [11]. In fact, dose to patients who are much smaller than the standard acrylic phantoms are underestimated by as much as a factor of three [12, 13]. In response to the danger of interpreting CTDI_vol as actual dose for pediatric patients, factors were developed to convert the CTDI_vol to a size-specific dose estimate (SSDE) [12]. The SSDE corrects for the difference in patient size compared to the acrylic phantom and offers an improved metric for assessing average absorbed dose.

However, CTDI_vol and SSDE remain poor estimates of individual organ dose because they measure the average absorbed dose in a homogeneous volume and do not account for tissue differences. Organ dose cannot be directly measured, and its calculation is based on a number of factors, including body composition and density, patient morphology and the portion of the body exposed to radiation during the CT examination. Assessment of effective dose requires knowledge of absorbed dose to important radiosensitive organs [14]. Effective dose has been estimated from DLP using age-specific conversion coefficients [8, 15, 16], but these coefficients were calculated using standard stylized anthropomorphic phantoms that may not be representative of actual patient populations.

Recent efforts have focused on developing Monte Carlo simulation routines to calculate organ dose from CT examinations [17–20]. These simulation codes model the CT scanner photon energy spectrum, inherent and bowtie filtration, and track particle transport through patient anatomy represented by a voxel-based geometry. Doses calculated from simulation studies are specific to the individual scanner model, and large variability occurs among scanners even when similar acquisition protocols are used. Scanner-independent values are necessary to compare results, and using CTDI_vol as a normalization factor reduces organ dose variability to less than 10% [21]. CTDI_vol-normalized organ doses have been reported for reference pediatric phantoms [22] and patient-specific models for pediatric and adult abdominopelvic CT [23, 24]. Similarly, scanner-independent estimates of effective dose are achieved by normalization by DLP [22, 25].

Body characteristics are known to influence CT dose, and several studies have investigated the dose relationship to patient size. DeMarco et al. [26] explored the effects of body size on organ and effective dose by simulation of whole-body CT of voxel phantoms. Li et al. [27] reported linear correlations between organ dose and chest diameter from chest CT of patient-specific models. Turner et al. [28] determined an exponential relationship between CTDI_vol-normalized organ doses and patient circumference. Studies involving large numbers of patient-specific models have observed similarly exponentially decreasing dose as a function of body diameter [23–25].

We investigated organ dose from Monte Carlo simulations of chest–abdomen–pelvis examinations from a Brilliance 64 CT multi-detector scanner (Philips Healthcare, Andover, MA) using 40 pediatric patient models generated from CT images. Reported organ doses from the Philips Brilliance 64 scanner have been limited to abdominal CT of voxel phantoms [21, 28]. Child-specific studies have modeled chest and abdominopelvic exams from GE Healthcare and Siemens Healthcare commercial scanners [23–25]. The purpose of this study was to determine the dependence of CTDI_vol-normalized organ doses and DLP-normalized effective dose on patient size and to investigate the effect of using a body bowtie filter for both adult and pediatric patients compared to a pediatric-specific bowtie filter. These data should allow a prospective estimation of body-size-adjusted radiation dose prior to examination.

Materials and methods

Patient data

Children who underwent chest–abdomen–pelvis CT scans as part of their care at Monroe Carrell, Jr., Children's Hospital at Vanderbilt were chosen from our archives by pediatric radiologists. Our institutional review board approved this retrospective study and did not require informed patient consent. All images were anonymized prior to use in accordance with the Health Insurance Portability and Accountability Act. A total of 40 children and 40 corresponding image sets were selected to represent pediatric patients of all ages, weights and heights. Patients varied in age from 7 months to 17 years (mean 7.8±4.7 years) and weighed 7–100 kg (mean 34 kg, median 25 kg). There were 19 girls (0–17 years, 9–84 kg) and 21 boys (0–16 years, 7–100 kg).

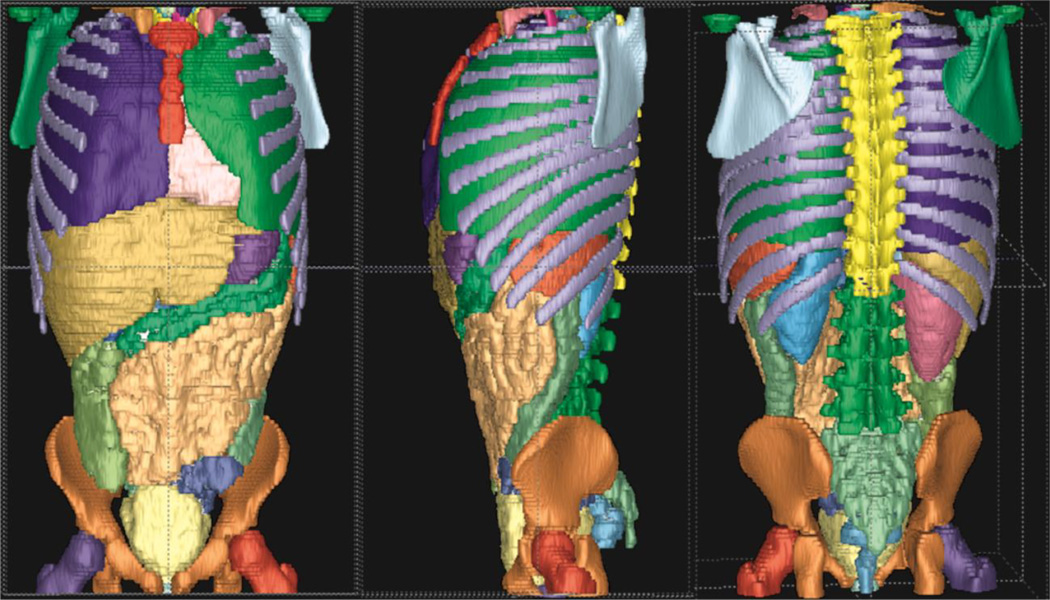
Organs within the image field of view were defined by a combination of manual and semiautomatic segmentation using the ITK-SNAP software [29]. A voxel-based organ map (Fig. 1) was generated with a unique integer identifier for each organ to assign materials and track energy deposition during Monte Carlo simulation. The outer 1–2 voxels (2–3 mm) of the body was delineated as skin.

Fig. 1.

Segmentation of body images. Voxel-based organ map shows various views of a segmented pediatric CT data set of a 7-year-old boy. Maps are colored-coded based on the organ identification numbers used in the computer model

Because of the difficulty of segmenting marrow cavities directly from an image, the percentage of cortical bone and marrow in the skeleton was calculated based on a method used for the GSF (German National Research Center for Environment and Health) voxel phantoms [30]. First, the average Hounsfield unit (HU) was calculated for each segmented bone. Then, the percentage of cortical bone and marrow was estimated by linearly interpolating between the HU of pure hard bone and total marrow. The HU of cortical bone was determined using an age-dependent density from ICRP 70 [31] and a bi-linear fit of material density to HU from calibration data [32]. The HU of total marrow was defined as a weighted value of pure red and yellow marrow by linear interpolation of age-specific marrow cellularity [33]. The cortical bone surface consists of a shell approximately one voxel layer thick. The voxels inside the shell were randomly assigned to be red or yellow marrow based on the age-specific cellularity. If cortical bone remained, additional inner-cavity voxels were randomly assigned as bone. Because it is limited by voxel size, this method does not properly model the microstructure of some bones, but it provides an improved representation of the overall bone composition compared to assigning a homogeneous density to the whole skeleton.

Monte Carlo simulation of CT examinations

We performed simulations of helical CT examinations using a Geant4-based Monte Carlo particle radiation transport code previously described [34] and briefly summarized here. Specific properties of the Philips Brilliance 64 scanner including the photon-energy spectrum, inherent and bowtie filtration, and geometry were incorporated into the simulation. An equivalent energy-fluence source model for the simulated CT scanner was created following methods in Turner et al. [35]. This fluence model includes the effects of the body bowtie filter that provides X-ray filtration across the transverse direction of the patient. The simulation has a beam collimation of 42.1 mm based on physical measurements. The exam table was also measured, for size and thickness, and is modeled as a trapezoidal volume of carbon fiber.

A normalization factor was determined by comparing simulated doses to physical measurements taken using a CT pencil ionization chamber in air. The accuracy of the simulation was determined using CT dose indices (CTDI₁₀₀) calculated following AAPM Report 96 [8] for standard 16-cm- and 32-cm-diameter phantoms. Simulated CTDI₁₀₀ values were calculated and directly compared to the actual dose indices with overall average agreement within 6%.

Calculation of organ doses

Monte Carlo simulations were run with a 120-kVp tube voltage, 100 mAs, and a pitch of 1 for all patient scans. The source moved in 1° increments and tracked 3.6×10⁶ total photon histories per tube rotation. The scan length ranged 1 cm above the apex of the lungs to the bottom of the ischium. Half the total beam collimation (2 cm) was added to each end to include the overscan required for reconstructing helical tomographic images. The material definitions for tissues used in the simulation (Table 1) were chosen to best represent pediatric anatomy. Soft tissues were taken from body compositions tabulated in ICRU Publication 46 [36]. The material for cortical bone was selected based on patient age, with densities and elemental compositions defined in ICRP Publication 70 [31]. Simulation times ranged 2–8 h depending on the patient size and length of scan.

Table 1.

Summary of materials used in the Monte Carlo simulation model

Material	Density (g/cm3)	H	C	N	Chemical composition (% by mass)					K	Other
					O	Na	P	S	Cl
Air	1.21×10−3		0.01	75.5	23.2						1.3 (Ar)
Soft tissuea	1.03	10.5	25.6	2.7	60.2	0.1	0.2	0.3	0.2	0.2
Brainb	1.04	10.7	14.5	2.2	71.2	0.2	0.4	0.2	0.3	0.3
GI tract/intestinesc	1.03	10.6	11.5	2.2	75.1	0.1	0.1	0.1	0.2	0.1
Heartd	1.06	10.3	12.1	3.2	73.4	0.1	0.1	0.2	0.3	0.2	0.1 (Fe)
Kidneye	1.04	10.6	9.4	2.1	77.0	0.2	0.2	0.1	0.2	0.2
Liverf	1.06	10.2	13.9	3.0	71.6	0.2	0.3	0.3	0.2	0.3
Lung tissueg	0.26	10.3	10.5	3.1	74.9	0.2	0.2	0.3	0.3	0.2
Mammary glandh	1.06	10.2	15.8	3.7	69.8	0.1	0.1	0.2	0.1	0.1
Ovaryb	1.05	10.5	9.3	2.4	76.8	0.2	0.2	0.2	0.2	0.2
Pancreasb	1.04	10.6	16.9	2.2	69.4	0.2	0.2	0.1	0.2	0.2
Skinb	1.09	10.0	20.4	4.2	64.5	0.2	0.1	0.2	0.3	0.1
Spleenb	1.06	10.3	11.3	3.2	74.1	0.1	0.3	0.2	0.2	0.3
Testesb	1.04	10.6	9.9	2.0	76.6	0.2	0.1	0.2	0.2	0.2
Thyroidb	1.05	10.4	11.9	2.4	74.5	0.2	0.1	0.1	0.2	0.1	0.1 (I)
Urinary bladderi	1.04	10.5	9.6	2.6	76.1	0.2	0.2	0.2	0.3	0.3
Cortical bonej (0 y)	1.65	4.0	15.7	4.5	45.4		10.1				0.2 (Mg) 20.1 (Ca)
Cortical bonej (1 y)	1.66	4.0	15.7	4.5	45.4		10.1				0.2 (Mg) 20.1 (Ca)
Cortical bonej (5 y)	1.70	4.0	15.7	4.5	45.4		10.1				0.2 (Mg) 20.1 (Ca)
Cortical bonej (10 y)	1.75	3.9	15.8	4.4	45.0		9.8				0.2 (Mg) 20.9 (Ca)
Cortical bonej (15 y)	1.80	3.9	15.8	4.4	45.0		9.8				0.2 (Mg) 20.9 (Ca)
Red marrow	1.03	10.5	41.4	3.4	43.9		0.1	0.2	0.2	0.2	0.1 (Fe)
Yellow marrow	0.98	11.5	64.4	0.7	23.1	0.1		0.1	0.1

^aICRU 46, Appendix A adult ICRU-44 male

^bICRU 46, Appendix A adult

^cICRU 46, Appendix A adult GI tract

^dICRU 46, Appendix A adult blood-filled

^eICRU 46, Appendix A child 2 years

^fICRU 46, Appendix A adult healthy

^gICRU 46, Appendix A adult healthy inflated

^hICRU 46, Appendix A breast-mammary gland adult #3

ⁱICRU 46, Appendix A adult empty

^jICRP 70, Table 27

Ar argon, C carbon, Ca calcium, Cl chlorine, Fe iron, H Hydrogen, I iodine, K potassium, Mg magnesium, N nitrogen, Na sodium, O oxygen, P phosphorus, S sulfur

The Monte Carlo simulation tallied the energy deposited in each voxel, and the 3-D output was converted to absorbed dose using assigned tissue densities (Table 1). Relative statistical uncertainties, defined as the 1σ standard deviation of the energy deposited divided by the average energy deposited, were less than 1% in each organ. A normalization factor (1.4×10⁶ mGy/100 mAs) determined during simulation validation was applied to convert data to absolute dose. Average absorbed doses to radiosensitive organs were calculated, and the effective dose was determined using tissue-weighting factors from ICRP publication 103 [14]. Scanner-specific variability was reconciled by normalizing organ doses using the CTDI_vol obtained from the 16-cm-diameter phantom (Table 2). Similarly, effective dose was normalized by the DLP.

Table 2.

CTDI measurements for simulated scan protocol

Tube potential (kVp)	Pitch	Collimation (mm)	CTDI100 (mGy/100 mAs)		CTDIvol (mGy/100 mAs)
			Center	Periphery
120	1.00	40 (64×0.625)	9.8	14.0	12.6

The relationship between organ doses and patient body size was investigated for several anthropometric measurements. Average patient diameters were determined for the chest and abdominopelvic regions assuming a cylindrical volume from the following relationship:

$$d=2\sqrt{\frac{V}{\pi H}}$$

where V is the volume of the region and H is the height. Abdominopelvic diameter was calculated using an axial range of 1 cm above the liver to 1 cm below the ischium. Chest diameter was determined from a region 1 cm above the lung apex to 1 cm below the lung base. Additionally, body circumference was measured at the central slice of the image series. A test of correlation between the measurements was performed, and abdominopelvic diameter was determined to best correlate with chest diameter and body circumference (Pearson's r >0.99). Previous studies [23–25, 28] have shown that CTDI_vol-normalized organ doses (nD_O) decrease exponentially with body diameter, and the following expression was chosen to obtain fit parameters from nonlinear regression:

$$n{D}_O(d_{AP})=\text{exp}({\alpha }_O{d}_{AP}+{\beta }_O).$$

The parameters α_O and β_O are unique to each organ and may be used to estimate patient-specific organ dose using the abdominopelvic diameter of a patient and scanner-specific CTDI_vol prior to performing the CT examination. Nonlinear regression was also performed to determine the fit parameters relating effective dose normalized by DLP (nED) to abdominopelvic diameter using the form:

$$nED(d_{AP})=\text{exp}({\alpha }_E{d}_{AP}+{\beta }_E).$$

Our results for both CTDI_vol-normalized organ doses and DLP-normalized effective dose were compared to previous studies [15, 22, 24, 25, 28]. Turner et al. [28] fit CTDI_vol-normalized organ doses from abdominal CT examinations to patient circumference. The study by Tian et al. [24] simulated chest and abdominopelvic CT examinations using bowtie filters for pediatric body. In the Li et al. study [25], CTDI_vol-normalized organ doses were fit to average chest diameter for various protocols to assess the effect of scanning parameters. To facilitate comparisons between our results and these independent research groups, we simulated chest and abdominopelvic scans in addition to chest–abdomen–pelvis examinations for each patient. The chest scan length ranged from 1 cm above the lung apex to 1 cm below the lung base. The abdominopelvic scan length ranged from 1 cm above the liver to 1 cm below the ischium. Absorbed doses for liver, stomach, adrenals, kidney, pancreas, spleen and gallbladder were compared to doses derived from the exponential regression curves reported by Turner et al. [28] using our measured patient circumferences. Similarly, comparisons were made between CTDI_vol-normalized doses for organs within the image coverage of chest and abdominopelvic studies and the dose coefficients in Tian et al. [24] and Li et al. [25].

Results

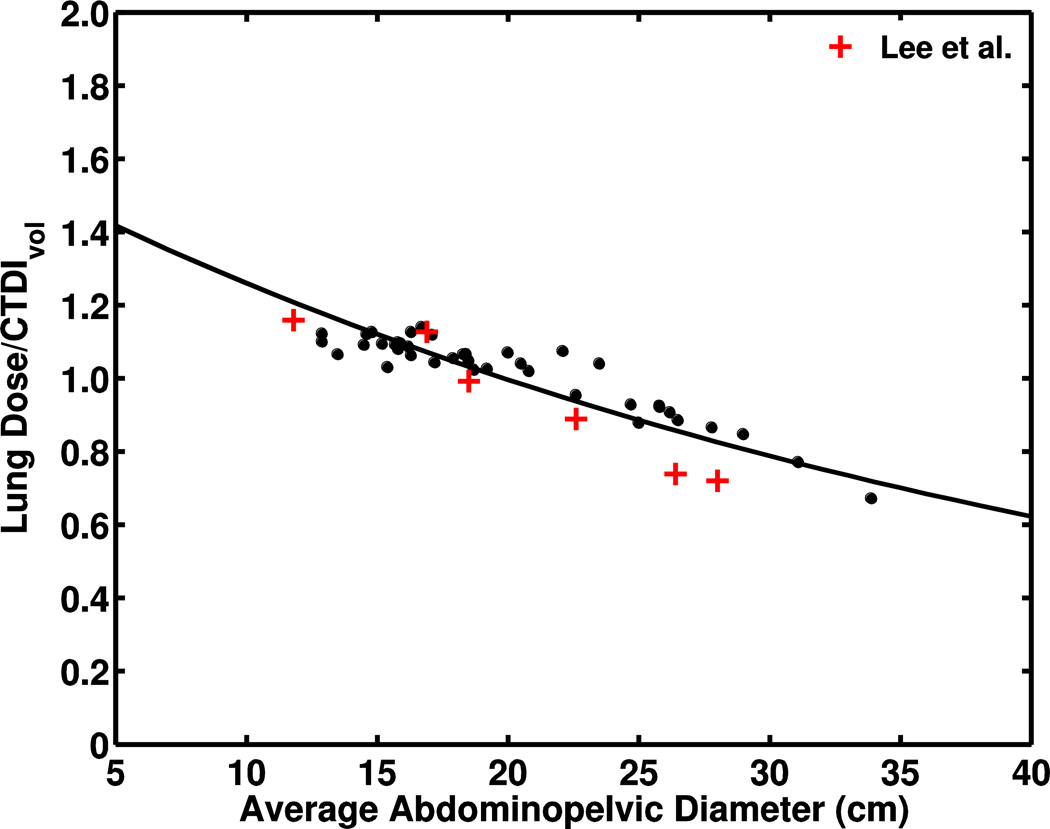
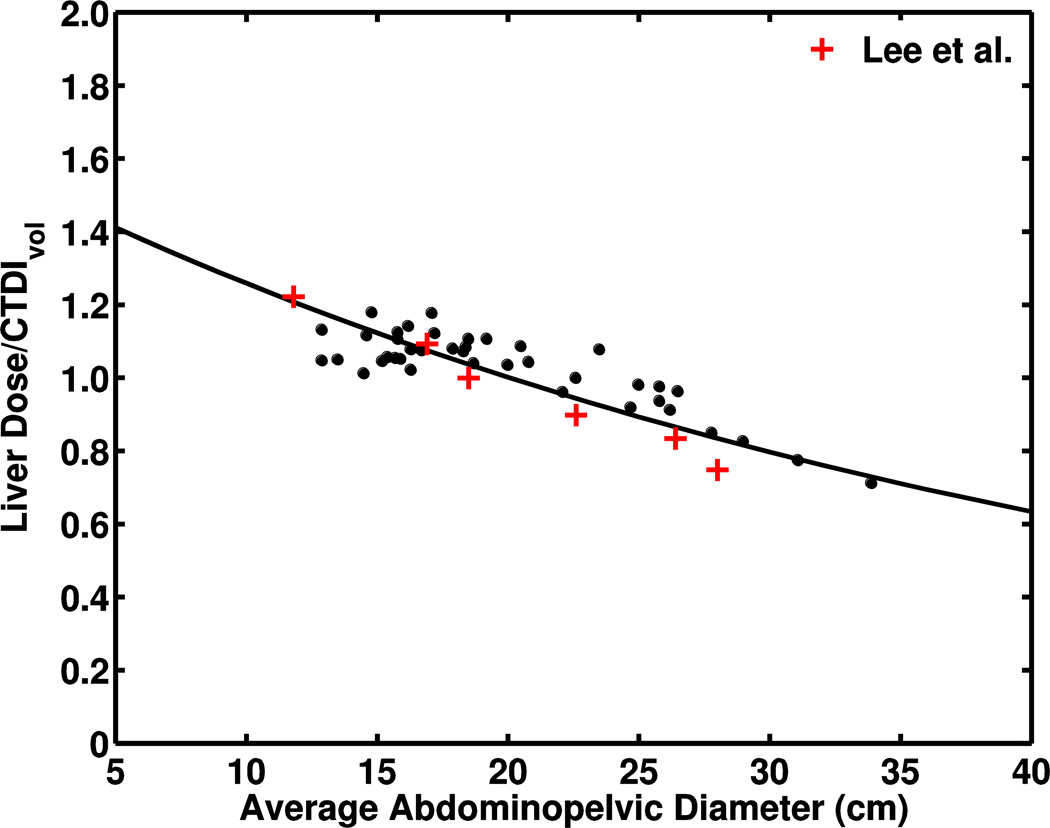
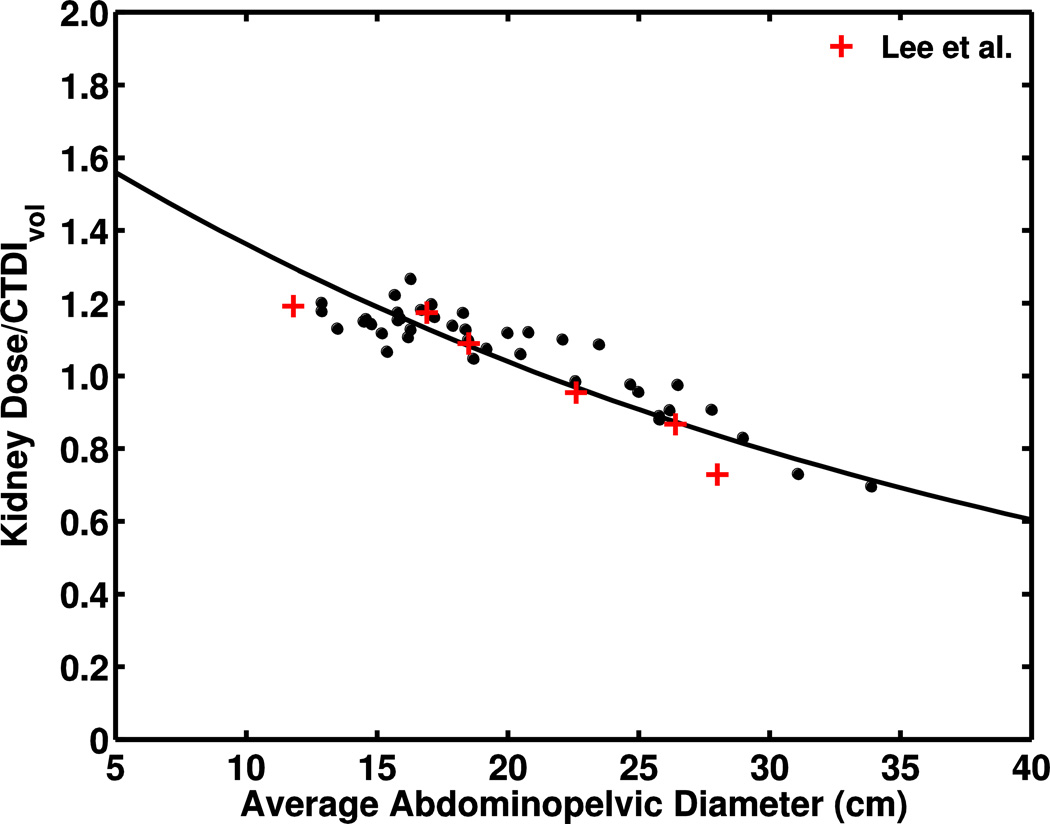
Typical organ doses for two patients are included in Table 3. The fit parameters from the linear regression of CTDI_vol-normalized dose for all organs completely within the scan range and for DLP-normalized effective dose are given in tables 4, 5 and 6 for chest–abdomen–pelvis, chest, and abdominopelvic studies, respectively. The R² correlation coefficient and root-mean squared error indicate a strong correlation between body diameter and dose. One exception is the prostate, a small organ on the edge of the scan coverage in both chest-abdomen-pelvis and abdominopelvic examinations. Figure 2 shows graphs of chest–abdomen–pelvis CTDI_vol-normalized organ doses as a function of average abdominopelvic diameter for four organs. For comparison, CTDI_vol-normalized organ doses from chest–abdomen–pelvis examinations of pediatric reference phantoms [22] are included in the plots. The relationship between average abdominopelvic diameter and DLP-normalized effective dose is shown in Fig. 3. For reference, k coefficients for trunk exams from Shrimpton et al. [15] are included in Fig. 3 and show differences of 9–37% from our fit. DLP-normalized effective dose was also fit to average chest diameter and plotted with results for pediatric chest CT examinations by Li et al. [25] (Fig. 3).

Table 3.

Organ doses from chest–abdomen–pelvis CT studies for two patients

Organ	Dose (mGy/100 mAs)
	8-month-old girl	15-year-old boy
Adrenals	13.5	9.7
Bladder wall	14.6	10.8
Esophagus	13.3	10.5
Gallbladder	14.0	11.2
Heart	15.0	12.3
Kidneys	15.1	11.4
Large intestines	14.6	11.6
Liver	14.2	11.5
Lungs	14.1	11.4
Pancreas	14.3	10.9
Skin	12.3	9.1
Small intestines	14.6	12.4
Spleen	13.3	10.4
Stomach wall	13.7	11.0
Prostate	—	8.4
Testes	—	11.2
Ovaries	14.2	—
Uterus	13.8	—
Breast (mammary)	N/A	11.2
Bone surface	44.5	29.9
Red marrow	12.1	8.6

Table 4.

Regression fit coefficients for CTDI_vol-normalized organ doses and DLP-normalized effective dose for chest–abdomen–pelvis CT studies

Organ	αOa	βOb	R2c	RMSEd
Adrenals	−0.027	0.49	0.92	0.050
Bladder	−0.034	0.62	0.83	0.088
Esophagus	−0.029	0.49	0.90	0.071
Gallbladder	−0.023	0.46	0.84	0.089
Heart	−0.021	0.53	0.89	0.066
Kidneys	−0.027	0.58	0.92	0.069
Large intestines	−0.022	0.45	0.93	0.050
Liver	−0.023	0.46	0.92	0.070
Lungs	−0.023	0.47	0.93	0.055
Pancreas	−0.024	0.51	0.89	0.061
Small intestines	−0.022	0.47	0.93	0.052
Spleen	−0.022	0.39	0.77	0.087
Stomach	−0.020	0.42	0.86	0.066
Prostate	−0.032	0.19	0.33	0.165
Ovaries	−0.032	0.57	0.88	0.053
Uterus	−0.031	0.52	0.89	0.049
Bone surface	−0.034	1.86	0.98	0.123
Red marrow	−0.033	0.44	0.97	0.037
Effective dose	−0.057	−2.8	0.95	0.0022

^{a, b}α_O and β_O are fit coefficients for the equation relating CTDIvol-normalized organ dose to abdominopelvic diameter, nD_O(d_AP) = exp(α_Od_AP + β_O) and DLP-normalized effective dose, nED(d_AP) = exp(α_Ed_AP + β_E)

^cR² is the coefficient of determination for the fit

^dRMSE is the root mean squared error, defined as $\sqrt{\frac{1}{n}{\sum }_{i=1}^n{(n{D}_i-{\widehat{nD}}_i)}^2}$, where ${\widehat{nD}}_i$ is the CTDI_vol-normalized organ dose is estimated from the exponential relationship with fit parameters α_O and β_O, DLP dose-length product

Table 5.

Regression fit coefficients for CTDI_vol-normalized organ doses and DLP-normalized effective dose for chest CT studies

Organ	αOa	βOb	R2c	RMSEd
Esophagus	−0.034	0.57	0.89	0.075
Heart	−0.024	0.56	0.86	0.076
Lungs	−0.026	0.49	0.91	0.058
Effective dose	−0.060	−2.4	0.84	0.0041

^{a, b}α_O and β_O are fit coefficients for the equation relating CTDI_vol-normalized organ dose to chest diameter, nD_O(d_Chest) = exp(α_Od_Chest + β_O) and DLP-normalized effective dose, nED(d_Chest) = exp(α_Ed_Chest + β_E)

^cR² is the coefficient of determination for the fit

^dRMSE is the root mean squared error, defined as $\sqrt{\frac{1}{n}{\sum }_{i=1}^n{(n{D}_i-{\widehat{nD}}_i)}^2}$, where ${\widehat{nD}}_i$ is the CTDI_vol-normalized organ dose is estimated from the exponential relationship with fit parameters α_O and β_O, DLP dose-length product

Table 6.

Regression fit coefficients for CTDI_vol-normalized organ doses and DLP-normalized effective dose for abdominopelvic CT studies

Organ	αOa	βOb	R2c	RMSEd
Adrenals	−0.028	0.46	0.91	0.055
Bladder	−0.034	0.61	0.83	0.087
Gallbladder	−0.021	0.39	0.76	0.089
Kidneys	−0.025	0.52	0.91	0.062
Large intestines	−0.022	0.43	0.91	0.053
Liver	−0.023	0.37	0.89	0.064
Pancreas	−0.025	0.46	0.84	0.073
Small intestines	−0.022	0.47	0.93	0.052
Spleen	−0.018	0.23	0.53	0.080
Stomach	−0.021	0.37	0.82	0.071
Prostate	−0.034	0.21	0.35	0.162
Ovaries	−0.029	0.52	0.86	0.055
Uterus	−0.031	0.52	0.87	0.053
Bone surface	−0.020	1.33	0.32	0.381
Red marrow	−0.036	−0.02	0.66	0.065
Effective dose	−0.077	−2.5	0.92	0.0025

^{a, b}α_O and β_O are fit coefficients for the equation relating CTDIvol-normalized organ dose to abdominopelvic diameter, nD_O(d_AP) = exp(α_Od_AP + β_O) and DLP-normalized effective dose, nED(d_AP) = exp(α_Ed_AP + β_E)

^cR² is the coefficient of determination for the fit

^dRMSE is the root mean squared error, defined as $\sqrt{\frac{1}{n}{\sum }_{i=1}^n{(n{D}_i-{\widehat{nD}}_i)}^2}$, where ${\widehat{nD}}_i$ is the CTDI_vol-normalized organ dose estimated from the exponential relationship with fit parameters α_O and β_O, DLP dose-length product

Fig. 2.

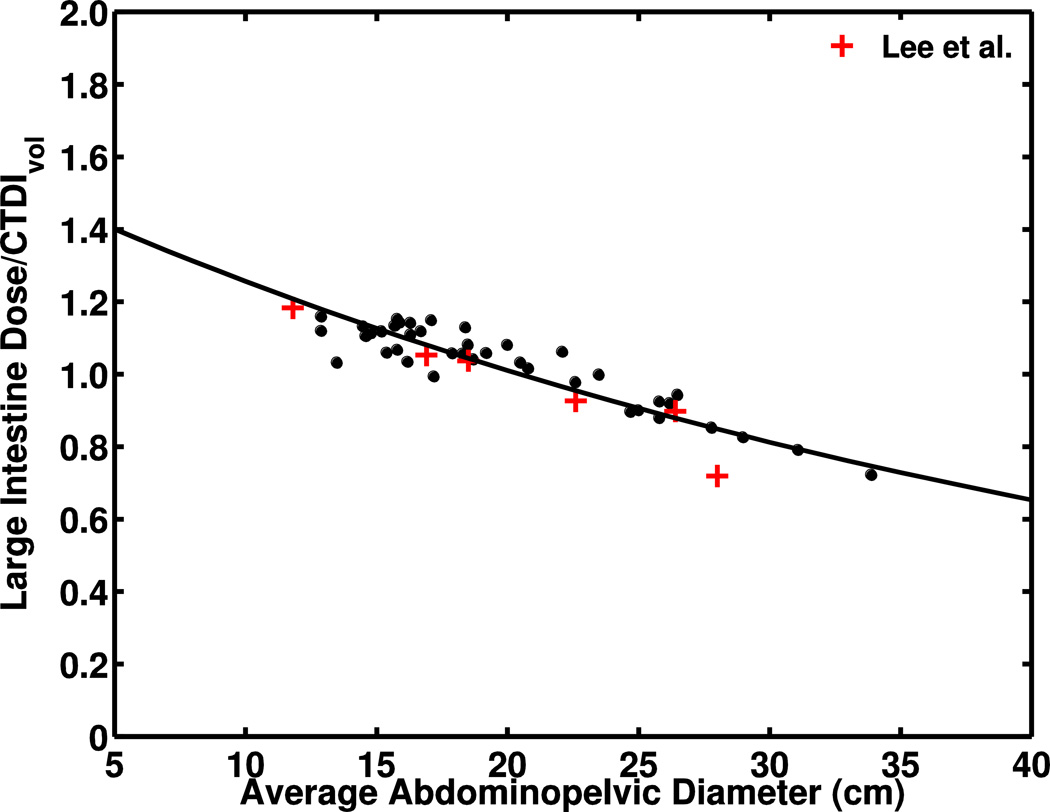
Chest–abdomen–pelvis CTDI_vol-normalized organ doses as a function of average abdominopelvic diameter for four organs. Plots show the dependence of CTDI_vol-normalized dose for (a) lungs, (b) liver, (c) kidneys and (d) large intestine on abdominopelvic diameter with comparison to data from Lee et al. [22], signified by (+) and derived from reference pediatric phantoms

Fig. 3.

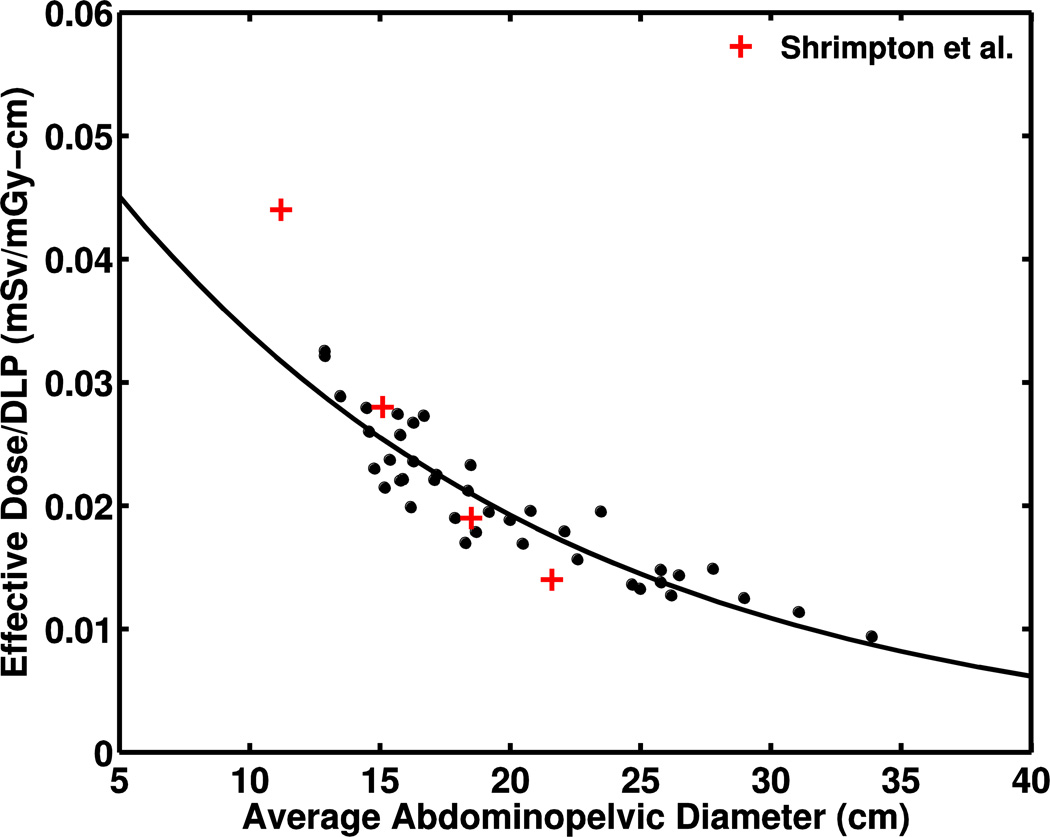
DLP-normalized effective dose to diameter. a Plot shows exponential fit of DLP-normalized effective dose to abdominopelvic diameter with comparison to k coefficients from Shrimpton et al. [15] for trunk examinations (Shrimpton data presented as +) of reference pediatric patients developed by Cristy and Eckerman [37] at age 0, 1 year, 5 years and 10 years. The average abdominopelvic diameters of the reference phantoms were determined from the geometric definitions of the trunk. b Plot shows exponential fit of DLP-normalized effective dose to chest diameter with comparison to data from Li et al.’s [25] protocol C for chest examination (120 kVp, large bowtie filter, pitch 1.375, 40-mm collimation) (dashed line). Data normalized to DLP from 32-cm-diameter phantom. DLP dose-length product

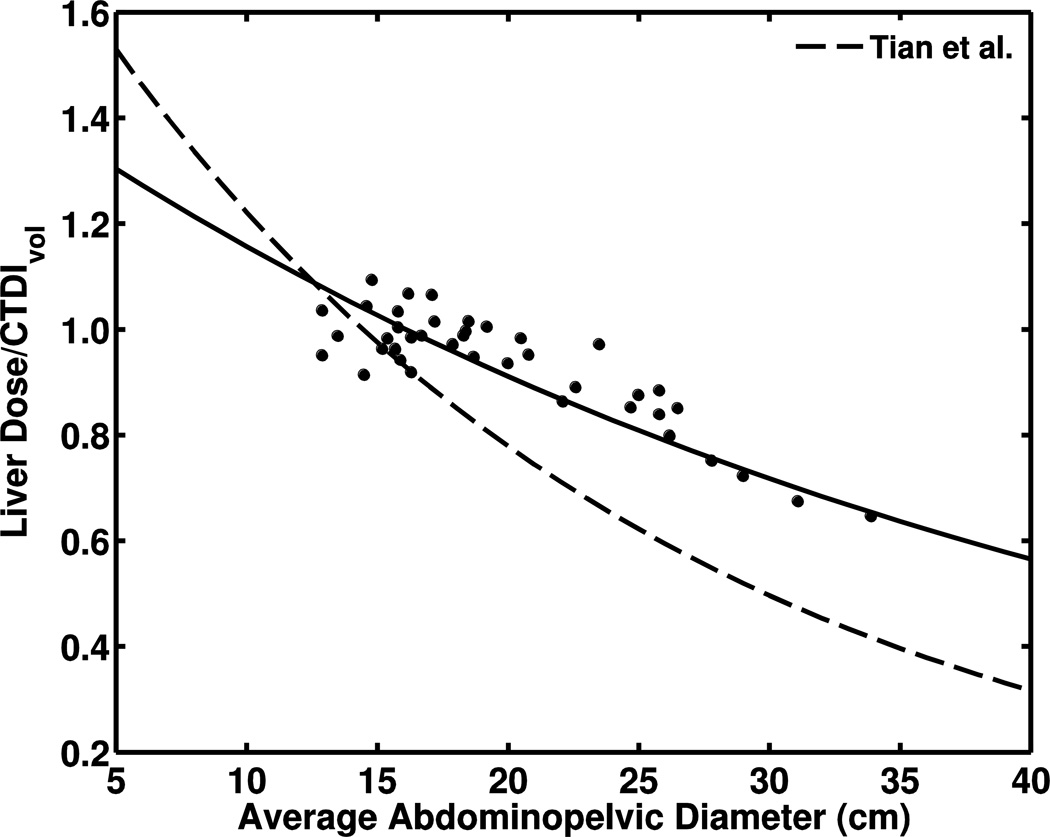
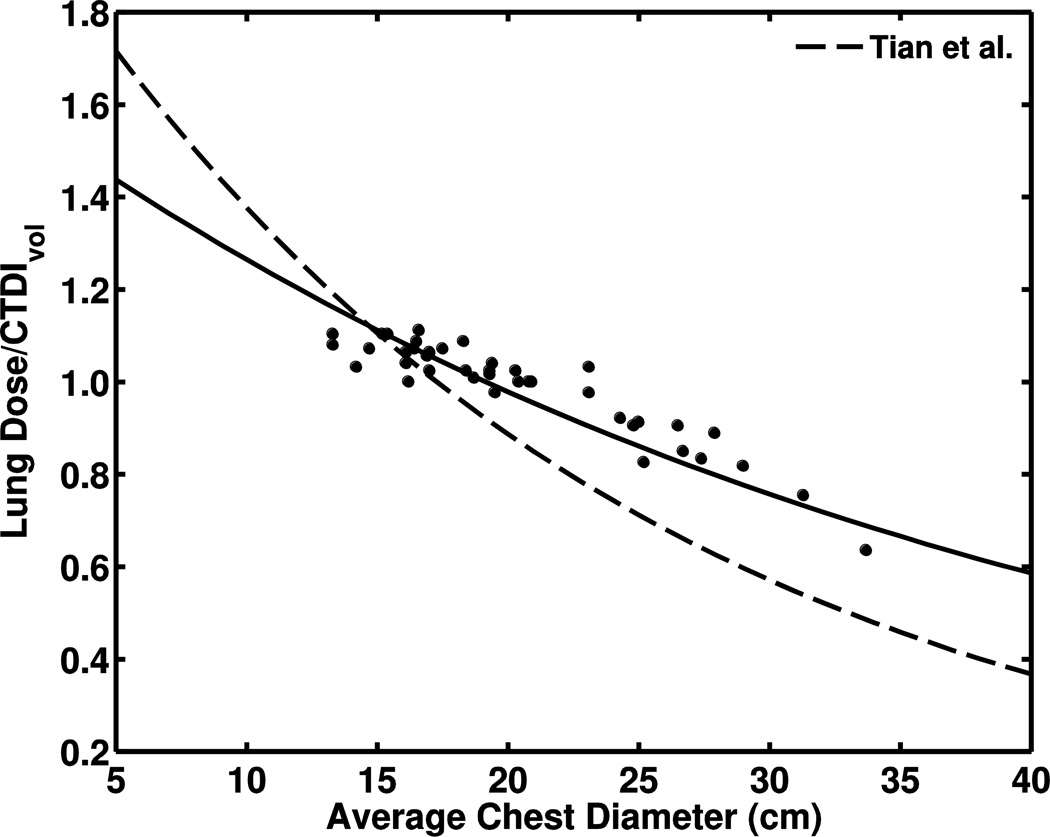
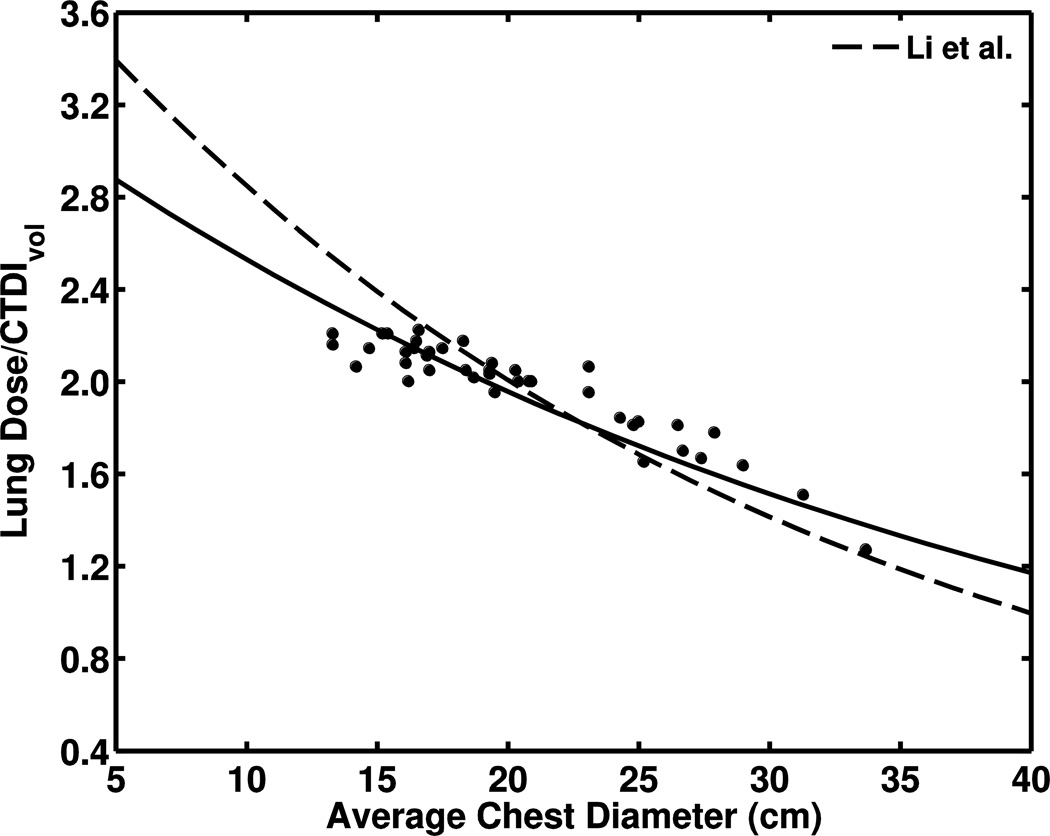
Average differences between absorbed doses from an abdominopelvic CT examination calculated from the organ-specific regression coefficients in Turner et al. [28] and our simulated organ doses ranged 8–12%. Figure 4 illustrates the comparison to our results for liver dose. Doses for the same abdominal organs calculated from fitting parameters for abdominopelvic CT studies in Tian et al. [24] had average differences of 15% for pancreas to up to 25% for kidney. Figure 4 also shows the comparison of our regression fit for liver dose. Additionally, absorbed doses to lung, heart and esophagus from fitting parameters for chest CT studies in Tian et al. [24] resulted in average differences of 13–15%. Figure 5 compares lung dose from chest CT. When we compared results from chest CT to exponential fits of CTDI_vol-normalized organ dose to chest diameter by Li et al. [25], differences between the studies were within 10% (Fig. 5).

Fig. 4.

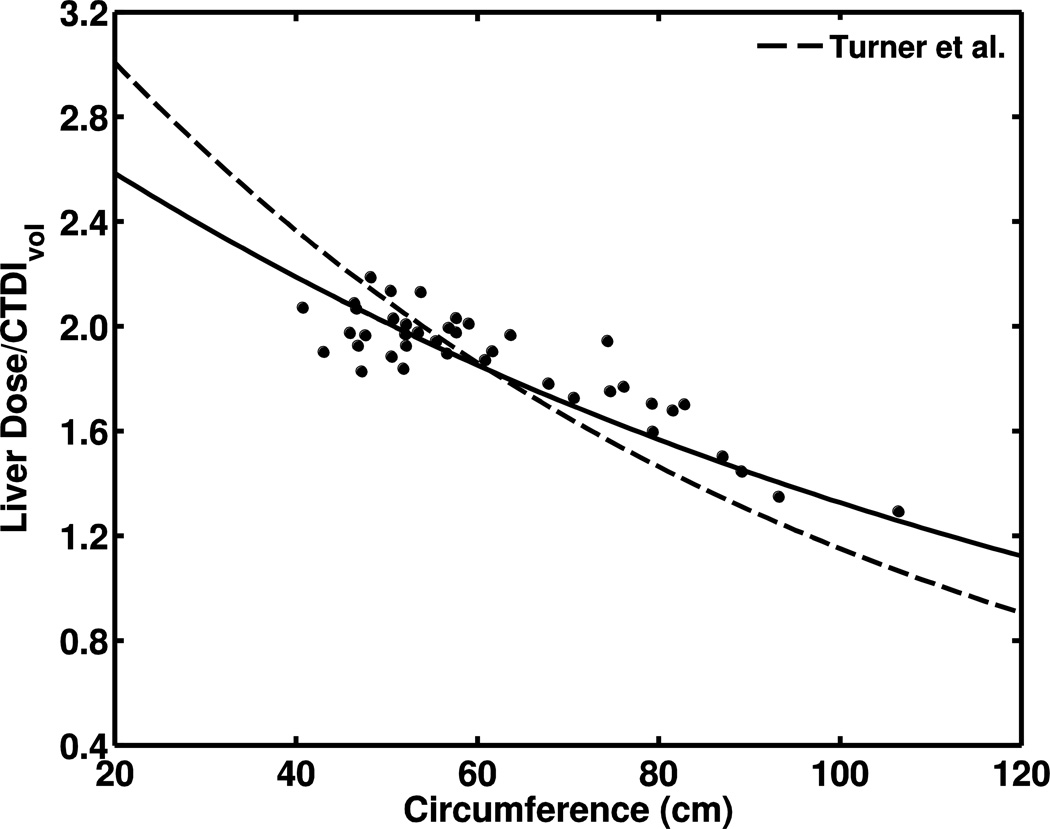
Comparison of liver-dose results. a Plot of CTDI_vol-normalized liver-dose relationship with body circumference as compared to findings of Turner et al. [28] (dashed line) for abdominopelvic study (120 kVp, body bowtie filter, pitch 1.0 and collimation 28.8–40 mm). Data normalized to CTDI_vol from 32-cm-diameter phantom. b Plot of exponential fit of CTDI_vol-normalized liver dose to abdominopelvic diameter as compared to data from Tian et al. [24] (dashed line) for abdominopelvic study (120 kVp, small bowtie filter, pitch 1.375, 40-mm collimation)

Fig. 5.

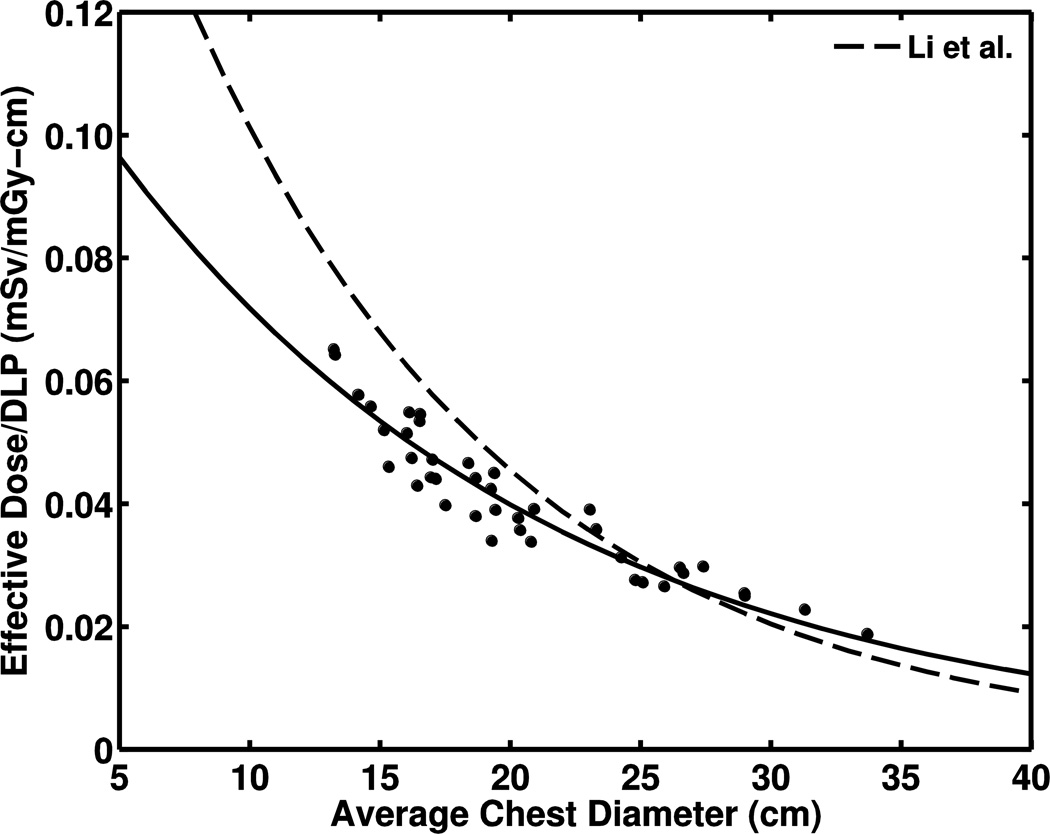
Comparison of lung-dose results. Plot of CTDI_vol-normalized lung-dose relationship with chest diameter as compared with data from Tian et al. [24] (dashed line) for chest examination. b Plot of exponential fit of CTDI_vol-normalized lung dose to chest diameter as compared to data from Li et al.’s [25] protocol c for chest examination (120 kVp, large bowtie filter, pitch 1.375, 40-mm collimation) (dashed line). Data normalized to dose-length product from 32-cm-diameter phantom

Discussion

CT chest–abdomen–pelvis exam of pediatric patients is a valuable diagnostic tool spanning the range of pediatric chronic and acute pathology. To date, studies of patient-specific organ doses have focused on pediatric chest or abdominopelvic CT examinations [24, 25], and reported organ doses from chest–abdomen–pelvis studies using pediatric reference phantoms [22]. Moreover, these results have been limited to data from GE and Siemens commercial CT scanners. In this study we determined patient-specific organ and effective doses from chest, abdominopelvic, and chest–abdomen–pelvis scans using manually segmented organ maps as input into a Monte Carlo model of the Philips Brilliance 64 CT scanner (Philips Healthcare, Best, The Netherlands). Our simulations calculated organ and skin doses for a diverse range of pediatric anatomies. We determined a strong correlation between CTDI_vol-normalized organ dose and average patient diameter for organs contained within the scan region (R²>0.8 for most organs). This relationship is expressed in the form of an exponential function based on the observation that organ dose is directly related to the attenuation of the X-ray beam by tissue along its path. As the depth of the organ increases, the attenuated X-ray beam deposits less dose, as observed in patients with large amounts of subcutaneous fat and therefore larger abdominopelvic diameters.

Organ doses normalized by scanner-specific radiation output are scanner-independent, with variations typically less than 10% [21, 28]. Patient-specific organ doses from chest–abdomen–pelvis CT examinations may be predicted from exponential fits of CTDI_vol-normalized dose to patient diameter (Fig. 2). A similar predictive relationship was determined for DLP-normalized effective dose (Fig. 3). Organ doses may by estimated for patients imaged by other CT scanners through application of the fit parameters (tables 4, 5 and 6) using measurements of patient diameter and scanner-specific CTDI_vol. It is noted that doses estimated for organs completely covered in the scan region from the fit parameters for chest–abdomen–pelvis examinations are within 10% of those derived from the chest and abdominopelvic studies. In general, these predicted doses are higher using the fit parameters relating organ dose to patient diameter for chest–abdomen–pelvis studies, because of additional scatter from the larger irradiated volume. However, this affect is small, and the fitting parameters in Table 4 can be applied to chest and abdominopelvic studies in addition to chest–abdomen–pelvis studies without contributing substantial error to the predicted organ dose. Our results, combined with fit parameters for other scan protocols (i.e. different tube voltage, collimation, pitch, or bowtie filter size) [24, 25], offer an improved method for tracking organ doses from diagnostic imaging studies of children compared to the current use of radiation dose indices such as CTDI_vol, dose-length product (DLP) and size-specific dose estimate (SSDE).

We compared CTDI_vol-normalized organ doses of completely irradiated organs reported by Lee et al. [22] with agreement within 4–12%. In general, CTDI_vol-normalized organ doses obtained from the phantoms were lower (Fig. 2), mostly likely because of differences in scan protocol. The organ doses for the reference phantoms were derived from axial scans with a 10-mm nominal beam, whereas our simulation modeled helical image acquisition with a 40-mm nominal beam width. It has been shown that larger beam collimation increases CTDI_vol-normalized organ doses [25]. Also, the over-ranging distance required to reconstruct images from helical acquisition contributes additional dose compared to axial scans.

Absorbed organ doses were calculated for each child using regression coefficients derived by Turner et al. [28] and compared to our simulation results for abdominopelvic examinations (Fig. 4). For organs completely covered in the scan length, the average difference for each CTDI_vol-normalized organ dose was less than 12%. Additionally, absorbed organ doses were calculated using dose coefficients from child-specific models [24]. For the same organs, average differences between CTDI_vol-normalized organ doses increased to 16–25%, with bigger deviations for large abdominopelvic diameter (Fig. 4). The type of bowtie filter was the only major variation between scan protocols that may not be compensated through normalization by CTDI_vol. The bowtie filter shapes the X-ray beam to compensate for variation in body thickness across the patient, eliminating low energy photons that contribute to patient dose without improving the image quality. Bowtie filters vary in size to modify the beam profile based on the type of examination (body or head) and patient size. Thus, filters of different size and thickness alter the X-ray energy spectrum differently. The Philips Brilliance 64 CT scanner has a single body bowtie filter that is used regardless of patient size and may not reduce the amount of low-energy X-rays reaching a child during chest, abdominal and pelvic examinations as much as a smaller filter would. We would expect higher organ doses from a softer X-ray beam created by a using a large bowtie filter on children, as shown in Fig. 4.

To further investigate the effect of a large bowtie filter on organ doses to children, we compared our doses to chest CT results from Li et al. [25] for a scan protocol using a large bowtie filter (Fig. 5). The average differences for lung and heart doses were 7–10%. The average differences increased to 13–15% using coefficients from scans with a small bowtie filter [24], with differences exceeding 25% for chest diameters greater than 25 cm (Fig. 5). This analysis indicates that the effect of the size of the bowtie filter might not be as modest as previously reported [21, 23, 25]. Additional studies of patients with large diameters are necessary to more fully quantify this result.

This study had several limitations. Our patient cohort lacked newborn individuals and the absence of children with very small body diameters might affect the slope of the exponential fits; however, our study did include patients as young as 7 months, and the results show very reasonable behavior for a broad range of patient diameters. Where our data agree less with previous studies, a number of factors including patient (or phantom) geometry differences, differences in beam quality, and variation in Monte Carlo simulation methods likely explain the dissimilarities in the results. Patient models were created by segmentation of CT images, which limited reported doses to organs contained within the length of the scan. Doses to distributed organs, including bone and red marrow, are artificially high because the models are missing the skull and some of the appendicular skeleton. Furthermore, the lack of dose information outside the scan length influences the accuracy of the effective dose because we were unable to measure dose to partly irradiated organs (e.g., thyroid and testes) and non-irradiated organs (e.g., salivary glands and brain). Despite this limitation, our results agree with k coefficients from stylized pediatric phantoms that are commonly used to convert dose-length product to effective dose [15] (Fig. 3), with the exception of the newborn because of our lack of data for infants younger than 7 months. Li et al. [38] found effective dose to be underestimated by 4–22% as a result of exclusion of dose to organs outside the image coverage. Our comparison of DLP-normalized effective dose to fit parameters from Li et al. [25] (Fig. 3) follows this general trend, with larger differences for small diameters. We are investigating the use of pediatric anthropomorphic phantoms in Monte Carlo CT simulation; this will allow calculation of doses to all organs, including contributions from scatter to regions outside the scan length.

In this paper, we have shown how DLP-normalized effective dose can be estimated using patient abdominopelvic diameter and that this method produces a superior quantity compared to a single vendor-supplied value assigned to all patients, regardless of body size or age. However, effective dose is meant to apply to populations, with tissue-weighting factors averaged over all ages and both genders, and designation of effective dose to individual patients is inconsistent with the intended use of the quantity. Therefore, we caution applying effective dose derived from Fig. 3 to an individual and instead consider this value as the effective dose to a population of patients of similar body size and anatomy.

Conclusion

We determined organ doses to pediatric patients from chest–abdomen–pelvis CT. Our results demonstrate the ability to estimate dose from different CT scanners using measurements of patient diameter and scanner output (CTDI_vol). We observed that factors such as beam collimation, bowtie filtration, and scan length may significantly affect the relationship between CTDI_vol-normalized organ dose and patient size and conclude that care must be used when applying dose coefficients. Nonetheless, this method offers a generalized approach to dose estimation from chest–abdomen–pelvis CT and, most important, predicts patient dose prior to the examination.