The General Base in the Thymidylate Synthase Catalyzed Proton Abstraction

Abstract

The enzyme thymidylate synthase (TSase), an important chemotherapeutic drug target, catalyzes the formation of 2′-deoxythymidine-5′-monophosphate (dTMP), a precursor of one of the DNA building blocks. TSase catalyzes a multi-step mechanism that includes the abstraction of a proton from the C5 of the substrate 2′-deoxyuridine-5′-monophosphate (dUMP). Previous studies on ecTSase proposed that an active-site residue, Y94 serves the role of the general base abstracting this proton. However, since Y94 is neither very basic, nor connected to basic residues, nor located close enough to the pyrimidine proton to be abstracted, the actual identity of this base remains enigmatic. Based on crystal structures, an alternative hypothesis is that the nearest potential proton-acceptor of C5 of dUMP is a water molecule that is part of a hydrogen bond (H-bond) network comprised of several water molecules and several protein residues including H147, E58, N177, and Y94. Here, we examine the role of the residue Y94 in the proton abstraction step by removing its hydroxyl group (Y94F mutant). We investigated the effect of the mutation on the temperature dependence of intrinsic kinetic isotope effects (KIEs) and found that these KIEs are more temperature dependent than those of the wild-type enzyme (WT). These results suggest that the phenolic –OH of Y94 is a component of the transition state for the proton abstraction step. The findings further support the hypothesis that no single functional group is the general base, but a network of bases and hydroxyls (from water molecules and tyrosine) sharing H-bonds across the active site can serve the role of the general base to remove the pyrimidine proton.

Introduction

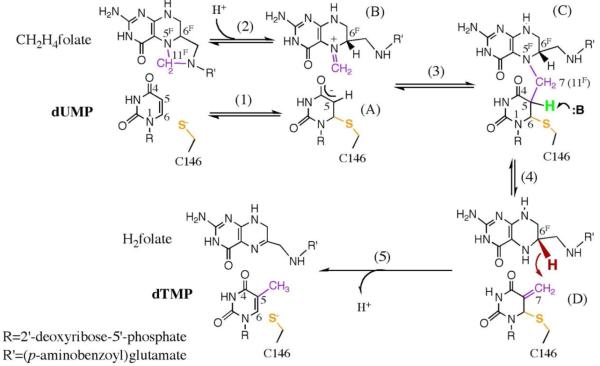
Thymidylate synthase (TSase, EC 2.1.1.45) catalyzes the reductive methylation of 2′-deoxyuridine-5′-monophosphate (dUMP) to form 2′-deoxythymidine-5′-monophosphate (dTMP), one of the DNA building blocks.¹ Therefore, the activity of this enzyme is crucial for DNA biosynthesis, making it a common target for chemotherapeutic drugs such as tomudex and 5-fluorouracil.^{2, 3} TSase utilizes N⁵, N¹⁰-methylene-5,6,7,8-tetrahydrofolate (CH₂H₄folate) as a cofactor that donates both a methylene and a hydride to the C5 of dUMP, thus generating the product dTMP (Scheme 1).¹ The detailed mechanistic features of the TSase-catalyzed reaction have been developed from a wide variety of kinetic, spectrophotometric and crystallographic studies.^{1, 4-7} In the proposed mechanism, a conserved cysteine residue (C146 in ecTSase) attacks the C-6 of the substrate dUMP to form an enolate at C5-C4=O (compound A in Scheme 1), which, in turn, attacks the pre-activated cofactor CH₂H₄folate, forming a covalent ternary complex of TSase-dUMP-CH₂H₄folate (compound C).^{1, 8, 9} Then an abstraction of the proton from the C5 of dUMP (step 4 in Scheme 1) leads to the formation of an exocyclic methylene intermediate (compound D),¹⁰ which is followed by a transfer of hydride from the C-6 of H₄folate that generates the final product dTMP. The hydride transfer is irreversible and rate limiting on both the first order (k_cat)⁷ and the second order rate constants (k_cat/K_M or V/K),¹¹ while the proton abstraction is much faster and reversible.⁴ Even though extensive experimental and theoretical studies^{12, 13} have been carried out on the mechanism of proton abstraction, the identity of the general base and the overall mechanism of proton abstraction remain elusive.^{9, 14-17} Hardy et al.¹⁴ proposed that the deprotonation of C5 of dUMP and the protonation of N-5 of CH₂H₄folate are tightly coupled and a nearby water molecule acts as a proton conduit that concertedly remove the pyrimidine proton and add it to the N5 of folate. The protonation of N5 of folate is crucial for the breakdown of the C7-N5 bond and to form the exocyclic methylene intermediate. On the other hand, Hyatt et al.⁹ and also Stroud and co-workers^{4, 5} postulated that the phenolate anion of Y94 might abstract the proton based on its proximity to the fluorine in a crystal structure of TSase-5FdUMP-CH₂H₄folate. Recent QM/MM calculations on this proton abstraction step also suggested that a nearby water molecule in the vicinity of Y94 serves as the initial proton acceptor.¹³ Y94 is one of the five most essential residues for catalysis⁴ and mutations at this position result in dramatic reduction in the enzyme’s activity and an accumulation of the ternary complex TSase-dUMP-CH₂H₄folate during the reaction, clearly indicating its importance in the turnover rate.¹⁷ Based on QM/MM calculations¹³ and previous experiments,¹⁸ we have hypothesized that Y94 may not be the sole general base but rather part of a more comprehensive basic-system,¹⁸ however this hypothesis has not been examined in the past.

Scheme 1.

Proposed chemical mechanism for TSase Catalyzed Reaction (reproduced from ref.¹³ with permission from ACS). The proton being abstracted in step 4 is shown in green.

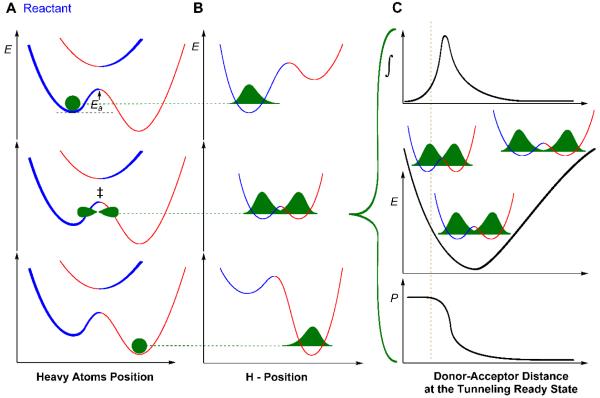
Ref 18 assessed the intrinsic KIE for the proton abstraction with Y94F at 25 °C, but the intrinsic KIE at one temperature cannot provide information about the structure or distribution of the transition state (TS).^19-25 Often isozymes with very different TSs have intersecting temperature dependences of KIEs, thus at one temperature their KIEs could be identical, but very different above or below that temperature. Before examining the mutant, it is important to note that the temperature dependence of intrinsic KIEs on the proton abstraction in the WT TSase are steeply temperature dependent,¹⁹ which contrasts with the temperature independent KIEs on the following hydride transfer.¹¹ A phenomenological model, known in literature as environmentally coupled tunneling,^{26, 27} Marcus-like model,^{28, 29} vibrationally enhanced tunneling^{23, 30} and other terms,^31-33 has been used to interpret temperature dependence of KIEs. A general form of such a model was discussed in greater detail in numerous published research and review articles.^{20, 24, 25, 34, 35} Briefly, in a reaction where H-transfers are involved, quantum mechanical (QM) tunneling occurs when the heavy atom motion brings the system to a state where the energies of the H-donor and acceptor are degenerate and the donor and acceptor distance (DAD) is short enough, so the H-tunneling probability is non-zero. This state is called tunneling ready state (TRS), which is a QM delocalized transition state (illustrated in the middle panel of Figure 1).³⁵ The tunneling probability at the TRS depends on the width and height of the barrier as well as the mass of the particle being transferred, thus it is isotopically sensitive. The heavy atoms motion of the protein, solvent, and reactants that bring the system to the TRS is not significantly sensitive to whether the bond to be cleaved is C-H or C-D, thus most of the measured KIE reflects the nature of the TRS for the C-H activation per se. In an adiabatic system²⁴ that assumes a strong electronic coupling between reactant and product potential surfaces, the motion of the heavy atoms brings the system to the TRS close to the top of the barrier (i.e., small curvature tunneling),³⁶ as represented by Eq. 1 and illustrated in Figure 1.

Figure 1.

Graphical representation of the phenomenological model for an electronically adiabatic H-transfer reaction. This figure illustrates Eq. 1 with blue and red wells representing the reactant and the product states, respectively. Panel A represents the heavy atom coordinate with the electronic ground-state potential and the first electronic-excited-state at the reactant (top), TRS (middle) and the product (bottom) state, with the green structures representing the position of transferring hydrogen. Panel B shows an orthogonal view to the panel A, showing the coordinates for H-transfer. In top row of A and B, the heavy atom position and the hydrogen wave function are localized in the reactant well. In the middle row of A and B, the ZPEs of donor and acceptor are degenerate and the tunneling probability is non-zero (TRS), so the H-wave function can tunnel through the barrier, or be transferred over the barrier if the DAD is short enough for the ZPEs to be above the barrier. Further reorganization of the heavy atom breaks the degeneracy, trapping the transferred hydrogen in the product well. Panel C illustrates the transmission probability P as function of DAD (bottom panel; first term in the integral of Eq. 1), the potential energy surface along the DAD coordinate (middle panel; second term in the integral of Eq. 1) with different level of overlaps between the reactant and the product wave functions at different DADs. The contribution to the H-transfer at each DAD as a function of the P and population is shown in the top panel (the product of both terms in the integral as function of DAD). The vertical line separates the shorter DADs where the zero point energy (ZPE) of the transferred H is above the energy barrier (over the barrier transfer) from the tunneling conformations.

This model is represented by equation 1:

$$k={\mathrm{C}}_{\left(\mathrm{T}\right)}{\mathrm{e}}^{-\Delta G^{‡}∕\mathrm{RT}}{\int }_0^{\infty }{P}_{(m,DAD)}{\mathrm{e}}^{-({\mathrm{E}}_{\left(\mathrm{DAD}\right)}∕\left({\mathrm{k}}_{\mathrm{B}}\mathrm{T}\right))}\mathrm{dDAD}$$ (1)

where the expression in front of the integral represents the rate of reaching the TRS or the TS according to the adiabatic transition state theory, which depends on the free energy difference between the ground state and TRS (ΔG^‡), the absolute temperature (T), the gas constant (R), and the fraction of the reactive complexes, C_(T). Inside the integral, P_{(m, DAD)} represents the probability of tunneling as a function of mass of the particle being transferred (m) and the donor-acceptor distance (DAD). The second term in the integral represents the Boltzmann distributions of DADs, where E_(DAD) is the DAD’s electronic potential surface. As discussed above, the expression in front of the integral does not depend on the mass of the isotope to be transferred and thus is dropped in the equation describing the KIE (Eq. 2):

$$\mathrm{KIE}=\frac{k_l}{k_h}=\frac{{\int }_0^{\infty }{P}_{\left(DAD\right)}^l{e}^{-(E_{\left(\mathrm{DAD}\right)}∕\left(k_{B}T\right))}\mathrm{dDAD}}{{\int }_0^{\infty }{P}_{\left(DAD\right)}^h{e}^{-(E_{\left(\mathrm{DAD}\right)}∕\left(k_{B}T\right))}\mathrm{dDAD}}$$ (2)

where k_l and k_h denote the rate constants for the light (l) and heavy (h) isotopes, respectively while P^l_(DAD) and P^h_(DAD) their transfer probabilities. In the framework of this kind of phenomenological models, temperature independent KIE results from a narrow distribution of DADs at the TRS, i.e., well defined TS with narrow distribution of DADs. Temperature dependent KIEs, on the other hand, results from a loose TRS with a broad distribution of DADs, i.e., broad ensemble of TSs, which leads to larger population of shorter DADs at higher temperature.^{21, 23-26, 35} Consequently, the reported temperature dependent KIEs on the non-rate limiting proton abstraction for the WT TSase indicates a poorly organized TRS, and as a result, it can attain a large distribution of DADs that changes with temperature. The temperature independent KIEs on the rate-limiting hydride transfer, on the other hand, demonstrate a well organized TRS with a narrow distribution of DADs. A perturbation of the reaction coordinates for a given H-transfer may change the physical nature of the TRS, and thus the distribution of DADs, which will be reflected as a change in the temperature dependence of KIEs.³⁵ To reemphasize, in order for a mutation to change the temperature dependence of intrinsic KIEs that residue has to be a component of the TS for the reaction.

In this study, this tool is applied to investigate the role of Y94 in the proton abstraction (step 4 in Scheme 1). The coordinating hydroxyl is removed by mutating Y94 to phenylalanine (F), which introduces a minimal structural perturbation, as evident from comparison of the crystal structures of the WT and mutant, PDB IDs 2FTO and 1TYS, respectively. We compared the temperature dependence of intrinsic KIEs for the Y94F mutant to that of the WT, and observed a significance increase in intrinsic KIEs and their temperature dependence. This finding implicates Y94 as part of the reaction coordinate for the proton transfer, in spite of its low basicity and indirect contact to the active site bases. As the hydroxyl of Y94 forms part of the H-bond network through several water molecules, these findings support the hypothesis that a network of hydrogen bond connecting several active-site residues and water molecules is the actual general base that deprotonate the C5 of the pyrimidine.

Materials and Methods

Materials and Instruments

[2-¹⁴C] dUMP (specific radioactivity 53.2 mCi/mmol) and [5-³H]-dUMP (specific radioactivity 14.3 Ci/mmol) were from Moravek Biochemicals. CH₂H₄folate was from MERK and scintillation cocktail (Ultima Gold) was from PerkinElmer. WT TSase was expressed and purified following the published procedure.³⁷ Agilent Technologies model 1100 HPLC system with Discovery C18 analytical column (25cm×4.6mm, 5µm) from Sigma-Aldrich was used for all the purifications and analytical separations. Liquid Scintillation Counter (TRI-CARB, 2900TR) was from Packard. All other chemicals were purchased from Sigma and used without further purification.

Construction, expression and purification of mutant TSase

pBluescript vector containing the TSase encoding thyA gene was used to generate the mutant Y94F by site-directed mutagenesis. Both the forward and reverse primers were designed by changing the appropriate DNA bases and were synthesized by Integrated DNA Technologies (IDT). The sequences of the mutagenic forward and reverse primers are 5'-GGC GAC CTC GGG CCA GTG TTT GGT AAA CAG TGG-3' and 5'-CCA CTG TTT ACC AAA CAC TGG CCC GAG GTC GCC-3', respectively. These primers were used to introduce a single point mutation in the thyA gene. The mutated gene was sequenced by the University of Iowa DNA core facility, which confirmed successful site directed mutagenesis. Finally, E.coli ΔthyA-BL21(DE3) cells were used to express and purify Y94F TSase according to a published procedure.³⁷

Synthesis of [2-¹⁴C, 5-D] dUMP

To measure the D/T KIEs on the second order rate constant (V/K), [2-¹⁴C, 5-D] dUMP was synthesized by following the method published by Wataya and Hayatsu.³⁸ In short, 1M L-cysteine and ~1mM of [2-¹⁴C] dUMP solutions were prepared in D₂O (> 99.9% atom D) and were lyophilized twice to replace all of the exchangeable hydrogens with deuterium and were then purged with argon. The pD of both solutions was maintained at 8.8 (37°C) prior to mixing. The reaction, performed in an NMR tube, was initiated by mixing the solutions. The extent of deuteration was verified using ¹H NMR and complete deuteration (>99.5%) was achieved after ~8 days of incubation.

Observed and intrinsic KIEs for Y94F were measured as described before for the WT TSase.¹⁹ A short summary of these procedures is provided below:

Competitive Observed KIE on proton abstraction

The 1° KIEs on the V/K for the proton transfer step were measured competitively. It is noteworthy to mention that in enzyme catalyzed reactions it is challenging to examine any chemical step that is not rate limiting within the complex catalytic cascade. This challenge was overcome by following the methods previously developed by Wang et al. in our lab.¹⁹ In short, the reaction mixture consisted of 50 mM magnesium chloride (MgCl₂), 5 mM formaldehyde, 1 mM ethylenediamine tetraacetic acid (EDTA), 2mM tris(2-carboxyethyl)phosphine (TCEP), 10μM CH₂H₄folate, 0.33 Mdpm of [2-¹⁴C] dUMP (for H/T KIE experiments) or [2-¹⁴C, 5-D] dUMP (for D/T KIE experiments) and 1.8 Mdpm [5-³H dUMP]. The reaction was performed in 140mM tris(hydroxymethyl)aminomethane (Tris/HCl) buffer and the pH was adjusted to 7.5 at each temperature and was conducted at four different temperatures (5, 15, 25 and 35°C). After incubating at the desired temperature for 2 min, the reaction was initiated by adding enzyme. At different time points, four to five 50 μL aliquots of the reaction mixture were withdrawn and quenched using 50 μM 5-fluoro-2'-deoxyuridine-5'-monophosphate (5-F dUMP, a nanomolar inhibitor of TSase).¹⁸ The quenched reaction mixtures were immediately put on dry ice and stored at −80 °C and were then analysed using HPLC. Three independent control reactions were performed without adding the enzyme to detect contaminations in the starting material. Additionally, after incubating the reaction mixtures for about two hours with mutant enzyme, 50 μM wild-type TSase was added to the reaction mixture for completion of the reaction, and yielded the R_∞ values used in Eq. 3 below (ratio of ³H/¹⁴C in the productafter completion of the reaction). After measuring the ratio of ³H/¹⁴C in the product ([³H] H₂O and [¹⁴C] dTMP) at each time point (R_t) and the fraction conversion (f), the observed KIEs on the proton abstraction step were calculated using equation 3.^{34, 39, 40}

$$KI{E}_{obs}=\frac{ln(1-f)}{ln(1-f\frac{R_t}{R_{\infty }})}$$ (3)

Here, the fraction conversion (f) is the ratio of the amount of ¹⁴C present in the product (dTMP) to the total amount of ¹⁴C present in the reactant (dUMP) and product (dTMP) at any particular time point and was calculated using equation 4.¹⁸

$$f=\frac{{[}^{14}CdTMP]}{{[}^{14}CdTMP]+{[}^{14}CdUMP]}$$ (4)

Assessment of Intrinsic KIE from Observed KIE

The intrinsic KIEs were calculated from observed H/T and D/T KIEs using Northrop method^{34, 41}

$$\frac{{}^T{(V∕K)}_{H_{obs}}^{-1}-1}{{}^T{(V∕K)}_{D_{obs}}^{-1}-1}=\frac{k_T∕k_H-1}{{(k_T∕k_H)}^{1∕3.34}-1}$$ (5)

where k_T/k_H is the reciprocal of intrinsic H/T KIE, ^T(V/K)_Hobs represents the observed H/T KIE and ^T(V/K)_Dobs represents the observed D/T KIE on the second order rate constant. This method allows the calculation of intrinsic KIE from observed KIE by measuring both H/T and D/T KIE at an identical condition for both reaction systems. The equation was solved numerically to get the intrinsic KIEs from all possible combinations of observed KIEs.^{18, 19} These calculated intrinsic KIEs were then used to determine the temperature dependence of KIEs and isotope effect on Arrhenius parameter by nonlinear regression.

Results and Discussion

Binding mechanism of Y94F

Due to a strictly ordered binding mechanism of ligands in wild-type TSase the observed KIEs on V/K for the proton abstraction step, where the labeled substrate, dUMP, binds first, depend on the concentration of the second binding ligand CH₂H₄folate.^{4, 18, 42} A mutation may cause a change in the binding mechanism, which alters the relation between the ligand concentration and the observed KIEs. Eq. 6 describes the relationship between the observed KIEs (KIE_obs) on the second order rate constant (V/K) and the KIEs after the formation of the ternary complex (complex EAB in Scheme 2), i.e. ^Tk₉. In this equation, the terms C_f and C_r represent the forward and reverse commitments, respectively and EIE denotes the equilibrium isotope effect.^{43, 44}

Scheme 2.

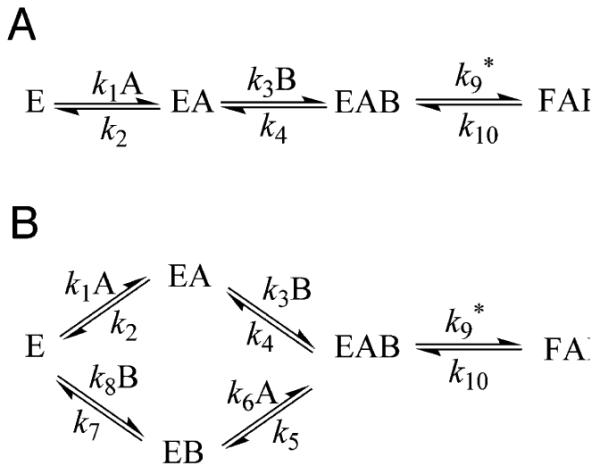
Schemes for an ordered (A) and a random (B) binding mechanisms. For TSase A and B represent dUMP and CH₂H₄folate, respectively. Asterisk (*) and number sign (#) denote the proton abstraction (k₉) and the hydride transfer (k₁₃), respectively.

$$KI{E}_{obs}=\frac{T_{k_9}+C_f+C_{r}EIE}{1+C_f+C_r}$$ (6)

The EIE on the proton abstraction was measured and found to be unity,¹⁸ and since the T-release from C5 is irreversible (labeled tritium at C5 of dUMP dilutes to 110 M of protiated water), we assume a negligible C_r, which simplifies the Eq. 6 to the following:

$$KI{E}_{obs}=\frac{T_{k_9}+C_f}{1+C_f}$$ (7)

The C_f is defined as the ratio of the rate constant of the isotopically sensitive forward step (k₉) to the net rate of isotopically insensitive steps proceeding backward; thus, it depends on the reaction kinetic scheme and the binding order. Eq. 8 and 9 represent the expression for C_f on V/K for an ordered and a random binding mechanisms, respectively:⁴³

$$C_f=\frac{k_9}{k_4}+\frac{k_3\left[B\right]}{k_2{k}_4}$$ (8)

$$C_f=\frac{k_9}{k_5+\frac{k_2{k}_4}{k_2+k_3\left[B\right]}}$$ (9)

where [B] is the concentration of the CH₂H₄folate. It is evident from Eq. 8 that in the ordered mechanism, C_f varies from infinity at a very high concentration of B to a finite value (k₉/k₄) at a very low concentration of B. As a result, the KIE_obs changes between unity at high B and a normal value at low B. On the other hand, C_f in the random mechanism (Eq. 9) changes between two finite values, k₉/k₅ and k₉/(k₅ + k₄), at B = ∞ and B = 0, respectively, yielding KIE_obs > 1 at any concentration of B. Therefore, measuring the KIEs as a function of the concentration of CH₂H₄folate can determine the binding order of ligands. The effect of CH₂H₄folate concentration on the KIE_obs for both the wild-type and the mutant Y94F are compared in Figure 2.¹⁸

Figure 2.

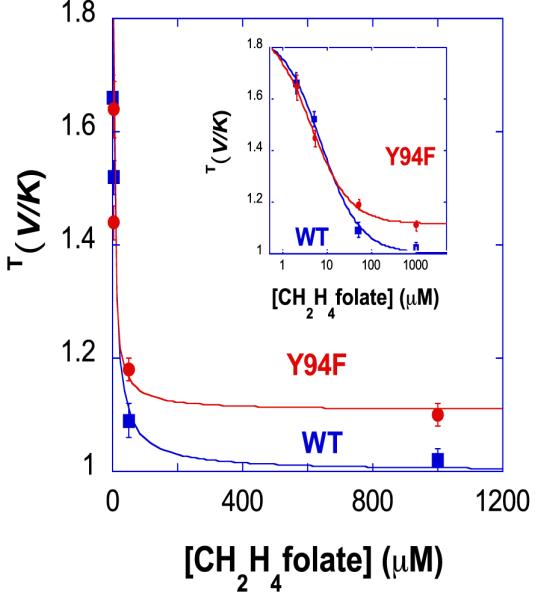
Observed H/T KIEs on V/K on the proton abstraction step for the wild-type (●) and Y94F (■) as a function of the concentration of CH₂H₄folate. The inset presents the same on a log scale. The figure is reproduced from ref 18 with the permission from ACS.

It is apparent from Figure 2 that the KIE_obs in the mutant enzyme at the high concentration of CH₂H₄folate reaches an asymptote larger than unity, indicating a less-ordered mechanism for Y94F than for the WT.

Temperature dependence of Intrinsic KIEs

The competitive H/T and D/T KIEs for the proton abstraction for the Y94F mutant at temperatures ranging from 5 to 35°C were measured at 10 μM CH₂H₄folate. The low CH₂H₄folate concentration was chosen to reduce the commitment factors (see Figure 2), and obtain larger H/T and D/T KIE_obss and thus smaller experimental errors. Other than that detail, the methods employed here are identical to those used to study the WT TSase.¹⁹ As for the WT TSase,¹⁹ the observed KIEs for Y94F do not follow Swain-Schaad relationships, indicating the proton abstraction in Y94F is not rate-limiting for both enzymes.^{28, 40, 43} The intrinsic KIEs for both enzymes were assessed as described in ref ¹⁹, and Figure 3 shows Arrhenius plots of intrinsic KIEs for both the WT and Y94F TSases. The H/T intrinsic KIEs were then fitted to the Arrhenius Equation (Eq. 10) via non-linear regression to obtain the isotope effect on the Arrhenius pre-exponential factor (A_H/A_T) and the activation energy (ΔE_a,T/H), which are presented in Table 1.

Figure 3.

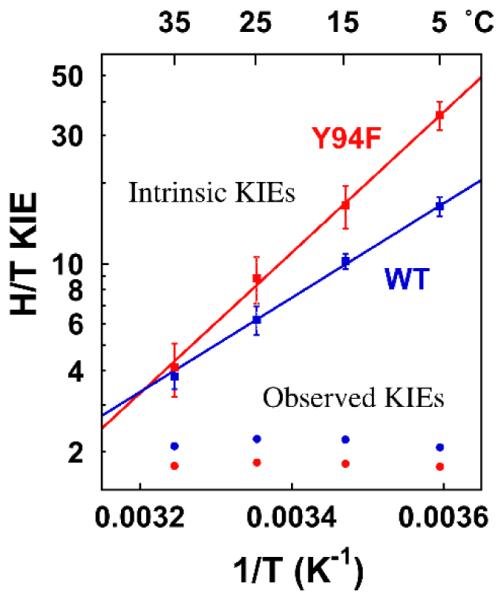
Arrhenius plots of the observed (sphere) and the intrinsic (cube) H/T KIEs on the proton abstraction for the wild-type (blue line) and Y94F (red line). The KIEs are shown as average values with their standard deviations (error bars), and the lines are the nonlinear fittings of all calculated intrinsic KIEs to the Arrhenius equation. Please note that for the observed KIEs, the error bars are smaller than the spheres.

Table 1.

Isotope effects on the Arrhenius parameters (A_H/A_T) and the activation energy (ΔE_aT/H) for the proton abstraction in the wild-type and Y94F.

	Wild-type19	Y94F
Ah/At	8.3 (±1.0) ⟂10−6	1.46 (±1.2) ⟂10−8
ΔEa,H/T (kcal/mol)	−8.0 (±0.1)	−11.9 (±0.45)

$$KIE=\frac{k_H}{k_T}=\frac{A_H}{A_T}\exp \left(\frac{-\Delta E_a}{RT}\right)$$ (10)

where k_H and k_T represent the isotopically sensitive microscopic rate constants (step 4 in Scheme 1) for the protium (H) and tritium (T) isotopologues, respectively.

As evident in Figure 3 and Table 1, up to 35 °C the H/T intrinsic KIEs are larger in Y94F than in the WT TSase with steeper temperature dependence. In the light of the phenomenological models discussed above, these observations suggest that the Y94F mutation significantly increased the average DAD and broadened its distributions at the TRS, indicating that Y94 is part of the proton transfer reaction coordinate. It appears that even though a tyrosine (phenol) that is not ligated to stronger bases is not very basic (pKa ≈ 10), its effective pKa in the WT TSase active site shifts by conjugation to other active site bases, prior to the proton abstraction step. The hydroxyl group can activate the pyrimidine proton directly or by coordinating with a near by water molecule acting as the general base to deprotonate the pyrimidine.

The effect of Y94F on the hydride transfer was insignificant down to 20 °C as evident form invariant intrinsic KIEs relative to the WT at physiological temperature.¹⁸ This observation carries an important significance because it emphasizes the unique role of Y94 in proton abstraction (step 4 in Scheme 1), and also suggests that the observed alteration in the intrinsic KIEs on the proton abstraction in Y94F does not result from a change in global conformations of the protein caused by the mutation, which would affect the both H-transfers. Indeed, a comparison of the crystal structures of wild-type and Y94F confirmed a perfect overlap of the backbones between the two structures, which further supports unaltered overall protein conformations in the mutant Y94F. In the overlaid structures (Figure 4), the obvious exception is the absence of the hydroxyl group at residue 94, and the rearrangements of water molecules that maintain a H-bond network at the proton transfer site between at least three active-site residues (H147, E58 and N177). It appears that the absence of the phenolic hydroxyl in Y94F disrupted the H-bond network. Consequently, the changes in the nature of the proton abstraction as evident from altered intrinsic KIEs in Y94F appear to arise from the alteration in the H-bond network, supporting the hypothesis that the whole H-bond network at the proton transfer site serves as the general base.

Figure 4.

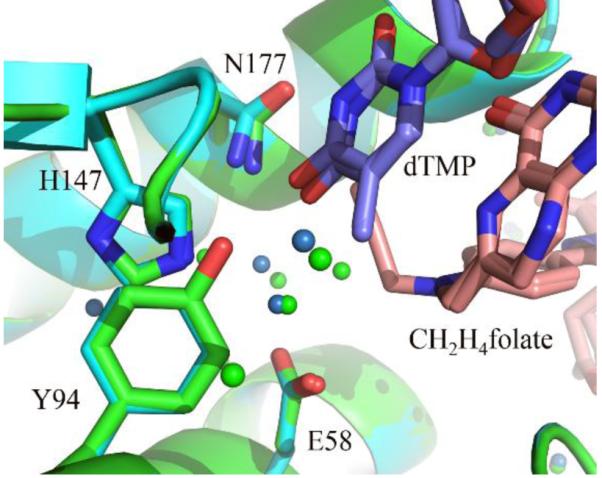
Structural comparison of WT TSase (green, PDB ID: 1TYS) and Y94F TSase (blue, PDB ID: 2FTO). Y/F 94, H147, E58, N177, dTMP and CH₂H₄folate molecules are shown in sticks and all the water molecules close to proton abstraction site as spheres.

Additional Analysis of the Intrinsic KIEs

Although the fitting of the intrinsic KIEs to the Arrhenius equation yields isotope effect on activation parameters, nonlinear regression of intrinsic KIEs to a phenomenological model based on Eq. 2 and Figure 1 can generate two alternative parameters that might be more physically meaningful than isotope effects on entropy and enthalpy (ΔE_a,T/H, A_H/A_T).⁴⁵ Nonlinear regression to the phenomenological model assuming adiabatic H-tunneling produces an average DAD and its population distribution. Since a single exponent can fit the data, only two parameters are meaningful for any alternative regression. In this kind of fitting, KIEs with small or no temperature dependence (ΔE_a,T/H < 1 kcal/mol) can be fit to a one-population DAD model, which generates the average DAD₀ and the force constant of DAD fluctuations (f). However, KIEs with steeper temperature dependence (ΔE_a,T/H >1 kcal/mol), like those relevant to this case (see Table 1), require a two-populations DAD model, one with ZPE already over the energy barrier (population with a KIE = 1) and one from which H tunnels (with a finite KIE at 0 °K). This last model yields a DAD for the dominant tunneling population (DAD_L) and the free energy difference between the two populations (ΔG°).⁴⁵ The parameters for the WT and Y94F TSase KIEs fitted to this model are summarized in Table 2.

Table 2.

Fitting parameters from the nonlinear regression of KIEs to the phenomenological model presented in ref⁴⁵.

	Wild-type	Y94F
DADL (Å)	3.61±0.03	3.78±0.03
ΔG° (kcal/mol)	9.44±0.5	12.80±0.6

As apparent in Table 2, Y94F possesses a significantly longer DAD_L with a larger ΔG° between the two populations, indicating a larger population centered at the longer DAD in Y94F than in the wild-type TSase. Since only the population with longer DAD contributes to the KIE, and it is more populated in the mutant, this finding accord well with the larger KIEs measured for the mutant. Furthermore, since the change of temperature shifts the population from DAD_L to the short DAD via Boltzmann distribution (), a larger ΔG° leads to a steeper temperature dependence of the KIEs, as observed for the mutant relative to the WT TSase.

General Base for the Proton Abstraction

The proton transfer site in TSase consists of several residues including Y94, E58, H147 and N177 that are connected to each other via H-bonds coordinated by at least two highly localized (W387, W453 in PDB ID 1TLS) and many disordered water molecules. Montfort et al.⁹ suggested that the hydroxyl of Y94 is in van der Waals contact with 5F-dUMP (a C5-substitued dUMP analog) in a crystal structure of the ternary complex of TSase-5FdUMP-CH₂H₄folate, prompting them to propose the phenolate anion acting as a base directly removing C5-H, although the authors acknowledged that the unassisted ionization of tyrosine presents a dilemma. H147, one of the basic residues that may assist the ionization of Y94, can be mutated without any significant loss in activity,^{4, 15} although its effect on the proton abstraction per se has not been determined. The nearest localized water molecule (W387) could be a candidate to serve as a proton acceptor (Figure 5), but, due to much higher pKa of C5 of dUMP, it has to be activated by more basic functional group. The current finding that Y94 is part of the reaction coordinate for that proton abstraction supports the hypothesis that the proton acceptor is W387, which is oriented by the phenolic hydroxyl of Y94 and activated through other water molecules by H147, N177, and E58, as found in the QM/MM calculations.¹³ According to this hypothesis the general base in TSase is not a single residue, but a whole network of residues connected via H-bonds.

Figure 5.

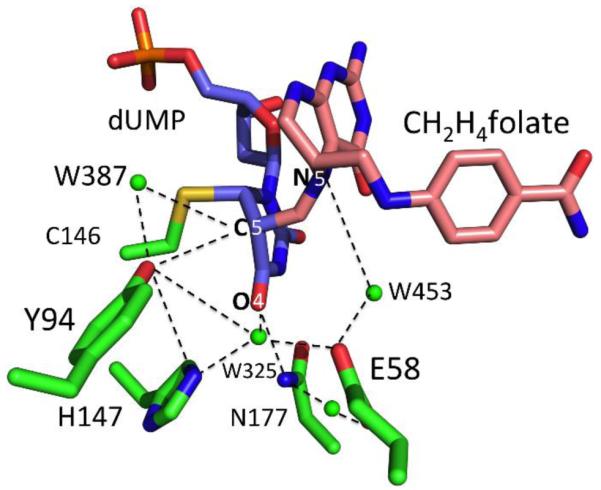
The network of H-bonds in TSase Active Site: Structure of wild-type ecTSase (PDB ID 1TLS) covalently bound to FdUMP-CH₂H₄folate (a mimic of the state prior to the proton abstraction) showing several relevant active site residues and water molecules. Potential H-bonds are marked by dashed line. Also marked are N5 of CH₂H₄folate, O4 carbonyl of dUMP, and the H-donor (C5 of dUMP). The fluorine atom is removed from C5 for clarity.

The removal of the C5 proton of dUMP might also be assisted by N5 of H₄folate, and protonation of that N5 is essential for the breakdown of C7-N5 bond that occurs in elimination step that follows the proton abstraction and leads to the formation of the exocyclic methylene intermediate (D in Scheme 1). In addition to the basic H147, this network may include the negatively charged E58. The anionic E58 is also a base that coordinates with both the N5 of folate and the C4=O4 carbonyl of dUMP through W453. It has been independently proposed that E58 plays a role in the protonation of the N5 of folate and the following cleavage of C7-N5 bond.¹⁶

Kinetic Complexities

Based on the alteration of C_f by the Y94F mutation, it is apparent that in addition to its role in the proton abstraction step, Y94 seems to play a role in other kinetic steps. The larger difference between the intrinsic and the observed KIEs in Y94F relative to the WT indicates larger kinetic complexity, as reflected in the commitment to catalysis (C_f) in the mutant. The commitments to catalysis (C_fs) on V/K of the proton abstraction were calculated from the observed and intrinsic KIEs using Eq. 7 and are presented as Arrhenius plots in Figure 6. The exponential relationships of C_fs with the inverse of temperature could indicate that the commitments arise from a single preceding kinetic step. According to the Eq. 8, the C_f at the low concentrations of CH₂H₄folate in the WT TSase approaches k₉/k₄ (Scheme 2), where the rate constant k₄ represents the release of the second binding ligand, CH₂H₄folate. However, due to the random binding mechanism for Y94F, its C_f reaches k₉/(k₅ + k₄) with k₅ and k₄ denoting the rates of dissociation of CH₂H₄folate and dUMP, respectively, from the ternary complex EAB (Eq. 9 and Scheme 2). Thus even if Y94F has no effect on the proton abstraction (k₉) and CH₂H₄folate (k₄), the very fact it leads to random binding mechanism (adding k₅ to the denominator) is sufficient to explain its larger C_f. However, the fact that Y94F changes the binding mechanism from ordered to random indicates its role in other kinetic steps than the proton abstraction.

Figure 6.

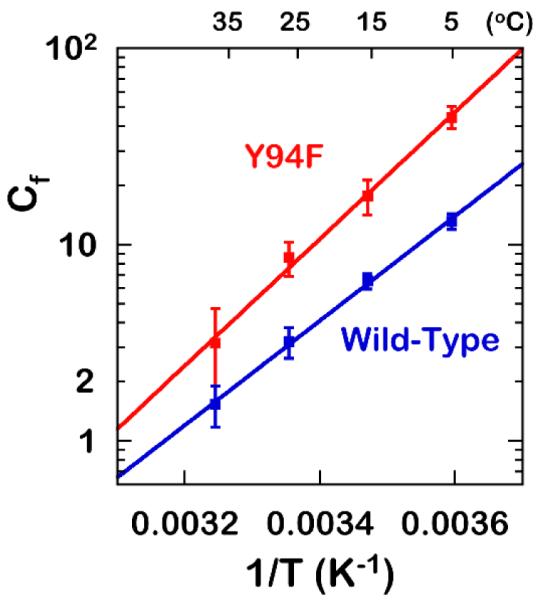
Arrhenius plots of forward commitments C_f on V/K for the wild-type¹⁹ and Y94F.

Conclusions

Understanding of how enzymes activate C-H bonds is of both intellectual and practical interest.^{2, 3} The current study examines the role of Y94 as a potential base in the deprotonation of C5 of dUMP (step 4 in Scheme 1). Mutations of Y94 adversely affects the activity and leads to the accumulation of the ternary complex.¹⁷ Previous saturation mutagenesis studies concluded that Y94 is one of the five most essential residues and critical for the function of enzyme.⁴ We investigate the effect of Y94F mutation on the proton abstraction step by comparing its temperature dependence of intrinsic KIEs with that of the WT TSase. The mutation causes a significant increase in intrinsic KIEs and their temperature dependence, implicating Y94 as a component of the general base facilitating the removal of the proton from C5 of dUMP, either directly or through a water-mediated H-bond network. Modulating the basicity of the water molecule by the H-bond network connecting several active site residues seems more likely than the direct effect due to the distance between Y94 and the C5-H of dUMP observed in most crystal structures.^{5, 46, 47} These results also corroborate recent findings from QM/MM calculations, which suggested that the acceptor of the proton is a water molecule H-bonded to Y94 and other residues in the proton transfer site.¹³ It seems that the TSase achieves this fast proton-transfer from C5 to a water molecule via an H-bond network involving several active site residues that together serve as the functional-general-base.