Traction Forces of Endothelial Cells under Slow Shear Flow

Abstract

Endothelial cells are constantly exposed to fluid shear stresses that regulate vascular morphogenesis, homeostasis, and disease. The mechanical responses of endothelial cells to relatively high shear flow such as that characteristic of arterial circulation has been extensively studied. Much less is known about the responses of endothelial cells to slow shear flow such as that characteristic of venous circulation, early angiogenesis, atherosclerosis, intracranial aneurysm, or interstitial flow. Here we used a novel, to our knowledge, microfluidic technique to measure traction forces exerted by confluent vascular endothelial cell monolayers under slow shear flow. We found that cells respond to flow with rapid and pronounced increases in traction forces and cell-cell stresses. These responses are reversible in time and do not involve reorientation of the cell body. Traction maps reveal that local cell responses to slow shear flow are highly heterogeneous in magnitude and sign. Our findings unveil a low-flow regime in which endothelial cell mechanics is acutely responsive to shear stress.

Main Text

The ability of endothelial cells (ECs) to sense and adapt to shear flow is one of the best-studied phenomena in all mechanobiology. In response to flow, ECs are known to change their orientation, remodel cell-cell and cell-matrix adhesions, modify patterns of gene expression, and alter protein localization at the cell membrane (1). Because these responses are downstream of a mechanical stimulus, a number of studies have analyzed the time evolution of cell-matrix tractions during the application of shear flow. Some of these studies reported increases in traction forces with shear flow (2, 3, 4), whereas others reached the opposite conclusion (5, 6).

Previous studies of traction forces exerted by ECs in the presence of constant shear flow focused on the application of shear stresses >1 Pa (10 dyn/cm²). Shear stresses in this range are characteristic of arterial flow during physiological function. In many other physiological and pathological conditions, however, shear stresses are much weaker. This is the case of shear stresses during venous (7) and interstitial flow (8), as well as during atherosclerosis (9) and intracranial aneurysm (10). The biochemical and structural responses of ECs to high versus low shear stress have been extensively shown to differ in terms of cell morphology, orientation, and expression of vasoactive agents, antioxidant enzymes, growth regulators, inflammatory mediators, and adhesion molecules (reviewed by Malek et al. (9)). Moreover, in the presence of ultraslow flow such as interstitial flow (11), ECs are capable of forming numerous capillary-like structures and have a greater rate of invasion (12). Many of the phenomena described above are likely to involve a synergy between flow sensing and force generation (13), but the link between slow flow and cell contractility is unknown.

To address this question, we combined traction microscopy (TM) and monolayer stress microscopy (MSM) with microfluidic techniques and explored cellular traction forces in reaction to slow shear flow (Fig. 1). TM maps the magnitude, location, and direction of the forces exerted by cells against their underlying soft substrate (14). Substrate displacements caused by cell tractions are mapped using fiduciary markers embedded in the soft substrate. The displacement fields are then used to compute tractions by inverting the elasticity equations in Fourier space.

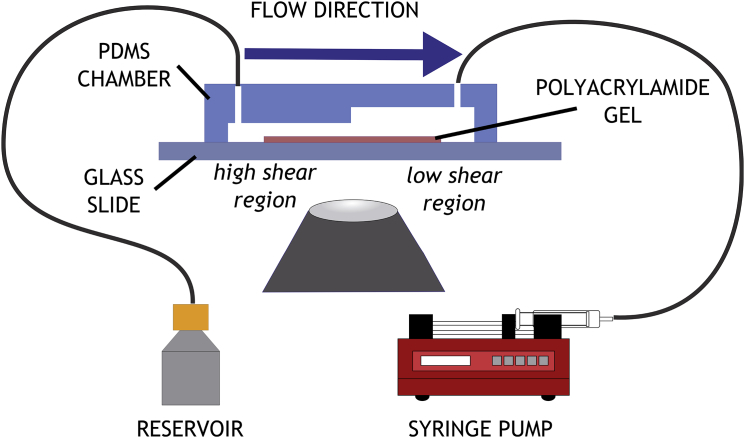
Figure 1.

Microfluidic traction assay. A PDMS flow chamber is assembled over a strip of polyacrylamide (E = 1.25 KPa) polymerized on a glass coverslip. The chamber is divided into two sections of varying heights. The flow is controlled by a syringe pump. To see this figure in color, go online.

TM was integrated into a microfluidic chamber, created in PDMS (polydimethylsiloxane) by soft lithography. A mold was machined from Plexiglas to create rectangular flow channel of 2 mm in width and 2 cm in length. The channel was designed to have two different heights over its length, thus creating a channel with two different shear stress values (15). The circulating media entered a chamber with an initial height of 300 μm, and moved into a chamber with a height of 600 μm. Corresponding shear stress values can be found in Table S1 in the Supporting Material. Cell tractions were monitored in both chambers, away from the transition zone between the two.

Monolayers of human umbilical vein endothelial cells were exposed to a time-varying protocol alternating no-flow and applied flow in the range 0.014–0.133 Pa (see Fig. 2 and the Supporting Material). The temporal stress pattern consisted of two consecutive flow steps of 30-min duration and increasing magnitude (5 and 10 mL/h), followed by a 30-min period of no flow. After this period, we applied a second pulse of flow (10 mL/h) lasting 30 min.

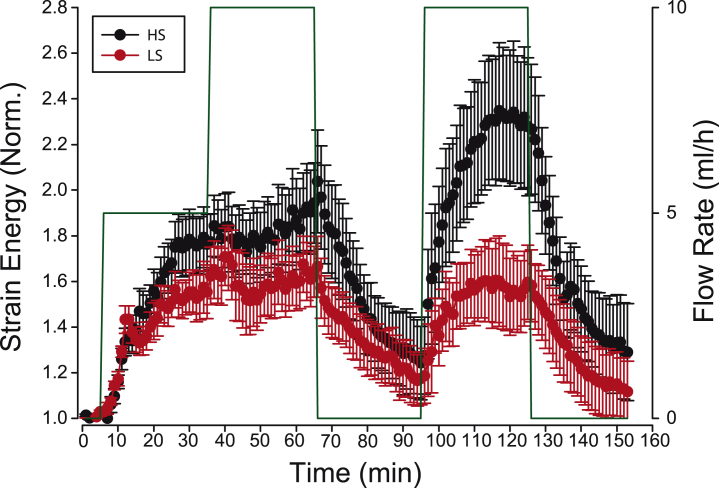
Figure 2.

ECs display acute responses to slow shear flow. Strain energy was normalized to its baseline (t = 0). (Green line) Flow values. (Red and black lines) High shear (HS) stress and low shear (LS) stress; both shear stresses were at least one order-of-magnitude lower than previously reported shear stresses in TM experiments. n = 6 monolayers per condition. Differences between HS and LS are only significant during the second shear pulse (t = 105 min and t = 125 min, p ≤ 0.05). The slopes of the strain energy between the first and second flow periods were not significant. To see this figure in color, go online.

Upon exposure to flow, we observed an acute increase in strain energy (the total energy transmitted by the cells on the substrate) with no significant differences between the two flow levels (Fig. 2). Subsequent doubling of the shear flow did not trigger a second increase in traction forces. Instead, cells tended to plateau at values that were 50–100% higher than baseline levels. Quickly after stopping the flow, the strain energy relaxed toward baseline levels, thus indicating reversibility of responses to flow. Application of an additional flow pulse triggered a second acute increase in tractions, with pronounced differences between the two flow levels, which is suggestive of a memory effect. Finally, stopping the flow led to a relaxation toward baseline levels.

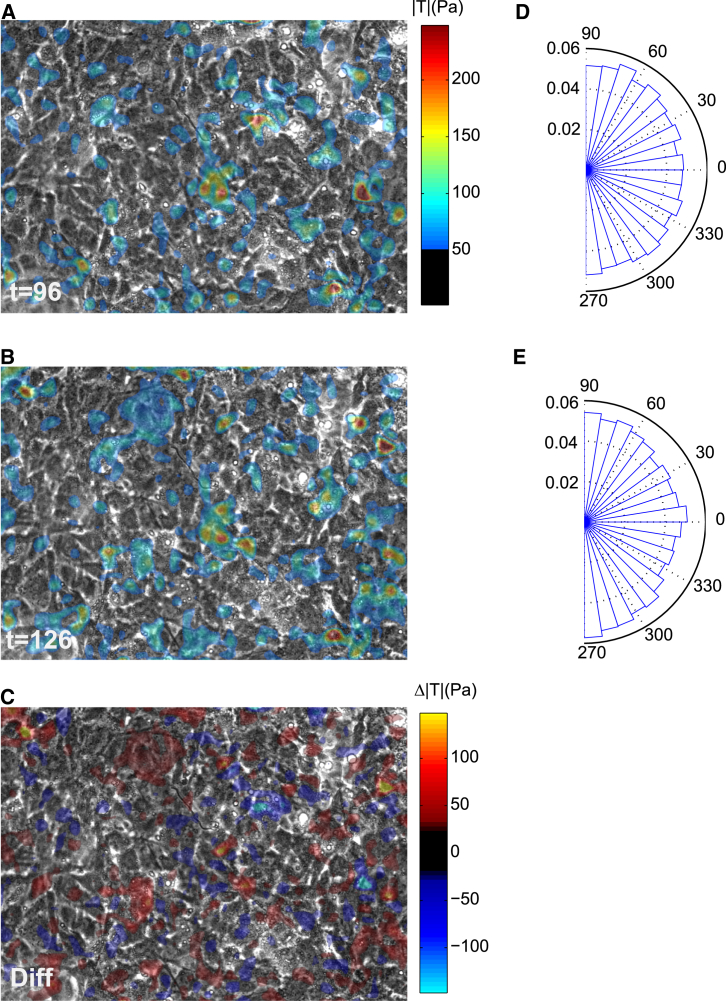
The responses shown in Fig. 2 are spatial averages of traction maps. As previously shown in a diversity of cell types (6, 16), these maps exhibited a punctate distribution with large spatial heterogeneities (Fig. 3, A and B). The response to shear flow was also heterogeneous; although the overall traction of the monolayer increased, several cells displayed significant traction drops (Fig. 3 C). The magnitude of local changes in traction in response to shear was similar to the global traction average. Upon flow application, tractions showed a weak but significant tendency to orient perpendicular to the direction of flow (p < 0.001, Rayleigh test, Fig. 3, D and E).

Figure 3.

Instantaneous maps of traction forces of an endothelial monolayer at (A) t = 96 min and (B) t = 126 min. (C) Difference between (A) and (B). Distribution of the angle between traction vectors and the direction of flow at (D) t = 96 min and (E) t = 126 min. To see this figure in color, go online.

Finally, we used MSM to measure cell-cell stresses (14). As reported previously (6, 14), cell-cell stresses showed supracellular spatial fluctuations (see Fig. S1). Upon flow application, these fluctuations increased in magnitude but cell-cell stresses did not change in orientation. Unlike cell-substrate tractions, cell-cell stresses did not show significant differences depending on flow magnitude.

Traction forces in the presence of constant shear stresses of relatively high magnitude (>1 Pa) have been extensively characterized in previous studies, with conflicting results (2, 3, 4, 5, 6). Here we used shear stresses between one and two orders-of-magnitude smaller than those applied in previous studies based on TM. In response to these low stresses, ECs exhibited acute but reversible increases in traction. These responses were fast and more pronounced than those reported in previous studies using higher shear flows (2, 3, 4, 5, 6). The low shear stresses applied here fall within the range of physiological interstitial flow (8). Because interstitial flow induces angiogenesis, we speculate that increased traction forces observed here might recapitulate those required to initiate the formation of new blood vessels in vivo (17). Low flows are also characteristic of pathological conditions such as intracranial aneurysm (10) and atherosclerosis (9); our findings raise the question of whether increases in traction forces might be protective or disruptive in these conditions.

A remarkable feature of our experiments was the heterogeneity of the responses. Heterogeneous responses of ECs to flow have been previously reported (18) in terms of protein and mRNA levels, calcium signaling, and organelle localization. Heterogeneity has been attributed to the topography of the monolayer (19), the heterogeneous location, properties of cytoskeleton elements (20), and flow sensors. Our findings of heterogeneous force distributions might underlie heterogenous responses in signaling and molecular localization through mechanotransduction activity. Whether such activity is dominated by cell-matrix or cell-cell stresses could be elicited based on the differences in the characteristic lengths of the corresponding fluctuations.

In conclusion, we used a new device, to our knowledge, to combine microfluidics, TM, and MSM to assess the mechanical response of ECs to slow shear flow. The observed acute increases in traction generation provide fresh insights into the synergy between flow and the biomechanical reaction of cells, with potential implications in morphogenesis and disease.

Author Contributions

C.M.P., D.L., and X.T. designed the study; C.M.P. implemented the flow chamber and carried out experiments; C.M.P., A.B., and E.B. processed data; C.M.P. and X.T. wrote the article; P.R. calculated shear and gel displacement in the chamber; and all authors discussed and interpreted results and commented on the article.

Editor: Gijsje Koenderink.

Supporting Citations

References (21, 22, 23, 24) appear in the Supporting Material.