Abstract
This feature article reviews the thermal dissipation of nanoscopic gold under radiofrequency (RF) irradiation. It also presents previously unpublished data addressing obscure aspects of this phenomenon. While applications in biology motivated initial investigation of RF heating of gold nanoparticles, recent controversy concerning whether thermal effects can be attributed to nanoscopic gold highlight the need to understand the involved mechanism or mechanisms of heating. Both the nature of the particle and the nature of the RF field influence heating. Aspects of nanoparticle chemistry and physics, including the hydrodynamic diameter of the particle, the oxidation state and related magnetism of the core, and the chemical nature of the ligand shell may all strongly influence to what extent a nanoparticle heats in an RF field. Aspects of RF include: power, frequency and antenna designs that emphasize relative strength of magnetic or electric fields, and also influence the extent to which a gold nanoparticle heats in RF. These nanoparticle and RF properties are analysed in the context of three heating mechanisms proposed to explain gold nanoparticle heating in an RF field. This article also makes a critical analysis of the existing literature in the context of the nanoparticle preparations, RF structure, and suggested mechanisms in previously reported experiments.
Introduction
The interaction of electromagnetic radiation with metal nanoparticles is presently explored for a wide range of applications, such as hyperthermal therapy,1 catalysis,2,3 biomedical contrast,4,5 and waste treatment.6 Nearly every region of the electromagnetic spectrum is examined (figure 1), with some spectral selectivity conferred by particle size and morphology.
Figure 1.

Nanoscopic gold and interactions with the electromagnetic spectrum.
The heating of metal nanoparticles in electromagnetic radiation is investigated with both infrared radiation and radio-frequency/microwave radiation. Nanoparticle-localized heat is used in the nascent field of remote control biology.7 Visible and infrared light can excite surface plasmon resonance in gold nanoparticles, provoking photothermal heating through well understood mechanisms.8,9 In the case of radiofrequency and microwave irradiation of metal nanoparticles, mechanisms of heating are poorly understood. In fact, several reports question both experimentally10–12 and theoretically11,13 whether metal nanoparticles heat in RF or microwave radiation at all.
Radiofrequency is especially desirable in many downstream applications because it penetrates through most non-conductive materials. This property is of course the basis for wireless communication.
Mechanistic insight may allow for more effective heating by revealing the effects of AuNP properties such as size, shape, oxidation state, and magnetic moment, as well as RF characteristics, including relative emphasis of electric (E-field) or magnetic (B-field), field strength, and chosen frequency.
The literature on heating of AuNPs with RF contains experiments with dramatically different RF and nanoparticle properties. In terms of nanoparticles, spherical diameters used range from 1.4nm to 100nm, a size regime over which size dependent physical chemistry evolves markedly. In terms of RF, investigations include RF that emphasizes E-field, RF that emphasizes B-field, and frequencies that range from kHz to GHz. While the higher frequencies used in this literature are technically microwave frequency, we will use RF as a shorthand in this review to encompass experiments done with both RF and microwave frequency radiation.
In this article we distil this complex and contradictory literature into a set of plausible heating mechanisms, and reinterpret much of the historical literature that invoked mechanisms that are now apparently discarded by researchers active in the field.
We first make a brief overview of the history of the field, then review tuneable RF field characteristics and AuNP properties. Then we synthesize this literature, presenting mechanisms and a unified set of mechanistic predictions in terms of particle size and RF nature. Finally we present a critical analysis of the literature in which we reinterpret some older papers in terms of presently accepted mechanisms.
The History of AuNP Heating in RF Fields
Investigation of AuNP heating in RF initially proceeded along two independent lines of research, both of which initially emphasized biological application over mechanistic understanding. The earlier line of research aimed to thermally manipulate molecules with nano-localized heat.14,15 The later line of research focused on hyperthermal therapy of cancer.16,17 These two independent lines of research differed initially in two important aspects. First, in the size (and therefore underlying physical chemistry) of gold nanoparticle used; second, in the nature of the radiofrequency used (in terms of power, frequency and antenna design.) A unified literature emerged recently, where attempts to integrate the phenomena across a wide range of experimental approaches are made.11–13,18,19
The first report of gold nanoparticles heating in a radiofrequency field came from a group led by a trained chemist in the MIT Media Lab. 14 In this landmark work, a 1.4nm diameter commercial Nanogold™ particle in a 0.4 W 1GHz solenoid generated radiofrequency magnetic (RFMF) field could generate localized heat sufficient to melt a covalently attached stretch of hairpin DNA (whose melting temperature was ~35°C) without, apparently, heating the surrounding solution. (Figure 2) An inductive or Joule-type mechanism of heating, with some theoretical support, was postulated to explain the heat. The Joule-type heating arises from inductive coupling, from the applied magnetic field to the metal cluster. This results in creation of eddy currents in the metal cluster, via Faraday induction. The phenomenon is well understood for macroscopic systems, such as transformer or inductor core materials.
Figure 2.
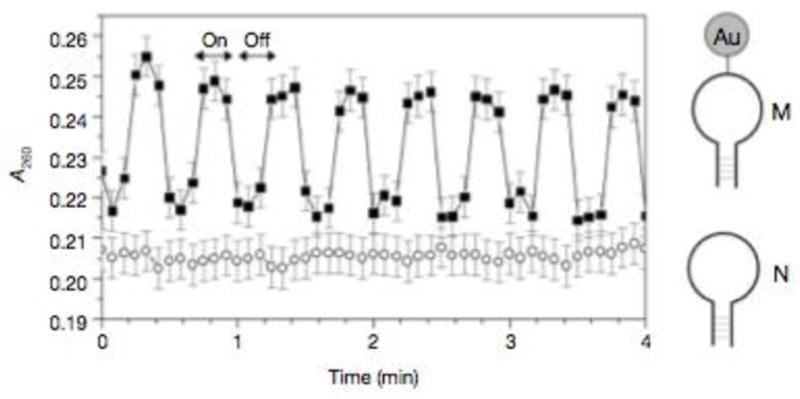
Absorbance at 260 nm (e260) of a solution of M in RFMF (squares). Arrows indicate when the RFMF is on/off. Circles, response of N (no nanocrystals) in RFMF. Gold nanocrystals also show an absorbance increase under RFMF, qualitatively attributed to the change in the optical absorption due to eddy currents. However, the absorbance increases nearly uniformly over 200±300 nm with RFMF and is small relative to the oligo change in absorbance. Reproduced from reference 14.
Experimental follow ups by the authors of this paper are minimal.20 Other direct experimental follow ups that cited this initial report used substantially different experimental conditions,15,21,22 and will be discussed below.
In a set of studies that did not cite initial study of RF interacting with nanoparticles,16,17,23 groups lead by surgeons began investigating the heating of nanomaterials including metal nanoparticles under RF irradiation for the destruction of cancer. RF ablation is used in clinical practice to treat tumours, and academic surgeons familiar with the technique began publishing experiments on the thermal properties of gold nanoparticles in the presence of RF irradiated cells16,17,23. These initial papers focused on killing cancer cells in cell culture and animal cancer models and made use of the so-called “Kanzius Machine” (Therm-Med LLC, Erie, PA).24 The Kanzius Machine generates a capacitively coupled radiofrequency electric field at 13.56 MHz, and is generally operated at higher power output (up to 1000W.) Figure 3 shows an example of the destruction of cultured model cancer cells with RF irradiated gold nanoparticles in the first paper reporting this. All experiments so far reported with the Kanzius machine utilize AuNPs in the 5 – 100 nm diameter regime. While initial reports did not make in-depth investigation of the mechanism for AuNP heating, a subsequent report postulated a Joule-type mechanism of heating,25 similar to the mechanism suggested by the original report of Hamad-Schifferli.14
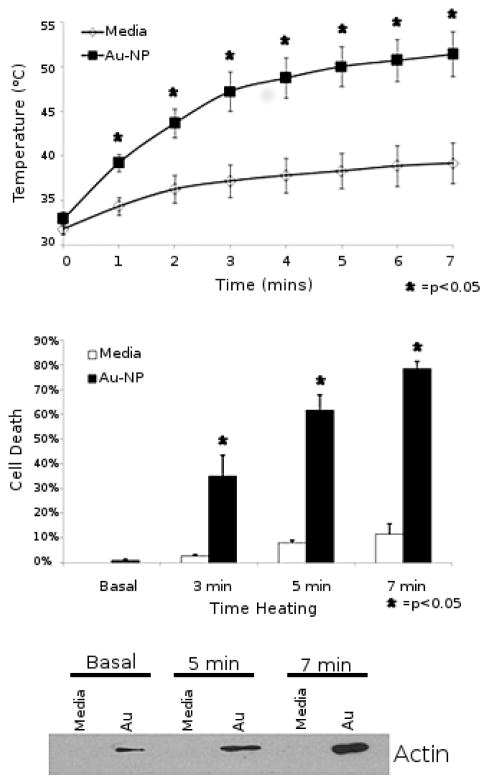
Figure 3.
In vitro cell culture demonstrates effective heating and cell death with Au-NP treated cells in the RF field. A, Temperature of HepG2 cells exposed to 35 W in the RF field in the presence (squares) or absence (diamonds) of Au-NP over a time course. Results reported are the average of 3 separate experiments. B, Percent cell death as assessed by LDH assay of HepG2 cells exposed to 35 W in the RF field for 3, 5 or 7 minutes in the presence (black) or absence (white) of Au-NP. Results reported are the average of 3 separate experiments. C, Western blot for b-actin on the supernatants of HepG2 cells exposed to 35 W in the RF field in the presence or absence of Au- NP for 5 or 7 minutes. Reproduced with permission from reference 16.
Most successive reports of AuNP heating in RF build directly on either the Hamad-Schifferli report14 or use the Kanzius machine. Although a unified literature that attempts to rationalize both experimental starting points has emerged, we suggest (vide infra) that these are potentially different experiments. Technically, they differ in both the nature of the RF and the nature of the gold nanoparticles used. In terms of RF, they are using different RF antenna designs, dramatically different frequencies and markedly different applied power. These lines of research also use different sizes of inorganic gold nanoparticles. All of these experimental modifications may be important in the interpretation of the work (vide infra). Despite all these differences in experimental setup, Joule-type nanoparticle heating was proposed in each case.
The validity of Joule-type heating of metal nanoparticles in RF is questioned on both experimental10–12,26 and theoretical13 grounds. One study attributes the observed heating to Joule-type heating not of nanoparticles but of surrounding electrolytes, observing that when particles are dissolved in rigorously deionized water, little to no heat is observed.12 Other experimental studies conclude that they cannot reproduce the amount of nanoparticle attributed thermal dissipation reported by others.10,11,26 Theoretically, Joule-heating is difficult to reconcile with nanoparticles of the size used in these experiments.13
Two novel mechanisms for nanoparticle heating in RF emerged after the reports disputing the possibility of Joule-type heating. Two groups show both experimentally and theoretically that an electrophoretic mechanism can account for heat attributable to nanoparticles.27,28 This mechanism becomes prominent when for nanoparticles 10nm in diameter or smaller.27 We also recently found that an unexpected magnetic mechanism can account for heating of sub 2 nanometre diameter nanoparticles.19 Furthermore, the question of the role of salts in heating is complicated by recent reports. Some reports suggest that dissolved salts enhance the heat that is attributable to nanoparticles.19,28,29 In addition, a recent report highlighted that the shape of a vessel that holds the nanoparticles in an RF field is a critical and previously unrecognized component in whether heat attributable to particles is observed.30 The interest and importance of some of these previously unrecognized experimental aspects was highlighted in a Science perspective18.
Thus, the history of gold nanoparticles heating in RF is one in which technically quite different experiments produced results that were attributed to the same underlying phenomenon—joule heating. Today, Joule heating as a mechanism for heating is essentially dismissed, even by research groups that previously attributed their heating to that mechanism.27 It is now also questionable whether any spherical AuNP larger than 10nm does heat in RF. As a not-very-unified field of inquiry, current interest lies in deciphering which mechanisms produce heating under different experimental conditions, as well as elucidating the role of salt solutions.
The area of study, as it has emerged, is highly interdisciplinary, with groups lead by disciplinary chemists, 19,20 surgeons,16,17 electrical engineers,31 and physicists10 all making contributions, often in multidisciplinary teams. Straightforward comparison of results reported by different groups is confounded by different RF properties, different particle formulations, and different reporting rubrics for disclosing how much heat dissipation is attributable to nanoparticles.
To enable a critical analysis of the heating of metal nanoparticles in RF, we review nanoparticle structure and RF, focusing especially on the aspects of nanoparticle structure that may contribute to heating in RF. Following this introduction to the components in the system, we will summarize each of the mechanisms hypothesized so-far to contribute to heating. After reviewing these components of the phenomenon, we make a critical analysis of the field as it stands and its prospects in the future.
The Mystery of Hot Gold Nanoparticles in RF
A debate is open regarding whether gold nanoparticles heat in an RF at all, and if AuNPs do heat in an RF, what is the mechanism? There are three mechanisms proposed in the current literature: Joule or inductive heating, magnetic heating and electrophoretic heating. Each mechanism has a strong dependence on the frequency of the applied RF and the diameter of the nanoparticle. Which mechanisms dominate heating may depend on the exact experimental setup, with parameters of the RF field character and nanoparticle formulation both playing a role.
Physical Properties of Gold Nanoparticles
The early literature on RF heating of AuNPs assumes that very small pieces of gold (with diameters between 1 – 100 nm) behaves as bulk gold.14,25 This possibly erroneous assumption motivated original hypotheses of induction heating. Research on the size-dependant physical properties of AuNPs reveals profound physical insights into the size and morphology dependant evolution of physical properties. In the 1–3 nm diameter size range, even the exact number of gold atoms and electrons strongly effects stability,32–34 electronic and optical properties,35–37 and magnetism.38,39
Many of these properties, including molecular vs metallic behaviour, magnetic behaviour and net charge may strongly influence interactions with RF. To fully account for gold nanoparticle interaction with RF fields, we enumerate the properties of nanoscopic gold that may allow interaction with the RF field under each mechanistic consideration. Figure 4 shows the chemical construction of a gold nanoparticle as an inorganic core and a ligand shell. As we will show below, the nature of both the organic and inorganic parts play a role in the mechanism of gold nanoparticle heating in RF.
Figure 4.
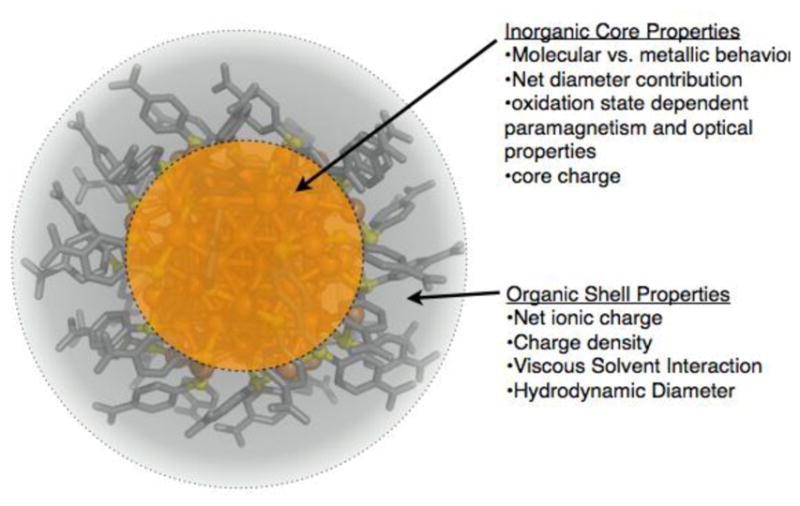
Illustration of the core and organic ligand shell of Au102(SR)44 nanocluster. The properties that are enumerated as belonging to the core or the ligand shell are generalizable to other sizes. Each of the enumerated properties may affect heating under one or more of the mechanistic considerations.
Structure
All of the AuNPs used in RF interaction studies are protected by an organic shell, which stabilizes the AuNPs against aggregation and sintering and solubilizes AuNPs in solvent. The organic ligands that stabilize the clusters used in reported studies are organophosphines, organothiolates, citrate, or proprietary commercial ligands of unknown composition. These ligands are generally present early in the synthesis and both control the size of the resulting particle and stabilize the particle against reversible and irreversible aggregation or sintering.
Ligand Shell
The ligand shell encodes two properties of potential importance for RF heating mechanisms: charge and thickness. Water-soluble AuNPs used universally in RF studies so far have carboxylic acid terminated ligand shells, conveying (ionic) charge and charge density to AuNPs. The interaction of this negatively charged ligand shell with RF is suggested as important in electrophoretic heating.27,28 The other property of the ligand shell of potential importance is the “monolayer thickness” of the ligand shell, which plays a key role in the electrochemical properties of clusters,35,37,40 as well as influencing hydrodynamic diameter. As discussed below, electrochemical properties and paramagnetism are tightly linked.
Inorganic Core
The range of sizes of spherical AuNPs that are studied for RF heating lie on the ‘molecular to metallic continuum’, meaning that the physical chemistry of the smaller particles tested for RF heating is very different than that of the larger particles tested for RF heating. The particle size at which transition from molecular-to-bulk or metallic like behaviour is not discrete, and depends on which properties are considered. Properties that evolve dramatically in this size regime include electrochemical,35 optical (notably plasmon emergence) and collapse of the HOMO-LUMO gap,41 and mechanism of stabilization.32
Mechanism of stabilization for metal nanoclusters is understood as either electronic or geometric, where electronic stabilization is favoured for smaller nanoclusters and geometric stabilization for larger.34 In the case of ligand protected gold, Au11(PPh3)7Cl3, Au25(SR)38, Au38(SR)24, Au39(PPh)14Cl6−, Au102(SR)44 among others are understood as electronically stabilized, as substantiated by generally low symmetry and conformance to electron counting rules.32 For the larger clusters Au144(SR)60, Au333(SR)~80 and Au~530(SR)~100, 42–44 structures are not yet available and the role of superatom orbitals is not fully defined. For instance, in the case of Au144 and Au333, geometrically perfect models are proposed,42,44 and yet evidence in each case for presence of superatom-type orbitals persists. 42,45
Electronically Stabilized (Superatom) Nanoclusters
The ‘superatom’ concept is useful in explaining both what is meant by ‘electronic stabilization’ as well as some of the stability, reactivity, and magnetic properties of electronically stabilized clusters. To make the simplest explanation of the superatom concept, recall that the total filling of electron shells in atoms results in the well-known noble gas stability. Thus, the total filling of 1s | 2s 2p | 3s 3p | 3d 4s 4p| electron shells implies a ‘magic number of electrons’ for noble-gas-like stability of 2, 10, 18, 36, … For metal clusters in the gas phase, which may be in the simplest case considered as a collection of positive charged nuclei in an approximately spherical shape, interacting with electrons, the accepted (simple) treatment is the Schrodinger equation solved for a spherically symmetric square well potential. This gives the electron orbitals 1S | 1P | 1D | 2S | 1F | 2P 1G | etc, giving magic numbers of electrons of 2, 8, 18, 20, 34, 40, 58, to arrive at clusters of special stability.32,34,46
Superatom stabilization concepts were first adapted for gold nanoclusters (ligated by phosphines and thiolates) in 2008, following the crystal structure of Au102SR44.32,47 The atomic structures enabled DFT calculations that showed that the relatively simple predictions of the superatom model are confirmed by all-electron DFT calculations which reveal that the frontier orbitals of Au102(SR)44, Au39(PR3)14X6−, Au13(PR3)10X23+, and Au11(PR3)7X3 have dominant angular momentum character and degeneracy predicted by simple application of the superatom theory. Later work showed the success of superatom theory in predicting the stability of other crystallographically resolved gold clusters.48–50
So far, superatom theory is used primarily to explain the special stability of apparently stable clusters, as resulting from a noble-gas-like superatom electron configuration. The effects of ‘open shell’ electron configurations are only recently beginning to be investigated explicitly. The “superatom electron configuration” of a gold nanocluster can be modified through well-established electrochemical methods.33,35 These modifications can influence magnetism of AuNPs.
Larger Nanoparticles
The practical preparation of well defined (in terms of molecular formula and atomistic structure) nanoparticles larger than Au~530(SR)~100 (approximately 2.5 nm inorganic diameter) is the current frontier of research. There is some debate about the isolability of exactly defined particles larger than the currently identified upper limit, as the energetic differences between ‘highly stable’ numbers of atoms and less stable numbers of atoms become small. In this ‘metallic materials regime’ the inorganic portion of nanoparticles are characterized in terms of size (usually diameter for spherical particles) and dispersity, where a commonly used definition of ‘monodisperse’ allows for 10% standard deviation in a collection of particle diameter measurements. There is little evidence for superatomic orbitals in particles larger than 2.5nm diameter. Such electronic structure is now well established for particles 1.5nm in inorganic diameter (i.e., Au102(SR)44) and smaller.
Magnetism in Gold Nanoparticles
Magnetism in AuNPs is of importance for AuNP heating in RF, since the magnetic moments of the cluster may interact with the magnetic portion of the applied RF field to produce heat. However, magnetism in gold nanoparticles is poorly understood, with the literature rife with results that are not repeated across other labs or even within the same lab, as highlighted in a recent review.38
The oxidation state dependence of paramagnetism, however, is increasingly well established in the case of Au25(SR)18. In this case, the majority of magnetism measured can be attributed to the superatom nature of these small clusters.
From a superatom perspective, Au25(SR)18−, which is the most stable redox state of the cluster,32,33 is an 8e− system, corresponding to the total filling of the 1S and 1P superatom orbitals. Multiple reports now use EPR, SQUID and redox chemistry to compare the anionic and neutral forms of Au25(SR)18x (where x= −1, 0 and +1) and these reports conclude universally that the anion is diamagnetic and the neutral compound paramagnetic.39,51,52 This is consistent with the superatom theory predicted doublet state.
The picture is somewhat murky for the Au25(SR)18+ cluster. Naïve superatom theory predicts a triplet spin state for the Au25(SR)18+ compound, but the cluster may also distort to adopt an singlet state. Experimentally both paramagnetic and diamagnetic Au25(SR)18+ are reported.52,53 Thus it is not perfectly clear if the assumptions of naïve superatom theory hold with regard to spin multiplicity of highly oxidized species. Our results for Au102 suggest the latter possibility, that spin multiplicity of superatoms might increase until the orbital is ½ filled.19 This area of research, however, is not settled science. The role of the ligand shell in enforcing core symmetry, underlying flexibility of the gold core allowing Jahn-Teller like distortions, and instability of clusters charged to large charge states may all contribute to the effect of oxidation on magnetism.
Radio Frequency Field Background
RF is nominally electromagnetic radiation with frequencies between 1/2 MHz to 500 MHz. Above 500 MHz frequency is the beginning of the microwave region. The behaviour of macroscopic pieces of metal (conductors) in RF circuits acting as loads is well understood and can be robustly modelled. But parasitic elements must be incorporated in models to account for capacitive coupling. Nevertheless, there remains, a substantial element of ‘art’ in RF circuit modelling; In short, quantitatively, models vary with metal cluster environments and changing parasitic components in the RF model of the loads circuit.
Three primary characteristics of an RF field determine the thermal dissipation of a ‘piece of metal’ in the near field: (1) The applied frequency of the RF fields (usually reported in Hz); (2) The magnetic or electric emphasis of the field (determined by the inductive or capacitive antenna design) and (3) the maximum power of the RF field.
The behaviour of nanoscopic pieces of metal in both near fields (where RF B fields dominate) and far RF fields (where B and E fields both play roles) remains poorly understood. There is presently not sufficient data in the literature to enable improved understanding, which we aim to address by calorimetric means of quantifying heat adsorption versus location from the antenna and from frequency variations of the RF field. The present literature contains sparse systematic investigation of field composition (B- vs E-) and gleaned not from a single report but by comparing multiple reports. The effect of RF frequency on thermal dissipation is studied theoretically13,27, but there are no experimental reports of frequency dependence effects.
Mechanisms that Contribute to AuNP Heating in RF
There are three mechanisms discussed in the literature for heating of AuNPs in RF. Here we review each mechanism, and how it quantitatively interacts with the particles. We also synthesize a comparison of how the expected thermal dissipation of each heating mechanism pathway changes as either frequency or particle size change.
Magnetic Heating
Magnetic heating is relevant in the case of gold nanoparticles because tailored gold nanoparticles can be magnetic.19,38,39 For the magnetic moment of a nanocluster to interact with an external alternating magnetic field to produce heat, two mechanisms may be considered. One mechanism, Brownian or viscous heating, assumes that the entire magnetic particle rotates to follow the directed and time varying alternating magnetic field (RFMF).54 The resulting viscous friction between the particle and the supporting solvent manifests as heat. The other mechanism considered, Néel relaxation,55,56 occurs in media where the magnetic moment of the particle realigning with the magnetic field occurs without the particle rotating. Both mechanisms produce heat, but the fastest mechanism of relaxation dominates54.
The Brownian power dissipation (P) of a suspension of magnetic particles rotating in response to a magnetic field depends on several experimental variables. These include the size or volume of the individual particles, the concentration of the particles in solution (i.e, volume fraction) how magnetic the particles are, the magnitude of the magnetic field, the viscosity of the solvent, and the frequency of the RF.
The interaction of each of these experimental variables in as they relate to power absorption (and subsequent generation of heat) was quantified theoretically by Rosensweig in the following equation54:
| (1) |
where and . Here V is the particle volume, Md the particle magnetization, η the dynamic shear viscosity of the solvent, kBT is the thermal energy, B is the magnetic field, φ is the volume fraction of the particles, and ω is the angular frequency which depends on the frequency of applied RF.
In contrast to Brownian dissipation of power, Néel dissipation does not depend on solvent viscosity, since Néel relaxation occurs in a stationary particle. The Néel relaxation times depend on the ability of the magnetic moment of the particle to rotate within a fixed particle. These times are described by the following equation:
| (2) |
Where τ0 is the attempt time (~10−9 s), K is the anisotropy energy density and V is the magnetic volume.54 Here the magnetic volume is used because it’s assumed that the majority of the magnetic response comes from the core with little contribution from the presumably diamagnetic ligands.
Since the Brownian and Néel relaxation processes happen in parallel, Néel relaxations can be included in equation (1) by taking the harmonic average of the two relaxation times: 54
| (3) |
This gives a better approximation of heating rates from equation (1) but also requires more involved calculations with approximations of the size-dependent anisotropy constant, and the attempt time. Therefore we do not include Néel relaxations in our current models.
The fact that the relaxation mechanisms depend on different factors may allow for investigation of the heat produced by changing the relaxation times. The viscosity of the solvent is varied by changing the Brownian relaxation time. Many studies investigating the relationships between the relaxation times and heat generation for macroscopic size superparamagnetic iron oxide particles have been conducted over the past few decades.57 We can tailor the Brownian relaxation time of our nanosize particles by changing the ligand coating, which impacts the hydrodynamic volume. The Néel relaxation times are more difficult to change without also changing the Brownian times.
Electrophoretic Heating
Most soluble AuNPs incorporate a net ionic charge, which depends on both the charge of the inorganic core and the charge of the ligands that passivate the particles against sintering. Commercially produced and water-soluble laboratory syntheses generally produce particles with a net negative charge. Charged particles migrate in an applied electric field toward their complementary charge. In an alternating electric field, charged particles will follow the alternating electric field. The absorption of power as a result of this electrophoretic movement is described by the dielectric constant. The dielectric constant has real and imaginary components, with the imaginary component containing any variables affected by experimental parameters. The imaginary component corresponding to the power loss is quantified by Sassaroli28:
| (4) |
Where and β = 6πηa. Here q is the particle charge, η the dynamic shear viscosity of the solvent, E is the electric field strength, ρ is the particle density, φ is the volume fraction of the particles, and a is the radius of the particle. As in magnetic heating, this mechanism depends on variables that we test experimentally, including AuNP net charge, AuNP particle density, AuNP volume fraction (modifiable through size of ligand shell), and frequency.
Inductive (or Joule) Heating
Several early papers attribute gold nanoparticle heating in RF to Joule-type or inductive mechanisms.14,15,25. However, the tiny area that nanoclusters present to the applied magnetic field attenuates such eddy current effects.
The frequency dependence of inductive power absorption by a suspension of conductive spheres is given by Smythe58:
| (5) |
where and . Here a is the particle diameter, σ the particle conductivity, μ the partice permeability, μ0 the permeability of the solvent, ω the angular frequency, Φ the particle volume fraction and B the magnetic field strength. As highlighted by Hanson13 and Sassaroli28, we also calculate that direct inductive heating proves much too small to rationalize the thermal dissipation for the size of particles used in the literature, even when plasmon and surface roughness are considered.
Comparative Modelling of Potential Heating Mechanisms
The main goal of the modelling exercise was to determine if different heating mechanisms should be experimentally distinguishable. To compare the how the heating rate that results from each considered mechanism changes as a function of experimental parameters, we modelled the mechanistic dependencies on both nanoparticle size and frequency of RF (fRF). We used Mathematica to model the expected heating rate of each mechanism based on equations 1, 4 and 5 above. Due to the magnitude of this modelling exercise we made some simplifications that are not perfectly realistic in the experimental case, and we detail these below. We also did not include Néel relaxation (equation 2) in the present exercise, although it is almost certainly important.
Figure 5 shows expected heating rate as a function of particle radius for the three mechanisms represented by equations 1, 4 and 5. The Y axis of heating rate is given as units of power (Watts) normalized by B2, m3 and φ. This normalization is necessary so that heating rates can be compared without imposing explicit B-field and volume fraction values.
Figure 5.
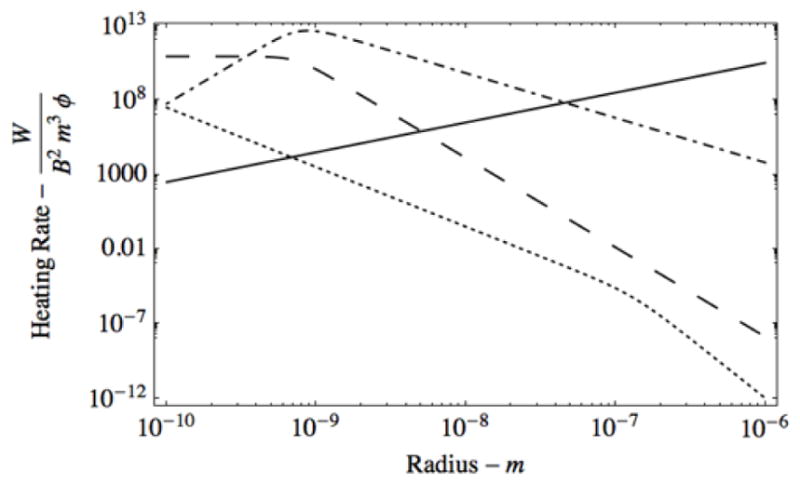
The plots of heating in vs particle radius (in meters) at 13.56 MHz for induction (solid line, equation (5)), superatom (large dash, magnetic heating from equation (1)), ferromagnetic (dash-dot, magnetic heating from equation (1)) particles, and electrophoretic (dot, from equation (4)). The electrophoretic dissipation is normalized by f E2 and scaled to fit on this graph.
The heating dependencies in this figure are varied only with AuNP diameter. Thus, the falloff in heat dissipation for the electrophoretic and magnetic mechanisms is accounted for in-part by the effective dilution of a fixed amount of charge or unpaired spin over a larger and larger volume.
Figure 6 shows the expected heating rate as a function of the fRF for the three mechanisms represented by equations 1, 4 and 5. The Y axis in figure 6 is the same as in figure 5. For the inductive mechanism that drove initial work14,25 heat varies with fRF squared. In the electrophoretic mechanism27,28 heating saturates and then falls off with varying fRF. In the Brownian relaxation (magnetic) mechanism highlighted in our recent work19, we model a sublinear dependence on fRF.
Figure 6.
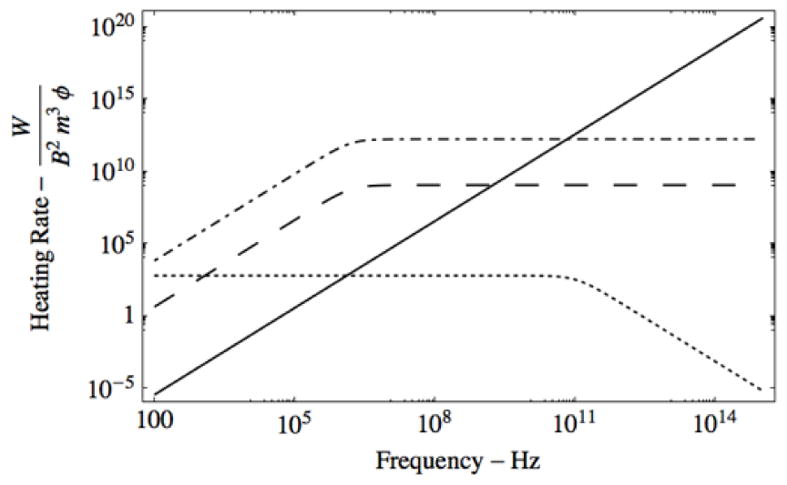
The plots of heating in vs frequency in Hz for 1.5 nm gold particles for induction (solid line, equation (5)), superatom (large dash, magnetic heating from equation (1)), ferromagnetic (dash-dot, magnetic heating equation (1)) particles, and electrophoretic (dot, from equation (4)). The simple electrophoretic model shows the effect of inertia reducing the loss at high frequency.
In figures 5 and 6 we considered two cases for the magnetic heating of equation 1: The heating of a ‘superatom’ and the heating of an ultra-small paramagnetic iron oxide (USPIO) of the same radius. The ‘superatom’ heating assumes the best-possible case for a superatom—that of a ½ filled G orbital in Au102(SR)44, giving 9 unpaired electrons. An USPIO of the same radius has less magnetization- and therefore typically less magnetic heating-- because the electron spins in magnetic iron oxides smaller than 3nm are typically not well ordered.59
Thus, the mechanisms should be experimentally distinguishable, and we expect that a unified picture of AuNP heating in RF may emerge that combines contributions from each mechanism or perhaps presently unconsidered mechanisms. To our knowledge, figures 5 and 6 contain the first simultaneous examination of frequency and nanoparticle size dependence of these mechanisms.
Heating of Salt Solutions
(Joule-type) heating of saline solutions is well known to occur. In this literature, it is shown that multiple antenna designs are capable of heating simple saline solutions at 13.56MHz, 12,19 presumably through Joule-type heating. Some reports that dismiss RF heating of AuNPs, suggest that all of heating previously attributed to gold nanoparticles can instead be attributed to joule-type heating of saline.12,13
The role of salts in particle heating may be the most unresolved aspect of thermal dissipation by gold nanoparticles in RF. Given the presence of relatively high concentrations of dissolved salts in biological tissues, and the interest in using this approach in biological systems, elucidating the role of dissolved salts in RF heating with and without nanoparticles is of high importance.
Biological applications so-far drive the majority of research into RF heating of gold nanoclusters. In these applications a complex background that necessarily contains salts is present. Understanding of how that complex background affects salt based heating is a missing link in this literature.
Other investigations suggest experimentally or theoretically that dissolved salts enhance heat transfer from the RF field to the gold nanoparticles.19,28,29. One study assesses several mechanisms of heating and concludes that most likely heat generation is due to concentration of the electric field at the surface of a nanoparticle.29 Therefore, the removal of ions and thus the conducting medium diminishes this mechanism. We also previously suggested a cooperative effect between saline and nanoparticles. Specifically, we observed upon exposure to RF, solutions of nanoparticles + salt produce notably more heat than either species alone.19 A study of electrophoretic heating mechanisms also supports cooperative effects for salts.28
In salt-containing systems more complex than saline solutions, several reports show nanoparticle dependent tumour treatment in a complex biological background. 16,60 Background heating of physiological saline is not noted and would be catastrophic if it occurred.
We show here explicitly that the heating of salts in setups that minimize ion-mobility, such as biological tissues may be minimal, even while the heating of salts in simple saline solutions is significant. We show this for both a large molecule (a dendrimer), and a biological tissue model.
PAMAM dendrimers are large simple molecules with a number of carboxylic acid groups that doubles with each “generation.”61 We hypothesized that we could interrogate the effect of free ions in this system by comparing the response of equivalent number of ions as either “free” simple ions or large polyionic molecules. In our experiments, we used a generation 3 dendrimer with 23+2 = 32 carboxylic acid functional groups and a molecular weight of 6909 g/mol. When dissolved at a concentration of 140μM, the concentration of ions is equivalent to free ions at 4.4mM.
We compared the heating response of such a 140μM solution of a generation 3 PAMAM dendrimer that is dialyzed against NH4OH to the heating of a 4.4mM solution of NH4OH. The results of this comparison are shown in Figure 7. The macromolecular nature of the counter ion in the dendrimer appears to substantially suppress heating compared to the ‘free ion’ case. We showed similar heating of ‘free ions’ in a previous report.19 This suggests that the ions must be ‘free’ in order to contribute maximally to salt based heating.
Figure 7.
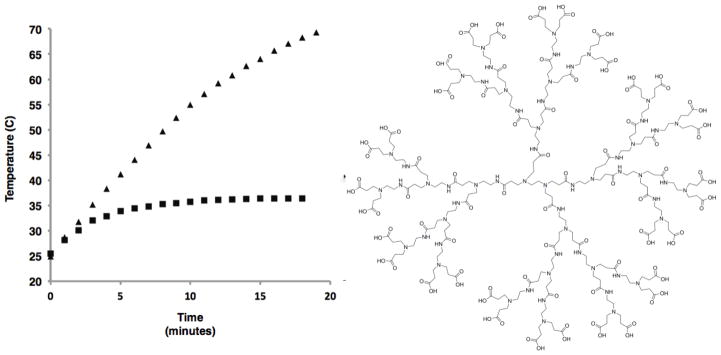
Left panel shows the time dependent thermal response of a solution containing PAMAM dendrimer (squares) and another solution containing an equivalent number of ammonium hydroxide ions (triangles). In the PAMAN solution the dendrimer concentration is 140μM, thus the concentration of carboxylic acid groups is 4.4mM and in the other solution total concentration of free ammonium ions is 4.4mM. The heating of this solution is compared to the heating of a 4.4mM solution of ammonium hydroxide. The right panel shows a Lewis diagram of the dendrimer used in this experiment.
The PAMAM dendrimer adds only a small amount of complexity to the system compared to a simple salt solution. Tissues are inordinately more complex than the PAMAM dendrimer, yet contain physiological amounts of salt. Food based models, such as chicken breast, are sometimes used as an inexpensive model of tissues.62 Figure 8 shows the time-dependent heating response of chicken breast in a 13.56 MHz 50 W solenoid generated B-field. This piece of complex tissue, which contains ~150 mM NaCl, shows no apparent thermal dissipation. We showed earlier that oxidation of Au102(SR)44 substantially increases thermal dissipation for this compound. Figure 8 shows that the effect is preserved even in the complex matrix of biological tissue.
Figure 8.
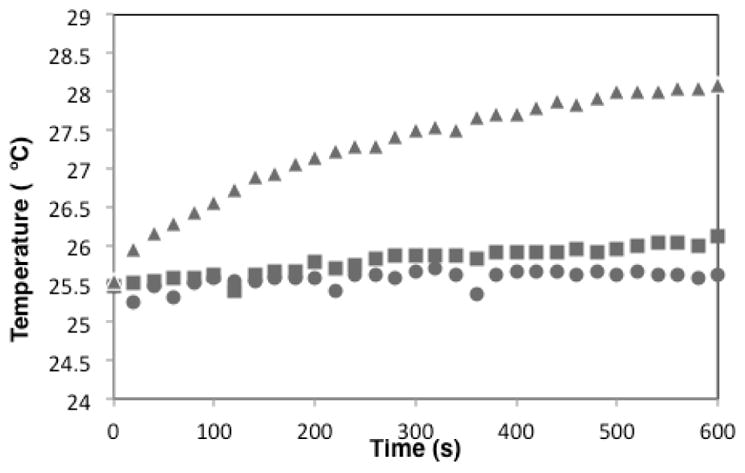
Samples of chicken muscle exposed to RF before soaking in Au102(SR)44 (circles), after soaking in Au102(SR)44 (squares) and after soaking in oxidized Au102(SR)44 (triangles).
In summary, the role of salts in radiofrequency heating of gold nanoparticles is unclear. Salts clearly confounded some earlier experimental interpretations of nanoparticle heating in simple solutions.12,25,27 It appears, however, that salts in biological systems may not contribute to background heating, perhaps because they are comparatively immobile. Background salts may help elicit the maximum amount of thermal dissipation from metal nanoparticles immersed in RF fields.28,29
Critical Assessment of the Heating of Metal Nanoparticles with Applied Radio Frequencies
Twenty-five papers so far examine the heating of gold nanoparticles in RF (Table 1). Five of these papers challenge some aspect of gold nanoparticles heating in RF,10–13,26 if not dismissing the entire phenomena. Parsing this controversy is complicated, because of differences in experimental approach that include frequency, antenna design, and nanoparticle preparation. We categorize the literature in terms of antenna design used in each experiment, as this commonality allows facile comparison of reports made with the same antenna design. Table 1 also organizes the literature secondarily according to the diameter of AuNPs reported.
Table 1.
Summary and comparison of reports of RF and microwave heating of AuNPs. Many reports do not report specific absorption rate and do not include enough data for independent calculation.
| Antenna Design
|
Operating Frequency
|
Operating Power
|
Particle Diameter
|
Application
|
Reference
|
SAR
|
|---|---|---|---|---|---|---|
| Kanzius | 13.56 MHz | 200 – 800 W | 5 nm | Cancer Hyperthermia | 17 | - |
| Kanzius | 13.56 MHz | 600 W | 5 nm | Cancer Hyperthermia | 23 | ~300 kW/g |
| Kanzius | 13.56 MHz | 600 W | 5 – 250 nm | Mechanistic Study | 25 | 380 kW/g |
| Kanzius | 13.56 MHz | 25 W | 5 – 200 nm | Mechanistic Study | 12 | 50nm; 8*10–17 W/AuNP |
| Capacitively Coupled | 13.56 MHz | 125 W | 5 – 50 nm | Cancer Hypertherma | 31 | 5nm, 356 kW/g |
| Kanzius | 13.56 MHz | 100 – 950 W | 5 – 50 nm | Mechanistic Study | 27 | 5nm, 1.82 W/kg 10nm, 1.24 W/kg |
| Kanzius | 13.56 MHz | 600 W | 10 nm | Cancer Hyperthermia | 64 | - |
| Kanzius | 13.56 MHz | 600 W | 10 nm | Mechanistic Study | 70 | - |
| Kanzius | 13.56 MHz | 10 – 100 W | 13 nm | Cancer Hyperthermia | 16 | |
| Kanzius | 13.56 MHz | 200 – 250 W | 20 nm | Cancer Hyperthermia | 66 | |
| Kanzius | 13.56 MHz | 200 W | 20 nm | Cancer Hyperthermia | 65 | |
| Kanzius | 13.56 MHz | 25 W | 100 nm | Mechanistic Study | 30 | |
| Theoretical E-field | 13 MHz | Not Applicable | 20 nm | Mechanistic Study | 13 | |
| Capacitively Coupled E-field | 13.56 MHz | 125 W | 5 – 50 nm | Cancer Hypertherma | 31 | 5nm, 356 kW/g |
| Solenoid | 1GHz | 0.4 – 4W | 1.4 nm | DNA Melting | 14 | - |
| Solenoid | 600 – 1000 kHz | Not reported | 1.4 nm | Mechanistic Study | 10 | - |
| Solenoid | 1 GHz | 1.5 W | 1.4nm | Aptamer Control | 67 | - |
| Multiple | 13.56 MHz | 50 W | 1.5 nm | Mechanistic Study | 19 | 9.1 W/g |
| Solenoid | 100 KHz – 100 MHz | 100 W | 7.8 nm Fe Doped | Mechanistic Study | 20 | 1.84 W/g @ 40 MHz |
| Resonating Chamber | 12 GHz | 0.1W | 10 nm | Amyloid Dissolution | 15 | 989 W/g |
| Not Reported | 12 GHz | 0.1 W | 10 nm | Amyloid Dissolution | 22 | 989 W/g |
| Resonating Chamber | 10 MHz – 50 GHz | 0.1 W | 12.5 nm | Amyloid Dissolution | 21 | - |
| Microstrip Waveguide | 13.56 MHz | 600W | 15 nm | Mechanistic Study | 11 | |
| Microstrip Waveguide | 13.56 MHz | 600 W | 10 – 30 nm | Mechanistic Study | 26 | - |
In terms of antenna design, capacitively coupled designs and solenoid antennae dominate the literature, accounting for 19 of the 24 reports. 11 of the reports use the commercial Kanzius machine. There are 5 reports of solenoid generated RFMF, from 5 different labs. Other designs used that have not been adopted outside of a single lab include resonating chambers and microstrip waveguides, with unclear emphasis of B- or E- field. What these entire reports share in common is the examination of thermal dissipation of small pieces of gold in radio or microwave-frequency irradiation.
Capacitively Coupled Antennae
There are 13 reports using capacitively coupled electric fields, coming from a 4 different research groups. An apparent catalyst for this work was a cancer patient and retired radio-engineer, John Kanzius, who began working with academic surgeons to develop technology for non-invasive nanoparticle/RF based cancer hyperthermia.24 One of the products of this collaboration is the Kanzius Machine, a capacitively coupled RF antenna. This instrument generates 13.56 MHz RF. The frequency is presumably chosen because it is in the industrial/medical frequency band, not regulated by the Federal Communications Commission (FCC). Industrial 13.56 MHz RF plasmas are commonly used to process semiconductor wafers and for RF-based surgical practices.
Early work with the Kanzius machine focused on cancer hyperthermia in both tissue culture and animal models, with some apparent success.16,17,23
In response to the suggestion that gold nanoparticles do not heat, a novel electrophoretic mechanism was proposed.27,28 This electrophoretic mechanism empirically fails to heat nanoparticles larger than 10 nm in diameter.27 The theory for electrophoretic heating also predicts more heat than is yet observed for this system, meaning the system is not completely understood. Nonetheless, the heating appears real and independently confirmed among 3 labs. Notably, though, the heat observed for simple solutions of gold nanoparticles is much less than observed in earlier work with the Kanzius machine. This is most easily noted by comparing reported Specific Absorption Rate (SAR) values in recent and older papers (Table 1).
Early papers with the Kanzius machine reported SAR values on the order of 300,000 W/g (Table 1). More recent mechanistic work reports SAR values on the order of 2 W/g.27 The more recent SAR value is on carefully desalted material and is concordant with the SAR value we reported in a different experimental setup of 9.1 W/g. A complete comparison of SAR values across this literature isn’t possible because while reporting of SAR values is widespread for the heating of magnetic iron oxides in RF, but is not universally reported in the gold nanoparticle heating literature.
Much of the earlier literature with the Kanzius machine must be reinterpreted then. SAR values larger than ~100W/g currently seem unrealistic, and the heating of AuNPs larger than 10nm, as reported in previous papers, is an experimental result that is difficult to reconcile with current understandings.16,25,31,63–66 Thus some of the early work may be artifactual, for instance attributing heating to particles that may be more appropriately attributed to saline.12,13
In summary, heat attributable to nanoparticles in Kanzius machine generated RF appears real when AuNPs are smaller than 10 nm in diameter. The Kanzius foundation website reports that the approach is moving forward into large-animal preclinical trials, suggesting that the approach has proven effective at treating cancers in tissue culture and small animals.71a
Solenoid Generated RF Fields
There are 5 reports examining AuNPs heating in solenoid based antennae, from 5 different research labs.10,14,19,20,67 Three of these reports examine the heating of the commercial product Nanogold™,10,14,67 a 1.4 nm cluster suggested as Au69(PR3)20Cl12−121,68,69. One report examines the heating of iron-doped magnetic gold nanoparticles.20 One report examines the heating of Au102(SR)44.19 Notably, except for the iron doped 7.8 nm nanoparticle—which is an outlier in having iron content -- all of the nanoparticles used in solenoid based experiments are 1.4–1.5 nm in diameter, and significantly smaller than the nanoparticles used in Kanzius machine based experiments, the smallest of which are 5 nm.
Four of the papers attribute heating to nanoclusters in RF,14,19,20,67 while one paper fails to observe heat attributable to nanoparticles.10 In aggregate, this literature is surprising in that there is very little direct experimental follow-up to a very prominent and widely cited Nature paper.14 The absence of direct experimental follow-up suggests some difficulty in reproducibility. In the report that fails to observe heat, Gupta and Kane examined local temperature of Nanogold™ conjugated to CdSe quantum dots (QD). They suggested that even subtle temperature changes at the nanocluster surface should induce a measureable change in fluorescence due to the close proximity of the gold cluster to the QD, and they fail to observe the change in fluorescence that they do observe for iron oxides which undoubtedly heat in RF. The frequency used in this report – 1000 kHz is lower than in others (13.56 MHz, 1 GHz), which could possibly account for the observational difference, but otherwise the report appears robust.
Another possible explanation for the small number of direct experimental follow-ups to the original paper, as well as the failure to observe heat in one report, may lie with the oxidation state and therefore magnetism of the clusters. In one case, the gold nanoparticles are iron doped explicitly to make them magnetic, and indeed this work represents a bridge between the SPION literature.20 In all other cases, with both Nanogold™ and Au102(SR)44, it is likely that the underlying superatomic structure is that of a 58e− superatom.32,47,68 It is known that ambient atmospheric oxygen is sufficient to oxidize diamagnetic Au25(SR)18−1 to Au25(SR)180 which is a superatom paramagnet.33 We showed that heat attributable to AuNPs is qualitatively related to oxidation state and resulting paramagnetism for Au102(SR)44.19 We suggest that serendipitous oxidation, likely with atmospheric oxygen dissolved in the aqueous buffer that the Nanogold™ is dissolved in, may render this compound paramagnetic and capable of heating in an RFMF. This aspect of Nanogold™ heating in RF may help explain the small number of follow-up reports and also the failure to observe heat in one of the follow-up reports.10
Other Antenna Designs
One research group has reported on resonating chamber antennae, operated primarily in GHz frequency ranges for the explicit purpose of dissolving amyloid aggregates implicated in neurodegeneracy, specifically Alzheimer’s disease.15,21,22 Another research group has made fundamental inquiry into the nature of nanoparticle heating using microstrip waveguide antennae.11,26 Neither of these strategies are reproduced by other research labs.
The use of a resonating chamber antenna to heat 10nm AuNPs is inspired directly by the original report of DNA melting. These studies, however, use larger particles, different frequencies, and different antennae compared to the original report, making direct comparison difficult. These studies do report SAR values of ~989W/g, which is a much larger SAR value than is observed in more recent and carefully controlled experiments (Table 1).
This work was always clearly aimed at the applied goal of dissolving the amyloid aggregates that are a central feature of Alzheimer’s disease. These authors note in their later works, citing the works of others in amyloid research, that dissolving amyloid aggregates may actually aggravate the disease, as a dissolved aggregate produces several new nucleation sites for formation of additional aggregates. In other words, dissolving aggregates does not neutralize them, and may accelerate the disease process. It is likely for this reason that this particular line of research appears to have ceased, with the last publication made in 2008.
The use of microstrip waveguides is reported by a single group that investigates the mechanism of heating. This group reports some heat from particles, but notes that the heat they observe is miniscule compared to the heating rates reported by other groups.11 The conclusions made in this report are similar to those made in other reports that question heating of AuNPs in RF: The heat observed is miniscule, greater heating is observed in samples that are not purified, presumably away from free salts, and that no presently considered mechanism can theoretically account for the amount of heat produced in experiments by groups using the Kanzius machine. Since this report focuses only on the thermal behaviour of ~15 nm diameter AuNPs, the results have little bearing on the electrophoretic and magnetic mechanisms that emerged after publication of this work, which are empirically effective only for 10 nm and smaller particles.
Conclusions
The literature that reports on heating of AuNPs in RF electromagnetic fields contains a wide variety of experimental approaches. Despite the wide variety of approaches, some global conclusions can be drawn. The chief conclusion is that in some cases gold nanoparticles immersed in RF fields heat, and in other cases they do not. All reports of AuNPs larger than 10 nm in diameter heating in RF are at this stage questionable. Also, reports that claim an SAR larger than a ~100 W/gram are questionable. All things considered, it seems probable that these heating rates arise from conductivity of the sample.
Just as in the empirical case, where it seems clear now that some reports may be artifactual, some conclusions regarding mechanism appear safe to make. First, the pure Joule or inductive heating mechanism is unlikely. Other considered mechanisms, relying on dielectric or Mie theory are also unlikely as noted in papers that investigate them.11,13 Particles larger than ~10 nm diameter probably do not heat detectably, consistent with the recent experimental and theoretical reports.19,27,28 Two mechanisms proposed within the past 18 months may explain heating of sub-10nm diameter particles. Electrophoretic mechanisms may heat AuNPs 10nm or smaller in concentrated electric fields. Magnetic mechanisms may function for sub-2.5 nm AuNPs and iron doped AuNPs.
If a combination of magnetic and electrophoretic mechanisms account for heating of particles smaller than 10nm in diameter, then essentially every report that questions whether AuNPs heat in RF at all is problematic. Theoretical reports that question the phenomena don’t consider these cooperative mechanisms, which emerged for consideration only after the theoretical reports were published.11,13 Experimental reports that completely dismiss the phenomena are similarly problematic. Some of these reports only use AuNPs that are larger than 10nm diameter.11 Another study that questions the phenomena is difficult to evaluate as the applied frequency is lower than in other studies and the applied power is not reported.10 Yet another study that dismisses the phenomenon12 is followed up by the authors with a subsequent study highlighting that container shape is important in whether heat is observed.18,30 In total, every report that questions the phenomenon of AuNPs heating does not dismiss electrophoretic heating of 10 nm or smaller particles, nor magnetic heating of 2.5 nm and smaller particles.
Future of AuNP heating in RF
For widespread adoption of this approach, it is clear that an empirically supported mechanism or set of mechanisms for heating must be validated. Presently, the electrophoretic mechanism overestimates heating and the magnetic mechanism underestimates observed heat. These mechanisms are not yet rigorously tested in terms of frequency dependence, field type, and particle composition and topology. In many cases both mechanisms may be simultaneously operative. We expect that a full testing of all of these experimental variables will allow clarification of which heating mechanisms apply in various experimental conditions, ideally allowing accurate prediction and modelling of nanoparticle heat at varying distances from the surface of a particle. Such understanding may usher in a new era of nanoparticle mediated remote-thermal control of biology.7
Acknowledgments
The authors acknowledge support from Colorado State University and the National Institutes of Health (5R21EB014520). We thank Dr. Joseph Diverdi for useful discussions.
Biographies

Christopher Ackerson earned his PhD in biophysics at Stanford University, under the direction of Roger Kornberg (2005). He did postdoctoral work in both the Kornberg lab and later with Dan Feldheim in the Chemistry and Biochemistry department of the University of Colorado – Boulder (2006–2009). In 2009 he joined the Chemistry Department at Colorado State University – Fort Collins, where he directs a lab that broadly focuses on the interface of metal nanoclusters and biology.

Christian Collins earned his BA in Chemistry and Mathematics from Western State College of Colorado in 2012. He is currently a physical chemistry PhD student at Colorado State University in Prof. Christopher Ackerson’s lab. His research focuses on applications and fundamental properties of heating gold nanoparticles in oscillating electromagnetic fields.

Ruthanne McCoy earned a BA in Biology and Chemistry and an MS in Chemistry at the University of Colorado – Colorado Springs. She worked in the Ackerson lab at Colorado State University from 2011 to 2013, investigating the interaction between radiofrequencies and gold nanoparticles. She is currently in medical school at the University of Colorado – Anschutz medical campus.

George Collins earned his PhD in Engineering and Applied Science at Yale University University. He did postdoc work in Nagoya Univ. Japan and Oxford University U.K. He joined the Electrical and Computer Engineering Dept at Colorado State University Fort Collins, where he is a Full Professor. He presently directs a laboratory that broadly focuses on the interface of RF generated reactive plasmas and tissues

Bruce Ackerson earned his PhD at the University of Colorado – Boulder. After postdoctoral work at the National Bureau of Standards & Measurement in Boulder (now NIST) he established a lab in the Physics department of Oklahoma State University, where he is now a full professor. His research focuses on the dynamics of colloidal particles.
Notes and references
- 1.Glazer ES, Curley SA. The Ongoing History of Thermal Therapy for Cancer. Surgical Oncology Clinics of North America. 2011;20:229–235. doi: 10.1016/j.soc.2010.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mukherjee S, et al. Hot electrons do the impossible: plasmon-induced dissociation of H2 on Au. Nano Lett. 2013;13:240–247. doi: 10.1021/nl303940z. [DOI] [PubMed] [Google Scholar]
- 3.Thomas J. Particle size effect in microwave-enhanced catalysis. Catal Lett. 1997;49:137–141. [Google Scholar]
- 4.Hainfeld JF, Slatkin DN, Focella TM, Smilowitz HM. Gold nanoparticles: a new X-ray contrast agent. The British journal of radiology. 2006;79:248–253. doi: 10.1259/bjr/13169882. [DOI] [PubMed] [Google Scholar]
- 5.Muhammed MAH, et al. Bright, NIR-emitting Au23 from Au25: characterization and applications including biolabeling. Chemistry. 2009;15:10110–10120. doi: 10.1002/chem.200901425. [DOI] [PubMed] [Google Scholar]
- 6.Neumann O, et al. Compact solar autoclave based on steam generation using broadband light-harvesting nanoparticles. Proceedings of the …. 2013;110:11677–11681. doi: 10.1073/pnas.1310131110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ball P. Material witness: Nano contraception. Nature Materials. 2013;12:602–602. doi: 10.1038/nmat3701. [DOI] [PubMed] [Google Scholar]
- 8.Huang X, Jain PK, El-Sayed IH, El-Sayed MA. Plasmonic photothermal therapy (PPTT) using gold nanoparticles. Lasers Med Sci. 2008;23:217–228. doi: 10.1007/s10103-007-0470-x. [DOI] [PubMed] [Google Scholar]
- 9.Dreaden EC, Alkilany AM, Huang X, Murphy CJ, El-Sayed MA. The golden age: gold nanoparticles for biomedicine. Chem Soc Rev. 2012;41:2740–2779. doi: 10.1039/c1cs15237h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gupta A, Kane RS, Borca-Tasciuc DA. Local temperature measurement in the vicinity of electromagnetically heated magnetite and gold nanoparticles. J Appl Phys. 2010;108:064901. [Google Scholar]
- 11.Liu X, Chen HJ, Chen X, Parini C, Wen D. Low frequency heating of gold nanoparticle dispersions for non-invasive thermal therapies. Nanoscale. 2012;4:3945–3953. doi: 10.1039/c2nr30166k. [DOI] [PubMed] [Google Scholar]
- 12.Li D, et al. Negligible absorption of radiofrequency radiation by colloidal gold nanoparticles. J Colloid Interface Sci. 2011;358:47–53. doi: 10.1016/j.jcis.2011.01.059. [DOI] [PubMed] [Google Scholar]
- 13.Hanson GW, Monreal RC, Apell SP. Electromagnetic absorption mechanisms in metal nanospheres: Bulk and surface effects in radiofrequency-terahertz heating of nanoparticles. J Appl Phys. 2011;109 [Google Scholar]
- 14.Hamad-Schifferli K, Schwartz John J, Santos Aaron T, Zhang S, Jacobson Joseph M. Remote electronic control of DNA hybridization through inductive coupling to an attached metal nanocrystal antenna. Nature. 2002;415:152–5. doi: 10.1038/415152a. [DOI] [PubMed] [Google Scholar]
- 15.Kogan MJ, et al. Nanoparticle-mediated local and remote manipulation of protein aggregation. Nano Lett. 2006;6:110–115. doi: 10.1021/nl0516862. [DOI] [PubMed] [Google Scholar]
- 16.Cardinal J, et al. Noninvasive radiofrequency ablation of cancer targeted by gold nanoparticles. Surgery. 2008;144:125–132. doi: 10.1016/j.surg.2008.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gannon CJ, Patra CR, Bhattacharya R, Mukherjee P, Curley SA. Intracellular gold nanoparticles enhance non-invasive radiofrequency thermal destruction of human gastrointestinal cancer cells. J Nanobiotechnology. 2008;6:2. doi: 10.1186/1477-3155-6-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kim HK, Hanson GW, Geller DA. Chemistry. Are gold clusters in RF fields hot or not? Science. 2013;340:441–442. doi: 10.1126/science.1237303. [DOI] [PubMed] [Google Scholar]
- 19.McCoy RS, Choi S, Collins G, Ackerson BJ, Ackerson CJ. Superatom Paramagnetism Enables Gold Nanocluster Heating in Applied Radiofrequency Fields. Acs Nano. 2013;7:2610–2616. doi: 10.1021/nn306015c. [DOI] [PubMed] [Google Scholar]
- 20.Wijaya A, Brown KA, Alper JD, Hamad-Schifferli K. Magnetic field heating study of Fe-doped Au nanoparticles. Journal of Magnetism and Magnetic Materials. 2007;309:15–19. [Google Scholar]
- 21.Araya E, et al. Gold Nanoparticles and Microwave Irradiation Inhibit Beta-Amyloid Amyloidogenesis. Nanoscale Res Lett. 2008;3:435–443. [Google Scholar]
- 22.Bastus N, Kogan M, Amigo R. ScienceDirect.com - Materials Science and Engineering: C - Gold nanoparticles for selective and remote heating of β-amyloid protein aggregates. Materials Science and …. 2007 [Google Scholar]
- 23.Curley SA, et al. Noninvasive radiofrequency field-induced hyperthermic cytotoxicity in human cancer cells using cetuximab-targeted gold nanoparticles. J Exp Ther Oncol. 2008;7:313–326. [PubMed] [Google Scholar]
- 24.Schmidt C. The Kanzius Machine: A New Cancer Treatment Idea From an Unexpected Source. JNCI Journal of the National Cancer Institute. 2008;100:985–986. doi: 10.1093/jnci/djn246. [DOI] [PubMed] [Google Scholar]
- 25.Moran CH, et al. Size-Dependent Joule Heating of Gold Nanoparticles Using Capacitively Coupled Radiofrequency Fields. Nano Res. 2009;2:400–405. [Google Scholar]
- 26.Liu X, et al. Dielectric Property Measurement of Gold Nanoparticle Dispersions in the Millimeter Wave Range. J Infrared Milli Terahz Waves. 2013;34:140–151. [Google Scholar]
- 27.Corr SJ, et al. Citrate-Capped Gold Nanoparticle Electrophoretic Heat Production in Response to a Time-Varying Radio-Frequency Electric Field. J Phys Chem C. 2012;116:24380–24389. doi: 10.1021/jp309053z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sassaroli E, Li KCP, O’Neill BE. Radio frequency absorption in gold nanoparticle suspensions: a phenomenological study. J Phys D: Appl Phys. 2012;45:075303. [Google Scholar]
- 29.Pearce JA, Cook JR. 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. 2011 33rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society; IEEE; 2011. pp. 5577–5580. [DOI] [PubMed] [Google Scholar]
- 30.Li D, et al. The effect of sample holder geometry on electromagnetic heating of nanoparticle and NaCl solutions at 13.56 MHz. IEEE Trans Biomed Eng. 2012;59:3468–3474. doi: 10.1109/TBME.2012.2219049. [DOI] [PubMed] [Google Scholar]
- 31.Kruse DE, et al. A radio-frequency coupling network for heating of citrate-coated gold nanoparticles for cancer therapy: design and analysis. IEEE Trans Biomed Eng. 2011;58:2002–2012. doi: 10.1109/TBME.2011.2124460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Walter M, et al. A unified view of ligand-protected gold clusters as superatom complexes. Proc Natl Acad Sci U S A. 2008;105:9157–9162. doi: 10.1073/pnas.0801001105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tofanelli MA, Ackerson CJ. Superatom Electron Configuration Predicts Thermal Stability of Au(25)(SR)(18) Nanoclusters. J Am Chem Soc. 2012;134:16937–16940. doi: 10.1021/ja3072644. [DOI] [PubMed] [Google Scholar]
- 34.DEHEER W. THE PHYSICS OF SIMPLE METAL-CLUSTERS - EXPERIMENTAL ASPECTS AND SIMPLE-MODELS. Rev Mod Phys. 1993;65:611–676. [Google Scholar]
- 35.Murray RW. Nanoelectrochemistry: Metal nanoparticles, nanoelectrodes, and nanopores. Chem Rev. 2008;108:2688–2720. doi: 10.1021/cr068077e. [DOI] [PubMed] [Google Scholar]
- 36.Huang T, Murray R. Visible Luminescence of Water-Soluble Monolayer-Protected Gold Clusters. Journal of Physical Chemistry B. 2001;105:12498–12502. [Google Scholar]
- 37.Sardar R, Funston A, Mulvaney P, Murray R. Gold Nanoparticles: Past, Present, and Future (dagger) Langmuir. 2009 doi: 10.1021/la9019475. [DOI] [PubMed] [Google Scholar]
- 38.Nealon GL, et al. Magnetism in gold nanoparticles. Nanoscale. 2012;4:5244–5258. doi: 10.1039/c2nr30640a. [DOI] [PubMed] [Google Scholar]
- 39.Zhu M, et al. Reversible switching of magnetism in thiolate-protected Au25 superatoms. J Am Chem Soc. 2009;131:2490–2492. doi: 10.1021/ja809157f. [DOI] [PubMed] [Google Scholar]
- 40.Hicks J, et al. The Monolayer Thickness Dependence of Quantized Double-Layer Capacitances of Monolayer-Protected Gold Clusters. Anal Chem. 1999;71:3703–3711. doi: 10.1021/ac990432w. [DOI] [PubMed] [Google Scholar]
- 41.Mulvaney P. Surface plasmon spectroscopy of nanosized metal particles. Langmuir. 1996;12:788–800. [Google Scholar]
- 42.Qian H, Zhu Y, Jin R. Atomically precise gold nanocrystal molecules with surface plasmon resonance. Proc Natl Acad Sci U S A. 2012 doi: 10.1073/pnas.1115307109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dass A. Faradaurate Nanomolecules: A Superstable Plasmonic 76.3 kDa Cluster. J Am Chem Soc. 2011;133:19259–19261. doi: 10.1021/ja207992r. [DOI] [PubMed] [Google Scholar]
- 44.Lopez-Acevedo O, Akola J, Whetten RL, Gronbeck H, Hakkinen H. Structure and Bonding in the Ubiquitous Icosahedral Metallic Gold Cluster Au-144(SR)(60) J Phys Chem C. 2009;113:5035–5038. [Google Scholar]
- 45.Yi C, Tofanelli MA, Ackerson CJ, Knappenberger KL. Optical Properties and Electronic Energy Relaxation of Metallic Au144(SR)60 Nanoclusters. J Am Chem Soc. 2013 doi: 10.1021/ja409998j. [DOI] [PubMed] [Google Scholar]
- 46.Martin T. Shell Structure of Cluster. Journal of Physical Chemistry B. 1991;95:6421. [Google Scholar]
- 47.Jadzinsky PD, Calero G, Ackerson CJ, Bushnell DA, Kornberg RD. Structure of a thiol monolayer-protected gold nanoparticle at 1.1 A resolution. Science. 2007;318:430–433. doi: 10.1126/science.1148624. [DOI] [PubMed] [Google Scholar]
- 48.Zeng C, Li T, Das A, Rosi NL, Jin R. Chiral Structure of Thiolate-Protected 28-Gold-Atom Nanocluster Determined by X-ray Crystallography. J Am Chem Soc. 2013 doi: 10.1021/ja404058q. [DOI] [PubMed] [Google Scholar]
- 49.Qian H, Eckenhoff WT, Zhu Y, Pintauer T, Jin R. Total structure determination of thiolate-protected Au38 nanoparticles. J Am Chem Soc. 2010;132:8280–8281. doi: 10.1021/ja103592z. [DOI] [PubMed] [Google Scholar]
- 50.Cheng L, Ren C, Zhang X, Yang J. New insight into the electronic shell of Au38 (SR) 24: a superatomic molecule. Nanoscale. 2013 doi: 10.1039/c2nr32888g. [DOI] [PubMed] [Google Scholar]
- 51.Venzo A, et al. Effect of the charge state (z = −1, 0, +1) on the nuclear magnetic resonance of monodisperse Au25[S(CH2)2Ph]18(z) clusters. Anal Chem. 2011;83:6355–6362. doi: 10.1021/ac2012653. [DOI] [PubMed] [Google Scholar]
- 52.Antonello S, Perera NV, Ruzzi M, Gascón JA, Maran F. Interplay of Charge State, Lability, and Magnetism in the Molecule-like Au25(SR)18 Cluster. J Am Chem Soc. 2013 doi: 10.1021/ja407887d. [DOI] [PubMed] [Google Scholar]
- 53.Akbari-Sharbaf A, Hesari M, Workentin MS, Fanchini G. Electron paramagnetic resonance in positively charged Au25 molecular nanoclusters. The Journal of chemical physics. 2013;138:024305. doi: 10.1063/1.4773061. [DOI] [PubMed] [Google Scholar]
- 54.Rosensweig RE. Heating magnetic fluid with alternating magnetic field. Journal of Magnetism and Magnetic Materials. 2002;252:370–374. [Google Scholar]
- 55.Brown WF., Jr Thermal fluctuations of a single-domain particle. Physical Review. 1963;130:1677–1686. [Google Scholar]
- 56.Pike CR, Roberts AP, Verosub KL. First-order reversal curve diagrams and thermal relaxation effects in magnetic particles. Geophysical Journal International. 2001;145:721–730. [Google Scholar]
- 57.Dennis CL, Ivkov R. Physics of heat generation using magnetic nanoparticles for hyperthermia. Int J Hyperthermia. 2013;29:715–729. doi: 10.3109/02656736.2013.836758. [DOI] [PubMed] [Google Scholar]
- 58.Smythe WR. Static and dynamic electricity. 1950. [Google Scholar]
- 59.Kim BH, et al. Large-Scale Synthesis of Uniform and Extremely Small-Sized Iron Oxide Nanoparticles for High-Resolution T1Magnetic Resonance Imaging Contrast Agents. J Am Chem Soc. 2011;133:12624–12631. doi: 10.1021/ja203340u. [DOI] [PubMed] [Google Scholar]
- 60.Cherukuri P, Glazer ES, Curley SA. Targeted hyperthermia using metal nanoparticles. Adv Drug Deliv Rev. 2010;62:339–345. doi: 10.1016/j.addr.2009.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Svenson S, Tomalia DA. Dendrimers in biomedical applications—reflections on the field. Adv Drug Deliv Rev. 2012;64:102–115. doi: 10.1016/j.addr.2005.09.018. [DOI] [PubMed] [Google Scholar]
- 62.Song KH, Kim C, Cobley CM, Xia Y, Wang LV. Near-infrared gold nanocages as a new class of tracers for photoacoustic sentinel lymph node mapping on a rat model. Nano Lett. 2009;9:183–188. doi: 10.1021/nl802746w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kruse DE, et al. Spatial and temporal-controlled tissue heating on a modified clinical ultrasound scanner for generating mild hyperthermia in tumors. IEEE Trans Biomed Eng. 2010;57:155–166. doi: 10.1109/TBME.2009.2029703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Glazer ES, et al. Noninvasive radiofrequency field destruction of pancreatic adenocarcinoma xenografts treated with targeted gold nanoparticles. Clin Cancer Res. 2010;16:5712–5721. doi: 10.1158/1078-0432.CCR-10-2055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Glazer ES, Massey KL, Zhu C, Curley SA. Pancreatic carcinoma cells are susceptible to noninvasive radio frequency fields after treatment with targeted gold nanoparticles. Surgery. 2010;148:319–324. doi: 10.1016/j.surg.2010.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Glazer ES, Curley SA. Radiofrequency field-induced thermal cytotoxicity in cancer cells treated with fluorescent nanoparticles. Cancer. 2010;116:3285–3293. doi: 10.1002/cncr.25135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Taira K, Abe K, Ishibasi T, Sato K, Ikebukuro K. Control of aptamer function using radiofrequency magnetic field. J Nucleic Acids. 2011;2011:103872. doi: 10.4061/2011/103872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Walter M, Moseler M, Whetten RL, Häkkinen H. A 58-electron superatom-complex model for the magic phosphine-protected gold clusters (Schmid-gold, Nanogold®) of 1.4-nm dimension. Chemical Science. 2011;2:1583–1587. [Google Scholar]
- 69.Hainfeld JF, Furuya FR. A 1.4-nm gold cluster covalently attached to antibodies improves immunolabeling. J Histochem Cytochem. 1992;40:177–184. doi: 10.1177/40.2.1552162. [DOI] [PubMed] [Google Scholar]
- 70.Raoof M, Zhu C, Kaluarachchi WD, Curley SA. Luciferase-based protein denaturation assay for quantification of radiofrequency field-induced targeted hyperthermia: developing an intracellular thermometer. Int J Hyperthermia. 2012;28:202–209. doi: 10.3109/02656736.2012.666318. [DOI] [PMC free article] [PubMed] [Google Scholar]