Thermodynamic Interrogation of the Assembly of a Viral Genome Packaging Motor Complex

Abstract

Viral terminase enzymes serve as genome packaging motors in many complex double-stranded DNA viruses. The functional motors are multiprotein complexes that translocate viral DNA into a capsid shell, powered by a packaging ATPase, and are among the most powerful molecular motors in nature. Given their essential role in virus development, the structure and function of these biological motors is of considerable interest. Bacteriophage λ-terminase, which serves as a prototypical genome packaging motor, is composed of one large catalytic subunit tightly associated with two DNA recognition subunits. This protomer assembles into a functional higher-order complex that excises a unit length genome from a concatemeric DNA precursor (genome maturation) and concomitantly translocates the duplex into a preformed procapsid shell (genome packaging). While the enzymology of λ-terminase has been well described, the nature of the catalytically competent nucleoprotein intermediates, and the mechanism describing their assembly and activation, is less clear. Here we utilize analytical ultracentrifugation to determine the thermodynamic parameters describing motor assembly and define a minimal thermodynamic linkage model that describes the effects of salt on protomer assembly into a tetrameric complex. Negative stain electron microscopy images reveal a symmetric ring-like complex with a compact stem and four extended arms that exhibit a range of conformational states. Finally, kinetic studies demonstrate that assembly of the ring tetramer is directly linked to activation of the packaging ATPase activity of the motor, thus providing a direct link between structure and function. The implications of these results with respect to the assembly and activation of the functional packaging motor during a productive viral infection are discussed.

Introduction

The assembly of an infectious virus requires the coordinated activity of a number of proteins and nucleoprotein complexes of both viral and host origin (1, 2). Genome packaging is an essential step in virus development that involves loading of genomic information, i.e., DNA or RNA, into a protective protein coat. For most complex double-stranded DNA (dsDNA) viruses, including adenovirus, the herpes viruses, and several bacteriophages, this reaction is catalyzed by a viral motor that inserts the DNA into a preformed procapsid shell, fueled by the energy derived from ATP hydrolysis (3, 4, 5, 6, 7). Terminase enzymes serve as packaging motors and are responsible for genome packaging in the complex dsDNA viruses. In general, the packaging substrate is a linear concatemer of individual genomes linked in a head-to-tail fashion (immature DNA). Terminase enzymes are responsible for excising an individual genome from the concatemer (genome maturation) and concomitant packaging of the mature DNA into the procapsid (3, 6, 7, 8).

Assembly of multimeric packaging motors from monomeric precursors is a central feature in the development of many dsDNA viruses, both prokaryotic and eukaryotic (6, 7, 8, 9). Given the essential role of the terminase motors in virus development, the mechanisms mediating motor assembly and activation are of significant interest. The aggregate genetic, biochemical, and structural data accumulated over many years of investigation suggest that all packaging motors possess similar structural and functional properties; they are generally oligomeric complexes composed of a large TerL subunit that possesses all of the catalytic activities required to mature and package individual genomes, and a smaller TerS subunit that is required for specific recognition of viral DNA. (A notable exception is the terminase enzyme from bacteriophage ϕ29. This virus does not encode a TerS subunit and packages monomeric genomes using only a TerL subunit. A second distinction is that ϕ29 utilizes an oligomeric ring of RNA that is bound to the portal (pRNA) and plays an essential role in genome packaging. We note that there is considerable debate as to the stoichiometry of the pRNA in the functional packaging motor; structural studies suggest a pentameric complex (10, 11), while biochemical and biophysical studies support a hexameric complex (12, 13).) Once assembled, the motors translocate DNA into the procapsid through a doughnut-shaped portal complex situated at a unique vertex in the icosahedral shell. All of the characterized motors translocate the duplex at incredible rates (>600 bp/s) and are capable of producing remarkably high packaging forces (∼60 pN), as required to fully insert the genome into the confines of the capsid shell (14, 15, 16).

Early models suggested that the packaging motors were functional hexamers in analogy to the translocating hexameric helicases (17, 18). Structural studies have suggested that the motors in phages T7, T4, and ϕ29 are composed of five TerL subunits assembled into a ring-like configuration at the portal vertex of a procapsid (see above) (10, 19, 20). Structural studies have further demonstrated that the isolated TerS subunits can assemble into oligomeric ring-like complexes containing 2, 8, 9, 11, or 12 subunits, and 22 subunit double-ring complexes depending on the virus and the protein construct (21, 22, 23, 24, 25, 26, 27). As of this writing, there is no structural data available for a functional motor complex assembled from both TerS and TerL subunits.

Bacteriophage-λ has been extensively studied and provides an ideal model system in which to interrogate the mechanistic details of virus assembly, and in particular the genome packaging machinery. Lambda-terminase is composed of a catalytic TerL subunit (gpA, 74.2 kDa) and a small TerS DNA-recognition subunit (gpNu1, 20.4 kDa) (9, 28). The purified enzyme affords a mixture of a protomeric holoenzyme (TerL₁•TerS₂) in slow equilibrium with a tetramer of protomers [(TerL₁•TerS₂)₄], each of which can be purified to homogeneity (28, 29, 30). The packaging pathway for terminase-mediated genome packaging can be summarized as follows (Fig. 1). The λ-protomer and Escherichia coli integration host factor (IHF) cooperatively assemble at the cohesive end site (cos) of immature λ-DNA (31). This engenders a catalytically competent maturation complex that nicks the duplex to yield the 12-base, single-stranded end of the mature genome in preparation for packaging; kinetic studies demonstrate that this complex contains 4 or 5 terminase protomers (28). The enzyme complex remains tightly bound to the matured left genome end and next binds to the portal vertex of an empty procapsid to afford the packaging motor complex in which packaging ATPase activity has been activated; kinetic data suggest that this complex similarly contains 4–5 terminase protomers (32). The activated motor translocates along the duplex, threading DNA through the portal ring and into the capsid interior. Packaging triggers expansion of the procapsid shell and the gpD decoration protein adds to stabilize the structure. Upon encountering the next downstream cos sequence (the genome end), the translocating motor reverts to a specifically bound maturation complex that again nicks the duplex to generate the mature right genome end and to release the DNA-filled capsid. Note that a unit-length genome is packaged in this process. Finishing proteins and a viral tail are added to the nucleocapsid to afford the infectious virus and the terminase-DNA complex binds a second procapsid to initiate the next round of processive packaging. In this manner, λ-terminase alternates between a highly stable, site-specifically bound maturation complex and a dynamic packaging motor complex that sequentially excises and packages individual genomes from the concatemeric DNA precursor.

Figure 1.

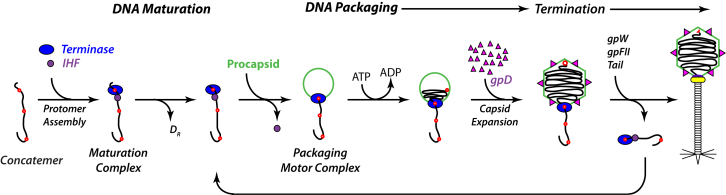
Genome packaging pathway for phage-λ. A two genome concatamer is depicted with cos sites indicated as red dots. The upstream D_R duplex end is ejected from the complex during duplex maturation. Details are presented in the text. To see this figure in color, go online.

The ability to purify λ-terminase as a structurally homogenous complex in solution and the well-characterized enzymatic properties of the enzyme provide a defined and tractable system to study motor assembly, structure, and function. As discussed above, we have previously demonstrated that the functional λ-motor consists of four or five protomers. Here, we greatly expand on these initial observations using an integrated analytical ultracentrifugation, electron microscopy, and enzyme kinetic approach. We confirm that the motor consists of four protomers assembled into a ring-like complex and provide a rigorous thermodynamic analysis of the self-association reaction. We further demonstrate that ring tetramer assembly is directly linked to activation of the packaging ATPase activity. The implications of these results with respect to motor assembly and activation during a productive viral infection in vivo are discussed. Although mechanistic details may differ between the complex dsDNA viruses, the essential features of virus assembly (both prokaryotic and eukaryotic) are recapitulated in all of them, and these results have broad biological implications.

Materials and Methods

Proteins and DNA substrates

All protein purifications utilized the Amersham Biosciences AKTApurifier core 10 System from GE Healthcare Life Sciences (Pittsburgh, PA). Terminase was purified as previously described in Andrews and Catalano (28) and Chang et al. (33) and the protomer and tetramer species were isolated by published protocol (28, 29), with modification. Briefly, purified terminase was dialyzed into Buffer P (20 mM sodium phosphate buffer, pH 6.8, 10% glycerol, 1 mM TCEP-HCl) containing 100 mM NaCl to afford the protomer species, which was isolated by size exclusion chromatography in the same buffer. Appropriate fractions were pooled and the protomer was stored at −80°C until further use. To prepare the tetramer, the purified protomer was then dialyzed into Buffer T (20 mM Tris, pH 8.6 at 4°C, 0.1 mM EDTA, 7 mM β-ME, 5% glycerol) containing 300 mM NaCl to reassemble the tetramer, which was isolated by size exclusion chromatography as previously described in Andrews and Catalano (28) and Maluf et al. (30). The purified protein was stored at −80°C until further use. Unless otherwise indicated, the concentration of terminase is expressed in terms of the protomer (TerL•TerS₂).

Sedimentation velocity experiments

Sedimentation velocity experiments were performed using an XLA analytical ultracentrifuge (Beckman Coulter, Brea, CA). The purified tetramer was dialyzed into Buffer P containing NaCl at the concentration indicated in each individual experiment. After dialysis, the protein was diluted to the indicated concentration using the dialysate and kept at 4°C for ∼50 h before loading into two-sector Epon charcoal-filled (Miller-Stephenson, Danbury, CT) centerpieces. The samples were placed in the centrifuge and equilibrated at 4°C for at least 1.5 h before initiation of the experiment. Unless otherwise indicated, the experiments were performed at 4°C and 42 K RPM. Data were collected at the indicated wavelengths, every 0.002 cm with two averages in the continuous mode. The raw sedimentation velocity data were corrected for timestamp errors (34) and the data were independently evaluated using three separate programs, SEDFIT, SEDPHAT (35, 36), and SedAnal (37, 38), as indicated.

Thermodynamic analysis of the protomer-tetramer equilibrium using sedimentation velocity data

Terminase establishes a slow equilibrium between the protomer and the tetramer without detectable intermediates (28, 29, 30). The c(s) distributions obtained from SEDFIT were utilized to determine K_A^∗, the macroscopic association constant of the monomer-tetramer equilibrium, as follows. The weight-average sedimentation coefficient, 〈s_20,w〉, for each concentration of protomer was calculated in SEDFIT; this reflects the ensemble concentration of all protomer species present in solution. Specifically, the terminase protomer self-assembles into a tetramer and by mass action,

$$\langle s_{20,w}\rangle =f_P\times s_P+f_{P4}\times s_{P4},$$ (1)

where s_P is the sedimentation coefficient (s_20,w) of the protomer, s_P4 is the sedimentation coefficient of the tetramer, and f_P and f_P4 are the fractions of protomer and tetramer in solution, respectively. Expressions for f_P and f_P4 are derived in Eqs. S1g and S1h (where n = 4), in the Supporting Material; by substitution and rearrangement, one obtains

$$\langle s_{20,w}\rangle =\frac{s_P\times \left[P\right]+s_{P4}\times 4\times K_A^{\ast }\times {\left[P\right]}^4}{\left[P\right]+4\times K_A^{\ast }\times {\left[P\right]}^4},$$ (2)

where [P] is the concentration of free protomer in solution, which was calculated from the total protein added to the reaction mixture, [P_T], by mass conservation. The 〈s_20,w〉 versus [P_T] data were analyzed according to Eq. 2 by nonlinear least-squares (NLLS) fitting of the data using the Scientist program (Micromath Research, St. Louis, MO) holding s_P and s_P4 to their experimentally determined values (5.28 and 14.77 S, respectively, obtained from SEDPHAT analysis; see Table S1 in the Supporting Material) and allowing K_A^∗ to float to its best fit values.

Sedimentation equilibrium experiments

The samples were prepared as described for the sedimentation velocity studies above and loaded into either two-sector (150 μL) or six-sector (120 μL) Epon (Miller-Stephenson) charcoal-filled centerpieces. The experiments were performed at 4°C and at the rotor speed indicated in each individual experiment. Sedimentation equilibrium was confirmed by the absence of deviation between successive scans using Winmatch; all experiments reached equilibrium within 50–60 h for the first speed. Absorbance data were collected at the indicated wavelength every 0.001 cm in the step mode, with 20 averages per step. The data sets were globally analyzed using NLLS analysis, programmed in Scientist, according to a monomer-tetramer equilibrium model (35, 39),

$${\text{Abs}}_r={\epsilon }_{\lambda }\times 1.2\times \left[C_{p,o}\times \text{exp}\left(\sigma \times \frac{r^2-r_o^2}{2}\right)+4\times K_A^{\ast }\times C_{p,o}^4\times \text{exp}\left(4\times \sigma \times \frac{r^2-r_o^2}{2}\right)\right]+b,$$ (3a)

where Abs_r is the absorbance at radial position r, ε_λ is the extinction coefficient of the protein at wavelength λ, C_p,o is the monomer concentration at reference position r₀, K_A^∗ is the apparent association constant for the monomer-tetramer equilibrium, b is the baseline offset, and

$$\sigma =M_p\times \left(1-\overline{\upsilon }\times \rho \right)\times \left(\frac{{\omega }^2}{R\times T}\right),$$ (3b)

where M_p is the molar mass of the protomer, $\overline{\upsilon }$ is the partial specific volume of the protomer, ρ is the buffer density, ω is the angular velocity of the rotor, R is the ideal gas constant, and T is the absolute temperature of the experiment. The raw equilibrium data were globally analyzed using NLLS approaches according to Eq. 3a: σ was calculated from protomer molar mass, 115.2 kDa; $\overline{\upsilon }$ = 0.733 mL/g was based on the protomer sequence (using SEDNTERP; Biomolecular Interactions Technology Center, University of New Hampshire, Durham, NH); the experimental parameters ω, ρ, and temperature, were held as global constants; r₀ was fixed as a local constant at the first data point for each data set; and C_p,o, b, and K_A^∗ were allow to float as global variables to obtain the best fit to the experimental data.

Because of the long experimental duration (>80 h), buffer components can contribute to the absorbance signal, resulting in a sloping baseline. The amplitude parameter, a, was therefore included in the analysis, where

$${\text{Abs}}_r={\epsilon }_{\lambda }\times 1.2\times C_r\times a\times \left(\frac{r^2-r_o^2}{2}\right)+b.$$ (3c)

Effect of NaCl on terminase self-association

Salt strongly affects the experimental K_A^∗ obtained for the protomer-tetramer equilibrium and this effect was quantified according to a simple thermodynamic linkage model presented later in Fig. 5 C. Based on this model, the following equation can be derived as described in the Supporting Material,

$$\begin{array}{c}2\times {\left(\frac{1}{4\times K_A^{\ast }}\right)}^{1/3}={\left(\frac{1+K_3^{1/4}\times {\left[L\right]}^m}{4\times K_1+4\times K_1\times K_2\times {\left[L\right]}^{4\times m}}\right)}^{1/3}+K_3^{1/4}\times {\left[L\right]}^m\times {\left(\frac{1+K_3^{1/4}\times {\left[L\right]}^m}{4\times K_1+4\times K_1\times K_2\times {\left[L\right]}^{4\times m}}\right)}^{1/3}\\ +4\times K_1\times {\left(\frac{1+K_3^{1/4}\times {\left[L\right]}^m}{4\times K_1+4\times K_1\times K_2\times {\left[L\right]}^{4\times m}}\right)}^{4/3}+4\times K_1\times K_2\times {\left[L\right]}^{4\times m}\times {\left(\frac{1+K_3^{1/4}\times {\left[L\right]}^m}{4\times K_1+4\times K_1\times K_2\times {\left[L\right]}^{4\times m}}\right)}^{4/3},\end{array}$$ (4)

where K_A^∗ is the experimentally determined macroscopic equilibrium constant determined at a salt concentration [L]; m is the net flux of NaCl involving in protomer self-assembly; and K₁, K₂, and K₃ represent the equilibrium association constants described later in Fig. 5 C. The K_A^∗ versus [NaCl] data were analyzed according to Eq. 4 by NLLS fitting of the data using the Scientist program (Micromath Research), allowing m, K₁, K₂, and K₃ to float to their best fit values.

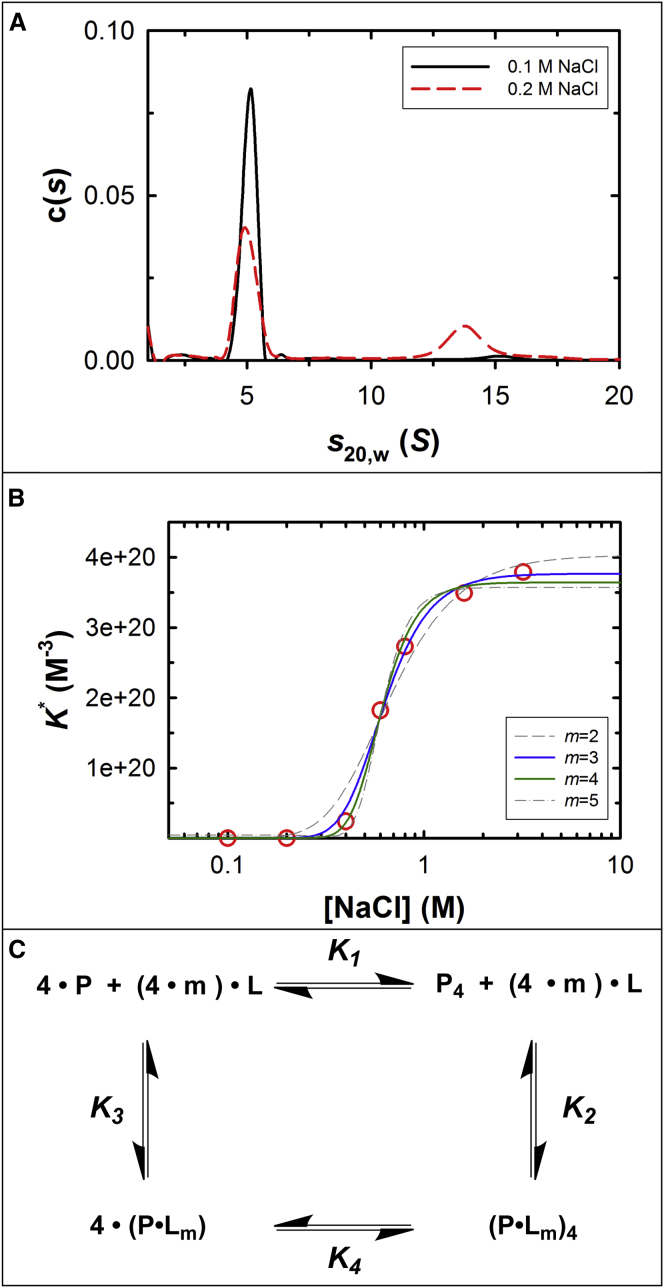
Figure 5.

Dependence of self-association on NaCl concentration. (A) Sedimentation velocity of terminase analyzed by c(s) analysis, showing different species distribution under different NaCl conditions (0.1 and 0.2 M, black solid and red dashed lines, respectively). Note that there is the slight decrease in s_20,w of the large species at the higher NaCl concentration, a phenomenon that we have observed previously (30). We interpret this to indicate that the conformation of the tetramer is affected by salt to afford a more extended shape, and thus a smaller s_20,w value. (B) (Red circles) Sedimentation equilibrium data presented in Table 1; (superimposed lines) nonlinear least-squares fits to the model presented in (C) using Eq. 4, with m fixed at the indicated value. The results of the NLLS fits are presented in Table 2. (C) Model for thermodynamic linkage of the monomer-tetramer equilibrium and NaCl binding. P is protein monomer, P₄ is tetramer, and m is the net number of NaCl (L) binding or releasing in the equilibria. The individual association constants are defined as follows: K₁ is the association constant of protomer-tetramer equilibrium with no net NaCl participating; K₂ is the association constant of NaCl binding to tetramer; K₃ is the association constant of NaCl binding to monomer; and K₄ is the association constant of monomer-tetramer equilibrium under saturated NaCl binding condition. The model assumes that the number of ions that bind to the protomer in isolation and in the context of the tetramer is identical. To see this figure in color, go online.

Electron microscopy

The terminase tetramer was diluted to a final concentration of 192 nM in buffer T without glycerol. An aliquot (4 μL) was applied to freshly plasma-cleaned electron microscopy (EM) grids that had been coated with a thin layer of carbon. After 1 min of adsorption, excess protein was wicked away with a Whatman No. 1 filter paper (GE Healthcare Life Sciences), and 2% (w/v) uranyl formate solution (4 μL) was immediately applied to the grid. The grid was then inverted and placed on four 50 μL droplets of uranyl formate solution for 10 s each, in succession. Excess stain was then wicked away with filter paper and the grid set to dry on the edge of a fume hood to provide airflow.

Data were acquired using a Tecnai Spirit (FEI, Hillsboro, OR) transmission electron microscope, operating at 120 keV at a nominal magnification of 52,000× (pixel size of 2.05 Å/pixel at the specimen level). A total of 318 micrographs was acquired using the LEGINON automated data acquisition system (40), using a F416 CMOS 4K× camera (T-VIPS, Oslo, Norway) at an electron dose of 20 electrons/Ų, with a defocus range from 0.3 to 1.5 μm. Image analysis was performed using the Appion image processing pipeline (41). Particles were selected from the micrographs using a difference-of-Gaussians-based automated particle picking program (42) and the contrast transfer function (CTF) of each micrograph was estimated using CTFFIND3 (43). Using the estimated CTF, phases for each micrograph was corrected before extracting particles with a box size of 224 pixels. Particles were binned by a factor of 2 and normalized for analysis. The resulting stack of 55,094 particles was subjected to four rounds of iterative multivariate statistical analysis and multireference alignment in Appion to remove damaged, aggregated, or erroneously selected particles. The resulting stack of 49,789 particles was then used for reference-free two-dimensional alignment and classification using the ISAC program (70), which is part of the SPARX software package (44). Of the particles examined, 38,211 (77%) were classified into stable classes depicting open or closed conformations. The remaining particles likely represent damaged/misfolded particles or sample contaminants that were not identified in the earlier coarse classification step.

ATPase activity assay

Terminase (1 μM) was preincubated in Buffer P containing 100, 300, 400, or 600 mM NaCl for 50 h at 4°C as described for the analytical ultracentrifugation studies. The ATPase activity of the enzyme was then measured as previously described in Andrews and Catalano (28) and Yang et al. (45) with minor modification. Briefly, the reactions contained 100 nM terminase protomer and 1 mM ATP in 20 mM Tris buffer, pH 8, containing 200 mM NaCl, 10 mM MgCl₂, 5% glycerol, and 7 mM β-mercaptoethanol. The reaction was allowed to proceed for 30 min at 37°C and ATP hydrolysis quantified by a thin-layer chromatography assay.

Results

Characterization of the λ-terminase protomer-tetramer self-association reaction: sedimentation velocity approach

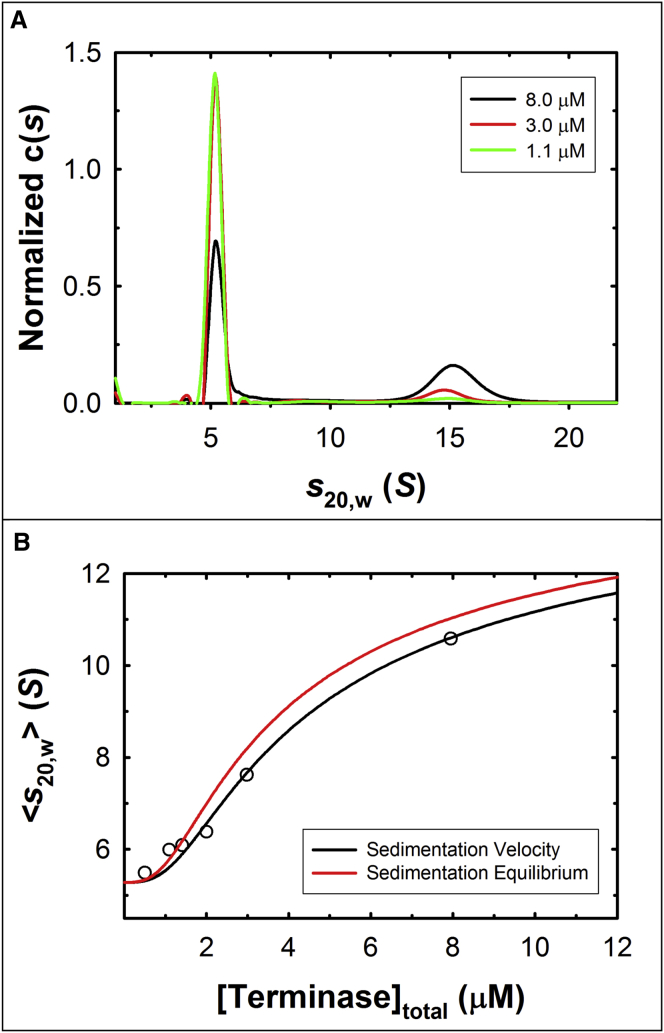
Lambda-terminase can be purified to homogeneity and the preparation contains a mixture of the protomer in slow equilibrium with a tetramer of protomers (28, 29, 30, 32). Here we expand upon these initial observations and describe a rigorous hydrodynamic characterization of the protomer-tetramer equilibrium reaction using sedimentation velocity (SV) analytical ultracentrifugation approaches. A concentrated preparation of the terminase tetramer was isolated as described in Materials and Methods and the enzyme was diluted to afford mixtures containing terminase at concentrations between 0.5 and 8 μM (Buffer P, pH 6.8, containing 100 mM NaCl). The samples were examined by SV analytical ultracentrifugation and the velocity data were first analyzed using SEDFIT; three representative c(s) distributions are displayed in Fig. 2 A. Consistent with published data, under these buffer conditions, purified terminase partitions between two species—a small 5.3 S species and a larger 15 S species. The presence of two distinct peaks in the c(s) distribution indicates that the rate of interconversion between them is slow under these conditions and with respect to the time course of the experiment.

Figure 2.

Terminase self-associates in a concentration-dependent manner. (A) The c(s) distributions of terminase at three loading concentrations (1.1 μM, green; 3.0 μM, red; and 8.0 μM, black) were calculated using SEDFIT as described in the Materials and Methods in buffer containing 100 mM NaCl. (B) (Open circles) The weight-average sedimentation coefficient of terminase at the indicated protomer concentrations was calculated using SEDFIT. (Black line) Best fit of the data according to a monomer-tetramer equilibrium model (Eq. 2). (Red line) Simulation of the theoretical 〈s_20,w〉 value as a function of protomer concentration assuming K_A^∗ = 1.72 × 10¹⁶ M⁻³ (from equilibrium data), and s_20,w = 5.23 S and s_20,w = 15.66 S for the protomer and tetramer, respectively (from velocity data; see Table S1). To see this figure in color, go online.

A c(M) analysis of six data sets comprising terminase concentrations between 0.5 and 8 μM yields an average molecular mass of 105 (91, 119) kDa and 486 (447, 525) kDa for the 5.3 S and 15.0 S species, respectively (data not shown). (All data are presented as a resolved value with 68.3% confidence intervals indicated in parentheses.) These values are consistent with the molecular masses of the terminase protomer (TerL•TerS₂, 115 kDa) and a tetramer of protomers (460 kDa) calculated from the known protein sequences. Importantly, the data demonstrate that within this concentration range, 1) TerS and TerL remain stably associated as a protomeric complex, and that 2) the protomer self-assembles into the tetramer with no significant population of intermediate species.

The velocity data reveal that terminase establishes a concentration-dependent, dynamic equilibrium between the protomer and tetramer species. Thus, the weight average sedimentation coefficient, 〈s_20,w〉, captures the ensemble distribution of the protomer and tetramer species in solution at each terminase concentration. The value of 〈s_20,w〉 was calculated from the c(s) distributions over a wide range of protomer concentrations (0.5–8 μM), which demonstrates that 〈s_20,w〉 increases from 5.3 S to 10.6 S over the 16-fold concentration range (open circles, Fig. 2 B); this is diagnostic of a self-association reaction. The data were directly fit to a simple monomer-tetramer equilibrium model to obtain a macroscopic association constant (K_A^∗) for the reaction (Eq. 2). The data are well described by this model (solid black line, Fig. 2 B) and the analysis affords $K_A^{\ast }$ = 7.50 (6.20, 9.20) × 10¹⁵ M⁻³.

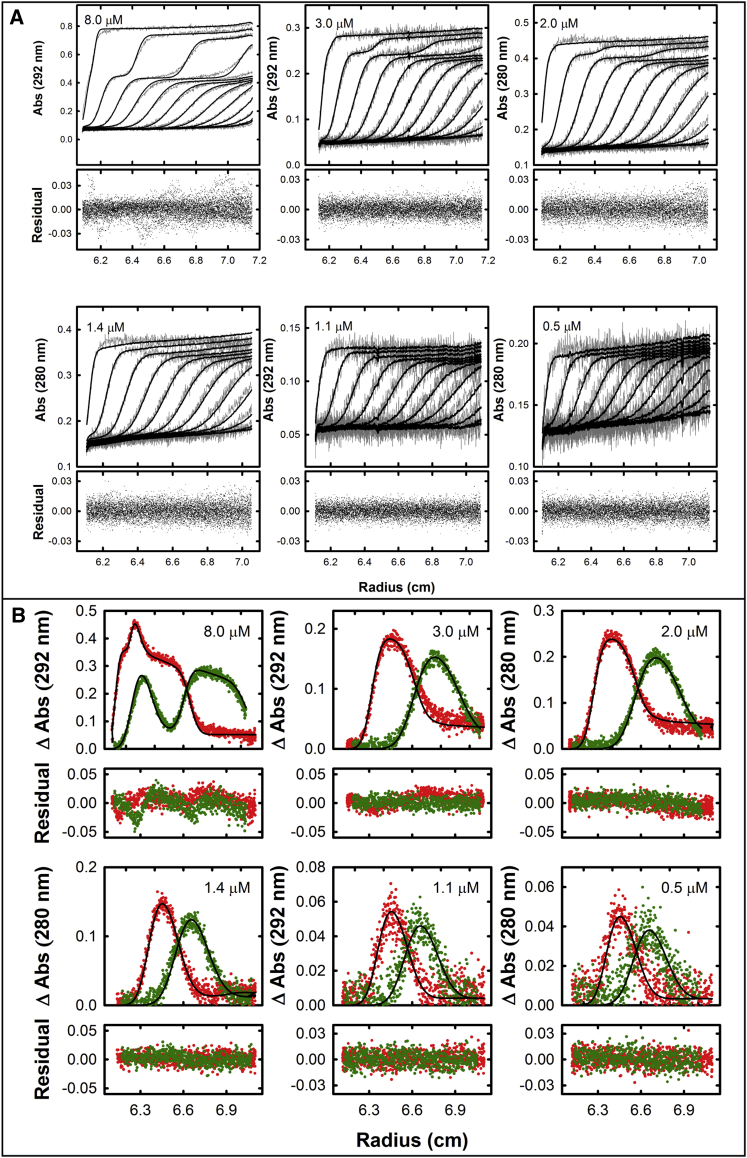
As an independent approach to the analysis of the sedimentation velocity data, we used SEDPHAT to globally analyze the raw data obtained at the six different terminase concentrations according to a noninteracting, two species model (35). The ensemble of data sets is well described by this model (Fig. 3 A) and the analysis provides a constrained determination of the sedimentation coefficients of the two terminase species in solution: best fit values were s_20,w = 5.28 (5.23, 5.32) S and s_20,w = 14.77 (14.58, 14.96) S for the protomer and tetramer, respectively. As expected, these values are in good agreement with the above analysis and with our previously published data for the isolated protomer and tetramer species, respectively (Table S1) (29, 30).

Figure 3.

(A) Global analysis of the sedimentation velocity data using SEDPHAT. Raw sedimentation velocity data for six different concentrations of protomer in buffer containing 100 mM NaCl are displayed. The ensemble of data was globally fit to a two-species model using SEDPHAT. (Solid lines) Best fit in each data set with fitting residuals presented beneath each plot; the resolved values for s_20,w for the protomer and the tetramer species are presented in Table S1. (B) Global analysis of the sedimentation velocity data using SedAnal. The subtracted absorbance traces (in pairs) from the same data sets shown in (A) are plotted against radius and globally fit to a monomer-tetramer equilibrium model (solid lines). Only the first and last traces (red and green, respectively) are shown for clarity. The residuals are shown below the subtracted absorbance plots. To see this figure in color, go online.

Finally, we applied a direct boundary analysis of the ensemble of velocity data using SedAnal according to a monomer-tetramer association model (37, 38, 46). This approach allows simultaneous fitting of the ensemble of data to obtain not only the sedimentation coefficients for the two species, but also the apparent association constant (K_A^∗) for the self-assembly reaction. Floating of these parameters in the global analysis affords an excellent fit to the data (Fig. 3 B) and yields the best fit s_20,w for the terminase protomer and tetramer of 5.23 (5.23, 5.25) and 15.66 (15.58, 15.71), respectively, and a derived K_A^∗ = 7.63 (7.34, 7.93) × 10¹⁵ M⁻³. Overall, independent analysis of the ensemble of sedimentation velocity data using three different approaches yields similar results for the derived sedimentation coefficients and the equilibrium constant for the protomer self-association reaction (Table S1).

Characterization of the λ-terminase protomer-tetramer self-association reaction: sedimentation equilibrium approach

Hydrodynamic modeling of sedimentation velocity data provides a reasonably accurate estimation of the apparent association constant for a reaction and the two analytic approaches described above provide virtually identical values for the K_A^∗; however, sedimentation equilibrium (SE) analytical ultracentrifugation approaches are most appropriate to rigorously determine thermodynamic information on solution-based association interactions (39, 47). We therefore utilized SE analytical ultracentrifugation to interrogate the thermodynamic features of the terminase protomer self-association reaction under conditions identical to those used in the velocity studies. As a first step, equilibrium scans were carried out at three concentrations of terminase and at two rotor speeds (Fig. 4). The velocity data described above indicates that the protomer self-assembles into a tetramer of protomers with no detectable intermediates; therefore, the ensemble of SE analytical ultracentrifugation data was modeled according to a monomer-tetramer equilibrium model as described in Materials and Methods (Eq. 3a). This global analysis adequately describes all six data sets and the best-fit curves are displayed as solid black lines on the data in Fig. 4. The analysis affords a resolved apparent association constant K_A^∗ = 1.72 (1.59, 1.85) × 10¹⁶ M⁻³.

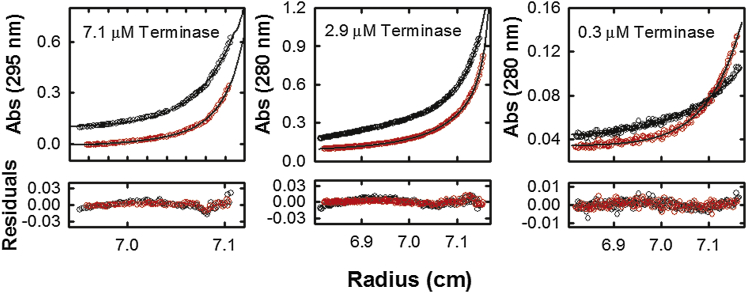
Figure 4.

Sedimentation equilibrium analysis by monomer-tetramer model. Absorbance traces of sedimentation equilibrium at three loading concentrations of terminase, sedimented at two different speeds (8000 and 12,000 RPM, black and red, respectively), plotted as a function of radius. The experiments were carried out in the presence of 100 mM NaCl and absorbance monitored at 295 nm (7.1 μM) or 280 nm (2.9 and 0.3 μM). (Solid lines) Best fit determined from a monomer-tetramer equilibrium model. The residuals were shown below the absorbance traces. To see this figure in color, go online.

We note that the K_A^∗ obtained from the equilibrium study is slightly greater than that obtained from the SV analytical ultracentrifugation analysis above (see Table S1). Close inspection of the data presented in Fig. 2 A reveals that the position of the ∼15 S species increases slightly with protomer concentration. This suggests that while slow, some dynamic information is apparent in the velocity data, which is not fully accounted for in the sedimentation velocity fitting models (48). This results in an underestimation of the 〈s_20,w〉 for the tetramer resulting in a concomitant underestimation of K_A^∗ obtained from the velocity analysis. To illustrate this point, we simulated the anticipated value of 〈s_20,w〉 in a velocity experiment over a wide terminase concentration range. The simulation used the experimental s_20,w values obtained from SedAnal analysis of the velocity data, 5.23 S and 15.66 S for protomer and tetramer, respectively; and the K_A^∗ = 1.72 × 10¹⁶ M⁻³ values obtained from the sedimentation equilibrium experiment (see Table S1). This simulation affords the predicted curve displayed as a solid red line in Fig. 2 B. While comparable, the simulation predicts a slightly larger value of 〈s_20,w〉, relative to the experimental velocity data, as a function of protomer concentration. This is consistent with the observation that the velocity models employed fail to adequately capture the slow, but dynamic nature of the equilibrium at 4°C. We therefore favor the use of K_A^∗ = 1.72 (1.59, 1.85) × 10¹⁶ M⁻³ obtained from the sedimentation equilibrium studies.

In sum, the sedimentation velocity and sedimentation equilibrium data both indicate that terminase undergoes a slow, reversible protomer-tetramer equilibrium in the concentration range of 0.5–8 μM protomer, with no evidence for a significant population of intermediate species or further self-association. The apparent equilibrium dissociation constant for the reaction under these conditions (100 mM NaCl) is K_D,app = 3.9 μM (Table S1). The implications of this thermodynamic analysis with respect to the assembly and activation of a viral maturation and motor complex during a viral infection in vivo are discussed below.

Effect of salt on λ-terminase self-assembly

We previously demonstrated that terminase assembly into the tetramer is favored at elevated concentrations of NaCl (29). We here expand on these initial observations and systematically examine the general effect of salt on the equilibrium reaction. SV analytical ultracentrifugation experiments were conducted as described in the Materials and Methods (1 μM terminase) except that the indicated salt was included in the reaction mixture. The concentration of each salt was adjusted to maintain a constant ionic strength (relative to 500 mM NaCl) and the c(s) distribution for each experimental condition was calculated using SEDFIT. The data presented in Table S2 indicate that the protomer-tetramer equilibrium is not significantly affected by salt type, which is consistent with a nonspecific salt effect.

Effect of NaCl concentration on λ-terminase self-assembly

We next examined the effect of NaCl concentration on the protomer-tetramer equilibrium reaction. Terminase (1 μM) was allowed to equilibrate between the protomer and tetramer species in phosphate buffer, pH 6.4, containing either 100 or 200 mM NaCl (50 h at 4°C). The samples were then analyzed under sedimentation velocity conditions and the c(s) distributions were calculated using the software SEDFIT. The data presented in Fig. 5 A demonstrate that both the protomer (low S) and the tetramer (high S) species are present at equilibrium under both conditions; however, the fraction of tetramer present is significantly greater in the presence of elevated NaCl concentration.

We next used a sedimentation equilibrium approach for a more detailed interrogation of how NaCl affects the terminase protomer-tetramer equilibrium reaction. Two concentrations of terminase over a >20-fold concentration range were allowed to come to equilibrium in phosphate buffer, pH 6.4, containing NaCl in the concentration range of 0.1–3.2 molar. For each of the six independent salt concentrations, the four equilibrium data sets (two protein concentrations at two rotor speeds) were globally fit using a monomer-tetramer equilibrium model as described in the Materials and Methods and the best fits of the data are presented as solid black lines in each of the panels presented in Fig. S2. The analysis affords the K_A^∗ for protomer self-assembly at each salt concentration, which is presented in Table 1 and displayed graphically in Fig. 5 B (red circles). Importantly, the experimentally derived K_A^∗ values approach asymptotic values at both low and high salt concentrations, an indication that the salt effect is a saturable process.

Table 1.

Sodium chloride affects the protomer-tetramer equilibrium

[NaCl] (Molar)	KA∗ (M−3)	ΔG (kcal/mol)b
0.1	1.72 (±0.13) × 1016	−6.9
0.2	2.87 (±0.70) × 1016	−7.0
0.4	2.38 (±1.86) × 1019	−8.2
0.6a	1.82 × 1020	−8.6
0.8a	2.73 × 1020	−8.7
1.6a	3.49 × 1020	−8.7
3.2a	3.79 × 1020	−8.7

The sedimentation equilibrium data presented in Fig. S2 were analyzed as described in the Materials and Methods to derive the apparent association constant, K_A^∗, for tetramer assembly at each concentration of NaCl.

^aThe equilibrium concentration of the protomer at these NaCl concentrations was extremely low and difficult to accurately quantify due to the detection limit of an analytical ultracentrifuge. This precludes an accurate estimate of the error and thus, no estimates are provided.

^bThe ΔG for protomer-tetramer association was calculated from ΔG = −RT ln(K^∗), where K^∗ = (K_A^∗)^1/3, R is the gas constant, and T is the absolute temperature of the experiment.

Thermodynamic linkage between NaCl binding and protomer self-assembly

The data presented in Fig. 5 B demonstrate that NaCl strongly affects the equilibrium between the terminase protomer and the tetramer species. This behavior is consistent with a thermodynamic linkage between salt binding to the protomer and self-assembly into an oligomeric complex (49). A simple model describing this linkage is presented in Fig. 5 C, where binding of m ions to the protomer (Na⁺ and/or Cl−, designated as L) affects the association equilibrium constant for tetramer assembly. In this model, K₁ and K₄ represent the protomer self-association equilibrium constants in the absence and in the presence of bound ions, respectively, while K₃ and K₂ represent the association equilibrium constant for the binding of m ions to the protomer in isolation and in the context of the tetramer, respectively. Based on this model, Eq. 4 (Materials and Methods) can be derived to describe the thermodynamic linkage between salt binding and protomer self-assembly. The data presented in Fig. 5 B were evaluated according to this model allowing all of the parameters to float in the NLLS analysis. This analysis yields a good fit (not shown) and affords a best-fit value m = 3.5 ± 0.4, which suggests that a net flux of 3–4 ions is involved in the terminase self-association equilibrium reaction.

The above analysis allows four degrees of freedom in the fit (K₁, K₂, K₃, and m). To constrain the analysis and allow more meaningful values for the equilibrium constants, we repeated the analysis fixing m (number of bound salt ions) at physically meaningful integral values of 2–5, but allowing K₁, K₂, and K₃ to float to their best-fit values. As anticipated, the data are best described by this simple model when m is fixed at either 3 or 4 (Fig. 5 B) and the analysis returns constrained values for the individual association constants presented in Table 2.

Table 2.

Thermodynamic linkage between NaCl binding and protomer self-assembly

Fitting Parameters	Best Fit Values
	m = 3 (Fixed)	m = 4 (Fixed)
K1	K1 = 2.6 × 1013 M−3	K1 = 9.1 × 1016 M−3
(K1)1/3 = 3.0 × 104 M−1	(K1)1/3 = 4.5 × 105 M−1
K2	K2 = 3.2 × 1012 M−12	K2 = 8.8 × 109 M−16
(K2)1/12 = 11.0 M−1	(K2)1/16 = 4.2 M−1
K3	K3 = 2.2 × 105 M−12	K3 = 2.2 × 106 M−16
(K3)1/12 = 2.8 M−1	(K3)1/16 = 3.4 M−1
K4a	K4 = 3.8 × 1020 M−3	K4 = 3.6 × 1020 M−3
(K4)1/3 = 7.2 × 106 M−1	(K4)1/3 = 7.1 × 106 M−1

The data presented in Fig. 5B were analyzed according to the thermodynamic linkage model presented in Fig. 5C. The number of ions involved, m, was fixed at either 3 or 4, as indicated, while the microscopic equilibrium constants K₁, K₂, and K₃ were allowed to float in the NLLS analysis. (Solid blue and green lines) Best fits of the data, respectively, are presented in Fig. 5B.

^aK₄ was calculated from K₁, K₂, and K₃ based on the model presented in Fig. 5C.

While the data are equally well described by a net flux of either three or four ions in the equilibrium reaction, close inspection of Table 2 reveals that the resolved values for K₁ (protomer-tetramer K_A in the absence of salt; note that K₁ cannot be measured experimentally due to significant aggregation of the protomer at NaCl concentrations <100 mM) is significantly closer to the experimentally determined values when m is constrained to four ions (see Table 1). Given this observation and the tetrameric nature of terminase, we are tempted to speculate that one ion interacts with each protomer to promote tetramer assembly (i.e., m = 4). Whatever the case, the data presented in Fig. 5 and Tables 1 and 2 clearly demonstrate that salt binding to the protomer and self-assembly are thermodynamically linked processes and that salt preferentially stabilizes the tetramer by ∼1.8 kcal/mol at 3.2 vs. 0.1 molar NaCl. This stabilization could be due to either a specific interaction between Na⁺ and/or Cl⁻ with terminase, and/or a nonspecific electrostatic rearrangement of terminase complex structure (50, 51, 52).

Structure of the terminase tetramer

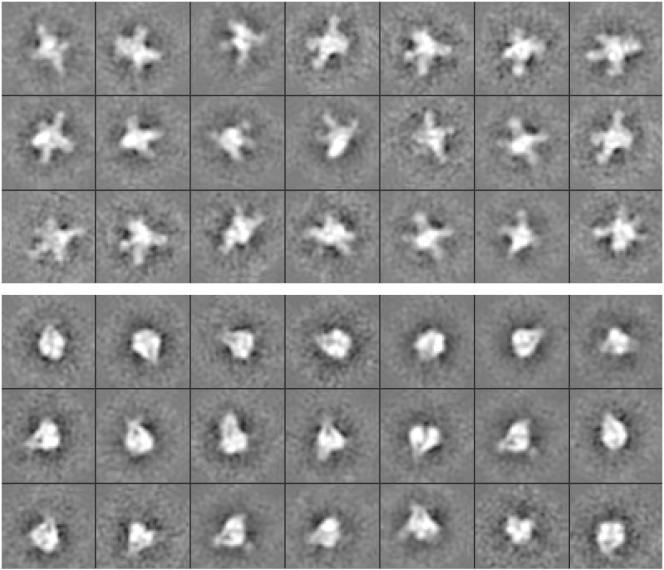
The analytical ultracentrifugation data presented above clearly demonstrates that the terminase protomer self-associates into a tetramer of protomers. Micrographs previously published from our lab suggested a ring-like structure for the assembled species, but the stoichiometry of the complex was ambiguous (30). Therefore, we here investigate the structure of the assembled terminase species using EM. The micrographs reveal a tetrameric ring-like complex that is composed of a compact stem, and four extended arms exhibiting a wide range of conformation states (Fig. 6). In some cases they are completely splayed out in an open conformation, while in others they are retracted and in contact with each other in a closed conformation. The implication of these two conformations is unclear; however, we note that while TerS must bind specifically to cos during packaging initiation, the subunits must interact weakly, if at all with the duplex when the motor is packaging DNA (see Fig. 1). Indeed, we have previously suggested that the TerS subunits are completely disengaged from the duplex during translocation (9), which could be accommodated by an open ring conformation. Structural studies are now underway in our lab to directly test this hypothesis.

Figure 6.

The terminase protomer assembles into a ring-like tetramer. The imaged particles could be classified into either open (58%, upper panel) or closed (42%, lower panel) conformations, as described in the Materials and Methods.

Effect of NaCl on the ATPase activity of bacteriophage λ-terminase

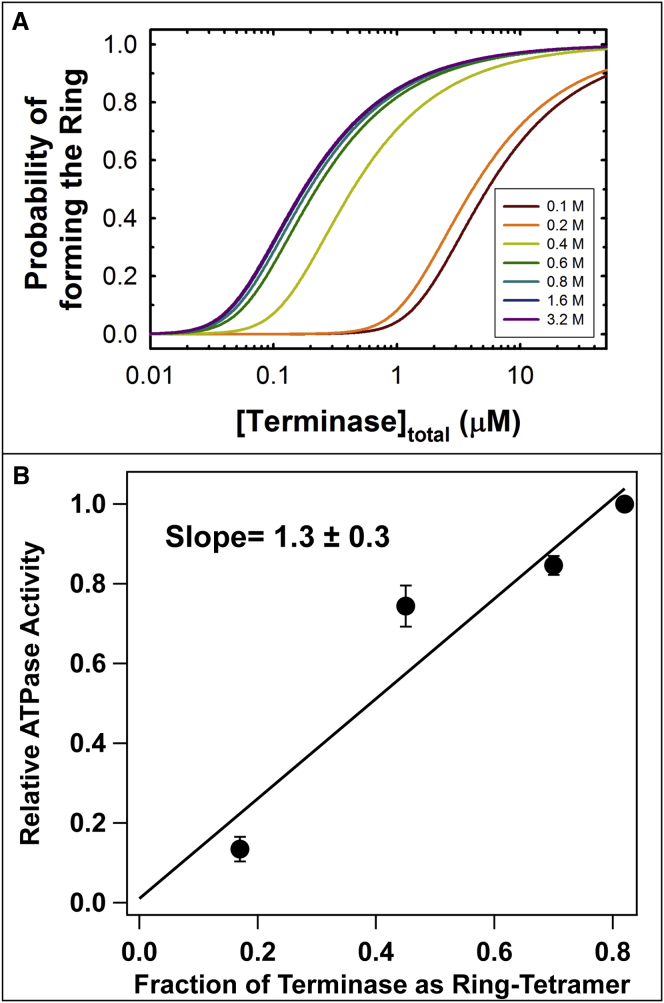
The terminase ring tetramer possesses all of the catalytic activities required to mature and package λ-DNA while the protomer is catalytically silent (29, 30); however, the exact relationship between ring assembly and activation of motor function remains unclear. The observation that salt promotes ring assembly in solution provides an opportunity to directly interrogate the relationship between structure and function of the motor. Unfortunately, the genome maturation and packaging reactions are strongly inhibited by NaCl as a result of diminished DNA binding interactions (53, 54, 55, 56). In contrast, the packaging ATPase activity of terminase is optimal at 200 mM NaCl (57) and this allows direct interrogation of ATPase activity as a function of ring tetramer concentration. Terminase (1 μM) was allowed to equilibrate between the protomer and tetramer species in phosphate buffer, pH 6.4, containing the indicated concentration of NaCl (50 h at 4°C). The ATPase activity of each sample was then quantified as previously described, except that NaCl was maintained at 200 mM in all of the assay mixtures (see the Materials and Methods). The data presented in Fig. 7 demonstrate that activation of the packaging ATPase activity of the motor tracks linearly with the fraction of terminase present as ring tetramer in solution. These data establish a direct linkage between protomer assembly into the ring tetramer and activation of motor function.

Figure 7.

(A) Simulation of the fraction of terminase present as the ring tetramer at various NaCl concentrations. (B) Effect of salt on the packaging ATPase activity of terminase. ATPase activity assays were performed as described in the Materials and Methods using enzyme (1 μM) that was preequilibrated at 4°C for 50 h in the presence of 100, 300, 400, or 600 mM NaCl to reach equilibrium between the protomer and tetramer species. To see this figure in color, go online.

Discussion

Terminase enzymes are essential to the development of most complex double-stranded DNA viruses, both eukaryotic and prokaryotic (3, 5, 6, 7, 8). They function as powerful molecular motors that are responsible for tightly packaging viral DNA into a preassembled procapsid shell, ultimately condensing DNA to liquid crystal density, which generates over 25 atmospheres of internal capsid pressure (14, 16, 58). Not surprisingly, these ATP-fueled motors are among the most powerful biological motors characterized to date. As with most biological motors, the viral terminase enzymes function as oligomeric complexes.

In this study, we have examined the physical properties of λ-terminase in solution and the data demonstrate that 1) the terminase protomer, which is composed of one large TerL and two small TerS subunits, is stable over at least a tenfold concentration range; that 2) the protomer undergoes a reversible, protomer-tetramer equilibrium with no evidence of intermediate species or further aggregation; and that 3) protomer self-assembly is thermodynamically linked to salt interaction. We have further demonstrated that the tetramer assembles into a ring-like structure with a compact central stem and four flexible extended arms, and that activation of the packaging ATPase directly correlates with ring-tetramer assembly. Importantly, the results provide a rigorous characterization of protomer self-assembly under physiologically relevant conditions (200–300 mM salt). This serves as an essential foundation toward our understanding of the complex interactions among terminase, E. coli IHF, and viral DNA in the assembly of a powerful genome packaging motor. Of what biological significance are these observations?

The functional λ-motor complex is a ring-tetramer of terminase protomers

Terminase enzymes serve two essential functions in the assembly of a viral particle—excision of a single genome from a concatemeric precursor (genome maturation) and concomitant translocation of the duplex into a preformed procapsid shell (genome packaging). Lambda-terminase possesses a number of catalytic activities that work in concert to perform these functions, including a cos-cleavage endonuclease activity that matures the genome end, a duplex translocation (DNA packaging) activity, and an ATPase activity that fuels the translocation reaction. The mechanism by which motor activity is regulated for specific and efficient packaging of viral DNA is not clearly understood in any system. We have proposed that a terminase ring tetramer is responsible for all of these reactions (29, 30, 33). The analytical ultracentrifugation and EM structural data presented here confirm that the protomer indeed assembles into a tetrameric ring structure and the kinetic data demonstrate that the packaging ATPase activity of the enzyme is directly associated with this complex. Thus, the data directly links ring-tetramer assembly and motor activation.

Assembly of a functional λ-motor in vivo

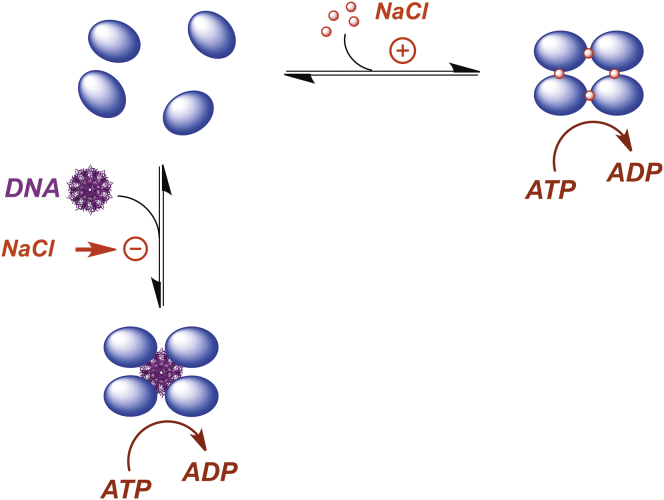
The studies presented here reveal the thermodynamic features associated with ring-tetramer assembly and suggest a mechanism for how motor assembly, and thus catalytic activity, may be controlled in vivo. The terminase concentration during a productive infection is 50–100 nM (59, 60). Given that the concentration of salt in the E. coli cell is 200–300 mM and that the K_D,app for ring assembly is 3–4 μM under these conditions, the data indicate that terminase remains predominantly a protomer in vivo. Importantly, the protomer is catalytically silent and the first step in genome packaging must be assembly of the functional motor. In vitro, salt can be used to shift the equilibrium toward the tetramer, with a concomitant activation of catalytic activity. Of course, increasing the salt concentration is not an option in vivo where viral DNA mediates the assembly of a catalytically competent motor complex (28, 32, 33). Preliminary studies in our lab suggest that four protomers and IHF cooperatively bind to cos-DNA with a K_D ∼20 nM, commensurate with in vivo concentrations (T.-C.Y. D.O., S.J. Sanyal, Q. Yang, and C.E.C., unpublished data). We suggest that salt ions in vitro serve as a surrogate for the phosphodiester backbone, which drives ring tetramer assembly in vivo, as depicted in Fig. 8.

Figure 8.

Model for ion-linked (in vitro) and DNA-linked (in vivo) packaging motor assembly. (Blue oval) The terminase protomer is a stable complex composed of one large TerL subunit tightly associated with a dimer of TerS subunits, shown as a blue oval for simplicity. In vitro, assembly and activation of the ring tetramer motor is thermodynamically linked to salt binding. Under typical in vivo concentrations (100 nM), the protomer is the predominant species in solution. We suggest that the phosphate backbone of DNA mediates ring-tetramer assembly in vivo with concomitant activation of the packaging motor. Note that salt strongly inhibits terminase•DNA binding interactions. To see this figure in color, go online.

While admittedly speculative, this model is consistent with 1) the salt linkage data demonstrating that 3–4 ions are associated with ring tetramer assembly; 2) the kinetic data suggesting that four protomers are required for optimal activation of the maturation and packaging activities of the enzyme (28, 32); and 3) the observation that nonspecific DNA activates the ATPase activity of the protomer, ostensibly due to assembly of the catalytically competent ring tetramer on the duplex (28). As discussed above, preliminary analytical ultracentrifugation studies suggest four protomers assemble on DNA and activate the packaging ATPase under conditions of low salt (50 mM), consistent with the proposed model. This provides an ideal mechanism to regulate terminase such that neither the nuclease nor ATPase activities of the enzyme are turned on until after the motor has assembled onto duplex DNA; this prevents unbridled ATP hydrolysis and/or nonspecific nuclease activity that could be detrimental to virus development.

General features of viral genome packaging motors

Terminase enzymes alternate between highly stable, site-specifically bound maturation complexes and dynamic packaging motor complexes that sequentially excise and package individual genomes from a concatemeric DNA precursor (Fig. 1) (a notable exception is phage ϕ29, as discussed earlier). In the case of λ, the enzyme both initiates and terminates packaging at a specific cos sequence and thus packages a unit-length genome with complementary ends. The TerS subunit is responsible for specific recognition of cos at both ends of the packaging cycle and it is not surprising that the protomeric λ-terminase contains TerS stably bound to TerL to enable processive packaging of unit-length genomes. We note that the packaging motors found in the herpes virus groups are unit-length packagers that recognize specific a-sequences in a concatemeric genome precursor (61, 62). These eukaryotic motors are composed of three protein subunits (63), but the stoichiometry of the proteins in the functional motor remains unknown.

In contrast, the head full terminase enzymes exemplified in phages SPP1, T7, and T4 similarly initiate packaging at a specific pac sequence. Unlike λ, however, the motors translocate beyond the next downstream pac until the capsid (i.e., head) is fully filled with DNA. This affords a packaged duplex that is 102–110% of the full genome length (64) and possesses terminally redundant ends (8, 65). In these cases, the TerS subunits are only required to initiate packaging and there is no essential requirement for a stable TerL•TerS complex in the reaction. Indeed, this appears to be the case in phages T4 and T7 where the subunits interact weakly, if at all, in solution (20, 66, 67). The isolated TerL subunit from phage T4 exists as a stable monomer in solution but assembles as an apparent pentameric ring at the portal vertex of a procapsid to engender a functional packaging motor (while the TerS subunit, gp16, is essential for specific packaging of the T4 genome in vivo, it is dispensable to the packaging of nonspecific DNA in vitro (65, 66, 68, 69); thus, a functional, though nonspecific T4 motor may be assembled with only TerL subunits) (8, 19).

Interestingly, the TerL subunit from phage T7 distributes between a monomer and ring pentamer in solution, with the latter possessing ATPase activity; a pentameric ring is similarly observed bound to the T7 portal, which presumably represents the functional packaging motor (20). Thus, functional packaging motors in the head full phages appear to consist of a pentameric TerL ring without an associated TerS subunit. This is in contrast to the TerS-containing ring tetramer observed with λ and it is interesting to speculate that this may reflect the different packaging termination requirements in the unit-length versus head full packaging machines. These differential termination mechanisms possess distinct requirements for downregulation of the packaging ATPase and physically stopping the translocating motor so that the terminal cleavage event can take place. Whatever the case and despite these differences, the essential features of mechano-chemical coupling, translocation, and force generation by the motors are likely conserved among the systems. Thus, the thermodynamic features describing protomer assembly into a functional motor complex described here is not only fundamental to our understanding of the λ-motor, but is relevant to the function of all of the viral packaging motors.

Author Contributions

T.-C.Y. performed and analyzed the analytical ultracentrifugation studies and co-wrote the article; D.O. performed and analyzed the ATPase kinetic studies and co-wrote the article; L.N. and G.C.L. performed electron microscopy and analysis; and C.E.C. co-wrote the article.

Editor: James Cole.