Abstract
We have investigated the role of electrostatic interactions in the transport of nucleic acids and ions through nanopores. The passage of DNA through nanopores has so far been conjectured to involve a free-energy barrier for entry, followed by a downhill translocation where the driving voltage accelerates the polymer. We have tested the validity of this conjecture by using two toxins, α-hemolysin and aerolysin, which differ in their shape, size, and charge. The characteristic timescales in each toxin as a function of temperature show that the entry barrier is ∼15kBT and the translocation barrier is ∼35kBT, although the electrical force in the latter step is much stronger. Resolution of this fact, using a theoretical model, reveals that the attraction between DNA and the charges inside the barrel of the pore is the most dominant factor in determining the translocation speed and not merely the driving electrochemical potential gradient.
Introduction
The dynamics of biological polymers going through narrow channels is crucial in many biological processes: RNA export through the nuclear pore complex, phage DNA ejection, and protein translocation through membranes. It is, as well, an important phenomenon to control in most of the DNA sequencing methods using nanopores. Polymer translocation experiments, theoretical models, and simulations, have been performed to study the translocation dynamics dependence on polymer type (1, 2, 3, 4, 5, 6), polymer length (7), voltage applied (6, 8), temperature (8, 9), ionic strength (10, 11), and nanopore nature (12, 13). Voltage dependence associated with barrier-crossing formalism allowed some authors to extract an entry barrier height (5, 8, 11, 14, 15). Some other publications modeled the energy landscape of translocation (16, 17) to get insight into the dynamics. Even though the temperature effect on transport dynamics has been already addressed, no interpretation of the thermodynamics of the process has been extracted except in the simulations of Matysiak (18) and, recently, a study by Mahendran and colleagues on the transport of polypeptides (19). The effect of the electrostatic interaction between the translocating chain and the pore wall charges have been studied by others (12, 20, 21) by tuning either the pore wall charges or the polymer charge. All underline the importance of electrostatic interactions in the transport.
The forces between the protein pore and DNA under nonequilibrium conditions are very complicated. As a result, the experimental data reported in the literature so far are only phenomenological. From the theoretical perspective, only simple models have been presented, without any quantitative comparison with experimental data or any validation of assumptions used in the models. Basically, there have been two models: 1) a particle-virtual-pore model, and 2) a polymer threading model (22). The major focus of theoretical predictions has been on the voltage dependence or DNA-length dependence of the average translation time. Although there have been several molecular dynamics simulations to explore the DNA motion inside a protein pore, the long time regime relevant to DNA translocation through protein pores remains to be explored. On the other hand, theoretical models are more suited to interpret experimental data due to their capacity to address longer time regimes relevant to experiments. However, there currently exists a critical need to interpret carefully acquired experimental data on different systems with any theoretical model. Furthermore, although free-energy barriers are invoked in theoretical models, the magnitude of these barriers remains to be established. An approach combining experiments and theory will enable a deeper understanding of the nature of various forces and barriers dictating the translocation kinetics of DNA through protein pores. That is the primary purpose of this article.
Toward achieving this goal, we have investigated two pores, α-hemolysin (αHL) and aerolysin (AL), and monitored the ionic current and DNA transport through them. Since the nature of the free-energy barriers for these transport processes is our focus, we have measured the effect of temperature on the ionic current and DNA translocation for both pores. Regarding an explanation of the observed ionic current through the pores, we used the one-dimensional (1D) Poisson-Nernst-Planck equation. In interpreting the DNA data, we theoretically modeled the free-energy landscape for threading by including a mean electrostatic interaction energy averaged over the whole length of the protein pore.
The main observations for the open-pore current are 1) rectification in the ionic current, and 2) Arrhenius-type temperature dependence. Modeling the rectification requires knowledge of the internal charge decoration of the pores. The inner structure of αHL is well known (23), but the crystal structure of the aerolysin pore is not yet available, although the group of F. Gisou van der Goot puzzled out a possible amino acid sequence which forms the β-barrel (24). In this article, we verify the adequacy of this sequence from the electrostatic point of view by measuring the open-pore current and its rectification as a function of temperature. The rectification is known to be strongly dependent on the electrostatic potential seen by the flowing ions, i.e., the amino acid sequence (25, 26, 27, 28). The two pores used here differ in their shape, size, and charge. αHL has a mushroom shape with a voluminous extramembrane part (the so-called vestibule) and a transmembrane part with a smaller constriction of ∼1.4 nm (23). Its overall charge is +7e. The AL pore has an extramembrane part lying on top of the membrane (no vestibule) and a transmembrane part with a constriction estimated to be between 1 and 1.7 nm (29). Its overall charge is −52e.When the details of charge distribution are included in the 1D Poisson-Nernst-Planck equation, the experimentally observed rectification can be readily accounted for. The observed Arrhenius-type barrier for the open-pore current is essentially due to the viscosity of the electrolyte solution.
One of the key results deduced from the temperature dependence of translocation dynamics through αHL and AL is that the energetics of DNA capture at the pore and the subsequent threading through the pore are distinctively different. Although both the capture and threading obey the Arrhenius-type law, the barrier for capture is about , whereas the barrier for threading is much higher, namely . This remarkable result is not anticipated, because the rate-limiting step of polymer translocation has so far been assumed to be the capture process, with the threading process as a downhill (in free energy), accelerated expulsion of DNA from the pore.
Toward an understanding of these intriguing experimental results, and to gain physical insight without much numerics, we have implemented the analytically tractable polymer threading model (30) for the experimental situation presented here. In this model, the segments of a flexible polyelectrolyte chain thread through a nanopore in single file under an electrophoretic force, and there is an attractive interaction between the pore and every polymer segment inside the pore. Calculations based on this model using the Fokker-Planck formalism show that the unexpected large free-energy barrier for the threading stage can be attributed to the amplification of local pore-polymer attraction by the pore length. The comparison between experimental results and the value of the pore-polymer interaction energy used in the theoretical model enables the tunability of the barrier for translocation and hence its speed.
Materials and Methods
The experimental setup is composed of a Teflon cell inside a Faraday cage. The cell is made of two 90 μL chambers connected by a U-shape tube ended at one side by a 10 to 20 μm hole on which the lipid bilayer is formed. Ag/AgCl electrodes are connected to each chamber to measure the ionic current, and the transmembrane voltage is applied using an Axopatch 200B amplifier (Molecular Devices, Sunnyvale, CA). The signal is first low-pass filtered by a four-pole Bessel filter with a cutoff frequency of 100 kHz (Khron-Hite, Brockton, MA), or 30 kHz in some cases using AL pores when the noise was too high to detect the events on the fly (especially at 60°C). It is then digitized at a sampling frequency of 1 MHz using a 16-bit acquisition card (National Instruments, Austin, TX) and finally saved directly to the hard drive of a computer. The acquisition card is controlled via a homemade program written with LabView (National Instruments).
The Teflon cell, embedded in a copper holder, is thermalized at a temperature varying from 5 to 70 ± 0.1°C using a Peltier module connected to a temperature controller (Newport, Irvine, CA). For temperatures of 25–70°C, the evaporation of water is not negligible, inducing an increase of the salt concentration and therefore a variation of the baseline current. We thus add water at a rate of 7 μL/h at 25°C to 64 μL/h at 70°C. This problem needs to be addressed carefully, because the frequency of entry of the DNA increases exponentially with salt concentration, as demonstrated in Bonthuis et al. (10). In the Supporting Material, we show an evolution of the event frequency as a function of the open-pore current while the water evaporates (see Fig. S6).
Lipids are diphytanoilphosphatidylcholine (Avanti Lipids, Alabaster, AL). The αHL toxin was purchased from Sigma Aldrich (St. Louis, MO) and dissolved in water at a concentration of 1 μg/μL and added directly to the chamber solution to a final concentration of 1–10 μg/mL. The AL toxin was synthetized using a procedure described in the literature (6, 31) and briefly in the Supporting Material. The final concentration of AL in the chamber is 1–10 μg/mL.
Single-stranded DNA (ssDNA) was purchased from Eurogentec (Liege, Belgium). Their sequence is and they were used with a final concentration in the cis chamber of 0.1–2 μM.
Results and Discussion
We first present results on the temperature dependence of the open-pore current through αHL and AL, followed by DNA transport through these pores.
Current-voltage curve of the open pores
The ionic current characteristics of the pores are measured by their current-voltage (I-V) curves and the asymmetry displayed in these curves. The I-V curves obtained at 15°C for both pores are presented in Fig. 1. The αHL I-V curve is very similar to those measured in numerous previous studies (for instance, Meller and Branton (8), Bonthuis et al. (,10), and Misakian and Kasianowicz (27). The only I-V curve of the AL pore that could be found in the literature is in the study by Pastoriza-Gallego et al. (6), using an upside-down orientation of the electrodes. The asymmetry observed on an I-V curve is defined from the open-pore currents measured at a voltage mV. Thus, it obviously depends on the orientation of the pore with respect to the electrode. Therefore, we followed the procedure detailed in the Supporting Material. We indeed observe that >90% of the pore insertions yielded to an I-V curve oriented as in Fig. 1.
Figure 1.
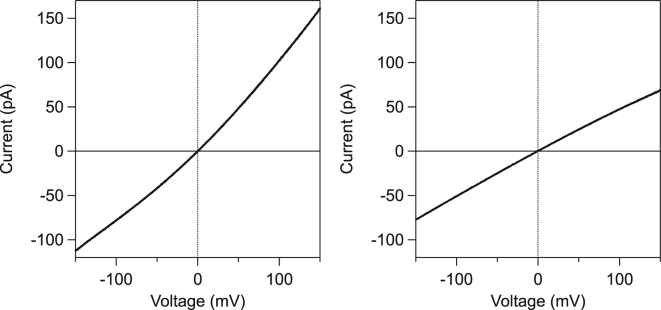
I-V curves at 15°C in 1 M KCl of (left) αHL pore and (right) AL pore. The αHL pore produces a convex I-V curve with an asymmetry of ∼30% . The AL pore produces a concave I-V curve with an asymmetry of ∼10% . Asymmetry, α, is defined in the text.
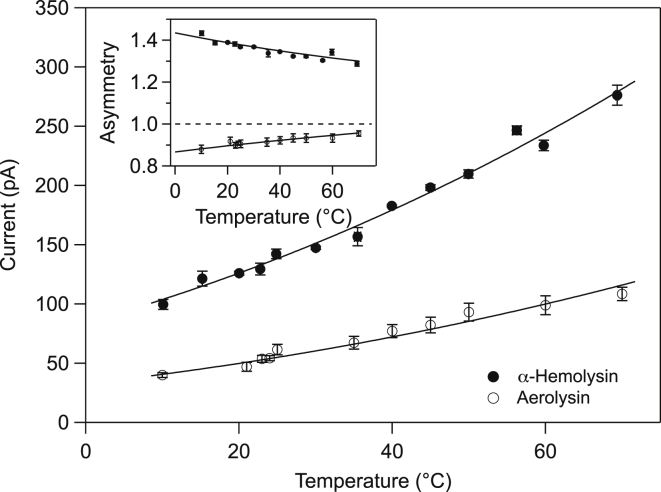
This measurement is repeated at different temperatures from 5 to 70°C. We represent in Fig. 2 the pore current as a function of temperature for an applied voltage of +120 mV. We observe a large increase of the current due to temperature (8, 32). The increase closely matches the change in viscosity of the solution as underlined in Meller and Branton (8) for a smaller range of temperature. It is common to associate the change of viscosity to a barrier-crossing process. Fitting the pore current as a function of temperature by an Arrhenius law gives an energy barrier of ∼ , which is very close to the value obtained in Mahandran and Lamichhane (19). This is consistent with the value obtained by considering tabulated measurements of the bulk conductivity (33). Therefore, the main contributor to the current increase with temperature is the bulk behavior itself.
Figure 2.
Ionic current for 120 mV applied voltage versus temperature for αHL (solid circles) and AL pores (open circles). The plain curves represent fits to Arrhenius law leading to an energy barrier of ∼5kBT. (Inset) The measured asymmetry factor, α, at 120 mV for both pores, with symbols defined as in the main figure. The plain curves are the asymmetry calculated following the procedure of Misakian and Kasianowicz (27) using the amino acids positions reported in Table S1.
In the inset of Fig. 2 is represented the asymmetry factor of the current, calculated as , where and are the current measured at and , respectively, as in Bhattacharya et al. (28). Therefore, α tends to 1 when the curve tends to be symmetrical. In addition, α is >1 if the I-V curve is convex, as for αHL (see Fig. 1, left) and α is <1 if the curve is concave as for AL (see Fig. 1, right).This definition eliminates the contribution of solvent conductivity to ionic-current variations.
The asymmetry observed depends on the interaction potential seen by the ions along the pore and can be modeled using the 1D Poisson-Nernst-Planck equation. Following the procedure of Misakian and Kasianowicz (27), we have calculated the asymmetry for αHL using the coordinates of the amino acids in the β-barrel from the Protein Data Bank file. For AL, we used the β-barrel sequence of amino acids defined by Iacovache et al. (24, 34) by sequence matching with toxin sequences of the same family. The positions of the charged amino acids along the pore are indicated in Table S1 and the potential is represented in Fig. S1. The calculated asymmetry versus temperature is displayed in the inset of Fig. 2 along with experimental results. Using this model, we obtain a good match between experiments and calculation for both pores; the mean diameter of the channel used to get the best match is 1.6 nm for αHL and 1.4 nm for AL. The sequence identified by Iacovache et al. (24) nicely characterizes the current measured.
It is usually considered that the pore-current asymmetry is a combination of pore geometry and surface charge density (see, for instance, Siwy et al. (35) on conical solid-state pores). The important part is really an asymmetry of the electrical potential felt by the ions flowing through the pore (due to the geometry or the asymmetric surface charge density). It is worth noticing that the αHL barrel is bearing five rings of charges (one positive and one negative at the cis entrance and two negative and one positive at the trans side of the pore), with a globally negative charge. The AL pore barrel is bearing seven rings of charges (four positive and three negative), with a positive global charge. Even though the pore is considered cylindrical, the differing distribution of the charges is enough to explain the differences in I-V curve between αHL and AL pores.
DNA transport dynamics
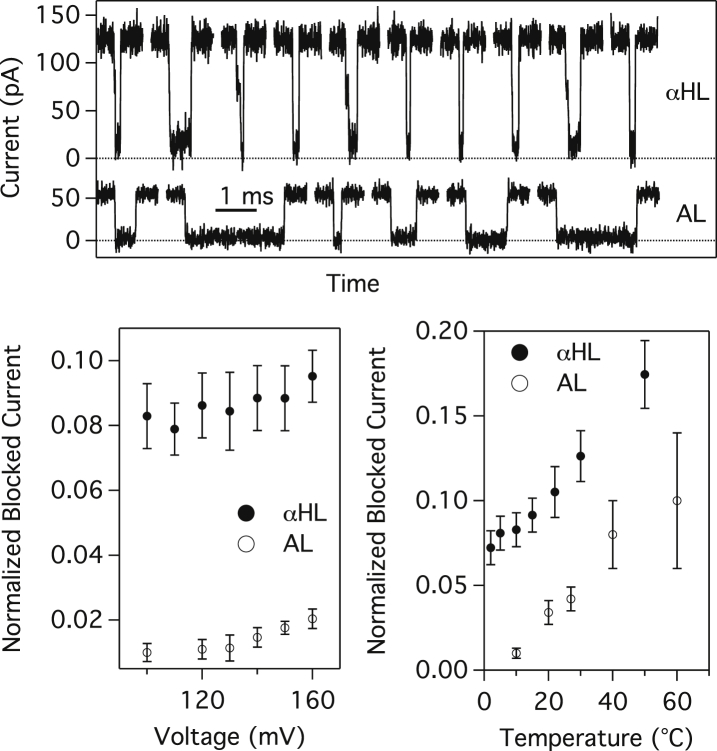
The DNA used to perform the translocation measurements are added to the solution of the cis chamber after stabilization of the desired temperature, T. We measure the translocation time and the event frequency either at constant T and as a function of the voltage applied, V, or at constant V and as a function of T. Typical traces of translocation events for αHL and AL are given in Fig. 3 (top).
Figure 3.
(Top) Examples of DNA translocation events observed in αHL and in AL at T = 20°C and V = 120 mV. The timescale is represented by a 1 ms bar. (Bottom) Variation of the normalized blocked current as a function of voltage applied at 10°C (left) and variation of the normalized blocked current as a function of temperature at a voltage of 120 mV (right) (αHL, solid circles; AL, open circles). The normalized blocked current increases slowly and uniformly with voltage and with temperature. The error bars represent the width of the normalized-blocked-current distribution.
First, for the AL pore, we observe at low voltage (70 mV) that the duration of the events is short (∼10 μs) and it increases with the voltage applied (see Fig. S2). We therefore conclude that these events do not represent molecules translocating through the pore. Starting at 100 mV, we observe much slower events ( 10 ms) with a lower blocked current. Their duration decreases with the voltage applied. We thus consider these slower events as translocation through the pore of aerolysin. The event frequency was calculated from these last events only. We therefore chose to perform the measurement at various temperatures at mV.
The mean current during DNA translocation divided by the open-pore current defines the normalized blocked current. For αHL, the normalized-blocked-current histogram always shows two distinctive peaks. These two peaks were previously reported (36) as the blockade obtained by translocation of the DNA by its 3′ end or by its 5′ end. As a function of the voltage (Fig. 3, bottom left), the normalized current peak increases slightly between 100 mV and 160 mV from 0.079 to 0.095. This peak corresponds to the major one, meaning the 3′ peak. The behavior of the 5′ peak is very similar but shifted up to a mean normalized blocked current of 0.11 (not shown). The relative amplitudes of the two peaks do not significantly change with voltage. For AL pores, only one main peak is observed centered around a normalized blocked current of 0.010 (at 120 mV) up to 0.020 (at 160 mV). We could distinguish rare events with a normalized current of 0.04 at the highest voltages. As the AL pore is narrower than the αHL pore, it is normal to observe a lower blockade current in similar conditions. As a function of temperature, we observe as well an increase of the blocked current, which is similar for both pores. If we consider an Arrhenius behavior for the blocked current, as was found for the open-pore current, we obtain energy barriers of ∼5kBT and 12kBT for the αHL and AL pores, respectively. The large difference between the two pores may be due to the energy needed to confine the ion in the remaining space between the pore and the DNA. Considering the energy barrier calculation in Bonthuis et al. (10) and a diameter of 1.6 nm and 1.4 nm for αHL and AL, the ratio of the energy barrier should be 2.2, close to what we obtain experimentally. Nevertheless, the current measurements are extremely sensitive to the filtering of the signal, especially at short event duration (31). This explains the increasing error bar at high temperatures, where the AL pores are not as stable as at lower temperatures, and it was necessary to filter the signal to 30 kHz.
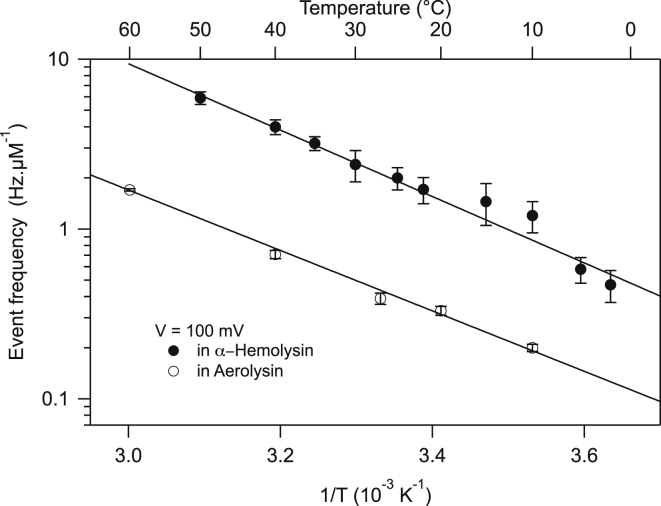
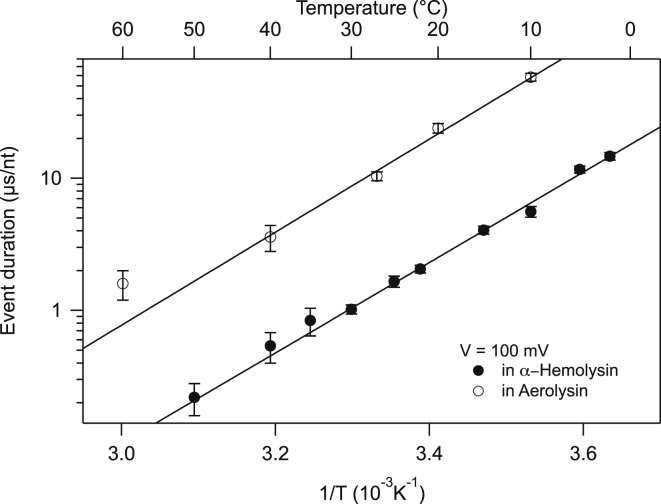
We represent in Figs. 4 and 5 our measurements under the conditions previously stated for the frequency of entry into the pore and the translocation time, respectively. As a reference, we show in Figs S3 and S4 the frequency of events and translocation times at constant C as a function of voltage. These results are very similar to what can be found in the literature (8, 14), although we could not find extensive study of DNA transport through AL pores.
Figure 4.
Event frequency per unit of concentration versus temperature for αHL (solid circles) and AL pores (open circles) measured at a voltage of 100 mV. The plain curves are fits to Arrhenius law, leading to an enthalpic barrier of 15kBT for both pores.
Figure 5.
Translocation time per nucleotide versus temperature for αHL (solid circles) and AL pores (open circles) measured at a voltage of 100 mV. The plain curves are fits to the model presented in the text. They could equally be fitted to Arrhenius law, leading to an enthalpic barrier of 35kBT for both pores. At high temperature, the value of the translocation time in AL deviates significantly from the fit. This is due to the fact that at this short timescale, our detection system reaches its limits. This effect has already been reported for protein transport through αHL and AL (9). Here, the αHL data set is not affected by this because of its much higher signal/noise ratio.
The translocation of a polymer through a protein pore involves two steps of first nucleating across a free-energy barrier of entry into the pore and subsequently moving down a free-energy landscape along the pore by a combination of diffusion and drift processes. The free-energy landscape for a particular combination of polymer and pore is nonuniversal and depends sensitively on the polymer sequence, the distribution of hydrophobic and charged amino acid residues inside the pore, and the magnitude of the electrochemical potential gradient driving the translocation. During translocation, the monomers are subjected to highly heterogeneous patterns of charges, dipoles, and hydrophobic patches. A precise computation of the free-energy landscape for transporting through αHL and AL pores is impossible due to the lack of adequate knowledge of electrohydrodynamic forces inside the protein pore environment. Nevertheless, it is widely recognized that electrostatic interactions play an important role in the translocation process of DNA through αHL, as noted in Rincon-Restrepo et al. (12). Those authors observed that the translocation time is exponentially dependent on the number of positively charged amino acids in the barrel of the channel. From their measurements, and considering the number of charges present in the barrels of αHL (14 total) and AL (28 total), the translocation times should display an ∼10-fold difference, as is observed in our experiments. It was also proposed in theoretical and numerical work that attractive interaction between polymer and pore plays an important role in the transport dynamics (37, 38, 39). In that respect, we model the DNA-pore interactions by an electrostatic contribution globally located all along the pore. Given the complexity of chemical details on the pore surface, and the necessity to account for the pore-polymer interaction, we coarse-grain the chemical details and assume that there is a uniform interaction energy per monomer, , all along the pore (30).
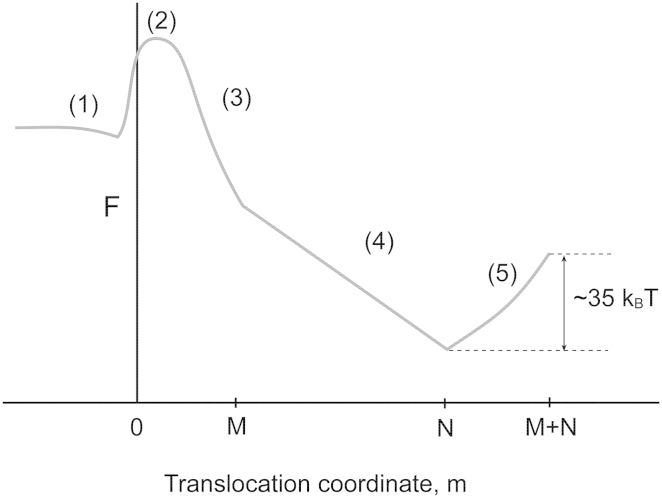
The generic nature of the free-energy landscape can be seen in Fig. 6. For the sake of clarity of the basic conceptual issues, we consider a uniform pore of length and a uniformly charged polymer of length , where a is the monomer length and . Under an applied voltage, , the monomers in the polymer chain translocate through the pore in single file.
Figure 6.
Sketch of the free-energy landscape for single-file translocation of a chain of N monomers through a pore of M monomer lengths. The translocation coordinate, m, denotes the number of monomers depleted from cis until it reaches the value N (with either m monomers inside the pore and monomers in cis or with M monomers inside the pore, monomers in cis and monomers in trans). For , the pore is partially filled, with the rest of the chain solely in trans. The key steps in the free-energy landscape are 1) placement of one chain end at the pore entrance; 2) entropic barrier crossing to nucleate a successful translocation by squeezing a large enough number of monomers into the pore; 3) a gain in electrostatic energy and pore-polymer interaction energy as more monomers enter an attractive pore under a favorable voltage gradient; 4) transfer of monomers from cis to trans with the pore remaining fully filled; and 5) an uphill process of polymer depletion from the pore. Steps 1 and 2 constitute the nucleation barrier controlling the translocation frequency. Steps 3–5 contribute to the translocation time. The barrier for the translocation time is attributed to the depletion of M monomers from the pore. Using , , and , the effective free-energy barrier for extraction of the last M monomers is ∼35kBT.
The essential features of the free-energy profile for translocation are 1) drift diffusion followed by an entropic barrier associated with placement of one chain end at the pore entrance; 2) an entropic barrier of squeezing enough monomers into the pore to ensure successful nucleation; 3) a free-energy gain (attractive pore, ) or loss (repulsive pore, ) associated with filling the pore in addition to the electrostatic energy gain for packing monomers into the pore; 4) a free-energy gain associated with the transfer of monomers from cis to trans while the pore is filled with M monomers; and 5) a free-energy barrier for removing M monomers trapped inside the attractive pore into trans. These five steps are depicted in Fig. 6. The translocation coordinate, m, denotes the number of monomers depleted from cis until m reaches N. For , it corresponds to a state where the pore is partially filled, with the rest of the chain being in the trans.
In general, the frequency of events is the nucleation rate across the initial barrier (associated with steps 1 and 2) and the translocation time (associated with steps 3 to 5). Clearly, the effective barriers for the event frequency and translocation time can be uncorrelated. Writing the nucleation barrier, , as , for steps 1 and 2 of Fig. 6, the event frequency, , is
| (1) |
where is the entropic contribution to the barrier.
Experimentally, the event frequency at constant 10°C follows the two regimes in αHL already reported (8) (see Fig. S3). At low voltage, the frequency is reaction-limited by an energy barrier of entry, and at high voltage, the frequency is diffusion-limited. Comparing the data obtained at 10°C, the frequency of entry is six to eight times smaller in AL than in αHL. Using the barrier-crossing formalism introduced in Henrickson et al. (14) (reviewed in the Supporting Material), we deduce an energy barrier of entry of 10kBT for both pores. This value is of the same order as entry barriers in the literature: 8kBT for DNA (14) and for proteins (15) or 10kBT for dextran sulfate (5). At constant voltage, the frequency displays an Arrhenius behavior as a function of temperature, yielding an enthalpic barrier contribution of . The difference between the two estimates of this barrier comes from physical parameters like the solvent viscosity that are influenced by temperature but not by voltage. The six- to eightfold difference in event frequency between the two pores underlines an entropic contribution that is twice as large in AL as in αHL, certainly due to the vestibule shape of αHL acting as a funnel and favoring entry. It is also due to the AL constriction being smaller than that for αHL.
Regarding the event duration, at constant T, we observe a decrease of the translocation time with an increase in applied voltage (see Fig. S4), and the time measured in AL is ∼10-fold larger than in αHL. Again, the AL constriction is smaller than that for αHL. The constriction size deduced from the current and asymmetry measurements yields a difference in pore size of only ∼10%. Thus, this huge difference in event duration has to be due to interactions between the pore and the DNA molecule.
The free-energy profile felt by the DNA along the translocation process (steps 3 to 5 of Fig. 6) is written as follows, as originally described in Muthukumar (30). In step 3, m monomers are inside the pore without completely filling the pore and the rest of the monomers are in cis. The free energy of this state has three contributions. a) There is attractive energy between the m monomers and the pore, . b) There is an electrostatic energy gain. At a distance from the pore entrance, the potential energy of a monomer is , where q is the effective charge of the monomer, e the electronic charge, and the electric field across the pore (assuming that the voltage drops linearly across the pore of length ). Therefore, when m segments are inside the pore, the electrostatic energy gain for all of these monomers is the integral of this expression over , which gives . c) There is a conformational entropic penalty from monomers in cis. This contribution to free energy is , where is ∼0.69 for the conditions of typical nanopore experiments and kB is the Boltzmann constant. As it turns out that the logarithmic term is negligible in comparison with the other two contributions, this part may safely be neglected. Therefore the free energy of the state with m monomers inside the pore but not filling it is given by
| (2) |
where and . It is to be noted that the timescale for equilibration of the polymer tail with monomers in cis is a moot issue in the model presented here, since is negligible in comparison with the two terms on the righthand side of the above equation.
It is straightforward to extend the above argument for steps 4 and 5, as given by Muthukumar (30), and obtain
| (3) |
and
| (4) |
The translocation time corresponds to the time taken by a chain to pass through the pore from the entry point to the exit point . As also recognized in the literature, this is a stochastic variable and this quantity can be determined only in some statistical sense. The theoretical machinery most suited to connecting the free-energy landscape and the time evolution of the probability of realizing a particular state is the Fokker-Planck formalism (40). In general, the Fokker-Planck equation for the situation presented here is
| (5) |
where D is the monomer diffusion coefficient inside the pore (30, 40, 41). Substitution of Eqs. 2–4 into Eq. 5 gives the time dependence of the probability of realizing a particular value of m in the translocation coordinate. The translocation time corresponds to the state of . Using standard procedures in the Fokker-Planck formalism, the average translocation time, τ, is given by
| (6) |
where is given by Eqs. 2–4. In defining τ, we used the reflecting boundary condition at and the absorbing boundary condition at .
For the ssDNA, we took the average monomer length, a, as 0.34 nm and N as 50. Taking the length of the β-barrel of the protein pore as 5 nm, . For (as suggested by the Manning condensation), and , the calculated τ is given in Fig. 5 along with the experimental data for αHL and AL pores. In making the comparison, the arbitrary shift factor is chosen as . The effective barrier is 35kBT and arises from the last step (step 5) of depletion of the polymer from the pore. Although the pore-monomer interaction is rather weak (∼2.5kBT), the barrier for translocation is amplified by the depletion stage. We observe a similar enthalpic contribution in αHL and AL pores. The main difference between the translocation times in the two pores arises from the entropic contribution, even though the pore barrels do not bear the same charges.
Because the main feature of the free-energy landscape of Fig. 6 is the energy of extraction of the M last monomers out of the pore, the temperature dependence is similar to a single barrier process. This is indeed what is observed experimentally despite the apparent complexity of the free-energy landscape. Although the theoretical model uses an interaction energy between a DNA segment and the pore, the precise nature of the molecular origin of the barrier remains to be explored.
Conclusions
In conclusion, we have used the electrostatic interactions created by the pore-wall charges with either the ions or the translocating DNA chain to model the ionic I-V curve and the DNA transport dynamics, respectively, in αHL and AL nanopores. The ionic current rectification versus temperature arises from the local energy landscape felt by the ions when going through the pore. Furthermore, our rectification analysis validates the sequence presumed in the literature to be responsible for the barrel formation of AL pores. This barrel bears twice as many positively charged residues as the αHL pore, which can thus greatly influence the polyelectrolyte transport.
About the dynamics of transport of DNA through the pores, the existing paradigm is that there is one energy barrier in the translocation process for entry into the pore followed by a downhill fall along the electric potential. From the Arrhenius plots of the translocation time in both pores, we observe that there is as well an energy barrier to exit the pore. This could only be demonstrated by studying the temperature influence on the transport dynamics. Previous articles on DNA transport have focused on the voltage dependence of the translocation time leading to an effective charge, a sort of lever arm to decrease the barrier height. Surprisingly, the entry barrier (15kBT) is much smaller than the barrier of translocation (35kBT), despite a much stronger driving electric field in the pore compared to the outside.
The model we present reveals the mechanism of the process. We model the electrostatic interaction felt by the DNA in the pore by a mean interaction potential per monomer, and the experimental results are fitted by this model. The global energy barrier of ∼35kBT for both pores leads to a 2.5kBT interaction energy per monomer inside the pore channel.
The experimental data along with the theoretical model reveal the importance of the interaction between DNA and the charge decoration inside the pore, which dominates the DNA translocation kinetics. This has profound implications for controlling the speed of DNA transport. The full energy landscape, including electrostatics and hydrophobicity, is very complex, and a later study will take into account local features of the energy landscape, allowing a more precise description of the process and a better understanding of the tunable parameters to control the translocation kinetics.
Author Contributions
L.P. and M.M. did the DNA translocation experiments in AL and αHL pores. C.M. did open-pore measurements of aerolysin pores. M.P.G. and J.P. produced the AL protein monomers. V.V. and L.A. were involved in data analysis and in the discussion of this article. M.M. developed the theoretical model and wrote the article. J.M. designed the experiment, did the IV curve calculations and the data analysis, and wrote the article.
Acknowledgments
We thank F. Gisous Van Der Goot for the vector recombinant aerolysin.
At the time of the data acquisition, L.P. and M.M. were postdoctoral fellows of Genopole. This work was supported by grant funding from the Agence Nationale de la Recherche, Blanche project TRANSFOLDPROT (ANR-BLAN08-1_339991), the National Institutes of Health (grant R01HG002776-11), and the Air Force Office of Scientific Research (grant FA9550-14-1-0164).
Editor: Hagan Bayley.
Footnotes
Supporting Materials and Methods, six figures, and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00926-1.
Supporting Material
References
- 1.Akeson M., Branton D., Deamer D.W. Microsecond time-scale discrimination among polycytidylic acid, polyadenylic acid, and polyuridylic acid as homopolymers or as segments within single RNA molecules. Biophys. J. 1999;77:3227–3233. doi: 10.1016/S0006-3495(99)77153-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Meller A., Nivon L., Branton D. Rapid nanopore discrimination between single polynucleotide molecules. Proc. Natl. Acad. Sci. USA. 2000;97:1079–1084. doi: 10.1073/pnas.97.3.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Muthukumar M. Theory of sequence effects on DNA translocation through proteins and nanopores. Electrophoresis. 2002;23:1417–1420. doi: 10.1002/1522-2683(200205)23:10<1417::AID-ELPS1417>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 4.Oukhaled A.G., Biance A.-L., Bacri L. Transport of long neutral polymers in the semidilute regime through a protein nanopore. Phys. Rev. Lett. 2012;108:088104. doi: 10.1103/PhysRevLett.108.088104. [DOI] [PubMed] [Google Scholar]
- 5.Brun L., Pastoriza-Gallego M., Pelta J. Dynamics of polyelectrolyte transport through a protein channel as a function of applied voltage. Phys. Rev. Lett. 2008;100:158302. doi: 10.1103/PhysRevLett.100.158302. [DOI] [PubMed] [Google Scholar]
- 6.Pastoriza-Gallego M., Rabah L., Pelta J. Dynamics of unfolded protein transport through an aerolysin pore. J. Am. Chem. Soc. 2011;133:2923–2931. doi: 10.1021/ja1073245. [DOI] [PubMed] [Google Scholar]
- 7.Meller A., Nivon L., Branton D. Voltage-driven DNA translocations through a nanopore. Phys. Rev. Lett. 2001;86:3435–3438. doi: 10.1103/PhysRevLett.86.3435. [DOI] [PubMed] [Google Scholar]
- 8.Meller A., Branton D. Single molecule measurements of DNA transport through a nanopore. Electrophoresis. 2002;23:2583–2591. doi: 10.1002/1522-2683(200208)23:16<2583::AID-ELPS2583>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 9.Payet L., Martinho M., Mathé J. Thermal unfolding of proteins probed at the single molecule level using nanopores. Anal. Chem. 2012;84:4071–4076. doi: 10.1021/ac300129e. [DOI] [PubMed] [Google Scholar]
- 10.Bonthuis D.J., Zhang J., Meller A. Self-energy-limited ion transport in subnanometer channels. Phys. Rev. Lett. 2006;97:128104. doi: 10.1103/PhysRevLett.97.128104. [DOI] [PubMed] [Google Scholar]
- 11.Oukhaled A.G., Bacri L., Auvray L. Effect of screening on the transport of polyelectrolytes through nanopores. Europhys. Lett. 2008;82:48003. [Google Scholar]
- 12.Rincon-Restrepo M., Mikhailova E., Maglia G. Controlled translocation of individual DNA molecules through protein nanopores with engineered molecular brakes. Nano Lett. 2011;11:746–750. doi: 10.1021/nl1038874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pastoriza-Gallego M., Gibrat G., Pelta J. Polyelectrolyte and unfolded protein pore entrance depends on the pore geometry. Biochim. Biophys. Acta. 2009;1788:1377–1386. doi: 10.1016/j.bbamem.2009.03.011. [DOI] [PubMed] [Google Scholar]
- 14.Henrickson S.E., Misakian M., Kasianowicz J.J. Driven DNA transport into an asymmetric nanometer-scale pore. Phys. Rev. Lett. 2000;85:3057–3060. doi: 10.1103/PhysRevLett.85.3057. [DOI] [PubMed] [Google Scholar]
- 15.Oukhaled G., Mathé J., Auvray L. Unfolding of proteins and long transient conformations detected by single nanopore recording. Phys. Rev. Lett. 2007;98:158101. doi: 10.1103/PhysRevLett.98.158101. [DOI] [PubMed] [Google Scholar]
- 16.Kowalczyk S.W., Wells D.B., Dekker C. Slowing down DNA translocation through a nanopore in lithium chloride. Nano Lett. 2012;12:1038–1044. doi: 10.1021/nl204273h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Christensen C., Baran C., Lee J.S. Effect of charge, topology and orientation of the electric field on the interaction of peptides with the α-hemolysin pore. J. Pept. Sci. 2011;17:726–734. doi: 10.1002/psc.1393. [DOI] [PubMed] [Google Scholar]
- 18.Matysiak S., Montesi A., Clementi C. Dynamics of polymer translocation through nanopores: theory meets experiment. Phys. Rev. Lett. 2006;96:118103. doi: 10.1103/PhysRevLett.96.118103. [DOI] [PubMed] [Google Scholar]
- 19.Mahendran K.R., Lamichhane U., Winterhalter M. Polypeptide translocation through mitochondrial TOM channel: temperature dependent rates at single molecule level. J. Phys. Chem. Lett. 2013;4:78–82. doi: 10.1021/jz301790h. [DOI] [PubMed] [Google Scholar]
- 20.Maglia G., Restrepo M.R., Bayley H. Enhanced translocation of single DNA molecules through α-hemolysin nanopores by manipulation of internal charge. Proc. Natl. Acad. Sci. USA. 2008;105:19720–19725. doi: 10.1073/pnas.0808296105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Buchsbaum S.F., Mitchell N., Howorka S. Disentangling steric and electrostatic factors in nanoscale transport through confined space. Nano Lett. 2013;13:3890–3896. doi: 10.1021/nl401968r. [DOI] [PubMed] [Google Scholar]
- 22.Muthukumar M., Katkar H.H. Reading nanopore clocks in single-molecule electrophoresis experiments. Biophys. J. 2015;108:17–19. doi: 10.1016/j.bpj.2014.11.3452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Song L., Hobaugh M.R., Gouaux J.E. Structure of staphylococcal α-hemolysin, a heptameric transmembrane pore. Science. 1996;274:1859–1866. doi: 10.1126/science.274.5294.1859. [DOI] [PubMed] [Google Scholar]
- 24.Iacovache I., Paumard P., van der Goot F.G. A rivet model for channel formation by aerolysin-like pore-forming toxins. EMBO J. 2006;25:457–466. doi: 10.1038/sj.emboj.7600959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Noskov S.Y., Im W., Roux B. Ion permeation through the α-hemolysin channel: theoretical studies based on Brownian dynamics and Poisson-Nernst-Plank electrodiffusion theory. Biophys. J. 2004;87:2299–2309. doi: 10.1529/biophysj.104.044008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Aksimentiev A., Schulten K. Imaging α-hemolysin with molecular dynamics: ionic conductance, osmotic permeability, and the electrostatic potential map. Biophys. J. 2005;88:3745–3761. doi: 10.1529/biophysj.104.058727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Misakian M., Kasianowicz J.J. Electrostatic influence on ion transport through the αHL channel. J. Membr. Biol. 2003;195:137–146. doi: 10.1007/s00232-003-0615-1. [DOI] [PubMed] [Google Scholar]
- 28.Bhattacharya S., Muzard L., Viasnoff V. Rectification of the current in α-hemolysin pore depends on the cation type: the alkali series probed by molecular dynamics simulations and experiments. J. Phys. Chem. C Nanomater. Interfaces. 2011;115:4255–4264. doi: 10.1021/jp111441p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Parker M.W., Buckley J.T., Tsernoglou D. Structure of the Aeromonas toxin proaerolysin in its water-soluble and membrane-channel states. Nature. 1994;367:292–295. doi: 10.1038/367292a0. [DOI] [PubMed] [Google Scholar]
- 30.Muthukumar M. Polymer escape through a nanopore. J. Chem. Phys. 2003;118:5174–5184. [Google Scholar]
- 31.Merstorf C., Cressiot B., Mathé J. DNA unzipping and protein unfolding using nanopores. Methods Mol. Biol. 2012;870:55–75. doi: 10.1007/978-1-61779-773-6_4. [DOI] [PubMed] [Google Scholar]
- 32.Kang X.-F., Gu L.-Q., Bayley H. Single protein pores containing molecular adapters at high temperatures. Angew. Chem. Int. Ed. Engl. 2005;44:1495–1499. doi: 10.1002/anie.200461885. [DOI] [PubMed] [Google Scholar]
- 33.Wu Y., Koch W., Tomek A. A dc method for the absolute determination of conductivities of the primary standard KCl solutions from 0°C to 50°C. J. Res. Natl. Inst. Stand. Technol. 1994;99:241–246. doi: 10.6028/jres.099.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Degiacomi M.T., Iacovache I., Dal Peraro M. Molecular assembly of the aerolysin pore reveals a swirling membrane-insertion mechanism. Nat. Chem. Biol. 2013;9:623–629. doi: 10.1038/nchembio.1312. [DOI] [PubMed] [Google Scholar]
- 35.Siwy Z., Gu Y., Korchev Y. Rectification and voltage gating of ion currents in a nanofabricated pore. Europhys. Lett. 2002;60:349–355. [Google Scholar]
- 36.Mathé J., Aksimentiev A., Meller A. Orientation discrimination of single-stranded DNA inside the α-hemolysin membrane channel. Proc. Natl. Acad. Sci. USA. 2005;102:12377–12382. doi: 10.1073/pnas.0502947102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Luo K., Ala-Nissila T., Bhattacharya A. Influence of polymer-pore interactions on translocation. Phys. Rev. Lett. 2007;99:148102. doi: 10.1103/PhysRevLett.99.148102. [DOI] [PubMed] [Google Scholar]
- 38.Luo K., Ala-Nissila T., Bhattacharya A. Translocation dynamics with attractive nanopore-polymer interactions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;78:061918. doi: 10.1103/PhysRevE.78.061918. [DOI] [PubMed] [Google Scholar]
- 39.Anderson B.N., Muthukumar M., Meller A. pH tuning of DNA translocation time through organically functionalized nanopores. ACS Nano. 2013;7:1408–1414. doi: 10.1021/nn3051677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Muthukumar M. CRC Press; Boca Raton, FL: 2011. Polymer Translocation. [Google Scholar]
- 41.Muthukumar M. Communication: charge, diffusion, and mobility of proteins through nanopores. J. Chem. Phys. 2014;141:081104. doi: 10.1063/1.4894401. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.