Education, HIV, and Early Fertility: Experimental Evidence from Kenya

Abstract

A seven-year randomized evaluation suggests education subsidies reduce adolescent girls’ dropout, pregnancy, and marriage but not sexually transmitted infection (STI). The government’s HIV curriculum, which stresses abstinence until marriage, does not reduce pregnancy or STI. Both programs combined reduce STI more, but cut dropout and pregnancy less, than education subsidies alone. These results are inconsistent with a model of schooling and sexual behavior in which both pregnancy and STI are determined by one factor (unprotected sex), but consistent with a two-factor model in which choices between committed and casual relationships also affect these outcomes.

Early fertility and sexually transmitted infections (STIs), chief among them HIV, are arguably the two biggest health risks facing teenage girls in sub-Saharan Africa.¹ Since unprotected sex can lead to both early pregnancy and STIs, a natural assumption is that any policy that reduces unprotected sex will be effective at fighting both. However, policies which affect the choice between having a committed relationship with a single partner and having multiple casual partners may differentially affect teen pregnancy and STIs. Pregnancy may be relatively more likely in committed relationships while STIs may be relatively more likely in casual relationships. We argue that taking this distinction into account is essential to understanding the impact of different policies on teen pregnancy and STIs.

This paper provides evidence on how STI prevalence and teen pregnancy are affected by two leading policy instruments (and their interaction): education subsidies and HIV prevention education focused on abstinence until marriage. In conjunction with the Kenya Ministry of Education, the Kenya National AIDS Control Council, and the non-profit ICS Africa, we conducted a large randomized evaluation involving 328 schools in Western Kenya to compare the effectiveness of two programs conducted stand-alone or jointly: 1) the Education Subsidy program, which subsidized the cost of education for upper primary school students by providing two free school uniforms over the last three years of primary school; and 2) the HIV Education program in which three teachers in each primary school received government-provided training to help them deliver Kenya’s national HIV/AIDS curriculum, which, like many other curricula in Africa and some U.S. states, emphasizes abstinence until marriage as the way to prevent infection. We also estimate the impact of the HIV education program augmented with a small add-on component explicitly stressing condoms within the boundaries of the curiculum. We assess the short-, medium- and long-term impacts of these two programs, implemented alone or jointly, on sexual behavior, fertility, and infection with HIV and another STI, Herpes Simplex Virus type 2 (HSV2), using a panel dataset that covers a cohort of around 9,500 girls and 9,800 boys over 7 years. For both HIV and HSV2, a positive test result at a point in time reflects having ever been infected with the disease.

The study involved 328 schools in Kenya’s Western Province. All students enrolled in grade 6 in 2003 were sampled for the study and followed for seven years, from age 13.5 to 20.5 on average. Follow-up rates were very high. After 7 years, 54 percent of the sample could be interviewed and almost all of them agreed to be tested for HIV and HSV2. A random subsample of 29 percent of the remainder was then selected for intensive tracking, and 81 percent of them could be found and surveyed, for an effective follow-up rate at endline of 91 percent. The resulting data set is unique due to the combination of its size, the length of the panel, the successful tracking rate, the availability of biomarkers for HSV2 and HIV, and the randomized two-by-two design. HIV prevalence was extremely low in the sample, so we focus on HSV2 as our measure of exposure to STIs. Fertility is much less easily observable for boys, so we focus on girls for the fertility results.

We find a nuanced set of results:

1. When implemented alone, the education subsidy program significantly reduced primary school dropouts for both boys and girls and delayed the onset of girls’ fertility. Specifically, the program reduced the dropout rate after three years from 19 percent to 16 percent for girls and from 13 percent to 10 percent for boys, and the girls’ teen pregnancy rate fell from 16 percent to 13 percent within that time period. This reduction came entirely through a reduction in the number of pregnancies within marriage, and there was no change in the out-of-wedlock pregnancy rate. By year 7, there was still a 7 percent gap in the childbearing rate between girls exposed to the education subsidy program and those in the control group (46 percent vs. 49 percent). However, the education subsidy alone did not reduce the HSV2 infection rate among either girls or boys.

2. The HIV education program implemented alone did not significantly reduce teenage pregnancy, the risk of HSV2 infection, or schooling attainment among either boys or girls. For girls, the program led to more early pregnancies within marriage and fewer early pregnancies outside of wedlock, however.

3. When the two programs were implemented jointly, fertility fell less than when the education subsidy was provided alone, but HSV2 infections fell more (and significantly). Girls who received the combined program were 20 percent less likely to be infected with HSV2 after 7 years (a drop from 11.8 percent to 9.5 percent). There was no significant impact on the HSV2 infection rate among boys.

4. Finally, the add-on component to the education program that specifically introduced a discussion on condoms led to greater knowledge of condoms but no more reported use, and did not significantly change results (2) and (3) above.

The results for girls are surprising because the STI and teenage pregnancy results are not aligned. The only program that reduced STI prevalence (the joint program) is not the program that had the largest impact on pregnancy (the stand-alone education subsidy). The joint program had a smaller effect on girls’ teenage pregnancies than the stand-alone education subsidy, but a larger effect on HSV2 prevalence. We argue that this result is not compatible with a simple one-factor model in which the level of unprotected sex jointly determines both pregnancy and STI rates.

These results are, however, consistent with a richer model of sexual behavior with three features which are realistic in our context. First, teenage girls choose not only a level of unprotected sex, but also choose between “committed” partnerships (in which girls have a single partner who they believe is also committed to them, and will marry them in the event of a pregnancy), and casual sex, in which there is no expectation of marriage. The costs of pregnancy are perceived to be lower in committed than in casual relationships. Second, schooling and pregnancy are incompatible. This is a reasonable feature since, in many settings, including ours, pregnant girls historically have been expelled from school and the practice continues de facto if not de jure.² This makes the opportunity cost of pregnancy higher for girls who want to and are financially able to go to school than for girls who (or whose parents) have already chosen not to invest in schooling. The third feature is that girls perceive STI risk to be higher in casual than committed relationships, and the government’s HIV/AIDS education program focused on abstinence until marriage strengthens this perception. Since the cost of pregnancy and the risk of STIs are lower in committed relationships, in the model girls have more unprotected sex in committed relationships than in casual relationships.

While we do not present a formal test of the model, we show that it generates a series of comparative statics consistent with the data. First, education subsidies lead girls to have less unprotected sex (to avoid pregnancy), conditional on choosing either committed or casual relationships, but can also lead some girls to switch to casual relationships, since committed relationships entail a higher risk of becoming pregnant and having to leave school. Thus, education subsidies reduce teenage pregnancy, but they may not reduce STIs if casual relationships indeed carry greater STI risk and if unprotected sex is relatively inelastic to STI risk for a substantial fraction of girls. This seems plausible in our context, since just over one third of sexually active unmarried 15–19 year old girls in Kenya had ever used a male condom as of 2008/2009 (KNBS and ICF Macro, 2010).

Second, when the perceived STI risk from casual relationships increases, as with the abstinence until marriage message of Kenya’s national HIV prevention curriculum, unprotected sex within casual relationships decreases. But a change in perceived STI risk from casual sex also causes some girls to shift from casual to committed relationships. Since unprotected sex is more frequent within committed relationships than casual ones, the overall effect on teenage pregnancies and STIs is ambiguous, but the share of teenage pregnancies that are out-of-wedlock unambiguously decreases (and this is indeed the only significant impact we observe for the stand-alone HIV education program).

Finally, when both programs are implemented jointly, girls have greater incentive to avoid pregnancy so they can take advantage of cheaper education, but they also think that casual relationships carry higher STI risk. As a result, the joint program may have qualitatively different effects than would be suggested by a reduced form analysis of the two programs considered individually. In particular, for appropriate parameter values, the joint program will reduce unprotected sex within each type of relationship, but without causing the switches between relationship types generated by either program in isolation. A joint program may thus reduce STI risk, even if neither program does so in isolation. However it will lead to a smaller drop in pregnancy and a smaller increase in education than an education subsidy program alone. While the quantitative predictions depend on specific parameters, we show that the set of results we observe can indeed be obtained. This does not rule out other multi-factor models and we discuss alternative interpretations as we discuss the model. The main take-away, though, is that we are able to rule out a single-factor model.

The model suggests that certain institutions and features common in much of Africa may influence the results. In particular, results might differ if pregnant girls did not have to leave school, or if the elasticity of unprotected sex to perceived risk was higher, for example due to more widespread acceptance of condoms. HIV curricula in African schools typically emphasize abstinence until marriage, but one could imagine alternative programs designed to increase condom acceptability.

The paper contributes to three distinct strands of literature. First, we contribute to the literature on the link between education and fertility. In developing countries, studies have generally found a strong causal relationship between increases in education and reduced fertility (see for example Breierova and Duflo (2004) in Indonesia, Osilii and Long (2008) in Nigeria, Ozier (2011) in Kenya, Keats (2014) in Uganda, and Lavy and Zablotsky (2011) on Israeli-Arab women).³ Our finding that girls at the margin of dropping out of school in Kenya are able to delay pregnancy when the cost of education is reduced suggests that, for that age group, fertility and schooling decisions are often jointly made. This is consistent with recent evidence from India presented in Jensen (2012), who finds that an increase in young women’s perceived returns to education increased educational attainment and reduced marriage and fertility.

Second, we contribute to the literature on prevention of sexually transmitted infections among African girls. It is sometimes feared that involuntary sex is so common that education or incentive programs focusing on girls will have no impact on STIs. Yet, there are surprisingly few rigorous studies with objective biomarker outcome data on this issue (see McCoy, Kangwende and Padian 2010, for a review). An important exception is in Malawi, in which monthly cash transfers to the families of out-of-school girls significantly reduced HIV infection rates after 18 months (Baird et al., 2012). Another exception is a community trial in rural Tanzania, which found that a comprehensive adolescent sexual health program (which combined in-school sexual health education with community-based condom promotion and distribution) significantly affected HIV knowledge and attitudes, but did not consistently reduce STIs (including HIV) in either the short-or the long-run (Ross et al., 2007; Doyle et al. 2010). With 20 communities, the study may have lacked power, however. Dupas (2011), in the same setting as ours, shows that informing girls that cross-generational relationships are particularly risky is more effective in reducing early pregnancies than Kenya’s official abstinence-until-marriage message curriculum, but she does not have STI data.

Third, we contribute to the literature on the link between education and STI risk. Evidence from both developed countries (see Cutler and Lleras-Muney, 2010, for a review) and developing countries (Thomas, Strauss and Henriques, 1991) suggest that greater educational attainment reduces unprotected sex. Existing evidence on the relationship between educational attainment and HIV status in Sub-Saharan Africa is mixed, however.⁴ In the Kenyan context, we find that for girls at the margin of dropping out of school, the increase in educational attainment brought about by the education subsidy was not sufficient, by itself, to reduce exposure to STIs – at least over the first seven years.

The remainder of the paper proceeds as follows. Section I provides some background on the context and the study design. Section II describes the data. We discuss the short- and medium-run results in Section III, and the long-run results in Section IV. Section V presents a model of sexual behavior and schooling decisions that can account for the findings.

I. Background: Context and Study Design

A. Background

Education

Though Kenya abolished school fees in 2003, primary education still entails other expenditures. All children in Kenyan schools wear uniforms, and at around $6 (or 1.6 percent of per-capita GDP) in 2003, uniforms constitute by far the largest out-of-pocket cost of education in government primary schools. Historically, headmasters often sent children home telling them that they could only return when they had a uniform. With the introduction of free primary education, the Ministry of Education announced that this practice should not continue, but de facto, students face strong social pressure to wear a uniform and most do. The provision of free uniforms has been shown to reduce absenteeism in younger grades (Evans, Kremer and Ngatia, 2009).

Since grade repetition and late school entry are common, many students are 15, 16, or even older, by the time they reach the end of primary school in eighth grade, and many pupils in upper grades are sexually active. While enrollment in the early grades of primary school is nearly universal, many students leave school before completing eighth grade, especially girls. In the comparison schools in our sample, about 30 percent of girls and 21 percent of boys who reach sixth grade drop out before completing eighth grade.

Sexual Norms

Primary school children in Kenya are not supposed to be sexually active. Girls who become pregnant typically have to leave school. Conversely, once a girl leaves school, sex and marriage are expected. Traditional marriage involves a brideprice, but most couples in our sample “elope” without a brideprice payment and without a marriage ceremony. Indeed for teenage girls who are not in school there is little stigma to pre-marital sex and pregnancy that quickly leads to marriage, and marriage is potentially more attractive than staying at the parental home, where teenage girls bear a large share of household chores. Couples are considered married if they are living together, and we use that definition in this paper.

Some scholars argue that condoms are seen as something one uses with casual partners, not committed partners, and therefore part of the meaning of not using a condom is that one is in a trusted, committed relationship (Mash, Mash and De Villiers, 2010). Condom use within marriage remains limited, with only 1.8 percent of married women reporting using condoms in the latest nationally representative Kenya Demographic and Health Survey (KNBS and ICF Macro, 2010). Condom use among sexually active unmarried women was 18 percent.

School-Based HIV education

The Kenyan government established a national HIV/AIDS curriculum for primary school with the assistance of UNICEF. Following the UNICEF-backed model, the planning process was based on extensive consultation within Kenyan civil society. Kenya is a religious society, and the Catholic church, various protestant denominations, including very active evangelical groups, and Muslim organizations are the most organized and politically influential civil-society stakeholders on this issue. These religious groups favored prevention messages focusing on abstinence until marriage. The resulting curriculum teaches the biology of AIDS and HIV transmission, care for people living with AIDS, and prevention. The prevention component stresses abstinence until marriage, followed by faithfulness in marriage as the most effective way to prevent sexually transmitted infections, and teaches skills such as saying no and resisting peer pressure. The official textbook does not mention condoms or contraception. Condoms can be discussed in class at the teacher’s discretion or in response to questions, but the teachers’ handbook only mentions condoms as a prevention strategy for married individuals. This type of curriculum is far from unique to Kenya: the UNICEF model Kenya followed is a standard one, and the underlying strength of religious organizations is also common. Curricula stressing abstinence until marriage are the norm in many African countries, and in much of the U.S. as well.

In our detailed review of the teaching-learning material, we identified a single (narrow) window of opportunity to discuss condoms, however: the teachers’ handbook proposes to organize a debate on whether condoms should be discussed in class. As discussed below we took advantage of this opportunity to explicitely control the degree to which condoms were mentioned in some schools.

B. Study Design

We study two programs implemented through a partnership between the NGO ICS Africa, the Kenyan Ministry of Education, the Kenya Institute of Education, and the Kenya National AIDS Control Council. The first program reduced the cost of education by providing free school uniforms. The second program trained teachers on how to deliver the national HIV/AIDS prevention curriculum to upper primary school students. We also evaluate a small add-on component to the government-run teacher training designed to foster the discussion of condoms, in order to check whether an explicit discussion of condoms in a curriculum otherwise focused on abstinence and fidelity could affect behavior.

Sample and Randomization

The study took place in all 328 public primary schools in seven divisions of two districts of Western Kenya: Butere-Mumias and Bungoma.⁵ None of these schools had participated in any prior randomized evaluation that we know of. All schools agreed to participate. Schools were stratified and assigned to one of four arms using a random number generator: (1) Control (82 schools); (2) Stand-Alone Education Subsidy program (83 schools); (3) Stand-Alone HIV Education program (83 schools); (4) Joint Program (80 schools).⁶

Table 1 presents school-level summary statistics by treatment group. Differences across treatment groups are small in magnitude, and only four of 65 p-values estimated are smaller than 0.10, suggesting that the randomization was effective at creating balance between the groups.

Table 1.

Baseline Characteristics, by Treatment Group

Panel A. Baseline Characteristics of Schools	Stand-Alone Education Subsidy (S)	Stand-Alone HIV Education (H)	Joint Program (SH)	Control (C)	Balance Tests p-val for test that:
					S = C	H = C	SH = C	SH = S SH = H
Average Score on Primary School Graduation Exam in 2003	255.2 [29.6]	249.4 [24.8]	248.6 [32.04]	249.3 [26.1]	0.097*	0.66	0.468	0.146 0.857
School Size (total number of students)	464.6 [203.1]	489.3 [208.8]	473.8 [185.7]	498.9 [194.3]	0.292	0.777	0.587	0.764 0.611
Sex Ratio (Female/Male) among Students in 2002	1.016 [.124]	1.024 [.127]	1.012 [.105]	1.016 [.135]	0.945	0.455	0.823	0.857 0.556
Number of Latrines on school compound	11.6 [6.3]	11.2 [6.4]	9.9 [5.7]	11.1 [5.5]	0.215	0.635	0.081*	0.068* 0.173
Number of primary schools within 2 km radius	2.01 [1.95]	2.16 [1.82]	2.06 [1.8]	2.06 [1.76]	0.845	0.521	0.925	0.86 0.742
Total Number of Teachers in 2003	14.2 [4.2]	14.6 [5.3]	13.8 [4.4]	14.6 [4.7]	0.786	0.439	0.282	0.613 0.257
Average Age of Teachers in 2003	40.0 [3.1]	39.6 [3.8]	39.6 [3.8]	39.6 [3.5]	0.455	0.796	0.845	0.57 0.975
Sex Ratio (Female/Male) among Teachers in 2003	1.22 [1.]	1.18 [.848]	1.30 [.987]	1.15 [.829]	0.856	0.788	0.281	0.575 0.405
Panel B. Baseline Characteristics of Study Cohort (Grade 6 in 2003)
Number of Girls in Grade 6	29.3 [15.4]	28.8 [15.3]	28.0 [14.4]	29.4 [14.]	0.859	0.862	0.451	0.566 0.717
Number of Boys in Grade 6	28.2 [13.3]	30.7 [14.6]	30.3 [14.7]	30.4 [14.1]	0.225	0.498	0.739	0.348 0.839
Sex Ratio (Female/Male) among Grade 6 students	1.065 [.412]	0.968 [.297]	0.964 [.356]	1.011 [.325]	0.127	0.184	0.156	0.071* 0.939
Averge Age among Girls (at baseline)	13.21 [.56]	13.12 [.64]	13.18 [.59]	13.14 [.6]	0.464	0.378	0.856	0.741 0.519
Averge Age among Boys (at baseline)	13.79 [.62]	13.72 [.69]	13.77 [.62]	13.77 [.66]	0.878	0.362	0.965	0.905 0.601
Number of Schools (Total = 328)	83	83	80	82

Notes: School Averages. Standard deviations in brackets. p-values in italics.

Education Subsidy

Between february and July 2003, ICS distributed free school uniforms to boys and girls enrolled in grade 6 at the onset of the school year (January).⁷ In fall 2004, ICS distributed a second uniform to the same students, if they were still enrolled in the same school (regardless of their grade). It was announced at the onset of the program that students still enrolled in the same school would be eligible for a second uniform after 18 months.⁸ The total education subsidy, delivered over two years, amounted to just around $12 per student, or 2.5 percent of average annual household income in the study area at the time.⁹ Given these magnitudes the income effect created by the education subsidy was likely negligible, and we expect the subsidy to mostly affect the demand for education and fertility through a price effect.

HIV education

In 2002 the Kenya government started a large-scale effort to train teachers on HIV education, based in part on data suggesting that in the absence of training, many teachers were uncomfortable teaching the official HIV/AIDS curriculum. In 2003, ICS Africa helped implement the national training program for 184 primary schools by providing logistical and financial support. The 184 schools selected for the HIV Education program were asked to send three upper primary teachers to participate in a five-day training program.¹⁰

The training sessions were conducted jointly by one facilitator from the AIDS Control Unit of the Ministry of Education (MoE), two facilitators from the Kenya Institute of Education (KIE), and one trained staff member from ICS Africa. Teacher training included basic facts on HIV/AIDS, a condom demonstration, information on voluntary counseling and testing, and HIV/AIDS education methodology. Because training was primarily done by MoE and KIE staff and was based on the officially approved curriculum, the content should be similar to that delivered in other parts of Kenya. At the same time, since the sessions were facilitated and observed by ICS Africa and members of the research team, we do know they were well run and teacher attendance was good. In addition to receiving training on how to deliver HIV information in the classroom, teachers were advised to set up health clubs to deliver HIV information outside of the classroom. A year after the training, 86 percent of the schools in the program had established health clubs.¹¹

Since the curriculum leaves almost no space for teachers to provide information about condoms, we were interested in testing whether exploiting the existing window to the maximum extent possible would affect the impact of teacher training on student knowledge and behavior. This is important for policy, since only an intervention taking place within the existing curriculumn could be potentially scaled up (if effective) without major rethinking. From the perspective of understanding adolescent behavior, it was also important to try to generate exogenous variation in awareness of condoms (a potential way to protect oneself against both STI and pregnancy) without affecting access to condoms. Thus, during the school year 2005, two years after the implementation of the education subsidy and HIV education teacher training, a random subset of schools that had participated in the teacher training were sampled for an additional intervention called “Critical Thinking” (CT). This add-on was targeted at students in grades 7 and 8 in 2005 (many of whom, given the high repetition rate, were in grade 6 in 2003, i.e. in our study cohort). Schools sampled for CT were encouraged to organize a debate on the motion: “School children should be taught how to use condoms”, a motion suggested in the official Facilitators’ Handbook (p. 66, KIE 1999). The debate was followed by an essay competition on the theme: “Discuss ways in which you can protect yourself from HIV infection now and at later ages in your life”.¹² Both debates and essay writing are established practices in Kenyan schools, and teachers agreed to organize these activities in 95 percent of sampled schools. At the time, none of these schools had previously organized a debate or essay competition on these specific topics, which suggests that these topics were most likely never discussed in non-CT schools, and thus the CT encouragement appears to have created the intended exogenous gap in students exposure.

II. Data and Estimation Strategy

A. The Data

The sample consists of 19,289 students (9,487 girls and 9,802 boys) enrolled in grade 6 at the onset of the study (2003). Short- and medium-run data on school enrollment, attendance, marital status and childbearing status was collected through regular school visits between 2003 and 2007. A rich array of longer-run data was collected through a follow-up survey with study participants in 2009–2010.

Short- and Medium-Run Outcomes: “Roll Call” Data

Seven unannounced school visits were conducted over five years. At each visit, the list of all those in our baseline sample was read aloud to upper-grade students present at the time of the visit, and for each name on the list, attendance was recorded, and for absent students, the following questions were asked: Is X still in school? If yes, in what grade? If no, does she still live in the area? Is she married? Does she have any children? If so, how many? How old is her first born? Is she currently pregnant? We use this roll call data to create dummy variables for “dropout”, “ever married”, “ever pregnant”, etc.

To check whether this roll call method generates accurate data on childbearing and marital outcomes, a random subsample of 1,420 girls were visited at home in 2006 for a quality control exercise. Girls reported as having started childbearing were oversampled. Information was collected from the subject in 44 percent of cases and in other cases it was collected from a relative, typically the mother. Table A1 in the Web Appendix presents the rates of consistency between the roll call data and the data collected through the quality control exercise, as well as how these rates vary across treatment groups. Since there was up to a four-month gap between the roll call and the home visit data, the home visit data is itself not 100 percent accurate, and therefore the consistency between the two would not be 100 percent even if the roll call data were perfect. Given this, the level of consistency appears high. 83 percent of those who were reported as not having started childbearing had indeed not started, and 79 percent of those who were reported as having started childbearing by their former schoolmates had indeed started childbearing. The longer the time between the roll call and the home visit, the lower the consistency rate, unsurprisingly. The consistency level is greater when we look at the “ever had a child” outcome (rather than ever started childbearing, which includes current pregnancies). Overall, the roll call method appears to provide remarkably accurate information (if we take the information obtained through home visits as “true”). Importantly, the level of consistency between the two sources does not appear to vary across groups.

Long-Run Outcomes: The Long-run Biomarkers Follow-Up Survey

In 2009–2010, on average seven years after the two programs had taken place, a long-run follow-up was conducted, including measurement of two biomarkers: HIV and Herpes Simplex Virus Type 2 (HSV2). Herpes is almost exclusively sexually transmitted and is a serious disease in its own right. What’s more, herpes can create lesions which can facilitate HIV transmission (Grosskurth et al., 1995; Corey et al., 2004). Oster (2005) estimates that high prevalence of STIs such as herpes is a major contributor to the HIV/AIDS epidemic in sub-Saharan Africa. Herpes leads to the lifelong presence in the blood of antibodies against HSV2, thereby providing a permanent marker of having ever been infected with HSV2, and thus an objective proxy for relatively risky sexual behavior in the past (Obasi, 1999). HSV2 was selected as the primary biomarker because a preliminary study we conducted with a similarly aged cohort found HSV2 prevalence to be greater than 10 percent, but prevalence of other sexually transmitted infections was much lower (Chlamydia, Gonorrhea, Trichomonas Vaginalis and HIV were all less than 5 percent.)

The long-run follow-up survey was administered either at a local meeting location to which the respondent had been invited, or at the respondent’s home if she had not come to the meeting point. The survey included questions on sexual behavior, past and current sexual partners, marriage, and fertility, as well as educational attainment. Half of the study participants had been pre-selected randomly to be offered voluntary counseling and HIV testing (VCT). VCT was done at the end of the survey by the surveyors, who were all government-certified VCT counselors. Finally, at the end of the follow-up survey, all respondents were directed to a mobile clinic for HSV2 testing. (Those surveyed at home were given a voucher for a free HSV2 test to be performed at the mobile clinic).

Conditional on being successfully tracked for the follow-up survey, compliance with HSV2 testing was remarkably high, at 96 percent on average, and comparable across groups. Compliance with VCT was also very high: 87 percent of girls and 88 percent of boys surveyed agreed to receive VCT, and this was not differential across groups.

The long-run follow-up survey started in March 2009. By August 2010, 10,651 youths (55 percent of the study cohort) had been tracked. This is a relatively high rate given the challenges in locating members of a mobile population of school-leavers, many of whom had married outside their initial villages. Of these, 97.5 percent had been interviewed, 2 percent had been identified as dead, and less than 1 percent had refused to be interviewed or were deemed mentally unfit for the interview.¹³

In August 2010, 29 percent of the 8,638 respondents who had not been tracked yet were randomly sampled for intensive tracking.¹⁴ Between September 2010 and March 2011, teams of field officers and lab technicians traveled to various locations in Kenya and Uganda to interview selected respondents at their current homes. 77.5 percent of girls and 84 percent of boys sampled for intensive tracking were successfully surveyed. This brings the effective tracking rate (in the terminology of Orr et al., 2003 and Baird, McIntosh and Özler, 2011) to 0.51+0.49×0.775 = 89% for girls, and 0.59 + (0.41) × (0.84) = 93% for boys.¹⁵

B. Attrition

Table A2 in the Web Appendix shows attrition in the roll-call data on school participation, marriage and fertility after three and five years. There is no evidence of differential attrition for any outcome, except for dropout information after five years.

Table A3 shows attrition in the long-term (7-year) follow-up data. Survey rates during the first phase of tracking (the regular tracking, or RT, phase) were significantly higher in the treatment groups than in the control group, especially among girls (column 2). Column 3 presents estimates of the survey rates, showing that intensive tracking (IT) rates were insignificantly greater among those exposed to either program than among the control group, and significantly greater under the joint program than in the control group. All in all, the sample that could be followed up after 7 years over-represents those that received the education subsidy only or the joint program (column 4). Incorporating sampling weights (column 5) does not solve this problem fully for girls in the joint program arm, since the intensive tracking rate was higher in that arm.¹⁶ Finally, there is a 25 to 30 day difference between the average survey date for the control group and the average survey date for the three treatment groups, but no difference across treatment groups (column 9). Given that the daily incidence of HSV2, pregnancy and other outcomes is very low, this difference, while significant statistically, is negligible in magnitude.

To test whether attrition in the long-run follow-up survey was differential in terms of underlying, unobserved characteristics, we check whether the treatment effects observed in the roll call data are changed when we estimate them on the follow-up subsample rather than the full sample. The idea is that, if attrition in the long-run follow-up biased the comparability of our groups in any way, then short-run treatment effects estimated using that subsample would differ from the “true” short-run treatment effects estimated on the full sample. We perform this analysis in Table A4 for one outcome (having ever started childbearing – results for other outcomes are similar and available upon request). We find that the estimates of the short- and medium-run treatment effects on childbearing measured through the roll call method are very much comparable when estimated on the full sample for which roll call data is available (columns 1 and 4 – those are the “true” effects), or on the subsample for which long-run data could be collected after 7 years (columns 2 and 5 – again, these would be biased estimates of the true effects if attrition were differential). Not surprisingly since the estimates are virtually identical in the full sample and the sample with attrition, the sampling weights correction, while decreasing precision, does not affect the estimates much (columns 3 and 6). All in all, the estimated short-run treatment effects using only the long-run follow-up sample are virtually identical to those using the full sample, even without using the sampling weights. This provides some confidence that differences in other long-run outcomes (in particular STI, the one variable for which we do not have roll call data) can be interpreted as causal treatment effects.

C. Estimation Strategy

The impact of the two stand-alone programs and the joint program can be evaluated by comparing outcomes across groups in a simple regression framework. For each individual-level outcome, the estimation equation is:

$$Y_{is}=\alpha +\beta S_s+\gamma H_s+\delta S{H}_s+{\mathbf{X}}_s^{\prime }\mu +\eta {\mathit{Age}}_i+{\epsilon }_{is}$$ (1)

where Y_is is the outcome for student i enrolled in school s at baseline; S_s is a dummy variable equal to 1 for schools in the stand-alone education subsidy arm; H_s is a dummy variable equal to 1 for schools in the stand-alone HIV education arm; SH_s is a dummy variable equal to 1 for schools in the joint program arm; X_s is a vector of school level controls (timing of the data collection, school size, and randomization stratum); and Age_i is student i’s age. Error terms are assumed to be independent across schools, but are allowed to be correlated across observations in the same school (i.e. the standards errors are clustered at the school level). We present results with sampling weights, which ensure that our final follow-up database is representative of (almost) the entire initial study population, but as mentioned above results are very similar when the estimation is done without sampling weights.

In equation 1, β measures the effect of the stand-alone education subsidy; γ measures the effect of the stand-alone HIV education program; and δ measures the effect of the joint program.

In all tables that follow, we present estimates of equation 1 for a series of outcomes. In each table, Panel A presents the estimates for girls and Panel B presents the estimates for boys. At the bottom of each panel, we show the mean of the dependent variable for the control group, and we present the p-values for tests of the hypotheses that the effect of the joint program is equal to that of either of the two stand-alone programs, or equal to the sum of the two stand-alone programs (i.e., we test for β = δ, γ = δ and γ = β + δ). We report OLS linear probability model regressions. The results are qualitatively unchanged with probit or logit specifications for binary outcomes (results available upon request). The results are unchanged when we add school-level controls (such as teacher-pupil ratio, school performance on national exams, whether the school is rural or semi-urban, etc.).

For brevity, we ignore the randomized critical thinking (CT) intervention among H and SH schools in the main analysis (Tables 2, 3 and 4). We show the CT results in Table 5, using the following specification:

$$Y_{is}=\alpha +\beta S_s+\gamma {\mathit{HnoCT}}_s+\delta {\mathit{SHnoCT}}_s+{\delta }_{ct}{\mathit{HCT}}_s+{\gamma }_{ct}\mathit{SHCT}+{\mathbf{X}}_{\mathbf{s}}^{\prime }\mu +\eta {\mathit{Age}}_i+{\epsilon }_{is}$$ (2)

where HnoCT_s is equal to 1 for the subset of stand-alone HIV Education schools that were not selected for the add-on critical thinking intervention (CT) in 2005, SHnoCT_s is equal to 1 for the subset of joint program schools not selected for the CT intervention, HCT_s is equal to 1 for the subset of stand-alone HIV Education schools randomly selected for the CT intervention, and SHCT_s is equal to 1 for the subset of joint program schools randomly selected for the CT intervention.

Table 2A.

Short- and Medium Run Impacts: Roll Call Data

Panel A. Girls	(1)	(2)	(3)	(4)	(5)	(6)
	Impacts after 3 years
	Dropped Out of Primary School	Attendance rate (while enrolled)	Ever Married	Ever Pregnanta	Ever Pregnant but Never Married	Ever Married but Never Pregnant
Stand-Alone Education Subsidy (S)	−0.031 (0.012)**	−0.002 (0.006)	−0.026 (0.010)**	−0.027 (0.011)**	−0.004 (0.006)	−0.002 (0.003)
Stand-Alone HIV Education (H)	0.003 (0.011)	−0.008 (0.006)	0.011 (0.009)	−0.007 (0.011)	−0.014 (0.006)**	0.005 (0.003)*
Joint Program (SH)	−0.016 (0.012)	0.000 (0.006)	0.000 (0.009)	−0.011 (0.010)	−0.013 (0.006)**	−0.001 (0.003)
Observations	9116	8232	9107	9072	9072	9072
Mean of Dep. Var. (Control)	0.188	0.939	0.128	0.160	0.046	0.011
p-val (Test: S = SH)	0.240	0.716	0.011**	0.145	0.09*	0.809
p-val (Test: H = SH)	0.102	0.204	0.235	0.742	0.866	0.058*
p-val (Test: S = H)	0.005***	0.328	0***	0.084*	0.092*	0.021**
p-val (Test: SH = S + H)	0.474	0.237	0.278	0.133	0.539	0.311
Panel B: Boys
Stand-Alone Education Subsidy (S)	−0.024 (0.011)**	−0.001 (0.008)	−0.008 (0.004)*	−0.002 (0.003)	0.001 (0.001)	−0.004 (0.003)
Stand-Alone HIV Education (H)	0.010 (0.010)	−0.021 (0.008)***	0.000 (0.005)	−0.002 (0.002)	0.000 (0.001)	0.001 (0.004)
Joint Program (SH)	−0.015 (0.010)	0.000 (0.008)	−0.010 (0.004)**	−0.006 (0.002)**	0.000 (0.001)	−0.004 (0.003)
Observations	9461	8985	9393	9433	9382	9382
Mean of Dep. Var. (Control)	0.127	0.908	0.022	0.011	0.002	0.012
p-val (Test: S = SH)	0.357	0.853	0.601	0.206	0.119	0.834
p-val (Test: H = SH)	0.014**	0.005***	0.004***	0.093*	0.421	0.042**
p-val (Test: S = H)	0.001***	0.011**	0.04**	0.756	0.403	0.097*
p-val (Test: SH = S + H)	0.983	0.038**	0.720	0.664	0.162	0.663

Notes: Data Source: Roll Call Data (see test section 2.1 for details). Data collected through five school visits conducted at regular intervals over three academic years (2003, 2004, 2005). Estimates obtained through OLS regressions that include controls controls for year of birth, the timing of the roll call visits, school size and randomization strata dummies. Standard errors clustered at the school level. ***, **, * indicate significance at 1, 5 and 10%.

^aFor boys, “ever pregnant” is equal to 1 if the respondent ever had a child or a pregnant partner.

Table 3.

Long-Run Impacts: Individual Long-term Follow-up Survey Data (after 7 years)

Panel A. Girls	(1)	(2)	(3)	(4)	(5)	(6)	(7)
	Reached 8th grade	Grades Completed	Ever Married	Ever pregnant1	Ever Pregnant but Never Married	Ever Married but Never Pregnant	Had started childbearing by age 16
Stand-Alone Education Subsidy (S)	0.039 (0.017)**	0.206 (0.091)**	−0.039 (0.021)*	−0.032 (0.021)	0.006 (0.012)	−0.001 (0.004)	−0.020 (0.012)*
Stand-Alone HIV Education (H)	−0.004 (0.017)	−0.020 (0.089)	0.020 (0.020)	0.017 (0.022)	−0.007 (0.014)	−0.004 (0.005)	−0.009 (0.014)
Joint Program (SH)	−0.009 (0.018)	0.006 (0.097)	−0.012 (0.021)	−0.008 (0.022)	0.006 (0.013)	0.001 (0.006)	−0.005 (0.012)
Sampling Weights	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Observations	5685	5685	5715	5719	5715	5715	5719
Mean of Dep. Var. (Control)	0.802	9.181	0.392	0.493	0.114	0.014	0.085
p-val (Test: S = SH)	0.009***	0.039**	0.218	0.275	0.995	0.621	0.176
p-val (Test: H = SH)	0.793	0.776	0.144	0.253	0.332	0.276	0.777
p-val (Test: S = H)	0.019**	0.017**	0.007***	0.027**	0.328	0.448	0.362
p-val (Test: SH = S + H)	0.069*	0.154	0.821	0.821	0.708	0.313	0.171
Panel B. Boys
Stand-Alone Education Subsidy (S)	0.036 (0.014)**	0.070 (0.083)	0.008 (0.016)	−0.002 (0.018)	−0.009 (0.009)	0.002 (0.006)	−0.005 (0.004)
Stand-Alone HIV Education (H)	0.000 (0.014)	−0.043 (0.080)	−0.003 (0.016)	0.004 (0.017)	0.002 (0.008)	−0.007 (0.005)	−0.006 (0.003)*
Joint Program (SH)	0.021 (0.014)	−0.010 (0.091)	0.004 (0.016)	−0.002 (0.016)	−0.004 (0.009)	0.002 (0.006)	−0.002 (0.004)
Sampling Weights	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Observations	6557	6557	6591	6595	6591	6591	6595
Mean of Dep. Var. (Control)	0.854	9.521	0.186	0.211	0.051	0.026	0.015
p-val (Test: S = SH)	0.316	0.369	0.791	0.999	0.583	0.951	0.392
p-val (Test: H = SH)	0.124	0.701	0.621	0.690	0.450	0.105	0.282
p-val (Test: S = H)	0.013**	0.158	0.465	0.721	0.147	0.106	0.892
p-val (Test: SH = S + H)	0.481	0.755	0.966	0.864	0.820	0.365	0.072*

Notes: Source: Long-run follow-up survey (see text section 2.1 for details). Estimates obtained through OLS regressions that include controls for year of birth, the timing of the survey, school size and randomization strata dummies. Standard errors clustered at the school level. ***, **, * indicate significance at 1, 5 and 10%.

1For boys, “ever pregnant” is equal to 1 if the respondent ever had a child or a pregnant partner.

Table 4.

Long-Run Impacts on Sexually Transmitted Infections (after 7 years)

Panel A. Girls	(1)	(2)
	Blood Test: HIV positive	Blood Test: HSV2 positive
Stand-Alone Education Subsidy (S)	0.004 (0.006)	0.009 (0.014)
Stand-Alone HIV Education (H)	−0.002 (0.006)	0.004 (0.013)
Joint Program (SH)	−0.002 (0.006)	−0.023 (0.013)*
Sampling Weights	Yes	Yes
Observations	2382	5509
Mean of Dep. Var. (Control)	0.009	0.118
p-val (Test: S = SH)	0.404	0.013**
p-val (Test: H = SH)	0.907	0.026**
p-val (Test: S = H)	0.312	0.699
p-val (Test: SH = S + H)	0.699	0.051*
Panel B: Boys
Stand-Alone Education Subsidy (S)	0.001 (0.002)	0.005 (0.009)
Stand-Alone HIV Education (H)	0.000 (0.002)	−0.002 (0.010)
Joint Program (SH)	0.003 (0.003)	−0.009 (0.010)
Sampling Weights	Yes	Yes
Observations	2659	6302
Mean of Dep. Var. (Control)	0.001	0.074
p-val (Test: S = SH)	0.595	0.145
p-val (Test: H = SH)	0.421	0.502
p-val (Test: S = H)	0.483	0.460
p-val (Test: SH = S + H)	0.759	0.380

Data Sources: Col 1: Rapid HIV tests administered to consenting individuals at the end of the long-run follow-up survey, among a randomly selected subsample. Col 2: Lab Tests performed on blood draws taken during after follow-up survey. See text section 2.1 for details.

Estimates obtained through OLS regressions that include controls for year of birth, the timing of the survey, school size and randomization strata dummies. Standard errors clustered at the school level. ***, **, * indicate significance at 1, 5 and 10%.

Table 5.

Main outcomes (short, medium and long run), breakdown by Critical Thinking (CT) intervention treatment

		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
	Data Source:	In-class survey after two years			Roll Call Data, 3-yr impacts		Roll Call Data, 5-yr impacts
	Outcome shown in:	Table A5, col 6	Table A5, col 7	Table A5, col 9	Table 2, col 1	Table 2, col 4	Table 2, col 9	Table 4, col 2	Table 6, col 8
Panel A. Girls		Knows that condoms can prevent HIV infection	Mentions abstinence when asked for ways to avoid HIV infection	Mentions faithfulness when asked for ways to avoid HIV infection	Dropped Out of Primary School	Ever pregnant	Ever pregnant	HSV-2 positive	Used a condom last time had sex
Stand-Alone Education Subsidy (S)		−0.009 (0.019)	0.022 (0.020)	0.037 (0.013)***	−0.031 (0.012)**	−0.027 (0.011)**	−0.044 (0.017)***	0.009 (0.014)	0.017 (0.021)
Stand-Alone HIV education (H), no CT		0.001 (0.023)	0.090 (0.028)***	0.051 (0.015)***	−0.006 (0.015)	−0.010 (0.015)	−0.007 (0.020)	0.014 (0.018)	−0.029 (0.027)
Joint Program (SH), no CT		0.005 (0.021)	0.016 (0.028)	0.021 (0.012)*	−0.017 (0.016)	0.000 (0.013)	−0.001 (0.020)	−0.031 (0.014)**	−0.034 (0.029)
Stand-Alone HIV education (H), with CT		0.039 (0.021)*	−0.021 (0.024)	0.011 (0.015)	0.011 (0.013)	−0.006 (0.013)	0.007 (0.020)	−0.005 (0.016)	0.009 (0.029)
Joint Program (SH), with CT		0.075 (0.023)***	0.035 (0.030)	0.039 (0.015)**	−0.015 (0.015)	−0.022 (0.014)	−0.021 (0.021)	−0.014 (0.017)	−0.007 (0.030)
Sampling weights								Yes	Yes
Observations		13338	13338	13338	9116	9072	8302	5509	3700
Mean of Dep. Var. (Control)		0.461	0.461	0.461	0.188	0.160	0.329	0.118	0.282
p-val (Test: S = SH no CT)		0.568	0.568	0.568	0.401	0.055*	0.046**	0.008***	0.065*
p-val (Test: H no CT = SH no CT)		0.882	0.028**	0.088*	0.571	0.554	0.821	0.017**	0.883
p-val (Test: S = H no CT)		0.674	0.014**	0.349	0.108	0.223	0.062*	0.791	0.107
p-val (Test: SH no CT = S + H no CT)		0.696	0.013**	0.003***	0.390	0.087*	0.106	0.023**	0.560
Panel B: Boys
Stand-Alone Education Subsidy (S)		0.018 (0.015)	0.026 (0.020)	0.016 (0.010)*	−0.024 (0.011)**	−0.002 (0.003)	0.005 (0.005)	0.005 (0.009)	−0.041 (0.022)*
Stand-Alone HIV education (H), no CT		0.012 (0.018)	0.080 (0.030)***	0.035 (0.016)**	0.007 (0.014)	−0.001 (0.004)	0.005 (0.007)	0.000 (0.012)	−0.011 (0.029)
Joint Program (SH), no CT		0.032 (0.020)	0.057 (0.025)**	0.003 (0.012)	−0.003 (0.014)	−0.004 (0.003)	0.002 (0.007)	−0.034 (0.013)***	−0.012 (0.030)
Stand-Alone HIV education (H), with CT		0.018 (0.023)	0.030 (0.025)	0.012 (0.012)	0.013 (0.012)	−0.002 (0.003)	0.002 (0.007)	−0.003 (0.013)	0.011 (0.026)
Joint Program (SH), with CT		0.060 (0.022)***	0.077 (0.029)***	0.026 (0.013)*	−0.026 (0.012)**	−0.007 (0.003)**	−0.002 (0.006)	0.016 (0.012)	0.032 (0.025)
Sampling weights								Yes	Yes
Observations		13559	13636	13636	9461	9433	8897	6302	4759
Mean of Dep. Var. (Control)		0.655	0.393	0.079	0.127	0.011	0.032	0.074	0.489
p-val (Test: S = SH no CT)		0.898	0.898	0.898	0.140	0.507	0.789	0.002***	0.325
p-val (Test: H no CT = SH no CT)		0.365	0.487	0.083*	0.563	0.378	0.793	0.029**	0.970
p-val (Test: S = H no CT)		0.749	0.063*	0.233	0.038**	0.672	0.962	0.688	0.302
p-val (Test: SH no CT = S + H no CT)		0.926	0.214	0.022**	0.473	0.798	0.514	0.027**	0.342

Notes: See respective tables for data sources and specifications. See text section 1.2 for a description of the CT intervention and section 2.3 for econometric specification. ***, **, * indicate significance at 1, 5 and 10%.

III. Short- and Medium Run Results: Roll Call Data

Tables 2A and 2B present estimated effects within three to five academic years after the onset of the study, obtained from the roll call data. We report the results first for girls, and then for boys. Note that fertility is much better observed for girls, which makes the results for girls more interesting. As discussed above, we pool the schools with and without the add-on CT intervention when estimating the impact of the HIV education program and the joint programs. We will break those down by CT treatment status in section IV.C.

Table 2B.

Short- and Medium Run Impacts: Roll Call Data

Panel A. Girls	(1)	(2)	(3)	(4)	(5)
	Impacts after 5 years
	Dropped Out of Primary School	Ever Married	Ever Pregnant	Ever Pregnant but Never Married	Ever Married but Never Pregnant
Stand-Alone Education Subsidy (S)	−0.053 (0.017)***	−0.030 (0.015)**	−0.044 (0.017)***	−0.009 (0.007)	0.005 (0.004)
Stand-Alone HIV Education (H)	−0.015 (0.015)	0.022 (0.014)	0.001 (0.015)	−0.014 (0.007)**	0.009 (0.004)**
Joint Program (SH)	−0.023 (0.016)	0.004 (0.015)	−0.011 (0.016)	−0.002 (0.007)	0.011 (0.004)***
Observations	8865	8391	8302	8302	8302
Mean of Dep. Var. (Control)	0.300	0.265	0.329	0.080	0.012
p-val (Test: S = SH)	0.102	0.034**	0.056*	0.320	0.215
p-val (Test: H = SH)	0.590	0.250	0.458	0.091*	0.757
p-val (Test: S = H)	0.024**	0.001***	0.006***	0.468	0.393
p-val (Test: SH = S + H)	0.061*	0.597	0.165	0.039**	0.496
Panel B: Boys
Stand-Alone Education Subsidy (S)	−0.039 (0.016)**	−0.006 (0.008)	0.005 (0.005)	0.000 (0.002)	−0.010 (0.004)**
Stand-Alone HIV Education (H)	0.010 (0.014)	0.006 (0.008)	0.004 (0.005)	−0.002 (0.002)	0.001 (0.005)
Joint Program (SH)	−0.011 (0.015)	−0.003 (0.008)	0.000 (0.005)	−0.002 (0.002)	−0.003 (0.005)
Observations	9261	8577	8897	8558	8558
Mean of Dep. Var. (Control)	0.211	0.059	0.032	0.006	0.029
p-val (Test: S = SH)	0.071*	0.733	0.458	0.547	0.098*
p-val (Test: H = SH)	0.128	0.248	0.567	0.913	0.492
p-val (Test: S = H)	0.001***	0.153	0.872	0.459	0.02**
p-val (Test: SH = S + H)	0.382	0.751	0.321	0.856	0.316

Notes: see Table 2A notes. Roll call information updated through school visits conducted in 2006 and 2007.

A. Impact of the stand-alone education subsidy on girls

The stand-alone education subsidy led some girls to remain in school (Table 2A, column 1). While 18.8 percent of girls in control schools had dropped out after three years, those in the education subsidy program were 3.1 percentage points less likely to do so, a 16.5 percent decrease significant at the 5 percent level. Note that this is a suprisingly large effect for a small transfer that had presumably little or no income effect. Also note that “marginal” girls were not less likely to regularly attend school: The program did not affect attendance conditional on enrollment (column 2).

The stand-alone education subsidy also substantially reduced teenage pregnancy. After three years, 16 percent of girls in the control group had ever been pregnant. This share was 2.7 percentage points (17 percent) lower in schools with the stand-alone subsidy (Table 2A, column 4). After five years, there was still a gap of 4.4 percentage points in the likelihood of having ever been pregnant between the stand-alone subsidy group and the control group (Table 2B, column 3). This gap is larger in absolute terms than after three years, but corresponds to a smaller treatment effect in percentage terms, since the childbearing rate in the control group rose from 16 percent in year 3 to 33 percent in year 5 for the control group. Nonetheless, it suggests that fertility among girls in the subsidy group did not catch up as soon as the subsidy ended. Indeed, we can reject not only the hypothesis that demand for fertility was simply bottled up during the program years when girls were in school and released afterwards, but also the hypothesis that the hazard rate of starting childbearing was the same in the stand-alone education subsidy group and the comparison group after year 3, when girls who did not repeat grades would have left school.¹⁷ This suggests that at least part of the effect of education on fertility goes beyond what Black, Devereux, and Salvanes (2004) refer to as the “incarceration effect” of schooling on teen fertility.

Column 5 of Table 2 shows that the stand-alone education subsidy did not decrease unwed (i.e., single-parenthood, given our definition of marriage) pregnancy, suggesting that it exclusively reduced within-marriage pregnancy. Column 6 shows that the incidence of marriage with no child did not increase. Together these results suggest that the pregnancies averted were primarily among girls who, had it not been for the education subsidy, would have dropped out of school and settled in a committed relationship. Indeed, girls in the subsidy program were 2.6 percentage points (20 percent) less likely to be married (column 3).

Overall, the reduction in the number of girls who started childbearing was almost as large as the reduction in the number who dropped out of school. It would seem tempting to use columns 1 and 4 of Table 2A (or columns 1 and 3 of Table 2B) as, respectively, the first stage and the reduced form of an instrumental variable strategy of the effect of education on early fertility. However, this would not be legitimate: this instrumental strategy would be valid only under the assumption that the education subsidy had no direct effect on the pregnancy status of girls. Under the model we develop in section V, this identification restriction will not hold because sexual activity and the propensity to drop out are jointly determined. The model implies that reducing the cost of education will induce some girls to reduce unprotected sexual activity to avoid becoming pregnant and to stay in school longer, invalidating the use of the education subsidy as an instrument for education. But it remains that for each girl who stayed in school thanks to the program, there was one early pregnancy averted. This is a large effect and suggests that investing in ways to keep girls in school could have large returns in terms of preventing early fertility.¹⁸

B. Impact of the stand-alone HIV education program on girls

Several pieces of evidence suggest that the teacher training affected teacher behavior in the classroom. Focus group discussions (not shown) confirmed that the training increased the likelihood that teachers talked about HIV in class. In particular, students in schools where teachers had been trained were 50 percent more likely to report that at least one teacher had mentioned HIV/AIDS in the previous week.¹⁹ A self-administered survey, distributed among students enrolled in grades 7 and 8 in 2005, suggests the HIV education program increased the likelihood that students report that teachers mentioned HIV in class and moderately increased students’ knowledge about HIV (see Table A5 in the Web Appendix).

While the HIV education program changed the content of education, it did not affect educational attainment. Coefficient estimates of the impact of the stand-alone HIV education program on schooling attainment are very small in magnitudes and insignificant (column 1, row 2, of Tables 2A and 2B). The teenage pregnancy rate also did not fall significantly in response to the stand-alone HIV education program. The point estimate of program impact on pregnancy is close to zero after 3 years, and almost exactly zero after 5 years (Table 2A, column 4 and Table 2B column 3). We can reject equality with the effects of the stand-alone education subsidy on pregnancy and on dropout at a level below 1 percent in all cases.

Although the HIV education program did not reduce overall teen fertility, it changed the type of pregnancies (in or out of wedlock). Unwed pregnancy is 1.4 percentage points lower among teenage girls exposed to the HIV education curriculum (Table 2, columns 5 and 10). This corresponds to a drop of 30 percent over the first three years and 18 percent over the first five years.²⁰ The point estimates for the effect on marriage are positive but insignificant (Table 2A column 3 and Table 2B column 2), but the likelihood of marriage without pregnancy was significantly increased by the HIV education program, however: such early, non-shotgun marriages are rare (only 1.2 percent of girls had engaged in such a marriage after 5 years), but almost doubled in the stand-alone HIV education group (+0.9 percent, Table 2B column 5).

Taken together, these results suggest that the stand-alone HIV education program may have switched unprotected sexual activity from outside to within marriage. Consistent with this, the HIV education program also increased the likelihood that students mention faithfulness as a means to prevent HIV, consistent with the idea that it moved pupils toward committed relationships (Table A5 column 9).

C. Impact of the joint program on girls

Arguably the most surprising result in the roll call data is that the HIV education program, which is ineffective on its own, seems to reduce the impact of the education subsidy, both on schooling and on fertility. Indeed, the effect of the joint program on dropout is only half that of the stand-alone subsidy, and not significant at conventional levels (the t-statistic for the effect on education is 1.33 after 3 years (Table 2A column 1) and 1.5 after 5 years (Table 2B column 1)). After 3 years, we cannot reject the hypothesis that the effect of the joint program is the sum of the effects of the two stand-alone programs, but after 5 years, we can reject additivity (the effect of the joint program is lower than the sum of the two stand-alone programs).

When it comes to pregnancy risk, the estimated effect of the joint program is less than half that of the stand-alone education subsidy. Again, that effect is not significant after three years (Table 2A column 4). Two years later, the effect of the joint program on pregnancy had diminished even further compared to that of the stand-alone education subsidy (Table 2B column 3).

Finally, the point estimate suggests that girls who received the joint program were exactly as likely to be married as girls who received neither program (Table 2A column 3). For pregnancy and marriage, we can reject the null hypothesis that the effects are the same for the joint program and for the stand-alone education subsidy. We cannot reject the null hypothesis that the joint program has the same effect as the stand-alone HIV education program, however.

D. Impacts on boys

The impacts of the programs on boys’ education are similar to those observed for girls: the stand-alone education subsidy program reduced the dropout rate after 3 years by 2.5 percentage points, corresponding to a 19 percent reduction compared to the control group. After 5 years, the dropout rate was still 3.9 percentage points lower. The point estimate of the impact of the joint program on educational attainment is somewhat smaller (1.5 percentage points after 3 years, with a t-stat of 1.5). There is also a small but significant drop in marriage within three years (similar across the stand-alone education program and the joint program) and even a reduction in observed paternity after three years, significant only for the joint program (0.6 percentage point, out of a mean of 1.1 percentage points). The stand-alone HIV education program had no impact whatsoever except for a negligible impact (in terms of magnitude) on attendance while enrolled.

The effects on boys could be direct program effects or the equilibrium consequences of changed incentives for their female classmates. We favor the first explanation for two reasons. First, because we see similar impacts of the stand-alone education subsidy and joint program on education, marriage and fertility, which suggests a simple direct causal link from the desire to stay in school to reduction in early marriage and acknowledged paternity (our understanding is that only those children who are supported by their father show up boys’ reports of paternity). Second, the effect on marriage and fertility for boys appear too big to be an equilibrium consequence of the changed incentives for the girls in their class. Teenage girls typically marry men who are about six years older on average, not their classmates. Our follow-up data suggests that in the comparison group, only 4 percent of the 12.8 percent of girls who had married by year 3 (so overall 0.5 percent of girls) had married a boy their age or up to one year older. Even under the extremely conservative assumptions that (1) these are all within-school marriages (which is itself unlikely since marriage among even distant relatives is not culturally allowed and students in a given school are often related to each other), and (2) this proportion falls to zero in the stand-alone education subsidy group, the GE effect would explain only about half of the fall in marriage we observe among boys.

IV. Long-Run Effects: The Biomarkers and Survey Data

A. Education, Marriage, and Fertility

The estimations of equation (1) on the long-run outcomes measured through the follow-up survey are presented in Tables 3 and 4.

Reassuringly, the estimated program effects on schooling, marriage and fertility after seven years are consistent with the estimated effects based on the roll call data. Namely, the stand-alone education subsidy increased educational attainment and decreased the risk of teenage pregnancy and marriage. The probability of being pregnant by age 16 falls by 2.2 percentage points in the stand-alone education subsidy group (Table 3, column 7), a magnitude similar to the 2.7 percent reduction in teen pregnancy found in the roll call data after three years. The fertility effect, which persisted from the three-year to the five-year follow-up, continues through the seven-year follow-up, although estimates are noisy. The point estimate of the impact of the stand-alone education subsidy on the probability of having ever started childbearing in the long-run follow-up is 3.4 percentage points (Table 3, column 4). The p-value is just 0.12 however. As in the roll call data, the stand-alone HIV education program had no significant impact on schooling and overall fertility; its effect on being unmarried while having ever been pregnant is still negative but it is not significant anymore after seven years. This is not too surprising since it is common for single teenage mothers to marry someone else later. Finally, the joint program had the previously discussed muting effect on the ability of the education subsidy to improve schooling and decrease pregnancy for girls.

B. Long-Run Impacts on Sexually Transmitted Infections

Besides confirming the roll call results, the key new piece of evidence provided by the long-run follow-up data is STI exposure. These results are presented in Table 4. Column 1 shows the estimated program effects on infection with HIV, and column 2 shows those for infection with HSV2. The first interesting result is that HIV infection in our cohort is remarkably low – at less than 1 percent among both boys and girls in the control group. While it implies that this particular study, despite its very large sample size, is not powered to estimate the impact of the programs on HIV transmission, this low infection rate is extremely good news, and an important result in its own right. The overall STI risk level is not negligible, however, as evidenced by the relatively high rate of infection with HSV2, at 11.8 percent among girls and 7.4 percent among boys in the control group (column 2).

Despite reducing teen pregnancy, the stand-alone education subsidy program did not decrease HSV2 infection. This is not a statistical power issue: the estimated coefficient is positive, though not statistically significant, and we can reject any reduction of 1.8 percentage points (15 percent) or more in girls’ risk of being infected with HSV2 at the 5 percent level. At best, any reduction in STI is therefore very modest. Likewise, the stand-alone HIV education program also did not have any significant impact on HSV2 infection for either gender, and once again the point estimate is positive.

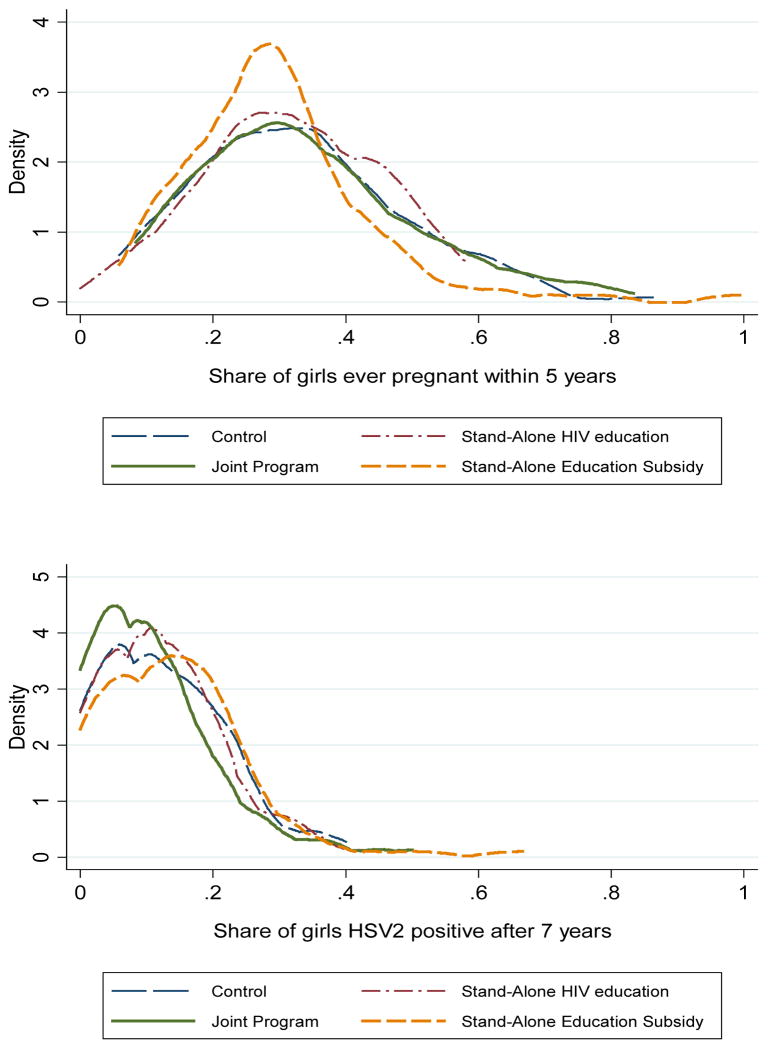
The joint program, in contrast, reduced HSV2 prevalence by 2.3 percentage points (significant at the 10 percent level) among girls, a 19 percent decrease compared to the control group. Furthermore, we can reject equality of the effect of the joint program and either of the stand-alone programs at the 5 percent level. The effect of the joint program relative to the stand-alone subsidy on STI infection is opposite of that observed for pregnancy: HSV2 prevalence is 3.2 percentage points lower under the joint program group than under the stand-alone education subsidy (p-value: 0.013), while in Table 2 (column 9) we saw that teen pregnancy was 3.3 percentage points higher under the joint program than under the stand-alone education subsidy (p-value: 0.058). These differences in means are not driven by outliers or a number of specific schools. Figure 1 shows the distribution of pregnancy (Panel A) and HSV2 (Panel B) rates across schools by treatment groups – the distributions for the stand-alone education subsidy group and the joint program group are markedly different throughout, and Kolmogorov-Smirnov tests reject equality between these distributions at the 5 percent level.

Figure 1.

Distribution of Pregnancy and HSV2 rates, by Treatment Groups

Notes: School-level averages.

Two-sample Kolmogorov-Smirnov tests for equality of distribution between Stand-alone Education Subsidy and Joint Program:

p-value for share ever pregnant (top panel): .024**

p-value for share HSV2 positive (bottom panel): .044**

For boys, however, the joint program had no significant effect on HSV2 infection rates, and we cannot reject that all three programs had the same effect.

Note that these results do not tell us the effect of the various programs on lifetime STI risk. We cannot, for example, rule out the possibility that girls who marry later will be exposed to the same risk of infection within marriage but have a greater chance of infection prior to marriage. Alternatively, girls who marry later may have more power within the relationship and therefore a lower risk of infection within marriage.

C. Impact of the Critical Thinking (CT) Intervention

Table 5 presents estimates of equation 2, in which the joint program and stand-alone HIV education groups are subdivided into two subgroups, with and without the CT intervention. We present results on all the main outcomes discussed so far (in the short-, medium- and long-run).

Column 1 of Table 5 shows that the CT intervention was successful in reaching its proximate objective: students in schools sampled for CT are more likely to mention condoms as a way to protect themselves in schools where it was conducted. This is the case in no other subgroup, which is consistent with our understanding of the curriculum and the way it was taught in schools. However, there is no report of greater use of condoms among either girls or boys in response to the CT intervention (column 11). This is not because condoms are never used: 49 percent of boys and 28 percent of girls report using a condom last time they had sex. For the other outcomes, the group with CT seems to behave similarly to the groups without CT. For example, the reduction in drop out rate after 3 years is 1.8 percentage points in the joint program without CT and 1.5 percentage points with CT (column 4) (compared to 3.1 percentage points for the education subsidy program alone), and the reduction in the rate of HSV2 is 3.1 percentage points in the joint program without CT and 1.4 percentage points in the joint program with CT (this is a smaller reduction than without CT and is not significant, but this is the second highest point estimate after the joint without CT). We interpret this evidence as suggesting that information about condoms is not, by itself, sufficient to significantly affect behavior. Indeed, even in the CT schools, there was no strong endorsement or effort to shift norm: condoms were mentioned only as something that should (or should not) be talked about, and both positions were argued in the debates.

D. Summary of Results

The stand-alone education subsidy program reduced dropout rates, pregnancy, and marriage, but did not reduce HSV2 infection. The stand-alone HIV education program had no effect on HSV2 infection or pregnancies, although it reduced the fraction of out-of-wedlock teen pregnancies. An add-on critical thinking intervention introducing a debate on condoms in schools where teachers were trained does not change this result.

Each of these sets of effects make sense on its own. Yet the combination of these effects and those of the joint program poses a puzzle: Why did the joint program have a smaller effect on girls’ teenage pregnancies than the stand-alone education subsidy, but a larger effect on HSV2 prevalence? In the next section, we propose a model which captures important aspects of sexual behavior among adolescents in our context and which, under reasonable assumptions, can yield such a pattern of results.

V. Model

Understanding the education subsidy results clearly calls for a model in which education and levels of unprotected sex are jointly determined. We now propose such a model. We will argue that understanding the full pattern of results requires moving beyond a model in which both STI risk and pregnancy are determined by a single factor, the level of unprotected sex, to a two-factor model with at least one factor differentially affecting pregnancy and STI probabilities. We introduce relationship type (committed vs casual) as such a second factor and show that the resulting two-factor model can match all our empirical results.

In the model, girls choose whether to invest in education, whether to have sex within casual or committed relationship(s) (or conceivably both), and how often to have unprotected sex. When choosing how much unprotected sex to have and in which type of relationship, girls take into account the risks and costs of sexually transmitted infection and pregnancy. Committed relationships may have lower pregnancy costs and lower perceived and actual risks of STI per unprotected sex act. We model Kenya’s HIV prevention curriculum as affecting the perceived relative risk of casual relationships.

The model nests a simpler model with no distinction between committed and casual relationships, and thus only one relationship type, as a special case. We show that our empirical results are inconsistent with the predictions of this simpler one-factor model but can be generated by the two-factor model.

Note that the decision of how much unprotected sex to have encompasses both how much sex to have and whether to use condoms. This is done for concision. One could instead separate the two decisions: how much sex to have, and how much protection to use (with a convex cost of protection). We had done this in a previous version of the model, but this does not yield useful insights: the two margins respond similarly to the variations in the environment that we consider, and have the same impact in terms of observable objective outcomes, namely HSV2 and pregnancies.²¹

A. Setup

Suppose that girls can have sex in two types of relationships: committed (that is, a faithful relationship with a fixed partner, with the view of future marriage, particularly in case of pregnancy), indexed by m (as in marriage), or casual, indexed by c. Denote the level of engagement in these types of unprotected sexual relationships as s_m and s_c respectively, and let the total amount of unprotected sex be s = s_m+s_c. In theory, agents may participate in both kinds of relationships simultaneously such that s_m > 0 and s_c > 0, but for simplicity of the analysis we assume in what follows that such “mixing”, as we refer to it, is not optimal. In the Web Appendix, we discuss conditions under which it is not optimal to mix, and we carry out the analysis below assuming these conditions hold.

It is useful to begin by separately analyzing the benefits and costs of unprotected sex by relationship type. Denote the benefit of having unprotected sex s in the absence of pregnancy or STI risk as u(s). Note that u(s) includes any possible inducements from partners, including gifts and payments. We assume that in the absence of STI and pregnancy risks, there is some utility-maximizing level of unprotected sex s̄, so u′(·) > 0 for all s less than s̄, and u′(·) < 0 above s̄. The idea that the optimal level of sex is bounded above in the absence of any risk will be helpful to rule out such high level of sex that individuals become fatalistic. It also matters for the conditions needed to avoid mixing different types of sex (given the functional forms below). We also assume u″(·) < 0. We do not rule out the possibility that u′(0) < 0, so some girls prefer abstinence. Note that we use the same utility function u(s) for both types of sex, which means that we abstract from the fact that girls may prefer either committed or casual relationships, depending on their own preference for relationship type, the inducements offered for each type of relationship, and any idiosyncratic preferences for particular partners, who may themselves prefer, or be eligible for, particular types of relationship (e.g. boys the girls’ age may not be able to afford to marry, while older men may be more able to do so). Adding such idiosyncratic preferences for one type of relationship or the other does not affect the predictions below. Note also that depending on the shape of the u(·) function, unprotected sex may either be elastic or inelastic to pregnancy cost and STI risk. If many girls are on the margin of whether or not to use condoms, for example, even small increases in either pregnancy cost or STI risk could have large effects on pregnancy and STI rates.

Unprotected sex carries risks of both STI and pregnancy. The perceived probability of getting an STI is π(s_c, s_m, a_m, a_c), where a_i is the perceived chance of infection per unprotected sex act. This perceived chance of infection per unprotected sex act is indexed by i as it may potentially depend on the nature of the relationship, committed or casual. We assume that the perceived risk of infection per unprotected act is weakly lower in committed than in casual relationships: a_m ≤ a_c. There could be a number of reasons for this. First, casual partners may be perceived as more likely to be infected; second, having multiple partners increases opportunities for exposure; and third, riskier sexual acts may be chosen in casual relationships (e.g. anal sex to avoid pregnancy). Also note that a_i, the perceived chance of infection per sex act, which is what enters the maximization problem, may be different from the actual probabilities of infection per unprotected sex act, which we denote as $a_i^{\ast }$.

For any agent, the overall perceived probability of contracting an STI takes the form

$$\pi (s_c,s_m,a_c,a_m)=1-{(1-a_c)}^{s_c}{(1-a_m)}^{s_m}$$

If an agent chooses to have only sex of type i, s_−i = 0 and this function collapses to π(s, a_i) = 1 − (1 − a_i)^s.

The cumulative perceived probability of pregnancy is v(s_c, s_m, b_c, b_m), where v ∈ [0, 1] is increasing in the level of any kind of unprotected sex, s_i, and the perceived chance of pregnancy per unprotected sex act of this type, b_i. We assume that the perceived risk of pregnancy is lower in casual relationships than in committed relationships: b_m ≥ b_c. This is a somewhat “reduced form” way of allowing the cost of preventing pregnancy (but not necessarily STI) to be lower in casual relationships; e.g. girls could have a greater ability to shift sexual activity away from fertile time periods, or in the choice of sex acts; for example, anal sex, as above, would increase the probability of contracting an STI but reduce the probability of pregnancy per sex act.²² We impose the same specific functional form for the perceived overall probability of pregnancy as for the probability of STI, that is,

$$v(s_c,s_m,b_c,b_m)=1-{(1-b_m)}^{s_m}{(1-b_c)}^{s_c}.$$

Now that we have specified the probabilities for STI and pregnancy, we turn to the utility impacts of each of these two risks.

Contracting an STI generates a utility cost D. Pregnancy generates a direct utility increment, B, but this utility sharply decreases in the event that the agent is not supported by the child’s other parent, which may happen with some probability if the agent is having sex with more than one person. Thus, B_m, the benefit of pregnancy under exclusive marital sex is greater than B_c and, importantly for the proof in the Web Appendix that girls will typically not chose to mix even if we allow it in the model, the benefit of pregnancy is B_c for any level of casual sex.²³ This utility structure follows the literature in anthropology and evolutionary biology concerning monogamy in humans and other primates (see for example Fortunato and Archetti 2009, Low 2007, Reichard and Boesch 2003, and Marlowe 2000): the idea is that if a father finds out that the mother has been engaged in any level of sex with anyone else at the same time as the committed relationship, he cannot be sure the baby carries his genes, and loses interest in supporting her.

Finally, pregnancy also affects utility because girls who become pregnant typically have to leave school.²⁴ The cost of this expulsion risk varies in the population due to heterogeneity in the return to education. We assume earnings are y₀ + θy(e), with y(0) = 0, y′(e) > 0, y″(e) < 0, lim_e→0 y′(e) = +∞, and lim_e→+∞ y′(e) = 0. Once a girl gets pregnant she cannot invest in education: she then earns y₀. We assume the return to education varies among girls due to differences in θ. We assume that the utility of having a child as a teenager is never, in itself, worth the opportunity cost of pregnancy: B_i − θ_jy(e) is negative for i = m, c. Finally let the cost of education be given by C(e) = eγ.²⁵

For simplicity in the analysis of the model, we focus on invidual variations in θ (returns to education). Girls could of course differ in other ways, including in an intrinsic preference in one kind of sexual activity over the other.

If a girl chooses not to mix, utility for girl j under relationship type i and level of unprotected sex s is:

$$\begin{array}{l}{U}_{ij}(s,e)=u_i(s)-\pi (s,a_i)D+v(s,b_i)(B_i+y_0)+(1-v(s,b_i))[y_0+{\theta }_{j}y(e)]-e\gamma \\ =u_i(s)-\pi (s,a_i)D+v(s,b_i)B_i+(1-v(s,b_i)){\theta }_{j}y(e)+y_0-e\gamma .\end{array}$$

With this set-up, we model the education subsidy program as lowering the cost of education γ, and the HIV education program as increasing the perceived STI risk associated with unprotected sex in casual relationships, a_c. In the nested case without a distinction between casual and committed relationships, it would raise both a_c and a_m. The next subsections provide comparative statics with respect to the two parameters γ and a_c.

In this analysis, we rule out the idea that, given high a_i, a further increase in a_i makes people fatalistic so they choose to have more unprotected sex (for an example of this logic see Kremer, 1996). The prevalence of HIV in our study population is low enough that abstracting from fatalism in our context seems reasonable. To rule this out, we assume that the utility-maximizing level of unprotected sex, s̄, satistifes: $\overline{s}\le \frac{-1}{ln(1-a_i)}\forall i$. This implies that the cross derivative of π with respect to s_i and a_i is positive in every case, that is, $\frac{{\partial }^2\pi (s_i,a_i)}{\partial s_i\partial a_i}>0$.²⁶ Likewise we rule out fatalism with regards to the risk of pregnancy by assuming $\overline{s}\le \frac{-1}{ln(1-b_i)}\forall i$. This implies that the cross derivative of v with respect to s_i and b_i is positive in every case, that is, $\frac{{\partial }^{2}v(s_i,b_i)}{\partial s_i\partial b_i}>0$.

Before we move on, it is worth mentioning a few limitations of the model as we set it up. First, the model does not include a risk of rape. While this risk is real, the comparative statics in the model would be qualitatively similar if all girls were subject to some constant risk of pregnancy or STI infection through rape, unless this risk were so large as to induce a fatalistic response to HIV/AIDS education, which our results do not suggest.

Second, all costs and benefits of various types of relationships and of unprotected sex are taking the marriage market and any transfers that are part of other sexual relationships as given. We thus assume these do not change substantially in response to the programs. We believe this assumption is reasonable for the purpose of understanding the treatment effects in our field experiment, since only one cohort of students (those in grade 6 in 2003) was affected by the programs, representing only a minority of adolescents in a given village. Moreover, as discussed earlier, sexual partners of teenage girls are typically several years older and therefore the boys directly impacted by the programs were unlikely to have been potential partners for girls in the sample. Finally, strong norms against sex with even distant relatives mean most marriages are outside of the immediate neighborhood, and while the program covered many schools in the area, the treatment arm assignment of neigboring schools would not be correlated with the treatment arm of a student’s own school.

B. Choice of relationship type, unprotected sex, and education

To solve the utility maximization problem, we assume that agents must choose between the two types of relationships (i.e. don’t mix). In the Web Appendix we provide (realistic) conditions on parameters under which this is true in our model. The underlying intuitions for these conditions are straightforward. First, think about girls for whom the returns to being in a committed relationship are positive. Introducing any positive amount of casual sex is very costly for them, in the sense that it leads to an immediate drop in utility (since once there is any casual sex in the mix, the girl cannot convince the supposed marital partner that he is the father so the benefits of pregnancy drops from B_m to B_c). Thus as long as the the utility-maximizing level of unprotected sex, s̄, is not too high, they will not want to introduce casual sex. Second, think about girls who choose some non-zero casual sex. The main advantage for them to add marital sex in the mix (rather than more casual sex) would be to decrease the STI risk, but this comes at the cost of increased pregnancy risk and therefore increased risk of having to forego education. As long as this cost outweighs the gain in terms of STI risk (which is not very restrictive a condition since girls who choose casual sex have high returns to education), they will choose not to mix.

In what follows, we assume these conditions (formalized in the Web Appendix) hold. We thus drop all i, j subscripts when the analysis is for a given individual and relationship type. To solve for the optimal level of s, e and relationship type, it is necessary to consider the Kuhn-Tucker conditions since the optimum could potentially be at a corner where e = 0 or s = 0. As discussed in the Web Appendix, comparative statics at the corners are either similar to those at the interior solution or uninteresting because there is no change in behavior in response to variations in the cost of education or perceived STI risk. We therefore focus on interior optima below, leaving exposition of the general case for the appendix.

Interior optima must satisfy the following first-order conditions:

$$\begin{array}{l}\frac{\partial U}{\partial s}=u^{\prime }(s)-\frac{\partial \pi (s,a)}{\partial s}D+\frac{\partial v(s,b)}{\partial s}[B-\theta y(e)]=0\\ \frac{\partial U}{\partial e}=(1-v(s,b))\theta y^{\prime }(e)-\gamma =0\end{array}$$

Finally, for an interior solution the Hessian matrix must be negative definite, and hence its determinant must be positive and the top-left entry negative. After replacing the second order derivatives and the partial derivatives, this implies that interior solutions must satisfy:

$$\begin{array}{c}\frac{{\partial }^{2}U}{\partial s^2}=u^{″}(s)-\frac{{\partial }^2\pi (s,a)}{\partial s^2}D+\frac{{\partial }^{2}v(s,b)}{\partial s^2}[B-\theta y(e)]<0\\ \mathit{detH}=\frac{{\partial }^{2}U}{\partial e^2}\frac{{\partial }^{2}U}{\partial s^2}-{\left(\frac{{\partial }^{2}U}{\partial s\partial e}\right)}^2>0.\end{array}$$

C. Comparative statics for s and e conditional on relationship type

We start with comparative statics conditional on relationship type, committed or casual, and then examine (in the next subsection) how changes in parameters affect switching between relationship types. We prove only the first lemma in the text: the other proofs follow exactly the same logic and are in the Web Appendix.

LEMMA 1

When γ (the cost of education) increases, conditional on relationship type, the optimal e decreases and s increases.

PROOF

Taking the total derivative of the first-order conditions with respect to γ yields:

$$\begin{array}{c}\frac{{\partial }^{2}U}{\partial s^2}ds+\frac{{\partial }^{2}U}{\partial s\partial e}de=0\\ \frac{{\partial }^{2}U}{\partial s\partial e}ds+\frac{{\partial }^{2}U}{\partial e^2}de-d\gamma =0.\end{array}$$

Solving these expressions for $\frac{de}{d\gamma }$ and $\frac{ds}{d\gamma }$, we obtain:

$$\begin{array}{l}\frac{\frac{{\partial }^{2}U}{\partial s^2}}{\mathit{detH}}=\frac{de}{d\gamma }\\ \frac{-\frac{{\partial }^{2}U}{\partial s\partial e}}{\mathit{detH}}=\frac{ds}{d\gamma }.\end{array}$$

The second-order conditions allow us to sign these expressions: $\frac{de}{d\gamma }<0$ and $\frac{ds}{d\gamma }>0$.

LEMMA 2

When a (the perceived risk of STI) increases, conditional on relationship type, s decreases and e increases.

LEMMA 3

When b (the risk of pregnancy per sex act) increases, conditional on relationship type, e decreases and the probability of pregnancy increases.

LEMMA 4

When B (the benefit of pregnancy) increases, conditional on relationship type, s increases and e decreases.

LEMMA 5

When θ (the return to education) increases, conditional on relationship type, s decreases and e increases.

D. Comparative statics: relationship type

LEMMA 6

Given a_c, a_m, b_c, b_m, B_c, B_m, θ and γ, the incidence of pregnancy is lower and e is higher in casual relationships than committed relationships.

PROOF

This is trivially true given the lemmas above and the assumptions that in casual relationships the benefit of pregnancy is lower (B_c ≤ B_m), the probability of pregnancy per sex act is lower (b_c ≤ b_m), and the STI risk is higher (a_c ≥ a_m).

The next step is to assess how changes in the parameters a_i (perceived STI risk by relationship type) and γ (the cost of education) affect which relationship type is chosen. We focus in this section on the case in which casual and committed relationships are distinct, and thus the inequalities discussed above (a_c ≥ a_m b_c ≤ b_m, B_c ≤ B_m) are strict. First, note that lower returns to education make committed relationships relatively more attractive and higher returns make casual relationships relatively more attractive.

LEMMA 7

Given a_c, a_m, b_c, b_m, B_c, B_m, and γ, then either:

1. all girls choose casual relationships or 

2. all girls choose committed relationships or 

3. there exists a threshold return to education θ_tsuch that girls with θ< θ_tchoose committed relationships and girls with θ> θ_tchoose casual relationships. 

PROOF

Both U_c and U_m increase in θ, but at different rates: $\frac{{dU}_i}{d\theta }=(1-v(s_i,b_i))y(e_i)$. Given the result in lemma 6, v(s_m, b_m) > v(s_c, b_c) and e_m < e_c. Therefore, $\frac{{dU}_m}{d\theta }<\frac{{dU}_c}{d\theta }$. This implies that, as long both types are chosen, there is a threshold level θ_t such that the individual chooses to engage in type m (a committed relationship) if and only if θ < θ_t.

The next step is thus simply to determine how the programs affect the threshold θ_t. The following two lemmas are proven in the Web Appendix:

LEMMA 8

When γ (the cost of education) decreases, θ_t (the threshold return to education above which girls choose casual relationships) decreases.

LEMMA 9

When a_c (the perceived chance of infection from an unprotected sex act in a casual relationship) increases and a_m does not change, θ_t increases.

These results are intuitive. Reductions in the cost of education, such as under the education subsidy program, increase utility in both committed and casual relationships, but increase utility more in casual relationships (because e tends to be larger in casual relationships). This leads more girls to choose casual relationships, and thus lowers the threshold return to education beyond which casual relationships are chosen. Meanwhile, increasing the perceived risks associated with casual sex, as we assume the official HIV prevention curriculum does, decreases the relative value of casual relationships and thus increases the threshold below which girls choose committed relationships.

E. Predictions

We are now ready to discuss the predictions regarding the impact of the three programs (education subsidy, HIV training and joint program) on educational attainment, pregnancies, and STIs.

Main predictions

Assume first that the impact of the education subsidy program is to reduce the cost of education (model parameter γ), while the impact of the HIV education program is to increase the spread between the perceived probability of contracting HIV and other STIs in casual and marital relationships (a relative increase in a_c compared to a_m).

PROPOSITION 1

A stand-alone education subsidy program reduces pregnancy and increases educational attainment. It may either increase or decrease STIs.

PROOF

Since the education subsidy reduces the cost of education, it reduces s and increases e for girls in both casual and committed relationships. Moreover, it increases the number of girls who choose casual, rather than committed, relationships. The education subsidy thus unambiguously increases education and reduces teenage pregnancy.

The education subsidy reduces STIs for girls who choose a committed relationship, but by inducing some to choose casual relationships it may increase their risk. If $a_c^{\ast }$ is sufficiently greater than $a_m^{\ast }$ and s remains positive, then STI risk will increase for those who switch to a casual relationship. If a sufficient proportion of the population is close enough to the threshold that they switch, overall STI prevalence will increase. On the other hand, if no one switches to casual relationships or if $a_m^{\ast }$ is sufficiently close to $a_c^{\ast }$, the reduction in s will reduce STI prevalence.

In the Web Appendix, we introduce a numerical example which illustrates the ambiguous effect of the education subsidy on STIs.

PROPOSITION 2

If casual and committed relationships differ, the stand-alone HIV education program increases early marriages and reduces the share of single-parenthood pregnancies, but the overall impact on pregnancy and education is ambiguous. Likewise, it may either increase or decrease STIs.

If there is no difference between casual and committed relationships, the HIV education program reduces both pregnancy and STIs.

PROOF

An increase in the perceived risk of STI per casual sex act, a_c, due to the HIV education program, reduces unprotected sex and increases educational effort for those who choose casual relationships. If committed relationships differ, they become relatively more attractive, and so some may switch to those relationships. Since the probability of pregnancy is higher in committed than in casual relationships, the effect on teenage pregnancy is ambiguous. However, there is an unambiguous decline in the share of teen pregnancies that are out of wedlock. The effect on STIs is ambiguous. If no one switches relationship type, then STIs will fall. If enough people switch to committed relationships and if $a_m^{\ast }$ is sufficiently close to $a_c^{\ast }$, then STIs may rise because the optimum s is higher in committed relationships.

Proposition 2 thus provides one way of distinguishing the proposed two-factor model from the nested one-factor model without a relationship type distinction. Proposition 3 below provides another.

PROPOSITION 3

If there is only one relationship type, i.e. if committed and casual relationships are identical ( $a_m^{\ast }=a_c^{\ast }$, a_m= a_c, b_m= b_c, and B_m= B_c), then if the joint program causes a greater reduction in STIs than either of the stand-alone programs, the joint program should also cause a greater reduction in pregnancy than either of the stand-alone programs. If there are two relationship types, this need not be the case.

PROOF

If there is only one type of relationship, there is no switching. The only way programs affect pregnancy or STI risk is by changing s. From Lemmas 1 and 2, we know that both stand-alone programs reduce s, thereby reducing both pregnancy and STIs. If the joint program causes a greater reduction in STIs than either of the stand-alone programs, then it implies that it reduces the level of unprotected sex more than either program in isolation, and therefore the reduction in pregnancy should also be greater.

If there are two relationship types, the joint program may either increase or decrease the threshold θ_t, because it pushes individuals in opposite directions: the education subsidy reduces the relative appeal of committed relationships, but raising the perceived risk of casual relationships pushes people towards committed relationships. Because switching from committed to casual relationships reduces the probability of pregnancy and increases educational effort, the joint program may reduce pregnancy by less than the stand-alone education subsidy. However, the joint program can lead to a larger decrease in STIs than under education subsidies alone, because the joint program generates fewer incentives to switch to casual relationships.

Alternative interpretation of the interventions

In the previous section we have limited the effect of the education subsidy to matter only through its impact on the opportunity cost of pregnancy. Education could also affect sexual behavior via other channels. First, by reducing the opportunities to have sex. Second, by increasing access to information, through direct exposure to education, and through a better ability to process the information that is available in the environment (Rosenzweig and Schultz 1989, Thomas, Strauss, and Henriques 1991). Third, the subsidized (new) uniforms could also have increased girls’ dignity and self-respect, making it easier to say no to sex, or to impose the use of condoms.

These effects can in principle all be captured within the framework of our model. The empowerment effect could be modeled as a reduction in the utility from unprotected sex (which includes monetary inducement and intimidation), potentially both casual and marital. The reduction in the opportunities to have sex can also be modeled in the same way (the increase in the value of time reduce the marginal utility of sex, marital or casual). In both cases, we would thus expect the education subsidy programs to reduce both pregnancies and STIs.

The information effect is the most interesting and potentially most complicated alternative mechanism to what we propose here, since it could have very different effects depending on the information that is in fact provided in school and elsewhere in the environment. To the extent the education subsidy intervention acts by increasing the exposure to information available in school, however, one clear prediction is that it should re-inforce any impact of the HIV education treatment. This implies that the joint program should have effects that are larger in absolute value than those of the HIV education treatment (in the same direction). This implies in particular that if the stand-alone HIV education program decreases the number of unmarried pregnancies, the effect of the joint program on unmarried pregnancies should be larger. Also, to the extent that the HIV education training mainly reinforces the message that is usually delivered in schools, the stand-alone education subsidy intervention would have an impact that is similar to the impact of the HIV-education program 

There could also be alternative interpretations of how the HIV education program affects the model parameters. We model it as increasing the perceived probability of STI in casual, but not in marital, sexual relationships. This is based on our understanding of the salient aspects of the HIV education curicu-lum. However, the implementation by teachers, or children understanding of it, may be different from what we believe, leading to different impacts. A first possibility is that condoms are in fact introduced by teachers, and that increasing the knowledge of condoms does reduce the cost of protected sex. We can directly address this thanks to the randomized critical thinking add-on program. A second possibility (raised by a referee) is that, perhaps due to fatalism, the HIV education program increases the value of a pregnancy (possiby on top of the effect we introduce). Assuming the increase is larger in committed relationships, this would lead to the same kind of comparative statics as the predictions in our model (increase in the share of pregnancies within marriage, shift towards marital relationships, and ambiguous impacts on STIs). This however seems unlikely since we do not find evidence that the HIV education program affected the likelihood that the first pregnancy was desired. There could also be an increase in pregnancies, but this may not happen if the perceived probability of contracting STIs in a casual relationship increases sufficiently.

F. Interpreting the data in light of the model

The data is compatible with the predictions of the model allowing for two relationship types. The education subsidy reduced dropout and teenage pregnancy rates significantly, but not STI rates, perhaps because casual relationships are indeed somewhat more likely to lead to STIs than committed relationships. Training teachers on the official HIV curriculum did not reduce teenage pregnancies but reduced the share of teen pregnancies out of wedlock, consistent with the idea that it pushed people to choose committed relationships.

The HIV education program did not reduce STI risk, presumably because the increase in unprotected sex associated with moving to committed relationships counteracts the lower average per-act risk of transmission in committed relationships. The joint program had a weaker effect on both dropout and teen pregnancy rates than the stand-alone education subsidy, but it reduced STI risk more than the stand-alone education subsidy.

The finding that the joint program has a larger effect on STI than the education subsidy alone (p-value = 0.013, Table 4, column 2) but a smaller effect on pregnancy (p-value = 0.058, Table 2, column 9) allows us to reject the prediction of the single factor model (proposition 3) that if the joint program causes a greater reduction in STI than either stand-alone programs, it should also cause a greater reduction in pregnancy than that program. Note that we do not just see an absence of this effect, which could then potentially be due to sampling error, but statistically significant effects (at the 6 percent and 2 percent level) in opposite directions.

To understand how the richer model’s predictions can indeed account for this pattern of results, it is useful to consider an example in which girls are equally divided between four levels of θ, such that in the control group, the two types with lower θ choose committed relationships, and the two types with higher θ choose casual relationships. The HIV education program reduces the STI risk unless it leads to a switch in relationship type (towards committed relationships) for those with the second to highest level of θ. If it leads to a switch, it may increase transmission since s is higher among those in committed relationships. The stand-alone education subsidy decreases STI risk, unless it leads the second to lowest type to switch to casual relationships, in which case STI risk may remain unchanged or increase. Finally, note that if the two stand-alone programs generate switching, but the groups that switch are close enough to the threshold after the policy change, these groups will not switch under the joint program and hence STI rates will fall unambiguously under the joint program.

In the Web Appendix, we provide a simple (and plausible) numerical example following the discussion above, and show that we can replicate the patterns of our empirical results. When the model’s parameters are set to match pregnancy and STI rates in the control group, the numerical example delivers pregnancy and STI rates for each treatment group similar to those observed in the data. Moreover, the direction and relative magnitudes of the effects of each treatment in the numerical example match the data. In particular, with our parameterization, the joint program produces the biggest drop in STI rates, but it does not reduce pregnancy or dropout rates by as much as the stand-alone education subsidy program.

In contrast, our results do not appear to be compatible with the alternative interpretations of the interventions. Starting with the education subsidy intervention, the fact that we do not see a reduction in both STI and pregnancies suggest that the effects of education do not come only through the empowerment and opportunities to have sex. The fact that the education subsidy intervention and the HIV education intervention have very different effects, and that the impact of the joint program is in between, suggest that the main impact of education is not to increase exposure to information provided in school. As for the HIV education program, the results of the add-on critical thinking intervention suggest that the introduction of information on condoms does not affect behavior (not even reported use of condoms), suggesting that information on condoms cannot be the way the program operates. The comparative statics we observe are in principle compatible with an increase in the value of pregnancy within marriage but only if there is also an increase in the fear of STI outside marriage (otherwise we would see a net increase in pregnancies). We will show below additional evidence suggesting that the value of pregnancies has not gone up significantly.

G. Additional evidence

The long-run follow-up survey includes self-reported sexual behavior data that can help check whether we observe some of the pathways for the effects predicted under the model. This data, shown in Table 6 with specifications identical to those in Tables 3 and 4, needs to be treated with considerable caution, as self-reports are easily tainted by social desirability bias.²⁷ Nevertheless, it is broadly consistent with the model. First, girls in the stand-alone education subsidy schools are significantly less likely to report faithfulness as a way they use to protect themselves (column 3). This is consistent with the model’s prediction that education subsidies may lead girls to switch to casual relationships (assuming faithfulness is an indicator of a committed relationship). The other effects are insignificant but all have the right sign: girls in the stand-alone education subsidy schools are more likely to report that they have never had sex, and more likely to report abstinence as one of the methods they use to protect themselves from HIV, and they also have younger partners, consistent with the shift to casual sex and away from sex with “committed” older men, i.e., those able to marry them if a baby is conceived (Dupas, 2011).

Table 6.

Long-Run Impacts: Self-Reported Sexual Behavior of Girls

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
		When asked about own behavior to prevent HIV infection…			First pregnancy / child was wanted	Age of oldest partner ever	If ever had sex:
	Ever had sex	Reports Abstinence	Reports Faithfulness	Reports Condom Use			Age at first sex	condom last time had sex
Stand-Alone Education Subsidy (S)	−0.029 (0.021)	0.017 (0.015)	−0.030 (0.017)*	−0.001 (0.010)	−0.009 (0.029)	−0.269 (0.226)	0.069 (0.095)	0.017 (0.021)
Stand-Alone HIV Education (H)	0.010 (0.023)	0.012 (0.016)	0.033 (0.019)*	−0.011 (0.010)	0.037 (0.029)	0.196 (0.256)	−0.096 (0.092)	−0.010 (0.022)
Joint Program (SH)	−0.008 (0.021)	0.025 (0.016)	0.023 (0.020)	−0.014 (0.010)	−0.025 (0.030)	0.051 (0.248)	0.061 (0.089)	−0.021 (0.023)
Sampling Weights	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Observations	5717	5713	5713	5713	2450	3681	3577	3700
Mean of Dep. Var. (Control)	0.680	0.211	0.274	0.069	0.304	24.953	16.997	0.282
p-val (Test: S = SH)	0.297	0.567	0.006***	0.190	0.586	0.205	0.931	0.094*
p-val (Test: H = SH)	0.409	0.438	0.612	0.764	0.034**	0.612	0.109	0.604
p-val (Test: S = H)	0.069*	0.755	0.001***	0.286	0.075*	0.09*	0.097*	0.224
p-val (Test: SH = S + H)	0.720	0.884	0.467	0.866	0.206	0.728	0.531	0.363

Notes: Data Source: Individual long-run follow-up survey conducted after 7 years. Estimates obtained through OLS regressions that include controls for year of birth, the timing of the survey, school size and randomization strata dummies. Standard errors clustered at the school level. ***, **, * indicate significance at 1, 5 and 10%.

Second, girls in the stand-alone HIV education schools report having had their first sexual experience at a younger age than the control group and, consistent with the model’s prediction that HIV education may lead girls to switch to committed relationships, they are significantly more likely to report faithfulness as a way they protect themselves from HIV. They have slightly older partners, consistent with the idea that they are moving away from casual relationships with men who are not likely to mary them. They are less likely to report condom use, consistent with the model’s suggestion that the level of unprotected sex s will be higher in committed relationships. While most of these effects have the sign predicted by the model, we note that they are not statistically significant, except for the results on faithfulness. The point estimate for the effect of the stand-alone HIV education program on the likelihood that the first pregnancy was wanted is positive and relatively large (a 3.7 percentage points increase off of a 30 percent mean) but not significant. This suggests that the HIV education program may have increased the value of pregnancy within marriage, although this is not the case in the joint program.

For the joint program, the impact on faithfulness is not significant in either direction. The increase in the number of girls mentioning abstinence is twice as high under the joint program than under the stand-alone HIV education program, but that difference is not significant. (Note that the model does not necessarily predict abstinence, just reduced unprotected sexual activity, for which we do not have a good self-reported proxy).

Table 7 provides further suggestive evidence, by looking at HSV2 prevalence within marital status and education categories. Of course such categories are endogenous, and therefore comparing HSV2 rates across categories (i.e., across rows of Table 7) is not particularly informative. For example, married women are much more likely to be infected with HSV2 than unmarried women, but this likely reflects the fact that married women have more unprotected sex (now and probably in the past as well) – it does not necessarily mean that, conditional on the level of sexual activity, committed sex is riskier. What is potentially more informative, however, is to compare categories across experimental arms (i.e., make comparisons across columns of Table 7). For example, compared to the control group, under the stand-alone education subsidy young women are slightly more likely to be HSV2 positive within each category, which is consistent with them moving towards more risky, casual relationships. The reason why, despite this, the overall level of STI does not significantly increase in the education subsidy group relative to the control group is that, as we saw earlier in Tables 3 and 4, more girls stay in school (and hence unmarried), the safest group. In contrast, prevalence is lower for girls in the joint program within each category, consistent with the model’s prediction that the reduction in STIs does not come from a composition change, but from a decline in unprotected sexual activity within each category.

Table 7.

HSV2 Prevalence Among Girls, by Marital/Schooling status and Treatment Group

	# Obs	All	Stand-Alone Education Subsidy (S)	Stand-Alone HIV Education (H)	Joint Program(SH)	Control (C)
Ever Married	1838	18.1%	20.6%	17.9%	15.4%	18.2%
Never Married	3694	7.6%	8.8%	7.8%	6.0%	7.9%
In school	2183	5.8%	6.4%	6.1%	3.8%	6.4%
Out of school	3346	14.6%	16.8%	14.7%	12.3%	14.7%
Out of school and never married	1517	10.3%	12.4%	10.6%	8.8%	10.1%
Reports that Ever had sex	3589	14.6%	16.7%	14.7%	12.4%	14.6%
Reports that Never had sex	1945	4.6%	5.1%	4.7%	3.0%	5.3%

Notes: Data Source: Individual Follow-up Survey conducted after 7 years. We present the raw (unweighted) means.

VI. Conclusion

It is widely believed that increasing female education is a critical step in reducing fertility and improving maternal and child health in developing countries. This paper sheds light on this important question. Using data from a randomized evaluation, we show that reducing the cost of education by providing free uniforms reduces school dropout, teen childbearing and early marriage. This suggests that girls have some agency regarding sexual activity. Whether girls defer childbearing, however, depends on their beliefs about the value of marriage. We find that HIV prevention curricula that focus on an abstinence-until-marriage message increase early marriage and counteract the effects of increased access to schooling on fertility.

We also show that the interplay between perceived HIV risk, schooling opportunities and early fertility is complex, and policies that focus on only one of these issues at a time may have unanticipated effects. We find that combining an education subsidy with Kenya’s abstinence-until-marriage curriculum can reduce the rate of STIs for young women, but it does not reduce their risk of early fertility and it does not increase their schooling attainment as much as the education subsidy implemented alone.

We develop a model to interpret these results and can use the model to think through counterfactual HIV prevention education programs. Indeed, it is important to recognize that our results apply to a particular type of HIV education program in a particular context, even if both the program type and broad content are common. The model first suggests that programs that increase the perceived risk of HIV associated with both casual and committed relationships, rather than just casual relationships, could lead to less switching to committed relationships, and thus potentially have greater effects on pregnancy, STI, and dropout rates. The model also suggests results would be different in a context with greater elasticity of unprotected sex due to greater condom acceptability. And of course a program actively promoting condoms would have different effects.

Despite the fact that we followed up with our study participants for an unusually long period of time, our results are relatively “short-run.” The youths in our sample are only at the onset of their adult life and we cannot speak to what their lifetime STI risk will be. More than 50 percent of the girls in our study cohort were not yet married as of our last survey. These girls will eventually marry and, depending on who they marry, might get infected through their spouse.

Nevertheless, our findings imply a particularly important role of the ability (and the incentives) to stay in school: the reduction in teenage pregnancies obtained through the education subsidy alone is almost as large as the reduction it caused in school dropouts. This does not imply that every girl who did not drop out because of the program would have had a child otherwise; some girls who would have stayed in school anyway if not pregnant may also have been induced by the program to remain sexually inactive or use contraception. Instead, this suggests that giving girls additional motivation to delay their first pregnancy (the opportunity to go to school if they want to do so) is an extremely powerful (and inexpensive) way to reduce early fertility. Most government and international efforts have focused on ease of access to basic education (up to grade 6 or 9). Our results suggest that education gains in the upper end of that range, or even secondary school, especially for girls, may have a much larger impact on reducing early fertility than we would expect based on the causal effect of years of primary education on early fertility.