Abstract
The American Community Survey (ACS) multiyear estimation program has greatly advanced opportunities for studying change in the demographic and socioeconomic characteristics of U.S. communities. Challenges remain, however, for researchers studying years prior to the full implementation of the ACS or areas smaller than the thresholds for ACS annual estimates (i.e., small counties and census tracts). We evaluate intercensal estimates of the demographic and socioeconomic characteristics of U.S. counties and census tracts produced via linear interpolation between the 2000 census and both the 2010 census and 2005–2009 ACS. Discrepancies between interpolated estimates and reference estimates from the Population Estimates Program, the Small Area Income and Poverty Estimates, and ACS are calculated using several measures of error. Findings are discussed in relation to the potential for measurement error to bias longitudinal estimates of linearly interpolated neighborhood change, and alternative intercensal estimation models are discussed, including those that may better capture non-linear trends in economic conditions over the 21st century.
Keywords: Intercensal estimates, Linear interpolation, American Community Survey (ACS)
Introduction
Research on the role of neighborhoods and communities in shaping the experiences of individuals has expanded rapidly over the last two decades buoyed both by a renewed interest in the role of place in public health and human development (Kearns 1993; National Research Council and Institute of Medicine 2000; Macintyre et al. 2002), as well as by innovations in data collection, computing, and statistical analysis (Entwisle 2007; Voss 2007; Auchincloss et al. 2012). Among the recommended directions for future research on individuals and place is the need to rigorously embrace the consequences of time. This includes questions motivated by life course theories about historical context, critical age periods, timing, sequencing, and the accumulation of advantages and disadvantages of place as individuals age (Sampson et al. 2002; Robert 2010). A notable obstacle to explore these unanswered questions, however, has been the limited availability of contextual data that is updated annually. Until 2000, the only publicly available source of spatially detailed, social, and economic information with consistent measurement over long periods of time and for the entirety of the U.S. has been the decennial census long form (MacDonald 2006). In order to pursue research requiring small area contextual data at a periodicity greater than every 10 years—for example in studies considering neighborhood selection and neighborhood inequality (Sampson and Sharkey 2008; Crowder et al. 2012) and accumulated exposure to neighborhood disadvantage (Kling et al. 2007; Do 2009; Wodtke et al. 2011; Ludwig et al. 2012)—the standard approach has been to apply linear interpolation to produce data estimates for intercensal years.
A primary rationale for developing the American Community Survey (ACS) was to address the limitations of the decennial census by providing annually updated estimates of population and housing characteristics (Torrieri 2007). Although the ACS data have greatly advanced opportunities for studying time and place, challenges remain for researchers interested in time trends for places (such as small counties and census tracts) that are smaller than the ACS population size thresholds for annual estimates and for researchers interested in incorporating trends prior to 2006 when the ACS was fully implemented.
In order to be economically feasible, the increased periodicity of the ACS data has had to come at the cost of reduced precision (MacDonald 2006; Spielman et al. 2014). This means that, although the ACS does provide 1-year estimates of nearly all (and some additional) demographic, social, economic, and housing characteristics previously covered in the census long form, these estimates are only available for places with populations of at least 65,000 persons. Thus 1-year estimates are unavailable for almost three-quarters of the counties in the U.S., almost half of the metropolitan statistical areas, nearly all school districts, and all census tracts (U.S. Census Bureau 2014b). Estimates for the full range of places covered by the decennial censuses are available annually, but only in 5-year estimates (e.g., 2005–2009, 2006–2010, and etc.).1 These multiyear estimates have a different temporal reference than the previously released decennial census point estimates; they describe a continuous window of time, while point estimates describe a snapshot of time (Beaghen and Weidman 2008; McElroy 2009; U.S. Census Bureau 2009a).
In addition, although the ACS began to provide the selected annual and multiyear estimates as early as 2001, full implementation of the ACS was not achieved until 2006 (U.S. Census Bureau 2009b). Prior to 2006, the ACS was not representative of the entire U.S. population; people living in group quarters (GQ) such as correctional facilities, nursing facilities, and college residence halls were excluded with consequent sampling bias for populations over-represented in GQ (e.g., racial/ethnic minorities, older adults, young adults, and disabled populations). Moreover, sampling was conducted at a lower rate, so that (with the exception of ACS test areas) 1-year estimates prior to 2006 are only available for populations of size 250,000 persons or larger. As a result, researchers requiring annual estimates of the demographic and socioeconomic conditions of small geographies over the 21st century must employ an estimation procedure with the only publicly available, nationally comprehensive, and geographically detailed data sources being the 2000 Census, the ACS 5-year multiyear estimates (beginning with the 2005–2009 estimate), and the 2010 Census. Among these sources, only the 2000 Census and the ACS provide information on a full range of demographic, social, economic, and housing variables.
While linear interpolation between census point estimates is a commonly employed method for producing annual intercensal estimates of small geographies for longitudinal research (Kling et al. 2007; Sampson and Sharkey 2008; Do 2009; Crowder et al. 2012; Ludwig et al. 2012), these interpolated estimates are seldom validated. In addition, with the advent of the ACS, it is unknown whether and how linear interpolation should be applied between the 2000 census (point estimate) and the first available ACS 2005–2009 (multiyear estimate). Although the Census Bureau advises against interpreting the multiyear estimates as a mid-year point estimate (Beaghen and Weidman 2008; McElroy 2009; U.S. Census Bureau 2009a), there are no alternative census tract point-estimate data for socioeconomic variables after 2000. Thus, in all but one known longitudinal research study considering the individual or household consequences of neighborhood socioeconomic conditions over the 21st century (Crowder et al. 2012), researchers employed a midpoint assumption to the ACS multiyear estimate and linearly interpolated between the 2000 Census and the 2005–2009 ACS (Do 2009; Do et al. 2013; Ludwig et al. 2012). For the one exception, the period of study did not extend beyond 2005 and so Crowder et al. (2012) instead conducted linear projection from the 2000 Census.
In this study, we examine how well linear interpolation performs for obtaining annual estimates of the demographic and socioeconomic characteristics of U.S. communities using the 2000 Census, 2010 Census, and 2005–2009 ACS. We evaluate the extent to which the performance of linear interpolation depends on the demographic or socioeconomic indicator, the population size of the geographic unit, and the year. In addition, although it is beyond the scope of this paper to fully examine the midpoint assumption required to employ the 2005–2009 ACS multiyear estimates in linear interpolation, we also examine whether annual trends in population characteristics across the 5-year period support the decision to use 2007 as an endpoint.
Methods
Interpolated Data
The interpolated data comprised a series of linearly interpolated estimates of the demographic and socioeconomic characteristics of U.S. counties and census tracts. For demographic characteristics, we linearly interpolated annual population counts by age, gender, and race/ethnicity between the 2000 and 2010 Census. For socioeconomic characteristics, we selected four indicators (i.e., annual population counts of persons with household income below the poverty level; annual population counts of persons by highest educational attainment; annual population counts of persons in the labor force by occupation; and the median household income) and conducted linear interpolation between the 2000 Census and the 2005–2009 ACS multiyear estimates. For the socioeconomic interpolations, we defined the endpoint as the midpoint of the 2005–2009 interval (i.e., 2007), and we examined the appropriateness of this assumption as described below. All decennial census data and ACS data were obtained from the U.S. Census Bureau FTP Server (U.S. Census Bureau 2014a). Additional information about the construction of the ACS and the differences in the construction relative to the decennial census is detailed elsewhere (Spielman et al. 2014).
For all demographic and socioeconomic indicators (with the exception of median household income), we obtained linearly interpolated population counts for each respective indicator at the tract level and the county level, and then calculated the tract-level and county-level percent distributions by the indicators. Linear interpolation of the median household income of tracts was conducted using the tract-level 2000 Census and tract-level 2005–2009 ACS estimates, and a separate linear interpolation of the median household income of counties was conducted using the county-level 2000 Census and the county-level 2005–2009 ACS estimates.
In order to interpolate tract-level demographic characteristics, we first needed to address the change in tract boundaries between the 2000 and 2010 Censuses. We employed spatial interpolation to estimate 2010 demographic characteristics for 2000 boundaries using public-use population and areal weighting tools from the Longitudinal Tract Data Base (LTDB) (Logan et al. 2014).2 In addition, 10 counties changed boundaries between 2000 and 2010, and these counties were dropped from the analysis. For the interpolation of socioeconomic characteristics, both the 2000 Census and the 2005–2009 are provided using 2000 Census tract boundaries.
Comparison Data
The U.S. Census Bureau provides the annual intercensal estimates of demographic and selected socioeconomic characteristics with nationally comprehensive estimates for geographies as small as counties through the Population Estimates Program (PEP) and Small Area Income and Poverty Estimates (SAIPE). The PEP is the only known data source with intercensal estimates of population counts by gender, age, race, and Hispanic origin available for all counties for every year from 2001 through 2009. The PEP produces an updated ‘vintage’ of postcensal population estimates in each year using a modified cohort–component methodology that incorporates data on birth, migration, and death; the intercensal 2000–2010 vintage of the PEP estimates are additionally adjusted to fall within the bounds of the 2000 and 2010 Census (U.S. Census Bureau 2014c). The 2000–2010 intercensal PEP data series is thus selected as the best available Census Bureau reference data source for the demographic indicators.
The SAIPE is the only known data source with estimates of socioeconomic characteristics (i.e., the median household income and the percentage of the population with household income below the poverty level) for every county in the U.S. for each year from 2001 through 2009. Estimates are produced using a statistical model that combines direct estimates of income and poverty for states and counties from a reference data source [i.e., the Current Population Survey (CPS) Annual Social and Economic Supplement (ASEC) through 2004 and the 1-year ACS estimates thereafter] with additional summary data (i.e., from federal income tax returns, food stamp benefits data, decennial census data, postcensal PEP estimates, Supplemental Security Income recipiency, and economic data from the Bureau of Economic Analysis) (U.S. Census Bureau 2014d). This model-based estimation methodology is designed to improve the precision of state and county income and poverty estimates and provide estimates of small geographic areas (i.e., small counties and school districts) otherwise unavailable through other sources. The SAIPE is thus selected as the best available Census Bureau reference data source for these two socioeconomic indicators.
For the other socioeconomic characteristics included in this study, the ACS 1-year county estimates provide the only known annual data source. As described above, full implementation of the ACS occurred in 2006, with 1-year estimates available for counties above the 65,000 person annual reporting threshold. At the sub-county level, the 2005–2009 ACS provides the first available nationally comprehensive and fully geographically detailed estimates of demographic and socioeconomic characteristics after the 2000 Census.
Analytic Strategy
In order to answer our research questions, we estimate the error in linearly interpolated estimates of community social and economic characteristics compared to the fine-grained, publicly available annual comparison data from the U.S. Census Bureau. We first calculate the error in linearly interpolated estimates of county characteristics compared to the following sets of reference data:
PEP annual estimates of total population counts, percent female, percent non- Hispanic White, percent non-Hispanic Black, and percent Hispanic for all counties in each year 2001–2009;
SAIPE annual estimates of percent of population with household income below the poverty line and median household income (in constant 1999 dollars) for all counties in each year 2001–2009; and
ACS 1-year estimates of the percent population distribution by education, and percent employed in professional and managerial occupations for the subset of available counties in 2006.
We evaluate error over all counties for all of the years possible for each of the above three comparisons. In order to assess the distribution of the error in terms of direction (i.e., underestimation or overestimation), we calculate the algebraic error. This is defined as (interpolated estimate) - (reference estimate). We calculate the mean and standard deviation of the algebraic error and identify the values of the 5th, 25th, 50th, 75th, and 95th percentiles. The mean and median (50th percentile) describe the central tendency of the error, while the standard deviation and the range of values between the 5th and 95th and between the 25th and 50th percentiles provide information about the variability of the error. Comparison of the absolute value of the 5th versus the 95th and the 50th versus the 75th percentile values provide additional information about the skew of the algebraic error. In addition, in order to summarize the magnitude of the error, we employ the median and the 90th percentile of the absolute error (i.e., calculated as the absolute value of the algebraic error). When error is balanced between underestimation and overestimation, the median absolute error is about one half of the range between the 25th and the 75th percentiles of the algebraic error and the 90th percentile of the absolute error is about one half of the range between the 5th and the 95th percentiles of algebraic error.
We calculate all of the above error statistics for all counties and all years for which reference data are available. Thus, for the analyses of the demographic variables using the PEP and for the analyses of socioeconomic variables using the SAIPE, error is reported for county years. For analyses employing ACS data on social and economic variables (for which only 1 year of comparison data is available), error is reported for counties. These statistics are presented in tabular form. In addition, we assess whether the performance of linear interpolation differs by the size of the county and the year of the estimation. We categorize counties depending on their population size in the 2000 Census (i.e., less than 5000 persons; 5000–9999 persons; 10,000–24,999 persons; 25,000–59,000 persons; 60,000–149,999 persons; and 150,000 or more persons). Error analyses by the size of the county and the year of estimation are displayed using box plots (where the values of the 25th and the 75th percentiles define the box and the 5th and 95th percentiles define the whiskers).
We also employ the above measures of error to evaluate whether trends in the 1-year ACS estimates support the 2007 midpoint year assumption for the endpoint of the linear interpolation between the 2000 Census and the 2005–2009 ACS. As a summary statistic, the mean absolute error allows us to assess the average difference between each of the nationally representative 1-year ACS county estimates and the overall 5-year ACS county estimate for the period 2005–2009 and to evaluate the extent to which differences between the 1-year and 5-year estimate are minimized in 2007. Recall that 1-year ACS estimates did not become nationally representative until 2006, so the series of 1-year ACS estimates we compare are for 2006, 2007, 2008, and 2009.
Finally, we employ the 2005–2009 ACS tract-level data to produce an estimate of the error in tract-level linear interpolation between the 2000 and 2010 Census. Due to the temporal alignment problem of appropriately matching the timing of the interpolated point estimates and ACS multiyear estimates (that is evaluated in part above), we compare the interpolated estimates of demographic characteristics for each year in the 5-year window (i.e., 2005, 2006, 2007, 2008, and 2009) to the respective tract-level demographic estimates from the 2005–2009 ACS. We calculate the measures of algebraic and absolute error described above.
Findings
Table 1 summarizes the findings from comparing the interpolated estimates against the best source of U.S. Census Bureau reference data for the total number of counties and years observed over the interpolation period. For the demographic indicators, we compare the interpolations between the 2000 and 2010 Census to annual intercensal estimates from the PEP for 3131 counties in each year from 2001 through 2009. Overall, we find that the algebraic error for the demographic indicators is centered at nearly zero and that the variability of the algebraic error is small relative to variability in the estimated indicators.
Table 1.
Comparison of interpolated estimates of county demographic, social, and economic characteristics to estimates from the Population Estimate Program (PEP), the Small Area Income and Poverty Estimates (SAIPE), and the American Community Survey (ACS), calculated over county-years
| Algebraic error over county-years |
Absolute error over county-years |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Percentiles |
Percentiles |
||||||
| 5th | 25th | 50th (Median) | 75th | 95th | 50th (Median) | 90th | |||
| Interpolated Demographic Indicators Compared to PEP, 2001–2009 | |||||||||
| Total population | −242 | 4,934 | −2,663 | −229 | 13 | 168 | 1300 | 191 | 1940 |
| Percent female | 0.04 | 0.36 | −0.37 | −0.07 | 0.03 | 0.14 | 0.49 | 0.11 | 0.43 |
| Percent non-Hispanic white | −0.04 | 0.47 | −0.64 | −0.19 | −0.04 | 0.10 | 0.58 | 0.15 | 0.62 |
| Percent non-Hispanic black | −0.05 | 0.29 | −0.43 | −0.09 | −0.02 | 0.02 | 0.25 | 0.05 | 0.35 |
| Percent Hispanic | −0.06 | 0.29 | −0.45 | −0.12 | −0.03 | 0.03 | 0.26 | 0.08 | 0.35 |
| Interpolated Socioeconomic Indicators Compared to SAIPE, 2001–2006 | |||||||||
| Percentage below poverty level | 0.58 | 2.36 | −2.53 | −0.61 | 0.36 | 1.55 | 4.42 | 1.06 | 3.64 |
| Median household income | 1070 | 1714 | −1496 | 73 | 1029 | 1945 | 3751 | 1244 | 3030 |
| Interpolated Socioeconomic Indicators Compared to 1-year ACS, 2006 | |||||||||
| Percent less than high school | 0.01 | 1.21 | −1.94 | −0.67 | −0.01 | 0.67 | 1.99 | 0.67 | 1.97 |
| Percent high school graduate | −0.74 | 1.57 | −3.35 | −1.72 | −0.72 | 0.24 | 1.7 | 1.09 | 2.87 |
| Percent greater than high school | 0.74 | 1.76 | −2.18 | −0.21 | 0.73 | 1.9 | 3.32 | 1.19 | 3.05 |
| Percent professional/managerial | 0.27 | 2.25 | −3.27 | −1.17 | 0.39 | 1.6 | 3.66 | 1.38 | 3.51 |
SD Standard deviation
Annual interpolated county-level estimates of demographic indicators are obtained by linearly interpolating between the 2000 Census and 2010 Census for demographic indicators and between the 2000 Census and 2005–2009 ACS for socioeconomic indicators
Error is defined as (interpolated estimate) - (reference estimate)
On average, the interpolated total population counts underestimate the PEP by less than 250 persons, with a standard deviation of fewer than 5000 persons and a median absolute error of about ±200 persons. Recognizing that the average size of a U.S. county over this period was about 90,000 persons with a standard deviation of over 300,000 persons, the interpolated error is comparatively small.
For the compositional indicators by gender and race/ethnicity, the interpolations are also centered at approximately zero with 90 % of the estimates within about a 1 % point range. The indicator with the largest absolute error (percent non-Hispanic white) has a mean algebraic error of −0.04 % points, with a 0.47 %point standard deviation and 90 % of the counties within ±0.62 % points. As observed for the total population counts, the magnitude and range of error is small given that the average county is 80 % non-Hispanic white and that there is a 20 % point standard deviation in the distribution of this indicator across counties and years. Similarly, although the average county percent non-Hispanic black and Hispanic are much lower (i.e., on average less than 10 %), error is small relative to the distribution of these indicators across counties and over time (i.e., standard deviation of 13 and 14 %-points, respectively). For gender, the magnitude of the error is also very small relative to the fact that counties are on average 50 % female.3
For the socioeconomic indicators, we are able to compare estimates of percent poverty and median household income (obtained by linearly interpolating between the 2000 Census and 2005–2009 ACS) to annual estimates from the SAIPE for each of the years 2001–2006. These comparisons comprise 3130 counties over 18,783 county years.4 For interpolated estimates of the educational and occupational composition of communities, reference data come from the ACS 1-year estimates for 2006 (i.e., 779 counties). We find that the magnitude and variability of the error for the socioeconomic indicators is larger than for the demographic indicators and, especially for the economic indicators, more skewed. For example, algebraic error for percent poverty is centered at a mean of 0.58 %point and median of 0.36 %points, indicating an overestimation of the SAIPE. The standard deviation of the error is 2.36 % points, with 90 % of the error within a range of about 7 % points (i.e., between −2.53 and 4.42 % points) and 50 % of the error within a range of about 2 % points. Moreover, this non-parametric (percentile) estimation of the distribution of the error shows that the 75th and 95th percentile upper bounds of these ranges tend to be larger in magnitude than the respective 25th and 5th percentile lower bounds. Error for median household income is even more strongly skewed, with a median algebraic overestimate of over 1000 dollars and 50 % of the interpolated estimates overestimating the SAIPE by about 70–2000 dollars. For the socioeconomic indicators observed only in the ACS, even the variable with the smallest error (percent less than high school) is found to have median absolute error of ±0.67 % points.
Not only is the magnitude of the error we observe for the socioeconomic indicators relatively large compared to our findings for the demographic indicators but error is also relatively large with respect to the average values and distribution of these indicators in the reference data. For example, given that the mean value of the percent poverty across counties and years in the SAIPE is 13.3 (with a standard deviation of 5.8 %-points) and the percent less than high school across the counties in the ACS is 14.8 (with a standard deviation also of 5.8 %-points), median absolute error of about 1 % points for these indicators is sizable.
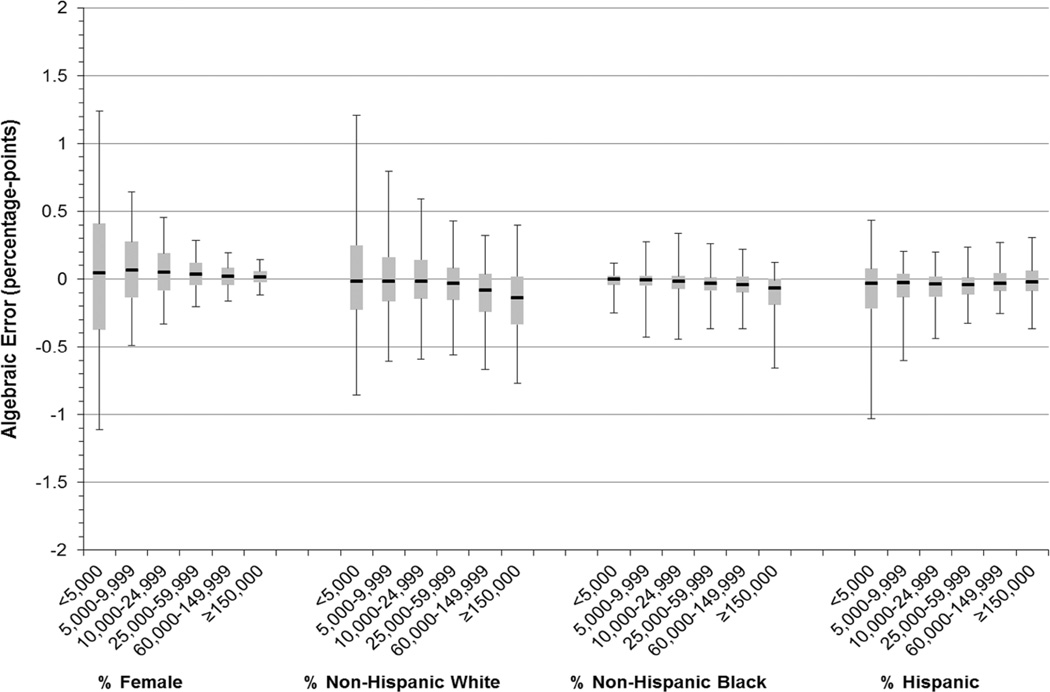
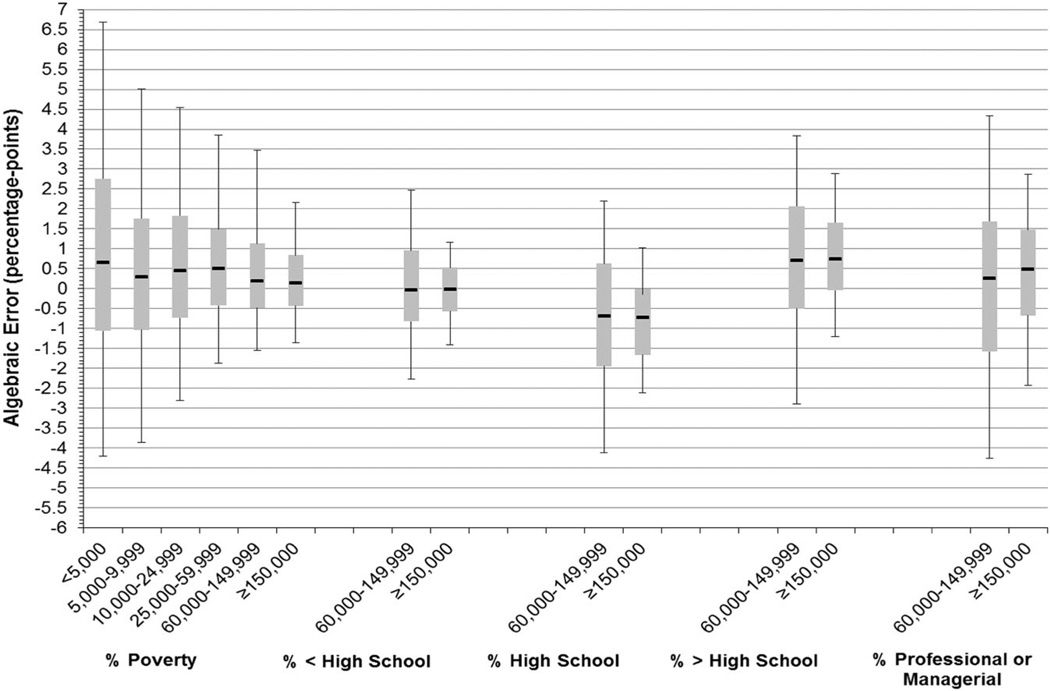
Error by County Population Size
In Figs. 1 and 2, we use box plots to display the median algebraic error and its range by the county population size in 2000. Analyses of the error for the interpolated demographic indicators compared to the PEP (for the years 2001–2009) and for the percent poverty indicator compared to the SAIPE (for the years 2001–2006) are conducted for the 290 counties with less than 5000 persons, 402 counties with 5000–9999 persons, 884 counties with 10,000–24,999 persons, 755 counties with 25,000–149,999 persons, 445 counties with 60,000–149,999 persons, and 355 counties with at least 150,000 persons. Counties for which reference data on the educational and occupational composition are available from the ACS in 2006 are included only in the last two largest county groups.5 In general, we observe a trend of increasing variability in the algebraic error (and thus also a larger magnitude of absolute error) with decreased county population size. In addition, we find that the above findings of greater error for the socioeconomic indicators than for the demographic indicators persist when comparing groups of counties with the same population size.
Fig. 1.
Algebraic error of interpolated estimates of county demographic characteristics, box plots by county population size in 2000 Note: The marker ‘‘–’’ identifies the median, the box extends to the 25th and 75th percentiles, and the whiskers extend to the 5th and the 95th percentiles
Fig. 2.
Algebraic error of interpolated estimates of county socioeconomic characteristics, box plots by county population size in 2000 Notes: The marker ‘‘–’’ identifies the median, the box extends to the 25th and 75th percentiles, and the whiskers extend to the 5th and the 95th percentiles. Comparison data on educational and occupational composition are unavailable for counties with less than 65,000 persons
Among the demographic indicators in Fig. 1, smaller county population size is most strongly associated with increased error for percent female. The range of the error contained between the 5th and 95th percentiles increases in a step-wise pattern from 0.3 % points for counties with at least 150,000 persons, to 0.4 % points for counties with 60,000–149,999 persons, and 0.5 % points for counties with 25,000–59,999 persons. It expands more rapidly in smaller counties from 0.8 % points for counties with 10,000–24,999 persons to 1.1 % points for counties with 5000–9999 persons, and it more than doubles to 2.4 % points for counties with less than 5000 persons. Similarly, the range of error for the percent non-Hispanic white indicator is also maximized at over 2 %-points in the smallest counties and is almost 1.5 % points for the percent Hispanic indicator in the smallest counties.
In Fig. 2, for percent poverty, the range of the error between the 5th and 95th percentiles increases from a range of about 3.5 %-points for counties with at least 150,000 persons to a range of nearly 11 % points for counties with less than 5000 persons. Similarly, although only the two largest county sizes are observed for the educational and occupational indicators, error is the smallest for counties with the largest population size.
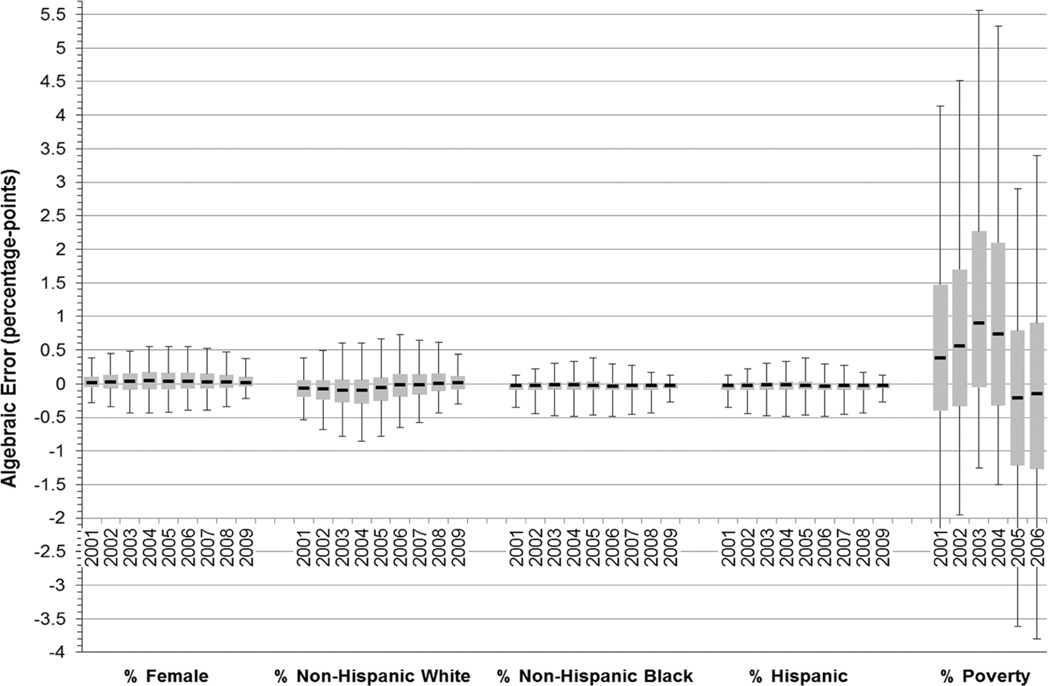
Error by Year
In Fig. 3, we display the trends in the error by year for the demographic indicators and the percent poverty and median household income socioeconomic indicators using box plots. For the demographic indicators, we observe no appreciable temporal pattern to the central tendency of the algebraic error. In all years, interpolated estimates are about evenly balanced between underestimation and overestimation. There is, however, a temporal pattern to the range of the algebraic error (and thus also the central tendency of the absolute error, not shown but available upon request). Both of these indicators of the magnitude of the error (i.e., the range of the algebraic error and the central tendency of the absolute error) show a step-wise increase and then decrease over time with the maximum value at the midpoint year of 2005 (or 1 year prior).
Fig. 3.
Algebraic error of interpolated estimates of county demographic characteristics and percent below the poverty level, box plots by year. Note: The marker ‘‘–’’ identifies the median, the box extends to the 25th and 75th percentiles, and the whiskers extend to the 5th and the 95th percentiles
In contrast with the demographic indicators, annual trends in the algebraic error for the percent below the poverty level and the median household income (not shown but available upon request) do vary over time. Figure 3 shows that for the percent below the poverty level, the interpolated estimates increasingly overestimate the SAIPE through 2003, continue to overestimate the SAIPE in 2004 by nearly a percentage point, and then become more evenly balanced between overestimation and underestimation in 2005 and 2006. It is noteworthy that, consistent with this discontinuous time pattern to the error, there was a change in the SAIPE estimation methodology that produced a break in the SAIPE time series of estimates between 2004 and 2005.6 Despite the differences in the annual trend of the direction of the error for percent poverty compared to the demographic indicators, the time trends in the absolute magnitude of the error (as measured by the range of the algebraic error and central tendency of the absolute error) are similar. As observed for the demographic indicators, the absolute error for poverty and median household income is greatest in the middle of the linear interpolation, albeit of a size 2–3 times larger than the absolute magnitude of demographic error in any given year.
Comparison of 1-year ACS County-Level Estimates for 2006, 2007, 2008, and 2009 to the 5-year ACS County-Level Estimate for 2005–2009
In Table 2, we detail our findings from investigating whether a midpoint year assumption for the timing of the ACS 2005–2009 is supported by the annual trends in the 1-year ACS estimates. We compare ACS 1-year estimates of the demographic and socioeconomic characteristics of counties to the ACS 2005–2009 5-year county-level estimates for each of the 4 years within this period in which the survey was fully implemented (i.e., 2006, 2007, 2008, and 2009). There are 779 counties that meet the ACS reporting guidelines in all 4 years of having a population of at least 65,000 persons. In Table 2, we report the median algebraic error by year and the median absolute error by year as measures of the comparability between the 1-year and 5-year estimates. For all of the demographic indicators (except percent female and percent non-Hispanic black, for each of which there is very little change in the absolute error over time), there is a convex pattern to the absolute error with the minimum value in 2007. Similarly, for all of the socioeconomic indicators except two—the percent below poverty level and median household income—the absolute error is also convex and minimized in 2007 or shows very little absolute change over time (i.e., for percent high school graduate).
Table 2.
Comparisons between the 2005–2009 ACS 5-year county-level estimates and the ACS 1-year county-level estimates of demographic and socioeconomic indicators
| Indicator | Median algebraic error by year |
Median absolute error by year |
||||||
|---|---|---|---|---|---|---|---|---|
| 2006 | 2007 | 2008 | 2009 | 2006 | 2007 | 2008 | 2009 | |
| Demographic | ||||||||
| Total population | 855 | −221 | −1230 | −2773 | 1689 | 523 | 1536 | 2878 |
| Percent Female | −0.04 | 0.01 | −0.01 | 0.02 | 0.18 | 0.18 | 0.20 | 0.16 |
| Percent non-Hispanic white | −0.47 | −0.05 | 0.29 | 0.75 | 0.49 | 0.20 | 0.33 | 0.75 |
| Percent non-Hispanic black | −0.04 | −0.07 | −0.02 | −0.08 | 0.23 | 0.22 | 0.21 | 0.26 |
| Percent Hispanic | 0.32 | 0.08 | −0.13 | −0.41 | 0.33 | 0.13 | 0.15 | 0.42 |
| Socioeconomic | ||||||||
| Percent below poverty level | 0.21 | 0.54 | 0.30 | −0.81 | 0.90 | 0.98 | 1.00 | 1.19 |
| Percent less than high school | −0.52 | −0.06 | 0.58 | 0.62 | 0.77 | 0.62 | 0.82 | 0.83 |
| Percent high school graduate | −0.65 | −0.74 | 0.78 | 0.71 | 1.07 | 1.11 | 1.09 | 1.04 |
| Percent greater than high school | 1.15 | 0.79 | −1.33 | −1.39 | 1.42 | 1.19 | 1.47 | 1.51 |
| Percent professional/managerial | 1.19 | 0.50 | −0.49 | −1.75 | 1.64 | 1.24 | 1.25 | 1.93 |
| Median household income | 62 | −736 | −470 | 784 | 951 | 1114 | 1078 | 1253 |
Error is defined as (interpolated estimate) - (reference estimate)
In addition, we found that for all but these same two socioeconomic indicators, the median algebraic error is either stable and very small over the period (i.e., for percent female and percent non-Hispanic black) or displayed a generally linear trend in which median algebraic error crossed zero on or shortly after 2007 (and prior to 2008). For the two exceptions (i.e., the percent below poverty level and median household income), the trend in the algebraic error is non-linear with a convex pattern over time for percent below the poverty level and a concave pattern over time for the median household income. For both indicators, the greatest absolute error occurs in 2009 when the 1-year estimates are at the greatest point above the 5-year estimate for income and below the 5-year estimate for poverty.
Comparison of the Annual Interpolated Tract-level Estimates to the ACS 5-year Tract-level Estimates for 2005–2009
In our final set of analyses, we compare the tract-level interpolated estimates of the demographic characteristics (obtained from linear interpolation between the 2000 and 2010 Census) with the ACS 5-year tract-level estimates for 2005–2009. We compare the interpolated estimates for each year in the 5-year ACS window to the ACS 2005–2009 estimate. Consistent with our county-level findings on the midpoint year assumption reported above, we determined (in analyses not shown but available upon request) that the central tendency of the absolute tract-level error and the variability of the algebraic tract-level error was the smallest for 2007. Thus in Table 3, we report our findings on the algebraic and absolute error for linearly interpolated estimates of 2007 tract demographics relative to the ACS 5-year 2005–2009 estimates (i.e., 65,174 tracts).
Table 3.
Comparisons between the interpolated tract-level estimates of demographic characteristics for 2007 and the ACS 5-year tract-level estimates for 2005–2009, all U.S. tracts
| Algebraic error |
Absolute error |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Percentiles |
Percentiles |
||||||
| 5th | 25th | 50th | 75th | 95th | 50th | 90th | |||
| All U.S. census tracts | |||||||||
| Total population | −16 | 594 | −840 | −247 | 1 | 238 | 753 | 242 | 795 |
| Percent female | 0.18 | 4.48 | −5.18 | −1.75 | 0.12 | 1.94 | 5.39 | 1.85 | 5.29 |
| Percent non-Hispanic white | −0.50 | 6.10 | −8.50 | −2.92 | −0.43 | 1.89 | 7.10 | 2.43 | 7.86 |
| Percent non-Hispanic black | 0.16 | 4.56 | −5.85 | −1.03 | 0.23 | 1.32 | 5.68 | 1.20 | 5.77 |
| Percent Hispanic | 0.25 | 4.54 | −6.17 | −1.27 | 0.43 | 1.79 | 6.05 | 1.58 | 6.12 |
SD Standard deviation
Interpolated tract-level estimates of demographic indicators for 2007 are obtained by linearly interpolating between the 2000 Census and 2010 Census
Error is defined as (interpolated estimate) - (reference estimate)
We find that the magnitude of the tract-level error is notably larger than the county-level error we report in Table 1 for the same demographic indicators. The distribution of the algebraic error at the tract level, however, is generally balanced between overestimation and underestimation as we also observed at the county level. For example, for the indicator with the least county-level error (percent non- Hispanic white), mean county-level algebraic error is −0.04 % points with a standard deviation of about 0.5 % points and a median absolute error of less than ±0.2 % points (Table 1). By comparison, mean tract-level algebraic error for this indicator is −0.50 % points, with a standard deviation of over 6 % points and a median absolute error of over ±2 % points (Table 3). For this and the other indicators, the standard deviation of the algebraic error and median absolute error at the tract level is generally an order of magnitude larger than at the county level.
Discussion
In this study, we evaluated linearly interpolated annual estimates of county and census tract demographic characteristics and county socioeconomic characteristics for the 21st century respective to the best available reference data from the U.S. Census Bureau. Despite the widespread and longstanding use of linear interpolation as a practical method for estimating annual change in neighborhood and community characteristics on a national scale (Massey and Shibuya 1995; Quillian 1999; Mayer 2002; Cubbin and Winkleby 2005; Do 2009; Do et al. 2013; Ludwig et al. 2012), our study provides the first known analysis of the validity of this method for intercensal estimation of 21st century social and demographic characteristics. For demographic characteristics, we found that linear interpolation performed well overall at the county level. However, for the smallest counties (i.e., those with fewer than 5000 persons in 2000 or about the size of a census tract7), the magnitude of the error was about twice as large as it was for all counties combined. Similarly, although we were able to only produce rough estimates of the performance of linear interpolation for estimating census tract demographics (due to the lack of annual intercensal reference data for census tracts), we determined that tract-level error was at least an order of magnitude larger than the county-level error. Our findings that demographic error was generally balanced between overestimation and underestimation irrespective of population size were reassuring as were our findings about the relatively small county-level error for larger counties. However, a final assessment of whether the magnitude of error we observed for smaller geographies is large or not will ultimately depend on the specific research question and analytical model, which as we discuss below could be achieved using study specific sensitivity analyses.
For the socioeconomic indicators, the magnitude of error also increased with decreased population size. On average, though, error was about an order of a magnitude larger for the socioeconomic indicators than for the demographic indicators. In addition, for both the demographic and economic indicators with reference data on multiple years, we found that the performance of linear interpolation was worse for the midpoint years. Although, we also observed a discontinuous time pattern to the direction of the algebraic error for the two economic indicators, we suspect this most reflects changes that the Census Bureau made in the estimation methodology of these reference data (U.S. Census Bureau 2014e, 2014f).
Finally, we determined that trends in the 1-year ACS estimates lend cautious support to making a midpoint year assumption for the timing of the 2005–2009 ACS estimates when these data must be used in annual research applications. For nearly all indicators, the differences between the 1-year and 5-year estimates were smallest in 2007. These findings are an important first step in helping researchers understand whether and how to use multiyear estimates in research applications requiring annual precision. While we fully appreciate that analyses considering the temporal relationships between the 1-year and 5-year estimates have found no full solution to the problem of incomparability between these series of estimates (McElroy 2009), our findings have practical implications for researchers who must either make an assumption about the single-year timing of the multiyear estimates or employ no data at all.
The exceptions to these findings on the midpoint year assumption, however, were notable. For the two economic indicators most closely linked to the economic conditions of the county (i.e., the percent below the poverty level and median household income), absolute error was not minimized in 2007, but rather increased over time. And, there was a non-linear pattern to the direction of the algebraic error such that the 5-year estimates tended to increasingly overestimate poverty and underestimate household income through 2007 and then reversed to a maximum underestimation of poverty and overestimation of income in 2009. These findings are entirely consistent with the dramatic changes in economic wellbeing that occurred over this period including the collapse of U.S. housing and financial markets and onset of the Great Recession (Elsby 2010), Moreover, our findings underscore the limitations of a 5-year estimate in describing community conditions in the context of rapid economic change.
Before proceeding with the implications of the study findings, it is important to highlight several analytical issues bearing on our findings. First, our county-level analyses employed what we determined to be the best source of reference data; however, there are alternative potential county-level reference data from the 1-year ACS (for the subset of larger counties beginning in 2006). That said, in sensitivity analyses, we determined that our overall findings on the differences in the magnitude of county-level error for demographic versus socioeconomic indicators were similar when we employed the ACS instead of the PEP or SAIPE.8 Second, our tract-level analyses required a spatial interpolation methodology to address the changes in tract boundary definitions between the 2000 and 2010 Census, and it is possible that the need to conduct spatial interpolation introduced additional error which may have confounded or exacerbated the findings on the temporal interpolations reported here. Although we applied a population and areal weighting methodology that employs fine-grained, sub-tract ancillary information about the block-level population distribution and the geographic distribution of land and water surfaces (Logan et al. 2014), there are alternative spatial interpolation methods (e.g., see review by Reibel 2007). Future research might evaluate the extent to which the choice of spatial interpolation methods influences error in temporal interpolation. Third, although we have examined differences in error across a range of indicators and by county population size and year, there may be other distinguishing factors such as geographic region or the pace of population growth within a community which impact on the performance of linear interpolation. Finally, although all of our error assessments employ reference data that are also only estimates of the ‘true’ demographic and socioeconomic characteristics, our tract-level assessment of error is likely most impacted by the estimation limitations of the ACS reference data. Recall that for the ACS census-tract estimates geographic precision is obtained by losing annual temporal precision. Our concerns about the greater magnitude of the tract-level error are, however, strengthened by the consistent findings we observe for small counties.
In light of the findings (and limitations) of this study, what is a researcher interested in studying small community trends to do? As a starting point, we suggest that studies employing small area annual interpolated data evaluate the sensitivity of their findings to the potential for bias introduced by estimation error. We know of only one previous and recent study to have conducted such evaluation (Massoglia et al. 2013), albeit with an approach that largely involved comparing analyses that restricted the number of waves of interpolated data employed or dropped the interpolated data altogether. Based on the findings reported here, an alternative approach might be to evaluate whether the findings of a given study hold up in the context of measurement error of the magnitude observed here. For example, in the context of neighborhood effects literature, the absence of neighborhood observations for the intercensal period might be reconceptualized as a missing data problem. As such, the linear interpolations provide estimates of these missing data, and following the literature on multiple imputation (Little and Rubin 2002), a failure to address the uncertainty of these missing data estimates will lead to an increased likelihood of type I error (i.e., rejection of a ‘true’ hypothesis). Thus, we suggest that a distribution of error in the interpolated values, such as those identified in this study, might be used to simulate the uncertainty in the interpolated estimates of the intercensal ‘missing values’ and then estimate their specific analytical model employing standard statistical techniques for combining estimates from multiply imputed data (Schafer and Graham 2002).
Should error from linearly interpolated estimates in fact prove large enough to bias the results of a given research study, there are alternative intercensal estimation methods that may still be practical even for a research study with national scope. For example, multilevel regression and poststratification (MRP) is one such method that has become increasingly employed to estimate public opinion statistics using survey data at various geographic levels (Lax and Phillips 2009; Buttice and Highton 2013; Ghitza and Gelman 2013). Incorporation of these richer time series of data from higher geographical levels potentially offers the particular advantage of better capturing non-linearity of 21st century economic trends through the Great Recession.
Although social science studies employing interpolated neighborhood data seldom recognize the uncertainty of their interpolated estimates as a potential source of bias, failure to evaluate and address such bias could have important policy implications. This might be particularly the case for research on the individual consequences of neighborhood change for which there is already considerable debate about the strength of evidence and its relationship to methodological considerations (Sampson et al. 2002; Oakes 2004; Sampson 2008; Oakes 2014). The advent of the ACS has provided new opportunities for informing discussion about time-varying and multilevel social processes, and we hope that future studies build upon the questions and insights drawn here about best to apply and integrate these data.
Footnotes
The ACS also releases 3-year estimates annually, but these estimates are restricted to areas with a population of 20,000 persons or more and are thus unavailable for all census tracts, most school districts and about two-fifths of the U.S. counties (U.S. Census Bureau 2014b).
The LTDB provides a tract correspondence matrix for the 2000 to 2010 tract boundary changes identifying whether 2000 census tracts remained unchanged, split, consolidated, or had complex changes involving both splits and consolidations. They also provide a matrix of weights constructed from population counts at the sub-tract level (e.g., block groups) that allows users to produce estimates for 2000 tract boundaries using data provided in 2010 tract boundaries. We calculated a set of ‘reverse’ weights from these weights to estimate 2010 data using 2000 boundaries that are equivalent to the ‘backwards’ LTDB weights that the LTDB has now made available since the initiation of this study.
Percent female differs little across counties and over time (i.e., a standard deviation of about 2 % points), so the absolute value of the interpolated error and the distribution of algebraic error is more sizeable in comparison.
Estimates for one county (Kalawao County, Hawaii) were unavailable in the SAIPE.
Due to the 65,000 person lower threshold for ACS data, we observe only 409 counties with a size of 60,000–149,999 persons in 2000; however, we observe all 355 counties with at least 150,000 persons.
In 2005, the SAIPE switched the data source for its model-based estimates from the Current Population Survey Annual Social and Economic Supplement (CPS ASEC) to the data source used as the reference data in this study, i.e., the ACS (U.S. Census Bureau 2014e).
The smallest two groups of counties had on average about 1.5 tracts and 2.5 tracts in 2007.
Error tended to be larger compared to the ACS than compared to the 2000–2010 vintage of PEP data used in this study. We ascribe this finding to a number of methodological differences in the estimation methodologies (U.S. Census Bureau 2009b, 2014c). The 2000–2010 vintage of PEP data incorporates the 2010 Census into the estimation methodology. By contrast, while the ACS estimates come from continuous sampling of the U.S. population, ACS population counts are controlled to the vintage of PEP for the estimated year. Thus, the ACS estimation methodology employs older vintages of the PEP (that are estimated without alignment to the 2010 Census) than the 2000–2010 vintage of the PEP employed as the best available demographic reference data source in this study.
References
- Auchincloss AH, Gebreab SY, Mair C, Diez Roux AV. A review of spatial methods in epidemiology, 2000–2010. Annual Review of Public Health. 2012;33:107–122. doi: 10.1146/annurev-publhealth-031811-124655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaghen M, Weidman L. Statistical issues of interpretation of the American Community Survey’s one-, three-, and five-year period estimates. Washington, D.C.: U.S. Census Bureau; 2008. [Google Scholar]
- Buttice MK, Highton B. How does multilevel regression and poststratification perform with conventional national surveys? Political Analysis. 2013;21(4):449–467. [Google Scholar]
- Crowder K, Pais J, South SJ. Neighborhood diversity, metropolitan constraints, and household migration. American Sociological Review. 2012;77(3):325–353. doi: 10.1177/0003122412441791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cubbin C, Winkleby MA. Protective and harmful effects of neighborhood-level deprivation on individual-level health knowledge, behavior changes, and risk of coronary heart disease. American Journal of Epidemiology. 2005;162(6):559–568. doi: 10.1093/aje/kwi250. [DOI] [PubMed] [Google Scholar]
- Do DP. The dynamics of income and neighborhood context for population health: Do long-term measures of socioeconomic status explain more of the black/white health disparity than single-pointin- time measures? Social Science and Medicine. 2009;68(8):1368–1375. doi: 10.1016/j.socscimed.2009.01.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do DP, Wang L, Elliot M. Investigating the relationship between neighborhood poverty and mortality risk: A marginal structural modeling approach. Social Science & Medicine. 2013;91:58–66. doi: 10.1016/j.socscimed.2013.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsby MW, Hobijn B, Sahin BA. National Bureau of Economic Research No. w15979. 2010. The labor market in the Great Recession. [Google Scholar]
- Entwisle B. Putting people into place. Demography. 2007;44(4):687–703. doi: 10.1353/dem.2007.0045. [DOI] [PubMed] [Google Scholar]
- Ghitza Y, Gelman A. Deep interactions with MRP: Election turnout and voting patterns among small electoral subgroups. American Journal of Political Science. 2013;57(3):762–776. [Google Scholar]
- Kearns RA. Place and health—Towards a reformed medical geography. Professional Geographer. 1993;45(2):139–147. [Google Scholar]
- Kling JR, Liebman JB, Katz LF. Experimental analysis of neighborhood effects. Econometrica. 2007;75(1):83–119. [Google Scholar]
- Lax JR, Phillips JH. How should we estimate public opinion in the states? American Journal of Political Science. 2009;53(1):107–121. [Google Scholar]
- Little RJA, Rubin DB. Statistical analysis with missing data. New York: Wiley; 2002. [Google Scholar]
- Logan JR, Xu Z, Stults B. Interpolating US decennial census tract data from as early as 1970 to 2010: a longitudinal tract database. Professional Geographer. 2014;66(3):412–420. doi: 10.1080/00330124.2014.905156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludwig J, Duncan GJ, Gennetian LA, Katz LF, Kessler RC, Kling JR, Sanbonmatsu L. Neighborhood effects on the long-term well-being of low-income adults. Science. 2012;337(6101):1505–1510. doi: 10.1126/science.1224648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacDonald H. The American Community Survey: Warmer (more current), but fuzzier (less precise) than the decennial census. Journal of the American Planning Association. 2006;72(4):491–503. [Google Scholar]
- Macintyre S, Ellaway A, Cummins S. Place effects on health: How can we conceptualise, operationalise and measure them? Social Science and Medicine. 2002;55(1):125–139. doi: 10.1016/s0277-9536(01)00214-3. [DOI] [PubMed] [Google Scholar]
- Massey DS, Shibuya K. Unraveling the tangle of pathology—The effect of spatially concentrated joblessness on the well-being of African–Americans. Social Science Research. 1995;24(4):352–366. [Google Scholar]
- Massoglia M, Firebaugh G, Warner C. Racial variation in the effect of incarceration on neighborhood attainment. American Sociological Review. 2013;78(1):142–165. doi: 10.1177/0003122412471669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer SE. How economic segregation affects children’s educational attainment. Social Forces. 2002;81(1):153–176. [Google Scholar]
- McElroy T. Incompatibility of trends in multi-year estimates from the American Community Survey. The Annals of Applied Statistics. 2009;3(4):1493–1504. [Google Scholar]
- National Research Council and Institute of Medicine. From Neurons to Neighborhoods: The Science of Early Childhood Development. Washington, D.C.: National Academy Press; 2000. [PubMed] [Google Scholar]
- Oakes JM. The (mis)estimation of neighborhood effects: causal inference for a practicable social epidemiology. Social Science and Medicine. 2004;58(10):1929–1952. doi: 10.1016/j.socscimed.2003.08.004. [DOI] [PubMed] [Google Scholar]
- Oakes JM. Invited commentary: repeated measures, selection bias, and effect identification in neighborhood effect studies. American Journal of Epidemiology. 2014;180(8):785–787. doi: 10.1093/aje/kwu231. [DOI] [PubMed] [Google Scholar]
- Quillian L. Migration patterns and the growth of high-poverty neighborhoods, 1970–1990. American Journal of Sociology. 1999;105(1):1–37. [Google Scholar]
- Reibel M. Geographic information systems and spatial data processing in demography: A review. Population Research and Policy Review. 2007;26(5–6):601–618. [Google Scholar]
- Robert SA, Cagney KA, Weden MM. A life-course approach to the study of neighborhoods and health. In: Conrad P, Bird CE, Fremont AM, Timmermans S, editors. Handbook of medical sociology. 6th ed. Nashville, TN: Vanderbilt University Press; 2010. [Google Scholar]
- Sampson RJ. Moving to inequality: Neighborhood effects and experiments meet social structure. American Journal of Sociology. 2008;114(1):189–231. doi: 10.1086/589843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sampson RJ, Morenoff JD, Gannon-Rowley T. Assessing neighborhood effects: Social processes and new directions in research. Annual Review of Sociology. 2002;28(1):443–478. [Google Scholar]
- Sampson RJ, Sharkey P. Neighborhood selection and the social reproduction of concentrated racial inequality. Demography. 2008;45(1):1–29. doi: 10.1353/dem.2008.0012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer JL, Graham JW. Missing data: Our view of the state of the art. Psychological Methods. 2002;7(2):147–177. [PubMed] [Google Scholar]
- Spielman SE, Folch D, Nagle N. Patterns and causes of uncertainty in the American Community Survey. Applied Geography. 2014;46:147–157. doi: 10.1016/j.apgeog.2013.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torrieri NK. America is changing, and so is the census. The American Statistician. 2007;61(1):16–21. [Google Scholar]
- U.S. Census Bureau. A compass for understanding and using American Community Survey data: What researchers need to know. Washington, D.C.: U.S. Government Printing Office; 2009a. [Google Scholar]
- U.S. Census Bureau. Design and methodology, American Community Survey. Washington, D.C.: U.S. Government Printing Office; 2009b. [Google Scholar]
- U.S. Census Bureau. FTP server. 2014a Retrieved December 15, 2014 from http://www2.census.gov/.
- U.S. Census Bureau. Geographic areas published, American Community Survey. 2014b Retrieved December 15, 2014 from www.census.gov/acs/www/data_documentation/areas_published/.
- U.S. Census Bureau. Intercensal estimates. 2014c Retrieved December 15, 2014 from http://www.census.gov/popest/data/intercensal/index.html.
- U.S. Census Bureau. SAIPE methodology: Estimation details for counties and states data. 2014d Retrieved December 15, 2014 from https://www.census.gov/did/www/saipe/methods/statecounty/index.html.
- U.S. Census Bureau. SAIPE methodology: Estimation procedure changes for the 2005 estimates. 2014e Retrieved December 15, 2014 from https://www.census.gov/did/www/saipe/methods/05change.html.
- U.S. Census Bureau. SAIPE methodology: General cautions about comparing estimates. 2014f Retrieved December 15, 2014 from https://www.census.gov/did/www/saipe/methods/cautions.html.
- Voss PR. Demography as a spatial social science. Population Research and Policy Review. 2007;26(5–6):457–476. [Google Scholar]
- Wodtke GT, Harding DJ, Elwert F. Neighborhood effects in temporal perspective. American Sociological Review. 2011;76(5):713–736. doi: 10.1177/0003122411420816. [DOI] [PMC free article] [PubMed] [Google Scholar]