Learning the opportunity cost of time in a patch-foraging task

Abstract

Although most decision research concerns choice between simultaneously presented options, in many situations options are encountered serially and the decision is whether to exploit an option or search for a better one. Such problems have a rich history in animal foraging but we know little about the psychological processes involved. In particular, it is unknown whether learning in these problems is supported by the well studied neurocomputational mechanisms involved in more conventional tasks.

We investigated how humans learn in a foraging task, which requires deciding whether to harvest a depleting resource or switch to a replenished one. The optimal choice (given by the Marginal Value Theorem; MVT) requires comparing the immediate return from harvesting to the opportunity cost of time, which is given by the long-run average reward. In two experiments, we varied opportunity cost across blocks. Subjects adjusted their behavior to blockwise changes in environmental characteristics. We examined how subjects learned their choice strategies by comparing choice adjustments to a learning rule suggested by the MVT (where the opportunity cost threshold is estimated as an average over previous rewards) and to the predominant incremental learning theory in neuroscience, temporal-difference learning (TD). Trial-by-trial decisions were better explained by the MVT threshold learning rule.

These findings expand on the foraging literature, which has focused on steady-state behavior, by elucidating a computational mechanism for learning in switching tasks that is distinct from those used in traditional tasks, and suggest connections to research on average reward rates in other domains of neuroscience.

Introduction

Extensive research in neuroscience, psychology, and economics concerns choice between a number of simultaneously presented alternatives, as in economic lotteries, “bandit” problems, and choice between concurrent schedules in operant conditioning (Krajbich et al., 2010; Tom et al., 2007; Hampton et al., 2006; Frank et al., 2004; Behrens et al., 2007; Hare et al., 2011; Barraclough et al., 2004; Herrnstein, 1961; Baum, 1974; Herrnstein, 1991; Sugrue et al., 2004). In such problems, attention has centered on a hypothesized neural mechanism for learning an estimate of the value of different options (Schultz et al., 1997). More recently, there has been increased interest in neuroscience in a different class of decision problems, in which alternatives are not compared simultaneously but are instead considered serially (Hayden et al., 2011; Hutchinson et al., 2008; Jacobs and Hackenberg, 1996; Wikenheiser et al., 2013; Kolling et al., 2012; Cain et al., 2012). The relevant decision in this class of problems is whether to engage with a current option or search for a better one. Such switching or stopping problems arise in many real-world settings, such as employment (whether to accept a job offer or candidate), internet search, mate selection and foraging, and have a rich theoretical and experimental history in ethology, ecology and economics (Charnov, 1976; Kacelnik, 1984; Freidin and Kacelnik, 2011; McCall, 1970; McNickle and Cahill, 2009; Smith and Winterhalder, 1992; Stephens and Krebs, 1986).

Decisions of this sort pose a dilemma for the widely studied neurocomputational mechanisms of choice, which largely center on comparing estimated values across available alternatives (Rangel et al., 2008; Rustichini et al., 2008), as well as for the related psychological mechanisms of matching and melioration in operant choice (Herrnstein, 1961; Baum, 1974; Herrnstein, 1991), which also require balancing time among multiple alternatives. If the alternatives are not directly known at choice time, to what alternative value should the current option be compared when deciding whether to accept it or when to leave it? And how is this more nebulous expected value or aspiration level learned, adjusted, or optimized from previous experience? Predominant theories of choice in the ethological foraging literature suggest quite different answers to this learning question (McNamara and Houston, 1985; Bernstein et al., 1988; Charnov, 1976; Stephens and Krebs, 1986) than would be provided by standard neurocomputational theories of learning (Sutton, 1988; Sutton and Barto, 1998).

The ethology literature has considered a class of stylized switching tasks modeling foraging problems, in which an animal encounters a series of depleting “patches” of resources and must decide whether to spend time exploiting the current patch or instead allocate that time towards seeking a new, replenished one. In such tasks, it has been proved (the Marginal Value Theorem; MVT; Charnov, 1976) that the reward rate-maximizing choice of whether to stay or search at each step simply requires comparing the current option’s immediate reward to a threshold given by the opportunity cost of the time spent engaging with it. The opportunity cost of time is given by the long-run average reward per timestep – a measure of the overall environmental richness that is foregone by harvesting. Whenever you expect to earn less than this quantity, you would be better off doing something else. The MVT thus poses an answer to the question of how to value the nebulous alternative of searching: equate it with the overall average reward rate.

Although the MVT concerns a steady-state choice policy, at the trial-by-trial level it suggests an extremely simple learning rule for deriving that policy by trial and error: estimate the long-run reward rate by a recency weighted average of received rewards over time and use this quantity as a dynamic aspiration level against which to accept or reject the current option (Charnov, 1976; McNamara and Houston, 1985; Krebs and Inman, 1992; Ollason, 1980; Stephens and Krebs, 1986). Variants of this simple model have been suggested in the ethological foraging literature, which finds that bees and starlings use dynamically adjusting threshold estimates to inform their search decisions (Cuthill et al., 1990; McNamara and Houston, 1985; Krebs and Inman, 1992; Hodges, 1985; Ollason, 1980). Although, as discussed below, this model is quite distinct from common theories of reinforcement learning in the brain, it suggests close connections with a number of other disjoint phenomena in neuroscience, which also turn on the average reward as the opportunity cost of time, including response vigor (Niv et al., 2006; Niv et al., 2007; Guitart-Masip et al., 2011; Beierholm et al., 2013) and temporal discounting (Cools et al., 2011; Daw and Touretzky, 2002; Kacelnik, 1997). These connections relate the simple average reward rate learning in foraging to the suggestion that this rate may be tracked and signaled by tonic levels of the neuromodulator dopamine (Niv et al., 2007; Niv et al., 2006).

An alternative hypothetical approach to learning in the foraging problem is to ignore its special structural features and instead treat the problem of learning the value of searching for a new option as equivalent to any other case of action value learning. This requires extending the notion of an action’s value to encompass the (non-immediate) value of seeking new, sequentially encountered options. Accordingly, much research in neuroscience has focused on the temporal difference (TD) learning algorithm, an incremental update rule that learns, via a series of recursive backups “chaining” rewards to earlier predictors, to estimate the cumulative future reward associated with different actions in different circumstances (Sutton, 1988; Sutton and Barto, 1998).

There is considerable neural and behavioral support for TD learning in humans and other animals, notably in recordings from midbrain dopaminergic neurons, whose phasic responses quantitatively match the prediction error signal used in TD learning (Schultz et al., 1997; Montague et al., 1996; Houk et al., 1995). A key feature of the TD rule is that it assigns value to the different options; however, unlike in the classic operant conditioning theories, this value is defined as cumulative future return following a choice. In this way, these models extend choice among options to sequential decision tasks, in which current choices affect future choices and the optimal solution requires considering the interdependent consequences of a series of decisions on the cumulative reward ultimately achieved. Importantly for the foraging task – since the value of switching is the deferred consequences of harvesting at subsequent patches – this feature allows treating the nebulous expected value of switching to an unknown option in the same way one learns the value of known options. TD learning applied to these problems incrementally updates estimates of the cumulative expected future reward associated with each local stay or switch option and compares these estimates to choose an action.

In this article we investigate these hypothesized learning rules for serial decision problems by examining human behavior in two sequential patch-foraging experiments. By varying the characteristics of the reward environment (and thus the opportunity cost of time) across blocks, we were able to compare these different accounts of how organisms learn in such tasks. We started by considering the asymptotic strategies. These two learning approaches arrive at the same optimal policy (assuming equivalent choices about parameters such as time discounting or risk sensitivity) and thus make equivalent predictions about asymptotic switching behavior in the different environments. These predictions have been tested extensively in animals (Charnov, 1976; Kacelnik, 1984; Freidin and Kacelnik, 2011; McNickle and Cahill, 2009; Stephens and Krebs, 1986) and more rarely in humans (Kolling et al., 2012; Hutchinson et al., 2008; Jacobs and Hackenberg, 1996). Next, we examined the choice adjustments visible in the trial-by-trial dynamics. Because these approaches learn different decision variables (average one-step rewards vs expected cumulative rewards) by different learning rules, they predict different path dynamics to reach the same asymptotic strategy.

For instance, according to the MVT strategy, an unusually large reward (e.g., a lucky harvest) increases the estimated average reward rate, and thus should directly and immediately raise the leaving threshold, favoring exit. In contrast, TD learns about the value of actions when they are chosen. Here, the long-run value of exiting is estimated indirectly, via chaining. When exit is chosen, the value of exiting is updated according to the expected value of the new tree one encounters; this value was in turn learned from the rewards received from previous stay decisions. The effect of an individual lucky harvest, on this theory, thus first affects the vaue of “stay” – increasing the chance of staying the next time the same tree state is encountered – and only later, through a series of further updates, propagates to increase the value of exiting. Differences of this sort capture the two distinct strategies for how the models search for the optimal policy - by estimating the local cost of time vs. the long-run value of switching - and allow us to compare the two learning models (and some plausible variants) in terms of how well they fit the trial-by-trial fluctuations in choice behavior.

The results suggest that learning in patch-foraging problems implicates a distinct computational mechanism from those that have been successful in more traditional choice problems. This additional mechanism may be broadly applicable to many decisions that can be framed as switching or stopping problems, and suggests links between choice and other behavioral phenomena such as response vigor.

Methods

Subjects

52 healthy subjects (age 19–35; 33 female) participated in the study: 11 in experiment 1a, 11 in 1b and 30 in experiment 2. Subjects were paid based on performance in the task ($15–$22). The study was approved by the Institutional Review Board of New York University.

A small number of subjects showed a qualitatively different response strategy (nearly always choosing the “harvest” option, even down to zero apples), and were excluded from all analyses. Specifically, we excluded subjects who had a mean number of harvests per tree that fell more than 2.3 standard deviations (99% quantile) above the group mean; this included one subject from experiment 1B and 3 subjects from experiment 2. Although these subjects were excluded out of caution, their inclusion or exclusion does not appreciably affect the learning analyses depicted in Figure 3. One subject was additionally excluded from experiment 2 due to a problem with the instructions. Thus, all results reported here concern 11, 10, and 26 subjects from Experiments 1A, 1B and 2, respectively.

Figure 3. Model comparison.

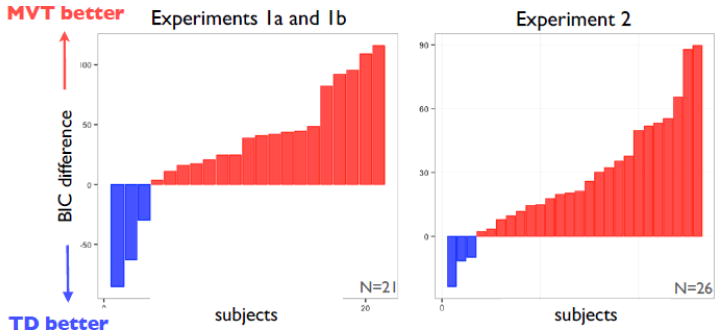
Approximate log Bayes factors (difference in BIC scores) favoring MVT vs TD learning models, shown for each subject separately for Experiments 1A and 1B (left) and 2 (right).

Experimental Design and Task

Subjects performed a virtual patch-foraging task: a discrete-trial adaptation of a class of tasks from the ecology literature (Cuthill et al., 1990; Hayden et al., 2011; Charnov, 1976; Stephens and Krebs, 1986). On each trial, subjects were presented with a tree and had to decide whether to harvest it for apples or go to a new tree. Subjects indicated their choice by one of two key presses when prompted by a response cue. If they decided to harvest the tree they incurred a short harvest time delay, during which the tree shook and the harvested apples were displayed (as an integer number of apple icons plus a fractional apple icon for the remainder), followed by a response cue. As the subject continued to harvest apples at the same tree, the apples returned were exponentially depleted.

If the subject chose to go to a new, replenished tree, they incurred a travel time delay, during which the old tree faded and moved off the screen while a new tree moved on to the screen, followed by a response cue. Trees were never revisited; each new tree had never been harvested and its starting quality was correlated with subsequent outcomes (and thus signaled the quality of the overall tree) in experiment 2 and uncorrelated in experiment 1. The total time in the game was fixed and each choice’s reaction time was counted toward the ensuing harvest or travel delay. (Subjects who responded too slowly were penalized by a timeout lasting the length of a single harvest trial.) Thus, subjects visited a different number of trees depending on their harvest decisions, but apart from timeouts (which occurred on a negligible 1.7% of trials) they were able to influence the reward rate only through their harvest or leave choices, not their reaction times. This design ensured that the optimal choice policy was invariant to the speed of responding.

Subjects experienced four foraging environments in a counterbalanced block design. The decision-relevant parameters that define an environment are the harvest time, the travel time, the rate at which apples were depleted and the tree quality distribution. By varying travel time and depletion rate across blocks, we produced environments that differed in terms of richness, with some having a higher achievable average reward rate than others.

The environment changed every 14 minutes and this was signaled by a change in background color and a short message. Subjects were not instructed about the type of environment they were entering or what aspects of the environment had changed. They were also not told the form or rate of the depletion or the exact duration of a foraging environment but were informed that they would have a fixed and equal time in all four environments and that the experiment would last approximately one hour, that trees could never be revisited, that new trees had never been harvested and were a priori identical, and that harvesting a tree would tend to return fewer apples over time. They were told that they would be paid a half-cent for every apple collected and that they should try to collect as many apples as possible.

Experimental parameters

Each foraging environment is defined by the average initial tree richness S₀, the average depletion rate per harvest κ, the travel time d and the harvest time h. We denote the state (current expected harvest) of a tree at trial i as s_i.

In experiments 1A and 1B, each travel decision led to a new tree that was initialized to the same value, s_i = S₀. Each harvest decision depleted the tree’s state by a fixed multiplicative decay κ, such that s_i+1 = κs_i. The reward r_i returned for harvesting a tree with state s_i was distributed as 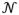(s_i, s_i · σ_r). Across environments, the proportional variance of the rewards was chosen such that the probability of the next observed reward falling more than one depletion rate from the current reward was 20 percent (P(r_i < κs_i) = 0.2). We varied travel time d or depletion rate κ across blocks in experiment 1A and 1B, respectively, to create high and low average reward rate foraging environments. Subjects encountered both environments twice in alternation, with counterbalanced orders ABAB or BABA.

The noise process in experiment 2 was changed in order to decorrelate a counting based policy rule from one explicitly based on observed rewards. In this setup, new trees were initialized with a state of variable quality: s_i ~ 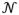(S₀, σ_s) and the decay factor applied after each harvest was stochastically drawn, κ_i ~ (κ, σ_κ). This creates an effective distribution of different quality trees with different possible reward paths through the trees. The reward for each harvest was a noiseless reflection of the state of the tree, r_i = s_i. We crossed two levels of depletion rate with two levels of travel time, resulting in four environment types. Subjects encountered each environment type once and the orders were counterbalanced in order to achieve an approximately equal number of subjects encountering short or long travel delays and steep and shallow depletion rates in the first block.

The parameters for the experiments are shown in Table 1.

Table 1.

Parameter values defining the different environment types in experiments 1A, 1B and 2.

block	Experiment 1A: Travel		Experiment 1B: Depletion		Experiment 2: Travel x Depletion
	Long	Short	steep	shallow	Long-steep	Long-shallow	Short-steep	Short-shallow
h (sec)	4.5	4.5	4.5	4.5	3	3	3	3
d (sec)	13.5	4.5	9	9	9	9	6	6
κ, σκ	.85 0	.85 0	.68 0	.89 0	.88 .07	.94 .07	.88 .07	.94 .07
S0, σS	10 0	10 0	10 0	10 0	10 1	10 1	10 1	10 1
σr	.18	.18	.37	.13	0	0	0	0

The Marginal Value Theorem & optimal behavior

Charnov (1976) proved that the long run reward-rate optimizing policy for this class of tasks is given by a simple threshold rule. In the context of our discrete-trial version of the task, the optimal policy is to exit a tree when the expected reward from one more harvest, κs_i, drops below the opportunity cost of the time that would be spent harvesting it. The opportunity cost of harvesting is the time it takes to harvest, h, times the long-run average reward rate, ρ. Note that in both experiments, the state s_i of a tree is observable: in experiments 1A and 1B it depends only on the number of times the current tree has been harvested (for a tree harvested n times s_i = κⁿ⁻¹S₀) and in experiment 2 it is equal to the received reward (s_i = r_i).

A sketch of the MVT proof for our setting is to consider the differential (average reward) Bellman equation for the task (Puterman, 2009). The future value of exiting, Q*(s_i, exit) = Q*(exit), is independent of the state; the value of harvesting is

$$Q^{\ast }(s_i,\mathit{harvest})=-\rho h+{\mathbb{E}}_{s_{i+1}}[r_{i+1}+\underset{a_{i+1}}{\text{max}}{Q}^{\ast }(s_{i+1},a_{i+1})]$$

where s_i+1 is the state produced by harvesting in state s_i. One should exit when Q*(s_i, harvest) < Q*(exit). Substituting the value of Q*(s_i, harvest) into this inequality and noting that if exit is optimal at t (i.e. if the inequality is satisfied), then the action a_i+1 that maximizes the continuation value Q* at the next state will also be exit (this is because trees decay monotonically¹), results in the following exit rule:

$$-\rho h+{\mathbb{E}}_{s_{i+1}}[r_{i+1}]+Q^{\ast }(\mathit{exit})<Q^{\ast }(\mathit{exit})$$

which can be simplified to [r_i+1] < ρh, where [r_i+1] = κs_i

Dependent variable & threshold estimates

Gross, tree-level threshold estimates

In experiments 1A and 1B, the trees’ state is discretized and the optimal decision rule can be expressed equivalently as a threshold on the integral number of harvests or on the (real-valued but still quantized) expected reward. To examine behavior and its optimality in units of reward, we estimated a subject’s leaving threshold per block as the across-tree average number of expected apples at exit, i.e. κⁿ⁻¹S₀, for a tree exited after n harvests. The optimal threshold to which we compare these blockwise estimates is given by the expected number of apples received after n* harvests, where n* is the number of harvests that optimizes the total average reward rate.

In experiment 2, the trees’ state is not discretized, so we estimate the subject’s exit threshold as the average of the last two rewards r_i and r_i−1 received before an exit decision. These rewards represent an upper and lower bound on the (continuously valued) threshold, respectively, since exiting at i implies that κr_i is lower than the subject’s threshold and not exiting in the preceding decision implies that κr_i−1 was greater. The corresponding optimal threshold is ρh/κ, since 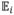[r_i+1] = κs_i.

For Figures 2c and 2f (the scatterplots), to visualize compliance with the MVT threshold condition κs_i = ρh, we plotted for each subject and block the total number of apples obtained in the block divided by the total length of the block in periods h(ρh), against the expected next reward at exit (κ times s_i, where the threshold s_i was taken as the average of rewards r_i−1 and r_i preceding each exit, further averaged over all trees in the block, since the MVT is expressed for both experiments in terms of the continuously valued threshold).

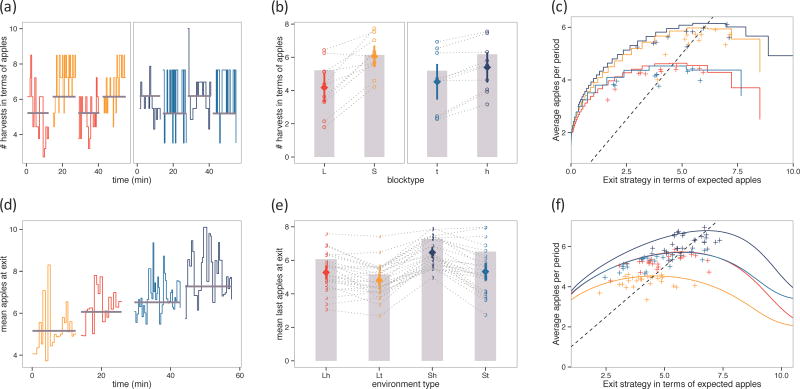
Figure 2. Foraging behavior.

Behavioral results compared to the optimal (ideal observer) performance in the task. (Top) Experiment 1a (travel time; L=long, S=short) and 1b (depletion rate; t=steep, h=shallow), (Bottom) Experiment 2 (Lh=long-shallow, Lt=long-steep, Sh=short-shallow, St=short-steep). (a,d) Example subject tree-by-tree exit points over time in the experiment. Colors indicate environments and grey lines indicate the optimal exit threshold. (b,e) Group performance by block. Height of the grey bars indicates optimal thresholds. Open circles connected by grey lines are individual subject mean exit thresholds and adjustment across environments. Filled diamonds are the mean exit threshold with 95% confidence intervals. (c,f) Colored curves show the achievable average reward per period for any given threshold policy in the different environments. Pluses are individual subjects’ mean exit thresholds. The dashed line is the MVT rule – points where the average reward rate is equal to the expected reward; it intersects the colored curves at the optimal exit thresholds.

Trial-by-trial choices

We can also model the trial-by-trial decisions using a logistic regression. In particular, we assume subjects make noisy harvest-or-exit choices a_i according to a logistic choice rule of the form:

$$P(a_i=\mathit{stay})=\frac{1}{1+exp(-(c_k+\beta [{\kappa }_k{s}_i]))}$$

for some block-specific threshold (intercept) c_k, trial and block specific explanatory variable κ_ks_i, and logistic weight (akin to a softmax inverse temperature) β. For a given environment with average reward rate ρ_k, the MVT predicts that c_k = −βρ_kh, resulting in a stochastic (logistic decision noise) version of the optimal policy. We estimated the parameters of this model (the thresholds c_k and temperature β) for each subject. The dependent variable was the binary choice a_i on each trial and the explanatory variables were the reward expected from harvesting on each trial, computed using the block-specific depletion rate, κ_ks_i, and four block-specific indicators corresponding to c_k.

This model defines a likelihood function over the sequence of choices, allowing us to use Bayesian model comparison to contrast different explanatory variables corresponding to different rules for estimating the state s_i of the tree. In particular, to compare counting-and reward-based strategies in experiment 2, we tested whether the choices were better fit by assuming $s_i={\kappa }_k^{n-1}{S}_0$ (the number of harvests, expressed in units of reward) or s_i = r_i (the most recent received reward, which is the actual state of the tree in experiment 2). We used the Bayesian information criterion (BIC) to estimate the marginal likelihood of each model given the data and submitted these values to the SPM_BMS function from SPM version 8 to compute exceedance probabilities (Stephan et al., 2009).

Learning

MVT Learning Model

The optimal policy from the MVT is to harvest whenever the immediate expected reward is greater than the average reward: κs_i ≥ ρh. Note that the appearance of the fixed harvest time h and the expected depletion rate κ in this equation are artifacts of the discrete-trial/discrete-time structure of our task; they do not appear in the MVT for a more classic continuous-time foraging task, like fishing, in which the agent can exit a patch at any instant. Thus, to execute this policy exactly, the subject must have an estimate of both quantities. We assume the fixed harvest time h (which is easily observed) is known, or equivalently that subjects learn ρ in units of reward per harvest period and that subjects estimate κ with a simple within-block running average of experienced depletion rates over adjacent harvests.

The MVT motivates a simple threshold learning model that requires specifying a learning rule for ρ and deciding whether to harvest by comparing the two sides of the MVT equation, κs_i and ρh (Table 2). We implement this comparison stochastically using a logistic (softmax) rule on the difference κs_i − ρh, with inverse temperature β and intercept c. The decision maker’s trial-by-trial estimate of ρ is constructed by a standard delta rule with learning rate α, taking into account the time τ_i = h or d of each choice step.

Table 2.

MVT-learning update-rule

Parameters: α, c, β

P(ai= harvest) = 1/(1 + exp(−c − β(κksi − ρih)))

δi ← ri/τi − ρi

ρi+1 ← ρi + (1 −(1 − α)τi) · δi

$${\rho }_i={(1-\alpha )}^{{\tau }_i}\frac{r_i}{{\tau }_i}+(1-{(1-\alpha )}^{{\tau }_i}){\rho }_{i-1}$$

At the beginning of the experiment, the depletion rate was initialized to 1 and the average reward rate ρ_init to the average across the experiments of the reward rates attained by an ideal observer. Fitting the initial condition as an additional free parameter, in both the MVT and TD models, did not appreciably affect the results; results not shown. In subsequent environments, the initial average reward rate estimate was taken as the last ρ estimate in the previous environment.

TD Learning Model

The TD algorithm learns the expected future discounted reward of continuing at each state Q(s, harvest) and a value of exiting Q(s, exit) = Q(exit) that is not state specific (Table 3). (Note that maintaining separate, state-specific values for exiting would only slow the learning of the task and accentuate the underperformance of TD. Furthermore, this assumption seems natural since subjects are told they can exit a tree on any trial and that this will lead to a new, randomly drawn tree.) The choice is taken to be logistic (softmax) in the difference between these values, with inverse temperature β and intercept c. The action values are incrementally updated by temporal-difference learning.

Table 3.

TD-learning update-rule

Parameters: α, γ, c, β

P(ai= harvest) = 1/(1 + exp(−c − β(Qi(si, harvest) − Qi(exit))))

Di~ Bernoulli(P(ai))

δi ← ri+ γτi(Di • Qi(si) + (1 − Di) • Qi(exit)) − Qi(si−1, ai−1)

Qi(si−1, ai−1) ← Qi+1(si−1, ai−1) + α • δi

This model has four parameters – the same three as MVT and an additional discount factor γ, which ensures that the infinite horizon cumulative future rewards are finite. For states s_i we use the actual state of the tree as defined by the experiment specifications. Thus, the state s_i is discrete in experiment 1 and is given by the number n of previous harvests at the current tree, whereas the state in experiment 2 is the most recently observed reward r_i, a continuous variable. In order to implement the update rule in this case, we approximate the value function by a linear combination of functions that are constant over predefined bins. To match the discretization of the state to the true exponentially depleting dynamics of the trees, the bins were logarithmically spaced and the width was chosen so that on average each subsequent harvest falls in a subsequent bin. More precisely, if b_j, b_j+1 are the lower and upper bounds of the jth bin, respectively, and κ̄ is the average depletion across the environments, the bins were spaced according to log(b_j+1) − log(b_j) = −logκ̄. At the beginning of the experiment, the starting values for Q(s, harvest) and Q(exit) were initialized with a constant for all s, equal to the discounted sum of rewards associated with earning ρ_init on average, $\frac{{\rho }_{\mathit{init}}}{1-\gamma }$. This starts the algorithm in the approximate range of the correct Q values, given a discount factor of γ and the same initial guess for the long-run reward rate as the MVT learning algorithm. In subsequent environments, the Q values are initialized to the Q values at the end of the previous block.

Note that both models were given explicit knowledge of the delays (h, t).

We fit the free parameters to each subject’s choices separately using maximum likelihood, and used these likelihoods to compute per-subject BIC scores as a measure of model fit. We used SPM_BMS to compare the models.

Variants of TD

In addition to the standard TD learning algorithm, we also compared the performance of two TD variants: TD(λ), which improves the efficiency of the algorithm by allowing faster back propagation, and R-learning, an undiscounted, average reward reinforcement learning model (Sutton, 1998; Schwartz, 1993). TD(λ) allows learning to immediately back propagate not just one step but through many preceding states by the introduction of an exponentially decaying eligibility trace (Table 4). The decay rate of the eligibility trace is governed by an additional free parameter λ, where λ = 0 is the one-step back up of the standard TD model presented above.

Table 4.

TD(λ) update-rule

Parameters: α1, λ, γ, c, β

P(ai = harvest) = 1/(1 + exp(−c − β(Qi(si, harvest) − Qi(exit))))

Di ~ Bernoulli(P(ai))

δi ← ri+ γτi (Di • Qi(si) + (1 − Di) • Qi(exit)) − Qi(si−1, ai−1)

Ei(si, ai) ← 1

∀s, a Ei+1(s,a) ← Ei(s,a) + λ • γτiEi(s,a)

∀s, a Qi+1(s,a) ← Qi(s,a) + α1 • Ei(s,a) • δi

R-learning aims to optimize the average reward per time step rather than the cumulative discounted reward, and so asymptotically it implements the same strategy as MVT. It produces this behavior in a different manner, however, as it uses a TD algorithm to learn a different notion of state-action value appropriate to this goal: the expected undiscounted cumulative average-adjusted reward. In this model, rewards are measured relative to the long-run average reward per timestep, a stateless quantity that is separately learned according to an additional learning rate parameter α₂. The full R-learning algorithm is presented in Table 5.

Table 5.

R-learning update-rule

Parameters: α1, α2, γ, c, β

P(ai = harvest) = 1/(1 + exp(−c − β(Qi(si, harvest) − Qi(exit))))

Di ~ Bernoulli(P(ai))

δi ← ri − ρi • τi + Di • Qi(si, havest) + (1 − Di) • Qi(exit) − Qi(si−1, ai−1)

Qi(si−1, ai−1) ← Qi+1(si−1, ai−1) + α1 • δi

ρi+1 ← ρi + α2 • δi

In both of these variants, the state-space and initialization were the same as in standard TD. In R-learning, the average reward term was initialized as in MVT-learning.

Over-harvesting

The intercept in the learning models above can capture a fixed policy bias, early or late exiting relative to the optimal exit threshold. However, plausible factors that might underlie the observed tendency toward over-harvesting include temporal discounting and decreasing marginal utility for money (one way of parameterizing risk-sensitive preferences). Decreasing marginal utility (sublinear increases in the value of each additional unit of money, which produce risk-averse choices in gambling tasks; Bernoulli, 1954) results in increased harvesting relative to a linear utility, since the larger rewards at a replenished tree are worth proportionally less. To test whether decreasing marginal utility captured this tendency, we fit the MVT model with a power-function utility on rewards ( $U(r_i)=r_i^{\eta }$), which affects both the expected next reward and the average reward rate, and looked at the effect this had on the intercept term estimate using an across subjects t-test. To examine discounting, we were constrained to the TD algorithm since there is no discounted equivalent of the MVT model. We again ran an across-subjects t-test on the intercept estimate to test whether deviations from optimal were fully captured by the discount parameter.

Results

Across two experiments, we presented human subjects (n=47) with foraging environments that varied in richness, as measured by the maximally achievable average reward rate, across a series of blocks (see Figure 1 and Methods). At each step of the task, subjects were presented with apples earned from the last harvest at the current tree and had to decide whether to continue harvesting or switch to a new, randomly drawn tree. Harvesting caused trees to deplete — each successive harvest earned fewer apples, on average — but traveling to a new, replenished tree cost additional time. Apples were converted to money at the end of the experiment.

Figure 1. Task Display.

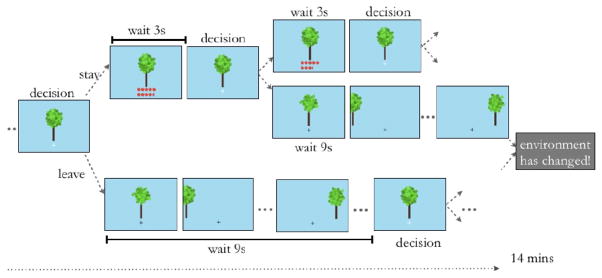
Subjects foraged for apples in four 14-minute virtual patch-foraging environments. They were presented with a tree and had to decide whether to harvest it for apples and incur a short harvest delay or move to a new tree and incur a longer travel delay. Harvests at a tree earn apples, albeit at an exponentially decelerating rate. New trees are drawn from a Gaussian distribution. Environmental richness or opportunity cost of time was varied across blocks by changing the travel time and/or the apple depletion rate. The quality of the tree, depletion rate and richness of the environment are a priori unknown to the subject (see Methods for a detailed explanation).

Environmental richness was manipulated by changing the travel delay between trees (experiment 1A), the tree depletion rate (experiment 1B) or both factors simultaneously (experiment 2). All else held constant, a longer travel delay or a steeper depletion rate reduces the rate at which apples can be earned. This reduces the opportunity cost of time spent harvesting and leads an ideal forager to harvest a tree down to a lower number of apples. Accordingly, the MVT states that the optimal policy for this class of tasks is to abandon a tree when the expected marginal intake from one more harvest falls below the overall average reward rate of the environment (see Methods; Charnov, 1976; Stephens and Krebs, 1986). The characteristics and richness of the environment were a priori unknown by the subject and had to be learned through experience.

Experiment 1

Each subject completed four 14-minute task blocks that alternated between high and low travel delay (experiment 1A, n=11) or depletion rate (experiment 1B, n=10) in counterbalanced order. The number of apples earned for each harvest was drawn randomly around an underlying average, which decayed exponentially with harvests in a manner that was deterministic and identical across trees. Thus, the expected reward for a harvest was a function of the number of times the tree had already been harvested. Subjects made an average of 611 harvest-or-exit decisions and visited an average of 103 trees.

First, we asked whether subjects’ overall strategies were modulated by environmental richness in the manner predicted by the optimal analysis. The optimal rule compares the expected reward for a harvest to a threshold; in Experiments 1A and 1B, the expected reward from harvesting is a function of the number of times the current tree has been harvested. Therefore, as an indicator of subjects’ exit thresholds, we considered the number of times each tree was harvested and expressed this quantity in units of the equivalent expected apple reward at the final harvest (Figure 2b.). Comparing the empirical thresholds to the values predicted under optimal switching, we found a tendency across all conditions to harvest longer (i.e. exhibit a lower exit threshold) than optimal but this was only significant in the long travel time condition (t₉ = −2.3, p = .045, all other environments p > .1). Next, comparing thresholds within-subjects and across blocks to examine whether, notwithstanding any over- or under-harvesting, subjects adjusted to changing reward rates in the optimally predicted direction, we found that subjects indeed harvested to lower thresholds in lower-quality environments: (paired t-tests across subjects, t₁₀ = 5.7, p < .001 for travel delay; t₉ = 5.1, p < .001 for depletion) with almost every subject adjusting in the predicted direction. These results suggest that subjects behave in a way qualitatively consistent with the MVT, though potentially with a slight bias to over-stay.

Another way to visualize compliance with the optimal policy is to consider overall earnings. The points in Figure 2c. show the obtained average reward for each subject and environment pair plotted against their empirical average exit thresholds. The dotted line shows the MVT prediction (where the threshold equals the average earnings), and the step function shows the achievable average reward per period as a function of different possible fixed exit thresholds in each environment. Subjects cluster around the MVT threshold, but with a tendency to lie to the left (reflecting overharvesting) and below the reward expected if the mean exit strategy had been executed consistently (implying variation in the strategy over the block, which is apparent in the individual subject data shown in Figure 2a.). Accordingly, subjects earned on average $17.9 ± 1.4 (mean ± SD), which represents a −10% loss on optimal earnings. In addition to comparing earnings to an upper bound given by the optimal strategy, it can be useful to situate them relative to a lower benchmark, given by random stay-or-exit responding according to a coin flip at each decision. To be conservative, we define this “random” policy generously by optimizing the weight on the coin to maximize earnings in each environment. The best such constant hazard rate policy deviates from optimal by −33%.

Learning & trial-by-trial choices

Next, rather than considering overall blockwise measures of thresholds and earnings, we examined trial-by-trial choices using models to explain the series of stay-or-exit decisions in terms of time series of candidate decision variables. Since subjects were not explicitly informed about the parameters of the environments, their ability to systematically adjust their exit thresholds between environments must reflect learning. Choice adjustments due to learning may also help to explain the substantial within-block dynamics of the exit strategies (as in the individual raw data shown in Figure 2a.). We compared the fits of two qualitatively different candidate models.

The first is a learning rule that has been suggested in the foraging literature and is based directly on the MVT policy: a stateless model in which subjects simply estimate the long-run average reward per timestep by taking a recency-weighted average over observed rewards. An exit decision occurs when the expected reward for harvesting drops below this opportunity cost estimate (McNamara and Houston, 1985; Krebs and Inman, 1992). An alternative model, the Q-learning algorithm, instead learns a state-action value function, which represents the cumulative future expected value of harvesting or leaving a tree at each state (where the state is given by the number of previous harvests on a tree). These action values are compared in each state to reach a decision (Watkins, 1989).

While TD methods like Q learning are more general and learn the full value function, which is required for optimal performance in many sequential decision tasks, MVT learns a summary variable that is sufficient for optimal choice in this class of tasks (see Methods). Learning these different decision variables results in different trial-by-trial choice adjustments. Generally, the two algorithms differ in how individual experiences affect future choices over the entire state space of the task. Whereas the MVT updates a single threshold (and the behavioral policy) at each observation, TD maintains a set of state-action values specifying the appropriate behavior for each step in the tree. These values are more difficult to learn, both because there are many of them and because they represent a prediction about long-run cumulative future reward, which is updated only locally via a process of chaining or “bootstrapping” of received rewards and value estimates across a series of successively encountered states (Sutton, 1988; Sutton and Barto, 1998).

Because both models specify different, complex trial-by-trial relationships between received rewards and subsequent choices, we used model comparison to determine which provided a better fit to the data. We computed the two learning models’ fit to each subject’s choice data using the Bayesian Information Criterion, having optimized the free parameters using maximum likelihood, and then compared the fits at the population level using (Stephan et al., 2009)’s group model comparison technique. This model comparison method allows for the possibility that the true model varies across subjects and estimates the proportion of subjects in the population expressing either model. This analysis showed overwhelming evidence in favor of the simpler MVT learning rule (Figure 3, left; with expected frequency 0.83, and exceedance probability, or posterior probability, that it is the more common model of 0.999). Note that the MVT model optimizes undiscounted reward rate, whereas TD optimizes cumulative exponentially discounted reward with a free discount rate. However, the model fit difference is not simply due to the penalty for the inclusion of the additional discount rate parameter in TD, since the BIC penalty for a single parameter is small with respect to the differences in model fit. Neglecting the penalty for the extra parameter still produces an exceedance probability of 0.999. The model differences remain significant even when the likelihood is computed without the initial 20% of observations, suggesting that the differences are not due to starting values (exceedence probability of 0.999); and when removing the first half of each block (exceedence probability of 0.993), suggesting that MVT does better not only at the environment transitions but also at explaining the within-environment dynamics.

In order to assess the robustness of our results, we also compared the MVT threshold learning model to two other variants of TD learning. First, motivated by the possibility that TD’s poor performance was due to slow learning over the state space, we considered TD(λ), a generalization of the standard TD model that allows for faster, nonlocal back propagation of information across multiple states. Second, we considered R-learning (Schwartz, 1993), an average-reward RL algorithm that updates state-action values relative to a stateless average reward term that is updated at every step. We reasoned that R-learning might perform more similarly to the MVT rule because it optimizes the same objective as MVT and does so, in part, by learning an additional average reward rate term similar to the MVT’s decision variable. These analyses again found overwhelming evidence in favor of the simpler MVT learning rule as compared to TD(λ) (expected frequency of 0.78 and exceedence probability of 0.997) and R-learning (expected frequency of 0.87 and exceedence probability of 0.999), suggesting that the simple, stateless, threshold learning rule outperforms a broad class of TD models in this task.

Over-harvesting

The above learning models each contain an intercept parameter that encodes any constant bias toward or away from harvesting, in addition to the effect of the learned decision variables. A tendency toward overharvesting, which was noticeable but for the most part non-significant in the cruder blockwise analyses above, should be visible here as a negative estimate for the intercept term in the MVT learning model. Indeed, the estimated intercept was significantly negative in the MVT model (t₂₀ = − 4.87, p < .001 across subjects for MVT), demonstrating a bias toward overharvesting.

Several factors may jointly contribute to this over-harvesting tendency. First, any persistent behavioral variability or deviations from consistently executing the optimal policy will reduce the obtained average reward and imply a lower steady-state opportunity cost of time and exit threshold. In other words, to the extent a subject’s actual long-run earnings fall below the rewards expected for consistently executing a strategy (stepped functions in Figure 2c), that implies variability around her average strategy. Her best response to the resulting effective reward environment is to aim to harvest longer than otherwise would be optimal (dotted line). Two such sources of variability are already accounted for in the learning model estimated above: trial-to-trial threshold variation (due to learning) and additional decision stochasticity (captured by the logistic choice rule). The finding that the intercept is still significantly negative demonstrates residual over-harvesting even after taking these sources of variability into account.

The MVT-predicted policy maximizes reward rate, but subjects may differ from this objective in their preferences over delay (time discount factor, as assumed in TD) or amount (nonlinear marginal utility of money, a standard way to parameterize risk sensitive preferences; (Bernoulli, 1954)), which would also contribute to over-harvesting. For a subject with decreasing marginal utility (one for whom $10 is worth less than twice $5, which in expected utility is functionally equivalent to risk aversion), exiting later is predicted because the marginal value of a replenished tree is reduced. The reverse pattern is predicted for subjects with increasing marginal utility (risk-seeking preferences). We re-estimated the MVT model with an additional risk sensitivity parameter (curvature in the function mapping money to utility). With this parameter, the intercept was no longer significant (t₂₀ = −1.33, p = .2 across subjects), suggesting that over-harvesting was substantially accounted for by risk aversion.

Additionally, a decision-maker who discounts future rewards will exit a patch later because the value of leaving is discounted by the travel delay, predicting discount-dependent over-harvesting. Indeed, the TD model optimizes cumulative exponentially discounted reward, and included a free parameter controlling the sharpness of discounting. The intercept in the TD model was not significantly different from zero (t₂₀ = − 1.03, p = .317 across subjects) indicating that exponential discounting can, on average, also account for over-harvesting. (However, note that some individual subjects under-harvest. Under-harvesting cannot be explained by conventional time discounting, though it could in principle be taken as a preference for later rewards, e.g. “savoring” delays. This is empirically unusual and also computationally problematic, since the infinite horizon value function then diverges. Such behavior can be explained more straightforwardly by convex utility curvature, which is less exotic.)

Experiment 2

A disadvantage of the design in Experiment 1 is that because the expected reward decayed deterministically with harvests, the reward-thresholding strategy predicted by the MVT is equivalent to a counting strategy: harvesting a fixed number of times. Therefore, we conducted an additional study, in which the initial qualities of new trees and the rates of depletion following each harvest were drawn randomly. These features require the ideal agent to monitor obtained rewards rather than simply count harvests. In this version, the obtained rewards at each step noiselessly reflected the current state of the tree and the expected reward from harvesting can thus be constructed by depleting the last observed reward. The optimal policy thus involves directly comparing the obtained reward to a threshold at which a tree should be exited, regardless of its starting quality or the number of preceding harvests.

In this experiment, we simultaneously varied both depletion rate and travel time within-subjects, crossing two levels of each to create four environment types with three levels of achievable average reward rates: one high, two medium and one low. Subjects made an average of 913 harvest-or-exit decisions and visited an average of 95 trees over the experiment.

The results of Experiment 2 echo those of Experiment 1 and verify that the behaviors studied there extend to this more complex setting. Exit thresholds were estimated as the average of rewards obtained before and at each exit in each condition, since these rewards should bracket the true threshold (Figure 2e.). These were significantly lower than optimal for three of the four conditions (t’s₂₅ < 3.6, p’s < .002; with a trend in the long-steep block, t₂₅ = −1.7, p = .09), again demonstrating an overharvesting tendency. Despite this tendency, most individual subjects adjusted their thresholds in the expected direction in response to blockwise changes in the average reward rate, a consistency that was reflected in a repeated-measures ANOVA as main effects of depletion, F(1,25) = 82, p < .001, and travel time, F(1,25) = 42.1, p < .001.

A quantitative analysis of the deviations from optimal found that subjects earned on average $18.7 ± 1.4 (mean ± SD), which represents a −9% loss relative to optimal earnings. For comparison, the best constant hazard rate policy, optimized to each environment, deviates from optimal earnings by −25%. When earnings are plotted against thresholds, strategies again cluster around the MVT’s predictions (Figure 2f.), albeit with a tendency to fall to the left of the line, indicating over-harvesting.

Trial-by-trial choices

Unlike Experiment 1, this experiment allowed us to distinguish between an exit policy based on thresholding observed rewards, as the MVT predicts, and a simple count of the number of times a tree has been harvested. We investigated this question by fitting two logistic regression models to subjects’ trial-by-trial stay or exit decisions, differing only in whether the main explanatory variable was the preceding reward or the preceding number of harvests. The analysis showed strong evidence in favor of the optimal reward-based strategy (Stephan et al.’s, 2009, Bayesian model selection): expected frequency .93, exceedance probability .999).

Learning

Finally, individual behavioral traces again demonstrate rapid threshold adjustments between and within environments (Figure 2d.). We compared the TD and MVT incremental learning model fits to the trial by trial decisions and found evidence in favor of the simpler MVT learning rule (Figure 3, right; expected frequency 0.85, exceedance probability of 0.999). Robustness checks showed the MVT model was still favored even without including the initial 20% of observations, suggesting that the differences are not due to starting values (exceedence probability of 0.823); and when removing the first half of each block, suggesting that MVT does better not only at the environment transitions but also at explaining the within environment dynamics (exceedence probability of 0.999).

A comparison between MVT and the two TD variants mentioned above, suggests that this simple threshold learning model better describes decisions in this type of task than a broad class of reinforcement learning models. A Bayesian model comparison finds an expected frequency of .93 and an exceedence probability of 0.999 in favor of MVT over R-learning, and an expected frequency of .73 and exceedence probability of .9941 when compared to TD(λ).

Over-harvesting

The results of experiment 2 again reveal a tendency to over-harvest relative to the reward maximizing policy. This is reflected in the MVT learning model fits, which include a negative intercept estimate (bias toward harvesting) that is significant across subjects (t₂₀ = −7.48, p < .001). This result again suggests that the tendency toward overharvesting is not fully captured by decision noise or threshold variation (due to learning). We again investigated whether this tendency could be explained by delay discounting or decreasing marginal utility (e.g. risk sensitivity) by looking at the effect of these additional preference parameters in TD and MVT, respectively. As in Experiment 1, the TD model incorporates a free time discounting parameter, but in this case still has a significantly negative intercept, suggesting that time discounting cannot by itself explain the result (t₂₀ = −4.47, p < .001 across subjects). However, when we added an additional parameter controlling risk sensitivity (value curvature) to the MVT model, the mean intercept was close to zero and no longer significant across subjects (t₂₀ = −1.71, p = .10), suggesting that over-harvesting may be substantially accounted for by risk sensitivity.

Discussion

Following on a long tradition of work in neuroscience and psychology about decision making in tasks where multiple options are presented simultaneously, there has been a recent interest in a different class of tasks, largely inspired by the ethological foraging literature: switching or stopping tasks in which options are presented serially and the choice is whether to accept the current option or search for a better one (Hayden et al., 2011; Hutchinson et al., 2008; Jacobs and Hackenberg, 1996; Wikenheiser et al., 2013; Kolling et al., 2012; Cain et al., 2012). Although most previous work in this class of foraging task has considered steady-state choice, these tasks pose a particularly interesting problem for learning, which we consider here: how to learn the (deferred and implicit) value of the alternative option.

Consistent with a body of ethological work in animals (Charnov, 1976; Kacelnik, 1984; Freidin and Kacelnik, 2011; McNickle and Cahill, 2009; Hayden et al., 2011; Stephens and Krebs, 1986) and a smaller literature in humans (McCall, 1970; Smith and Winterhalder, 1992; Jacobs and Hackenberg, 1996; Hutchinson et al., 2008; Kolling et al., 2012), we show across two experiments that humans consistently adjust their foraging choices to manipulations of the richness of the environment in the directions predicted by the optimal analysis. However, both experiments find a tendency to harvest a patch longer than would be optimal for maximizing reward rate, which is consistent with previous findings in patch foraging experiments (Hutchinson et al., 2008). In our data, this apparent suboptimality disappears if we assume that subjects optimize a currency with a nonlinear marginal utility for money (e.g., risk sensitivity). Thus, the choices are consistent with the MVT, when stated in terms of utility, rather than the raw monetary amount. A less satisfactory explanation for overharvesting (e.g., because it failed to fully account for overharvesting in Experiment 2) is that subjects discount delayed rewards. Had we needed to appeal to time discounting, this would have been harder to reconcile with the MVT, which concerns the undiscounted reward rate. A more direct test of either explanation would require assessing risk sensitivity (or time discounting) independently in order to investigate whether those estimates predict a subject’s overharvesting. It is also possible that many factors contribute jointly to this tendency.

With respect to learning, subjects’ trial-by-trial choice adjustments are consistent with a simple learning rule in which they track the average reward per timestep and use it as a threshold or aspiration level against which to compare their immediate gains (McNamara and Houston, 1985; Krebs and Inman, 1992). This learning rule is notably different from the reinforcement learning rules more often studied in neuroscience, which solve sequential decision tasks by estimating cumulative long-term rewards (Schultz et al., 1997; Montague et al., 1996; Houk et al., 1995).

In analyzing learning, we relied on formal model comparison to examine which of the two learning accounts better explains the observed relationship between outcomes and choices. This was necessitated because the correlated structure of rewards over time in the task — especially in Experiment 2 — makes it difficult to find a simple, local feature of the reward-choice relationship (such as the relationship between individual rewards and subsequent exits) that unambiguously captures the qualitative difference between the models. Thus, we compared how well each model explained the full joint probability of all the choices, conditional on all the rewards. However, disadvantages of this approach, interpretationally, are that it is relatively opaque as to what features of the data drive the difference in model fit, and that the conclusion is also specific to the particular models tested. The possibility therefore exists that some variant model not explored, and in particular some version of TD, might outperform the models considered here. We addressed this problem by considering what we take to be a canonical representative of the set of TD models, further improved with task-specific knowledge (e.g. a stateless value of exiting), and by additionally considering other TD variants, which together represent a reasonably large class of TD models. The magnitude of the difference in fit and its robustness to these algorithmic variations suggest that MVT learning is a better model of subjects’ trial-by-trial decisions than a broad range of plausible TD models.

One important dimension where there are many possible variants of TD learning is how the algorithm construes the space of possible states of the task. This is less of an issue in Experiment 1, where the objective state space of the task is small, discrete and well defined and does not require any generalizing function approximator. Two other TD variants that we considered were TD(λ), which increases the efficiency of the algorithm by introducing eligibility traces that allow for faster back propagation of information across states (making the particular representation of states less important); and R-learning, a TD algorithm that learns state-action values relative to an average reward term equivalent to that used in the MVT. Since this model maximizes the same currency as MVT learning, it rules out the possibility that the difference in fit between MVT and the other TD variants was driven by the slightly different objective (cumulative discounted reward) optimized by the latter.

Another difference between the models is that the MVT rule, as we have simulated it, relies on learning the depletion rate of the trees, and (unlike TD) is given the knowledge that this process takes an exponential form². Although it is difficult to see how to imbue TD with equivalent knowledge (since its action values are derived in a complex way from the one-step rewards and continuation values), we believe that this disadvantage does not explain away the difference in fit between the models. In particular, although we have included this factor in the MVT for consistency with the ideal observer (where this term occurs as an algebraic infelicity owing to the discrete trial setup of our task), leaving it out altogether (i.e., omitting κ) from the modeled MVT choice rule, and thus removing any built in knowledge about the form of the depletion, results only in a slight decision bias relative to optimal and does not change the dynamics of the algorithm. Accordingly, repeating the model comparison analyses omitting the depletion rate term from the decision rule does not appreciably change the model comparison (results not presented).

Our results suggest an important role for the average reward rate in guiding choice in serial switching or stopping tasks. These results tie decision-making in this class of tasks to a diverse set of behavioral phenomena and neural mechanisms that have been previously associated with average reward rates. Notably, the average reward rate has arisen in the analysis of a number of other seemingly disparate behaviors, including behavioral vigor, risk sensitivity, labor-leisure tradeoffs, self-control, and time discounting (Niv et al., 2006; Niv et al., 2007; Cools et al., 2011; Kacelnik, 1997; Niyogi et al., 2014; Keramati et al., 2011; Kurzban et al., 2012; Gallistel and Gibbon, 2000; Daw and Touretzky, 2002; Guitart-Masip et al., 2011). The notion of the average reward rate as the opportunity cost of time links these seemingly disparate domains: it indicates, for instance, the potential reward foregone by behaving less vigorously, by waiting for a delayed reward in a discounting task, or, in the case of foraging, by spending more time with the current option rather than searching for a better one (Niv et al., 2006; Niv et al., 2007). A very similar comparison – of current rewards to the long-run average – has also been suggested to govern the explore-exploit tradeoff (Aston-Jones & Cohen, 2005; Gilzenrat et al. 2010). Indeed, in the case of vigor, it has been shown that trial-by-trial fluctuations in behavioral vigor as assessed by reaction times are consistent with modulation by an ongoing estimation of the average reward rate (Guitart-Masip et al., 2011; Beierholm et al., 2013). The present results extend this rate-sensitive adjustment from modulations of arousal to discrete foraging decisions.

That such diverse phenomena implicate the same decision variable invites the possibility that they might share neural mechanisms. In particular, whereas TD learning about cumulative future action values is widely linked to phasic dopamine signaling (Schultz et al., 1997; Montague et al., 1996; Houk et al., 1995), it has been argued that longer-timescale (“tonic”) extracellular dopamine levels might be a neural substrate for tracking average rewards and for controlling behaviors that depend on them (Niv et al., 2006; Niv et al., 2007; Cools, 2008; Beierholm et al., 2013). Accordingly, dopamine is well known to affect response vigor and time discounting and we hypothesize that it may play a similar role in the current task (Robbins and Everitt, 2007; Salamone, 1988; Beierholm et al., 2013). However, while dopaminergic involvement in response vigor appears to focus on the nucleus accumbens (Lex and Hauber, 2008; Salamone, 1988), foraging decisions, switching to non-default courses of action, average-reward tracking, cognitive control, and decisions involving costs, all appear to involve another important dopaminergic target, the anterior cingulate cortex (ACC; Hayden et al., 2011; Kolling et al., 2012; Walton et al., 2009; Boorman et al., 2013; Gan et al., 2009; Seo et al., 2007; Curtis and Lee, 2010; Kurzban et al., 2012; Shenhav et al., 2013). Neurons in the ACC track reward history with a range of time constants (Seo et al., 2007; Bernacchia et al., 2011), and the slower of these may also serve as a signal for the average reward rate. Finally, the cingulate’s projections to another neuromodulatory nucleus, the locus coeruleus norepinephrine system, have been implicated in average reward effects governing explore-exploit tradeoffs (Aston-Jones and Cohen, 2005).

A different choice mechanism that has been argued to be at least partly distinct from the dopaminergic/TD system is “model-based” learning. Such a system learns a cognitive map or model of the structure of the task and then evaluates options by explicit simulation or dynamic programming (Daw et al., 2005; Daw et al., 2011; Doya, 1999). Although model based learning in the current task — that is, incrementally estimating the state transitions and rewards and solving the Bellman equation at each step for the cumulative expected value of harvesting and exiting — would likely result in behavior quite similar to the MVT learning rule, this seems an implausible account of choice behavior in the current study. Humans have been shown to use model-based evaluation in problems with very small state spaces (most often for sequences of only two actions; Daw et al., 2011), whereas quantitatively computing the optimal exit threshold by dynamic programming would require a very deep and precise search. TD and the MVT rule represent two different and more plausible “model-free” ways to short-circuit this computation by learning decision variables directly while foregoing the global model.

Indeed, it has recently been proposed that, perhaps in addition to the model-free/model-based distinction, the brain contains psychologically and anatomically distinct mechanisms for solving (bandit-type) simultaneous choice tasks vs. (patch-foraging type) serial stopping or switching tasks (Rushworth et al., 2012; Kolling et al., 2012), as with our TD vs. MVT models. On the basis of the imaging and physiological evidence discussed above, the ACC seems a likely substrate for foraging, whereas a long line of research implicates nearby ventromedial PFC in more symmetric economic choices, such as bandit tasks (e.g., Behrens et al., 2007; Hare et al., 2011; O’Doherty, 2011). The two sorts of choice have been most directly contrasted in a recent fMRI study (Kolling et al., 2012), supporting this anatomical dissociation, though another study using the task argued for a different intepretation of the ACC response (Shenhav et al, 2014). The present study, in the context of previous RL work, suggests a computational counterpart to such a distinction. In particular, learning in bandit tasks has been well described by TD and related delta-rule learning models (Sugrue et al., 2004; Daw et al., 2006; Li and Daw, 2011; Ito and Doya, 2009; Barraclough et al., 2004). Our finding that learning in a serial switching problem is instead more consistent with a structurally different threshold learning rule is consistent with the idea that these two sorts of choices employ distinct computational mechanisms and helps to flesh out the function of this proposed additional mode of choice.

This computational distinction sets the stage for future work directly comparing both approaches against a range of tasks, so as to understand in what circumstances the brain favors each approach. It has been suggested that organisms may approach many problems like foraging tasks, including even classic symmetric or simultaneous ones like economic lotteries and bandit tasks (Brandstatter et al., 2006; Hills et al., 2012; Hills and Hertwig, 2010; Kacelnik et al., 2010). One might hypothesize a rational tradeoff: that the brain favors the simpler MVT rule in tasks for which it is optimal, or nearly so, but favors more complex decision rules in tasks where these would earn more effectively. The MVT threshold learning rule differs from TD in two respects, by essentially neglecting two sorts of information that are inessential to patch-foraging and analogously structured tasks. The first difference is that foraging models neglect the value of any other alternatives in a simultaneous choice set, since they assume options are evaluated sequentially. Subjects must accept or reject each option by comparing it to some global aspiration level (the average reward), which can account for alternatives only in the aggregate via their long run statistics. This approach could be applied to arbitrary problems, such as bandit tasks, by assuming that even when options are proffered simultaneously, subjects evaluate them serially, taking some option as “default.” Regardless of how the default is set, this should produce a sort of satisficing relative to a maximizing model (like TD) that evaluates each option and chooses among them, since subjects will select a “good enough” default even when a better option is available. This inefficiency should be especially pronounced – and, perhaps, TD methods most favored – when the choice set changes from trial to trial (e.g., Behrens et al. 2007).

The second difference has to do with sequential credit assignment. An MVT rule, unlike TD, neglects the longer-run consequences of engaging with an option by myopically considering only its instantaneous or next-step reward rate. For patch-leaving, such myopic evaluation results in the optimal long-run choice rule as long as patches degrade monotonically. (The same rule is optimal in models of serial prey selection, e.g. Krebs et al., 1977, because encounters are independent and the gain for processing each prey is a single event.) However, in a modified foraging-like task where options can improve – consider deciding whether to sell a stock whose dividend might decrease and increase cyclically, or to fire an employee whose productivity could be improved with training – then the MVT will undervalue staying. The myopia of foraging rules has also been noted in time discounting problems (e.g., Stephens et al., 2004). Finally, long-run credit assignment is important to many differently structured multistep choice tasks, such as spatial navigation or multiplayer games. For instance, in a two-choice Markov decision task, that we have elsewhere argued is learned by a combination of TD and model-based RL (Daw et al., 2011), the MVT rule would be at chance in selecting a first-stage move since they earn no immediate reward and are only distinguished by the reward earned following an additional state transition and choice. Different tasks will vary in the degree to which myopic credit assignment results in inefficient returns.

Overall, although the class of switching tasks for which the MVT solution is optimal is small, the idea of staying or switching by comparing short-run returns to the expected long-run average is a plausible, albeit suboptimal, heuristic across many domains. MVT may be an overall favorable algorithm across a broader range of tasks because the resources saved in simplified computation may outweigh the reward losses. Thus, the choice and learning mechanisms isolated in simple patch foraging problems may shed light on broadly applicable systems, different from but complementary to those that have seen more attention so far.