A positive-negative mode of population covariation links brain connectivity, demographics and behavior

Abstract

We investigated the relationship between individual subjects’ functional connectomes and 280 behavioral and demographic measures, in a single holistic multivariate analysis relating imaging to non-imaging data from 461 subjects in the Human Connectome Project. We identified one strong mode of population co-variation; subjects were predominantly spread along a single “positive-negative” axis, linking lifestyle, demographic and psychometric measures to each other and to a specific pattern of brain connectivity.

The Human Connectome Project (HCP)¹ is acquiring high quality in vivo macroscopic-level connectome imaging data from over a thousand healthy adult subjects, in an effort to elucidate the neural pathways and networks that underlie brain function and behavior. An overarching aim is to reveal much about what makes us uniquely human and what makes individuals different from each other, by understanding how brain networks integrate information through the complex pattern of neural connections. To date, datasets from 500 subjects have been publicly released, including imaging data measuring functional and structural brain connectivity, as well as 280 non-imaging subject measures (SMs) including demographics (age, sex, income, education level, drug use, etc.), psychometrics (IQ, language performance, etc.) and other behavioral measures such as “rule-breaking behavior”.

Here we aimed to relate functional connectomes to behavior in a single integrated analysis. This goes further than simply investigating which SMs correlate with other SMs; we wanted to discover whether any specific patterns of brain connectivity are associated with specific sets of correlated demographics and behavior - as brain-behavior modes of population co-variation.

We used resting-state functional MRI data from 461 HCP subjects, and network modeling tools from FSL (FMRIB Software Library). A population-average brain parcellation was estimated using independent component analysis², giving 200 distinct brain regions; these constitute the nodes in our network modeling. The functional connections (edges) between these nodes were estimated using Tikhonov-regularised partial correlation, resulting in a 200×200 connectome for each subject. These connectomes were combined into a single large connectome matrix (containing all connectomes from all subjects; Supplementary Fig. 1). Separately, 158 behavioral and demographic non-imaging SMs from the same set of subjects were formed into a subject measure matrix. We regressed potential confounds (including brain size and head motion) out of both matrices. Redundancies among connectomes and SMs were reduced by (separately) keeping just the first 100 principal components of each matrix.

A natural choice of method for investigating underlying relationships between two sets of variables is canonical correlation analysis (CCA)³, a procedure that seeks maximal correlations between combinations of variables in both sets. Using CCA we estimated pairs of canonical variates along which sets of SMs and patterns of brain connectivity co-vary in a similar way across subjects. We refer to each such pair of variates as a mode of co-variation. Strict tests were applied to avoid over-fitting and false-positive inflation. Statistical significance was determined with a permutation test that accounted for the family structure of the HCP data⁴. This analysis revealed a single highly significant CCA mode that relates functional connectomes to subject measures (r=0.87, P<10⁻⁵ corrected for multiple comparisons across all modes estimated). These analyses were driven by and report only correlations; inferring and interpreting the (presumably complex and diverse) causalities remains a challenging issue for the future.

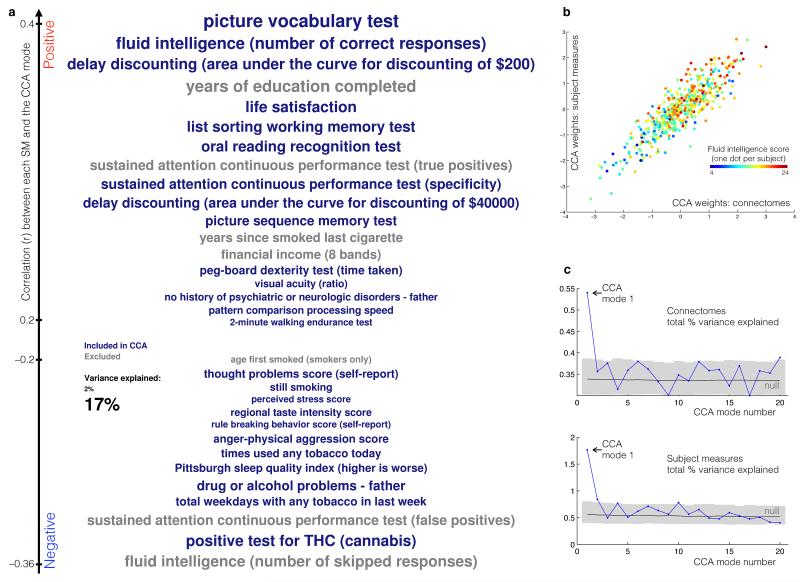
Fig. 1a displays the SMs most strongly associated (positively or negatively) with the identified CCA mode (see also Supplementary Table 1). Also plotted (Fig. 1b) are the relationships of all subjects with this mode, i.e., individual subject scores in the SM canonical variate vs. subject scores in the connectome canonical variate (one point per subject). This mode of population co-variation resembles descriptions of a general intelligence g factor⁵, but extends it to include key aspects of real-life function, including years of education, income, and life satisfaction. Remarkably, this can be considered a one-dimensional “positive-negative” axis, insofar as nearly all the positively correlated SMs are commonly considered as positive personal qualities or indicators (e.g., high performance on memory and cognitive tests, life satisfaction, years of education, income), and all negatively correlated SMs relate to negative traits (e.g., those related to substance use, rule breaking behavior, anger). One striking example is the strongly negative position of cannabis usage on the scale (though this is not on its own driving the overall results, which are almost unchanged if cannabis users are excluded from the CCA - see Online Methods). High-scoring subjects (top-right points in the scatter-plot) have high relative values for “positive” SMs (at the top of the SM list), and low relative values for “negative” SMs (at the bottom). In low-scoring subjects (bottom-left points), the pattern is reversed, with high values for negative SMs and low values for positive ones.

Figure 1.

(a) The set of SMs (subject measures) most strongly associated with the CCA mode of population variability. SMs included in the CCA are colored blue, while others (grey) were correlated with the CCA mode post-hoc. Vertical position is according to correlation with the CCA mode, while font size indicates SM variance explained by the CCA mode. Here we do not report “secondary” SMs that are highly redundant with those shown here (Supplementary Table 1 shows the complete set of SMs that correlate highly with the CCA mode). See wiki.humanconnectome.org/display/PublicData/HCP+Data+Dictionary+Public-+500+Subject+Release for details of the SMs. (b) The principal CCA mode - a scatter-plot of SM weights versus connectome weights, with one point per subject, and an example subject measure (fluid intelligence) indicated with different colors. The high correlation visualised here indicates significant co-variation between the two datasets. (c) The total variance explained of the original data matrices (shown separately for connectomes and subject measures) is plotted for the first 20 CCA modes. In black/grey is shown the mean and the 5^th to 95^th percentiles of the null distribution of the same measures, estimated via permutation testing. Using the null distributions to normalize variance explained accounts for the fact that the initial modes are expected to have higher correlations, even in the null scenario, but, as can be seen from the nulls, this is in any case a very small effect.

We next investigated whether this one CCA mode is indeed unique in modeling a substantially larger fraction of the total population variance (in the connectome and SM matrices) than the other 99 modes estimated. It is clear (Fig. 1c) that the first CCA mode explains a much larger fraction of the total data than any other mode, and is the only one to fall far outside the null confidence interval. Using the null distributions to normalise the variance explained into z-scores, the primary CCA mode has Z=7.7 for connectomes (the largest of any of the other 99 modes is 2.7) and Z=9.2 for SMs (the largest of any other mode is 2.4).

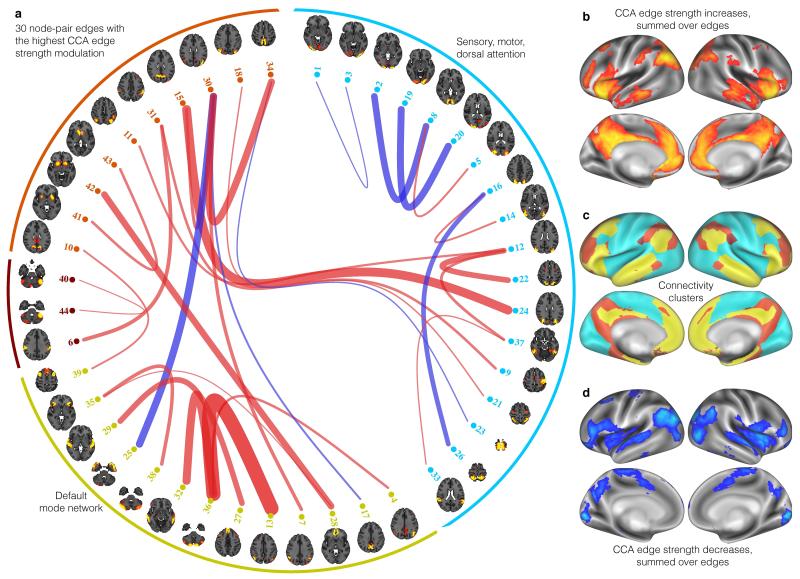
Fig. 2a displays the brain connections most strongly associated with the CCA mode. The thickest curves represent connections with largest CCA weights; for more quantitative results, see Supplementary Fig. 2. Red indicates stronger connections and blue weaker, for high-scoring subjects (and vice versa for low-scoring subjects). There is positive overall correlation (across edges, r=0.20) between the CCA connectome-modulation weights and the original population mean connectome shown in Supplementary Fig. 3, meaning that subjects that score highly in this CCA mode have stronger connectivity overall than low-scoring subjects – reflected in the dominance of red-colored edges.

Figure 2.

(a) The 30 brain connections most strongly associated with the CCA mode of population variability. To aid interpretation, the CCA edge modulation weights are multiplied by the sign of the population mean correlation; hence red indicates stronger connections and blue weaker, for high-scoring subjects (and vice versa for low-scoring subjects). (b) Map of CCA connection strength increases (each node’s parcel map is weighted by CCA edge-strength increases, summed across edges involving the node). (c) Group-mean functional clustering: 4 clusters from a hierarchical analysis of all 200 nodes’ population-average full correlation (Supplementary Fig. 3). These fall into two groups: one cluster (blue) contains sensory, motor, insula and dorsal attention regions, and a group of 3 correlated clusters (brown, red, yellow) primarily covering the default mode network and subcortical/cerebellar areas. (d) As b, but showing CCA connection strength decreases. Maps d and b are largely non-overlapping except in insula. b has spatial correlation of +0.40 with the default-mode areas in c (i.e., high overlap), while d shows negative correlation (−0.12). The average connectivity strength increase is approximately double that of the average decrease (as reflected in the predominance of red edges in a; also, a single map averaging across all 200 edges for each node shows a pattern of overall increase highly similar to b; finally, both b and d are thresholded at the 80^th percentile of their respective distributions, and if the threshold applied to b were applied to d, none of the strength reductions shown would survive).

When the data is summarised according to brain regions that most strongly contribute to these connections, a striking pattern emerges (Fig. 2b and Supplementary Table 2) that includes bilaterally symmetric peaks in medial frontal and parietal cortex, in the temporo-parietal junction and in anterior insula and frontal operculum. These areas, taken together, have high spatial overlap with the default mode network^6,7. While precise anatomical dissociations and functional specialisations among these regions is the subject of debate in cognitive neuroscience, they have been associated with many higher-level aspects of human cognition, including episodic and semantic memory^7,8, imagination and construction⁸, value-guided decision-making⁹, delay discounting¹⁰, spatial reasoning¹¹ and high order social process such as theory of mind¹². With deference to the caution required when making reverse inferences¹³, it may be expected that these aspects of cognitive function would have an influence on life in a complex society. While there are peaks in dorsal prefrontal cortex, it is notable that the highest node strengths are not centered on the dorsolateral prefrontal regions often associated with fluid intelligence^14,15.

An obvious exception to the positive-negative interpretation of SMs is peg-board dexterity (time-taken), where high-scoring subjects perform worse. That exception, however, is consistent with the connectome result (Fig. 2) insofar as the within-early-visual connections are weaker in high-scoring subjects, as are connections with two sensory/motor nodes (23 and 26 - likely Brodmann areas 4 and 5 respectively).

In summary, we found one significant mode of population variation that links a specific pattern of brain connectivity to a specific pattern of covariance between many behavioral and demographic subject measures. The vast majority of the SMs that correlate positively with this mode are “positive” subject traits/measures (education, income, IQ, life-satisfaction); those that correlate negatively are mostly “negative” subject measures. However, while strongly resembling the known general intelligence g factor for many of the subject measures, this mode does not trivially map onto just the strongest single principal component of the subject measures (see Supplementary Fig. 4; the CCA mode maps strongly onto the top three SM principal components and not just the first). It is plausible that the CCA mode includes a neural correlate of g, but is a more general mode of positive brain function, and is more directly tied into to the underlying biology (specifically, connectivity between brain regions), given that it is driven both by structured population covariance in behavioral measures and by intrinsic brain connectivity. We note a common criticism of the g factor, that there could be many distinct uncorrelated neural systems underlying high-level cognitive function, and that different cognitive tasks will involve different but overlapping sets of these latent processes, resulting in “artificial” correlation between subject measures, and hence the appearance of a g factor¹⁶. In future work it will be important to determine whether this known “unresolvable” ambiguity in g factor interpretation might be resolved through more fine-grained analysis of the data source newly available – the subject-specific functional connectomes – potentially even allowing direct investigation of the latent neural systems¹⁷, which may help us understand the coordinated interactions among brain systems that give rise to a general mode of positive function in humans.

ONLINE METHODS

Data

We used resting-state functional magnetic resonance imaging (rfMRI) data from 461 subjects taking part in the Human Connectome Project. All subjects were healthy adults (ages 22-35 y, 271 females) scanned on a 3 T Siemens connectome-Skyra scanner (customised to achieve 100 mT/m gradient strength). For each subject there were 4 × 15-minute runs of rfMRI timeseries data with temporal resolution 0.73 s and spatial resolution 2 mm isotropic. This high spatial and temporal resolution was made possible through the use of multiband echo-planar imaging, with a simultaneous-multi-slice acceleration factor of 8¹⁸. To aid in cross-subject registration and surface mapping, T1-weighted and T2-weighted structural images of resolution 0.7 mm isotropic were also acquired, and B0 field mapping was also carried out to aid in correcting EPI distortions. The original set of subject measures was all the behavioral, demographic and other measures reported in the “open access” and “restricted” subject information spreadsheets available from the HCP database website (http://humanconnectome.org/data).

Data pre-processing

Data pre-processing was carried out with tools from FSL¹⁹, FreeSurfer²⁰ and HCP workbench tools²¹. Each 15-minute run of each subject’s rfMRI data was preprocessed according to²²; spatial preprocessing was applied²³, and structured artefacts were then removed using ICA+FIX (independent component analysis followed by FMRIB’s ICA-based X-noiseifier^24,25). FIX removes more than 99% of the artefactual ICA components found in each dataset. The rfMRI data was represented as a timeseries of grayordinates - a combination of cortical surface vertices and subcortical standard-space voxels²³.

Group-ICA parcellation

Group-ICA was performed to generate a set of group-average nodes (or parcels). For this, 4 15-minute runs from 468 HCP subjects were temporally demeaned and had variance normalisation applied². These were fed into the MIGP algorithm²⁶, which carried out a 4500-dimensional principal component analysis (PCA) from the 4×468 timeseries. The output of MIGP is a very close approximation to PCA applied to temporal concatenation of the 4×486 timeseries, but can be calculated even when the full concatenated matrix is too large to form. The MIGP output (PCA spatial eigenvectors) was fed into group-ICA, run using FSL’s MELODIC tool², applying spatial-ICA at several different ICA dimensionalities (D = 25, 50, 100, 200, 300). The dimensionality determines the number of distinct ICA components (spatial maps); a higher dimensionality typically means that the regions within individual spatial component maps will be smaller. A set of ICA maps can be considered as a parcellation, though it lacks some properties often assumed for parcellations: ICA maps are not binary masks but contain a continuous range of weight values, and a given map can include multiple spatially separated peaks/regions.

Node timeseries (individual subjects)

For a given group-ICA parcellation, the set of ICA spatial maps was mapped onto each subject’s rfMRI timeseries data to derive one timeseries per ICA component per subject. For these purposes we consider each ICA component as a network “node”. For each subject, these 25 (or 50, 100, 200 or 300) timeseries can then be used in network analyses. The method used to estimate the node-timeseries was “dual-regression stage-1”, in which the full set of ICA maps was used as spatial regressors against the full timeseries data, estimating one timeseries for each ICA map²⁷. This results in 25-300 nodes’ timeseries of 4800 timepoints for each subject.

Network matrices (individual subjects and group averages)

Network matrices (also referred to as netmats or parcellated connectomes) were then derived from the node-timeseries. For each subject, the D (25-300) node-timeseries were fed into network modeling, creating a D×D matrix of connectivity estimates. Network modeling was carried out using the FSLNets toolbox (fsl.fmrib.ox.ac.uk/fsl/fslwiki/FSLNets). Netmats were estimated for the 461 subjects that have fully complete timeseries of 4800 timepoints (7 subjects whose data were fed into the group-ICA were missing some timepoints, and so were excluded from the subsequent quantitative subject-level network modeling). We applied network modeling using partial temporal correlation between nodes’ timeseries. This aims to estimate direct connection strengths more accurately than is achieved by full correlation²⁸. To improve the stability of the estimates of partial correlation coefficients, a small amount of L2 regularization is applied (setting rho=0.01 in the Ridge Regression netmats option in FSLNets). Netmat values were converted from Pearson correlation scores (r-values) into z-statistics with Fisher’s transformation. Partial correlation z-statistic netmats were estimated separately for each 15-minute dataset, and then averaged across the 4 runs for each subject, resulting in a single netmat (for a given group-ICA dimensionality) per subject. Group average partial and full correlation network matrices were estimates by averaging the z-statistic netmats across all subjects.

For display/interpretational purposes (Fig. 2, Supplementary Figs. 2, 3), hierarchical clustering of the group-average full correlation network matrix was carried out using Ward’s method implemented in Matlab. This was applied to all 200 nodes (from the 200-dimensional group-ICA). For more quantitative evaluation of specific connectivities (e.g., as used for our CCA), partial correlation is preferable, as it is more successful (than full correlation) in identifying the strengths of connections that are considered direct in a functional sense²⁸. However, for display of hierarchical network matrix clustering, we consider full correlation to be useful because of the extra robustness in identifying densely connected clusters that is achieved by also considering indirect connections. Additionally, this approach can help interpretability of the hierarchy/clustering, because it better matches the information that drives a low-dimensional clustering (e.g., a low-dimensional ICA that identifies a small number of gross resting-state networks, where there is no equivalent process to partial correlation occurring in the within-cluster modeling); hence this helps relate the results to typical low-dimensional network representation in the literature. Because this is a hierarchical clustering (see Supplementary Fig. 3), there is no single dimensionality (number of clusters) identified, but rather a continuum of clustering levels. However, large-scale clustering into 4 clusters allows simple interpretation relative to the literature: one cluster (blue) relates to sensory, motor and dorsal attention network (“task positive network”) areas⁶; the other dominant cortical cluster (yellow) identifies the default mode network⁶, and the two others (brown and red) relate to extended/secondary default-mode areas and subcortical/cerebellar areas.

The PTN data release

The above-described Parcellations, node Timeseries and Netmats (PTN) were publicly released via the central HCP ConnectomeDB database in late 2014. These same subject-specific netmats were used for the current study.

CCA modeling of many SMs and functional connectomes

We carried out a single integrated multivariate analysis using CCA, to simultaneously co-analyse a full set of functional networks (from all subjects) along with a large subset of the SMs. This aims to identify symmetric linear relations between the two sets of variables. Each significant CCA component (or mode) identifies a linear combination of netmat-edges (connectome connections) and a linear combination of SMs, where the variation in strength of involvement across subjects is maximally correlated. That is, we used CCA to find modes that relate sets of functional brain connections to sets of subjects’ demographics and behavioral measures.

In our main analysis, we used the netmats from the 200-dimensional group-ICA. This was a somewhat arbitrary choice, as all dimensionalities within reason are valid, but we also found that the other dimensionalities gave very similar CCA results (see below). As the parcellated network matrices (netmats) are symmetric, we only kept values on one side of the diagonal, resulting in 19900 unique edges (200×199/2). Combining across subjects resulted in a 461×19900 (s×edges) matrix N₁.

From the original set of 478 SMs, we formed a 461×478 matrix S₁.

Whereas CCA ignores variable scaling of individual variables, the PCA dimension-reduction step used prior to CCA (see below) is influenced by the relative scaling of each variable. In particular, PCA would not equally treat edges showing strong absolute variation versus edges showing strong fractional variation (relative to the population mean), and strong variations of both kinds are arguably of interest. Hence we formed additional matrix N₂ where each column was normalised (scaled) according to its mean value, removing resulting columns that were badly conditioned due to a very low (z<0.1) mean value. We then demeaned (columnwise) and globally variance-normalised (matrixwise, separately for the two matrices) N₁ and N₂ before concatenating them horizontally to give N₃, a matrix that therefore includes both preferences. (Nevertheless, we show below that this gave almost identical CCA results to only using N₁ or N₂.)

We used a rank-based inverse Gaussian transformation²⁹, to enforce Gaussianity for each of the SMs, producing S₂. This transformation was used to avoid undue influence of potential outlier values, although we later confirmed that this normalisation made almost no difference to the final CCA results (see below).

We identified 9 confound SMs, whose potential effect we wished to remove from our main analysis:

1. Acquisition reconstruction software version (as an improved MRI reconstruction method was implemented in the third quarter of acquisition year 1).

2. A summary statistic quantifying average subject head motion during the resting-state fMRI acquisitions (this is the average, across all timepoints, of the timepoint-to-timepoint head motion, that measure being the linear distance moved, averaged across the head).

3. Weight.

4. Height.

5. Blood pressure – systolic.

6. Blood pressure – diastolic.

7. Hemoglobin A1C measured in blood.

8. The cube-root of total brain volume (including ventricles), as estimated by FreeSurfer.

9. The cube-root of total intracranial volume, as estimated by FreeSurfer.

In addition to identifying these 9 confound SMs, we also demeaned and squared measures 2-9 (the first is a binary indicator), to create additional confound measures, to help account for potentially nonlinear effects of these confounds. All confounds were demeaned, and any missing data treated as zeros. We then regressed the 17 resulting confounds out of both data matrices (resulting in N₄ and S₃). (The CCA result was virtually unchanged if we did not regress the confounds out of N and S, or if we only regressed them out of N.)

We excluded any SMs from any further consideration (including post-hoc reporting) where fewer than 60 subjects had valid measures (6 SMs). We also excluded race (partly because the race measure is not quantitative, but consists of several distinct categories).

To focus our primary CCA on core behavioral measures of most interest, we excluded from the CCA a further set of SMs (but did include these in the final post hoc testing):

1. All 9 confound SMs.

2. 69 SMs, which were quantitatively poor measures according to one or more of the following criteria:

   1. An SM contained very extreme outlier values, as measured by most extreme value from the median. Specifically, if x_s is an SM value for subject s, and y_s=(x_s-median(x_s))², we consider an SM to have extreme outliers if max(y_s) >100×mean(y_s) .
   2. Fewer than 250 subjects had valid measures (too much missing data).
   3. Discreteness with severe imbalance, defined as >95% of all subjects having the same SM value.

3. 191 supplied measures from the T1-weighted structural brain analysis using FreeSurfer (including volumes of subcortical structures, and average thickness and surface area of many cortical regions). These are of course imaging-derived, but are supplied along with all the other SMs in the HCP database. We did not want these to drive the CCA, as we wanted the only imaging-derived measures utilised to be the functional connectomes.

4. 45 variables considered undesirable to feed into the core CCA, in some cases because they are not sufficiently likely to be measures relating to brain function, and in some cases where “minor” measures are highly correlated with more major related measures. For example, some measures would not necessarily be considered a confound, but we did not want them to be driving the main CCA result, to avoid complicating later interpretation. Thus we removed: “Is the subject in college?”; “Is the subject in a live-in relationship?”; “Is the subject born in Missouri?”; BMI (body mass index) and BMI self-report (note that as height and weight are confounds, BMI is essentially a confound and already removed); thyroid/hypothyroid/endocrine measures; menstruation-related measures; fluid intelligence secondary measures of skipped tests and reaction time (as we included the highly correlated major measure of correct responses); all minor Delayed Discounting measures (i.e., all except for the two major ones of area-under-the-curve for $200 and $40,000); all minor Sustained Attention (Short Penn Continuous Performance Test) measures (keeping the major measures of sensitivity and specificity; the minor Verbal Episodic Memory (Penn Word Memory Test) measure of reaction time; the minor Emotion Recognition (Penn Emotion Recognition Test) measure of Correct Responses Median Response Time; the minor visual Contrast Sensitivity (Mars Contrast Sensitivity) measure of error count; Sex; Age; Handedness; Employment status; Income level; Education level; “Whether blood was drawn for testing and measured hematocrit levels?”; Walking Endurance and Gait Speed; Physical Grip Strength.

This resulted in a 461×158 matrix S₄ (which still included some missing data). These 158 SMs fed into the CCA are now listed using their formal database naming; see wiki.humanconnectome.org/display/PublicData/HCP+Data+Dictionary+Public-+500+Subject+Release for detailed descriptions of these measures:

PicVocab_Unadj PicVocab_AgeAdj PMAT24_A_CR DDisc_AUC_200 THC LifeSatisf_Unadj ListSort_AgeAdj ReadEng_Unadj SCPT_SPEC ReadEng_AgeAdj ListSort_Unadj DDisc_AUC_40K Avg_Weekday_Any_Tobacco_7days Num_Days_Used_Any_Tobacco_7days Total_Any_Tobacco_7days PicSeq_AgeAdj FamHist_Fath_DrgAlc PicSeq_Unadj Avg_Weekday_Cigarettes_7days Avg_Weekend_Any_Tobacco_7days Total_Cigarettes_7days Dexterity_AgeAdj Avg_Weekend_Cigarettes_7days Dexterity_Unadj Times_Used_Any_Tobacco_Today PSQI_Score AngAggr_Unadj Taste_AgeAdj ASR_Rule_Raw Taste_Unadj ASR_Thot_Raw EVA_Denom SSAGA_TB_Still_Smoking FamHist_Fath_None ASR_Thot_Pct PercStress_Unadj ProcSpeed_AgeAdj ASR_Rule_Pct ProcSpeed_Unadj DSM_Antis_Raw ER40_CR NEOFAC_A ASR_Crit_Raw VSPLOT_TC NEOFAC_O ER40ANG VSPLOT_OFF SSAGA_Times_Used_Stimulants ASR_Soma_Pct SSAGA_Mj_Times_Used DSM_Antis_Pct CardSort_AgeAdj ASR_Extn_Raw ASR_Oth_Raw ASR_Totp_T ASR_Extn_T ASR_Totp_Raw EmotSupp_Unadj DSM_Anxi_Pct PercReject_Unadj ER40NOE DSM_Anxi_Raw ASR_TAO_Sum SSAGA_TB_Smoking_History CardSort_Unadj PosAffect_Unadj SSAGA_ChildhoodConduct Odor_AgeAdj ASR_Witd_Raw SSAGA_Alc_Hvy_Frq_Drk ASR_Soma_Raw DSM_Depr_Pct ASR_Aggr_Pct SSAGA_Alc_12_Max_Drinks DSM_Depr_Raw Mars_Final PercHostil_Unadj DSM_Somp_Pct SSAGA_Alc_Age_1st_Use ASR_Witd_Pct IWRD_TOT PainInterf_Tscore MMSE_Score SSAGA_Alc_12_Frq_Drk Odor_Unadj SSAGA_Alc_D4_Ab_Sx SSAGA_Mj_Use ASR_Aggr_Raw SSAGA_Mj_Ab_Dep DSM_Somp_Raw FearSomat_Unadj SSAGA_Alc_12_Drinks_Per_Day Mars_Log_Score SelfEff_Unadj SCPT_SEN NEOFAC_N SSAGA_Agoraphobia ASR_Intn_T AngHostil_Unadj Num_Days_Drank_7days SSAGA_Times_Used_Cocaine Loneliness_Unadj ASR_Intn_Raw SSAGA_Alc_Hvy_Drinks_Per_Day MeanPurp_Unadj DSM_Avoid_Pct NEOFAC_E Total_Beer_Wine_Cooler_7days DSM_Avoid_Raw Avg_Weekday_Wine_7days Flanker_AgeAdj ASR_Anxd_Pct Avg_Weekend_Beer_Wine_Cooler_7days SSAGA_Alc_D4_Ab_Dx Total_Drinks_7days SSAGA_Alc_Hvy_Max_Drinks FearAffect_Unadj Total_Wine_7days Avg_Weekday_Drinks_7days ER40SAD Flanker_Unadj ER40FEAR Avg_Weekday_Beer_Wine_Cooler_7days SSAGA_Times_Used_Illicits Avg_Weekend_Drinks_7days SSAGA_Alc_D4_Dp_Sx NEOFAC_C Total_Hard_Liquor_7days Correction SSAGA_Alc_Hvy_Frq_5plus DSM_Adh_Pct ASR_Attn_Pct VSPLOT_CRTE SSAGA_Depressive_Ep AngAffect_Unadj SSAGA_PanicDisorder Avg_Weekend_Hard_Liquor_7days FamHist_Moth_Dep ASR_Anxd_Raw SSAGA_Times_Used_Opiates SSAGA_Times_Used_Sedatives SSAGA_Alc_Hvy_Frq SSAGA_Alc_12_Frq_5plus Friendship_Unadj SSAGA_Depressive_Sx ASR_Attn_Raw ASR_Intr_Raw SSAGA_Alc_12_Frq FamHist_Fath_Dep InstruSupp_Unadj ASR_Intr_Pct SSAGA_Times_Used_Hallucinogens Avg_Weekend_Wine_7days FamHist_Moth_None Sadness_Unadj DSM_Hype_Raw DSM_Adh_Raw DSM_Inat_Raw

To avoid overfitting in the CCA, we used PCA to reduce the dimensionality of both N₄ and S₄ to c=100, reducing each to size 461×100 (i.e., keeping the top 100 subject-weight-eigenvectors N₅ and S₅ to feed into the CCA). In the case of applying PCA to S, we accounted for missing data in the SMs (4% of matrix entries) by estimating the subjects×subjects covariance matrix one element at a time, where, for any two subjects, SMs missing for either subject are ignored. This approximation to the covariance matrix was projected onto the nearest valid (positive-definite) covariance matrix using the nearestSPD (http://www.mathworks.com/matlabcentral/fileexchange/42885-nearestspd) matlab toolbox; this projection was extremely mild, with the correlation between the before vs after covariance values being very high (r=0.99996), but is important in order for the covariance matrix to be valid. The resulting covariance was therefore formed without any need to impute missing SM values. It was fed into an eigenvalue decomposition (of order 100) to estimate the top 100 subject-wise SM eigenvectors S₅, for feeding into the CCA, which represented 98.5% of the total SMs variance in S₄. The top 100 subject-wise connectome eigenvectors (N₅) represented 41.5% of the total connectomes population variance in N₄.

CCA (via canoncorr in Matlab) estimated 100 components (modes), optimising de-mixing matrices A and B such that the resulting U=N₅ A and V=S₅ B (461×100) matrices were maximally similar to each other. The correlation between a corresponding pair of columns (one each from U and V) indicates the strength with which a mode of population variation is common to both brain networks and behavioral measures; significance was estimated via 100,000 permutations of the rows of one matrix relative to the other. CCA was then re-run after each permutation. There are many related subjects in the HCP data, and family structure was kept intact when permuting the data⁴, therefore building up a valid null distribution of CCA results.

We identified just one CCA mode that related functional connectomes to SMs with high significance (r=0.8723, P<10⁻⁵, corrected-p 5% critical r threshold = 0.840). This mode was by definition the one component (out of 100 estimated) whose correlation between the connectome-subject-weights and the SM-subject-weights was maximal, and as this is compared against the null distribution of maximal correlation values, the quoted p-value is explicitly corrected for multiple testing (searching across all CCA modes estimated). This CCA mode represents one significant mode of population co-variation, for which individual subjects’ strength of involvement with this mode is highly similar for both a subset of the functional connectome and a subset of the SMs. The mode comprises 4 vectors:

• U₁, a 461×1 vector of individual subject weights derived from the connectomes matrix (in which each value describes the extent to which a given subject is positively or negatively correlated with this mode of population variation with respect to brain connectivity)

• V₁, a 461×1 vector, also of individual subject weights, derived from the SMs matrix (and which is highly correlated with U₁, r=0.87)

• A₁, a 100×1 vector of CCA mode weights relating to the 100 connectome PCA components fed into the CCA (i.e., the extent to which combinations of edge strength relate to mode weights-vector U₁)

• B₁, a 100×1 vector describing the extent to which each SM PCA component relates to mode weights-vector V₁.

CCA finds the A and B that maximise the correlation between U and V. To obtain relative weights (and signs) of involvement of the original sets of connectome edges and SMs, we correlated U₁ and V₁ respectively against N and S, even for those SMs not used for the CCA, resulting in “full length” edge/SM weight vectors A_F1 and B_F1. This simple approach for mapping CCA modes onto the original data matrices (to get connectomes and SM weights) allows for the estimation of the same test statistic for those SMs included in the CCA and those that were excluded.

In order to generate the CCA edge strength “increase” and “decrease” maps shown in Figs. 2b and 2d, we carried out the following. Using vector A_F1 (CCA edge modulation weights), we multiplied each element by the sign of the population mean edge connectivity, converting the modulation weights into measures of edge strength modulation. We reshaped the resulting vector into a square nodes×nodes matrix containing the same values (i.e., reversing the reshaping depicted top-left in Supplementary Fig. 1). For each column (node), we then estimated the average of the lowest 25% of values, and also the average of the highest 25% of values. This gave us estimates of the mean (across edges involving each node) strength decrease and increase, respectively. These values were then plotted spatially by multiplying each nodes’ spatial map by its edge strength decrease/increase, and averaging across all nodes for a given grayordinate. Note that a given node could in theory have both strong edge strength decreases (i.e., for certain edges involving that node) as well as strong increases (for other edges), but in general the maps of decrease and increase show little overlap.

Code availability

The full CCA script is freely available at: http://www.fmrib.ox.ac.uk/analysis/HCP-CCA .

Additional CCA validation tests

Several additional analyses were performed to further increase confidence that the CCA mode is a, robust, interpretable, mode of variation associating factors internal to the brain and subject measures. In general each test is evaluated in terms of 4 correlations [1 2 3 4]:

1. CCA mode 1 subject weights (connectomes): U_1(original) vs U_{1(alternative)}

2. CCA mode 1 subject weights (SMs): V_1(original) vs V_{1(alternative)}

3. CCA mode 1 connectome weights: A_F1(original) vs A_{F1(alternative)}

4. CCA mode 1 SM weights: B_F1(original) vs B_{F1(alternative)}

We now list the additional tests carried out:

• If we did not Gaussianise the distributions of all SMs before the PCA (and hence CCA), there was almost no change in the results – the correlations are: [0.86 0.86 0.85 0.96].

• If we changed the connectome normalisation to only use N₁ or N₂ instead of N₃ (feeding into the pre-CCA PCA), there was almost no change in results – the two sets of correlations are: [0.75 0.69 0.84 0.93] (N₁) and [0.74 0.70 0.84 0.93] (N₂).

• The pre-CCA SVD reduction of netmats and SMs was run using a much smaller number of PCA components for each (30 instead of 100), with almost no change in the results – original vs alternative correlations: [0.68 0.69 0.82 0.93].

• The CCA result was virtually unchanged if we did not regress the confounds out of N and S [0.75 0.76 0.78 0.92], or if we only regressed them out of N [0.82 0.84 0.82 0.94].

• If we use the 50-dimensional group-ICA parcellation to derive netmats and re-run the CCA, the results are very similar [0.61 0.68 - 0.88] (the third correlation cannot be computed as the netmats are not compatible between the analyses). Also, if we combine across all 5 dimensionalities, concatenating the matrices of netmats across all, again we get a very similar CCA output [0.88 0.91 - 0.97].

• If we added age into the confounds, which subsumes the effect of removing all the age-adjusted SMs from feeding into the CCA, the results were almost unchanged [0.99 0.99 0.99 1.00].

• Similarly, in order to explicitly determine whether there was a strong effect of feeding in both age-adjusted and non-adjusted SMs into the CCA, we carried out two additional CCA tests. In the first we excluded all age-adjusted measures previously fed into the CCA, for which non-adjusted SMs were also being used; this removed 10 SMs. In a second test we did the opposite, removing 10 non-adjusted SMs. In both cases we re-ran the CCA and compared the 4 primary CCA weight vectors against the original vectors. The results were virtually unchanged, with the smallest correlation across the 8 new-old vector pairs (two CCA re-runs and 4 weight vectors) being r=0.997.

• THC is the strongest-involved negative SM; hence, we tested the effect of removing THC from feeding into the CCA. The result is virtually unchanged [1.00 1.00 1.00 1.00]. More stringently, if we further remove all subjects who tested positive for THC, the results are still almost unchanged [0.78 0.78 0.79 0.81].

• In order to evaluate whether information similar to that in the connectomes might also be present in structural volume measures, we re-ran the CCA using the 47 FreeSurfer structural measures (volumes of individual tissue components and brain sub-structures) instead of the functional connectomes. Because this number of variables was much smaller, it was necessary to reduce the number of PCA components to 30. The correlation between U₁ and V₁ (from the resulting dominant CCA mode) was reduced to 0.56 (p=0.002). The correlations between the original V₁ and B_F1 and the volumetric-feature-based estimates of these were 0.51 and 0.78 respectively, i.e., lower than the corresponding connectome-based correlations reported above when reducing the number of PCA components from 100 to 30 without making any other changes. Thus, while the relationship between “brain” and SMs is weaker when using volumetric brain measures instead of functional connectivity measures, the results are still partially present. We also re-ran the original CCA, but after adding the 47 FreeSurfer structural volumes as additional confounds (to be regressed out of the connectomes and SMs). The correlation between U₁ and V₁ was 0.86 (i.e., nearly as high as in the original result), and the CCA weight vectors were similar to the original results [0.59 0.63 0.70 0.81]; these values are quite similar to the those reported above when re-running the original analysis with a reduction of PCA components to 30. We conclude that there is some shared variance between brain sub-volumes and functional connectomes (and hence the primary CCA result is to a limited extent recapitulated when co-modeling structural volumes and SMs), but the original CCA result (using functional connectomes) is stronger, and is largely unchanged when regressing out the brain structure volumes.

• As a simple sanity check of the permutation scheme that respects family structure, we replaced all rows (in both connectomes and SMs matrices) from a given family with the average row across all family members, for each family, and re-ran the CCA. We reduced the number of PCA components kept to 40, given the greatly reduced new “subject” numbers (157). The result is virtually unchanged [- - 0.74 0.88], and the significance of this first CCA mode remains at p~1/N_permutations.

• Although we have no reason to doubt the validity of the permutation-based significance test (of the main CCA result), we carried out a separate train-test validation analysis in which the CCA was only run on a subset of the data, and the outputs tested against the rest. We randomly kept approximately 80% of the subjects in a “train” analysis, leaving the other 20% as a test validation subset, without splitting any families across the train/test subsets. We ran the CCA on the train dataset, and confirmed that the main CCA mode estimated was virtually the same as the main original result (with weight vector similarities in the range r=0.85:0.99). We then took the CCA SM and connectome weight vectors from the train dataset and multiplied those into the left-out test dataset SM and connectome matrices, in order to estimate subject weight vectors U₁ and V₁ for the test dataset. We correlated U₁ and V₁, and carried out a (within the test dataset) permutation test (again respecting family structure, 1000 permutations) in order to measure the significance of the test dataset subject weight vectors’ correlation. We ran this train-test process 10 times, each with a randomly different set of subjects in the train and test subjects. The mean correlation between the left-out (test) U₁ and V₁ was 0.25 (N_subjects~90); the mean correlation in the null (permuted data) was 0.03 and the standard deviation was 0.1. In all 10 cases the correlation between the test dataset subject weight vectors was maximally significant at p=1/N_permutations (i.e., p=0.001). Hence the main CCA mode result is strongly supported by these train/test evaluations.