Establishing Good Practices for Exposure–Response Analysis of Clinical Endpoints in Drug Development

Abstract

This tutorial aims at promoting good practices for exposure–response (E-R) analyses of clinical endpoints in drug development. The focus is on practical aspects of E-R analyses to assist modeling scientists with a process of performing such analyses in a consistent manner across individuals and projects and tailored to typical clinical drug development decisions. This includes general considerations for planning, conducting, and visualizing E-R analyses, and how these are linked to key questions.

Exposure–response (E-R) analyses have become an integral part of clinical drug development and regulatory decision-making over the last decades.1 However, the regulatory guidances and industry recommendations for E-R are still lacking behind more mature areas such as population pharmacokinetic (PK) and pharmacokinetic/pharmacodynamic (PK/PD) modeling analyses. Population PK analysis is a mature discipline, and numerous methodological papers on model building, covariate selection, and model diagnostics exist2–6; PK/PD modeling, on the other hand, started to evolve at a later stage but rapidly evolved to an established research field with a dedicated journal (JPKPD). PK/PD modeling involves linking the concentration timecourse, including variation across dosing intervals, to the timecourse of the pharmcodynamic response.7,8

E-R analysis, in its broad definition, includes PK/PD modeling as a special case where the exposure variable is drug concentration, but most often the term E-R refers to analyses that differ from PK/PD models in several aspects: I) The exposure variable is a summary variable such as area under the curve (AUC), rather than the concentration timecourse. II) The response is often a clinical endpoint, typically expressed as the change of response variable from baseline to the end of trial. III) Response and variability in the placebo group (potentially due to changes over time, concomitant medication, or a placebo effect) is central to the analysis. IV) In many instances, E-R analysis is conducted by simple regression type of analysis, rather than timecourse models. For the present tutorial, we shall focus on E-R in the more narrow sense as described above, and only briefly refer to PK/PD and timecourse modeling.

The objective of this publication is to provide a common basis for how E-R analysis may be applied in the clinical drug development process. The scope of the tutorial is not to go into theoretical considerations but to highlight practical aspects of E-R analyses to facilitate consistent implementation across individuals and projects. This includes general considerations for planning, conducting, and visualizing E-R analyses, and furthermore how to link the questions that are addressed to the specific analysis. Finally, we discuss the limitations and assumptions for E-R analysis along with the perspectives for future applications in clinical drug development. The focus is on analysis of continuous response data but similar principles apply to categorical type data. Likewise, as mentioned above, we focus on the response at a single timepoint, and share only a few thoughts on the extension to timecourse E-R analysis, for which a standard remains to be developed.

We hope that by sharing our perspectives the pharmacometrics community will join forces and begin standardizing these types of analyses to increase the impact on key drug development decisions, similarly as Byon and Pfizer colleagues have done for population PK analyses.9

GOOD PRACTICES FOR EXPOSURE–RESPONSE ANALYSIS

One of the primary purposes of E-R analyses in clinical drug development is to ensure adequate dose selection and justification after each phase of development and at the time of submission utilizing the totality of evidence available. To facilitate this, the following sections provide general recommendations for conducting E-R analysis aligned with key questions. Specific examples are presented in a subsequent section.

Key questions

Relevant key questions at each stage of drug development are being utilized to move modeling support towards statistical inferences and quantitative analysis providing more direct answers, e.g., for justifications of selected doses. Table 1 suggests key questions to be considered for design and interpretation purposes across the phases of clinical drug development in patients. The aim is to focus on questions addressed by E-R, but for completeness also including questions addressed by PK/PD and meta-analysis (e.g., based on summary level data providing an overview of trial effects for a given indication). The design questions typically focus on choice of trial parameters such as dose regimen, trial duration, and sample size, including the power of the trial to provide evidence of E-R, whereas interpretation questions focus on E-R evaluation of trial data, i.e., identification of a treatment effect or higher response at higher exposure, or aiming at characterizing the E-R relationship.

Table 1.

Generic key questions to be considered for design and interpretation purposes across the phases of clinical drug development

Phase	Design questions	Interpretation questions
Phase I-IIa	Does PK/PD analysis, e.g. based on preclinical data support the starting dose, the regimen, and the dose range explored? Do simulations indicate that E-R based on phase I/IIa data can inform development decisions? Does the design provide power to detect a signal via E-R analysis for a biomarker or clinical endpoint? Is the design optimized with respect to duration, sample size, and dose levels? Consider if other design options reduce the risk of poor decisions, and what decision criteria should be used? Based on meta-analysis for this indication, do Phase 1 biomarker endpoints reliably predict late stage endpoints?	Does the E-R relationship indicate treatment effects? If safety signals are present: Does the E-R relationship support or challenge a relation to treatment? ∘Are safety issues more pronounced in the subjects with highest exposure? Does the E-R relationship indicate a potential therapeutic window? For PD markers, similar questions may be addressed with PK/PD analysis, which with more assumptions likely provides higher power than E-R analysis to detect a signal and identify a therapeutic window.
Phase IIb	Do PK/PD and E-R analyses based on available data support the suggested dose range and regimen? A phase IIB design should explore a dose range, including sub clinical, and supra clinical doses (if safe). What is the PD timecourse, including variability between subjects? Do simulations indicate that E-R based on phase IIb data can inform development decisions? What is the predicted power of the primary analysis/E-R analysis based on exposure-response? Does the design provide power to detect if treatment effect increases with exposure? Can E-R analysis assist to determine phase 3 dose levels? Is the design optimized with respect to duration, sample size, and dose levels? Consider if other design options reduce the risk of poor decisions, and what decision criteria should be used? Based on meta-analysis for this indication, do Phase II endpoints reliably predict Phase III outcome (if different)?	Does the E-R relationship support evidence of a treatment effect? What are the characteristics of the E-R relationship for efficacy and main safety/tolerability parameters? Does treatment effect increase with dose/exposure? What is the minimal effective concentration, EC50, maximum effect level? Does the effect level off at high exposure? What is the expected therapeutic dose/exposure window? For PD biomarkers: what are the characteristics of the PK/PD relationship, including variability in response over time, in particular for trials with different treatment regimens? If critical safety signals are present: Does E-R relationship support or challenge a relation to treatment?
Phase III and submission	Do E-R simulations based on phase II data support the phase III design, dose, and regimen, also for subpopulations with different exposure and/or response? What is the predicted power of the primary analysis/E-R analysis? What is the expected E-R outcome following phase III, overall and for relevant subgroups? Consider: ∘Uncertainty for the overall population? ∘Position on the E-R curve for relevant subgroups? If peak-to-trough ratio is high: Do PK/PD simulations based on phase II support the phase III dose and regimen? What is the predicted PD timecourse (including variation between subjects)? Does meta-analysis indicate an impact of PD fluctuations on the clinical endpoints?	Does the E-R relationship obtained from combined phase 2 and phase 3 data support evidence of a treatment effect? What are the characteristics of the E-R relationship of efficacy and main safety/tolerability parameters? Consider: Does treatment effect increase with dose? What are the minimal effective concentration, EC50, maximum effect level, and does the effect level off at high exposure? What is the expected therapeutic dose/exposure window? For critical safety issues: Does E-R support or challenge a relation to treatment? Is the proposed dose and dose regimen supported by E-R analyses (overall and in subpopulations)? What is the predicted effect of dose changes? Is an effect compared to placebo expected in all subgroups?

The questions in Table 1 should be regarded as generic options. It is recommended to supplement or replace these with specific questions tailored for each separate occasion in collaboration with relevant stakeholders.

Design questions

E-R analysis is a powerful tool in the planning stages of the trial to optimize the design to detect and quantify signals of interest based on current quantitative information of the compound and/or the drug class. Simulations and quantitative explorations of the proposed design should be performed prior to conducting the trial in order to understand the impact of design parameters on the outcome. This includes capturing the likelihood of obtaining a prespecified response in a specific population of patients and furthermore exploring inclusion criteria, demographic distributions, doses, dose regimens, treatment duration, and models for data analysis.

Careful planning of the trial and of the analysis is crucial for a successful utilization of E-R analyses in clinical drug development. Relevant stakeholders involved in the trial design and analysis discussions should be included to secure buy-in and focus of the expected analyses as well as effective utilization of results. For predefined analyses, the details of the analyses should be defined beforehand in a modeling analyses plan. For exploratory analyses, plans should focus on nontechnical aspects, in particular identifying the key questions to be addressed by the analyses in support of internal decision making (Table 1).

Interpretation questions

The key questions for interpretation are focused on informing the design of the next clinical trial or submission to regulatory authorities. In contrast to classical statistical testing confined to drawing evidence for the actual clinical trial, E-R and PK/PD analyses focus on drawing inferences through integration of prior knowledge based on pharmacology and physiological principles. A robust characterization of the dose–exposure–response relationships provides better understanding of the efficacy and safety of a drug, and enables quantitative decisions, e.g., for dose selection. Some of the suggested interpretation questions are relevant across the clinical development phases, e.g., questions pertaining to the treatment effect; and since these may often be satisfactorily addressed by classical statistics, timely application of E-R analysis will avoid redundant analyses. However, when uncertainty remains in the statistical evaluation, E-R analysis may contribute with critically important evidence, e.g., in the sense that a causal relationship to exposure will increase confidence in observed effects. Additionally, when results indicate the need for new studies, e.g., with another dose, E-R models can be used to simulate, predict, and extrapolate beyond the observed data and thereby be used to optimize the dose, design, and analyses, or altogether alleviate the need for further clinical data.

Data considerations

In general, studies are powered to demonstrate effect against placebo, and not powered to investigate differences between dose levels. Multiple trials should therefore, if possible, be included for E-R analysis. At the end of phase IIa, it would also be relevant to include patient data from phase I trials, and at submission it would be relevant to include, both the larger phase III and the phase IIb dose-finding trials, which typically span a broader dose range. However, such analyses across trials need to take into account differences in trial design and study populations, e.g., healthy subjects vs. patients, which may prohibit a meaningful joint analysis. Furthermore, response data from early clinical trials may be limited to include biomarkers rather than clinical efficacy endpoints, in which case the analysis will rely on available methods to link biomarker data to clinical outcome.

Exposure data may not be available from all patients, and so the E-R population from a clinical trial can be defined as the subset of patients from the full analysis set (FAS) for which exposure data are available. The response data obtained at the time of the primary endpoint evaluation should be used with appropriate imputation of missing data consistent with the primary analysis method; often Mixed-Effects Model Repeated Measures.10–12 Consider excluding patients who dropped out before PK steady-state was obtained in order to reduce the risk of obtaining a biased E-R evaluation. For timecourse analysis, all data are included as observed, and analyzed, e.g., by a Mixed-Effects Model that takes into account that response may be lower if subjects drop out early. The results of both the single timepoint and the timecourse analysis will reflect the outcome if all subjects had remained on-treatment. Alternatively, it may be relevant to investigate dropouts more thoroughly by dropout modeling, to provide a more detailed picture of the effect of changing the dose.

The most obvious summary measure of drug exposure is the area under the concentration–time curve (AUC) in a dosing interval at steady-state, but other measures such as maximal drug concentration (C_max) or trough concentration (C_trough) may be more appropriate, depending on the indication, the endpoint, and the PK properties of the drug. During early drug development the exposure data can be derived by noncompartmental methods. In late-stage development, sparse blood sampling often requires the use of population PK analysis, in which case the individual post-hoc AUC estimates can be used as the exposure measure.

Type of response variable

For E-R analysis, the response variable could be continuous, categorical, or time-to-event data. Models for continuous endpoints are typically estimated via nonlinear least-squares procedures. The same type of models can be used for binary endpoints, but data are typically logit-transformed in order to apply nonlinear logistic regression, with an underlying model such as the E_max model, similar to models of continuous data. Examples of model code used for analyzing continuous and categorical data are provided in the online Appendix to this tutorial. Time-to-event analysis may apply similar models in a proportional hazards model,13 or use a model independent analysis such as Kaplan–Meier plots for subjects in different exposure quantiles or placebo.

Assumptions and limitations

E-R analyses are associated with assumptions and limitations that should be considered before collecting the data, conducting the analyses, or interpreting the results, as follows.

Assumptions

• The exposure variable (potentially model-derived) accurately reflects the individual average effective concentration: i.e., that E-R analysis is independent of dose. This may be addressed graphically by comparing the E-R relationship for different dose levels.

• Exclusion of subjects without adequate exposure measurements does not bias the results. This may be addressed by comparing the response over time for subjects with and without adequate exposure measurements.

• The use of imputation for efficacy endpoints is assumed not to bias the results. As the true outcome for subjects dropping out is unknown, any imputation may create biased results. For late-stage trials, the primary analysis is often subject to sensitivity analysis to address this.

• All relevant confounding covariates have been taken into account in the analysis (see Choice of analysis method, below). This may be explored by checking the consistency between the E-R model predictions for the tested dose levels and the observed dose–response relationship, since if patients are randomized between dose levels, no confounding covariates should exist for the dose–response relationship with, e.g., higher response and dose levels for a certain subgroup. However, in general it is not possible to fully validate this assumption.

• The parametric model adequately represents the shape of the true E-R relationship. This may be evaluated by goodness-of-fit plots.

• Values of EC₅₀ and the Hill coefficient (see next section) are assumed identical in the contributing trials or between populations. Any differences in these parameters are unlikely to be identified at the same time as differences in E_max, since data may be insufficient. However, if data are insufficient to identify differences between populations, violation of this assumption is unlikely to have a significant influence.

Limitations

• E-R analysis is generally based on unbalanced data, since, e.g., heavy subjects could have different exposure than light-weight subjects, and this may limit applications in terms of statistical testing. The lack of balancing with respect to exposure is an inherent limitation due to the fact that clinical trials are typically controlled with respect to dose, whereas exposure is an uncontrolled variable. Some scientists find this to be a critical limitation, leading to skepticism towards E-R analysis in general, but we need to stress that most often the lack of randomization is not an issue, and the strengths of these analyses should encourage general applications of E-R analyses adding to the totality of evidence for decision making.

• The most important limitation of E-R analyses is the possible presence of unrecognized confounders. This is discussed further in the section on Choice of analysis method.

• The aim of the E-R analysis is to analyze the response for a specific endpoint, i.e., at a given timepoint, which does not necessarily reflect the long-term effects of the drug.

The above-mentioned assumptions and limitations are not likely to invalidate the analysis unless high rates of data exclusions have occurred. This is particularly true for late-phase applications where the important covariates for exposure and response are likely to have been identified, and confounders have been taken into account.

Choice of analysis method

The method used for conducting E-R analysis should be carefully adjusted to the question that is being addressed.

Fundamentally, we are addressing E-R questions using three different types of analyses, depending on the question, as summarized in Table 2. Whereas the first question concerns the effect relative to placebo, the two latter analyses elucidate various aspects relevant for selecting and supporting the dose.

Table 2.

Generic key questions with suggested models used for addressing the questions

Type	Question	Analysis*
A	Does data indicate a treatment effect?	ECFB ∼ EBASE + COVs + Slope*Exposure +Intercept (analysis based on all data)
B	Does treatment effect increase with dose?	ECFB ∼ EBASE + COVs + Slope*Exposure +Intercept (data from placebo excluded)
C	What are the characteristics of the E-R relationship? What is the predicted effect of dose changes?	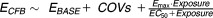+Intercept, (analysis based on all data)

^*E_CFB indicates the change from baseline of the primary endpoint, E_BASE is the baseline value of the effect variable. Exposure is an exposure variable such as the area under the concentration-time curve in a dosing interval at steady-state. COV is the contribution from covariates for the effect. Slope is the estimated slope of the E-R relationship on a linear scale. The E_max model (Type C) is parameterized by E_max, the maximal effect obtained at infinite exposure and EC₅₀, the exposure at half-maximal effect. For any of the analysis, an intercept, representing the response at zero exposure (i.e., placebo) is included. The equations are written with E_CFB as the dependent variable, assuming a continuous endpoint. Similar analyses may be applied for categorical binary endpoints, following logit transformation, and using the response rate as the dependent variable.

The first two types of analyses, Type A and Type B, should be predefined or relatively generic to ensure an interpretable P-value, by avoiding multiple testing. The third analysis for characterization and prediction (Type C) implies initiation of model development in order to obtain the best description of the structural relationship and covariate effects. The structural model could be reduced to a (log) linear relationship or expanded with a Hill coefficient, as implied by the data, and covariates should be selected for the relevant parameters in order to obtain the best and most realistic description. These fundamentally different types of analyses may assist to answer different questions throughout clinical drug development, as further discussed below.

For any key question, we recommend applying the simplest possible analysis, which includes the fewest assumptions and which readily can be communicated to a wide range of stakeholders. Therefore, the simplistic single timepoint analyses outlined above are recommended as the firm starting point. However, it is a gross simplification that these three types of analyses constitute a sufficient toolbox for E-R, as many aspects have not been addressed. In particular, dropout models and mixed-effects analysis using the entire timecourse of data can provide valuable additional insights. Application of these more advanced techniques are typically explorative in nature, being developed based on the data rather than being predefined. A number of potential model extensions to account for dropout, tolerance development, and disease progression should be considered on a case-by-case basis. Thorough recommendations for these options are outside the scope of this tutorial. Rather, our recommendations are focusing on the use of relatively simple models to evaluate relationships between exposure and treatment outcome at a single timepoint, which we believe will be adequate for the majority of situations in drug development and closest to the primary analysis specified in the protocol. However, the following sections provide general remarks to guide timecourse E-R analysis and situations where dropout needs to be accounted for.

Timecourse E-R models

In principle, models of the timecourse of response data constitute the hallmark of E-R analysis, providing more insight than single timepoint analysis at the expense of more assumptions.14 In particular, if the response is not at steady state, e.g., due to tolerance development or disease progression, a time series model may provide long-term predictions that can be highly relevant for real-world use. However, for investigations of clinical endpoints at a certain point in time, the single timepoint analysis is often sufficient. In general, we recommend to supplement the single timepoint analysis outlined in Table 2 with a timecourse analysis when:

1. The interoccasion variability in response is high.

2. The response at the primary endpoint appears inconsistent with the entire timecourse of the response.

3. In situations with frequent or informative dropouts.

For E-R analysis, the response in the placebo group is an important element that needs to be taken into account. Similarly, timecourse models need to include a placebo component changing with time. A frequently applied placebo model is:

where E_max,pl is the maximum placebo effect and k_pl is the rate constant for placebo effect development.15 The total response in the active group may be expressed as the sum of the placebo effect and the treatment effect.

Although E-R analysis is usually based on a summary exposure statistic such as the AUC rather than the complete PK timecourse, E-R models may borrow approaches from classical PK/PD modeling such as indirect response models to describe the treatment effect over time, taking into account if, e.g., the dose changes with time. However, a simple alternative is to use only a single value for the steady-state exposure, and a similar model as for the placebo effect described above, e.g.:

where Exposure_ss is a steady-state exposure variable such as AUC, k_tr is the rate constant for development of the full treatment effect, and E_max is the maximal response.

One issue with this setup, where an underlying placebo effect and a treatment effect are added together, is that placebo effects and treatment effects cannot always be separated, i.e., if a subject responds more than average, this may be due to an elevated placebo response or an elevated treatment effect. In single timepoint analysis, one often captures such an elevated response by a single residual with similar variance across placebo and active treatment. For timecourse analysis, the corresponding approach would be not to include random interindividual variability for the treatment effect but only for the placebo effect. Whereas this would be an appealing starting point, it may not be the optimal option, and should be explored on a case-by-case basis.

Dropout models

If patient dropout is ignored, the results of both the single timepoint and the timecourse analysis will reflect the response which would have been obtained if all subjects had remained on treatment. If a substantial number of subjects dropped out of a trial it may be relevant to investigate dropouts more thoroughly by including a dropout component in the model, in order to provide a more realistic evaluation. Thus, for predicting the effects of changing the dose it can be relevant to predict which patients would actually complete the trial. This allows for predicting the response for completers as well as for subjects dropping out of the trial. Furthermore, the dropout pattern (all dropouts, dropouts due to lack of efficacy or due to adverse events) may be considered as a clinical endpoint in itself, and would thereby be relevant to include in E-R analyses.

Dropout models are time-to-event analysis, typically based on the principles of proportional hazard models, extended with terms that depend on concentration/exposure, level of side effects, and efficacy. Inspiration for implementation of dropout models, in particular for informative dropouts, can be obtained elsewhere.15,16

In this tutorial we argue for simplicity, and do not recommend a general implementation of dropout models across E-R analysis. In fact, it may often be most informative and reasonably sufficient to evaluate the outcome expected if patients adhere to treatment (as provided by models that ignore dropouts), rather than aiming at predicting the true outcome for the intention-to-treat population. However, for dropout rates above 20% we recommend investigating these as independent clinical endpoints, in particular for dropouts related to adverse events. Such evaluations should be included in the evaluation of benefits and risks, e.g., when predicting the outcome of different dosing options.

Evaluation of covariates and subgroups

Covariates are important for evaluation of the E-R relationship in subgroups of patients and for adjusting for confounding factors (covariates that influence both the PK and the response variable). Known and unknown confounding factors may compromise the analysis if not properly accounted for, and this is probably the single most important source of error in E-R analyses. Figure 1 illustrates the importance of including sex as a covariate in the model in order to account for a higher exposure in females than in males. From Figure 1a it appears that an E_max model with Hill coefficient represents a good fit to the data. However, by including the confounding covariate (sex) it becomes evident that the true model (a simple E_max relationship) is more appropriate, demonstrating now that response is almost constant across the exposure range, as seen in Figure 1b.

Figure 1.

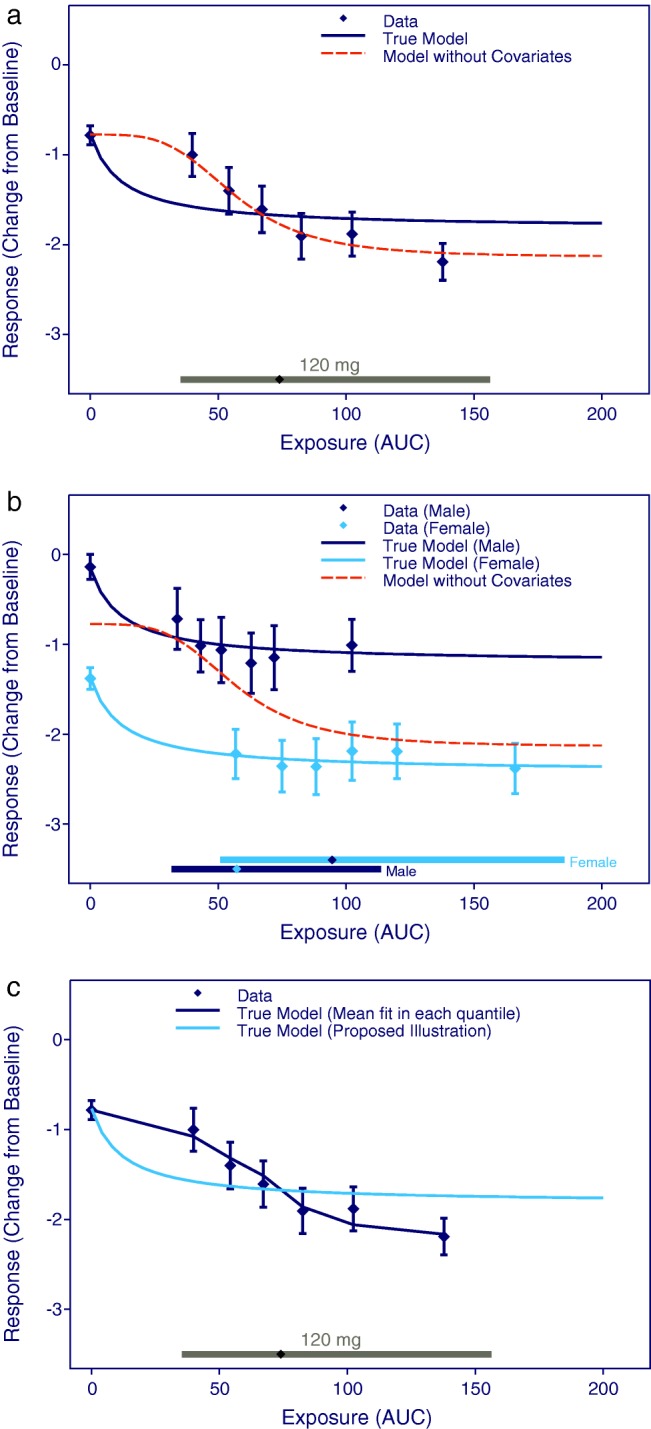
Visualization of E-R relationships (a) without and (b) with stratification for a confounding covariate (gender). (c) The proposed method for model visualization compared to the model fit for each quantile. Data points are mean effects with 95% CIs for quantiles of AUC values and the lines represent the estimated E-R relationships. The horizontal lines with diamonds along the abscissa represent medians and 90% exposure ranges at each dose level. The three panels are based on identical datasets generated by simulation of 1,000 subjects equally distributed between males and females.

Thus, the analysis needs to take into account possible confounding factors by including these as covariates. Case-control adjustment as a sensitivity analysis has recently been published as a way to adjust for known confounding factors in a model-independent analysis.17

In general, it is recommended to limit the number of covariates based on criticality. The following covariates should be considered:

• Always include the response variable at baseline and covariates that are known to be relevant for PK and/or response. Investigation of other covariates may be relevant, such as:

  • ○ Trial/population/add-on-treatment.
  • ○ Age, body weight, sex, region of the world.
  • ○  Additional demographics (e.g., other non-PK relevant covariates), relevant concomitant medication/illness etc.

Implementation of covariates can be tricky, since too many covariates on too many parameters will increase the uncertainty and potentially render parameter estimation impossible. In general, more covariates can be included for parameters that are estimated with high precision, e.g., covariates on the baseline effect (see below) that have the same effect on active treatment and placebo, compared to more uncertain parameters, such as the E_max or EC₅₀.

1. Covariates on the baseline effect (with similar impact on active treatment and placebo). Several covariates may be included without problems, but should be kept to relevant and uncorrelated covariates:

   • For phase III data with large numbers of patients: Include the most important covariates listed above. Consider additional covariates, only if required.
   • If the number of patients is limited, e.g., phase IIa: Include only the baseline value of the response as covariate. For known confounding covariates (or prespecified analysis), e.g., if sex is relevant for both PK and response, conduct additional analysis separately in males and females.
2. Covariates on treatment effects:

   • These covariates should be investigated, preferably for E_max. Only a few (e.g., 0–2) covariates should be included in the final model, to avoid over parameterization.
   • Do not include such covariates for statistical testing of evidence for E-R (Type A analysis). If relevant, test subgroups of patients separately.
   • Do not implement covariates for EC₅₀ unless data from different dose levels are available for individual subjects, or if such covariates are obvious from the data. Covariates on EC₅₀ can usually be substituted by covariates on E_max.

Visualization of results

E-R analysis may be performed as graphical data analysis and/or model-based analysis. Graphical data analysis is most often performed prior to initiating model-based analysis and to qualify the model-based analysis, when possible. Occasionally, graphical analysis may be the single method of choice for particular tasks.

Visualization of observations

Graphical analysis as scatterplots of individual response vs. exposure often turn out to be complex and difficult to interpret due to variability in response. This is certainly the case for categorical endpoints, but most often also in the continuous setting. Instead, we recommend dividing subjects into exposure quantiles, as follows. For each subgroup/trial in the graphical plot, subjects on active treatment are divided into quantiles based on their exposure values. For each quantile (or placebo) the mean and 95% confidence interval (CI) for the response is plotted against the median exposure level, with a value of 0 exposure for subjects treated with placebo. For multiple analyses conducted on small datasets, it may be advantageous to use the same exposure quantiles for all analyses, in order to better compare one timepoint/endpoint to another. In other cases, it may be more important to ensure that the same or similar number of subjects is included in all quantiles. Such quantile plots usually provide useful information of the trends of the data, and hence can be used also for qualifying the model-based predictions.

Visualization of model-derived predictions

A key purpose of the model-based analysis is to take into account that the subjects with the highest exposure are more likely to be of a different demographic composition than subjects with the lowest exposure. To address such issues, it is recommended to generate a mean exposure–response model prediction by the following procedure:

1. For each subject in the dataset, take the actual covariates (sex, body weight, etc.), and use the model to predict the response across the entire exposure range for a number of discrete prefixed exposure values.

2. At each of these exposure values, calculate the mean model prediction for all subjects within each trial/subgroup.

This procedure ensures that the model-predicted differences in response across the exposure range are driven by differences in exposure, rather than by a shift in covariate distributions across the exposure range. The proposed method for presenting model results has been used for all models and figures throughout this tutorial. Figure 1c illustrates the importance of this method by comparing the proposed method to the mean model fit obtained for each quantile of exposure. As seen, the proposed method for model visualization illustrates that the true E-R relationship is flat and thereby provides additional information besides a simple illustration of data. On the other hand, if we choose to present the mean model fit in each quantile (which may be a relevant model diagnostic plot), we may falsely conclude that the model supports that higher exposure provides higher response.

Often, visualizations of E-R include different extensions, e.g., variability between subjects, or uncertainty in the predictions. Inclusion of prediction uncertainty can be relevant, e.g., for a statistical conclusion, or when analyzing and comparing the benefits and risks from several different endpoints. However, a general introduction of model uncertainty may be less relevant, as uncertainty may depend heavily on the assumptions, parameterization, and complexity. For example, if the modeler includes components that are not monotonically increasing with dose, these could easily provide a similar mean E-R relationship, but with large changes to the uncertainty estimates. Confidence intervals around the quantiles, as presented in this tutorial provide a model independent assessment of the uncertainty.

Visualizing the timecourse of response

Diagnostic plots of timecourse models most often include response data vs. time with overlay of model predictions. To focus the application of timecourse models towards the influence of exposure, we recommend also including quantile plots of response vs. exposure, e.g., at end of trial with model predictions, with similar analysis overall, and for subgroups (similar to the recommendation for the single timepoint analysis described above). In situations where timecourse models are not pursued, we recommend including exploratory graphs of response vs. time for subgroups of exposure/dose to investigate if a single endpoint analysis is sufficient.

EXAMPLES: LINKING KEY QUESTIONS AND ANALYSES

The link between key questions and the corresponding E-R analyses is introduced in Table 2. The following section explains in more detail when and why to apply the different types of analyses.

Do data indicate a treatment effect? (Type A question)

During early development, the most important question is whether the compound has an effect or not, i.e., to establish clinical proof of principle following phase I/IIa, in order to decide whether to proceed with full clinical drug development. Due to the limited number of patients contributing data at this stage, the power may be limited when using classical statistical testing of treatment outcome vs. placebo for each dose. For this reason, an E-R analysis using all available data across doses may provide important supportive evidence of effectiveness.

Although the true E-R relationship may be more complicated, a generic analysis using a linear approximation is recommended for this purpose using the prespecified model (see Type A in Table 2). As depicted in Figure 2, the variability in data from phase I/IIa trials may preclude any conclusions regarding the shape of the E-R relationship, but nevertheless, a treatment effect may be established using the assumption of a linear relationship and testing if the slope of the line is significantly different from zero.

Figure 2.

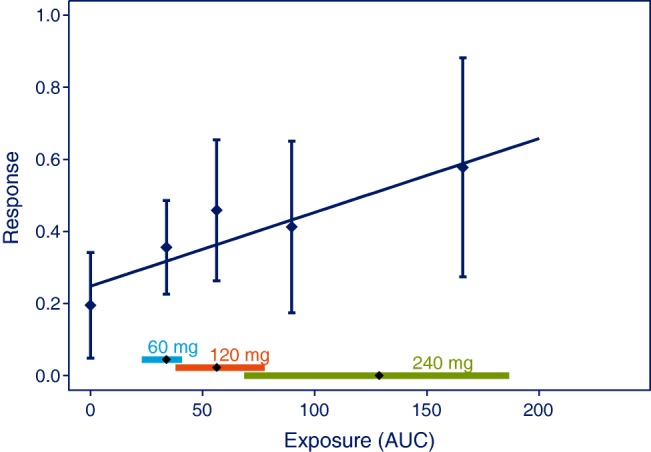
Plot to visualize a prespecified analysis for establishing supportive evidence of effectiveness. Data points are mean and 95% CI of effects for quantiles of AUC values. The horizontal lines with diamonds along the abscissa represent medians and 90% exposure ranges at each dose level. Data was simulated with 8 active + 4 placebo subjects at the two lower dose levels, and 16 active + 8 placebo subjects at the highest dose level.

Obviously, identification of a treatment effect as statistically significant will be relevant, not only at the end of phase I/IIa, but for many questions throughout the development. This may not be relevant for primary endpoints in phase III, but in other situations E-R analyses may assist in concluding if a borderline effect is real. For example, for safety data, it can be extremely important to conduct E-R analyses as part of the totality of evidence, either to support or challenge findings that appear unclear or questionable using classical statistical analyses.

Does the drug effect increase with higher doses? (Type B question)

For an already established effect, it is often relevant to test if the effect increases across the studied dose range to evaluate the benefits and risks for one dose level against another. Such a question is generally applicable when using E-R analysis to bridge from one dose level to another, e.g., by illustrating that the response for a safety biomarker is similar at all dose levels, as seen in Figure 3. This question may be particularly useful at the submission phase, when attempting to reach solid (yes/no) conclusions for different endpoints to justify a recommended dose. At earlier phases in drug development, e.g., when designing phase III trials, dose selection may be based on the expected E-R relationship, i.e., using a Type C analysis (Table 2) to ensure that phase III dose levels will provide adequate efficacy and safety, also in subjects with particularly high or low exposures.

Figure 3.

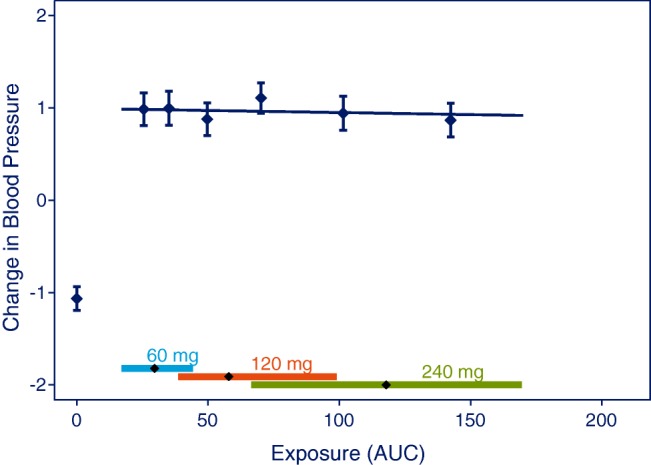
Plot to visualize the analysis used to test if already established effects increase with dose in the studied dose range. Data points are mean and 95% CI of effects for quantiles of AUC values. The vertical lines with diamonds along the abscissa represent medians and 90% exposure ranges at each dose level. Data were simulated with 240 subjects at each dose level or placebo.

Similar to Type A questions, Type B questions (Table 2) can be addressed by establishing a P-value for the slope using a prespecified linear model of effects vs. exposure. However, in this analysis the placebo data must be excluded from the analysis to ensure that the placebo group does not drive a false-positive conclusion. As seen in Figure 3, a treatment effect may be obvious when comparing to placebo data, but nonetheless, an E-R relationship may be absent when considering only the studied dose range and disregarding the placebo effect in the analysis.

What are the characteristics of the E-R relationship? (Type C question)

A model of the E-R relationship based on primary efficacy endpoints to support proposed dose levels is perhaps the most common type of E-R analysis. More so for phase IIb/III, compared to early clinical drug development, where less information is available. Often phase III is conducted with one or two doses, and as seen in Figure 4, the inclusion of phase II data for this analysis may be crucial in order to cover a sufficiently large dose range.

Figure 4.

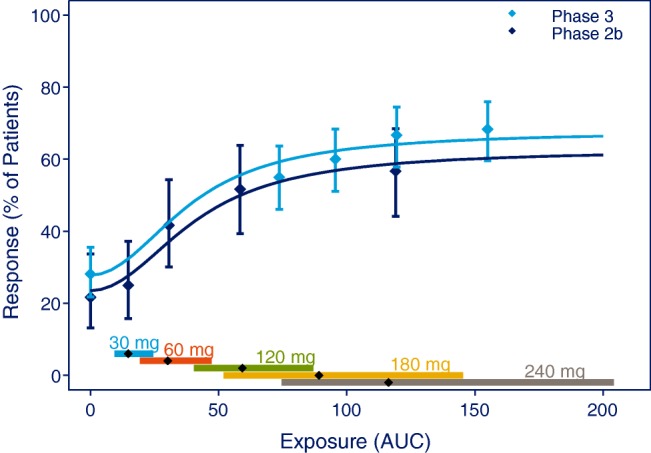
E-R relationship obtained from phase II and phase III trials. Data points are mean effects with 95% CI for quantiles of AUC values and the line represents the estimated E-R relationship. The vertical lines with diamonds along the abscissa represent medians and 90% exposure ranges at each dose level. Data were a simulated phase IIb trial including 60 subjects at each dose level 30, 60, 120, 240 mg, or placebo, and a simulated phase III trial randomizing 160:160:320 subjects to placebo, 180 mg, or 240 mg.

Whereas these thorough Type C analyses are currently more common for efficacy endpoints, they would be equally important for safety or tolerability endpoints, in order to justify the benefit–risk of different dose levels, e.g., summarized in a table such as Table 3, for the population as a whole, and for selected subpopulations. This may involve exploration of alternative doses, e.g., to illustrate that a lower dose would provide insufficient effects and that higher doses would be associated with limited additional benefit or unacceptable tolerability. In order to provide an accurate description of the data and the best possible predictions, it will most often be necessary to adapt the structural model and covariates to the actual data. Whereas this type of analysis provides the most accurate predictions of the expected impact of a dose change, a Type B analysis (Table 2) would be more useful to provide firm conclusions, whether a difference exists between effects of e.g., the two highest dose levels.

Table 3.

Predicted response by hypothetical dose increase from 120 to 180 mg

Dose increase 120 mg→180 mg	Predicted effect increase	Predicted increase in percentage of subjects with tolerability issues
All subjects	5%	7%
10% Heaviest subjects	8%	9%
10% Lightest subjects	3%	5%

In addition to such Type B analysis, comparing one dose to another, a Type C analysis with characterization of the entire dose/exposure–response relationship is often applied to substantiate that the dose is adequate, providing exposure within the therapeutic range. Before entering into phase III, it is relevant to apply this overall E-R characterization to illustrate the expected outcome for subjects with extreme exposure and to ensure that at least one of the dose levels included is expected to provide adequate safety and efficacy. Similar analyses should be applied for the submission, both for the population as a whole, and for relevant subgroups of patients.

DISCUSSION

E-R analysis has evolved as a discipline in its own right during the past decade, and many specific cases have been presented in the scientific literature during this period.18–23

Summary of recommendations for E-R analyses

This tutorial emphasizes the importance of applying E-R analyses throughout clinical drug development as tools for understanding efficacy and/or safety data and as quantitative support for decision making. An overview of key recommendations is provided in Table 4.

Table 4.

Summary of key recommendations provided in this tutorial

Key questions	• Apply key questions, aligned with stakeholders as a central part of the Modeling Analysis Plan.
	• Supplement generic questions with tailored questions for each investigational drug.
	• Consider if traditional PK/PD models or E-R models will be most appropriate to address the questions.
Data considerations	• Specify the relevant dataset and data imputations that will allow useful interpretation of exposure-response results without obvious bias of the results.
	• For medium to high dropout rates, dropout may be relevant to study as an independent clinical endpoint.
	• Argue for the choice of exposure variable (AUC is a common choice, but is not always appropriate).
	• Include PK sampling in late stage clinical drug development when it makes sense.
Assumptions and limitations	• Address the assumptions when possible, e.g., by diagnostic graphs and sensitivity analysis.
	• E-R analyses will most often be supportive evidence rather than the primary analysis, due to the possible presence of unknown confounders.
Choice of analysis method	Align the analysis with the key questions. Consider if the model should be prespecified or if data based model development/selection is more appropriate. Always estimate a single time point model and investigate, possibly by explorative graphs, if more advanced models are relevant. ∘Timecourse E-R models may be relevant due to high inter-occasion variability or bias due to dropouts. ∘Dropout modeling may also be relevant to provide a more nuanced picture of the response when looking into completer populations or ITT analysis with specific imputation strategies.
Covariates	Covariates are important, in order to adjust for confounding factors. More covariates can be included for parameters that are estimated with high precision. ∘Several covariates (with limited correlation) can be included for baseline effects; also in prespecified models. ∘Limit the number of covariates for Emax (reduce by forward inclusion and backwards elimination). ∘Include covariates for EC50 and Hill coefficients only when obvious from data and when predictions are physiologically plausible.
Visualization of results	• Visualize results by quantile plots, showing e.g. mean and 95% CI of response vs. median exposure.
	• Always add a model prediction that takes into account the known confounders.
	• The model prediction should reflect all subjects at all exposure levels.
	• Consider if prediction intervals or confidence intervals provides relevant and objective additional information.

Of major importance, we recommend linking the specific E-R analyses with key questions in order to provide clarity of results and to facilitate communication with internal and external stakeholders, including regulatory agencies. For communication purposes, it is important to show relationships between exposure and response as model-derived estimates overlaid with data. Use of individual data points for this purpose will often blur the trends of the data, and for this reason we recommend using quantiles of exposure values for display of the observed data. The number of quantiles may be adjusted in order to display data with the appropriate resolution.

The use of model-based E-R analyses is generally based on assumptions that should be defined and communicated to stakeholders. In principle, it may not be possible to verify all assumptions and so it may be considered to use a pure data summary as an alternative to a model-based analysis. However, using model-based analysis the presence of confounders may be investigated by inclusion of appropriate covariates in the model. This is not always possible by means of stratifications in graphical data analysis. Moreover, model-based E-R analyses provide additional opportunities in terms of investigating subgroups of patients and exploring doses, which have not been tested in a trial. For these reasons we consider model-based analyses to be the method of choice unless evidence against it has appeared.

Applications of E-R analyses in clinical drug development

At the outset, E-R analyses were explored mainly as a tool for late-stage clinical drug development. The widespread use of sparse PK sampling and population PK analyses in confirmatory clinical trials have opened the possibility of providing individual steady-state estimates of drug exposure in terms of AUC values, which are suitable for E-R analyses. Since then, many applications have emerged covering the entire chain from early- to late-stage clinical drug development, as outlined in this tutorial.

In general, E-R analyses aim to quantify effects at specific exposure ranges rather than providing statistical proof of effect. As such, E-R analyses are often regarded as supportive evidence of effectiveness, supplementing the statistical evaluation of trial endpoints because the underlying data are generally unbalanced and the model assumptions cannot always be verified.

Nevertheless, the use of model-based evaluation of clinical trials has been shown to increase power considerably24 and time will show if this approach has an increasingly important role as a primary analysis tool in future clinical trials.

On the other hand, in this tutorial we have shown that E-R analyses have a clear potential for establishing early-phase clinical proof of principle. This can be accomplished in terms of statistical verification of a significant slope in a linear approximation of exposure vs. response. Such confirmatory applications may be of value for the decision to move into full clinical drug development with a drug candidate.

Currently, applications of E-R analyses in clinical drug development may be summarized as follows:

1. Establishing clinical proof of principle.

2. Providing a rationale for the recommended dose(s).

   • Rationale for the recommended dose in subpopulations;

   • Bridging results from one dose level to another;

   • Exploring hypothetical dose changes.

3. Interpretation of unexpected findings.

4. Providing supportive evidence of effectiveness.

5. Exploring if adverse effects are related to drug exposure.

Perspectives

The successful application of E-R analyses in many contexts raises the question of whether new and more widespread applications are likely to emerge in the future.21 One possible development could be to use model-based E-R analyses for evaluation of trial outcome as a replacement or supplement to a classical statistical evaluation. As mentioned above, studies have shown superior power compared to statistical testing using model-based E-R analyses as the primary trial analysis. Examples of the use of such tools for evaluation of trial outcome exist for Parkinson's disease and hypertension.24 Whether the inherent limitations and assumptions for model-based evaluation of treatment outcome will limit development of this particular application remains to be seen.

In order to facilitate E-R analyses, it is recommended to include PK sampling in late-stage clinical drug development,22 when it makes sense. We have experienced that such analysis facilitates a deeper understanding of the data to support the recommended dose(s), not the least in order to address regulatory questions, both in terms of efficacy and safety. However, we do acknowledge that for some programs widespread PK sampling will not make sense, e.g., for a drug where the dose is titrated to effect.

An E-R model may be used for estimating trial outcome at doses not included in the pivotal trials, and cases exist where such doses have been approved based on E-R.25 Time will show if increased focus on E-R analyses will stimulate more applications of this kind, thus providing attractive opportunities in terms of cost and time reduction.

Given the widespread use of E-R analyses for drug approval, not only for efficacy but also for safety evaluation, the question arises whether model-based analyses will develop into a standard tool for benefit–risk evaluation. Movement towards this situation has already been seen, but many barriers need to be “removed” to further continue this development.26

Development of guidelines and good practices

The expanded use of E-R analyses during the last decade has been driven in part by regulatory initiatives such as the US Food and Drug Administration (FDA)'s End of Phase 2a meetings27 and the question-based clinical pharmacology review, which includes several E-R questions.28,29

Regulatory guidance is available from the FDA and European Medicines Agency (EMA) for E-R analysis.30,31 It is believed that revised guidelines with more specific recommendations are likely to further stimulate consistent use of E-R analyses by sponsors. Such guidelines would benefit from specific recommendations for I) collecting PK samples across late-stage clinical trials; II) expectations for establishing a therapeutic window; III) evaluation for the entire patient population as well as for subgroups of patients including analysis of patients with extreme demographic characteristics such as low and high body weight; and IV) for evaluation of doses not specifically tested in clinical trials. One step in this direction is the current EMA/EFPIA initiative to develop a good practice guidance with the aim to improve consistency, quality, and transparency for model informed drug discovery and development (MID3).32

This good practices document is a first attempt to share industry good practices for conducting E-R analyses in clinical drug development. The authors encourage other companies to share their internal recommendations to facilitate an informed discussion of how to standardize these types of analyses for maximum impact on clinical drug development decisions.

Author Contributions. R.V.O., C.W.T., and S.H.I. designed research and wrote the article. R.V.O. analyzed the data.

Conflict of Interest/Disclosure. R.V.O., S.H.I., and C.W.T. are employees and shareholders of Novo Nordisk A/S.

Supporting Information

Additional Supporting Information may be found in the online version of this article.

Supporting Information