What Do Arabic Numerals Mean to Macaques (Macaca mulatta)?

Abstract

In the past, rhesus macaques (Macaca mulatta) have demonstrated an ability to use Arabic numerals to facilitate performance in a variety of tasks. However, it remained unclear whether they understood the absolute and relative values of numerals. In Experiment 1, numeral-trained macaques picked the larger stimuli when presented with pairwise comparisons involving numerals and analog quantities. In Experiment 2, macaques were provided with numeral cues indicating the number of times a behavior could be performed in one location for a reward. Of the 4 monkeys, 3 performed above chance, but they often erred by performing more behaviors than indicated. The results of these studies indicate that the monkeys have knowledge of the approximate quantities represented by each numeral.

A range of nonhuman animals including dolphins (Mitchell, Yao, Sherman, & O'Regan, 1985), pigeons (Olthof & Roberts, 2000; Xia, Emmerton, Siemann, & Delius, 2001), a parrot (Pepperberg, 1994, 2006), squirrel monkeys (Olthof, Iden, & Roberts, 1997), capuchin monkeys (Beran et al., 2008), rhesus monkeys (Beran, Beran, Harris, & Washburn, 2005; Washburn & Rumbaugh, 1991), and chimpanzees (Beran & Rumbaugh, 2001; Biro & Matsuzawa, 2001; Boysen & Berntson, 1989, 1995; Matsuzawa, 1985; Murofushi, 1997; Rumbaugh, Hopkins, Washburn, & Savage-Rumbaugh, 1989) have learned to make numerical judgments using arbitrary symbols that represent quantities. The advantage to using arbitrary symbols, such as Arabic numerals, in numerical tasks rather than food items or analog stimuli is that the symbols provide no inherent non-numerical cues such as surface area, density, or complexity to indicate the relation between one quantity and another.

Over the past decade, the rhesus monkeys in our laboratory have participated in a variety of studies aimed at assessing their ability to perform numerical tasks using Arabic numerals. This research began when Washburn and Rumbaugh (1991) presented rhesus monkeys with pairs of the numerals 0 through 9 and reinforced them with a corresponding number of pellets for choosing either of the numerals. The monkeys learned to choose the larger numeral, and they performed accurately even when presented with probe trials of unfamiliar pairings of numerals. None of the probe pairings could be solved on the basis of logical transitivity. For instance, knowledge that 8 > 7 and 8 > 6 does not provide sufficient information to conclude that 7 > 6. When the monkeys were later presented with arrays of up to five numerals, they tended to select stimuli in the correct reverse ordinal sequence.

Across the years, dozens of additional monkeys have been trained and tested at our laboratory or at the Ames Research Center (Moffett Field, CA) using our software and the protocols originally described for the 2 monkeys by Washburn and Rumbaugh (1991). For these monkeys, the relative numerousness judgment task with Arabic numerals, described earlier, was administered as one of many training tasks to prepare the monkeys for subsequent cognitive studies. We have never reported the data from these training sessions, but the findings replicated the earlier results. We currently have summary data for 66 of those monkeys. After receiving training with randomly paired numerals (0 to 9, as described earlier and by Washburn & Rumbaugh, 1991), with proportional rewards for whichever numeral they selected, these monkeys averaged 84% accuracy on familiar (trained) pairings. On the first presentation of novel test trials—pairings of numerals the monkeys had never seen before—the monkeys were correct on a total of 367 of the 462 probe trials (seven novel probes for each of the 66 monkeys). This accuracy level (79%) is substantially and significantly in excess of what would be predicted by chance and is in fact very near the monkeys' levels of accuracy for familiar, overtrained pairings.

Despite these demonstrations of numerical ability, the following question remained: What exactly do these monkeys know about Arabic numerals? In the Washburn and Rumbaugh (1991) study, for example, it is possible that the monkeys learned a complex matrix involving the relative difference and degree of difference between all possible pairs of numerals. For example, knowledge that 8 is greater than 7 by one pellet (the smallest unit of difference) and greater than 6 by two pellets (the second smallest unit of difference) would allow the monkeys to solve a novel pairing of 8 and 7 and also of 7 and 6. A different explanation is that the monkeys gained an understanding of the absolute quantity of pellets represented by each number. Perhaps the most parsimonious explanation is that the monkeys associated each numeral with a different hedonic value on the basis of how much food was presented for that numeral. In others words, the largest numerals evoked the strongest positive hedonic states.

There is some evidence that monkeys may understand the quantitative values represented by Arabic numerals. In a study of Stroop-like effects (Washburn, 1994), rhesus monkeys at our laboratory learned to select the larger of two arrays of one to nine letters (e.g., to select five As rather than four Cs). When the arrays of letters were replaced with arrays of numerals, incongruous numerals (e.g., four 1s vs. two 5s) disrupted performance and congruous numerals (four 5s vs. two 4s) did not. In other words, it was more difficult for the monkeys to choose the array with more stimuli when that array was composed of the smaller numeral than when it was composed of the larger numeral. This effect suggests that these monkeys processed the quantitative meanings of the numerical symbols automatically because of their prior training with these numerals, despite the fact that these meanings were irrelevant to the task.

Experiment 1 of this study further tests the hypothesis that number-trained monkeys understand the absolute and the relative values of numerals by presenting them with pairwise comparisons involving numerals and analog quantities. If the monkeys had originally learned a complex matrix of values using knowledge of the relative difference and degree of relative difference between pairs of numerals, then they should be incapable of comparing symbols with actual quantities. Conversely, if the monkeys acquired knowledge of the absolute quantity of pellets represented by each Arabic numeral, then they might be able to compare symbols with analog dot arrays.

Additionally, the study includes a test of whether it is number or hedonic value that determines the monkeys' behavior. Brannon and Terrace (1998) criticized the proportional reinforcement procedure previously used in some numerical studies (e.g., Washburn & Rumbaugh, 1991) because it confounds numerousness and hedonic value, making it possible that the monkeys were not responding to the stimuli on the basis of numerosity, but rather on the richer reinforcement history provided by certain numerals that led to larger numbers of food pellets. That is, Brannon and Terrace (1998) suggested that the monkeys in our laboratory chose 7 instead of 6 not because 7 is more than 6, but because 7 is better than 6. We acknowledge this possibility, but note that monkeys could also perceive that 7 is better than 6 because 7 is more likely to be reinforced, as in such studies as Brannon and Terrace (1998) that used probabilistic (rather than proportional) reinforcement in which the animal is rewarded only for selecting the correct number. To address this criticism empirically, five monkeys in Experiment 1 received proportional rewards for every selection and a sixth monkey (Hank) was rewarded with a proportional number of pellets for numerals (e.g., picking the 4 netted four pellets) but probabilistic rewards for dot selections (e.g., correctly picking the bigger array always netted one pellet).

Experiment 2 was designed to further assess the monkeys' use of absolute numerical knowledge using a sequential task in which the monkeys were required to enumerate their own responses. In a previous study, we used a similar method to investigate the ability of four of our number-trained rhesus monkeys to use Arabic numeral cues to discriminate between different series of maze trials and anticipate the final trial in each series (Harris & Washburn, 2005). The monkeys were trained on a computerized task consisting of three reinforced maze trials followed by one nonreinforced trial. The goal of the maze was an Arabic numeral 3, which corresponded to the number of reinforced maze trials in the series. Two of the four monkeys developed a “slow, fast, faster, slow” pattern, which suggested that they were anticipating the final nonreinforced trial. The other two monkeys performed gradually slower on each trial in a series, which made it impossible to ascertain whether they were predicting precisely when the final trial would occur.

During testing, two monkeys were given probe series of the numerals 2 and 4 intermixed with the familiar numeral 3 series, and the remaining two monkeys were given probe series of the numerals 2 through 8. As was true during training, the Arabic numeral displayed in the maze corresponded to the number of reinforced trials that would occur before one nonreinforced trial. The monkeys receiving probe trials of the numerals 2 and 4 showed some generalization to the new numerals and developed a pattern of performing more slowly on the nonreinforced trials than on the reinforced trials, indicating the use of the changing target numeral cues to anticipate those final nonreinforced trials. The monkeys receiving probe trials of the numerals 2 through 8 did not use the changing numeral to predict precisely when the nonreinforced trial would occur in each series, but they did incorporate the changing numerals into their strategy by performing faster overall on series with greater target numerals.

The Harris and Washburn (2005) study provided evidence that number-trained rhesus monkeys could use Arabic numerals as a cue to facilitate performance on a task involving sequential responses, also known as a “constructive” enumeration task (Beran & Rumbaugh, 2001; Xia, Siemann, & Delius, 2000). However, the pattern established by two of the monkeys during training of performing gradually slower on each trial in a series and the failure of the monkeys receiving probe trials of the numerals 2 through 8 to generalize the pattern learned during training to new target numerals highlighted the need for a task that specifically addressed the monkeys' understanding of when a series is finished. Thus, in Experiment 2, monkeys were provided with Arabic numeral cues indicating the number of times a behavior could be performed in one location for a reward. After receiving all of the possible rewards from one location, the monkeys could behaviorally indicate that the series was complete by moving on to a second location. This design allowed us to assess their understanding of the cardinal value of the numerals. Together, these two experiments provided us with a greater understanding of what Arabic numerals mean to the macaques in our laboratory.

Experiment 1: Do Monkeys Know, for Example, That 4 > ⋯?

Method

Subjects

Six male rhesus monkeys (Macaca mulatta) were tested in this study. The monkeys (age range = 4–16 years) had previously been trained following the procedures described else- where (Rumbaugh, Richardson, Washburn, Savage-Rumbaugh, & Hopkins, 1989) to manipulate a joystick so as to control a computer-graphic cursor in response to stimuli displayed on a computer screen. The monkeys were not deprived of food or water and had continuous access to the apparatus and computerized tasks so that they could work or rest ad libitum. Each of the monkeys had been tested in numerous experiments before this study, and each had previously learned to respond to Arabic numerals in accordance with the number of pellets associated with each (see Washburn & Rumbaugh, 1991, for the details of this task and the procedure by which all of these monkeys learned to select the greater of any pair or array of Arabic numerals). That is, each monkey could generally select the larger of any two Arabic numerals (0 to 9) to receive the corresponding number of pellets and could generally select the array of letters or numerals with more items (Washburn, 1994). More important, none of the monkeys had received any training to directly link these two dimensions of numerousness (e.g., no training to label four items with the numeral 4, to pick three stimuli when presented with the numeral 3, or to determine whether the numeral 2 is greater than or less than some number of dots).

Apparatus

An analog joystick was connected to a computer that displayed stimuli on a 13-in. (33-cm) color monitor, presented auditory feedback through an external speaker–amplifier, and delivered 97-mg fruit-flavored chow pellets (Noyes, Lancaster, NH) via a pellet dispenser (5210, Gerbrands, Arlington, MA) and relay interface (ERA01 and PIO12, Keithley, Cleveland, OH). The mounting and protection of this apparatus has been described in detail elsewhere (Rumbaugh, Richardson, et al., 1989; Washburn & Rumbaugh, 1992). Each monkey worked at a dedicated computerized test system, and the monkey could reach through the mesh of his home cage to manipulate the joystick and to retrieve pellets.

Task

Each trial began with the cursor (a white plus sign) randomly positioned on the screen and a small (1.25-cm diameter) circle presented midscreen. Trials were initiated by manipulating the joystick so as to direct the cursor into the circle, whereupon the numerical stimuli were presented on either side of the cursor. Three stimulus conditions were used in these experiments. Some trials were numeral:numeral trials, in which two different Arabic numerals (1 to 9) were selected at random and positioned randomly to the left and right of the cursor. Other trials were dot:dot trials, in which two different arrays of one to nine randomly positioned 2.5-cm diameter white dots were displayed, one array on each side of the cursor. During training, each trial was randomly determined to be a numeral:numeral or a dot:dot trial. During subsequent probe testing, some trials were numeral:dot trials in which a randomly selected Arabic numeral was presented on the screen with a randomly selected (but different) quantity of dots. The position of the stimuli was randomized for all conditions (i.e., the numeral did not always appear on the left for numeral:dot trials). The monkeys' choices and response times were recorded for each trial.

Training procedure, proportional reinforcement

Five of the monkeys (Murph, Lou, Baker, Gale, and Willie) were trained to criterion with a version of the task that rewarded them for choosing the larger numeral or dot array by delivering a number of reinforcements proportional to the numeral or array selected. Selecting the smaller numeral or dot array resulted in a 1-s buzz tone and no food reward. That is, a monkey presented with the numerals 6 and 7 received seven pellets for picking the numeral 7 and no reward for picking the numeral 6. Likewise, a monkey presented with an array of four dots and an array of three dots received four pellets for picking the four dots and no reward for picking the three dots.

Training procedure, probabilistic reinforcement

To assess the hedonic criticism outlined earlier, we decided to implement two control conditions in the training and testing of Hank. First, Hank was reinforced proportionally for choosing the larger of two numerals, but he was only reinforced with a single pellet for choosing the larger of two dot arrays, irrespective of the number of dots in the array. He received a 1-s buzz tone and no reward for choosing the smaller numeral or quantity of dots. Second, we withheld some of Hank's dot:dot training trials, so that he never received an array in which five dots was the smaller quantity. That is, every one of Hank's choices of five dots was correct and reinforced during training.

Probe test procedure

After the monkeys reached a criterion of at least 76% accuracy on numeral:numeral trials and on dot:dot trials, the 72 possible novel numeral:dot trials were interspersed randomly within the next session. Note that one could claim that more than 72 novel numeral:dot trials exist, given that the position of the dots and the numeral were randomized each trial; however, the first exposure of each numeral with each quantity of dots (irrespective of position) was considered a probe trial for this study. These trials were reinforced in the same way described earlier for the training conditions: All monkeys received proportional reinforcement for correct numeral selections, Hank received one pellet for correct dot selections, and all other monkeys received proportional reinforcement for correct dot selections. All monkeys heard a buzz and received no reward for selecting the smaller numeral or quantity of dots.

Results

Each monkey achieved the training criterion in fewer than 1,500 trials (about 1 day of testing). Overall accuracy averaged 84% for numeral:numeral comparisons and 82% for dot:dot comparisons. As was reported by Washburn (1994) and Brannon and Terrace (1998, 2000), accuracy and response time varied as a function of the absolute difference between the quantities or numerals (e.g., 7:2 responses were faster and more accurate than 3:2 responses or three dot:two dot responses).

In the probe–test phase of the study, performance for each of the 6 monkeys was significantly better than chance (p < .05, binomial test), with the novel numeral:dot trials averaging 81.5% accuracy (see Table 1). No reliable differences were observed in the probe–trial tests between the numeral:numeral, dot:dot, and numeral:dot conditions.

Table 1. Overall Accuracy Levels Across Trial Type for Experiment 1.

Trial type	Mean % correct	No. trials	SD
Numeral–numeral (training)	84.5a	2,399	11.82
Dot–dot (training)	89.3a	2,385	4.72
Numeral–dot probes (testing)	81.5a	360	2.52

^aPerformance is significantly better than chance, p < .01.

Particular attention should be directed to Hank's responses in this probe–test phase given that Hank was reinforced probabilistically, rather than proportionally, for dot:dot trials and never received an array in which five dots was the smaller quantity during training. In the initial 36 novel numeral:dot trials, Hank showed a reliable numeral bias and thus was correct on 100% of the trials in which the numeral was larger but only 6% of the trials in which the dot array was larger. After 1 additional day of testing on numeral:numeral, dot:dot, and these 36 numeral:dot trials, he was tested on the final 36 novel probes. Hank was correct on 89% of these novel probes, and accuracy on the other trial types remained high (93%). It is also noteworthy that Hank was correct on 7 of the 8 (88%) novel trials in which an array of five dots was paired with a larger array or numeral.

For all of the monkeys, most of the errors on the numeral:dot probe trials were made on trials in which the numerical distance (i.e., the difference between the numerical values of the numeral and dot array) of the two stimuli was very small. Analysis of variance revealed a significant effect of numerical distance for the accuracy data, F(7, 28) = 10.02, p < .05. A post hoc analysis using Tukey's Honestly Significant Difference revealed that performance for the numerical distance of 1 was significantly worse than performance for numerical distances of 2 and larger; performance for the distance of 2 was significantly worse than performance for the distances of 4, 5, and 8; and performance for the distance of 3 was significantly worse than performance for the distances of 4 and 8.

Discussion

The monkeys accurately interdigitated Arabic numerals and random arrays of dots, even on the first exposure to these trials. This indicates that the monkeys were not relying solely on a complex matrix of two-choice discriminations learned during the training phase. Knowledge that the numeral 7 is the correct choice when presented with the numeral 6 and that an array of seven dots is the correct choice when presented with six dots is not sufficient information to compare the numeral 7 and six dots.

Additionally, the data from Hank indicate that this ability is not based solely on the numerals' hedonic value. Although Hank initially favored all numerals, probably because of their substantial advantage in terms of reinforcement history, he did come to respond at levels significantly better than chance to first-trial presentations of stimulus pairs in which numerical value opposed hedonic value. For example, Hank, like the other monkeys, responded that four dots is greater than the numeral 3, even though the numeral 3 was associated with a rich reinforcement history, whereas arrays of four dots were only occasionally reinforced, and then with only a single pellet. This point is further supported by the observation that Hank did not base his responses solely on probability of reward either. Although arrays of five dots were always reinforced during training, Hank correctly selected larger arrays or Arabic numerals greater than 5 on 88% of the subsequent probe trials involving five dots.

Hank's data are also interesting because they indicate that he was able to use the ordinal information inherent in the dot quantities to perform the numeral and dot comparisons. Dot quantities are different from symbolic stimuli such as numerals because they have visible properties that relate to their ordinal position in a sequence (i.e., the quantity three consists of fewer dots than the quantity four). During training Hank was only reinforced with a single pellet for correct dot:dot responses, and he never received an array in which five dots was the smaller quantity. Thus, he did not have an opportunity to associate specific quantities of pellets with specific dot quantities or to learn the order of the dot quantities 5 through 9 using reinforcement history. The fact that Hank was able to solve the novel trials in which an array of five dots was paired with a larger array or numeral indicates that he was responding to the inherent ordinal value present in the analog dot displays. These data match those from another study with rhesus monkeys in which those monkeys also spontaneously responded to analog dot displays in a comparison task on the basis of their ordinal relations (Harris, Beran, & Washburn, 2007).

On the basis of the combined data from all of the monkeys, we are able to rule out a matrix of learned values and also hedonic value as the basis for responding to the novel numeral:dot comparisons. The data therefore suggest that the monkeys had acquired knowledge about the absolute quantity of things represented by each Arabic numeral and could, even on probe trials, compare this represented quantity accurately with a visible array of dots.

Another possibility that must be noted is that performance reflected integration of two learned sequences instead of comparisons of quantity. Research has indicated that monkeys trained to order two lists of four arbitrary stimuli (e.g., A₁B₁C₁D₁ and A₂B₂C₂D₂) immediately respond correctly at a greater than chance level when presented with comparisons of two items from different lists (e.g., A₁-C₂ or B₁-D₂; D'Amato & Colombo, 1988; Terrace, Son, & Brannon, 2003). It is possible that the monkeys in this study perceived the numerals as one arbitrary list of stimuli and the dot quantities as another arbitrary list and ordered pairs of numerals and dots using only knowledge of their ordinal position. It is unlikely, however, that the differentially reinforced monkeys completely disregarded quantity information during the novel probe comparisons given that quantity information was readily available during training. We know that Hank did not represent the dot arrays as arbitrary stimuli in a list with no inherent order because he was able to solve novel numeral:dot probe trials, despite the fact that some dot pairs were withheld during training so he had no opportunity to learn the complete order of dot quantities by trial-and-error.

In fact, the use of pairwise comparisons leaves open the question of whether any of the monkeys learned a complete ordered list of numerals or dot quantities. Knowing that 8 > 7 and 7 > 6 is not the same as knowing that 8 > 7 > 6. Subsequent studies have produced mixed findings pertaining to the formation of an ordered list on the basis of pairwise comparison training. When 2 of the monkeys in this study were subsequently trained to respond to an array of Arabic numerals in descending order and an array of colored squares in a stable order determined by the experimenter, they showed no advantage when learning to order the Arabic numerals, which suggests that they had no previous representation of Arabic numerals as an ordered list (Harris, Beran, et al., 2007). In another study, however, capuchin and rhesus monkeys from our laboratory were presented with random pairings of the Arabic numerals 0 through 9 and learned to choose the larger numeral when rewarded with one pellet for each correct choice. The monkeys were subsequently presented with arrays of five familiar numerals and arrays of five novel letters, and both species performed better with the numerals. This indicates that they had learned a sequence of numerals during the pairwise comparison training despite the lack of quantity information (Beran et al., 2008). Regardless of the exact nature of the knowledge used in the current task, the monkeys were able to compare novel numerals and dot quantities only on the basis of information acquired during training with randomly presented pairwise comparisons.

Overall, the data from this experiment provide insight regarding what the monkeys know about the numeric symbols with which they have experience. It appears that the numeral 4 does not simply mean “greater than 3 and less than 5” or “better than 3 and not as good as 5” but rather represents a quantity that can be compared directly and accurately with visible arrays of analog stimuli. However, it is important to note that performance suffered when the numerical distance between the numeral and dot quantity was small, which suggests that any quantity information was approximate rather than exact.

Experiment 2: Do Monkeys Know, for Example, That “4” Means Four Actions?

The monkeys in the sequential study by Harris and Washburn (2005) that was discussed in the introduction were clearly using the numeral values to alter their behavior on a sequence of maze trials. They solved nonreinforced trials more slowly than reinforced trials. They could have produced this effect in the way suggested by Harris and Washburn, by solving the maze slowly in anticipation of a lack of reward when the number of reinforced trials performed matched the value of the target numeral. However, they could also have accomplished this by performing more slowly on each successive trial (without keeping track of the number of reinforced trials or even knowing the cardinal value of the target number) and resetting back to rapid responding after the nonreinforced trial. Indeed, 2 monkeys appeared to do this. It is important to note that even if this was the strategy, the monkeys were still using the numeral values to adjust performance speeds differentially, so that the slope of successive slowing was steeper when the target number was 3 than when it was 5.

The results of the Harris and Washburn (2005) study indicated the need for an alternative procedure that allowed a monkey to solve a maze a specified number of times and then behaviorally indicate “I'm done.” We reasoned that by placing two target numerals in the maze, a monkey could travel to the larger number the corresponding number of times and then indicate that he knew he had exhausted the pellets at this location by traveling to the smaller number. In contrast, if the monkeys know only ordinal and not absolute values corresponding to the numerals, then the animals have no basis for knowing when to stop responding to the larger of the two numerals and move to the smaller stimulus.

Method

Subjects

Four rhesus monkeys were available to be tested in this experiment. The animals (Hank, Gale, Willie, and Murph) had previously been trained to select between visual arrays or Arabic numerals and had participated in some of the experiments discussed earlier. All were familiar with moving a cursor through a two-dimensional maze (Harris & Washburn, 2005; Harris, Washburn, Beran, & Sevcik, 2007), although none had seen the task with two Arabic-numeral targets before this study.

Task

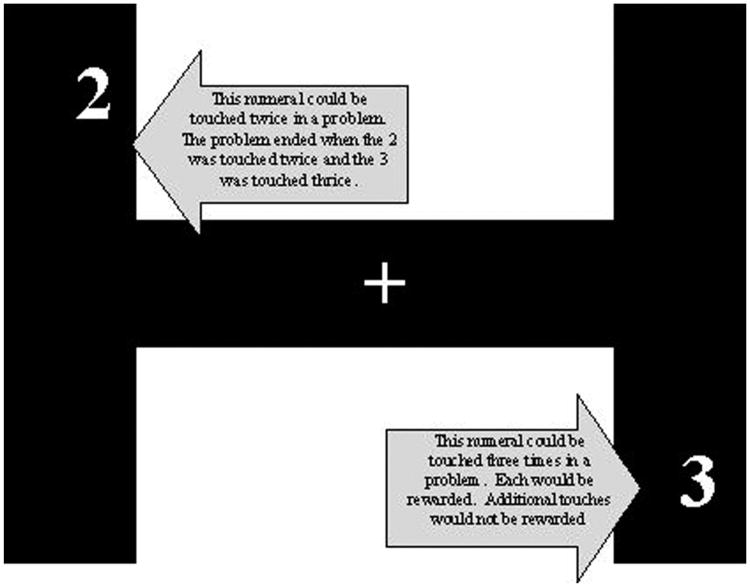
Each trial began with a white plus-sign cursor (measuring 1.25 cm × 1.25 cm) presented midscreen against a black background. White rectangles were displayed on the screen to form a basic two-dimensional H-maze (see Figure 1). Two randomly selected Arabic numerals were presented in two terminus points of the maze, equidistant from the cursor. For each trial within a problem, these numeral positions remained constant. Each numeral was “baited” with the corresponding number of pellets. Moving the cursor into contact with either numeral resulted in the delivery of a pellet, unless the monkey had already earned the corresponding number of pellets for that problem (e.g., a 4 would only be reinforced four times in a problem). Pellet delivery was accompanied by a short beep, and the cursor immediately reset to the center of the screen in preparation for the next trial. Additional responses to a numeral were scored as errors. When the monkeys made an error, they received a negative buzzing sound and the cursor reset to the center of the screen. The monkey could make as many errors as needed to obtain all the pellets for each problem. The problem ended automatically when all of the pellets that could be obtained had been earned. The end of a problem was signaled by a melodic tone and a 30-s interval before the beginning of the next problem. New numerals and random positions for the numerals were generated for each new problem.

Figure 1.

Example of the type of display used in Experiment 2 (the arrows and annotations within the arrows did not appear on the monkeys' screens).

Procedure

Gale and Hank were trained for 200 problems in which the target numerals were always 2 and 3. Between problems, the location of the numerals was changed randomly. For each of these 200 problems, an ideal solution was to move the cursor through the maze to the 3 on three (and only three) trials and to the 2 on two (and only two) trials. Note that nothing constrained the monkeys to select the numerals in this order (i.e., touching the 2 twice and then the 3 thrice would also have been errorless performance, as would other combinations of responses that did not involve moving to a numeral more times than its value). After these 200 problems, a transfer phase began in which another numeral (1 to 6) was introduced every 50 problems. For example, the Arabic numerals on Gale's Problems 201–250 were 2, 3, or 5 and for Hank they were 2, 3, or 4.

We used an identical procedure for Willie and Murph, except that their first 200 training problems used 2 and 4 as targets. As with Hank and Gale, an additional numeral was selected at random every 50 problems to be included in the stimulus pool.

Results

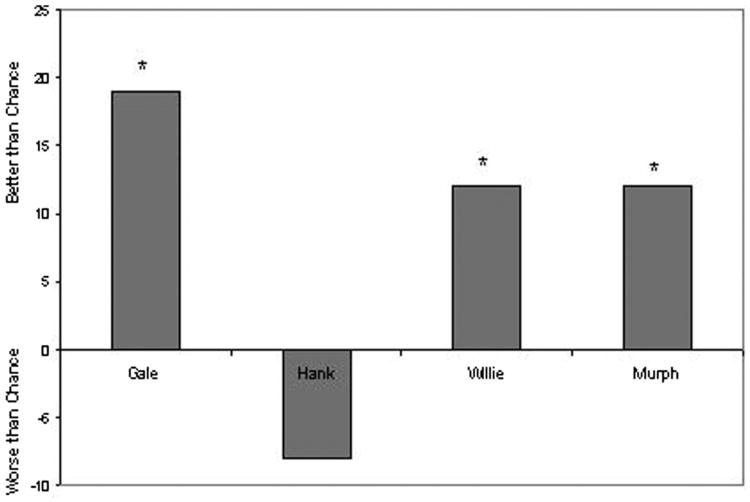
All 4 monkeys learned to correctly complete problems during the initial training period. Gale completed 40% of the training problems without error (i.e., without visiting a numeral more times than its value), Murph and Willie completed 41% without error, and Hank completed 48% without error. Of the 4 monkeys, 3 generalized to new numerals when they were added to the sequence. Figure 2 shows the percentage of problems completed without error compared with chance level during the transfer phase. We computed chance level separately for each monkey using a computer simulation because each monkey received a different pairings of numerals. Gale, Willie, and Murph performed significantly better than chance across target–numeral pairings (p < .05, binomial test).

Figure 2.

Percentage of problems completed without error compared with chance level in the transfer phase of Experiment 2. * Performance was significantly better than chance, p < .05.

Hank showed a different pattern. During the initial training problems, he developed the strategy of alternating between the target numerals, starting with the larger numeral. That is, he learned that he could touch the 3, 2, 3, 2, 3, in sequence to end each trial without error. Of course, this was a perfectly acceptable strategy, but one that would not work when most other combinations of numerals were used as targets. Consequently, Hank's performance was statistically at chance levels on the test trials.

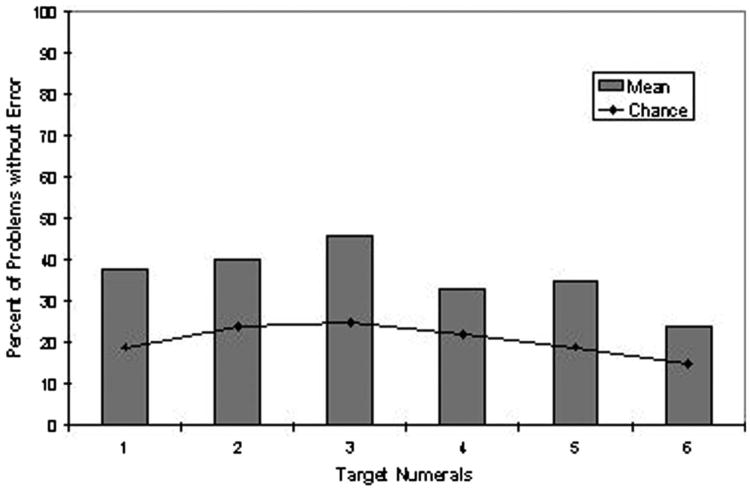
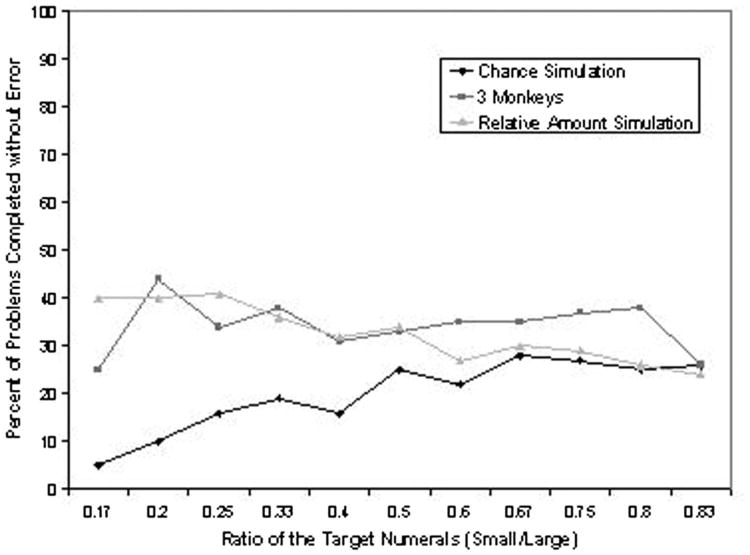
Examining the data for the other 3 monkeys, trials without error were seen at levels in excess of chance across target numerals and target–numeral ratios. Figure 3 depicts average performance across target numerals, and Figure 4 depicts average performance across target–numeral ratios. Note that performance was essentially stable across ratios—consistently above and showing a different distribution than chance levels (as determined by computer simulation). Performance was significantly better than chance (p < .01) at every ratio except 0.67 and 0.83 (each p > .10). Observed behavior was better simulated by an algorithm that selected numerals in proportion to their relative magnitudes (i.e., to be twice as likely to select 4 rather than 2 when they were paired together) versus having a .50 chance of selecting each numeral. However, even this simulation failed to capture the level of errorless trials that was observed with target:target ratios of 0.6 and greater. The monkeys performed significantly better than the relative-amount simulation for the target pairings 5:3, 4:3, and 5:4 (p < .05). The monkeys' performance on these problems required knowledge beyond the relative magnitudes of the numerals.

Figure 3.

Percentage of problems completed without error that included a given target numeral for Gale, Willie, and Murph in the transfer phase of Experiment 2.

Figure 4.

Percentage of problems completed without error by ratio (small–large target numerals) for Gale, Willie, and Murph in the transfer phase of Experiment 2 compared with computer simulations of chance performance and a strategy based on relative amount.

To determine how the monkeys solved these problems, we examined the pattern of responding and found several patterns that the monkeys routinely used in this task. Some of the problems were solved with a pattern we labeled as the numeral pattern. This pattern involved clearing out the bigger numeral first before moving to the smaller numeral. For example, if the problem contained a numeral 2 and a numeral 3, the monkeys would contact the 3 on three consecutive trials before contacting the 2 on the last two trials.

Other problems were solved with a pattern we labeled the pellet pattern. This pattern involved contacting the numeral with the greater number of remaining pellets on every trial in a problem. For example, when presented with a 2 and a 4, a monkey following the pellet pattern would touch 4, 4, 4, 2, 2, 4, in that order. After contacting the 4 on three trials, the numeral 2 would have more remaining pellets (one pellet for the 4 and two for the 2), so the monkey would switch to the numeral 2. After contacting the numeral 2 twice, the numeral 4 would have more remaining pellets (one pellet for the 4 and zero for the 2), so the monkey would switch back to the 4 to finish the problem. We must note, however, that the same pattern for the numerals 2 and 4 could be obtained using a slightly different rationale. The monkey could attempt to clear out the numeral 4 first, but move prematurely to the 2. If he knew that he had exhausted the pellets at the 2 and the problem did not end, he could then move back to the 4 and retrieve the last pellet. This would produce the same pattern as choosing the numeral with the larger number of pellets on every trial. This rationale, however, would not produce the same behavior as the pellet pattern for other pairings, such as 4 and 3.

The alternating pattern was scored as a special case of the pellet pattern. In the alternating pattern, the monkeys started with the larger numeral and alternated between the two numerals on each response until the pellets had been exhausted. So if they were presented with a 3 and a 2 they would touch 3, 2, 3, 2, 3, in that order. Note that this response pattern would never produce an errorless trial when the target numerals differed by more than one (e.g., 5 and 3). Note also that for correct alternating-pattern responses, the outcome is also consistent with what would be expected for the pellet pattern (i.e., the monkey never goes to a numeral associated with the lesser remaining number of pellets). Finally, problems in which the smaller number was cleared first (e.g., 1, 2, 2) or there was no predictable pattern were labeled other pattern.

We determined the proportion of errorless trials as a function of response pattern for Gale, Willie, and Murph. The proportion was approximately 5% for the numeral pattern, 20% for the pellet pattern, 20% for the alternating pattern, and 55% for the other pattern. We then computed how often the monkeys' behavior would conform to these patterns by chance, given the numeral pairings that were used in the study. We used a computer simulation to perform this calculation.

Simulations were conducted by creating a computer program that responded to the same kinds of problems the monkeys saw. That is, we simulated the choices between numerals, not the maze-running itself. The simulation chose randomly between the two numerals available in the problem. Responding continued in this way until the trial was completed (i.e., until each numeral had been selected the corresponding number of times). Errors were calculated for the computer in the same way as they were operationalized for the monkeys (e.g., choosing the 4 more than four times in a problem). The computer was tested with blocks of problems, as was done with the monkeys; however, for purposes of generating the normal distribution, at least 10,000 blocks of trials were simulated for each possible pairing of numerals (1 to 6). One million trials were simulated in total.

After each block of problems, we calculated the proportion of trials completed without error, producing a sampling distribution of errorless trials that could be expected by chance alone. Each simulated errorless trial was also scored according to whether it matched the pellet pattern (including its variation, the alternating pattern) described earlier. In this way, we obtained statistical estimates of the likelihood by chance alone of selecting the numeral associated with the larger number of pellets on every trial (response) of a problem. Of course, the probability of this pattern of responses varied as a function of the numeral pairing. For 2:1 problems, two-thirds of the problems fit this pattern (i.e., only by selecting the 1 on the first response could a trial be completed without error and without following the pellet pattern). By comparison, only 7% of the errorless 6:5 trials fit this pattern by chance alone.

We analyzed only the correct problems to provide a conservative estimate of chance against which to compare our monkeys' performance. Responding according to the pellet or numeral strategies occurs relatively infrequently by chance alone in the correct problems and can never occur, by definition, on the incorrect problems. A monkey that makes an error on a problem must have responded at one point to a numeral with zero pellets remaining, and thus by definition the probability of pellet and numeral patterns on incorrect problems equals 0.0. The proportion of all trials (correct and incorrect) that followed the pellet or numeral strategies by chance alone would have been much lower than the proportion of correct trials that followed these strategies by chance alone.

Overall, only 20% of the trials that were completed without error by the computer simulation matched the pellet pattern. The 40% of errorless trials performed by the monkeys that actually fell into this category significantly exceeded the 20% chance level determined by the computer simulation (p < .05). This suggests that the monkeys were purposefully using this pattern to facilitate performance and not just behaving at random with some of their behavior conforming to the pellet pattern by chance.

No other strategy was observed at levels in excess of chance. Analysis revealed that 8% of the simulated trials fit the numeral pattern (e.g., 5, 5, 5, 5, 5, 2, 2), which is a number statistically identical to the 5% the monkeys produced (p > .10). Errorless responses that fit the alternating pattern (e.g., 2, 1, 2) alone were even less probable by chance (3%), but the monkeys did not produce this subset of the pellet pattern at levels significantly in excess of chance (p = .06). Recall that the alternating variant of the pellet pattern could only produce errorless performance on five numeral pairings (1:2, 2:3, 3:4, 4:5, and 5:6).

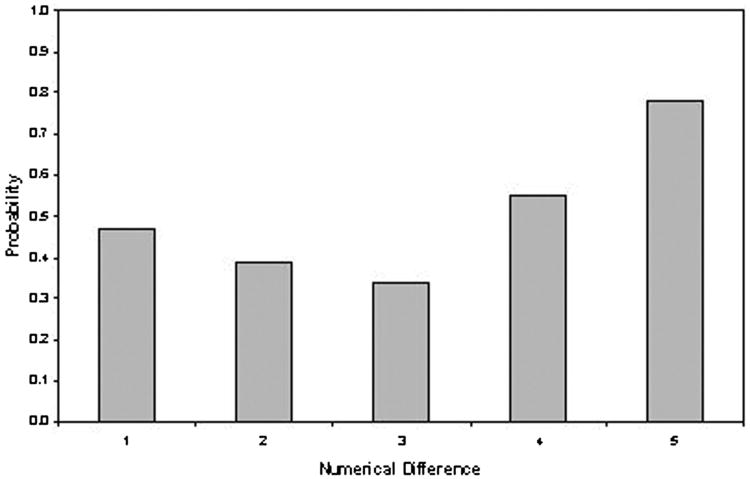
To further understand the monkeys' behavior, we examined descriptive data on the distribution of observed errors. Specifically, we examined error patterns as a function of the difference between the numerals. Results revealed that the first error was more likely to result from contact with the larger numeral when the distance between the two numerals was large (see Figure 5). These results are based on different patterns of responding for the different pairs of numerals. When the numbers differed by a value of one, the monkeys tended to alternate unpredictably between the numerals so the error could occur on either numeral. However, when the numerals differed by a larger amount, the monkeys tended to try and clear out the larger numeral first before moving to the smaller numeral, which led to more errors on the larger numeral.

Figure 5.

Probability that the first error was a result of contact with the larger numeral, as a function of the difference between the two numerals in the transfer phase of Experiment 2.

Discussion

Of the four monkeys, three performed better than chance, and better than would be expected if they knew only the relative magnitudes of the numerals. The pattern of responding indicated that the monkeys learned strategies to simplify the task, such as choosing the numeral with the greater number of remaining pellets or alternating between the numerals, beginning with the larger. Correct execution of these strategies required knowledge beyond ordinality (which numeral is bigger) or even ratio (the relative magnitude of the difference in proportions). For instance, the pellet strategy was successful when the monkeys correctly judged the exact number of pellets separating the two numerals, and therefore switched from the larger numeral to the smaller numeral on the correct trial.

Despite these performance strategies, errorless problems were still the minority. On most trials, the monkeys touched a target more times than was represented by the numeral. Of course, the memory demands of this task were substantial, requiring a monkey not only to keep track of how many times he had touched a specific target, but potentially also to remember how many times he had touched the other target, and in any case to reset these representations for each new problem. Under these demands, it seems unreasonable to expect errorless performance on the vast majority of trials; still, our data do not compel a conclusion that the monkeys were enumerating responses toward some exact and absolute quantity (e.g., move to the 3 exactly three times). Instead, the results indicate that the monkeys had an understanding of the approximate values represented by the numerals.

General Discussion

Over the past 2 decades, researchers have provided clear evidence that nonhuman primates can use Arabic numerals to perform a variety of tasks (e.g., Beran & Rumbaugh, 2001; Biro & Matsuzawa, 2001; Boysen & Berntson, 1989, 1995; Matsuzawa, 1985; Murofushi, 1997; Olthof et al., 1997; Rumbaugh et al., 1989; Washburn & Rumbaugh, 1991). Despite these impressive displays of numerical competence, it is difficult to ascertain exactly what numerals represent to these primates. When adult humans look at the Arabic numeral 4 they understand several things about that numeral. They understand that the numeral 4 is larger than the numeral 3 and smaller than the numeral 5 and that it symbolizes the quantity four. They also understand that the numeral 4 is an even number that can be divided by the numeral 2 with no remainder. Obviously, we do not expect the monkeys to understand the concept of even numbers or the operation of division, but it is possible that they understand the order of numerals (their ordinal value) and that the numerals represent specific quantities (their cardinal value). It is also possible that the monkeys do not understand the order of the numerals or the quantities associated with them, but instead respond to the numerals on the basis of a complex matrix of memorized response patterns (e.g., pick the numeral 7 when presented with 6, not when presented with 8) or their hedonic value. The results of the two current studies provided us with a clearer picture of what Arabic numerals mean to the rhesus macaques in our laboratory.

In Experiment 1, the monkeys accurately compared Arabic numerals and analog dot arrays, even on the first exposure to these trials. This indicates that the monkeys were not relying on a complex matrix of learned discriminations. Additionally, the data from Hank suggest that the monkeys were not solving the comparisons only on the basis of the hedonic value of the numerals. Although Hank was reinforced proportionally for numerals but not for dot displays, his responses to the last half of the novel numeral: dot probes were similar to the responses of the other monkeys, even when numerical value opposed hedonic value. For example, Hank was able to correctly respond to a comparison of four dots and the numeral 3, despite the fact that the numeral 3 had a much richer reinforcement history. The results also indicated that Hank did not base his responses on the probability of reward. He responded correctly on the majority of trials in which an array of five dots was paired with a larger array or numeral, even though he had always been reinforced for choosing arrays of five dots during training. The fact that the monkeys were not responding to numerical pairs on the basis of a complex matrix of memorized responses or hedonic values suggests that these monkeys understood that the Arabic numerals represented absolute values that could be ordered and compared on a relative basis.

Although the results of Experiment 1 suggest that the monkeys were using quantity information to make comparisons between numerals and dot quantities, the quantity information appears to be approximate rather than exact. Performance suffered when the numerical distance between the numeral and dot quantity was small, which is a hallmark of the analog magnitude model of numerical ability (e.g., Brannon & Roitman, 2003; Gibbon, 1977; Meck & Church, 1983). According to this model, numerical performance is based on a continuous representation of magnitude rather a representation of the exact number of items in a set. Memory for the magnitudes associated with each numeral is imperfect, so it is more difficult to compare numerals that are close in distance than numerals that are far apart (Dehaene, 1992, 2003; Gallistel & Gelman, 1992, 2000; Whalen, Gallistel, & Gelman, 1999). This model has been used by a number of researchers to explain animal numerical behavior in studies involving analog stimuli (e.g., Beran, 2001, 2004; Beran & Rumbaugh, 2001; Nieder & Miller, 2004).

The results of Experiment 2 provide additional information on the representations underlying the monkeys' use of Arabic numerals. Of the 4 monkeys, 3 performed better than chance in a task requiring them to make a number of responses equaling an Arabic numeral. However, on most trials, the monkeys touched a target more times than was represented by the numeral. These data, like the data from Experiment 1, suggest that the monkeys had some understanding of the quantity symbolized by the numerals, but were not representing that quantity precisely. In other words, the monkeys were not enumerating exactly three responses to the numeral 3, but were instead responding in a more approximate manner. Overall, these two studies provide evidence that the rhesus macaques in our laboratory understand the relative values of Arabic numerals and can use this knowledge to compare two numerals. These monkeys also understand that Arabic numerals represent approximate quantity information and can use that information to compare numerals with analog stimuli and to perform a task requiring the enumeration of sequential responses.

Although these numerical abilities are impressive, it is clear that the monkeys do not have a humanlike understanding of numerals. Humans use number words and symbols to move beyond the realm of approximation and communicate the precise numerical values required for formal mathematics. The monkeys in this study understood the order of the numerals and could use them to facilitate responding in tasks requiring knowledge of quantity information. In contrast to humans, however, they behaved as if the representations underlying the Arabic numerals were fuzzy approximations of true set size rather than precise quantities. Therefore, what seems to distinguish the symbolic numerical competence of monkeys from that of humans is the representation of exact set sizes across a large range of quantities. Only humans need the exactness of representing numbers such as 9, 13, 142, or even 4 for that matter.

Nonhuman animals may need to judge between small sets so that they can make important choices between things like four pieces of food and three pieces or two predators versus three, but even these judgments do not require exact numerical knowledge, just an ability to distinguish relative numerousness. In addition, perceptual dimensions of stimuli, such as density, surface area, configuration, and temporal pattern often naturally covary with number and can be used as a cue to responding. For example, crows that respond differentially to vocal messages that vary in the number of calls may be responding to the different temporal patterns of the call sequences rather than the number of calls (Thompson, 1968, 1969). Outside of laboratory tasks like the ones in this study, monkeys probably never need to know that there are exactly six predators or to distinguish 16 pieces of fruit from 18, for example. In those cases, reliance on perceptual features, relative numerousness judgments, or approximate representation of number provides all of the information necessary to aid decision making that increases survival odds. The present findings indicate that although nonhuman primates do not need to know absolute numerousness in the wild, they can learn symbols that represent such numerousness and use those symbols in a variety of different contexts.