Partitioning heritability by functional annotation using genome-wide association summary statistics

Abstract

Recent work has demonstrated that some functional categories of the genome contribute disproportionately to the heritability of complex diseases. Here, we analyze a broad set of functional elements, including cell-type-specific elements, to estimate their polygenic contributions to heritability in genome-wide association studies (GWAS) of 17 complex diseases and traits with an average sample size of 73,599. To enable this analysis, we introduce a new method, stratified LD score regression, for partitioning heritability from GWAS summary statistics while accounting for linked markers. This new method is computationally tractable at very large sample sizes, and leverages genome-wide information. Our results include a large enrichment of heritability in conserved regions across many traits; a very large immunological disease-specific enrichment of heritability in FANTOM5 enhancers; and many cell-type-specific enrichments including significant enrichment of central nervous system cell types in body mass index, age at menarche, educational attainment, and smoking behavior.

Introduction

In GWAS of complex traits, much of the heritability lies in single-nucleotide polymorphisms (SNPs) that do not reach genome-wide significance at current sample sizes [1, 2]. However, many current approaches that leverage functional information [3, 4] and GWAS data to inform disease biology use only SNPs in genome-wide significant loci [5–8], assume only one causal SNP per locus [9], or do not account for linkage disequilibrium (LD) [10]. We aim to improve power by estimating the proportion of genome-wide SNP-heritability [1] attributable to various functional categories, using information from all SNPs and explicitly modeling LD.

Previous work on partitioning SNP-heritability has used restricted maximum likelihood (REML) as implemented in GCTA [1, 11–14]. REML requires individual genotypes, but many of the largest GWAS analyses are conducted through meta-analysis of study-specific results, and so typically only summary statistics, not individual genotypes, are available for these studies. Even when individual genotypes are available, using REML to analyze multiple functional categories becomes computationally intractable at sample sizes in the tens of thousands. Here, we introduce a method for partitioning heritability, stratified LD score regression, that requires only GWAS summary statistics and LD information from an external reference panel that matches the population studied in the GWAS.

We apply our novel approach to 17 complex diseases and traits with an average sample size of 73,599. We first analyze non-cell-type-specific annotations and identify heritability enrichment in many of these functional annotations, including a large enrichment in conserved regions across many traits and a very large immunological disease-specific enrichment in FANTOM5 enhancers. We then analyze cell-type-specific annotations and identify many cell-type-specific heritability enrichments, including enrichment of central nervous system (CNS) cell types in body mass index, age at menarche, educational attainment, and smoking behavior.

Results

Overview of methods

Our method for partitioning heritability from summary statistics, called stratified LD score regression, relies on the fact that the χ² association statistic for a given SNP includes the effects of all SNPs that it tags [15,16]. Thus, for a polygenic trait, SNPs with high LD score will have higher χ² statistics on average than SNPs with low LD score [16]. This might be driven either by the higher likelihood of these SNPs to tag an individual large effect, or their ability to tag multiple weak effects. If we partition SNPs into functional categories with different contributions to heritability, then LD to a category that is enriched for heritability will increase the χ² statistic of a SNP more than LD to a category that does not contribute to heritability. Thus, our method determines that a category of SNPs is enriched for heritability if SNPs with high LD to that category have higher χ² statistics than SNPs with low LD to that category.

More precisely, under a polygenic model [1], the expected χ² statistic of SNP j is

$$E[{\chi }_j^2]=N{\mathrm{\sum }}_C{\tau }_C\ell (j,C)+Na+1$$ (1)

where N is sample size, C indexes categories, ℓ(j, C) is the LD score of SNP j with respect to category C (defined as $\ell (j,C)={\mathrm{\sum }}_{k\in C}{r}_{jk}^2$), a is a term that measures the contribution of confounding biases [16], and if the categories are disjoint, τ_C is the per-SNP heritability in category C; if the categories overlap, then the per-SNP heritability of SNP j is Σ_C:j∈C τ_C Equation (1) allows us to estimate τ_C via a (computationally simple) multiple regression of χ² against ℓ(j, C), for either a quantitative or case-control study. We define the enrichment of a category to be the proportion of SNP-heritability in the category divided by the proportion of SNPs. We estimate standard errors with a block jackknife [16], and use these standard errors to calculate z-scores, P-values, and FDRs. We have released open-source software implementing the method (URLs); for further details see the Online Methods and Supplementary Note.

To apply stratified LD score regression (or REML) we must first specify which categories we include in our model. We created a “full baseline model” from 24 publicly available main annotations that are not specific to any cell type (Supplementary Table 1; see URLS and Online Methods). Below, we show that including many categories in our model leads to more accurate estimates of enrichment. The 24 main annotations include: coding, UTR, promoter, and intron [14, 17]; histone marks H3K4me1, H3K4me3, H3K9ac [3–5] and two versions of H3K27ac [18, 19]; open chromatin reflected by DNase I hypersensitivity Site (DHS) regions [5, 14]; combined chromHMM/Segway predictions [20], which make use of many ENCODE annotations to produce a single partition of the genome into seven underlying “chromatin states”; regions that are conserved in mammals [21, 22]; super-enhancers, which are large clusters of highly active enhancers [19]; and enhancers with balanced bidirectional capped transcripts identified using cap analysis of gene expression in the FANTOM5 panel of samples, which we call FANTOM5 enhancers [23]. For the histone marks and other annotations that differ among cell types, we combined the different cell types into a single annotation for the full baseline model by taking a union (except for Repressed, where we took an intersection). To prevent our estimates from being biased upwards by enrichment in nearby regions [14], we also included 500bp windows around each functional category in the full baseline model, as well as 100bp windows around ChIP-seq peaks when appropriate (see Online Methods). This yielded a total of 53 (overlapping) functional categories in the full baseline model, including a category containing all SNPs.

In addition to the analyses using the full baseline model, we performed analyses using cell-type-specific annotations from the four histone marks H3K4me1, H3K4me3, H3K9ac, and H3K27ac. Each cell-type-specific annotation corresponds to a histone mark in a single cell type—for example, H3K27ac in liver cells—and there are 220 such annotations in total (Supplementary Table 2, Online Methods). When ranking these 220 cell-type-specific annotations, we want to control for overlap with the functional categories in the full baseline model, but not for overlap with the 219 other cell-type-specific annotations. Thus, we add these annotations individually to the baseline model, creating 220 separate models, each with 54 annotations. Then for a given phenotype, we run LD score regression once each on the 220 models and rank the cell-type-specific annotations by the P-value of the coefficient τ_C of the annotation in the corresponding analysis. This P-value tests whether the annotation contributes significantly to per-SNP heritability after controlling for the effects of the annotations in the full baseline model.

We also divided the 220 cell-type-specific annotations into 10 groups: adrenal/pancreas, CNS, cardiovascular, connective/bone, gastrointestinal, immune/hematopoietic, kidney, liver, skeletal muscle, and other. We took a union of cell-type-specific annotations within each group, resulting in 10 new cell-type group annotations (for example, SNPs with any of the four histone modifications in any CNS cell type). We then repeated the cell-type-specific analysis described above with these 10 cell-type groups instead of 220 cell-type-specific annotations.

Simulation results: power and lack of bias

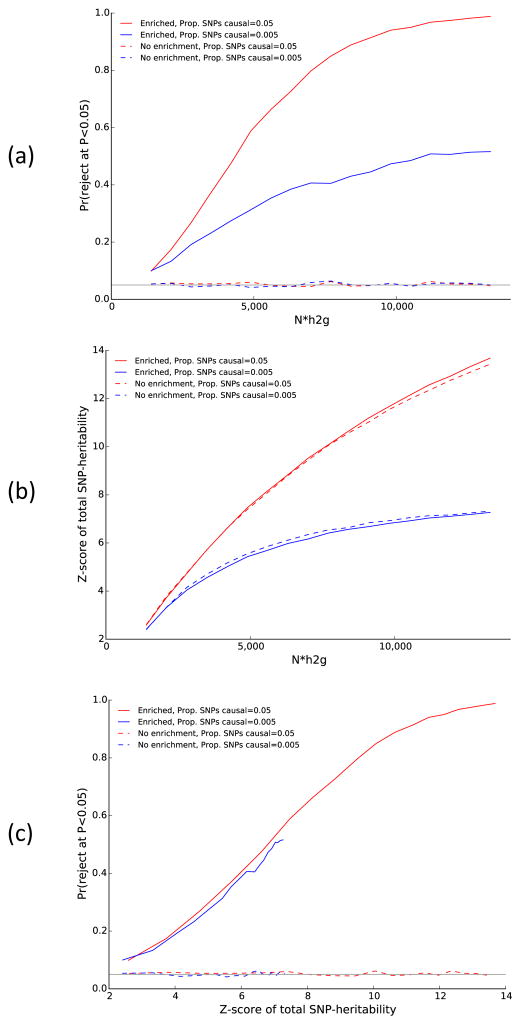
In our first set of simulations, we assessed the power and bias of the method at a variety of settings of SNP-heritability (h_g²), sample size (N), and proportion of causal SNPs (p_causal) (Online Methods). These simulations demonstrated well-calibrated type 1 error at all settings of h_g², N, and p_causal tested (Figure 1). At a fixed p_causal, power depends on N and h_g² only through N·h_g² (Supplementary Figure 1), and increases as N·h_g² increases and as p_causal increases (Figure 1a). We also looked at the z-score for total SNP-heritability in our analysis, which increases as N·h_g² and p_causal increase (Figure 1b). We found that the relationship of heritability z-score to power was the same for both values of p_causal (Figure 1c), indicating that the heritability z-score is a good indicator of power at a variety of sample sizes, heritabilities, and values of p_causal. For this paper, we chose to analyze only traits with a heritability z-score above 7, which corresponds to N·h_g² of roughly 4,500 for very polygenic traits and 12,500 for less polygenic traits.

Figure 1.

Simulation results: null calibration and power. We simulated genetic architectures with positive total SNP-heritability, with and without functional enrichment, for two values of p_causal and a range of values of N·h_g². (a) Proportion of simulations in which a null of no functional enrichment is rejected, as a function of N·h_g² and p_causal. (b) The z-score of total SNP-heritability depends on N·h_g² and p_causal, but does not depend on the presence or absence of functional enrichment. (c) Proportion of simulations in which a null of no functional enrichment is rejected, as a function of the z-score of total SNP-heritability. Here, the z-score of total SNP-heritability for p_causal = 0.005 did not exceed 7.3 even at maximum N·h_g².

In each of these simulations, stratified LD score regression gave unbiased estimates of heritability and of the heritability of the CNS cell-type group (Supplementary Figures 2a,b, 3a,b). While in theory the ratio of these two unbiased estimators could be a biased estimator of the proportion of heritability (and therefore the estimates that we report here), in practice we saw only negligible bias in our estimates of proportion of heritability (Supplementary Figures 2c, 3c). Using out-of-sample LD caused some downward attenuation bias in estimates of total SNP-heritability and heritability of the CNS cell-type group, but also gave unbiased estimates of proportion of heritability and properly calibrated type 1 error (Supplementary Figure 4).

Simulation results: model misspecification

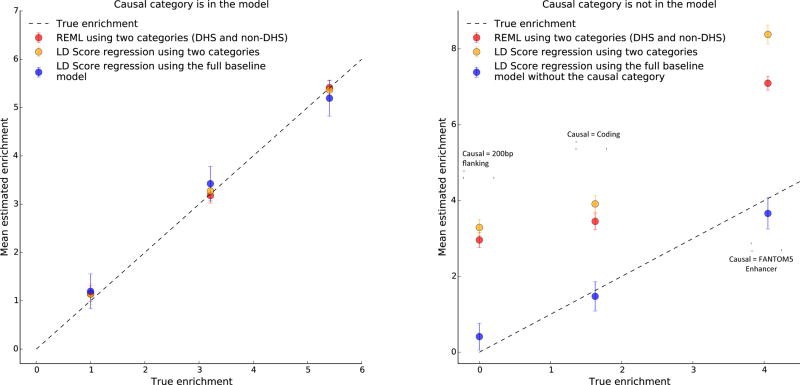
In our second set of simulations, we compared stratified LD score regression to REML, a method that also estimates partitioned heritability but requires genotype data, in scenarios with and without model misspecification (Online Methods). We estimated the enrichment of the DHS category, i.e., (Prop. h_g²)/(Prop. SNPs), using three methods: (1) REML with two categories (DHS/non-DHS), (2) stratified LD score regression with two categories (DHS/non-DHS), and (3) stratified LD score regression with the full baseline model (53 categories, described above). Since REML with 53 categories did not converge at this sample size and would be computationally intractable at sample sizes in the tens of thousands, we did not include it in our comparison; an advantage of stratified LD score regression is that it is possible to include a large number of categories in the underlying model. We report means and standard errors of the mean over 100 independent simulations.

We first performed three sets of simulations without model misspecification; i.e., where the causal pattern of enrichment was well modeled by the two-category (DHS/non-DHS) model. In these simulations, enrichment of the DHS region varied from 1x (i.e., no enrichment) to 5.5x (i.e., full enrichment, DHS SNPs explain 100% of heritability). All three methods gave unbiased estimates, although stratified LD score regression with the full baseline model had larger standard errors around the mean (Figure 2a).

Figure 2.

Simulation results: model misspecification. Enrichment is the proportion of heritability in DHS regions divided by the proportion of SNPs in DHS regions. Bars show 95% confidence intervals around the mean of 100 trials. (a) From left to right, the simulated genetic architectures are 1x DHS enrichment, 3x DHS enrichment, and 5.5x DHS enrichment (100% of heritability in DHS SNPs). (b) From left to right, the simulated genetic architectures are 200bp flanking regions causal, coding regions causal, and FANTOM5 Enhancer regions causal. For simulations with coding or FANTOM5 Enhancer as the causal category, we removed the causal category and the 500bp window around that category from the full baseline model in order to simulate enrichment in an unknown functional category.

Next, to explore the realistic scenario where the model used to estimate enrichment does not match the (unknown) causal model, we performed three sets of simulations where all causal SNPs were in a particular category, but the model used to estimate heritability did not include this causal category. The three sets of simulations were (1) all causal SNPs in coding regions, yielding a true 1.6x DHS enrichment due to coding/DHS overlap, (2) all causal SNPs in FANTOM5 enhancers, yielding a true 4.0x DHS enrichment due to FANTOM5 enhancer/DHS overlap, and (3) all causal SNPs in 200bp DHS flanking regions, yielding a true 0x DHS enrichment. For the coding and FANTOM5 enhancer causal simulations, we transformed the full baseline model into a misspecified model by removing the causal category and window around the causal category; the baseline model includes a 500bp window around DHS but not a 200bp window, and so is misspecified also in that case. Results from these simulations are displayed in Figure 2b. The two-category estimators were not robust to model misspecification and consistently over-estimated DHS enrichment by a wide margin. Stratified LD score regression with the full baseline model gave more accurate mean estimates of enrichment.

In summary, while these simulations include exaggerated patterns of enrichment (e.g., 100% of heritability in DHS flanking regions), the results highlight the possibility that two-category estimators of enrichment can yield incorrect conclusions. Although we cannot entirely rule out model misspecification as a source of bias for stratified LD score regression with the full baseline model, we have shown here that it is robust to a wide variety of patterns of enrichment, because including many categories gives it the flexibility to adapt to the unknown causal model.

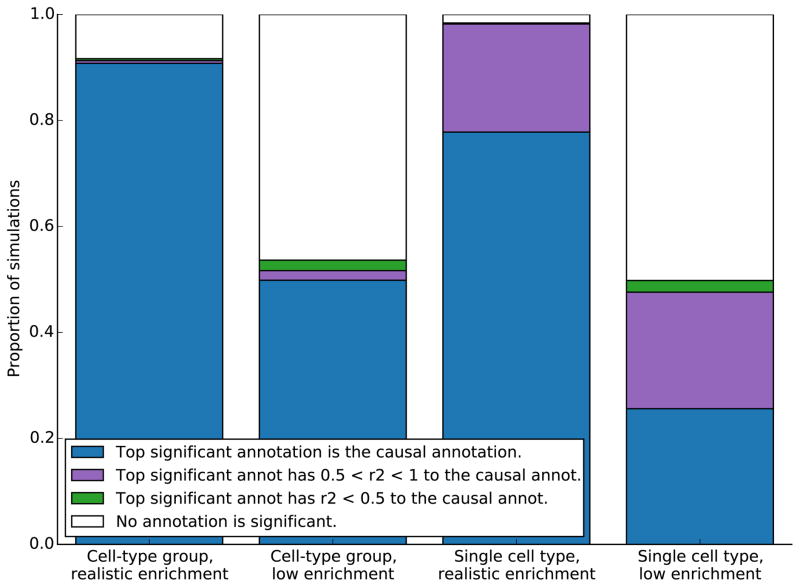
Simulation results: cell-type and cell-type group analyses

We simulated realistic baseline enrichment plus enrichment in a cell-type group (see Online Methods), and we performed our cell-type group analysis on the resulting summary statistics. First, we calibrated simulated enrichment of the causal cell-type group to give us a realistic average top −log₁₀(P) based on results for the real data sets analyzed below (Online Methods). Of the simulations in which at least one cell-type group reached significance, we found that the top cell-type group was the cell-type group simulated to be causal 99% of the time (Figure 3). Next, we simulated weaker enrichment, calibrated so that only 50% of replicates included a significant cell-type group. In these simulations, the cell-type group simulated to be causal was the top cell-type group in 95% of simulations with at least one significant cell-type group, and a cell-type group with r² > 0.5 to the causal group was the top cell-type group in half of the remaining simulations with at least one significant cell type (Figure 3). Results separated into the ten individual cell-type groups are displayed in Supplementary Figure 5.

Figure 3.

Simulation results for ranking cell-type groups and cell types. For each cell-type group, 500 simulations were performed with baseline enrichment and either realistic enrichment or low enrichment in that cell-type group. Results for the left two columns are aggregated over the ten cell-type groups; results for individual groups are displayed in Supplementary Figure 5. The right two columns represent 500 simulations each of realistic or low enrichment of a single cell-type-specific annotation, H3K4me3 in fetal brain cells.

We next repeated these simulations with a cell-type-specific mark—H3K4me3 in fetal brain cells—instead of a cell-type group as the simulated causal category. There are many more pairs of cell types that are highly correlated than there are highly correlated pairs of cell-type groups, and we are testing all cell types every time (Supplementary Figure S6). We found that when the level of enrichment was calibrated to give a realistic −log₁₀(P) (based on results for the real data sets analyzed below; Online Methods), the simulated causal cell type was the most significant cell type in 78% of simulations, a cell-type with r² > 0.5 to the causal cell type was most significant in 20% of simulations, and there was no significant cell type in 2% of simulations. In simulations with weak enrichment—again calibrating so that 50% of simulations have at least one significant cell type—we found that of the simulations with at least one significant cell type, only 4% had as the top cell type a cell type with r² < 0.5 to the causal cell type.

In conclusion, the cell-type group analysis reliably reports the causal annotation as the top annotation, if at least one cell-type group passes statistical significance. The analysis of individual cell types, because it is testing more cell types that are more correlated, often gives a highly correlated cell type as the top cell type—just as in a GWAS the top SNP in a locus is not always the causal SNP.

Analysis of 17 traits using the full baseline model

We applied stratified LD score regression to 17 diseases and quantitative traits: height, BMI, age at menarche, LDL levels, HDL levels, triglyceride levels, coronary artery disease, type 2 diabetes, fasting glucose levels, schizophrenia, bipolar disorder, anorexia, educational attainment, smoking behavior, rheumatoid arthritis, Crohn’s disease, and ulcerative colitis [18, 24–36] (Supplementary Table 3, URLS). This includes all traits with publicly available summary statistics with sufficient sample size, SNP-heritability, and polygenicity measured by the z-score of total SNP-heritability; specifically, we restricted to traits for which the z-score of total SNP-heritability was at least 7 (Supplementary Note). We removed the MHC region from all analyses, due to its unusual LD and genetic architecture.

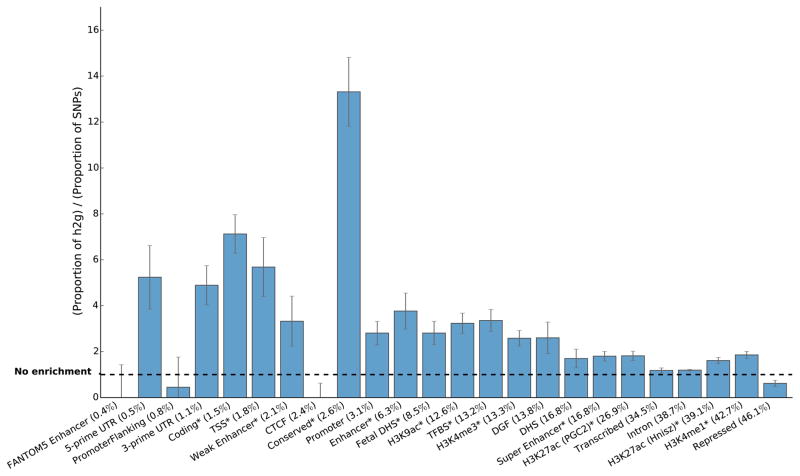
We applied stratified LD score regression with the full baseline model to the 17 traits. Figure 4 shows results for the 24 main functional annotations, averaged across nine independent traits (Supplementary Note). Figure 5 shows trait-specific results for selected annotations and traits (Supplementary Note). Supplementary Tables 4 and 5 show meta-analysis and trait-specific results for all traits and all 53 categories in the full baseline model.

Figure 4.

Enrichment estimates for the 24 main annotations, averaged over nine independent traits. Annotations are ordered by size. Error bars represent jackknife standard errors around the estimates of enrichment, and stars indicate significance at P < 0.05 after Bonferroni correction for 24 hypotheses tested. Negative point estimates, significance testing, and the choice of nine independent traits are discussed in the Online Methods and Supplementary Note.

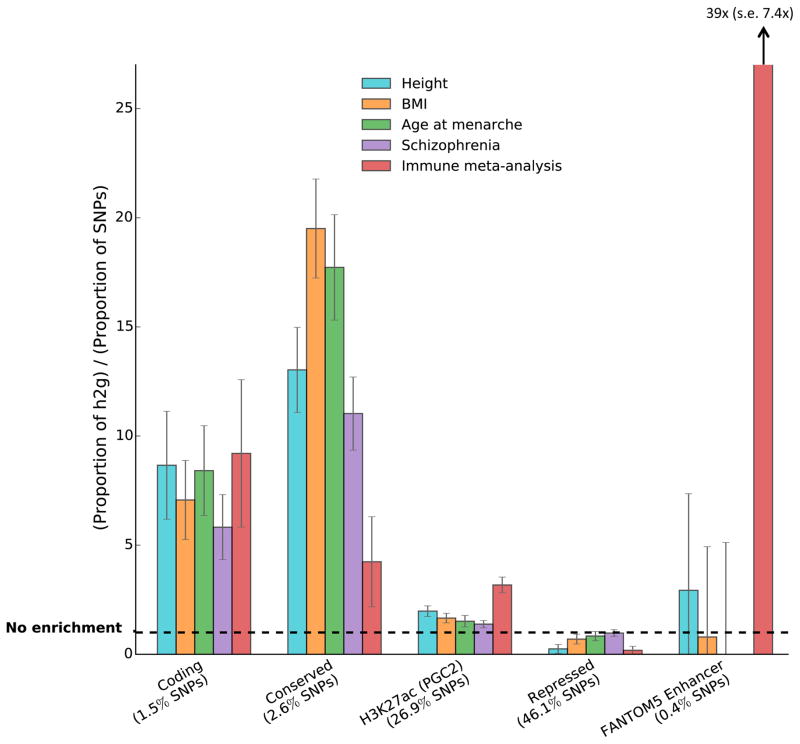
Figure 5.

Enrichment estimates for selected annotations and traits. Error bars represent jackknife standard errors around the estimates of enrichment.

We observed large and statistically significant enrichments for many functional categories. A few categories stood out in particular. First, regions conserved in mammals [21] showed the largest enrichment of any category, with 2.6% of SNPs explaining an estimated 35% of SNP-heritability on average across traits (P < 10⁻⁶ for enrichment). This is a significantly higher average enrichment than for coding regions, and provides evidence for the biological importance of conserved regions, despite the fact that the biochemical function of many conserved regions remains uncharacterized [37]. Second, FANTOM5 Enhancers [23] were extremely enriched in the three immunological diseases, with 0.4% of SNPs explaining an estimated 15% of SNP-heritability on average across these three diseases (P = 10⁻⁴, 2×10⁻⁴, and 0.03 for Crohn’s disease, Ulcerative Colitis, and Rheumatoid arthritis, respectively), but showed no evidence of enrichment for non-immunological traits (Figure 5). The immune-specific enrichment could be because immune cells have better coverage, altered degradation, and/or a higher number of enhancers. We did not see a large enrichment of super-enhancers vs. regular enhancers; the estimates for enrichment were 1.8x (s.e. 0.2) for super-enhancers vs. 1.6x (s.e. 0.1) for regular enhancers from the same paper [19] (denoted “H3K27ac (Hnisz)” in Figure 4). We also did not see increased cell-type-specificity in super-enhancers (Supplementary Note). This lack of enrichment supports the hypothesis that super-enhancers may not play a much more important role in regulating transcription than regular enhancers [38]. For many annotations, there was also enrichment in the 500bp flanking regions (Supplementary Table 4); this could be because the boundaries are not well defined, because the boundaries of the regions are different in different individuals, or because unknown regulatory elements often appear close to known regulatory elements. Analyses stratified by derived allele frequency produced broadly similar results (Supplementary Table 6; see Online Methods).

Cell-type-specific analysis of 17 traits

We performed two different cell-type-specific analyses: an analysis of 220 individual cell-type-specific annotations, and an analysis of 10 cell-type groups (see Overview of Methods). For the analysis of single cell types, we assessed statistical significance at the 0.05 level after Bonferroni correction for 220×17=3,740 hypotheses tested, and for the cell-type group analysis, we corrected for 10×17=170 hypotheses tested. This is conservative, since the 220 cell-type-specific annotations are not independent, and neither are the 10 cell-type group annotations. We also report results with false discovery rate (FDR) < 0.05, computed over 220 cell types for each trait for the cell-type specific analysis, and over all cell-type groups and traits for the cell-type group analysis. For 15 of the 17 traits, the top cell type passed an FDR threshold of 0.05, while for 16 of the 17 traits (all traits except anorexia), the top cell-type group passed an FDR threshold of 0.05. The top cell type for each trait is displayed in Table 1, with additional top cell types reported in Supplementary Table 7. Cell-type group results for the 11 traits with the most significant enrichments (after pruning closely related traits) are shown in Figure 6, with remaining traits in Supplementary Figure 7.

Table 1.

Enrichment of individual cell types. We report the cell type with the lowest P-value for each trait analyzed.

Phenotype	Cell type	Tissue	Mark	-log10(P)
Height	Chondregenic dif**	Bone	H3K27ac	6.81
BMI	Fetal brain*	Fetal brain	H3K4me3	4.48
Age at menarche	Fetal brain**	Fetal brain	H3K4me3	12.25
LDL	Liver*	Liver	H3K4me1	4.76
HDL	Liver*	Liver	H3K4me1	4.51
Triglycerides	Liver*	Liver	H3K4me1	3.99
Coronary artery disease	Adipose nuclei*	Adipose	H3K4me1	4.21
Type 2 diabetes	Pancreatic islets	Pancreas	H3K4me3	2.87
Fasting glucose	Pancreatic islets*	Pancreas	H3K27ac	3.93
Schizophrenia	Fetal brain**	Fetal brain	H3K4me3	18.51
Bipolar disorder	Mid frontal lobe*	Brain	H3K27ac	4.42
Anorexia	Angular gyrus	Brain	H3K9ac	2.61
Years of education	Angular gyrus**	Brain	H3K4me3	6.63
Ever smoked	Inferior temporal lobe*	Brain	H3K4me3	3.21
Rheumatoid arthritis	CD4+ CD25− IL17+ stim Th17**	Immune	H3K4me1	6.76
Crohn’s disease	CD4+ CD25− IL17+ stim Th17**	Immune	H3K4me1	7.59
Ulcerative colitis	CD4+ CD25− IL17+ stim Th17**	Immune	H3K4me1	6.37

^*denotes FDR < 0.05.

^**denotes significant at P < 0.05 after Bonferroni correction for multiple hypotheses. Sample sizes are in Supplementary Table 3.

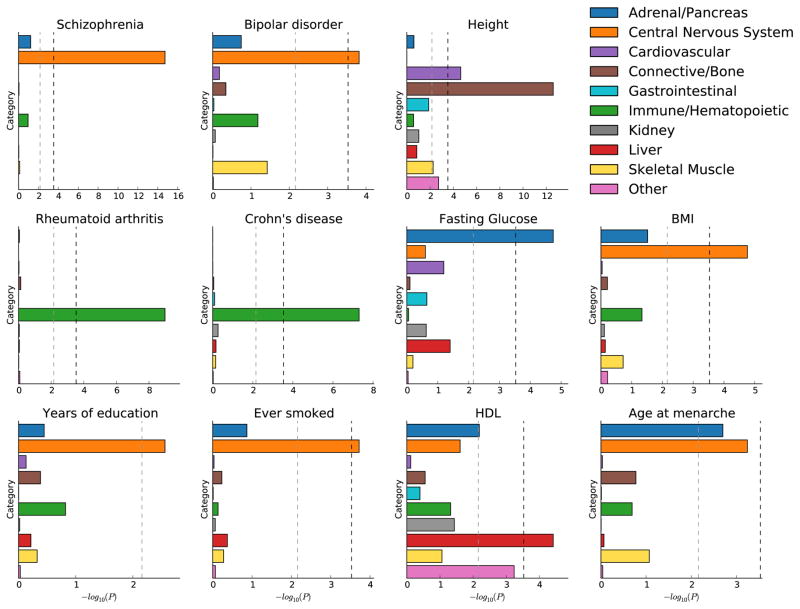
Figure 6.

Enrichment of cell-type groups. We report significance of enrichment for each of 10 cell-type groups, for each of 11 traits. The black dotted line at −log₁₀(P) = 3.5 is the cutoff for Bonferroni significance. The grey dotted line at −log₁₀(P) = 2.1 is the cutoff for FDR < 0.05. For HDL, three of the top individual cell types are adipose nuclei, which explains the enrichment of the “Other” category.

These two analyses are generally concordant, and show highly trait-specific patterns of cell-type enrichment. They also recapitulate several well-known findings. For example, the top cell type for each of the three lipid traits is liver (FDR < 0.05 for all three traits). For both type 2 diabetes and fasting glucose, the top cell type is pancreatic islets (FDR < 0.05 for fasting glucose but not type 2 diabetes). For the three psychiatric traits, the top cell type is a brain cell type and the top cell-type group is CNS (FDR < 0.05 for schizophrenia and bipolar disorder but not for anorexia). These results are concordant with the medical literature [39, 40] and with previous analysis of these GWAS datasets [9, 18, 27, 31, 41, 42].

There are also several new insights among these results. For example, the three immunological disorders show patterns of enrichment that reflect biological differences among the three disorders. Crohn’s disease has 40 cell types with FDR < 0.05, of which 39 are immune cell types and one (colonic mucosa) is a GI cell type. On the other hand, the 39 cell types with FDR < 0.05 for ulcerative colitis include nine GI cell types in addition to 30 immune cell types, whereas all 39 cell types with FDR < 0.05 for rheumatoid arthritis are immune cell types. The top cell type for all three traits is CD4+ CD25- IL17+ PMA Ionomycin simulated Th17 primary. Th17 cells are thought to act in opposition to Treg cells, which have been shown to suppress immune activity and whose malfunction has been associated with immunological disorders [43].

We also identified several non-psychiatric phenotypes with enrichments in brain cell types. For both BMI and age at menarche, cell types in the central nervous system (CNS) ranked highest among individual cell types, and the top cell-type group was CNS, all with FDR < 0.05. These enrichments support previous human and animal studies that propose a strong neural basis for the regulation of energy homeostasis [44]. For educational attainment, the top cell-type group is CNS (FDR < 0.05) and of the ten cell types that are significant after multiple testing, nine are CNS cell types. This is consistent with our understanding that the genetic component of educational attainment, which excludes environmental factors and population structure, is highly correlated with IQ [45]. Finally, for smoking behavior, the CNS cell-type group is significant and the top cell type is again a brain cell type, likely reflecting CNS involvement in nicotine processing.

Discussion

We developed a new statistical method, stratified LD score regression, for identifying functional enrichment from GWAS summary statistics that uses genome-wide information from all SNPs and explicitly models LD. We applied this method to summary statistics from 17 traits with an average sample size of 73,599. Our method identified strong enrichment for conserved regions across all traits, and immunological disease-specific enrichment for FANTOM5 enhancers. Our cell-type-specific enrichment results confirmed previously known enrichments, such as liver enrichment for HDL levels and pancreatic islet enrichment for fasting glucose. In addition, we identified enrichments that would have been challenging to detect using existing methods, such as CNS enrichment for smoking behavior and educational attainment—traits with only one and three genome-wide significant loci, respectively [33, 34]. Stratified LD score regression represents a significant departure from previous methods that require raw genotypes [11], use only SNPs in genome-wide significant loci [5–8], assume only one causal SNP per locus [9], or do not account for LD [10] (see Online Methods and Figure 7 for a discussion of other methods and comparison on simulated data). Our method is also computationally efficient, despite the 53 overlapping functional categories analyzed.

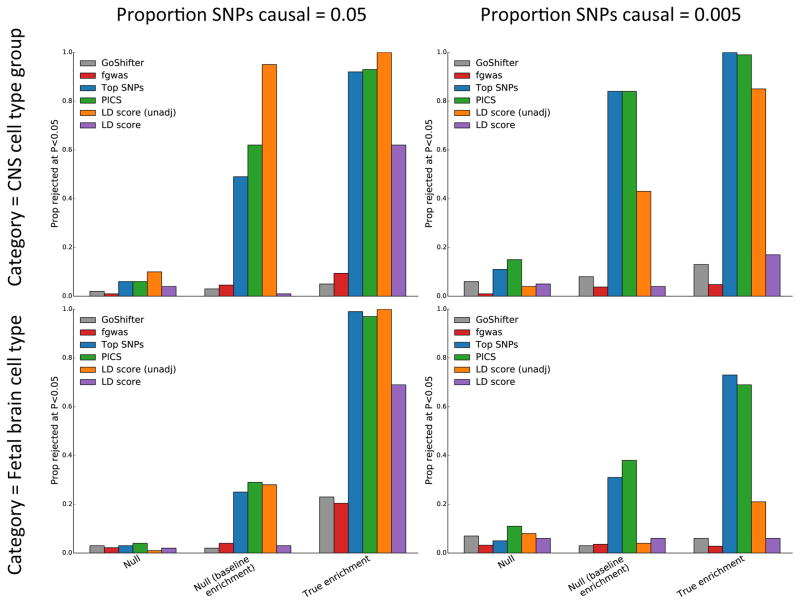
Figure 7.

Comparison to other methods for identifying enriched cell types. In “Null” simulations, there is no enrichment. In “Null (baseline enrichment)” simulations, there is enrichment in the baseline categories, some of which overlap the cell type or cell-type group, but no additional enrichment in the cell type or cell-type group. In the “True enrichment” simulations, there is enrichment in either the CNS cell-type group (top panels) or the fetal brain cell type (bottom babels). In all simulations, N = 14000, h_g² = 0.7. We report the proportion of 100 simulations in which the null is rejected by six methods: GoShifter [6], fgwas [9], Top SNPs [10], PICS [7], stratified LD score (unadjusted), and LD score. LD score (unadj) refers to total unadjusted enrichment, i.e., (Prop. h_g²)/(Prop. SNPs); LD score refers to the coefficient β of the category, controlling for all other categories in the model.

Although our polygenic approach has enabled a powerful analysis of genome-wide summary statistics, it has several limitations. First, for the method to have reasonable power, the dataset analyzed must have a very large sample size and/or large SNP-heritability, and the trait analyzed must be polygenic (Figure 1). Second, the method requires an LD reference panel matched to the population studied to give accurate results; all results here are from European datasets and use 1000G Europeans as a reference panel (see Online Methods and Supplementary Figure 4). Third, our method is currently not applicable to studies using custom genotyping arrays (e.g., Metabochip; see Supplementary Note). Fourth, our method is based on an additive model and does not consider the contribution of epistatic or other non-additive effects, nor does it model causal contributions of SNPs not in the reference panel; in particular, it is possible that patterns of enrichment at extremely rare variants may be different from those inferred using this method (see Online Methods). Fifth, the method is limited by available functional data: if a trait is enriched in a cell type for which we have no data, we cannot detect the enrichment. Sixth, our method currently gives large standard errors when applied to very small categories (Supplementary Figure 8 and Supplementary Note). Last, though we have shown our method to be robust in a wide range of scenarios, we cannot rule out bias due to model misspecification caused by enrichment in an unidentified functional category as a possible source of bias; however our simulations show that our method gives nearly unbiased results even under very extreme scenarios of unmodeled functional categories (Figure 2).

In conclusion, the polygenic approach described here is a powerful and efficient way to learn about functional enrichments from summary statistics. It will likely become increasingly useful as functional data continues to grow and improve, and as GWAS studies of larger sample size are conducted.

Online Methods

Stratified LD score regression

We assume a linear model:

$$y_i=\sum _j{X}_{ij}{\beta }_j+{\epsilon }_i$$

where y_i is a quantitative phenotype in individual i, X_ij is the standardized genotype of individual i at the j-th SNP, β_j is the effect size of SNP j, and ε_i is mean-zero noise. We define heritability by

$$h^2=\sum _j{\beta }_j^2$$

and the heritability of a category C to be

$$h^2(C)=\sum _{j\in C}{\beta }_j^2$$

We model β as a mean-zero random vector with independent entries. We have C functional categories C₁, …, C_C, and we allow the variance of β_j —i.e., the per-SNP heritability at SNP j—to depend on these functional categories that we include in our model via the equation

$$\mathit{Var}({\beta }_j)={\mathrm{\sum }}_{c:j\in C_c}{\tau }_c.$$ (2)

In the case that the C_c are disjoint, we have τ_c = h²(C_c)/M(C_c), where M(C_c) is the number of SNPs in C_c. Each SNP must be in at least one category; in practice we either have a set of categories that forms a disjoint partition of the genome, or we include the set of all SNPs as one of the categories.

In the Supplementary Note, we show that under this model,

$$E\left[{\chi }_j^2\right]=N{\mathrm{\sum }}_c{\tau }_c\ell (j,c)+1,$$ (3)

whereχ²_j is the marginal association test statistic at SNP j, N is the sample size and $\ell (j,c):={\mathrm{\sum }}_{k\in C_c}{r}_{jk}^2$. An extension of this derivation to case-control traits is in Bulik-Sullivan et al. [45].

Given a vector of χ² statistics and LD information either from the sample or from a reference panel, Equation (3) allows us to obtain estimates τ̂_c of τ_c by computing ℓ(j, c) and regressing χ²_j on ℓ(j, c). For some analyses—including the cell-type and cell-type group analyses in this manuscript—estimating τ_c is the goal. For other analyses—including the baseline analyses in this manuscript—the goal is to estimate $h^2(C_c):={\mathrm{\sum }}_{j\in C_c}{\beta }_j^2$, or h²(C_c)/h². Because the β_j have mean zero, we can approximate h²(C_c) with its expectation, Σ_j∈Cc Var(β_j). When the categories are disjoint, Var(β_j) = τ_c, where SNP j is in category C_c, and so ĥ²(C_c) = |C_c|·τ̂_c. When the categories overlap, we apply Equation (2), which gives us

$$\begin{array}{l}{\widehat{h}}^2(C_c)=\sum _{j\in C_c}\widehat{\mathit{Var}}({\beta }_j)\\ =\sum _{j\in C_c}\sum _{c^{\prime }:j\in C_{c^{\prime }}}{\widehat{\tau }}_c.\end{array}$$

In this paper, we use HapMap Project Phase 3 (HapMap3 [46]) SNPs for our regression, 1000G SNPs [47] for our reference panel, and we only partition the heritability of SNPs with minor allele frequency above 5% (see Supplementary Note). The details of the regression, including outlier removal, out-of-bounds estimates, regression weights, and GC correction are in the Supplementary Note.

Significance testing

We estimate standard errors using a block jackknife over SNPs with 200 equally-sized blocks of adjacent SNPs [16]. This gives us an empirical covariance matrix of coefficient estimates. In the baseline analysis, to evaluate whether a category is enriched for heritability, we want to test whether $\frac{h^2(C)}{h^2}>\frac{\mid C\mid }{M}$. This is the same as testing whether the per-SNP heritability is greater in the category than out of the category; i.e., whether $\frac{h^2(C)}{\mid C\mid }-\frac{h^2-h^2(C)}{M-\mid C\mid }>0$. Because our estimates of the regression coefficients are approximately normally distributed, and therefore $\frac{h^2(C)}{h^2}$ is not normally distributed but $\frac{h^2(C)}{\mid C\mid }-\frac{h^2-h^2(C)}{M-\mid C\mid }$ is, we use the latter expression to test for significance. Because this expression is linear in the coefficients, we can estimate its standard error using the covariance matrix for the coefficient estimates, and then we compute a z-score to test for significance. This procedure is well-calibrated; see Figure 1. We also report jackknife standard errors of the proportion of heritability even though this is not what we use to assess significance.

For the cell-type-specific analyses, we use the z-score of the coefficient directly.

Code availability

Stratified LD score regression is available as open source software at github.com/bulik/ldsc.

Full baseline model

The 53 functional categories, derived from 24 main annotations, were obtained as follows:

• Coding, 3′-UTR, 5′-UTR, promoter, and intron annotations from the RefSeq gene model were obtained from UCSC [17] and post-processed by Gusev et al. [14]

• Digital genomic footprint and transcription factor binding site annotations were obtained from ENCODE [3] and post-processed by Gusev et al. [14]

• The combined chromHMM/Segway annotations for six cell lines were obtained from Hoffman et al. [20]. The CTCF, promoter flanking, transcribed, transcription start site, strong enhancer, and weak enhancer categories are each a union over the six cell lines; the repressed category is an intersection over the six cell lines.

• DNase I hypersensitive sites (DHSs) are a combination of ENCODE and Roadmap data, postprocessed by Trynka et al. [5]. We combined the cell-type-specific annotations into two annotations for inclusion in the full baseline model: a union of all cell types, and a union of only fetal cell types.

• Cell-type-specific H3K4me1, H3K4me, and H3K9ac data were all obtained from Roadmap and postprocessed by Trynka et al. [5] For each mark, we took a union over cell types for the full baseline model, and used the individual cell types for our cell-type-specific analysis.

• Cell-type-specific H3K27ac was obtained from Roadmap and post-processed [18]. A second version of H3K27ac was obtained from the data of Hnisz et al. [19] For each mark, we took a union over cell types for the full baseline model. We also used the individual cell types of the Roadmap H3K27ac data for our cell-type-specific analysis.

• Super-enhancers were also obtained from Hnisz et al [19], and comprise a subset of the H3K27ac annotation from that paper. We took a union over cell types for the full baseline model

• Regions conserved in mammals were obtained from Lindblad-Toh et al. [21], post-processed by Ward and Kellis [22].

• FANTOM5 enhancers were obtained from Andersson et al. [23]

• For each of these 24 categories, we added a 500bp window around the category as an additional category to keep our heritability estimates from being inflated by heritability in flanking regions [14].

• For each of DHS, H3K4me1, H3K4me3, and H3K9ac, we added a 100bp window around the ChIP-seq peak as an additional category.

• We added an additional category containing all SNPs.

When we report results in Supplementary Tables 4, 5, and 6, we do not report results from the category containing all SNPs, as it has 100% of the heritability with standard error zero. (It might have a coefficient τ_c that is non-trivial, but in these tables we report proportions of heritability.)

According to our simulations (Figure 2), including these 53 categories in our baseline model allows us to obtain unbiased or nearly unbiased estimates of enrichment for a wide range of potential new categories. To estimate the enrichment of a new annotation, we perform analyses using a model with these 53 annoations plus the new annotation. For example, for the cell-type-specific analysis, we add each cell-type-specific annotation to the baseline model one at a time, and asses enrichment using the z-score of the cell-type-specific annotation.

Simulations: Figure 1

For these simulations, we used genotypes from the Wellcome Trust Case Control Consortium [48]. QC was performed as described in Gusev et al. [14]: we removed any SNPs that were below a MAF of 0.01, were above 0.002 missingness, or deviated from Hardy-Weinberg equilibrium at a P < 0.01. The resulting dataset had 14,526 individuals and 162,574 SNPs. We let heritability vary between 0.1 and 0.9, with the proportion of causal SNPs equal to 0.05 and 0.005 (i.e., 8,129 and 813 causal SNPs on average, respectively), and we simulated quantitative phenotypes from an additive model. For each simulation, effect sizes for causal SNPs were drawn from a normal distribution with mean zero and variance (i.e., average per-SNP heritability) determined by functional categories. To simulate realistic enrichment for the 53 categories in the baseline model plus the CNS cell-type group, we fit the model to the schizophrenia summary statistics [18] and took the resulting coefficients, replacing negative coefficients with 0. We then scaled these coefficients as needed to give the desired heritability at the desired level of polygenicity. For each simulation, we used stratified LD score regression to estimate total heritability, the heritability of the CNS cell-type group, and the proportion of heritability in the CNS cell-type group.

Simulations: out of sample LD

In this paper, we use LD scores computed from an out-of-sample reference panel. To evaluate this, we used the summary statistics simulated above, but ran stratified LD score regression using a 1000G reference panel rather than in-sample LD. We found that estimates of total h_g² and category-specific h_g² were biased downwards, but that estimates of proportion of h_g² were approximately unbiased and type 1 error was well calibrated (Supplementary Figure 4).

Simulations: Figure 2

For computational ease using REML, we decreased our sample size to the 2,680 samples in the NBS and 1966BC control cohorts of the WTCCC1 dataset, and we correspondingly restricted ourselves to only SNPs on chromosome 1. For this set of simulations, a dense set of SNPs was particularly important, so we used genotypes imputed to integrated phase1 v3 1000 Genomes [47] (URLs), giving us 360,106 SNPs after quality control. We again simulated quantitative phenotypes using an additive model, with effect sizes of causal SNPs drawn from a normal distribution with mean zero and variance determined by functional categories. Heritability was set to 0.5, and all SNPs were causal unless in a category simulated to have zero variance.

Simulations: Figure 3

We began with the simulations of realistic enrichment in the baseline categories and the CNS cell-type group as in Figure 1. Then for each other cell-type group, we removed the CNS cell-type group and added the new cell-type group to the model, scaling the coefficient τ_c of the new cell-type group to keep the total heritability constant. We then increased the coefficients of the cell-type groups by a multiplicative constant so that the average top z-score over 5,000 simulations (10 cell-type groups × 500 replicates each) was close to the mean top z-score found in our analysis of 17 real traits. In a second set of simulations, we decreased the coefficients so that the top cell-type group was significant 50% of the time.

We then repeated the process with the H3K4me3 fetal brain annotation (though with just one annotation instead of 10 cell-type-groups). First we fit a model with this annotation plus the baseline model to the schizophrenia summary statistics [18]. We then scaled the coefficient of the cell-type-specific annotation until the mean z-score over 500 replicates matched the mean z-score in real data. In a second set of simulations, we decreased the coefficient so that that the top cell-type group was significant in 50% of 500 replicates.

Meta-analysis across traits

We chose nine phenotypes with low phenotypic correlation and sample overlap: Height, BMI, menarche, LDL levels, coronary artery disease, schizophrenia, educational attainment, smoking behavior, and rheumatoid arthritis (see Supplementary Note). We performed a random-effects meta-analysis of proportion of heritability over the nine phenotypes listed above for each functional category. The results are in Figure 4 and Supplementary Table 4. Results meta-analyzed over all 17 traits are in Supplementary Figure 9; however these results have artificially deflated standard errors due to correlated traits such as HDL/LDL/Triglycerides being treated as independent.

Robustness to derived allele frequency

Stratified LD score regression is based on the assumption that the per-normalized-genotype effect size of a SNP is drawn i.i.d. with mean zero, conditioned on functional annotation. So if allele frequency bins are not included as annotations in the model, then we are assuming that per-allele effect sizes have variance proportional to (p(1−p))⁻¹ for allele frequency p.

To check that our results are not affected by an allele-frequency-dependent genetic architecture, we repeated the meta-analysis over traits using the full baseline model with seven derived allele frequency bins as extra annotations. This allowed for effect size to depend on derived allele frequency, independently of functional annotation. These results are very similar to our results without derived allele frequency bins, and are displayed in Supplementary Table 6.

In this paper, we do not consider heritability of very rare SNPs. If stratified LD score regression were to be used to analyze a dataset with rare variants, then there would be several issues to consider that did not come up in our analysis. For example, in the current analysis, we could use LD estimates from a reference panel because the LD patterns in the reference panel matched the LD patterns in our samples for the allele frequency range we were interested in; this might not hold for rare variants [49]. Also, our analysis described above shows that allele-frequency dependent architectures are not causing bias in our current analyses, but this robustness result may not extend to potential future analyses of datasets with rare variants.

Comparison to other methods

We are not aware of any other methods designed to estimate genome-wide components of heritability from summary statistics. However, there are existing methods that identify enriched functional categories and cell types from summary statistics. We compared our method to four other methods, described below; each of these methods has provided valuable biological insights. For each of these methods, we assessed the rejection rate over 100 simulations for true cell-type-specific enrichment, null baseline enrichment (i.e., baseline enrichment with no cell-type-specific signal), and null simulations with no enrichment in any category. We performed this analysis for both a cell type (fetal brain in H3K4me3) and cell-type group (CNS), and for two proportions of causal SNPs, 0.05 and 0.005. All simulations had a sample size of 14000 and h_g² of 0.7. Results are displayed in Figure 7; below, we discuss the results for each method individually.

GoShifter is a recent method of Trynka et al. [6] (see also their previous published work [5]). Goshifter is conservative in its identification of enrichment, comparing to a null obtained by local shifting rather than a genome-wide null, and it only uses statistically significant SNPs. It had properly calibrated type 1 error in all four situations we simulated. Of these four situations, stratified LD score regression had higher power than GoShifter in the more polygenic scenarios, and the two methods performed comparably in the less polygenic scenarios, in which there were more significant SNPs.

A paper by Pickrell [9] combines GWAS data with functional data to identify enriched and depleted functional categories, and leverages the resulting model to increase GWAS power. The method, called fgwas, is effective at increasing association mapping power and identifies many interesting enrichments in the published paper. In our simulations we saw good null calibration, but low power to detect enrichment. Of the four simulations with true enrichment, fgwas performed best for when identifying enrichment of the smaller category (fetal brain) in the more polygenic trait (p_causal = 0.05); however, stratified LD score regression had higher power than fgwas in all four situations. Fgwas could have an advantage for annotations smaller than the ones tested in this manuscript, but we do not explore that issue here.

Maurano et al. [10] use enrichment of SNPs passing P-value thresholds of increasing stringency to identify important cell types. Using this method, Maurano et al. found striking patterns of cell-type-specific enrichment. However, this approach implicitly assumes that the functional annotation at a GWAS SNP matches the functional annotation at the causal SNP, which could be true for functional annotations composed of very wide regions, but is not likely to be true for functional annotations composed of smaller regions, such as conserved regions. Moreover, the method does not account for total LD, and so could give biased results if used to compare functional annotations with different average amounts of total LD [1]. We implemented a “top SNPs” method analogous to the method of Maurano et al. that tests for enrichment of the functional category among SNPs that pass statistical significance. Because the method is not intended to control for any other annotations, it had a high rejection rate for the null baseline simulations, detecting cell-type-specific signal where there was none. Thus, its high rejection rate for the cell-type-specific simulations were not reflective of true power. It remains a powerful method for traits with many significant SNPs, if the goal does not include controlling for other categories.

Similarly, PICS, a recent method from Farh et al. [7] focuses on fine-mapping and considers only genome-wide significant loci. On real data [7], the results from this method were compelling and consistent with our understanding of biology. This method performed similarly to the top SNPs method in our simulations, with a high rejection rate in null simulations with baseline enrichment and also a high rejection rate for true enrichment.

In addition to stratified LD score regression as used in this manuscript for cell-type-speciifc analyses, we also compared to “unadjusted” stratified LD score regression; i.e., LD score regression used to test for enrichment in total proportion of heritability, not controlling for other methods, in a way analogous to the top SNPs and PICS methods. As expected, this unadjusted version had a high rejection rate both for null baseline enrichment as well as for true cell-type-specific signal, for the same reasons that the top SNPs and PICS methods did.

Of the three methods with properly calibrated rejection rates for the null simulations with baseline enrichment (GoShifter, fgwas, and stratified LD score regression), stratified LD score regression was the most powerful for the polygenic traits. For the less polygenic traits, stratified LD score regression had power similar to GoShifter for the cell-type group, and none of the three methods had any power for the single cell type with less polygenic genetic architecture.

In very recent work, Kichaev et al. [8] introduce a new method (PAINTOR) that leverages functional data for improved fine-mapping. The method also outputs annotations associated with disease. While the method is clearly effective in increasing fine-mapping resolution, it is unclear whether the method is effective at ranking cell types; for example, cell types identified as contributing the most to HDL, LDL, and Triglycerides (using data from Teslovich et al. [27]) are muscle, kidney, and fetal small intestine, respectively, whereas the top cell types for those three phenotypes identified using our method (also using data from Teslovich et al. [27]) are liver, liver, and liver. The uncertain effectiveness of this method in ranking cell types may be because it is primarily aimed at fine-mapping and thus considers only genome-wide significant loci.