A Novel Approach to Measuring Efficiency of Scientific Research Projects: Data Envelopment Analysis

Abstract

Purpose

Measuring the efficiency of resource allocation for the conduct of scientific projects in medical research is difficult due to, among other factors, the heterogeneity of resources supplied (e.g., dollars or FTEs) and outcomes expected (e.g., grants, publications). While this is an issue in medical science, it has been approached successfully in other fields by using data envelopment analysis (DEA). DEA has a number of advantages over other techniques as it simultaneously uses multiple heterogeneous inputs and outputs to determine which projects are performing most efficiently, referred to as being at the efficiency frontier, when compared to others in the data set.

Method

This research uses DEA for the evaluation of supported translational science projects by the Oregon Clinical and Translational Research Institute (OCTRI), a NCATS Clinical & Translational Science Award (CTSA) recipient.

Results

These results suggest that the primary determinate of overall project efficiency at OCTRI is the amount of funding, with smaller amounts of funding providing more efficiency than larger funding amounts.

Conclusion

These results, and the use of DEA, highlight both the success of using this technique in helping determine medical research efficiency and those factors to consider when distributing funds for new projects at CTSAs.

Purpose

The National Center for Advancing Translational Sciences (NCATS) of the National Institutes of Health supports a national consortium of more than 60 medical research institutions throughout the United States via the Clinical and Translational Science Awards (CTSA).1 A primary function of the CTSA program includes “maximizing investment in core and other resources to increase efficiency and help NIH support a wide range of researchers and projects.” To evaluate the success of funding investments in specific programs, overall performance statistics are compiled by each CTSA with metrics like return on investment, number of investigators trained, or number of supported publications. These metrics, while good to evaluate a single dimension of performance, are problematic because CTSAs typically provide a range of services to their investigators, including additional funding or research infrastructure support, while expecting a range of outcomes, such as papers, patents, and trained investigators. How then does one overcome the difficulty of developing a uniform measure of performance when there are numerous factors that might define and contribute to success? This issue is not unique to CTSAs, as it is not uncommon for academic health centers (AHCs) to support projects in much the same way, with anticipation of much the same results.

Faced with a similar problem, researchers in other fields developed the technique of data envelopment analysis (DEA). DEA was designed to simultaneously evaluate heterogeneous contributing factors to compute the most efficient use of resources (inputs) for a given set of performance metrics (outputs). One use of the technique is to evaluate the performance of bank branches, where each branch is in a different area (thus having a different customer base) but each needs to be evaluated on similar set of performance criteria, for example successful loans or new acquisition of new customers. DEA generates the relative efficiency of each branch bank compared to the other branches. Those branches that are most efficient in using their resources (inputs) to generate results (outputs) are considered to be at the efficient frontier. Hence, this technique might be one solution to the current AHC and CTSA problem on how to most efficiently allocate the limited amount of resources available.

Here we apply DEA to assess the efficiency of the pilot project funding process at one CTSA: the Oregon Clinical and Translational Research Institute (OCTRI). Our results suggest that DEA can be useful in evaluating the efficiency of pilot projects selected for support, the processes used to support projects, and outcome measures selected to assess project success.

Method

Data envelopment analysis

DEA focuses on identifying those decision‐making units (DMUs) in the data set that are optimal in utilizing of a set of invested resources (inputs) in delivering a set of expected results (outcomes). DEA has been characterized as “balanced benchmarking” effort.2 Using nonparametric linear programing methods, DEA computes both: (1) the “best practice” or efficiency frontier, in the set of DMUs, and (2) the relative inefficiencies of those DMUs not on this frontier (Figure 1). Mathematically, a DMU at the frontier will have an efficiency ratio of 1, and those DMUs not at the frontier will have a ratio less than unity but not less than zero. The amount a DMU is less than 1 can be viewed as its degree of inefficiency where the DMU was either: (1) given too many inputs for the outputs, (2) provided too little outputs for the inputs, or (2) both, compared to other DMUs in the analysis. For a simple example, assume Clinic X had a budget of $10 million (single input) and saw 2,000 patients (single output). Clinic Y had a budget of $8 million and saw 2,000 patents and Clinic Z had a budget of $10 million and saw 2,500 patients. From an efficiency standpoint, Clinic X was less efficient than Clinic Y (Y used less budget to see the same number of patients) and less efficient than Clinic Z (Z saw more patients for the same budget).

Figure 1.

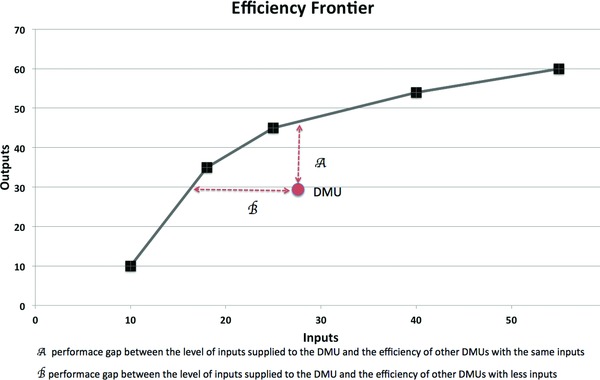
Sample DEA for DMUs with one input and one output. The figure shows an example of efficiency and inefficiency. In this example, the x‐axis represents the inputs (for example, funds and services supplied for a project) the y‐axis is the outputs (for example, number of publications and new grants from a project), DMUs (funded projects) are represented by boxes and circle, and the efficiency frontier, computed by DEA, is represented by the black boxes linked by the black line. The red circle represents a DMU not at the efficiency frontier, hence a project that either underperformed for the level of inputs (A) or was over funded for the level of outputs (B) relative to other projects. It is expected that most DMUs in a data set will have some level of inefficiency and, with further statistical analysis, it is possible to determine how to better allocate scarce input resources. For example, once DEA has computed an efficiency frontier, it is possible to use more typical statistical techniques, such as regression analysis. This analysis would use the efficiency frontier value for each project as the dependent variable and the inputs as independent variables.

Importantly, the efficiency ratio is only valid within the data set being analyzed. That is, it is an expression of efficiency in relation to other DMUs in the analysis and is not an absolute measure of efficiency in a global sense, i.e., it does not imply any absolute maximization of resource utilization.

Data source (OCTRI)

The setting for the study is OCTRI, an institute serving all researchers at the Oregon Health and Science University in Portland Oregon.3 It has four primary aims: to contribute to major scientific advances in clinical and translational biomedical research, help build careers in clinical and translational science research, provide critical research infrastructure to support these efforts, and to continuously evaluate the success of these efforts. This research falls in the final category, as it is attempting to evaluate how “efficient” OCTRI has been in its project funding for translational research, referred to as the awards program. This program provides grants, seed money, and other nonfinancial support to investigators (for more information, see Ref. 3).

In the 7‐year period of interest for this research, OCTRI and its partners provided over $4 million in funds for 85 specific projects, which generated over $56 million in grant and other funds, representing a return‐in‐investment (ROI) of approximately 14×, hence, in general OCTRI was a good steward of its resources. However, the question for this research is: are there insights that can be gleaned from DEA to make it even better at utilizing ever‐scarcer resources?

Input variables

There are three input variables of interest for this study. The first variable is the amount of funding supplied by OCTRI and its partners to a particular project. Second is the number of OCTRI programs that provided in‐kind support to the project. While a more effective measure would include the level of in‐kind support, these data are not available for the total study period. Third is the number of collaborators who are members of the project team. This variable was initially difficult to classify as an input or output as the collaborations could have preexisted or the provision of research funds could have spawned the collaboration. After considerable thought, it was decided that the number of collaborators is one of the evaluation characteristics used to select projects, hence it is an input variable. Characteristics of the input variables are shown in Table 1. As can be seen in this table, not all projects required all types of inputs. For example, 45.9% of all projects required no additional in‐kind services.

Table 1.

Demographics of the DMUs (projects)

Projects (n = 85)		Mean	Median	Min	Max	% Zero value
	Months since launch	47.7	49.0	12	84	0%
Inputs	Funded supplied (dollars)	48,160	30,000	7,084	247,375	0%
	Number of support services supplied	1.3	1.0	0	8	45.9%
	Number of collaborators	2.8	2.0	0	20	16.5%
Output	Funds acquired (annualized dollars)	155,336	0	0	1,648,104	51.8%
	Publications per year (annualized)	0.2745	0.0000	0.0000	4.0000	54.1%
	Grants per year (annualized)	0.0004	0.0000	0.0000	0.0049	51.8%
% of DMUs with no output						36.5%

Output variables

For output variables, OCTRI regularly surveys investigators on each funded project to verify the reported financial output information in the OHSU grants system, and to discover what publications, if any, have been the result of the project. OCTRI follows projects for 5 years.

The three output variables analyzed are: (1) the additional dollar amount of funds acquired as a result of the pilot award, (2) the number of published papers, and (3) the count of new grants received (see Table 1). Again, not all projects generated all output variables. For example, 51.8% of projects generated zero additional funding. Interestingly, and of importance for the DEA results, 36.5% of the 85 funded projects resulted in zero outputs on any the three outputs measured.

Projects are funded on a rolling basis throughout the year, and projects have been in existence for a variable amount of time since they received funding, (from 0 to 7 years). To account for these variable times, all output variables were normalized by dividing each output by the number of years since the project was initially funded. This normalization assumes that projects in existence for longer time period have more opportunities to create outputs. Any projects in existence less than 12 months (<1 year) were excluded.

Overall DEA model and key DEA criteria selection

The nonlinear mathematical formulation of the problem is shown in the Appendix. For a good and relatively nontechnical description of the technique in healthcare, see Huang and McLaughlin.5 The software used for DEA is MaxDEA, available as a free download.6 The critical settings for the DEA analysis are: (1) the use of Charnes, Cooper, Rhodes (CCR) radial measure of efficiency, (2) input‐oriented structure, and (3) a variable return to scale. These setting were selected as they are the most common settings in DEA and, as this study is initial exploratory research it is a “proof of concept.”

Statistical analysis

To determine which, if any of the input variables could predict the results of DEA, namely the project efficiency scores, regression analysis was completed using the input variables as independent variables and the DMUs efficiency score as the dependent variable. To verify these results, projects were coded, or “binned,” into quintile groups based on their level of efficiency. Additionally, for each project, input variables were compared to the median for that variable and coded into two categories: below median or above median. Using this binning method, it was possible to complete chi‐square analysis. All analyses were done using IBM SPSS Version 22.

Results

Figure 2 shows the resulting DEA scores in a graphical form. Regression analysis was used to identify the relationship between the individual DEA scores and each input variable (Table 2) The only statistically significant input variable is funds supplied (p < 0.001). There was a negative relationship between funds supplied and DEA efficiency score. Neither of the other two input variables was statistically significant at the 0.10 level. The beta weights in this case are not easily interpretable, thus we used binning to help explain the results. Projects were binned in quintiles based on their efficiency scores. Figure 2 shows the efficiency scores (y‐axis) for each project (x‐axis). These bins are color‐coded and binned values of the inputs and outputs are shown in Table 3.

Figure 2.

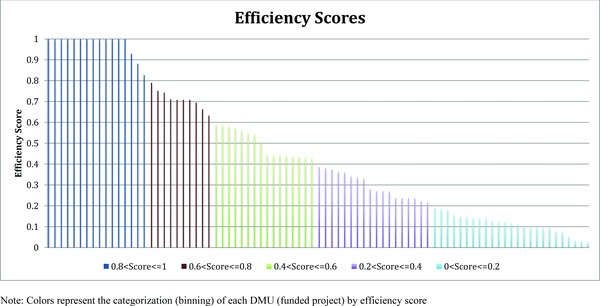
Efficiency scores by DMU (all projects).

Table 2.

Regression results

	Unstandardized coefficients		Standardized coefficients
	B	Std. error	Beta	t‐score	Sig.
(Constant)	0.643	0.054		11.986	0.000	***
Funds supplied (dollars)	–3.40E‐06	0	–0.514	–5.428	0.000	***
Number of support services	0.002	0.019	0.013	0.133	0.895
Number of collaborators	–0.009	0.009	–0.091	–0.956	0.342
R 2	0.275		F value	10.237
Adjusted R 2	0.248		Sig.	0.000***

***Significant at the 0.001 level.

Table 3.

Binned efficiency scores of DMUs (quintiles of DMU scores)

DMU Categories	1	2	3	4	5	Total
Bin efficiency range	0.8 < Score ≤ 1	0.6 < Score ≤ 0.8	0.4 < Score ≤ 0.6	0.2 < Score ≤ 0.4	0 < Score ≤ 0.2	n/a
Number of DMUs in bin	16	10	16	18	25	85
Months since funding	53.6	40.4	49.7	55.0	40.2	47.7
Inputs (mean)
Funded supplied ($000)	$20.5	$36.1	$29.4	$35.4	$91.9	$48.16
Number of support services supplied	1.4	1.5	0.8	1.3	1.4	1.3
Number of collaborators	2.8	1.4	2.3	4.0	2.8	2.8
Outputs, (annualized, mean)
Funds acquired ($000)	$411.3	$161.3	$153.2	$102.0	$29.0	$155.34
Number of publications	0.7483	0.3128	0.2195	0.1812	0.0584	0.2745
Number of grants	0.0013	0.0001	0.0005	0.0003	0.0000	0.0004

Figure 3.

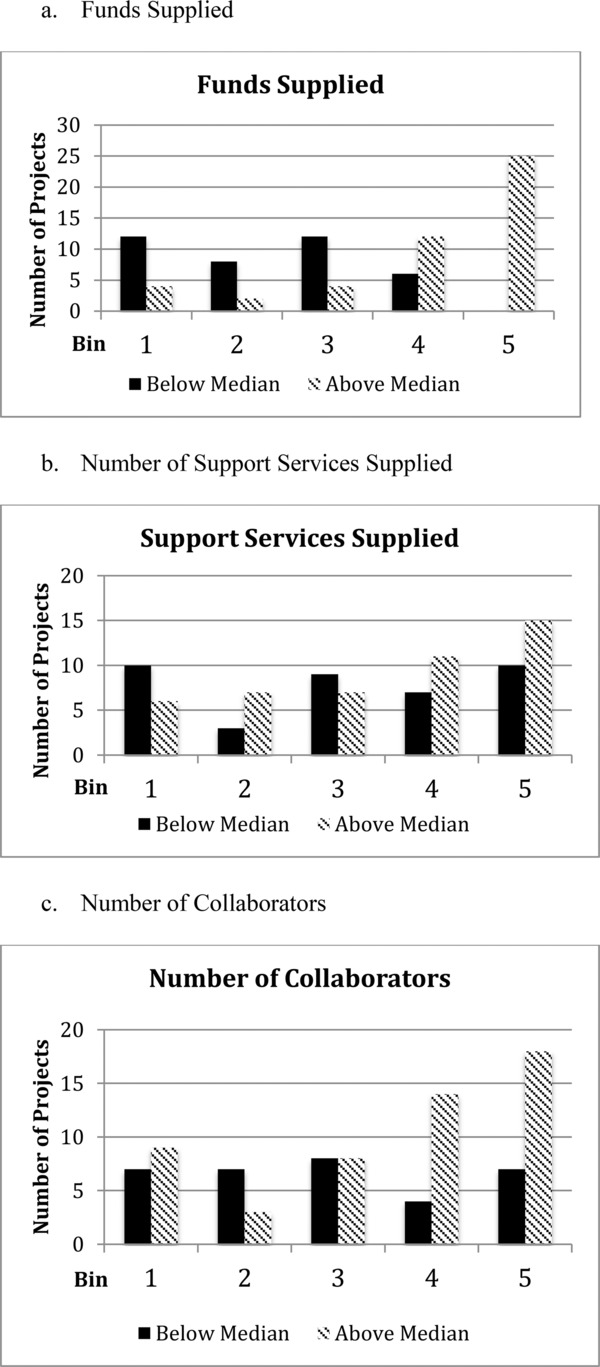
Binned above and below median comparisons.

Using chi‐square analysis, the only statistically significant difference in input variables was funds supplied (p < 0.0001). Thus, this supports the findings of the regression analysis: input dollars is most predictive of eventual performance, with lower funds supplied predicting a higher likelihood of efficiency.

Comparing bin 1 (highest efficiency) versus Bin 5 (lowest efficiency) reveals that the lowest efficiency projects required five times the amount of input dollars ($91.9 vs. $20.5). However, the highest efficiency projects generated more than 14 times the new funds acquired ($411.3 vs. $29.0) and almost 13 times the number of annualized publications (0.7483 vs. 0.0584). Again, there is a strong negative relationship between funds supplied and eventual performance. One possible explanation of this result might lie in the differences in “months since funding” as projects in the most efficient bin were open for over a year longer than in the least efficient bin (bin 1 vs. bin 5; 53.6 months vs. 40.2 months). Looking more broadly, this explanation does not explain the difference as the second most efficient (bin 2) was similar in time since funding to lowest (bin 5; 40.4 vs. 40.2), and the second lowest (bin 4) was similar to the highest (bin 1, 55.0 vs. 53.6).

Conclusions

We have used DEA to evaluate the efficiency of a pilot project support program for biomedical research. Our results indicate that the primary predictor of project efficiency is the level of funding supplied. Somewhat unexpectedly, projects supported with smaller investments were more efficient than those with larger budgets. These and similar analyses could assist in project selection, in the design or pilot project support programs, and in determining how to best train researchers in being efficient in the use of funds As such, it could help academic health centers, CTSAs and other funding institutions in evaluating the most efficient use of their resources.

The finding of better performance by projects supported by smaller investments is very similar to that from the venture capital and angel investor communities; in anticipation that a high proportion of projects will be less than maximally efficient (i.e., fail), it is better to fund many small projects rather than a few, larger projects.7 While there could be a number of reasons why smaller funding was most efficient, these data are not available for analysis. Of course, there may be objectives other than maximal efficiency that drive the choice of funding level. For instance, some desirable outcomes may not be feasible with small investments. Nevertheless, the use of DEA to assess the efficiency of any level of support should be advantageous.

DEA has a rich history since its initial inception in by Charnes et al.,8 with over 4,000 published articles and 3,000 unpublished dissertations, theses, and conference presentations since 1978.9 In health care, it has been use to analyze settings as diverse as community care settings,10 primary health practices,11 individual physician practices,12 and hospital performance in Zambia.13 Interestingly, we have been unable to discover that it has been previously applied to the medical research environment, in our case evaluating supported research projects.

DEA has several advantages compared to other analysis techniques. First, it is designed to utilize heterogeneous inputs and outputs. Hence there is no need to convert variables into a common unit of measure, provided that the same variables are used for every DMU. Second, because it simultaneously analyzes multiple inputs and outputs, and it generates relative‐efficiency information, it provides information that is not available with other techniques. With a given set of data on projects, this technique effectively blends inputs and outputs and evaluates which projects have been most efficient in the use of the inputs compared to the other projects. Importantly, DEA only compares the efficiency of resources within the evaluated data set; to DEA there is no “universally optimal” efficiency. Another advantage of DEA over other statistical techniques, such as regression analysis, is that it does not attempt to find the “best‐fit” of the data. Rather, it determines those DMUs that have maximized the use of inputs to create an “efficiency frontier.” Thus, identifying “average” performance is not the goal; it is distinguishing “most efficient” performance. Rather than attempting to “best‐fit” the data, as regression analysis does, DEA looks explicitly for the maximal performers in a data set.

There are a number of limitations to this study. First, all results rely on the quality of the data set. If investigators neglected to provide accurate output data, then the results are suspect. We do not believe this was a major issue because extensive effort was expended in acquiring accurate data from investigators. Second, actual levels of in‐kind support (in dollars expended) were not collected—only counts of number of different types of support requested, for example grant writing support or database creation. Other data are currently being collected so it will be available for future analysis. Moreover, the assumption that the number of collaborators is an input, and not an output, requires further consideration. There were also analytical challenges. As previously mentioned, the data matrix of output variables is sparse, i.e., there are numerous zero values, for instance when no publications or no grants resulted from a supported project. Also, the output variables were annualized. In a typical DEA analysis, similar units are compared for an identical time frame (typically a year). The benefit of annualizing is the acknowledgement that a longer time frame provides additional opportunities to create output but it is coupled with the problem that it penalizes projects that have been in existence for a long time, demanding that these projects perform at high levels over the entire time frame. Perhaps better input and output variables could have been selected for the study. For instance, the impact of articles as measured by citation indices or journal impact factors may be more appropriate than the absolute number publications that result from a pilot project; one key, paradigm‐shifting publication may be a more desirable outcome than multiple, more incremental research findings. Refinement of the output variables used for these analyses should be a future goal. Finally, as with all DEA, only a relative efficiency measure is generated. That is, each DMU or project is compared only to its peers within the same umbrella organization. While this is good for analyzing internal organizational efforts, it does not imply that the results can be generalized across other programs that rest on fundamentally different assumptions. Additional research should be completed to address these limitations.

With ever decreasing budgets, it is important to carefully determine how to best allocate the scarce resources available for biomedical pilot project support. We have shown that it is possible and desirable to use the DEA technique to assess the efficiency of a portfolio of projects. Our results suggest that DEA provides a flexible approach to assess a variety of inputs that may affect project success, and to understand the performance of a pilot project support program. In our analyses, smaller amounts of project support were more efficient in yielding the specified outcomes (additional grant funding, publications). Additional refinements in the selection of inputs and desired outputs should improve the utility of the approach.

While this paper demonstrates how DEA can be used to evaluate efficiency of projects within an individual CTSA, an advantage of DEA is that is can be used at various levels of scale. It could just as easily have been used to examine the efficiency of the project support process in a larger setting, including across multiple institutions using similar pilot project funding models (e.g. at the NCATS level). The National Institute of Health and other funding agencies support billions of dollars of research annually and most NIH institutes collect a myriad of data concerning their grants, contracts, and other funded efforts. To the best of our knowledge, these data are typically only used for internal purposes. They could be analyzed utilizing DEA, or a similar technique, so that investigators, centers, and institutes can better understand how to become more efficient in the use of these resources.

Appendix A. Mathematical Problem Formulation

Objective Function:

$$\mathrm{Max}{h}_j=\left(u_1{O}_1+u_2{O}_2+...u_M{O}_M\right)/(v_1{I}_1+v_2{I}_2+...+v_N{I}_N).$$

Subject to:

$$\begin{array}{c}{h}_j\le 1,j=1,2,...,\mathrm{J}\\ 0<\varepsilon \le O_1,O_2,...O_m\\ 0<\varepsilon \le I_1,I_2,...I_n\end{array},$$

where

Variable	Description	Values in Study
J	Total number of DMUs in the data set,	85
M	Total number of Output Variables	3
O i	output variable i,	(all annualized)
		O1 = funds acquired (dollars)
		O2 = number of publications
		O3 = number of grants
N	The number of Input Variables	3
I k	Input variable k,	I1 = funds supplied, (dollars)
		I2 = number of support services supplied,
		I3 = number of collaborators
j	An individual DMU	e.g., one funded project
h j	Efficiency ratio for DMU j
u's and v's	Weights generated by the model for outputs and inputs respectivelyε
ε	A non‐Archimedean infinitesimal