Analysis of transtheoretical model of health behavioral changes in a nutrition intervention study – A continuous time Markov chain model with Bayesian approach

Summary

Continuous time Markov chain (CTMC) models are often used to study the progression of chronic diseases in medical research, but rarely applied to studies of the process of behavioral change. In studies of interventions to modify behaviors, a widely used psychosocial model is based on the transtheoretical model (TTM) that often has more than three states (representing stages of change) and conceptually permits all possible instantaneous transitions. Very little attention is given to the study of the relationships between a CTMC model and associated covariates under the framework of TTM. We developed a Bayesian approach to evaluate the covariate effects on a CTMC model through a log-linear regression link. A simulation study of this approach showed that model parameters were accurately and precisely estimated. We analyzed an existing data set on stages of change in dietary intake from the Next Step Trial using the proposed method and the generalized multinomial logit model (GMLM). We found that the GMLM was not suitable for these data since it ignores the unbalanced data structure and temporal correlation between successive measurements. Our analysis not only confirms that the nutrition intervention was effective, but also provides information on how the intervention affected the transitions among the stages of change. We found that, compared to the control group, subjects in the intervention group, on average, spent substantively less time in the precontemplation stage and were more/less likely to move from an unhealthy/healthy state to a healthy/unhealthy state.

1 Introduction

Continuous time Markov chain (CTMC) models are often used to describe longitudinally measured categorical variables. In medical applications, the states of a Markov chain may refer to stages of a chronic disease, such as stages of breast cancer in cancer screening trials [1, 2], classifications of severity in studies of asthma control [3, 4] and stages of infection in patients with HIV [5, 6]. Indeed, CTMC models are widely applied in the field of public health, including health promotion [7–9]. In these studies, subjects are often followed intermittently and the exact transition times between states are generally not observed. As a result, model fitting and model parameter estimation are complex since the exact likelihood function involves calculating a matrix exponential, which may require unstable numerical methods and cumbersome algebra[10, 11]. Much of the existing literature focuses on models in which one-step direct transitions are restricted or three/fewer states are allowed [12–15]. We define “one-step direct transitions” as instantaneous transitions across states that do not require any intermediate transitions from one state to another. In both cases, the likelihood function may be obtained analytically without requiring matrix exponentiation.

Furthermore, these analytic solutions are not available for a general form of CTMC model that has more than three states and allows for all possible instantaneous transitions. Examples of this type of data are the nutrition intervention study from the Next Step Trial [16] and the study of smoking cessation [17]. In these behavioral studies, the Markov chain states are “stages of change”, based on a well-developed psychosocial theory known as the transtheoretical model (TTM). Usually, the TTM has four or more states and assumes that an individual makes consistent, logical plans [18]. However, studies often show that individuals make “spontaneous” decisions such as unplanned attempts to quit smoking [19] or that they may progress from an unhealthy state by jumping to the healthy state without experiencing an intermediate stage of preparation [20]. Although these process characteristics fit well with the CTMC, the application of CTMC models to the TTM is very limited [17].

It is possible that the usefulness of CTMC models has not been well recognized in the community of psychosocial researchers, and that fitting general CTMC models is statistically challenging. A general framework for CTMC models was well developed by Kalbfleisch and Lawless [10], followed by some applications and extensions [4, 6]. A multi-state Markov (MSM) R package was developed to implement some frequentist approaches, where the likelihood involves matrix exponentials, calculated using eigensystem decomposition (distinct eigenvalues) or Padé approximants (repeated eigenvalues) [11, 21]. Some researchers employed numerical integration techniques to approximate the likelihood [2] and others used the expectation-maximization algorithm for estimation [22]. However, the increased number of parameters complicates the likelihood function for general CTMC models, especially when covariates are incorporated [4]. To overcome these issues, the matrix exponential can be calculated numerically by solving an appropriate ordinal differential equation [23–25]. In our experience, this method has performed satisfactorily.

Recently, Ma [25] showed that in comparison to the MSM package, the Bayesian approach performed better in terms of biases and nominal coverage probabilities, especially when the number of parameters is large (e.g., five-state models with 20 parameters). The MSM package is a very useful tool when fitting CTMC models without covariates, but the parameter estimation failed to converge for the Next Step trial data when covariates were incorporated. This lack of convergence in parameter estimation was also reported by Mhoon et al. [7] when a general CTMC model with covariates was encountered. It may be that the maximum likelihood (ML) method searches the surface of the likelihood; whereas the Bayesian approach samples from the posterior distributions. When the sample size of a data set is relatively small for a given number of parameters, the surface of the likelihood tends to be flat, causing convergence failure or unstable estimates [21, 26, 27]. In contrast, Bayesian methods average the posterior samples; hence, they may still offer reasonable estimates, and the estimation might be further improved by incorporating prior knowledge into the modeling process [27]. Bayesian approaches have been developed for CTMC models with covariates [23, 24]. However, to the best of our knowledge, Bayesian modeling methods for general four-state CTMC models with multiple covariates have not been examined yet.

In this article, we present a Bayesian estimating procedure that can simultaneously evaluate the effects of multiple covariates on the transition rates under a general CTMC framework. We conduct empirical studies to assess model performance. We illustrate the application of this method to the nutrition intervention data on stages of change from the Next Step Trial, including model selection, model checking and calculation of the mean sojourn times and one-year transition probabilities. In addition, we discuss differences between the CTMC and a generalized multinomial logit model (GMLM) when analyzing the stages of change in the original report on the nutrition intervention data [16].

2 Methods

2.1 Continuous time Markov chain models

Consider a longitudinal study consisting of M subjects, where each subject can move independently among S states within the state space of 1, 2, 3,…, S, (state and stage are synonymous in this article). Let y(t_m,k) represent the outcome of the stage observed at time t_m,k for m = 1, 2,… M and k = 1, 2, … K_m, where K_m represents the number of observations on subject m. Assume that the underlying process for each subject follows a first-order homogeneous continuous-time Markov chain that can be fully described by the infinitesimal rate matrix Q = {q_{i j}} where q_{i j} ≥ 0 for j ≠ i and −q_ii = Σ_i≠j q_{i j} for i, j = 1, 2, 3,…, S. Under our assumption, the future and past states are independent given the present state, and transition rate q_{i j} is constant over time. In this model, the time a subject spends in state i is exponentially distributed, with the mean of 1/q_ii. Further, the transition rate q_{i j} can be interpreted as the hazard rate of change from state i to state j, which can be derived as in competing risk models [28]. The transition probability for subject m moving from state i at time t_m,k−1 to state j at time t_m,k is defined as p_{i j}(t) = Pr{y(t_m,k) = j|y(t_m,k−1) = i}, where t = (t_m,k − t_m,k−1) ≥ 0 for i, j = 1, 2, 3,…, S and k = 2, 3,… K_m. The S × S transition probability matrix P(t) = {p_{i j}(t)} is determined by the infinitesimal rate matrix Q and can be expressed as $P(t)=e^{Qt}=I+{\sum }_{i=0}^{\infty }{Q}^n\frac{t^n}{n!}$ with P(0) = I. See Bhat and Miller [29] for more details of CTMC models.

2.2 Models with covariates

In practice, covariate effects on hazard rates are often of research interest, and can be evaluated by incorporating these covariates in the model as a regression-type relationship via a log transformation of the hazard rates q_{i j} for i, j = 1, 2, 3,…, S and i ≠ j. To see this, let z = (z₁, z₂,…, z_h) represent the covariate vector, and ${\beta }_{ij}=({\beta }_{ij}^1,{\beta }_{ij}^2,\dots ,{\beta }_{ij}^h)$ be the regression coefficients associated with vector z for the direct transition from i to j. The hazard rates depend on the covariate vector z through a log-linear model given by the following equation:

$$\mathit{log}(q_{ij})={\gamma }_{ij}+z{\beta }_{ij}^T,$$ (1)

where ${\beta }_{ij}^T={({\beta }_{ij}^1,{\beta }_{ij}^2,\dots ,{\beta }_{ij}^h)}^T$ and each γ_{i j} represents the intercept of the log-transformed hazard rate for i, j = 1, 2, 3,…, S and i ≠ j.

Fitting a general CTMC model with covariates can be complicated and computationally expensive due to a potentially large number of parameters. The total number of parameters in a model is S × (S−1) × (1 + number of covariates). Saint-Pierre et al. [4] pointed out that the more parameters in the model, the more information and more computational resources that are required. As a consequence, convergence issues and numerical problems have been reported [6, 21]. There are two ways to reduce the number of parameters and to retain a model that well describes the data. One approach is to put constraints on some one-step transitions. Jackson [21] argued that some one-step transitions may occur only between “adjacent” states for a chronic disease; thus, an observation of transition from state 1 to 3 must have gone through state 2, for instance. This is a reasonable assumption and has been adopted by many researchers [24, 30–32]. If some one-step direct transitions are not allowed, the transition rates and corresponding covariate effects are automatically dropped from the model. The other method is to decrease the number of coefficients on the parameters. For example, we can assume that ${\beta }_{i1}^h={\beta }_{i2}^h=\cdots ={\beta }_{iS}^h$, i.e., the h^th covariate effects are the same on all hazard rates from state i to any other state [7].

Following the above argument, we assume that we have three covariates z = (z₁, z₂, z₃) in a four-state model with coefficient vector of ${\beta }_{ij}^T={({\beta }_{ij}^1,{\beta }_{ij}^2,{\beta }_{ij}^3)}^T$ for the one-step transition from i to j. The infinitesimal matrix is given as

$$Q=\left[\begin{array}{cccc}-& e^{{\gamma }_{12}+z{\beta }_{12}^T}& e^{{\gamma }_{13}+z{\beta }_{13}^T}& e^{{\gamma }_{14}}\\ e^{{\gamma }_{21}+z{\beta }_{21}^T}& -& e^{{\gamma }_{23}+z{\beta }_{23}^T}& e^{{\gamma }_{24}}\\ e^{{\gamma }_{31}}& e^{{\gamma }_{32}+z{\beta }_{32}^T}& -& e^{{\gamma }_{34}+z{\beta }_{34}^T}\\ e^{{\gamma }_{41}}& e^{{\gamma }_{42}+z{\beta }_{42}^T}& e^{{\gamma }_{42}+z{\beta }_{42}^T}& -\end{array}\right]$$ (2)

where each diagonal element equals the negative value of the sum of all hazard rates in their corresponding row. Assume for a moment that there is only one treatment covariate (e.g., intervention versus control) in this model. As discussed in Section 2.1, the hazard rates of change from state i to state j, except for the zero covariate effect terms, are $e^{{\gamma }_{ij}+{\beta }_{ij}^1}$ and e^{γ_{i j}}, respectively, for subjects in the intervention and control groups. The interpretation of the coefficient ${\beta }_{ij}^1$ is the log hazard rate ratio of change from state i to state j for the intervention compared to the control. Note that the model described by the above matrix Q is the same as assuming zero covariate effects on the hazard rates of 1 → 4, 2 → 4, 3 → 1, 4 → 1. In principle, one can fit CTMC models with any number of zero covariate effects and/or put restrictions on any one-step transition. However, the model has to be biologically reasonable and must have enough data for estimation.

2.3 Bayesian model implementation

The likelihood function can be written as $L(\theta \mid y)={\prod }_{m=1}^M{\prod }_{k=2}^{K_m}{p}_{y(t_{m,k-1})y(t_{m,k})}(t_{m,k}-t_{m,k-1})$ , where θ is the vector of the model parameters that does not explicitly appear in the above expression. We selected a set of independent N(0,σ²) as priors for the parameters of interest. Often σ² = 100 is large enough to cover the parameter space and is considered as a flat prior. The implementation of the proposed Bayesian approach is similar to what was described in Ma [25]. Under that Bayesian approach for estimating general CTMC models without covariates [25], the likelihood was numerically evaluated using ordinary differential equations (GSL-GNU scientific library; http://www.gnu.org/software/gsl/). Specifically, the method of fourth-order Rungekutta was used to solve the transition probability of p_{y(tm,k−1)y(tm,k})(t_m,k − t_m,k−1). We developed a C program to sample the posterior distribution with the generic Metropolis Hastings algorithm. The C code is available at http://go.uth.edu/ctmc-with-covariate.

Informative priors can be employed as well, and may be derived using data from similar, previous studies. For example, the mean of q_{i j} can be approximately estimated for models without covariates [12]. Using historical data, we can specify a prior as a normal distribution with relatively small variance (e.g., 1) and centered at the resulting quantity for the mean of q_{i j}. Similarly, we may stratify the data to derive informative priors for covariate coefficients [7]. With different prior distributions, the posterior inferences will be inevitably affected, especially when the sample size is small [33]. Because prior knowledge is difficult to precisely specify, studies on prior sensitivities are conducted by comparing posterior inferences with a set of reasonable priors [33]. In this article, we exploited the flat priors of N(0, σ² = 100) for both our empirical and case studies. This setting of the prior distributions worked very well in both cases; hence, we did not further explore other priors.

2.4 Model comparisons and goodness-of-fit

We ran three parallel chains with over-dispersed initial values for both the empirical studies and analysis of the Next Step Trial data. We used the Brooks-Gelman statistic R̂ to monitor the convergence; if it was less than or equal to 1.1, the chains are considered to have converged [32]. Note that all results reported in this article meet the convergence criteria of R ≤ 1.1. Models are compared with the deviance information criterion (DIC), a broadly used Bayesian equivalent to Akaike’s information criterion (AIC) [32, 34–36]. Let y and θ denote the data and parameters, respectively. The DIC is based on the posterior distribution of the deviance statistic of D(y, θ) = −2log(L(y|θ)) and is defined as $\mathit{DIC}=2\overline{D(y,\theta )}-D(y,\overline{\theta })$, where θ̄ is a vector for the posterior means and $\overline{D(y,\theta )}$ is the average of the deviance over the posterior distribution. Similar to the formula of the AIC, the DIC can be defined as $\mathit{DIC}=\overline{D(y,\theta )}+p_D$. A smaller value of DIC indicates a better fitting model. The term of $\overline{D(y,\theta )}$ is an approximation of E{D(y, θ)} that captures the model fit; and the increasing model complexity is penalized by the effective number of parameters, which is defined as $p_D=\overline{D(y,\theta )}-D(y,\overline{\theta })$.

Much literature has addressed goodness-of-fit for CTMC models. Often this can be done by comparing the observed value to the expected value on the basis of a model [4, 6, 10, 21, 37]. A Pearson-type goodness-of-fit test statistic was derived to examine the stationary assumption of the Markov process; however, the test statistic does not have a known distribution [38]. Indeed, a bootstrap-based test was recommended [38]. Titman [39] recently developed a method that offers an improved approximation to the distribution of the Pearson-type test statistic. Under the Bayesian framework, we utilize the posterior predictive method to check the goodness-of-fit, which is similar to the bootstrap technique [25, 32, 38]. Let y^rep represent the predicted values of the data from our model and T(y, θ) be the test quantity (i.e., number of observed transitions in this study). The discrepancy between the fitted model and the data is measured by the Bayesian predictive p value, which is defined as p_B = Pr{T(y^rep, θ) ≥ T(y, θ)} [32]. A serious lack of fit is suggested if we observe that p_B ≥ 0.95 or p_B ≤ 0.05.

3 Empirical studies

In this section, we assess the accuracy of estimation for the proposed method. A total of one thousand duplicated data sets were simulated for a four-state CTMC model with three covariates, i.e., one binary type, one categorical type and one continuous type. For each generated data set, six hundred subjects were measured twenty-one times with observation time intervals equal to one. A Bernoulli distribution with probability equal to 0.5 was selected for the binary covariate. For the categorical covariate, a random sample from (0,1,2) was generated for each subject with probability of (1/3,1/3,1/3). The continuous covariate was generated from a normal distribution with N(0,36). The outcomes were assumed to follow a continuous time Markov chain with 4 possible states (1, 2, 3 or 4) specified in the infinitesimal rate matrix Q (equation 2) in Section 2.2. The true parameters are given in Tables 1 and 2. The observation time intervals were set to be equal to one for all subjects. For details of simulating continuous Markov chain data, see Ma [25]. Tables 1 and 2 are based on 933 data sets that have results that met the convergence criteria. A total of 80,000 samples were generated for each data set for implementing the Bayesian procedure, and the first half were dropped, leaving the second half for inferences. The sampling acceptance rates (the fraction of candidate draws that are accepted) were about 24%.

Table 1.

Bias, precision and coverage probabilities of the intercepts of the log-transformed transition rates using the proposed method; results are based on 933 duplicated data sets and observation intervals are equal to 1 time unit; PB: percentage of bias; SD: standard deviations of the point estimates; SE: square roots of the means of the estimated variances; MSE: means of the squared errors; CP: nominal coverage probabilities.

	γ12	γ13	γ14	γ21	γ23	γ24	γ31	γ32	γ34	γ41	γ42	γ43
TRUE	−1.050	−1.610	−2.120	−1.200	−0.690	−1.900	−2.300	−0.920	−1.200	−2.210	−1.560	−1.270
Bias	−0.006	−0.032	−0.010	0.002	−0.001	−0.017	−0.012	−0.001	−0.009	−0.002	−0.020	−0.016
PB(%)	0.590	2.015	0.477	−0.163	0.126	0.885	0.526	0.122	0.758	0.073	1.249	1.241
SD	0.126	0.190	0.138	0.106	0.096	0.122	0.133	0.103	0.090	0.107	0.148	0.119
SE	0.116	0.183	0.134	0.109	0.093	0.126	0.130	0.101	0.088	0.104	0.145	0.116
MSE	0.016	0.037	0.019	0.011	0.009	0.015	0.018	0.011	0.008	0.012	0.022	0.014
CP	0.924	0.948	0.936	0.955	0.941	0.953	0.946	0.933	0.943	0.939	0.937	0.944

Table 2.

Bias, precision and coverage probabilities of the covariate effects using the proposed method; results are based on 933 duplicated data sets and observation intervals are equal to 1; PB: percentage of bias; SD: standard deviations of the point estimates; SE: square roots of the means of the estimated variances; MSE: means of the squared errors; CP: nominal coverage probabilities.

Coefficients for a binary covariate
	${\beta }_{12}^1$	${\beta }_{13}^1$	${\beta }_{21}^1$	${\beta }_{23}^1$	${\beta }_{32}^1$	${\beta }_{34}^1$	${\beta }_{42}^1$	${\beta }_{43}^1$
TRUE	0.300	0.210	0.120	0.150	−0.210	0.110	−0.110	0.060
Bias	0.011	−0.023	0.000	0.011	0.001	0.009	0.003	0.006
PB(%)	3.720	−10.697	−0.303	6.971	−0.502	7.782	−2.310	9.393
SD	0.125	0.202	0.113	0.101	0.118	0.087	0.153	0.124
SE	0.127	0.202	0.116	0.099	0.113	0.085	0.149	0.124
MSE	0.016	0.041	0.013	0.010	0.014	0.008	0.023	0.015
CP	0.960	0.949	0.961	0.950	0.943	0.950	0.939	0.951

Coefficients for a 3-category covariate
	${\beta }_{12}^2$	${\beta }_{13}^2$	${\beta }_{21}^2$	${\beta }_{23}^2$	${\beta }_{32}^2$	${\beta }_{34}^2$	${\beta }_{42}^2$	${\beta }_{43}^2$
TRUE	0.150	0.100	0.100	0.050	−0.070	0.100	0.050	−0.070
Bias	0.008	−0.011	0.001	0.003	−0.001	0.002	0.001	0.002
PB(%)	5.522	−10.685	1.229	5.161	2.016	1.452	2.187	−3.089
SD	0.082	0.129	0.071	0.062	0.071	0.051	0.090	0.077
SE	0.079	0.125	0.072	0.060	0.069	0.051	0.091	0.075
MSE	0.007	0.017	0.005	0.004	0.005	0.003	0.008	0.006
CP	0.936	0.940	0.955	0.946	0.936	0.956	0.944	0.949

Coefficients for a continuous covariate
	${\beta }_{12}^3$	${\beta }_{13}^3$	${\beta }_{21}^3$	${\beta }_{23}^3$	${\beta }_{32}^3$	${\beta }_{34}^3$	${\beta }_{42}^3$	${\beta }_{43}^3$
TRUE	−0.025	−0.020	0.030	−0.020	0.018	0.015	−0.020	−0.016
Bias	0.000	0.002	0.001	0.000	0.000	0.000	0.000	0.000
PB(%)	0.591	−7.264	1.661	0.855	0.945	−1.689	1.801	−0.312
SD	0.011	0.017	0.010	0.008	0.010	0.007	0.013	0.011
SE	0.011	0.017	0.010	0.008	0.010	0.007	0.013	0.010
MSE	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
CP	0.936	0.949	0.952	0.954	0.945	0.953	0.951	0.936

This model contains a relatively large number of parameters. To fully examine the proposed method, the percentage of bias (PB) for each parameter is reported along with its bias, standard deviation (SD), square root of the mean of the estimated variance (SE), mean of the squared error (MSE), and nominal coverage probability (CP). Note that the percentage bias is calculated as the bias divided by the true value times 100. As we can see, all the biases are small, albeit there are three parameters with PB around 10% in Table 2. In addition, most parameters have a nominal coverage probability near 95%, and the range of the CP for all parameters is between 92.4% and 96.0%. We conclude that, overall, the proposed method offers accurate and precise estimates. The R package of MSM has the option to fit models with covariates [21]. Using that package, we experienced a high rate of convergence failure; therefore, we did not apply that package here.

4 Case study

In this section, we introduce data from the Next Step Trial and then describe our application of the proposed method of CTMC models.

4.1 The Next Step Trial

We used the CTMC model to examine the nutrition intervention effect on stages of change in fat intake using data from the Next Step Trial, a randomized trial of colorectal cancer screening promotion and nutrition intervention programs. In this two-year study, twenty-eight worksites were randomized to a control program (a company-sponsored screening program) or an intervention program (an enhanced screening program) [40–42]. The sites randomized to the screening intervention were also given the Next Step Trial nutrition intervention. The control sites were not given the nutrition intervention. Less than 5% of the participants were female; therefore, the female participants were excluded from the analysis. Of the 4,845 male subjects enrolled at baseline, 56.8% (n=2,754) completed dietary assessments with no missing values for the stages of change in fat intake. We included only subjects with a baseline assessment of the stages of change, for reasons discussed by Tilley et al. [42] and as in the Catch trial [43].

In the Catch trial, subjects who did not give blood samples at baseline were excluded. In the Next Step Trial, subjects who did not have the stages of change measured at baseline were excluded from the analysis of the stages of change. In addition, to compare our results to those of Kristal et al.[16], we included only the subgroup of 1,758 (response rate of 63.8%) subjects who completed the dietary assessments at three survey time points: baseline, year 1 and year 2. Among the subjects in this subgroup, the mean age at baseline (±SE) was 58.3 ± 10.6 years and the mean years of education (±SE) was 13.6 ± 2.6. Almost half of this study population was retired (48.5%); the majority was white (97%) and married (90%). Compared to the total male subjects (n=4,845) enrolled at baseline, subjects included in this analysis (n=1,758) were more likely to be older, retired, married, and white. Given the randomized design, the Next Step Trial investigators concluded that, “comparison of intervention and control worksites {the 2,754 subjects who completed the baseline survey} would not be biased unless there was a differential response to the survey between intervention and control sites, a situation that did not occur” [40], p. 234. There was also no difference in response by the intervention and control in the 1,758 subjects (p-value=0.18). Sixteen subjects who had missing values of years of education, were also excluded from the data analysis. The observational time intervals varied among subjects. The average length of observational time intervals between surveys in the 1,758 subjects was 1.04 years, and the median was 1.03 years (95% were within 0.78–1.29 years).

The Next Step Trial was randomized by worksites rather than by subjects. We investigated how the intervention, and the age and educational levels of the subjects affected the stages of change in fat intake. Years of education was redefined as educational levels with three categories: less than or equal to 12 years, greater than 12 years and less than 16 years, and equal to or greater than 16 years. Age was centered at the mean to avoid numerical issues. Originally, there were five stages of the outcome variable under the TTM framework: precontemplation, contemplation, preparation, action, and maintenance [44]. The number of observed transitions from/to the stage of preparation was not large enough for estimation, and it was combined with the stage of contemplation. Thus, there were four stages of the outcome variable: precontemplation (P, coded as 1), contemplation (C, coded as 2), action (A, coded as 3), and maintenance (M, coded as 4). The number of observed transitions were (125, 65, 74, 23) from stage P to stages P, C, A and M; (72, 217, 265, 58) from stage C to stages P, C, A and M; (54, 220, 896, 305) from stage A to stages P, C, A and M; and (32, 83, 259, 736) from stage M to stages P, C, A and M, respectively.

4.2 Results from CTMC models

Three parallel Markov chain Monte Carlo (MCMC) chains were run for each model, and each chain was generated with 120,000 iterations. The first half of the iterations was discarded as burn-in, and inferences were based on the second half of the samples. All results reported here were with R ≤ 1.1. The acceptance rates were all around 23%.

When fitting CTMC models, especially models with covariates, it is important to know that some parameters may not be well estimated due to the lack of information from the data. Numerical problems may occur and some additional assumptions may be needed for estimation[6]. In the study of Ma [25], a model with the same data set without any covariates was run, and the hazard rates were estimated as 0.002 and 0.017 for one-step transitions of 2 → 4 and 3 → 1. Thus, we did not allow for the one-step transition of 2 → 4 for all models, but allowed for the one-step transition of 3 → 1 for some models (Table 3).

Table 3.

Modeling summary and statistics; parameters of ${\beta }_{13}=({\beta }_{13}^1,{\beta }_{13}^2,{\beta }_{13}^2),{\beta }_{41}=({\beta }_{41}^1,{\beta }_{41}^2,{\beta }_{41}^3)$, are set to zero for all models; P_D: effective number of parameters; DIC: deviance information criteria; (γ₁₃ = γ₁₃ = −∞) indicates that one-step transitions 3→1 and/or 2→4 are not allowed. Intervention n=845, control n=897.

Model	PD	Nominal number parameters	DIC	Covariates	Restrictions on baseline transition parameters
A	27.4	29	7259.5	Intervention, age and education level	γ24 = ∞
B	21.3	23	7254.9	Intervention and age	γ24 = ∞
C	19.8	22	7256.0	Intervention and age	γ24 = ∞, γ13 = ∞
D	22.0	23	7285.3	Intervention and education level	γ24 = ∞
E	21.4	22	7285.7	Intervention and education level	γ24 = ∞, γ13 = ∞

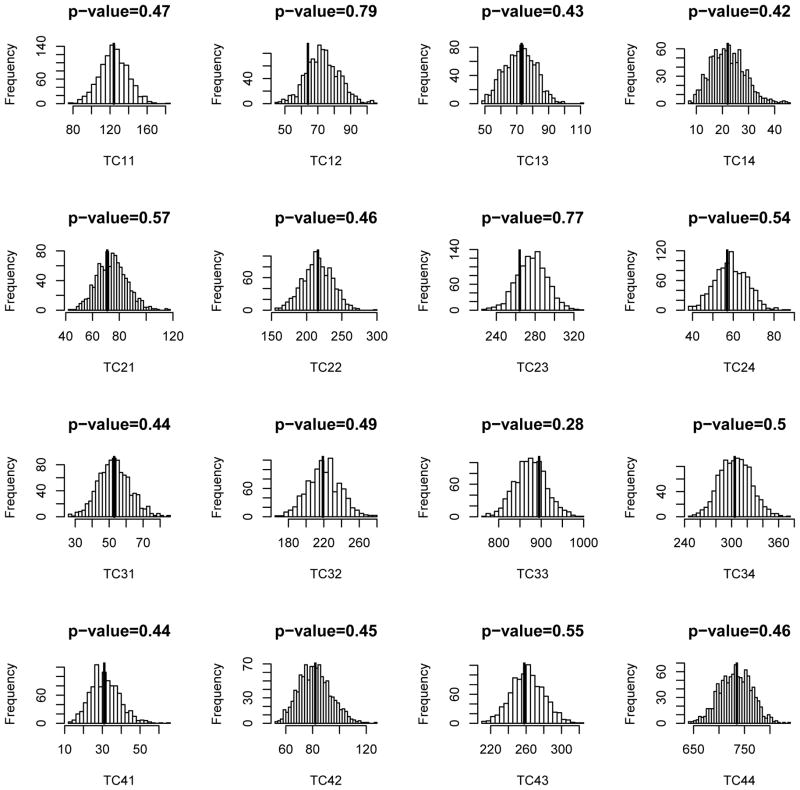
The goal is to find the most parsimonious model that adequately describes the data. This can be done through model selection strategies using DIC. Five models were considered and their corresponding specifications along with the values of DIC are displayed in Table 3. In model A, three covariates were considered: intervention (binary), educational levels (categorical) and age (continuous). Also, the one-step transition of 2 → 4 was not allowed (or equivalently γ₂₄ = −∞); and parameters of ${\beta }_{13}=({\beta }_{13}^1,{\beta }_{13}^2,{\beta }_{13}^3)$ and ${\beta }_{41}=({\beta }_{41}^1,{\beta }_{41}^2,{\beta }_{41}^3)$ were set equal to zero due to the convergence issue. Indeed, β₁₃ and β₄₁ were set equal to 0 for all models in Table 3. Similarly, specifications of models B, C, D and E can be found in Table 3. Educational level had no statistically significant effect on any hazard rates, so it is not surprising that models D and E have relatively large values of DIC compared to the others. Model B had the smallest value of DIC, thus we consider it to be the best model among those we investigated here. The results for model B are displayed in Tables 4 and 5. The goodness-of-fit was also checked (Figure 1). Since all Bayesian p values are moderate, we conclude that there is no observed discrepancy between the fitted model and the data.

Table 4.

Estimates of the intercepts of the log-transformed transition rates; SE: standard errors; LB/UB: lower/upper bound of 95% credible intervals. Intervention n=845, control n=897.

	γ12	γ13	γ14	γ21	γ23	γ31	γ32	γ34	γ41	γ42	γ43
Mean	−0.819	−1.988	−2.832	−1.205	0.020	−4.472	−0.903	−1.151	−3.514	−2.509	−0.975
SE	0.223	0.804	0.775	0.194	0.110	1.308	0.131	0.088	0.409	0.297	0.120
LB	−1.274	−4.343	−4.870	−1.614	−0.191	−7.742	−1.160	−1.326	−4.461	−3.151	−1.218
UB	−0.392	−1.062	−1.875	−0.851	0.242	−3.009	−0.644	−0.978	−2.841	−2.011	−0.754

Table 5.

Estimates of covariate effects of the transition matrix parameters*; SE: standard errors; LB/UB: lower/upper bound of 95% credible intervals; credible intervals that do not cover 0 are highlighted in boldface. Intervention n=845, control n=897. Upper script “1” and “2” represent coefficients of intervention and age, respectively; lower script “i j” represents transition from i to j. For example, ${\beta }_{12}^1$ is the intervention coefficient for transition 1 to 2, and ${\beta }_{43}^2$ is the age coefficient for transition 4 to 3.

	Intervention Effects						Age Effects
	${\beta }_{12}^1$	${\beta }_{21}^1$	${\beta }_{23}^1$	${\beta }_{32}^1$	${\beta }_{34}^1$	${\beta }_{43}^1$	${\beta }_{12}^2$	${\beta }_{21}^2$	${\beta }_{23}^2$	${\beta }_{32}^2$	${\beta }_{34}^2$	${\beta }_{43}^2$
Mean	0.986	0.281	0.132	−0.269	0.185	−0.118	−0.005	0.018	−0.004	0.002	0.027	−0.004
SE	0.257	0.293	0.144	0.181	0.119	0.157	0.011	0.013	0.006	0.008	0.006	0.007
LB	0.471	−0.274	−0.164	−0.627	−0.051	−0.423	−0.026	−0.007	−0.016	−0.015	0.016	−0.018
UB	1.476	0.852	0.408	0.090	0.420	0.182	0.018	0.044	0.008	0.019	0.039	0.010

Figure 1.

Bayesian predictive p-values for Model B and results are based on 1000 duplicated data sets. The dark lines represent the observed transition counts. Precontemplation, contemplation, action and maintenance are represented by 1, 2, 3, and 4, respectively; TC12, for example, is for transitions from precontemplation to contemplation

As we can see in Table 5, there was a statistically significant effect of the intervention on the hazard rate from precontemplation to contemplation, ${\beta }_{21}^1$ (0.968, CI: 0.471–1.476). The abbreviation CI represents the Bayesian 95% credible interval throughout this article, unless otherwise specified. The coefficients can be interpreted as log hazard rate ratios as in the Cox model [13, 21]. The hazard rate ratio is defined, for example, as $e^{{\beta }_{21}^1}$, and can be calculated from the posterior MCMC samples, which is 2.77 (CI: 1.601–4.378). Note that all the hazard rate ratios hereafter are similarly calculated. Thus for subjects in the intervention group, the hazard rate of the change in state from precontemplation to contemplation (a relatively higher and healthier status), on average, was about 2.77 times the hazard rate for subjects in the control group after adjusting for age. Note that the hazard rate ratio and the 95% credible interval were calculated using an MCMC algorithm, with half of the posterior samples. Further, for age, the hazard rate ratio for the one-step transition from action to maintenance was 1.027 (CI: 1.016–1.039) in the model that includes the intervention. Hence, on average, the hazard rate increases 1.027 times for every one-year increase in age after adjusting for the intervention.

In practice, we may be interested in the mean sojourn time on each state and the one-year transition probabilities for a subgroup or a specific subject. These statistics were calculated with an MCMC algorithm, using the samples for the posterior distributions. The results shown in Table 6 and Table 7 are based on model B. Table 6 presents the one-year transition probabilities for subjects who were 58.3 years of age (the mean age of the population) in the control and intervention groups, respectively; and the differences between these probabilities were also calculated. As one can see from Table 6, a subject who was 58.3 years of age and was treated with the control program had higher probability of transferring from relatively higher stages to lower stages. These differences (and their credible intervals) in the probability of transferring stages are reported as M→C (0.01; CI: 0–0.021), M→P (0.006; CI: 0.001–0.011), and A→C (0.042; CI: 0.006–0.076). Similarly, this individual had lower probability of moving from relatively lower stages to higher stages, with differences in the probabilities reported as P→C (−0.118; CI: −0.183–0.044), P→A (−0.1; CI: −0.164–0.042), C→M (−0.025;CI: −0.049–0.002) and A→M (−0.044; CI:−0.083–0.006). One may also notice that this individual had much higher probability of being at stage P, with the difference in the probability (and the credible interval) P→P (0.231; CI: 0.113–0.335). This is reflected by the mean sojourn time in Table 7, i.e., on overage, an individual spent 0.752 (CI:0.343–1.166) more years in the stage of precontemplation when randomized to the control group compared with those in the intervention group who were of the same age (58.3 years).

Table 6.

Comparisons of the estimated one-year transition probabilities for subjects who are 58.3 years of age (mean age of the study population), between intervention and control groups in the Next Step Trial. Difference is calculated as transition probabilities for subjects in control group minus those for subjects in the intervention group; Stages in this study are precontemplation (P), contemplation (C), action (A) and maintenance (M). Credible intervals (CI) that do not cover 0 are highlighted in boldface. Intervention n=845, control n=897.

Transition	Control			Intervention			Difference
	Mean	CI(95%)		Mean	CI(95%)		Mean	CI(95%)
P-P	0.534	0.460	0.605	0.303	0.222	0.390	0.231	0.113	0.335
P-C	0.200	0.148	0.260	0.318	0.254	0.378	−0.118	−0.183	−0.044
P-A	0.198	0.142	0.263	0.298	0.244	0.351	−0.100	−0.164	−0.042
P-M	0.068	0.036	0.107	0.081	0.056	0.110	−0.013	−0.028	0.001
C-P	0.128	0.094	0.165	0.109	0.078	0.145	0.020	−0.027	0.065
C-C	0.366	0.316	0.420	0.327	0.279	0.381	0.039	−0.029	0.107
C-A	0.425	0.381	0.470	0.459	0.411	0.505	−0.034	−0.096	0.032
C-M	0.080	0.066	0.097	0.106	0.088	0.124	−0.025	−0.049	−0.002
A-P	0.040	0.029	0.053	0.032	0.023	0.041	0.009	−0.003	0.020
A-C	0.173	0.146	0.201	0.131	0.108	0.156	0.042	0.006	0.076
A-A	0.601	0.565	0.636	0.607	0.573	0.641	−0.006	−0.053	0.042
A-M	0.186	0.161	0.213	0.230	0.201	0.260	−0.044	−0.083	−0.006
M-P	0.030	0.020	0.043	0.024	0.017	0.034	0.006	0.001	0.011
M-C	0.078	0.063	0.095	0.068	0.053	0.085	0.010	0.000	0.021
M-A	0.244	0.207	0.281	0.229	0.196	0.265	0.015	−0.034	0.065
M-M	0.648	0.606	0.689	0.679	0.640	0.716	−0.031	−0.087	0.023

Table 7.

Comparisons of the estimated mean sojourn times of being at stages of precontemplation (P), contemplation (C), action (A), and maintenance (M) for subjects who are 58.3 years of age (mean age of the study population) between intervention and control groups in the Next Step Trial. Difference is calculated as mean sojourn time for subjects in control group minus those for subjects in intervention group; credible interval that does not cover 0 is highlighted in boldface.

Stages	Control			Intervention			Difference
	Mean	CI(95%)		Mean	CI(95%)		Mean	CI(95%)
P	1.457	1.144	1.830	0.705	0.495	0.941	0.752	0.343	1.166
C	0.758	0.617	0.913	0.639	0.511	0.787	0.118	−0.064	0.294
A	1.349	1.143	1.573	1.409	1.210	1.623	−0.059	−0.345	0.236
M	2.026	1.721	2.372	2.215	1.880	2.591	−0.190	−0.678	0.278

5 Discussion

We reanalyzed the Next Step Trial data using a generalized multinomial logit model. We included only age and the intervention as covariates. The dependent variables were all the possible transitions, consisting of sixteen categories for the entire duration of the study. The transition from precontemplation to precontemplation was used as the referent outcome. Some confusing results were found in this analysis. For example, the calculated odds ratio of making a transition from A to C was 2.005 (confidence interval: 1.248–3.221) for subjects in the intervention group compared with those in the control group; however, the results in Table 6 show that subjects in the intervention group had lower probabilities of moving from A to C. Further investigation revealed that the proportions in the action state at baseline were 43.7% and 38.4% for the intervention and control groups, respectively. As a result, the odds ratio was still large even though the transition probability from A to C was lower in the intervention group compared with the control group (Table 6). This is well understood because the temporal correlation between successive measurements is ignored by the GMLM. In addition, a more sensible modeling strategy is to fit multiple GMLMs with outcome variables (transitions) conditional on the previous states. Specifically, each GMLM has S-level outcomes that represent the state at the next observation, conditional on the state at the current observation. This approach correctly models the relations between the covariates and transitions; however, it still does not take into account the varying time intervals between observations. Its application is limited to studies in which the observational time intervals are fixed. Hence, predictions may not be made for time intervals other than the fixed intervals [17].

In contrast, CTMC models incorporate the information of the observation time intervals, which is especially useful when time intervals are unequally spaced, such as in our case study. Results from this method consistently show the existence of the intervention effects. For example, a statistically significant hazard rate ratio in favor of the intervention was found for the transition rate moving from precontemplation to contemplation (Table 5). The absolute differences in the transition probabilities between the control and intervention groups were 0.231, −0.118 and −0.1 for transition probabilities from precontemplation to precontemplation, and contemplation, respectively (Table 6). The hazard rate ratios for the intervention of moving from action to contemplation and maintenance were 0.776 (CI: 0.537–1.095) and 1.212 (CI: 0.950–1.521), respectively (calculated from posterior samples). Although the hazard rate ratio for change from action to maintenance was not statistically significant, its lower bound is close to 1. Similarly, for the hazard rate of the change from action to contemplation, it seems that subjects in the intervention group had less risk of moving to a relatively less healthy state, though the finding was not statistically significant. These are reflected by differences (between the control and intervention groups) in the transition probabilities from action to maintenance (−0.044, CI: −0.083–0.006) and contemplation (0.042, CI: 0.006–0.076), respectively.

When fitting a CTMC model, several researchers have reported a numerical issue and suggested some strategies to handle these problems [4, 6, 7, 21, 24]. In our approach, we first fit the model without the covariates, and assign zero to those hazard rates that are around zero. In some cases, we only assign zero to coefficients of that one-step transition and keep the hazard rate positive. Indeed, we estimated covariate effects on adjacent states while keeping all intercepts of the log-transformed hazard rates in our case study, except for the one-step transition of contemplation to maintenance. A common model fitting strategy available in the literature is to assume the same covariate effects as discussed in Section 2.2. In this approach, although parameters are dramatically reduced, the assumptions are stronger and hence less attractive. While researchers try to find a model that answers the scientific question, model assumptions and issues of estimations need to be carefully considered.

From the methodology point of view, the proposed method is attractive in that the complicated analytical form can be avoided and the method can be easily extended to models with more than four states. However, models must be biologically reasonable and have enough data for estimation. Another benefit of using the Bayesian approach in estimating the CTMC model is that many statistics can be calculated using an MCMC technique, as illustrated in Section 4.2. Since these statistics are often functions of model parameters, the asymptotic normality assumptions may be required to calculate the standard errors under the frequentist framework. Due to the complex form of the likelihood function, the asymptotic assumption may not work as desired. Previous knowledge may be incorporated as informative priors under our Bayesian framework, which is helpful, especially in scenarios when a data set is relatively small for a given number of parameters [27, 32]. However, one shall be cautious in assigning priors that reflect substantive information. As Muller [27] demonstrated, models that use “incorrect” priors are unstable and may generate misleading results.

6 Limitations and conclusions

It is important to acknowledge that the approach for estimating the intervention effects in our analysis has some limitations, and the results found in this article may only apply to our baseline population with complete information. Compared to the total survey response sample (n=2,754) with at least one measurement, participants (n=1,758) who completed all three assessments were more likely to be older and retired. Compared to subjects (n=996) who completed the baseline assessment but not all the follow-up assessments, subjects included in this analysis (n=1,758) were more likely to be older, married and retired [16]. However, the response rates are similar between the intervention and control groups. In addition, there were no detected differential responses in terms of age, race, employee status (retirees versus active employees), or marital status (married versus others) for the intervention and control groups. Thus, we believe the comparison of intervention and control groups are unlikely to be biased due to response bias, as discussed by Tilley et al. [40].

Another limitation is the complexity of the CTMC models. We considered only three covariates of intervention, age and educational levels, and did not adjust for marital status and employee status. We fitted a GMLM with intervention, age and an interaction term against transitions for stages of change in fat intake; we found that the interaction term was not statistically significant using the likelihood ratio test. Similar results were found for the covariates of marital status and employee status. Thus, age, marital status and employee status were unlikely to be confounders.

Moreover, we ignored the fact that the Next Step Trial was randomized by twenty-eight work-sites, and therefore the correlation among subjects within the same worksite was not taken into consideration in our models. As a result, our findings of the intervention effects may be less conservative compared with results that adjusted for the within-cluster correlation. One way to handle this issue is to use random-effect models to account for the cluster effects. Although using random-effect models is not new in CTMC models [14, 22, 23], applications in our setting, e.g., general CTMC models, have not yet been published. In future research, we will evaluate the intervention effects of the Next Step Trial data while considering the cluster effects due to the worksite randomization. In our analysis, subjects are assumed to follow a homogeneous first-order continuous time Markov process, but this assumption may be violated. Some methods have been proposed to address situations where the homogeneity does not hold, e.g., using piecewise constant transition intensities [4], or using time transformation [45]. This can be another direction for future applications of our modeling approach.

An important question for our study is whether it is plausible in psychological studies that individuals change their current states directly to any of the other states, including jumping, say, from contemplation to maintenance. This issue is important when fitting CTMC models as they must be biologically reasonable [6]. Regarding behavioral changes, several studies showed that individuals make “spontaneous” decisions. For instance, more than half of the smokers in one study made sudden decisions to attempt to quit smoking without making any preparations [19]. Another study reported that quite a few individuals experienced progressions from pre-action stages to the maintenance stage, and the authors argued that “spontaneous transitions in stages of change may occur” [20], p. 5. Furthermore, discrete time Markov chain models have been employed in the setting of TTM, and the authors have correctly pointed out that this approach is limited due to the lack of providing important information of the process within the observational time intervals [17]. Nevertheless, without considering any covariates, we conducted an analysis, assuming only adjacent instantaneous transitions in both directions, between P and C, between C and A, and between A and M. The goodness-of-fit test detected obvious discrepancies (Bayesian p-values greater than 0.95 or less than 0.05) between the data and the model (results not shown); hence, alternative models may fit the data well [25]. Though these results are supportive, further investigations might be needed; however, these are beyond the scope of this article.

The proposed CTMC model incorporates the observational time intervals and is very useful when these intervals are unequally spaced. This novel Bayesian approach enabled us to fit different CTMC models without requiring an analytical form of the likelihood, which can be mathematically difficult [12]. The CTMC model was evaluated via a simulation study that showed that the parameters were accurately and precisely estimated. This model not only confirms that the nutrition intervention in the Next Step Trial was effective, but also provides information on how the intervention affected the transitions among the stages of change. Information on the patterns of transition may be helpful to improve the intervention design for future studies in health promotion. To the best of our knowledge, this is the first use of the Bayesian approach to analyze the relationship between longitudinal categorical outcome data and multiple covariates under the framework of the general four-state CTMC model.