Incorporating the sampling design in weighting adjustments for panel attrition

Abstract

We review weighting adjustment methods for panel attrition and suggest approaches for incorporating design variables, such as strata, clusters and baseline sample weights. Design information can typically be included in attrition analysis using multilevel models or decision tree methods such as the CHAID algorithm. We use simulation to show that these weighting approaches can effectively reduce bias in the survey estimates that would occur from omitting the effect of design factors on attrition while keeping the resulted weights stable. We provide a step-by-step illustration on creating weighting adjustments for panel attrition in the Galveston Bay Recovery Study, a survey of residents in a community following a disaster, and provide suggestions to analysts in decision making about weighting approaches.

1. Introduction

Panel surveys collect similar measurements on the same sample at multiple points of time [1]. As with other longitudinal studies, panel surveys are subject to dropout or panel attrition. If individuals who respond are different from those who drop out, statistical analysis based only on complete respondents can lead to biased statistical inference.

In cross-sectional surveys, weighting adjustments are often made for unit nonresponse when a sampled individual does not respond to the entire survey, and imputation is commonly used to handle item nonresponse for individuals who do not respond to particular questions. Unit and item nonresponse also arise in panel surveys and can be handled similarly using weighting and imputation, respectively. However, the choice between weighting and imputation is more complicated with panel attrition. Specifically, with weighting, information collected for panel nonrespondents in the initial waves is discarded, which results in a waste of costly collected data. On the other hand, with imputation, missing responses in the entire wave need to be imputed, which causes concerns about attenuation of covariance between variables. Further discussion of weighting and imputation for panel attrition can be found elsewhere [2–5]. Imputation with well-chosen models is more efficient than weighting, but we focus on weighting in this paper given that weighting has been widely used in many public health studies.

To remove attrition bias in estimating population quantities, weighting adjustments need to account for the large amount of information available on both respondents and nonrespondents, such as the survey responses collected in the initial waves of the survey [6]. When complex designs are used in the baseline survey, the set of variables about the sampling design also need to be considered. Because of confidentiality restrictions, not all such variables might be available. Instead, it is common for datasets to include a single weight variable that accounts for both sampling design and unit nonresponse in the baseline, and also strata and clusters if stratified or cluster sampling is used. With the availability of design information in the forms of base weights, strata and clusters, no consensus exists as to the best way to incorporate design information into the weighting adjustment for panel attrition. Survey practitioners would benefit from clear guidelines on how to create weighting adjustments using all the available information, most notably with these three design variables.

This paper has four parts. First, we review weighting adjustment methods and suggest approaches for incorporating the design variables, such as base weights, strata and clusters. Second, we provide a step-by-step demonstration on the application of various weighting approaches for panel attrition in a real data example. Third, we illustrate through simulation that these approaches for incorporating design variables are effective in reducing attrition bias while keeping the resulted survey estimates stable. Finally, we make suggestions to analysts in decision making about weighting approaches for panel attrition.

2. Methods for Creating Weighting Adjustments

2.1. Adjustment Cell Weighting

A common method to compensating for panel attrition is to form weighting adjustment cells of homogeneous sample units based on p auxiliary variables, X = (X₁, X₂, …, X_p)^T, that are observed for both respondents and nonrespondents [7]. Continuous variables are categorized, so that X_j has c_j levels, j = 1, 2, …, p. These variables are cross-classified to form $L={\prod }_{j=1}^p{c}_j$ adjustment cells, with n_l units of respondents and nonrespondents combined in the lth adjustment cell, l = 1, 2, …, L. Let r_il denote the panel response status for the ith unit in the lth cell, with 1 for respondents and 0 for nonrespondents, so that the number of respondents in the lth cell is $m_l={\sum }_{i=1}^{n_l}{r}_{il}$. The response rate in the lth cell is then estimated using π̂_l = m_l/n_l, and the weighting adjustment for respondents in the lth cell is 1/π̂_l. The nonresponse adjustment cell method requires both m_l and n_l to be large enough in each cell to obtain a stable response rate estimate. When p is large, some of the adjustment cells can be small. As a result, some cells may contain few or even no respondents, and the estimated response rates π̂_l may vary a lot in different cells. Therefore, adjacent adjustment cells with similar estimated response rates are often collapsed to ensure a certain number of respondents and a certain ratio of respondents to nonrespondents in each cell.

When many variables are available, the chi-square automatic interaction detection (CHAID) algorithm [8] is often used to select variables for forming adjustment cells [3, 4, 9–11]. CHAID splits a dataset progressively via a tree structure by choosing variables that maximize a chi-square criterion in each split. Specifically, the algorithm proceeds with two steps: merging and splitting. For each predictor X_j, a chi-square test is used to test independence between any pair of categories and attrition. The pair of categories that has the largest p-value is merged into a single category if the p-value is larger than the user-specified alpha-level for merging. The merging step continues until no more non-significant pairs of categories for each predictor. The p-value is then calculated using Bonferroni adjustments to account for the number of possible ways each predictor can be merged. These adjusted p-values are used to split the node. The predictor that has the smallest adjusted p-value defines the first split. The tree-growing process continues until no more predictors have adjusted p-values less than a user-specified alpha-level for splitting or until the split of a node results in a child node that has too few cases. At the end of the tree-building process we have a series of terminal nodes that are significantly different from one another on the attrition rate. The terminal nodes define the adjustment cells.

2.2. Response Propensity Weighting

Another method frequently used to handle nonresponse in sample surveys is response propensity weighting, an extension of the propensity score method of Rosenbaum and Rubin [12] to survey nonresponse [13]. Let r_i denote the panel response status for the ith unit in the sample and X_i = (X_i1, X_i2, …, X_ip) denote auxiliary variables that are important predictors of r_i. A logistic regression model is often used to estimate the response propensity:

$$\text{logit}\{Pr(r_i=1\mid {\mathit{X}}_i)\}={\beta }_0+{\beta }_1{X}_{i1}+\cdots +{\beta }_p{X}_{ip}.$$ (1)

To obtain the list of predictors X_i in model (1), an initial screening is often first performed to reduce the number of predictors to a more manageable size, by examining bivariable associations between each of the auxiliary variables and attrition. Model (1) is then fitted on the identified subset of auxiliary variables and coupled with additional steps such as variable selection and inclusion of interactions. Weighting adjustments for panel respondents are equal to the reciprocals of estimated response propensities $\widehat{Pr}(r_i=1\mid {\mathit{X}}_i)$ obtained from model (1).

Response propensity weighting has been widely used in practice. Some applications include the Survey of Income and Program Participation Survey [9] and the Medical Expenditure Panel Survey [14, 15]. But the method has two potential limitations. First, the effect of weighting adjustments in reducing nonresponse bias largely relies on correct specification of the response propensity model. If model (1) is misspecified, the weighted estimators of the population quantities are likely to be biased. To remedy this problem, Giommi [16] proposes kernel smoothing and daSilva and Opsomer [17] propose local polynomial regression to estimate the response propensities. Secondly, some respondents can have very small estimated response propensities and thus receive very large weights, which in turn leads to high variance of the weighted estimators of the population quantities. A common remedy is to trim large weights [18–20]. The most common form of weight trimming method is to pick a cutpoint w₀, force weights above this cutpoint to be w₀, and multiply weights under this cutpoint by a constant so that the sum of the trimmed weights equal to the sum of weights before trimming.

Alternatively, Little [21] proposes a response propensity stratification method, which forms adjustment cells based on the estimated response propensities. Specifically, the estimated response propensities from model (1) are first ordered; respondents and nonrespondents with similar estimated response propensities are grouped to form adjustment cells; and respondents in each cell are weighted by the inverse of response rate in that cell. Since the estimated response propensities are used only for the purpose of forming adjustment cells, the response propensity stratification method relies less on correct specification of the response propensity model. Furthermore, by forming adjustment cells, we can avoid large weighting adjustments due to small estimated response propensities.

2.3. Auxiliary Variables for Weighting Adjustments

Rizzo, Kalton, and Brick [9] suggest that the choice of auxiliary variables could be more important than the choice of methods for creating weighting adjustments. The auxiliary variables used for weighting adjustments should be predictors of panel attrition and predictors of outcomes of interest, so that including these variables in creating weighting adjustments can generally reduce attrition bias and improve efficiency in the survey estimates [21–23]. Such variables include survey responses in the initial waves of the panel survey and variables measuring sample units’ cooperation. Variables measuring cooperation include the amount and patterns of item nonresponse in the initial waves of the survey and call history variables, such as number of calls and whether a respondent was ever a refusal in the baseline survey [24–27]. These cooperation variables can have great predictive power for panel attrition, because a sampled individual being hard to reach in the first wave interview can be considered as a negative reaction to the request to participate in the survey, thus increasing the probability of attrition in the subsequent waves. With a large number of candidate auxiliary variables, a desirable weighting adjustment method should be able to incorporate a large number of auxiliary variables without creating weighting adjustments that are too noisy to be useful.

2.4. Simple Approaches for Incorporating Design Variables

When complex sample designs are used to select sample units in the initial waves of survey, design features also need to be considered in the weighting adjustment for panel attrition. However, the set of variables used in the sample design are usually not included in the datasets because of confidentiality restrictions. Instead, it is more common to only include a single base weight variable that reflects the complex sampling design and unit nonresponse in the baseline. If stratified or cluster sampling is used, the strata and clusters are also included. A question then arises on how to incorporate the base weights, strata and clusters into attrition analysis. In the adjustment cell method, it is common practice to include the base weights by calculating the weighting adjustment using the inverse of weighted response rate in each adjustment cell, where units are weighted by their base sample weights. In the response propensity model, the coefficients in model (1) are estimated using weighted logistic regression. Little and Vartivarian [28] show that the weighted response rate yields biased estimates of population quantities if design variables are related to nonresponse and is unnecessary if design variables are unrelated to nonresponse, and that weighting the logistic regression by the sample weight does not offer any advantage over unweighted regression. Instead they suggested cross-classifying design variables with other auxiliary variables to create weighting adjustment cells or including the design variables as predictors in the response propensity model.

Following Little and Vartivarian [28], we suggest some simple approaches for incorporating these three design variables in the adjustment cell and response propensity methods. Our goal is to create weighting adjustments that can minimize the bias that would occur from omitting key design factors while keeping the resulted weights stable. The first approach is to include design variables as categorical variables in the CHAID model for attrition. Specifically, the classification tree for panel attrition is built from inputs of (X, Z), where Z are design variables including strata, clusters and base weights and X are other auxiliary variables. Clusters with similar response rates are collapsed in the merging step of the CHAID algorithm and the collapsed clusters with response rates that are significantly different from others are used to split data into different adjustment cells. To account for the effect of stratification and weighting in the sample design, strata with similar response rates and proxy variables (e.g. geographically location) are first collapsed and the base weight is then dichotomized at the median in each collapsed stratum to catch the interaction effect between stratum and sample weight on attrition.

The second approach is to incorporate the design variables in the response propensity weighting using multilevel models. A multilevel response propensity model can naturally handle the cluster effect using varying intercepts across clusters. When there are no interaction effects on attrition between strata, base weights and other auxiliary variables X, they can all be included in the multilevel model as predictors. To avoid extremely large weights, propensity score categories with approximately equal numbers of cases are then created using the quintiles of the estimated response propensities. When the interaction effects on attrition exist, alternatively, an ad hoc two-step approach is considered. Specifically, the multilevel response propensity model with only X as predictors is first fitted to create propensity score categories, which are further cross-classified with the stratum-weight variable used in the above CHAID approach to form weighting adjustment cells. This can be considered a hybrid approach of response propensity and adjustment cell methods, where the response propensity score of attrition, strata and base weights are used to form adjustment cells. Weighting adjustments are then taken to be the reciprocal of the unweighted response rate in each cell.

3. Application to the Galveston Bay Recovery Study

In this section we provide a step-by-step demonstration on how to incorporate base weights, strata, clusters and a large number of other auxiliary variables into weighting for panel attrition, using as an example the second wave of the Galveston Bay Recovery Study (GBRS). The GBRS was a three-wave panel survey conducted after Hurricane Ike struck the Galveston Bay area in Texas on September 13–14, 2008 [29]. The goal of the GBRS was to characterize trajectories and determinants of post-disaster mental health outcomes. The study population consists of residents living in Galveston and Chalmers counties who were present in the county when Hurricane Ike hit and had been living in the area for at least one month before the storm. The two-county area was divided into five damage geographic strata, with differing sampling rates to oversample the areas that were expected to be more affected by the storm. Seventy-seven area segments composed of Census blocks were then selected proportional to Census 2000 number of occupied households. Using an address list purchased from Experian with some basic household information, each household in the sampling frame was further classified as high versus low risk of experiencing post-traumatic stress disorder (PTSD) based on their household characteristics. Households with high risk of PTSD were over-sampled. There were 658 individuals participating in the baseline survey, with 239 from stratum 1, 68 from stratum 2, 123 from stratum 3, 33 from stratum 4, and 195 from stratum 5. Two follow-up interviews were conducted approximately two and twelve months after the baseline interview, with 529 participating in wave 2 and 487 participating in wave 3. In this paper, we focus on the weighting adjustment for the wave 2 attrition.

3.1. Strata and Sample Weights

The wave 2 response rate in the five sampling strata is 84%, 84%, 75%, 91%, and 76%, respectively. Since sample size is relatively small in stratum 4 (n = 33), and the wave 2 response rate is similar in the first two strata and is similar between stratum 3 and 5, and also strata 1–2 and strata 3–5 are geographically closer to each other, we create a new stratum indicator that combines strata 1–2 and strata 3–5, which in turn yields a new response rate of 84% and 77%, respectively. Since sampling strata were ordered by the damage level with the worst damage in stratum 1 and the least damage in stratum 5, this suggests that people who were less affected by Hurricane Ike were more likely to drop out the study. To examine the effect of base weight on panel attrition, we further divide the sample units in each of the two newly combined strata by the median of the base weight, which is 98 in the combined stratum 1–2 and 255 in the combined stratum 3–5. As a result, the combined stratum 1–2 has a response rate of 86% in the small weight group and 82% in the large weight group, and the combined stratum 3–5 has a response rate of 76% and 79% in the small and large weight group, respectively. This suggests that sample units who had a large base weight were more likely to drop out the study in the area with more damage, while were less likely to drop out in the area with less damage.

3.2. Other Auxiliary Variables for Weighting Adjustments

Other auxiliary variables that can be used to improve weighting adjustments include the 112 survey response variables to the baseline survey and participants’ cooperation variables in the baseline interview (e.g., ever a refusal, number of calls, number of item nonresponse). Item nonresponse is less a concern here. The proportion of missing data for each individual variable is between zero and four percents. To avoid losing any observations in the weighting adjustments, missing survey responses are imputed using sequential regression imputation method [30]. Variables summarizing item nonresponse in the baseline survey are created, including number of item nonresponse and item nonresponse indicators for each of the 30 survey variables with more than 20 (3%) missing observations.

3.3. Screening for Important Predictors of Panel Attrition

Before attempting the adjustment cell or response propensity modeling, an initial screening analysis of the auxiliary variables is performed to reduce the large number of variables to a more manageable set. With the wave 2 panel attrition as the dependent variable, survey weighted logistic regression is used to examine the bivariable association between each auxiliary variable and the panel attrition. With a moderate sample size (n = 658), variables having p-values less than or equal to 0.1 are retained for later analysis. The screening analysis reduces the number of baseline survey variables from 112 to 26 and removes all the item nonresponse indicators.

3.4. The CHAID Model

We use the CHAID algorithm to create weighting adjustment cells. Predictors include the 26 survey response variables identified in the screening step, three cooperation variables (ever being a refuser, number of calls and number of item nonresponse in the baseline survey), and the design variables (the new stratum-weight variable, area segments). A significance level of 0.05 is used for both merging categories of predictors and splitting a node. The CHAID model yields five terminal nodes. Figure 1 shows that the first split of node is determined by callnumcat (number of calls in the baseline survey; 1=1–5; 2=6–10; 3=11–15; 4=15+ calls). The splitting of node 1 yields nodes 2 and 6, where node 2 includes individuals whom were called 1–15 times, and node 6 includes individuals whom were called more than 15 times in the baseline survey. The splitting of node 2 yields three terminal nodes 3–5, defined by the past month depression severity, with “1 = minimal” for node 3, “2 = mild & 3 = moderate” for node 4, and “4 = severity” for node 5. The splitting of node 6 yields two terminal nodes 7 and 8, defined by the stratum-weight variable, with “strata 3–5 and base weight ≤ 225” for node 8 and the others for node 7. The weighting adjustment from the CHAID model is then equal to the inverse of response rate in each of the five terminal nodes. The terminal nodes yield very different response rates, ranging from 0.50 to 0.94, with the shaded area in the terminal nodes of Figure 1 representing proportions of response. The algorithm is implemented using the CHAID package in R.

Figure 1.

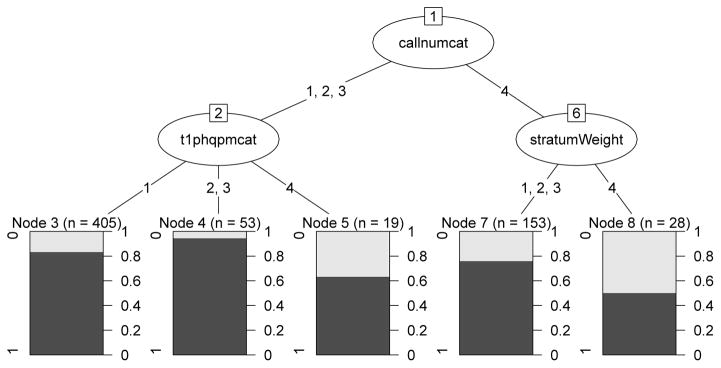
Using the CHAID algorithm to model panel attrition in the wave 2 survey of the Galveston Bay Recovery Study. The weighting adjustment cells are formed by number of calls in the baseline survey (callnumcat; 1=1–5, 2=6–10, 3=11–15, and 4=15+ calls), past month depression severity (t1phqpmcat; 1=minimal, 2=mild, 3=moderate, and 4=severity), and the design variable (stratumWeight; 1=strata 1–2 and base weight > 98, 2=strata 1–2 and base weight ≤ 98, 3=strata 3–5 and base weight > 225, and 4=strata 3–5 and base weight ≤ 225). The shaded area in the terminal nodes represents proportions of response in each terminal node.

3.5. Response Propensity Model

We use a lasso logistic regression [31] to identify important predictors of panel attrition from the list of 26 survey response variables, the three cooperation variables and the four-category stratum-weight variable. The lasso model selects 12 of them into the final model. To estimate the response propensity, we re-fit the response propensity model on these 12 important predictors using a Bayesian multilevel model with varying intercepts to account for the effect of the area segment. The final model is shown in Table 1. In additional to the number of calls, past month depression severity variables, and stratum-weight variable identified in the CHAID model, variables used in the response propensity model also include education, self or household member performed dangerous activity during storm, number of previous hurricane exposure, displaced from home or financial loss due to Ike, post-disaster emotional support, lifetime generalized anxiety disorder severity, alcohol drinking, and use help services after Ike. We first calculate the response propensity (RP) adjustment using the reciprocal of the estimated response probability, which has a median of 1.17 (min = 1.02, max = 4.48). We then order the estimated response propensities and divide the baseline sample units into five approximately equal-sized categories to obtain the response propensity stratification (RPS) adjustments. To practice the two-step hybrid approach, we repeat the above multilevel model without the stratum-weight variable. The resulted response propensity categories are further cross-classified with the stratum-weight variable resulting in 20 adjustment cells. The hybrid approach yields weighting adjustments varying from 1.00 to 2.41. The lasso logistic regression model is fitted using the glmnet package and the Bayesian model is fitted using the rstan package in R [32, 33].

Table 1.

Odds ratio (OR) estimates and 95% credible intervals (CI) of the response propensity model for response to the wave 2 survey of the Galveston Bay Recovery Study.

Predictors	OR (95% CI)
Number of calls (15+ vs. 1–15)	0.4 (0.2, 0.6)
Past month depression severity (moderately severe vs. others)	0.4 (0.2, 1.3)
Highest level of education completed (>high school vs. ≤high school)	1.4 (0.9, 2.2)
Self or houseold member performed dangerous activity during storm (yes vs. no)	0.6 (0.3, 1.2)
Number of previous hurricane exposure (3 vs. others)	1.7 (1.0, 3.1)
Displaced from home for > 1 week (yes vs. no)	1.3 (0.8, 2.2)
Financial loss as a result of Ike (yes vs. no)	0.7 (0.4, 1.0)
Postdisaster emotional support (median vs. low)	0.7 (0.4, 1.2)
Postdisaster emotional support (high vs. low)	1.5 (0.9, 2.6)
Lifetime generalized anxiety disorder severity (severe vs. others)	0.5 (0.2, 1.0)
Ever had ≥3 alcoholic drinks within a 3 hour period on ≥3 occasions	1.6 (1.0, 2.4)
Need help and use services (yes vs. no)	1.8 (0.9, 3.4)
Strata 1–2 and weight lower than median	1.1 (0.6, 2.1)
Strata 3–5 and weight lower than median	0.8 (0.4, 1.3)

3.6. Final Panel Weights

As a final step, the base weight is multiplied by the panel attrition weighting adjustment and post-stratified to obtain the final wave 2 weight using the raking method. The post-stratification is conducted using American Community Survey data for the relevant counties based on the post-stratification variables: age, gender, marital status, race/ethnicity, whether born in the United States, education, employment status, and household income. The raking is implemented using the survey package in R.

3.7. Survey Data Analysis

Figure 2 shows the results of the population mean estimate of the baseline post-disaster stress disorder score among wave 2 respondents (n = 529) using the final panel weights. To serve as a benchmark for comparison, we also provide the estimate using the complete wave 1 sample (n = 658) and the base weight. Without adjustment for panel attrition, using the wave 2 respondents and the base weight the NULL estimate is about one point lower than the other estimates. The four weighted estimators (RP, RPS, Hybrid, and CHAID) are effective in reducing bias in estimating the population mean of the stress score, with their point estimates close to the benchmark estimate. The point estimates from the CHAID and hybrid approaches are closer to the benchmark than that of RPS, which might be explained by the interaction effect between the stratum-weight variable and other covariates as shown in the CHAID analysis. CHAID yields the largest standard error among all the approaches.

Figure 2.

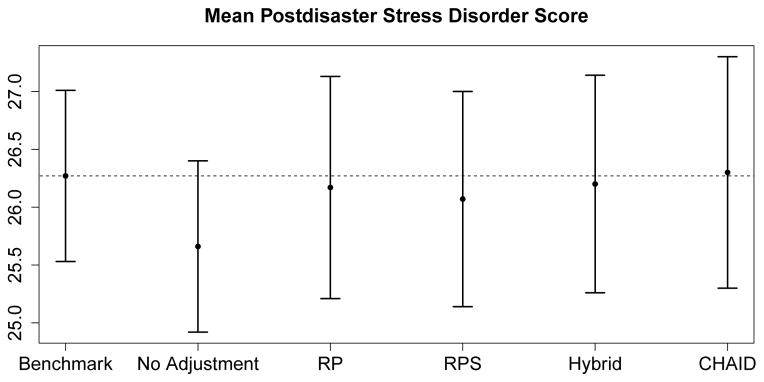
The estimates of mean postdisaster stress disorder score measured at the baseline survey of the Galveston Bay Recovery Study. The estimates using the wave 2 survey respondents and the final wave 2 panel weights (including no adjustment or using the response propensity (RP), the response propensity stratification (RPS), the hybrid adjustment or the CHAID algorithm to adjust for the panel attrition) are compared to the benchmark estimate using the complete data in the baseline survey. The black dots represent point estimates and the bars represent one standard error.

4. Simulation Study

4.1. Design of the Simulation Study

We use a simulation to show that the weighting approaches discussed in Section 2.4 that incorporate design variables, such as base weights, strata and clusters, in the attrition analysis can effectively reduce bias when attrition is related to design features. The simulation is conducted using the data of the 658 individuals who participated in the wave 1 data collection of the Galveston Bay Recovery Study. Let X be the age of sample units at the first wave of data collection and Z be the natural log-transformed base weight. Both X and Z are standardized to have zero mean and unit standard deviation. We generate three outcome variables: Y₁|X, Z ~ Norm(0, 1), Y₂|X, Z ~ Norm(X, 1), and Y₃|X, Z ~ Norm(X + Z, 1), and consider the following four different wave 2 response propensity models:

$$\begin{array}{l}\text{logit}Pr(R_1=1\mid X,Z)=0.5,\\ \text{logit}Pr(R_2=1\mid X,Z)=0.5+X,\\ \text{logit}Pr(R_3=1\mid X,Z)=1+X+Z+XZ,\end{array}$$

and

$$Pr(R_4=1\mid X,Z)=\{\begin{array}{ll}0.2+0.4\mathrm{I}(Z>q_1)\hfill & \text{if}X\le 0\hfill \\ 0.8\hfill & \text{if}X>0,\hfill \end{array}$$

where q₁ is the first quartile of Z. These models result in an average response rate of 60% – 70%.

We compare eight attrition weighting adjustments, including a naive method without any adjustment (NULL), two CHAID models (CHAID_[x], CHAID_[x,z]), two response propensity models (RP_[x], RP_[x,z]) and their corresponding response propensity stratification adjustments (RPS_[x], RPS_[x,z]), and the hybrid approach that cross-classifies RPS_[x] with design variables (Hybrid_[x,z]). For CHAID_[x] and CHAID_[x,z], we first categorize the continuous X and Z into quartiles. A significance level of 0.05 is used both for merging of predictor categories and for splitting of a node. The subscript [x] and [x, z] denote which variables are used to grow the trees. Similar subscript notations are also used to denote which variables are included as predictors in the response propensity model (1), with [x] for main effect of X and [x, z] for the main effects of X and Z plus their interaction. The response propensity categories are created using the quintiles of the predicted response propensities from the corresponding models. Finally, the weighting adjustment of Hybrid_[x,z] is created by cross-classifying the response propensity strata of RPS_[x] with Z that is dichotomized at the median. Let w_nr denote any of the eight panel attrition adjustment and w₁ be the base weight. The attrition adjusted weight w₂ for the wave 2 respondents is

$$w_2=w_1\times w_{nr}.$$ (2)

For each response model, we replicate 1000 simulations and compare the absolute empirical bias and root mean squared error (RMSE) of the eight adjustments in estimating mean Y:

$$\begin{array}{c}\text{Absolute}\text{Bias}=\left|\frac{1}{1000}\sum _{t=1}^{1000}({\widehat{\mu }}^{(t)}-\stackrel{\sim }{\mu })\right|,\\ \text{RMSE}=\sqrt{\frac{1}{1000}\sum _{t=1}^{1000}{({\widehat{\mu }}^{(t)}-\stackrel{\sim }{\mu })}^2},\end{array}$$

where, μ̂^(t) is the Hájek estimate of mean Y [34] in the tth replicate of simulation using the attrition adjusted weight among the m respondents,

$${\widehat{\mu }}^{(t)}=\frac{{\sum }_{i=1}^m{w}_{2i}^{(t)}{y}_i^{(t)}}{{\sum }_{i=1}^m{w}_{2i}^{(t)}},$$

and μ̃ is the Hájek estimate of mean Y using the base weight and the n complete data without dropout,

$$\stackrel{\sim }{\mu }=\frac{{\sum }_{i=1}^n{w}_{1i}{y}_i}{{\sum }_{i=1}^n{w}_{1i}}.$$

Weighting adjustments that yield smaller values of absolute bias and RMSE are desirable.

4.2. Simulation Results

Table 2 displays the absolute empirical bias of the estimates of mean Y using the eight weighting adjustments. In the response model R₁ where response is independent of X and Z, the bias is close to zero for all eight weighting adjustments. In the response models R₂ – R₄, the NULL estimator performs poorly with large bias, especially when Y is related to X or Z. In the response model R₂ where response is related to X only, the two RP adjustments achieve the smallest bias followed by the Hybrid_[x,z] adjustment. In the response model R₃ where response is related to both X and Z, the adjustments that account for the design variable Z (CHAID_[x,z], RP_[x,z], RPS_[x,z], and Hybrid_[x,z]) yield smaller bias than the corresponding adjustments that do not account for Z, and RP_[x,z] achieves the smallest bias. This is not surprising because the true response model is used in RP_[x,z]. In the response model R₄ where response is a step function of X and Z, the CHAID_[x,z] performs best in this case with close to zero bias followed by the Hybrid_[x,z] adjustment, while the estimates using RP_[x,z] and RPS_[x,z] are subject to some degree of bias due to model misspecification. Overall the weighting approaches using [x, z] perform well in all scenarios with small bias.

Table 2.

Comparison of absolute bias of the estimates of mean Y between various weighting adjustments under four response propensity models in the simulation study: Y₁|X, Z ~ Norm(0, 1), Y₂|X, Z ~ Norm(X, 1), and Y₃|X, Z ~ Norm(X + Z, 1).

Response model	R1			R2			R3			R4
Outcome	Y1	Y2	Y3	Y1	Y2	Y3	Y1	Y2	Y3	Y1	Y2	Y3
NULL	.000	.000	.005	.024	.363	.344	.016	.313	.407	.014	.139	.152
CHAID[x]	.000	.001	.005	.014	.033	.040	.006	.161	.245	.011	.055	.024
CHAID[x,z]	.000	.001	.006	.014	.033	.041	.016	.076	.078	.000	.003	.003
RP[x]	.000	.000	.005	.001	.003	.002	.001	.152	.232	.002	.055	.028
RP[x,z]	.000	.001	.002	.001	.006	.000	.001	.012	.004	.016	.042	.035
RPS[x]	.000	.000	.004	.001	.029	.022	.003	.165	.234	.004	.038	.018
RPS[x,z]	.000	.001	.003	.004	.035	.020	.000	.078	.040	.016	.039	.033
Hybrid[x,z]	.000	.000	.004	.002	.018	.015	.001	.069	.064	.003	.008	.014

Table 3 compares the RMSE of the eight weighting adjustments. For Y₁ that is not related to X or Z, all eight weighting adjustments yield small RMSE in all response models and the NULL achieves the smallest RMSE in most of cases. This suggests that while weighting can effectively reduce attrition bias, the increase in variance due to weighting can lead to a slightly increased RMSE than the NULL when Y is independent of X and Z. When Y is related to either X or Z, the NULL is subject to not only large bias but also large RMSE, and weighting adjustments improve efficiency in the survey estimates. In the response models of R₃ and R₄, the adjustments that account for Z yield smaller RMSE than the corresponding adjustments that fail to do that. In the response models of R₁ and R₂ where response is unrelated to Z, there is minimal penalty by including Z. The CHAID_[x,z] yields a slightly larger RMSE than the counterparts.

Table 3.

Comparison of root mean square error of the estimates of mean Y between various weighting adjustments under four response propensity models in the simulation study: Y₁|X, Z ~ Norm(0, 1), Y₂|X, Z ~ Norm(X, 1), and Y₃|X, Z ~ Norm(X + Z, 1).

Response model	R1			R2			R3			R4
Outcome	Y1	Y2	Y3	Y1	Y2	Y3	Y1	Y2	Y3	Y1	Y2	Y3
NULL	.046	.091	.108	.046	.373	.355	.028	.317	.409	.039	.157	.172
CHAID[x]	.046	.090	.108	.055	.106	.099	.034	.170	.248	.042	.094	.082
CHAID[x,z]	.046	.090	.108	.056	.109	.099	.043	.098	.088	.038	.072	.077
RP[x]	.046	.085	.105	.055	.104	.091	.031	.161	.235	.040	.091	.081
RP[x,z]	.046	.077	.090	.056	.091	.084	.058	.090	.061	.039	.070	.073
RPS[x]	.046	.086	.105	.055	.107	.091	.034	.175	.237	.040	.081	.078
RPS[x,z]	.046	.080	.094	.054	.098	.085	.044	.103	.057	.038	.070	.078
Hybrid[x,z]	.046	.084	.104	.057	.102	.088	.044	.097	.075	.038	.067	.075

5. Discussion

In public health research it is standard to use weighting to adjust for panel attrition. Given that weighting is being widely used, our goal of this paper is review weighting approaches and provide suggestions to analysts in decision making in weighting for panel attrition. In the attrition analysis, we need to consider not only the large amount of auxiliary information available on both respondents and nonrespondents, but also the set of variables about the sampling design. Since the variables about sampling designs are often not available to analysts because of confidentiality restrictions, we focus on the attrition analysis that uses base weights, strata and clusters. We review two commonly used weighting methods, i.e. the adjustment cell weighting and the response propensity weighting. We explore the application of these two weighting methods to panel attrition using the CHAID algorithm and multilevel models, both of which are appealing in that they can handle a large number of auxiliary variables and can naturally incorporate the design variables into weighting.

To form adjustment cells using the CHAID algorithm, the data are partitioned into mutually exclusive, exhaustive adjustment cells that best describe the panel attrition using all auxiliary variables including base weights, strata and clusters. The CHAID algorithm requires all the continuous predictors to be converted into categorical variables. In practice, we can divide the continuous predictors into a number of categories with an approximately equal number of observations. For the continuous base weight variable, we suggest to dichotomize it at its median within each stratum because the range of base weight tends to vary across strata. To incorporate the cluster effect, the CHAID algorithm merges clusters that are similar in the response rates and splits nodes when the smallest adjusted p-value is smaller than an alpha-level for splitting. The CHAID requires rather large sample sizes, so that the number of cases in each terminal nodes would not be too small to yield reliable estimate of response rate. The CHAID has advantageous features. Specifically, it can naturally handle interactions between various auxiliary variables, and its output is highly visual and easy to understand.

For response propensity models, Little and Vartivarian [28] suggest including design variables as predictors. With the limited available design information in the forms of base weights, strata and clusters, we suggest using multilevel models where the cluster effect is taken into account by allowing intercepts to vary across clusters. All the other auxiliary variables can be included as predictors in the model. To allow for possible modification effects of strata and base weights on other auxiliary variables, we consider a two-step hybrid approach. We first obtain response propensity categories based on the multilevel model, and then cross-classify the propensity categories with strata and the dichotomized base weights within each stratum. In panel surveys with many auxiliary variables, it is often not a trivial task to include design variables as predictors, because the models need to include not only the correct functional forms of the design variables but also their possible interactions with other predictors. Simply including design variables as predictors in the propensity models can yield biased survey estimates when model is misspecified, but model misspecification is less a concern in the two-step approach, as shown in the simulation study. However, the two-step approach is rather ad hoc and involves a number of arbitrary decisions. Multilevel models that can incorporate base weights and strata and are robust to model misspecification will be the focus of future research.

Both the adjustment cell weighting using the CHAID algorithm and the response propensity weighting using multilevel models are easy to implement. Both approaches are shown to work well in the simulation study and the real data application. They both can effectively reduce the attrition bias that would occur by omitting important auxiliary variables and design factors that are related to attrition, although the CHAID algorithm tends to yield larger mean squared errors in the survey estimates than the other weighting approaches. The simulation study also shows that when the design features are not related to panel attrition there is minimal penalty for including well-constructed design variables.

Although our limited simulation does not show any adverse effect of including irrelevant variables in the weighting adjustment, the inclusion of many irrelevant auxiliary and design variables might increase the variability in the adjusted weight and thus in survey estimates. Caution is needed in selecting variables for weighting adjustment. In practice, we often screen important predictors of panel attrition prior to the CHAID or multilevel models. We would include all the auxiliary variables that are predictors of not only attrition but also survey outcomes. Including predictors of survey outcomes in the attrition analysis has been shown to improve efficiency in the survey estimates in our simulation study and in literature [21–23]. We also suggest to collapse small sampling strata with similar proxy variables (e.g. geographic location) that yield similar panel response rates and dichotomize the base weight by their medians in each collapsed stratum. The ultimate goal of weighting is to reduce attrition bias without a serious loss of precision in the survey estimates.

In this paper we focus on attrition in panel surveys with two waves of data collection, but these weighting approaches can also be applied to panel surveys with three or more waves, in which adjustments need to be repeated in each of the follow-up waves [35]. For example in a three-wave panel survey, to create weighting adjustments for wave 3 respondents, the attrition analysis will be conducted among the sampled units who respond to wave 2 and use survey responses in both waves 1 and 2 as auxiliary variables in the CHAID and multilevel models. The weighting adjustments for non-attrition nonresponse can be more challenging. Analysts can consider turning non-attrition patterns into attrition patterns either through imputation or discarding interviews that fall outside the attrition patterns [3, 5] and then apply the weighting approaches for panel attritions.