Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies

Abstract

The propensity score is defined as a subject's probability of treatment selection, conditional on observed baseline covariates. Weighting subjects by the inverse probability of treatment received creates a synthetic sample in which treatment assignment is independent of measured baseline covariates. Inverse probability of treatment weighting (IPTW) using the propensity score allows one to obtain unbiased estimates of average treatment effects. However, these estimates are only valid if there are no residual systematic differences in observed baseline characteristics between treated and control subjects in the sample weighted by the estimated inverse probability of treatment. We report on a systematic literature review, in which we found that the use of IPTW has increased rapidly in recent years, but that in the most recent year, a majority of studies did not formally examine whether weighting balanced measured covariates between treatment groups. We then proceed to describe a suite of quantitative and qualitative methods that allow one to assess whether measured baseline covariates are balanced between treatment groups in the weighted sample. The quantitative methods use the weighted standardized difference to compare means, prevalences, higher‐order moments, and interactions. The qualitative methods employ graphical methods to compare the distribution of continuous baseline covariates between treated and control subjects in the weighted sample. Finally, we illustrate the application of these methods in an empirical case study. We propose a formal set of balance diagnostics that contribute towards an evolving concept of ‘best practice’ when using IPTW to estimate causal treatment effects using observational data. © 2015 The Authors. Statistics in Medicine Published by John Wiley & Sons Ltd.

1. Introduction

Researchers are increasingly using observational studies to estimate the effects of treatments, exposures, and interventions on health outcomes. In randomized controlled trials, randomization ensures that, on average, treated subjects will not differ systematically from control subjects in both measured and unmeasured baseline characteristics. Therefore, the effect of treatment can be estimated by directly comparing outcomes between the treatment groups. However, non‐randomized studies of the effect of treatment on outcomes can be subject to treatment‐selection bias in which treated subjects differ systematically from control subjects. Therefore, in non‐randomized studies, the effect of treatment cannot be estimated by simply comparing outcomes between treatment groups.

Propensity score methods are being used with increasing frequency to estimate treatment effects using observational data. The propensity score is defined as the probability of treatment assignment conditional on measured baseline covariates 1, 2, 3. Rosenbaum and Rubin demonstrated a key property of the propensity score: conditional on the propensity score, treatment status is independent of measured baseline covariates 1. Thus, the propensity score is a balancing score: treated and control subjects with the same propensity score will have similar distributions of observed baseline covariates.

Four methods of using the propensity score have been described in the statistical literature: covariate adjustment using the propensity score, stratification or subclassification on the propensity score, matching on the propensity score, and inverse probability of treatment weighting (IPTW) 1, 4. Rubin argues that an advantage to the use of propensity score methods is that they allow observational studies to be designed similar to randomized experiments: the design of the study is separated from the analysis of the effect of exposure on the outcome 5. Rubin states that ‘diagnostics for the successful design of observational studies proposed on estimated propensity scores …is a critically important activity in most observational studies’ 6. Such diagnostics enable applied researchers to determine whether conditioning on the estimated propensity score has removed observed systematic differences between treated and control subjects. Diagnostics have been developed for stratification on the propensity score 2, 7, 8, matching on the propensity score 9, 10, and covariate adjustment using the propensity score 11. However, diagnostics have been less well described in the context of IPTW using the propensity score.

The objective of the current study is to describe methods to assess whether the use of IPTW has induced a weighted sample in which the distribution of measured baseline covariates is similar between treated and control subjects. These methods are based on comparing the distribution of measured baseline covariates between treated and control subjects in the sample weighted by the estimated inverse probability of treatment. We refer to these methods as balance diagnostics. The paper is structured as follows. In Section 2, we briefly review methods based on IPTW. In Section 3, we report on a review of the literature examining the frequency with which appropriate diagnostics were employed when using IPTW. In Section 4, we describe balance diagnostics for use with IPTW and methods for assessing the validity of the positivity assumption. We first describe quantitative methods to compare means, prevalences, higher‐order moments, and interactions between covariates across treatment groups in the weighted sample. We then describe how graphical methods can be used to compare the distribution of continuous covariates between treated and control subjects in the weighted sample. These graphical methods are complemented by a numerical method to compare the distribution of continuous covariates between treated and control subjects. In Section 5, we describe a case study illustrating the application of these methods. Finally, in Section 6, we discuss our proposed methods in the context of the existing literature and provide recommendations for practice.

2. Inverse probability of treatment weighting

2.1. Potential outcomes framework and average treatment effects

We consider the setting in which there is a binary or dichotomous exposure. Thus, we assume that there are two possible treatments (e.g., active treatment vs. control treatment). The potential outcomes framework assumes that each subject has a pair of potential outcomes: Y_i(0) and Y_i(1), the outcomes under the control treatment and the active treatment, respectively, when received under identical circumstances 12. However, each subject receives only one of the control treatment or the active treatment. Let Z denote an indicator variable denoting the treatment received (Z = 0 for control treatment vs. Z = 1 for active treatment). Thus, only one outcome, Y_i, is observed for each subject: the outcome under the actual treatment received. The observed outcome is equal to Y_i=Z_iY_i(1) + (1 − Z_i)Y_i(0). Thus, Y_i is defined to be equal to Y_i(0) if Z_i=0, and to be equal to Y_i(1) if Z_i=1.

For each subject, the effect of treatment is defined as Y_i(1) − Y_i(0): the difference between the two potential outcomes. The average treatment effect (ATE) is defined to be: E[Y_i(1) − Y_i(0)] 13, with the expectation taken across the population of interest. The ATE is the average effect, at the population level, of moving an entire population from control to treated.

If treatment were assigned at random, we would have that E[Y|Z = 1] = E[ZY(1) + (1 − Z)Y(0)|Z = 1] = E[ZY(1)|Z = 1] + E[(1 − Z)Y(0)|Z = 1] = E[Y(1)|Z = 1] = E[Y(1)]. The last equality holds because, under randomization, treatment assignment is independent of the potential outcomes: (Y(1),Y(0))⊥⊥Z. Similarly, E[Y(0)] = E[Y|Z = 0]. Therefore, under randomization, one has that E[Y_i(1) − Y _i(0)] = E[Y|Z = 1] − E[Y|Z = 0]13. Thus, randomization provides an unbiased estimate of the average treatment effect. However, in an observational study, we have that, in general, E[Y(1)|Z = 1] ≠ E[Y(1)]. Thus, in an observational study simply comparing outcomes between the two treatment groups does not necessarily yield an unbiased estimate of the average treatment effect.

2.2. The propensity score and inverse probability of treatment weighting

As previously discussed, let Z denote treatment assignment (Z = 1 denoting treatment; Z = 0 denoting absence of treatment), and let X denote a vector of observed baseline covariates. The propensity score is defined as e = P(Z = 1|X): the probability of a subject receiving the treatment of interest conditional on their observed baseline covariates 1. The inverse probability of treatment weight is defined as $w=\frac{Z}{e}+\frac{1-Z}{1-e}$. Each subject's weight is equal to the inverse of the probability of receiving the treatment that the subject received 4.

Lunceford and Davidian provide a review of methods for estimating treatment effects that use weighting by the inverse of the probability of treatment 14. If Y denotes an outcome variable, the average treatment effect (ATE) can be estimated by $\frac{1}{n}\sum _{i=1}^n\frac{Z_i{Y}_i}{e_i}-\frac{1}{n}\sum _{i=1}^n\frac{(1-Z_i)Y_i}{1-e_i}$, where n denotes the number of subjects. An alternative estimator of the ATE is ${\left(\sum _{i=1}^n\frac{Z_i}{e_i}\right)}^{-1}\sum _{i=1}^n\frac{Z_i{Y}_i}{e_i}-{\left(\sum _{i=1}^n\frac{1-Z_i}{1-e_i}\right)}^{-1}\sum _{i=1}^n\frac{(1-Z_i)Y_i}{1-e_i}$ 14. When the propensity score model is correctly specified, both estimators are consistent estimators of the true treatment effect 14. However, Lunceford and Davidian found that in empirical studies, in general, the variance of the former estimator is greater than that of the latter estimator 14.

Joffe et al. describe how weighting by the inverse probability of treatment results in an artificial population in which baseline covariates are independent of treatment status 15. Furthermore, Joffe et al. describe how regression models can be combined with weighting by the inverse probability of treatment to estimate causal treatment effects. While weighting by the inverse probability of treatment allows the comparison of expectations and distributions between treated and control subjects, methods that account for the weighting must be used in estimating variances and significance levels 14, 15. For instance, Joffe et al. suggest that a robust, sandwich‐type variance estimator be used to account for the fact that the weights are estimated, rather than known with certainty. Other alternatives to variance estimation include bootstrap‐based methods.

A difficulty that can arise when using the weights described previously is that treated subjects with a very low propensity score can result in a very large weight. Similarly, a control subject with a propensity score close to one can result in a very large weight. Such weights can increase the variability of the estimated treatment effect 16. An alternative to the conventional weights described previously is to use stabilized weights: $w=\frac{Z\mathrm{Pr}(Z=1)}{e}+\frac{(1-Z)\mathrm{Pr}(Z=0)}{1-e}$ 16. Pr(Z = 1) and Pr(Z = 0) denote the marginal probability of treatment and control in the overall sample. Another alternative to address the problems that can arise with very large weights is to use trimmed or truncated weights, in which weights that exceed a specified threshold are each set to that threshold 16, 17. The threshold is often based on quantiles of the distribution of the weights (e.g., the 1^st and 99^th percentiles).

The weights described previously $\left(w_{\text{ATE}}=\frac{Z}{e}+\frac{1-Z}{1-e}\right)$ permit estimation of the ATE. However, a different set of weights permit estimation of the average treatment effect in the treated (ATT): $w_{\text{ATT}}=Z+\frac{e(1-Z)}{1-e}$ 18. These weights are obtained by multiplying the conventional weights by e, so that treated subjects receive a weight of one. Thus, the treated sample is being used as the reference population to which the treated and control samples are being standardized. While the current article is focused on the use of the ATE weights, the balance diagnostics discussed are equally applicable to situations in which the ATT weights are employed.

2.3. Variable selection for the propensity score model

The propensity score is defined as the probability of treatment selection conditional on measured baseline covariates. A natural question that arises is what variables should be included in the propensity score model. A reasonable suggestion would be to include those variables that influence the treatment selection process. A different answer can be obtained by remembering the primary property of the propensity score: that it is a balancing score 1. Thus, conditioning on the propensity score permits one to balance the distribution of measured baseline covariates between treated and control subjects. Accordingly, Rosenbaum suggests that one ask ‘which covariates do you wish to balance by matching on the propensity score?’ 19 (page 356). The goal of propensity score analyses should be to induce balance in measured baseline covariates between treatment groups. However, when considering balance, not all covariates are of equal importance. It is more important to balance prognostically important covariates than those covariates that influence treatment selection but have no effect on the outcome. Indeed, prior evidence has suggested that it is preferable to include either the prognostically important covariates (those related to outcomes) or the confounding covariates (those related to treatment and outcomes) in the propensity score model than to include those variables that affect the treatment‐selection process 8. In a similar vein, Myers et al. state that conditioning on instruments (i.e., variables that affect treatment‐selection but not the outcome) can result in increased bias and variance of the treatment‐effect estimate 20.

The identification of the set of variables that are prognostically important or that confound the treatment–outcome relationship can be identified using causal diagrams 21 in conjunction with a review of the subject‐matter literature and expert opinion. We suggest that statistical hypothesis testing in the analytic sample not be used to identify the requisite variables, in the spirit of separating ‘design’ from ‘analysis’ and not using the outcome data in the propensity score process 22. A further reason for this caution is the possibly low statistical power to detect all of the prognostically important or confounding covariates. Having identified the appropriate set of variables, the objective of IPTW using the propensity score is to create a weighted sample in which the distribution of these covariates is the same between treated and control subjects.

2.4. Assumptions of propensity score methods

Causal inference using the propensity score requires four assumptions: consistency, exchangeability, positivity, and no misspecification of the propensity score model 16. Consistency means that a subject's potential outcome under the treatment actually received is equal to the subject's observed outcome. Exchangeability, also known as ignorable treatment assignment, is the assumption that there are no unmeasured confounders: that one has measured and has access to all of the variables that affect treatment selection and outcomes. Positivity is the assumption that all subjects have a non‐zero probability of receiving each treatment: 0< Pr(Z = 1) < 1. Cole and Hernan note that the assumption of no unmeasured confounding cannot be formally tested 16. Instead, subject matter knowledge is required in designing the study so that all confounders are collected.

Rosenbaum and Rubin suggest that there are multiple balancing scores (of which f(X) = X is the finest and the propensity score is the coarsest) 1. The use of any of these balancing scores would induce balance on the measured baseline covariates. Given that conditioning on any balance score will induce balance, it may not be possible to assess whether the propensity score model has been correctly specified; that is, it may be that we have an ‘incorrect’ propensity score but yet have something that is still a balancing score. We would argue that while the specification of the propensity score model may be unverifiable, the important issue is whether weighting using the estimated propensity score induced balance of measured covariates between treated and control subjects. Thus, rather than assessing the accuracy of the specification of the propensity score model, we focus on assessing balance of measured covariates between treated and control subjects in the weighted sample.

3. Literature review of the use of balance diagnostic with IPTW in the applied medical literature

We conducted a review of the applied biomedical literature to determine the frequency with which IPTW methods are applied and how often appropriate balance diagnostics are employed in this context.

3.1. Methods

We conducted a literature search using the Web of Science ©(Thomson Reuters) to address two objectives. The first objective was to determine the frequency with which applied articles reported using IPTW methods. The second was to examine in detail all the articles published in a recent year to determine the frequency with which authors reported using balance diagnostics in conjunction with IPTW methods. We limited our literature search to articles published between 1987 and 2014. The start date was selected as the year in which Rosenbaum's original article on inverse probability of treatment weighting was published 4.

We searched the Web of Science Core Collection on 30 March 2015 using the following search strategy: TOPIC: (“inverse probability of treatment weight*”) AND YEAR PUBLISHED: (1987–2014) Refined by: DOCUMENT TYPES: (ARTICLE) AND [excluding] WEB OF SCIENCE CATEGORIES: (STATISTICS PROBABILITY OR MATHEMATICS INTERDISCIPLINARY APPLICATIONS OR MATHEMATICAL COMPUTATIONAL BIOLOGY OR COMPUTER SCIENCE INTERDISCIPLINARY APPLICATIONS OR MEDICAL INFORMATICS OR SOCIAL SCIENCES MATHEMATICAL METHODS OR COMPUTER SCIENCE INFORMATION SYSTEMS)

The last set of exclusions was used to exclude articles published in the methodological literature, because we were interested in the application of IPTW in the applied literature.

3.2. Results

The search identified 139 articles published between 1987 and 2014 that used IPTW. The number of identified studies published each year is reported in Figure 1. No applied studies were identified that used IPTW until 2000, when two studies used this method. From 2000 until 2007, few studies were identified as having used IPTW, with a total of 10 published studies during this 8‐year period. From 2007 onwards, the annual number of published studies that used IPTW grew in an approximately linear fashion. In 2014, 34 articles were identified that employed IPTW.

Figure 1.

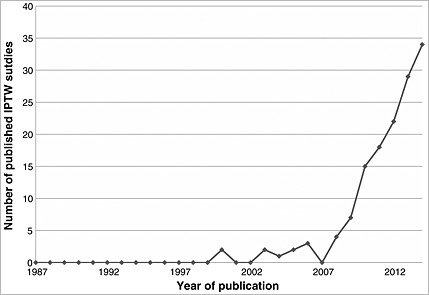
Number of published IPTW studies.

We examined in detail the 34 articles published in 2014. The most frequent research areas (using the Web of Science Research Area classification system) were ‘Cardiovascular system cardiology’ (9 articles), followed by ‘Surgery’ (6 articles), and ‘Respiratory system’ (5 articles). Upon a more detailed examination of these 34 articles, five were excluded because they used inverse probability of treatment weighting in the context of marginal structural models (MSMs) (4 articles) or considered a continuous exposure (1 article). This left 29 articles for assessment of the use of balance and weight diagnostics. Of these 29 articles, three (10.3%) presented some assessment of the distribution of weights, while 14 (48.3%) assessed the distribution of baseline covariates after implementing IPTW. Only two studies conducted an assessment of baseline covariate balance and examined the distribution of the weights 23, 24.

Of the three studies that assessed the distribution of the weights, one article computed the mean and standard deviation of the weights, as well as reported the range of the weights 24. This study conducted separate analyses using stabilized weights and trimmed weights. A second study conducted three separate analyses using conventional weights, standardized weights, and trimmed weights 23. The authors used boxplots to examine the distribution of the weights. Finally, the third study reported the range of the weights 25.

Of the 14 studies that examined the distribution of baseline covariates between treated and control subjects in the weighted sample, a range of methods were used. These included using standardized differences in the weighted sample 23, 24, 26, 27, 28, 29, 30, 31, the Kolmogorov–Smirnov statistic 26, a crude comparison of baseline characteristics 32, and statistical significance testing in the weighted sample 30, 33, 34, 35. Two studies reported that comparisons were carried out but did not report the results 36, 37.

While it was not the focus of the review, we noted that several sets of authors incorrectly defined the weights as the reciprocal of the propensity score, rather the reciprocal of the probability of receiving the treatment that was actually received.

4. IPTW diagnostics

In this section, we describe both quantitative and qualitative methods for assessing balance in observed baseline covariates between treated and control subjects in a sample weighted by the inverse probability of treatment. We also describe methods for assessing the validity of the positivity assumption.

4.1. Balance diagnostics

In this sub‐section, we consider diagnostics for assessing the balance of baseline covariates between treated and control subjects in a sample weighted by the inverse probability of treatment. As noted previously, the objective of IPTW analyses is to create a weighted sample in which the distribution of either the confounding variables or the prognostically important covariates is the same between treated and control subjects.

4.1.1. Comparison of means and proportions of baseline variables

The first quantitative method compares the means of observed baseline covariates between treated and control subjects in the weighted sample. For a continuous variable, let ${\overline{x}}_{\text{treatment}}$ and ${\overline{x}}_{\text{control}}$ denote the sample mean of X in treated and control subjects, respectively, while $s_{\text{treatment}}^2$ and $s_{\text{control}}^2$denote the sample variance of X in treated and control subjects, respectively. Similarly, for a dichotomous variable, ${\widehat{p}}_{\text{treatment}}$ and ${\widehat{p}}_{\text{control}}$ denote the sample prevalence of the variable in treated and control subjects, respectively. In an unweighted sample, the standardized difference is defined as

$$d=100\times \frac{({\overline{x}}_{\text{treatment}}-{\overline{x}}_{\text{control}})}{\sqrt{\frac{s_{\text{treatment}}^2+s_{\text{control}}^2}{2}}}$$ (1)

for continuous variables. The standardized difference was developed for comparing continuous variables; however, it can justifiably be used for comparing dichotomous variables 38. For dichotomous variables the standardized difference is defined as

$$d=100\times \frac{({\widehat{p}}_{\text{treatment}}-{\widehat{p}}_{\text{control}})}{\sqrt{\frac{{\widehat{p}}_{\text{treatment}}(1-{\widehat{p}}_{\text{treatment}})+{\widehat{p}}_{\text{control}}(1-{\widehat{p}}_{\text{control}})}{2}}}$$ (2)

The standardized difference compares the difference in means in units of the pooled standard deviation 39. Unlike t‐tests and other statistical tests of hypothesis, the standardized difference is not influenced by sample size. Thus, the use of the standardized difference can be used to compare balance in measured variables between treated and control subjects in the same sample when different weights are assigned to the same subjects. Furthermore, it allows for the comparison of the relative balance of variables measured in different units (e.g., age in years vs. systolic blood pressure in mm Hg) by calculating each on the standard deviation scale.

The sample means, sample variances, and sample prevalences in formulas (1) and (2) are unweighted estimates. However, each sample estimate can be replaced by its weighted equivalent. The weighted mean is defined as ${\overline{x}}_{\text{weight}}=\frac{\sum w_i{x}_i}{\sum w_i}$, while the weighted sample variance is defined as $s_{\text{weight}}^2=\frac{\sum w_i}{{\left(\sum w_i\right)}^2-\sum \underset{i}{\overset{2}{w}}}\sum w_i{(x_i-{\overline{x}}_{\text{weight}})}^2$, where w _i is the weight assigned to the i‐th subject. In our context, the weight is the inverse probability of treatment received, as defined in Section 2. The use of standardized differences allows researchers to quantitatively compare balance in measured baseline covariates between treated and control subjects in the sample weighted by the inverse probability of treatment.

4.1.2. Comparison of interactions and higher‐order moments of continuous variables

The methods described in the previous section allow one to compare means and prevalences of continuous and dichotomous variables, respectively, between treated and control subjects in the weighted sample. However, one desires to balance not only means and prevalences but also other characteristics of the distribution. In particular, higher‐order moments and interactions between variables should be similar between treatment groups in the weighted sample. In the context of propensity‐score matching, both Ho et al. and Austin have suggested comparing interactions and higher‐order moments between treatment groups 9, 10. Therefore, we suggest that standardized differences be used to compare the mean of higher‐order moments (e.g., squares and cubes of continuous variables) and interactions between continuous variables. Comparing the mean of squares of continuous variables is equivalent to comparing the variance of that variable between treatment groups. One wants to ensure that the variance, and not only the mean, of a continuous variable is similar between treatment groups in the weighted sample.

4.1.3. Graphical comparisons of the distribution of continuous variables

Standardized differences allow for the comparison of means and higher‐order terms between treated and control subjects. However, one wants to induce balance on the entire distribution of continuous covariates, not just means and higher‐order terms of baseline variables. We now describe graphical methods that permit a broader, qualitative, comparison of the distribution of a continuous variable between two groups in a sample that has been weighted by the inverse probability of treatment.

Side‐by‐side boxplots 40 and empirical cumulative distribution functions (CDFs) 41 can be used to compare the distribution of continuous baseline covariates between treated and control subjects in the weighted sample. The use of side‐by‐side boxplots to compare the distribution of baseline covariates between treated and control subjects in the weighted sample has previously been described by Joffe et al. 15. These methods allow one to assess whether the variability of a continuous baseline variable differs between treatment groups and whether the tails of the distribution of the variable differ between treatment groups.

4.1.4. Numerical comparisons of the distribution of continuous variables

The graphical methods described in the previous sub‐section permit the analyst to compare the distribution of continuous baseline covariates between treated and control subjects, both in the original sample as well as in the weighted sample. A limitation of the graphical approach is that it relies on a subjective comparison of graphs, especially when comparing two different specifications of the propensity score model. In this section, we propose a numerical method for comparing the distribution of continuous baseline covariates between treatment groups. In the preceding section, we proposed that empirical CDFs be used to compare the distribution of continuous baseline covariates between treatment groups. The Kolmogorov–Smirnov test permits a formal comparison of the distribution of a continuous variable between two independent groups. The test statistic is defined to be the maximal vertical distance between the two empirical CDFs of the variable in the two groups 42. The use of the Kolmogorov–Smirnov test statistic permits a quantification of the difference in the distribution of a continuous baseline covariate between treated and control subjects.

We suggest that analysts restrict their use of this method to estimation of the Kolmogorov–Smirnov test statistic, rather than use it for formal hypothesis testing to detect statistically significant differences in the distribution of the covariate between treatment groups. While there is precedent for the use of statistical hypothesis testing for assessing balance in baseline covariates 2, other authors have suggested that the balance‐test fallacy precludes the use of hypothesis testing when conducting balance assessment 43. One reason for this criticism of statistical hypothesis testing is that one is interested in assessing balance in the particular analytic sample, rather than in the super‐population from which the sample was drawn. Furthermore, while the Kolmogorov–Smirnov test statistic can be computed when using weighted data, we are unaware of a statistical test that permits one to formally use the weighted test statistic to test whether the distribution is different between the two groups However, if an analyst were to conduct formal hypothesis testing using the Kolmogorov–Smirnov test, it could be possible to use a permutation‐based approach to assess the statistical significance of the difference in the distributions between treatment groups.

4.2. Diagnostics for assessing the positivity assumption

In this section, we describe methods for assessing the validity of the positivity assumption. In the context of MSMs, which use IPTW to account for time‐varying treatment and confounding, Cole and Hernan recommend that analysts should determine the mean stabilized weight (note that this recommendation pertains only to when stabilized weights are used) and the standard deviation of the stabilized weights 16. Similarly, they suggest determining the minimum and maximum weights. They suggest that if the mean of the stabilized weights is far from one or if there are very extreme values, then this can be indicative of non‐positivity or that the propensity score model has been misspecified. The standard deviation of the weights can be useful when comparing between different specifications of the propensity score model. Everything else being equal, one would select the specification that resulted in weights with the lowest standard deviation.

5. Case study

5.1. Data sources

We used data on 9107 patients who were discharged alive with an acute myocardial infarction (or heart attack) from 102 hospitals in Ontario, Canada, between 1 April 1999 and 31 March 2001. These data were collected as part of the Enhanced Feedback for Effective Cardiac Treatment (EFFECT) study, an initiative that is focused on improving the quality of care for cardiovascular disease patients in Ontario 44. Data on patient demographics, presenting signs and symptoms, classic cardiac risk factors, comorbid conditions and vascular history, vital signs on admission, and results of laboratory tests were abstracted directly from patients' medical records. The exposure of interest was whether the patient was prescribed a beta‐blocker at hospital discharge.

Overall, 6178 (67.8%) of patients received a prescription for a beta‐blocker at discharge, while 2929 (32.2%) did not receive a prescription at discharge. Table 1 compares the characteristics of patients who did and did not receive a beta‐blocker at hospital discharge. Standardized differences were used to compare the balance in measured baseline covariates between those who did and did not receive a prescription for a beta‐blocker at discharge. Eighteen of the 24 measured baseline covariates had standardized differences that exceeded 10%. While there is no consensus as to what value of a standardized difference can be taken to indicate the presence of meaningful confounding, some authors have suggested that a standardized difference in excess of 10% may be indicative of meaningful imbalance in a covariates between treated and control subjects 10, 45, 46. The largest observed standardized differences were for age (−34.1%) and respiratory rate (−33.2%).

Table 1.

Baseline characteristics of treated and control subjects in original sample.

Variable	Beta‐blocker: No (N=2929)	Beta‐blocker: Yes (N=6178)	Standardized difference
Demographic characteristics
Age	69.6 ± 13.5	65 ± 13.3	−34.1
Female	1144 (39.1%)	1984 (32.1%)	−14.5
Presenting signs and symptoms
Cardiogenic shock	26 (0.9%)	32 (0.5%)	−4.4
Acute congestive heart failure (CHF)/pulmonary edema	214 (7.3%)	224 (3.6%)	−16.2
Classic cardiac risk factors
Diabetes	842 (28.7%)	1494 (24.2%)	−10.4
Current smoker	916 (31.3%)	2158 (34.9%)	7.8
Hyperlipidemia	767 (26.2%)	2132 (34.5%)	18.2
Hypertension	1343 (45.9%)	2793 (45.2%)	−1.3
Family history of coronary artery disease	745 (25.4%)	2195 (35.5%)	22.1
Comorbid conditions
Cerebrovascular disease/transient ischemic attack (CVA/TIA)	354 (12.1%)	493 (8%)	−13.7
Angina	975 (33.3%)	1982 (32.1%)	−2.6
Cancer	110 (3.8%)	154 (2.5%)	−7.3
Congestive heart failure (CHF)	189 (6.5%)	177 (2.9%)	−17.1
Renal disease	21 (0.7%)	26 (0.4%)	−3.9
Vital signs on admission
Systolic blood pressure	146.8 ± 31.4	149.9 ± 30.9	10.2
Diastolic blood pressure	81.8 ± 18.6	84.9 ± 18.3	17.3
Heart rate	86.9 ± 25.9	82.1 ± 22.7	−19.9
Respiratory rate	22.2 ± 6.5	20.3 ± 4.8	−33.2
Laboratory tests
Glucose	9.8 ± 5.2	9.2 ± 5.2	−11.8
White blood count	10.6 ± 5.5	10 ± 4.3	−12.4
Hemoglobin	135.2 ± 20	140.2 ± 17.7	26.1
Sodium	138.7 ± 4.2	139.2 ± 3.5	10.8
Potassium	4.1 ± 0.6	4.1 ± 0.5	−12.5
Creatinine	114.2 ± 77.4	98.8 ± 50.3	−23.5

Note: Continuous variables are represented as mean ± standard deviation, while dichotomous variables are represented as N (%).

5.2. IPTW diagnostics

The propensity score was estimated using a logistic regression model in which treatment assignment (beta‐blocker vs. no beta‐blocker) was regressed on the 24 covariates listed in Table 1. We considered two different specifications of the propensity score model. In the first specification, each covariate entered the propensity score model as a main effect only. For the 11 continuous covariates, it was assumed that each covariate was linearly related to the log‐odds of receiving a prescription for a beta‐blocker at hospital discharge. In the second specification, restricted cubic smoothing splines with five knots were used to model the relationship between each of the continuous variables and the log‐odds of treatment 47. We refer to these two specifications as the simple and complex specifications, respectively. Stabilized weights were computed as described previously. The methods described in Section 4 were then used to assess whether, in the sample weighted by the inverse probability of treatment (using the stabilized weights), treated and control subjects had similar distributions of the covariates listed in Table 1, all of which are plausible predictors of outcomes in patients with acute myocardial infarction. By comparing diagnostics between the two different specifications of the propensity score model, we are able to assess whether one specification was preferable to the other.

5.2.1. Diagnostics based on the stabilized weights

When using the simple specification of the propensity score model, the mean stabilized weight was equal to 1.002, while the standard deviation of the stabilized weights was equal to 0.29. The minimum and maximum weights were 0.353 and 4.656, respectively. When using the complex specification of the propensity score model, the mean stabilized weight was equal to 1.001, while the standard deviation of the stabilized weights was equal to 0.30. The minimum and maximum weights were 0.361 and 3.793, respectively. There was no evidence of non‐positivity or of misspecification of the propensity score model based on an examination of the distribution of the weights derived from either specification of the propensity score model. Based on these diagnostics, neither specification was clearly preferable over the other.

5.2.2. Comparison of means and prevalences in the weighted sample

When using the simple specification of the propensity score model, the largest absolute standardized difference in the weighted sample was 2.1% (age) among the 24 baseline covariates. When using the complex specification of the propensity score model, the largest absolute standardized difference in the weighted sample was 1.7% (hyperlipidemia) among the 24 baseline covariates. In contrast, the standardized differences in the unweighted sample exceeded 10% for 18 (75%) of the 24 baseline covariates. Figure 2 reports the absolute standardized differences for each of the 24 baseline covariates in the unweighted sample and in the two samples weighted by weights derived from the simple and complex specifications of the propensity score model. We have superimposed a vertical line on this figure denoting a standardized difference of 10%, as some authors consider standardized differences below this threshold as indicative of negligible imbalance. These diagnostic assessments suggest that weighting by the inverse probability of treatment has created a sample in which the means of continuous baseline covariates and the prevalence of binary baseline variables are similar between treated and control subjects. While better balance was achieved using the complex specification of the propensity score model, differences between the two specifications were at most modest.

Figure 2.

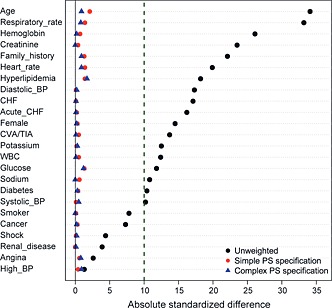
Absolute standardized differences in unweighted and weighted samples.

5.2.3. Comparison of higher‐order moments and interactions

The mean of the square of each continuous variable was compared between treatment groups in both the original unweighted sample and in each of the two weighted samples. The 11 absolute standardized differences comparing the square of the continuous variables between treatment groups in the original unweighted sample ranged from a low of 5.1% to a high of 35.3%. The 25^th percentile, median, and 75^th percentile were 9.6%, 14.1%, and 25.6%, respectively. In the sample weighted using the weights derived from the simple specification of the propensity score model, the 11 absolute standardized differences comparing the squares of continuous variables between treatment groups ranged from a low of 0.1% to a high of 2.5%. The 25^th percentile, median, and 75^th percentile were 0.2%, 0.8%, and 1.5%, respectively. In the sample weighted using the weights derived from the complex specification of the propensity score model, the 11 absolute standardized differences comparing the squares of continuous variables between treatment groups ranged from a low of 0% to a high of 1.9%. The 25^th percentile, median, and 75^th percentile were 0.1%, 0.5%, and 0.8%, respectively. Similar results were obtained when we compared the mean of cubes of continuous variables between treatment groups.

The 55 interactions between pairs of continuous variables were computed in the original sample. The absolute value of standardized differences comparing the mean of the product of a pair of variables between treated and control subjects in the original unweighted sample ranged from a low of 2.4% to a high of 43.3%. The 25^th percentile, median, and 75^th percentile were 10.7%, 18.0%, and 24.6%, respectively. Thus, in the original unweighted sample, approximately 75% of the standardized differences comparing pairs of interactions between groups exceeded 10%. In the sample weighted by the weights derived from the simple specification of the propensity score model, the absolute value of the standardized differences comparing the 55 means of products of continuous variables ranged from a low of 0% to a high of 2.3%. The 25^th percentile, median, and 75^th percentile were 0.5%, 1.0%, and 1.5%, respectively. In the sample weighted by the weights derived from the complex specification of the propensity score model, the absolute value of the standardized differences comparing the 55 means of products of continuous variables ranged from a low of 0% to a high of 1.4%. The 25^th percentile, median, and 75^th percentile were 0.3%, 0.6%, and 0.9%, respectively.

These analyses suggest that by weighting by the inverse probability of treatment, a sample has been created in which the means of higher‐order terms and interactions between continuous variables are similar between treated and control subjects. Better balance was achieved using the weights derived from the complex specification of the propensity score model than using the simple specification; however, differences between the two approaches were at most modest.

5.2.4. Graphical comparisons of the distribution of continuous covariates

Figures 3, 4, 5, 6 display side‐by‐side boxplots and the empirical CDFs comparing the distribution of age, respiratory rate, creatinine, and haemoglobin between treated and control subjects. This is performed in both the original unweighted sample and in the two weighted samples. The three top panels display the side‐by‐side boxplots in the original unmatched sample and in the two weighted samples. The three lower panels display the empirical cumulative distribution functions in the unweighted sample and in the two weighted samples.

Figure 3.

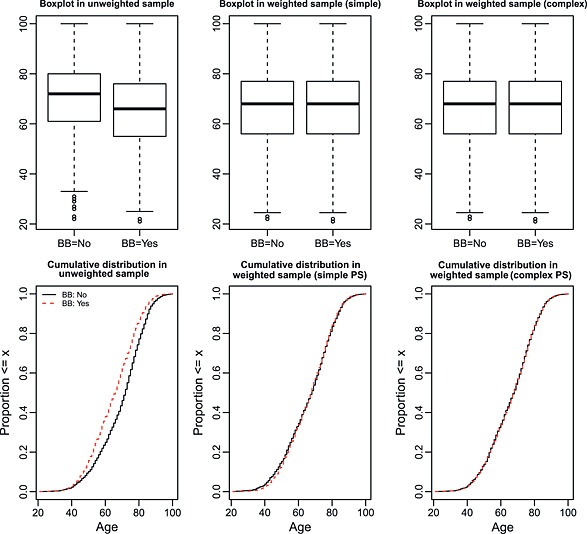
Distribution of age between treated and control subjects.

Figure 4.

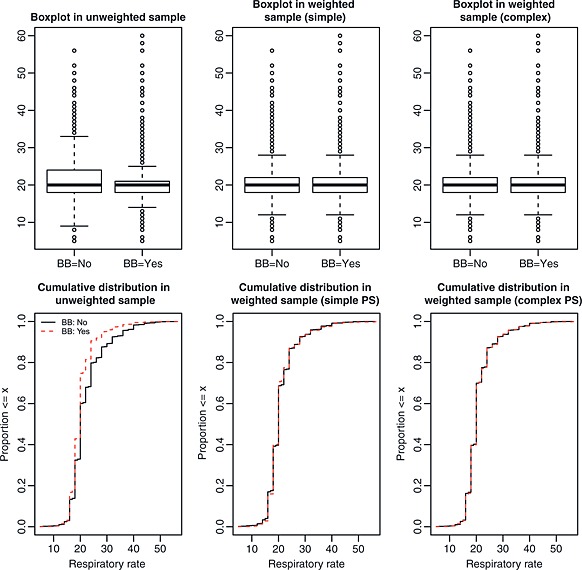
Distribution of respiratory rate between treated and control subjects.

Figure 5.

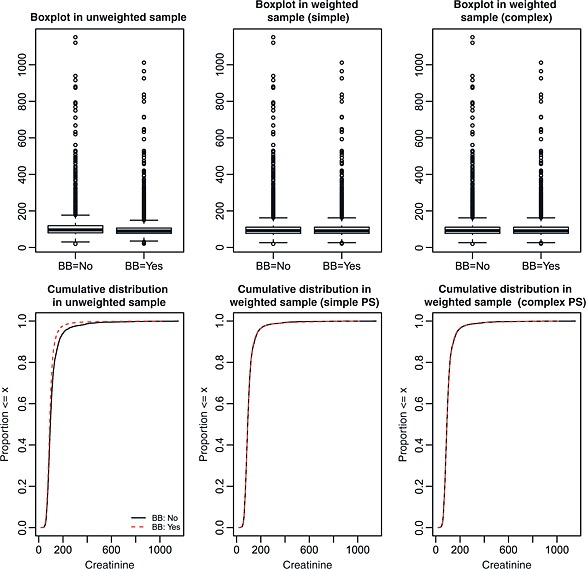
Distribution of creatinine between treated and control subjects.

Figure 6.

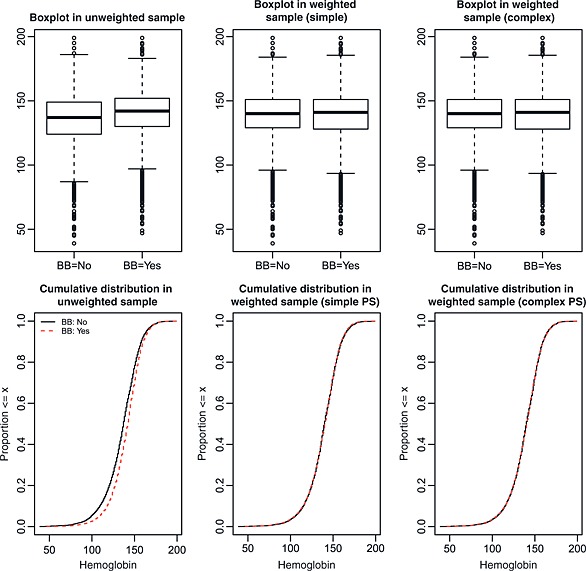
Distribution of hemoglobin between treated and control subjects.

In examining the boxplots in the upper left panel of Figure 3, one observes that the median age is greater in patients who did not receive a beta‐blocker compared with patients who did receive a prescription for a beta‐blocker at discharge. Furthermore, the distribution of age is shifted upwards in those who did not receive a prescription compared with those who did receive a prescription. However, after weighting by the inverse probability of treatment, the two side‐by‐side boxplots appear nearly identical. Similarly, the empirical cumulative distribution is nearly identical between treated and control subjects in both weighted samples. Both graphical diagnostics indicate that the distribution of age is nearly identical between treated and control subjects in the two weighted samples. Modest improvement in balance was achieved with the complex specification of the propensity score model compared with the simple specification of the propensity score model.

Figures 4, 5, 6 depict the graphical balance diagnostics for respiratory rate, creatinine, and haemoglobin, respectively. These figures (Figure 5 in particular) illustrate a limitation to the use of boxplots. When the interquartile range is very small compared with the range of the data, the box portion of the plot can be very compressed, and it can be difficult to qualitatively compare the similarity of the two boxplots. However, the cumulative distribution plots do not suffer from this limitation. In examining the lower panels of Figures 4, 5, 6, it is evident that weighting using the inverse probability of treatment has resulted in a sample in which the distributions of respiratory rate, creatinine, and haemoglobin are nearly identical between treated and control subjects. In order to address the difficulty of interpreting the boxplots for creatinine, Figure 7 compares the distribution of the natural logarithm of creatinine (thereby reducing the influence of extreme observations on the interpretability of the boxplots) between treated and control subjects. Figure 7 reinforces the conclusion that weighting by the inverse probability of treatment has resulted in a sample in which the distribution of creatinine is very similar between treated and control subjects.

Figure 7.

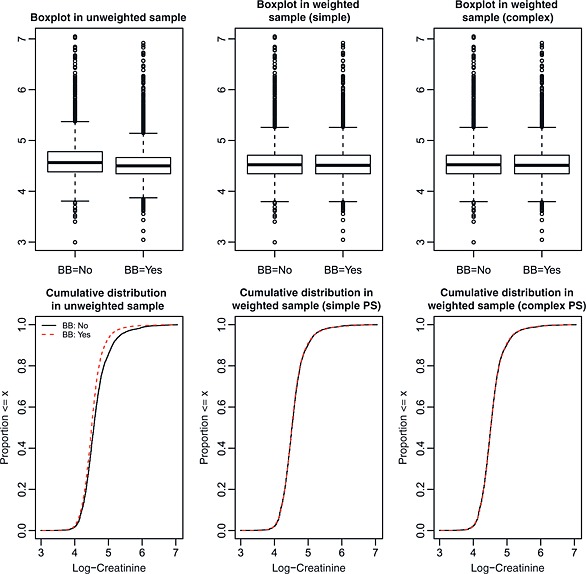
Distribution of log‐creatinine between treated and control subjects.

These analyses suggest that by weighting by the inverse probability of treatment, a sample has been created in which the univariate distribution of continuous variables are similar between treated and control subjects. While the specifications of the propensity score resulted in weighted samples with comparable balance between treated and control subjects, one could prefer the more complex specification because of its minor improvement in balancing the distribution of age between treated and control subjects.

5.2.5. Kolmogorov–Smirnov test statistic for comparing distribution of baseline covariates between treatment groups

The Kolmogorov–Smirnov test statistic for the 11 continuous covariates in the original unweighted sample ranged from a low of 0.050 (sodium) to a high of 0.164 (age). The Kolmogorov–Smirnov test statistic for the 11 continuous covariates in the sample weighted using the simple specification of the propensity score model ranged from a low of 0.014 (creatinine) to 0.027 (diastolic blood pressure). The Kolmogorov–Smirnov test statistic for the 11 continuous covariates in the sample weighted using the complex specification of the propensity score model ranged from a low of 0.005 (respiratory rate) to a high of 0.020 (heart rate). The test statistic for each of the 11 variables was higher in the sample weighted by the simple specification of the propensity score than it was in the sample weighted by the complex specification of the propensity score (differences ranged from a low of 0.003 to a high of 0.017). As with the graphical tests considered in the previous sub‐section, one would express a slight preference for the more complex specification of the propensity score, as it resulted in slight improvements in balance compared with that observed for the simple specification of the propensity score model.

6. Discussion

We have described methods to assess the adequacy of assumptions necessary for making causal inferences when using IPTW using the propensity score. We described a comprehensive suite of diagnostics to assess whether weighting the sample by the inverse probability of treatment received induced a sample in which the distribution of measured baseline covariates is the same between treated and control subjects. Diagnostics for assessing balance have not been developed formally in the context of IPTW, nor has their use been forcefully advocated. Likely in part because of this, applied researchers commonly do not use appropriate diagnostics. We propose that the weighted standardized difference be used to compare means and prevalences of continuous and binary variables, respectively, between treated and control subjects in the weighted sample and also to compare higher‐order moments and interactions between continuous variables. Furthermore, the use of cumulative distribution functions and side‐by‐side boxplots allows researchers to qualitatively compare the distribution of continuous variables between treated and control subjects in the sample weighted by the inverse probability of treatment. The Kolmogorov–Smirnov test statistic permits a numerical comparison of the distribution of continuous baseline covariates between treatment groups in the weighted sample. If, in the sample weighted by the estimated inverse probability of treatment, systematic differences persist between treated and control subjects, this may be an indication that the specification of the propensity score model requires modification. If this occurs, an iterative approach to developing the propensity score model, similar to the one suggested by Rosenbaum and Rubin, may be required 2. Finally, when using stabilized weights, examining the distribution of the weights (in particular the mean weight) permits an examination of whether the propensity score model had been correctly specified and whether the positivity assumption had been violated.

Diagnostics for the adequacy of the specification of the propensity score model have been developed in the context of propensity score matching, stratification on the propensity score, and covariate adjustment using the propensity score. Methods have been developed to assess whether matching on the propensity score has resulted in a matched sample in which the distribution of measured baseline covariates are similar between treated and control subjects. Ho et al. suggest comparing higher‐order moments and important two‐way interactions between treated and control subjects 9. Furthermore, Austin described a comprehensive set of methods, including graphical approaches, for assessing the comparability of treated and control subjects in the matched sample 10. Similarly, balance diagnostics have been proposed for when stratification on the quintiles of the propensity score is employed. In the first application of propensity score methods, Rosenbaum and Rubin used two‐way analysis of variance models to regress each measured baseline covariate on propensity score quintile (as a five‐level categorical variable), an indicator variable for treatment selection, and the two‐way interaction between these two factors 2. The significance of either the treatment indicator or the interaction variable was used to infer that the mean of that baseline covariate differed between treated and control subjects within at least one quintile of the propensity score. Other authors have proposed the use of within‐quintile standardized differences to compare the distribution of baseline covariates between treated and control subjects 8, 48. In the context of covariate adjustment using the propensity score, weighted conditional absolute standardized differences and quantile regression have been proposed to assess the balance in measured baseline covariates between treated and control subjects with the same propensity score 11. While several applied studies have reported the area under the receiver operating characteristic curve of the propensity score model (equivalent to the model c‐statistic), recent research has indicated that this does not serve as a test of whether the propensity score model has been correctly specified 10, 49. Similarly, in the context of propensity score matching, comparing the empirical distribution of the propensity score does not serve as an indication of whether the propensity score model has been correctly specified 10.

In our literature review, we observed that of the 29 studies published in 2014 that used IPTW methods, fewer than half described a comparison of baseline covariates between treated and control subjects in the weighted sample (regardless of the quality or appropriateness of the method for comparison). Further, only a small minority of studies (10.3%) reported examining the distribution of weights. These observations can be compared with those from a previous review of the use of propensity score matching in studies published in the medical literature between 1996 and 2003 50. Of the 47 articles that employed propensity score matching, in only eight (17%) was there no reported assessment of the comparability of the treatment groups. In the large majority of papers (83%), some form of balance assessment was conducted and reported. Thus, it appears that when analysts use propensity score matching, there is a general awareness of the need to compare the distribution of measured baseline covariates between treatment groups. However, there is a much more limited recognition that this is equally important when using IPTW. These observations highlight the need for guidance on optimal statistical practice when using IPTW. As our review also demonstrated, the use of IPTW has grown substantially in recent years. Given the increasing interest in this method for estimating causal effects and the poor statistical practice that is evident when this method is used, it is imperative that information on best statistical practice be disseminated to a wide audience.

We acknowledge that the balance diagnostics described in this paper are not particularly novel. Indeed, they are all weighted versions of methods that have been proposed for examining covariate balance in the context of propensity score matching. Furthermore, some of the proposed methods have been used previously in the literature. In a case study comparing the effect of Catholic schooling versus public school on student outcomes, Morgan and Todd used standardized differences to compare means of covariates between the two educational systems in the weighted sample 30. They compared the variance of continuous variables between groups. Similarly, Joffe et al. used side‐by‐side boxplots to compare the distribution of continuous variables between treatment groups in the weighted sample 15. Thus, some of the diagnostics that we have described have been previously employed in the causal inference literature. By having a paper focussed on balance diagnostics in the context of IPTW, our objective is to contribute towards the evolvement of what constitutes best practice when using IPTW. Morgan and Todd suggest that a comparison of characteristics between treated and control subjects should be a step in an analysis of causal treatment effects using IPTW 18. Our hope is that formal balance diagnostics will become a well‐accepted and formal step in any analysis that uses propensity score weighting. The methods described in this paper can serve as a template on how to conduct this step. Our literature review indicated that the use of IPTW has become increasingly popular in recent years and that the use of appropriate balance and weight diagnostics are frequently omitted from published studies. This suggests that there is an urgent need for the dissemination of appropriate diagnostics to complement the reporting of effect estimates.

As noted in the Introduction, there are four primary methods of using the propensity score to estimate treatment effects: matching, stratification (or subclassification), weighting, and covariate adjustment using the propensity score. Of these, the last two use the propensity score directly in estimating the effect of treatment, while the first two use the propensity score only for grouping subjects but not in estimating the effect of treatment. Rubin has suggested that for this reason, the latter two methods may be more sensitive to misspecification of the propensity score model than the first two methods 6. For this reason, it is imperative that balance and weight diagnostics accompany analyses that use IPTW.

The interpretation of balance diagnostics is, to a certain extent, inherently subjective. The degree of imbalance that is acceptable likely depends on the magnitude of the effect of the covariate on the outcome. Thus, greater imbalance may be acceptable for covariates that are weakly prognostic than for covariates that are strongly prognostic. Furthermore, the analyst may be faced with a situation in which one specification of the propensity score model results in better balance of a given covariate and worse balance of a different covariate compared with a different specification of the propensity score model. In such a setting, the analyst would need to consider the relative effects of each covariate on the outcome when deciding which specification to use in the final analyses.

There are avenues for future extensions of the proposed diagnostics. Our discussion of diagnostics for use with IPTW using the propensity score has been in the context of a binary or dichotomous treatment. While not considered in the current paper, these methods can be extended to settings with polytomous exposures. Furthermore, we have restricted our focus to settings in which propensity score methods are most commonly used: cohort designs in which there is a point‐exposure that is applied and defined at baseline. MSMs are a family of models for use with longitudinal studies in which there is both time‐varying treatment and time‐varying confounding 15, 51, 52, 53. The parameters of these models are often estimated using IPTW. While more complex, the methods described in the current paper should be modifiable for use with MSMs.

In summary, we found that the use of IPTW is increasing rapidly in the applied literature. However, many published studies omit the crucial step of assessing the comparability of the treated and control groups in the weighted sample. To address this weakness in published studies, we have described diagnostics for assessing the balance of baseline covariates between treatment groups in the sample weighted by the inverse probability of treatment. Our hope is that increased use of these diagnostics will improve the practice of IPTW for estimating average treatment effects using observational data. Adherence to the methods described in this paper may contribute towards the evolvement of what is considered ‘best practice’ when using IPTW to estimate causal treatment effects.

Disclaimer

The opinions, results, and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred.

Austin, P. C. , and Stuart, E. A. (2015) Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies. Statist. Med., 34: 3661–3679. doi: 10.1002/sim.6607.