Ascending thoracic aortic aneurysm wall stress analysis using patient-specific finite element modeling of in vivo magnetic resonance imaging

Abstract

OBJECTIVES

Rupture/dissection of ascending thoracic aortic aneurysms (aTAAs) carries high mortality and occurs in many patients who did not meet size criteria for elective surgery. Elevated wall stress may better predict adverse events, but cannot be directly measured in vivo, rather determined from finite element (FE) simulations. Current computational models make assumptions that limit accuracy, most commonly using in vivo imaging geometry to represent zero-pressure state. Accurate patient-specific wall stress requires models with zero-pressure three-dimensional geometry, material properties, wall thickness and residual stress. We hypothesized that wall stress calculated from in vivo imaging geometry at systemic pressure underestimates that using zero-pressure geometry. We developed a novel method to derive zero-pressure geometry from in vivo imaging at systemic pressure. The purpose of this study was to develop the first patient-specific aTAA models using magnetic resonance imaging (MRI) to assess material properties and zero-pressure geometry. Wall stress results from FE models using systemic pressure were compared with those from models using zero-pressure correction.

METHODS

Patients with aTAAs <5 cm underwent ECG-gated computed tomography angiography (CTA) and displacement encoding with stimulated echo (DENSE)-MRI. CTA lumen geometry was used to create surface contour meshes of aTAA geometry. DENSE-MRI measured cyclic aortic wall strain from which wall material property was derived. Zero- and systemic pressure geometries were created. Simulations were loaded to systemic pressure using the ABAQUS FE software. Wall stress analyses were compared between zero-pressure-corrected and systemic pressure geometry FE models.

RESULTS

Peak first principal wall stress (primarily aligned in the circumferential direction) at systolic pressure for the zero-pressure correction models was 430.62 ± 69.69 kPa, whereas that without zero-pressure correction was 312.55 ± 39.65 kPa (P = 0.004). Peak second principal wall stress (primarily aligned in the longitudinal direction) at systolic pressure for the zero-pressure correction models was 200.77 ± 43.13 kPa, whereas that without zero-stress correction was 156.25 ± 25.55 kPa (P = 0.02).

CONCLUSIONS

Previous FE aTAA models from in vivo CT and MRI have not accounted for zero-pressure geometry or patient-specific material property. We demonstrated that zero-pressure correction significantly impacts wall stress results. Future computational models that use wall stress to predict aTAA adverse events must take into account zero-pressure geometry and patient material property for accurate wall stress determination.

INTRODUCTION

Dissection and/or rupture of ascending thoracic aortic aneurysms (aTAAs) are often lethal cardiovascular emergencies. Pre-hospital mortality is 40%, with 1% death/hr thereafter without surgery [1]. Operative mortality is still 25% despite advances in intensive care and surgery according to the International Registry of Acute Aortic Dissection (IRAD) [2]. While elective surgical aTAA repair is based on size, growth, symptoms and family history or connective tissue disorder, diameter measured radiographically remains the primary determinant for risk stratification and surgical repair to prevent adverse events [3]. However, we and others have shown that diameter alone is not adequate to predict dissection [4–6] and nearly 60% of patients with type A dissection had aortic diameters <5.5 cm, whereas 40% had diameters <5.0 cm [5]. Alarmingly, significant numbers of patients develop aortic dissection with mean aortic diameters <5.0 cm. Conversely, many patients with aTAAs <5.0 cm have been clinically followed successfully for extended periods without adverse consequences. Simply lowering the size criteria for surgical intervention of aTAAs would subject many patients to the unnecessary risk of surgery. A better predictor of dissection or rupture for <5 cm aTAAs is clearly needed.

From a biomechanics perspective, rupture or dissection is a mechanical failure that occurs when aneurysm wall stress exceeds wall strength. Wall stress may be a better predictor of adverse events. Unfortunately, neither wall stress nor wall strength is directly measurable in vivo. Guidelines use diameter as a surrogate for wall stress based on LaPlace's Law. However, accurate determination of wall stress requires finite element analysis (FEA). FEA in physiological studies is a valuable method to obtain important biomechanical data about complicated real-world systems that otherwise would be impossible to measure, i.e. in vivo wall stress. In the setting of patient-specific aTAAs, wall stress can be determined by FEA of realistic three-dimensional (3D) computational models, whereas wall strength is determined by failure testing. Failure testing of aTAA surgical specimens has elucidated generalized aTAA wall strength for better understanding of dissection [7, 8]. Accurate patient-specific wall stress requires FE models with precise 3D geometry in the zero-pressure state, regional material properties, wall thickness and residual stress. We and others have previously studied stress–strain relationships to determine aTAA mechanical properties [7, 9, 10]. However, current in vivo aTAA FE models [11–15] are plagued with assumptions that limit the accuracy and validity of the results [16, 17]. The most common assumption is to use in vivo geometry at systemic pressure from computed tomography (CT) or magnetic resonance imaging (MRI) as the reference zero-pressure geometry and loading the already pressurized geometry to systemic pressure. We hypothesized that wall stress derived from systemic pressure geometry underestimates that using zero-pressure geometry. We developed a novel method to derive zero-pressure geometry from in vivo imaging at systemic pressure. The purpose of this study was to develop the first patient-specific aTAA models using in vivo MRI to assess material properties and zero-pressure geometry and compare stress differences between simulations using zero-pressure and systemic pressure geometry.

MATERIALS AND METHODS

Nine patients with aTAA size <5.0 cm were recruited for the study. Our aTAA patients are followed clinically with ECG-gated 64-slice CT angiography (CTA) gated to systole for maximum aTAA dimension. Informed consent was obtained for subjects to undergo displacement encoding with stimulated echo (DENSE)-MRI for research purposes. The study was approved by the Committee on Human Research at the University of California at San Francisco Medical Center and Institutional Review Board at San Francisco Veterans Administration Medical Center. Three patients underwent DENSE-MRI for optimization of the sequences to obtain the requisite data for material properties, but were not used in the study. An additional 2 patients had sufficient motion artifact during DENSE acquisition that prevented use during analysis. The remaining 4 patients were investigated in this study. The stress distribution in each patient was determined using four steps: (i) FE model development from CTA images, (ii) optimization of the material properties using DENSE-MRI data, (iii) derivation of the zero-pressure configuration and (iv) FE simulations with and without the zero-pressure configuration.

Development of finite element model geometry from in vivo imaging

Each patient underwent ECG-gated 64-slice CTA in systole with 0.625 mm axial slice thickness through the chest. An FE model for each patient was developed. First, CT scan images (Fig. 1) were exported as Digital Imaging and Communications in Medicine (DICOM) files and imported into MeVisLab, an open source surface reconstruction software (http://www.mevislab.de/home/about-mevislab) for image segmentation. Next, a smooth 3D surface was constructed and imported into ABAQUS (Dassault Systèmes, Waltham, MA, USA), a commercially available FE software package to develop the FE model. ABAQUS was used for pressure loading simulations and data analysis.

Figure 1:

Computed tomography scan images used for surface reconstruction.

In vivo patient-specific material properties

FE models require input of mechanical behaviour of the patient's aTAA wall. The Ogden hyperelastic material is widely used to model nonlinear arterial tissues and was used here, defined by a strain energy density function, W, as

$$W={\sum }_{i=1}^N\frac{2{\mu }_i}{{\alpha }_i^2}({\overline{\lambda }}_1^{{\alpha }_i}+{\overline{\lambda }}_2^{{\alpha }_i}+{\overline{\lambda }}_3^{{\alpha }_i}-3)+{\sum }_{i=1}^N\frac{1}{D_i}{(J^{el}-1)}^{2i},$$ (1)

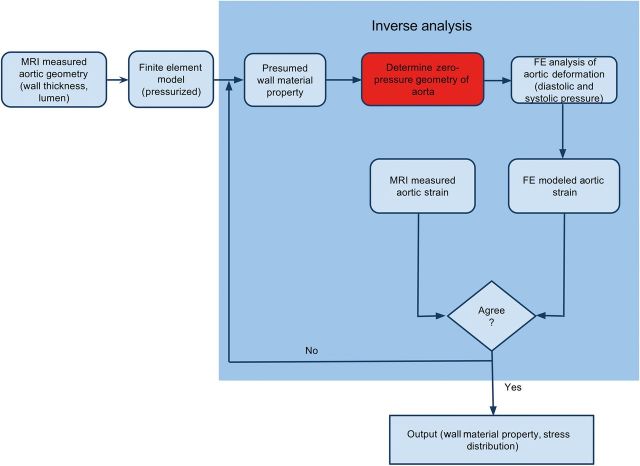
where ${\overline{\lambda }}_i$ is the deviatoric principal stretches, $J^{el}$ is the elastic volume ratio and N, ${\mu }_i$, ${\alpha }_i$ and $D_i$ are material parameters. We have previously performed biaxial tensile testing to obtain stress–strain data for aTAA material properties [9]. We demonstrated that aTAA mechanical behaviour is variable among patients. To determine patient-specific aTAA material properties in this study, we used a previously described inverse analysis method [18]. Unlike forward analysis, which predicts aortic wall strain from a set of known material parameters, inverse analysis determines the unknown material parameters using measured aortic wall strain using the iterative approach given in Fig. 2. The goal of inverse analysis is to determine material properties by optimizing material parameters (Equation 1) to match measured aortic wall strain. We used the experimental stress–strain curve for a 4.5-cm aTAA as a starting point for the optimization. Patients underwent in vivo DENSE-MRI to determine cyclic aortic strain using our published protocol [19].

Figure 2:

Flow chart of the inverse analysis technique for in vivo wall material property. MRI: magnetic resonance imaging; FE: finite element.

Zero-pressure configuration

Since CTA data acquired in vivo represented aTAA at systolic pressure, we needed to reconstruct zero-pressure geometry from in vivo configuration. We developed an innovative solution for determining zero-pressure geometry. In the first step, aTAA was assumed to have supra-physiological stiffness (Young's modulus, E = 1 × 10⁹ Pa), such that application of systolic pressure would not deform the geometry. The aTAA wall was loaded to systolic pressure. The stress distribution for the individual elements of the aortic wall was determined. Then in the second step, the results of the stress distribution from the first step were specified as the initial wall stress. The supra-physiological stiff material was replaced by the patient-specific aTAA wall material property as determined above in the inverse analysis. Zero-pressure geometry was calculated by gradually reducing the inner surface pressure load to 0 mmHg.

Finite element analyses of aneurysms at diastolic and systolic pressure

FE simulations were performed using an ABAQUS explicit solver. The reconstructed aTAA wall surface from the sinotubular junction to the aortic arch was modelled using two-dimensional shell elements with an average element size of 1.5 mm. Mesh refinement studies were performed to determine the ideal mesh size for the stress analysis. Boundary conditions were applied to the outer nodes of the model to restrict any rigid body motions. For each patient, we conducted two simulations, one using the above-determined zero-pressure geometry and the other, using in vivo geometry at systemic pressure. Simulation was performed by applying human physiological arterial pressure loading conditions to aTAA inner lumen. Initial pressurization during simulation featured ramp up from 0 mmHg to systolic pressure (120 mmHg) over 100 ms duration, followed by a decrease in pressure to diastolic pressure (80 mmHg) over another 100 ms period. Application of pressure in this fashion eliminated any unrealistic inertial forces and improved numerical stability during simulation [20]. After initial ramp up to systolic pressure and decrease to diastolic pressure, one cardiac cycle of 800 ms duration was applied. The cardiac cycle was composed of 300 ms ramp upwards to maximum systolic pressure, followed by 500 ms ramp downwards to minimum diastolic pressure. Systole comprised 38% of cardiac cycle. All remaining elements were unconstrained.

Data and statistical analysis

Simulation results were examined at times corresponding to peak systolic and minimum diastolic pressures to measure wall stress. First principal stress corresponding to stress primarily aligned in the circumferential direction and second principal stress corresponding to stress primarily aligned in the longitudinal direction were calculated by the ABAQUS post-processing software. For statistical analysis, independent-samples t-tests were utilized to compare maximum principal stresses of FE models from zero- and systemic pressure geometries at diastolic and systolic pressures. Reported values are quoted as mean ± standard deviation (SD), and a P-value of <0.05 was considered statistically significant. Statistical analyses were performed using IBM SPSS.

RESULTS

Finite element models and validation

An FE aTAA model at systemic pressure configuration for each of the 4 patients was created from in vivo CTA at systolic pressure. Patient-specific material properties were obtained from the DENSE data and are reported in Table 1. Zero-pressure configuration for each patient was determined. For each patient, the zero-pressure geometry model was validated by running a simulation from 0 mmHg to the patient's systolic pressure at the time of CT imaging. Matching of predicted systolic geometry from the model with in vivo CT imaging provided confidence in our zero-pressure geometry. Figure 3 illustrates a comparison of the zero-pressure geometry at 0 mmHg and a model predicted systolic pressure geometry superimposed on in vivo CT imaging geometry. FE models for all 4 patients demonstrated excellent matching with systolic geometry from in vivo CTA imaging. Figure 3 also demonstrates predicted systolic geometry when using in vivo CTA geometry as the FE model. The superimposed predicted geometry does not match in vivo CTA geometry and demonstrates the inaccuracy of that commonly used FE method. Figure 4 illustrates the two FE models per patient, the systemic pressure geometry and corresponding zero-pressure configuration.

Table 1:

Patient-specific material properties and haemodynamics

Patient	Systolic pressure (mmHg)	Diastolic pressure (mmHg)	Stretch ratio	Young's modulus (kPa)	Aneurysm diameter (cm)
1	125	75	1.0154	5.0E3	4.5
2	180	94	1.0129	6.0E3	4.3
3	134	81	1.0040	1.0E4	4.5
4	115	67	1.0176	5.2E3	4.2

Young's modulus is a measure of stiffness of the elastic aTAA wall.

aTAA: ascending thoracic aortic aneurysm.

Figure 3:

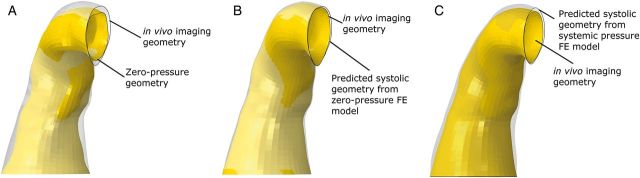
(A) Zero-pressure geometry superimposed on in vivo imaging geometry. (B) Predicted systolic geometry from the zero-pressure FE model superimposed on in vivo imaging geometry. (C) Predicted systolic geometry from the systemic pressure FE model superimposed on in vivo imaging geometry. FE: finite element.

Figure 4:

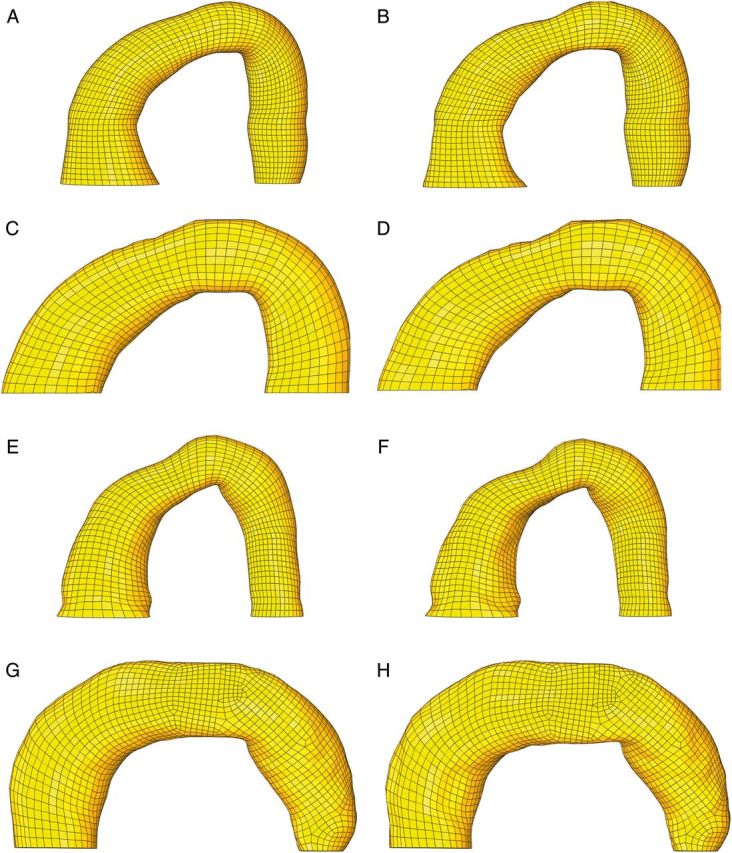
FE mesh of the systolic pressure geometry (left) and the corresponding zero-pressure geometry (right) for Patients 1 (A and B), 2 (C and D), 3 (E and F) and 4 (G and H). FE: finite element.

Finite element analyses of aneurysms

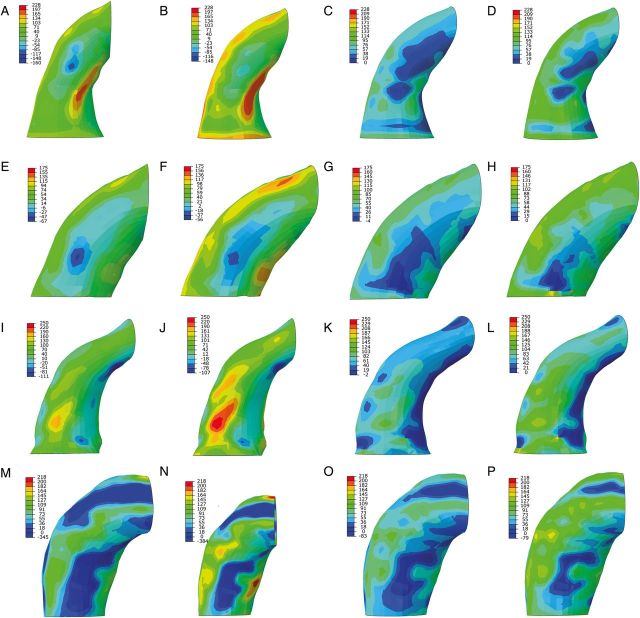
Peak first principal stress corresponding to wall stress primarily aligned in the circumferential direction was analysed at diastole (80 mmHg) and systole (120 mmHg). Peak second principal stress corresponding to wall stress primarily aligned in the longitudinal direction was also determined at diastole and systole. Peak first and second principal stresses were compared from FE models with zero-pressure geometry and systemic pressure geometry (Table 2). Peak stress values for the zero-pressure FE models were significantly greater than those for the systemic pressure models. The regions of peak first principal stress were located on outer surface of the aTAA wall, inner curvature as well as close to the pulmonary artery (Fig. 5). Peak first principal stress in diastole for the zero-pressure models was 323.65 ± 58.64 kPa, whereas systemic pressure models predicted 212.87 ± 27.84 kPa (P = 0.004). Peak first principal stress at systole for the zero-pressure models was 430.62 ± 69.69 kPa, whereas systemic pressure models predicted 312.55 ± 39.65 kPa (P = 0.004). Regions of peak second principal stress were also located on the outer curvature of the aTAA wall, as well as inner curve and close to the pulmonary artery (Fig. 6). Peak second principal stress in diastole for the zero-pressure models was 150.69 ± 35.26 kPa, whereas systemic pressure models predicted 107.11 ± 14.03 kPa (P = 0.03). Peak second principal stress at systole for the zero-pressure models was 200.77 ± 43.13 kPa, whereas systemic pressure models predicted 156.25 ± 25.55 kPa (P = 0.02).

Table 2:

Peak stress for each patient using zero- or systemic pressure geometry at diastole (80 mmHg) and systole (120 mmHg)

Patient	First principal stress using zero-pressure geometry (kPa)		First principal stress using systemic pressure geometry (kPa)		Second principal stress using zero-pressure geometry (kPa)		Second principal stress using systemic pressure geometry (kPa)
	Diastole	Systole	Diastole	Systole	Diastole	Systole	Diastole	Systole
1	412.9	535	256	370.5	184.1	227.9	105.7	155.8
2	249.2	350.5	179.1	258.6	96.27	133.1	92.07	121.8
3	324.6	448.7	213.5	313.2	179.6	246.6	129.9	193.9
4	307.9	388.3	202.9	307.9	142.8	195.5	100.8	153.5
Mean	323.65	430.62	212.87	312.55	150.69	200.77	107.11	156.25
SD	58.64	69.69	27.84	39.65	35.26	43.13	14.03	25.55

First principal stress is primarily aligned in the circumferential direction.

Second principal stress is primarily aligned in the longitudinal direction.

Figure 5:

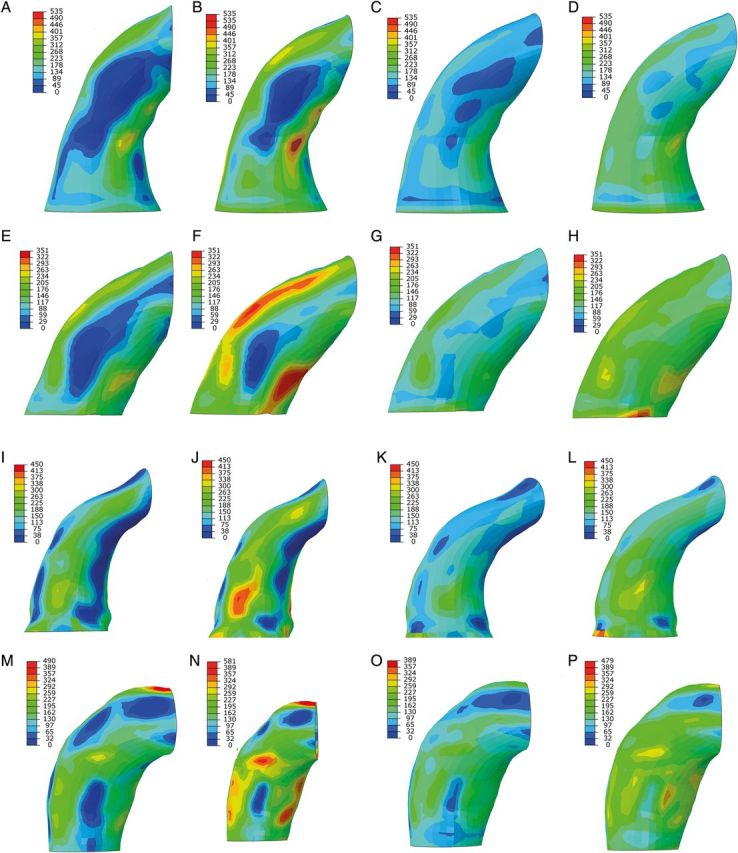
First principal aTAA stress for zero-pressure and systemic pressure FE models in Patients 1 (A–D), 2 (E–H), 3 (I–L) and 4 (M–P). The first two images represent wall stress at diastole and systole, respectively, for the zero-pressure FE model. The last two images represent wall stress at diastole and systole, respectively, for the systemic pressure FE model. FE: finite element; aTAA: ascending thoracic aortic aneurysm.

Figure 6:

Second principal aTAA stress for zero-pressure and systemic pressure FE models in Patients 1 (A–D), 2 (E–H), 3 (I–L) and 4 (M–P). The first two images represent wall stress at diastole and systole, respectively, for the zero-pressure FE model. The last two images represent wall stress at diastole and systole, respectively, for the systemic pressure FE model. FE: finite element; aTAA: ascending thoracic aortic aneurysm.

DISCUSSION

The aTAA models in the literature thus far [11–15] have estimated wall stress without accounting for zero-pressure geometry or patient-specific aTAA mechanical property. In this study, we developed the first aTAA models, to our knowledge, that incorporated both patient-specific material property and zero-pressure geometry. We demonstrated that aTAA wall stresses were significantly greater when FE models were corrected for zero-pressure geometry. If wall stress is to be used in the future as a predictor of adverse aTAA events, then FE models determining wall stress must account for zero-pressure geometry since models using systemic pressure geometry would greatly underestimate the risk of dissection or rupture.

Patient-specific aneurysm material properties and measurement of aneurysm stiffness

In this study, we used an inverse analysis method to determine patient-specific aTAA mechanical properties from DENSE-MRI. DENSE-MRI enabled measurement of aortic cyclic strain and aTAA wall stiffness. Other methods of measuring arterial wall stiffness in a patient-specific fashion include pulse wave velocity, the most validated method to non-invasive quantity arterial stiffness, and applanation tonometry [21]. Either method could be used in an inverse analysis to determine material properties. Carotid-femoral pulse valve analysis is the most frequently used index of arterial stiffness, given its simplicity and reproducibility; however, the arterial stiffness calculated reflects the aorta between the carotid and femoral arteries and would be less relevant to the aTAA. To determine aTAA stiffness would require assessment of pulse wave velocity non-invasively by MRI or echocardiography with pulse wave Doppler, which has good correlation with applanation tonometry. Applanation tonometry allows pulse wave analysis using a sensor probe to assess the augmentation of the pulse pressure waveform and the pulse wave velocity. The advantages of MRI are detection of regional stiffness, 3D vessel visualization and measurement of changes in aortic cross-sectional area for stiffness [21].

Wall stress of aneurysm models with zero-pressure correction

Peak aTAA first principal wall stress in systole was roughly 25% greater than the average wall stress. Overall, mean first principal wall stress from diastole to systole was 324–431 kPa, higher than the peak stress range seen in normal aortic roots [22]. Peak wall stress ranged from 242 to 535 kPa primarily in the circumferential direction and 179 to 370 kPa primarily in the longitudinal direction from diastole to systole. Wall stress distribution in these patients demonstrated that peak wall stress concentrated in the outer and inner curvature in the ascending aorta and towards the pulmonary artery. These regions would be most prone to dissection/rupture during periods of sudden increased systolic pressure.

We have previously studied the locations of the primary entry tear in acute type A aortic dissection. We found that for the majority of patients, the site of entry tear was at the sinotubular junction or ascending aorta, with the remaining in the sinus of Valsalva and aortic arch [4]. Our results in this study demonstrate areas in the greater and lesser curvature that may be prone to dissection and correlate with areas of dissection and higher wall stress in other studies [4, 14, 23].

Wall strength

Pichamuthu et al. [8] demonstrated greater aTAA strength circumferentially than longitudinally in 15 aTAA patients with the tricuspid aortic valve (TAV) and mean aTAA diameter of 5.7 cm and in 23 aTAA patients with the bicuspid aortic valve (BAV) and mean aTAA diameter of 5 cm. TAV-associated aTAA tensile strength was 961 ± 610 kPa circumferentially and 540 ± 370 kPa longitudinally, whereas BAV aTAA tensile strength was 1656 ± 980 kPa circumferentially and 698 ± 310 kPa longitudinally. Similarly, Duprey et al. [24] performed uniaxial testing for failure. Maximum elastic modulus was 834 and 905 kPa circumferentially for greater and lesser curvature, respectively; and 565 and 297 kPa longitudinally for greater and lesser curvature, respectively. Since aTAA wall strength is significantly lower in the longitudinal direction, the intimal tear would be predicted to occur as a transverse tear, giving a circumferential dissection spiral. Thubrikar et al. [14] predicted this transverse tear based on wall stress calculations. Given the range of our patients' peak aTAA wall stresses that were far below the mean tensile strength but within its lower limits, these aTAAs would not be expected to rupture unless their strength was within the lower limits of failure. Patient-specific FE models like the ones we created here may be useful clinically to assess the need for surgical intervention in select <5 cm aTAA patients whose wall stress exceeds the failure strength.

Aneurysm growth and systolic flow displacement

The major contributor of aortic wall stress is blood pressure, thus FEA to determine wall stress may be predictive of risk of dissection or rupture. For patients with aTAA <5 cm, another important consideration is the rate of aTAA growth. Unlike dissection or rupture, which represents a mechanical failure when stress exceeds strength, aTAA growth may be more influenced by not only genetic and biological factors, but also aortic flow characteristics. We have previously demonstrated using phase-contrast MRI that systolic flow displacement, a quantitative measure of systolic flow eccentricity, strongly correlated with future ascending aortic growth in patients with the BAV [25]. Wall shear stress and changes in aortic flow helicity as seen in 4D-flow MRI (time-resolved 3D phase-contrast MRI) may reveal other parameters that predict aTAA growth.

Study limitations

We assumed that the aTAA regions were homogeneous. Regional variations can exist, but we successfully defined patient-specific aTAA material properties which had not been done in in vivo computational models to date. We derived zero-pressure aTAA geometry, but were not able to confirm that geometry with true zero-pressure geometry from surgical specimens since these patients did not meet criteria for surgery. However, we have confidence in those derivations since our simulations of patient-specific pressurized geometry so closely matched the in vivo imaging geometry. Our simulations were performed to determine wall stress based on arterial pressurization, but do not account for fluid–structure interaction (FSI) with asymmetric or turbulent flow patterns from the valve. FEA of wall stress as demonstrated here ranged from 350 to 535 kPa primarily in the circumferential direction and ranged from 133 to 247 kPa primarily in the longitudinal direction. In contrast, the contribution of fluid shear stress was reported as a maximum value of 0.0023 kPa, several orders of magnitude less [13]. FSI to determine wall shear stress may be important for evaluation of aTAA development and growth, which is believed to depend on eccentricities of flow. However, such investigation of growth was beyond the scope of our study. Finally, DENSE-MRI was unable to completely the full stress–strain curve, particularly in the low-strain region since scans only gate to the cardiac cycle from diastole to systole but not from zero-pressure. Further experimental characterization of material properties for <5.0 cm aTAAs will be required in the future.

CONCLUSIONS

We developed the first to our knowledge patient-specific aTAA FE models from DENSE-MRI that incorporated zero-pressure geometry and patient-specific material properties. Peak wall stresses in these patients were significantly less than the average circumferential and longitudinal aTAA strength reported in the literature. Peak aTAA wall stresses were significantly greater for the zero-pressure correction models, which demonstrate the importance of incorporating zero-pressure geometry. Patient-specific computational models that use systemic pressure geometry from in vivo CT or MRI will underestimate aTAA wall stress and be unlikely to accurately predict aTAA adverse events. Creation of such patient-specific FE models using zero-pressure correction and patient-specific material properties is an important first step in the development of a biomechanically based clinical paradigm for in-vivo patient-specific aTAA risk prediction.

Funding

This work was supported by the University of California, proof-of-concept grant 246590.

Conflict of interest: none declared.

APPENDIX. CONFERENCE DISCUSSION

Dr L. Weltert (Rome, Italy): I will agree the overall concept you presented: many patients present with acute type A aortic dissection not having an aneurysm greater than 5 cm which in turns means that there are a lot of people around, with aneurysms measuring 4 to 5 cm who are at risk, but we don't know how to actually determine which way they will go.

The big question here is, is there a better way to predict the dissection rupture? I guess it would be the holy grail of biomechanics to have a reproducible tool to verify that precise stress for that specific patient in that peculiar anatomical configuration.

Once you determine stress, how do you assess risk in relation to strength? To date we can only measure strength by having the tissue to test for failure. There are literature-based studies on overall aneurysm strength, but at this point we don't have a way to determine individual patient wall strength.

I've seen as well that you, run the simulation at the systolic blood pressure of 120 mmHg. Then what if the patient has bursts of hypertension? Once you determine the zero pressure state, can you run the simulation up to higher BPs to see what blood pressure might result in stresses exceeding the literature-based aneurysm wall strength? I guess this could suggest how much blood pressure control would be required in that specific patient.

Dr Tseng: Thank you for your questions. Those are excellent points. Wall strength can only be determined at this time with experimental testing. The goal would be to determine wall strength on actual samples. In a grant that will be funded next year, we plan to study patients that require aneurysm surgery because these analyses of stress and strength can be determined in patients that require surgery by experimentally testing the tissue specimens. Using preoperative DENSE MRI with 4D flow, you can estimate material properties and perform computational studies to determine stress.

Then at the time of operation the excised tissue, provides the parameters to validate those computational models. The tissue specimen has geometry at zero pressure and the simulations can be performed to determine what the true stresses are to compare with the predicted stresses from MRI. The tissue provides the patient-specific material properties as well as the failure strength using tensile testing.

Among the parameters obtained from imaging and tissue specimens, we hope to develop a method to estimate failure strength noninvasively. This will be important for developing the patient specific risk benefit ratio.

With respect to the second question, we can run simulations to higher blood pressures to determine at what pressures the stresses may potentially exceed the wall strength estimate. Running the simulations to the patients’ blood pressure at the time of scan allowed us to validate the model. Each one of these patients had their CTs done at a given blood pressure, and so when the simulations were reloaded to that blood pressure, we were able to match the geometries from the scan to those of the model to show the accuracy of the simulation. The simulations can be loaded to any higher level of blood pressure to see what the risk of rupture would be at those higher levels.

Certainly sudden elevations in blood pressure could explain some type A dissections presenting in the ER, particularly those after cocaine or methamphetamine use.

Dr A. Moritz (Frankfurt, Germany): In your wall load pictures, there was always a very punctual increase in load, and it was usually on the inner side of the curvature.

In physics, the wall tension circumference is twice that when longitudinal. Despite this, in most cases of acute A dissections, the membrane rupture is circumferential.

This does not correlate to the increased stress pictures you showed us. So if this is true, the line of most load of the wall should be circumferential because that's the area where they rupture.

Dr Tseng: When an aneurysm dissects, the circumferential direction has not only the highest stress, but also the greatest strength. The circumferential tear represents a failure in the longitudinal direction.

Our preliminary study began with a few surgical aneurysm patients in whom we determined actual zero-pressure geometry, material properties and developed computational models of wall stress. In those patients, while longitudinal stress was lower than circumferential stress, the longitudinal stress was greater than the estimated longitudinal strength, validating the need for surgery in those patients. Those patients are expected to have a higher risk of rupture in the longitudinal direction corresponding to a circumferential tear. Circumferential stress was not greater than the estimated circumferential strength. In this study of these non-surgical patients, the longitudinal stress was quite low, so presumably these patients are less likely to dissect. However, in other future patients with small aneurysms, if the predicted stress is higher than the estimated strength, it would be concerning for potential dissection and rupture.

Dr A. Della Corte (Naples, Italy): Intuitively, it seems that this type of stress that you're measuring here is not the type of stress that may be causally related to dissection. This is without flow, isn't it?

Dr Tseng: It is without flow.

Dr Della Corte: Without computing the flow. So it does not take into account wall shear stress, which is probably more important in the pathogenesis of aortic dissection.

Dr Tseng: The magnitude of wall shear stress is magnitudes of order less than wall stress from blood pressure.

Dr Della Corte: Very different, yes.

Dr Tseng: The magnitude of wall shear stress is approximately of 0.002 kPa. So the contribution of wall shear stress is actually very minimal in comparison to wall stress. Where we do think wall shear stress is important is its impact on the endothelium and the biological aspects that relate to growth, potentially alterations in shape of the aneurysms.

Dr Della Corte: But again, dissection occurs with the increase in wall shear stress, independent of absolute magnitude.

Dr Tseng: The concept of rupture and dissection is based on biomechanics where stress exceeds strength. Since strength is also in the order of hundreds of kPas as is wall stress from blood pressure, blood pressure and corresponding wall stress plays a much greater contribution than actual flow stress of 0.002 kPa.

Dr Della Corte: Yes. But wall rupture is different from intimal tear that is dissection.

Dr Tseng: True, but dissection is still a mechanical failure and rupture or dissection begins with stress exceeding strength. The magnitude of shear stress is significantly lower than wall stress and, from an engineering perspective, plays a relatively minor role.