Abstract
Although many studies have evaluated the effects of type 2 diabetes mellitus (T2DM) on the pharmacokinetics (PK) of low molecular weight molecules, there is limited information regarding effects on monoclonal antibodies. Our previous studies have reported significant increases in total (2–4 fold) and renal (100–300 fold) clearance of human IgG, an antibody isotype, in Zucker diabetic fatty (ZDF) rats. Pioglitazone treatment incompletely reversed the disease-related PK changes. The objective of this study was to construct a mechanistic model for simultaneous fitting plasma and urine data, to yield physiologically relevant PK parameters. We propose an extended minimal physiologically based PK (mPBPK) model specifically for IgG by classifying organs as either leaky or tight vascular tissues, and adding a kidney compartment. The model incorporates convection as the primary mechanism of IgG movement from plasma into tissues, interstitial fluid (ISF) in extravascular distribution space, and glomerular filtration rate (GFR), sieving coefficient and fraction reabsorbed in the kidney. The model captured the plasma and urine PK profiles well, and simulated concentrations in ISF. The model estimated a 2–4 fold increase in nonrenal clearance from plasma and 30–120 fold increase in renal clearance with T2DM, consistent with the experimental findings, and these differences in renal clearance were related to changes in GFR, sieving coefficient, and proximal tubular reabsorption. In conclusion, the mPBPK model offers a more relevant approach for analyzing plasma and urine IgG concentration-time data than conventional models and provides insight regarding alterations in distributional and elimination parameters occurring with T2DM.
KEY WORDS: IgG, monoclonal antibody, mPBPK, renal clearance, Zucker diabetic fatty rat
INTRODUCTION
Diabetes mellitus is a group of endocrine metabolic disorders in which a person suffers from hyperglycemia, either because the body is unable to produce enough insulin, or because the receptor cells become desensitized to the insulin that is present (1,2). Globally, as of 2010, around 285 million people have been diagnosed with diabetes; and type 2 diabetes mellitus (T2DM) accounts for 90% of these cases. It is estimated that the prevalence of T2DM will reach around 500 million people worldwide by 2030 (3–5). Approximately 25–33% of T2DM patients develop diabetic nephropathy (DN) (5,6). As DN progresses, renal function becomes further compromised, exhibited by increases in urinary albumin excretion, observed initially as microalbuminuria and progressing to macroalbuminuria (6,7). Furthermore, with increasing severity of DN, about 20% of individuals progress to end-stage renal diseases (ESRD) (8,9).
Significant effects of DM/DN on small molecules have been reported (10), but there are only a few studies that have evaluated the impact of DM/DN on the pharmacokinetics (PK) of antibodies. Our previous studies have demonstrated that diabetes significantly impacts the renal and total clearance of human IgG (hIgG) in the T2DM Zucker Diabetic Fatty (ZDF) rat model (11). Since IgG is the most abundant antibody isotype found in the circulation, we dosed our animals with hIgG (12). Our studies demonstrated increases in renal clearance of IgG along with a significant increase in nonrenal clearance. Furthermore, treatment with the antihyperglycemic drug pioglitazone resulted in significant reductions in the total and renal clearances of IgG and demonstrated the importance of hyperglycemia and effects related to the hyperglycemia in the alterations in clearance of IgG.
Our findings in ZDF rats are consistent with clinical findings. In one such study in Pima Indians with T2DM and DN, dextrans were used as probes to demonstrate the development of large pores in the glomerular basement membrane (GBM), and a 2-fold increase in urinary IgG concentrations was observed with significant microalbuminuria (13). Other studies have also used dextrans or Ficoll as probes to evaluate the changes in the sieving function of kidneys with DM/DN (14–16). These studies have also evaluated the renal clearance of IgA (160 kDa) and IgM (970 kDa) (proteins larger than IgG in their molecular weight and size), and observed significantly larger amounts being eliminated through the urine (17). Another study assessed the role of clearance pathways involved in adalimumab elimination in patients with focal segmental glomerulosclerosis (18). This study reported 2- to 5-fold higher clearance with the disease, with a greater contribution of nonrenal clearance to the total clearance, as compared to renal clearance.
Previously, we had used a two-compartment model (2CM) (Fig. 1) to describe the concentration-time profiles of hIgG. A 2CM has been commonly used to describe and fit hIgG and monoclonal antibody PK data in animals (19). However, there are certain limitations to the use of a 2CM in protein therapeutics (20,21). The basic assumption of mammillary model is that same rate or clearance occurs for inward and outward distribution between central and peripheral compartments, thus keeping their concentrations at equilibrium. This assumption, however, fails to incorporate convection, which is the primary mechanism for IgG extravascular distribution and leads to lower concentrations of IgG in interstitial fluids (ISF), unlike small molecules. Furthermore, 2CM assumes elimination only from the central compartment and hence provides poor estimation of the peripheral compartment, especially in the case of mAbs which are metabolized in tissues such as the kidneys, spleen, skin, and liver. Physiologically based pharmacokinetic models (PBPK) provide a more mechanistic approach as compared to mammillary models since they can utilize anatomical and physiological parameters in the model (22). However, PBPK models require intensive biological sample collection and measurements of drug concentrations in various tissues. Recently, minimal PBPK (mPBPK) models have been developed for fitting limited data sets of blood or plasma (20,21,23). mPBPK takes a reductionist outlook and lumps organs of similar physiological characteristics together to form fewer compartments. Thus, the objective of this study was to develop an extended mPBPK model for hIgG disposition, using our plasma and urine data. We wanted to incorporate the effect of DM on total and renal clearance changes, along with the effect of pioglitazone treatment. An mPBPK model developed recently for mAbs was extended to include a kidney compartment to account for alterations in renal clearance of IgG with and without DM (20,21,23,24).
Fig. 1.

A schematic representation of the two compartment pharmacokinetic model for human IgG disposition. Human IgG was dosed IV into the central compartment. Linear antibody elimination clearance (CLT) is assumed to occur solely from the central compartment. Linear distribution clearance (CLd) occurs between the central and peripheral tissue compartments. V c and V p represent the volumes of distribution of the central and peripheral tissue compartments, respectively. A c and A p are the amounts in the central and peripheral compartments, respectively
MATERIALS AND METHODS
The data used in model development was obtained from a previous publication (11). In that study, ZDF rats were used as the animal model of Type 2 DM/DN as they exhibit the pertinent clinical signs of this disease including initial DM and progression to DN, allowing for assessment of the effects of DM with and without renal dysfunction, as well as with concomitant obesity. Male obese ZDF rats develop progressive DN causally related to their DM and represent a well-characterized animal model of DM/DN (25). Nondiabetic Zucker fatty rats were used as age‐matched controls. Another group of diabetic ZDF rats were treated with pioglitazone (10 mg/kg orally, daily) to treat hyperglycemia. The disposition of hIgG was studied at the age of 12–13 weeks (phase A; the observed age for the development of diabetes in the ZDF obese diabetic model) and then at the age of 29–30 weeks (phase B; when the ZDF diabetic rats demonstrated nephropathy with progressive albuminuria and rising urinary albumin to creatinine ratios (ACR)) (25,26). Animals were dosed with 1 mg/kg of hIgG IV through the jugular cannula or penile vein, with 6–8 animals per group. Blood and urine samples were collected over 4–5 half-lives and analyzed using commercially available ELISA kits.
Pharmacokinetic Models
2CM
Plasma and urine data obtained after the administration of hIgG (1 mg/kg) IV were reassessed using a 2CM (Fig. 1). The equations for the model are provided below:
| 1 |
| 2 |
where CLT is the hIgG elimination clearance (assumed to occur solely from the central compartment), CLD is the distribution clearance (that occurs between the central and peripheral tissue compartment), V c and V p are the volumes of distribution of the central and peripheral tissue compartments, respectively. A c and A p are the amounts of hIgG in central and peripheral compartments, respectively. IC represents the initial condition.
Previously reported parameters (CLD, CLT, V c, V p, k a and F) were obtained from simultaneously fitting data obtained after IV and SC administration of IgG (11).
mPBPK Model
The extended mPBPK model was based on a second-generation mPBPK model developed to describe the unique PK characteristics of mAbs (20,21). The model structure is based upon certain important considerations. The PK of IgG and mAbs are governed by the unique distribution of these proteins in extravascular space. Unlike small molecules, mAbs have poor transcapillary and cellular permeability. Similarly, convection is predominantly responsible for transcapillary escape rate, with insignificant diffusion involved (27,28). More than 50% of endogenous IgG is distributed in extravascular space and since mAbs have limited cellular permeability, ISF is assumed to be the primary extravascular distributable space (29).
The model structure (Fig. 2) is described by the following differential equations:
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
where A p represents the amount of hIgG amounts in the plasma compartment. A tight, A leaky, and A kid are the ISF amounts of hIgG in tissues, with volumes V tight, V leaky, and V kid, respectively. V tight defines the volume of ISF in tissues having continuous capillaries (brain, muscle, skin, and adipose), while V leaky defines the volumes of ISF in tissues having fenestrated or discontinuous capillaries (including liver, heart, pancreas, lung, and spleen) (20,21,30), with the exclusion of the kidneys since it was treated as an individual compartment. A lymph is the amount of hIgG in the lymph compartment having a volume of V lymph. The V lymph is assumed to be equal to the blood volume (20,23). The L is defined as total lymph flow, which is equal to the sum of L 1 and L 2, the lymph flow for V tight and V leaky, respectively. The σ1 and σ2 are vascular reflection coefficients for V tight and V leaky. The σL is the lymphatic capillary reflection coefficient. Lymphatic capillaries are very porous and, since their diameter is much larger than the paracellular pore diameter, a value of 0.2 for σL correlates with the assumption that there will be very little resistance to the convective transport of IgG via the lymphatic capillaries (31,32). CLi and CLp are clearances from ISF (V tight and V leaky) and plasma, respectively. For identifiability of clearance, the model structure is defined in such a way that either CLi will be estimated, with CLp set as 0, or vice-versa. Q kid is the blood flow rate to the kidney, glomerular filtration rate (GFR) is the glomerular flow rate, Ф is the sieving coefficient of a solute and is a measure of its transport rate in relation to that of water, F r is the fraction of IgG reabsorbed after clearing the glomerulus, while S is a scaling factor used to calculate changes in renal function (33). When GFR, Ф, and F r are fixed, changes in renal function are directly correlated to the values of S. IC is the initial condition of each compartment.
Fig. 2.

A schematic representation of the pharmacokinetic model for human IgG disposition. Human IgG was dosed IV into the plasma compartment. A p is the amount of hIgG in the plasma compartment, A tight, A leaky, and A kid are ISF amounts of hIgG in tissues with volumes V tight, V leaky, and V kid; A lymph is the amount of hIgG in the lymph compartment with the volume V lymph. L is the total lymph flow (L = L 1 + L 2). σ1 and σ2 are the vascular reflection coefficients for V tight and V leaky. σL is lymphatic capillary reflection coefficient. CLi and CLp are the clearances from ISF (V tight and V leaky) and plasma. GFR is the glomerular flow rate, Ф is the sieving coefficient of a solute, F r is the fraction of IgG reabsorbed after filtration at the glomerulus
The values of various volumes (34), ISF (35), GFR (25), and Ф (33,36) (Table I) were obtained from the literature. In our studies, weight differences were significant among the three animal groups and were also significant between phase A and phase B of the studies. To account for the weight variations as well as a separate kidney compartment, we deviated in the calculations for relative volume fractions from the literature (V tight:V leaky = 65:35) and based on animal weight, animal organ weights and values used in PBPK models, we calculated the ratio of individual group volumes (V Tcal ranged between 65 and 72%, V Lcal ranged between 27 and 34%, and V kid ranged between 0.4 and 1.1%) for phases A and B. Thus, the volumes were defined as:
| 9 |
where ISF is the total system ISF and K p is the available fraction of ISF for hIgG distribution. As in the literature, K p was fixed as 0.8 (20,21). Similarly, L 1 and L 2 were calculated and values of 0.33 and 0.67 were fixed, respectively (20,21,32,37). σ1 and σ2 were fixed or estimated between values of 0 and 1. Based on initial estimates in the control group, σ1 always was estimated with values of 0.95–1.0, so it was fixed at 0.95 for all 3 groups. Also, keeping the reflection coefficients σ1 and σ2 less than 1 limits the extravasation rate so that it is not higher than total lymph flow (L). Furthermore, the model settings assume σ1 as larger than σ2, since tight vascular endothelium is expected to have higher reflection than leakier vessels. The “lumped” tissue concentrations were simulated and compared among the animal groups. Model fittings were performed by nonlinear regression analysis using the maximum likelihood algorithm in ADAPT 5. All PK data was naïve pooled before analysis. Model performance was evaluated by goodness-of-fit parameters including Akaike Information Criterion, visual inspection, and coefficient of variation (CV) of the estimated parameters.
Table I.
Literature Values Used for Pharmacokinetic Parameters of hIgG in Rats (Fixed in the mPBPK Model)
| Parameter | Value |
|---|---|
| V p | 27 mL/kg |
| V L | 65 mL/kg |
| ISF | 0.2 L/kg |
| L | 0.708 mL/h |
| GFR Control rats (phase A) | 0.621 L/kg/h |
| GFR Diabetic rats (phase A) | 0.693 L/kg/h |
| GFR Pioglitazone-treated ZDF rats (phase A) | 0.406 L/kg/h |
| GFR Control rats (phase B) | 0.608 L/kg/h |
| GFR Diabetic rats (phase B) | 0.730 L/kg/h |
| GFR Pioglitazone-treated ZDF rats (phase B) | 0.284 L/kg/h |
| Ф | 2.30E-03 |
| Q kid | 36.9 mL/kg/min |
V p volume of plasma, V L volume of lymph, ISF interstitial fluid volume, L Total lymph flow, GFR glomerular filtration rate, Ф sieving coefficient for rat, Q kid kidney blood flow rate
RESULTS
2CM
The parameter estimates for plasma concentrations of hIgG IV dose are shown in Table II (phase A) and Table III (phase B). The model fits the data well (fittings not shown). Both the renal clearance as well as the total clearance of hIgG increased significantly (∼100-fold and ∼2.3-fold, respectively) in the diabetic animals. The changes in clearances were more pronounced in phase B with DM/DN present. Diabetic rats treated with pioglitazone demonstrated significantly decreased total and renal clearance, both in phase A and phase B. However, the renal clearance values with pioglitazone treatment were still significantly higher than the nondiabetic control rats. The estimated peripheral volume of distribution was significantly lower in the diabetic rats compared with the control and pioglitazone-treated rats.
Table II.
Analysis by a 2CM for Human IgG after IV Administration to ZDF Nondiabetic Control, Diabetic and Pioglitazone-Treated Diabetic Rats (phase A; 12–13 weeks of Age)
| Parameter (Units) |
Phase A Estimates (%CV) | ||
|---|---|---|---|
| Control | Pioglitazone-treated | Diabetic | |
| V C (mL/kg)a | 68.8 (8.54) | 68.8 (8.54) | 68.8 (8.54) |
| V p (mL/kg) | 63.1 (16.9) | 103 (15.7)* # | 53.5 (12.4) |
| CLD (mL/day/kg)a | 16.0 (16.1) | 16.0 (16.1) | 16.0 (16.1) |
| CLT (mL/day/kg) | 6.60 (4.43) | 7.53 (5.85) # | 14.9 (3.46) * |
| CLR (mL/day)b | 1.03E-02 ± 4.76E-03 | 0.230 ± 0.0843 * # | 1.33 ± 0.270 * |
*Statistically significant from control group; and #Statistically significant from Diabetic group at p ≤ 0.05 [One way ANOVA with Tukey’s Test]; (n = 6–8)
V C volume (central) of distribution; V p volume (peripheral) of distribution; CL T total clearance; CL D distribution clearance
a V C and CLD were modeled to be same for all the three groups, in phases A and B simultaneously.
bCLR renal clearance (calculated as urinary amount0-t/AUC0-t; mean ± SD) IV data (plasma and urine) of human IgG 1 mg/kg from the previous studies (11) was reassessed using a 2CM
Table III.
Analysis by a 2CM of Human IgG after IV Administration to ZDF Nondiabetic Control, Diabetic and Pioglitazone-Treated Diabetic Rats (phase B; 29–30 weeks of Age)
| Parameter (Units) |
Phase B Estimates (%CV) | ||
|---|---|---|---|
| Control | Pioglitazone-treated | Diabetic | |
| V C (mL/kg)a | 68.8 (8.54) | 68.8 (8.54) | 68.8 (8.54) |
| V p (mL/kg) | 56.7 (18.3) | 73.9 (12.7)* # | 23.7 (16.4)* |
| CLD (mL/day/kg)a | 16.0 (16.1) | 16.0 (16.1) | 16.0 (16.1) |
| CLT (mL/day/kg) | 5.44 (3.69) | 6.31 (3.63)# | 22.2 (3.29)* |
| CLR (mL/day)b | 3.50E-02 ± 1.04E-02 | 0.307 ± 0.119 *# | 6.27 + 1.49 * |
*Statistically significant from control group; and #Statistically significant from Diabetic group at p ≤ 0.05 [One way ANOVA with Tukey’s Test]; (n = 6–8). V C = volume (central) of distribution; V p volume (peripheral) of distribution; CL T total clearance; CL D distribution clearance
a V C and CL D were modeled to be same for all the three groups, in phases A and B simultaneously. bCLR renal clearance (calculated as urinary amount0-t/AUC0-t; mean ± SD)
IV data (plasma and urine) of human IgG 1 mg/kg from the previous studies (11) was reassessed using a 2CM
mPBPK Model
The mPBPK model provides a simple modeling approach, useful for the PK analysis of IgG and mAbs. The model involves different assumed physiologic parameters and is able to characterize the plasma and urine concentrations very well. All parameters have been estimated with reasonable precision.
The mPBPK model structure was designed to allow either CLp or CLi to be estimated. These two clearances cannot be both identified in this model. In our studies, estimating CLp provided better fittings as compared to estimating CLi (lower AIC function; data not shown). The model was able to fit the plasma and the urine data well, and simulated the lumped leaky and tight tissue compartments (Fig. 3. phase A; Fig. 4. phase B). Hence all the model estimations have CLi assumed to be 0. The CLp values for the diabetic group were significantly higher than the control group in phase A, and increased more during phase B (2.21- and 2.60-fold, respectively). Pioglitazone treatment reduced the effects of diabetes, but incompletely. These trends are similar to those of the 2CM (which also indicated a 2- to 4-fold increase in nonrenal clearance and changes with pioglitazone treatment; Tables II and III).
Fig. 3.
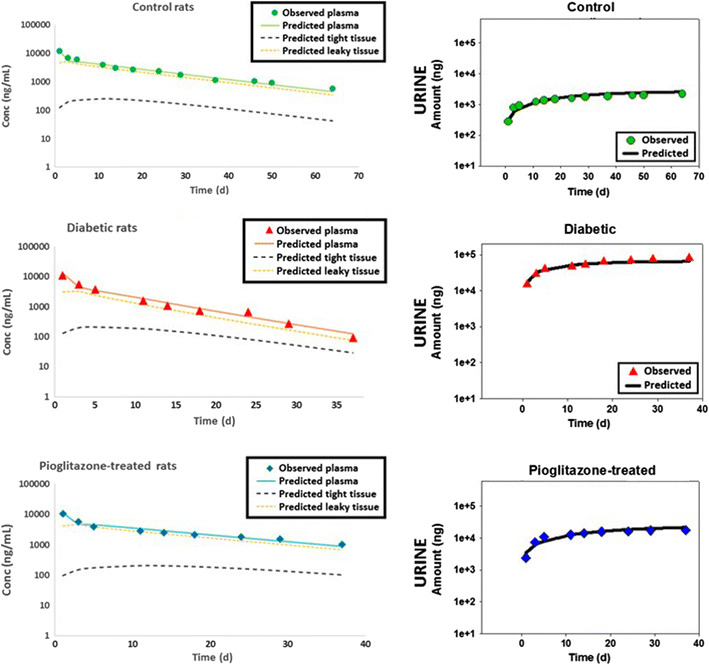
Plasma concentrations and urine amounts of human IgG after IV administration to ZDF diabetic, nondiabetic control rats, and pioglitazone-treated ZDF diabetic rats (phase A, age 12–13 weeks; n = 6–8). Symbols represent data and lines represent model fittings of mPBPK model 2. Data presented as mean ± SD
Fig. 4.
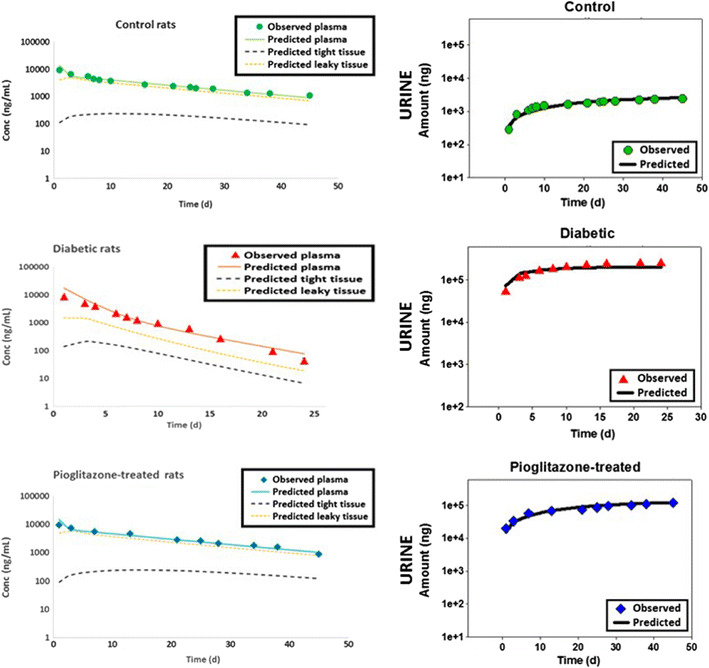
Plasma concentrations and urine amounts of human IgG after IV administration to ZDF diabetic, nondiabetic control rats, and pioglitazone-treated ZDF diabetic rats (phase B, age 29–30 weeks; n = 6–8). Symbols represent data and lines represent model fittings of mPBPK model 2. Data presented as mean ± SD
To mechanistically evaluate the renal changes, the amounts of hIgG present in urine were characterized by three functions GFR, Ф, and F r. Significant changes have been observed in GFR with the DM and pioglitazone treated DM groups (25). While the GFR of ZDF diabetic rats was significantly higher than nondiabetic control rats, pioglitazone-treated rats demonstrated significantly lower values for GFR. Another choice in modeling was whether to estimate changes associated with tubular reabsorption efficiency, F r (Model 1) or changes, possibly due to multiple reasons, in renal function via a scaling factor S (Model 2). Among the three groups, the GFR was fixed to the individual rates based on the literature (25), while either the F r (Table IV) or S (Table V) was estimated. With model 1 (estimating F r), the control rats had values of 97.1 and 98.3% in phases A and B, respectively. Model 1 also estimated a decrease in efficiency and thus, a significant decrease in F r, with values of 5.24E-01% and 5.41E-05% in DM and with increasing DN, respectively (phases A and B) in the diabetic animals. In the case of the pioglitazone treatment DM group, the model estimated F r to be 72.9 and 69.2% during phases A and B. However, the values of F r had very high CV% and poor model fittings (Table IV). The model parameters suggested that the model structure is limited in its ability to identify F r when in DM/DN the filtered load increases significantly.
Table IV.
mPBPK MODEL 1 Pharmacokinetic Parameters of Human IgG in ZDF Rats
| Group | Phase A | Phase B | ||||
|---|---|---|---|---|---|---|
| Parameter | Final | %CV | Parameter | Final | %CV | |
| Control | σ2 | 0.306 | 27.5 | σ2 | 0.631 | 16.3 |
| CLp (mL/day) | 2.10 | 4.74 | CLp (mL/day) | 2.42 | 3.65 | |
| F r | 0.971 | 0.220 | F r | 0.983 | 0.08 | |
| Diabetic | σ2 | 1.00 | 2.81E-05 | σ2 | 0.896 | 3.74 |
| CLp (mL/day) | 2.41 | 5.74 | CLp (mL/day) | 5.06 | 5.62 | |
| F r | 0.0 | 2.39E + 03 | F r | 5.41E-07 | 4.56E + 05 | |
| Pioglitazone | σ2 | 9.52E-06 | 1.35E + 06 | σ2 | 0.200 | 80.1 |
| CLp (mL/day) | 3.38 | 5.21 | CLp (mL/day) | 2.69 | 5.44 | |
| F r | 0.73 | 2.86 | F r | 0.693 | 2.84 | |
Analysis by a mPBPK model for human IgG after IV administration to ZDF nondiabetic control, diabetic and pioglitazone-treated diabetic rats (phase A; 12–13 weeks of age; phase B; 29–30 weeks of age). In this mPBPK model, the CLi (clearance from ISF) was fixed to zero. GFR and Ф was fixed to specific values from literature. σ2, CLp and F r were estimated
σ 2 vascular reflection coefficient for V leaky compartment; CLp nonrenal clearance; F r fraction reabsorbed
Table V.
mPBPK MODEL 2 Pharmacokinetic Parameters of Human IgG in ZDF Rats
| Phase A | Phase B | |||||
|---|---|---|---|---|---|---|
| Parameter | Final | %CV | Parameter | Final | %CV | |
| Control | σ2 | 0.282 | 22.1 | σ2 | 0.293 | 22.0 |
| CLp (mL/day) | 2.13 | 3.80 | CLp (mL/day) | 2.59 | 3.26 | |
| S | 1.00 | Fixed | S | 1.13 | 5.03 | |
| Diabetic | σ2 | 0.530 | 15.8 | σ2 | 0.819 * | 5.72 |
| CLp (mL/day) | 4.71 * | 6.47 | CLp (mL/day) | 5.55 * | 5.80 | |
| S | 36.5 * | 9.28 | S | 121 * | 8.14 | |
| Pioglitazone | σ2 | 0.227 | 8.19 | σ2 | 0.200 | 80.5 |
| CLp (mL/day) | 2.78 # | 14.2 | CLp (mL/day) | 2.69 # | 5.46 | |
| S | 8.78 *# | 11.3 | S | 10.3 *# | 6.41 | |
Analysis by a mPBPK model for human IgG after IV administration to ZDF nondiabetic control, diabetic and pioglitazone-treated diabetic rats (phase A; 12–13 weeks of age; phase B; 29–30 weeks of age). In this mPBPK model, the CLi (clearance from ISF) was fixed to zero. GFR and Ф was fixed to specific values from literature. F r was fixed to 0.971. S was fixed for phase A control animals, and was estimated for other groups. σ2 and CLp were estimated
*Statistically significant from control group; and #Statistically significant from diabetic group at p ≤ 0.05 [One way ANOVA with Tukey’s Test]; (n = 6–8).
σ 2 vascular reflection coefficient for V leaky compartment; CLp total clearance; S factor describing fold change as compared to control animals of phase A
Model 2 had fixed GFR, Ф, and F r and the renal changes were quantified with a scaling factor S (Table V). For phase A, model 2 estimated a 36.5- and 8.78-fold increase in S for diabetic and pioglitazone treatment groups, respectively. For control animals in phase B, S was estimated to be 1.13 thus showing no changes throughout the study. For phase B, S was estimated to be 121- and 10.3-fold higher (diabetic rats and pioglitazone-treated diabetic rats, respectively) compared to the control group.
The vascular reflection coefficient σ2 predictions were similar between control and pioglitazone treatment groups. However, σ2 was significantly higher for the diabetic group, compared to the other two groups (2- and 3-fold in phases A and B, respectively).
DISCUSSION
Around 10–12% of the American population has been diagnosed with T2DM (1,38), with approximately one third to one fourth of T2DM patients developing DN (5,6). Since DM is highly associated with comorbidities including cardiovascular diseases, nephropathy, retinopathy, neuropathy, and transplantation, the use of mAbs in these populations may be necessary for various indications.
Previously, we had used a 2CM to describe hIgG concentration-time profiles in ZDF rats after the IV and SC administration of hIgG (11). A 2CM has been commonly used to describe and fit hIgG and mAb data in different species (19). Using a 2CM for plasma mAb PK data yields estimates of the volume of central compartment (V C) similar to plasma volume, which have been observed to be physiologically reasonable, since the hydrophilic nature and large molecular size of mAbs restricts them to plasma. On the other hand, estimates of the volume of the peripheral compartment are typically underestimated (23,32) since this model assumes elimination only from the central compartment. This assumption then becomes a limiting factor for large molecules where tissue also contributes to the elimination of the drug (23,39).
The use of physiologically based PK (PBPK) models provides a more mechanistic approach. Unlike the 2CM, PBPK models characterize drug disposition by incorporating physiologically based properties to describe mAb disposition in plasma, lymph node, and various other peripheral organs (24,40). However, the characterization and validation of these models requires extensive plasma and tissue data. Many studies are limited with data for plasma, or plasma and urine only. For such cases, mPBPK models provide an intermediate approach, where the organs can be segregated according to their physiologic and anatomical characteristics (20,21,23,24). The estimated parameters from the mPBPK models can be compared across species, and species scale-up has been described for mAbs (20,21). Moreover, similar to full PBPK models, the mPBPK models can incorporate different clearance sites and mechanisms and absorption processes in their structures.
In our model, we have extended the mPBPK model to include kidney and urine compartments, in addition to the leaky and tight compartments, since we utilized not only plasma but also urine data and T2DM/DN is associated with changes in renal function. Furthermore, the model allows a comparison of clearances from either the ISF or plasma, along with renal clearance. Although many studies have elucidated different elimination pathways through tissues and plasma, there is no clear consensus regarding the primary pathway (41). Our model had better fittings and estimations with clearance from the plasma rather than ISF. However, since the model is limited in its ability to identify both clearances simultaneously, this does not mean ISF is not contributing to clearance since both CLi and CLp processes contribute to mAb elimination (20,21).
This model retains the full PBPK feature that assigns plasma volume as the initial distribution space and helps to better characterize the distribution rates of mAbs, unlike the 2CM. The uptake of mAbs by endocytosis is very efficient and rapidly establishes equilibrium with plasma. However, this would not play any significant role in distribution due to the small volume of endothelial endosomes. Furthermore, due to rapid endocytosis and subsequent lysosomal degradation, the clearance parameters are similar to those from plasma (CLp) rather than from ISF (CLi). Thus, the CLp would also include degradation in endothelial lysosomes as well as plasma clearance (20,24,42).
In estimating F r, the control rats had values of 97.1 and 98.3% in phases A and B (Table IV), respectively. These values are similar to those reported in the literature with albumin and other proteins (43,44). Under normal conditions, only a fraction of proteins of intermediate molecular weight (albumin) and almost none of the high molecular weight (HMW) proteins (IgG, IgM) are present in the tubular lumen (Fig 5). Insignificantly low amounts of <0.01% of IgG are eliminated in the urine (43,45). One of the main reasons for the limited elimination of proteins is the very efficient mechanism of reabsorption of proteins by proximal tubule epithelial cells. An estimate of the efficiency of this system can be gauged by studies that inhibited proximal tubular reabsorption with lysine; in the presence of lysine, up to 450- and 5-fold increases in renal clearance can be seen with low and high molecular weight proteins, respectively (43,44,46). In the case of DM/DN and CKD, increases in the urinary elimination of proteins have been widely reported (13,18,47). These changes are a result of an increase in the filtered load, because of increased permeability of the glomerular capillary wall, or due to defects in the tubular uptake mechanisms (33,43). Alterations in the restrictive barrier properties of the glomerular wall lead to significant increases in the filtered amounts of albumin (intermediate molecular weight protein) and IgA and IgG (high molecular proteins). Unlike high MW proteins, low molecular weight proteins do not exhibit large increases in urinary elimination since the glomerular permeability is high under normal conditions and cannot increase substantially more. Thus, the small increase in glomerular permeability for larger molecular weight proteins would lead to large increases in their filtered amounts and subsequently, saturate proximal tubular reabsorption (33,43). mPBPK model 1 also estimated a decrease in efficiency of tubular reabsorption, with increasing DN. Major caveats associated with model 1 include extremely low values of F r, very high CV%, and poor model fittings (Table IV). For the pioglitazone treatment diabetic group, the model estimated F r to be 72.9 and 69.2% during phases A and B, respectively. Similar to other antihyperglycemic drugs, pioglitazone treatment ameliorates the diabetes effects significantly; however, the reversal is incomplete (11,48). Although model 1 is unable to completely capture the plasma and urine profiles, the trends in model predictions are similar to those observed in the literature. This suggests that changes in renal function and increases in urinary excretion of hIgG go beyond changes associated with proximal tubular reabsorption only. Thus, model 1 is unable to define and quantify the changes in DM/DN, with only F r as the parameter for renal change.
Fig. 5.

Schematic representation of transglomerular transfer to the tubular lumen followed by reabsorption by the tubular cells and elimination in the urine of plasma proteins of low molecular weight (<69 kDa, i.e., smaller than albumin), intermediate molecular weight (such as albumin), and high molecular weight proteins (>80 kDa) in physiologically normal conditions and during proteinuria conditions
To better evaluate the renal changes occurring with DM and DM/DN, mPBPK model 2 was constructed with a scaling factor S to accommodate renal changes with disease. The model predictions suggest that DM/DN produces significant changes in renal function, and these changes will be associated with altered GFR, sieving ability of the glomerulus membrane, and tubular efficiency. With pioglitazone treatment, the scaling factor S is significantly reduced, but still is 8.78- and 10.3-fold higher than the control animals (phases A and B, respectively). Based on goodness-of-fit parameters for CLp and S (AIC, visual inspection and CV of the estimated parameters), mPBPK model 2 is better able to describe the hIgG data in all the groups, as compared to model 1. Thus, model 2 is able to quantify changes associated with the DM/DN and predicts the reversal of the impact of the disease on renal function with pioglitazone treatment.
The vascular reflection coefficient σ2 predicts the extent of distribution of IgG in leaky tissues. Predictions of σ2 were similar between control and pioglitazone treatment groups. However, σ2 was significantly higher for the diabetic group, compared to the other two groups (2- and 3-fold higher than control group, in phases A and B, respectively). A significantly higher σ2 indicates lower concentrations of hIgG in leaky tissues as seen in the fittings (Fig. 3. phase A; Fig. 4. phase B). The high σ2 may be due to a more rapid clearance or metabolism in these tissues resulting in model predictions of much lower concentrations in the DM or DM/DN groups as compared to the control and pioglitazone-treated groups.
The estimation of a limited number of parameters in our model reduces the complexity and increases the ease of interpretation of the model. The model is able to describe the effect of diabetes on tissue distribution and renal and nonrenal clearances, including the severity in changes with progressing DM/DN. Similarly, the model is able to characterize the pioglitazone-mediated effects on clearance and demonstrates incomplete reversal of DM.
It is important to address some of the limitations of the model. This model follows the “reductionist” approach and lumps the body into tissues. This limits the prediction of IgG distribution to specific tissues, the incorporation of the role of the neonatal Fc receptor (FcRn) binding affinities or the role of diffusion in extravasation of macromolecules. Although our mPBPK model reasonably captures the trends in the modulations in renal clearance, the predictions rely upon changes in renal function, while being limited in identifiability for other factors involved such as proximal tubular reabsorption (F r) and renal catabolism. Both have been found to be important for albumin (49,50). In these studies, filtered albumin load was elevated 50 to 70 days after induction of diabetes, and it was suggested that the enhanced albuminuria observed was partly glomerular and partly tubular in origin (49). Significant increases (20- to 40-fold) in Ф have been reported for rats with proteinuria as compared to control rats, due to changes in the glomerular barrier function and tubular reabsorption (36). Thus, the scaling factor S would encompass various disorders of the glomerular filtration barrier which lead to increases in filtered amounts of IgG across the membrane. These disorders include podocyte detachment, glomerular basement membrane rupture, and slit diaphragm dysfunction in focal segmental glomerulosclerosis, membranous nephropathy, and other diseases causing glomerulonephritis (44). Additionally, our studies have used a Ф value based on the literature (36), and there are a range of values reported for different proteins, including albumin and IgG, under normal conditions, as well as with changes in physiology and disease (51–53). Irrespective of the specificity of Ф value in our studies, the model shows the comparative changes between the three groups and helps to describe the role of progressive DM/DN in these changes. To mechanistically improve the model, the role of FcRn and other endocytic proteins such as megalin/cubilin and changes in expression of these proteins with disease would have to be incorporated in the model structure (54,55). FcRn may contribute to the increases in the renal and non‐renal clearances of IgG (56); it is expressed in podocytes, and helps to clear out IgG that has traversed the glomerular filtration barrier, while renal vascular endothelial FcRn facilitates the removal of IgG from the circulation into the interstitium.
CONCLUSION
mPBPK models represent one approach for mAb PK analysis. Although the model is limited in identifying the specific changes in glomerular barrier function and tubular reabsorption capacity, it is able to quantify renal changes as a scaling factor which describes changes due to diabetes progression and reversal in the disease effects with pioglitazone treatment. Furthermore, the model is able to predict IgG concentrations in the two major groups of tissues with “tight” and “leaky” vascular biology. We believe the model provides a good foundation for assessing mAb PK with limited datasets. The model provides a better approach than a 2CM, and provides an intermediary method if a full PBPK model cannot be established.
Acknowledgments
We would like to acknowledge the advice of Yanguang Cao in developing the mPBPK model. This study was supported by grants from the Center for Protein Therapeutics, University at Buffalo.
REFERENCES
- 1.Pandey A, Tripathi P, Pandey R, Srivatava R, Goswami S. Alternative therapies useful in the management of diabetes: a systematic review. J Pharm Bioallied Sci. 2011;3(4):504–12. doi: 10.4103/0975-7406.90103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Miller BR, Nguyen H, Hu CJ, Lin C, Nguyen QT. New and emerging drugs and targets for type 2 diabetes: reviewing the evidence. Am Health Drug Benefit. 2014;7(8):452–63. [PMC free article] [PubMed] [Google Scholar]
- 3.Guariguata L, Whiting D, Weil C, Unwin N. The International Diabetes Federation diabetes atlas methodology for estimating global and national prevalence of diabetes in adults. Diabetes Res Clin Pract. 2011;94(3):322–32. doi: 10.1016/j.diabres.2011.10.040. [DOI] [PubMed] [Google Scholar]
- 4.Wild S, Roglic G, Green A, Sicree R, King H. Global prevalence of diabetes: estimates for the year 2000 and projections for 2030. Diabetes Care. 2004;27(5):1047–53. doi: 10.2337/diacare.27.5.1047. [DOI] [PubMed] [Google Scholar]
- 5.Ritz E, Orth SR. Nephropathy in patients with type 2 diabetes mellitus. N Engl J Med. 1999;341(15):1127–33. doi: 10.1056/NEJM199910073411506. [DOI] [PubMed] [Google Scholar]
- 6.Bakris GL. Recognition, pathogenesis, and treatment of different stages of nephropathy in patients with type 2 diabetes mellitus. Mayo Clin Proc. 2011;86(5):444–56. doi: 10.4065/mcp.2010.0713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gross JL, de Azevedo MJ, Silveiro SP, Canani LH, Caramori ML, Zelmanovitz T. Diabetic nephropathy: diagnosis, prevention, and treatment. Diabetes Care. 2005;28(1):164–76. doi: 10.2337/diacare.28.1.164. [DOI] [PubMed] [Google Scholar]
- 8.Scheffel RS, Bortolanza D, Weber CS, Costa LA, Canani LH, Santos KG, et al. Prevalence of micro and macroangiopatic chronic complications and their risk factors in the care of out patients with type 2 diabetes mellitus. Rev Assoc Med Bras. 2004;50(3):263–7. doi: 10.1590/S0104-42302004000300031. [DOI] [PubMed] [Google Scholar]
- 9.Palmer AJ, Valentine WJ, Chen R, Mehin N, Gabriel S, Bregman B, et al. A health economic analysis of screening and optimal treatment of nephropathy in patients with type 2 diabetes and hypertension in the USA. Nephrol Dial Transplant: Off Publ Eur Dial Transplant Assoc - Eur Renal Assoc. 2008;23(4):1216–23. doi: 10.1093/ndt/gfn082. [DOI] [PubMed] [Google Scholar]
- 10.Dostalek M, Akhlaghi F, Puzanovova M. Effect of diabetes mellitus on pharmacokinetic and pharmacodynamic properties of drugs. Clin Pharmacokinet. 2012;51(8):481–99. doi: 10.1007/BF03261926. [DOI] [PubMed] [Google Scholar]
- 11.Chadha GS, Morris ME. Effect of type 2 diabetes mellitus and diabetic nephropathy on IgG pharmacokinetics and subcutaneous bioavailability in the rat. AAPS J. 2015;17(4):965–75. doi: 10.1208/s12248-015-9771-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hamilton RG. Human IgG subclass measurements in the clinical laboratory. Clin Chem. 1987;33(10):1707–25. [PubMed] [Google Scholar]
- 13.Lemley KV, Blouch K, Abdullah I, Boothroyd DB, Bennett PH, Myers BD, et al. Glomerular permselectivity at the onset of nephropathy in type 2 diabetes mellitus. J Am Soc Nephrol: JASN. 2000;11(11):2095–105. doi: 10.1681/ASN.V11112095. [DOI] [PubMed] [Google Scholar]
- 14.Ruggenenti P, Mosconi L, Sangalli F, Casiraghi F, Gambara V, Remuzzi G, et al. Glomerular size-selective dysfunction in NIDDM is not ameliorated by ACE inhibition or by calcium channel blockade. Kidney Int. 1999;55(3):984–94. doi: 10.1046/j.1523-1755.1999.055003984.x. [DOI] [PubMed] [Google Scholar]
- 15.Bakoush O, Tencer J, Tapia J, Rippe B, Torffvit O. Higher urinary IgM excretion in type 2 diabetic nephropathy compared to type 1 diabetic nephropathy. Kidney Int. 2002;61(1):203–8. doi: 10.1046/j.1523-1755.2002.00108.x. [DOI] [PubMed] [Google Scholar]
- 16.Lemley KV, Lafayette RA, Safai M, Derby G, Blouch K, Squarer A, et al. Podocytopenia and disease severity in IgA nephropathy. Kidney Int. 2002;61(4):1475–85. doi: 10.1046/j.1523-1755.2002.00269.x. [DOI] [PubMed] [Google Scholar]
- 17.Kerr MA. The structure and function of human IgA. Biochem J. 1990;271(2):285–96. doi: 10.1042/bj2710285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Roberts BV, Susano I, Gipson DS, Trachtman H, Joy MS. Contribution of renal and non-renal clearance on increased total clearance of adalimumab in glomerular disease. J Clin Pharmacol. 2013;53(9):919–24. doi: 10.1002/jcph.121. [DOI] [PubMed] [Google Scholar]
- 19.Kacskovics I, Kis Z, Mayer B, West AP, Jr, Tiangco NE, Tilahun M, et al. FcRn mediates elongated serum half-life of human IgG in cattle. Int Immunol. 2006;18(4):525–36. doi: 10.1093/intimm/dxh393. [DOI] [PubMed] [Google Scholar]
- 20.Cao Y, Balthasar JP, Jusko WJ. Second-generation minimal physiologically-based pharmacokinetic model for monoclonal antibodies. J Pharmacokinet Pharmacodyn. 2013;40(5):597–607. doi: 10.1007/s10928-013-9332-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cao Y, Jusko WJ. Survey of monoclonal antibody disposition in man utilizing a minimal physiologically-based pharmacokinetic model. J Pharmacokinet Pharmacodyn. 2014;41(6):571–80. doi: 10.1007/s10928-014-9374-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rowland M, Peck C, Tucker G. Physiologically-based pharmacokinetics in drug development and regulatory science. Annu Rev Pharmacol Toxicol. 2011;51:45–73. doi: 10.1146/annurev-pharmtox-010510-100540. [DOI] [PubMed] [Google Scholar]
- 23.Elmeliegy M, Lowe P, Krzyzanski W. Simplification of complex physiologically based pharmacokinetic models of monoclonal antibodies. AAPS J. 2014;16(4):810–42. doi: 10.1208/s12248-014-9591-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cao Y, Jusko WJ. Applications of minimal physiologically-based pharmacokinetic models. J Pharmacokinet Pharmacodyn. 2012;39(6):711–23. doi: 10.1007/s10928-012-9280-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hempe J, Elvert R, Schmidts HL, Kramer W, Herling AW. Appropriateness of the Zucker diabetic fatty rat as a model for diabetic microvascular late complications. Lab Anim. 2012;46(1):32–9. doi: 10.1258/la.2011.010165. [DOI] [PubMed] [Google Scholar]
- 26.Finegood DT, McArthur MD, Kojwang D, Thomas MJ, Topp BG, Leonard T, et al. Beta-cell mass dynamics in Zucker diabetic fatty rats. Rosiglitazone prevents the rise in net cell death. Diabetes. 2001;50(5):1021–9. doi: 10.2337/diabetes.50.5.1021. [DOI] [PubMed] [Google Scholar]
- 27.Baxter LT, Zhu H, Mackensen DG, Jain RK. Physiologically based pharmacokinetic model for specific and nonspecific monoclonal antibodies and fragments in normal tissues and human tumor xenografts in nude mice. Cancer Res. 1994;54(6):1517–28. [PubMed] [Google Scholar]
- 28.Flessner MF, Lofthouse J, el Zakaria R. In vivo diffusion of immunoglobulin G in muscle: effects of binding, solute exclusion, and lymphatic removal. Am J Physiol. 1997;273(6 Pt 2):H2783–93. doi: 10.1152/ajpheart.1997.273.6.H2783. [DOI] [PubMed] [Google Scholar]
- 29.Rossing N. Intra- and extravascular distribution of albumin and immunoglobulin in man. Lymphology. 1978;11(4):138–42. [PubMed] [Google Scholar]
- 30.Sarin H. Physiologic upper limits of pore size of different blood capillary types and another perspective on the dual pore theory of microvascular permeability. J Angiogenes Res. 2010;2:14. doi: 10.1186/2040-2384-2-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Garg A, Balthasar JP. Physiologically-based pharmacokinetic (PBPK) model to predict IgG tissue kinetics in wild-type and FcRn-knockout mice. J Pharmacokinet Pharmacodyn. 2007;34(5):687–709. doi: 10.1007/s10928-007-9065-1. [DOI] [PubMed] [Google Scholar]
- 32.Shah DK, Betts AM. Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. J Pharmacokinet Pharmacodyn. 2012;39(1):67–86. doi: 10.1007/s10928-011-9232-2. [DOI] [PubMed] [Google Scholar]
- 33.Haraldsson B, Nystrom J, Deen WM. Properties of the glomerular barrier and mechanisms of proteinuria. Physiol Rev. 2008;88(2):451–87. doi: 10.1152/physrev.00055.2006. [DOI] [PubMed] [Google Scholar]
- 34.Brown RP, Delp MD, Lindstedt SL, Rhomberg LR, Beliles RP. Physiological parameter values for physiologically based pharmacokinetic models. Toxicol Ind Health. 1997;13(4):407–84. doi: 10.1177/074823379701300401. [DOI] [PubMed] [Google Scholar]
- 35.Wiig H, Tenstad O. Interstitial exclusion of positively and negatively charged IgG in rat skin and muscle. Am J Physiol Heart Circ Physiol. 2001;280(4):H1505–12. doi: 10.1152/ajpheart.2001.280.4.H1505. [DOI] [PubMed] [Google Scholar]
- 36.Bertolatus JA, Abuyousef M, Hunsicker LG. Glomerular sieving of high molecular weight proteins in proteinuric rats. Kidney Int. 1987;31(6):1257–66. doi: 10.1038/ki.1987.139. [DOI] [PubMed] [Google Scholar]
- 37.Lindena J, Kupper W, Trautschold I. Catalytic enzyme activity concentration in thoracic duct, liver, and intestinal lymph of the dog, the rabbit, the rat and the mouse. Approach to a quantitative diagnostic enzymology, II. Communication. J Clin Chem Clin Biochem Zeitschrift fur klinische Chemie und klinische Biochemie. 1986;24(1):19–33. doi: 10.1515/cclm.1986.24.1.19. [DOI] [PubMed] [Google Scholar]
- 38.Foundation NK. About Chronic Kidney Disease 2012. Available from: http://www.kidney.org/kidneydisease/aboutckd.cfm.
- 39.Garzone PD, Atkinson AJ., Jr In search of physiologically based distribution volume estimates for macromolecules. Clin Pharmacol Ther. 2012;92(4):419–21. doi: 10.1038/clpt.2012.156. [DOI] [PubMed] [Google Scholar]
- 40.Baxter LT, Zhu H, Mackensen DG, Butler WF, Jain RK. Biodistribution of monoclonal antibodies: scale-up from mouse to human using a physiologically based pharmacokinetic model. Cancer Res. 1995;55(20):4611–22. [PubMed] [Google Scholar]
- 41.Tabrizi MA, Tseng CM, Roskos LK. Elimination mechanisms of therapeutic monoclonal antibodies. Drug Discov Today. 2006;11(1–2):81–8. doi: 10.1016/S1359-6446(05)03638-X. [DOI] [PubMed] [Google Scholar]
- 42.Chen Y, Balthasar JP. Evaluation of a catenary PBPK model for predicting the in vivo disposition of mAbs engineered for high-affinity binding to FcRn. AAPS J. 2012;14(4):850–9. doi: 10.1208/s12248-012-9395-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.D’Amico G, Bazzi C. Pathophysiology of proteinuria. Kidney Int. 2003;63(3):809–25. doi: 10.1046/j.1523-1755.2003.00840.x. [DOI] [PubMed] [Google Scholar]
- 44.Tojo A, Kinugasa S. Mechanisms of glomerular albumin filtration and tubular reabsorption. Int J Nephrol. 2012;2012:481520. doi: 10.1155/2012/481520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Norden AG, Lapsley M, Lee PJ, Pusey CD, Scheinman SJ, Tam FW, et al. Glomerular protein sieving and implications for renal failure in Fanconi syndrome. Kidney Int. 2001;60(5):1885–92. doi: 10.1046/j.1523-1755.2001.00016.x. [DOI] [PubMed] [Google Scholar]
- 46.Tencer J, Frick IM, Oquist BW, Alm P, Rippe B. Size-selectivity of the glomerular barrier to high molecular weight proteins: upper size limitations of shunt pathways. Kidney Int. 1998;53(3):709–15. doi: 10.1046/j.1523-1755.1998.00797.x. [DOI] [PubMed] [Google Scholar]
- 47.Mercuri SR, Naldi L. Potential role of ustekinumab in the treatment of chronic plaque psoriasis. Biol: Targets Ther. 2010;4:119–29. doi: 10.2147/btt.s4921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Xu X, Chen P, Zheng Q, Wang Y, Chen W. Effect of pioglitazone on diabetic nephropathy and expression of HIF-1alpha and VEGF in the renal tissues of type 2 diabetic rats. Diabetes Res Clin Pract. 2011;93(1):63–9. doi: 10.1016/j.diabres.2011.03.019. [DOI] [PubMed] [Google Scholar]
- 49.Andersen S, Blouch K, Bialek J, Deckert M, Parving HH, Myers BD. Glomerular permselectivity in early stages of overt diabetic nephropathy. Kidney Int. 2000;58(5):2129–37. doi: 10.1111/j.1523-1755.2000.00386.x. [DOI] [PubMed] [Google Scholar]
- 50.Tucker BJ, Rasch R, Blantz RC. Glomerular filtration and tubular reabsorption of albumin in preproteinuric and proteinuric diabetic rats. J Clin Invest. 1993;92(2):686–94. doi: 10.1172/JCI116638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Peti-Peterdi J, Sipos A. A high-powered view of the filtration barrier. J Am Soc Nephrol: JASN. 2010;21(11):1835–41. doi: 10.1681/ASN.2010040378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lund U, Rippe A, Venturoli D, Tenstad O, Grubb A, Rippe B. Glomerular filtration rate dependence of sieving of albumin and some neutral proteins in rat kidneys. Am J Physiol Renal Physiol. 2003;284(6):F1226–34. doi: 10.1152/ajprenal.00316.2002. [DOI] [PubMed] [Google Scholar]
- 53.Axelsson J, Mahmutovic I, Rippe A, Rippe B. Loss of size selectivity of the glomerular filtration barrier in rats following laparotomy and muscle trauma. Am J Physiol Renal Physiol. 2009;297(3):F577–82. doi: 10.1152/ajprenal.00246.2009. [DOI] [PubMed] [Google Scholar]
- 54.Akilesh S, Huber TB, Wu H, Wang G, Hartleben B, Kopp JB, et al. Podocytes use FcRn to clear IgG from the glomerular basement membrane. Proc Natl Acad Sci U S A. 2008;105(3):967–72. doi: 10.1073/pnas.0711515105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sarav M, Wang Y, Hack BK, Chang A, Jensen M, Bao L, et al. Renal FcRn reclaims albumin but facilitates elimination of IgG. J Am Soc Nephrol: JASN. 2009;20(9):1941–52. doi: 10.1681/ASN.2008090976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Brambell FW, Hemmings WA, Morris IG. A theoretical model of gamma-globulin catabolism. Nature. 1964;203:1352–4. doi: 10.1038/2031352a0. [DOI] [PubMed] [Google Scholar]


