Abstract
Disclosing the origin of convolutions in the mammalian brain remains a scientific challenge. Primary folds form before we are born: they are static, well defined, and highly preserved across individuals. Secondary folds occur and disappear throughout our entire life time: they are dynamic, irregular, and highly variable among individuals. While extensive research has improved our understanding of primary folding in the mammalian brain, secondary folding remains understudied and poorly understood. Here, we show that secondary instabilities can explain the increasing complexity of our brain surface as we age. Using the nonlinear field theories of mechanics supplemented by the theory of finite growth, we explore the critical conditions for secondary instabilities. We show that with continuing growth, our brain surface continues to bifurcate into increasingly complex morphologies. Our results suggest that even small geometric variations can have a significant impact on surface morphogenesis. Secondary bifurcations, and with them morphological changes during childhood and adolescence, are closely associated with the formation and loss of neuronal connections. Understanding the correlation between neuronal connectivity, cortical thickness, surface morphology, and ultimately behavior, could have important implications on the diagnostics, classification, and treatment of neurological disorders.
Keywords: brain, morphogenesis, cortical folding, instability, bifurcation, period-doubling
1. Motivation
Understanding the formation of brain convolutions remains a challenging task in modern neurosciences [1]. Recent advances in neuroimaging provide insight into the phenomenon of brain folding on different scales [2, 3]. However, the whole picture of brain growth and its convolutional development remain barely understood [4]. Figure 1 illustrates the characteristic surface morphology of the mammalian brain with its primary and secondary folds. Primary folding is remarkably well preserved across individuals [5] and is closely correlated with a sequence of well-defined genetic events [6]. Secondary and tertiary folding, however, distinctively vary among individuals and develop mainly after birth after primary folding is basically completed [7]. A possible stimulus for secondary and tertiary folding could be differential growth [8], with a growing or shrinking cortex as new connections between neurons form and dissolve.
Figure 1.
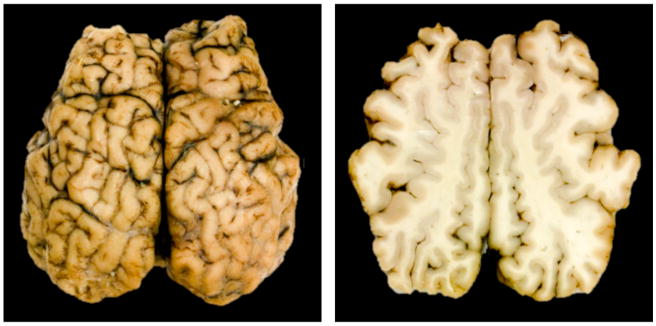
Characteristic surface morphology of the mammalian brain. Top view of the whole brain, left, and superior horizontal section, right. The gray matter layer, the cortex, displays a complex outer appearance with regular primary folds and irregular secondary and tertiary folds.
Folding phenomena induced by compressive stresses in layered media are relevant in various fields [9, 10]. Compressive stresses can be of different origin caused by either external phenomena such as pressure or by internal phenomena such as growth [11]. Applications range from undesired instabilities of layered engineering structures [12], and naturally folded rocks [13], via microfabrication of controlled surface patterns [14], to wrinkling phenomena in biological systems including the lung [16], the epithelial layer [17], the mucosa [19], and the brain [8].
Several studies address the critical conditions for primary and secondary instabilities of layered media, either analytically or numerically [18]. Yet, there are two major differences between these layered structures and the mammalian brain: the stiffness contrast, the stiffness ratio between layer and substrate, is typically of the order 100 – 1000, implying that the layer is significantly stiffer than the substrate [19, 20]; and the growth contrast, the ratio between layer and substrate growth, is typically infinite, meaning that the substrate is purely elastic [21]. While quite common for thin films, this seems unphysiological for the mammalian brain. Using indentation experiments of freshly excised brain, we have recently shown that the stiffness contrast between gray and white matter is much lower, effectively around the order of one [1]. In addition, brain tissue is a living material - not only its gray matter layer but also its white matter substrate grows as the brain develops and new connections form. The cortex experiences a period of maximum growth during weeks 23 and 37 of gestation, where it turns from a flat surface into a wrinkled structure and approximately triples its area. The expanding cortex imposes tension on the axons in the white matter, which can double their length within only two hours when stretched beyond their physiological limit [22]. This suggests that the growth contrast, the growth ratio between gray and white matter growth, is of the order of 100.
The objective of this work is to analyze secondary folding phenomena for biologically realistic stiffness contrasts, significantly smaller than 100, and biologically realistic growth contrasts, far from the elastic limit. Recent studies have shown how primary instabilities of a growing gray matter layer on a growing white matter substrate evoke uniform wrinkling modes [23, 24]. Here we focus on secondary instabilities that occur upon continuing growth, beyond the first instability point. Secondary instabilities are highly sensitive to small variations in geometry, loading, and boundary conditions [25], which may explain the increasingly complex and diverse cortical appearance with age [26]. Figure 2 illustrates this complex cortical morphology with its characteristic primary and secondary folds. Here we aim to explain these morphologies through growth-induced secondary bifurcations. We explicitly link progressive cellular maturation after birth to structural changes in the dynamically changing brain throughout childhood and early adolescence [27].
Figure 2.
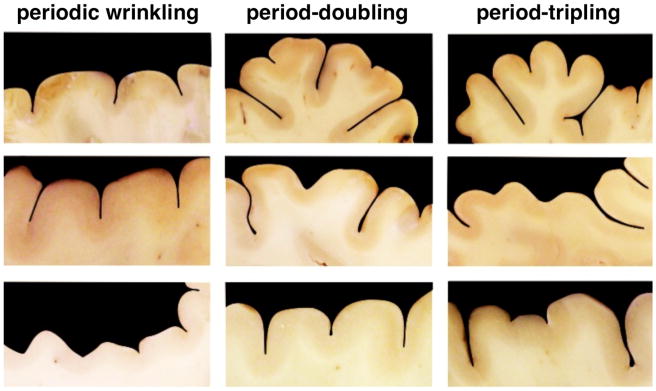
Primary and secondary folding in the mammalian brain. Periodic wrinkling, left, exhibits a constant folding amplitude. For period-doubling, middle, every second amplitude is larger than those in between. For period-tripling, right, every third amplitude is larger than those in between.
2. Methods
To explore secondary folding phenomena, we adopt the continuum model of differential growth [28]. To describe the kinematics of finite deformation, we introduce the deformation map φ, which maps points X from the initial ungrown configuration to their new positions x = φ(X, t) in the current configuration. To model growth, we multiplicatively decompose its spatial gradient F = ∇φ into an elastic part Fe and a grown part Fg [29],
| (1) |
A similar multiplicative decomposition holds for the Jacobian J = Je Jg, which is a measure of changes in volume. For simplicity, we assume that growth in both gray and white matter is purely isotropic, parameterized in terms of a single scalar-valued growth multiplier ϑ,
| (2) |
This implies that the grown volume Jg is identical to the growth multiplier cubed ϑ3. In the initial ungrown state, the growth multiplier is one, ϑ = 1, such that ϑ > 1 and ϑ < 1 characterize volume growth and shrinkage. Human brain tissue is a porous, fluid-saturated, nonlinear solid with very small volumetric drained compressibility, capable of permanent deformations [1]. On the time scales of traumatic brain injury, brain tissue is a highly viscous and porous material [30]. On the time scales of brain development, we can neglect viscous and porous effects, and assume that brain tissue is isotropic and elastic [23]. We characterize its constitutive behavior through the following Neo-Hookean free energy,
| (3) |
where λ and μ are the Lamé constants. Since only the elastic part of the deformation induces stress, the free energy depends exclusively on the elastic tensor Fe and its Jacobian Je. Following standard arguments of thermodynamics, we can introduce the Piola stress P as energetically conjugate to the deformation gradient F,
| (4) |
The Piola stress enters the standard balance of linear momentum, the equation of mechanical equilibrium,
| (5) |
It remains to define the kinetics of growth [31], the evolution equations for the growth multipliers for the cortex and for the subcortex, ϑc and ϑs. Since the cortex consists primarily of cell nuclei while the subcortex consists primarily of axons, we assume different growth kinetics. Cortical growth is a result of neural progenitor division, cell migration, and the formation of new connections, which we assume to be purely morphogenetic [32], independent of mechanical stress or strain [33]. We let the cortex grow homogeneously in space and linearly in time at a constant rate Gc,
| (6) |
Subcortical growth is a result of chronic axon elongation upon mechanical stretch [22] at the axon elongation rate Gs,
| (7) |
With 〈Je − J0〉 = Je − J0 for Je > J0 and 〈 Je − J0〉 = 0 otherwise, the term in the Macaulay brackets activates growth only if the elastic volume stretch Je exceeds the physiological baseline value of J0 [24]. Figure 3 summarizes the kinetics of cortical and subcortical growth.
Figure 3.
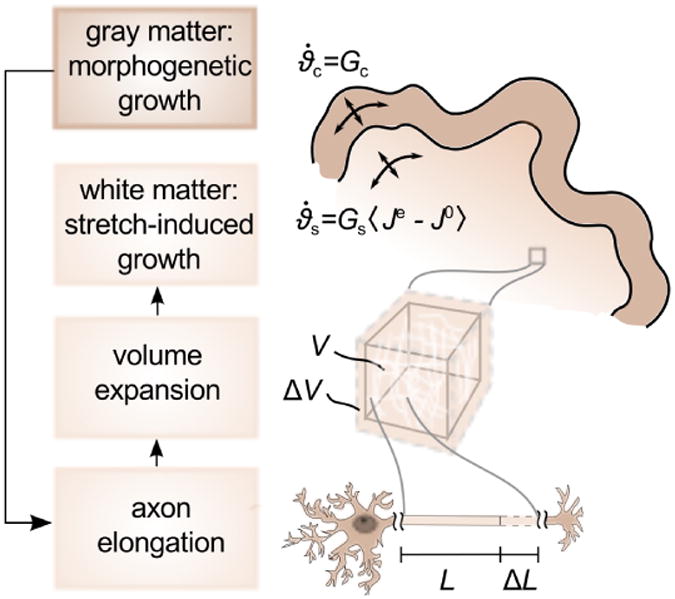
Growth kinetics in the developing mammalian brain. The gray matter layer grows morphogenetically at a constant rate Gc, which is correlated to neural progenitor division. Cortical growth induces subcortical deformation, which triggers subcortical growth. The white matter substrate grows at a stretch-dependent rate as Gs 〈Je − J0 〉, where Gs mimics the axon elongation rate and 〈Je − J0〉 activates growth only, if the elastic volume stretch Je exceeds its baseline value J0.
We solve the nonlinear set of equations using the finite element method and implement the resulting equations in a Matlab-based environment [28]. The growth multipliers for cortex and subcortex, which we introduce as internal variables on the integration point level, locally capture the amount of growth at the current time point. Motivated by Figure 2, we model cortical folding in a rectangular domain of height H and width W under plane strain conditions. We choose the sample height to H = 0.5, discretized with 80 elements, and the initial substrate thickness to T = 0.02, discretized with 4 elements. The sample width varies between W = 0.3625 and W = 0.5250, discretized with 58 to 84 elements, for the simulation of period doubling and W = 0.5875 and W = 0.7625, discretized with 94 to 122 elements, for the simulation of period tripling, depending on the corresponding stiffness and growth ratios.
We apply homogeneous Dirichlet boundary conditions perpendicular to the left, bottom, and right boundaries, but allow the nodes to slide freely along the three edges. To trigger an initial instability, we adapt an established protocol [23]: we add a small imperfection of 1% volumetric contraction, ϑs = 0.99, within a two-element wide vertical band in the center of the substrate, and verify numerically that this imperfection is small enough to not influence the wavelength of the overall wrinkling mode.
We model gray matter as Neo-Hookean elastic with Lamé constants λc = 34.2kPa and μc = 3.3kPa [34], and white matter with a stiffness contrast Ec/Es and Lamé constants λs = Es/Ec λc and μs = Es/Ec μc. In the linear regime, these parameters would correspond to a Young's modulus of E = 10kPa and a Possion's ratio of ν = 0.46, reflecting the soft and nearly incompressible behavior of brain tissue [1]. In contrast to studies of thin films with a large stiffness contrast [35], here we restrict our analysis to a range of stiffness ratios of 3 ≤ Ec/Es ≤ 12, such that the stiffnesses of layer and substrate are of the same order of magnitude.
We perform simulations for growth ratios within the range of 1/40 ≤ Gc/Gs ≤ ∞. The elastic limit of Gc/Gs = ∞ mimics non-growing white matter tissue, which seems physiologically unrealistic, but serves as a valuable control case. Once the growth-induced compressive stresses in the cortex reach a critical value, the cortex wrinkles into a periodic sinusoidal pattern. With further growth, advanced wrinkling modes emerge from secondary bifurcations at a second critical value.
To systematically study the characteristics of secondary instabilities we first determine the wavelength of primary folding λ on a wide domain of several wavelengths. Then, we select two different domain widths, W = 2λ and W = 3λ. The first setup triggers the emergence of a period-doubling mode. The second setup suppresses period-doubling and triggers a period-tripling mode instead.
3. Results
Figure 4 shows the temporal evolution of the folding pattern for a stiffness ratio of μc/μs = 5 and a growth ratio of Gc/Gs = 1/10. Initially, at ϑc = 1.22, the cortex is a flat thin layer. Once the growth in the cortex has passed a first instability point, at ϑc = 1.45 the cortex buckles into a sinusoidal pattern to partially release growth-induced residual stresses. With continuing growth, the solution of smooth wrinkling becomes unstable a second time and bifurcates into a split solution. In the case of period-doubling, beyond the second instability point at ϑc = 1.55, every second sulcus deepens, while those in between flatten out and become more shallow. In the case of period-tripling, beyond the second instability point at ϑc = 1.70, every third sulcus deepens, while those in between flatten out.
Figure 4.
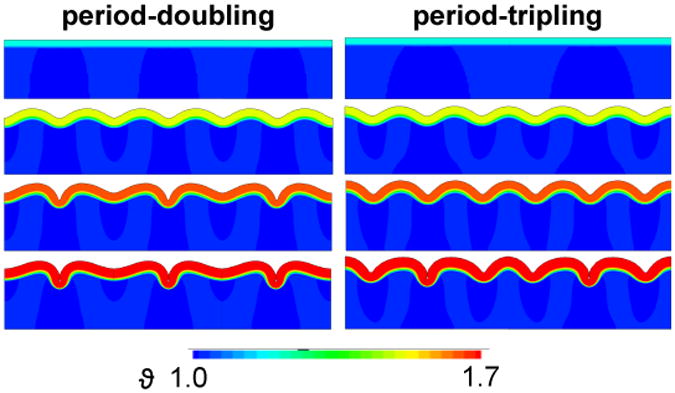
Spatio-temporal evolution of period-doubling and period-tripling. At ϑc = 1.22, growth-induced compressive stresses are still below the critical value and the surface remains flat, first row. At ϑc = 1.45, growth beyond the first instability point creates symmetric, sinusoidal folding patterns, which are similar for period-doubling and -tripling, second row. At ϑc = 1.55, growth has passed the second instability point for period-doubling, which initiates alternating increasing and decreasing sulcal depths, while the second bifurcation point for period-tripling has not been reached yet, third row. At ϑc = 1.70, growth has passed both second bifurcation points and contact forms along the edges of two neighboring sulci, fourth row.
Figure 5 illustrates more detailed characteristics of the folding amplitudes and the instability points for a stiffness ratio of μc/μs = 5 and growth ratios of Gc/Gs = ∞ and Gc/Gs = 1/10. Initially, the cortex is flat and the folding amplitudes equal zero. At the first instability point, ϑw, amplitudes begin to grow uniformly at a similar critical growth value for both growth ratios. The second instability point is different for period-doubling and period-tripling with ϑpd ≤ ϑpt. We observe a pitchfork bifurcation of the solution: Every second amplitude, red curve, or third amplitude, blue curve, continues to grow, while those in between decay. In the case of period-tripling, amplitudes grow uniformly even beyond the instability point for period-doubling ϑpd, but bifurcate into a period-tripling mode at a larger cortical growth value ϑpt. When comparing a purely elastic substrate, top graph, with a growing substrate, bottom graph, we conclude that subcortical growth stabilizes the system and shifts the second bifurcation points to the right. The stabilizing effect of subcortical growth is more apparent for period-tripling than for period-doubling.
Figure 5.
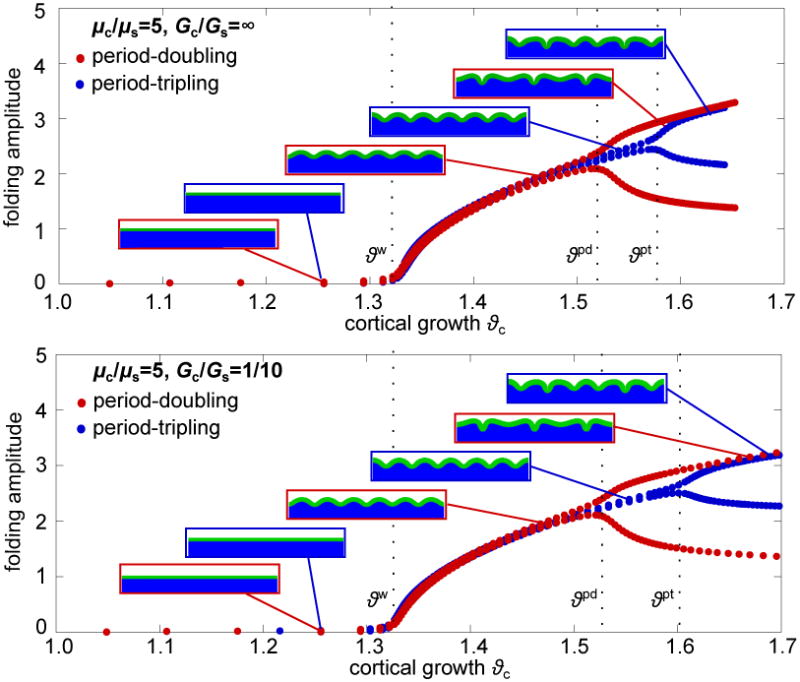
Evolution of folding amplitudes with successive cortical growth. Stiffness and growth ratios are μc/μs = 5, Gc/Gs = ∞, top, and Gc/Gs = 1/10, bottom. Initially the cortex is flat and the amplitudes equal zero. At the critical growth for periodic wrinkling ϑw, amplitudes begin to grow uniformly. With further growth the path reaches a second bifurcation point ϑpd , which initiates a period-doubling mode, red curve: Every second amplitude grows and those in between decay. A 50% wider domain suppresses the period-doubling mode and enforce a period-tripling bifurcation at an even higher critical growth value ϑpt: Every third amplitude grows and those in between decay.
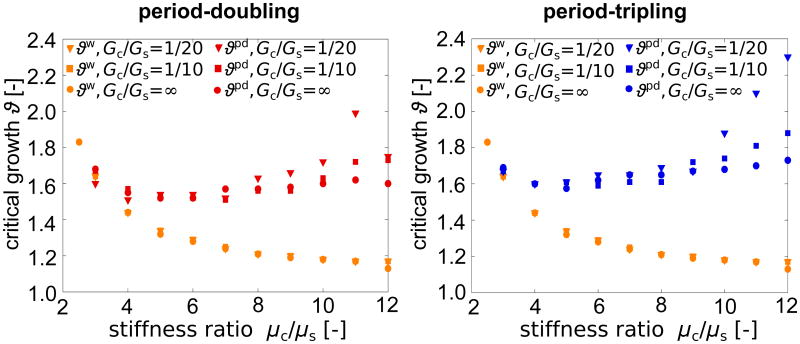
Figure 6 summarizes the critical growth values for periodic wrinkling ϑw, period-doubling ϑpd, and period-tripling ϑpt, for varying stiffness ratios, 2 ≤ μc/μs ≤ 12, and varying growth ratios, Gc/Gs = 1/20,1/10, ∞. We define the instability points through an accompanying eigenvalue analysis: Once the system becomes unstable, the lowest eigenvalue decreases until it reaches its minimum at the instability point. We observe that the critical growth value for periodic wrinkling decreases asymptotically with stiffness ratio μc/μs independent of the growth ratio Gc/Gs. For a purely elastic substrate with Gc/Gs = ∞, both second instability points ϑpd and ϑpt are almost independent of the stiffness ratio. For a growing substrate, however, ϑpd and ϑpt increase with increasing stiffness ratio. Critical growth for period-doubling is consistently lower than for period-tripling ϑpd < ϑpt, which indicates that period-doubling is energetically favorable over period-tripling.
Figure 6.
Effect of stiffness ratio μc/μs and growth ratio Gc/Gs olution of folding amplitudes with successive cortical growt, and for wrinkling and period-tripling, right. Critical growth for periodic wrinkling ϑw decreases asymptotically with increasing stiffness ratio independent of the growth ratio. Critical growth for period-doubling ϑpd and period-tripling ϑpt are only marginally influenced by the stiffness ratio for a growth ratio of Gc/Gs = ∞. For smaller growth ratios of Gc/Gs = 1/10 and Gc/Gs = 1/20, critical growth ϑpd and ϑpt increase with increasing stiffness ratio. Critical growth for period-doubling is consistently smaller than for period-tripling ϑpd < ϑpt.
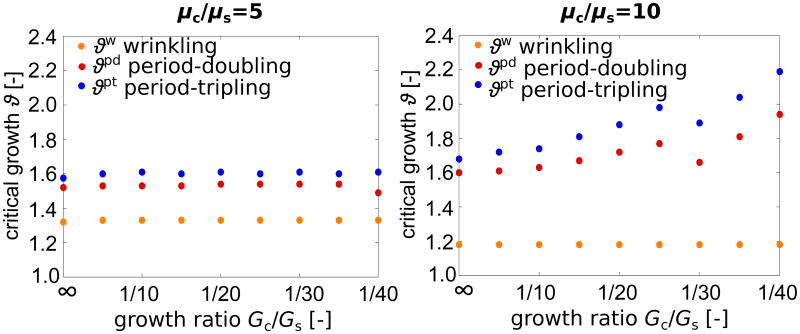
Figure 7 provides further evidence of the influence of the growth ratio Gc/Gs on the critical growth for primary and secondary bifurcations. The results show that the growth ratio does not affect critical growth for periodic wrinkling ϑw. For a stiffness ratio of μc/μs = 10, right, the critical growth values for period-doubling ϑpd and period-tripling ϑpt increase with decreasing growth ratio - each to the same extent. This effect almost vanishes for smaller stiffness ratios of μc/μs = 5, left. Within the investigated range of 1/40 ≤ Gc/Gs ≤ ∞, all critical growth values, ϑw, ϑpd, and ϑpt, are almost entirely independent of Gc/Gs. We attribute this to small folding amplitudes that fail to induce subcortical growth to stabilize the system.
Figure 7.
Effect of growth ratio Gc/Gs on the critical conditions for primary and secondary bifurcations. The growth ratio does not affect critical growth for periodic wrinkling ϑw. For a stiffness ratio of μc/μs = 5, left, the critical growth values for period-doubling ϑpd and period-tripling ϑpt are also independent of the growth ratio. For a stiffness ratio of μc/μs = 10, right, ϑpd and ϑpt increase with decreasing growth ratio.
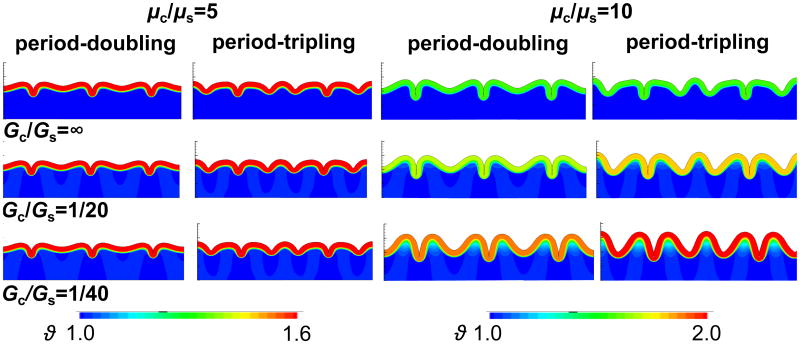
Figure 8 illustrates how stiffness and growth ratios affect the folding pattern. An increased stiffness ratio generates longer wavelengths and larger amplitudes. Similar to the results in Figure 7, the growth ratio Gc/Gs barely influences the folding pattern for a small stiffness ratio of μc/μs = 5 as the overall folding amplitudes are small and subcortical growth is hardly activated. For a higher stiffness ratio of μc/μs = 10, however, the higher folding amplitudes induce remarkably larger subcortical growth, which leads to an increasing amplitude with decreasing growth ratio. The growing substrate not only influences the critical condition for secondary bifurcation, but also the wavelength of folding: the distance between two neighboring gyri slightly increases with increasing subcortical growth [23].
Figure 8.
Effect of stiffness ratio μc/μs and growth ratio Gc/Gs on the folding pattern. Both wavelength and amplitude increase with increasing stiffness ratio and decreasing growth ratio. For a stiffness ratio of μc/μs = 5, left, the folding pattern is almost independent of the growth ratio with constant folding amplitudes and only marginal subcortical growth. For a stiffness ratio of μc/μs = 10, right, the folding pattern changes with decreasing growth ratio; both folding amplitude and subcortical growth noticeably increase. The influence of the growth ratio on the folding pattern is more prominent for period-tripling than for period-doubling.
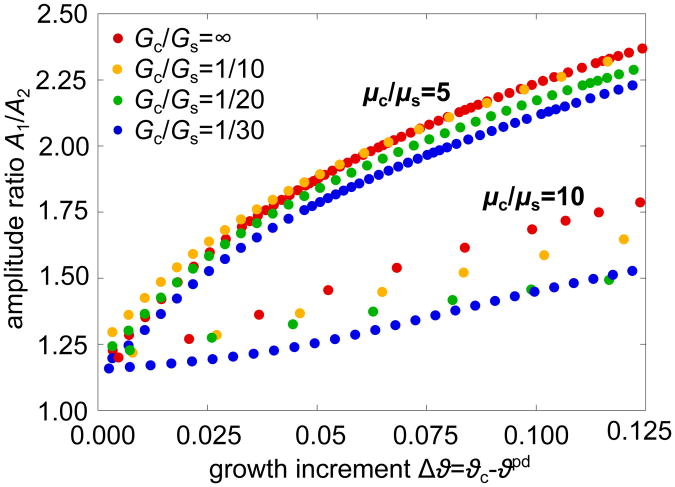
Figure 9 shows the evolution of the amplitude ratio A1/A2, the ratio between the growing amplitude A1 and the decaying amplitude A2, beyond the onset of period-doubling Δϑ = ϑc − ϑpd. In the uniformly wrinkled state between the first and second instability point ϑw and ϑpd, all amplitudes are equal and this ratio is equal to one. Once the secondary bifurcation sets in, the ratio begins to increase [21]. In this region, subcortical growth stabilizes the system: it not only shifts the second bifurcation point to larger growth values, as shown before, but also slows down the amplitude growth. Much more distinctive, however, is the effect of the stiffness ratio μc/μs on the development of the amplitude ratio. The stiffer the cortex compared to the subcortex, the higher the overall amplitude.
Figure 9.
Evolution of the amplitude ratio A1/A2, the ratio between the growing and decaying amplitudes A1 and A2, for varying stiffness ratios μc/μs = 5,10 and varying growth ratios Gc/Gs = 1/30,1/20,1/10, ∞. With decreasing growth ratio Gc/Gs the slope of the curves decreases. This effect is more distinct for higher stiffness ratios. In general, the slope of the curve decreases with increasing stiffness ratio.
4. Discussion
Our continuum model for differential growth - with a morphogenetically growing gray matter layer and a stretch-induced growing white matter core - explains a wide variety of folding phenomena observed in mammalian brains. It not only characterizes the formation of regular, sinusoidal wrinkles, but also the emergence of irregular, complex folds. Once the growth-induced stress in the cortex reaches a critical value, the cortex releases its stress by folding into a periodic sinusoidal pattern (Figure 2, left). The importance of the skull during cortical folding remains an issue of ongoing debate. While our intuition suggests that the stiff skull places a significant spatial constraint on cortical folding, recent studies indicate that there is a large degree of independence between the development of the brain and the skull, despite their close physical connection [36]. Our model neglects the spatial constraint of the skull and assumes that the expansion of the brain is primarily limited by the subcortical tissue itself. This creates a regular primary folding pattern of sinusoidal shape (Figure 4, second row).
The phenomenon of primary folding has been studied before, both analytically [8] and numerically [23, 24]. Here we show that beyond the onset of primary folding, with continuing growth, the sinusoidal solution bifurcates into irregular secondary modes (Figure 2, middle and right). These secondary modes explain the increasing complexity of the cortex during the later stages of development, childhood, and adolescence [26] (Figure 1).
Our simulations reveal that secondary instabilities are highly sensitive to the underlying geometry and domain size: Changing the width of the simulation domain from two wavelengths to three suppresses the early mode of period-doubling and triggers the later mode of period-tripling, associated with a larger critical growth multiplier (Figures 4, 5, and 8). While the numerical solution relies on finite-sized domains and is sensitive to the domain width, in an infinite domain, the energetically favorable mode of period-doubling would be the only secondary bifurcation mode (Figure 5).
Our results suggest that, for a purely elastic substrate, the second instability point is almost independent of the stiffness ratio (Figure 6, dots). For a growing substrate, however, the required growth to induce the second instability increases with increasing stiffness ratio (Figure 6, squares and triangles). At the same time, the first instability point is only marginally affected by growth in the substrate; yet, it decreases markedly with increasing stiffness ratio. We conclude that stretch-induced subcortical growth - triggered by the adaption of axons to mechanical stretch [37] - acts as stabilizer of the folding process: The faster the axons respond to mechanical loading, the more stable the primary sinusoidal pattern and the less likely the occurrence of secondary instabilities. These features are conceptually similar to folding phenomena on a time-dependent viscoelastic foundation in tectonics and orogenesis [38, 39].
The secondary instability phenomena discussed here are different from the formation of primary folds during early gestation [24]. Rather, they apply to secondary and tertiary sulci, which continue to emerge after birth. As such, they are more affected by non-genetic, environmental factors. Upon birth, the brain of full-term infants already displays the entire primary folding pattern of the adult human brain [7]. Yet, cortical complexity still increases after birth [26], and many secondary and tertiary gyri occur and disappear long after neuronal migration has ceased [40]. This agrees with the common belief that secondary and tertiary gyri are closely related to the formation of interneuronal connections, which require more space than the neurons themselves: the cortex keeps expanding after birth [41]. Our folding patterns suggest that continuing growth of the cortical layer triggers secondary instabilities, which explain the increasing cortical complexity with age (Figures 4, 5, and 8).
Interestingly, the gyrification index, a clinical metric to quantify the degree of cortical folding, increases significantly during the last trimester of gestation, but remains almost constant after birth [43]. The gyrification index is the ratio between the total cortical surface and the its convex hull [42]. Our results confirm that secondary folding phenomena such as period-doubling and period-tripling result in a more complex outer appearance (Figures 4 and 8). Yet, the ratio between total cortical surface and convex hull virtually remains the same: while some sulci deepen, others flatten out.
Our brain surface morphology never reaches a stationary state - it continues to change plastically as new interneuronal connections form and dissolve [44]. Learning new tasks triggers the formation of new connections, increases the gray matter volume, and changes the brain surface morphology [45]. Our model suggests that these changes are closely correlated to secondary and tertiary bifurcations. Morphological changes during childhood and adolescence are closely associated with enhanced neuronal connectivity. As such, they could serve as early markers for physiological disorders [44]. A classical example is Huntington's disease associated with a chronic loss in gray matter volume [46]. Understanding the correlation between neuronal connectivity, gray matter volume, surface morphology, and ultimately behavior, could have important implications on how we diagnose, classify, quantify, and treat neurological disorders.
Acknowledgments
This study was supported by the German National Science Foundation grant STE 544/50-1 to Silvia Budday and Paul Steinmann, by the Stanford Bio-X Interdisciplinary Initiatives Program, by the National Science Foundation CAREER award CMMI 0952021, and by the National Institutes of Health Grant U01 HL119578 to Ellen Kuhl.
References
- 1.Goriely A, Geers MGD, Holzapfel GA, Jayamohan J, Jerusalem A, Sivaloganathan S, Squier W, van Dommelen JAW, Waters S, Kuhl E. Biomechanics and Modeling in Mechanobiology. doi: 10.1007/s10237-015-0662-4. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Luhmann HJ, Kilb W, Hanganu-Opatz IL. Front Neuroanat. 2009;3:19. doi: 10.3389/neuro.05.019.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sun T, Hevner RF. Nat Rev Neurosci. 2014;15:217. doi: 10.1038/nrn3707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Welker W. Why does the cortex fissure and fold: a review of determinants of gyri and sulci. In: Jones EG, Peters A, editors. Cerebral Cortex. Plenum Press; New York: 1990. p. 3. [Google Scholar]
- 5.Lohmann G, Von Cramon DY, Colchester AC. Cereb Cortex. 2008;18:1415. doi: 10.1093/cercor/bhm174. [DOI] [PubMed] [Google Scholar]
- 6.Raghavan R, Lawton W, Ranjan SR, Viswanathan RR. J Theor Biol. 1997;187:285. [Google Scholar]
- 7.Gilles FH, Leviton A, Dooling EC. The Developing Human Brain: Growth and Epidemiologic Neuropathology. J Wright Psg Inc. 1983 [Google Scholar]
- 8.Richman DP, Stewart RM, Hutchinson JW, Caviness VS. Science. 1975;189:18. doi: 10.1126/science.1135626. [DOI] [PubMed] [Google Scholar]
- 9.Adamuszek M, Schmid DW, Dabrowski M. J Struct Geol. 2011;33:1406. [Google Scholar]
- 10.Li B, Cao YP, Feng XQ, Gao H. Soft Matter. 2012;8:5728. [Google Scholar]
- 11.Yin J, Chen X. J Phys D: Appl Phys. 2011;44:045401. [Google Scholar]
- 12.Allen HG. Analysis and Design of Structural Sandwich Panels. Vol. 51. Pergamon Press; Oxford: 1969. [Google Scholar]
- 13.Schmalholz SM, Schmid DW. Phil Trans R Soc A. 2012;370:1798. doi: 10.1098/rsta.2011.0421. [DOI] [PubMed] [Google Scholar]
- 14.Bowden N, Brittain S, Evans AG, Hutchinson JW, Whitesides GM. Nature. 1998;393:146. [Google Scholar]
- 15.Diamant H, Witten TA, Ege C, Gopal A, Lee KYC. Phys Rev E. 2001;63:061602. doi: 10.1103/PhysRevE.63.061602. [DOI] [PubMed] [Google Scholar]
- 16.Moulton DE, Goriely A. J Appl Physiol. 2011;110:1003. doi: 10.1152/japplphysiol.00991.2010. [DOI] [PubMed] [Google Scholar]
- 17.Nelson MR, Howard D, Jensen OE, King JR, Rose FRAJ, Waters SL. Biomech Model Mechanobio. 2011;10:883. doi: 10.1007/s10237-010-0280-0. [DOI] [PubMed] [Google Scholar]
- 18.Brau F, Vandeparre H, Sabbah A, Poulard C, Boudaoud A, Damman P. Nat Phys. 2011;7:56. [Google Scholar]
- 19.Li B, Cao YP, Feng XQ, Gao H. J Mech Phys Solids. 2011;59:758. [Google Scholar]
- 20.Cao YP, Li B, Feng XQ. Soft Matter. 2012;8:556. [Google Scholar]
- 21.Pocivavsek L, Dellsy R, Kern A, Johnson S, Lin B, Lee KYC, Cerda E. Science. 2008;320:912. doi: 10.1126/science.1154069. [DOI] [PubMed] [Google Scholar]
- 22.Dennerll TJ, Lamoureux P, Buxbaum RE, Heidemann SR. J Cell Bio. 1989;109:3073. doi: 10.1083/jcb.109.6.3073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bayly PV, Okamoto R, Xu G, Shi Y, Taber LA. Phys Biol. 2013;10:016005. doi: 10.1088/1478-3975/10/1/016005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Budday S, Raybaud C, Kuhl E. Sci Rep. 2014;4:5644. doi: 10.1038/srep05644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Budday S, Kuhl E, Hutchinson JW. Phil Mag. 2015 doi: 10.1080/14786435.2015.1014443. in press. doi:10.1080/14786435. 2015.1014443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Naidich TP, Castillo M, Cha S, Smirniotopoulos JG. Imaging of the Brain: Expert Radiology Series. Elsevier Health Sciences; Oxford: 2012. [Google Scholar]
- 27.Sowell ER, Thompson PM, Tessner KD, Toga AW. J Neurosci. 2001;21:8819. doi: 10.1523/JNEUROSCI.21-22-08819.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Budday S, Steinmann P, Kuhl E. J Mech Phys Solids. 2014;72:75. doi: 10.1016/j.jmps.2014.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rodriguez EK, Hoger A, McCulloch AD. J Biomech. 1994;27:455. doi: 10.1016/0021-9290(94)90021-3. [DOI] [PubMed] [Google Scholar]
- 30.Franceschini G, Bigoni D, Regitnig P, Holzapfel GA. J Mech Phys Solids. 2006;54:2592. [Google Scholar]
- 31.Menzel A, Kuhl E. Mech Res Comm. 2012;42:1. doi: 10.1016/j.mechrescom.2012.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.BenAmar M, Goriely A. J Mech Phys Solids. 2005;53:2284. [Google Scholar]
- 33.Ambrosi D, Ateshian GA, Arruda EM, Cowin SC, Dumais J, Goriely A, Holzapfel GA, Humphrey JD, Kemkemer R, Kuhl E, Olberding JE, Taber LA, Garikipati K. Perspectives on biological growth and remodeling. J Mech Phys Solids. 2011;59:863. doi: 10.1016/j.jmps.2010.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Soza G, Grosso R, Nimsky C, Hastreiter P, Fahlbusch R, Greiner G. Int J Med Robot Comp Assist Surg. 2005;1:87. doi: 10.1002/rcs.32. [DOI] [PubMed] [Google Scholar]
- 35.Cao Y, Hutchinson JW. J Appl Mech. 2012;79:031019. [Google Scholar]
- 36.Aldridge K, Kane AA, Marsh JL, Panchal J, Boyadjiev SA, Yan P, Govier D, Ahmad W, Richtsmeier JT. Anatom Rec Part A 285A. 2005:690. doi: 10.1002/ar.a.20201. [DOI] [PubMed] [Google Scholar]
- 37.Suter DM, Miller KE. Prog Neurobiol. 2011;94:91. doi: 10.1016/j.pneurobio.2011.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Biot MA. Geol Soc Am Bulletin. 1961;72:1595. [Google Scholar]
- 39.Adamuszek M, Schmid DW, Dabrowski M. J Struct Geol. 2013;48:137. [Google Scholar]
- 40.Volpe JJ. Neurology of the Newborn. Elsevier Health Sciences; 2008. [Google Scholar]
- 41.Braitenberg V, Schüz A. Cortex: Statistics and Geometry of Neuronal Connectivity. Springer-Verlag; 1998. [Google Scholar]
- 42.Zilles K, Armstrong E, Schleicher A, Kretschmann HJ. Anat Embryol. 1988;179:173. doi: 10.1007/BF00304699. [DOI] [PubMed] [Google Scholar]
- 43.Armstrong E, Schleicher A, Omran H, Curtis M, Zilles K. Cereb Cortex. 1995;5:56. doi: 10.1093/cercor/5.1.56. [DOI] [PubMed] [Google Scholar]
- 44.White T, Su S, Schmidt M, Kao CY, Sapiro G. Brain Cognition. 2010;72:36. doi: 10.1016/j.bandc.2009.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Draganski B, Gaser C, Busch V, Schuierer G, Bogdahn U, May A. Nature. 2004;427:311. doi: 10.1038/427311a. [DOI] [PubMed] [Google Scholar]
- 46.Mühlau M, Gaser C, Wohlschläger AM, Weindl A, Städtler M, Valet M, Zimmer C, Kassubek J, Peinemann A. Mov Disord. 2007;22:1169. doi: 10.1002/mds.21137. [DOI] [PubMed] [Google Scholar]