TEAMS: Toxicity- and Efficacy-based Dose Insertion Design with Adaptive Model Selection for Phase I/II Dose-Escalation Trials in Oncology

Summary

In many oncology clinical trials it is necessary to insert new candidate doses when the prespecified doses are poorly elicited. Formal statistical designs with dose insertion are lacking. We propose a dose insertion design for phase I/II clinical trials in oncology based on both efficacy and toxicity outcomes. We also implement Bayesian model selection during the course of the trial so that better models can be adaptively chosen to achieve more accurate inference. The new design, TEAMS, achieves great operating characteristics in extensive simulation studies due to its ability to adaptively insert new doses as well as perform model selection. As a result, appropriate doses are inserted when necessary and desirable doses are selected with higher probabilities at the end of the trial.

1 Introduction

Phase I clinical trials are usually the first test of a new drug on human beings. The main purpose of traditional phase I oncology clinical trials is to determine the maximum tolerated dose (MTD) of an experimental drug, which is then passed to subsequent phase II trials for further testing for efficacy. The MTD is defined as the dose at which the probability that a patient experiences dose limiting toxicity is less than (sometimes close to) a prespecified target response rate p_T, which is usually set up by physicians. Therefore traditional phase I oncology clinical trials only consider the toxicity of the experimental drugs without using the efficacy information. The underlying assumption that justifies traditional clinical trial designs is that both efficacy and toxicity response rates are non-decreasing with respect to the dose level, which is correct in the case of cytotoxic agents commonly used in classical oncology trials (Le Tourneau et al, 2009). Numerous statistical designs considering toxicity along have been proposed for phase I trials in the last two decades. Representative methods include the continual reassessment method (CRM) (O’Quigley et al, 1990), escalation with overdose control (Babb et al, 1998) and modified toxicity probability interval (mTPI) method (Ji et al, 2010; Ji and Wang, 2013), among many others.

As the paradigm of cancer drug development shifts from cytotoxic agents towards molecular targeted therapy (MTT), the monotonicity assumption might no longer hold (Hoff and Ellis, 2007; Korn, 2004). For example, for monoclonal antibodies that target either the vascular endothelial growth factor or epidermal growth factor receptor for metastatic colorectal cancer, it is not the case that efficacy will monotonically increase with dose. Similar results were obtained in Postel-Vinay et al (2009) and Jain et al (2010), demonstrating that MTD may not have the highest efficacy among the safe doses in the case of MTT. Hence, both toxicity and efficacy should be taken into consideration when designing dose-escalation trials for these novel therapies. Instead of identifying the MTD, one could consider the optimal biological dose (OBD), the definition of which takes into account both efficacy and toxicity. Such trials are categorized as phase I/II trials because efficacy is incorporated.

Statistical designs have been developed in the literature for phase I/II dose-escalation trials. Braun (2002) used the Euclidean distance from the estimated response rates pair of toxicity and efficacy to the desired response rates pair as well as its variations. Thall and Cook (2004) defined efficacy-toxicity trade-off contours to determine the OBD. Yin et al (2006) used toxicity and efficacy odds ratio as the assessment of dose desirability. Zhang et al (2006) and Ivanova et al (2009) used a linear combination of toxicity and efficacy.

As little is known about the experimental drugs in phase I or phase I/II dose-escalation studies, initial dose elicitation is usually quite ad hoc and does not guarantee that elicited doses are always acceptable as treatments. For instance, all prespecified doses may have lower efficacy and/or higher toxicity than the optimal dose, or the optimal dose might be bracketed by two adjacent prespecified doses. Therefore, a new dose that is more desirable than all of the prespecified doses should be extrapolated or interpolated. This practice is routinely done by physicians, although formal and principled statistical designs with dose insertion are lacking. Piantadosi and Liu (1996) proposed a sequential dose-finding method that adaptively calculates doses to be assigned to each cohort as the trial proceeds, which is a variant of the CRM. Hu et al (2013) developed an adaptive dose insertion strategy as an “add-on” to phase I trial designs. But neither of them is suitable for phase I/II trials since efficacy is not considered in their designs.

In this paper, we propose a toxicity- and efficacy-based dose insertion trial with adaptive model selection, or the TEAMS design, for phase I/II clinical trials. Our method can also be thought as an “add-on” to a phase I/II trial that would complement any appropriate dose-escalation designs as long as both efficacy and toxicity responses are recorded for each patient. The main features of TEAMS include a penalty-based assessment of dose desirability and a model-based inference that provides coherent outcome-adaptive decisions. Importantly and innovatively, to capture the potential non-monotone dose-response relationship of many novel oncology drugs, we propose an adaptive model selection procedure that allows the dose-response model to vary between the monotone pattern and non-monotone pattern as trial data accumulate. We construct non-local priors in Johnson and Rossell (2010) for the key parameters governing the model selection based on Bayes factor (BF).

The remainder of this article is organized as follows. In sections 2 and 3, we describe the probability model and TEAMS design. A variation of TEAMS using Bayesian model averaging (BMA) instead of Bayesian model selection (BMS) is also considered and discussed. In section 4, we evaluate the operating characteristics of the TEAMS design via simulation studies. We conclude with brief discussion in section 5.

2 Methods

2.1 Dose-response models

Consider a trial with D dose levels, denoted by x₁ < x₂ < ⋯ < x_D. For mathematical convenience, we assume that the dose values of x_i’s have been unitized so that the maximum dose x_D = 1 and x_i ∈ (0, 1], i = 1, ⋯, D. Let q_E(x_i) and q_T (x_i) denote probabilities of the efficacy event and toxicity event for the dose level x_i.

Assume that q_T(x) follows a linear logistic model

$$\text{logit}\{q_T(x)\}={\alpha }_0+{\alpha }_{1}x,$$ (1)

where α₁ > 0. To incorporate a non-monotone pattern in the dose-efficacy model, we assume that q_E(x) follows a quadratic logistic model:

$$\text{logit}\{q_E(x)\}={\beta }_0+{\beta }_{1}x+{\beta }_2{x}^2.$$ (2)

Denote α = (α₀, α₁)′ and β = (β₀, β₁, β₂)′, the vector of regression parameters in the dose-toxicity model (1) and dose-efficacy model (2), respectively. Here, we assume that the binary outcomes of efficacy and toxicity are independent. Although the independence assumption may not hold, it is suggested via sensitivity analysis in Cai et al (2014) that methods modeling efficacy and toxicity responses independently have a robust performance in the case that the two endpoints are correlated.

2.2 Penalty function and definition of OBD

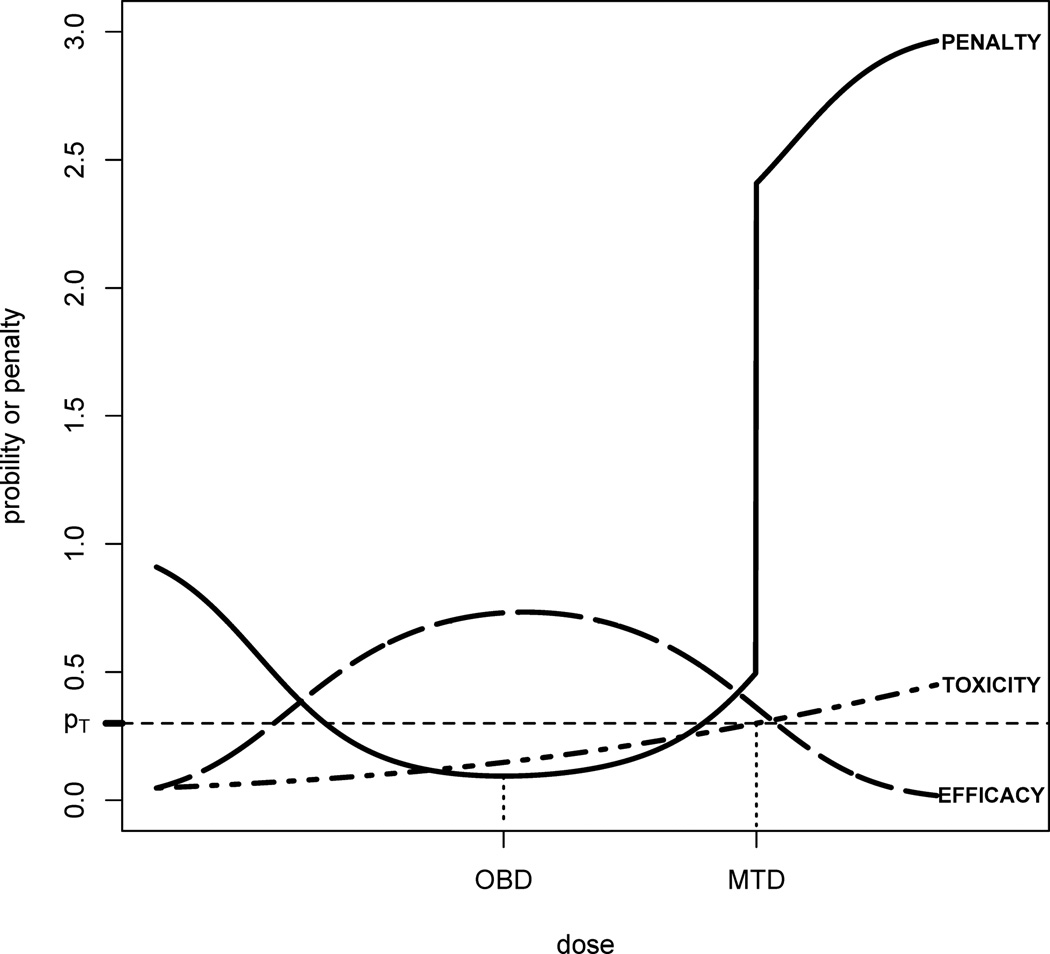
We construct a penalty function to evaluate doses based on the probabilities of efficacy and toxicity. Denote P(x, θ) the penalty for dose x, and define

$$P(x,\mathit{\theta })=q_T^2(x)·\mathbf{1}\{q_T(x)\le p_T\}+2·\mathbf{1}\{q_T(x)>p_T\}+{\{1-q_E(x)\}}^2,$$ (3)

where θ = (α′, β′)′ and 1{·} is the indicator function. Then the OBD x_opt is defined as the dose that minimizes the penalty function, i.e.

$$x_{\mathit{\text{opt}}}(\mathit{\theta })=\underset{x}{\text{argmin}}P(x,\mathit{\theta }).$$

See Figure 1 for an illustration. The intuition behind penalty P(x, θ) is originated from the distance from (q_T (x), q_E(x)) to (0, 1), the ideal point on the two dimensional probability space of efficacy and toxicity. The farther away the probabilities (q_T(x), q_E(x)) from (0, 1), the more penaltydose × receives. In practice, safety outweighs efficacy once a threshold is passed, say q_T(x) > p_T. Therefore, we define the penalty in such a way that when the toxicity probability of a dose is higher than p_T the associated penalty will drastically increase, by a factor of 2 · 1{q_T(x) > p_T} as shown in (3). It can be easily derived that the penalty P(x, θ) ≥ 2 if q_T(x) > p_T and P(x, θ) ≤ 2 if q_T(x) ≤ p_T, hence a dose higher the MTD can never be the OBD. This can be clearly seen in Figure 1. Note that one can use λ · 1{q_T(x) > p_T} for any λ ≥ 2 so that the defined OBD is always lower than the MTD.

Fig. 1.

Penalty function and the OBD: the penalty function defined in (3) is discontinuous at MTD and sharply increases, making doses above the MTD impossible to be OBD. The OBD is the minimizer of the penalty.

2.3 Adaptive model selection for the dose-efficacy model

Efficacy could be either monotone or non-monotone with respect to the dose, which depends on the pharmacology of the drug. Proposing adaptive model selection, we allow adaptation in model choice throughout the trial. Briefly, when the number of explored doses or the sample size is small, especially at the beginning of the trial with few enrollments, the estimation of dose-response curve could be noisy and susceptible to model mis-specification. In this case a simpler model, such as a linear logistic regression, may fit the data better; in contrast when more doses are explored and more patient data accumulate, better estimates may be obtained under more complex models such as a nonmonotone quadratic logit model. To enable the adaptive model selection as sample size increases, we introduce a method for selecting the dose-efficacy model. Consider a hypothesis test for the quadratic regression coefficient in (2) as following:

$$M_1:{\beta }_2=0\text{vs}{M}_2:{\beta }_2\ne 0.$$

To incorporate Bayesian model selection, we impose a non-local alternative prior on β₂ under M₂, which has no probability mass at the null point (β₂ = 0) (Johnson and Rossell, 2010). Specifically, inverse moment prior (iMOM) is used providing exponential convergence in favor of both true null hypothesis and true alternative hypothesis, which takes the form

$$\pi ({\beta }_2|M_2)=\frac{k{\tau }^{\nu /2}}{\Gamma (\nu /2k)}|{\beta }_2{|}^{-(\nu +1)}\text{exp}\left(\frac{{\tau }^k}{{\beta }_2^{2k}}\right),$$ (4)

for k, ν, τ > 0. Some examples of the iMOM prior are shown in Figure A.2 in Wed Appendix A.

The null prior is simply a point mass at zero, i.e.

$$\pi ({\beta }_2|M_1)=\mathbf{1}({\beta }_2=0).$$

We assume a prior Pr(M₁) = Pr(M₂) = 0.5 for the two hypothesis. We perform model selection through BF, similar to Yuan and Yin (2011), given by

$$BF=\frac{\int \pi (\mathit{\alpha },{\mathit{\beta }}_{\mathbf{1}}|M_1)ℒ(\mathit{\text{Data}}|\mathit{\alpha },{\mathit{\beta }}_{\mathbf{1}},M_1)d\mathit{\alpha }d{\mathit{\beta }}_{\mathbf{1}}}{\int \pi (\mathit{\alpha },{\mathit{\beta }}_{\mathbf{2}}|M_2)ℒ(\mathit{\text{Data}}|\mathit{\alpha },{\mathit{\beta }}_{\mathbf{2}},M_2)d\mathit{\alpha }d{\mathit{\beta }}_{\mathbf{2}}},$$

where ℒ(Data|α, β_j, M_j) is the likelihood function under model M_j, β₁ = {β₀, β₁, β₂ = 0} and β₂ = {β₀, β₁, β₂}. Since the integral does not have a closed form, numerical integration, such as Monte Carlo integration, is applied. Specifically, we use the harmonic mean of likelihood values here. Let ${\mathit{\beta }}_{\mathit{j}}^{(1)},{\mathit{\beta }}_{\mathit{j}}^{(2)},\dots ,{\mathit{\beta }}_{\mathit{j}}^{(R)}$ be a Markov chain Monte Carlo (MCMC) sample from the posterior distribution of β_j under model M_j; suppressing terms related to α it can be shown that

$$\int \pi ({\mathit{\beta }}_{\mathit{j}}|M_j)ℒ(\mathit{\text{Data}}|{\mathit{\beta }}_{\mathit{j}},M_j)d{\mathit{\beta }}_{\mathit{j}}\approx {\left\{\frac{1}{R}\sum _{r=1}^Rℒ{(\mathit{\text{Data}}|{\mathit{\beta }}_{\mathit{j}}^{(r)},M_j)}^{-1}\right\}}^{-1},$$

for j = 1, 2. Hence

$$BF\approx \frac{{\left\{\frac{1}{R}{\sum }_{r=1}^Rℒ{(\mathit{\text{Data}}|{\mathit{\beta }}_{\mathbf{1}}^{(r)},M_1)}^{-1}\right\}}^{-1}}{{\left\{\frac{1}{R}{\sum }_{r=1}^Rℒ{(\mathit{\text{Data}}|{\mathit{\beta }}_{\mathbf{2}}^{(r)},M_2)}^{-1}\right\}}^{-1}}.$$ (5)

Kass and Raftery (1995) showed that the harmonic mean approach is more efficient than directly sampling from the prior, especially when the likelihood function is highly concentrated in an area with low prior probabilities.

When applying the BF-based model selection, we define a rule for thresholding BF (Table 1). This rule is consistent with the interpretation of BF in Jeffreys (1961), in which BF between 1 and 3 was not considered as strong evidence supporting either model, and BF larger than 3 was considered substantial evidence supporting the more plausible hypothesis.

Table 1.

BF-based model selection rules. Note that we choose the linear logistic regression as the preferred model when BF ∈ [1/3, 3] to enforce parsimony.

BF	The Selected Dose-Efficacy Model
< 1/3	Q (quadratic logistic model, M2)
1/3 to 3	L (linear logistic model, M1)
> 3	L (linear logistic model, M1)

2.4 Likelihood and prior specification

Let y_i, z_i and n_i be the numbers of toxicity responses, efficacy responses and total patients treated at dose i, for i = 1, …, D. For the observed data Data ≡ {(y_i, z_i, n_i), i = 1,…, D}, the likelihood function under model M_j is the product of the binomial densities, i.e.

$$ℒ(\mathit{\text{Data}}|\mathit{\alpha },{\mathit{\beta }}_{\mathit{j}},M_j)\propto \prod _{i=1}^d{q}_T{(x_i|\mathit{\alpha })}^{y_i}{\{1-q_T(x_i|\mathit{\alpha })\}}^{n_i-y_i}{q}_E{(x_i|{\mathit{\beta }}_{\mathit{j}})}^{z_i}{\{1-q_E(x_i|{\mathit{\beta }}_{\mathit{j}})\}}^{n_i-z_i},$$

where j = 1, 2 index two different models. Denote π_E(β_j|M_j) and π_T(α) the priors for β_j and α. Assuming the prior independence between β_j and α, the joint posterior is given by

$$\pi ({\mathit{\theta }}_{\mathit{j}}|\mathit{\text{Data}},M_j)\propto ℒ(\mathit{\text{Data}}|\mathit{\alpha },{\mathit{\beta }}_{\mathit{j}},M_j){\pi }_E({\mathit{\beta }}_{\mathit{j}}|M_j){\pi }_T(\mathit{\alpha }),$$

where ${\mathit{\theta }}_{\mathit{j}}=(\mathit{\alpha }\prime ,{\mathit{\beta }}_{\mathit{j}}^{\prime })\prime$. Specifically, we assume

$${\alpha }_0,{\beta }_0~𝒩(-3,{0.5}^2),$$

$${\alpha }_1~\text{log}𝒩(0,2^2),$$

$${\beta }_1~𝒩(5,{10}^2).$$

We use an informative normal prior centered at −3 for α₀ and β₀ to reflect the belief that patients receiving no drug should not have any response for either efficacy or toxicity; having intercepts α₀ and β₀ around −3 reflects that belief since logit⁻¹(α₀) and logit⁻¹(β₀), both equal to 0.047 when plugging in the prior mean, are the prior probabilities of toxicity and efficacy when x = 0, i.e. no drug. The lognormal prior for α₁ reflects the belief that α₁ > 0, i.e. the dose-toxicity relationship is monotone increasing. We choose prior for β₁ with large variance allowing data-driven posterior inference.

For the iMOM prior for β₂ under the quadratic logistic model in (4), default values recommended by Johnson and Rossell (2010) are used for k and ν: k = ν = 1. Specifically, k = 1 provides adequate exponential convergence rates of BF in favor of the null hypothesis when it is true; and ν = 1 yields a Cauchy-like tail in the prior, which can improve the power under the alternative hypothesis for small sample sizes (Gelman et al, 2008). Regarding the choice of parameter τ, we use a sensitivity analysis to calibrate its value. In the sensitivity analysis, we test different τ values and examine the estimated β₂ values under 11 scenarios. We decide to set τ = 50 to balance the performance of selecting either M₁ or M₂ when it is the true model. Details of the sensitivity analysis can be found in Web Appendix A.

2.5 Dose insertion

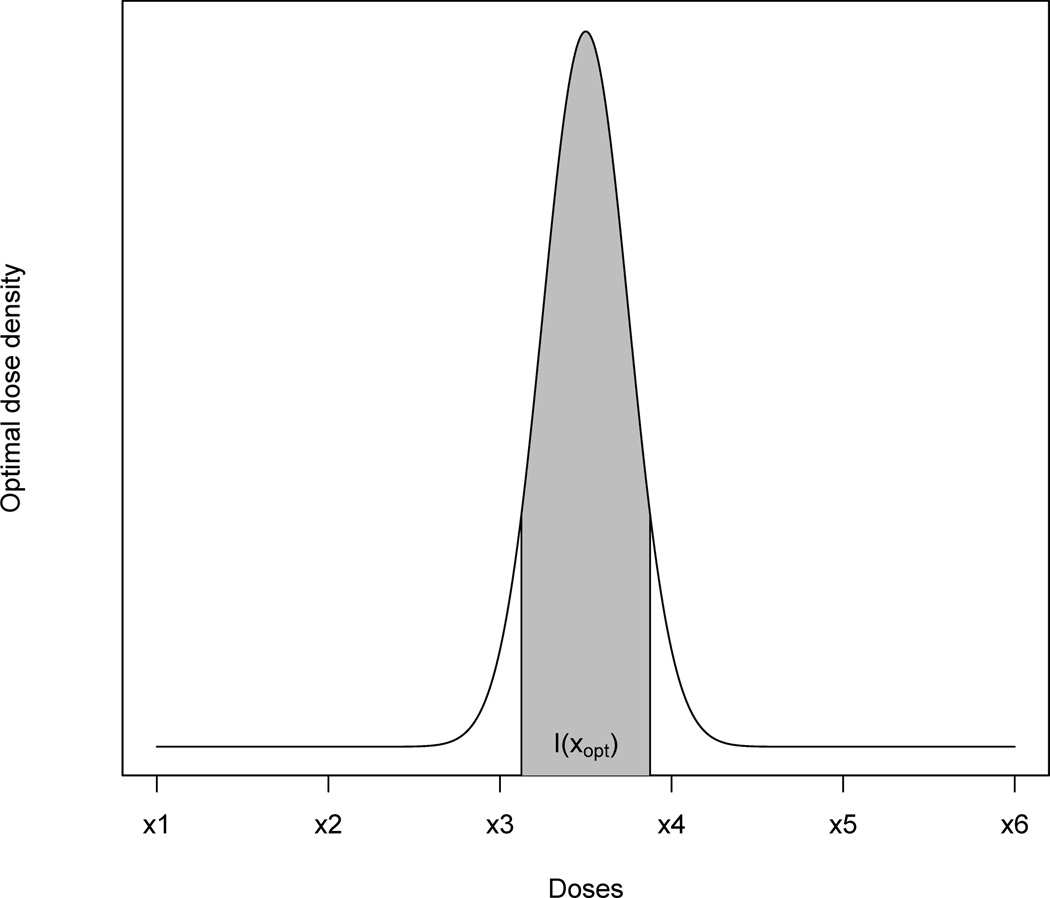
A new dose should be inserted when the OBD, x_opt, is distant to all the existing doses in the trial. Mathematically, we propose an activation rule for triggering the dose-insertion procedure. Let I_C(x_opt) denote the C% (e.g., C = 95) credible interval of x_opt. Define A as the indicator of dose insertion,

$$A=\{\begin{array}{c}1\text{if}{I}_C(x_{\mathit{\text{opt}}})\cap \{x_1,x_2,\cdots ,x_D\}=\varphi ,\hfill \\ 0\text{if}{I}_C(x_{\mathit{\text{opt}}})\cap \{x_1,x_2,\cdots ,x_D\}=\varphi ,\hfill \end{array}$$ (6)

where φ denotes the empty set. When A = 1, the dose-insertion procedure is activated. Otherwise, the trial proceeds by treating the next cohort at one of the existing doses. Figure 2 illustrates intuitively how the condition could be satisfied. In the figure, the posterior density of the OBD is plotted along with a credible interval I_C(x_opt). The interval does not cover any existing dose, in which case A = 1 and the dose-insertion procedure is activated.

Fig. 2.

A hypothetical probability density function of the estimated optimal dose x_opt for which a new dose should be inserted between x₃ and x₄.

3 TEAMS design

3.1 Dose-finding algorithm

Once a new cohort is recruited in the trial, we update the recorded outcome data from existing doses and enrolled patients, generate MCMC posterior samples of the parameters under M₁ and M₂ respectively, denoted by $\{{\mathit{\theta }}_1^{(r)},r=1,\cdots ,R\}$ and $\{{\mathit{\theta }}_2^{(r)},r=1,\cdots ,R\}$, and carry out the adaptive model selection based on BF using the updated data. Suppose M_j* is selected and currently we have an MCMC posterior sample of θ_j* under the selected M_j*. For each simulated values ${\mathit{\theta }}_{j^{*}}^{(r)}$ from the r-th MCMC iteration, r = 1,…, R, we minimize the penalty function P(x, θ_j*) with respect to dose x, to obtain a posterior sample of the OBD, i.e.

$${\hat{x}}_{\mathit{\text{opt}},j*}^{(r)}=\underset{x}{\text{argmin}}P(x,{\mathit{\theta }}_{j*}^{(r)}),j*\in \{1,2\},$$ (7)

from which the posterior mean

$${\hat{x}}_{\mathit{\text{opt}}}=\frac{{\sum }_{r=1}^R{\hat{x}}_{\mathit{\text{opt}},j*}^{(r)}}{R},$$

and posterior credible interval Î_C(x_opt) can be directly computed. For example,

$${Î}_C(x_{\mathit{\text{opt}}})=({\hat{x}}_{\frac{1-C\%}{2}},{\hat{x}}_{\frac{1+C\%}{2}})$$

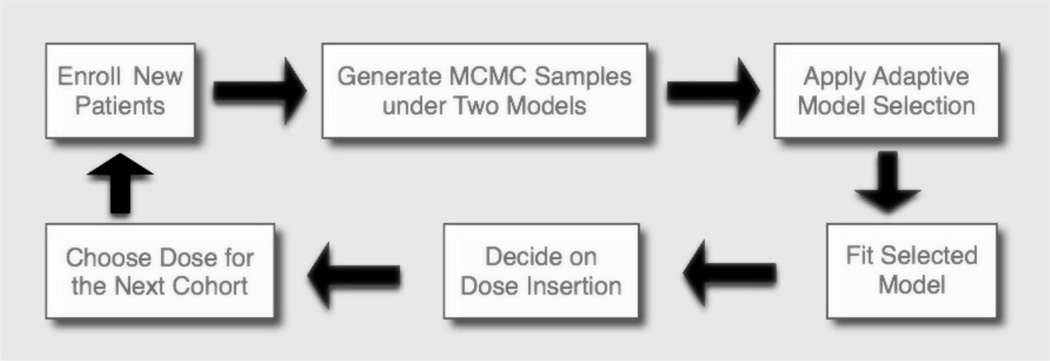
where x̂_k is the 100k-th percentile of the posterior sample $\{{\hat{x}}_{\mathit{\text{opt}},j^{*}}^{(r)},r=1,\dots ,R\}$. Using the estimated Î_C(x_opt), we obtain the decision A for dose insertion. A simple flow chart in Figure 3 depicts the flow of TEAMS.

Fig. 3.

A simple flow chart for TEAMS.

Given limited data from the first few cohorts at the beginning of the trial, estimates of the parameters are unstable which in turn affect the performance of the insertion procedure. To this end, we only apply the dose-insertion algorithm after treating N/2 patients, where N is the maximum sample size. Before applying the dose-insertion algorithm, the trial goes according to a default trial design. For example, we apply the mTPI design (Ji et al, 2010; Ji and Wang, 2013) for the first N/2 patients. Using a Bayesian statistical framework, mTPI computes the posterior probabilities of three intervals reflecting the distance between the toxicity rate of the treating dose and the target toxicity probability p_T, and generates a decision table containing dose-finding decisions - E, S, and D - representing escalating the dose, staying at the same dose, and de-escalating the dose.

The TEAMS design is summarized in Box 1. Additional rules are defined for ethics and stability concern. Although these rules would slow down the speed of exploring the dose space, they would reduce the probability of exposing patients to excessively toxic or inefficacious doses. The practical rules are listed in Box 2.

Box 1. The TEAMS design for phase I/II dose finding trials.

• Stage I Apply a default dose escalation design when ${\mathrm{\Sigma }}_{i=1}^D{n}_i<N/2$.

• Stage II When ${\mathrm{\Sigma }}_{i=1}^D{n}_i<N/2$.

  • II1 Treat a new cohort of patients at the current dose, and collect data on both efficacy and toxicity.
  • II2 Using the collected data, generate MCMC posterior samples of the parameters under M₁ and M₂ respectively, carry out adaptive model selection based on BF, and obtain an MCMC posterior sample $\{{\mathit{\theta }}_{j^{*}}^{(r)},r=1,\dots ,R\}$ under the selected dose-efficacy model M_j*, j^* ∈ {1, 2}.
  • II3 Obtain a posterior sample of x_opt under M_j*, i.e. $\{{\hat{x}}_{\mathit{\text{opt}},j^{*}}^{(r)},r=1,\dots ,R\}$, from (7). Then compute the posterior mean of OBD, ${\hat{x}}_{\mathit{\text{opt}}}=\frac{1}{R}{\mathrm{\Sigma }}_{r=1}^R{\hat{x}}_{\mathit{\text{opt}},j^{*}}^{(r)}$, and the decision indicator A given by (6).

    1. If A = 1, the new dose x̂_opt is inserted in the trial and assigned to the next cohort.
    2. If A = 0, compute the posterior mean of the penalty for each existing dose, i.e. $\frac{1}{R}{\mathrm{\Sigma }}_{r=1}^{R}P(x_i,{\mathit{\theta }}_{j^{*}}^{(r)})$ for i = 1, ⋯, D. Treat the next cohort on the dose ĩ that has the lowest mean penalty, where ĩ = argmin_i{P̄(x_i, θ_j*)}.
  • II4 Repeat steps II1-II3 until the maximum sample size N is achieved.
  • II5 Select as OBD the dose that has the lowest mean penalty among all tested doses, including prespecified doses and new inserted doses.

Box 2. Practical rules.

• –Rule 1 [Dose Extrapolation] The inserted new dose is not allowed to be more than twice the highest dose or less than half of the lowest dose that has been used in the trial.
• –Rule 2 [Early Termination] If the lowest dose x₁ is too toxic, i.e. Pr{q_T (x₁) > p_T|data} > ξ where ξ is close to 1, and no new dose is inserted, terminate the trial.
• –Rule 3 [Dose Exclusion] Suppose that a dose x_i is too toxic, i.e. Pr{q_T (x_i) > p_T|data} > ξ where ξ is close to 1. We exclude doses {x_i, ⋯, x_D}, i.e. these doses will never be used in the trial again.
• –Rule 4 [No Skipping Dose] Restrict the escalation to 1 level for doses that have not been used, i.e. there is no skipping in the escalation. Particularly, if the new dose intended for insertion is higher than any unexplored dose, pause the insertion and treat the next cohort on the lowest unexplored dose that has not been used, instead of the putative newly inserted dose.

3.2 Bayesian model averaging

Besides the BF-based model selection for the dose-efficacy model, we also consider the Bayesian model averaging (BMA) method to incorporate the uncertainty in the model specification. BMA for dose finding has been considered in Yin and Yuan (2009) as an extension of the CRM design.

TEAMS with BMA differs from TEAMS with model selection in three aspects. When estimating the mean penalty for each dose in stage II3, both models M₁ and M₂ must be taken into account, i.e.

$$\overline{P}(x,\mathit{\theta })=\mathrm{E}[\mathrm{P}(\mathrm{x},\mathit{\theta })|\text{Data}]=\sum _{j=1}^{2}E[P(x,{\mathit{\theta }}_j)|\mathit{\text{Data}},M_j]\mathit{\text{Pr}}(M_j|\mathit{\text{Data}})\approx \sum _{j=1}^2\mathit{\text{Pr}}(M_j|\mathit{\text{Data}})\sum _{r=1}^{R}P(x,{\mathit{\theta }}_j^{(r)})/R.$$ (8)

Given the definition of the Bayes factor BF in (5), the two posterior probabilities can be calculated as Pr(M₁|Data) = BF/(BF + 1) and Pr(M₂|Data) = 1/(BF + 1).

Let $x_{\mathit{\text{opt}},j}^{(r)}={\text{argmin}}_{x}P(x,{\mathit{\theta }}_j^{(r)})$, j ∈ {1, 2}. Regarding the dose insertion criterion A, we propose a minor modification to (6) to avoid joggling between two credible intervals for two models. Specifically, in stage II3 we calculate the c.d.f of posterior distribution for x_opt at a given x₀ using BMA, which is

$$\mathit{\text{Pr}}(x_{\mathit{\text{opt}}}<x_0|\mathit{\text{Data}})=\sum _{j=1}^2\mathit{\text{Pr}}(x_{\mathit{\text{opt}}}<x_0|\mathit{\text{Data}},M_j)\mathit{\text{Pr}}(M_j|\mathit{\text{Data}})\approx \sum _{j=1}^2\mathit{\text{Pr}}(M_j|\mathit{\text{Data}})\sum _{r=1}^R\mathbf{1}(x_{\mathit{\text{opt}},j}^{(r)}<x_0)/R.$$ (9)

If $\frac{1-C\%}{2}<\mathit{\text{Pr}}(x_{\mathit{\text{opt}}}<x_i|\mathit{\text{Data}})<\frac{1+C\%}{2}$, it can be implied that the dose x_i ∈ I_C(x_opt) and consequently the decision rule A based on BMA can be obtained.

Similarly, the posterior mean x_opt under BMA can also be calculated, i.e.

$$E[x_{\mathit{\text{opt}}}|\mathit{\text{Data}}]=\sum _{j=1}^{2}E[x_{\mathit{\text{opt}}}|\mathit{\text{Data}},M_j]\mathit{\text{Pr}}(M_j|\mathit{\text{Data}})\approx \sum _{j=1}^2\mathit{\text{Pr}}(M_j|\mathit{\text{Data}})\sum _{r=1}^R{x}_{\mathit{\text{opt}},j}^{(r)}/R.$$ (10)

With these calculations, TEAMS essentially is unchanged based on BMA. An almost identical dose-finding algorithm of TEAMS using BMA is given in Web Appendix B.

4 Simulation studies

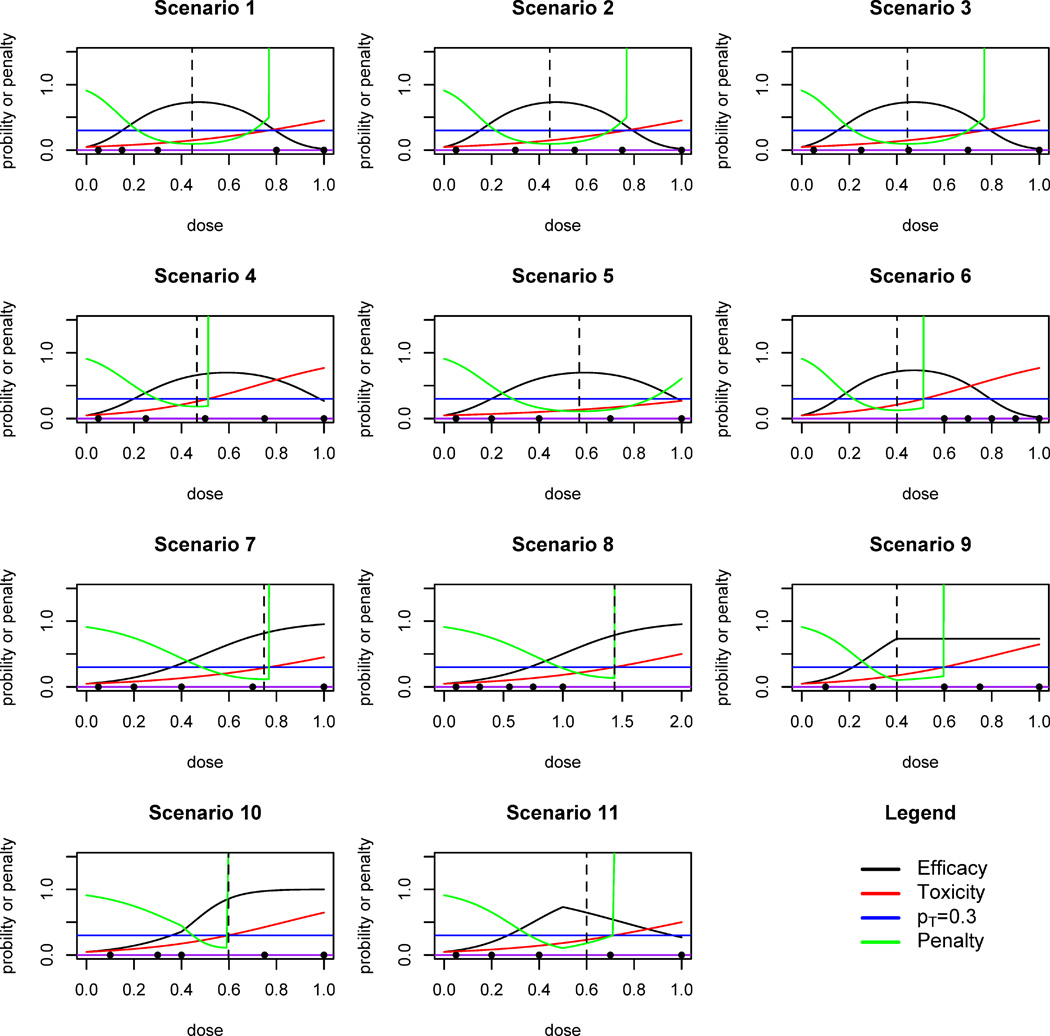
We consider eleven different scenarios in the simulation, which are shown in Figure 4. For each scenario, 1,000 simulated trials are conducted using the TEAMS design. Each simulated trial has five prespecified doses to begin with. In the first eight scenarios, toxicity and efficacy responses are generated from equations (1) and (2); for the last three scenarios which are conducted as a sensitivity study, we set the dose-efficacy model to consist of two linear logit regression models joined at a change point. Cohort size is 3 and the maximum samples size N is 54. The credible level C% of the interval Î(x_opt) is 95% and the MTD toxicity threshold p_T is 0.3. We start all trials at the lowest dose. The default dose escalation design for the first half of trial is mTPI. In the mTPI method, the choices of ε₁ and ε₂ are both 0.05, the default values suggested by Ji et al (2010). The probability threshold ξ = 0.95 for the practical rules. These trial parameters are determined based on an extensive review of literature to reflect a typical practical trial in real life.

Fig. 4.

Eleven scenarios in the simulation study. Dots represent the pre-specified doses. Dashed vertical line marks the true OBD. Black curve: dose-efficacy curve. Red curve: dose-toxicity curve. Green curve: dose-penalty curve. Blue horizontal line: p_T.

Regarding MCMC computation, we adopt a random walk Metropolis-Hasting algorithm with normal proposals. And for each chain, 10,000 samples are drawn with a burn-in size of 5,000 iterations.

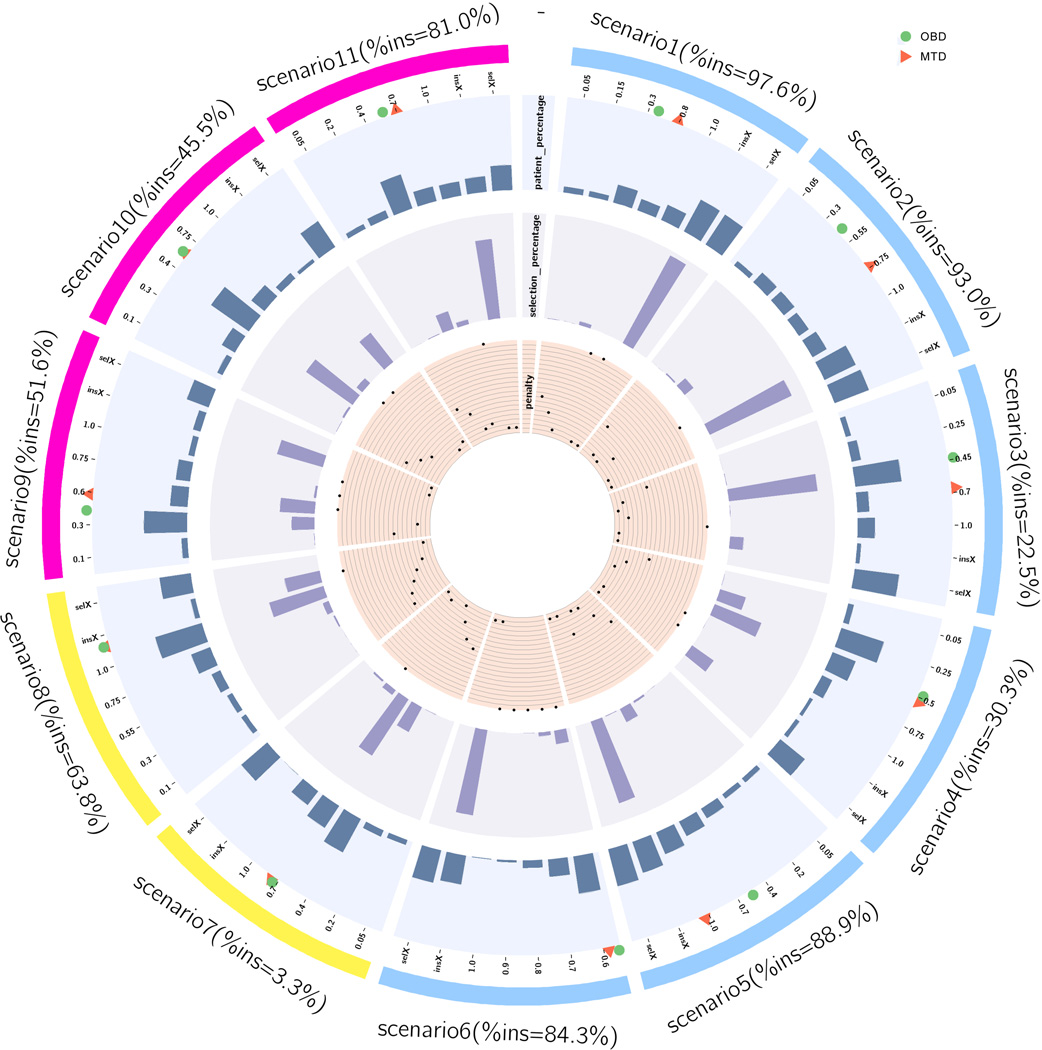
Figure 5 is a circos plot (Krzywinski et al, 2009) summarizing the operating characteristics of the TEAMS design on all the eleven scenarios, including the dose-insertion rates, the percentage of each dose selected as the OBD at the end of the trials, along with the percentage of patients assigned to each dose. To assist the comprehension of Figure 5, we provide a zoom-in version for Scenario 1 in the circos plot as Figure C.1 in Web Appendix C. Tabulated results can be found in Table 2, which presents simulation summaries by scenarios with four sections in the first eight scenarios and two sections in the last three scenarios. Section 1 gives a brief description of the true dose response and the need for insertion or not. Section 2 provides the average (standard deviation) of the posterior means across 1,000 simulated trials for the regression parameters. Section 3 summarizes the model selection and Section 4 presents the detailed operating characteristics of TEMAS in terms of patient allocation and dose selection. Overall, the results are encouraging.

Fig. 5.

A circos plot summarizing the operating characteristics of TEAMS in simulated trials for the eleven scenarios. For each scenario, different characteristics are plotted for all prespecified doses, the inserted doses (denoted by insX), and the selected doses (denoted by selX). MTD and OBD are marked by the red triangle dot and green circle dot in the dose axis. From inner to outer tracks, the plot displays characteristics as follows: penalties, with longer distances from the center to dots indicating higher penalties; histogram for percentages of all the tested doses selected as the OBD; histogram for percentages of patients assigned to all the tested doses and selected doses.

Table 2.

Simulation results for 11 scenarios using the TEAMS design. For each scenario, 1,000 trials are conducted on computer and operating characteristics of TEAMS are summarized in four sections. Section 1 gives a brief description of the true dose response and the need for insertion or not. Section 2 provides the average (standard deviation) of the posterior means across 1,000 simulated trials for the regression parameters. Section 3 summarizes the model selection and Section 4 presents the detailed operating characteristics of TEMAS (model selection or model averaging) in terms of patient allocation and dose selection. For Scenarios 9–11, the true dose-response curves do not follow either a linear or a quardratic logit model. Therefore, results for Sections 2 and 3 are not available for these scenarios.

Scenario 1
1. Quadratic; Efficacy peaks in the left side of MTD; Too low or Too high toxicity; Insertion is needed.
2. Tox Parameter Estimation				Eff Parameter Estimation
True (α0, α1) = (−3, 2.8)				True (β0, β1, β2) = (−3, 17, −18)
α̂0	α̂1		${\hat{\beta }}_0^L$	${\hat{\beta }}_1^L$	${\hat{\beta }}_0^Q$	${\hat{\beta }}_1^Q$	${\hat{\beta }}_2^Q$
−2.95(0.23)	2.71(0.85)		−2.85(0.27)	3.11(7.27)	−2.79(0.23)	15.44(2.60)	−16.58(3.77)
3. Model selection percentages: L – linear vs. Q – quadratic						L = 0.1%	Q = 99.0%
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.445, BMS: %ins=97.6%, BMA: %ins=98.4%
True Dose level	0.05	0.15	0.3	0.8	1.0	Dose inserted	Dose selected
True Eff/Tox	0.10/0.05	0.30/0.07	0.62/0.10	0.28/0.32	0.02/0.45
BMS insertion						0.440(0.058)	0.434(0.054)
BMA insertion						0.441(0.047)	0.437(0.047)
BMS % pts	0.063	0.059	0.196	0.126	0.176	0.380	0.374
BMA % pts	0.056	0.059	0.208	0.126	0.176	0.375	0.369
BMS % sel	0.005	0.001	0.036	0.000	0.000	0.958
BMA % sel	0.000	0.001	0.032	0.000	0.000	0.967
Scenario 2
1. Quadratic; Efficacy peaks in the left side of MTD; Bracket; Insertion is needed.
2. Tox Parameter Estimation				Eff Parameter Estimation
True (α0, α1) = (−3, 2.8)				True (β0, β1, β2) = (−3, 17, −18)
α̂0	α̂1		${\hat{\beta }}_0^L$	${\hat{\beta }}_1^L$	${\hat{\beta }}_0^Q$	${\hat{\beta }}_1^Q$	${\hat{\beta }}_2^Q$
−2.94(0.22)	2.67(0.76)		−2.72(0.23)	9.29(1.58)	−2.81(0.20)	15.45(2.61)	−16.26(3.94)
3. Model selection percentages: L – linear vs. Q – quadratic						L = 0.1%	Q = 98.2%
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.445, BMS: %ins=93.0%, BMA: %ins=91.5%
True Dose level	0.05	0.3	0.55	0.75	1.0	Dose inserted	Dose selected
True Eff/Tox	0.10/0.05	0.62/0.10	0.71/0.19	0.41/0.29	0.02/0.45
BMS insertion						0.435(0.031)	0.447(0.048)
BMA insertion						0.436(0.028)	0.447(0.050)
BMS % pts	0.057	0.140	0.142	0.124	0.172	0.366	0.387
BMA % pts	0.057	0.146	0.145	0.124	0.172	0.357	0.386
BMS % sel	0.001	0.016	0.109	0.000	0.000	0.874
BMA % sel	0.001	0.020	0.112	0.001	0.000	0.866
Scenario 3
1. Quadratic; Efficacy peaks in the left side of MTD; Bracket; Insertion is not needed.
2. Tox Parameter Estimation				Eff Parameter Estimation
True (α0, α1) = (−3, 2.8)				True (β0, β1, β2) = (−3, 17, −18)
α̂0	α̂1		${\hat{\beta }}_0^L$	${\hat{\beta }}_1^L$	${\hat{\beta }}_0^Q$	${\hat{\beta }}_1^Q$	${\hat{\beta }}_2^Q$
−2.94(0.22)	2.66(0.77)		−2.65(0.25)	7.30(3.45)	−2.82(0.20)	15.55(2.56)	−16.39(3.98)
3. Model selection percentages: L – linear vs. Q – quadratic						L = 0.2%	Q = 99.2%
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.445, BMS: %ins=22.5%, BMA: %ins=22.2%
True Dose level	0.05	0.25	0.45	0.7	1.0	Dose inserted	Dose selected
True Eff/Tox	0.10/0.05	0.53/0.09	0.73/0.15	0.52/0.26	0.02/0.45
BMS insertion						0.399(0.060)	0.444(0.038)
BMA insertion						0.398(0.060)	0.444(0.036)
BMS % pts	0.057	0.102	0.490	0.126	0.183	0.043	0.473
BMA % pts	0.056	0.103	0.490	0.126	0.183	0.043	0.472
BMS % sel	0.001	0.005	0.857	0.004	0.000	0.131
BMA % sel	0.000	0.005	0.859	0.005	0.000	0.131
Scenario 4
1. Quadratic; Efficacy peaks in the right side of MTD; Bracket; Insertion is not needed.
2. Tox Parameter Estimation				Eff Parameter Estimation
True (α0, α1) = (−3, 4.2)				True (β0, β1, β2) = (−3, 13, −11)
α̂0	α̂1		${\hat{\beta }}_0^L$	${\hat{\beta }}_1^L$	${\hat{\beta }}_0^Q$	${\hat{\beta }}_1^Q$	${\hat{\beta }}_2^Q$
−2.98(0.22)	4.25(1.00)		−2.74(0.23)	7.45(1.78)	−2.88(0.24)	12.46(2.03)	−10.61(2.89)
3. Model selection percentages: L – linear vs. Q – quadratic						L = 1.5%	Q = 73.9%
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.465, BMS: %ins=30.3%, BMA: %ins=25.4%
True Dose level	0.05	0.25	0.5	0.75	1.0	Dose inserted	Dose selected
True Eff/Tox	0.08/0.06	0.39/0.12	0.68/0.29	0.64/0.54	0.27/0.77
BMS insertion						0.392(0.032)	0.407(0.107)
BMA insertion						0.388(0.024)	0.404(0.110)
BMS % pts	0.061	0.472	0.263	0.121	0.037	0.044	0.334
BMA % pts	0.061	0.481	0.260	0.121	0.037	0.040	0.348
BMS % sel	0.003	0.259	0.484	0.001	0.000	0.253
BMA % sel	0.003	0.286	0.495	0.001	0.000	0.215
Scenario 5
1. Quadratic; All doses are safe; The dose range covers the main efficacy-dose curve; Insertion is needed.
2. Tox Parameter Estimation				Eff Parameter Estimation
True (α0, α1) = (−3, 2)				True (β0, β1, β2) = (−3, 13, −11)
α̂0	α̂1		${\hat{\beta }}_0^L$	${\hat{\beta }}_1^L$	${\hat{\beta }}_0^Q$	${\hat{\beta }}_1^Q$	${\hat{\beta }}_2^Q$
−2.91(0.20)	1.71(0.65)		−2.76(0.24)	6.22(2.00)	−2.92(0.20)	12.50(2.02)	−10.65(2.44)
3. Model selection percentages: L – linear vs. Q – quadratic						L = 0.1%	Q = 97.7%
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.569, BMS: %ins=88.9%, BMA: %ins=84.0%
True Dose level	0.05	0.2	0.4	0.7	1.0	Dose inserted	Dose selected
True Eff/Tox	0.08/0.05	0.30/0.07	0.61/0.10	0.67/0.17	0.27/0.27
BMS insertion						0.587(0.202)	0.575(0.072)
BMA insertion						0.555(0.032)	0.576(0.071)
BMS % pts	0.056	0.057	0.120	0.175	0.250	0.341	0.403
BMA % pts	0.056	0.057	0.136	0.197	0.249	0.205	0.388
BMS % sel	0.000	0.001	0.020	0.143	0.006	0.830
BMA % sel	0.000	0.001	0.025	0.168	0.002	0.804
Scenario 6 (% early stop = 0.333)
1. Quadratic; All doses are too toxic; Insertion is needed.
2. Tox Parameter Estimation				Eff Parameter Estimation
True (α0, α1) = (−3, 4.2)				True (β0, β1, β2) = (−3, 17, −18)
α̂0	α̂1		${\hat{\beta }}_0^L$	${\hat{\beta }}_1^L$	${\hat{\beta }}_0^Q$	${\hat{\beta }}_1^Q$	${\hat{\beta }}_2^Q$
−2.94(0.14)	3.89(0.48)		−2.95(0.09)	5.82(0.70)	−2.81(0.17)	14.42(2.11)	−14.48(4.28)
3. Model selection percentages: L – linear vs. Q – quadratic						L = 1.0%	Q = 82.0%
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.401, BMS: %ins=84.3%, BMA: %ins=78.0%
True Dose level	0.6	0.7	0.8	0.9	1.0	Dose inserted	Dose selected
True Eff/Tox	0.67/0.38	0.52/0.49	0.28/0.59	0.09/0.69	0.02/0.77
BMS insertion						0.429(0.039)	0.462(0.081)
BMA insertion						0.427(0.036)	0.471(0.085)
BMS % pts	0.397	0.185	0.081	0.023	0.006	0.309	0.353
BMA % pts	0.444	0.173	0.087	0.020	0.004	0.272	0.372
BMS % sel	0.132	0.037	0.000	0.000	0.000	0.831
BMA % sel	0.192	0.034	0.000	0.000	0.000	0.775
Scenario 7
1. Linear; Insertion is not needed.
2. Tox Parameter Estimation				Eff Parameter Estimation
True (α0, α1) = (−3, 2.8)				True (β0, β1) = (−3, 6)
α̂0	α̂1		${\hat{\beta }}_0^L$	${\hat{\beta }}_1^L$	${\hat{\beta }}_0^Q$	${\hat{\beta }}_1^Q$	${\hat{\beta }}_2^Q$
−2.95(0.21)	2.75(0.70)		−3.04(0.21)	6.18(0.81)	−3.08(0.14)	10.10(1.00)	−6.29(1.36)
3. Model selection percentages: L – linear vs. Q – quadratic						L = 68.0%	Q = 2.7%
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.748, BMS: %ins=3.3%, BMA: %ins=2.3%
True Dose level	0.05	0.2	0.4	0.7	1.0	Dose inserted	Dose selected
True Eff/Tox	0.06/0.05	0.14/0.08	0.35/0.13	0.77/0.26	0.95/0.45
BMS insertion						0.573(0.039)	0.631(0.162)
BMA insertion						0.537(0.012)	0.629(0.159)
BMS % pts	0.056	0.073	0.402	0.278	0.185	0.007	0.465
BMA % pts	0.056	0.073	0.368	0.267	0.185	0.003	0.361
BMS % sel	0.000	0.004	0.271	0.647	0.058	0.020
BMA % sel	0.000	0.006	0.266	0.662	0.048	0.018
Scenario 8
1. Linear; All doses are safe but too inefficient; Insertion is needed.
2. Tox Parameter Estimation				Eff Parameter Estimation
True (α0, α1) = (−3, 1.5)				True (β0, β1) = (−3, 3)
α̂0	α̂1		${\hat{\beta }}_0^L$	${\hat{\beta }}_1^L$	${\hat{\beta }}_0^Q$	${\hat{\beta }}_1^Q$	${\hat{\beta }}_2^Q$
−2.96(0.17)	1.42(0.43)		−3.02(0.17)	3.02(0.41)	−3.09(0.13)	7.92(0.95)	−5.86(1.23)
3. Model selection percentages: L – linear vs. Q – quadratic						L = 86.4%	Q = 2.1%
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=1.435, BMS: %ins=63.8%, BMA: %ins=12.6%
True Dose level	0.1	0.3	0.55	0.75	1.0	Dose inserted	Dose selected
True Eff/Tox	0.06/0.05	0.11/0.07	0.21/0.10	0.32/0.13	0.50/0.18
BMS insertion						1.719(0.147)	1.221(0.374)
BMA insertion						1.743(0.108)	1.011(0.235)
BMS % pts	0.056	0.062	0.102	0.215	0.514	0.052	0.333
BMA % pts	0.056	0.062	0.109	0.254	0.510	0.008	0.477
BMS % sel	0.001	0.001	0.016	0.062	0.547	0.346
BMA % sel	0.000	0.003	0.020	0.131	0.771	0.075
Scenario 9
1. Plateau; Insertion is needed.
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.4, BMS: %ins=51.6%, BMA: %ins=39.9%
True Dose level	0.1	0.3	0.6	0.75	1.0	Dose inserted	Dose selected
True Eff/Tox	0.12/0.07	0.50/0.13	0.73/0.30	0.73/0.43	0.73/0.65
BMS insertion						0.453(0.030)	0.480(0.117)
BMA insertion						0.448(0.029)	0.480(0.126)
BMS % pts	0.062	0.456	0.184	0.153	0.063	0.081	0.245
BMA % pts	0.062	0.485	0.181	0.152	0.063	0.056	0.254
BMS % sel	0.004	0.181	0.336	0.023	0.000	0.456
BMA % sel	0.005	0.219	0.393	0.022	0.000	0.361
Scenario 10
1. Insensitive to the dose under a threshold and sensitive to the dose above the threshold; Insertion is needed.
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.598, BMS: %ins=45.5%, BMA: %ins=46.5%
True Dose level	0.1	0.3	0.4	0.75	1.0	Dose inserted	Dose selected
True Eff/Tox	0.08/0.07	0.23/0.13	0.35/0.17	0.97/0.43	1.00/0.65
BMS insertion						0.558(0.021)	0.479(0.110)
BMA insertion						0.556(0.021)	0.480(0.111)
BMS % pts	0.063	0.160	0.485	0.177	0.077	0.039	0.328
BMA % pts	0.064	0.160	0.483	0.177	0.077	0.040	0.321
BMS % sel	0.003	0.020	0.549	0.072	0.000	0.356
BMA % sel	0.004	0.021	0.530	0.072	0.000	0.373
Scenario 11
1. Increasing under a threshold and decreasing above the threshold; Insertion is needed.
4. Bayesian model selection (BMS) vs. Bayesian model average (BMA)
		OBD=0.500, BMS: %ins=81.0%, BMA: %ins=75.0%
True Dose level	0.05	0.2	0.4	0.7	1.0	Dose inserted	Dose selected
True Eff/Tox	0.07/0.05	0.20/0.08	0.55/0.14	0.55/0.29	0.27/0.50
BMS insertion						0.534(0.033)	0.515(0.077)
BMA insertion						0.533(0.032)	0.515(0.083)
BMS % pts	0.056	0.085	0.380	0.161	0.152	0.166	0.266
BMA % pts	0.056	0.084	0.404	0.161	0.152	0.143	0.270
BMS % sel	0.001	0.007	0.178	0.047	0.000	0.767
BMA % sel	0.000	0.009	0.203	0.071	0.000	0.717

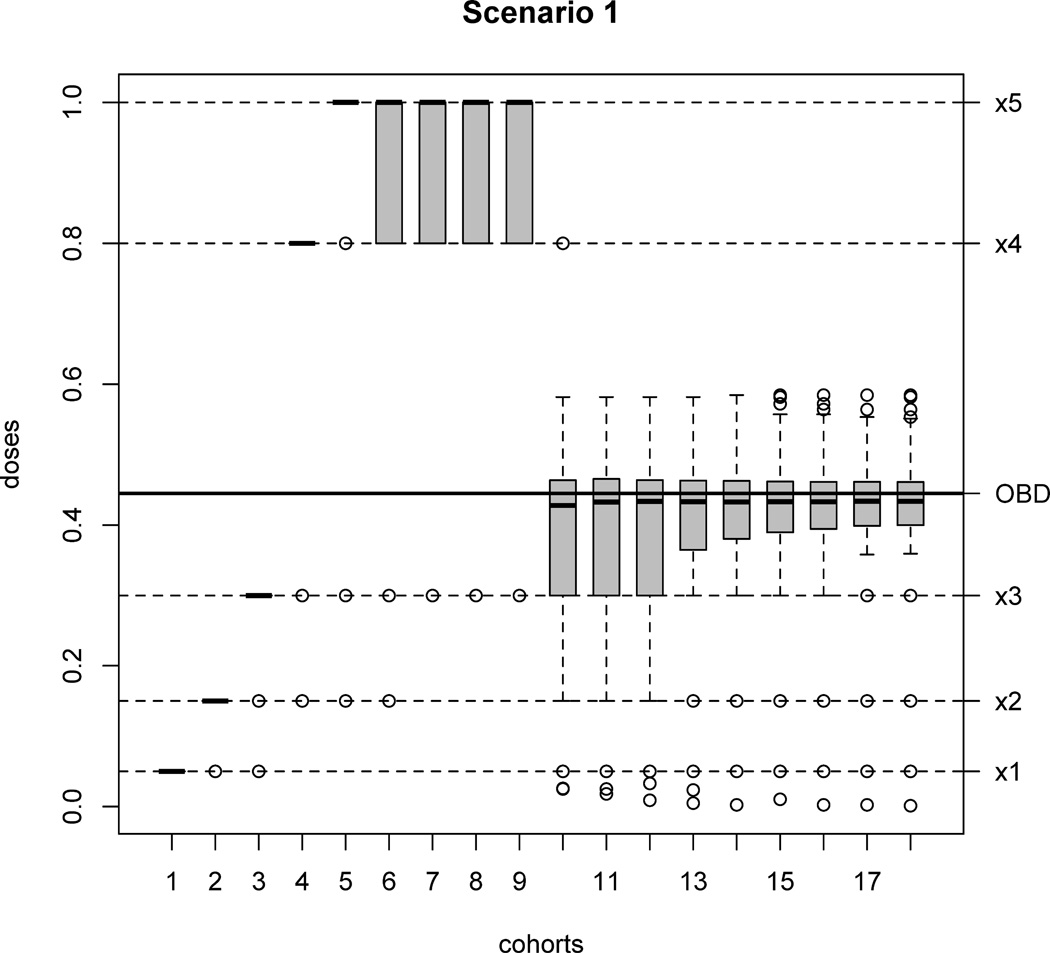
Scenarios 1–6 assume a true quadratic logistic model for the dose-efficacy relationship. In Scenario 1, the true OBD x_opt = 0.445 falls between doses x₃ = 0.3 and x₄ = 0.8. Apparently, in this scenario, new doses should be inserted because doses x₁, x₂ and x₃ have lower efficacy than the true OBD and x₄ and x₅ have higher toxicity than p_T (Figure 4, Scenario 1). Without a dose insertion rule, either an inefficacious dose or an excessively toxic dose could be chosen as OBD due to poor dose elicitation. By applying TEAMS, new doses with mean 0.440 are inserted among 97.6% of the simulated trials. The penalty of the mean inserted dose under the true model is 0.094, which is lower than that of all prespecified doses. Among all patients, 38.0% are treated at the inserted new doses. At the end of 96.7% of the simulated trials, an inserted dose is claimed to be the OBD. The mean selected OBD at the end of the trial is 0.434, close to the true OBD. Also, 99.0% of the trials correctly choose the quadratic logistic regression for the dose-efficacy curve at the end, and the posterior sample means of β under quadratic logistic model are close to the true values. Figure 6 shows a series of box-plots for the doses used on each cohort under Scenario 1. As simulated trials proceed, the mean of doses assigned to each cohort is getting closer to the true OBD and the variation is decreasing, i.e. the patients are closely treated around the true OBD.

Fig. 6.

Box-plots for doses used on each cohort across all 1,000 simulated trials under Scenario 1. It is clear when more cohorts are enrolled, more patients are put on doses closer to the true OBD.

Scenarios 2 and 3 have the same parameter specifications as Scenario 1, except that doses are closer to one another and more evenly spaced. From Figure 4, new doses are needed in Scenario 2, but not in Scenario 3. Correspondingly, the dose-insertion rate is 93.0% for Scenario 2, and only 22.5% for Scenario 3. The mean selected dose is 0.447 and 0.444, both close to the true OBD 0.445.

Scenarios 4 and 5 have wider bell-shaped curves for the dose-efficacy relationship compared to Scenarios 1–3 (Figure 4). The dose-insertion rates are 30.3% and 88.9% respectively, which is as expected since Scenario 4 does not need an insertion and Scenario 5 does. Notice that in Scenario 4 TEAMS has a relatively smaller proportion (73.9%) of selecting the true quadratic logistic model for the dose-efficacy relationship, compared to 97.7% in Scenario 5. Because only a few patients (15.8% in total) are assigned to the highest two doses due to their high toxicity in Scenario 4, TEAMS could not explore the dose spaces adequately, which in turn resulted in a less precise estimation. However, all doses in Scenario 5 are lower than MTD, and so all the doses are explored more frequently and a more precise estimation can be obtained.

In Scenario 6 all doses are higher than MTD, and hence 33.3% of the trials are stopped at an early stage according to Practical Rule 2. Among completed trials, the proportion of selecting the true quadratic model for efficacy is 82.0%. New doses with a mean 0.429 are inserted among 84.3% of the completed trials, and 83.1% end with selecting new doses as the OBD. The mean selected dose is 0.462, which is lower than the MTD and close to the true OBD (0.401). This scenario demonstrates the important safety feature of the TEAMS design. In words, TEAMS not only is able to stop the trial early due to toxicity, it also performs desirable dose insertion below all the prespecified doses and identify the correct OBD.

Unlike the previous six scenarios, Scenarios 7 and 8 assumes that the true dose-efficacy model is a linear logistic model. For Scenario 7, dose insertion is not needed. The insertion rate of Scenario 7 is 3.3%, which is expected. The mean selected OBD dose in Scenario 7 is 0.623, and the quadratic logistic model is selected at a very low rate (2.7%). In Scenario 8 all doses are safe but with low efficacy rates. Hence, higher doses are more desirable. For Scenario 8, the insertion rate is 63.8%, but only 34.6% of the trials select new doses as the OBD in the end. This is due to the challenge in estimating the dose-toxicity curve as the prespecified doses span a small range and data on these doses could not provide a good estimate of the entire curve. Therefore, the extrapolated new doses generally overshoot on toxicity due to poor extrapolation, although they would not be used once their high toxicities are recognized by our model. Due to a relatively small maximum sample size (N = 54), the simulated trials stop frequently before a second, more appropriate dose could be inserted. If a larger N is allowed, the dose insertion algorithm would perform better with a more appropriate new dose (results not shown).

In Scenarios 9–11 the dose-response curves for efficacy are based on neither linear nor quadratic logistic models. They are “irregularly” shaped and used to test the robustness of TEAMS. Scenario 9 has a plateau pattern after a change point; Scenario 10 consists of a change-point model in which a slowly ascending curve is joined with a fast ascending curve; Scenario 11 combines an ascending curve with a descending curve. In all three scenarios, dose insertion is needed. Under TEAMS with model selection, the average insertion rates are 51.6%, 45.5% and 81.0%, respectively. The mean selected doses are close to the true OBDs in all three scenarios. Therefore, TEAMS is quite robust even though the underlying dose-efficacy model varies from the linear or quadratic logistic model.

Comparing the results of TEAMS based on model selection and BMA, we can see that the performance of two methods are almost the same in terms of the mean selected OBD, patients allocation, and the percentage of being selected as the OBD. In general, insertion rates of TEAMS with model selection are slightly higher than that of the BMA-based design, because the latter has a wider I_C(x) due to the inflated variance.

In addition, to evaluate the role of model selection in TEAMS, we apply the dose-insertion design without model selection for the efficacy model on Scenarios 2 and 8, which are the representatives for scenarios with the quadratic logistic efficacy model and the linear logistic efficacy model, respectively. The results are shown in Table D.1 of Web Appendix D. We implement TEAMS without model selection in Step II2 and always assume a linear logistic model or a quadratic logistic model for the dose-efficacy relationship. We find that when the efficacy model is mis-specified, e.g., using the linear logistic model in Scenario 2, TEAMS without model selection fails to capture the non-monotone pattern of the efficacy model and performs poorly in dose insertion. Similarly, poor performance is seen for Scenario 8 when using the quadratic logistic model for inference. For example, TEAMS without model selection exhibits an insertion rate of only 1.6%. This is because with a quadratic model TEAMS believes that efficacy decreases when dose level x > 1. These results show the critical role of model selection in the TEAMS design.

5 Discussion

We propose a new Bayesian adaptive dose insertion design, TEAMS, for phase I/II oncology trials that account for novel treatments. The dose-insertion procedure based on both efficacy and toxicity enables us to locate more desirable doses. Bayesian model selection during the trial allows the dose-efficacy relationship to be adapted between linear and quadratic logistic model, resulting in high flexibility and much improved performance. Simulation results show that the TEAMS design has superior operating characteristics. High dose-insertion rates are observed in scenarios that are urgent for insertion, while much lower rates in scenarios in which dose insertion is not needed. This means TEAMS is stable and will not insert new doses if not needed.

One advantage of the TEAMS design is its “add-on” property so that it can be applied to any sensible trial design.

The TEAMS design could be considered as a penalty-based method. Clearly, the performance of TEAMS heavily depends on the penalty. Although we choose penalty based on Euclidean distance, one can use other reasonable alternative penalties. Choosing an appropriate penalty function has to be done for individual trials and through discussion between clinicians and statisticians. For different diseases and drugs, different trade-off between efficacy and toxicity might be allowed. This can be realized by imposing different weights to toxicity and efficacy in the penalty function. Fortunately, changes on the penalty function is a separate task and does not affect the overall statistical design illustrated in Boxes 1 and 2.