SPReM: Sparse Projection Regression Model For High-dimensional Linear Regression

Abstract

The aim of this paper is to develop a sparse projection regression modeling (SPReM) framework to perform multivariate regression modeling with a large number of responses and a multivariate covariate of interest. We propose two novel heritability ratios to simultaneously perform dimension reduction, response selection, estimation, and testing, while explicitly accounting for correlations among multivariate responses. Our SPReM is devised to specifically address the low statistical power issue of many standard statistical approaches, such as the Hotelling’s T² test statistic or a mass univariate analysis, for high-dimensional data. We formulate the estimation problem of SPREM as a novel sparse unit rank projection (SURP) problem and propose a fast optimization algorithm for SURP. Furthermore, we extend SURP to the sparse multi-rank projection (SMURP) by adopting a sequential SURP approximation. Theoretically, we have systematically investigated the convergence properties of SURP and the convergence rate of SURP estimates. Our simulation results and real data analysis have shown that SPReM out-performs other state-of-the-art methods.

1 Introduction

Multivariate regression modeling with a multivariate response y ∈ ℝ^q and a multivariate covariate x ∈ ℝ^p is a standard statistical tool in modern high-dimensional inference, with wide applications in various large-scale applications, such as genome-wide association studies (GWAS) and neuroimaging studies. For instance, in GWAS, our primary problem of interest is to identify genetic variants (x) that cause phenotypic variation (y). Specifically, in imaging genetics, multivariate imaging measures (y), such as volumes of regions of interest (ROIs), are phenotypic variables, whereas covariates (x) include single nucleotide polymorphisms (SNPs), age, and gender, among others. The joint analysis of imaging and genetic data may ultimately lead to discoveries of genes for neuropsychiatric and neurological disorders such as autism and schizophrenia (Scharinger et al., 2010; Paus, 2010; Peper et al., 2007; Chiang et al., 2011a,b). Moreover, in many neuroimaging studies, there is a great interest in the use of imaging measures (x), such as functional imaging data and cortical and subcortical structures, to predict multiple clinical and/or behavioral variables (y) (Knickmeyer et al., 2008; Lenroot and Giedd, 2006). This motivates us to systematically investigate a multivariate linear model with a multivariate response y and a multivariate covariate x.

Throughout this paper, we consider n independent observations (y_i, x_i) and a Multivariate Linear Model (MLM) given by

$$\mathbf{Y}=\mathbf{X}\mathbf{B}+\mathbf{E},\text{or}{\mathbf{y}}_i={\mathbf{B}}^T{\mathbf{x}}_i+{\mathbf{e}}_i,$$ (1)

where Y = (y₁, …, y_n)^T, X = (x₁, …, x_n)^T, and B = (β_jl) is a p × q coefficient matrix with rank(B) = r^* ≤ min(p, q). Moreover, the error term E = (e₁, …, e_n)^T has E(e_i) = 0 and Cov(e_i) = Σ_R for all i, where Σ_R is a q × q matrix. Many hypothesis testing problems of interest, such as comparison across groups, can often be formulated as

$$H_0:\mathbf{C}\mathbf{B}={\mathbf{B}}_0\mathrm{v}.\mathrm{s}.H_1:\mathbf{C}\mathbf{B}\ne {\mathbf{B}}_0,$$ (2)

where C is an r × p matrix and B₀ is an r × q matrix. Without loss of generality, we center the covariates, standardize the responses, and assume rank(C) = r.

We focus on a specific setting that q is relatively large, but p is relatively small. Such a setting is general enough to cover two-sample (or multi-sample) hypothesis testing for high-dimensional data (Chen and Qin, 2010; Lopes et al., 2011). There are at least three major challenges including (i) a large number of regression parameters, (ii) a large covariance matrix, and (iii) correlations among multivariate responses. When the number of responses and the number of covariates are even moderately high, fitting the conventional MLM usually requires estimating a p × q matrix of regression coefficients, whose number pq can be much larger than n. Although accounting for complicated correlations among multiple responses is important for improving the overall prediction accuracy of multivariate analysis (Breiman and Friedman, 1997; Cook et al., 2010), it requires estimating q(q+1)/2 unknown parameters in an unstructured covariance matrix.

There is a great interest in the development of efficient methods for handling MLMs with large q. Four popular traditional methods include the mass univariate analysis, the Hotelling’s T² test, partial least squares regression, and dimension reduction methods. As pointed by Klei et al. (2008) and many others, testing each response variable individually in the mass univariate analysis requires a substantial penalty of controlling for multiplicity. The Hotelling’s T² test is not well-defined, when q > n. Even when q ≤ n, the power of the Hotelling’s T² can be very low if q is nearly as large as n. Partial least squares regression (PLSR) aims to find a linear regression model by projecting y and x to a smaller latent space (Chun and Keles, 2010; Krishnan et al., 2011), but it focuses on prediction and classification. Although dimension reduction techniques, such as principal component analysis (PCA), are considered to reduce the dimensions of both the response and covariates (Formisano et al., 2008; Kherif et al., 2002; Rowe and Hoffmann, 2006; Teipel et al., 2007), most of the methods ignore the variation of covariates and their associations with responses. Thus, such methods can be sub-optimal for our problem.

Some recent developments primarily include regularization methods and envelope models (Peng et al., 2010; Tibshirani, 1996; Breiman and Friedman, 1997; Cook et al., 2010, 2013; Lin et al., 2012). Cook, Li and Chiaromonte (2010) developed a powerful envelope modeling framework for MLMs. Such envelope methods use dimension reduction techniques to remove the immaterial information, while achieving efficient estimation of the regression coefficients by accounting for correlations among the response variables. However, the existing envelope methods are limited to the n > max(p, q) scenario. Recently, much attention has been given to regularization methods for enforcing sparsity in B (Peng et al., 2010; Tibshirani, 1996). These regularization methods, however, do not provide a standard inference tool (e.g., standard deviation) on the regression coefficient matrix B. Lin et al. (2012) developed a projection regression model (PRM) and its associated estimation procedure to assess the relationship between a multivariate phenotype and a set of covariates without providing any theoretical justification.

This paper presents a new general framework, called sparse projection regression model (SPReM), for simultaneously performing dimension reduction, response selection, estimation, and testing in a general high dimensional MLM setting. We introduce two novel heritability ratios, which extend the idea of principal components of heritability from familial studies (Klei et al., 2008; Ott and Rabinowitz, 1999), for MLM and overcome over-fitting and noise accumulation in high dimensional data by enforcing the sparsity constraint. We develop a fast algorithm for both sparse unit rank projection (SURP) and sparse multi-rank projection (SMURP). Furthermore, a test procedure based on the wild-bootstrap method is proposed, which leads to a single p–value for the test of an association between all response variables and covariates of interest, such as genetic markers. Simulations show that our method can control the overall Type I error well, while achieving high statistical power.

Section 2 of this paper introduces the SPReM framework. We introduce a novel deflation procedure to extract the most informative directions for testing hypotheses of interest. Simulation studies and an imaging genetic example are used to examine the finite sample performance of SPReM in Section 3. We present concluding remarks in Section 4.

2 Sparse Projection Regression Model

2.1 Model Setup and Heritability Ratios

We introduce SPReM as follows. The key idea of our SPReM is to appropriately project y_i in a high-dimensional space onto a low-dimensional space, while accounting for the correlation structure Σ_R among the response variables and the hypothesis test in (2). Let W = [w₁, …, w_k] be a q × k nonrandom and unknown direction matrix, where w_j are q × 1 vectors. A projection regression model (PRM) is given by

$${\mathbf{W}}^T{\mathbf{y}}_i={(\mathbf{B}\mathbf{W})}^T{\mathbf{x}}_i+{\mathbf{W}}^T{\mathbf{e}}_i={\mathit{\beta }}_{\mathbf{w}}^T{\mathbf{X}}_i+{\epsilon }_i,$$ (3)

where β_w is a p × k regression coefficient matrix and the random vector ε_i has E(ε_i) = 0 and Cov(ε_i) = W^TΣ_RW. When k = 1, PRM reduces to the pseduo-trait model considered in (Amos et al., 1990; Amos and Laing, 1993; Klei et al., 2008; Ott and Rabinowitz, 1999). If k << min(n, q) and W were known, then one could use likelihood (or estimating equation) based methods to efficiently estimate β_w, and (2) would reduce approximately to

$$H_{0W}:\mathbf{C}{\mathit{\beta }}_{\mathbf{w}}={\mathbf{b}}_0\mathrm{v}.\mathrm{s}.H_{1W}:\mathbf{C}{\mathit{\beta }}_{\mathbf{w}}\ne {\mathbf{b}}_0,$$ (4)

where Cβ_w = CBW and b₀ = B₀W. In this case, the number of null hypotheses in (4) is much smaller than that of (2). It is also expected that different W’s strongly influence the statistical power of testing the hypotheses in (2).

A fundamental question arises “how do we determine an ‘optimal’ W to achieve good statistical power of testing (2)?” To determine W, we develop a novel deflation approach to sequentially determine each column of W at a time starting from w₁ to w_k. We focus on how to determine w₁ below and then discuss how to extend it to the scenario with k > 1.

To determine an optimal w₁, we consider two principles. The first principle is to maximize the mean value of the square of the signal-to-noise ratio, called the heritability ratio, for model (3). For each i, the signal-to-noise ratio in model (3) is defined as the ratio of mean to standard deviation of a signal or measurement w^T y_i, denoted by SNR_i = w^TB^T x_i/(w^TΣ_Rw)^0.5. Thus, the heritability ratio (HR) is given by

$$\mathrm{H}\mathrm{R}(\mathbf{w})=n^{-1}\sum _{i=1}^n{\text{SNR}}_i^2=\frac{{\mathbf{w}}^T{\mathbf{B}}^T{S}_X\mathbf{B}\mathbf{w}}{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}},$$ (5)

where $S_X=n^{-1}{\sum }_{i=1}^n{\mathbf{x}}_i{\mathbf{x}}_i^T$. The HR has several important interpretations. If the x_i are independently and identically distributed (i.i.d) with E(x_i) = 0 and Cov(x_i) = Σ_X, then as n → ∞, we have

$$\mathrm{H}\mathrm{R}(\mathbf{w}){\to }^p\frac{{\mathbf{w}}^T{\mathbf{B}}^T{\mathrm{\Sigma }}_X\mathbf{B}\mathbf{w}}{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}}=\frac{\text{Var}({\mathbf{w}}^T{\mathbf{B}}^T{\mathbf{x}}_i)}{\text{Var}({\epsilon }_i)},$$

where →^p denotes convergence in probability. Thus, HR(w) is close to the ratio of the variance of signal w^TB^T x_i to that of noise ε_i. Moreover, HR(w) is close to the heritability ratio considered in (Amos et al., 1990; Amos and Laing, 1993; Klei et al., 2008; Ott and Rabinowitz, 1999) for familial studies, but we define HR from a totally different perspective. With such new perspective, one can easily define HR for more general designs, such as cross-sectional or longitudinal design. One might directly maximize HR(w) to calculate an ‘optimal’ w₁, but such a w₁ can be sub-optimal for testing the hypotheses in (2) as discussed below.

The second principle is to explicitly account for the hypotheses in (2) under model (1) and the reduced ones in (4) under model (3). We define four spaces associated with the null and alternative hypotheses of (2) and (4) as follows:

$$S_{H_0}=\{\mathbf{B}:\mathbf{C}\mathbf{B}={\mathbf{B}}_0\},S_{H_W}=\{\mathbf{B}:\mathbf{C}\mathbf{B}\mathbf{W}={\mathbf{B}}_0\mathbf{W}\},S_{H_1}=\{\mathbf{B}:\mathbf{C}\mathbf{B}\ne {\mathbf{B}}_0\},S_{H_{1W}}=\{\mathbf{B}:\mathbf{C}\mathbf{B}\mathbf{W}\ne {\mathbf{B}}_0\mathbf{W}\}.$$

It can be shown that they satisfy the following relationship:

$$S_{H_0}\subset S_{H_W}\text{and}{S}_{H_{1W}}\subset S_{H_1}\text{for any}\mathbf{W}\ne \mathbf{0}.$$

Due to potential information loss during dimension reduction, both S_HW − S_H0 and S_H1 − S_H1W may not be the empty set, but we need to choose W such that S_H1 − S_H1W ≈ ø. The next question is how to achieve this.

We consider a data transformation procedure. Let C₁ be a (p−r) × p matrix such that

$$\text{rank}[{\mathbf{C}}^T{\mathbf{C}}_1^T]=p\text{and}\mathbf{C}{\mathbf{C}}_1^T=\mathbf{0}.$$ (6)

Let $\mathbf{D}={[{\mathbf{C}}^T{\mathbf{C}}_1^T]}^T$ be a p × p matrix and ${\tilde{\mathbf{x}}}_i=({\tilde{\mathbf{x}}}_{i1}^T,{\tilde{\mathbf{x}}}_{i2}^T)={\mathbf{D}}^{-T}{\mathbf{x}}_i$ be a p × 1 vector, where x̃_i1 and x̃_i2 are, respectively, the r × 1 and (p − r) × 1 subvectors of x̃_i. We define $\tilde{\mathbf{B}}={[{\tilde{\mathbf{B}}}_1^T{\tilde{\mathbf{B}}}_2^T]}^T=\mathbf{D}\mathbf{B}$, or B = D⁻¹B̃, where B̃₁ and B̃₂ are, respectively, the first r rows and the last p − r rows of B̃. Therefore, model (3) can be rewritten as

$${\mathbf{W}}^T{\mathbf{y}}_i={({\mathbf{D}}^{-1}\tilde{\mathbf{B}}\mathbf{W})}^T{\mathbf{x}}_i+{\mathbf{W}}^T{\mathbf{e}}_i={\mathbf{W}}^T{({\tilde{\mathbf{B}}}_1-{\mathbf{B}}_0)}^T{\tilde{\mathbf{x}}}_{i1}+{\mathbf{W}}^T{\mathbf{B}}_0^T{\tilde{\mathbf{x}}}_{i1}+{\mathbf{W}}^T{\tilde{\mathbf{B}}}_2^T{\tilde{\mathbf{x}}}_{i2}+{\mathbf{W}}^T{\mathbf{e}}_i.$$ (7)

In (7), due to (6), we only need to consider the transformed covariate vector x̃_i1, which contains useful information associated with B̃₁ − B₀ = CB − B₀.

We define a generalized heritability ratio based on model (7). Specifically, for each i, we define a new signal-to-noise ratio as the ratio of mean to standard deviation of signal w^T (B̃₁ − B₀)^T x̃_i1 + w^T e_i, denoted by SNR_i,C = w^T (B̃₁ − B₀)^T x̃_i1/(w^TΣ_Rw)^0.5. The generalized heritability ratio is then defined as

$$\text{GHR}(\mathbf{w};\mathbf{C})=n^{-1}\sum _{i=1}^n{\text{SNR}}_{i,\mathbf{C}}^2=\frac{{\mathbf{w}}^T{({\tilde{\mathbf{B}}}_1-{\mathbf{B}}_0)}^T{S}_{{\tilde{X}}_1}({\tilde{\mathbf{B}}}_1-{\mathbf{B}}_0)\mathbf{w}}{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}},$$ (8)

where $S_{{\tilde{X}}_1}=n^{-1}{\sum }_{i=1}^n{\tilde{\mathbf{x}}}_{i1}{\tilde{\mathbf{x}}}_{i1}^T$. If the x_is are random, then we have

$$\text{GHR}(\mathbf{w};\mathbf{C}){\to }^p\frac{{\mathbf{w}}^T{({\tilde{\mathbf{B}}}_1-{\mathbf{B}}_0)}^T\text{Cov}({\tilde{\mathbf{x}}}_{i1})({\tilde{\mathbf{B}}}_1-{\mathbf{B}}_0)\mathbf{w}}{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}}=\frac{{\mathbf{w}}^T{\mathrm{\Sigma }}_C\mathbf{w}}{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}},$$ (9)

where Σ_C = (B̃₁ − B₀)^T (D^−TΣ_XD⁻¹)_(r,r)(B̃₁ − B₀), and (D^−TΣ_XD⁻¹)_(r,r) is the upper r × r submatrix of D^−TΣ_XD⁻¹. Particularly, if C = [I_r 0], then Σ_C reduces to w^T (B̃₁ − B₀)^T (Σ_X)_(1,1)(B̃₁ − B₀)w, in which (Σ_X)_(1,1) is the upper r × r submatrix of Σ_X. Thus, GHR(w; C) can be interpreted as the ratio of the variance of w^T (B̃₁ − B₀)^T x̃_i1 relative to that of w^T e_i. We propose to calculate an optimal w_* as follows:

$${\mathbf{w}}_{*}=\underset{\mathbf{w}}{\text{argmax}}\text{GHR}(\mathbf{w};\mathbf{C}).$$ (10)

We expect that such an optimal w_* can substantially reduce the size of both S_H1 − S_H1W and S_HW − S_H0 and thus the use of such an optimal w_* can enhance the power of testing the hypotheses in (2). Without loss of generality, we assume B₀ = 0 from now on.

We consider a simple example to illustrate the appealing properties of GHR(w; C).

Example We consider model (1) with p = q = 5 and want to test the nonzero effect of the first covariate on all five responses. In this case, r = 1, C = (1, 0, 0, 0, 0), B₀ = (0, 0, 0, 0, 0), and D = I₅, which is a 5 × 5 identity matrix. Without loss of generality, it is assumed that (Σ_X)_(1,1) = 1.

We consider three different cases of Σ_R and B. In the first case, we set ${\mathrm{\Sigma }}_R=\text{diag}({\sigma }_1^2,\cdots ,{\sigma }_5^2)$ and the first column of B to be (1, 0, 0, 0, 0). It follows from (8) that

$$\text{GHR}(\mathbf{w};\mathbf{C})=\frac{w_1^2}{{\sigma }_1^2{w}_1^2+{\sigma }_2^2{w}_2^2+\cdots +{\sigma }_5^2{w}_5^2}\text{and}{\mathbf{w}}_{*}^T=(c_0,0,0,0,0),$$

where c₀ is any nonzero scalar. Therefore, w_* picks out the first response, which is the sole one that is associated with the first covariate.

In the second case, we set ${\mathrm{\Sigma }}_R=\text{diag}({\sigma }_1^2,\cdots ,{\sigma }_5^2)$ with ${\sigma }_1^2\ge \cdots \ge {\sigma }_5^2$ and the first row of B to be (1, 1, 0, 0, 0). It follows from (8) that

$$\text{GHR}(\mathbf{w};\mathbf{C})=\frac{{(w_1+w_2)}^2}{{\sigma }_1^2{w}_1^2+{\sigma }_2^2{w}_2^2+\cdots +{\sigma }_5^2{w}_5^2}\text{and}{\mathbf{w}}_{*}^T=(\frac{{\sigma }_2^2}{{\sigma }_1^2}{c}_0,c_0,0,0,0),$$

where c₀ is any nonzero scalar. Therefore, w_* picks out both the first and second response with larger weight on the second component. This is desirable since β₁₁ and β₂₁ are equal in terms of strength of effect and the noise level for the second response is smaller than that of the first one.

In the third case, we set the first row of B to be (1, 1, 0, 0, 0) and the first and second columns of Σ_R are set as σ²(1, ρ, 0, 0, 0) and σ²(ρ, 1, 0, 0, 0), respectively. It follows from (8) that

$$\text{GHR}(\mathbf{w};\mathbf{C})=\frac{{(w_1+w_2)}^2}{{\sigma }^2{w}_1^2+2{\sigma }_2^2\rho w_1{w}_2+{\sigma }_2^2{w}_2^2+Q(w_3,w_4,w_5)}\text{and}{\mathbf{w}}_{*}^T=(c_0,c_0,0,0,0),$$

where Q(w₃,w₄,w₅) is a non-negative quadratic form of (w₃,w₄,w₅). Thus, the optimal w_* chooses the first two responses with equal weight, since they are correlated with each other with same variance and β₁₁ = β₂₁ = 1.

For high dimensional data, it is difficult to accurately estimate w_*, since the sample covariance matrix estimator Σ̂_R can be either ill-conditioned or not invertible for large q > n. One possible solution is to focus only on a small number of important features for testing. However, a naive search for the best subset is NP-hard. We develop a penalized procedure to address these two problems, while obtaining a relatively accurate estimate of w. Let Σ̃_R and Σ̂_C be, respectively, estimators of Σ_R and Σ_C. Here we use Σ̃_R to denote the covariance estimator other than sample covariance matrix Σ̂_R. To obtain Σ̂_C, we need to plug B̂, an estimator of B, into Σ_C. Without loss of generality, we consider the ordinary least squares estimate of B. By imposing a sparse structure on w₁, we recast the optimization problem as

$$\text{max}\{\frac{{\mathbf{w}}^T{\widehat{\mathrm{\Sigma }}}_C\mathbf{w}}{{\mathbf{w}}^T{\tilde{\mathrm{\Sigma }}}_R\mathbf{w}}\}\mathrm{s}.\mathrm{t}.{\Vert \mathbf{w}\Vert }_1\le t,$$ (11)

where ‖·‖₁ is the L₁ norm and t > 0.

2.2 Sparse Unit Rank Projection

When r = 1, we call the problem in (10) as the unit rank projection problem and its corresponding sparse version in (11) as the sparse unit rank projection (SURP) problem. Actually, many statistical problems, such as two-sample test and marginal effect test problems, can be formulated as the unit rank projection problem (Lopes et al., 2011). We consider two cases including ℓ = (CB)^T = 0 and ℓ = (CB)^T ≠ 0. When ℓ = (CB)^T = 0, the solution set of (8) is trivial, since any w ≠ 0 is a solution of (8). As discussed later, this property is extremely important for controlling the type I error rate.

When ℓ = (CB)^T ≠ 0, (8) reduces to the following optimization problem:

$${\mathbf{w}}_{*}=\underset{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}=1}{\text{argmax}}{\mathbf{w}}^T{\mathrm{\Sigma }}_C\mathbf{w}=\underset{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}\le 1}{\text{argmax}}{\mathbf{w}}^T{\mathrm{\Sigma }}_C\mathbf{w}=\underset{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}\le 1}{\text{argmax}}{\mathbf{w}}^T\ell ,$$ (12)

where ℓ is the sole eigenvector of Σ_C, since Σ_C is a unit-rank matrix. To impose an L₁ sparsity on w, we propose to solve the penalized version of (12) given by

$${\mathbf{w}}_{\lambda }=\underset{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}\le 1}{\text{argmax}}{\mathbf{w}}^T\ell -\lambda {\Vert \mathbf{w}\Vert }_1.$$ (13)

Although (13) can be solved by using some standard convex programming methods, such methods are too slow for most large-scale applications, such as imaging genetics. We therefore reformulate our problem below. Without special saying, we focus on ℓ = (CB)^T ≠ 0.

By omitting a scaling factor ${\Vert {\mathrm{\Sigma }}_R^{-1/2}\ell \Vert }_2$, which will not affect the generalized heritability ratio, we note that (12) is equivalent to the following

$${\mathbf{w}}_0=\underset{\mathbf{w}}{\text{argmin}}\frac{1}{2}{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}-{\mathbf{w}}^T\ell .$$ (14)

We consider a penalized version of (14) as

$${\mathbf{w}}_{0,\lambda }=\underset{\mathbf{w}}{\text{argmin}}f(\mathbf{w})=\underset{\mathbf{w}}{\text{argmin}}\frac{1}{2}{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}-{\mathbf{w}}^T\ell +\lambda {\Vert \mathbf{w}\Vert }_1.$$ (15)

A nice property of (15) is that it does not explicitly involve the inequality constraint, which leads to a fast computation. We define (14) as the oracle, since w_λ converges to w₀ as λ → 0. It can be shown that

$${\mathbf{w}}_0={\sum }_R^{-1}\ell .$$ (16)

We obtain an equivalence between (15) and (13) as follows.

Theorem 2.1 Problem (15) is equivalent to problem (13) and w_λ ∝ w_0,λ.

We discuss some connections between our SURP problem and the optimization problem considered in Fan et al. (2012) for performing classification in high dimensional space.

However, rather than recasting the problem as in (12) and then (15), they formulate it as

$${\mathbf{w}}_c=\underset{{\Vert \mathbf{w}\Vert }_1\le c,{\mathbf{w}}^T\ell =1}{\text{argmin}}{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w},$$

which can further be reformulated as

$${\mathbf{w}}_{\lambda }=\underset{{\mathbf{w}}^T\ell =1}{\text{argmin}}\frac{1}{2}{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}+\lambda {\Vert \mathbf{w}\Vert }_1.$$ (17)

Since (17) involves a linear equality constraint, they replace it by a quadratic penalty as

$${\mathbf{w}}_{\lambda ,\gamma }=\text{argmin}\frac{1}{2}{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}+\lambda {\Vert \mathbf{w}\Vert }_1+\frac{1}{2}\gamma {({\mathbf{w}}^T\ell -1)}^2.$$ (18)

This new formulation requires the simultaneously tuning of λ and γ, which can be computationally intensive. However, in Fan et al. (2012), they stated that the solution to (18) is not sensitive to γ, since solution is always in the direction of ${\mathrm{\Sigma }}_R^{-1}\mathbf{\ell }$ when λ = 0, as validated by simulations. Their formulation (17) is close to the formulation (15). This result sheds some light on why w_λ,γ is not sensitive to γ. Finally, we can show that the solution path to (15) has a piecewise linear property.

Proposition 2.2 Let ℓ ∈ ℝ^q be a constant vector and Σ_R be positive definite. Then, w_0,λ is a continuous piecewise linear function in λ.

We derive a coordinate descent algorithm to solve (15). Without loss of generality, suppose that $\mathbf{w}={({\tilde{w}}_1,{\tilde{\mathbf{w}}}_2^T)}^T={({\tilde{w}}_1,\cdots ,{\tilde{w}}_q)}^T$, w̃_j for all j ≥ 2 are given, and we need to optimize (15) with respect to w̃₁. In this case, the objective function (15) becomes

$$f_1({\tilde{w}}_1,{\tilde{\mathbf{w}}}_2)=\frac{1}{2}({\tilde{w}}_1,{\tilde{\mathbf{w}}}_2^T)\left(\begin{array}{cc}{\sigma }_{11}& {\mathrm{\Sigma }}_{12}\\ {\mathrm{\Sigma }}_{21}& {\mathrm{\Sigma }}_{22}\end{array}\right)\left(\begin{array}{c}{\tilde{w}}_1\\ {\tilde{\mathbf{w}}}_2\end{array}\right)-({\tilde{\ell }}_1{\tilde{w}}_1+{\tilde{\ell }}_2^T{\tilde{\mathbf{w}}}_2)+\lambda |{\tilde{w}}_1|+\lambda {\Vert {\tilde{\mathbf{w}}}_2\Vert }_1,$$

where $\mathbf{\ell }=({\tilde{\ell }}_1,{\tilde{\mathbf{\ell }}}_2^T)$ and σ₁₁, Σ₁₂, and Σ₂₂ are subcomponents of Σ_R. Then, by taking the sub-gradient with respect to w̃₁, we have

$$f_1^{\prime }({\tilde{w}}_1,{\tilde{\mathbf{w}}}_2)={\tilde{w}}_1{\sigma }_{11}+{\mathrm{\Sigma }}_{12}{\tilde{\mathbf{w}}}_2+\lambda {\mathrm{\Gamma }}_1-{\tilde{\ell }}_1$$

where Γ₁ = sign(w̃₁) for w̃₁ ≠ 0 and is between −1 and 1 if w̃₁ = 0. Let S_λ(t) = sign(t)(|t|−λ)⁺ be the soft-thresholding operator. By setting $f_1^{\prime }({\tilde{w}}_1,{\tilde{\mathbf{w}}}_2)=0$, we have w̃₁ = S_λ(ℓ̃₁ − Σ₁₂w̃₂)/σ₁₁. Based on this result, we can obtain a coordinate descent algorithm as follows.

Algorithm 1

1. Initialize w at a starting point w⁽⁰⁾ and set m = 0.

2. Repeat:

   • (b.1) Increase m by 1: m ← m + 1
   • (b.2) for j ∈ 1, …, p, if ${\tilde{w}}_j^{(m-1)}=0$, then set ${\tilde{w}}_j^{(m)}=\mathit{0}$; otherwise: ${\tilde{w}}_j^{(m)}=\text{argmin}f({\tilde{w}}_1^{(m)},\cdots ,{\tilde{w}}_{j-1}^{(m)},{\tilde{w}}_j,{\tilde{w}}_{j+1}^{(m-1)},\cdots ,{\tilde{w}}_q^{(m-1)})$

3. Until numerical convergence: we require |f(w^(m))−f(w^(m−1))| to be sufficiently small.

2.3 Extension to Multi-rank Cases

In this subsection, we extend the sparse unit rank projection procedure to handle multiple rank test problems when r > 1. We propose the k–th projection direction as the solution to the following problem:

$$\text{argmax}\frac{{\mathbf{w}}_k^T{\mathrm{\Sigma }}_C{\mathbf{w}}_k}{{\mathbf{w}}_k^T{\mathrm{\Sigma }}_R{\mathbf{w}}_k}\mathrm{s}.\mathrm{t}.{\mathbf{w}}_k^T{\mathrm{\Sigma }}_R{\mathbf{w}}_j=0,{\forall }_j<k.$$ (19)

It can be shown that (19) is equivalent to

$$\text{argmax}{\mathbf{w}}_k^T{\mathrm{\Sigma }}_C{\mathbf{w}}_k\mathrm{s}.\mathrm{t}.{\mathbf{w}}_k^T{\mathrm{\Sigma }}_R{\mathbf{w}}_k\le 1,{\mathbf{w}}_k^T{\mathrm{\Sigma }}_R{\mathbf{w}}_j=0,{\forall }_j<k.$$ (20)

Following the reasoning in Witten and Tibshirani (2011), we recast (20) into an equivalent problem.

Proposition 2.3 Problem (20) is equivalent to the following problem:

$$\underset{\mathbf{w}}{\text{argmax}}\frac{{\mathbf{w}}^T{\mathbf{B}}^T{\mathbf{C}}^T{\mathrm{\Sigma }}_{11}^{1/2}{P}_{\perp }^{k-1}{\mathrm{\Sigma }}_{11}^{1/2}\mathbf{C}\mathbf{B}\mathbf{w}}{{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}},$$ (21)

where $P_{\perp }^{k-1}$ is the projection matrix onto the orthogonal space spanned by $\{{\mathrm{\Sigma }}_{11}^{1/2}{\mathbf{\text{CBw}}}_j,1\le j\le k-1\}$, in which Σ₁₁ = (D^−TΣ_X D⁻¹)_(r,r).

Based on Proposition 2.3, we consider several strategies of imposing the sparsity structure on w_k. A simple strategy is to consider the following problem given by

$$\underset{{\mathbf{w}}_k}{\text{argmax}}{\mathbf{w}}_k^T{\mathrm{\Sigma }}_C^k{\mathbf{w}}_k-\lambda {\Vert {\mathbf{w}}_k\Vert }_1\mathrm{s}.\mathrm{t}.{\mathbf{w}}_k^T{\mathrm{\Sigma }}_R{\mathbf{w}}_k\le 1,$$ (22)

where ${\mathrm{\Sigma }}_C^k={\mathbf{B}}^T{\mathbf{C}}^T{\mathrm{\Sigma }}_{11}^{1/2}{P}_{\perp }^{k-1}{\mathrm{\Sigma }}_{11}^{1/2}\mathbf{C}\mathbf{B}$. When the rank of C is greater than 1, the problem in (22) is no longer convex, since it involves maximizing an objective function that is not concave. A potential solution is to use the minorization-maximization (MM) algorithm (Lange et al., 2000). Specifically, for any fixed w^(m), we take a Taylor series expansion of ${\mathbf{w}}_k^T{\mathbf{\Sigma }}_C^k{\mathbf{w}}_k$ at w^(m) and get

$${\mathbf{w}}_k^T{\mathrm{\Sigma }}_C^k{\mathbf{w}}_k-\lambda {\Vert {\mathbf{w}}_k\Vert }_1\ge 2{\mathbf{w}}_k^T{\mathrm{\Sigma }}_C^k{\mathbf{w}}_k^{(m)}-{\mathbf{w}}_k^{(m)T}{\mathrm{\Sigma }}_C^k{\mathbf{w}}_k^{(m)}-\lambda {\Vert {\mathbf{w}}_k\Vert }_1.$$ (23)

Thus, the right hand side of (23) minorizes the objective function (22) at ${\mathbf{w}}_k^{(m)}$ and is a convex function, which can be solved by using some convex optimization methods. However, based on our extensive experience, the MM algorithm is too slow for most large-scale problems, such as imaging genetics.

To further improve computational efficiency, we consider a surrogate of (22). Recall the discussion in the second principle, we are only interested in extracting informative directions for testing hypotheses of interest. We consider a spectral decomposition of (D^−TΣ_XD⁻¹)_(r×r) as ${(D^{-T}{\mathrm{\Sigma }}_X{D}^{-1})}_{(r\times r)}={\sum }_{j=1}^r{\gamma }_j{\mathbf{\ell }}_j{\mathbf{\ell }}_j^T$, where (γ_j, ℓ_j) are eigenvalue-eigenvector pairs with γ₁ ≥ γ₂ ≥ … ≥ γ_r. Then, instead of solving (22), we propose to solve r SURP problems as

$${\mathbf{w}}_{\lambda }^k=\text{argmin}\frac{1}{2}{\mathbf{w}}_k^T{\mathrm{\Sigma }}_R{\mathbf{w}}_k-\sqrt{{\gamma }_k}{\ell }_k^T{\mathbf{\text{CBw}}}_k+{\lambda }_k{\Vert {\mathbf{w}}_k\Vert }_1\text{for}1\le k\le r.$$ (24)

Solving (24) leads to r sparse projection directions. In (24), since we sequentially extract the direction vector according to the input signal Σ_C, it may produce a less informative direction vector compared with those from (22). However, such formulation leads to a fast computational algorithm and our simulation results demonstrate its reasonable performance. Thus, (24) is preferred in practice.

2.4 Test Procedure

We consider three statistics for testing H_0W against H_1W in (4). Based on model (3), we calculate the ordinary least squares estimate of β_w, given by ${\widehat{\mathit{\beta }}}_{\mathbf{w}}={({\sum }_{i=1}^N{\mathbf{x}}_i{\mathbf{x}}_i^T)}^{-1}{\sum }_{i=1}^N{\mathbf{x}}_i{\mathbf{y}}_i^T\mathbf{W}$.

Subsequently, we calculate a k × k matrix, denoted by T_n, as follows:

$$T_n={(\mathbf{C}{\widehat{\mathit{\beta }}}_{\mathbf{w}}-{\mathbf{b}}_0)}^T{\mathrm{\Sigma }}_{\tilde{\mathrm{\Omega }}}^{-1}(\mathbf{C}{\widehat{\mathit{\beta }}}_{\mathbf{w}}-{\mathbf{b}}_0),$$ (25)

where Σ_Ω̃ is a consistent estimate of the covariance matrix of Cβ̂_w − b₀. Specifically, let β̃_w be the restricted least squares (RLS) estimate of β under H₀, which is given by

$${\tilde{\mathit{\beta }}}_{\mathbf{w}}={\widehat{\mathit{\beta }}}_{\mathbf{w}}-{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{C}}^T{[\mathbf{C}{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{C}}^T]}^{-1}(\mathbf{C}{\widehat{\mathit{\beta }}}_{\mathbf{w}}-{\mathbf{b}}_0).$$

Then, we can set ${\mathrm{\Sigma }}_{\tilde{\mathrm{\Omega }}}=\mathbf{C}{({\mathbf{X}}^T\mathbf{X})}^{-1}{\sum }_{i=1}^N{a}_i^2{\mathbf{x}}_i{\tilde{\mathbf{\epsilon }}}_i^T{\tilde{\mathbf{\epsilon }}}_i{\mathbf{x}}_i^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{C}}^T$, where $a_i=1/\{1-{\mathbf{x}}_i^T{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{x}}_i\}$ and ${\tilde{\mathbf{\epsilon }}}_i={\mathbf{W}}^T{\mathbf{y}}_i-{\tilde{\mathit{\beta }}}_{\mathbf{w}}^T{\mathbf{x}}_i$. When k > 1, we use the determinant, trace and eigenvalues of T_n as test statistics, which are given by

$$W_n=\text{det}(T_n),{\text{Tr}}_n=\text{trace}(T_n),{\text{and Roy}}_n=\text{max}(\text{eig}(T_n)),$$ (26)

where det, trace, and eig, respectively, denote the determinant, trace and eigenvalues of a symmetric matrix. When k = 1, all three statistics in (26) reduce to the Wald-type (or Hotelling’s T²) test statistic. For simplicity, we focus on Tr_n throughout the paper.

We propose a wild bootstrap method to improve the finite sample performance of the test statistic Tr_n. First, we fit model (1) under the null hypothesis (2) to calculate the estimated regression coefficient matrix, denoted by B̂₀, with corresponding residuals ${\widehat{\mathbf{e}}}_i={\mathbf{y}}_i-{\widehat{\mathbf{B}}}_0^T{\mathbf{x}}_i$ for i = 1, …, n. Then we generate G bootstrap samples ${\mathbf{z}}_i^{(g)}={({\widehat{\mathbf{B}}}_0)}^T{\mathbf{x}}_i+{\eta }_i^{(g)}{\widehat{\mathbf{e}}}_i$ for i = 1, …, n, where ${\eta }_i^{(g)}$ are independently and identically distributed as a distribution F, which is chosen to be ±1 with equal probability. For each generated wild-bootstrap sample, we repeat the estimation procedure for estimating the optimal weights and the calculation of the test statistic $\mathrm{T}{\mathrm{r}}_n^{(g)}$. Subsequently, the p-value of Tr_n is computed as $\frac{1}{G}{\sum }_{g=1}^{G}1(\mathrm{T}{\mathrm{r}}_n^{(g)}\ge \mathrm{T}{\mathrm{r}}_n)$, where 1(·) is an indicator function.

2.5 Tuning Parameter Selection

We consider several methods to select the tuning parameter λ. The first one is cross validation (CV), which is primarily a way of measuring the predictive performance of a statistical model. However, the CV technique can be computationally expensive for large-scale problems. The second one is the information criterion, which has been widely to measure the relative goodness of fit of a statistical model. However, neither of these two methods are applicable for SURP, since our primary interest is to find informative directions for appropriately testing the null and alternative hypotheses of (2). If the null hypothesis is true, it is expected that CB̂ only contains noisy components and the estimated direction vectors should be random. In this case, the test statistics Tr_n, W_n, and Roy_n should not be sensitive to the value of λ. This motivates us to use the rejection rate to select the tuning parameter as follows:

$$\widehat{\lambda }=\underset{0\le \lambda \le {\lambda }_{\text{max}}}{\text{argmax}}\{{(\text{Rejection Rate})}_{\lambda }\},$$ (27)

where λ_max is the largest λ to make w nonzero.

3 Asymptotic Theory

We investigate several theoretical properties of SURP and its associated estimator. By substituting Σ̃_R and ℓ̂ = CB̂ into (15), we can calculate an estimate of w₀ as

$${\widehat{\mathbf{w}}}_{\lambda }=\underset{\mathbf{w}}{\text{argmin}}\frac{1}{2}{\mathbf{w}}^T{\tilde{\mathrm{\Sigma }}}_R\mathbf{w}-{\mathbf{w}}^T\widehat{\ell }+\lambda {\Vert \mathbf{w}\Vert }_1.$$ (28)

The following question arises naturally:

• how close is ŵ_λ to w₀?

We address this question in Theorems 3.1 and 3.2.

We consider the scenario that there are a few nonzero components in w₀, that is, a few response variables are associated with the covariates of interest. Such a scenario is common in many large-scale problems. We make a note here that the sparsity of ${\mathbf{w}}_0={\mathrm{\Sigma }}_R^{-1}\mathbf{\ell }$ does not require neither ${\mathrm{\Sigma }}_R^{-1}\text{nor}\mathbf{\ell }$ to be sparse, and hence are more quite flexible. Let S₀ = {j : w_0,j ≠ 0} be the active set of w₀ = (w_0,1, …, w_0,q)^T and s₀ is the number of elements in S₀. We use the banded covariance estimator of Σ_R (Bickel and Levina, 2008) such that ${\Vert {\tilde{\mathrm{\Sigma }}}_R-{\mathrm{\Sigma }}_R\Vert }_2=O_p({(\frac{\text{log}q}{n})}^{\frac{\alpha }{2(\alpha +1)}})$ for some well behaved covariance class 𝒰(ε₀, α, C₁), which is defined as

$$𝒰({\epsilon }_0,\alpha ,C_1)=\{\mathrm{\Sigma }=({\sigma }_{jj\prime }):\underset{j}{\text{max}}\sum _{j\prime }\{|{\sigma }_{j\prime j}|:|j\prime -j|>k\}\le C_1{k}^{-\alpha }\text{for all}k>0\text{and}0<{\epsilon }_0\le {\lambda }_{\text{min}}(\mathrm{\Sigma })\le {\lambda }_{\text{max}}(\mathrm{\Sigma })\le 1/{\epsilon }_0\}.$$

We have the following results.

Theorem 3.1 Assume that Σ_R ∈ 𝒰(ε₀, α, C₁) and

$$\lambda =\text{max}\{(k_n{t}_1^0+C_1{k}_n^{-\alpha }){\Vert {\mathbf{w}}_0\Vert }_2,t_2^0\}\asymp {(\frac{\text{log}(q\vee n)}{n})}^{\frac{\alpha }{2(\alpha +1)}}{\Vert {\mathbf{w}}_0\Vert }_2,$$ (29)

where $k_n\asymp {(\frac{\text{log}(q\vee n)}{n})}^{-\frac{1}{2(\alpha +1)}},t_1^0≔\sqrt{2({\eta }_1+1)\frac{1}{\gamma ({\epsilon }_0,\delta )}}\sqrt{\frac{\text{log}(q\vee n)}{n}}$, and $t_2^0≔\frac{C_0}{{\epsilon }_0}\sqrt{2({\eta }_2+1)}\sqrt{\frac{\text{log}(q\vee n)}{n}}$, in which γ(ε₀, δ) and δ = δ(ε₀) only depends on (ε₀. Then, with probability at least 1 − (q ∨ n)^−η₁ − (q ∨ n)^−η₂, we have

$${\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_2\le C\lambda \sqrt{s_0},$$ (30)

where C is a constant not depending on q and n. Furthermore, for ‖ℓ‖₂ > δ₀, we have

$${\Vert \frac{{\widehat{\mathbf{w}}}_{\lambda }}{{\Vert {\widehat{\mathbf{w}}}_{\lambda }\Vert }_2}-\frac{{\mathbf{w}}_0}{{\Vert {\mathbf{w}}_0\Vert }_2}\Vert }_2\le \frac{2C\lambda \sqrt{s_0}}{{\Vert {\mathbf{w}}_0\Vert }_2}.$$ (31)

Theorem 3.1 gives an oracle inequality and the L₂ convergence rate of ŵ_λ in the sparse case, which indicates direction consistency and is important to ensure the good performance of test statistics. This result has several important implications. If $\sqrt{s_0}{(\frac{\text{log}q}{n})}^{\frac{\alpha }{2(\alpha +1)}}=o(1)$, then ‖ŵ_λ − w₀‖₂ converges to zero in probability. Therefore, our SURP should perform well for the extremely sparse cases with s₀ << n. This is extremely important in practice, since the extremely sparse cases are common for many large-scale problems. Although we consider the banded covariance estimator of Σ_R in Theorem 3.1 (Bickel and Levina, 2008), the convergence rate of ŵ_λ can be established for other estimators of Σ_R and ℓ as follows.

Theorem 3.2 Suppose that we have ‖Σ̃_R − Σ_R‖₂ = O_p(a_n) = o_p(1) and ‖ℓ̂ − ℓ‖_∞ = O_p(b_n) = o_p(1), then

$${\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_2=O_p((a_n\vee b_n)\sqrt{s_0}).$$ (32)

Furthermore, for ‖ℓ‖₂ > δ₀, we have

$${\Vert \frac{{\widehat{\mathbf{w}}}_{\lambda }}{{\Vert {\widehat{\mathbf{w}}}_{\lambda }\Vert }_2}-\frac{{\mathbf{w}}_0}{{\Vert {\mathbf{w}}_0\Vert }_2}\Vert }_2=O_p(\frac{(a_n\vee b_n)\sqrt{s_0}}{{\Vert {\mathbf{w}}_0\Vert }_2}).$$ (33)

Theorem 3.2 gives the L₂ convergence rate of ŵ_λ for any possible estimators of Σ_R and ℓ. A direct implication is that we can consider other estimators of Σ_R in order to achieve better estimation of Σ_R under different assumptions of Σ_R. For instance, if Σ_R has an approximate factor structure with sparsity, then we may consider the principal orthogonal complement thresholding (POET) method in Fan et al. (2013) to estimate Σ_R. Moreover, if we can achieve good estimation of ℓ for large p, then we can extend model (1) to the scenario with large p. We will systematically investigate these generalizations in our future work.

Remark The SPReM estimator ŵ_λ is closely connected with those estimators in Witten and Tibshirani (2011) and Fan et al. (2012) in the framework of penalized linear discriminant analysis. However, little is known about the theoretical properties of such estimators. To the best of our knowledge, Theorems 3.1 and 3.2 are the first results on the convergence rate of such estimators under the restricted eigen-vectors of problem (11).

Remark The SPReM estimator ŵ_λ does not have the oracle property due to the asymptotic bias introduced by the L₁ penalty. See detailed discussions in (Fan and Li, 2001; Zou, 2006). However, our estimation procedure may be modified to achieve the oracle property by using some non-concave penalties or adaptive weights. We will investigate this issue in more depth in our future work.

4 Numerical Examples

4.1 Simulation 1: Two Sample Test in High Dimensions

In this subsection, we consider high-dimensional two-sample test problems and compare SPReM with the High-dimensional Two-Sample test (HTS) method in Chen and Qin (2010) and the Random Projection (RP) method proposed by Lopes et al. (2011). Both HTS and RP are the state-of-the-art methods for detecting a shift between the means of two high-dimensional normal distributions. It has been shown in Lopes et al. (2011) that the random projection method outperforms several competing methods when q/n converges to a constant or ∞.

We simulated two sets of samples {y₁, …, y_n1} and {y_n1+1, …, y_n} from N(β₁, Σ_R) and N(β₂, Σ_R), respectively, where β₁ and β₂ are q × 1 mean vectors and Σ_R = σ²(ρ_jj′ ), in which (ρ_jj′) is a q × q correlation matrix. We set n = 2n₁ = 100 and the dimension of the multivariate response q is 50, 100, 200, 400, and 800, respectively. We are interested in testing the null hypothesis H₀ : β₁ = β₂ against H₁ : β₁ ≠ β₂. This two-sample test problem can be formulated as a special case of model (1) with n = n₁ + n₂. Moreover, we have B^T = [β₁, β₂] and C = (1, −1). Without loss of generality, we set β₁ = β₂ = 0 to assess type I error rate and then introduce a shift in the first ten components of β₂ to be 1 to assess power. We set σ² to be 1 and 3 and consider three different correlation matrices as follows.

• Case 1 is an independent covariance matrix with (ρ_jj′) = diag(1, …, 1).

• Case 2 is a weak correlation matrix with ρ_jj′ = 1(j′ = j) + 0.3 + 1(j′ ≠ j).

• Case 3 is a strong correlation covariance matrix with ρ_jj′ = 0.8^|j′−j|.

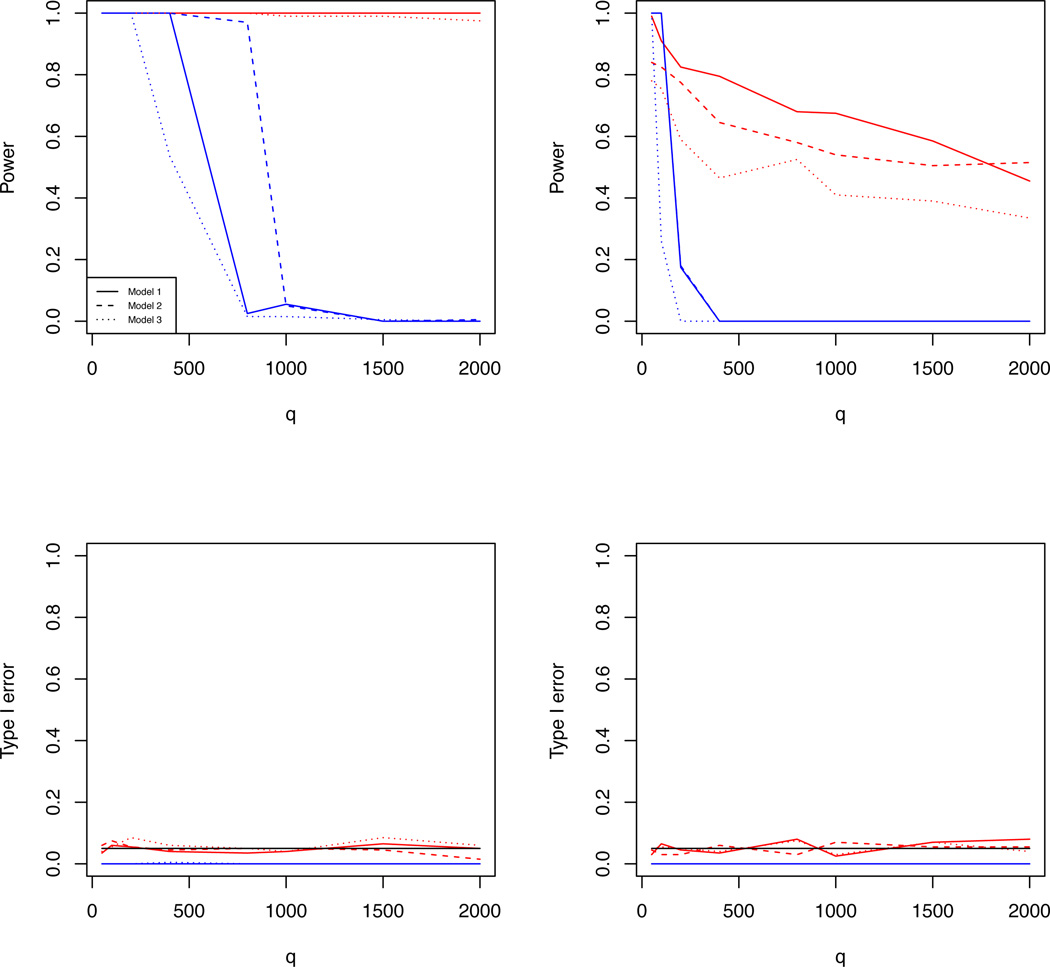
Simulation results are summarized in Tables 1 and 2. As expected, both HTS and RP perform worse as q gets larger, whereas our SPReM works very well even for relatively large q. This is consistent with our theoretical results in Theorems 3.1 and 3.2. Moreover, HTS and RP cannot control the type I error rate well in all scenarios, whereas our SPReM based on the wild bootstrap method works reasonably well. According to the best of our knowledge, none of the existing methods for the two sample test in high dimensions work well in this sparse setting. For cases (ii) and (iii), ${\mathrm{\Sigma }}_R^{-1}({\beta }_1-{\beta }_2)$ is not sparse, but SPReM performs reasonably well under the correlated scenarios. This may indicate the potential of extending SPReM and its associated theory to non-sparse cases. As expected, increasing σ² decreases statistical power in rejecting the null hypothesis. Since both SPReM and RP significantly outperform HTS, we increased q to 2,000 and presented some additional comparisons between SPReM and RP based on 100 simulated data sets in Figure 1.

Table 1.

Simulation 1: power and type I error are reported for two sample test at 5 different qs at significance level α = 5% when σ² = 1.

	Power					Type I error
q	50	100	200	400	800	50	100	200	400	800
case 1
SPReM	1.000	1.000	1.000	1.000	1.000	0.035	0.060	0.055	0.040	0.035
RP	1.000	1.000	1.000	1.000	0.025	0.000	0.000	0.000	0.000	0.000
HTS	0.965	0.320	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
case 2
SPReM	1.000	1.000	1.000	1.000	1.000	0.060	0.075	0.055	0.045	0.050
RP	1.000	1.000	1.000	1.000	0.970	0.000	0.000	0.000	0.000	0.000
HTS	1.000	0.245	0.030	0.005	0.000	0.000	0.000	0.000	0.000	0.000
case 3
SPReM	1.000	1.000	1.000	1.000	1.000	0.040	0.055	0.085	0.060	0.050
RP	1.000	1.000	1.000	0.535	0.015	0.000	0.000	0.000	0.005	0.000
HTS	1.000	0.140	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000

Table 2.

Simulation 1: power and type I error are reported for two sample test at 5 different qs at significance level α = 5% when σ² = 3.

	Power					Type I error
q	50	100	200	400	800	50	100	200	400	800
case 1
SPReM	0.990	0.910	0.825	0.795	0.680	0.030	0.065	0.045	0.035	0.080
RP	1.000	1.000	0.175	0.000	0.000	0.000	0.000	0.000	0.000	0.000
HTS	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
case 2
SPReM	0.840	0.825	0.775	0.645	0.580	0.045	0.030	0.030	0.060	0.030
RP	1.000	1.000	0.180	0.000	0.000	0.000	0.000	0.000	0.000	0.000
HTS	0.105	0.015	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000
case 3
SPReM	0.780	0.755	0.590	0.465	0.525	0.050	0.055	0.050	0.040	0.075
RP	1.000	0.260	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
HTS	0.095	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000

Fig. 1.

Simulation 1 results: the estimated rejection rates as functions of q for two different σ² values. The upper and lower rows are, respectively, for powers and for type I error rates, whereas the left and right columns correspond to σ² = 1 and σ² = 3, respectively. In all panels, the lines obtained from SPReM and RP are, respectively, presented in red and in blue, and the results for independence, weak, and strong correlation structures are, respectively, presented as thick, dashed, and dotted lines.

4.2 Simulation 2: Multiple Rank Cases

In this subsection, we evaluate the finite sample performance of SMURP. The simulation studies were designed to establish the association between a relatively high-dimensional imaging phenotype with a genetic marker (e.g., SNP or haplotype), which is common in imaging genetics studies, while adjusting for age and other environmental factors. We set the sample size n = 100 and the dimension of the multivariate phenotype q to be 50, 100, 200, 400 and 800, respectively, and then simulated the multivariate phenotype according to model (1). The random errors were simulated from a multivariate normal distribution with mean 0 and covariance matrix with diagonal elements 1. For the off-diagonal elements in the covariance matrix, which characterize the correlations among the multivariate phenotypes, we categorized each component of the multivariate phenotype into three categories: high correlation, medium correlation and very low correlation with the corresponding number of components (1, 1, q − 2) in each category, and then we set the three degrees of correlation among the different components of the multivariate phenotype according to Table 3. The final covariance matrix is set to be Σ_R = σ²(ρ_jj′), where (ρ_jj′) is the correlation matrix. We considered σ² = 1 and 3.

Table 3.

Correlation matrix of responses used in the simulation

	High	Med	Low
High	0.9	0.6	0.3
Med	0.6	0.9	0.1
Low	0.3	0.1	0.1

For the covariates, we included two SNPs with an additive effect and 3 additional continuous covariates. We varied the minor allele frequency (MAF) of the first SNP, whereas we fixed the MAF of the second SNP to be 0.5. For the first SNP, we considered 6 scenarios assuming the MAFs are 0.05, 0.1, 0.2, 0.3, 0.4, and 0.5, respectively. We simulated the three additional continuous covariates from a multivariate normal distribution with mean 0, standard deviation 1, and equal correlation 0.3. We first set B = 0 to assess type I error rate. To assess power, we set the first response to be the only components of the multivariate phenotype associated with the first SNP and the second response to be the component related to the second SNP effect. Specifically, we set the coefficients of the two SNPs to be 1 for the selected responses and all other regression coefficients to be 0. We are interested in testing the joint effects of the two SNPs on phenotypic variance.

We applied SPReM to 100 simulated data sets. Note that to the best of our knowledge, no other methods can be used to test the multi-rank test problem and thus we only focus on SPReM here. Table 4 presents the estimated rejection rates corresponding to different MAFs, q, and σ². Our SPReM works very well even for relatively large q under both σ² = 1 and 3. Specifically, the wild bootstrap method can control the type I error rate well in all scenarios. For the power, SPReM performs reasonably well under the small MAFs and q = 800. It may indicate that our method can perform well for much larger q if the sample size gets larger. As expected, increasing σ² decreases statistical power in rejecting the null hypothesis.

Table 4.

Simulation 2: the estimates of rejection rates were reported at 6 different MAFs, 5 different qs, and 2 different σ² values at significance level α = 5%. For each case, 100 simulated data sets were used.

	Power					Type I error
σ2 = 1
MAF\q	50	100	200	400	800	50	100	200	400	800
0.050	0.950	0.955	0.930	0.940	0.930	0.045	0.060	0.030	0.070	0.080
0.100	0.995	0.990	0.990	0.980	0.975	0.045	0.055	0.040	0.045	0.045
0.200	1.000	1.000	1.000	1.000	1.000	0.045	0.045	0.080	0.030	0.060
0.300	1.000	1.000	1.000	1.000	1.000	0.065	0.040	0.020	0.065	0.060
0.400	1.000	1.000	1.000	1.000	1.000	0.050	0.070	0.035	0.060	0.070
0.500	1.000	1.000	1.000	1.000	1.000	0.060	0.050	0.030	0.020	0.035
σ2 = 3
0.050	0.915	0.875	0.765	0.795	0.735	0.050	0.040	0.030	0.050	0.065
0.100	0.970	0.960	0.940	0.875	0.865	0.040	0.055	0.070	0.080	0.050
0.200	0.995	0.985	0.975	0.975	0.970	0.015	0.050	0.060	0.010	0.065
0.300	1.000	1.000	0.990	0.970	0.955	0.045	0.055	0.055	0.080	0.040
0.400	0.995	1.000	1.000	0.990	0.985	0.055	0.035	0.045	0.050	0.070
0.500	0.995	1.000	1.000	0.985	0.980	0.085	0.055	0.055	0.065	0.030

4.3 Alzheimer’s Disease Neuroimaging Initiative (ADNI) Data Analysis

The development of SPReM is motivated by the joint analysis of imaging, genetic, and clinical variables in the ADNI study. “Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.ucla.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year publicprivate partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California, San Francisco. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.”

The Huamn 610-Quad BeadChip (Illumina, Inc. San Diego, CA) was used to genotype 818 subjects in the ADNI-1 database, which resulted in a set of 620,901 SNPs and copy number variation (CNV) markers. Since the Apolipoprotein E (ApoE) SNPs, rs429358 and rs7412, are not on the Human 610-Quad Bead-Chip, they were genotyped separately and added to the data set manually. For simplicity, we only considered the 10, 479 SNPs collected on the chromosome 19, which houses the famous ApoE gene commonly suspected of having association with Alzheimer’s disease. A complete GWAS of ADNI will be reported elsewhere. The SNP data were preprocessed by standard quality control steps including dropping any SNP that has more than 5% missing data, imputing the missing values in each SNP with its mode, dropping SNPs with minor allele frequency < 0.05, and screening out SNPs violating the Hardy-Weinberg equilibrium. Finally, we obtained 8, 983 SNPs on chromosome 19, including the ApoE allele as the last SNP in our dataset.

Our problem of interest is to perform a genome-wide search for establishing the association between the 10, 479 SNPs collected on the chromosome 19 and the brain volume of 93 regions of interest (ROIs). We fitted model (1) with all 93 ROIs as responses and a covariate vector including an intercept, a specific SNP, age, gender, whole brain volume, and the top 5 principal components to account for population stratification. To reduce population stratification effects, we only used 761 Caucasians from all 818 subjects. Subjects with missing values were removed, which leads to 747 subjects. We set λ = λ_max in our SPReM for computational efficiency. To test the SNP effect on all 93 ROIs, we calculated the test statistic and its p–value for each SNP. We further performed a standard massive univariate analysis. Specifically, we fitted a linear model with the same set of covariates and calculated a p–value for every pair of ROIs and SNPs.

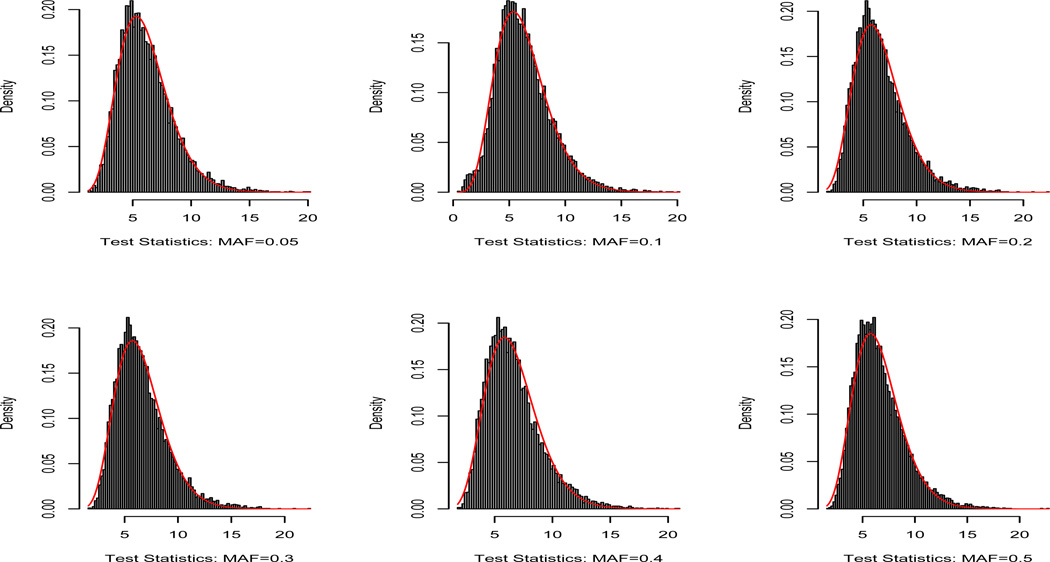
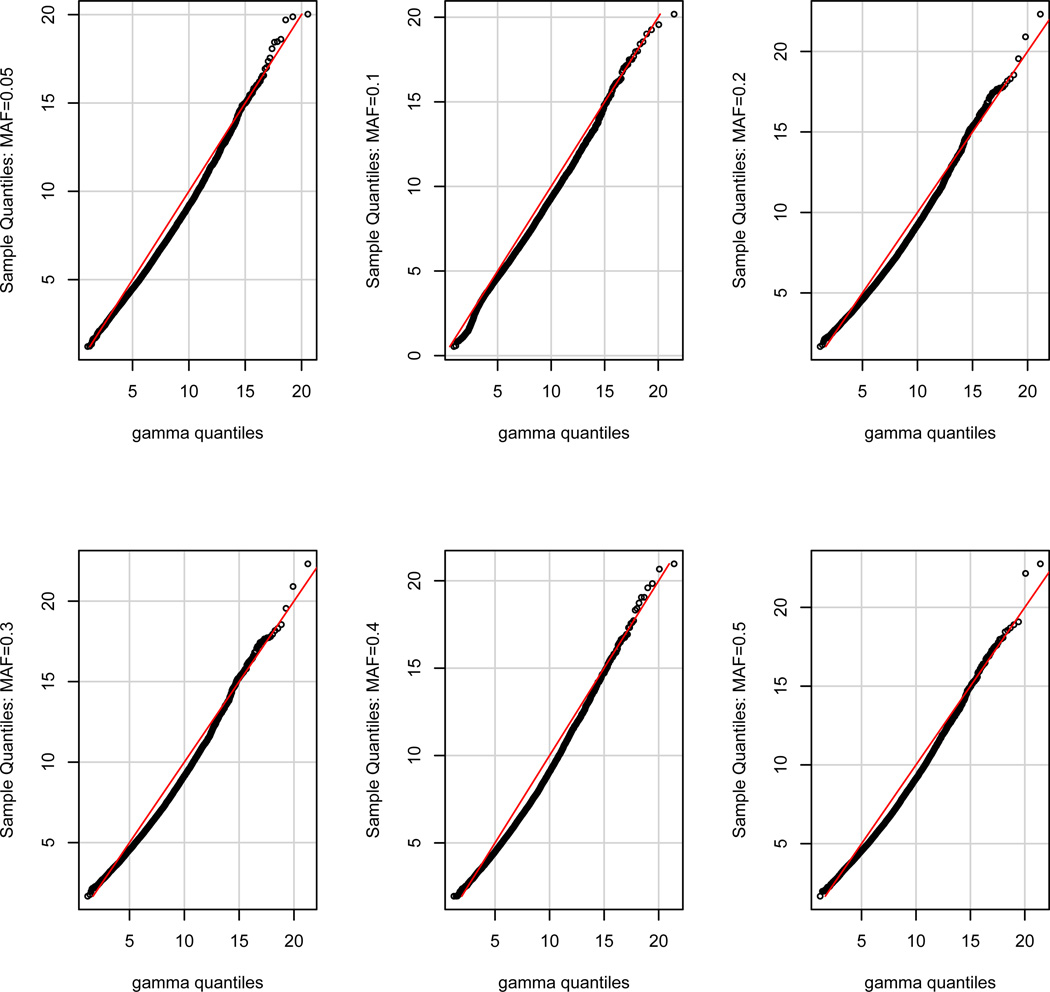
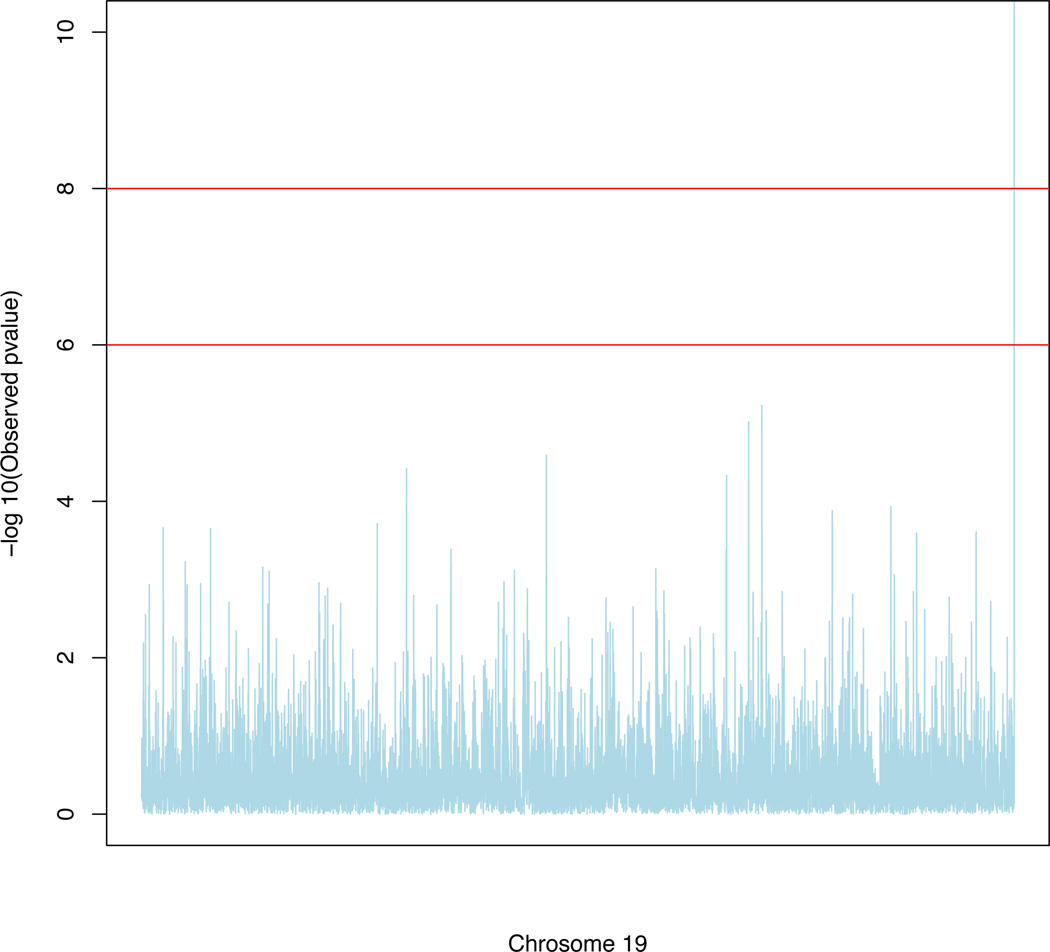
We developed a computationally efficient strategy to approximate the p–value of each SNP with different MAFs. In the real data analysis, we considered a pool of SNPs consisting of 6 MAF groups including MAF∈ (0.05, 0.075], MAF∈ (0.075, 0.15], MAF∈ (0.15, 0.25], MAF∈ (0.25, 0.35], MAF∈ (0.35, 0.45], and MAF∈ (0.45, 0.50]. Each MAF group contains 40 SNPs. For each SNP, we generated 10,000 wild bootstrap samples under the null hypothesis to obtain 10,000 bootstrapped test statistics. Then, based on 40 × 10, 000 bootstrapped samples for each MAF group, we use the Satterthwaite method to approximate the null distribution of the test statistic by a Gamma distribution with parameters (a_T, b_T). Specifically, we set a_T = ε²/ν and b_T = ν/ε by matching the mean (ε) and the variance (ν) of the test statistics and those of the Gamma distribution. The histograms and the fitted gamma distributions along with the QQ-plots are, respectively, presented in Figures 2–3. Figures 2 and 3 reveal that our gamma approximations work reasonably well for a wide range of MAFs when λ = λ_max. Since we only use Gamma(a_T, b_T ) to approximate the p–value of large test statistic, we only need a good approximation at the tail of the Gamma distribution. See Figure 3 for details. For each SNP, we matched its MAF with the closest MAF group in the pool and then calculated the p–value of the test statistic based on the approximated gamma distribution. We present the manhattan plot in Figure 4 and the top 10 SNPs with their p–values for SPReM and the mass univariate analysis in Table 5 for λ = λ_max.

Fig. 2.

Histograms and their gamma approximations based on the wild bootstrap samples under the null hypothesis for different MAFs for λ = λ_max.

Fig. 3.

QQ-plot of the gamma approximations based on the wild bootstrap samples under the null hypothesis for different MAFs for λ = λ_max.

Fig. 4.

ADNI GWAS results: Manhattan plot of −log₁₀(p)-values on chromosome 19 by SPReM for λ = λ_max.

Table 5.

Comparison between SPReM and the massive univariate analysis (MUA) for ADNI data analysis: the top 10 SNPs and their – log₁₀(p) values for λ = λ_max.

SNP	apoe_allele	rs11667587	rs2075650	rs7248284	rs3745341
SPReM	5.04E-16	5.95E-06	9.58E-06	2.56E-05	3.83E-05
MUA	3.43E-11	4.42E-04	1.12E-04	8.75E-04	1.00E-03
SNP	rs4803646	rs8106200	rs2445830	rs8102864	rs740436
SPReM	4.65E-05	1.16E-04	1.32E-04	1.93E-04	2.17E-04
MUA	7.56E-04	3.70E-03	1.33E-02	9.34E-04	1.63E-03

We have several important findings. The ApoE allele was identified as the top one significant covariate with −log₁₀(p) ~ 15 and 9 respectively, indicating a strong association between the ApoE allele and imaging phenotype, a biomarker of Alzheimer’s disease diagnosis. This finding agrees with the previous result in Vounou et al. (2012). We also found some interesting results regarding rs207650 on the TOMM40 gene, which is one of the top 10 significant SNPs with −log₁₀(p) ~ 5 and 4 respectively. The TOMM40 gene is located in close proximity to the ApoE gene and has also been linked to AD in some recent studies (Vounou et al., 2012). We are also able to detect some additional SNPs, such as rs11667587 on the NOVA2 gene, among others, on the chromosome 19, which are not identified in existing genome-wide association studies. The new findings may shed more light on further Alzheimer’s research. The p–values for those top 10 SNPs calculated from SPReM are much smaller than those calculated from the mass univariate analysis. In other words, to achieve comparable p–values, the mass univariate analysis requires many more samples. This strongly demonstrates the effectiveness of our proposed method.

5 Discussion

In this paper, we have developed a general SPReM framework based on the two heritability ratios. Our SPReM methodology has a wide range of applications, including sparse linear discriminant analysis, two sample tests, and general hypothesis tests in MLMs, among many others. We have systematically investigated the L₂ convergence rate of ŵ_λ in the ultrahigh dimensional framework. We further extend the SURP problem to the SMURP and offered a sequential SURP approximation algorithm. We carried out simulation studies and examined a real data set to demonstrate the excellent performance of our SPReM framework compared to other state-of-the-art methods.

6 Assumptions and Proofs

Throughout the paper, the following assumptions are needed to facilitate the technical details, although they may not be the weakest conditions.

• Assumption A1. C(n⁻¹X^TX)⁻¹C^T ≍ 1, that is, there exists constant c₀ and C₀ such that c₀ ≤ C(n⁻¹X^TX)⁻¹C^T ≤ C₀.

• Assumption A2. 0 ≤ ε₀ ≤ λ_min(Σ_R) ≤ λ_max(Σ_R) ≤ 1/ε₀.

• Assumption A3. The covariance estimator Σ̃_R satisfies: ‖Σ̃_R − Σ_R‖₂ = O_p(a_n) ≤ o_p(1).

Remark : Assumption A1 is a very weak and standard assumption for regression models. Assumption A2 has been widely used in the literature. Assumption A3 requires a relatively accurate covariance estimator in terms of spectral norm convergence. We may use some good penalized estimators of Σ_R under different assumptions of Σ_R (Bickel and Levina, 2008; Cai et al., 2010; Lam and Fan, 2009; Rothman et al., 2009; Fan et al., 2013).

Proof of Theorem 2.1 The Karush-Kuhn-Tucker (KKT) conditions for problem (13) are given by:

$$\ell -\lambda \mathrm{\Gamma }-\gamma {\mathrm{\Sigma }}_R\mathbf{w}=0,\gamma \ge 0,\gamma (\frac{1}{2}{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}-\frac{1}{2})=0,\frac{1}{2}{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}\le \frac{1}{2},$$

where Γ is a q × 1 vector and equals the subgradient of ‖w‖₁ with respect to w. We consider two scenarios. First, suppose that |ℓ_j| > λ for some j. We must have γΣ_Rw ≠ 0, which leads to γ > 0 and w^TΣ_Rw = 1. Thus, the KKT conditions reduce to

$$\ell -\lambda \mathrm{\Gamma }-\gamma {\mathrm{\Sigma }}_R\mathbf{w}=0,\gamma \ge 0,{\mathbf{w}}^T{\mathrm{\Sigma }}_R\mathbf{w}=1.$$

If we write w̃ = γw, this is equivalent to solving problem (15) with w̃ and then take normalization. Second, if |ℓ_j| ≤ λ for any j, then w = 0 and γ = 0, which is the solution of (15) as well. This finishes the proof.

Proof of Proposition 2.2 It follows from Theorem 2 of Rosset and Zhu (2007).

Proof of Proposition 2.3 The proof is similar to that of Proposition 1 of Witten and Tibshirani (2011). Letting ${\tilde{\mathbf{w}}}_k={\mathrm{\Sigma }}_R^{1/2}{\mathbf{w}}_k$, then problem (20) can be rewritten as

$$\text{argmax}{\tilde{\mathbf{w}}}_k^T{\mathrm{\Sigma }}_R^{-1/2}{\mathbf{B}}^T{\mathbf{C}}^T{\mathrm{\Sigma }}_{11}^{1/2}\mathbf{\text{CB}}{\mathrm{\Sigma }}_R^{-1/2}{\widehat{\mathbf{w}}}_k\mathrm{s}.\mathrm{t}.{\Vert {\widehat{\mathbf{w}}}_k\Vert }^2\le 1,$$

which is equivalent to

$$\text{argmax}{\tilde{\mathbf{w}}}_k\mathbf{A}{P}_{\perp }^{k-1}{\mathbf{u}}_k\mathrm{s}.\mathrm{t}{\Vert {\tilde{\mathbf{w}}}_k\Vert }^2\le 1,{\Vert {\mathbf{u}}_k\Vert }^2\le 1,$$ (34)

where $\mathbf{A}={\mathbf{B}}^T{\mathbf{C}}^T{\mathrm{\Sigma }}_{11}^{1/2}$. Thus, w̃_k and u_k that solve problem (34) are the k-th left and right singular vectors of A (Witten and Tibshirani, 2011). Therefore, we have $P_{\perp }^{k-1}=\mathbf{I}-{\sum }_{j=1}^{k-1}{\mathbf{u}}_j{\mathbf{u}}_j^T$ and u_k is the k-th eigenvector of A^TA, or equivalently the k-th right singular vector of A. For problem (34), w̃_k is the k-th left singular vector of A. Therefore, the solution of (21) is the k-th discriminant vector of (20).

Proof of Theorem 3.1 In this theorem, we specifically use the banded covariance estimator Σ̃_R = B_kn(Σ̃_R), where B_k(Σ) = [σ_jj′I(|j′ −j| ≤ k)] and Σ̂_R is the sample covariance matrix of y_i − B̂^T x_i.

First, we define 𝒥 = {‖Σ̃_R − B_kn(Σ_R)‖_∞ ≤ t₁} ∩ {‖ℓ̂ − ℓ‖_∞ ≤ t₂}, where t₁ and t₂ are specified as in Lemma 6.2. Then, it follows from Lemma 6.2 that P(𝒥) ≥ 1−3(q ∨ n)^−η₁ − 2(q ∨ n)^−η₂.

On the set 𝒥, by taking $\lambda =\text{max}\{k_n{t}_1+C_1{k}_n^{-\alpha },t_2\}$ and using Lemma 6.1, we have

$$\frac{1}{2}{({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)}^T{\tilde{\mathrm{\Sigma }}}_R({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)+\lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda }\Vert }_1\le ({\mathbf{w}}_0^T({\mathrm{\Sigma }}_R-{\tilde{\mathrm{\Sigma }}}_R)+{\epsilon }^T)({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)+\lambda {\Vert {\mathbf{w}}_0\Vert }_1\le {\Vert {\tilde{\mathrm{\Sigma }}}_R-{\mathrm{\Sigma }}_R\Vert }_2{\Vert {\mathbf{w}}_0\Vert }_2{\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_1+{\Vert \epsilon \Vert }_{\infty }{\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_1+\lambda {\Vert {\mathbf{w}}_0\Vert }_1\le (k_n{t}_1+C_1{k}_n^{-\alpha }){\Vert {\mathbf{w}}_0\Vert }_2{\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_1+t_2{\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_1+\lambda {\Vert {\mathbf{w}}_0\Vert }_1\le \lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_1+\lambda {\Vert {\mathbf{w}}_0\Vert }_1.$$

Let w₀,S₀ = [w_0,jI(j ∈ S₀)], where w_0,j is the j–th component of w₀. The above equation can be rewritten as

$${({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)}^T({\tilde{\mathrm{\Sigma }}}_R-{\mathrm{\Sigma }}_R+{\mathrm{\Sigma }}_R)({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)+\lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda ,S_0}\Vert }_1+\lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda ,S_0^c}\Vert }_1\le \lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda ,S_0}-{\mathbf{w}}_{0,S_0}\Vert }_1+\lambda {\Vert {\mathbf{w}}_{0,S_0}\Vert }_1+\lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda ,S_0^c}\Vert }_1,$$

which yields

$$\{{\lambda }_{\text{min}}-O(1){(\frac{\text{log}(q)}{n})}^{\frac{\alpha }{2(\alpha +1)}}\}{\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_2^2\le 2\lambda \sqrt{s_0}{\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_2.$$

Finally, we obtain the following inequality

$${\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_2\le \frac{2\lambda \sqrt{s_0}}{{\lambda }_{\mathit{\text{min}}}-O(1){(\frac{\text{log}(q)}{n})}^{\frac{\alpha }{2(\alpha +1)}}}\le C\lambda \sqrt{s_0},$$

which finishes the proof.

Proof of Theorem 3.2 It follows from Lemma (6.1) that

$$\frac{1}{2}{({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)}^T{\tilde{\mathrm{\Sigma }}}_R({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)+\lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda }\Vert }_1\le ({\mathbf{w}}_0^T({\mathrm{\Sigma }}_R-{\tilde{\mathrm{\Sigma }}}_R)+(\widehat{\ell }-\widehat{\ell }))({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)+\lambda {\Vert {\mathbf{w}}_0\Vert }_1\le ({\Vert {\tilde{\mathrm{\Sigma }}}_R-{\mathrm{\Sigma }}_R\Vert }_2{\Vert {\mathbf{w}}_0\Vert }_2+{\Vert \widehat{\ell }-\widehat{\ell }\Vert }_{\infty }){\Vert {\widehat{\mathbf{w}}}_{\lambda ,S}-{\mathbf{w}}_{0,S}\Vert }_1+\lambda {\Vert {\mathbf{w}}_{0,S}\Vert }_1$$

Note that ${\Vert {\widehat{\mathbf{w}}}_{\lambda }\Vert }_1\le {\Vert {\mathbf{w}}_{0,S_0}\Vert }_1-{\Vert {\mathbf{w}}_{0,S_0}-{\widehat{\mathbf{w}}}_{\lambda ,S_0}\Vert }_1+{\Vert {\widehat{\mathbf{w}}}_{\lambda ,S_0^c}\Vert }_1$. Then, by taking

$$\lambda ={\Vert {\tilde{\mathrm{\Sigma }}}_R-{\mathrm{\Sigma }}_R\Vert }_2{\Vert {\mathbf{w}}_0\Vert }_2+{\Vert \widehat{\ell }-\widehat{\ell }\Vert }_{\infty }\asymp O_p(a_n{\Vert {\mathbf{w}}_0\Vert }_2\vee b_n),$$

we have

$$\frac{1}{2}{({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)}^T{\tilde{\mathrm{\Sigma }}}_R({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)\le ({\Vert {\tilde{\mathrm{\Sigma }}}_R-{\mathrm{\Sigma }}_R\Vert }_2{\Vert {\mathbf{w}}_0\Vert }_2+{\Vert \widehat{\ell }-\widehat{\ell }\Vert }_{\infty })({\Vert {\widehat{\mathbf{w}}}_{\lambda ,S_0}-{\mathbf{w}}_{0,S_0}\Vert }_1+{\Vert {\widehat{\mathbf{w}}}_{\lambda ,S_0^c}\Vert }_1)-\lambda ({\Vert {\mathbf{w}}_{0,S_0}\Vert }_1-{\Vert {\mathbf{w}}_{0,S}-{\widehat{\mathbf{w}}}_{\lambda ,S_0}\Vert }_1+{\Vert {\widehat{\mathbf{w}}}_{\lambda ,S_0^c}|)+\lambda |{\mathbf{w}}_{0,S_0}\Vert }_1=O_p(a_n\vee b_n){\Vert {\widehat{\mathbf{w}}}_{\lambda ,S_0}-{\mathbf{w}}_{0,S_0}\Vert }_1\le O_p(a_n\vee b_n)\sqrt{s_0}{\Vert {\widehat{\mathbf{w}}}_{\lambda ,S}-{\mathbf{w}}_{0,S_0}\Vert }_2.$$

By using Weyl’s inequality, we have

$${({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)}^T{\tilde{\mathrm{\Sigma }}}_R({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)\ge ({\lambda }_{\text{min}}({\mathrm{\Sigma }}_R)-{\Vert {\tilde{\mathrm{\Sigma }}}_R-{\mathrm{\Sigma }}_R\Vert }_2){\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_2^2$$

where ‖Σ̃_R − Σ_R‖₂ = O_p(a_n) = o_p(1). Finally, we have

$${\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_2^2\le \frac{O_p(a_n\vee b_n)\sqrt{s_0}{\Vert {\widehat{\mathbf{w}}}_{\lambda ,S}-{\mathbf{w}}_{0,S}\Vert }_2}{{\lambda }_{\text{min}}(\mathrm{\Sigma })-O_p(a_n)},$$ (35)

which finishes the proof.

Lemma 6.1 We have the following basic inequality

$$\frac{1}{2}{({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)}^T{\tilde{\mathrm{\Sigma }}}_R({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)+\lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda }\Vert }_1\le \{{\mathbf{w}}_0^T({\mathrm{\Sigma }}_R-{\tilde{\mathrm{\Sigma }}}_R)+{(\widehat{\ell }-\ell )}^T\}({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)+\lambda {\Vert {\mathbf{w}}_0\Vert }_1.$$ (36)

Proof We rewrite the optimization problem (28) as

$${\widehat{\mathbf{w}}}_{\lambda }=\text{argmin}\frac{1}{2}{(\mathbf{w}-{\tilde{\mathrm{\Sigma }}}_R^{-1}\widehat{\ell })}^T{\tilde{\mathrm{\Sigma }}}_R(\mathbf{w}-{\tilde{\mathrm{\Sigma }}}_R^{-1}\widehat{\ell })+\lambda {\Vert \mathbf{w}\Vert }_1.$$

Thus, we have

$$\frac{1}{2}{({\widehat{\mathbf{w}}}_{\lambda }-{\tilde{\mathrm{\Sigma }}}_R^{-1}\widehat{\ell })}^T{\tilde{\mathrm{\Sigma }}}_R({\widehat{\mathbf{w}}}_{\lambda }-{\tilde{\mathrm{\Sigma }}}_R^{-1}\widehat{\ell })+\lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda }\Vert }_1\le \frac{1}{2}{({\mathbf{w}}_0-{\tilde{\mathrm{\Sigma }}}_R^{-1}\widehat{\ell })}^T{\tilde{\mathrm{\Sigma }}}_R({\mathbf{w}}_0-{\tilde{\mathrm{\Sigma }}}_R^{-1}\widehat{\ell })+\lambda {\Vert {\mathbf{w}}_0\Vert }_1,$$

which yields

$$\frac{1}{2}{\Vert {\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0\Vert }_{{\tilde{\mathrm{\Sigma }}}_R}^2+\lambda {\Vert {\widehat{\mathbf{w}}}_{\lambda }\Vert }_1\le {(\widehat{\ell }-{\tilde{\mathrm{\Sigma }}}_R{\mathbf{w}}_0)}^T({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)=\{{\mathbf{w}}_0^T({\mathrm{\Sigma }}_R-{\tilde{\mathrm{\Sigma }}}_R)+{(\widehat{\ell }-\ell )}^T\}({\widehat{\mathbf{w}}}_{\lambda }-{\mathbf{w}}_0)+\lambda {\Vert {\mathbf{w}}_0\Vert }_1,$$

in which we have used ℓ̂ = Σ_Rw₀ + ℓ̂ − ℓ in the last equality.

Lemma 6.2 For all $t_1\ge t_1^0$ and $t_2\ge t_2^0$, we have

$$P(𝒥)\ge 1-3{(q\vee n)}^{-{\eta }_1}-2{(q\vee n)}^{-{\eta }_2}.$$ (37)

Proof First, it follows from Lemma A.3 of Bickel and Levina (2008) that

$$P({\Vert {\tilde{\mathrm{\Sigma }}}_R-B_{k_n}({\mathrm{\Sigma }}_R)\Vert }_{\infty }\ge t_1)\le 2(k+1)q\text{exp}\{-n{(t_1^0)}^2\gamma ({\epsilon }_0,\delta )\}\le 2(k_n+1)(q\vee n)\text{exp}\{-2n({\eta }_1+1)\frac{1}{\gamma ({\epsilon }_0,\delta )}\frac{\text{log}(q\vee n)}{n}\gamma ({\epsilon }_0,\delta ))\}\le 3((q\vee n)k_n)\text{exp}\{-({\eta }_1+1)\text{log}((q\vee n)k_n))\}\le 3{((q\vee n)k_n)}^{-({\eta }_1+1)+1}\le 3{(q\vee n)}^{-{\eta }_1},$$

where $t_1^0=\sqrt{2({\eta }_1+1)\frac{1}{\gamma ({\epsilon }_0,\delta )}}\sqrt{\frac{\text{log}(q\vee n)}{n}}$.

Second, we know that $\frac{\sqrt{n}({\widehat{\ell }}_j-{\ell }_j)}{{\sigma }_j{C}_X}$ is Sub(1)-distributed, where $C_X=\mathbf{C}{(\frac{1}{n}{\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{C}}^T$. Then by the union sum inequality, we have

$$P(\underset{j}{\text{max}}|\frac{\sqrt{n}({\widehat{\ell }}_j-{\ell }_j)}{C_0/{\epsilon }_0}|\ge t_2)\le P(\underset{j}{\text{max}}|\frac{\sqrt{n}({\widehat{\ell }}_j-{\ell }_j)}{{\sigma }_j{C}_X}|\ge t_2)\le 2(q\vee n)\text{exp}\{-\frac{{(t_2^0)}^2}{2}\}.$$ (38)

By taking ${(t_2^0)}^2=2{\eta }_2\text{log}(q\vee n)$, we can rewrite the above inequality as

$$P({\Vert \widehat{\ell }-\ell \Vert }_{\infty }\ge \frac{C_0}{{\epsilon }_0}\sqrt{\frac{(2{\eta }_2+2)\text{log}(q\vee n)}{n}})\le 2{(q\vee n)}^{-{\eta }_2}$$

Finally, we get

$$P(𝒥)\ge 1-P({\Vert {\tilde{\mathrm{\Sigma }}}_R-B_k({\mathrm{\Sigma }}_R)\Vert }_{\infty }\ge t_1^0)-P({\Vert \widehat{\ell }-\ell \Vert }_{\infty }\ge \frac{C_0}{{\epsilon }_0}\sqrt{\frac{(2{\eta }_2+2)\text{log}(q\vee n)}{n}})\ge 1-3{(q\vee n)}^{-{\eta }_1}-2{(q\vee n)}^{-{\eta }_2},$$

which finishes the proof.