Skip to main content
PMC home page
The Journal of the Acoustical Society of America logoLink to The Journal of the Acoustical Society of America
letter
. 2015 Oct 26;138(4):2427–2429. doi: 10.1121/1.4932022

Comparison of glottal flow rate characteristics based on experimental and computational data

Liran Oren 1,a), Sid Khosla 1, Ephraim Gutmark 2
PMCID: PMC4627926  PMID: 26520324

Abstract

In a recent computational model, Farahani and Zhang [J. Acoust. Soc. Am. 136, EL369−EL375 (2014)] concluded that intraglottal vortices did not affect the closing mechanism of the folds. In order to determine the validity of any model that addresses the issue of vortex significance, it is important that the results of the computational model are comparable to experimental results. The results of Farahani and Zhang's model are inconsistent with data published for experimental models, which may challenge the validity of their conclusions.

I. INTRODUCTION

During phonation the amount of volumetric airflow (Q) that passes through the glottis changes during the opening and closing phases of the folds vibration. The changes in flow rate produce the source of acoustic energy,1–3 which is then filtered by vocal tract resonance according to classical source-filter theory.4 Although the flow rate is constantly changing, the greatest rate of change happens during the latter part of closing, which yields a flow rate waveform that is skewed towards the closing phase. The maximum flow declination rate (MFDR) has been shown to highly correlate with acoustic intensity, which is the objective physical variable that roughly correlates with loudness.3,5–8

There are several mechanisms that can affect MFDR. Recent experimental9–11 and computational12–14 models have shown that intraglottal vortices may form during the closing phase of vibration. These vortices are formed by the divergent shape of the glottis and their size is related to the degree of the divergence angle. In our canine experiments, these vortices augment the negative pressure (i.e., pressure that is less than atmospheric) that is formed near the superior aspect of the folds.10 We have hypothesized that the negative pressure then acts as an (additional) aerodynamic force that increases the closing speed of the vocal folds, resulting in increased MFDR.9,10 In our work, we have seen that an increase in the strength of the intraglottal vortices is correlated with an increase in skewing of the flow rate15 and area16 waveforms to the right. We also observed that the intraglottal vortices do not form in cases with no divergence during closing (at relatively low subglottal pressures),9 or they were reduced in cases with minimal divergence and scarring of the tissue.17 These findings are consisted with our hypothesis.

In their letter, Farahani and Zhang18 proposed a computational model that aimed to study the significance of the intraglottal vortices. The model used an equation that simulated the (negative) pressure produced by intraglottal vortices to then study their effect on the dynamics of the glottal wall and Q. The equation for the pressure was partially based on the experimental data of Oren et al.,10 which showed that the lowest value of the negative pressure acting on the glottal wall was approximately 30% of the magnitude of the subglottal pressure magnitude. The model used two cases for the elastic conditions of the vocal fold's tissue (soft and stiff) and examined the changes in Q at different subglottal pressures with different pressure levels added by the vortices. Farahani and Zhang found that the negative pressure from the vortices had no affect on Q thus concluding that the vortices had negligible affect on the closing mechanism of the folds.

II. LIMITATIONS OF THE MODEL

In the short discussion on the limitation of their model, Farahani and Zhang identified the lack of complete glottal closure and the limited number of values used to model the tissue elasticity. There are several other limitations of this particular model that suggest the conclusions may not be valid. However, we strongly agree that the significance of the intraglottal vortices has not been definitively shown and that the question of significance is best answered using a computational model.

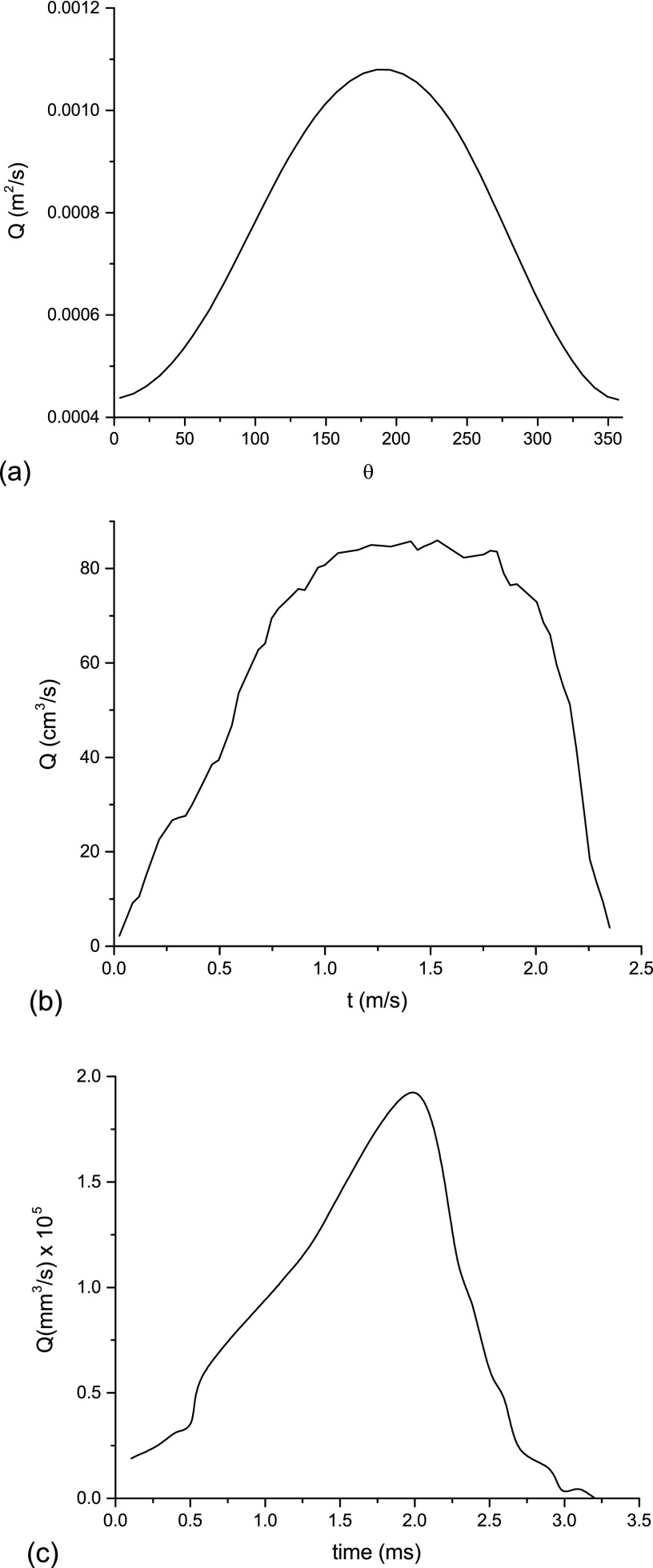
First, the most significant concern about Farahani and Zhang's model is the lack of agreement of their results with published experimental data. The results shown for the flow rate in their model do not match the waveform characteristics that were observed experimentally in canine larynges (Fig. 1). The maximum skewing of the flow rate predicted by the model has a value of 1.1 for the speed quotient, which is far less than values observed experimentally (1.5−2.5) in canine models.15,19 The results of Farahani and Zhang's model show minor skewing of the waveform towards closing and in some cases skewing towards opening (cf. Figs. 3 and 4 in their letter18). As far as we know, skewing towards opening was never observed experimentally in a canine larynx when the vocal folds are approximated symmetrically about the midline with no prephonatory gap.

FIG. 1.

FIG. 1.

Open in a new tab

Reproduced waveforms of the (a) glottal flow rate from Farahani and Zhang (Ref. 18) (cf. Fig. 3). The image shows minimal skewing (SQ = 1.1) in the stiff case with the highest magnitudes of subglottal pressure and the pressure from the vortices. (b) Example of flow rate measurement at the glottal exit in a canine larynx (Ref. 15) showing distinct skewing of the flow rate waveform. (c) Example of the flow rate measurement about 1 cm above the folds (Ref. 19) (cf. Fig. 8) also showing skewing.

Second, the imprecise properties of the tissue used to model the elasticity of the vocal folds are another significant limitation for the model used by Farahani and Zhang. Several studies have shown that the tissue stiffness (i.e., Young's modulus) changes along the vertical height of the fold.20,21 Other studies have also shown that the stiffness of the tissue changes in a non-linear fashion as a function of tissue strain, which is determined by the subglottal pressure and the mechanical properties of the tissue layers.22,23 Therefore, using a two-layer vocal fold model, which uses the same Young's modulus value(s) to characterize the elasticity of the tissue, is inadequate.

Third, the magnitudes of the elasticity values used in their model represents an exaggerated stiffness value of the tissue. The imprecision of the tissue properties comes from the mismatch between the Young's modulus values that Farahani and Zhang used and the values observed experimentally21 in canine larynges. The levels of the subglottal pressure are not high enough to produce the strain in the tissue that corresponds to the Young's modulus values that are used in the model. The exaggerated stiffness values that are used to model the tissue are likely to affect how the displacement of the folds occurs in the model in response to the deriving pressures from the subglottal and the vortices. The magnitudes of the elasticity values used in the model might be justifiable based on human data,23 but in order to correctly assess the effect of the vortices, the elasticity values should match what is measured in the same model (i.e., canine).

Finally, the use of Bernoulli's equation to predict the air pressure on the surface of the vocal folds is flawed because the assumptions, namely steady and inviscid flow, are invalid. The pressure predicted by Bernoulli's equation is related to the ratio of glottal area and will approach a singular value (i.e., infinite) when the opening area approaches zero (i.e., glottal closure). Farahani and Zhang did not simulate complete glottal closure thereby avoiding this problem; however, our experiments simulating “normal vibration” always showed complete glottal closure.

Other critical details have been omitted making it difficult to assess the significance of the intraglottal vortices. For example, it is unclear why the effect of the vortices was also applied during the opening phase, and if the direction of the aerodynamic force applied to the glottal wall was changed between opening and closing. The lapse that develops is evident in the results that show the glottal flow waveforms that develop from the same subglottal pressure with different levels of pressure produced by the vortices (cf. Fig. 3 in their letter18). During the opening phase the glottis assumes a convergent shape and the glottal flow separates from the glottal wall at the level of the glottal exit. Since intraglottal vortices do not form during the opening phase the only aerodynamic force that is applied to the glottal wall during opening is related to the subglottal pressure; inertance is not a factor since no vocal tract is used. It is unclear why the model of Farahani and Zhang predicts changes in the flow rate during opening for the same subglottal pressure. It is reasonable to assume that the erroneous flow characteristics during opening will propagate in the model and affect the flow characteristics during closing.

III. CONCLUSION

In order to determine the validity of any model that addresses the issue of vortex significance, it is important that the results of the computational model would be compared with actual experimental results. The results predicted by Farahani and Zhang's model18 are inconsistent with data published for other experimental and computational models, specifically regarding the waveform of Q and values for tissue elasticity. Given the inconsistency with experimental results and lack of agreement with published data, readers should be cautious regarding the authors' conclusion that the contribution from the intraglottal vortices is negligible. The significance of the intraglottal vortices is still debatable and further work is needed to substantiate their role.

ACKNOWLEDGMENT

The authors acknowledge the support of NIH Grant No. R01DC009435.

References

  • 1. Fant G., “ Preliminaries to analysis of the human voice source,” STL-QPRS 4, 1−27 (1983). [Google Scholar]
  • 2. Titze I. R., “ The physics of small amplitude oscillation of the vocal folds,” J. Acoust. Soc. Am. 83, 1536−1552 (1988). 10.1121/1.395910 [DOI] [PubMed] [Google Scholar]
  • 3. Stevens K. N., Acoustic Phonetics ( MIT Press, Cambridge, MA, 2000), pp. 75−126. [Google Scholar]
  • 4. Fant G., Acoustic Theory of Speech Production ( Mouton, The Hague, Netherlands, 1960), pp. 15−92. [Google Scholar]
  • 5. Sundberg J. and Gauffin J., “ Waveform and spectrum of the glottal voice source,” in Frontiers of Speech Communication Research, edited by Lindholm B. and Ohman S. ( Academic, New York, 1979), pp. 301−320. [Google Scholar]
  • 6. Holmberg E., Hillman R. E., and Perkell J. S., “ Glottal air flow and transglottal pressure measurements for male and female speakers in soft, normal and loud voice,” J. Acoust. Soc. Am. 84, 511−529 (1988). 10.1121/1.396829 [DOI] [PubMed] [Google Scholar]
  • 7. Gauffin J. and Sundberg J., “ Spectral correlates of glottal voice source waveform characteristics,” J. Speech Lang. Hear. Res. 32, 556−565 (1989). 10.1044/jshr.3203.556 [DOI] [PubMed] [Google Scholar]
  • 8. Sapienza C. M. and Stathopoulos E. T., “ Comparison of maximum flow declination rate: Children versus adults,” J. Voice 8, 240−247 (1994). 10.1016/S0892-1997(05)80295-4 [DOI] [PubMed] [Google Scholar]
  • 9. Khosla S., Oren L., Ying J., and Gutmark E., “ Direct simultaneous measurement of intraglottal geometry and velocity fields in excised larynges,” Laryngoscope 124, S1−S13 (2014). 10.1002/lary.24512 [DOI] [PubMed] [Google Scholar]
  • 10. Oren L., Khosla S., and Gutmark E., “ Intraglottal pressure distribution computed from empirical velocity data in canine larynx,” J. Biomech. 47, 1287−1293 (2014). 10.1016/j.jbiomech.2014.02.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11. Oren L., Khosla S., and Gutmark E., “ Intraglottal geometry and velocity measurements in canine larynges,” J. Acoust. Soc. Am. 135, 380−388 (2014). 10.1121/1.4837222 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12. Zhao W., Zhang C., Frankel S. H., and Mongeau L., “ Computational aeroacoustics of phonation, Part I: Computational methods and sound generation mechanisms,” J. Acoust. Soc. Am. 112, 2134−2146 (2002). 10.1121/1.1506693 [DOI] [PubMed] [Google Scholar]
  • 13. Mihaescu M., Khosla S., Murugappan S., and Gutmark E., “ Unsteady laryngeal airflow simulations of the intra-glottal vortical structures,” J. Acoust. Soc. Am. 127, 435−444 (2010). 10.1121/1.3271276 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14. de Luzan C. F., Chen J., Mihaescu M., Khosla S. M., and Gutmark E., “ Computational study of false vocal folds effects on unsteady airflows through static models of the human larynx,” J. Biomech. 48, 1248−1257 (2015). 10.1016/j.jbiomech.2015.03.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15. Oren L., Khosla S., Dembinski D., Ying J., and Gutmark E., “ Direct measurement of planar flow rate in an excised canine larynx model,” Laryngoscope 125, 383−388 (2015). 10.1002/lary.24866 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16. Khosla K., Oren L., and Gutmark E., “ An example of the role of basic science research to inform the treatment of UVFP,” Perspect. Voice Voice Disord. 24, 37−50 (2014). 10.1044/vvd24.1.37 [DOI] [Google Scholar]
  • 17. Murugappan S., Khosla S., Casper K., Oren L., and Gutmark E., “ Flow fields and acoustics in a unilateral scarred vocal fold model,” Ann. Otol. Rhinol. Laryngol. 118, 44−50 (2009). 10.1177/000348940911800108 [DOI] [PubMed] [Google Scholar]
  • 18. Farahani M. H. and Zhang Z., “ A computational study of the effect of intraglottal vortex-induced negative pressure on vocal fold vibration,” J. Acoust. Soc. Am. 136, EL369−EL375 (2014). 10.1121/1.4898743 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19. Verneuil A., Berry D. A., Kreiman J., Gerratt B. R., Ming Y. E., and Berke G. S., “ Modeling measured glottal volume velocity waveforms,” Ann. Otol. Rhinol. Laryngol. 112, 120−131 (2003). 10.1177/000348940311200204 [DOI] [PubMed] [Google Scholar]
  • 20. Chhetri D. K., Zhang Z., and Neubauer J., “ Measurement of young's modulus of vocal folds by indentation,” J. Voice 25, 1−7 (2011). 10.1016/j.jvoice.2009.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21. Oren L., Dembinski D., Gutmark E., and Khosla S., “ Characterization of the vocal fold vertical stiffness in a canine model,” J. Voice 28, 297−304 (2014). 10.1016/j.jvoice.2013.11.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22. Perlman A. L., Titze I. R., and Cooper D. S., “ Elasticity of canine vocal fold tissue,” J. Speech Lang. Hear. Res. 27, 212−219 (1984). 10.1044/jshr.2702.212 [DOI] [PubMed] [Google Scholar]
  • 23. Berke G. and Smith M. “ Intraoperative measurement of the elastic modulus of the vocal fold. Part 2. Preliminary results,” Laryngoscope 102, 770−778 (1992). 10.1288/00005537-199207000-00006 [DOI] [PubMed] [Google Scholar]

Articles from The Journal of the Acoustical Society of America are provided here courtesy of Acoustical Society of America

RESOURCES