Sensitivity estimation in time-of-flight list-mode positron emission tomography

Abstract

Purpose:

An accurate quantification of the images in positron emission tomography (PET) requires knowing the actual sensitivity at each voxel, which represents the probability that a positron emitted in that voxel is finally detected as a coincidence of two gamma rays in a pair of detectors in the PET scanner. This sensitivity depends on the characteristics of the acquisition, as it is affected by the attenuation of the annihilation gamma rays in the body, and possible variations of the sensitivity of the scanner detectors. In this work, the authors propose a new approach to handle time-of-flight (TOF) list-mode PET data, which allows performing either or both, a self-attenuation correction, and self-normalization correction based on emission data only.

Methods:

The authors derive the theory using a fully Bayesian statistical model of complete data. The authors perform an initial evaluation of algorithms derived from that theory and proposed in this work using numerical 2D list-mode simulations with different TOF resolutions and total number of detected coincidences. Effects of randoms and scatter are not simulated.

Results:

The authors found that proposed algorithms successfully correct for unknown attenuation and scanner normalization for simulated 2D list-mode TOF-PET data.

Conclusions:

A new method is presented that can be used for corrections for attenuation and normalization (sensitivity) using TOF list-mode data.

1. INTRODUCTION

Positron emission tomography (PET) is a molecular imaging technique that provides quantitative information of the biodistribution of an administered radiotracer in the subject under study. This quantitative information is relevant in many cases,^1–3 and it is one of the main advantages of PET over other imaging techniques. In order to obtain this quantitative information, some calibrations and corrections are required,⁴ being the sensitivity correction the most significant one in most cases. The sensitivity of a particular voxel in a PET scanner is defined as the probability that a positron emitted in that voxel is finally detected as a coincidence in a pair of detectors in the scanner. There are several factors that affect the sensitivity, like the geometry and configuration of the scanner (that will be considered fixed in this work), possible variations of the sensitivity of the scanner detectors (which is usually corrected by a normalization procedure), and the attenuation of the annihilation gamma rays in the object. These last two factors may change the sensitivity of coincidence detection in each line-of-response (LOR) of the PET scanner, ultimately affecting the overall sensitivity.

Normalization correction of the sensitivity of each pair of detector elements is commonly obtained using uniform sources⁵ and comparing the measured data with the expected outcomes. This is a tedious procedure which is routinely performed daily in clinical scanners because the sensitivity of each detector element may change over time.⁶ On the other hand, attenuation correction is currently performed based on a transmission source acquired before the PET scan. The source, which in early PET scanners usually consisted of a ⁶⁸Ga ring, has been replaced by a computed tomography (CT) scan. In this case, the attenuation measured by the x-rays from the CT scan is converted into 511 keV attenuation coefficients⁷ to obtain the attenuation map. The replacement of the long transmission acquisitions by fast CT scans was a significant improvement in the patient management in hospitals and facilitated the adoption of PET as one of the most important techniques in oncology, cardiology, and neurology. This was also motivated by the fact that the anatomical information provided by the CT was the perfect complement to the molecular and functional information provided by PET. Nevertheless, there are still two main concerns about the use of CT scans for PET attenuation correction. First, the motion of the heart and the lungs during the PET scan may create a mismatch respect to the still (usually holding breath) image obtained with the CT. This may generate artifacts in some regions of the torso.⁸ Second, a whole-body CT scan may deposit a very significant amount of radiation in the patients,⁹ which is an important concern for children and patients undergoing many radiological procedures.

In the last few years, the new combined PET and magnetic resonance (MR) scanners^10–12 and their lack of a CT scan have made nonCT-based attenuation correction methods to be revisited.^13,14 MR-derived images give a lot of useful anatomical information, but they are not fully related to the attenuation parameters, and therefore, they cannot be used for attenuation correction in a straightforward way. For instance, MR Dixon fat-water images can be segmented into four tissue classes (air, lung, fat, and water) and then assigned predetermined attenuation coefficients to each class.¹⁵ Nevertheless, as bones and patient-specific attenuation coefficients are not considered, this method does not provide enough accuracy.¹⁶ Many different solutions have been proposed to address this problem^17–19 but it continues to be an important issue for PET-MR modality.²⁰ It is worth mention that nonCT-based attenuation correction methods have been also proposed in dedicated breast PET scanners.²¹ In that case, the PET image is used to segment the volume into two tissues (water/air). This provides a first-order correction that may be valid in some studies.

With the introduction of modern time-of-flight (TOF)-PET scanners, new imaging capabilities have become available.²² As shown in Defrise et al.,²³ attenuation maps can be estimated from emission TOF data to the accuracy of an additive constant. This possibility has gained a lot of interest and several methods have been recently proposed to obtain the joint reconstruction of the activity and the attenuation.^24–28 These methods may remove the need of an additional acquisition to obtain the attenuation correction and hold the potential to avoid the aforementioned problems of CT-based and MR-based corrections.

In this work, we propose a new approach to handle TOF-PET data which allows performing either or both (1) attenuation correction and (2) LOR normalization correction (selfnormalization) using only TOF-PET data. By doing this, we extend previously published algorithms to handle unknown normalization as well.²⁹ Our approach has significant differences with respect to previously proposed methods that jointly estimate the activity and the attenuation using TOF data. On one hand, it is not based on a maximum-likelihood derivation, but on a fully Bayesian approach (Sec. 2.A) that does not use the assumption of Poisson statistics. This provides a different insight into the problem. On the other hand, instead of obtaining the image of the activity in each voxel and the attenuation in each LOR [like the MLACF (Refs. ^24–26) algorithm does], or obtaining the activity and the attenuation in each voxel [MLAA (Ref. ²⁷) and MLAA-GMM (Ref. ²⁸) algorithms], our proposed algorithm estimates the number of detected coincidences coming from each voxel and the total sensitivity of each voxel. As the sensitivity is connected with the attenuation factor in each LOR via a backward projection, our method in that sense lies between the MLAACF and the MLAA algorithms. Appendix B shows the connection between algorithms such as MLACF (Refs. ^24–26) and this work.

We use computer simulations to validate our approach; however, in the initial validations performed in this paper, we do not take into account randoms and Compton scatter which are important effects in order to achieve fully quantitative PET and we will investigate these effects in the future. In Sec. 2.D, we provide strategies to implement corrections for those effects in algorithms proposed in this work.

This paper presents in Sec. 2.A the fully Bayesian model of the problem of simultaneous sensitivity and image estimation from TOF-PET data. In Secs. 2.B and 2.C, we propose two algorithms to compute the sensitivity image and we evaluate them numerically with simulations in Sec. 3.

2. SENSITIVITY CORRECTION ALGORITHM

2.A. Theoretical derivation

Suppose a tomographic imaging system defined by I voxels indexed by i and K LORs indexed by k. In general, the size of the voxels can be made as small as needed, so the theory presented here applies in the limit of zero size and continuous image representation. We also assume that the TOF information for each LOR is available and there are T TOF bins per LOR. Therefore, the total number of detector elements is KT. The width of the TOF bins can be also made asymptotically zero.

The actual measured data, including TOF information, are denoted by the vector g with elements g_kt, k is the index of LOR, and t is the index of TOF in LOR k, while the sum over all TOF bins in the LOR k is denoted by $g_k={\mathbf{\sum }}_{t=1}^T{g}_{kt}$. We define unobservable complete data y_kti, which represent the number of decays that occurred in voxel i and were detected in LOR k in the TOF bin t. The total number of decays that occurred per voxel i and was detected in any projection element is represented by c_i. Therefore, $c_i={\mathbf{\sum }}_{k=1}^K{\mathbf{\sum }}_{t=1}^T{y}_{\mathit{kti}}$.

For such system, we define a system matrix with elements h_kti which represents the probability that a decay in voxel i is detected in the projection element indexed by k and t. h_kti does not include effects of attenuation and normalization. If we consider a vector a and an element a_k represents the attenuation/normalization factor of LOR k, with values between 0 and 1, we can then define the system matrix elements ${\tilde{h}}_{\mathit{kti}}$ which includes attenuation and normalization as ${\tilde{h}}_{\mathit{kti}}=h_{\mathit{kti}}{a}_k$. The sensitivity of a voxel i is then given by ${\tilde{\epsilon }}_i={\mathbf{\sum }}_{k=1}^K{\mathbf{\sum }}_{t=1}^T{\tilde{h}}_{\mathit{kti}}$, which is equivalent to ${\tilde{\epsilon }}_i={\mathbf{\sum }}_{k=1}^K{a}_k{\mathbf{\sum }}_{t=1}^T{h}_{\mathit{kti}}$. If we define ${\alpha }_{\mathit{ki}}={\mathbf{\sum }}_{t=1}^T{h}_{\mathit{kti}}$ (i.e., α_ki are the elements of the system matrix when TOF information is not used, there is no attenuation, and all normalization factors are 1), we can rewrite the voxel sensitivity as ${\tilde{\epsilon }}_i={\mathbf{\sum }}_{k=1}^K{a}_k{\alpha }_{\mathit{ki}}$.

As shown in Refs. ^30–33, the conditional probability of complete data is given by

$${\displaystyle p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)={\mathbf{\prod }}_{i=1}^I\frac{c_i!}{{\tilde{\epsilon }}_i^{c_i}}{\mathbf{\prod }}_{k=1}^K{\mathbf{\prod }}_{t=1}^T\frac{{\left({\tilde{h}}_{\mathit{kti}}\right)}^{y_{\mathit{kti}}}}{y_{\mathit{kti}}!}}$$ (1)

for y such that c_i = ∑_k∑_ty_kti and zero otherwise. Bold symbols y, a, and c indicate vectors with sizes KTI, K, and I, respectively. This notational convention is used throughout the paper. Equation (1) can be derived using general binomial statistics of nuclear decay without Poisson distribution approximation. The Poisson approximation is almost always assumed in other formulations of imaging statistics. We note that Eq. (1) can be rewritten as

$${\displaystyle p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)={\mathbf{\prod }}_{i=1}^I\frac{c_i!}{{\tilde{\epsilon }}_i^{c_i}}{\mathbf{\prod }}_{k=1}^K{\left(a_k\right)}^{y_{\mathit{ki}}}{\mathbf{\prod }}_{t=1}^T\frac{{\left(h_{\mathit{kti}}\right)}_{}^{y_{\mathit{kti}}}}{y_{\mathit{kti}}!},}$$ (2)

where we slightly simplified the notation by defining y_ki = ∑_ty_kti. The above probability distribution is insensitive to scaling of a, as $p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)=p\left(\mathbf{y}|x\mathbf{a},\mathbf{c}\right)$ for any scalar x > 0 if c_i = ∑_ky_ki, which holds from the definition given in Eq. (1). This is consistent with the results described by Defrise et al.²³ who showed that attenuation maps can be determined to the accuracy of a constant scalar factor. The model of the acquired data³¹ g is

$${\displaystyle p\left(\mathbf{g}|\mathbf{a},\mathbf{c}\right)=\mathbf{\sum }_{\mathrm{y}ϵY_{\mathrm{g}}{\cap }^{Y_{\mathrm{c}}}}p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right),}$$ (3)

where $Y_{\mathbf{g}}=\left\{\mathbf{y}:{\mathbf{\sum }}_i{y}_{\mathit{kti}}=g_{kt}\right\}$ and $Y_{\mathrm{c}}=\left\{\mathbf{y}:{\mathbf{\sum }}_k{\mathbf{\sum }}_t{y}_{\mathit{kti}}=c_i\right\}$ are subsets of Y. Equation (3) is simply the statements that probability of observed data is equal to sum of probabilities of complete data that are consistent with the observed data. Using the Bayes’ theorem, the posterior probability p(a, c|g) is

$${\displaystyle p\left(\mathbf{a},\mathbf{c}|\mathbf{g}\right)=\frac{p\left(\mathbf{g}|\mathbf{a},\mathbf{c}\right)p\left(\mathbf{a},\mathbf{c}\right)}{p\left(\mathbf{g}\right)}.}$$ (4)

Assuming flat prior of joint probability p(a, c) ∝ 1 for a_k ∈ [0, 1] and zero otherwise, we obtain the final form of the posterior distribution,

$${\displaystyle p\left(\mathbf{a},\mathbf{c}|\mathbf{g}\right)\propto \mathbf{\sum }_{\mathrm{y}ϵY_g{\cap }^{Y_{\mathrm{c}}}}p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right),}$$ (5)

where $p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)$ is given by Eq. (2). Note that the election of the range [0, 1] for a_k is arbitrary because of the freedom of scaling.

Both quantities a and c are unknown, but we are not directly interested in a, which makes it a nuisance quantity. In this work, we investigate two approaches to remove dependence of the posterior on the unknown a. We estimate it using a fixed-point (FP) iteration algorithm³⁴ (Sec. 2.B) or marginalize it (integrate out) with a Markov chain Monte Carlo (MCMC) algorithm (Sec. 2.C). Both approaches provide the posterior of c.

Once the posterior of c is estimated, other quantities that are proportional to the concentration of the tracer in the voxels (e.g., voxel activity or the number of total decays per voxel d) can be derived as described in Sec. 2.D and Appendix D.

2.B. Fixed-point algorithm for sensitivity correction

In this section, we derive an easy approach to implement iterative algorithm for finding the maximum of $p\left(\mathbf{a},\mathbf{c}|\mathbf{g}\right)$ for a fixed c. It can also be used with standard iterative image reconstruction methods (See Appendix B). The algorithm is derived by computing the derivative of the posterior $p\left(\mathbf{a},\mathbf{c}|\mathbf{g}\right)$ with respect to a and finding the conditions for which the derivative is equal to zero,

$${\displaystyle \frac{\partial p(\mathbf{a},\mathbf{c}|\mathbf{g})}{\partial a_{k^{\prime }}}\propto \mathbf{\sum }_{\mathrm{y}ϵY_{\mathrm{g}}{\cap }^{Y_{\mathrm{c}}}}\frac{\partial p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)}{\partial a_{k^{\prime }}}.}$$ (6)

Using Eq. (2), we arrive to (see the derivation in Appendix C)

$${\displaystyle \frac{\partial p\left(\mathbf{a},\mathbf{c}|\mathbf{g}\right)}{\partial a_{k^{\prime }}}\propto \mathbf{\sum }_{\mathrm{y}ϵY_{\mathrm{g}}{\cap }^{Y_{\mathrm{c}}}}\left(\frac{g_{k^{\prime }}}{a_{k^{\prime }}}-\mathbf{\sum }_i\frac{{\alpha }_{k^{\prime }i}{c}_i}{{\tilde{\epsilon }}_i}\right)p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right).}$$ (7)

The content of the parenthesis can be pulled before the sum because it is the same for a given g and c, and therefore, the derivative is zero if for each k,

$${\displaystyle \frac{g_k}{a_k}={\mathbf{\sum }}_{i=1}^I\frac{{\alpha }_{\mathit{ki}}{c}_i}{{\tilde{\epsilon }}_i}.}$$ (8)

To intuitively understand the above equation, we notice that $c_i/{\tilde{\epsilon }}_i$ is the estimate of the number of decays that occurred in voxel i during the scan. As a reminder, c_i is the number of decays that occurred and was detected, and ${\tilde{\epsilon }}_i$ is the voxel sensitivity that contains not only geometrical effects but also the nonperfect detection efficiency (normalization) and attenuation. Therefore, the right-hand side of the equation represents the estimate of the number of decays that would have been detected if there were perfect efficiency and no attenuation (α does not contain those effects). The left hand side of Eq. (8) represents the estimate of the same quantity from the acquired data. Rewriting Eq. (8), we obtain the relation,

$${\displaystyle a_k=\frac{g_k}{\mathbf{\sum }_{i=1}^I({\alpha }_{\mathit{ki}}{c}_i/{\tilde{\epsilon }}_i)}=\frac{g_k}{\mathbf{\sum }_{i=1}^I\left({\alpha }_{\mathit{ki}}{c}_i/\mathbf{\sum }_{k=1}^K{\alpha }_{\mathit{ki}}\hspace{0.17em}{a}_k\right)}.}$$ (9)

If we use the sensitivity obtained from the back-projection of the a_k factors in each LOR, to obtain the following relationship for ${\tilde{\epsilon }}_i$ which is the main theoretical result of this work,

$${\displaystyle {\tilde{\epsilon }}_i={\mathbf{\sum }}_{k=1}^K{\alpha }_{\mathit{ki}}{a}_k={\mathbf{\sum }}_{k=1}^K\frac{{\alpha }_{\mathit{ki}}{g}_k}{\mathbf{\sum }_{i=1}^I\left({\alpha }_{\mathit{ki}}{c}_i/{\tilde{\epsilon }}_i\right)}.}$$ (10)

Equation (10) can be solved iteratively using the fixed-point algorithm³⁴ given next. Let’s assume that an estimate $\hat{c}$ of the image of detected decays has been obtained from TOF-PET data based on a current estimate of the sensitivity ${\tilde{\epsilon }}_i$. In general, ${\tilde{\epsilon }}_i$ may be unknown due to a missing attenuation maps, normalization, or both. In such case, we can apply the following algorithm.

• 1.For each LOR for which g_k > 0, compute the projection ${\mathbf{\sum }}_{i=1}^I({\alpha }_{\mathit{ki}}{c}_i/{\tilde{\epsilon }}_i)$. This projection uses the same system matrix employed for the estimation of c_i, and it does not contain normalization or attenuation factors. Note that in this case, we do not make use of the TOF information, as we compute the sum over all the TOF bins of the LOR k.
• 2.Find an estimate of the factor ${\hat{a}}_k$ using Eq. (9).
• 3.Create a new estimation of ${\tilde{\epsilon }}_i$ by backward projecting the values of ${\hat{a}}_k$ [Eq. (10)]. The backward projection is again performed without TOF.
• 4.Go back to step 1. Repeat R times.

After R iterations of this algorithm, we end up with an estimator of the sensitivity ${\tilde{\epsilon }}_i$ (to the accuracy of multiplicative constant). Then, with the new sensitivity estimate, we can continue with the image reconstruction, performing new iterations for obtaining a better estimation of c_i’s using the origin ensemble (OE) algorithm.³⁰ After that, another R iterations of the proposed algorithm for sensitivity estimation can be performed. Therefore, the proposed method consists on alternating reconstructions of the image c_i for a fixed sensitivity ${\tilde{\epsilon }}_i$ and vice versa. Note that steps 2 and 3 can be performed together [using Eq. (10)], and no explicit computation of ${\hat{a}}_k$ is actually needed with this algorithm.

2.C. Markov chain Monte Carlo algorithm for sensitivity correction

The posterior probability distribution $p\left(\mathbf{a},\mathbf{c}|\mathbf{g}\right)$ can be also sampled using Markov chains as described in our previous publications.^30–33 As direct sampling the posterior $p\left(\mathbf{a},\mathbf{c}|\mathbf{g}\right)$ from Eq. (5) is difficult because of the sum, we instead derive MC samples from $p\left(\mathbf{a},\mathbf{y}|\mathbf{g}\right)$ and marginalize them to obtain samples of $p\left(\mathbf{a},\mathbf{c}|\mathbf{g}\right)$. This computational technique is an example of data augmentation for posterior computing.³⁵ Therefore, samples from a and c are obtained using the following stochastic algorithm which is a combination of previously published OE (Refs. ^30–33) algorithm that creates samples from c and another Markov chain algorithm which generated samples in a. The algorithm uses a parameter $\gamma \left(0<\gamma <1\right)$ which represents the branching ratio between the sampling of c and a. This constant determines the efficiency of the Markov chain algorithm and was empirically set to γ = 0.98.

Step 1—Initialize c: For each detected event, guess the location of its origin by placing it in a voxel of maximum TOF likelihood.³²

Step 2—Initialize $\tilde{\epsilon }$: If no prior estimation of a is available, set all elements of a to 1 (or any other nonzero number). Then, backward project it using the coefficients $\alpha \left({\tilde{\epsilon }}_i={\mathbf{\sum }}_{k=1}^K{a}_k{\alpha }_{\mathit{ki}}\right)$.

Step 3—Loop many times: Select a random number r (from 0 to 1).

If r < γ, perform step (3A), otherwise perform step (3B).

(3A)—Perform a standard OE algorithm move³⁰ generating a new sample of c.

(3B)—Generate a new sample of a and accept it or not using Metropolis–Hasting algorithm. If the new sample is accepted, update the sensitivity $\tilde{\epsilon }$ accordingly.

The OE algorithm of step (3A) was discussed in several previous publications. We briefly describe it here for sake of completeness. First, a single detected count is randomly selected. Next, a new voxel from which this count could have originated from TOF kernel h_kti is randomly chosen. The new location of the origin of that count is accepted if $p\left(\mathbf{a},{\mathbf{y}}^{\prime }|\mathbf{g}\right)\ge p\left(\mathbf{a},\mathbf{y}|\mathbf{g}\right)$. On the other hand, if $p\left(\mathbf{a},{\mathbf{y}}^{\prime }|\mathbf{g}\right)<p\left(\mathbf{a},\mathbf{y}|\mathbf{g}\right)$, it is accepted with a chance $p\left(\mathbf{a},{\mathbf{y}}^{\prime }|\mathbf{g}\right)/p\left(\mathbf{a},\mathbf{y}|\mathbf{g}\right)$, being y and y′ the configurations of origins (complete data indicating from which voxel each detected event originated) before and after the move. The ratio can be computed using Eq. (2). If a new sample $y_{\mathit{kti}}^{\prime }$ is accepted, we update c subtracting one count from the initial voxel and adding it to the final one. For more details, see Refs. ^30–33.

The algorithm (3B) used to generate a new sample of a is specified next. Note that algorithm (3B) is different than (3A) because a draw from a continuous distribution is made as opposed to discrete distribution used in (3A). We assume that the prior density $p\left(\mathbf{a}\right)=1$ for 0 ≤ a_k ≤ 1, and 0 otherwise. A new sample is generated by adding a random number δ in the range [ − Δ, Δ], with 0 < Δ < 1, to the factor a_k, where the LOR k is chosen randomly from all LORs for which g_k > 0. If we denote by a′ a new sample created by adding δ to a_k, we accept the change if the value of the posterior $p\left({\mathbf{a}}^{\prime },\mathbf{y}|\mathbf{g}\right)\ge p\left(\mathbf{a},\mathbf{y}|\mathbf{g}\right)$. Otherwise, if $p\left({\mathbf{a}}^{\prime },\mathbf{y}|\mathbf{g}\right)<p\left(\mathbf{a},\mathbf{y}|\mathbf{g}\right)$, we accept it conditionally with a probability $p\left({\mathbf{a}}^{\prime },\mathbf{y}|\mathbf{g}\right)/p\left(\mathbf{a},\mathbf{y}|\mathbf{g}\right)$. Using Eq. (2), we have

$${\displaystyle \frac{p\left({\mathbf{a}}^{\prime },\mathbf{y}|,\mathbf{g}\right)}{p\left(\mathbf{a},\mathbf{y}|,\mathbf{g}\right)}={\left(1+\frac{\delta }{a_k}\right)}^{g_k}{\mathbf{\prod }}_{i=1}^I{\left(1+\frac{{\alpha }_{\mathit{ki}}\delta }{{\tilde{\epsilon }}_i}\right)}^{-c_i}.}$$ (11)

The above equation can be simplified if δ is assumed small (see Appendix A), but for the purpose of this work, we used the exact formula expressed by Eq. (11).

If a_k + δ fell outside the allowed region [0, 1], the value a_k + δ is “folded” back. For example, if (a_k + δ) > 1, the new folded value is $1-\left(a_k+\delta -1\right)=(2-a_k-\delta )$, and if (a_k + δ) < 0, the new folded value is $0-\left(a_k+\delta -0\right)=-\left(a_k+\delta \right)$. This ensures that the probability of selecting $a_k^{\prime }$ when the current value of the chain is a_k, to be the same as the probability of selecting a_k when the chain value is $a_k^{\prime }$, which is a requirement for the Markov chain to achieve equilibrium. The above algorithm requires specification of Δ. Similarly to what happens with the parameter γ, the value of Δ will affect the efficiency of Markov chain but not the result of the analysis. In the results presented in this work, we have used Δ = 0.05, but we also tested the performance on a range of 0.01–0.5 and found the efficiency relatively unchanged. See Sec. 4 for more extensive discussion on the efficiency of Markov chains.

As indicated before, if a new sample of $a_k^{\prime }$ is accepted, the new sample of sensitivity is obtained by backward projecting δ and adding it to current $\tilde{\epsilon }$ using

$${\displaystyle {\tilde{\epsilon }}_i^{\prime }={\tilde{\epsilon }}_i+{\alpha }_{\mathit{ki}}\delta .}$$ (12)

The loop of the step 3 of the algorithm, repeated N times, constitutes one iteration.

In this work, we have not studied in depth the efficiencies of the Markov chain and empirically determined that the value γ = 0.98 provides well behaving chains in all experiments that were performed. We also found that if we vary γ between 0.5 and 0.99, the efficiency is not strongly affected indicating the robustness of the method respect to this parameter. Note that the efficiency does not affect the result of the method but only the computing time needed to achieve it.

2.D. Quantitative tracer concentration

So far, we formulated the inverse problem in terms of the quantity c; the number of events per voxel that were detected, which of course, is affected by attenuation/normalization effects. Nevertheless, we are typically not interested in c, but in a quantity that is proportional to the concentration of the tracer in each voxel. We define such quantity as d with elements d_i which describes the number of events that occurred (detected or not) during that scan. We would like to stress here that fd is not the same as the voxel activity f. Voxel activity f is a real number that describes the average number of emissions per unit time. Typically, these two quantities will be very close. The posterior, $p\left(\mathbf{d}|\mathbf{g}\right)$, of this quantity can be obtained using MCMC as described in Ref. 25. However, in this work, we use a more straightforward approach. We first determine the minimum mean square error (MMSE) estimate of c, $\hat{c}$, and then, the estimate of d is obtained simply by dividing it by the estimate of $\tilde{\epsilon }$. It can be shown (see Appendix D) that if $\hat{c}$ is the MMSE estimate, then $\hat{c}/\tilde{\epsilon }$ is the MMSE estimate of d, due to the conditional independence of d and g, given c. See Ref. 31 for proof of conditional independence.

In this paper, we do not address the issue of scatter and randoms. The correction for these effects can be done as in Ref. 32 and can be integrated into the algorithms presented here. In short, if estimates of randoms and scatter are available (rates at projection elements) that information can be used to construct an OE MCMC algorithm that would stochastically reject some of the detected counts effectively correcting c for these effects. Obviously, since the scatter fraction estimation is typically done based on attenuation maps which are unknown, we would have to use some iterative procedure in which scatter is computed every time a more accurate estimation of the attenuation maps is available.

3. RESULTS

3.A. Numerical phantom simulation

A 2D TOF simulation experiment was performed to illustrate the applications of method and to obtain the initial assessment of its performance. In this experiment, c_i’s and ${\tilde{\epsilon }}_i$’s are estimated from the TOF emission data using the OE algorithm for c_i and Monte Carlo and iterative algorithms for ${\tilde{\epsilon }}_i$. Other algorithms than OE can be used to estimate the detected emissions in each voxel, but the OE algorithm is perfectly suited for this task as it also provides estimate of Bayesian errors of the figures of merit.

Figure 1 shows the simulated activity distribution, the attenuation distribution, and the sensitivity image. The diameter of the field of view was 51.2 cm. The simulated TOF-resolution profile was Gaussian with a full-width at half-maximum (FWHM) between 133, 400, and 800 ps, corresponding to a spatial FWHM between 2, 6, and 12 cm, respectively. The attenuation coefficients were 0.095 cm⁻¹ for tissue, 0.0317 cm⁻¹ for lung, 0.142 cm⁻¹ for spine, and 0 cm⁻¹ for air. We used a grid of 128 × 128 and a pixel size of 0.4 cm for these images. Projecting the attenuation image of Fig. 1(B), calculating the exponent of the negative of that projection, and multiplying it by the normalization factors in Fig. 1(D) result in the sinogram shown in Fig. 1(E). The backward projection of this sinogram provides the true sensitivity in Fig. 1(C). We chose the normalization factors to be highly nonuniform and created an artificial pattern on the sinogram of normalization factors [Fig. 1(D)] in order to investigate the effects on the quality of the resulting images. This pattern is quite unrealistic and it is more challenging (i.e., less uniform) that the ones usually found in practice. It was chosen because our goal was to investigate the limits of the algorithms proposed in this paper.

FIG. 1.

(A) Simulated emission phantom. Activity values are 1 (“background”), 10 (“heart”), 0.2 (“lungs”), and 0 elsewhere. Two 8 by 8 black pixel squares correspond to two ROIs used for evaluation. (B) Attenuation: 0.009 66/mm (background tissues), 0.002 66/mm (lungs), 0.0187/mm (“spine”), and 0 elsewhere. (C) Sensitivity image, (D) sinogram of artificially created normalization factors, and (E) sinogram of normalization and attenuation factors. (F) Sinogram of the projections of the emission phantom multiplied by the normalization and attenuation factors for 100 000 total counts.

We obtained the noiseless sinograms of the projection data with 64 angular samples and 128 radial bins of 0.4 cm, by projecting image in Fig. 1(A) with the attenuation maps shown in Fig. 1(B). The resulting noiseless sinogram was multiplied by normalization factors shown in Fig. 1(D) and the sum of the sinogram was normalized to a desired number of total counts N that varied between 20 000 and 1 × 10⁶. The projection was done using exact idealized geometry using areas of pixels inside strips defined by projection bins. Next, the Poisson noise was added to each bin of the noiseless sinograms. Such generated data correspond to a standard PET data with no TOF information. An example noisy sinogram corresponding to 100 thousand counts is shown in Fig. 1(F).

The TOF information was generated for each simulated count by randomly assigning it to a location within the strip area where it could have originated proportionally to activity and pixel area in the strip. Therefore, we simulated the exact locations where detected events occurred (true c). Then, the locations were modified along the corresponding LORs using appropriate TOF kernel to simulate nonideal TOF measurement. Therefore, the generated data were in a list-mode format without any specific predefined number of TOF bins. The algorithms developed in this paper are for the list mode and are independent on the selected number of TOF bins and, in general, this number could be infinity. We note here that when generating the data, we used the Poisson statistics with the true image defined by activities [Fig. 1(A)]. This was done out of convenience. We also note that algorithm used to generate list-mode data makes relation between c and y correct from the statistical point of view and described by Eq. (2). The alternative was to use image of d, number of decays per voxel, as a true image which can also be done; however, creation of the correct dataset would be more complex.

3.B. Methods for estimating the posteriors

We compared three methods for posterior estimation. In method 1, we used the fully MCMC approach described in Sec. 2.C. We used γ = 0.05 and 20 000 iterations for the burn-in period, followed by 20 000 iterations in the equilibrium to obtain samples of the posterior. We allowed an ample number of iterations to achieve the equilibrium, which was confirmed using trace graphs.

For method 2, we used the FP algorithm described in Sec. 2.B. The updates consisted of 1000 repetition of twenty iterations of OE for estimating c (using a fixed $\tilde{\epsilon }$) and ten iterations of the FP algorithm for estimating $\tilde{\epsilon }$ (for a fixed c). After that, 20 000 iterations of OE were used to obtain samples of the posterior of c.

Method 3 was used as a reference, as in this case, the sensitivity image $\tilde{\epsilon }$ was considered known, and only the estimation of c was required. We used 20 000 iterations of OE as a burn-in period, followed by 20 000 iterations of OE algorithm for obtaining the posterior samples.

Figure 2 shows the variation of events with the number of iterations in the image c in two different ROIs with the MCMC (method 1). It can be seen that the variability in ROI 1, in the background, is higher than in the cardiac ROI, as the number of counts in that ROI is smaller.

FIG. 2.

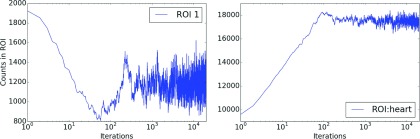
Trace plots corresponding to number of events in c in ROI 1 corresponding to the background (left) and ROI corresponding the heart (right) for method 1, TOF 6 cm, and 100 000 total counts. Equilibrium is achieved around 500–1000 iterations of the MCMC (method 1).

Samples were averaged to obtain MMSE estimates. For estimation of the variances, samples of some marginalized one-dimensional quantity (e.g., number of emissions from each ROI) were histogrammed and the variance of the histograms was computed. One of every 100 samples was used to minimize sample correlations. The estimate of d was obtained dividing the estimate of c by the estimate of the sensitivity. Because the sensitivity estimate was determined only to the accuracy of a constant, we rescaled all images d to have a total number of counts equal to 1.

3.C. Figures of merit

The main result of this work is the proposed method to the estimate of posterior, which cannot be efficiently presented in the paper because of the large dimensionality. Therefore, we decided to summarize the posterior using point estimates of c, d, and $\tilde{\epsilon }$ which can be presented as images, and the whole process can be considered an image reconstruction.

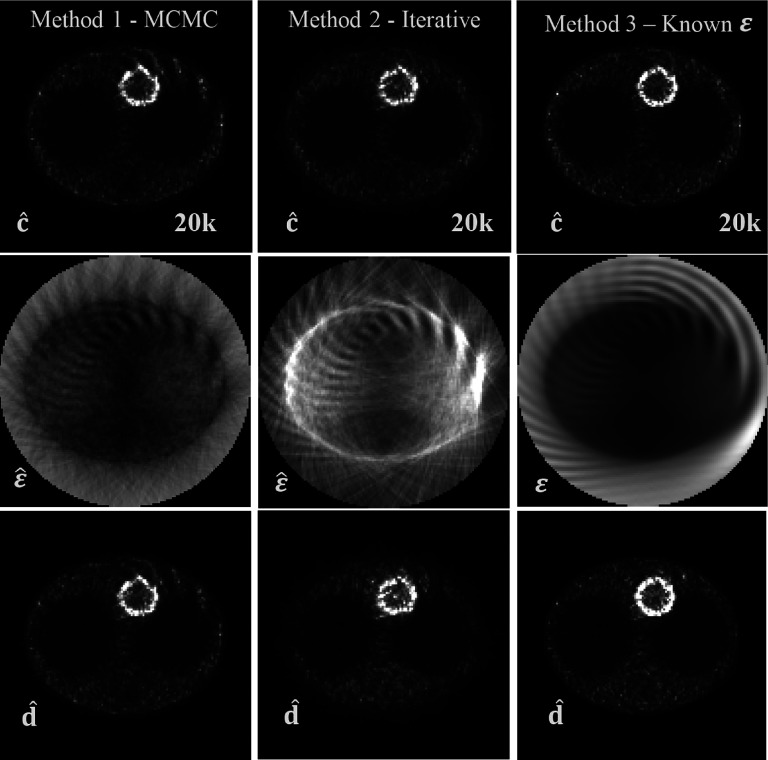
The most important quantity obtained with our approach is c, but we would like to caution the reader that this quantity, when considered as an image, will exhibit artifacts as evidenced in first rows of Figs. 3 and 4. This is because it corresponds to the number of emissions that were detected, and therefore, if a region in the image has a low sensitivity, it will appear as a cold spot on the image c. On the contrary, the image d, which represents the number of decays per voxel, should not exhibit those artifacts.

FIG. 3.

Results for the moderate-count (500k) experiment with TOF resolution 6 cm FWHM. Top row: image of c estimate obtained using three different approaches for the sensitivity estimation: using the MCMC of Sec. 2.B (left), using the fixed-point iterative algorithm of Sec. 2.C (middle), when true attenuation and normalization were used (right). Middle row: respective sensitivity estimates and true sensitivity used in method 3. Bottom row: images of estimates of d.

FIG. 4.

Results for the ultra-low-count (20k) experiment with TOF resolution 6 cm FWHM. Top row: image of c estimate obtained using three different approaches for the sensitivity estimation: using the MCMC of Sec. 2.B (left), using the fixed-point iterative algorithm of Sec. 2.C (middle), and when true attenuation/normalization was used (right). Middle row: respective sensitivity estimates and true sensitivity used in method 3. Bottom row: images of estimates of d.

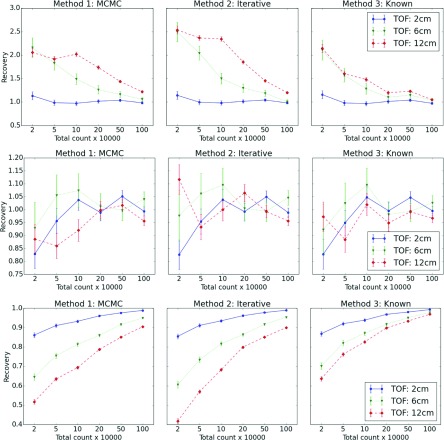
In addition to point estimates, we also evaluated the recovery coefficient for three ROIs. The first two ROIs are shown in Fig. 1 and the third ROI consists of all pixels that comprise the heart walls. The expected number of emissions from a ROI $r\left(rϵ\{1,2,3\}\right)$ that were detected was denoted by E_r and was obtained by multiplying the activity image that generated the data by the true sensitivity within ROIs.

The recovery coefficient was defined as

$${\displaystyle {\mathrm{recovery}}_r={\hat{c}}^r/E_r,}$$ (13)

where ${\hat{c}}^r$ is the number of events in ROI r in the MMSE estimate $\hat{c}$. The Bayesian variance³⁰ of those numbers was also estimated and the square root of the variance was used as the estimate of the error. The MCMC runs consisted of 20 000 iterations as burn-in period followed by 20 000 iterations during which the ${\hat{c}}^r$ was determined. We show trace plots for the burn-in time in Fig. 2 for 100k total counts, 6 cm TOF, and method 1, to demonstrate that equilibrium is reached quite rapidly.

3.D. Summary of results

Figure 3 presents results of the simulation when the total number of counts was 500k. In this case, there are no visible artifacts in the image of d with any of the methods.

However, it is clear that for a very low number of counts (Fig. 4), the images of d (Fig. 4 bottom row) exhibit some serious artifacts. We attribute it to the fact that for that case, there is insufficient information in the data to recover the image of the original object with no artifacts. This is confirmed by the third column in Fig. 4 where the true sensitivity was used and artifacts were still present. It is important to note that this figure has a total of 20k counts, which corresponds to detect only about 2 counts per background voxel. This constitutes an extreme count starvation condition.

With respect to the sensitivity images, it can be seen in row two of Fig. 3 that with the MCMC and the iterative methods, the obtained images both differ greatly in terms of the image texture with respect to the reference image in column 3. Because of the freedom of scaling and this difference in image features and texture, we did not compare those images directly. Interestingly, the general features of the true sensitivity are recovered even with a very low count level in Fig. 4.

Figure 5 shows the ability of the algorithm to recover the expected number of emitted and detected counts in various ROIs. It is quite clear that for a very low count level, the value in ROI 1 is grossly overestimated. This is a well-known effect that occurs in low-count ROIs and it happens with standard reconstruction methods as well. When better experimental evidence is available (better TOF or more counts), this effect is diminished. The number of c-counts recovered in the background ROI located in uniform region is very close to 1. For ROI 3, the heart ROI, the number of c-counts is not fully recovered when information in the data is weak (low count, poor TOF characteristics). It should be noted that because the total number of counts in c is preserved, if one region is underestimated, there must be another region in the image which is overestimated.

FIG. 5.

Rows correspond to recovery coefficient for the three ROIs. The first two ROIs are shown in Fig. 1 and the third corresponds to entire myocardium. Each column corresponds to a different method of analysis. Each inset contains data for three values of TOF. The ideal value of recovery is 1.

4. DISCUSSION

Simultaneous reconstruction of attenuation and activity distribution in nonTOF PET is known to be a strongly ill-posed problem. TOF information has been shown, not only to reduce the sensitivity of PET reconstructions due to attenuation correction errors and inconsistency in the data^22,36 but also to eliminate the problem of activity and attenuation cross-talk in joint estimation methods.²⁸ In this work, we propose a new approach to handle list-mode unbinned TOF-PET data which allows performing either the attenuation correction, LOR normalization correction (selfnormalization), or correction for both those effects simultaneously using TOF-PET data without transmission and without normalization information.

Our approach significantly differs in theory and in implementation from previously proposed methods. We do not use the assumption of Poisson statistics of the data and the method is based on a fully Bayesian view on the statistical description of the problem. Instead of Poisson statistics, the multinomial statistics of complete data is used,³⁰ and the estimated image c represents the number of events emitted from each voxel that was actually detected, rather than the voxel activities (mean of Poisson process) used in the classical approach. As no Poisson model is used, the selection of the main quantities of interest c and $\tilde{\epsilon }$ (the number of detected coincidences coming from each voxel and the total sensitivity of each voxel) requires fewer assumptions. Interestingly, for the case of the TOF reconstruction with unknown attenuation/normalization factors, the image of c is not affected by the inestimable scale factor of the TOF data-based attenuation/normalization correction. In this work, we do not compare performances of our algorithms with previously published methods.^24–28 We believe that a fair comparison deserves a careful and extensive study that is beyond the scope of this work. It is unclear for us how to optimally implement the correction for unknown normalization in the previously published algorithms and it is a future direction of our work. The main goal in TOF-PET reconstruction is to obtain the best possible information about the PET tracer distribution, while the sensitivity image or attenuation factors a are not of direct interest. In a classical treatment, they would be called nuisance parameters,²⁵ whose values are typically estimated. Because of our Bayesian treatment, we marginalize these quantities (method 1). We also propose a hybrid method in which we explore the posterior of c using MCMC but estimate sensitivity image using a fixed-point algorithm (method 2). This is an ad hoc method, as we were not able to find the proof of convergence of the algorithm. Nevertheless, we are confident that the algorithm is quite robust because it was successful in all studies that were performed, including ultra-low count cases and the results (c and d image) were very similar to method 1.

Interestingly, when comparing estimated images of sensitivity obtained with the different methods, they seem strikingly different, although at the same time, the resulting estimates of c and d are very similar, at least for high-information content data. For example, it can be seen (Fig. 3) that although ε is not accurate in regions where no activity is present, it does not significantly affect the accuracy of the image of c or d.

Estimating the attenuation from the emission data, independent of a CT image used for attenuation correction, does not suffer the disadvantage of mismatch between patient positions during PET and CT. This may reduce the effects of motion blurring (e.g., breathing, heartbeat) and possible misregistration problems between the PET and the CT images. The proposed method has been also shown to be robust against unknown normalization in detector pair sensitivities. However, it was also shown that under low-count regime, the normalization artifacts were not fully recovered. By increasing the information content in the data, either by acquiring more counts or by having a better TOF resolution, these artifacts were shown to disappear. As noted in Ref. 26, a normalization correction obtained with a dedicated high count calibration scans will be more precise than the estimation that can be derived from a method like this and our results from low-information-content data seem to confirm these findings. However, with increasing information content of data acquired by modern TOF-PET scanners, the data-derived corrections may find use in the future. More studies are needed to investigate the robustness of transmission/normalization-less approaches.

Equations (10) and (11) define algorithms used in this work to find unknown sensitivities. There is nothing in those equations specific to TOF and it seems that the TOF information is not needed. However, the algorithms [either iterative equation (10) or MCMC equation (11)] assume knowledge of c and the MCMC algorithm used to find inferences about c explicitly uses the TOF information, and therefore, the TOF is used indirectly in those algorithms. We demonstrate this in the paper by varying the TOF resolution and showing that for poor TOF timing resoling TOF = 12 cm, the quality of reconstructed images gets worse (see Fig. 5).

In this work, we have not considered randoms and scatter. If the estimation of these effects is available, they can be incorporated in the OE reconstruction algorithm.³² Because the OE iterations are independent of sensitivity image updates in our algorithms, these corrections can also be used in the framework proposed here in a straightforward manner. It is interesting to note that the attenuation estimate derived from the TOF-PET data may be used to obtain the scatter estimate²⁶ with an algorithm like the single scatter simulation (SSS).^37,38

As expected, the accuracy of the method depends on the number of counts of the acquisition. A comparison of the results showed in Figs. 3 and 4 reveals that artifacts present in the image of d for the low number of counts are removed when more counts are available. This raises a question about the existence of a theoretical threshold on how much information is needed for the artifact-free analysis of attenuation/normalizationless TOF-PET data. The effects of the TOF (sampling) and number of acquired counts (noise) need to be considered in such investigation, which we plan to do in the future. It is also apparent form Fig. 5 that Bayesian algorithm suffers from a similar problem of overestimating cold and underestimating hot regions as in the standard bias/variance analysis. However, the interpretation of this effect is different. From the Bayesian point of view, we start with a very inaccurate flat prior, as it says that any c is equally probable. Of course, this is not our actual prior belief, as we know that some values of c are impossible (for example, an image c with elements equal to infinity). In this work, we used a flat prior out of computational convenience, but this flat prior makes the posterior not accurate if there is not enough information in the data that can overcome the strength of the prior as evidenced in Fig. 5.

We already published other computationally efficient priors in Refs. ³⁰ and ³¹. More research is needed to investigate the use of better priors which are closer to the true prior beliefs and which are computationally efficient to improve this inherent problem in tomography. We think that Bayesian approaches offer this possibility.

We proposed a fixed-point iterative algorithm for the sensitivity correction which can be used in combination with other image reconstruction algorithms, like OSEM (instead of our OE algorithm). This is discussed in Appendix B. If several subsets are used, it would be required to compute and store a different sensitivity image for each subset. This is not a major problem considering the capabilities of current computers.

Our computational methods are based on Monte Carlo sampling techniques which, in general, are more time consuming than deterministic iterative methods. Most of them also require some care in order to make them efficient (this drawback does not apply to the OE algorithm which does not require specification of any parameters). In general, the efficiency of MCMC methods is investigated using trial-and-error approach. This seems to be a quite serious obstacle for proliferation of those methods. However, in our experience, we found that once the methods are optimized for efficiency, they work on a wide range of settings. For example, in the current implementation, we found the algorithm very robust to selection of parameters that affect efficiency and they were never changed for analysis of various TOF-values/count level settings used in this work. The advantage of MCMC methods is that they provide estimates of the posterior distributions. These distributions can be used to assess the precision of point estimates as can be seen in Fig. 5 (error bars). They can also be used to judge the combined effects of sampling and noise³⁹ or in multiple hypothesis testing (e.g., detection).³⁰ An example of use in the clinics includes the estimation of error in standardized uptake values (SUVs). The SUV is frequently utilized in clinical practice end knowledge of the error of the SUV may improve confidence in decision making.

In theory, the MCMC does not suffer from local minima problems; albeit in practice, efficiency has to be considered. The effects of null spaces of standard analyses are not applicable, as the results of MCMC-based methods are not point estimates. Of course, the posterior probability can have the same value in subspaces of the parameters, in a way emulating the problem of null spaces in standard analysis. However, in order to select a point estimate, the specification of a loss function is required, which, if the function is chosen properly, can remove any possible ambiguity. In our previous work³⁰ with optimized implementations, we found that MCMC methods based on OE algorithm are about two times slower than that of the standard iterative list-mode expectation maximization algorithm.

The feasibility of this novel approach to attenuation/normalization correction has been verified with a 2-D thorax phantom, but the formulation presented here is general and it is not limited to this case.

The extension of these results to 3-D realistic cases (with scatter and randoms) and clinical data will be considered in the future work. The proposed new method can be of great help for attenuation correction in new PET-MR TOF scanners and reduce the impact on the image quality of the absence of recent normalization measurements.

5. CONCLUSION

Algorithms were derived and their initial evaluation performed for corrections for unknown attenuation and unknown normalization using TOF-PET data. The approach derived here uses fully Bayesian view on statistical problem of emission tomography imaging. Although questions remain as to the robustness of proposed method to noise and whether the method can be reliably applied to a spectrum of objects (e.g., would the method work with a large cold attenuator), it shows a great promise for improvements in PET imaging, especially in PET-MR.

APPENDIX A: SIMPLIFICATION OF EQ. (11)

If we compute the logarithm of both sides of Eq. (11), we obtain

$${\displaystyle log\frac{p\left(\mathbf{a},{\mathbf{y}}^{\prime }|,\mathbf{g}\right)}{p\left(\mathbf{a},\mathbf{y}|,\mathbf{g}\right)}=g_{k}log\left(1+\frac{\delta }{a_k}\right)-{\mathbf{\sum }}_{i=1}^{\mathrm{I}}{c}_{i}log\left(1+\frac{{\alpha }_{\mathit{ki}}\delta }{{\tilde{\epsilon }}_i}\right).}$$ (A1)

Using log(1 + x) ≈ x for small x, we have

$${\displaystyle log\frac{p\left(\mathbf{a},{\mathbf{y}}^{\prime }|,\mathbf{g}\right)}{p\left(\mathbf{a},\mathbf{y}|,\mathbf{g}\right)}\approx \delta \left(\frac{g_k}{a_k}-{\mathbf{\sum }}_{i=1}^{\mathrm{I}}\frac{{\alpha }_{\mathit{ki}}{c}_i}{{\tilde{\epsilon }}_i}\right).}$$ (A2)

Therefore, for the fast numerical implementation, the approximation of the right hand side can be promptly evaluated.

APPENDIX B: RELATIONSHIP WITH THE MLACF ALGORITHM

ML-EM is the most common reconstruction algorithm in PET, especially its accelerated version OSEM. Therefore, it is useful to show the connection of our algorithm with previously proposed attenuation correction algorithms based on TOF data and ML-EM. The update equation of ML-EM with TOF using the notation used in this work is

$${\displaystyle f_i^{n+1}=\frac{f_i^n}{{\tilde{\epsilon }}_i}{\mathbf{\sum }}_{k=1}^K{\mathbf{\sum }}_{t=1}^T{\alpha }_{\mathit{kti}}\frac{g_{kt}}{p_{kt}^n},}$$ (B1)

where n represents the iteration number, $f_i^n$ is the estimated activity in voxel i, and $p_{kt}^n={\mathbf{\sum }}_j{\alpha }_{ktj}{f}_j^n$ is the estimated projection in LOR k and TOF bin t at iteration n. In Ref. 25, the estimate of the sensitivity was obtained followed by an EM update,

$${\displaystyle {\tilde{\epsilon }}_i={\mathbf{\sum }}_{k=1}^K{\alpha }_{\mathit{ki}}\frac{g_k}{p_k^n}\to f_i^{n+1}=\frac{f_i^n}{\mathbf{\sum }_{k=1}^K{\alpha }_{\mathit{ki}}\frac{g_k}{p_k^n}}{\mathbf{\sum }}_{k=1}^K{\mathbf{\sum }}_{t=1}^T{\alpha }_{\mathit{kti}}\frac{g_{kt}}{p_{kt}^n}.}$$ (B2)

In this work, we used several iterations or updates of the sensitivity [using the fixed-point algorithm defined by Eq. (12)]. This approach may also be used with MLACF. We can run the fixed-point algorithm followed by EM iterations. This is because the number of emissions per voxel that were detected can be estimated from $f_i^n$ using

$${\displaystyle {\widehat{\stackrel{ˆ}{c}}}_i^n=f_i^n\cdot {\tilde{\epsilon }}_i.}$$ (B3)

The symbol ${\widehat{\stackrel{ˆ}{c}}}_i^n$ has been used to differentiate this estimate of c based on value of f from the MMSE point estimates used in the rest of this work and denoted as $\hat{c}$ (single hat). Using ${\widehat{\stackrel{ˆ}{c}}}_i^n$, we can then perform several updates of ${\tilde{\epsilon }}_i$ using

$${\displaystyle {\tilde{\epsilon }}_i^{l+1}={\mathbf{\sum }}_{k=1}^K\frac{{\alpha }_{\mathit{ki}}{g}_k}{\mathbf{\sum }_{i=1}^I\left({\alpha }_{\mathit{ki}}{\widehat{\stackrel{ˆ}{c}}}_i^n/{\tilde{\epsilon }}_i^l\right)}}$$ (B4)

which is equivalent to Eq. (10). l represents the iteration number of the fixed-point algorithm. This appendix shows how the proposed procedure based on c_i instead of f_i can be combined with other existing reconstruction methods.

APPENDIX C: DERIVATIVE OF THE POSTERIOR

We calculate

$${\displaystyle \frac{\partial p(\mathbf{a},\mathbf{c}|\mathbf{g})}{\partial a_{k^{\prime }}}\propto \mathbf{\sum }_{\mathrm{y}ϵY_{\mathrm{g}}\cap Y_{\mathrm{c}}}\frac{\partial p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)}{\partial a_{k^{\prime }}},}$$ (C1)

where $p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)$ using Eq. (2) repeated for convenience is

$${\displaystyle p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)={\mathbf{\prod }}_{i=1}^I\frac{c_i!}{{\tilde{\epsilon }}_i^{c_i}}{\mathbf{\prod }}_{k=1}^K{\left(a_k\right)}^{y_{\mathit{ki}}}\mathbf{\prod }_t\frac{{\left(h_{\mathit{kti}}\right)}^{y_{\mathit{kti}}}}{y_{\mathit{kti}}!}.}$$ (C2)

Since ${\left(p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)\right)}^{{}^{\prime }}=p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right){\left(log\hspace{0.17em}p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)\right)}^{{}^{\prime }}$,

$${\displaystyle \frac{\partial p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)}{\partial a_{k^{\prime }}}=p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)\frac{\partial }{\partial a_{k^{\prime }}}\times \left(-{\mathbf{\sum }}_{i=1}^I{c}_i\hspace{0.17em}log\hspace{0.17em}{\tilde{\epsilon }}_i+{\mathbf{\sum }}_{i=1}^I{\mathbf{\sum }}_{k=1}^K{y}_{\mathit{ki}}\hspace{0.17em}log\hspace{0.17em}{a}_k+\mathrm{const}.\right).}$$ (C3)

We note that ∂a_k/∂a_k′ = δ_kk′ (Kronecker’s delta) and $\partial {\tilde{\epsilon }}_i/\partial a_{k^{\prime }}={\alpha }_{k^{\prime }i}$ and the above transforms to

$${\displaystyle \frac{\partial p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)}{\partial a_{k^{\prime }}}=p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)\left(-{\mathbf{\sum }}_{i=1}^I\frac{{\alpha }_{k^{\prime }i}{c}_i}{{\tilde{\epsilon }}_i}+{\mathbf{\sum }}_{i=1}^I{\mathbf{\sum }}_{k=1}^K{y}_{\mathit{ki}}\frac{{\delta }_{k^{\prime }k}}{a_k}\right)}$$ (C4)

because ∑_iy_ki = g_k for y ∈ Y_g, we obtain

$${\displaystyle \frac{\partial p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right)}{\partial a_{k^{\prime }}}=\left(\frac{g_{k^{\prime }}}{a_{k^{\prime }}}-{\mathbf{\sum }}_{i=1}^I\frac{{\alpha }_{k^{\prime }i}{c}_i}{{\tilde{\epsilon }}_i}\right)p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right).}$$ (C5)

Substituting to Eq. (C1), we obtain

$${\displaystyle \frac{\partial p\left(\mathbf{a},\mathbf{c}|\mathbf{g}\right)}{\partial a_{k^{\prime }}}\propto \mathbf{\sum }_{\mathrm{y}ϵY_{\mathrm{g}}{\cap }^{Y_{\mathrm{c}}}}\left(\frac{g_{k^{\prime }}}{a_{k^{\prime }}}-\mathbf{\sum }_i\frac{{\alpha }_{k^{\prime }i}{c}_i}{{\tilde{\epsilon }}_i}\right)p\left(\mathbf{y}|\mathbf{a},\mathbf{c}\right).}$$ (C6)

APPENDIX D: DERIVATION OF MMSE ESTIMATOR OF d

From the definition, the MMSE estimator of d is

$${\displaystyle \hat{d}=\mathbf{\sum }_{\mathbf{d}}\mathbf{d}p\left(\mathbf{d}|\mathbf{g}\right)=\mathbf{\sum }_{\mathbf{d}}\mathbf{d}\mathbf{\sum }_{\mathbf{c}}p\left(\mathbf{d}|\mathbf{c},\mathbf{g}\right)p\left(\mathbf{c}\right|\mathbf{g}).}$$ (D1)

Because of conditional independence,³¹ $p\left(\mathbf{d}|\mathbf{c},\mathbf{g}\right)=p\left(\mathbf{d}|\mathbf{c}\right)$ and interchanging the order of summations, we have

$${\displaystyle \hat{d}=\mathbf{\sum }_{\mathbf{c}}p\left(\mathbf{c}\right|\mathbf{g})\mathbf{\sum }_{\mathbf{d}}\mathbf{d}p\left(\mathbf{d}|\mathbf{c}\right).}$$ (D2)

Because emissions from different voxels are independent, we have $p\left(\mathbf{d}|\mathbf{c}\right)={\mathbf{\prod }}_{i=1}^{I}p\left(d_i\right|c_i)$ and because p(d_i|c_i) has the negative binomial distribution with expectation $c_i/{\tilde{\epsilon }}_i$, we arrive to

$${\displaystyle {\hat{d}}_i=\frac{1}{{\tilde{\epsilon }}_i}\mathbf{\sum }_{\mathbf{c}}{c}_{i}p\left(\mathbf{c}\right|\mathbf{g})=\frac{{\hat{c}}_i}{{\tilde{\epsilon }}_i}.}$$ (D3)