Variable Cadence Walking and Ground Adaptive Standing with a Powered Ankle Prosthesis

Abstract

This paper describes a control approach that provides walking and standing functionality for a powered ankle prosthesis, and demonstrates the efficacy of the approach in experiments in which a unilateral transtibial amputee subject walks with the prosthesis at variable cadences, and stands on various slopes. Both controllers incorporate a finite-state structure that emulates healthy ankle joint behavior via a series of piecewise passive impedance functions. The walking controller incorporates an algorithm to modify impedance parameters based on estimated cadence, while the standing controller incorporates an algorithm to modulate the ankle equilibrium angle in order to adapt to the ground slope and user posture, and the supervisory controller selects between the walking and standing controllers. The system is shown to reproduce several essential biomechanical features of the healthy joint during walking, particularly relative to a passive prosthesis, and is shown to adapt to variable cadences. The system is also shown to adapt to slopes over a range of ± 15 deg and to provide support to the user in a manner that is biomimetic, as validated by quasi-static stiffness measurements recorded by the prosthesis. Data from standing trials indicate that the user places more weight on the powered prosthesis than on his passive prosthesis when standing on sloped surfaces, particularly at angles of 10 deg or greater. The authors also demonstrated that the prosthesis typically began providing support within 1 s of initial contact with the ground. Further, the supervisory controller was shown to be effective in switching between walking and standing, as well as in determining ground slope just prior to the transition from the standing controller to the walking controller, where the estimated ground slope was within 1.25 deg of the actual ground slope for all trials.

I. Introduction

Transtibial amputees typically utilize passive dynamic elastic response (DER) foot/ankle prostheses, which are relatively stiff leaf springs, typically configured nominally with a 90 deg angle between the foot and the shank. The behaviors of the intact human ankle joint, however, are considerably more varied than those provided by the passive DER prosthesis. Among the behaviors which might be exhibited by the intact ankle are adaptive passive behaviors (i.e., passive behaviors that vary as a function of activity), as well as active behaviors such as powered push-off [1]. Regarding the latter, the intact human ankle joint supplies net positive energy during gait initiation [2] and during steady-state walking, particularly in self-selected medium to fast walking [3]. A passive DER prosthesis is inherently unable to produce net power generation in these instances, and is therefore deficient relative to the healthy joint.

Additionally, persons with below knee amputations walking on passive prosthetic devices have been shown to require up to 20% more oxygen uptake relative to healthy individuals [4], and their walking speed is significantly reduced [5] (between 10% and 22% [6, 7]). Walking speed and efficiency are substantially related to powered push-off (see, for example, [8, 9]), and as such, it is reasonable to hypothesize that restoring powered push-off could decrease cost of transport and increase walking speed for these individuals.

A. Prior Work

Recent advances in robotics technologies (battery, microprocessor, motor) have facilitated the emergence of powered prostheses which are capable of delivering power comparable to that which the biological joint generates during walking. Several such powered ankle designs are described in [10– 16]. The extent to which such a device can restore the biomechanical functionality of the absent ankle, however, is dependent on the ability of a control system to coordinate the action of the powered prosthesis with both the movement and the movement intent of the user.

A number of control methods have emerged in conjunction with powered prosthetic ankle designs, several of which are reviewed in [17]. Among these, Holgate et al. discuss several strategies including position control, velocity or stiffness control, impedance control, and proportional myoelectric control [18]. Additionally, two control strategies are proposed to augment position control, including one based on a continuous relationship between shank angle (relative to an inertial reference frame) and ankle angle [18, 19], in conjunction with a scaling factor based on speed, and one which continuously modulates the ankle period and amplitude based on stride time of the previous gait cycle [18]. A powered ankle control strategy presented by Au et al. [20] describes both a neural network model and a neuromuscular model which rely on electromyogram (EMG) signal inputs from the amputee’s residual limb to set the ankle angle. Another control strategy implements a four-state finite-state controller, where the control action within each state is a stiffness, a torque source, a position trajectory controller, or some combination of these [21]. This method is applied to both level ground walking and stair climbing in [22], and EMG signals from the user enable switching between controllers [22]. Additionally, [23] presents an approach based on a two state model, one for swing and the other for stance. The swing state employs position control and the stance state incorporates a Hill-type muscle model which reacts with a force in proportion to position and speed. Sun and Voglewede [24] present a finite-state controller comprised of four states: loading response, middle and terminal stance, pre-swing, and swing. During the stance phase (comprised of the first three finite states) output torque is controlled via PI feedback with a healthy subject torque profile as the reference, while the swing state is a PID position controller. Finally, Huang et al. present a proportional myoelectric controller for a pneumatic artificial plantar flexor muscle for a transtibial prosthesis [25].

This paper presents a walking controller which enables a biomimetic walking gait in a transtibial amputee with a powered ankle prosthesis prototype. The method incorporates a different control structure from the methods described above (i.e., [17, 21–24]), including different state behaviors and different switching conditions. Further, the paper describes a control methodology for ground adaptive standing–namely, a controller that provides adaptation to various ground slopes regardless of the user’s posture (the orientation of the shank with respect to the ground). A control method for such ground slope adaptation has not yet been demonstrated in the literature for a powered transtibial prosthesis. The authors have demonstrated similar functionality in a previous publication with a powered transfemoral prosthesis [26], although that method relies on measurement of ground reaction force, which is not measured or utilized in the system presented here. This work additionally describes the supervisory method by which the system determines how to switch between the walking and standing controllers. After a brief description of the powered ankle prosthesis prototype utilized herein, the authors describe the powered ankle prosthesis control structure for level walking with variable cadence and ground adaptive standing. Following the control description, the paper describes an experimental implementation and assessment of the prosthesis and each controller (variable slope standing, variable cadence walking, and the supervisory controller for switching between), and presents data demonstrating the ability of the prosthesis and controller to provide desired functionality during these activities and to select between them.

II. Prosthesis Design

A. Mechanical Design

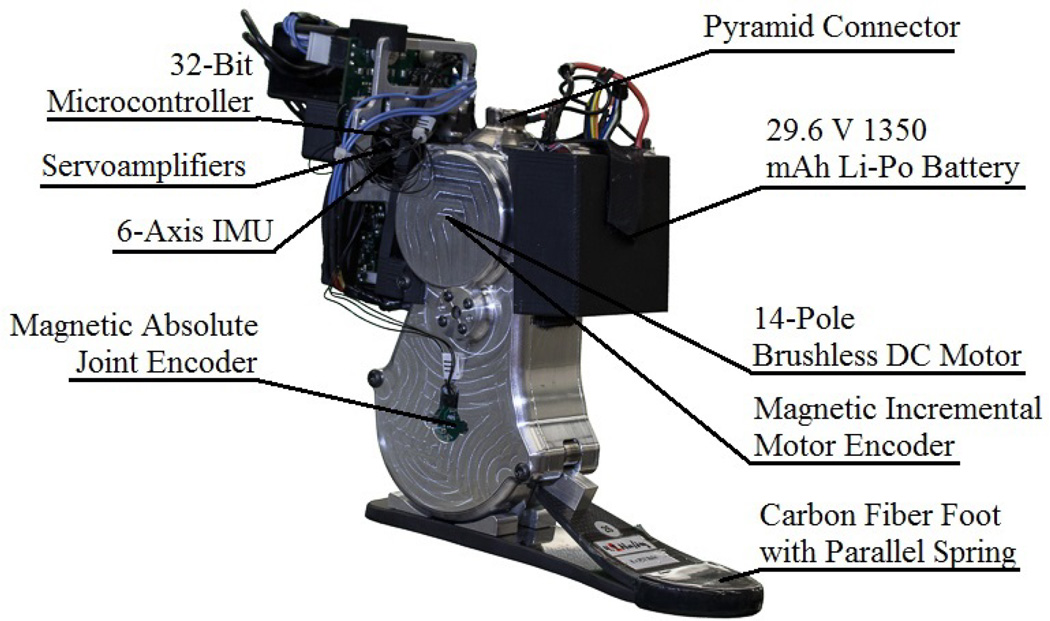
The Vanderbilt powered ankle prosthesis prototype, shown in Fig. 1, has a range of motion of 45 deg of plantarflexion and 20 deg of dorsiflexion. Note that the electronics and battery shown in Fig. 1 are temporary, as a (more compact and better integrated) custom embedded system and battery pack will be implemented at a later date. The prosthesis incorporates a Maxon EC60 14-pole brushless motor, which is speed reduced by a factor of 116:1 through a 3-stage belt/chain/chain transmission in order to produce a peak ankle joint torque of approximately 100 Nm. The ankle-foot complex additionally incorporates a carbon-fiber leaf spring into the foot, which is characterized by a stiffness of approximately 4.2 Nm/deg and engages at approximately 1.6 deg (dorsiflexion). The spring biases the output capabilities of the ankle toward plantarflexion, which is consistent with the biomechanical characteristics of the human ankle during locomotion. At typical peak (dorsiflexive) ankle angles in middle to late stance, the spring provides up to 50 Nm of supplemental torque, such that the prosthesis is capable of providing a (combined active and passive) plantarflexive torque in middle to late stance of up to 150 Nm. A custom embedded system integrates a 32-bit microcontroller for execution of high-level control code with a 16-bit digital signal processing chip, which performs low-level control functions, such as commutation and current control of the brushless motor, and signal conditioning of an absolute encoder at the joint, an incremental encoder at the motor, and a 6-axis inertial measurement unit (IMU) on the control board. Sensor information available to the high-level controller therefore includes ankle joint position and velocity (provided by the encoders), as well as shank absolute orientation and angular velocity information (provided by the IMU). The prosthesis is powered by an on-board lithium-polymer battery and attaches to a user’s socket via a standard pyramid connector. The mass of the prosthesis as shown in Fig. 1, including electronics and battery, is 2.3 kg. Note that this prosthesis is based on an earlier version of the Vanderbilt powered ankle prosthesis prototype, described in [27].

Fig. 1.

Vanderbilt powered prosthesis prototype.

B. Impedance-Based Control Design

Similar to the structure described by the authors for the control of a transfemoral prosthesis [28], the ankle control system consists of a finite-state machine (FSM) for each activity (e.g., walking, standing), where the behavior within each state is characterized by passive stiffness and damping terms. Specifically, for the controller described here, the ankle joint impedance within each state is given by

$$\tau =k_i(\theta -{\theta }_{e,i})+k_{5,i}{(\theta -{\theta }_{e,i})}^5+b_i\dot{\theta }$$ (1)

where k_i, k_5,i, b_i, and θ_e,i denote linear stiffness, fifth-order stiffness coefficient, damping coefficient, and equilibrium angle, respectively, for the i^th state during a gait cycle. The fifth-order stiffness coefficient k_5,i is nonzero only during the middle stance state of the walking controller, where it acts as a stiffening spring term to increase ankle support as the user’s center of mass (CoM) passes over the ankle joint. The fifth-order term was implemented as an approximation of the nonlinear stiffening behavior (between ankle angle and torque) observed in healthy subjects during the middle stance phase of walking [1, 29]. Transitions between finite states are triggered by pre-selected thresholds in sensor measurements. A supervisory controller selects which FSM (i.e., activity mode) is active based on the current activity mode and controller state, as well as sensor data. This paper describes the activity-level controller developed by the authors for walking at various cadences, the activity-level controller for ground adaptive standing, and the supervisory controller that switches between the two.

C. Walking Activity Mode Controller

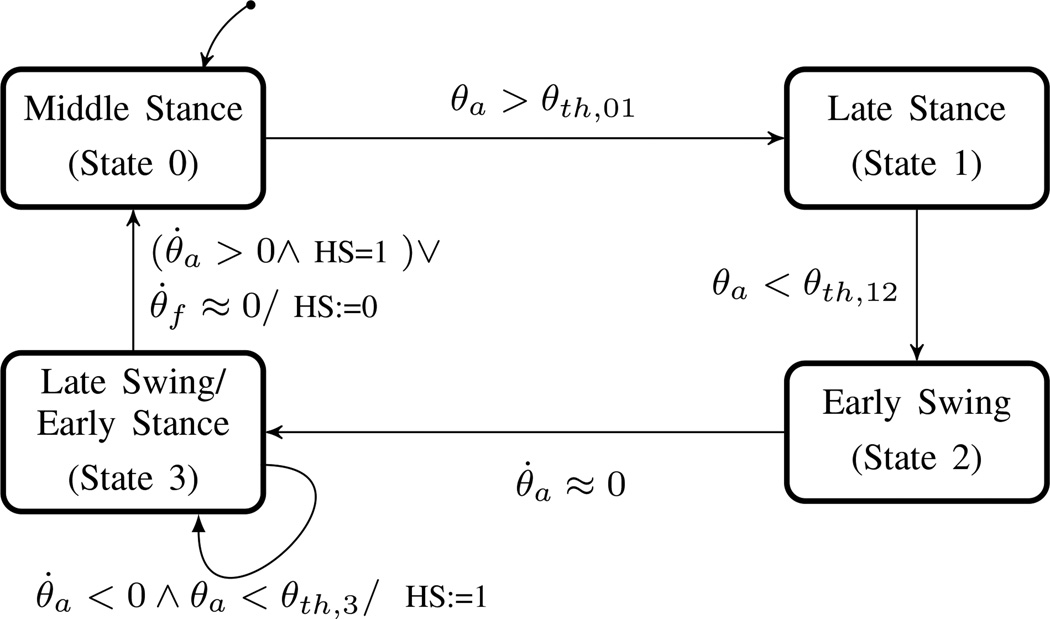
In the walking activity mode controller, the ankle behavior over a gait cycle can be characterized by four basic functions, which map directly to states in the FSM, presented as a state chart in Fig. 2. During the early stance phase of gait (state 3), the joint behaves essentially as a damper, allowing plantarflexion upon heel contact to provide shock absorption (i.e., corresponding to the loading response). The powered prosthesis emulates a nonlinear spring during middle stance (state 0), which may be initiated either by foot flat detection (foot angular velocity sufficiently close to zero) or by the detection of ankle dorsiflexion immediately following heel strike. Since the prosthesis neither incorporates a load cell nor measures ground contact, heel strike is detected by a negative (plantarflexive) ankle angular velocity during state 3 which occurs when the ankle angular position is dorsiflexed relative to the equilibrium position for that state. Late stance (state 1) is initiated when the ankle is dorsiflexed past a predetermined angle. This state effects power delivery (push-off in healthy walking) by emulating a stiffness with a virtual equilibrium point in a plantarflexed position. At this transition, the rate of change of the torque reference is limited such that the power delivery is less abrupt and better mimics that which is observed in healthy gait. Once push-off is complete (the ankle angle reaches a predetermined threshold), the controller enters early swing (state 2), during which the ankle returns to a nearneutral although slightly dorsiflexed position to facilitate toe clearance during swing. Late swing (state 3) begins once the ankle has reached equilibrium (indicated by an ankle angular velocity that is sufficiently close to zero). In this state, as described previously, the ankle behaves essentially as a damper (with a light spring to maintain its nominal configuration) in preparation for heel strike.

Fig. 2.

The FSM executed by the prosthesis for walking. θ_a is the ankle angle, which is compared to predetermined thresholds θ _th,01 θ _th,12, and θ _th,3, respectively. θ̇ _a is the angular velocity of the ankle, and θ_f is the angular velocity of the foot with respect to the ground. HS is a flag which when set to 1 indicates a heel strike event.

Note that all transitions in the state machine associated with ground contact (i.e., all those except termination of late stance (push-off) and entrance into the damping state) require active user input. Specifically, to achieve foot flat the user must load the foot after heel strike, and to initiate push-off (late stance), the user must continue to load the prosthesis as his center of mass moves forward over the foot. Late stance (state 1) will terminate automatically, based on either an angle or time condition, and as such this state is an inherently transient state that provides bounded movement and energy delivery. Ankle return (state 2) will also terminate once it has been completed. Therefore, in the absence direct user input, the prosthesis will default to passive behavior, and come to rest in either state 0 or 3. The dependency on user input to progress through the state machine, specifically during stance states, ensures that the user maintains control of ankle behavior, and that the device will default to passive behavior in the event that the user is not actively engaged in walking.

Note also that the walking controller does not enforce a specific walking speed, allowing the user to control his or her speed or cadence. Varied walking speeds, however, may be better accommodated by variation in power delivery in late stance and stiffness in middle stance. The controller accommodates such variation by measuring cadence, selecting one of three cadence ranges–slow, normal, or fast–and applying a corresponding set of controller parameters that provides increased push-off and stiffness with increasing cadence, in order to better match the biomechanical characteristics of the healthy ankle within those respective ranges of cadence. Cadence is measured by recording the time between each heel strike, with a moving window average of three strides. The controller switches between appropriate cadence regimes with a 2 step/min hysteresis in the switching in order to mitigate chatter between sets of control parameters.

D. Ground Adaptive Standing Activity Mode Controller

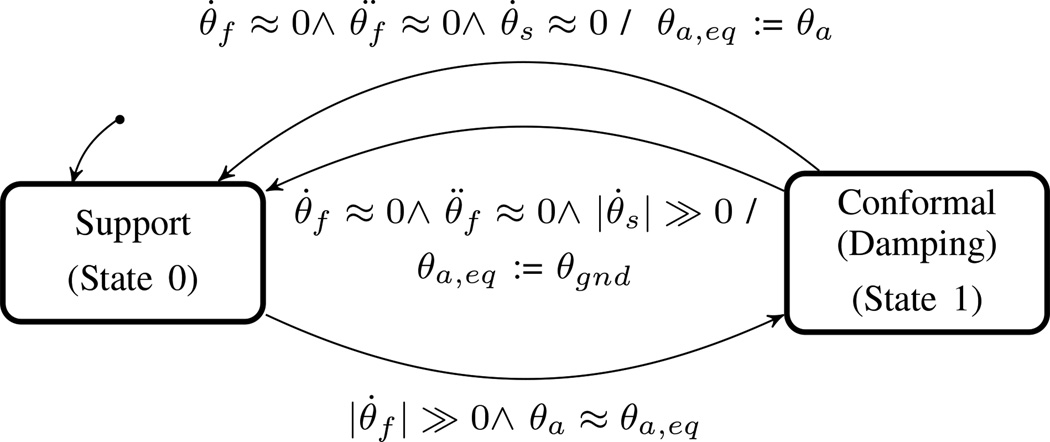
A powered prosthesis also benefits from a ground adaptive standing controller. This functionality is provided by the control structure depicted in Fig. 3, which is comprised of two impedance-based finite states: a support state and a conformal damping state, which are similar to the middle stance and late swing/early stance states, respectively, in the walking controller. The support state of the standing controller emulates a spring with light damping and is designed for use when the prosthesis is loaded; the conformal damping state is designed for use when the device first contacts the ground in order to facilitate foot flat according to the user’s posture and ground topology. Adaptation to the ground is achieved by establishing the support state equilibrium angle based on the configuration of the ankle and/or foot following foot flat. This adaptation mechanism facilitates standing on a surface which is not perpendicular to gravity–i.e. inclines and declines. This functionality is also beneficial when standing or sitting in a relaxed pose where foot flat is desired regardless of the orientation of the shank. This controller is designed to accommodate both circumstances.

Fig. 3.

The FSM executed by the prosthesis for the standing activity mode. θ̈_f is the angular acceleration of the foot. θ̇_s is the angular velocity of the shank, and θ̇_f is the angular velocity of the foot. θ_a is the ankle angle, which is compared to the ankle virtual equilibrium position θ_a,eq. Additionally, θ_gnd is the estimate of the ground slope.

The controller executes a transition from the support state to the conformal damping state if the angular velocity of the foot is greater than 30 deg/s while the ankle angle is within 1.5 deg of the equilibrium position. These conditions are intended to establish that the user is not loading the prosthesis and may subsequently contact the ground. The controller transitions from the conformal damping phase to the support phase if the estimated (sagittal plane) foot angular velocity and foot angular acceleration are both approximately zero (magnitudes are less than 5 deg/s and 50 deg/s², respectively). These conditions indicate that the foot is essentially stationary with respect to the inertial reference frame, and thus is either on the ground and loaded, or in the air and immobile, in which case it need not conform to the ground and can enter support state.

A new equilibrium position is established at each transition from conformal damping to support. The new equilibrium angle is established by either the ground slope or the user’s posture, depending upon the nature of the movement preceding the transition. In the case that the shank is rotating at the transition from conformal damping to support, as indicated by a magnitude of shank angular velocity greater than or equal to 10 deg/s, the new equilibrium angle is established as the mean of the estimated ground slope (orientation of the foot in the sagittal plane) during the 50 ms prior to the transition. These conditions might be met, for example, if the user is in prosthetic-side single support, while the sound-side foot is adjusting to the ground topology. Alternatively, these conditions might be met when the user initiates walking with the sound side, a circumstance which is discussed in more detail in the following subsection. In the case that the shank is essentially stationary at the transition from conformal damping to support, as indicated by a magnitude of shank angular velocity less than 10 deg/s, the new equilibrium angle is established as the mean of the ankle angle during the 50 ms prior to the transition. These conditions might be met if the user is in sound-side single support and the prosthetic foot is conforming to the ground, such as when sitting or when stepping onto a slope first with the sound side, followed by the prosthesis. Note that foot orientation is calculated as the sum of the sagittal plane shank orientation and ankle angle, and foot angular velocity as the sum of shank angular velocity and ankle angular velocity, where the shank orientation and angular velocity are provided by the IMU.

E. Supervisory Controller

A supervisory controller, depicted in Fig. 4, determines which of the two activity controllers, walking or standing, should be active. Switching from the standing activity controller to the walking activity controller is essentially equivalent to the push-off (late stance) trigger in walking– dorsiflexion of the ankle past a predetermined angle. In this case, the ankle must exceed a predetermined angle offset from the equilibrium position. The transition to the walking controller can only be made from the support state (state 0) of the standing controller to the late stance state (state 1) of the walking controller. A walking gait, however, can be initiated by a step with either the sound leg or the prosthesis. In the case of the former, as the sound leg swings forward to heel strike, push-off is triggered on the prosthesis when the ankle angle (dorsiflexion) threshold is met. In the case of the latter, since the conformal damping and support states of the standing controller are similar in function to the early stance and middle stance states, respectively, of the walking controller, the prosthesis can remain in the standing control during the early and middle stance phases of the first stride, while exhibiting biomechanical functionality similar to that of the walking controller. Specifically, the user will initiate a step with the prosthesis in the standing controller, in which case the prosthesis will reside in the conformal damping state during heel strike; the controller will transition to support state at foot flat with an equilibrium position set according to ground slope, and finally will enter the walking activity controller and trigger push-off in late stance. Therefore, a stride initiated with the prosthesis is essentially the same as one initiated with the sound leg, although middle stance is characterized in the first step by a linear rather than nonlinear stiffness. Additionally, in both cases, the strength of the first push-off after switching to the walking controller is diminished relative to that of subsequent steps.

Fig. 4.

The supervisory controller executed by the prosthesis. θ_a is the ankle angle, which is compared to a position threshold offset from the ankle equilibrium angle, represented here by θ_th,sw. θ̇_s is the angular velocity of the shank, T represents the amount of time that θ̇_s is approximately zero, and dt is the sample time of the controller. θ_a,eq is the ankle equilibrium position for the subsequent state (State 0 of Standing), and θ_a,eq,w0 is the ankle equilibrium position of State 0 of Walking, which is the previous state.

Switching from the walking controller to the standing controller takes place from middle stance (walking) to support (standing). While in middle stance (state 0), if the absolute angular velocity of the shank is near zero–i.e., magnitude less than 5 deg/s–for 0.5 s, the controller transitions into the support state of the standing controller, where the equilibrium position of the ankle persists from the middle stance state of walking.

III. Experimental Assessment

The two activity level controllers–variable cadence walking and variable slope standing–were implemented in the powered prosthesis prototype, along with the supervisory controller, and the collective behavior was assessed in experimental trials with a unilateral transtibial amputee subject. The subject was male, 44 years of age, 3 years post-amputation, with a body mass of 85.7 kg (189 lb). His limb loss was the result of a traumatic injury. Controller efficacy during walking and standing was assessed by comparing the behavior of the powered prosthesis to that of the subject’s passive prosthesis (an Össur Vari-Flex XC carbon fiber foot) and to that of the healthy limb, as well as by determining the ability of the controller to select the appropriate behavior for a given activity in a timely manner; the details of these assessments are provided in subsequent subsections. Approval for these assessments was granted by the Vanderbilt University Institutional Review Board; the subject gave informed consent, including permission for publication of (non-de-identified) photographs and video. A video is included in the supplemental material that depicts walking and standing activities representative of the experimental trials described below.

A. Controller Parameters

A nominal set of controller parameters (i.e., impedance values and transition conditions) for the walking controller were initially established using ankle joint angle, angular velocity, and torque data from healthy subjects [29], and these parameters were iteratively tuned for the amputee subject during treadmill and overground walking. Control parameters were specifically adjusted based on a combination of quantitative (ankle joint kinematic and kinetic data) and qualitative (user feedback, external observation) information, in order to provide appropriate kinematics and kinetics as well as reliable and natural state transitions. The process of parameter tuning is similar to the manner in which a prosthetist iteratively adjusts passive components during prosthesis fitting in order to achieve comfortable, stable, and functional walking and standing. While there are a relatively large number of parameters associated with the walking controller presented in this work (16 per cadence mode), the authors hypothesize that the set which would require tuning in a clinical setting would be significantly reduced and would be intuitive for the prosthetist. Firstly, the four parameters associated with early swing as well as the equilibrium position in late swing/early stance are assumed to be independent of the subject or patient. Further, damping and linear and nonlinear stiffness parameters could likely eventually be coupled and thus adjusted by a single mechanism for each state. Additionally, the equilibrium and stiffness/damping of push-off, or late stance (state 1), can be coupled and adjusted as the strength of push-off. Therefore, establishing the control parameters for the intermediate cadence regime essentially entails tuning five gait parameters: 1) the stiffness/damping parameter in middle stance (analogous to selecting stiffness of a DER foot); 2) the equilibrium angle in middle stance (analogous to adjusting alignment of a DER foot); 3) the strength of push-off; 4) the trigger angle for push-off; 5) the speed (rate limiting) of push-off. Further, once these parameters are established, the parameters that would require modification for the slow and fast cadence regimes are 1) the spring stiffness in early stance; 2) the spring stiffness in middle stance; 3) push-off strength; 4) push-off trigger angle; 5) speed of push-off. As such, an additional ten parameters establish all controller function for the remaining cadence regimes. Thus, despite the existence of 48 total parameters, tuning of 15 parameters at three cadence regimes is sufficient to establish control functionality. The authors note also that, once a larger number of subjects have been fitted with the device, it is likely that height and weight can be correlated to certain parameters, such that the controller could be tuned in a clinical setting by adjusting only a few nominal controller characteristics.

B. Evaluation of the Walking Controller

In order to assess the efficacy of the walking controller, the amputee subject walked on a treadmill at three speeds–0.98, 1.13, and 1.35 m/s–which represent the slow, self-selected, and fast cadence regimes, respectively, with the powered prosthesis, and subsequently with his passive prosthesis. The subject walked at each speed, and with each prosthesis, for a period of approximately 90 s, during which ankle and knee joint angle data were collected via a motion capture system. Motion capture was performed using an OptiTrack S250e infrared twelve-camera system (NaturalPoint, Inc.) to track a full skeletal marker set (similar to the Helen Hayes marker set) consisting of thirty-four reflective markers. Motion capture data were sampled at 120 Hz using ARENA software (Natu-ralPoint, Inc.) and subsequently exported to and processed in MATLAB in order to extract lower limb sagittal-plane joint angles. For each prosthesis and walking speed, 20 consecutive strides were selected from steady-state walking for analysis. The periodic data were parsed into strides in a manner similar to that presented in [30], using the inflection in ankle angle to determine heel strike in lieu of the minimum vertical position of the heel marker.

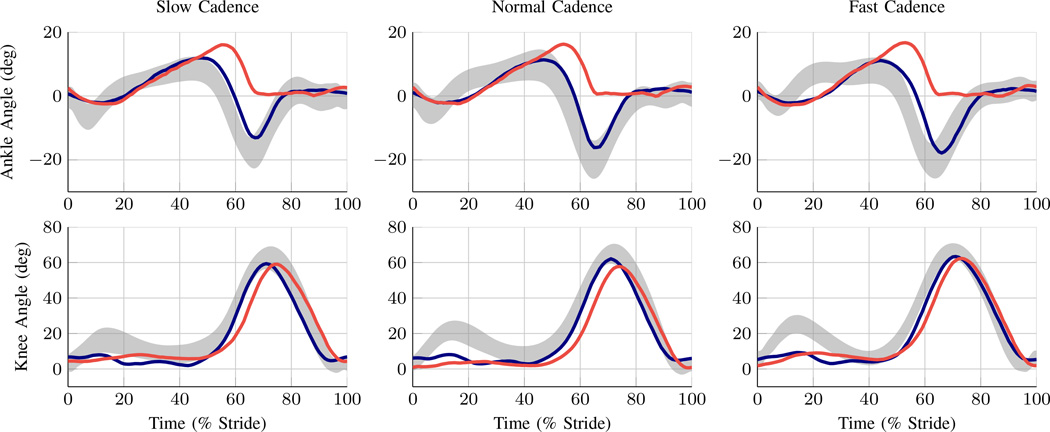
Figure 5 shows the knee and ankle kinematics for the subject walking with the powered prosthesis and the passive prosthesis, respectively, and also shows for reference the corresponding kinematic data for healthy subjects walking at similar cadences [29]. Specifically, the gray shaded area represents a plus and minus one standard deviation band around the healthy mean, the blue (dark) line is mean powered prosthesis data, and the red (light) line is mean passive prosthesis data, all at comparable cadences. Specifically, the three treadmill speeds used in the previously described experiments corresponded to respective cadences of 91, 101, and 112 steps/min with the powered prosthesis and 93, 104, and 110 steps/min for the passive prosthesis, respectively, while the healthy subject data corresponds to average cadences of 85, 105, and 125 steps/min.

Fig. 5.

Kinematics (knee and ankle angles) for slow, normal, and fast cadences. Healthy subject data ± 1 standard deviation are shaded in gray, powered prosthesis data are shown by blue (dark) lines, and passive prosthesis data are shown by red (light) lines. The maximum standard deviations of the mean at the ankle for the passive prosthesis are 1.90 deg at 65% stride, 1.48 deg at 62% stride, and 2.17 deg at 62% stride for slow, normal, and fast cadences respectively. The maximum standard deviations of the mean at the ankle for the powered prosthesis are 1.82 deg at 75% stride, 4.11 deg at 61% stride, and 4.28 deg at 62% stride for slow, normal, and fast cadences respectively. The maximum standard deviations of the mean at the knee for the passive prosthesis are 3.88 deg at 65% stride, 3.15 deg at 90% stride, and 4.24 deg at 85% stride for slow, normal, and fast cadences respectively. The maximum standard deviations of the mean at the knee for the powered prosthesis are 4.42 deg at 86% stride, 6.33 deg at 61% stride, and 6.60 deg at 89% stride for slow, normal, and fast cadences respectively.

As shown in the top row of Fig. 5, the ankle kinematics for the powered prosthesis falls largely within the healthy data band for all three speeds, while the kinematics of the passive prosthesis are much less representative of healthy patterns. Among the notable differences, powered push-off is not provided by the passive prosthesis, as evidenced by the absence of a plantarflexive peak in late stance/early swing. Additionally, notice that (for all three cadences) the peak dorsiflexion provided by the passive prosthesis in stance occurs at least 10% later in the stride than that of the powered prosthesis or healthy data.

One can observe in the healthy subject data a significant ankle dorsiflexion around 20% of stride, particularly for normal and fast cadences, and that neither prosthesis exhibits a similar pattern of dorsiflexion. Further, as shown in the bottom row of Fig. 5, the subject achieves a significantly smaller degree of stance knee flexion with both prostheses, compared to healthy. Because the trajectory of the ankle is highly influenced by that of the knee during stance, this deviation in knee behavior (presumably due to compensatory behaviors that are trained into the amputee) causes the ankle to exhibit less dorsiflexion (compared to healthy) during the same portion of the stride.

For the powered prosthesis, ankle angle, angular velocity, and motor current data were recorded by the embedded system on the prosthesis during another set of trials. For these data, heel strike was determined as the point during state 3 when the ankle angular velocity became substantially nonzero (i.e., by the heel strike flag described in Fig. 2). The joint torque experienced by the user was calculated using the recorded motor current in combination with a model of the known or estimated passive characteristics of the motor, transmission, and parallel spring (i.e. inertia, friction, and stiffness) according to:

$${\tau }_{\mathit{\text{jnt}}}=\{\begin{array}{cc}{\tau }_{\mathit{\text{mot}}}-J\ddot{\theta }-b\dot{\theta }-c\cdot \text{sgn}(\dot{\theta })-k(\theta -{\theta }_0)\hfill & \text{if}\theta \ge {\theta }_0\hfill \\ {\tau }_{\mathit{\text{mot}}}-J\ddot{\theta }-b\ddot{\theta }-c\cdot \text{sgn}(\dot{\theta })\hfill & \text{if}\theta \text{<}{\theta }_0\hfill \end{array}$$ (2)

where τ_mot represents the motor torque (transformed into joint space), J is rotor inertia (transformed into joint space), b is viscous damping coefficient, c is Coulomb friction, k is the spring constant for the parallel spring, and θ₀ is the equilibrium position (contact angle) for the parallel spring. The motor torque is calculated using the motor current, torque constant (from the motor datasheet), and the transmission ratio from the motor to the joint output. The parallel spring stiffness and engagement angle, k and θ₀, respectively, were determined experimentally and were implemented in the control code to offset the motor torque command and are therefore known for the purpose of this analysis. Rotor inertia J was derived from motor manufacturer specifications and the known transmission ratio. The remaining parameters, c and b, were determined using least squares estimation of a set of data taken from driving the prosthesis with the motors through a state space comparable to level ground walking with no external load. The calculated torque was then multiplied by joint velocity to obtain joint power. Note that joint position, velocity, and acceleration data were filtered in post-processing in MATLAB in order to avoid phase lag in the velocity and acceleration signals. Specifically, the ankle position was filtered using a Fast Fourier Transform (FFT) to remove the frequency content above 10 Hz and reconstructed with an inverse FFT; the velocity and acceleration were obtained by differentiation of the zero-phase-filtered position.

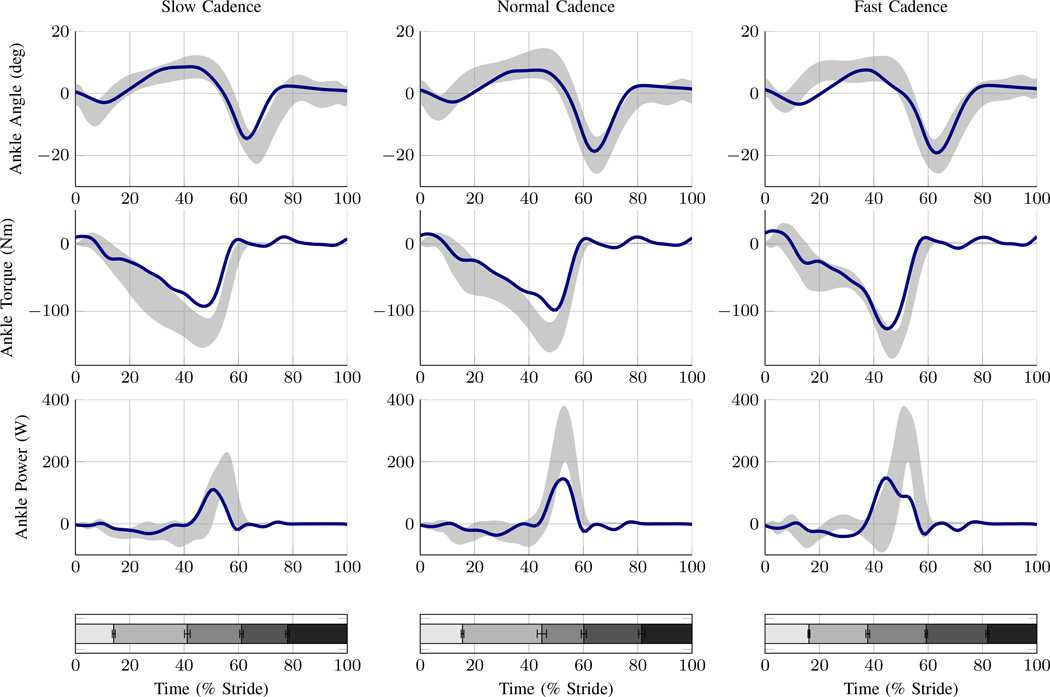
Figure 6 shows the powered ankle kinematic and kinetic data corresponding to the amputee subject walking with the powered prosthesis at the three cadences evaluated in this work, along with corresponding data representative of healthy subject walking, excerpted from [29]. In each plot, data characterizing plus and minus one standard deviation around the healthy mean are shaded in gray, providing a standard for comparison which incorporates inter-subject variability for healthy individuals, while the blue line is the mean data (over 20 strides) from the powered prosthesis. The respective cadences for healthy and prosthesis data are as listed previously.

Fig. 6.

Kinematics and kinetics for slow, normal, and fast cadences. Healthy subject data ± 1 standard deviation are shaded in gray, and powered prosthesis data are shown by blue (dark) lines. 1.35 deg at 68% stride, 7.12 Nm at 54% stride, and 16.54 W at 46% stride for slow cadence; 2.59 deg at 70% stride, 9.90 Nm at 47% stride, and 44.34 W 48% stride for normal cadence; and 1.14 deg at 69% stride, 6.88 Nm at 51% stride, and 15.29 W at 41% stride for fast cadence. State transition times (in percent of stride) with error bars representing ± 1 standard deviation are also shown in the bottom row of this figure.

The top row of Fig. 6 shows the ankle angle versus stride for the powered prosthesis and healthy norm, for the three respective walking speeds, while the second row of Fig. 6 shows the sagittal plane ankle torque for the powered prosthesis, relative to the healthy norm. The joint torque profiles for the powered are highly representative of healthy data, but with slightly lower magnitude. The third row of Fig. 6 shows the sagittal plane ankle joint power for the powered prosthesis, relative to the healthy norm, for the three walking speeds. The power delivery falls within the band of healthy subject data for slow walking (for the corresponding body weight), but is somewhat under-powered at normal and fast cadences. Note that in fast walking, the power pulse observed in the powered prosthesis leads that of healthy fast walking. Due to the aforementioned power limitations in the powered prosthesis, the authors chose to initiate power delivery slightly earlier than what is observed in healthy data in order to increase net energy delivery over the stride. Note that, while torque and power data are not available for the passive prosthesis, by nature it cannot deliver net positive power and will actually dissipate net power over a stride. The bottom row of Fig. 6 shows the state transition times in terms of percent of stride with error bars indicating ± one standard deviation, demonstrating a high degree of consistency in the transitions, thus indicating consistent, repeatable, and predictable prosthesis behavior during walking.

Average electrical power consumption of the powered prosthesis, as measured at the battery for the experimental trials conducted here, was 40.7 W, 69.8 W, and 88.2 W while walking at slow, normal (self-selected), and fast cadences, respectively. The battery currently implemented in the prosthesis, as shown in Fig. 1, has a capacity of 40 Wh (i.e., 1350 mAh @ 29.6 V), and as such, will provide approximately 3500 steps of walking on a battery charge at the self-selected walking cadence (i.e., 101 steps/min). Note that, as reported in [31, 32] an active amputee takes approximately 3000 – 4200 steps per day, and as such, the powered prosthesis as currently configured is estimated to provide a full day of walking on a battery charge. It should be noted, however, that an active healthy adult takes approximately 9500 steps per day [33], and providing this amount of activity would require either an increased battery capacity or replacement/charging of the battery during a day of use.

Note that the system is presently configured with a 4.2 Nm/deg parallel spring incorporated into the foot, which serves to effectively bias the torque capability of the device toward plantarflexion, reflecting the torque curve for walking in healthy subjects. A larger spring constant and/or a more plantarflexed engagement angle for this parallel spring would further bias the system toward plantarflexion, presumably reducing power consumption during walking, the extent to which has not yet been determined by the authors. Note, however, that as level ground walking is not the only activity supported by the powered prosthesis in this work, optimization of the spring stiffness and engagement angle should be based on power consumption in other activities, such as standing on inclines.

C. Evaluation of the Variable Cadence Control Algorithm

The performance of the variable cadence algorithm was assessed in a series of five trials during which the subject began walking on the treadmill at 0.78 m/s, after which the speed of the treadmill was increased at approximately 0.9 m/s increments to 1.7 m/s, and then subsequently decreased to the starting speed of 0.78 m/s. Cadence and cadence mode data from the prosthesis were collected from the embedded system on the prosthesis and synchronized with video from which cadence was later extracted as the time between apparent heel strikes. The first two strides were removed from each data set, since the cadence measurement onboard the prosthesis averages that of the current and two preceding strides. Figure 7 shows a plot from one representative trial of cadence estimated by the prosthesis (red or light-colored marks) and measured from the video footage (blue or dark-colored marks), and also indicates the cadence mode at each time step by shading to various degrees. The mean and standard deviation of the absolute value of the cadence error (measured versus estimated) were 2.64 and 3.36 steps/min, respectively, for the trial depicted in Fig. 7, and 3.00 and 5.36 steps/min for all five trials combined. Note that, as can be seen in Fig. 7, the largest errors in each trial are at the beginning and end of the trial, where the subject was walking so slowly that the controller did not detect a heel strike during some strides. Since the controller still selected the correct cadence regime, however, these estimate errors did not affect the performance of the device.

Fig. 7.

Cadence for a single variable cadence trial. The red (light-colored) marks are the cadence measured by the prosthesis, and the blue (dark-colored) marks are the cadence extracted from the video. The gray shaded areas indicate the cadence mode of the prosthesis. The lightest-colored area represents the slow cadence mode, and the darkest-colored area represents the fast cadence mode.

D. Evaluation of the Ground Adaptive Standing Controller

The ground adaptive standing controller was evaluated based on its ability to select the appropriate equilibrium position according to the slope and/or preference of the user, and then to provide support at that position. In a first experiment, the subject stood on various ground slopes while the average weight distribution between the sound and prosthetic legs was measured by force plates. This experiment was conducted with the powered and passive prostheses, respectively for slopes of ± 15, ± 10, ± 5, and 0 deg, respectively. For the 0 deg slope, the subject stood directly on the force plates–one under each foot. For nonzero slopes, a corresponding wooden wedge with non-slip tape was placed on top of each force plate. For this assessment, the subject was instructed to stand on the wedges as though he were going to be doing so for an extended period of time.

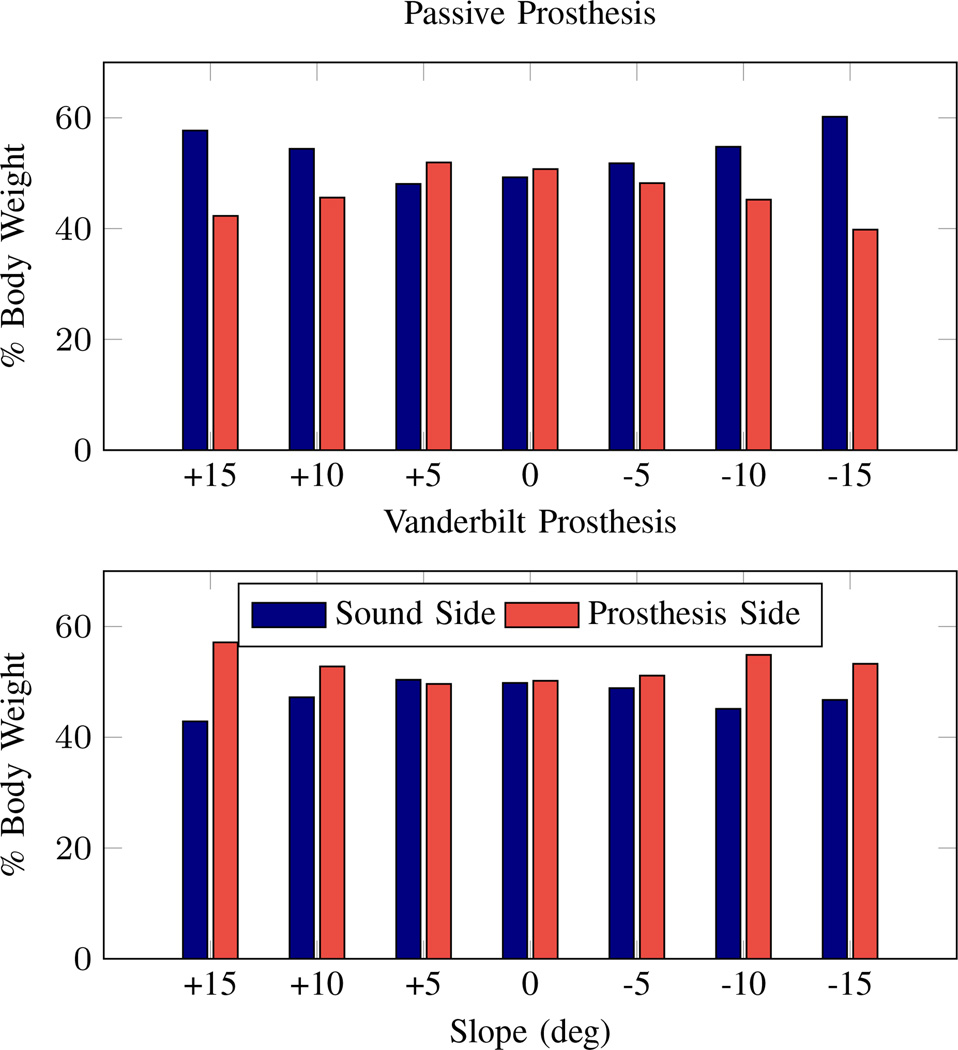
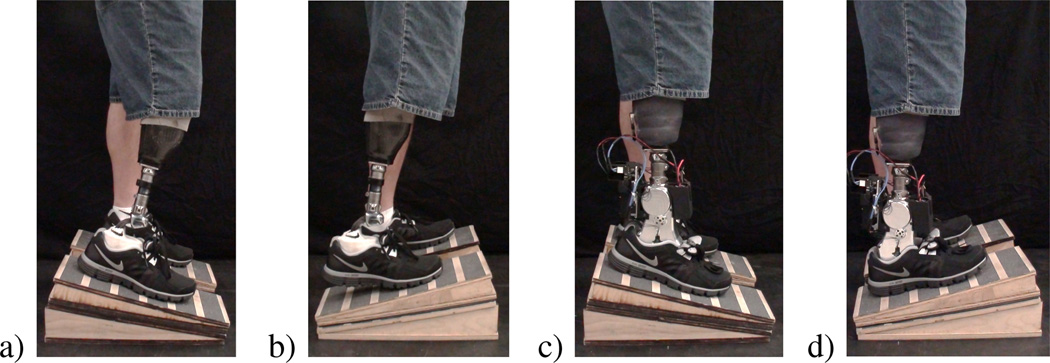
Figure 8 shows the relative load on each foot for the affected and sound sides with the powered and passive prostheses, respectively. Notice that for the passive prosthesis, the subject did not load the prosthesis as much as his sound side for the more extreme inclines and declines (± 15 and ± 10). Since the passive prosthesis maintains a 90-deg equilibrium angle between the foot and shank, the subject must stand with a bent knee (and therefore shortened leg) on the prosthetic side when standing on the downslope, and must stand on the toe of the prosthesis on the upslope, slightly posterior to his center of mass. This can be seen clearly in Fig. 9a–b, which depicts the subject standing with his passive prosthesis on negative and positive 15 deg slopes, respectively. In both cases, the amputee is unable to comfortably place equal weight on the prosthesis, as indicated by Fig. 8. In the case of the powered prosthesis, the subject loaded the prosthesis more than the sound leg on extreme inclines, perhaps because it alleviated muscle loading on the sound side at extreme ends of the muscle length/tension curve. Figure 9c–d depicts the subject standing on negative and positive 15 deg slopes, respectively, with the powered prosthesis, demonstrating the ability of the prosthesis to conform to the slope, which enables the subject to stand with a straight knee and with the prosthetic foot fully flat on the sloped surface.

Fig. 8.

Plot of percent body weight on the sound side and prosthesis side, respectively, during standing on slopes of ±15, ±10, ±5, and 0 degs with the passive prosthesis (top) and powered prosthesis (bottom).

Fig. 9.

Photos of the amputee subject standing on a 15-deg decline and incline with the powered and passive prostheses. From left to right: a) passive prosthesis, −15-deg slope; b) passive prosthesis +15-deg slope; c) powered prosthesis, −15-deg slope; d) powered prosthesis +15-deg slope.

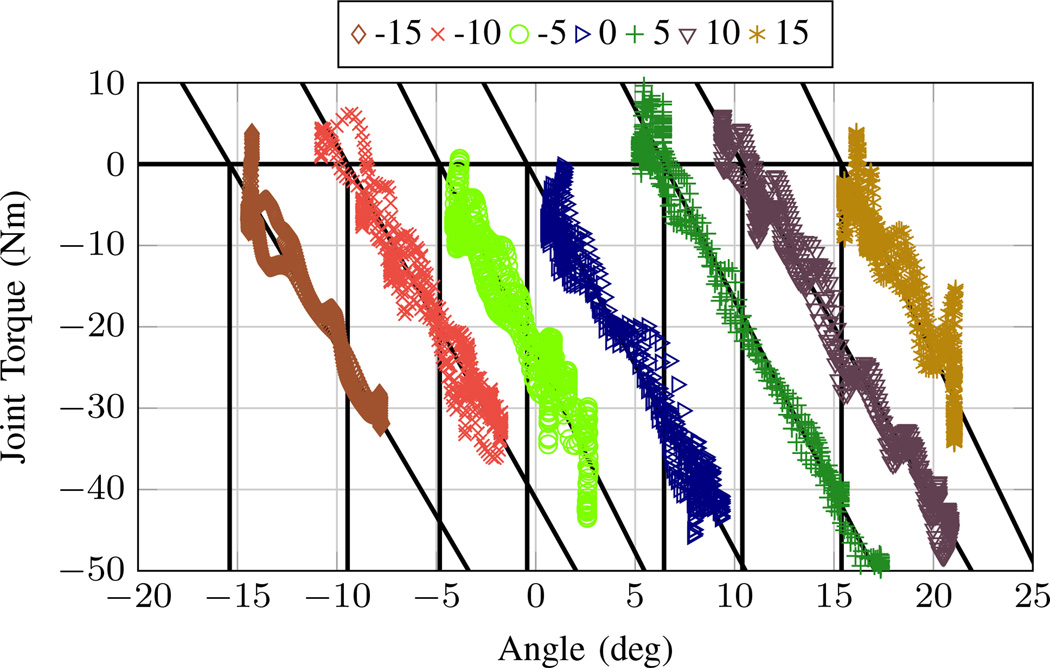
The ability to conform to a ground slope can of course be provided with a simple articulated ankle (e.g., a simple or damped revolute joint), without the associated powered prosthesis or standing controller. In that case, however, the user would not receive the benefit of postural support provided by ankle joint stiffness, which is one of the primary biomechanical roles of the ankle during standing. In order to demonstrate that the powered prosthesis is providing ankle stiffness around the desired equilibrium, a second experiment was conducted in which the subject stood on the same sets of slopes with the powered prosthesis, and was instructed to sway slightly forward and backward, during which time the prosthesis recorded the ankle torque and angle. Figure 10 shows a plot of the ankle angle versus torque for each slope on which the subject stood. The data were calculated from measurements taken and recorded by the prosthesis and filtered in post-processing in MATLAB using the same method described previously for the walking data. This plot verifies the ankle stiffness and equilibrium point, demonstrating that the ankle was supporting the user at the appropriate equilibrium position for each slope. Note that while the data shown indicate an equilibrium position approximately equal to the incline of each slope, the subject preferred increased dorsiflexion when standing on an incline, demonstrating the utility in allowing the user to position the ankle where comfortable prior to establishing an equilibrium angle.

Fig. 10.

Plot of stiffness (torque versus angle) for the passive prosthesis during standing on slopes of ±15, ±10, ±5, and 0 deg.

A third experiment was conducted to measure the time from initial contact between the prosthesis and the ground to the transition into the support state. All seven slope conditions listed previously were assessed, initially for stepping onto the slope with the prosthesis first, and then with the sound leg first. For this assessment, the force plate and wedges were used, and the prosthesis standing state was recorded by the embedded system and synchronized with force plate data. For each slope condition, the subject was instructed to step onto the force plate/wedge first with his prosthetic side and then with his sound side, pause until the prosthesis provided support, then dismount, repeating the procedure five times. The subject was then instructed to repeat this sequence five times beginning with the sound side instead. The subject was permitted to readjust the prosthesis once he stood on the wedge if desired.

From these trials, the time of initial ground contact of the prosthesis and of the transition to support state were recorded. Any trials for which the prosthesis entered support state before initial contact or for which the prosthesis entered damping state after the prosthesis was fully loaded were considered ineligible for assessment and discarded, since no meaningful value for response time in these cases could be extracted. Such trials might include ones wherein the subject paused just before contacting the wedge or force plate and chose not to reposition the foot, or repositioned the foot so quickly that the force plate signal did not return to zero before it was loaded once more by the subject. Response time was then calculated as the difference between the time at transition into support state and the time of initial contact of the prosthesis with the force plate. The mean and standard deviation of this response time for eligible trials wherein the subject stepped with his prosthesis side first were 786 and 306 ms, respectively, and for trials where the subject stepped with his sound side first were 535 and 207 ms, respectively. The mean response time of all eligible trials was 663 ms, and the condition with the smallest mean response time was the −5 deg slope, sound side stepping first, at 284 ms.

E. Evaluation of the Supervisory Controller

The supervisory controller was evaluated in a series of 11 trials during which the subject started from sitting, stood, took two strides leading with the sound side, paused, turned around, took two strides leading with the prosthesis side (wherein for the first step the equilibrium position during support state was established according to estimated ground slope), paused, turned around, and sat. This assessment procedure is somewhat similar to the timed-up-and-go test, although with the constraint that the sound side lead in the first two steps and the prosthetic side lead in the second two. Transition from standing to walking was expected at the beginning of each set of two strides, and transition from walking to standing was expected during each pause. Recall that the transition from walking to standing is based on a timer of inactivity (of shank motion).

In 10 of the 11 trials, the supervisory controller selected the expected activity modes. In the single trial in which the supervisory controller did not select the expected activity modes, the single error was a failure to select standing mode between the two-stride walking subsets. In this case, standing mode was not selected because the subject did not pause (standing quietly) long enough to reenter the standing mode. This error, however, was not noticeable to the subject, since the prosthesis remained in middle-stance state during the brief standing period, and thus provided essentially the same functionality. Had the subject stood on a sloped surface during that brief period, however, he would have noticed that the ankle would not have conformed to the surface. Since the second expected standing transition (which was the one to be initiated by the prosthesis side) could not take place in the aforementioned trial, it was considered ineligible for assessment of the equilibrium angle selection. For this series of trials, the expected equilibrium angle is the slope of the ground–in this case 0 deg. For the 10 eligible trials, the mean and standard deviation of the selected equilibrium angles were 0.67 and 0.44 deg, respectively, indicating that the controller was highly effective in selecting both an appropriate equilibrium angle, and the correct activity mode.

In addition to these trials, video was taken of the subject completing a series of tasks to demonstrate the functionality of the controllers presented in this work, including the supervisory controller and cadence mode selection. This video is included in supplemental material

IV. Conclusion

A variable cadence walking controller and ground adaptive standing controller for a powered ankle prosthesis were described in this paper. The prosthesis and controller were demonstrated on an amputee subject, and shown to provide several features of healthy walking and standing biomechanics, which were not provided by the subject’s passive prosthesis. The authors hope that this improved functionality in such a prosthesis can improve the extent of mobility, quality of life, and musculoskeletal health. Although clearly subjective, the single subject involved in the assessments presented here indicated a preference for functionality provided by the powered prosthesis, relative to his passive prosthesis, for the standing and walking activities characterized here. Future work will include the further development of prosthesis controllers for activities such as walking on uneven terrain, upslope and downslope, and for facilitating stair ascent and descent. Additionally, future work includes assessment of metabolic energy consumption while walking with a powered prosthesis, relative to walking with a passive prosthesis, and assessment of stresses on intact joints. Such studies will provide insight to support the extent to which such devices might provide health benefit relative to existing passive prostheses.